Keywords

1 Compatibility Condition and Multiple Approximations

The aim of this paper is to extend the “traditional” rough set model to be able to represent different levels of uncertainty. Rough sets were introduced by Pawlak in [8]. He assumed that our knowledge about the objects of a universe U is given in the terms of an information relation R reflecting their indiscernibility.

For any relation \(R\subseteq U \times U\) and \(x \in U\), denote \(R(x) = \{y \in U \mid (x,y) \in R\}\). Then for any subset \(X\subseteq U\) its lower approximation is defined as

$$ X_{R} =\{x\in U\mid R(x)\subseteq X\}, $$

and the upper approximation of X is given by

$$ X^{R} =\{x\in U\mid R(x)\cap X\ne \emptyset \}. $$

If R is a reflexive relation, then \(X_{R}\subseteq X\subseteq X^{R}\) and the elements of U may be divided into three disjoint classes:

  1. (C1)

    The elements which are certainly in X. These are the elements in \(X_{R}\), because if \(x\in X_{R}\), then all the elements to which x is R-related are in X.

  2. (C2)

    The elements which certainly are not in X. These are the elements x such that all the elements to which x is R-related are outside X.

  3. (C3)

    The elements which are possibly in X. These are the elements x which are R-related at least to one element from X and also at least to one element outside X. In other words, \(x\in X^{R} \setminus X_{R}\).

Initially, Pawlak assumed that R is an equivalence, that is, a reflexive, symmetric and transitive relation. There are many generalizations of Pawlak’s construction based on non-equivalence relations, and replacing equivalence classes by coverings; see [13, 14], for instance. A natural variant is to assume that our information is given by a tolerance relation, that is, a reflexive and symmetric binary relation, being not transitive in general. Authors of this paper have considered lattice-theoretical properties of rough sets defined by tolerances, for example, in [3, 5, 6].

In [4], we used both equivalences and tolerances to form approximations. As a motivation for this kind of setting consider the case in which U consists of a set of patients of a hospital and \(x \,E\,y\) means that all the attributes of x and y representing some medical information are the same. Let X be a set of patients with a certain disease. If \(x\in X^{E}\), then X contains a patient y such that x cannot be distinguished from y in terms of any attribute. On the other hand, sometimes it would be useful to know also those patients who have a risk to have the disease in the near future or who are at an initial phase of the disease. These persons may have different symptoms as the patients with illness have. But they may have, for instance, similar symptoms. Thus, we can use a tolerance relation T to represent this similarity. The upper approximation \(X^{T}\) consists of persons who are similar to patients with disease, thus they may have some risk to get the disease. It may be reasonable to introduce several tolerance relations to represent different types of risks and different types of similarity, and therefore in this paper we consider also multiple tolerances.

In [4] we considered tolerances compatible with equivalences, which turned to be closely related to “similarity relations extending equivalences” studied in [11]. In this work, we slightly generalize the notion of compatibility to be used also between tolerances.

Definition 1

Let R and T be two tolerances on U. If \(R \circ T=T\), then T is R -compatible.

If T is R-compatible, then \(R\subseteq T\) and \(R^{2} \subseteq R \circ T = T\), so R is “transitive” inside T. Since \(T^{-1}=T\) and \((R \circ T)^{-1} = T^{-1} \circ R^{-1} = T \circ R\) we get

$$\begin{aligned} R \circ T = T \iff (R \circ T)^{-1} = T^{-1} \iff T \circ R=T. \end{aligned}$$
(1.1)

Hence, \(R\circ T = T\) and \(T\circ R=T\) are equivalent conditions.

For a tolerance T, the kernel of T is defined by

$$\begin{aligned} \ker T = \{ (x,y) \mid T(x) = T(y) \}. \end{aligned}$$

Proposition 2

Let R and T be tolerances on U. The tolerance T is R-compatible if and only if \(R \subseteq \ker T\).

Proof

(\(\Rightarrow \)) Suppose that T is R-compatible. We show that \(R \subseteq \ker T\). Assume \((x,y) \in R\). Let \(z \in T(x)\). Then \(z \, T \, x\) and \(x \, R \, y\), that is, \((z,y) \in T \circ R = T\). Thus, \(z \in T(y)\) and \(T(x) \subseteq T(y)\). Similarly, we can show that \(T(y) \subseteq T(x)\): if \(z \in T(y)\), then \((x,z) \in R \circ T = T\) and \(z \in T(x)\). Thus, \(T(x) = T(y)\) and \((x,y) \in \ker T\). Therefore, \(R \subseteq \ker T\).

(\(\Leftarrow \)) Assume that \(R \subseteq \ker T\). Let \((x,y) \in R \circ T\). Then, there is z such that \(x \, R \, z\) and \(z \, T \, y\). Because \((x,z) \in \ker T\), \(y \in T(z) = T(x)\). Thus, \((x,y) \in T\) and \(R \circ T \subseteq T\). Because \(T \subseteq R \circ T\) holds always, we have \(T = R \circ T\) and T is R-compatible.    \(\square \)

We can also present the following characterization.

Proposition 3

Suppose R and T are tolerances on U. The tolerance T is R-compatible if and only if

$$\begin{aligned} T(x) = \bigcup \{ R(y) \mid y \in T(x) \} \end{aligned}$$
(1.2)

for all \(x \in U\).

Proof

(\(\Rightarrow \)) Assume that T is R-compatible. Let \(z \in T(x)\). Then \(z \in R(z)\) gives \(z \in \bigcup \{ R(y) \mid y \in T(x) \}\). On the other hand, if \(z \in \bigcup \{ R(y) \mid y \in T(x) \}\), then \(z \, R \, y\) and \(y \, T \, x\) give \((z,x) \in R \circ T = T\), that is, \(z \in T(z)\). So, (1.2) holds.

(\(\Leftarrow \)) Suppose (1.2) is true for any \(x \in U\). If \((x,z) \in T \circ R\), then there is y such that \(y \in T(x)\) and \(z \in R(y)\). By (1.2), these give \(z \in T(x)\). Thus, \((x,z) \in T\) and \(T \circ R \subseteq T\). Since, \(T \subseteq T \circ R\) holds always, T is R-compatible.    \(\square \)

Let \(X\subseteq U\) be arbitrary and let T be an R-compatible tolerance. The following properties can be proved:

$$\begin{aligned} (X^{T})^{R} = X^{T\circ R} = X^{T} = X^{R\circ T} = (X^{R})^{T}; \end{aligned}$$
(1.3)
$$\begin{aligned} (X_{T})_{R} = X_{T\circ R} = X_{T} = X_{^{R\circ T}} = (X_{R})_{T}. \end{aligned}$$
(1.4)

Indeed, \(X^{T\circ R}=X^{T}=X^{R\circ T}\) is clear by (1.1). Let us check \((X^{T})^{R} = X^{R\circ T}\) as an example:

$$\begin{aligned} x \in (X^{T})^{R}&\iff (\exists z) \, x \, R \, z \text { and } z \in X^T \\&\iff (\exists z)(\exists y) \, x \, R \, z \text { and } z \, T \, y \text { and } y \in X \\&\iff (\exists y) \, x \, (R \circ T) \, y \text { and } y \in X \\&\iff x \in X^{R \circ T} \end{aligned}$$

Hence (1.3) is satisfied. Equalities (1.4) are proved analogously.

If our knowledge about the attributes of the elements is incomplete, then classification (C1)–(C3) of the elements of U into three disjoint subsets

$$\begin{aligned} X_{E}\cup (X^{E}\setminus X_{E}) \cup (U \setminus X^{E}) \end{aligned}$$

may be insufficient [2]. For instance, beside those elements which are in the boundary \(X^{E}\setminus X_{E}\) of X, there may exist other elements in U whose attributes are not enough known to exclude that they are somehow related to X. Hence a division of the elements of U in four, or even more classes might be more convenient. In this work, we will consider several tolerances \(T_{1},\ldots ,T_{n}\) on U. This enables us to define multiple borders and consider cases in which there are several degrees of possibility. Our work is related to a multi-granulation rough set model (MGRS), where the set approximations are defined by using multi equivalence relations on the universe [10].

The tolerances \(T_{1},\ldots ,T_{n}\) are assumed to be E-compatible. This means that if x is \(T_{i}\)-similar to y, then any element E-indistinguishable with x must also be \(T_{i}\)-similar to y. The obtained tuples \((X_{E},X^{T_{1}},\ldots ,X^{T_{n}})\) can be considered as generalizations of rough sets.

2 Rough Sets of Multiple Approximations

For a binary relation R on U, the “traditional” R-rough set of X is defined as the pair \((X_{R},X^{R})\). We denote by

$$ RS (R)=\{(X_{R},X^{R})\mid X\subseteq U\} $$

the set of all R-rough sets. The set \( RS (R)\) can be ordered coordinatewise inclusion by

$$ (X_{R},X^{R})\le (Y_{R},Y^{R})\iff X_{R}\subseteq Y_{R} { \ \mathrm{and} \ } X^{R}\subseteq Y^{R}, $$

obtaining a partially ordered set \(( RS (R),\le )\), which we denote simply by \( RS (R)\). If E is an equivalence relation, then \( RS (E)\) is a complete lattice such that

$$\begin{aligned} \bigvee _{X\in \mathcal {H}}(X_{E},X^{E})&= \Big ( \bigcup _{X\in \mathcal {H}} X_{E},\bigcup _{X\in \mathcal {H}}X^{E} \Big ) \end{aligned}$$
(2.1)

and

$$\begin{aligned} \bigwedge _{X \in \mathcal {H}} (X_{E},X^{E})&= \Big ( \bigcap _{X\in \mathcal {H}}X_{E},\bigcap _{X\in \mathcal {H}}X^{E} \Big ) \end{aligned}$$
(2.2)

for all \(\mathcal {H}\subseteq \wp (U)\), where \(\wp (U)\) the powerset of U, that is, the set of all subsets of U. It is also known that a so-called regular double Stone algebra can be defined on \( RS (E)\) [1, 9]. If T is a tolerance, then in [3] it is proved that \( RS (T)\) is not necessarily even a semilattice.

In [4] we considered the following generalization

$$ RS (E,T)=\{(X_{E},X^{T})\mid X\subseteq U\} $$

of the traditional rough set system. The idea behind studying such pairs \((X_E, X^T)\) is that the equivalence E represents “strict” information (indistinguishability) and the information represented by T is “soft” (similarity). Hence \(X_E\) is defined as it is usual in rough set theory, but \(X^T\) is now more permissible, because \(E \subseteq T\) and thus \(X \subseteq X^E \subseteq X^T\). We proved several results about the structure of \( RS (E,T)\), particularly that it always forms a complete lattice.

First we generalize our setting to multiple E-compatible tolerances. If E is an equivalence on U and \(T_{1},\ldots ,T_{n}\) are tolerances on U, then

$$\begin{aligned} X^{T_{1}}\setminus X_{E},\ X^{T_{2}}\setminus X_{E}, \ \ldots ,X^{T_{n}}\setminus X_{E} \end{aligned}$$

may express uncertainties of different kinds. We denote

$$ RS (E,T_{1},\ldots ,T_{n})=\{(X_{E},X^{T_{1}},\ldots ,X^{T_{n}})\mid X\subseteq U\}. $$

As earlier, \( RS (E,T_{1},\ldots ,T_{n})\) is ordered coordinatewise.

Proposition 4

Let E be an equivalence on U and \(T_{1},\ldots ,T_{n}\) be E-compatible tolerances. Then \( RS (E,T_{1},\dots ,T_{n})\) is a complete lattice.

Proof

Because is the least element of \(\mathbf {RS}:= RS (E,T_{1},\ldots ,T_{n})\), it suffices to show that for any \(\emptyset \ne \mathcal {H} \subseteq \wp (U)\), the set \(\{(X_{E},X^{T_{1}}, \ldots , X^{T_{n}}) \mid X \in \mathcal {H}\}\) has a supremum in \(\mathbf {RS}\). Since \(\big ( \bigcup _{X\in \mathcal {H}} X_{E},\bigcup _{X\in \mathcal {H}}X^{E}\big )\) is an E-rough set by (2.1), there exists a set \(Y \subseteq U\) with

$$ Y_{E} = \bigcup _{X\in \mathcal {H}}X_{E}\quad \text {and} \quad Y^{E}=\bigcup _{X\in \mathcal {H}}X^{E}. $$

By Property (1.3) we have that for \(1\le i\le n\),

$$ Y^{T_{i}} = ( Y^{E})^{T_{i}} = \Big ( \bigcup _{X\in \mathcal {H}} X^{E} \Big )^{T_{i}} = \bigcup _{X\in \mathcal {H}} (X^{E})^{T_{i}} = \bigcup _{X\in \mathcal {H}}X^{T_{i}}. $$

This implies that

$$ \big ( \bigcup _{X\in \mathcal {H}}X_{E},\bigcup _{X\in \mathcal {H}}X^{T_{1}},\ldots ,\bigcup _{X\in \mathcal {H}}X^{T_{n}}\big ) =(Y_{E},Y^{T_{1}},\ldots ,Y^{T_{n}}) $$

belongs to \(\mathbf {RS}\).

Now \((Y_{E},Y^{T_{1}},\ldots ,Y^{T_{n}})\) is an upper bound of \((X_{E},X^{T_{1}},\ldots ,X^{T_{n}})\) for all \(X\in \mathcal {H}\). It is also clear that if

$$ (Z_{E},Z^{T_{1}},\ldots ,Z^{T_{n}}) $$

is an upper bound of \(\{(X_{E},X^{T_{1}},\ldots ,X^{T_{n}})\mid X\in \mathcal {H}\},\) then \(X_{E}\subseteq Z_{E}\) and \(X^{T_{i}}\subseteq Z^{T_{i}}\) for all \(X\in \mathcal {H}\) and \(1\le i\le n\). This gives

$$ \bigcup _{X\in \mathcal {H}}X_{E}\subseteq Z_E \quad \text {and} \quad \bigcup _{X\in \mathcal {H}}X^{T_{i}}\subseteq Z^{T_{i}}$$

for \(1\le i\le n\). Therefore,

$$ (Y_{E},Y^{T_{1}},\ldots ,Y^{T_{n}})\le (Z_{E},Z^{T_{1}},\ldots ,Z^{T_{n}}) $$

and \((Y_{E},Y^{T_{1}},\ldots ,Y^{T_{n}})\) is the supremum of \(\{(X_{E} ,X^{T_{1}},\ldots ,X^{T_{n}})\mid X\in \mathcal {H}\}\).    \(\square \)

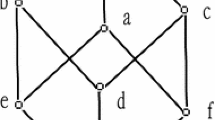
Example 5

Let \(U=\{1,2,3,4\}\) and E be an equivalence on U such that \(U/E = \{ \{1\},\{2,3\},\{4\}\}\). Assume \(T_1\) is an equivalence (and thus a tolerance) such that

$$\begin{aligned} T_1(1) = T_1(2) = T_1(3) = \{1,2,3\} \quad \text {and} \quad T_1(4) = \{4\}. \end{aligned}$$

In addition, let \(T_2\) be a tolerance such that

$$\begin{aligned} T_2(1) = U, \quad T_2(2) = T_2(3) = \{1,2,3\} \quad \text {and} \quad T_2(4) = \{1,4\}. \end{aligned}$$

Because \(E\subseteq \ker T_1 = T_{1}\) and \(E = \ker T_2\), \(T_{1}\) and \(T_{2}\) are E-compatible.

We have also \(T_{1}\subseteq T_{2}\), but \(T_{2}\) is not \(T_{1}\)-compatible, since \(T_{1} \nsubseteq \ker T_{2} = E\). The elements of

$$\begin{aligned} RS (E,T_{1},T_{2}) = \{(X_{E},X^{T_{1}},X^{T_{2}}) \mid X\subseteq U\} \end{aligned}$$

are given in Table 1. Note that here we denote sets just by sequences of their elements, the set \(\{1,2,4\}\) is written 124, for instance. The Hasse diagram of \( RS (E,T_{1},T_{2})\) can be found in Fig. 1.

Table 1. The 3-tuple approximations of subsets of U
Full size table

Let us note that if \(n=1\) and \(T_{1}=T\), we obtain the complete lattice \( RS (E,T) = \{(X_{E},X^{T})\mid X\subseteq U\}\) investigated in [4]. Our next theorem shows that adding T-compatible tolerances \(S_1,\ldots ,S_n\) to \( RS (E,T)\) does not change the lattice-theoretical structure. Notice that if T is an E-compatible tolerance and a tolerance S is compatible with T, then S is also E-compatible because

$$\begin{aligned} E \circ S \subseteq T \circ S \subseteq S , \end{aligned}$$

which implies \(E \circ S = S\), since \(S \subseteq E \circ S\).

Theorem 6

Let E be an equivalence on U and let T be an E-compatible tolerance. If \(S_{1},\ldots ,S_{n}\) are tolerances which are T-compatible, then

$$\begin{aligned} RS (E,T) \cong RS (E,T,S_{1},\ldots ,S_{n}). \end{aligned}$$
Fig. 1.
figure 1

The lattice \( RS (E,T_1,T_2)\)

Full size image

Proof

Note first that each \(S_1,\ldots ,S_n\) is E-compatible. This means that

$$\begin{aligned} RS (E,T,S_{1},\ldots ,S_{n}) \end{aligned}$$

is a complete lattice by Proposition 4. We define a map

$$ \varphi : RS (E,T) \rightarrow RS (E,T,S_{1},\ldots ,S_{n}),\ (X_{E},X^{T})\mapsto (X_{E},X^{T},X^{S_{1}},\ldots ,X^{S_{n}}). $$

The map \(\varphi \) is well defined, because if \((X_{E},X^{T})=(Y_{E},Y^{T})\), then by (1.3),

$$ X^{S_{k}}=(X^{T})^{S_{k}}=(Y^{T})^{S_{k}}=Y^{S_{k}} $$

for any \(1\le k\le n\), which yields \(\varphi (X_{E},X^{T})=\varphi (Y_{E},Y^{T})\). Next we prove that \(\varphi \) is an order-embedding, that is,

$$ (X_{E},X^{T})\le (Y_{E},Y^{T})\iff \varphi (X_{E},X^{T})\le \varphi (Y_{E},Y^{T}). $$

Suppose \((X_{E},X^{T})\le (Y_{E},Y^{T})\). Then \(X^{T}\subseteq Y^{T}\) and for any \(1\le k\le n\),

$$ X^{S_{k}}=(X^{T})^{S_{k}}\le (Y^{T})^{S_{k}}=Y^{S_{k}}. $$

Hence, \(\varphi (X_{E},X^{T})\le \varphi (Y_{E},Y^{T})\). It is trivial that if \(\varphi (X_{E},X^{T}) \le \varphi (Y_{E}, Y^{T})\), then \((X_{E},X^{T}) \le (Y_{E},Y^{T})\). The mapping \(\varphi \) is obviously surjective, because if \((X_{E},X^{T},X^{S_{1}},\ldots ,X^{S_{n}})\) belongs to \( RS (E,T,S_{1},\ldots ,S_{n})\), then \(\varphi (X_{E},X^{T})=(X_{E},X^{T},X^{S_{1}},\ldots ,X^{S_{n}})\).    \(\square \)

The following consequence is immediate. Notice that each equivalence E is compatible with itself, that is \(E \circ E = E\).

Corollary 7

Let E be an equivalence relation on U and \(T_{1},\ldots ,T_{n}\) be E-compatible tolerances. If \(T_{1}=E\), then

$$\begin{aligned} RS (E)\cong RS (E,T_{1},\ldots ,T_{n}). \end{aligned}$$

Let \(E_{0} \subseteq E_{1} \subseteq E_{2} \subseteq \cdots \subseteq E_{n}\) be equivalences on U. Note that the kernel of an equivalence is the equivalence itself. Therefore, \(E_1\) is \(E_0\)-compatible and \(E_2,\dots , E_n\) are \(E_1\)-compatible. By Theorem 6 we can write the following corollary.

Corollary 8

Let \(E_{0}\subseteq E_{1}\subseteq \cdots \subseteq E_{n}\) be equivalences on U. Then

$$\begin{aligned} RS (E_{0},E_{1},\ldots ,E_{n})\cong RS (E_{0},E_{1}). \end{aligned}$$

We end this section by presenting a couple of examples where multiple rough sets can be defined in a natural way.

Example 9

Let R be a fuzzy equivalence on U. This means that for all \(x,y\in U\), \(R(x,y) \in [0,1]\) and that R is

  • reflexive: \(R(x,x)=1\) for each \(x\in U\),

  • symmetric: \(R(x,y)=R(y,x)\) for all \(x,y\in U\), and

  • transitive: \(R(x,z) \ge \min \{ R(x,y),R(y,z) \}\) for any \(x,y,z\in U\).

It is known that for any \(\alpha \in [0,1]\) the \(\alpha \)-cut

$$ R_{\alpha }=\{(x,y)\in U\times U\mid R(x,y)\ge \alpha \} $$

of R is a “crisp” equivalence on U. Let \(0\le \alpha _{0} \le \alpha _{1} \le \cdots \le \alpha _{n} \le 1\). Then \(R_{\alpha _{0}}\subseteq R_{\alpha _{1}}\subseteq \cdots \subseteq R_{\alpha _{n}}\) are equivalences on U. By Corollary 8 we get

$$\begin{aligned} RS (R_{\alpha _{0}},R_{\alpha _{1}},\dots ,R_{\alpha _{n}})\cong RS (R_{\alpha _{0}},R_{\alpha _{1}}). \end{aligned}$$

Example 10

An information system in the sense of Pawlak [7] is a triple

$$\begin{aligned} (U,A,\{V\}_{a\in A}), \end{aligned}$$

where U is a set of objects, A is a set of attributes and \(V_{a}\) is the value set of \(a \in A\). Each attribute is a mapping \(a:U\rightarrow V_{a}\). For any \(\emptyset \ne B \subseteq A\), the strong indiscernibility relation of B is defined by

$$ \mathrm {ind}(B) = \{(x,y)\mid a(x)=a(y) \text { for all } a\in B\}. $$

The weak indiscenibility relation of B is given by

$$ \mathrm {wind}(B) = \{(x,y)\mid a(x)=a(y) \text { for some } a\in B\}. $$

Clearly, \(\mathrm {ind}(B)\) is an equivalence and \(\mathrm {wind}(B)\) is a tolerance.

Let \(\emptyset \ne C\subseteq B\subseteq A\). It is easy to see that \(\mathrm {wind}(C)\) is \(\mathrm {ind}(B)\)-compatible. Indeed, the inclusion \(\mathrm {wind}(C) \subseteq \mathrm {ind}(B) \circ \mathrm {wind}(C)\) is clear. In order to prove the converse inclusion, let \((x,y) \in \mathrm {ind}(B)\circ \mathrm {wind}(C)\). Then \((x,z) \in \mathrm {ind}(B)\) and \((z,y) \in \mathrm {wind}(C)\) for some \(z\in U\). As \(C \subseteq B\), \((x,z) \in \mathrm {ind}(B)\) yields \(a(x) = a(z)\) for all \(a \in C\). Because \((z,y) \in \mathrm {wind}(C)\), we have \(b(y) = b(z)= b(x)\) for some \(b \in C\). Thus, \((x,y) \in \mathrm {wind}(C)\). This means \(\mathrm {ind}(B) \circ \mathrm {wind}(C) \subseteq \mathrm {wind}(C)\), completing the proof.

Suppose \(\emptyset \ne C_{1},\ldots ,C_{n} \subseteq B\). Since \(\mathrm {wind}(C_{i})\) is \(\mathrm {ind}(B)\)-compatible for any \(1 \le i \le n\), we can form the generalized rough set complete lattice

$$\begin{aligned} RS (\mathrm {ind}(B),\mathrm {wind}(C_{1}),\ldots ,\mathrm {wind}(C_{n})). \end{aligned}$$

3 Comparison with the Fuzzy Set Approach

The relationship between rough set theory and fuzzy set theory is widely discussed in the literature. One of the key differences between these approaches is the fact that in fuzzy set theory the membership value does not depend on other elements. In contrast, the rough approximations and rough membership functions are defined in terms of a relation on the object set [15]. According to [12], one may treat rough set in set-oriented view as a special class of fuzzy sets. In this section, we argue that from the viewpoint of set approximation, rough sets with multiple borders significantly increase the functionality of the standard rough set model and it provides a more general model of uncertainty than the fuzzy model.

In the fuzzy set theory [16], a fuzzy set A on U is defined by a membership function

$$ f_A :U \rightarrow [0,1], $$

where the value \(f_A(x)\) for any \(x \in U\) denotes the “grade of membership” of x in A. For any \( \alpha \in [0,1]\), the closed alpha-cut set \(A_{\alpha }\) and the open alpha-cut set \(A_{> \alpha }\) are crisp sets, where

$$\begin{aligned} A_{\alpha }&= \{ x \in U \mid f_A(x) \ge \alpha \} \end{aligned}$$

and

$$\begin{aligned} A_{> \alpha }&= \{ x \in U \mid f_A(x) > \alpha \}. \end{aligned}$$

Let \(X \subseteq U\) be a (crisp) set. A fuzzy set A can be considered as a “rough approximation” of X, if

$$ A_{1} \subseteq X \subseteq A_{> 0}. $$

The set \(A_{1}\) denotes the elements which are certainly in X and the elements which may belong to X are contained in \(A_{> 0}\). In “fuzzy terminology”, \(A_{1}\) is called the core of A and \(A_{> 0}\) is the support of A.

Similarly as in case of multiple tolerances, we may use several cut sets to approximate X. More precisely, let \(X \subseteq U\) and suppose that there exists a fuzzy set A on U and \(1> \alpha _{1}> \alpha _{2}> \ldots> \alpha _{n} > 0\) such that

$$\begin{aligned} A_{1} \subseteq X \subseteq A_{\alpha _1} \subseteq A_{\alpha _2} \subseteq \cdots \subseteq A_{\alpha _n}. \end{aligned}$$

Our next proposition shows that we can always construct the same tuple

$$\begin{aligned} (A_{1}, A_{\alpha _1},\ldots A_{\alpha _n}) \end{aligned}$$

using multiple rough sets.

Proposition 11

Let A be a fuzzy set U and \(1> \alpha _{1}> \alpha _{2}> \ldots> \alpha _{n} > 0\). Then there exist a set \(X \subseteq U\), an equivalence E on U, and E-compatible tolerances \(T_1,\ldots ,T_n\) satisfying

$$\begin{aligned} (A_{1},A_{\alpha _{1}},\ldots ,A_{\alpha _{n}}) = (X_{E},X^{T_{1}},\ldots ,X^{T_{n}}) . \end{aligned}$$

Proof

Having \((A_{1},A_{\alpha _{1}},\ldots ,A_{\alpha _{n}})\), we define the equivalences:

$$\begin{aligned} E&= A_1 \times A_1 \cup \{ (x,x) \mid x \in U \}, \\ T_1&= A_{\alpha _1} \times A_{\alpha _1} \cup (U \setminus A_{\alpha _1}) \times (U \setminus A_{\alpha _1}),\\ T_2&= A_{\alpha _2} \times A_{\alpha _2} \cup (U \setminus A_{\alpha _2}) \times (U \setminus A_{\alpha _2}),\\&{\ \ \vdots } \\ T_n&= A_{\alpha _n} \times A_{\alpha _n} \cup (U \setminus A_{\alpha _n}) \times (U \setminus A_{\alpha _n}). \end{aligned}$$

It is clear that \(E \subseteq T_i\) for any \(1 \le i \le n\), so each \(T_1,\ldots ,T_n\) is E-compatible. We have that

$$\begin{aligned} X_E&= X = A_{1}, \\ X^{T_1}&= (A_{1})^{T_1} = A_{\alpha _{1}}, \\ X^{T_2}&= (A_{1})^{T_2} = A_{\alpha _{2}}, \\&{\ \ \vdots } \\ X^{T_n}&= (A_{1})^{T_n} = A_{\alpha _{n}}. \end{aligned}$$

Thus, \((A_{1},A_{\alpha _{1}},\ldots ,A_{\alpha _{n}}) = (X_{E},X^{T_{1}},\ldots ,X^{T_{n}})\).   \(\square \)

We end this section by showing that the converse is not true.

Proposition 12

Let U be a set with at least 3 elements. There exists an equivalence E on U, E-compatible tolerances \(T_1\) and \(T_2\), and a set \(X \subseteq U\), such that \((X_E,X^{T_1},X^{T_2})\) cannot be given in terms of \(\alpha \)-cut sets of some fuzzy set A on U.

Proof

If \(|U| \ge 3\), we may define tolerances \(T_1\) and \(T_2\) on U such that neither \(T_1 \subseteq T_2\) nor \(T_2 \subseteq T_1\) hold. In addition, let \(E = \{(x,x) \mid x \in U\}\). Then trivially \(T_1\) and \(T_2\) are E-compatible. Let us consider the case \(T_1 \nsubseteq T_2\) only, because \(T_2 \nsubseteq T_1\) can be treated similarly. Now \(T_1 \nsubseteq T_2\) means that there is \((x,y) \in T_1\) such that \((x,y) \notin T_2\). We get that \(\{x\}^{T_1} \nsubseteq \{x\}^{T_2}\).

Next consider the rough set 3-tuple \((\{x\}_{E},\{x\}^{T_{1}},\{x\}^{T_{2}})\). Suppose that there exists a fuzzy set A on U and \(\alpha _1\) and \(\alpha _2\) such that

$$\begin{aligned} (A_{1},A_{\alpha _{1}},A_{\alpha _{2}}) = (\{x\}_{E},\{x\}^{T_{1}},\{x\}^{T_{2}}). \end{aligned}$$

Because \(\alpha _1, \alpha _2 \in [0,1]\), without loss of generality we may assume that \(\alpha _1 \ge \alpha _2\). Then \(A_{\alpha _1} \subseteq A_{\alpha _2}\) would imply \(\{x\}^{T_1} \subseteq \{x\}^{T_2}\), a contradiction.   \(\square \)

These properties mean that every multiple alpha-cuts fuzzy model can be given using multiple rough set model, but not every multiple rough set model can be obtained with some alpha-cuts of a fuzzy set. From this point of view, the multiple rough set model is a more general model of uncertainty than the fuzzy set model with multiple cuts.

4 Conclusions

The paper presented an extension of the traditional rough set model introducing multiple upper approximations using more tolerance relations where the tolerance relations are compatible with the inner equivalence relation. Regarding the main properties of the proposed model, it can be proven that the set of multiple upper approximations rough sets form a complete lattice. In special cases, this lattice is isomorphic with the lattice generated from the base rough set pairs. The proposed model can be used to represent a novel multi-level uncertainty-based approximation of selected base sets. It is shown in the paper that for presenting multiple borders, this approximation model is more general than the widely used fuzzy approximation model.