Advances in Image and Video Compression Using Wavelet Transforms and Fovea Centralis

Abstract

It is well-known that there has been a considerable progress in multimedia technologies during the last decades, namely TV, photography, sound and video recording, communication systems, etc., which came into the world during at least half of the previous century and were developed as analog systems, and nowadays have been almost completely replaced by digital systems. The aforementioned motivates a deep study of multimedia compression and intensive research in this area. Data compression is concerned with minimization of the number of information carrying units used to represent a given data set. Such smaller representation can be achieved by applying coding algorithms. Coding algorithms can be either lossless algorithms that reconstruct the original data set perfectly or lossy algorithms that reconstruct a close representation of the original data set. Both methods can be used together to achieve higher compression ratios. Lossless compression methods can either exploit statistical structure of the data or compress the data by building a dictionary that uses fewer symbols for each string that appears on the data set. Lossy compression, on the other hand, uses a mathematical transform that projects the current data set onto the frequency domain. The coefficients obtained from the transform are quantized and stored. The quantized coefficients require less space to be stored. This chapter is focused on the recently published advances in image and video compression to date considering the use of the integer discrete cosine transform (IDCT), wavelet transforms, and fovea centralis.

FormalPara Acronyms

ABAC:

Adaptive binary arithmetic coding

AFV-SPECK:

Adaptive fovea centralis set partitioned embedded block codec

AVC:

Advance video coding

AWFV-Codec:

Adaptive wavelet/fovea centralis-based codec

BGR:

Blue green red color space

bpp:

Bits per pixel

CDF9/7:

Cohen–Daubechies–Feauveau wavelet

CIF:

Common intermediate format

CMYK:

Cyan magenta yellow black color space

CWT:

Continuous wavelet transform

dB:

Decibel

DCT:

Discrete cosine transform

DWT:

Discrete wavelet transform

FWT:

Fast wavelet transform

FVHT:

Fovea centralis hierarchical trees

GIF:

Graphics interchange format

HEVC:

High efficiency video coding

HVS:

Human visual system

iDCT:

Integer discrete cosine transform

iSPECK:

Inverse SPECK

iLWT:

Inverse LWT

JBIG:

Joint bi-level image group

JPEG:

Joint photographic experts group

JPEG2000:

Joint photographic experts group 2000

LCL:

Lossless compression limit

LIP:

List of insignificant pixels

LIS:

List of insignificant sets

LSP:

List of significant pixels

LWT:

Lifting wavelet transform

MPEG:

Moving picture experts group

MSE:

Mean squared error

PCX:

Personal computer exchange

pixel:

Picture element

PNG:

Portable network graphics

ppi:

Pixels per inch

PSNR:

Peak signal to noise ratio

RAR:

Roshal archive file format

RGB:

Red green blue color space

RLE:

Run length encoding

ROI:

Region of interest

SPECK:

Set partitioned embedded block codec

SPIHT:

Set partitioning in hierarchical tree

sRGB:

Standard red green blue color space

SSIM:

Structural similarity index

WebP:

WebP

WT:

Wavelet transform

Y’CBCR:

Luma chrominance color space

ZIP:

.ZIP file format

1 Introduction

The problem of storing images appeared along with the devices that allowed to capture and represent data in the form of visual information. Devices like image scanners (1950) and graphic processing units (1984) along with graphic manipulation software made possible to capture, create, and display images as digital images on a computer. A digital image is a numeric representation of a captured or software created image. This numeric representation is a discretization value made from a digital scanner device. The digital image can be represented as a two-dimensional numeric matrix. Each element of the matrix represents a small picture element (pixel). Such images are also known as raster images. Computer software such as Adobe Photoshop¹ or Gimp² allow to create raster images. Also, most capturing devices like cameras and image scanners capture the image as a raster image [38, 39].

Compression algorithms are encapsulated with its decompression counterpart on digital image formats. A digital image format or standard specifies the following: a compression algorithm, a decompression algorithm, which color space is used for representing the image, how the data is stored inside a binary file and headers with metadata for image software [28]. Digital image formats that use only one two-dimensional matrix are used for storing black and white images or gray scale images. Digital color images on the other hand require more than one matrix in order to represent color. Usually, the number of matrices used are three for color spaces such as Red Green Blue color space (RGB) [20], Luma Chrominance color space (Y ′C _B C _R) [33], and derivatives or four matrix for spaces such as Cyan Magenta Yellow Black color space (CMYK) [47]. Each matrix is known as a color channel. A common practice when using integer representation is to use one matrix of elements of 32 bits. The bits of each 32-bit element are split into four sets of 8 bits. Each 8-bit set is related to one color channel. When using a three channel color space, usually the four most significant bits set is either discarded as in RGB (or Blue Green Red color space (BGR) representation [62]) or used as a transparency information as in the Standard Red Green Blue color space (sRGB) format [20]. There are other digital image representations of an image such as vector images [48, 57]. However, this chapter will be focused only on raster type images. From now on the term image will be used to refer to digital raster images unless otherwise stated. Usually, the quality of an image grows as the amount of pixels taken per inch grows. This is known as pixels per inch (ppi).

Lossless compression is the best way to reduce the space needed to store a high quality image. Examples of such lossless compression algorithms are the Personal Computer Exchange (PCX) file format and the Graphics Interchange Format (GIF) file format. Nevertheless, it has been shown that the upper limit for an ideal lossless compression algorithm is around 30% [28]. Therefore, image file formats based on lossless compression algorithms are less convenient as the image increases in size. In consequence, new file formats were designed that take advantage of lossy compression algorithms. Lossy compression algorithms take into account the sensibility of the human visual system (HVS) in order to drop some of the details of the image when compressing. As a result, the reconstructed image is not the original image but a close representation of it. The aim of lossy compression is to build an algorithm that when reconstructing the image using the compressed stream, the reconstructed image will look almost the same for the user. Several lossy compression algorithms for images have been proposed; however, most of them are based on mathematical transformations that take the image matrix of color intensities and map it into a different space. The most common space used is the frequency space also known as frequency domain. When using the frequency domain, a matrix representing the intensity of each pixel of an image is considered to be in a spatial domain.

The Joint Photographic Experts Group (JPEG) and the JPEG2000 standards are examples of image lossy compression using a transform function [1, 50, 59]. Hybrid codecs based on the discrete cosine transform (DCT) are designed to attain higher compression ratios by combining loss and lossless compression algorithms. A modified version of the DCT is used in H.264/AVC (Advanced Video Coding) and H.265/HEVC (High Efficiency Video Coding) standards [6, 60, 63]. Algorithms based on the DCT are the one used in the JPEG file format [59] and the one used in the lossy definition of the WebP file format.³ The DCT is widely used because of its low computational complexity and its high quality when used for lossy compression. However, the wavelet transform (WT) shows better image reconstruction quality when used for lossy compression [5, 30]. By using the HVS based on fovea centralis, coding the quality of the reconstruction may be improved [12, 24, 40, 41]. Nowadays, few image formats use the WT for image compression. An example of these formats is the JPEG2000 file format [1].

There are several proposals for improving classic algorithms for current wavelet-based image compression methods such as the ones proposed in [13, 25]. However, there is no ideal algorithm that produces the best image reconstruction quality for any kind of image in any given application [3]. The reason is that when doing lossy compression, the algorithm must choose which details must be dropped in order to reach a given compression ratio. The main problem lies in which details to drop. For video compression, the problem of storage increases because a digital video is a set of several images, called frames, that represent a state of a taken video at a specific instant. Also, video file formats must store the information of sound, increasing the need of efficient lossy compression algorithms for images even if the sound is also compressed. Because sound compression is a related but different problem to image compression, from now on the rest of this chapter the term video compression will be used to refer only to the compression of the visual information or frames.

2 Data Compression

Lossless compression algorithms exploit the statistical behavior of the data to be compressed. The original data can be recovered perfectly after decompression. Lossless compression is used for generic data compression regardless of what the data represents images, sound, text, and so on. Current formats for data file compression like .Zip file format (ZIP) [44] and Roshal Archive file format (RAR) [45] use lossless compression algorithms. There are two main classifications of lossless compression: dictionary and statistical methods. These methods require data information. Information is an intuitive concept that deals with the acquisition of knowledge. This acquisition can be done in several ways such as through study, experience of past events, or in the form of a collation of data [3]. Thereof, an important aspect to take into account is how to measure data. Quantifying information is based on the observation of the content of a given message and evaluating how much it is learned from a previous pool of knowledge. The value of how much information is gained depends on the context. Claude Shannon, the precursor of information theory [18], proposed a way to measure how much information is transmitted or gain after transmitting a string of characters. Given an alphabet Σ, the amount of information H (entropy) from a string s is expressed in terms of the probability of each symbol where each symbol can be seen as a value of a random variable. The amount of information indicates how easily a set of data, in this case the given string, can be compressed. The entropy is expressed as

$$\displaystyle \begin{aligned} H (\mathbf{s}) = -\sum_{i=1}^nP_i\log_2P_i {} \end{aligned} $$

(19.1)

where n is the amount of symbols in the alphabet of s calculated as n = | Σ| and P _i is the probability of the i-th symbol.

Equation (19.1) can be interpreted as the amount of information gained from a string. This is known as the data entropy. The term entropy was coined by Claude Shannon [45]. The name entropy was chosen because the same term is used in thermodynamics to indicate the amount of disorder in a physical system. The meaning in the thermodynamics field can be related to the information theory field by expressing the information gained from a string s as the different frequencies each symbol of the alphabet appears on the string s. Using Eq. (19.1), the redundancy of R in the data is defined by the difference between the largest entropy of a symbol set and its actual entropy [44] defined by

$$\displaystyle \begin{aligned} R (\mathbf{s}) = \log_2n + H (\mathbf{s}). {} \end{aligned} $$

(19.2)

How much a data stream can be compressed is defined in terms of its redundancy R. If the stream has a redundancy R = 0, the data cannot be further compressed. Thus, the aim of a lossless compression algorithm is, from a given data stream with R > 0, to create a compressed data stream where its redundancy R = 0. The main theorem of Shannon of source coding states that [45] a stream of data cannot be compressed further to a limit without lossless. Such limit defined in this chapter by lossless compression limit (LCL) denoted by ρ is defined using Eq. (19.1) as follows.

$$\displaystyle \begin{aligned} \rho(\mathbf{s}) = mH(\mathbf{s}) {} \end{aligned} $$

(19.3)

where m is the amount of different symbols that appear on string s.

Dictionary and statistical coding algorithms use different approach to reduce the redundancy of a data stream. Dictionary methods encode the data by choosing strings and encoding them with a token. Each token is stored in a dictionary and is associated with a particular string. An example of this is to use a numerical index for each word on a dictionary. For a dictionary of length of N, it will be needed an index with a size close to ⌈log₂ N⌉ bits. Dictionary methods perform better as the size of the data stream to be compressed tends to infinity [46]. There are popular methods of dictionary source coding such as LZ77, LZ78, and LZW [43]. A common implementation of LZ77 is the DEFLATE algorithm used by the Unix operating system. The statistical methods for compression use a statistical model of the data to be compressed. It assigns a code to each of the possible symbols of the stream. The performance of the algorithms is determined by how such codes are assigned. These codes are variable in size, and usually the shortest one is assigned to the symbol with the higher frequency on the data stream. There are different variable size codes that allow to assign codes to each symbol without ambiguity. One of the most popular methods is the Huffman code. The Huffman code uses the statistical model of the data in order to assign a unique variable size code to each symbol. Huffman code is used in current standards such as JPEG and Portable Network Graphics (PNG). However, Huffman code only produces ideal size codes when the probabilities of each symbol are a negative power of two [45]. Arithmetic encoding on the other hand is known for its better performance against the Huffman codes [44].

The main disadvantage of lossless coding is that it is bounded by Shannon’s theorem (see Eq. (19.3)). However, a consequence of the Shannon’s theorem is that if a data stream is compressed beyond the LCL, the new data stream begins to lose information and a reconstruction of the original data cannot be made [46]. As a result, lossy algorithms must be designed in order to select which data will be lost in the compression and how to get a close representation of the original data using the compressed data stream. The data selected to be discarded is usually the one that contains the fewer information possible about the data stream. Thereof, lossy coding algorithms are designed for specific data sets in order to be able to select which data is significant and which data will be discarded. There are several ways to design lossy compression algorithms. There are lossy algorithms that operate over the original mathematical domain of the given stream such as the run-length encoding (RLE) for images. However, the best algorithms known are those that its output is calculated when using a mathematical transform.

A mathematical transform is a function that maps a set into either another set or itself. Mathematical transforms used in lossy compression, specifically on sound and image compression, are projections from one space to another. The inverse of the chosen transform must be invertible in order to reconstruct a close approximation of the original data. The use of mathematical transform for compression is also known as transform coding. Transform coding is widely used in multimedia compression and is known as perceptual coding. The preferred transformations for perceptual coding are the ones that present graceful degradation [3]. This property allows to discard some of the data on the projected space while the inverse of the transform can reconstruct a close approximation of the original data. The most common functions for perceptual coding are the ones related to the Fourier transform. When using a Fourier-related transform, it is said that the transform translates the original data from the spatial or time domain into the frequency domain. Being the data on the frequency domain which allows to discard some of the frequencies that are imperceptible to human perception. Hence the name of perceptual coding. Also, Fourier-related transforms degrade gracefully when decimal precision of some coefficients is lost. This allows to reduce the arithmetic precision of certain coefficients, thus reducing the number of bits required for its representation while retaining the most of the information of the original data. This process is known as quantization. The quantization method depends on how the data is represented by the transform on the frequency domain. There are several quantization algorithms for a given transform. The performance of the lossy compression algorithm depends on its transform and the quantization method. Several transforms have been proposed for multimedia coding such as the previously discussed DCT or the discrete WT (DWT).

Another common method used in lossy compression is the selection of regions of interest (ROIs) at different compression ratios. This feature mitigates such loss by conserving the details over a specific area. The ratio between the size of the compressed stream and the uncompressed stream is known as compression ratio [44]. In current standards such as MPEG4 and JPEG2000, ROIs can be defined [1, 19]. ROI-based algorithms are commonly used on image and video compression, and their main purpose is to assign more screen resources to a specific area [10]. ROIs are areas defined over an image selected by a given characteristic. ROI compression is when areas of the image are isolated using different desired final quality [19].

2.1 Fovea Centralis

The structure of the human eye (see Fig. 19.1) can also be exploited for compression. In applications wherever ROI is isolated, a selected part of the human eye called fovea centralis is utilized to increase the image quality for the human eye around ROI areas [49]. There are two main bodies on the tissue layer, particularly cones and rods. The number of cones in every eye varies between half a dozen and seven million. They are placed primarily within the central portion of the tissue layer, referred to as the fovea centralis, and are highly sensitive to color. The number of rods is much larger, some seventy five to one hundred fifty million are distributed over the retinal surface. In Fig. 19.1, the circle between the points b′ and c′ marks wherever the cones reside, such area is termed fovea centralis. The larger area of distribution and the fact that several rods are connected to a single nerve reduce the amount of detail discernible by these receptors. The distance x in Fig. 19.1 is the area where the perception of an user would be the most acute, where the size of x is determined by the distance d between the observer and the image, and the distance d′ between the retina and the back of the eye where the rods and cones reside. Anything outside of such area will be perceived with fewer details. This aliasing is exploited in fovea centralis compression. Fovea centralis compression can be applied over images with ROI; the use of fovea centralis around defined ROI improves the image quality for the human eye [15, 16, 24].

Fig. 19.1

Structure of the human eye

3 Wavelet Transforms

Fourier analysis is an useful tool for signal analysis. Fourier analysis is the study of general functions represented by using the Fourier transform [34]. The analysis is done by representing any periodic function as series of harmonically related sinusoids. It is useful in numerous fields, however it has some limitations [14]. Many of these limitations come from the fact that the Fourier basis elements are not localized in space. It is said that the basis of a transform is localized in space when its energy is concentrated around a given point. Accordingly, elements of the basis beyond certain radius will be 0 valued or close to 0. A basis that is not localized does not give information about how the frequency changes in relation to its position in time or space. There are refined tools that extend the capabilities of the Fourier transform in order to cover its weakness such as the windowed Fourier transform [27]. One mathematical tool that is able to analyze a signal and the structure of a signal at different sizes, thus yielding into information about the changes of frequency related to its position in time or space is the wavelet transform [2]. Time-frequency atoms are mathematical constructions that help to analyze a signal over multiple sizes. Time-frequency atoms are waveforms that are concentrated in time and frequency. The set of time-frequency atoms used for analyzing a signal is known as dictionary of atoms denoted by $\mathfrak {D}$. The wavelet transform builds this dictionary from a function $\psi (t) \in {\mathbf {L}}^2(\mathbb {R})$, where L ² is the Lebesgue space at power of 2, $\mathbb {R}$ is the set of real numbers, and ψ(t) denotes a wavelet function. ψ has several properties, it has zero average [27]

$$\displaystyle \begin{aligned} \int_{-\infty}^\infty \psi(t)dt = 0. {} \end{aligned} $$

(19.4)

It is normalized ||ψ|| = 1 and centered in the neighborhood of t = 0. ψ is known as the mother wavelet. In order to create a dictionary $\mathfrak {D}$, ψ is scaled by ℓ and translated by u, namely [27]

$$\displaystyle \begin{aligned} \mathfrak{D} = \left\{ \psi_{\ell,u}(t) = \frac{1}{\sqrt{\ell}}\psi \left(\frac{t-u}{\ell}\right)\right\}_{u\in\mathbb{R},\ell > 0} {} \end{aligned} $$

(19.5)

The atoms remain normalized ||ψ _ℓ,u|| = 1. The constant $\frac {1}{\sqrt {\ell }}$ is for energy normalization. The continuous wavelet transform (CWT) ω of $f(t)\in {\mathbf {L}}^2(\mathbb {R})$ at time u and scale ℓ is

$$\displaystyle \begin{aligned} \omega_{\ell,u}(f) = \langle f,\psi_{\ell,u} \rangle = \int_{-\infty}^\infty f(t)\frac{1}{\sqrt{\ell}}\psi^*\left(\frac{t-u}{\ell}\right)dt {} \end{aligned} $$

(19.6)

where ψ ^∗ is the complex conjugate of the mother wavelet ψ and 〈⋅, ⋅〉 denotes an inner product.

Because images are two-dimensional signals, a two-dimensional wavelet transform is needed. Let $\bar \psi _{\ell ,u}$ be

$$\displaystyle \begin{aligned} \bar\psi_{\ell,u}(t) = \frac{1}{\sqrt{\ell}}\psi^*\left(\frac{t-u}{\ell}\right), {} \end{aligned} $$

(19.7)

extending Eq. (19.6) to two dimensions, the wavelet transform at parameters u _v, ℓ _v, u _h, ℓ _h of $f(t,x)\in {\mathbf {L}}^2(\mathbb {R}^2)$ yields into

$$\displaystyle \begin{aligned} \begin{aligned} \omega^2_{\ell_v,u_v,\ell_h, u_h}(f) & = \langle\langle f,\bar\psi_{\ell_v,u_v} \rangle , \bar\psi_{\ell_h,u_h} \rangle\\ &= \int_{-\infty}^\infty\int_{-\infty}^\infty f(t,x)\bar\psi_{\ell_v,u_v}\bar\psi_{\ell_h,u_h}dtdx. {} \end{aligned} \end{aligned} $$

(19.8)

where ω is the wavelet operator. Also, because digital images are stored as a discrete finite signal, a discrete version of the CWT is needed. Let f[n] be a discrete signal obtained from a continuous function f defined on the interval [0, 1] by a low-pass filtering and uniform sampling at intervals N ⁻¹. The DWT can only be calculated at scales N ⁻¹ < ℓ < 1. Also, let ψ(n) be a wavelet with a support included in [−K∕2, K∕2]. For 1 ≤ ℓ = a ^j ≤ NK ⁻¹, a discrete wavelet scaled by a ^j is defined by [27]

$$\displaystyle \begin{aligned} \psi_j[n] = \frac{1}{\sqrt{a^j}}\psi\left(\frac{n}{a^j}\right). {} \end{aligned} $$

(19.9)

The DWT is defined by a circular convolution with $\bar \psi _j[n]$ defined as $\bar \psi _j[n] = \psi _j^*[-n]$ with DWT described as

$$\displaystyle \begin{aligned} \omega_{a^j}f[n] = \sum _{m=0}^{N-1}f[m]\psi^*_j[m-n] = f\ast \bar\psi_j[n] {} \end{aligned} $$

(19.10)

where ∗ is the convolution operator. Also, signal f is assumed to be periodic of length N in order to avoid border problems.

In order to speed up the computation of the wavelet coefficients, a second approach that simplifies the DWT is referred to as the lifting scheme. The lifting scheme [32, 51] is another way of looking at the DWT, where all the operations are performed in the time domain [1]. Computing the wavelet transform using lifting steps consists of several stages. The idea is to compute a trivial wavelet transform (the lazy wavelet) and then improve its properties by alternating the dual lifting or prediction step and the primal lifting or updating step [44]. The lazy wavelet only splits the signal into its even and odd indexed samples, namely

$$\displaystyle \begin{aligned} (even[n-1], odd[n-1]) = Split(f[n]). {} \end{aligned} $$

(19.11)

where f[n] is a given discrete signal, even and odd are the even and odd signals of the lazy wavelet, and Split is the split function. A dual lifting step consists of applying a filter to the even samples and subtracting the result from the odd ones. This is based on the fact that each value f[n]_2ℓ+1 of the next decomposition level in the odd set is adjacent to the corresponding value f[n]_2ℓ in the even set, where ℓ is the decomposition level. Thus, the two values are correlated and any can be used to predict the other. The prediction step is given by

$$\displaystyle \begin{aligned} d[n-1] = odd[n-1] - P(even[n-1]). {} \end{aligned} $$

(19.12)

where d is the difference signal of the odd part of the lifting wavelet and the result of the prediction P operator applied to the even part of the lazy wavelet. A primal lifting step does the opposite: applying a filter to the odd samples and adding the result to the even samples. The update operation U follows the prediction step. It calculates the 2[n − 1] averages s[n − 1]_ℓ as the sum

$$\displaystyle \begin{aligned} s[n-1] = even[n-1] + U(d[n-1]). {} \end{aligned} $$

(19.13)

where U is defined by

$$\displaystyle \begin{aligned} s[n-1]_\ell = f[n]_{2\ell} + \frac{d[n-1]_{\ell}}{2}. {} \end{aligned} $$

(19.14)

The process of applying the prediction and update operators is repeated as many times as needed. Each wavelet filter bank is categorized by its own U operator and the amount of rounds of the process. The calculation process of U is described in [26]. This scheme often requires far fewer computations compared to the convolution-based DWT, and its computational complexity can be reduced up to 50% [1, 11, 53]. As a result, this lifting approach has been recommended for implementation of the DWT in the JPEG2000 standard.⁴

4 Image Compression

Image data compression is concerned with coding of data to minimize the number of bits used to represent an image. Current image compression standards use a combination of lossless and lossy algorithms. These can be used over the same data set because both algorithms exploit different properties of the image. On the one hand, lossless-based compression exploits data redundancy, but on the other hand, lossy-based compression exploits its transform properties and quantization. The simplest quantization equation used in image coding is defined as [4, 17]

$$\displaystyle \begin{aligned} {\mathbf{C}}^q = \left \lfloor \frac{1}{\Delta q} \mathbf{C} \right \rfloor {} \end{aligned} $$

(19.15)

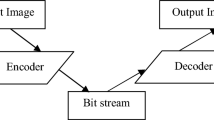
where ⌊⋅⌋ is the floor operation, Δq > 1 is known as the quantization delta, C is the matrix of coefficients obtained from applying a transform to the given image, and C ^q is the matrix of quantized coefficients. Spatial redundancy takes a variety of different forms in an image. For example, it includes strongly correlated repeated patterns in the background of the image and correlated repeated base shapes, colors, and patterns across an image. The combination of lossy and lossless compression allows achieving lower compression ratios. Figure 19.2 shows a block diagram of the classic lossy/lossless image coding scheme [4, 17].

Fig. 19.2

Block diagram of the classic image coding scheme [17]

In Fig. 19.2, the image is interpreted as a matrix I, then the coefficients matrix C of the chosen transform is calculated. Subsequently, the quantized coefficient matrix C ^q is calculated and the final lossless compressed stream S is calculated on the entropy coding block. The color space used for image compression is often the Y ′C _B C _R color space. This color space is chosen because it has been found that the human eye is more sensitive to changes on the luma channel (Y’) than on the color channels (C_BC_R) [33]. This allows compressing at lower ratios the color channels than the luma channel. As a result, compression algorithms are evaluated over the luma channel only. Thereof, all the analyses of the algorithms presented in this chapter are evaluated on the luma channel. The equation used for calculating Y ′C _B C _R from other common color space RGB suggested in [17] is the following:

(19.16)

where R, G, B are the values for each channel on the RGB color space of a given pixel. From Eq. (19.16), the luma is calculated as

$$\displaystyle \begin{aligned} Y' = 0.299R + 0.587G + 0.114B. {} \end{aligned} $$

(19.17)

One of the foremost image compression algorithms is the JPEG image coding standard (see Fig. 19.3). Outlined in [59], JPEG framework defines a lossy compression and a lossless compression algorithm used in tandem. The lossy compression algorithm of JPEG uses the DCT. However, in order to reduce the complexity of the algorithm [4], the image is split into non overlapping blocks of 8 × 8 pixels. Each block is referred to as macroblock. Processing macroblocks requires less computation and allows the algorithm to optimize transmission by sending the data of processed macroblocks while processing the rest of the images [19].

Fig. 19.3

Block diagram of the JPEG2000 standard [59]

In Fig. 19.3, the RGB image is transformed into the Y ′C _B C _R color space. Then, the image is split into macroblocks. Then, the DCT macroblock applies the transform to each macroblock individually. After the transformation of a macroblock is calculated, the coefficients are quantized by a fixed ratio. JPEG standard defines a quantization matrix. Because each coefficient has a different significance on the reconstruction of the image, the quantization matrix stores a quantization ratio for each of the coefficient of a macroblock. The standard provides with values for the quantization matrix. However, some manufacturers defined its own quantization matrices in order to improve the quality of the algorithm. After quantization, the next step is resorting each macroblock into zigzag order. This allows to exploit the entropy of the lower diagonal of the macroblocks [1]. The last block of the algorithm applies lossless compression to the quantized sorted coefficients. Early versions of the algorithm define RLE and Huffman coding as the lossless algorithms for JPEG. However, the last version of JPEG [45] also includes arithmetic coding in order to reduce the compression ratio. The final overall quality of JPEG is mostly given by the quantization matrix, however it is not possible to precalculate the final compression ratio [43].

It is well-known that in compression applications, wavelet-based approaches outperform the block-DCT methods [22, 35]. This is due to the fact that wavelet-based approaches can reduce the blocking artifacts, provide better energy compaction because of the multi-resolution feature of wavelet basis, and have better correspondence with the HVS system [58]. Therefore, wavelet-based compression algorithms have been recommended for the JPEG2000 standard [17, 45].

4.1 Foveated Images

Images with a non-uniform resolution that have been used in image and video compression are known as foveated images. Equation (19.18) shows a representation of a foveated image [9].

$$\displaystyle \begin{aligned} I^0_x = \int I_x c^{-1} (x)s\left( \frac{t-x}{\omega(x)}\right)dt {} \end{aligned} $$

(19.18)

where c(x) = $\left \| s\left (\frac {-x}{\omega (x)}\right )\right \|$, I _x is the pixel at position x of a given image, ω(x) is a weight function, and $I^0_x$ is the foveated image. The function s is known as the weighted translation of s by x [24]. A variation of the fast wavelet transform (FWT) is reported in [7] that operates over the wavelet transform. For an image I, its foveation is given by

$$\displaystyle \begin{aligned} I^0 = \langle I, \Phi_{\ell_0, 0, 0} \rangle + \sum_{u_v,\ell_v,u_h,\ell_h} c_j^k[\ell_v, u_h] \langle I, \Psi^{u_v}_{\ell_v, u_h, \ell_h} \rangle\Psi^{u_v}_{\ell_v, u_h, \ell_h} {} \end{aligned} $$

(19.19)

where $\Phi _{\ell _0, 0, 0}$ is the father wavelet, and $\Psi ^{u_v}_{\ell _v, u_h, \ell _h}$ is the mother wavelet scaled and translated with u _v = {h, v, d} and the operator 〈⋅, ⋅〉 is the convolution operator. $c_j^k[\ell _v, u_h]$ is defined as

$$\displaystyle \begin{aligned} \begin{aligned} c_j^k[\ell_v, u_h] & = \langle T\Psi^{u_v}_{0,\ell_v, u_h}, \Psi^{u_v}_{0,\ell_v, u_h} \rangle \\ & = \int_{-\infty}^\infty dy\int_{-\infty}^\infty dx \Psi^{u_v}_{0,\ell_v,u_h}(x,y)\int_{-\infty}^\infty dt\int_{-\infty}^\infty ds \Psi^{u_v}_{0,\ell_v, u_h}(s,t)g_{\omega(x,y)}(s,t) \end{aligned} \end{aligned} $$

(19.20)

where T is the fovea centralization operator and g _ω(x,y)(s, t) is the smoothing function defined as

$$\displaystyle \begin{aligned} g_{\omega(x,y)}(s,t) := \frac{1}{\omega(x,y)^2}g\left(\frac{s-x}{\omega(x,y)}, \frac{t-y}{\omega(x,y)} \right). \end{aligned} $$

(19.21)

where the weight function ω(x, y) is defined by

$$\displaystyle \begin{aligned} \omega(x,y) = \alpha||(x,y) - (\gamma_1,\gamma_2)||{}_2+\beta \end{aligned} $$

(19.22)

where α is the rate, γ = (γ ₁, γ ₂) is the fovea centralis, and β is the fovea centralis resolution [7].

5 Video Compression

Because video is just a sequence of several images called frames, video coding algorithms or video codecs use image compression extensively. To achieve high compression ratios is suitable to combine lossy and lossless compression algorithms. Classic video coding frameworks have three main algorithms (see Fig. 19.4), namely intra-frame coding (spatial transform and inverse spatial transform), inter-frame coding (motion estimation and compensation), and variable length coding (variable length coder).

Fig. 19.4

Block diagram of the classic video coding framework [6]

In intra-frame coding, which uses the information of previous or future frames, a frame of a video stream is normally compressed using lossy algorithms. The encoder should work out the variations (prediction error) between the expected frame and the original frame. The first step in the motion compensated video coder is to create a motion compensated prediction error of the macroblocks. This calculation requires only a single frame to be stored in the receiver. Notice that for color images, motion compensation is performed only for the luma component of the image. The decimated motion vectors obtained for luma are then exploited to form motion compensated chroma components. The resulting error signal for each of the components is transformed using DCT, quantized by an adaptive quantizer, entropy encoded using a variable length coder, and buffered for transmission over a fixed-rate channel. The main problem of the block matching motion compensation is its high computational complexity.

Most video coding standards such as the H.264 [36] or the newest proposed standard H.265/HEVC codec [52] rely on the DCT for lossy intra-frame coding applied to macroblocks of a dimension of 4 × 4. The smaller macroblock allows reducing artifacts on the reconstructed image [37]. However, in order to improve the speed of the algorithm, the transform used is the integer discrete cosine transform (IDCT) [8]. The IDCT is an approximation of the DCT used in JPEG standard. Instead of calculating a convolution, two different matrices are defined that are an approximation of the base of the DCT.

6 An Approach to Image Compression Based on ROI and Fovea Centralis

Image compression within the frequency domain based on real-valued coefficients is carried out through coefficient quantization. In this process of quantization, these coefficients become integer-valued for further compression employing either a RLE or an arithmetic encoding algorithms, which are known as variable quantization algorithms. The variable quantization algorithm exploits the fovea centralis result of the HVS based on a fovea centralis window, which is focused at a given fixation point to see a way to quantize each wavelet coefficient [15]. A modified version of the set partitioning in hierarchical tree (SPIHT) algorithm is utilized to quantize and compress these coefficients.

Figure 19.5 shows the block diagram of the compression approach based on ROIs and fovea centralis called here fovea centralis hierarchical tree (FVHT) algorithm. Assuming a video stream with frames F _i, the applied blocks can be described as follows [15]. In the Motion estimation block, the fovea centralis points are estimated using video frames F _i and F _i−1. The ROI estimation block outputs an array of fovea centralis points as ROI _i, where each pixel different of 0 is taken as a fovea centralis. The fovea centralis cutoff window is described in [15]. The Lifting Wavelet Transform (LWT) block generates the coefficients denoted as C(⋅)_i (see Sect. 19.3). The Quantization block maps to integers the coefficients C(⋅)_i into $C(\cdot )_i^q$ using a fixed quantization for compression. Finally, the FVHT block outputs a compressed stream of the quantized coefficients $C(\cdot )_i^q$ using the information of the estimated fovea centralis points ROI _i.

Fig. 19.5

Block diagram of compression approach based on ROI and fovea centralis [15]

Note that the fovea centralis points ROI _i are input parameters to the FVHT rather than using the motion estimation block. The window parameters and the cutoff window are calculated as long as there is a fixation point [15, 24]. The reported method permits defining ROIs of variable size around the fixation point that retains the best quality. Further details on the approach described here can be found in [15].

6.1 FVHT Algorithm

The compression bit rate can be computed by assessing the decaying window function on each algorithm pass at each coefficient coordinate as it is proposed in the FVHT algorithm [15]. First, the coefficient is encoded whether the current bit rate is lower than wavelet subband, otherwise it is discarded. The sorting pass is modified in order to classify the coefficients according to its distance to the scaled fovea centralis and the cutoff window. Each time an attempt to add a coefficient to the list of significant pixels (LSP) is done, the assigned bits per pixel (bpp) is calculated, and the coefficient is classified. However, it should be noted that on the significance pass, the positions of the coefficients are discarded from the list of insignificant pixels (LIP) and on the refinement pass, they are discarded from the LSP. The list of insignificant sets (LIS) will remain the same as in the SPIHT algorithm [15, 42]. The execution time of the algorithm was analyzed using Big O notation, concluding that the complexity of the algorithm is linear ($\mathcal {O}(n{})$) [15]. The memory usage was also analyzed, yielding a size of $\frac {71}{64}n$. The FVHT is memory intensive when compared with classic methods based on the DCT transform that can be computed using no extra storage.

6.2 Simulation Results

The FVHT algorithm is assessed using standard non-compressed 512 × 512 images. The fovea centralis is defined at the center pixel (256, 256) with two parameters, namely a radius of the ROI and the power law function (the ramp function), which are defined in [15]. As stated in the JPEG2000 standard and for a fair comparison, the biorthogonal Cohen–Daubechies–Feauveau (CDF) 9/7 is considered using four levels of decomposition [1]. The reported results are compared against the SPIHT algorithm. Figures 19.6 and 19.7 show the reconstructed wavelet coefficients of the cameraman image at 1 bit per pixel (bpp) with both SPIHT and FVHT, respectively. The same reconstructed wavelet coefficients at 1 bpp as its higher compression ratio and 0.06 bpp as its lower compression ratio are shown in Fig. 19.7. It is observed that the FVHT algorithm has better performance than SPIHT algorithm particularly over small areas around the fovea centralis or those closer to the fixation point. Further details on this approach can be found in [15].

Fig. 19.6

Reconstructed image (“cameraman”) using SPIHT algorithm at 1 bpp compression ratio [15]

Fig. 19.7

Reconstructed image (“cameraman”) using FVHT compression algorithm at 0.06–1 bpp compression ratio [15]. Fovea centralis at (256,256)

7 Wavelet-Based Coding Approaches: SPECK-Based Codec and Adaptive Wavelet/Fovea Centralis-Based Codec

Two wavelet-based coding approaches based on the LWT [27] are described in this section [16]. The first called Set Partitioned Embedded bloCK (SPECK)-based codec (SP-Codec) is shown in Fig. 19.8 [31]. In the Z-order block, all coefficients position are organized and mapped from 2D to 1D using the Z-transform. The quantization step is carried out on LWT and SPECK blocks. The adaptive binary arithmetic coding (ABAC) block, which is a lossless compression algorithm, allows compressing a data stream while at the same time computes the statistical model (see Sect. 19.7.1) [31]. The inverse LWT (iLWT) and inverse SPECK (iSPECK) are applied to the compressed stream generated in the SPECK block, and finally the motion compensation and estimation blocks compute the motion vectors based on the block matching algorithm for each inter-frame.

Fig. 19.8

Video coding framework SPECK-based codec (SP-Codec) [16]

The second proposal referred to as adaptive wavelet/fovea centralis-based codec (AWFV-Codec) reported in [16] aims to further increase the quality of the decoded frames (see Fig. 19.9). The reported adaptive fovea centralis-SPECK (AFV-SPECK) algorithm defines a center, a ROI area radius, and a decaying window [15, 16] and as a result various compression ratios may be considered. An external subsystem is assumed that computes the fovea centralis point of one observer, which is later provided to the AFV-SPECK coding algorithm.

Fig. 19.9

Video coding framework AWFV-Codec [16]

7.1 Adaptive Binary Arithmetic Coding

The adaptive binary arithmetic coding (ABAC) is a version of the arithmetic coding algorithm applied to an alphabet with only two elements Σ = 0, 1 [64]. This application is commonly used for bi tonal images [23]. Also, it does not require a previously calculated statistical model. Each time a symbol is read, the statistical model is updated. The adaptive part of the algorithm decreases its performance when compared against a static approach. However, the main advantage is that the input data is not preprocessed. As a result, the efficiency of the transmission of the compressed stream increases because there is no wait time for the calculation of the statistical model. There are several applications for ABAC as in JPEG and Joint Bi-level Image Group (JBIG)⁵ when dealing with black and white images. However, because SPECK encodes per bit, it makes ABAC suitable to compress the output of SPECK. In order to increase the computing time performance of the proposed framework, ABAC is included as its variable length encoder. Listing 19.1 shows the pseudocode for adaptive binary arithmetic coding.

Listing 19.1 ABAC algorithm

In classic arithmetic coding, the interval used for arithmetic compression is [0, 1). The function receives a string s to be compressed. The variable fq will store the frequency of the symbol 0. Because there are only two symbols on the alphabet, it is only needed to store one of the frequencies and compute the other by

$$\displaystyle \begin{aligned} P_1 = 1 - P_0 {} \end{aligned} $$

(19.23)

where P ₁ is the probability of the symbol i. The probability of the symbol 0 is given by

$$\displaystyle \begin{aligned} P_0 = \frac{fq}{r} {} \end{aligned} $$

(19.24)

where r is the amount of read symbols. The algorithm stores the lower bound of the main interval on l and the upper bound on u. Each time a symbol is read, the counter r is increased on 1 and the interval for the input symbol is updated by using the frequency of the symbol 0 stored on fq. If a 0 is read, the frequency fq is increased in 1. After updating the statistical model, the new main interval is computed and the next symbol is read. The process stops when there are no more symbols to read on s and the statistical model P. P is a set that contains the probabilities of all different symbols s of the alphabet of s.

7.2 AFV-SPECK Algorithm

In the AFV-SPECK algorithm, every time a new coefficient is categorized as significant it will also be tested for its individual compression ratio using the cutoff window for each wavelet decomposition subband [16] (see Fig. 19.10). Note that the main loop remains the same as with SPECK. The input is the set of quantized coefficients, while the output is stored on S (assessed for significance by the function ProcessS), and the sorting of the LSP set is also added. If S is significant and only has one element (x, y), the sign of quantized coefficient is stored on S and the set is removed from LIS. The function ProcessI evaluates I for its significance. As with FVHT, the computational complexity of AFV-SPECK will be expressed in terms of the Big O notation. The AFV-SPECK algorithm has a computational complexity of $\mathcal {O}({}n)$. The analysis of the memory usage yielded that AFV-SPECK uses more memory when implemented as proposed in [31]. Further details can be found in [16].

Fig. 19.10

Flowchart of the main AFV-SPECK algorithm loop [16]

7.3 Simulation Results

To assess the reviewed video coding frameworks, SP-Codec and AWFV-Codec standard test images and video sequences were used⁶ [16]. For intra-frame coding, H.265 standard based on the IDCT using a 4 × 4 pixel block size is compared against SPECK and AFV-SPECK algorithms. Both binary streams were further compressed using the ABAC algorithm. The delta used for quantization was set to Δ = 40, see e.g.,[52]. Note that the chosen quantization delta and other parameters were used as input for SPECK and AFV-SPECK algorithms [16]. This is due to the fact that the compression ratio of the H.265 cannot be specified beforehand.

It is well-known that there is no analytic method to represent the exact perception of the HVS [56]. As a result, there are different metrics for image quality metrics [55]. In this work, the peak signal-to-noise ratio (PSNR) is used as performance metric [37]. The PSNR is defined in terms of the mean squared error (MSE) given by the equation

$$\displaystyle \begin{aligned} \mathrm{MSE}(I,K) = \frac{1}{mn}\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}\left[I_{i,j} - K_{i,j}\right]^2 {} \end{aligned} $$

(19.25)

where m denotes the rows and n the columns of original image matrix, I is the matrix of the original image, and K represents the reconstructed image matrix. Using Eq. (19.25), the PSNR is given by

$$\displaystyle \begin{aligned} \mathrm{PSNR}(I,K) = 10 \log_{10}\left[\frac{\mathrm{MAX}^2_I}{\mathrm{MSE}(I,K)}\right] \end{aligned} $$

(19.26)

where $\mathrm {MAX}^2_I$ is the square of the maximum value that a pixel of the image I can take. Such value depends on the amount of bits used per channel. Commonly, an image of 8 bits per channel has $\mathrm {MAX}^2_I=255^2$. PSNR is measured in decibels (dB). Usually, it is considered that a reconstructed image with a PSNR of 40 dB or higher is of good quality for an average user [44]. However, trained users should require higher PSNR values. The 40 dB threshold is only a convention and has not been proved. Expected values of good reconstructions are between 20 dB and 50 dB [44].

As stated in the standard JPEG2000 and for a fair comparison, we use the biorthogonal CDF9/7 with four levels of decomposition [1]. Two metrics are used to assess the performance of the reported algorithms, namely PSNR and structural similarity index (SSIM) [54, 61]. This metric indicates that a reconstructed image with high quality should give a SSIM index closer to 1. Table 19.1 depicts comparisons in images for various video sequences using H.265, SPECK and AFV-SPECK algorithms, where CIF stands for common intermediate format. This table shows that the SPECK algorithm has a high PSNR (see e.g., [29]). It also observed that since the reported AFV-SPECK algorithm is based on ROIs and fovea centralis, it is expected that the result of these metrics to be equal or lower than the SPECK algorithm. Further details on these comparisons and other sequences are reported in [16].

Table 19.1 Comparisons between SPECK, AFV-SPECK and H.265 (see [16])

8 Conclusions

In this chapter, two wavelet-based algorithms were reviewed, namely FVHT and AFV-SPECK. Such algorithms exploit the HVS in order to increase the quality of the reconstructed image for an observer. The algorithms were assessed against classic compression algorithms such as the JPEG base algorithm and the algorithm used on the H.265 standard. Simple wavelet compression shows better performance when compressing images allowing to reach compression ratios of 0.06 bpp while retaining a good visual quality. The reported algorithms show similar behavior while increasing the quality of the compressed image over designed areas. However, when evaluated for overall quality, the reported algorithms show less performance than its non-fovea-based counterparts. This makes necessary an external subsystem that calculates the fixation point of the observers. Additionally, two wavelet-based video coding frameworks were surveyed, namely SP-Codec and AWFV-Codec [16]. The revised video frameworks increase the key frame reconstruction using wavelet-based compression that is also applied to motion compensation reconstruction. Fovea centralis coding also increases the quality of the reconstructed video as in AWFV-Codec, and in some cases, increases the quality of the reconstructed frames against non-fovea-based frameworks like SP-Codec. The reported AWFV-Codec is a viable choice for fast video streaming but it also reduces the utility of the stream when recorded. This is due to the fact that the video would be recorded without possibility of recovering the information discarded outside the fovea centralis. However, when stream recording is needed SP-Codec yields into better reconstruction quality than classic methods such as the H.265/HEVC video coding frameworks [15, 16]. The reported image compression algorithms FVHT and spatial transform AFV-SPECK require extra storage besides the wavelet coefficients. Methods will be investigated for in place computation for quantization in order to decrease the memory usage of both reported algorithms and for automatic foveation such as in [21].