Situation Calculus Meets Description Logics

Abstract

For more than six years, the groups of Franz Baader and Gerhard Lakemeyer have collaborated in the area of decidable verification of Golog programs. Golog is an action programming language, whose semantics is based on the Situation Calculus, a variant of full first-order logic. In order to achieve decidability, the expressiveness of the base logic had to be restricted, and using a Description Logic was a natural choice. In this chapter, we highlight some of the main results and insights obtained during our collaboration.

Prologue

We begin our contribution to celebrate Franz’ 60th birthday with some personal remarks by the second author, written as a first-person account. As these remarks are largely historical, they will also shed light on how the technical work described later came into being and how it is intimately connected to the work by Franz and his group in Dresden.

Franz and I first met, I believe, in 1990, when we both gave talks at AAAI in Boston. Indeed, in those early days, we mainly met at conferences, either at AAAI, IJCAI or KR. But apart from that, each of us was minding his own business, Franz working on Description Logics (DLs) and me on the Situation Calculus and the related action programming language Golog. This is not to say that I stayed away completely from DLs. While I was still in Bonn, Franz was nice enough to share his course notes with me so that I could teach a DL course, which I did exactly once! In 1994, I even published a paper on an epistemic version of CLASSIC, an early variant of modern DLs, at the German AI conference. But I soon realized that other people, in particular Franz, were much better at this, and I left DL to them without any intention to ever return, or so I thought.

In 1997, Franz and I became colleagues at RWTH Aachen University. Research-wise we continued our separate ways, but at least we now met regularly at (often boring) faculty meetings. It was only when Franz moved to Dresden that things took a different turn. Michael Thielscher, also at TU Dresden at the time, had the brilliant idea to gather researchers from different areas in KR and combine work on action formalisms with work on Description Logics, planning, and nonmonotonic reasoning. In the end, a DFG-funded Research Cluster on Logic-Based Knowledge Representation was established, initially started by Franz, Michael, Bernhard Nebel and myself, and later joined by Gerd Brewka. While I, together with my then Ph.D. student Jens Claßen, collaborated most closely with Bernhard’s group during this time, the meetings and workshops of the entire Research Cluster not only helped us to get to know each other better personally but to also appreciate each other’s research and the connections between the different areas much more.

At the time Hongkai Liu, a former Ph.D. student of Franz, worked on updating ABoxes, which is meant to reflect how a world changes. As the external examiner of Hongkai’s thesis I got to know his work quite well, and I was particularly intrigued by his chapter on decidable verification of infinite sequences of updates. At the same time, Jens had started work on the verification of nonterminating Golog programs. When the time came to re-apply for funding from DFG, this time in the form of a Research Unit on “Hybrid Reasoning for Intelligent Systems” [9], Franz had the idea that we should join forces and explore the verification of Golog programs when the underlying logic is restricted to a DL fragment with the aim of arriving at decidable forms of verification. When we received funding for our Research Unit, Jens joined our project on the Aachen side and Benjamin on the Dresden side. The rest, as they say, is history. We have collaborated now for almost seven years, and it has been a lot of fun. In the following, we highlight some of the main results obtained during this time, but before we begin: Happy Birthday, Franz!

1 Introduction

The agent language Golog [19, 33] allows one to describe an agent’s behaviour in terms of a program containing both imperative and nondeterministic aspects. Its basic building blocks are the primitive actions that are defined in a theory of some action logic, typically the Situation Calculus [40, 44] or its modal variant [31], but also formalisms based on Description Logics. Among Golog’s most promising application areas is the control of autonomous, mobile robots [11, 24].

As a very simple, illustrating example, consider a robot whose task it is to remove dirty dishes from a number of rooms in a building. A program for it might look like this:

The robot is initially in the kitchen. In each iteration of the infinite outer loop, it first unloads all dishes it carries, selects a room in the building, moves there, collects all dirty dishes from there, and returns to the kitchen. Here, $Dirty (x,y)$ means “dirty dish x is in room y”, and $load (x,y)$ stands for “load dish x from room y.” Constructs of the form moreover are to be read as “non-deterministically choose one object from the $Dish$ domain and do the following with it”. We furthermore assume that at any time during operation, some new dish x to be removed from room y may appear, which is represented through a special, “exogenous” $newdish (x,y)$ action. Now before deploying such a program onto the real robot, it is often desirable to verify it against some temporal specification, e.g. to make sure that every dish will eventually be removed.

While a large variety of temporal verification methods have been developed in the field of Model Checking [7, 12] over the last decades, the problem of verifying (typically non-terminating) Golog programs received surprisingly little attention among Situation Calculus researchers. Note that Model Checking is not directly applicable due to the fact that even though nowadays implicit, symbolic representations of state spaces are used, their input formalisms are very restricted in expressivity. Golog on the other hand relies on action descriptions in terms of (first-order) logical theories that correspond to a very large, if not infinite number of possible models. Instead of simply checking the property in question against a single model, theorem proving within the underlying logic is hence required.

De Giacomo, Ternovska and Reiter [21] were the first to address the verification of non-terminating Golog programs. They express programs and their properties using inductive definitions and fixpoint logics, thus heavily resorting to second-order quantification. They then do manual, meta-theoretic proofs to show that the program satisfies the desired properties. While this work was an important first step, an automated verification would be obviously much more preferable to a manual one since the latter tends to be tedious and error-prone.

Claßen and Lakemeyer [16] proposed such a method for properties expressed in a temporal logic that resembles the Computational Tree Logic $\textsc {CTL}$, but that allows for unrestricted first-order quantification. The algorithm is inspired by the classical symbolic model checking techniques for propositional $\textsc {CTL}$ in the sense that it does a similar fixpoint computation to systematically explore the system’s state space. The difference however is that it does not work on a single finite model, but, as explained above, uses a logical first-order action theory together with the Golog program (which possibly contains further first-order quantification). The method relies on regression-based reasoning, a newly proposed graph-based representation of the input program, and theorem proving for detecting convergence.

The overall verification problem for Golog is highly undecidable due to unrestricted first-order quantification in the underlying base logic, the kind and range of actions’ effects, and Golog being a Turing-complete programming language. Consequently, in [16] only soundness of the method was proved, but a termination guarantee could not be given. A natural next step is to try to identify restricted, yet non-trivial fragments of Golog where verification becomes decidable, while a great deal of expressiveness is retained.

A natural choice for a decidable base logic with first-order expressivity is a Description Logic. Baader, Liu and ul Mehdi [4] considered actions specified in an action formalism based on the Description Logic $\mathcal{A L C}$ [5], and furthermore abstracted from the actual execution sequences of a non-terminating program by considering infinite sequences of actions defined by a Büchi automaton. They expressed properties by a variant of $\textsc {LTL}$ over $\mathcal{A L C}$ axioms [2] and could show that under these restrictions, verification reduces to a decidable reasoning task within the underlying DL.

Their work was an important first step in the search for a way to overcome the above mentioned three “sources of undecidability” (i.e. undecidable base logic, range of action effects, Turing-complete program constructs), even though the restrictions employed were comparably harsh. In particular, their $\mathcal{A L C}$-based action formalism only allows for basic STRIPS-style addition and deletion of literals, and the very simple over-approximation of programs through Büchi automata loses important features such as the non-deterministic choice of argument and test conditions. Baader and Zarrieß [6] later showed that these results can indeed be lifted to a more expressive fragment of Golog that includes test conditions. They obtained decidability by proving that the potentially infinite transition system induced by the Golog program can always be represented by a finite one that admits the exact same execution traces. This was the start of a complementary line of research based on the approach of applying restrictions that allows one to compute a finite, propositional abstraction of the infinite state space, and then use a classical model checker to decide the query.

In this paper we want to give a brief, yet concrete impression of research conducted on both approaches, the Golog-specific fixpoint method as well as abstraction methods, within the aforementioned Research Unit on “Hybrid Reasoning for Intelligent Systems”. The following section introduces some formal preliminaries. Sections 3 and 4 then present the Golog-specific fixpoint method and the abstraction technique, respectively. DL-based representations, their relation to Situation Calculus formalizations, as well as computational complexities are then discussed in Sect. 5. Section 6 gives a survey of further research we conducted, followed by a conclusion in Sect. 7.

2 Preliminaries

2.1 The Logic $\mathcal E\! S$

We use a fragment of the first-order modal Situation Calculus variant $\mathcal E\! S$ [31], and corresponding Basic Action Theories (BATs) [44].

Syntax: There are terms of sort object and action. Variables of sort object are denoted by symbols $x,y,\ldots$, and a denotes a variable of sort action. $N_O$ is a countably infinite set of object constant symbols and $N_A$ a countably infinite set of action function symbols with arguments of sort object. We denote the set of all ground terms (also called standard names) of sort object by $\mathcal {N} _O$, and those of sort action by $\mathcal {N} _A$.

Formulas are built using fluent predicate symbols (predicates that may vary as the result of actions) of any arity and equality, using the usual logical connectives and quantifiers. In addition we have two modalities for referring to future situations, where $\Box \phi$ says that $\phi$ holds after any sequence of actions, and $[t]\phi$ means that $\phi$ holds after executing action t.

A formula without $\Box$ and $[\cdot ]$ is called fluent formula, one without $\Box$ bounded, and one without free variables a sentence.

Semantics: Let $\mathcal {Z}:= \mathcal {N} _A ^*$ be the set of all finite action sequences (including the empty sequence $\langle \rangle$) and $\mathcal {P}_F$ the set of all primitive formulas $F(n_1,...,n_k)$, where F is a k-ary fluent and the $n_i$ are object standard names. A world w maps primitive formulas and situations to truth values: $w : \mathcal {P}_F \times \mathcal {Z} \rightarrow \{0,1\}.$

The set of all worlds is denoted by $\mathcal {W}$.

Definition 1

(Truth of Formulas). Given a world $w \in \mathcal {W}$ and a sentence $\psi$, we define $w\,\models \,\psi$ as $w,{\langle \rangle } \,\models \,\psi$, where for any $z \in \mathcal {Z}$:

• 1. $w,z \,\models \, F(n_1,\dots ,n_k)$ iff $w[F(n_1,\dots ,n_k),z] = 1$;

• 2. $w,z \,\models \, (n_1 = n_2)$ iff $n_1$ and $n_2$ are identical;

• 3. $w,z \,\models \, \psi _1 \wedge \psi _2$ iff $w,z \,\models \, \psi _1$ and $w,z \,\models \, \psi _2$;

• 4. $w,z \,\models \, \lnot \psi$ iff $w,z \not \models \,\psi$;

• 5. $w,z \,\models \, \forall x.\phi$ iff $w,z \,\models \, \phi ^x_n$ for all $n \in \mathcal {N} _{x}$;

• 6. $w,z \,\models \, \Box \psi$ iff $w,z \cdot z' \,\models \, \psi$ for all $z' \in \mathcal {Z}$;

• 7. $w,z \,\models \, [t]\psi$ iff $w,z \cdot t \,\models \, \psi$.

Above, $\mathcal {N} _{x}$ refers to the set of all standard names of the same sort as x. We moreover use $\phi ^x_n$ to denote the result of simultaneously replacing all free occurrences of x in $\phi$ by n. Note that by rule 2 above, the unique names assumption for actions and object constants is part of our semantics. We understand $\vee , \exists , \supset , \equiv$ and $\top$ and $\bot$ as the usual abbreviations.

Definition 2

(Basic Action Theory). A basic action theory (BAT) $\mathcal {D} = \mathcal {D}_0 \cup \mathcal {D}_{\text {post}}$ is a set of axioms consisting of:

• 1. $\mathcal {D}_0$, the initial theory, a finite set of fluent sentences describing the initial state of the world;

• 2. $\mathcal {D}_{\text {post}}$ a finite set of successor state axioms (SSAs), one for each fluent relevant to the application domain, incorporating Reiter’s [43] solution to the frame problem, for encoding action effects. They have the form¹

  $$\begin{aligned} \Box [a] F(\mathbf {x}) \equiv \gamma _F^+ \vee F(\mathbf {x}) \wedge \lnot \gamma _F^-, \end{aligned}$$

  (1)

  where the positive (negative) effect condition $\gamma _F^+$ ($\gamma _F^-$) is a fluent formula with free variables a and $\mathbf {x}$.

Normally, BATs also feature action precondition axioms, which we ignore here for simplicity.

Example 1

For the aforementioned dish robot we may have

$$ \mathcal {D}_0 = \{ \lnot \exists x,y Dirty (x,y),~ \lnot \exists x OnRobot (x) \}. $$

Also, let $\mathcal {D}_{\text {post}}$ consist of the following SSAs (we abstract from the robot’s location for simplicity):

2.2 Golog Programs and Verification

The primitive actions defined in the BAT can be used as basic building blocks for Golog programs as follows.

Definition 3

A program $\delta$ is built according to the following grammar:

$$\begin{aligned} \delta \,::=\,t \mid \psi ? \mid \delta {;}\delta \mid \delta {|}\delta \mid {\delta }^* \mid \delta {|\!|}\delta . \end{aligned}$$

A program can thus be an action t, a test $\psi ?$ for some fluent formula $\psi$, or constructed from subprograms by means of sequence $\delta {;}\delta$, non-deterministic choice $\delta {|}\delta$, non-deterministic iteration ${\delta }^*$, and interleaving $\delta {|\!|}\delta$. We treat $\mathbf{if }$, $\mathbf{while }$, $\mathbf{loop }$ and the finitary non-deterministic choice of argument (“pick”) as abbreviations:

$$\begin{aligned} \mathbf{if }~\phi ~\mathbf{then }~\delta _1~\mathbf{else }~\delta _2~\mathbf{endIf }&{\mathop {=}\limits ^{def}}[\phi ? ; \delta _1] ~| ~ [\lnot \phi ? ; \delta _2]\\ \mathbf{while }~\phi ~\mathbf{do }~\delta ~\mathbf{endWhile }&{\mathop {=}\limits ^{def}}{[\phi ? ; \delta ]}^* ; \lnot \phi ? \\ \mathbf{loop }~\delta&{\mathop {=}\limits ^{def}}\mathbf{while }~\top ~ \mathbf{do }~\delta ~ \mathbf{endWhile }\\ \pi x \text{: } \{c_1,\dots ,c_k\}.~\delta&{\mathop {=}\limits ^{def}}\delta ^x_{c_1} ~| ~ \cdots ~| ~ \delta ^x_{c_k} \end{aligned}$$

An example for a program was presented in the introduction. Exogenous actions can be incorporated by having a loop that, in each cycle, executes one such action with non-deterministically chosen arguments

run concurrently with the actual control program $\delta _{ctl}$, i.e. in the verification one analyzes the behaviour of $\delta _{ctl}\,|\!| \,\delta _{exo}$.

Following [16] we define the transition semantics of programs meta-theoretically. A configuration $\langle z,\rho \rangle$ consists of an action sequence $z \in \mathcal {Z}$ (that has already been performed) and a program $\rho$ (that remains to be executed). Execution of a program in a world $w \in \mathcal {W}$ yields a transition relation $\xrightarrow {w}$ among configurations that is defined inductively over program expressions:

• 1. $\langle z,t \rangle \xrightarrow {w} \langle z \cdot t,\langle \rangle \rangle$;

• 2. $\langle z,\delta _1; \delta _2 \rangle \xrightarrow {w} \langle z \cdot t,\gamma ; \delta _2 \rangle$, if $\langle z,\delta _1 \rangle \xrightarrow {w} \langle z \cdot t,\gamma \rangle$;

• 3. $\langle z,\delta _1; \delta _2 \rangle \xrightarrow {w} \langle z \cdot t,\delta ' \rangle$, if $\langle z,\delta _1 \rangle \in \mathcal {F}^{w}$ and $\langle z,\delta _2 \rangle \xrightarrow {w} \langle z \cdot t,\delta ' \rangle$;

• 4. $\langle z,\delta _1| \delta _2 \rangle \xrightarrow {w} \langle z \cdot t,\delta ' \rangle$, if $\langle z,\delta _1 \rangle \xrightarrow {w} \langle z \cdot t,\delta ' \rangle$ or $\langle z,\delta _2 \rangle \xrightarrow {w} \langle z \cdot t,\delta ' \rangle$;

• 5. $\langle z,{\delta }^* \rangle \xrightarrow {w} \langle z \cdot t,\gamma ; {\delta }^* \rangle$, if $\langle z,\delta \rangle \xrightarrow {w} \langle z \cdot t,\gamma \rangle$;

• 6. $\langle z,\delta _1 |\!| \delta _2 \rangle \xrightarrow {w} \langle z \cdot t,\delta ' |\!| \delta _2 \rangle$, if $\langle z,\delta _1 \rangle \xrightarrow {w} \langle z \cdot t,\delta ' \rangle$;

• 7. $\langle z,\delta _1 |\!| \delta _2 \rangle \xrightarrow {w} \langle z \cdot t,\delta _1 |\!| \delta ' \rangle$, if $\langle z,\delta _2 \rangle \xrightarrow {w} \langle z \cdot t,\delta ' \rangle$.

For the set of final configurations $\mathcal {F}^{w}$ wrt. a world w we have:

• 1. $\langle z,\langle \rangle \rangle \in \mathcal {F}^{w}$;

• 2. $\langle z,\psi ? \rangle \in \mathcal {F}^{w}$, if $w,z \,\models \, \psi$;

• 3. $\langle z,\delta _1; \delta _2 \rangle \in \mathcal {F}^{w}$, if $\langle z,\delta _1 \rangle \in \mathcal {F}^{w}$ and $\langle z,\delta _2 \rangle \in \mathcal {F}^{w}$;

• 4. $\langle z,\delta _1| \delta _2 \rangle \in \mathcal {F}^{w}$, if $\langle z,\delta _1 \rangle \in \mathcal {F}^{w}$ or $\langle z,\delta _2 \rangle \in \mathcal {F}^{w}$;

• 5. $\langle z,{\delta }^* \rangle \in \mathcal {F}^{w}$;

• 6. $\langle z,\delta _1{\parallel }\delta _2 \rangle \in \mathcal {F}^{w}$, if $\langle z,\delta _1 \rangle \in \mathcal {F}^{w}$ and $\langle z,\delta _2 \rangle \in \mathcal {F}^{w}$.

Definition 4

(Transition System of a Program). Let $\delta$ be a program and $w \in \mathcal {W}$. Execution of $\delta$ in w yields the transition system wrt. $w,\delta$ given by ${\mathsf {T}^{w}_{\delta }} = \bigl ( \mathsf {S}, \rightarrow ),$ where the set of states $\mathsf {S} = \{\langle z',\delta ' \rangle ~|~ \langle {\langle \rangle },\delta \rangle \xrightarrow {w}{}\!\!^* \langle z',\delta ' \rangle \} \cup \{\mathfrak {e},\mathfrak {f} \}$ consists of configurations reachable from $\langle {\langle \rangle },\delta \rangle$ plus two special “sink” states for program termination and failure, and $\rightarrow$ is a transition relation such that $\mathsf {s} \rightarrow \mathsf {s} '$ iff one of the following holds:

• 1. $\mathsf {s} \xrightarrow {w} \mathsf {s} '$;

• 2. $\mathsf {s} ' = \mathfrak {e}$ and ($\mathsf {s} \in \mathcal {F}^{w}$ or $\mathsf {s} = \mathfrak {e}$);

• 3. $\mathsf {s} ' = \mathfrak {f}$ and (no $\mathsf {s} ''$ with $\mathsf {s} \xrightarrow {w} \mathsf {s} ''$ and $\mathsf {s} \not \in \mathcal {F}^{w}$ or $\mathsf {s} = \mathfrak {f}$).

Definition 5

(Temporal Properties of Programs). The syntax for temporal formulas is the same as for propositional $\textsc {CTL}^{*}$, but in place of propositions we allow fluent sentences $\psi$ in Boolean combinations with the special symbols $Succ$ and $Fail$ (for program termination and failure, respectively):

$$\begin{aligned} \varPsi&\,::=\, \psi \mid Succ \mid Fail \mid \lnot \varPsi \mid \varPsi \wedge \varPsi \mid \varvec{E}\varPhi \end{aligned}$$

(2)

$$\begin{aligned} \varPhi&\,::=\, \varPsi \mid \lnot \varPhi \mid \varPhi \wedge \varPhi \mid \varvec{X}\varPsi \mid \varPsi ~{\varvec{U}}~\varPsi \end{aligned}$$

(3)

Formulas according to (2) are temporal state formulas, and according to (3) temporal path formulas. We use the usual abbreviations ($\varPhi$ holds on all paths) for , (eventually $\varPhi$) for and (globally $\varPhi$) for .

Now let $\varPsi$ be a temporal state formula, ${\mathsf {T}^{w}_{\delta }}$ the transition system wrt. w, $\delta$, and $\mathsf {s} \in \mathsf {S}$. For an infinite path

$$ \pi = \mathsf {s} _0 \rightarrow \mathsf {s} _1 \rightarrow \mathsf {s} _2 \rightarrow \cdots $$

in ${\mathsf {T}^{w}_{\delta }}$, we denote for any $j \ge 0$ the state $\mathsf {s} _j$ by $\pi [j]$ and the suffix $\mathsf {s} _j \rightarrow \mathsf {s} _{j+1} \rightarrow \cdots$ by $\pi [j..]$. $\mathsf {Paths}(\mathsf {s},{\mathsf {T}^{w}_{\delta }})$ denotes the set of all paths starting in $\mathsf {s}$. Truth of $\varPsi$ in ${\mathsf {T}^{w}_{\delta }}, \mathsf {s}$ (written ${\mathsf {T}^{w}_{\delta }}, \mathsf {s} \,\models \, \varPsi$) is given by:

• ${\mathsf {T}^{w}_{\delta }}, \mathsf {s} \,\models \, \psi$ iff $\mathsf {s} = \langle z',\delta ' \rangle$ and $w,z' \,\models \, \psi$;

• ${\mathsf {T}^{w}_{\delta }}, \mathsf {s} \,\models \, Succ$ iff $\mathsf {s} = \mathfrak {e}$;

• ${\mathsf {T}^{w}_{\delta }}, \mathsf {s} \,\models \, Fail$ iff $\mathsf {s} = \mathfrak {f}$;

• ${\mathsf {T}^{w}_{\delta }}, \mathsf {s} \,\models \, \lnot \varPsi$ iff ${\mathsf {T}^{w}_{\delta }}, \mathsf {s} \not \models \,\varPsi$;

• ${\mathsf {T}^{w}_{\delta }}, \mathsf {s} \,\models \, \varPsi _1 \wedge \varPsi _2$ iff ${\mathsf {T}^{w}_{\delta }}, \mathsf {s} \,\models \, \varPsi _1$ and ${\mathsf {T}^{w}_{\delta }}, \mathsf {s} \,\models \, \varPsi _2$;

• iff $\pi \in \mathsf {Paths}(\mathsf {s},{\mathsf {T}^{w}_{\delta }})$ with ${\mathsf {T}^{w}_{\delta }}, \pi \,\models \, \varPhi$.

Let $\varPhi$ be a temporal path formula, ${\mathsf {T}^{w}_{\delta }}$ and $\mathsf {s}$ as above, and $\pi \in \mathsf {Paths}(\mathsf {s},{\mathsf {T}^{w}_{\delta }})$. Truth of $\varPhi$ in ${\mathsf {T}^{w}_{\delta }}, \pi$ (written ${\mathsf {T}^{w}_{\delta }}, \pi \,\models \, \varPhi$) is given by:

• ${\mathsf {T}^{w}_{\delta }}, \pi \,\models \, \varPsi$ iff ${\mathsf {T}^{w}_{\delta }}, \pi [0] \,\models \, \varPsi$;

• ${\mathsf {T}^{w}_{\delta }}, \pi \,\models \, \lnot \varPhi$ iff ${\mathsf {T}^{w}_{\delta }}, \pi \not \models \,\varPhi$;

• ${\mathsf {T}^{w}_{\delta }}, \pi \,\models \, \varPhi _1 \wedge \varPhi _2$ iff ${\mathsf {T}^{w}_{\delta }}, \pi \,\models \, \varPhi _1$ and ${\mathsf {T}^{w}_{\delta }}, \pi \,\models \, \varPhi _2$;

• iff ${\mathsf {T}^{w}_{\delta }}, \pi [1..] \,\models \, \varPhi$;

• iff $\exists k \ge 0 : {\mathsf {T}^{w}_{\delta }}, \pi [k..] \,\models \,\varPhi _2$ and $\forall j, 0 \le j < k : {\mathsf {T}^{w}_{\delta }}, \pi [j..] \models \, \varPhi _1$.

The sink states $\mathfrak {e}$, $\mathfrak {f}$ and the corresponding special symbols $Succ$, $Fail$ allow us to treat terminating programs simply as special cases of non-terminating ones, where once a program terminates successfully or due to failure, the program will indefinitely loop through $\mathfrak {e}$ or $\mathfrak {f}$, respectively. Furthermore, we can analyze the termination behaviour of a program simply by verifying appropriate temporal properties, e.g.  (the program is guaranteed to terminate) or (the program may fail).

Example 2

Some temporal properties for the (non-terminating) dish robot are:

In the following, we will use a restricted subset of temporal formulas that resembles $\textsc {CTL}$ without nesting of path quantifiers (but still with fluent sentences instead of propositions):

$$\begin{aligned} \varphi&\,::= \, \psi \mid Succ \mid Fail \mid \lnot \varphi \mid \varphi \wedge \varphi \end{aligned}$$

(4)

$$\begin{aligned} \varPsi&\,::=\, \varphi \mid \lnot \varPsi \mid \varPsi \wedge \varPsi \mid \varvec{E}\varvec{X}\varphi \mid \varvec{E}\varvec{G}\varphi \mid \varvec{E}(\varphi ~{\varvec{U}}~\varphi ) \end{aligned}$$

(5)

$\textsc {CTL}$ formulas according to (5) are obviously a subset of temporal state formulas. Note that the properties from Example 2 are all part of this subset using .

Definition 6

(Verification Problem). A temporal state formula $\varPsi$ is valid in a program $\delta$ for a BAT $\mathcal {D}$ iff for all worlds $w \in \mathcal {W}$ with $w \,\models \, \mathcal {D}$ it holds that ${\mathsf {T}^{w}_{\delta }}, \langle {\langle \rangle },\delta \rangle \,\models \, \varPsi$.

3 Verification by Fixpoint Computation

The first approach [13, 16, 17] is inspired by classical symbolic model checking [41] in the sense that a systematic exploration of the state space is made using a fixpoint computation of preimages of state sets, however now involving first-order reasoning about actions. For this purpose, an $\mathcal E\! S$ variant [31] of Reiter’s [43] regression operator is employed, which replaces fluent atoms in the scope of a [t] by the right-hand side of the corresponding SSA:

Definition 7

(Regression). Let $\psi$ be a bounded formula. We define ${\mathcal R} [\psi ] = {\mathcal R} [{\langle \rangle },\psi ]$, where for any $z \in \mathcal {Z}$,

• 1. ${\mathcal R} [{\langle \rangle },F(\mathbf {t})] = F(\mathbf {t})$ and ${\mathcal R} [z \cdot t,F(\mathbf {t})] = {(\gamma _F^+ \vee F(\mathbf {x}) \wedge \lnot \gamma _F^-)}^{\mathbf {x}~a}_{\mathbf {t}\,~t}$;

• 2. ${\mathcal R} [z,(t_1 = t_2)] = (t_1 = t_2)$;

• 3. ${\mathcal R} [z,\psi _1 \wedge \psi _2] = {\mathcal R} [z,\psi _1] \wedge {\mathcal R} [z,\psi _2]$;

• 4. ${\mathcal R} [z,\lnot \psi ] = \lnot {\mathcal R} [z,\psi ]$;

• 5. ${\mathcal R} [z,\forall x \psi ] = \forall x {\mathcal R} [z,\psi ]$;

• 6. ${\mathcal R} [z,[t]\psi ] = {\mathcal R} [z \cdot t,\psi ]$.

Theorem 1

If $\mathcal {D}$ is a BAT and $\psi$ a bounded formula, then $\mathcal {D} \,\models \,\Box (\psi \equiv {\mathcal R} [\psi ])$.

${\mathcal R} [\psi ]$ is hence equivalent to the original $\psi$ wrt. $\mathcal {D}$, but contains no $[\cdot ]$ and only talks about the initial (current) situation.

Fig. 1.

Characteristic graph for the dish-cleaning robot

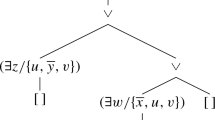
In addition to regression, another ingredient for the verification method are characteristic graphs, which are used to encode the reachable subprogram configurations. For any program $\delta$, the graph $\mathcal {G} _{\delta } = \langle V,E,v_0 \rangle$ consists of a set of vertices V, each of which corresponds to one reachable subprogram $\delta '$, or $\mathfrak {e}$ or $\mathfrak {f}$. The initial node $v_0$ corresponds to the overall program $\delta$. Edges E are labelled with tuples $t/\psi$, where t is an action term and $\psi$ a fluent formula (omitted when $\top$) denoting the condition required to take that transition. We omit the formal definition; the interested reader is referred to [13]. As an example, Fig. 1 shows the graph for the control program of the dish robot as presented in the introduction, assuming that the $Room$ domain only contains a single $room$. The asterisks in edge annotations such as $newdish (*, room )$ indicates that there is one such edge instance for every element in the $Dish$ domain. (Graphs for programs where the $Room$ domain is larger contain one “copy” of node $v_1$ for each room, with similar connections to $v_0$ and itself.) The algorithm uses a set of labels $\langle v,\psi \rangle$, one for each node $v \in V$, where $\psi$ is a fluent formula. Intuitively, if $v = \delta '$, then $\langle v,\psi \rangle$ represents all combinations of worlds w and configurations $\langle z,\delta \rangle$ with $w,z \,\models \, \psi$. Below is the procedure for formulas of form , similar ones exist for and [13]:

That is to say first the “old” labelling $L'$ is initialized to label every node with $\bot$ and the “current” labelling L marks every vertex with $\phi$. While L and $L'$ are not equivalent ($\psi \equiv \psi '$ for every $\langle v,\psi \rangle \in L$, $\langle v,\psi ' \rangle \in L'$), L is conjoined according to

$$\begin{aligned}&L_1~{\textsc {And}}~L_2 {\mathop {=}\limits ^{def}}\{ \langle v,\psi _1 \wedge \psi _2 \rangle ~|~ \langle v,\psi _1 \rangle \in L_1 \hbox {,~} \langle v,\psi _2 \rangle \in L_2 \} \end{aligned}$$

with its pre-image

$$\begin{aligned}&{\textsc {Pre}} [\langle V,E,v_0 \rangle ,L] {\mathop {=}\limits ^{def}}\{\langle v,{\textsc {Pre}} [v,L] \rangle ~|~ v \in V\} \end{aligned}$$

where ${\textsc {Pre}} [v,L]$ stands for

$$\begin{aligned} \bigvee ~ \{{\mathcal R} [\phi \wedge [t]\psi ] ~|~ v \xrightarrow {t/\phi } v' \in E,~ \langle v',\psi \rangle \in L\}. \end{aligned}$$

Note the use of regression to eliminate the action term t. Once the label set has converged, the method returns ${\textsc {InitLabel}} [\mathcal {G} _{\delta },L]$, the label formula at the initial node $v_0$. The algorithm is sound as follows:

Theorem 2

Let $\mathcal {D}$ be a BAT, $\delta$ a program, and $\phi$ a fluent formula. If the procedure terminates, then $\psi := {\textsc {CheckEG}} [\delta ,\phi ]$ is a fluent formula and is valid in $\delta$ for $\mathcal {D}$ iff $\mathcal {D}_0 \,\models \, \psi$.

Example 3

Suppose we want to verify whether a run of the program for the dish robot presented in the introduction (including possible exogenous actions) is possible where there is always some dirty dish x in some room y, i.e. whether it satisfies property . We hence call Procedure 1 with $\delta = \delta _{ctl}\,|\!| \,\delta _{exo}$ being the overall program and the axiom $\phi = \exists x,y Dirty (x,y)$. It starts with the following label set L:

$$L_0 = \{\langle v_0, \exists x,y\, Dirty (x,y)\rangle ,~ \langle v_1, \exists x,y\, Dirty (x,y)\rangle \}.$$

For determining the pre-image for a node in the characteristic graph, each of its outgoing edges has to be considered. Recall that we have multiple instances of each $newdish ( d _i, room )$ with different dishes $d _i$. One of the disjuncts of ${\textsc {Pre}} [v_0,L_0]$ thus is

$$\begin{aligned} {\mathcal R} [[ newdish ( d _1, room )]\exists x,y\, Dirty (x,y)] \end{aligned}$$

which (using unique names of actions) reduces to

$$\begin{aligned} \exists x,y.~ x= d _1 \vee Dirty (x,y). \end{aligned}$$

Using similar reductions for the other edges we get ${\textsc {Pre}} [v_0,L_0]$ and ${\textsc {Pre}} [v_1,L_0]$ both being equivalent to

if there are two dishes in total. Then $L_1 = \big ( L_0~{\textsc {And}}~{\textsc {Pre}} [\mathcal {G} _{\delta },L_0] \big )$, which reduces to

$$ \{\langle v_0, \exists x,y\, Dirty (x,y)\rangle , \langle v_1, \exists x,y\, Dirty (x,y)\rangle \} $$

Hence $L_0\equiv L_1$, i.e. the algorithm terminates and returns $\exists x,y\, Dirty (x,y)$. Thus, there is a run where there is always some dirty dish just in case there is some dirty dish somewhere initially. Intuitively, this is correct because means that $\phi$ persists to hold during the entire run, including the initial situation. Therefore, only if a dish is dirty initially it may happen that never all of them get cleaned. All we have to do now is to check whether $\mathcal {D}_0 \,\models \, \exists x,y\, Dirty (x,y)\rangle$, which is not the case according to the $\mathcal {D}_0$ from Example 1.

Naturally, the next interesting question is under what circumstances it can be guaranteed that the procedure terminates as it did here, thus rendering the verification problem decidable. As first-order logic is already undecidable, the first step is to ensure that the basic, first-order reasoning tasks of checking the equivalence of label formulas and whether the output of ${\textsc {CheckEG}} [\delta ,\phi ]$ is entailed by the BAT’s initial theory can be decided. We do so restricting the base logic to $\textsc {FO}^2$, the two-variable fragment of FOL. We hence require that

• fluents have at most two arguments;

• $\mathcal {D}_0$, tests $\phi ?$ in the program $\delta$ as well as axioms $\psi$ in temporal properties $\varPsi$ are formulas where x and y are the only variable symbols;

• the instantiations of $\gamma _F^+$ and $\gamma _F^-$ by any ground action from $\delta$ are formulas where x and y are the only variable symbols.

Note that in this paper we assume all actions in a program are ground (our definition of Golog does not include the general nondeterministic choice of argument $\pi$, but a finitary version where each $\pi$ only ranges over some finite domain). It can be shown [51] by means of a reduction of the Halting Problem for Turing Machines that otherwise, the Golog Verification Problem remains undecidable, even under all other restrictions we discuss here. The BAT from Example 1 and the properties from Example 2 all fulfill these requirements.

While there are other decidable fragments of first-order predicate calculus, note that not all are equally suited for our purposes. In particular, decidable quantifier prefix fragments for instance have the disadvantage that they are not closed under regression, i.e. the regression of such a formula may not be expressable by a formula in the same fragment. This is the case for $\textsc {FO}^2$ on the other hand, provided that the regression operator is slightly modified to rename variables where needed [26]. Moreover, note that the $\textsc {FO}^2$ fragment subsumes many Description Logics, so its choice paves the way for a method where representation and reasoning is handled entirely within a DL.

Now that we restricted the base logic and the class of programs we consider, the last restriction is on the range of action effects we allow. Again, it can be shown that without any such restriction, verification remains undecidable [51]. A popular subclass of action theories (originally studied within the context of progression) is that where actions only have local effects [37]:

Definition 8

(Local-Effect). An SSA is local-effect if the conditions $\gamma _F^+$ and $\gamma _F^-$ are disjunctions of formulas $\exists \mathbf {z} [a=A(\mathbf {y}) \wedge \phi ]$, where A is an action function, $\mathbf {y}$ contains $\mathbf {x}$, $\mathbf {z}$ are the remaining variables of $\mathbf {y}$, and $\phi$ is a fluent formula with free variables $\mathbf {y}$. A BAT is local-effect if all its SSAs are.

Intuitively, an action $A(\mathbf {c})$ is local-effect if it only changes fluents $F(\mathbf {d})$ all of whose arguments $\mathbf {d}$ are among the action’s parameters $\mathbf {c}$, i.e. all objects affected have to be mentioned in the action. Note that the SSAs in Example 1 are local-effect. In [17] it was shown that under these assumptions, the verification procedure becomes complete:

Theorem 3

The procedure ${\textsc {CheckEG}} [\delta ,\phi ]$ terminates if the BAT is local-effect and $\textsc {FO}^2$ is used as base logic.

There are similar theorems for the other cases and .

4 Verification by Abstraction

The second method we consider is verification by abstraction. Zarrieß and Claßen [52] show that for a Golog program $\delta$ with a local-effect BAT $\mathcal {D}$, the verification of a temporal formula $\varPsi$ can be reduced to classical model checking by constructing a finite, bisimilar abstraction of the original infinite transition system induced by $\delta$ and $\mathcal {D}$ wrt. $\varPsi$. This is achieved by identifying finitely many equivalence classes for worlds, whose computation reduces to consistency checks in the underlying decidable base logic $\textsc {FO}^2$.

4.1 Regression with Sets of Effects

The first ingredient is the observation that by unique names of actions, the instantiation of a local-effect SSA on a ground action $t = A(\mathbf {c})$ can be significantly simplified [38], as any ${\gamma _F^+}^a_t$ or ${\gamma _F^-}^a_t$ is equivalent to

$$ \mathbf {x} = \mathbf {c}_1 \wedge \phi _1 \vee \cdots \vee \mathbf {x} = \mathbf {c}_n \wedge \phi _n $$

where $\mathbf {c}_i$ is a vector of names contained in $\mathbf {c}$, and $\phi _i$ is a quantifier-free sentence. We use the notation $(\mathbf {c}_i,\phi _i) \in {\gamma ^+_F}^a_t$ and $(\mathbf {c}_i,\phi _i) \in {\gamma ^-_F}^a_t$ to express that there is a disjunct of the form $\mathbf {x} = \mathbf {c}_i \wedge \phi _i$ in ${\gamma ^+_F}^a_t$ or ${\gamma ^-_F}^a_t$, respectively. Let $\mathsf {L}$ be the set of all positive and negative ground fluent literals:

$$ \begin{aligned} \mathsf {L} = \{ F(\mathbf {c}), \lnot F(\mathbf {c}) \,\mid \,&t \in \delta :\, (\mathbf {c},\phi ) \in {\gamma ^+_F}^a_t \text { or } (\mathbf {c},\phi ) \in {\gamma ^-_F}^a_t \} \end{aligned} $$

One can then define a variant of regression wrt. an effect set, given a consistent set of fluent literals and a fluent sentence.

Definition 9

(Regression with Effects). If $F(\mathbf {v})$ is a fluent atom where $\mathbf {v}$ is a vector of variables or constants, and $E \subseteq \mathsf {L}$ a consistent set of fluent literals, then the regression of $F(\mathbf {v})$ through E, written as ${\mathcal R} [E,F(\mathbf {v})]$ is given by:

$$ {\mathcal R} [E,F(\mathbf {v})] = \biggl ( F(\mathbf {v}) \wedge \bigwedge _{\lnot F(\mathbf {c}) \in E} (\mathbf {v} \not = \mathbf {c}) \biggr ) \vee \bigvee _{F(\mathbf {c}) \in E} (\mathbf {v} = \mathbf {c}) $$

For any fluent sentence $\alpha$, ${\mathcal R} [E,\alpha ]$ denotes the result of replacing any occurrence of a fluent $F(\mathbf {v})$ by ${\mathcal R} [E,F(\mathbf {v})]$.

Example 4

For the dish robot, the ground actions to consider are all instances of $newdish (*, room )$, $unload (*)$, $load (*, room )$, $goto ( room )$, and $goto ( kitchen )$. For $t = newdish ( d _1, room )$ we have:

$$ \begin{aligned} {\gamma _{ Dirty }^+}^a_t&= (x = d _1 \wedge y = room )\\ {\gamma _{ Dirty }^-}^a_t&= \bot \end{aligned} $$

The literals that are possible effects of the ground actions hence are:

$$ \begin{aligned} \mathsf {L} = ~\{~&(\lnot ) Dirty ( d _1, room ),\, (\lnot ) Dirty ( d _2, room ),\,\\ {}&(\lnot ) OnRobot ( d _1),\, (\lnot ) OnRobot ( d _2) ~\} \end{aligned} $$

Let $E = \{ Dirty ( d _1, room )\}$. Then for example,

$$ {\mathcal R} [E, \lnot \exists x,y\, Dirty (x,y)] = \exists x,y\, \lnot \big ( Dirty (x,y) \vee (x = d _1 \wedge y = room ) \big ) $$

Clearly, the regression result ${\mathcal R} [E,\alpha ]$ is again a fluent sentence. We note that an iterated application of the regression operator can be reduced to an application of the operator for a single set of fluent literals. For a set $E \subseteq \mathsf {L}$ we define $\lnot E := \{ \lnot l \mid l \in E \}$ (modulo double negation). For two consistent subsets $E,E'$ of $\mathsf {L}$ and a sentence $\alpha$ it holds that

$$\begin{aligned} {\mathcal R} [E,{\mathcal R} [E',\alpha ]] \equiv {\mathcal R} [(E \setminus \lnot E' \cup E'),\alpha ]. \end{aligned}$$

(6)

The idea is that any such set of literals then represents a class of action sequences that all bring about the same set of accumulated effects.

4.2 Finite Abstraction

To construct the abstract transition system, we identify the context $\mathcal {C}(\mathcal {D},\delta )$, the set of all relevant fluent sentences

• in the initial theory $\mathcal {D}_0$;

• in all tests $\psi ?$ occurring in the program $\delta$;

• all $\phi$ with $(\mathbf {c},\phi ) \in {\gamma ^+_F}^a_t$ or $(\mathbf {c},\phi ) \in {\gamma ^-_F}^a_t$ for some t in $\delta$;

• all $F(\mathbf {c})$ with $(\mathbf {c},\phi ) \in {\gamma ^+_F}^a_t$ or $(\mathbf {c},\phi ) \in {\gamma ^-_F}^a_t$ for some t in $\delta$;

• all axioms occurring in temporal properties.

Furthermore, $\mathcal {C}(\mathcal {D},\delta )$ is assumed to be closed under negation. Intuitively, worlds satisfying the same maximal consistent set of context formulas are considered to be members of the same equivalence class, called a type. To incorporate actions, also the regressions of these formulas wrt. all consistent $E' \subseteq \mathsf {L}$ have to be taken into account. States belonging to the same equivalence class can be shown to simulate one another, i.e. they are indistinguishable through temporal properties. This bisimulation justifies the construction of the corresponding quotient system as an abstraction, which can be obtained as follows. Abstract states are tuples $\langle v,\,\varGamma ,\,E \rangle$, where v is a node of the characteristic graph of $\delta$, $\varGamma$ is a consistent set of (regressed) context formulas representing worlds, and $E \subseteq \mathsf {L}$ is a consistent set of accumulated effects representing situations. There is a transition $\langle v,\,\varGamma ,\,E \rangle {\mathop {\rightarrow }\limits ^{t}} \langle v',\,\varGamma ,\,E' \rangle$ between abstract states in case

• 1. there is an edge $v \xrightarrow {t/\psi } v'$ in $\delta$’s characteristic graph,

• 2. $\varGamma \,\models \,{\mathcal R} [E,\psi ]$, and

• 3. $E' = (E \setminus \lnot E^* \cup E^*)$, where $E^* = \mathcal {E}(\varGamma ,E,t)$.

Above, $\mathcal {E}(\varGamma ,E,t)$ denotes the set of effects induced by action t wrt. the type given by $\varGamma$ and E:

$$ \begin{aligned} \mathcal {E}(\varGamma ,E,t) \,=\,&\{ {\quad } F(\mathbf {c}) \mid (\mathbf {c},\phi ) \in {\gamma ^+_F}^a_t,\, \varGamma \,\models \, {\mathcal R} [E,\phi ] \}\ \cup \\&\{ \lnot F(\mathbf {c}) \mid (\mathbf {c},\phi ) \in {\gamma ^-_F}^a_t,\, \varGamma \,\models \, {\mathcal R} [E,F(\mathbf {c}) \wedge \phi ] \} \end{aligned} $$

Example 5

In our running example, the relevant fluent sentences are

One possible type (in fact the only one consistent with the initial theory of the BAT from Example 1) is given by

$$ \varGamma _0 = \{\lnot \exists x,y\, Dirty (x,y),\, \lnot \exists x\, OnRobot (x) \} $$

One abstract state is

$$ \mathsf {s} _1 = \langle v_0,\varGamma _0,\{ Dirty ( d _1, room )\} \rangle , $$

which intuitively represents any configuration where the overall program $\delta = \delta _{ctl}\,|\!| \,\delta _{exo}$ remains to be executed, whose initial situation was as described by $\mathcal {D}_0$, and where a sequence of actions has been performed that caused $Dirty ( d _1, room )$ to come about (e.g. a single $newdish ( d _1, room )$, but also any sequence where other dirty dishes except $d _1$ have been removed already).

The characteristic graph depicted in Fig. 1 shows three kinds of outgoing edges for $v_0$, all of which correspond to potential transitions from $\mathsf {s} _1$. $newdish ( d _i, room )$ edges have no transition condition. Their effects are given by

$$ \mathcal {E}(\varGamma _0,\{ Dirty ( d _1, room )\}, newdish ( d _i, room )) = \{ Dirty ( d _i, room )\}, $$

hence we have $\mathsf {s} _1 \rightarrow \mathsf {s} _i$ for

$$ \mathsf {s} _i = \langle v_0,\varGamma _0,\{ Dirty ( d _1, room ), Dirty ( d _i, room )\} \rangle $$

(i.e. for $i=1$ we remain in $\mathsf {s} _1$). For any $unload ( d _i)$ edge, condition $\exists x OnRobot (x)$ regresses to

$$ {\mathcal R} [\{ Dirty ( d _1, room )\}, \exists x OnRobot (x)] = \exists x OnRobot (x) $$

(adding a dirty dish has no effect on whether the robot is holding something). Since , there is no $unload ( d _i)$ transition from $\mathsf {s} _1$. Finally, for the $goto ( room )$ edge, the transition condition similarly regresses to

$$ {\mathcal R} [\{ Dirty ( d _1, room )\}, \lnot \exists x OnRobot (x)] = \lnot \exists x OnRobot (x). $$

As $\varGamma _0 \,\models \, \lnot \exists x OnRobot (x)$, there is a transition $\mathsf {s} _1 \rightarrow \mathsf {s} _1'$ with

$$ \mathsf {s} _1' = \langle v_1,\varGamma _0,\{ Dirty ( d _1, room )\} \rangle . $$

Recall that in this simple encoding, $goto$ actions do not have any effect, i.e.

$$ \mathcal {E}(\varGamma _0,\{ Dirty ( d _1, room )\}, goto ( room )) = \emptyset . $$

There are only finitely many nodes in the characteristic graph, relevant fluent sentences, and ground fluent literals as effects. The abstract transition system is hence finite, and can be effectively computed due to the fact that the necessary consistency and entailment checks in $\textsc {FO}^2$ are all decidable.

Finally, we can replace every relevant fluent sentence with a propositional atom (both in abstract states and temporal properties) and then call a propositional $\textsc {CTL}$ model checker.

The complexity of this decision procedure is mainly determined by the complexity of consistency checks in $\textsc {FO}^2$, which we have to do for exponentially large knowledge bases. Knowledge base consistency in $\textsc {FO}^2$ is $\textsc {NexpTime}$-complete [25], so determining a single type can be done in $\textsc {N2ExpTime}$. It turns out that co-N2ExpTime is an upper bound for the overall complexity.

Theorem 4

The verification problem is decidable for a temporal state formula $\varPsi$, a program $\delta$ over ground actions and a local-effect BAT $\mathcal {D}$ in co-N2ExpTime.

5 Golog Programs over Description Logic Actions

Motivated by the idea of obtaining a decidable yet expressive fragment of the Situation Calculus, a first DL-based action formalism was introduced by Baader and his colleagues in [5]. Next, we briefly review some of the basic definitions of a simple formalism that we have used in [50, 54] to analyze the complexity of the verification problem in a DL-based setting. It is a bit different from the one in [5] but adopts its main ideas.

The expressive DL $\mathcal {ALC{}QI{}O}$, which can be viewed as a fragment of the two variable fragment of first-order logic with counting, is the underlying logic. It is used for representing an incomplete initial situation (ABox part of the KB), general domain knowledge (TBox) and for formulating pre-conditions and effect conditions of primitive actions by means of action descriptions.

The signature for describing complex concepts consists of pairwise disjoint sets of concept names $\mathsf {N_C}$ (unary predicates), role names $\mathsf {N_R}$ (binary predicates) and individual names $\mathsf {N_I}$. Several constructors can be used to form complex concepts from $A \in \mathsf {N_C}$, $s \in \mathsf {N_R} \cup \{ r^- \mid r \in \mathsf {N_R} \}$ (a role name or the inverse thereof), $a \in \mathsf {N_I}$ and $n \in \mathbb {N}$ as shown in the first two columns of Table 1. Fragments of $\mathcal {ALC{}QI{}O}$ are obtained by restricting the available constructors for building concepts. For example, the basic DL $\mathcal{A L C}$ is obtained by disallowing at-most and at-least restrictions (the letter $\mathcal {Q}$ in the name of the DL indicates that those restrictions are allowed), inverse roles ($\mathcal {I}$) and nominals ($\mathcal {O}$).

As usual, axioms are grouped in boxes. The TBox is a finite set of concept inclusions and the ABox a finite set of concept and role assertions as shown in the first two columns of Table 2.

The semantics is defined in terms of an interpretation $\mathcal {I} = (\varDelta _{\mathcal {I}},\cdot ^\mathcal {I})$, where $\varDelta _{\mathcal {I}}$ is the non-empty domain of $\mathcal {I}$, and $\cdot ^\mathcal {I}$ a function that maps concept names to subsets of the domain, role names to binary relations, individual names to elements, and is extended to complex concepts as shown in Table 1. Satisfaction of an axiom in an interpretation is defined as shown in Table 2. An interpretation $\mathcal {I}$ is a model of an ABox $\mathcal {A}$, a TBox $\mathcal {T}$ or a KB $\mathcal {K}$ iff all axioms in $\mathcal {A}$, $\mathcal {T}$ or $\mathcal {K}$, respectively, are satisfied in $\mathcal {I}$.

Obviously, a DL like $\mathcal {ALC{}QI{}O}$ is too inexpressive to formulate basic action theories as a whole like the ones in Definition 2. An alternative approach would be to take an axiomatization in form of a BAT and a program formulated in $\mathcal E\! S$ and restrict the formulas used for domain specific knowledge in the initial theory, the successor state axioms, and tests in the program to be $\mathcal {ALC{}QI{}O}$-axioms. However, for the DL-based formalism in [5] and its variants and successors, a different approach was taken which we briefly review below.

Table 1. Syntax and semantics of roles and concepts

Table 2. Syntax and semantics of axioms

The overall idea is not to axiomatise the meaning of actions using quantification, but introduce action descriptions meta-theoretically. The syntax is similar to planning languages like STRIPS or ADL: the domain designer explicitly provides a complete list of effects for each primitive action name. The semantics of an action is defined in terms of a transition relation between interpretations such that the frame assumption is respected. First, we define the syntax of an effect.

Definition 10

(Effect Description). Let $\mathcal {L}$ be a sub-DL of $\mathcal {ALC{}QI{}O}$ and let $A \in \mathsf {N_C}$, $r \in \mathsf {N_R}$ and $a,b \in \mathsf {N_I}$ and $\varphi$ an $\mathcal {L}$-axiom (or Boolean combination of axioms). An $\mathcal {L}$-effect description ($\mathcal {L}$-effect for short) has one of the following forms

where $\varphi$ is called effect condition. In case the effect condition $\varphi$ is a tautology like for example $\top \sqsubseteq \top$, the effect is called unconditional and is written without the effect condition.

For a set of effects and an interpretation, the corresponding updated interpretation is defined in a straightforward way.

Definition 11

(Interpretation Update). Let $\mathcal {I} = (\varDelta _{\mathcal {I}},\cdot ^\mathcal {I})$ be an interpretation and $\mathsf {E}$ a set of unconditional effects. The update of $\mathcal {I}$ with $\mathsf {E}$ is an interpretation denoted by ${\mathcal {I}}^{\mathsf {E}} = (\varDelta _{{{\mathcal {I}}^{\mathsf {E}}}},\cdot ^{{\mathcal {I}}^{\mathsf {E}}})$ and is defined as follows:

$$\begin{aligned}&\varDelta _{{{\mathcal {I}}^{\mathsf {E}}}} := \varDelta _{\mathcal {I}}; \\&A^{{\mathcal {I}}^{\mathsf {E}}} := A^\mathcal {I} \setminus \{ a^\mathcal {I} \mid {\langle A(a) \rangle }^- \in \mathsf {E} \} \cup \{ b^\mathcal {I} \mid {\langle A(b) \rangle }^+ \in \mathsf {E} \} \text { for all } A \in \mathsf {N_C}; \\&r^{{\mathcal {I}}^{\mathsf {E}}} := r^\mathcal {I} \setminus \{ (a^\mathcal {I},b^\mathcal {I}) \mid {\langle r(a,b) \rangle }^- \in \mathsf {E} \} \cup \{ (a^\mathcal {I},b^\mathcal {I}) \mid {\langle r(a,b) \rangle }^+ \in \mathsf {E} \} \text { for all } r\!\in \!\mathsf {N_R};\\&a^{{\mathcal {I}}^{\mathsf {E}}} := a^\mathcal {I} \text { for all } a \in \mathsf {N_I}. \end{aligned}$$

Let $\mathsf {E}$ be a set of (possibly conditional) effects. The update of $\mathcal {I}$ with $\mathsf {E}$, denoted by ${\mathcal {I}}^{\mathsf {E}}$, is given by the update

$$\begin{aligned} {\mathcal {I}}^{\mathsf {E} (\mathcal {I})} \text { with } \mathsf {E} (\mathcal {I}) := \{ \mathsf {l} \mid (\varphi \triangleright \mathsf {l} ) \in \mathsf {E},\, \mathcal {I} \,\models \, \varphi \}. \end{aligned}$$

An action theory in this setting just consists of an initial KB and a finite set of actions, each associated with a finite set of effects.

Definition 12

An $\mathcal {L}$-action theory $\varSigma$ is a tuple $\varSigma = (\mathcal {K},\mathsf {Act},\mathsf {Eff})$, where $\mathcal {K}$ is an $\mathcal {L}$-KB describing the initial state, $\mathsf {Act}$ is a finite set of action names, and for each $\alpha \in \mathsf {Act}$, the effects of$\,\,\alpha$, denoted by $\mathsf {Eff}(\alpha )$, is a finite set of $\mathcal {L}$-effects.

We can now extend the definition of an interpretation update to sequences of actions. Let $\mathcal {I}$ be an interpretation, $\varSigma = (\mathcal {K},\mathsf {Act},\mathsf {Eff})$ an action theory, and $\sigma \in \mathsf {Act}^*$ a sequence of action names. The update of $\mathcal {I}$ with $\sigma$ is an interpretation $\mathcal {I} ^\sigma$ defined by induction on the length of $\sigma$ as follows: $\mathcal {I} ^{\langle \rangle } := \mathcal {I}$ for the empty sequence and $\mathcal {I} ^{\sigma '\cdot \alpha } = {\mathcal {I} ^{\sigma '}}^{\mathsf {E}}$, where $\mathsf {E} = \mathsf {Eff}(\alpha )(\mathcal {I} ^{\sigma '})$.

Definition 13

The projection problem is a simple instance of the verification problem that can now be defined as follows. Let $\varSigma = (\mathcal {K},\mathsf {Act},\mathsf {Eff})$ be an action theory, $\sigma \in \mathsf {Act}^*$ a sequence of action names, and $\varrho$ an axiom. We say that $\varrho$ is true after doing $\sigma$ in $\varSigma$ iff for all models $\mathcal {I}$ of $\mathcal {K}$ we have that $\varrho$ is satisfied in $\mathcal {I} ^\sigma$.

For the formalism in [5] it was shown that the projection problem can be solved by a polynomial reduction to a standard KB consistency task. Thus, the complexity is the same as for standard reasoning.

As an example consider an action theory

$$\begin{aligned} \varSigma = (\mathcal {K} = \mathcal {A} \cup \mathcal {T}, \mathsf {Act} = \{ discon (d,p), turn\text {-}on (d) \},\mathsf {Eff}) \end{aligned}$$

for a domain with concept names $DishWasher$, $PowerSupply$, $On$ and a role name $connected$. The following concept assertions describe an initial situation involving individuals d and p:

$$\begin{aligned} \mathcal {A} = \{ d : \left( DishWasher \sqcap \exists connected . PowerSupply \right) ,\, p : PowerSupply \}. \end{aligned}$$

(7)

As a concept inclusion we can express that a dish washer that is powered on must be connected to some power supply:

$$\begin{aligned} \mathcal {T} = \{ DishWasher \sqcap On \sqsubseteq \exists connected . PowerSupply \}. \end{aligned}$$

(8)

We consider two actions $discon (d,p)$ (for disconnecting d and p) and $turn\text {-}on (d)$ with the following conditional effects:

$$\begin{aligned}&\mathsf {Eff}( turn\text {-}on (d)) := \{ \left( d : \left( \exists connected . PowerSupply \right) \right) \triangleright {\langle On (d) \rangle }^+ \}; \\&\mathsf {Eff}( discon (d,p)) := \{ \begin{aligned}&{\langle connected (d,p) \rangle }^-, \\&\left( d : \left( \forall connected . (\{ p \} \sqcup \lnot PowerSupply ) \right) \right) \triangleright {\langle On(d) \rangle }^- \}. \end{aligned} \end{aligned}$$

The action $turn\text {-}on (d)$ only is effective if d is connected to some power supply, and $discon (d,p)$ in addition to disconnecting d and p makes sure that d is no longer an instance of $On$ in case p was the only power supply connected to d before the disconnection. Note that the effect conditions make sure that axiom (8) is never violated due to an action execution.

It is rather straightforward to provide a Situation Calculus semantics for $\mathcal {ALC{}QI{}O}$-action theories. That is, for an action theory $\varSigma = (\mathcal {K},\mathsf {Act},\mathsf {Eff})$, sequence $\sigma \in \mathsf {Act}^*$, and axiom $\varrho$ as projection query, one can construct a corresponding basic action theory $\mathcal {D} _\varSigma$ such that $\varrho$ is true after doing $\sigma$ in $\varSigma$ iff the following entailment

$$\begin{aligned} \mathcal {D} _\varSigma \,\models _\mathcal{E\! S}\,[\sigma ] \mathsf {fol}(\varrho ), \end{aligned}$$

holds in $\mathcal E\! S$, where $\mathsf {fol}(\cdot )$ denotes the translation from DL syntax to FOL syntax. For instance, the effect condition of the delete effect ${\langle On(d) \rangle }^-$ of $discon (d,p)$ is equivalent to the FOL sentence

Since actions only affect named individuals in effect descriptions, the resulting BAT is one with only local effects. We can now describe Golog programs over Description Logic actions as follows.

Definition 14

The base logic $\mathcal {L}$ is a DL between $\mathcal{A L C}$ and $\mathcal {ALC{}QI{}O}$, and the initial knowledge and effects of atomic actions are described in an $\mathcal {L}$-action theory $\varSigma = (\mathcal {K},\mathsf {Act},\mathsf {Eff})$. A program expression $\delta$ over $\varSigma$ is obtained as in Definition 3 with the following restrictions for atomic actions and tests: we require $t \in \mathsf {Act}$ and that $\psi$ in a test $\psi ?$ is a Boolean combination of $\mathcal {L}$-axioms. We call $(\varSigma ,\delta )$ an program.

To describe properties of programs, $\textsc {CTL}^{*}$ temporal formulas over $\mathcal {L}$-axioms are used. Validity of a $\textsc {CTL}^{*}$ state formula over $\mathcal {L}$-axioms in an program is then defined according to Definitions 5 and 6. For the verification problem we have obtained the following tight complexity bounds:

Theorem 5

Let $(\varSigma ,\delta )$ be an program and $\varPsi$ a $\textsc {CTL}^{*}$ temporal state formula over $\mathcal {L}$-axioms. Checking validity is

• $2\textsc {ExpTime}$-complete if $\mathcal {L} \in \{ \mathcal{A L C O}, \mathcal {ALCI{}O}, \mathcal {ALC{}Q{}O} \}$, and

• co-N2ExpTime-complete if $\mathcal {L} = \mathcal {ALC{}QI{}O}$.

The upper bounds are obtained by using the abstraction technique described in Sect. 4. For more details and for the proofs of the lower bounds we refer to [50]. Note that in our formalism there is no direct interaction between the TBox that is part of the initial KB $\mathcal {K}$ and the transition semantics of actions and programs. It is possible that TBox axioms are violated in some program states, which might seem not desirable because usually TBox axioms are assumed to be global state constraints. However, the property that a global TBox is satisfied in all program states can be expressed as a $\textsc {CTL}^{*}$ formula, and the corresponding check is an instance of the verification problem. Different approaches with a tighter integration of TBox axioms as state constraints and action semantics have been investigated, for instance, in [3, 5, 36].

6 Further Results

The results summarized in the previous sections laid the foundation for extensions in various directions.

Knowledge-based programs, which are suited for more realistic scenarios where the agent possesses only incomplete information about its surroundings and has to use sensing in order to acquire additional knowledge at run-time, were considered in [53, 54]. As opposed to classical Golog, knowledge-based programs [15, 45] contain explicit references to the agent’s knowledge, thus enabling it to choose its course of action based on what it knows and does not know. The work introduces a new epistemic action formalism based on the basic Description Logic $\mathcal{A L C}$, obtained by combining and extending earlier proposals for DL action formalisms [5] and epistemic DLs [23]. It turned out that the corresponding verification problem is in general again undecidable in the presence of pick operators, even under severe restrictions on the knowledge base and actions. Decidability can however be obtained by syntactically limiting the domain of pick operators to contain named objects only, yielding a $2\textsc {ExpSpace}$ upper bound.

Actions with non-local effects were considered in [55], where two new classes of action theories are introduced that generalize the previously discussed local-effect ones. Instead of imposing any bound on the number of affected objects, decidability of verification is obtained by restricting certain dependencies between fluents in the successor state axioms. This allows for a much wider range of application domains, including classical examples such as the briefcase domain [42] and exploding a bomb [35]: When a briefcase is moved, all (unboundedly many, unmentioned) objects that are currently in it are being moved along, and if a bomb explodes, everything in its vicinity is destroyed.

Decision-theoretic Golog  (DTGolog) extends classical Golog by decision-theoretic aspects in the form of stochastic actions and reward functions [8, 48]. Here, a stochastic action refers to an operator that can have a limited number of possible outcomes, each of which is a regular, deterministic action with an associated probability. The program together with the action theory and reward function thus essentially induce an infinite-state Markov Decision Process (MDP), and the objective is to verify properties expressed in first-order variants of probabilistic temporal logics such as $\textsc {PCTL}$ [28] or $\textsc {PRCTL}$ [1]. Using similar techniques and restrictions as discussed above, Claßen and Zarrieß [18] showed that the infinite-state MDP can effectively be abstracted to a finite one, which then can be fed into any state-of-the-art probabilistic model checker such as PRISM [30] and STORM [22].

Probabilistic beliefs constitute a more involved notion of uncertainty. Instead of just having stochastic actions affect the objective truth of world-state fluents as above, an agent is now considered to have a certain probabilistic degree of belief. For such a setting, Zarrieß [49] studied the complexity of the projection problem, a subproblem of verification where one wants to determine whether a formula (here: about the agent’s probabilistic beliefs) is true after executing a given sequence of (here: stochastic) actions. He proposed a formalization where deterministic actions (the possible outcomes of stochastic ones) are once again described similar to [5], and where initial beliefs as well as queries refer to subjective probabilities applied to ABox facts and TBox statements formulated in the DL $\mathcal{A L C O}$, which can be seen as a member of the Prob-$\mathcal{A L C}$ family of probabilistic DLs [39] and is a decidable fragment of Halpern’s Type 2 probabilistic first-order logic [27]. It turned out that the combination of including both stochastic actions and probabilistic beliefs increases the complexity from $\textsc {ExpTime}$-complete to $2\textsc {ExpTime}$-complete, while the problem remains $\textsc {ExpTime}$-complete when only deterministic actions are used.

Timed Golog is a variant where instead of employing a qualitative notion of time, the more realistic assumption is made that actions may have a certain (discrete-time) duration. Consequently, verification is with respect to properties expressed in a metric temporal logic such as $\textsc {TCTL}^{*}$ [32]. Koopmann and Zarrieß [29] studied the complexity of verification under these assumptions over a DL representation of actions for various DLs in the $\mathcal{A L C}$ family as well as a lightweight DL. They were able to establish $2\text {-}\textsc {ExpTime}$-completeness for almost all variants, except for the case of full $\mathcal {ALC{}QI{}O}$ ($\mathcal{A L C}$ with qualified number restrictions, inverse roles, and nominals), which yields co-N2ExpTime-completeness. They also show that these tight complexity bounds apply for the non-metric, untimed case (cf. Theorem 4), and the corresponding abstraction techniques are indeed worst-case optimal.

A prototypical implementation of the methods from Sects. 3 and 4 was presented in [14], with the motivation that most results so far on Golog verification remained purely theoretical. In particular the very high worst-case complexities mentioned above are widely considered intractable, and hence may appear discouraging. On the other hand, experience from other areas (such as classical planning and SAT solving) is that in practical cases, most instances are comparatively easy to solve, and only few exhaust the full theoretical complexity. A prototype was hence implemented which uses a new Golog interpreter that supports full first-order reasoning by means of an embedded theorem prover [47]. One major challenge was that regression as is used by the fixpoint method causes a severe, exponential blow-up of formulas, and therefore – once again drawing inspiration from symbolic propositional model checking – a representation based on a first-order variant [46] of ordered binary decision diagrams [10] was used. A subsequent experimental evaluation showed that the fixpoint method is often preferable since it only explores parts of the state space that are relevant for the query property, while constructing a complete, bisimilar abstraction (which can be up to double-exponential in size) is often too expensive.

7 Conclusion

We presented an overview of our work on the temporal verification of Golog programs, both from a (modal) Situation Calculus and a Description Logic perspective. The problem can be approached in two different ways, namely by means of a Golog-specific fixpoint computation method based on characteristic program graphs and regression-based reasoning, or by determining a finite abstraction and applying a classical model checker. Golog’s high expressiveness renders the general verification problem highly undecidable, and so the main challenge has been to identify restrictions on the input formalism that yield decidable, yet non-trivial fragments.

Other groups of researchers have conducted work that complements ours. To name but a few, Li and Liu [34] also present a sound, but incomplete verification method based on first-order theorem proving, however addressing the (somewhat different) task of proving Hoare-style partial correctness of terminating Golog programs. De Giacomo et al. [20] study the class of theories that have an infinite overall domain of objects, but where fluent extensions in each situation are bounded, which also admits finite abstractions and thus renders temporal verification decidable. Achieving decidable projection through a Description Logic representation in the Situation Calculus is analyzed in depth by Gu and Soutchanski [26].

While through this work, we have gained a deeper understanding of the problem and possible approaches to it, many avenues for future work remain. Probably the most interesting, and also most challenging, are those that strive to advance the current state of the art further towards realistic applications in robotics (or cyber-physical systems in general), where representations of quantitative, dynamic, and probabilistic aspects are needed, and that, beyond what was presented above, require e.g. notions of continuous change, noisy sensing, and uncertain beliefs.