Keywords

1 Introduction

The technical level of the technological and transport equipment largely predetermines the technical and economic indicators of the mechanical drives contained in them. This explains the relevance of research aimed at improving existing types of engagement gearing and creating their fundamentally new modifications which are introduced in the paper.

1.1 Formulation of the Problem

Improving the technical level of gearing engagement is associated with a set of problems optimizing the design parameters of mechanisms [1,2,3,4], upgrading devices already used [5,6,7,8], modifying working surface shapes [9,10,11,12] and researching tribological factors in the contact zone [13,14,15,16]. This article presents the research material connected with using the conical surfaces as axoids for pinions and wheels with parallel axes of rotation proposed by the authors [17].

The task is to perform a comparison of some classical cylindrical gear geometric characteristics for involute gearing with chevron teeth (hereinafter referred to as CGCh) and its analog [17]—gear on parallel axes. The axoids of the considered gear are treated as cones with tangential teeth (hereinafter referred to as CGA). It is required to achieve the possibility of increasing the length of the gear teeth and wheel in gearbox transmission without changing the gear engagement width, which will give an advantage in terms of the load capacity of the gearbox in comparison with the CGCh transmission with other things being equal. There is a need to prove the possibility of increasing the load capacity of the CGA gearing by the main criterion—the contact endurance of the teeth, as compared with the existing type of gear on parallel axes—chevron gearing with the same overall dimensions and other conditions being equal.

2 Theoretical Part

  1. 1.

    Since the CGCh consists of two helical gears (hemi-chevron) with opposite teeth at the same angle of inclination, to calculate the length of the CGCh teeth we use the parametric equation of the helical teeth surface for the involute engagement [18].

    $$ \left\{ {\begin{array}{*{20}l} {x = r_{O1} \cdot \cos v + u \cdot \cos \beta_{O} \cdot \sin v;} \hfill \\ {y = r_{O1} \cdot \sin v - u \cdot \cos \beta_{O} \cdot \cos v;} \hfill \\ {z = P \cdot v - u \cdot \sin \beta_{O} .} \hfill \\ \end{array} } \right. $$
    (1)

    here, v—an independent variable that varies within \( [v_{1} ;v_{2} ] \); \( u,r_{O1} ,\beta_{O} ,P \)—constants; the coordinate z passes along the axis of gears rotation. The limits of variable v change are of the obvious condition: \( z = [0;b_{{W\Sigma }} ] \), where \( b_{{W\Sigma }} = 2 \cdot b_{W} \)—the width of the CGCh engagement gearing, equal to the width of the two hemi-chevrons \( b_{W} \), Fig. 1a. As a result,

    Fig. 1
    figure 1

    a Gear of CGCh; b gear of CGA

    Full size image
    $$ v = [v_{1} ;v_{2} ] = \left[ {u \cdot \frac{{\sin \beta_{O} }}{P};\quad \frac{{u \cdot \sin \beta_{O} + b_{{W\Sigma }} }}{P}} \right], $$
    (2)

    where \( \beta_{O} = \text{arctg}(r_{1} /r_{O1} \cdot \text{tg}\,\beta ) \)—the angle of the teeth on the base cylinder pinion CGCh; \( r_{1} = 0,5 \cdot m_{n} \cdot z_{1} /\cos \beta \) and \( r_{O1} = r_{1} \cdot \cos \alpha_{t} \)—the radii of the pitch and base pinion cylinders, respectively; \( \alpha_{t} = {\text{arctg}}({\text{tg}}\,\alpha_{n} /\cos \beta ) \)—face angle of the teeth profile on the pitch cylinder of the pinion, \( (\alpha_{n} = 20^{ \circ } ) \); β—slope angle of the teeth on the pitch cylinder pinion; \( P = r_{1} \cdot {\text{tg}}(\pi /2 - \beta ) \)—helix teeth parameter.

The parameter u that determines the position of a point on the pitch circle of the tooth surface (1) is found from the condition:

$$ \sqrt {x^{2} + y^{2} } = r_{1} . $$

After substituting the coordinates [x, y] from the system of equations (1), we get

$$ u = \frac{{m_{n} \cdot z_{1} }}{2} \cdot \frac{{\sin \alpha_{{_{t} }} }}{{\cos \beta \cdot \cos \beta_{O} }}, $$
(3)

where \( \alpha_{t} = {\text{arctg}}({\text{tg}}\,\alpha_{n} /{\text{tg}}\,\beta ) \)—the angle of the tooth profile on the pitch cylinder in the face section.

The joint consideration of dependencies (1) and (3) allows to determine the coordinates of the tooth longitudinal line on the hemi-chevron of the CGCh transmission (Fig. 1a), which is a helical cylindrical line. Its length L is

$$ L = \int\limits_{{v_{1} }}^{{v_{2} }} {\sqrt {\dot{x}_{v}^{2} + \dot{y}_{v}^{2} + \dot{z}_{v}^{2} } \cdot {\text{d}}v} , $$
(4)

where \( \dot{x}_{v} = {\text{d}}x/{\text{d}}v;\dot{y}_{v} = {\text{d}}y/{\text{d}}v;\dot{z}_{v} = {\text{d}}z/{\text{d}}v. \)

$$ \left\{ {\begin{array}{*{20}l} {\dot{x}_{v} = u \cdot \cos \beta_{O} \cdot \cos v - r_{O1} \cdot \sin v;} \hfill \\ {\dot{y}_{v} = u \cdot \cos \beta_{O} \cdot \sin v + r_{O1} \cdot \cos v;} \hfill \\ {\dot{z}_{v} = P.} \hfill \\ \end{array} } \right. $$
(5)

After integrating the function (4) with the substitution of derivatives (5) and the limits of integration (2) into it, we obtain

$$ L = \frac{{b_{W} }}{P} \cdot \sqrt {u^{2} \cdot \cos^{2} \beta_{O} + r_{O1}^{2} + P^{2} } . $$
(6)

For practical calculations, a simpler version of the dependency is proposed for calculating the length of the CGCh tooth (Fig. 1a):

$$ L^{{\prime }} = b_{{W\Sigma }} /\cos \beta $$
(7)

Calculations show that numerical values L and \( L^{{\prime }} \) differ by a fraction of a percent.

  1. 2.

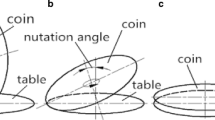
    Considering the limited volume of the article and the more cumbersome structure of analytical dependencies for the CGA surface of the teeth, we will calculate their length LK for the CGA pinion based on the following assumptions (Fig. 1b). The longitudinal direction of the tangential tooth on each hemi-chevron of the bevel gear is determined by the conical helix:

    $$ \left\{ {\begin{array}{*{20}l} {x = a \cdot v \cdot \cos v;} \hfill \\ {y = a \cdot v \cdot \sin v;} \hfill \\ {z = b \cdot v.} \hfill \\ \end{array} } \right. $$
    (8)

Therefore, the length of the tangential tooth can be considered as the length of the conical helix (8) on a truncated cone with dimensions:

  • \( r_{F1} = r_{m1} - 0,5 \cdot b_{W} \cdot {\text{tg}}\,\delta \)—radius of the smaller base of the cone, \( (r_{m1} = r_{1} ) \);

  • bW—the height of the truncated cone between its bases (coordinate z), equal to the width of one CGA hemi-chevron;

  • β—the angle between the tangent to the helix and generating line a cone;

  • δ—the angle between the generatrix of the cone and the axis z.

These parameters are given.

In the environment KOMPAS-3D, three-dimensional models of cylindrical gear transmission with chevron teeth (Fig. 2a) and gear transmission on parallel axes with gear axoids and wheels in the form of truncated cones on parallel axes (Fig. 2b) are developed. In this case, the “shafts and mechanical transmission” application included in the KOMPAS-3D [19,20,21,22].

Fig. 2
figure 2

a 3D model gear of CGCh; b 3D model gear of CGA

Full size image

When determining a helical cylindrical line, the following parameters are determined:

  • bW—the height of the truncated cone between its bases (coordinate z), equal to the width of one CGA hemi-chevron; β—the angle between the tangent to the helix and generating line a cone; δ—the angle between the generatrix of the cone and the axis z.

  • These parameters are given.

In contrast to bevel gears with intersecting axes of links in CGA gearing (Fig. 1b), the angles of the pitch cones of the pinion \( (\delta_{1} ) \) and the wheel \( (\delta_{2} ) \) are the same that is \( \delta_{1} = \delta_{2} = \delta \), and their numerical values are set independently of the gear ratio, but with one restriction:

$$ \delta \le {\text{arctg}}\left( {\frac{{r_{m1} - 3,5 \cdot \sqrt[3]{{T_{1} }}}}{{0,5 \cdot b_{W} }}} \right), $$
(9)

where \( T_{1} \)—the torque on the pinion shaft, N m; \( r_{m1} \)—the average pitch radius of the toothed hemi-chevron of the CGCh pinion, mm; (the size \( r_{m2} \) in Fig. 1b denotes the average pitch radius of the toothed hemi-chevron of the CGA wheel); \( b_{W} \)—in mm.

3 Experimental Part

The specified limitation for the angle β is aimed at preventing possible flanking of the pinion teeth on a smaller base of the cone with a radius \( r_{F1} \) (Fig. 1b) into the shaft body with a diameter \( {\text{d}}_{B} \), that is, for the realization of a constructive condition \( r_{F1} \ge {\text{d}}_{B} /2 \). We illustrate the constraint (9) as applied to the CGA, whose parameters are given in the numerical calculation of the function (13) given below in the article. Determine the values of the parameters included in the formula (9)

$$ r_{m1} = m_{\text{tm}} \cdot z_{1} /2 = 39.9\,{\text{mm}}, $$

where \( m_{\text{tm}} = m_{n} /\cos \beta = 4/\cos 17.82^\circ = 4.2 \)—the average face module CGA;

$$ T_{1} = \frac{{T_{2} }}{u \cdot \eta } = \frac{3097.8}{5.26 \cdot 0.97} = 607.1\,{\text{N}}\,{\text{m}}, $$

where \( u = \frac{{z_{2} }}{{z_{1} }} = \frac{100}{19} = 5.26 \) and \( \eta = 0.97 \), respectively, the gear ratio and the coefficient of performance for the CGA.

After substituting these parameters in condition (9), we obtain the restrictive value of the angle δ:

$$ \delta_{\hbox{max} } = {\text{arctg}}\left( {\frac{{39.9 - 3.5 \cdot \sqrt[3]{607.1}}}{0.5 \cdot 42}} \right) \approx 26^\circ . $$

Thus, for the CGA with the specified parameters, the pitch angle of the axoid cones of the pinion and wheels should be assigned with the restriction:

$$ \delta \le \delta_{\hbox{max} } = 26^\circ . $$

The length of the conical helix (8) is determined from the following dependence [20]:

Conical helix length:

$$ L_{K} = \int\limits_{{v_{1} }}^{{v_{2} }} {\sqrt {\dot{x}_{v}^{2} + \dot{y}_{v}^{2} + \dot{z}_{v}^{2} } \cdot {\text{d}}v} = \int\limits_{{v_{1} }}^{{v_{2} }} {\sqrt {a^{2} \cdot (v^{2} + 1) + b^{2} } \cdot {\text{d}}v} , $$
(10)

where

$$ \begin{aligned} \dot{x}_{v} & = {\text{d}}x/{\text{d}}v = a \cdot (\cos v - v \cdot \sin v); \\ \dot{y}_{v} & = {\text{d}}y/{\text{d}}v = a \cdot (\sin v + v \cdot \cos v); \\ \dot{z}_{v} & = {\text{d}}z/{\text{d}}v = b. \\ \end{aligned} $$

The limits of integration of the function (10) are determined by the parameters of the pinion axoid, that is, the truncated cone on which the conical helix (8) is located:

$$ \begin{aligned} v_{1} & = \frac{{{\text{tg}}\,\beta }}{\sin \delta }; \\ v_{2} & = v_{1} \cdot \left( {1 + \frac{{b_{W} }}{{r_{F1} }} \cdot {\text{tg}}\,\delta } \right) = \frac{{{\text{tg}}\,\beta }}{\sin \delta } \cdot \left( {1 + \frac{{b_{W} }}{{r_{F1} }} \cdot {\text{tg}}\,\delta } \right). \\ \end{aligned} $$
(11)

Constant values:

$$ a = r_{F1} \cdot \sin \delta /{\text{tg}}\,\beta ;\quad b = a/{\text{tg}}\,\delta = r_{F1} \cdot \cos \delta /{\text{tg}}\,\beta . $$
(12)

As a result,

$$ L_{K} = \left. {2 \cdot (L_{K2} - L_{K1} )} \right|_{{v_{1} }}^{{v_{2} }} , $$
(13)

where

$$ L_{K1,2} = \frac{{v_{1,2} }}{2} \cdot \sqrt {a^{2} \cdot (v_{1,2}^{2} + 1) + b^{2} } + \frac{{a^{2} + b^{2} }}{2 \cdot a} \cdot \ln \left[ {\sqrt {a^{2} \cdot (v_{1,2}^{2} + 1) + b^{2} } + v_{1,2} \cdot a} \right]. $$
(14)

The factor “2” in the formula (13) takes into account the fact that the pinion in the CGA transmission consists of two hemi-chevrons, that is, of two truncated cones, each of which has parameters \( [r_{F1} ,b_{W} ,\beta ,\delta ] \).

The calculations of function (13) show a nonlinear dependence \( L_{K} = L_{K} (\delta ) \). In Fig. 3 shows the graph of this function, built on the dependencies (8)–(13) for transmission with the parameters:

Fig. 3
figure 3

Lengths of teeth in CGCh (L) and CGA \( (L_{K} ) \)

Full size image
$$ a_{W} = 250\,{\text{mm}};\quad m_{n} = 4\,{\text{mm}};\quad z_{1} /z_{2} = 19/100;\quad \beta = 17.82^\circ ;\quad b_{W} = 42.5\,{\text{mm}}. $$

For comparison, Fig. 3 shows a graph of the CGCh teeth length with the same engagement parameters as in the transmission of the CGA. An increase in the length of CGA teeth in comparison with CGCh with their identical overall dimensions will lead to an increase in the load capacity of CGA for bending and contact endurance of the teeth.

The increase in the teeth length of the CGA compared with the CGCh is from 5.3% at \( \delta = 15^{ \circ } \) up to 65% at \( \delta = 45^{ \circ } \). For a preliminary assessment of the reduction of contact stresses in the teeth during the transition from the CGCh transmission to the CGA transmission, we use the Hertz dependence for the linear contact of two surfaces [19]. With other things being equal, contact stresses in CGA and CGCh are connected by the relation:

$$ \sigma_{H(K)} /\sigma_{H} = \sqrt {L/L_{(K)} } . $$

For the specified gains \( L_{K} \), we get

$$ \sigma_{H(K)} /\sigma_{H} = \left\{ {\begin{array}{*{20}l} {0.97 - {\text{for}}\,\delta = 15^\circ ;} \hfill \\ {0.8 - {\text{for}}\,\delta = 45^\circ .} \hfill \\ \end{array} } \right. $$

That is the reduction of contact stresses in the CGA as compared with the CGCh is from 3 to 20%. It is obvious that for a more significant reduction, it is advisable to take large values of the axoids angle, but taking into account the restrictive condition (9).

  1. 3.

    Pinion 1 CGA transmission performed together with the shaft. Wheel CGA is an assembly unit consisting of two wheels—2 and 3, each of which has tangential teeth. Conical semi-chevrons mounted on the centers and bolted to them. In order to exclude vibrations when the transmission is in operation, the semi-chevrons should be centered in three directions:

  • radial—due to the interference fit of rims on the centers;

  • axial—with the help of a shim gasket;

  • circumferential—by means of annular grooves in which fastening bolts are placed (in Fig. 2, only the teeth rims of the hemi-chevrons are depicted, and the centers on which they are mounted with the help of bolts, annular grooves and shim gasket are not shown.

Wheels 2 and 3, bolted 4 and centered in three directions:

  • radial—by fit on the bead diameter \( D_{6} H_{7} /m_{6} \);

  • axial—using the shim 5;

  • circumferential—through the annular grooves in which the bolts 4 are placed.

  1. 4.

    The following calculation algorithm is recommended for the design of the CGA transmission.

  2. 4.1.

    The allowable stresses, as well as the design calculation, in which the axial distance \( a_{W} \) and the main engagement parameters \( m_{n} ,b_{W} ,\beta ,z_{1} ,z_{2} \) of the condition of the teeth contact endurance are performed according to the existing design of cylindrical helical transmission [23] (here, \( m_{n} \)—the average normal engagement modulus used in the calculations of modern bevel gears).

  3. 4.2.

    The angle of the pitch cones of the pinion and the wheel \( \delta \approx 30^\circ \ldots 60^\circ \) is assigned, taking into account the obtained limitation—formula (9). To accept the numerical value of the angle, the average face module \( m_{tm} = m_{nm} \cos \beta \) is preliminarily calculated, along which the average pitch diameters of the pinion and wheel are \( r_{m1} = m_{tm} \cdot z_{1} /2;r_{m2} = m_{tm} \cdot z_{2} /2 \) (wherein \( r_{m1} + r_{m2} = r_{1} + r_{2} = a_{w} \)).

  4. 4.3.

    Tests for contact points \( (\sigma_{H} ) \) and bending \( (\sigma_{F1} ,\sigma_{F2} ) \) stresses are carried out using the existing method of calculating cylindrical helical gears [23, 24] with one difference—calculations \( \sigma_{F1} \) and \( \sigma_{F2} \) are carried out using tooth shape factors \( Y_{F1} \) and \( Y_{F2} \) according to the graph [23] or table depending on biequivalent numbers of CGA pinion teeth and wheel teeth: \( z_{Vni} = z_{i} /(\cos^{3} \beta \cdot \cos \delta ),\;(i = 1,2) \) as in bevel gears. This is due to the fact that the pitch surfaces of the CGA transmission links are cones, which is different from the CGCh transmission where axoids are cylinders.

4 Conclusion

  1. 1.

    An analytical base for designing CGA bevel transmission on parallel axes with tangential pinion teeth and wheel teeth has been developed.

  2. 2.

    A comparative assessment of the CGA transmission with its analog—a cylindrical transmission with chevron teeth CGCh with the same dimensions is made. The result of an increase in the teeth length of the CGA is an increase in the transmission capacity according to the main criterion for the performance of closed gears—the contact endurance of the teeth.

  3. 3.

    An enlarged scheme of the algorithm for the practical calculation of the CGA transmission with reference to the current method of calculating the CGCh is proposed.