Contingency Tables

Abstract

This chapter introduces permutation methods for the analysis of contingency tables. Included in this chapter are six example analyses illustrating computation of permutation methods for goodness-of-fit tests, analysis of contingency tables composed of two nominal-level (categorical) variables, analysis of contingency tables composed of two ordinal-level (ranked) variables, analysis of contingency tables composed of one nominal-level variable and one ordinal-level variable, analysis of contingency tables composed of one nominal-level variable and one interval-level variable, and analysis of contingency tables composed of one ordinal-level variable and one interval-level variable. Included in this chapter are permutation versions of Pearson chi-squared goodness-of-fit test, Pearson’s chi-squared test of independence, Cramér’s symmetrical measure of nominal association, Goodman and Kruskal’s τ _a and τ _b asymmetric measures of association for two categorical variables, Goodman and Kruskal’s G measure of association for two ranked variables, Somers’ d _yx and d _xy asymmetric measures of association for two ranked variables, Freeman’s θ measure of association for a categorical independent variable and a ranked dependent variable, Pearson’s point-biserial correlation coefficient for one dichotomous variable and one interval-level variable, and Jaspen’s correlation coefficient for one ranked variable and one interval-level variable.

This chapter introduces exact and Monte Carlo permutation statistical methods for selected measures of relationship among nominal-, ordinal-, and interval-level variables, commonly called contingency table analysis. The analysis of contingency tables with their associated measures of effect size and tests of significance constitutes a substantial portion of nonparametric statistical methods.

In this last chapter, exact and Monte Carlo permutation statistical methods for the analysis of contingency tables are illustrated with six types of analyses. The first section of the chapter considers permutation statistical methods applied to conventional goodness-of-fit tests; for example, Pearson’s chi-squared goodness-of-fit test. The second section is devoted to permutation statistical methods for analyzing contingency tables composed of two cross-classified nominal-level (categorical) variables; for example, Pearson’s symmetric chi-squared test of independence for two categorical variables and Goodman and Kruskal’s t _a and t _b asymmetric measures of association for two categorical variables. The third section utilizes permutation statistical methods for analyzing contingency tables composed of two cross-classified ordinal-level (ranked) variables; for example, Goodman and Kruskal’s symmetric G measure of association for two ranked variables and Somers’ d _yx and d _xy asymmetric measures of association for two ranked variables. The fourth section is the first of three sections utilizing permutation statistical methods for analyzing contingency tables composed of two cross-classified mixed-level variables. In this fourth section permutation statistical methods are utilized for analyzing contingency tables composed of one nominal-level (categorical) variable cross-classified with one ordinal-level (ranked) variable; for example, Freeman’s θ measure for one categorical independent variable and one ranked dependent variable. The fifth section utilizes permutation statistical methods for analyzing contingency tables composed of one nominal-level variable cross-classified with one interval-level variable; for example, Pearson’s point-biserial correlation coefficient for one dichotomous variable and one interval-level variable. The sixth section utilizes permutation statistical methods for analyzing contingency tables composed of one ordinal-level variable cross-classified with one interval-level variable; for example, Jaspen’s correlation coefficient for one ranked variable and one interval-level variable. ¹

There exist a vast array of measures of association and correlation. The few measures described here illustrate the application of permutation statistical methods to the analysis of two-way contingency tables at various levels of measurement and were selected for their popularity in the research literature and inclusion in various introductory textbooks. For a more comprehensive treatment of permutation statistical methods applied to measures of association and correlation see a 2018 book on The Measurement of Association by the authors [2].

11.1 Goodness-of-Fit Tests

Goodness-of-fit tests are essential for determining how well observed data conform to hypothetical models. When at all reasonable, exact goodness-of-fit tests are preferred over asymptotic tests. More specifically, goodness-of-fit tests are designed to compare the observed values in k discrete, unordered categories with values that are expected to occur under chance conditions. For example, for a fair coin the expectation for 100 independent trials is 50 heads and 50 tails over many, many trials of 100 tosses. The observed values, say 60 heads and 40 tails, are then compared with expected values under the null hypothesis, H ₀: p(H) = p(T) = 0.50.

The most popular goodness-of-fit test for k discrete, unordered categories is Pearson’s chi-squared test, although Wald’s likelihood-ratio test is occasionally encountered in the contemporary literature. Utilizing the conventional notation presented in many introductory textbooks, Pearson’s chi-squared goodness-of-fit test for k discrete, unordered categories is given by

$$\displaystyle \begin{aligned} \chi^{2} = \sum_{i=1}^{k} \frac{O_{i}^{2}}{E_{i}}-N\;, \end{aligned}$$

where O _i and E _i denote the observed and expected frequency values, respectively, for i = 1, …, k. Under the Neyman–Pearson null hypothesis, H ₀: O _i = E _i for i = 1, …, k, χ ² is asymptotically distributed as Pearson’s χ ² with k − 1 degrees of freedom, under the assumption of normality.²

Consider the random assignment of N objects to k discrete, unordered categories where the probability that any one of the N objects occurs in the ith category is p _i > 0 for i = 1, …, k. Then the probability that O _i objects occur in the ith category for i = 1, …, k is the multinomial probability given by

$$\displaystyle \begin{aligned} P(O_{1},O_{2},\,\ldots,\,O_{k}|p_{1},p_{2},\,\ldots,\,p_{k},N) = \frac{N!}{\displaystyle\prod_{i=1}^{k}O_{i}!}\prod_{i=1}^{k}p_{i}^{O_{i}}\;, \end{aligned}$$

where

$$\displaystyle \begin{aligned} \sum_{i=1}^{k}O_{i} = N \quad \mbox{and} \quad \sum_{i=1}^{k}p_{i} = 1\;. \end{aligned}$$

11.1.1 Example 1

Two example analyses will serve to illustrate the permutation approach to goodness-of-fit-tests. For the first analysis under the Neyman–Pearson population model of statistical inference, consider a small example set of data with k = 3 unordered categories, N = 6 total objects, O ₁ = 5 objects in the first category, O ₂ = 1 object in the second category, and O ₃ = 0 objects in the third category. The observed and expected frequencies along with the associated theoretical proportions are listed in Table 11.1. For the example data listed in Table 11.1 with N = 6 observations, Pearson’s chi-squared goodness-of-fit test statistic is

$$\displaystyle \begin{aligned} \chi^{2} = \sum_{i=1}^{k}\frac{O_{i}^{2}}{E_{i}}-N = \frac{5^{2}}{2}+\frac{1^{2}}{2}+\frac{0^{2}}{2}-6 = 7.00\;. \end{aligned}$$

Under the Neyman–Pearson null hypothesis, H ₀: O _i = E _i for i = 1, …, k, χ ² is asymptotically distributed as Pearson’s χ ² with k − 1 degrees of freedom. With k − 1 = 3 − 1 = 2 degrees of freedom, the asymptotic probability value of χ ² = 7.00 is P = 0.0302, under the assumption of normality.

Table 11.1 Example data for Pearson’s chi-squared goodness-of-fit test statistic with k = 3 discrete, unordered categories and N = 6 observations

11.1.2 An Exact Permutation Analysis

For the example data listed in Table 11.1 under the Fisher–Pitman permutation model of statistical inference there are exactly

$$\displaystyle \begin{aligned} M = \binom{N+k-1}{k-1} = \binom{6+3-1}{3-1} = \binom{8}{2} = 28 \end{aligned}$$

possible, equally-likely arrangements in the reference set of all permutations of the example data listed in Table 11.1. Table 11.2 lists the M = 28 arrangements of the observed data, the associated χ ² values, and the multinomial point probability values to six decimal places, ordered by the χ ² values from lowest ($\chi _{1}^{2} = 0.00$) to highest ($\chi _{28}^{2} = 12.00$). The exact probability value of χ ² = 7.00 is the sum of the multinomial point probability values associated with values of χ ² that are equal to or greater than the observed χ ² value. There are only nine arrangements of the observed data with χ ² test statistic values that are equal to or greater than the observed value of χ ² = 7.00: six values of χ ² = 7.00 and three values of χ ² = 12.00, all in rows indicated with asterisks in Table 11.2. Thus if all M arrangements of the N = 6 observations listed in Table 11.1 occur with equal chance under the Fisher–Pitman null hypothesis, the exact probability value of χ ² = 7.00 computed on the M = 28 possible arrangements of the observed data with k = 4 categories preserved for each arrangement is

$$\displaystyle \begin{aligned} P = 6(0.008230)+3(0.001372) = 0.053496\;. \end{aligned}$$

Table 11.2 Example discrete probability distribution for the data given in Table 11.1 with χ ² test statistic values and associated multinomial probability values

There is a substantial difference between the exact probability value of P = 0.0535 and the asymptotic probability value of P = 0.0302; that is,

$$\displaystyle \begin{aligned} \Delta_{P} = 0.0535-0.0302 = 0.0233\;. \end{aligned}$$

With the sparse data given in Table 11.1 there are only M = 28 possible arrangements of cell frequencies given the marginal frequency totals and it would be unreasonable to expect a continuous mathematical function such as Pearson’s χ ² to fit such a small discrete distribution consisting of only six different values with any precision.

11.1.3 Example 2

Gregor Mendel (1822–1884) is notable for his studies of hybridization utilizing the common garden pea while he resided in the Augustinian monastery of St. Thomas at Brünn in Austrian Silesia.^{3 , 4} In one of his many studies of garden peas, Mendel crossed hybrid plants producing round yellow peas with hybrid plants producing wrinkled green peas. To produce his hybrids, Mendel carefully brushed the pollen of one pea plant onto the pistils of another plant. The first generation, as expected, produced all round yellow peas—both dominant characteristics. However, the second generation yielded four varieties of peas: round yellow, wrinkled yellow, round green, and wrinkled green.⁵

Figure 11.1 displays the different varieties of peas in a Punnett square where RY denotes round yellow peas, Ry denotes round green peas, rY denotes wrinkled yellow peas, and ry denotes wrinkled green peas.⁶ In the Punnett diagram in Fig. 11.1, the round-yellow hybrids, RYRY, RYRy, RYrY, RYry, RyRY, RyrY, rYRY, rYRy, and ryRY, are indicated by nine black circles ([black,fill=black] (0,0) circle (0.6ex);), the round-green hybrids, RyRy, Ryry, and ryRy, are indicated by three dark gray circles ([gray,fill=gray] (0,0) circle (0.6ex);), the wrinkled-yellow hybrids, rYrY, rYry, and ryrY, are indicated by three light gray circles ([lightgray,fill=lightgray] (0,0) circle (0.6ex);), and the single wrinkled-green ryry hybrid is indicated by a white circle ([black,fill=white] (0,0) circle (0.6ex);).

Fig. 11.1

Punnett square depicting RYRY, RYRy, RYrY, RYry, RyRY, RyrY, rYRY, rYRy, and ryRY hybrids with nine black circles, RyRy, Ryry, and ryRy hybrids with three dark gray circles, rYrY, rYry, and ryrY hybrids with three light gray circles, and the sole ryry hybrid with a single white circle

Mendel’s 15 double-hybrid plants produced a sample of N = 556 peas. Mendel’s data for the N = 556 second-generation hybrids are listed in Table 11.3, along with the expected values which approximate the ratios 9:3:3:1.

Table 11.3 Mendel’s second-generation hybridization frequency data for N = 556 common garden peas

For Mendel’s hybridization data listed in Table 11.3, Pearson’s chi-squared goodness-of-fit test statistic is

$$\displaystyle \begin{aligned} \chi^{2} = \sum_{i=1}^{k} \frac{O_{i}^{2}}{E_{i}}-N = \frac{315^{2}}{312.75}+\frac{101^{2}}{104.25}+\frac{108^{2}}{104.25}+\frac{32^{2}}{34.75}-556 = 0.4700\;. \end{aligned}$$

Under the Neyman–Pearson null hypothesis, H ₀: O _i = E _i for i = 1, …, k, χ ² is asymptotically distributed as Pearson’s χ ² with k − 1 degrees of freedom. With k − 1 = 4 − 1 = 3 degrees of freedom, the asymptotic probability value of χ ² = 0.4700 is P = 0.9254, under the assumption of normality.

In a 1936 paper published in Annals of Science, R.A. Fisher , Galton Professor of Eugenics at University College, London, re-examined Mendel’s hybridization data, questioned Mendel’s recording of his observations, and concluded that the very close agreement between Mendel’s observed and expected series was unlikely to have arisen by chance [4]. Fisher submitted his paper at Christmas time in 1936 to Annals of Science with a comment to the editor, Dr. Douglas McKie:

I had not expected to find the strong evidence which has appeared that the data had been cooked. This makes my paper far more sensational than ever I had intended…(quoted in Box [3, p. 297]).

11.1.4 An Exact Permutation Analysis

Under the Fisher–Pitman permutation model, the exact probability value of an observed chi-squared value of χ ² = 7.00 is given by the sum of the multinomial point probability values associated with the values of χ ² that are equal to or greater than the observed χ ² value. For the Mendel hybridization data listed in Table 11.3 under the permutation model there are

$$\displaystyle \begin{aligned} M = \binom{N+k-1}{k-1} = \binom{556+4-1}{4-1} = \binom{559}{3} = 28{,}956{,}759 \end{aligned}$$

possible, equally-likely arrangements in the reference set of all permutations of Mendel’s hybridization data listed in Table 11.3, making an exact permutation analysis feasible. If all M arrangements of the N = 556 observations listed in Table 11.3 occur with equal chance under the Fisher–Pitman null hypothesis, the exact probability value of the observed chi-squared value of χ ² = 0.4700 computed on the M = 28, 956, 759 possible arrangements of the observed data with k = 4 categories preserved for each arrangement is P = 0.9381; that is, the sum of the multinomial probability values associated with values of χ ² = 0.4700 or greater.

11.1.5 A Measure of Effect Size

A chi-squared test of goodness-of-fit and its associated probability value provide no information as to the closeness of the fit between the observed and theoretical values, only whether they are statistically significant under the Neyman–Pearson population-model null hypothesis. Measures of effect size are essential in such cases as they index the magnitude of the fit between the observed and expected frequencies and indicate the practical significance of the research. A maximum-corrected measure of effect size is easily specified for a chi-squared goodness-of-fit test [1].

Define

$$\displaystyle \begin{aligned} q = \min(E_{1},\,E_{2},\,\ldots,\,E_{k}) \end{aligned}$$

for k disjoint, unordered categories. Then with q determined, the maximum value of χ ² is given by

$$\displaystyle \begin{aligned} \chi_{\text{max}}^{2} = \frac{N(N-q)}{q} \end{aligned} $$

(11.1)

and a maximum-corrected measure of effect size for Pearson’s chi-squared goodness-of-fit test is given by

$$\displaystyle \begin{aligned} \mathit{ES}(\chi^{2}) = \frac{\chi_{\text{o}}^{2}}{\chi_{\text{max}}^{2}}\;, \end{aligned}$$

where $\chi _{\text{o}}^{2}$ denotes the observed value of χ ² [8].

For Mendel’s hybridization data listed in Table 11.3, the minimum expected frequency value is

$$\displaystyle \begin{aligned} q = \min(E_{1},\,E_{2},\,E_{3},\,E_{4}) = \min(312.75,\, 104.25,\, 104.25,\, 34.75) = 34.75\;, \end{aligned}$$

and the maximum possible Pearson’s χ ² test statistic value given k = 4, q = 34.75, and N = 556 is

$$\displaystyle \begin{aligned} \chi_{\text{max}}^{2} = \frac{N(N-q)}{q} = \frac{556(566-34.75)}{34.75} = 8340\;. \end{aligned}$$

To illustrate the function of Eq. (11.1) imagine that all N = 556 observations are concentrated in the one category with the smallest expected value and the remaining k − 1 categories contain zero observations. In this case all N = 556 observations are concentrated in the last category with the minimum expected value of E ₄ = 34.75, such as depicted in Table 11.4. Then the maximum value of Pearson’s chi-squared goodness-of-fit test statistic is

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} &\displaystyle &\displaystyle \chi^{2}_{\text{max}} = \sum_{i=1}^{k} \frac{O_{i}^{2}}{E_{i}}-N\\ &\displaystyle &\displaystyle \qquad \qquad \quad \qquad {}= \frac{0^{2}}{312.75}+\frac{0^{2}}{104.25}+\frac{0^{2}}{104.25}+\frac{556^{2}}{34.75}-556 = 8340\;, \end{array} \end{aligned} $$

and the maximum-corrected measure of effect size is

$$\displaystyle \begin{aligned} \mathit{ES}(\chi^{2}) = \frac{\chi^{2}}{\chi_{\text{max}}^{2}} = \frac{0.4700}{8340} = 0.5636 {\times} 10^{-4}\;, \end{aligned}$$

indicating that the observed value of χ ² = 0.4700 is an insignificantly small proportion of the maximum possible χ ² value, given the expected values E ₁ = 312.75, E ₂ = 104.25, E ₃ = 104.25, and E ₄ = 34.75.

Table 11.4 Maximum arrangement of cell frequencies for Mendel’s second-generation hybridization frequency data with N = 556 observations

11.2 Contingency Measures: Nominal by Nominal

The most popular test for the cross-classification of two nominal-level (categorical) variables is Pearson’s chi-squared test of independence, which is presented in every introductory textbook. Utilizing the conventional notation presented in many introductory textbooks for a contingency table with r rows and c columns, Pearson’s chi-squared test statistic is given by

$$\displaystyle \begin{aligned} \chi^{2} = N \left( \sum_{i=1}^{r}\,\sum_{j=1}^{c}\frac{O_{ij}^{2}}{R_{i}C_{j}}-1 \right)\;, \end{aligned} $$

(11.2)

where O _ij denotes the observed frequency in the ith row and jth column for i = 1, …, r and j = 1, …, c, R _i denotes a row marginal frequency total for i = 1, …, r, C _j denotes a column marginal frequency total for j = 1, …, c, and N denotes the total number of values in the observed contingency table.

11.2.1 Example 1

Two examples will serve to illustrate Pearson’s chi-squared test of independence for an r×c contingency table. For an analysis under the Neyman–Pearson population model, consider the sparse example data given in Table 11.5 with r = 3 rows, c = 3 columns, and N = 9 observations. Under the Neyman–Pearson population model, the chi-squared test statistic value for the example data given in Table 11.5 is

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} &\displaystyle &\displaystyle \chi^{2} = N \left( \sum_{i=1}^{r}\,\sum_{j=1}^{c}\frac{O_{ij}^{2}}{R_{i}C_{j}}-1 \right)\\ &\displaystyle &\displaystyle \ \ \qquad {}= 9 \bigg[ \frac{0^{2}}{(2)(2)}+\frac{0^{2}}{(2)(3)}+\frac{2^{2}}{(2)(4)}+\frac{0^{2}}{(3)(2)}+\frac{3^{2}}{(3)(3)}+\frac{0^{2}}{(3)(4)}\\ &\displaystyle &\displaystyle \qquad \qquad \qquad \qquad \quad \qquad {}+\frac{2^{2}}{(4)(2)}+\frac{0^{2}}{(4)(3)}+\frac{2^{2}}{(4)(4)}-1 \bigg] = 11.2500\;. \end{array} \end{aligned} $$

Table 11.5 Example data for Pearson’s chi-squared test of independence with r = 3 rows, c = 3 columns, and N = 9 cross-classified observations

Under the Neyman–Pearson null hypothesis, H ₀: O _ij = E _ij for i = 1, …, r and j = 1, …, c, where the expected cell values are given by

$$\displaystyle \begin{aligned} E_{ij} = \frac{O_{ij}}{R_{i}C_{j}} \end{aligned}$$

for i = 1, …, r and j = 1, …, c, χ ² is asymptotically distributed as Pearson’s χ ² with (r − 1)(c − 1) degrees of freedom. With (r − 1)(c − 1) = (3 − 1)(3 − 1) = 4 degrees of freedom, the asymptotic probability value of χ ² = 11.2500 is P = 0.0239, under the assumption of normality.

11.2.2 A Measure of Effect Size

The fact that a chi-squared statistical test produces a low probability value indicates only that there are differences among the response measurement scores between the two variables that (possibly) cannot be attributed to error. The obtained probability value does not indicate whether these differences are of any practical value. Measures of effect size express the practical or clinical significance of an obtained chi-squared value, as contrasted with the statistical significance of a chi-squared value. The most popular measure of effect size for Pearson’s chi-squared test of independence is Cramér’s V  given by

$$\displaystyle \begin{aligned} V = \sqrt{ \frac{\chi^{2}}{N \big[\min(r-1,c-1)\big]}}\;. \end{aligned}$$

For the example data given in Table 11.6 with χ ² = 11.2500, Cramér’s measure of effect size is

$$\displaystyle \begin{aligned} V = \sqrt{ \frac{11.2500}{9\big[ \min(3-1,3-1) \big]}} = \sqrt{\frac{11.2500}{18.00}} = 0.7906\;. \end{aligned}$$

For a critical evaluation of Cramér’s V  measure of effect size, see a discussion in The Measurement of Association by the authors [2, pp. 80–82].

Table 11.6 All M = 39 arrangements of the frequency data given in Table 11.5 with associated chi-squared values and hypergeometric point probability values

Occasionally in the contemporary literature, Cohen’s measure of effect size for a chi-squared test of independence is encountered. Cohen’s measure is given by

$$\displaystyle \begin{aligned} w = \sqrt{\frac{\chi^{2}}{N}}\;. \end{aligned}$$

For the example data given in Table 11.5, Cohen’s measure of effect size is

$$\displaystyle \begin{aligned} w = \sqrt{\frac{11.2500}{9}} = 1.1180\;. \end{aligned}$$

11.2.3 An Exact Permutation Analysis

Given the observed marginal frequency totals for the example data, there are only M = 39 possible, equally-likely arrangements of cell frequencies in the reference set of all permutations of the N = 9 observations given in Table 11.5, making an exact permutation analysis possible. Table 11.6 lists the M = 39 arrangements of cell frequencies, the associated chi-squared test statistic values, and the hypergeometric point probability values given by

$$\displaystyle \begin{aligned} p(O_{11},\,\ldots,O_{rc}|R_{1},\,\ldots,\,R_{r},C_{1},\,\ldots,\,C_{c},N) = \frac{ \left( \displaystyle\prod_{i=1}^{r}R_{i}!\right) \left( \displaystyle\prod_{j=1}^{c}C_{j}! \right)}{N! \displaystyle\prod_{i=1}^{r}\,\prod_{j=1}^{c}O_{ij}!}\;. \end{aligned}$$

Because the observed marginal frequency totals are fixed, Table 11.6 lists only cell frequencies O ₁₁, O ₁₂, O ₂₁, and O ₂₂, as the remaining five cell frequencies can be determined from the observed marginal frequency totals.

Under the Fisher–Pitman permutation model, the exact probability value of χ ² = 11.2500 is the sum of the hypergeometric point probability values associated with the chi-squared values that are equal to or greater than the observed chi-squared value. For the results listed in Table 11.6, there are four chi-squared test statistic values that are equal to or greater than the observed value of χ ² = 11.2500: $\chi _{1}^{2} = 18.0000$, $\chi _{2}^{2} = 14.0625$, $\chi _{3}^{2} = 13.0000$, and $\chi _{4}^{2} = 11.2500$, in rows 1, 2, 3, and 4, respectively, and indicated by asterisks. Thus the exact probability value of χ ² = 11.2500 is

$$\displaystyle \begin{aligned} 0.7937 {\times} 10^{-3}+0.3175 {\times} 10^{-2}+0.2381 {\times} 10^{-2}+0.4762 {\times} 10^{-2} = 0.0111\;. \end{aligned}$$

There is a substantial difference between the exact probability value of P = 0.0111 and the asymptotic probability value of P = 0.0239; that is,

$$\displaystyle \begin{aligned} \Delta_{P} = 0.0239-0.0111 = 0.0128\;. \end{aligned}$$

With such sparse data as given in Table 11.5 there are only M = 39 possible arrangements of cell frequencies given the marginal frequency totals with only 25 different chi-squared values and it would be unreasonable to expect a continuous mathematical function such as Pearson’s χ ² to fit such a small discrete distribution with any precision.

11.2.4 Example 2

For a second example of a chi-squared analysis of a nominal-nominal contingency table, consider the 3×5 contingency table with cell frequencies given in Table 11.7. Following Eq. (11.2), Pearson’s chi-squared test statistic for the frequency data given in Table 11.7 is

$$\displaystyle \begin{aligned} \begin{array}{rcl} \chi^{2} &\displaystyle =&\displaystyle N \left( \sum_{i=1}^{r}\,\sum_{j=1}^{c}\frac{O_{ij}^{2}}{R_{i}C_{j}}-1 \right)\\ {}&\displaystyle =&\displaystyle 63 \bigg[ \frac{6^{2}}{(21)(7)}+\frac{2^{2}}{(21)(11)}+ \cdots +\frac{6^{2}}{(17)(21)}+\frac{3^{2}}{(17)(8)} -1 \bigg] = 16.6279\;. \end{array} \end{aligned} $$

Under the Neyman–Pearson null hypothesis the chi-squared test statistic is asymptotically distributed as Pearson’s χ ² with (r − 1)(c − 1) degrees of freedom. With (r − 1)(c − 1) = (3 − 1)(5 − 1) = 8 degrees of freedom, the asymptotic probability value of χ ² = 16.6279 is P = 0.0342, under the assumption of normality.

Table 11.7 Example data for Pearson’s chi-squared test of independence with r = 3 rows, c = 5 columns, and N = 63 cross-classified observations

11.2.5 A Measure of Effect Size

For the frequency data given in Table 11.7, Cramér’s measure of effect size is

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} &\displaystyle &\displaystyle V = \sqrt{ \frac{\chi^{2}}{N \big[\min(r-1,c-1)\big]}}\\ &\displaystyle &\displaystyle \qquad \qquad \qquad \qquad \qquad {}= \sqrt{ \frac{16.6279}{63\big[ \min(3-1,5-1) \big]}} = \sqrt{\frac{16.6279}{126.00}} = 0.3633 \end{array} \end{aligned} $$

and Cohen’s measure of effect size is

$$\displaystyle \begin{aligned} w = \sqrt{\frac{\chi^{2}}{N}} = \sqrt{\frac{16.6279}{63}} = 0.2639\;. \end{aligned}$$

11.2.6 An Exact Permutation Analysis

Given the observed marginal frequency totals for the example data, there are M = 11, 356, 797 possible, equally-likely arrangements of the cell frequencies in the reference set of all permutations of the N = 63 observations given in Table 11.7, making an exact permutation analysis possible. Under the Fisher–Pitman permutation model, the exact probability of χ ² = 16.6279 is the sum of the hypergeometric point probability values associated with the chi-squared values calculated on all M possible arrangements of the cell frequencies, given the observed marginal frequency totals. For the frequency data given in Table 11.7, there are M = 11, 356, 797 possible, equally-likely arrangements of the cell frequencies given the observed marginal frequency totals, of which 10,559,996 chi-squared test statistic values are equal to or greater than the observed chi-squared value of χ ² = 16.6279, yielding an exact hypergeometric probability value of P = 0.0306. Note that with M = 11, 356, 797 possible arrangements of the data given in Table 11.7, the asymptotic χ ² probability value of P = 0.0342 closely approximates the exact hypergeometric probability value of P = 0.0306.

11.2.7 Goodman–Kruskal’s t _a and t _b Measures

While all measures of association based on Pearson’s chi-squared are symmetric measures, Goodman and Kruskal’s two asymmetric proportional-reduction-in-error measures (t _a and t _b) allow researchers to specify an independent and a dependent variable. Consider two cross-classified, unordered polytomies, A and B, with variable A the dependent variable and variable B the independent variable. Table 11.8 provides notation for the cross-classification, where a _j for j = 1, …, c denotes the c categories for dependent variable A, b _i for i = 1, …, r denotes the r categories for independent variable B, N denotes the total of cell frequencies in the table, n _i. denotes a marginal frequency total for the ith row, i = 1, …, r, summed over all columns, n _.j denotes a marginal frequency total for the jth column, j = 1, …, c, summed over all rows, and n _ij denotes a cell frequency for i = 1, …, r and j = 1, …, c.

Table 11.8 Notation for the cross-classification of two categorical variables, A _j for j = 1, …, c and B _i for i = 1, …, r

Goodman and Kruskal’s t _a test statistic is a measure of the relative reduction in prediction error where two types of errors are defined. The first type is the error in prediction based solely on knowledge of the distribution of the dependent variable, termed “errors of the first kind” (E ₁) and consisting of the expected number of errors when predicting the c dependent variable categories (a ₁, …, a _c) from the observed distribution of the marginals of the dependent variable (n _.1, …, n _.c). The second type is the error in prediction based on knowledge of the distributions of both the independent and dependent variables, termed “errors of the second kind” (E ₂) and consisting of the expected number or errors when predicting the c dependent variable categories (a ₁, …, a _c) from knowledge of the r independent variable categories (b ₁, …, b _r).

To illustrate the two error types, consider predicting category a ₁ only from knowledge of its marginal distribution, n _.1, …, n _.c. Clearly, n _.1 out of the N total cases are in category a ₁, but exactly which n _.1 of the N cases is unknown. The probability of incorrectly identifying one of the N cases in category a ₁ by chance alone is given by

$$\displaystyle \begin{aligned} \frac{N-n_{.1}}{N}\;. \end{aligned}$$

Since there are n _.1 such classifications required, the number of expected incorrect classifications is

$$\displaystyle \begin{aligned} \frac{n_{.1}(N-n_{.1})}{N} \end{aligned}$$

and, for all c categories of variable A, the number of expected errors of the first kind is given by

$$\displaystyle \begin{aligned} E_{1} = \sum_{j=1}^{c} \frac{n_{.j}(N-n_{.j})}{N}\;. \end{aligned}$$

Likewise, to predict n ₁₁, …, n _1c from the independent category b ₁, the probability of incorrectly classifying one of the n _1. cases in cell n ₁₁ by chance alone is

$$\displaystyle \begin{aligned} \frac{n_{1.}-n_{11}}{n_{1.}}\;. \end{aligned}$$

Since there are n ₁₁ such classifications required, the number of incorrect classifications is

$$\displaystyle \begin{aligned} \frac{n_{11}(n_{1.}-n_{11})}{n_{1.}} \end{aligned}$$

and, for all cr cells, the number of expected errors of the second kind is given by

$$\displaystyle \begin{aligned} E_{2} = \sum_{j=1}^{c}\,\sum_{i=1}^{r} \frac{n_{ij}(n_{i.}-n_{ij})}{n_{i.}}\;. \end{aligned}$$

Goodman and Kruskal’s t _a statistic can then be defined as

$$\displaystyle \begin{aligned} t_{a} = \frac{E_{1}-E_{2}}{E_{1}}\;. \end{aligned}$$

An efficient computation form for Goodman and Kruskal’s t _a test statistic is given by

$$\displaystyle \begin{aligned} t_{a} = \frac{N \displaystyle\sum_{i=1}^{r}\,\sum_{j=1}^{c} \displaystyle\frac{n_{ij}^{2}}{n_{i.}}-\sum_{j=1}^{c}n_{.j}^{2}}{N^{2}-\displaystyle\sum_{j=1}^{c}n_{.j}^{2}}\;. \end{aligned} $$

(11.3)

A computed value of t _a indicates the proportional reduction in prediction error given knowledge of the distribution of independent variable B over and above knowledge of only the distribution of dependent variable A. As defined, t _a is a point estimator of Goodman and Kruskal’s population parameter τ _a for the population from which the sample of N cases was obtained. If variable B is considered the dependent variable and variable A the independent variable, then Goodman and Kruskal’s test statistic t _b and associated population parameter τ _b are analogously defined.

11.2.8 An Example Analysis for t _a

To illustrate Goodman and Kruskal’s t _a measure of nominal-nominal association, consider the contingency table given in Table 11.9 with r = 3 rows, c = 4 columns, and N = 110 cross-classified ordered observations. Following Eq. (11.3), the observed value of Goodman and Kruskal’s t _a test statistic is

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} &\displaystyle &\displaystyle t_{a} = \frac{N \displaystyle\sum_{i=1}^{r}\,\sum_{j=1}^{c} \displaystyle\frac{n_{ij}^{2}}{n_{i.}}-\sum_{j=1}^{c}n_{.j}^{2}}{N^{2}-\displaystyle\sum_{j=1}^{c}n_{.j}^{2}}\\ &\displaystyle &\displaystyle \ \quad {}= \frac{110 \left( \displaystyle\frac{24^{2}}{37}+\frac{2^{2}}{37}+\cdots+\frac{17^{2}}{38}+\frac{19^{2}}{38} \right)-(25^{2}+25^{2}+27^{2}+33^{2})}{110^{2}-(25^{2}+25^{2}+27^{2}+33^{2})}\\ &\displaystyle &\displaystyle \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad {}= 0.2797\;. \end{array} \end{aligned} $$

Table 11.9 Example data for Goodman and Kruskal’s t _a and t _b measures of nominal-nominal association with r = 3 rows, c = 4 columns, and N = 110 cross-classified observations

Under the Neyman–Pearson null hypothesis, H ₀: τ _a = 0, t _a(N − 1)(r − 1) is asymptotically distributed as Pearson’s χ ² with (r − 1)(c − 1) degrees of freedom. With (r − 1)(c − 1) = (3 − 1)(4 − 1) = 6 degrees of freedom, the asymptotic probability value of t _a = 0.2797 is P = 0.2852×10⁻¹⁰, under the assumption of normality.

11.2.9 An Exact Permutation Analysis for t _a

Under the Fisher–Pitman permutation model, the exact probability value of an observed value of Goodman and Kruskal’s t _a is given by the sum of the hypergeometric point probability values associated with t _a test statistic values that are equal to or greater than the observed value of t _a = 0.2797. For the frequency data given in Table 11.9, there are M = 26, 371, 127 possible, equally-likely arrangements in the reference set of all permutations of cell frequencies given the observed row and column marginal frequency distributions, {37, 35, 38} and {25, 25, 27, 33}, respectively, making an exact permutation analysis possible. There are exactly 1,523,131 t _a test statistic values that are equal to or greater than the observed value of t _a = 0.2797. The exact probability value of the observed t _a value under the Fisher–Pitman null hypothesis is P = 0.0578; that is, the sum of the hypergeometric point probability values associated with values of t _a = 0.2797 or greater.

11.2.10 An Example Analysis for t _b

Now consider variable B as the dependent variable. A convenient computing formula for t _b is

$$\displaystyle \begin{aligned} t_{b} = \frac{N \displaystyle\sum_{j=1}^{c}\,\sum_{i=1}^{r} \displaystyle\frac{n_{ij}^{2}}{n_{.j}}-\sum_{i=1}^{r}n_{i.}^{2}}{N^{2}-\displaystyle\sum_{i=1}^{r}n_{i.}^{2}}\;. \end{aligned}$$

Thus, for the frequency data given in Table 11.9 the observed value of t _b is

$$\displaystyle \begin{aligned} t_{b} = \frac{110 \left( \displaystyle\frac{24^{2}}{25}+\frac{2^{2}}{25}+\cdots+\frac{17^{2}}{27}+\frac{19^{2}}{33} \right)-(37^{2}+35^{2}+38^{2})}{110^{2}-(37^{2}+35^{2}+38^{2})} = 0.4428\;. \end{aligned}$$

Under the Neyman–Pearson null hypothesis, H ₀: τ _b = 0, t _b(N − 1)(c − 1) is asymptotically distributed as Pearson’s χ ² with (r − 1)(c − 1) degrees of freedom. With (r − 1)(c − 1) = (3 − 1)(4 − 1) = 6 degrees of freedom, the asymptotic probability value of t _b = 0.4428 is P = 0.9738×10⁻²⁸, under the assumption of normality.

11.2.11 An Exact Permutation Analysis for t _b

Under the Fisher–Pitman permutation model, the exact probability value of an observed value of Goodman and Kruskal’s t _b is given by the sum of the hypergeometric point probability values associated with t _b test statistic values that are equal to or greater than the observed value of t _b = 0.4428. For the frequency data given in Table 11.9, there are M = 26, 371, 127 possible, equally-likely arrangements in the reference set of all permutations of cell frequencies given the observed row and column marginal frequency distributions, {37, 35, 38} and {25, 25, 27, 33}, respectively, making an exact permutation analysis possible. There are exactly 991,488 t _b test statistic values that are equal to or greater than the observed value of t _b = 0.4428. The exact probability value of the observed t _b value under the Fisher–Pitman null hypothesis is P = 0.0376; that is, the sum of the hypergeometric point probability values associated with values of t _b = 0.4428 or greater.

11.2.12 The Relationships Among t _a, t _b, and χ ²

While no general equivalence exists between Goodman and Kruskal’s t _a and t _b measures of nominal-nominal association and Pearson’s χ ² test of independence, certain relationships hold among t _a, t _b, and χ ² under some limited conditions. Four of the relationships can easily be specified.

First, if n _i. = N∕r for i = 1, …, r, then χ ² = N(r − 1)t _b and t _b = χ ²∕N(r − 1). To illustrate the relationship between Goodman and Kruskal’s t _b asymmetric measure of nominal-nominal association and Pearson’s χ ² test of independence when n _i. = N∕r for i = 1, …, r, consider the frequency data given in Table 11.10 with r = 3 rows, c = 3 columns, N = 30 cross-classified observations, and n _i. = N∕r = 10 for i = 1, …, r. For the frequency data given in Table 11.10 with N = 30 observations,

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle t_{b} = \frac{N \displaystyle\sum_{j=1}^{c}\,\sum_{i=1}^{r} \displaystyle\frac{n_{ij}^{2}}{n_{.j}}-\sum_{i=1}^{r}n_{i.}^{2}}{N^{2}-\displaystyle\sum_{i=1}^{r}n_{i.}^{2}}\\ &\displaystyle &\displaystyle \qquad \quad {}= \frac{30 \left( \displaystyle\frac{2^{2}}{5}+\frac{3^{2}}{10}+\cdots+\frac{3^{2}}{10}+\frac{6^{2}}{15} \right)-(10^{2}+10^{2}+10^{2})}{36^{2}-(10^{2}+10^{2}+10^{2})}\\ &\displaystyle &\displaystyle \quad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad {}= \frac{10}{600} = 0.0167 \end{array} \end{aligned} $$

and

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} &\displaystyle &\displaystyle \chi^{2} = N \left( \sum_{i=1}^{r}\,\sum_{j=1}^{c}\frac{n_{ij}^{2}}{n_{i.}n_{.j}}-1 \right)\\ &\displaystyle &\displaystyle \ \qquad \quad {}= 30 \left[ \frac{2^{2}}{(10)(5)}+\frac{3^{2}}{(10)(10)}+ \cdots +\frac{3^{2}}{(10)(10)}+\frac{6^{2}}{(10)(15)} \right]\\ &\displaystyle &\displaystyle \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad {}= 30 \left(1.0333-1\right) = 1.00\;. \end{array} \end{aligned} $$

Then the observed value of Pearson’s χ ² test statistic with respect to the observed value of Goodman and Kruskal’s t _b test statistic is

$$\displaystyle \begin{aligned} \chi^{2} = N(r-1)t_{b} = 30(3-1)(0.0167) = 1.00 \end{aligned}$$

and the observed value of Goodman and Kruskal’s t _b test statistic with respect to the observed value of Pearson’s χ ² test statistic is

$$\displaystyle \begin{aligned} t_{b} = \frac{\chi^{2}}{N(r-1)} = \frac{1.00}{30(3-1)} = 0.0167\;. \end{aligned}$$

Table 11.10 Example data for χ ² and t _b with r = 3 rows, c = 3 columns, and N = 30 cross-classified observations

Second, if n _.j = N∕c for j = 1, …, c, then χ ² = N(c − 1)t _a and t _a = χ ²∕N(c − 1). To illustrate the relationship between Goodman and Kruskal’s t _a measure of nominal-nominal association and Pearson’s χ ² test of independence when n _.j = N∕c for j = 1, …, c, consider the frequency data given in Table 11.11 with r = 2 rows, c = 4 columns, N = 40 cross-classified observations, and n _.j = N∕c = 10 for j = 1, …, c. For the frequency data given in Table 11.11 with N = 40 observations,

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle t_{a} = \frac{N \displaystyle\sum_{i=1}^{r}\,\sum_{j=1}^{c} \displaystyle\frac{n_{ij}^{2}}{n_{i.}}-\sum_{j=1}^{c}n_{.j}^{2}}{N^{2}-\displaystyle\sum_{j=1}^{c}n_{.j}^{2}}\\ &\displaystyle &\displaystyle \ \ \ \quad {}= \frac{40 \left( \displaystyle\frac{7^{2}}{25}+\frac{6^{2}}{25}+\cdots+\frac{2^{2}}{15}+\frac{6^{2}}{15} \right)-(10^{2}+10^{2}+10^{2}+10^{2})}{40^{2}-(10^{2}+10^{2}+10^{2}+10^{2})}\\ &\displaystyle &\displaystyle \ \ \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad {}= \frac{37.3333}{1200} = 0.0311 \end{array} \end{aligned} $$

Table 11.11 Example data for χ ² and t _a with r = 2 rows, c = 4 columns, and N = 40 cross-classified observations

and

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} &\displaystyle &\displaystyle \chi^{2} = N \left( \sum_{i=1}^{r}\,\sum_{j=1}^{c}\frac{n_{ij}^{2}}{n_{i.}n_{.j}}-1 \right)\\ &\displaystyle &\displaystyle \ \quad \qquad {}= 40 \left[ \frac{7^{2}}{(25)(10)}+\frac{6^{2}}{(25)(10)}+ \cdots +\frac{2^{2}}{(15)(10)}+\frac{6^{2}}{(10)(15)} \right]\\ &\displaystyle &\displaystyle \quad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad {}= 40 \left(1.0933-1\right) = 3.7333\;. \end{array} \end{aligned} $$

Then the observed value of Pearson’s χ ² test statistic with respect to the observed value of Goodman and Kruskal’s t _a test statistic is

$$\displaystyle \begin{aligned} \chi^{2} = N(c-1)t_{a} = 40(4-1)(0.0311) = 3.7333 \end{aligned}$$

and the observed value of Goodman and Kruskal’s t _a test statistic with respect to the observed value of Pearson’s χ ² test statistic is

$$\displaystyle \begin{aligned} t_{a} = \frac{\chi^{2}}{N(c-1)} = \frac{3.7333}{40(4-1)} = 0.0311\;. \end{aligned}$$

Third, if r = 2, then χ ² = Nt _a and t _a = χ ²∕N, which is Pearson’s ϕ ² coefficient of contingency. Also, if c = 2, then χ ² = Nt _b and t _b = χ ²∕N. Thus, if r = c = 2, then χ ² = Nt _a = Nt _b. To illustrate the relationships between Goodman and Kruskal’s t _a and t _b measures of nominal-nominal association and Pearson’s χ ² test of independence with r = c = 2, consider the frequency data given in Table 11.12 with r = 2 rows, c = 2 columns, and N = 90 cross-classified observations. For the frequency data given in Table 11.12 with N = 90 observations,

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle t_{a} = \frac{N \displaystyle\sum_{i=1}^{r}\,\sum_{j=1}^{c} \displaystyle\frac{n_{ij}^{2}}{n_{i.}}-\sum_{j=1}^{c}n_{.j}^{2}}{N^{2}-\displaystyle\sum_{j=1}^{c}n_{.j}^{2}}\\ &\displaystyle &\displaystyle \quad \quad \qquad \quad {}= \frac{90 \left( \displaystyle\frac{20^{2}}{30}+\frac{10^{2}}{30}+\frac{20^{2}}{60}+\frac{40^{2}}{60} \right)-(40^{2}+50^{2})}{90^{2}-(40^{2}+50^{2})}\\ &\displaystyle &\displaystyle \quad \quad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad {}= \frac{400}{4000} = 0.10\;, \end{array} \end{aligned} $$

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle t_{b} = \frac{N \displaystyle\sum_{j=1}^{c}\,\sum_{i=1}^{r} \displaystyle\frac{n_{ij}^{2}}{n_{.j}}-\sum_{i=1}^{r}n_{i.}^{2}}{N^{2}-\displaystyle\sum_{i=1}^{r}n_{i.}^{2}}\\ &\displaystyle &\displaystyle \ \ \ \quad \quad \qquad \quad {}= \frac{90 \left( \displaystyle\frac{20^{2}}{40}+\frac{10^{2}}{50}+\frac{20^{2}}{40}+\frac{40^{2}}{50} \right)-(30^{2}+60^{2})}{90^{2}-(30^{2}+60^{2})}\\ &\displaystyle &\displaystyle \ \ \ \quad \quad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad {}= \frac{360}{3600} = 0.10\;, \end{array} \end{aligned} $$

and

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} &\displaystyle &\displaystyle \chi^{2} = N \left( \sum_{i=1}^{r}\,\sum_{j=1}^{c}\frac{n_{ij}^{2}}{n_{i.}n_{.j}}-1 \right)\\ &\displaystyle &\displaystyle \quad \quad \qquad \quad {}= 90 \left[ \frac{20^{2}}{(30)(40)}+\frac{10^{2}}{(30)(50)}+\frac{20^{2}}{(60)(40)}+\frac{40^{2}}{(60)(50)} \right]\\ &\displaystyle &\displaystyle \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad {}= 90 \left(1.1000-1\right) = 9.00\;. \end{array} \end{aligned} $$

Then the observed value of Pearson’s χ ² test statistic with respect to the observed value of Goodman and Kruskal’s t _a test statistic is

$$\displaystyle \begin{aligned} \chi^{2} = Nt_{a} = 90(0.10) = 9.00 \end{aligned}$$

Table 11.12 Example data for χ ², t _a, and t _b with r = 2 rows, c = 2 columns, and N = 36 cross-classified observations

and the observed value of Goodman and Kruskal’s t _a test statistic with respect to the observed value of Pearson’s χ ² test statistic is

$$\displaystyle \begin{aligned} t_{a} = \frac{\chi^{2}}{N} = \frac{9.00}{90} = 0.10\;. \end{aligned}$$

Also, the observed value of Pearson’s χ ² test statistic with respect to Goodman and Kruskal’s t _b test statistic is

$$\displaystyle \begin{aligned} \chi^{2} = Nt_{b} = 90(0.10) = 9.00 \end{aligned}$$

and the observed value of Goodman and Kruskal’s t _b test statistic with respect to the observed value of Pearson’s χ ² test statistic is

$$\displaystyle \begin{aligned} t_{b} = \frac{\chi^{2}}{N} = \frac{9.00}{90} = 0.10\;. \end{aligned}$$

Fourth, if n _i. = N∕r and n _.j = N∕c for i = 1, …, r and j = 1, …, c, then χ ² = N(c − 1)t _a = N(r − 1)t _b. To illustrate the relationships between Goodman and Kruskal’s t _a and t _b asymmetric measures of nominal association and Pearson’s χ ² test of independence with n _i. = N∕r = 12 for i = 1, …, r and n _.j = N∕c = 9 for j = 1, …, c, consider the frequency data given in Table 11.13 with r = 3 rows, c = 4 columns, and N = 36 cross-classified observations. For the frequency data given in Table 11.13 with N = 36 observations,

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle t_{a} = \frac{N \displaystyle\sum_{i=1}^{r}\,\sum_{j=1}^{c} \displaystyle\frac{n_{ij}^{2}}{n_{i.}}-\sum_{j=1}^{c}n_{.j}^{2}}{N^{2}-\displaystyle\sum_{j=1}^{c}n_{.j}^{2}}\\ &\displaystyle &\displaystyle \quad \qquad {}= \frac{36 \left( \displaystyle\frac{3^{2}}{12}+\frac{2^{2}}{12}+\cdots+\frac{3^{2}}{12}+\frac{4^{2}}{12} \right)-(9^{2}+9^{2}+9^{2}+9^{2})}{36^{2}-(9^{2}+9^{2}+9^{2}+9^{2})}\\ &\displaystyle &\displaystyle \quad \quad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad {}= \frac{24}{972} = 0.0247\;, \end{array} \end{aligned} $$

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle t_{b} = \frac{N \displaystyle\sum_{j=1}^{c}\,\sum_{i=1}^{r} \displaystyle\frac{n_{ij}^{2}}{n_{.j}}-\sum_{i=1}^{r}n_{i.}^{2}}{N^{2}-\displaystyle\sum_{i=1}^{r}n_{i.}^{2}}\\ &\displaystyle &\displaystyle \quad \qquad {}= \frac{36 \left( \displaystyle\frac{3^{2}}{9}+\frac{2^{2}}{9}+\cdots+\frac{3^{2}}{9}+\frac{4^{2}}{9} \right)-(12^{2}+12^{2}+12^{2})}{36^{2}-(12^{2}+12^{2}+12^{2})}\\ &\displaystyle &\displaystyle \quad \quad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad {}= \frac{32}{864} = 0.0370\;, \end{array} \end{aligned} $$

Table 11.13 Example data for χ ², t _a, and t _b with r = 3 rows, c = 4 columns, and N = 36 cross-classified observations

and

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} &\displaystyle &\displaystyle \chi^{2} = N \left( \sum_{i=1}^{r}\,\sum_{j=1}^{c}\frac{n_{ij}^{2}}{n_{i.}n_{.j}}-1 \right)\\ &\displaystyle &\displaystyle \qquad \qquad {}= 36 \left[ \frac{3^{2}}{(12)(9)}+\frac{2^{2}}{(12)(9)}+ \cdots +\frac{3^{2}}{(12)(9)}+\frac{4^{2}}{(12)(9)}\right]\\ &\displaystyle &\displaystyle \quad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad {}= 36 \left( \frac{116}{108}-1\right) = 2.6667\;. \end{array} \end{aligned} $$

Then the observed value of Pearson’s χ ² test statistic with respect to the observed value of Goodman and Kruskal’s t _a test statistic is

$$\displaystyle \begin{aligned} \chi^{2} = N(c-1)t_{a} = 36(4-1)(0.0247) = 2.6667\end{aligned} $$

and the observed value of Goodman and Kruskal’s t _a test statistic with respect to the observed value of Pearson’s χ ² test statistic is

$$\displaystyle \begin{aligned} t_{a} = \frac{\chi^{2}}{N(c-1)} = \frac{2.6667}{36(4-1)} = 0.0247\;.\end{aligned} $$

Also, the observed value of Pearson’s χ ² test statistic with respect to Goodman and Kruskal’s t _b test statistic is

$$\displaystyle \begin{aligned} \chi^{2} = N(r-1)t_{b} = 36(3-1)(0.0370) = 2.6667\end{aligned} $$

and the observed value of Goodman and Kruskal’s t _b test statistic with respect to the observed value of Pearson’s χ ² test statistic is

$$\displaystyle \begin{aligned} t_{b} = \frac{\chi^{2}}{N(r-1)} = \frac{2.6667}{36(3-1)} = 0.0370\;. \end{aligned}$$

11.2.13 The Relationships Among t _b, δ, and $\Re$

Goodman and Kruskal’s t _b measure of nominal-nominal association is directly related to the permutation test statistic δ and, hence, to the permutation-based, chance-corrected $\Re$ measure of effect size. To illustrate the relationships among test statistics t _b, δ, and $\Re$, consider the frequency data given in Table 11.9 on p. 426, replicated in Table 11.14 for convenience. The conventional notation for an r×c contingency table is given in Table 11.8 on p. 423 where the row marginal frequency totals are denoted by n _i. for i = 1, …, r, the column marginal frequency totals are denoted by n _.j for j = 1, …, c, the cell frequencies are denoted by n _ij for i = 1, …, r and j = 1, …, c, and

$$\displaystyle \begin{aligned} N = \sum_{i=1}^{r}n_{i.} = \sum_{j=1}^{c}n_{.j} = \sum_{i=1}^{r}\,\sum_{j=1}^{c}n_{ij}\;. \end{aligned}$$

Then for the frequency data given in Table 11.14, Goodman and Kruskal’s t _b test statistic is

$$\displaystyle \begin{aligned} \begin{array}{rcl} t_{b} &\displaystyle =&\displaystyle \frac{N \displaystyle\sum_{j=1}^{c}\,\sum_{i=1}^{r} \displaystyle\frac{n_{ij}^{2}}{n_{.j}}-\sum_{i=1}^{r}n_{i.}^{2}}{N^{2}-\displaystyle\sum_{i=1}^{r}n_{i.}^{2}}\\ {}&\displaystyle =&\displaystyle \frac{110 \left( \displaystyle\frac{24^{2}}{25}+\frac{2^{2}}{25}+\cdots+\frac{17^{2}}{27}+\frac{19^{2}}{33} \right)-(37^{2}+35^{2}+38^{2})}{110^{2}-(37^{2}+35^{2}+38^{2})} = 0.4428\;. \end{array} \end{aligned} $$

Table 11.14 Example data for illustrating the relationships among t _b, δ, and $\Re$ with r = 3 rows, c = 4 columns, and N = 110 cross-classified observations

In 1971 Richard Light and Barry Margolin developed test statistic R ², based on an analysis of variance technique for categorical response variables [6]. Light and Margolin were unaware that R ² was identical to Goodman and Kruskal’s t _b test statistic and that they had asymptotically solved the long-standing problem of testing the null hypothesis that the population parameter corresponding to Goodman and Kruskal’s t _b was zero; that is, H ₀: τ _b = 0. The identity between R ² and t _b was first recognized by Särndal in 1974 [9] and later discussed by Margolin and Light [7], where they showed that t _b(N − 1)(c − 1) was distributed as Pearson’s chi-squared with (r − 1)(c − 1) degrees of freedom.

Following Light and Margolin in the context of a completely-randomized analysis of variance for the frequency data given in Table 11.14, the sum-of-squares total is

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle \mathit{SS}_{\mathrm{Total}} = \frac{N}{2}-\frac{1}{2N}\sum_{i=1}^{r}n_{i.}^{2}\\ &\displaystyle &\displaystyle \ \qquad \qquad \qquad \qquad {}= \frac{110}{2}-\frac{1}{(2)(110)}\big( 37^{2}+35^{2}+38^{2} \big) = 36.6455\;, \end{array} \end{aligned} $$

the sum-of-squares between treatments is

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle \mathit{SS}_{\mathrm{Between}} = \frac{1}{2} \left( \sum_{i=1}^{r}\,\sum_{j=1}^{c} \frac{n_{ij}^{2}}{n_{.j}} \right)-\frac{1}{2N}\sum_{i=1}^{r}n_{i.}^{2}\\ &\displaystyle &\displaystyle \ \ {}= \frac{1}{2}\left( \frac{24^{2}}{25}+\frac{2^{2}}{25}+ \cdots +\frac{19^{2}}{33} \right)-\frac{1}{(2)(110)}\big( 37^{2}+35^{2}+38^{2} \big) = 16.2281\;, \end{array} \end{aligned} $$

the sum-of-squares within treatments is

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} &\displaystyle &\displaystyle \mathit{SS}_{\mathrm{Within}} = \sum_{j=1}^{c}\left( \frac{n_{.j}}{2}-\frac{1}{2n_{.j}} \sum_{i=1}^{r}n_{ij^{2}} \right)\\ &\displaystyle &\displaystyle \ \ {}= \frac{25}{2}-\frac{1}{(2)(25)} \big( 24^{2}+0^{2}+1^{2} \big)+ \cdots +\frac{33}{2}-\frac{1}{(2)(33)}\left( 6^{2}+8^{2}+19^{2} \right)\\ &\displaystyle &\displaystyle \quad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad {}= 20.4174\;,\vspace{-2pt} \end{array} \end{aligned} $$

and Light and Margolin’s test statistic is

$$\displaystyle \begin{aligned} R^{2} = \frac{\mathit{SS}_{\mathrm{Between}}}{\mathit{SS}_{\mathrm{Total}}} = \frac{16.9857}{36.6455} = 0.4428\;,\end{aligned} $$

which is identical to Goodman and Kruskal’s t _b = 0.4428.

The essential factors, sums of squares (SS), degrees of freedom (df), mean squares (MS), and variance-ratio test statistic (F) are summarized in Table 11.15 where df _Between = c − 1 = 4 − 1 = 3, df _Within = N − c = 110 − 4 = 106, and df _Total = N − 1 = 110 − 1 = 109. Under the Neyman–Pearson null hypothesis, H ₀: n _ij = n _i.∕c for i = 1, …, r and j = 1, …, c, where each of the c treatment groups possesses the same multinomial probability structure, test statistic F is asymptotically distributed as Snedecor’s F with ν ₁ = r − 1 and ν ₂ = N − r degrees of freedom. With ν ₁ = r − 1 = 4 − 1 = 3 and ν ₂ = N − r = 110 − 4 = 106 degrees of freedom, the asymptotic probability value of F = 28.0835 is P = 0.1917×10⁻¹², under the assumptions of normality and homogeneity.

Table 11.15 Source table for the data listed in Table 11.14

For the frequency data given in Table 11.14, the permutation test statistic is

$$\displaystyle \begin{aligned} \delta = \frac{2\mathit{SS}_{\mathrm{Within}}}{N-c} = \frac{2(20.4174)}{110-4} = 0.3852\;, \end{aligned}$$

the exact expected value of test statistic δ under the Fisher–Pitman null hypothesis is

$$\displaystyle \begin{aligned} \mu_{\delta} = \frac{2\mathit{SS}_{\mathrm{Total}}}{N-1} = \frac{2(36.6455)}{110-1} = 0.6724\;, \end{aligned}$$

and Mielke and Berry’s chance-corrected measure of effect size is

$$\displaystyle \begin{aligned} \Re = 1-\frac{\delta}{\mu_{\delta}} = 1-\frac{0.3852}{0.6724} = +0.4271\;, \end{aligned}$$

indicating approximately 43% agreement between variables A and B above what is expected by chance.

Alternatively, in terms of a completely-randomized analysis of variance model the chance-corrected measure of effect size is

$$\displaystyle \begin{aligned} \Re = 1-\frac{(N-1)(\mathit{SS}_{\mathrm{Within}})}{(N-c)(\mathit{SS}_{\mathrm{Total}})} = 1-\frac{(110-1)(20.4174)}{(110-4)(36.6455)} = +0.4271\;. \end{aligned}$$

Then the observed value of test statistic δ with respect to the observed value of Goodman and Kruskal’s t _b test statistic is

$$\displaystyle \begin{aligned} \delta = \frac{2\mathit{SS}_{\mathrm{Between}}(1-t_{b})}{t_{b}(N-c)} = \frac{2(16.2281)(1-0.4428)}{(0.4428)(110-4)} = 0.3852 \end{aligned}$$

and the observed value of Goodman and Kruskal’s t _b test statistic with respect to the observed value of test statistic δ is

$$\displaystyle \begin{aligned} t_{b} = \frac{2\mathit{SS}_{\mathrm{Between}}}{\delta(N-c)+2\mathit{SS}_{\mathrm{Between}}} = \frac{2(16.2281)}{(0.3852)(110-4)+2(16.2281)} = 0.4428\;. \end{aligned}$$

The observed value of test statistic δ with respect to the observed value of Fisher’s F-ratio test statistic is

$$\displaystyle \begin{aligned} \delta = \frac{2\mathit{SS}_{\mathrm{Between}}}{F(c-1)} = \frac{2(16.2281)}{(28.0835)(4-1)} = 0.3852 \end{aligned}$$

and the observed value of Fisher’s F-ratio test statistic with respect to the observed value of test statistic δ is

$$\displaystyle \begin{aligned} F = \frac{2\mathit{SS}_{\mathrm{Between}}}{\delta(c-1)} = \frac{2(16.2281)}{(0.3852)(4-1)} = 28.0835\;. \end{aligned}$$

The observed value of Goodman and Kruskal’s t _b test statistic with respect to the observed value of Mielke and Berry’s $\Re$ measure of effect size is

$$\displaystyle \begin{aligned} t_{b} = \frac{\Re(N-c)+c-1}{N-1} = \frac{(0.4271)(110-4)+4-1}{110-1} = 0.4428 \end{aligned}$$

and the observed value of Mielke and Berry’s $\Re$ measure of effect size with respect to Goodman and Kruskal’s t _b test statistic is

$$\displaystyle \begin{aligned} \Re = 1-\frac{(N-1)(1-t_{b})}{N-c} = 1-\frac{(110-1)(1-0.4428)}{110-4} = +0.4271\;. \end{aligned}$$

The observed value of Mielke and Berry’s $\Re$ measure of effect size with respect to the observed value of Fisher’s F-ratio test statistic is

$$\displaystyle \begin{aligned} \Re = 1-\frac{(N-1)\mathit{SS}_{\mathrm{Between}}}{F(c-1)\mathit{SS}_{\mathrm{Total}}} = 1-\frac{(110-1)(16.2281)}{(28.0835)(4-1)(36.6455)} = +0.4271 \end{aligned}$$

and the observed value of Fisher’s F-ratio test statistic with respect to the observed value of Mielke and Berry’s $\Re$ measure of effect size is

$$\displaystyle \begin{aligned} F = \frac{\mathit{SS}_{\mathrm{Between}}(N-1)}{\mathit{SS}_{\mathrm{Total}}(c-1)(1-\Re)} = \frac{(16.2281)(110-1)}{(36.6455)(4-1)(1-0.4271)} = 28.0835\;. \end{aligned}$$

11.3 Contingency Measures: Ordinal by Ordinal

There exist numerous measures of association for the cross-classification of two ordinal (ranked) variables. Three popular measures of ordinal-ordinal association are Goodman and Kruskal’s symmetric measure of ordinal association denoted by G and two asymmetric measures of ordinal association by Somers denoted by d _yx and d _xy.⁷ These three measures and several others are based on the numbers of concordant and discordant pairs present in the observed contingency table. To illustrate the calculation of concordant and discordant pairs, consider the 3×5 contingency table given in Table 11.16 with N = 63 observations.

Table 11.16 Example data for Goodman and Kruskal’s G measure of ordinal-ordinal association with r = 3 rows, c = 5 columns, and N = 63 cross-classified observations

For any ordered contingency table there are five types of pairs to be considered: concordant pairs (C), discordant pairs (D), pairs that are tied on variable x but not tied on variable y (T _x), pairs tied on variable y but not tied on variable x (T _y), and pairs tied on both variable x and variable y (T _xy). Together they sum to the number of possible pairs in the table; that is,

$$\displaystyle \begin{aligned} C+D+T_{x}+T_{y}+T_{xy} = \frac{N(N-1)}{2}\;. \end{aligned}$$

To demonstrate the calculation of concordant (C) and discordant (D) pairs, consider the two sets of rank scores listed in Table 11.17, where there are no tied ranks. Consider the first pair of objects: Objects 1 and 2. For Object 1, x ₁ = 1 and y ₁ = 3, and for Object 2, x ₂ = 3 and y ₂ = 4. Since x ₁ < x ₂ and y ₁ < y ₂ (1 < 3 and 3 < 4), the pair is considered to be concordant. Now consider a second pair of objects: Objects 1 and 3. For Object 1, x ₁ = 1 and y ₁ = 3, and for Object 3, x ₃ = 2 and y ₃ = 1. Since x ₁ < x ₃ and y ₁ > y ₃ (1 < 2 and 3 > 1), the pair is considered to be discordant. For the untied rank data listed in Table 11.17, the number of concordant pairs is C = 23 and the number of concordant pairs is D = 5. The

$$\displaystyle \begin{aligned} \frac{N(N-1)}{2} = \frac{8(8-1)}{2} = 28 \end{aligned}$$

concordant (C) and discordant (D) pairs for the rank-score data listed in Table 11.17 are listed in Table 11.18.

Table 11.17 Two sets of N = 8 rank scores with no tied scores

Table 11.18 Paired differences: concordant (C) and discordant (D) values for the rank scores listed in Table 11.17

To illustrate the calculation of the T _x, T _y, and T _xy tied pairs, consider the two sets of rank scores listed in Table 11.19, where there are multiple tied rank scores on both variable x and variable y. For the rank scores listed in Table 11.19, N = 6, the number of concordant pairs is C = 8, the number of discordant pairs is D = 2, the number of pairs tied on variable x is T _x = 1, the number of pairs tied on variable y is T _y = 2, and the number of pairs tied on both variable x and variable y is T _xy = 2. Table 11.20 lists the

$$\displaystyle \begin{aligned} \frac{N(N-1)}{2} = \frac{6(6-1)}{2} = 15 \end{aligned}$$

paired differences: concordant pairs (C), discordant pairs (D), pairs tied on variable x (T _x), pairs tied on variable y (T _y), and pairs tied on both variable x and variable y (T _xy).

Table 11.19 Two sets of rank scores with tied scores

Table 11.20 Paired differences: C, D, T _x, T _y, and T _xy values for the rank scores listed in Table 11.19

11.3.1 An Example Analysis for G

For the example rank data given in Table 11.16 on p. 438 with N = 63 observations, the number of concordant pairs is

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle C = \sum_{i=1}^{r-1} \,\sum_{j=1}^{c-1}n_{ij} \left( \,\sum_{k=i+1}^{r} \,\sum_{l=j+1}^{c} n_{kl} \right)\\ &\displaystyle &\displaystyle \ \ \quad {}= (6)(8+5+8+4+1+6+6+3)+(2)(5+8+4+6+6+3)\\ &\displaystyle &\displaystyle \ \ \quad \qquad \qquad \qquad \qquad \qquad \qquad \qquad {}+ \cdots +(5)(6+3)+(8)(3)) = 653\;, \end{array} \end{aligned} $$

the number of discordant pairs is

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} &\displaystyle &\displaystyle D = \sum_{i=1}^{r-1} \,\sum_{j=1}^{c-1} n_{i,c-j+1} \left( \: \sum_{k=i+1}^{r} \,\sum_{l=1}^{c-j} n_{kl} \right)\\ &\displaystyle &\displaystyle \ \ \quad {}= (1)(0+8+5+8+1+1+6+6)+(7)(0+8+5+1+1+6)\\ &\displaystyle &\displaystyle \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad {}+ \cdots +(5)(1+1)+(8)(1) = 372\:, \end{array} \end{aligned} $$

and Goodman and Kruskal’s measure of ordinal-ordinal association is

$$\displaystyle \begin{aligned} G = \frac{C-D}{C+D} = \frac{653-372}{653+372} = +0.2741\;. \end{aligned}$$

Under the Neyman–Pearson null hypothesis, H ₀: γ = 0, Goodman and Kruskal’s G measure of ordinal-ordinal association is asymptotically distributed N(0, 1) as N →∞ with a standard error given by

$$\displaystyle \begin{aligned} s_{G} = \sqrt{\frac{N(1-G^{2})}{C+D}}\;. \end{aligned}$$

For the frequency data given in Table 11.16,

$$\displaystyle \begin{aligned} z = \frac{G}{\sqrt{\displaystyle\frac{N(1-G^{2})}{C+D}}} = \frac{+0.2741}{\sqrt{\displaystyle\frac{63[1-(0.2741)^{2}]}{653+372}}} = +1.1496\;, \end{aligned}$$

yielding an asymptotic upper-tail N(0, 1) probability value of P = 0.1252, under the assumption of normality.

11.3.2 An Exact Permutation Analysis for G

Under the Fisher–Pitman permutation model, the exact probability value of an observed value of Goodman and Kruskal’s G measure of ordinal-ordinal association is given by the sum of the hypergeometric point probability values associated with values of test statistic G that are equal to or greater than the observed value of G = +0.2741. For the frequency data given in Table 11.16 with N = 63 observations, there are M = 11, 356, 797 possible, equally-likely arrangements in the reference set of all permutations of cell frequencies given the observed row and column marginal frequency distributions {21, 25, 17} and {7, 11, 16, 21, 8}, respectively, making an exact permutation analysis feasible. The exact probability value of the observed value of test statistic G is P = 0.0336; that is, the sum of the hypergeometric point probability values associated with values of G = +0.2741 or greater.

11.3.3 The Relationship Between Statistics G and δ

The functional relationships between test statistic δ and Goodman and Kruskal’s G measure of ordinal-ordinal association are given by

$$\displaystyle \begin{aligned} \delta = \frac{N(N-1)-2G(C+D)}{2N} \quad \mbox{and} \quad G = \frac{N\left( \displaystyle\frac{N-1}{2}-\delta \right)}{C+D}\;. \end{aligned}$$

For the frequency data given in Table 11.16, the observed value of test statistic δ with respect to the observed value of Goodman and Kruskal’s G measure of ordinal-ordinal association is

$$\displaystyle \begin{aligned} \delta = \frac{63(63-1)-1(+0.2741)(653+372)}{(2)(63)} = 26.5404 \end{aligned}$$

and the observed value of Goodman and Kruskal’s G measure of ordinal-ordinal association with respect to the observed value of test statistic δ is

$$\displaystyle \begin{aligned} G = \frac{63 \left( \displaystyle\frac{63-1}{2}-26.5404 \right)}{653+372} = +0.2741\;. \end{aligned}$$

11.3.4 Somers’ d _yx and d _xy Measures

While Goodman and Kruskal’s G measure of ordinal-ordinal association is a symmetric measure, Somers’ two asymmetric proportional-reduction-in-error (PRE) measures (d _yx and d _xy) allow researchers to specify an independent and a dependent variable. For Somers’ d _yx, the dependent variable is typically the column variable labeled y and for Somers’ d _xy, the dependent variable is typically the row variable labeled x. The two asymmetric measures are given by

$$\displaystyle \begin{aligned} d_{yx} = \frac{C-D}{C+D+Ty} \quad \mbox{and} \quad d_{xy} = \frac{C-D}{C+D-T_{x}}\;, \end{aligned} $$

(11.4)

where C is the number of concordant pairs, D is the number of discordant pairs, T _x is the number of pairs tied on the row variable, and T _y is the number of pairs tied on the column variable. As is evident in Eq. (11.4), Somers included in the denominators of d _yx and d _xy the number of tied pairs on the dependent variable: T _y for d _yx and T _x for d _xy. The rationale for including the tied pairs is simply that when variable y is the dependent variable (d _yx), then if two values of the independent variable x differ, but the corresponding two values of the dependent variable y do not differ (are tied), there is evidence of a lack of association and the ties on dependent variable y (T _y) should be included in the denominator where they act to decrease the value of d _yx. The same rationale holds for Somers’ d _xy where the ties on dependent variable x (T _x) are included in the denominator.

11.3.5 An Example Analysis for d _yx

For the frequency data given in Table 11.16 on p. 438, replicated in Table 11.21 for convenience, the number of concordant pairs is

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle C = \sum_{i=1}^{r-1} \,\sum_{j=1}^{c-1}n_{ij} \left( \,\sum_{k=i+1}^{r} \,\sum_{l=j+1}^{c} n_{kl} \right)\\ &\displaystyle &\displaystyle \qquad {}= (6)(8+5+8+4+1+6+6+3)+(2)(5+8+4+6+6+3)\\ &\displaystyle &\displaystyle \ \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad {}+ \cdots +(5)(6+3)+(8)(3)) = 653\;, \end{array} \end{aligned} $$

Table 11.21 Example data for Somers’ d _yx and d _xy measures of ordinal-ordinal association with r = 3 rows, c = 5 columns, and N = 63 cross-classified observations

the number of discordant pairs is

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle D = \sum_{i=1}^{r-1} \,\sum_{j=1}^{c-1} n_{i,c-j+1} \left( \: \sum_{k=i+1}^{r} \,\sum_{l=1}^{c-j} n_{kl} \right)\\ &\displaystyle &\displaystyle \qquad {}= (1)(0+8+5+8+1+1+6+6)+(7)(0+8+5+1+1+6)\\ &\displaystyle &\displaystyle \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad {}+ \cdots +(5)(1+1)+(8)(1) = 372\:, \end{array} \end{aligned} $$

the number of pairs tied on variable x is

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle T_{x} = \sum_{i=1}^{r} \,\sum_{j=1}^{c-1} n_{ij} \left( \, \sum_{k = j+1}^{c} n_{ik} \right)\\ &\displaystyle &\displaystyle \ \ \qquad {} = (6)(2+5+7+1)+(2)(5+7+1)+(5)(7+1)+(7)(1)\\ &\displaystyle &\displaystyle \qquad \qquad \qquad \qquad {}+ \cdots +(1)(6+6+3)+(6)(6+3)+(6)(3) = 494\:, \end{array} \end{aligned} $$

the number of pairs tied on dependent variable y is

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} &\displaystyle &\displaystyle T_{y} = \sum_{j=1}^{c} \,\sum_{i=1}^{r-1} n_{ij} \left( \;\sum_{k=i+1}^{r} n_{kj} \right)\\ &\displaystyle &\displaystyle \qquad \qquad \qquad {}= (6)(0+1)+(0)(1)+(2)(8+1)+(8)(1)\\ &\displaystyle &\displaystyle \ \qquad \quad \qquad \qquad \qquad \qquad \qquad \qquad {}+ \cdots +(1)(4+3)+(4)(3) = 282\:, \end{array} \end{aligned} $$

and Somers’ d _yx asymmetric measure of ordinal-ordinal association is

$$\displaystyle \begin{aligned} d_{yx} = \frac{C-D}{C+D+T_{y}} = \frac{653-372}{653+372+282} = +0.2150\;. \end{aligned}$$

For an r×c contingency table, d _yx is asymptotically distributed N(0, 1) under the Neyman–Pearson null hypothesis as N →∞ with a standard error given by

$$\displaystyle \begin{aligned} s_{d_{yx}} = \frac{2}{3r}\sqrt{\frac{(r^{2}-1)(c+1)}{N(c-1)}}\;. \end{aligned}$$

For the frequency data given in Table 11.21,

$$\displaystyle \begin{aligned} z = \frac{d_{yx}}{\displaystyle\frac{2}{3r}\sqrt{\frac{(r^{2}-1)(c+1)}{N(c-1)}}} = \frac{+0.2150}{{\displaystyle\frac{2}{(3)(3)}}\sqrt{\displaystyle\frac{(3^{2}-1)(5+1)}{(63)(5-1)}}} = +2.2168\;, \end{aligned}$$

yielding an asymptotic upper-tail N(0, 1) probability value of P = 0.0133, under the assumption of normality.

11.3.6 An Exact Permutation Analysis for d _yx

Under the Fisher–Pitman permutation model, the exact probability value of an observed value of Somers’ d _yx is given by the sum of the hypergeometric point probability values associated with values of test statistic d _yx that are equal to or greater than the observed value of d _yx = +0.2150. For the frequency data given in Table 11.21, there are M = 11, 356, 797 possible, equally-likely arrangements in the reference set of all permutation of cell frequencies given the observed row and column marginal frequency distributions {21, 25, 17} and {7, 11, 16, 21, 8}, respectively, making an exact permutation analysis feasible. The exact probability value of d _yx = +0.2150 is P = 0.0331; that is, the sum of the hypergeometric point probability values associated with values of d _yx = +0.2150 or greater.

11.3.7 The Relationship Between Statistics d _yx and δ

The functional relationships between test statistic δ and Somers’ d _yx asymmetric measure of ordinal-ordinal association are given by

$$\displaystyle \begin{aligned} \delta = \frac{N-1}{2}-\frac{d_{yx}(C+D+T_{y})}{N} \quad \mbox{and} \quad d_{yx} = \frac{N \left( \displaystyle\frac{N-1}{2}-\delta \right)}{C+D+T_{y}}\;. \end{aligned}$$

For the frequency data given in Table 11.21, the observed value of test statistic δ with respect to the observed value of Somers’ d _yx measure of ordinal-ordinal association is

$$\displaystyle \begin{aligned} \delta = \frac{63-1}{2}-\frac{+0.2150(653+372+282)}{63} = 26.5396 \end{aligned}$$

and the observed value of Somers’ d _yx measure of ordinal-ordinal association with respect to the observed value of test statistic δ is

$$\displaystyle \begin{aligned} d_{yx} = \frac{63 \left( \displaystyle\frac{63-1}{2}-26.5396 \right)}{653+372+282} = +0.2150\;. \end{aligned}$$

11.3.8 An Example Analysis for d _xy

For the frequency data given in Table 11.21, the number of concordant pairs is C = 653, the number of discordant pairs is D = 372, the number of pairs tied on dependent variable x is T _x = 494, and Somers’ d _xy asymmetric measure of ordinal-ordinal association is

$$\displaystyle \begin{aligned} d_{xy} = \frac{C-D}{C+D+T_{x}} = \frac{653-372}{653+372+494} = +0.1850\;. \end{aligned}$$

For an r×c contingency table, d _yx is asymptotically distributed N(0, 1) under the Neyman–Pearson null hypothesis as N →∞ with a standard error given by

$$\displaystyle \begin{aligned} s_{d_{yx}} = \frac{2}{3c}\sqrt{\frac{(c^{2}-1)(r+1)}{N(r-1)}}\;. \end{aligned}$$

For the frequency data given in Table 11.21,

$$\displaystyle \begin{aligned} z = \frac{d_{yx}}{\displaystyle\frac{2}{3c}\sqrt{\frac{(c^{2}-1)(r+1)}{N(r-1)}}} = \frac{+0.1850}{{\displaystyle\frac{2}{(3)(5)}}\sqrt{\displaystyle\frac{(5^{2}-1)(3+1)}{(63)(5-1)}}} = +2.2480\;, \end{aligned}$$

yielding an asymptotic upper-tail N(0, 1) probability value of P = 0.0123, under the assumption of normality.

11.3.9 An Exact Permutation Analysis for d _xy

Under the Fisher–Pitman permutation model, the exact probability value of an observed value of Somers’ d _xy is given by the sum of the hypergeometric point probability values associated with values of test statistic d _xy that are equal to or greater than the observed value of d _xy = +0.1850. For the frequency data given in Table 11.21, there are M = 11, 356, 797 possible, equally-likely arrangements in the reference set of all permutation of cell frequencies given the observed row and column marginal frequency distributions {21, 25, 17} and {7, 11, 16, 21, 8}, respectively, making an exact permutation analysis feasible. The exact probability value of d _xy = +0.1850 is P = 0.0331; that is, the sum of the hypergeometric point probability values associated with values of d _xy = +0.1850 or greater.

11.3.10 The Relationship Between d _xy and δ

The functional relationships between test statistic δ and Somers’ d _xy asymmetric measure of ordinal-ordinal association are given by

$$\displaystyle \begin{aligned} \delta = \frac{N-1}{2}-\frac{d_{yx}(C+D+T_{x})}{N} \quad \mbox{and} \quad d_{xy} = \frac{N \left( \displaystyle\frac{N-1}{2}-\delta \right)}{C+D+T_{x}}\;. \end{aligned}$$

For the frequency data given in Table 11.21, the observed value of test statistic δ with respect to the observed value of Somers’ d _xy measure of ordinal-ordinal association is

$$\displaystyle \begin{aligned} \delta = \frac{63-1}{2}-\frac{+0.1850(653+372+494)}{63} = 26.5394 \end{aligned}$$

and the observed value of Somers’ d _xy measure of ordinal association with respect to the observed value of test statistic δ is

$$\displaystyle \begin{aligned} d_{xy} = \frac{63 \left( \displaystyle\frac{63-1}{2}-26.5394 \right)}{653+372+494} = +0.1850\;. \end{aligned}$$

11.3.11 Probability Values for d _yx and d _xy

It may appear inconsistent that while Somers’ two measures of effect size differ (d _yx = +0.2150 and d _xy = 0.1850), they both yield the same probability value of P = 0.0331. It follows from the fact that the denominators of d _yx and d _xy (C + D + T _y and C + D + T _x, respectively) can be computed from just the marginal frequency distributions, which are fixed for all possible arrangements of cell frequencies and are, therefore, invariant under permutation.

It is easily shown that C + D + T _y can be obtained from N and the row marginal frequency distribution. Recall that for the frequency data listed in Table 11.21 on p. 443, the number of concordant pairs is C = 653, the number of discordant pairs is D = 372, the number of pairs tied on variable y is T _y = 282, and C + D + T _y = 653 + 372 + 282 = 1307. Then with N = 63,

$$\displaystyle \begin{aligned} C+D+T_{y} = \frac{1}{2}\left( N^{2}-\sum_{i=1}^{r} n_{i.}^{2} \right) = \frac{1}{2}\Big[ 63^{2}-\big(21^{2}+25^{2}+17^{2}\big) \Big] = 1307\;. \end{aligned}$$

In such manner C + D + T _x can be obtained from N and the column marginal frequency distribution. For the frequency data listed in Table 11.21, the number of concordant pairs is C = 653, the number of discordant pairs is D = 372, the number of pairs tied on variable x is T _x = 494, and C + D + T _x = 653 + 372 + 494 = 1519. Then with N = 63,

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} &\displaystyle &\displaystyle C+D+T_{x} = \frac{1}{2}\left( N^{2}-\sum_{j=1}^{c} n_{.j}^{2} \right)\\ &\displaystyle &\displaystyle \qquad \qquad \qquad \qquad \qquad {}= \frac{1}{2}\Big[ 63^{2}-\big(7^{2}+11^{2}+16^{2}+21^{2}+8^{2}\big) \Big] = 1519\;. \end{array} \end{aligned} $$

11.4 Contingency Measures: Nominal by Ordinal

There exist any number of measures of association for which the standard error is unknown. Permutation statistical methods do not rely on knowledge of standard errors and therefore provide much-needed probability values for a number of otherwise very useful measures of association. One measure without a known standard error is Freeman’s θ measure of nominal-ordinal association [5, pp. 108–119].

Consider an r×c contingency table where the r rows are a nominal-level (categorical) independent variable (x) and the c columns are an ordinal-level (ranked) dependent variable (y). For Freeman’s θ it is necessary to calculate the absolute sum of the number of concordant pairs and number of discordant pairs for all combinations of the nominal-level independent variable (rows) considered two at a time. Assuming that the column ordered variable (y) is underlying continuous and that ties in ranking result simply from a crude classification of the continuous variable, Freeman’s nominal-ordinal measure of association is given by

$$\displaystyle \begin{aligned} \theta = \frac{\displaystyle\sum_{i=1}^{r-1}\,\sum_{j=i+1}^{r} \big| C_{ij}-D_{ij} \big|}{C+D+T_{y}}\;.\end{aligned} $$

11.4.1 An Example Analysis for θ

To illustrate the calculation of Freeman’s θ measure of nominal-ordinal association, consider the 4×5 contingency table given in Table 11.22 with N = 40 observations. For the frequency data given in Table 11.22 with N = 40 observations, the number of concordant pairs is

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle C = \sum_{i=1}^{r-1} \,\sum_{j=1}^{c-1}n_{ij} \left( \,\sum_{k=i+1}^{r} \,\sum_{l=j+1}^{c} n_{kl} \right)\\ &\displaystyle &\displaystyle \ \ \quad \qquad {}= (1)(5+5+0+0+0+2+2+1+0+0+2+3)\\ &\displaystyle &\displaystyle \quad \qquad \quad \qquad {}+(2)(5+0+0+2+2+1+0+2+3)\\ &\displaystyle &\displaystyle \ \ \qquad \qquad \qquad \qquad \qquad \qquad \qquad {}+ \cdots +(2)(2+3)+(2)(3)) = 304\;, \end{array} \end{aligned} $$

Table 11.22 Example data for Freeman’s θ measure of nominal-ordinal association with r = 4 rows, c = 5 columns, and N = 40 cross-classified observations

the number of discordant pairs is

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle D = \sum_{i=1}^{r-1} \,\sum_{j=1}^{c-1} n_{i,c-j+1} \left( \: \sum_{k=i+1}^{r} \,\sum_{l=1}^{c-j} n_{kl} \right)\\ &\displaystyle &\displaystyle \qquad \qquad {}= (0)(10+5+5+0+0+0+2+2+0+0+0+2)\\ &\displaystyle &\displaystyle \qquad \qquad \qquad {}+(2)(10+5+6+0+0+2+0+0+0)\\ &\displaystyle &\displaystyle \quad \qquad \qquad \qquad \qquad \qquad \qquad \qquad {}+ \cdots +(2)(0+0)+(0)(0) = 141\:, \end{array} \end{aligned} $$

the number of pairs tied on variable y is

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle T_{y} = \sum_{j=1}^{c} \,\sum_{i=1}^{r-1} n_{ij} \left( \;\sum_{k=i+1}^{r} n_{kj} \right)\\ &\displaystyle &\displaystyle \quad \qquad \qquad {}= (1)(10+0+0)+(10)(0+0)+(0)(0)\\ &\displaystyle &\displaystyle \ \qquad \qquad \quad \qquad {}+ \cdots +(0)(0+1+3)+(1)(1+3)+(1)(3) = 80\;, \end{array} \end{aligned} $$

the concordant and discordant pairs for the r = 4 rows considered two at a time are

$$\displaystyle \begin{aligned} C_{12} &= (1)(5+5+0+0)+(2)(5+0+0)+(5)(0+0)+(2)(0) = 20\;,\\ {} D_{12} &= (0)(10+5+5+0)+(2)(10+5+5)+(5)(10+5)+(2)(10) = 135\;,\\ C_{13} &= (1)(0+2+2+1)+(2)(2+2+1)+(5)(2+1)+(2)(1) = 32\;,\\ {} D_{13} &= (0)(0+0+2+2)+(2)(0+0+2)+(5)(0+0)+(2)(0) = 4\;,\\ C_{14} &= (1)(0+0+2+3)+(2)(0+2+3)+(5)(2+3)+(2)(3) = 46\;,\\ {} D_{14} &= (0)(0+0+0+2)+(2)(0+0+0)+(5)(0+0)+(2)(0) = 0\;,\\ C_{23} &= (10)(0+2+2+1)+(5)(2+2+1)+(5)(2+1)+(0)(1) = 90\;,\\ {} D_{23} &= (0)(0+0+2+2)+(0)(0+0+2)+(5)(0+0)+(5)(0) = 0\;,\\ C_{24} &= (10)(0+0+2+3)+(5)(0+2+3)+(5)(2+3)+(0)(3) = 100\;.\\ {} D_{24} &= (0)(0+0+0+2)+(0)(0+0+0)+(5)(0+0)+(5)(0) = 0\;,\\ C_{34} &= (0)(0+0+2+3)+(0)(0+2+3)+(2)(2+3)+(2)(3) = 16\;,\\ {} D_{34} &= (1)(0+0+0+2)+(2)(0+0+0)+(2)(0+0)+(0)(0) = 2\;, \end{aligned} $$

and Freeman’s θ is

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} &\displaystyle &\displaystyle \theta = \frac{\displaystyle\sum_{i=1}^{r-1}\,\sum_{j=i+1}^{r} \big| \,C_{ij}-D_{ij} \big|}{C+D+T_{y}}\\ &\displaystyle &\displaystyle \quad {}= \frac{|20-135|+|32-4|+|46-0|+|90-0|+|100-0|+|16-2|}{304+141+80}\\ &\displaystyle &\displaystyle \ \ \quad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad {}= 0.7486\;. \end{array} \end{aligned} $$

11.4.2 An Exact Permutation Analysis for θ

Under the Fisher–Pitman permutation model, the exact probability value of an observed value of θ = 0.7486 is given by the sum of the hypergeometric point probability values associated with the values of test statistic θ calculated on all M possible arrangements of the cell frequencies that are equal to or greater than the observed value of θ = 0.7486. For the frequency data given in Table 11.22, there are only M = 6, 340, 588 possible arrangements in the reference set of all permutations of cell frequencies consistent with the observed row and column marginal frequency distributions, {10, 20, 5, 5} and {11, 7, 12, 6, 4}, respectively, making an exact permutation analysis feasible.

If all M possible arrangements of the observed data occur with equal chance, the exact probability value of Freeman’s θ under the Fisher–Pitman null hypothesis is the sum of the hypergeometric point probability values associated with the arrangements of cell frequencies with values of θ that are equal to or greater than the observed value of θ = 0.7486. Based on the underlying hypergeometric probability distribution, the exact probability value of θ = 0.7486 is P = 0.2105×10⁻¹⁰.

11.5 Contingency Measures: Nominal by Interval

Pearson’s point-biserial correlation coefficient, denoted by r _pb, measures the association between a nominal-level (categorical) variable with two categories and an interval-level variable. Pearson’s point-biserial correlation coefficient is an important measure in fields such as education and educational psychology where it is typically used to measure the correlation between test questions scored as correct (1) or incorrect (0) and the overall score on the test for N test takers. A low or negative point-biserial correlation coefficient indicates that the test takers with the highest scores on the test answered the question incorrectly and the test takers with the lowest scores on the test answered the question correctly, alerting the instructor to the possibility that the question failed to discriminate properly and may be faulty.

11.5.1 An Example Analysis for r _pb

To illustrate the calculation of Pearson’s point-biserial correlation coefficient, consider the dichotomous data listed in Table 11.23 for N = 20 observations where variable x is the dichotomous variable and variable y is an unspecified interval-level variable. The point-biserial correlation coefficient is often expressed as

$$\displaystyle \begin{aligned} r_{pb} = \frac{\bar{y}_{0}-\bar{y}_{1}}{s_{y}}\sqrt{\frac{n_{0}n_{1}}{N(N-1)}}\;, \end{aligned}$$

where n ₀ and n ₁ denote the number of y values coded 0 and 1, respectively, N = n ₀ + n ₁, $\bar {y}_{0}$ and $\bar {y}_{1}$ denote the means of the y values coded 0 and 1, respectively, and s _y is the sample standard deviation of the y values given by

$$\displaystyle \begin{aligned} s_{y} = \sqrt{\frac{1}{N-1} \sum_{i=1}^{N} \big( y_{i}-\bar{y} \big)^{2}}\;. \end{aligned}$$

For the data listed in Table 11.23, n ₀ = n ₁ = 10,

$$\displaystyle \begin{aligned} \bar{y}_{0} = \frac{1}{n_{0}} \sum_{i=1}^{n_{0}}y_{i} = \frac{99+99+ \cdots +89}{10} = 88.40\;, \end{aligned}$$

$$\displaystyle \begin{aligned} \bar{y}_{1} = \frac{1}{n_{1}} \sum_{i=1}^{n_{1}}y_{i} = \frac{98+98+ \cdots +60}{10} = 95.60\;, \end{aligned}$$

$$\displaystyle \begin{aligned} s_{y} = \sqrt{\frac{1}{N-1} \sum_{i=1}^{N}\big( y_{i}-\bar{y} \big)^{2}} = \sqrt{\frac{1456}{20-1}} = 8.7539\;, \end{aligned}$$

and Pearson’s point-biserial correlation coefficient is

$$\displaystyle \begin{aligned} r_{pb} = \frac{\bar{y}_{0}-\bar{y}_{1}}{s_{y}}\sqrt{\frac{n_{0}n_{1}}{N(N-1)}} = \frac{88.40-95.60}{8.7539}\sqrt{\frac{(10)(10)}{20(20-1)}} = -0.4219\;. \end{aligned}$$

Table 11.23 Example (0, 1) coded data for Pearson’s point-biserial correlation coefficient

Alternatively, with

$$\displaystyle \begin{gathered} {} \sum_{i=1}^{N}x_{i} = 10\;, \quad \sum_{i=1}^{N}x_{i}^{2} = 10\;, \quad \sum_{i=1}^{N}y_{i} = 1840\;, \quad \sum_{i=1}^{N}y_{i}^{2} = 170{,}736\;,\\ \mbox{and} \quad \sum_{i=1}^{N}x_{i}y_{i} = 884\;, \end{gathered} $$

Pearson’s point-biserial correlation coefficient is simply the product-moment correlation between dichotomous variable x and interval-level variable y. Thus,

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} &\displaystyle &\displaystyle r_{pb} = \frac{N \displaystyle\sum_{i=1}^{N}x_{i}y_{i}-\displaystyle\sum_{i=1}^{N}x_{i}\displaystyle\sum_{i=1}^{N}y_{i}}{\sqrt{\left[N \displaystyle\sum_{i=1}^{N}x_{i}^{2}-\left( \displaystyle\sum_{i=1}^{N} x_{i} \right)^{2}\,\right]\left[N \displaystyle\sum_{i=1}^{N}y_{i}^{2}-\left( \displaystyle\sum_{i=1}^{N} y_{i} \right)^{2}\,\right]}}\\ &\displaystyle &\displaystyle \quad \qquad \quad \qquad {}= \frac{(20)(884)-(10)(1840)}{\sqrt{\big[ (20)(10)-10^{2} \big]\big[ (20)(170{,}736)-1840^{2} \big]}} = -0.4219\;. \end{array} \end{aligned} $$

The conventional test of significance for Pearson’s point-biserial correlation coefficient is

$$\displaystyle \begin{aligned} t = r_{pb} \sqrt{\frac{N-2}{1-r_{pb}^{2}}} = -0.4219 \sqrt{\frac{20-2}{1-(-0.4219)^{2}}} = -1.9743\;. \end{aligned}$$

Under the Neyman–Pearson null hypothesis, H ₀: ρ _pb = 0, test statistic t is asymptotically distributed as Student’s t with N − 2 degrees of freedom. With N − 2 = 20 − 2 = 18 degrees of freedom, the asymptotic two-tail probability value of t = −1.9743 is P = 0.0639, under the assumption of normality. For a critical evaluation of the point-biserial correlation coefficient, see a discussion in The Measurement of Association by the authors [2, pp. 417–424].

11.5.2 An Exact Permutation Analysis for r _pb

For the bivariate observations listed in Table 11.23, there are only

$$\displaystyle \begin{aligned} M = \frac{(n_{0}+n_{1})!}{n_{0}!\;n_{1}!} = \frac{(10+10)!}{10!\;10!} = 184{,}756 \end{aligned}$$

possible, equally-likely arrangements in the reference set of all permutations of the observed scores, making an exact permutation analysis possible. Under the Fisher–Pitman permutation model, the exact probability of an observed value of Pearson’s |r _pb| is the proportion of |r _pb| values calculated on all possible arrangements of the observed data that are equal to or greater than the observed value of |r _pb| = 0.4219. There are exactly 11,296 |r _pb| values that are equal to or greater than the observed value of |r _pb| = 0.4219. If all arrangements of the N = 20 observed scores occur with equal chance, the exact probability value of |r _pb| = 0.4219 computed on the M = 184, 756 possible arrangements of the observed data with n ₀ = n ₁ = 10 preserved for each arrangement is

where denotes the observed absolute value of test statistic r _pb and M is the number of possible, equally-likely arrangements of the N = 20 bivariate observations listed in Table 11.23.

11.6 Contingency Measures: Ordinal by Interval

The best-known and most-widely reported measure of ordinal-by-interval association is Jaspen’s multiserial correlation coefficient, which is simply the Pearson product-moment correlation coefficient between an interval-level variable, Y , and a transformation of an ordinal-level variable, X. Given N values on the interval variable and k disjoint, ordered categories on the ordinal variable, the mean standard score of the underlying scale for a given category is given by

$$\displaystyle \begin{aligned} \bar{Z}_{j} = \frac{Y_{L_{j}}-Y_{U_{j}}}{p_{j}} \qquad \mbox{for }j = 1,\,\ldots,\,k\;, \end{aligned}$$

where $Y_{L_{j}}$ and $Y_{U_{j}}$ are the lower and upper ordinates of the segment of the N(0, 1) distribution corresponding to the jth ordered category, and where p _j is the proportion of cases in the jth of k ordered categories. Given the obtained values of $\bar {Z}_{j}$, j = 1, …, k, and the original N values of the interval-level variable, a standard Pearson product-moment correlation between the Y  and $\bar {Z}$ values yields the multiserial correlation coefficient.

11.6.1 An Example Analysis for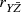

To illustrate the calculation of Jaspen’s multiserial correlation coefficient, consider the small set of data given in Table 11.24 where N = 32 interval-level variables are listed in k = 4 disjoint, ordered categories: A, B, C, and D. Table 11.25 illustrates the calculation of Jaspen’s multiserial correlation coefficient. The first column, headed X in Table 11.25, lists the k = 4 ordered categories of variable X. The second column, headed n, lists the number of observations in each of the k ordered categories. The third column, headed p, lists the proportion of observations in each of the k ordered categories. The fourth column, headed P, lists the cumulative proportion of observations in each of the k ordered categories. The fifth column, headed z, lists the standard score that defines the cumulative proportion from the fourth column under the unit-normal distribution for each of the k ordered categories. For example, for category A the standard score that defines the lowest (left-tail) of the normal distribution with proportion P = 0.1250 is z = −1.1503. The sixth column, headed Y _L, lists the height of the ordinate at the standard score listed in the fifth column below the specified segment of the unit-normal distribution. For example, for category A,

$$\displaystyle \begin{aligned} Y_{L_{A}} = \frac{\exp(-z^{2}/2)}{\sqrt{2\pi}} = \frac{\exp \big[-(-1.1503)^{2}/2 \big]}{\sqrt{2(3.1416)}} = 0.2059\;. \end{aligned}$$

The seventh column, headed Y _U, lists the height of the ordinate at the standard score listed in the fifth column above the specified segment of the unit-normal distribution. For example, for category C,

$$\displaystyle \begin{aligned} Y_{U_{C}} = \frac{\exp(-z^{2}/2)}{\sqrt{2\pi}} = \frac{\exp \big[-(-0.1573)^{2}/2 \big]}{\sqrt{2(3.1416)}} = 0.3940\;. \end{aligned}$$

The last column, headed $\bar {Z}$, lists the average standard scores for the k ordered categories. For example, for category B,

$$\displaystyle \begin{aligned} \bar{Z}_{B} = \frac{Y_{L_{B}}-Y_{U_{B}}}{p_{B}} = \frac{0.3940-0.2059}{0.3125} = +0.6019 \end{aligned}$$

Table 11.24 Example ordinal-by-interval data for Jaspen’s correlation coefficient with N = 32 observations

Table 11.25 Calculation of the mean standard scores for the k = 4 ordinal categories

Jaspen’s multiserial correlation coefficient is the Pearson product-moment correlation between the Y  interval-level values given in Table 11.24 and the transformed $\bar {Z}$ values given in Table 11.25. Table 11.26 lists the Y , $\bar {Z}$, Y ², $\bar {Z}^{2}$, and values, along with the corresponding sums.

Table 11.26 Calculation of the sums needed for the Pearson product-moment correlation between variables Y  and $\bar {Z}$

For the summations given in Table 11.26, the Pearson product-moment correlation between the Y  and $\bar {Z}$ values is

Jaspen’s multiserial correlation coefficient is known to be biased. The bias is due to the grouping of the values into k categories. When k is small, the bias can be pronounced. For the example data listed in Table 11.24, the correction for grouping is

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} &\displaystyle &\displaystyle S_{\bar{Z}} = \left( \frac{1}{N} \sum_{j=1}^{k} n_{j}\bar{Z}_{j}^{2} \right)^{1/2}\\ &\displaystyle &\displaystyle \quad \qquad {}=\left\{ \frac{1}{32}\Big[ (4)(+1.6472)^{2}+(10)(+0.6019)^{2}+(11)(-0.2877)^{2}\right.\\ &\displaystyle &\displaystyle qquad\qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad {}+(7)(-1.3487)^{2}\Big]\bigg\}^{1/2} = 0.9374 \end{array} \end{aligned} $$

and the corrected multiserial correlation coefficient is

Jaspen’s is asymptotically distributed as Student’s t under the Neyman–Pearson null hypothesis with N − 2 degrees of freedom. If the population parameter, ρ _c, is assumed to be zero, then for the observed data in Table 11.24,

and with N − 2 = 32 − 2 = 30 degrees of freedom the asymptotic two-tail probability value of is P = 0.1308×10⁻², under the assumption of normality.

11.6.2 A Monte Carlo Permutation Analysis for

Because there are

$$\displaystyle \begin{aligned} M = N! = 32! = 263{,}130{,}836{,}933{,}693{,}530{,}167{,}218{,}012{,}160{,}000{,}000 \end{aligned}$$

possible, equally-likely arrangements in the reference set of all permutations of the observed values listed in Table 11.24, an exact permutation analysis is not possible and a Monte Carlo analysis is mandated. Let indicate the observed value of r _c. Based on L = 1, 000, 000 randomly-selected arrangements of the observed data, there are 3069 |r _c| values that are equal to or greater than , yielding a Monte Carlo probability value of

where denotes the observed value of r _c and L is the number of randomly-selected, equally-likely arrangements of the ordinal-interval data listed in Table 11.24.

11.7 Summary

Under the Neyman–Pearson model of statistical inference, this chapter examined various measures of nominal-nominal, ordinal-ordinal, nominal-ordinal, nominal-interval, and ordinal-interval association. Asymptotic probability values were provided under either Pearson’s χ ² probability distribution, Student’s t distribution, Snedecor’s F distribution, or the N(0, 1) probability distribution. Under the Fisher–Pitman permutation model of statistical inference, procedures for both exact and Monte Carlo probability values were developed.

Six sections provided examples and illustrative analyses of permutation statistical methods for contingency tables. In the first section, goodness-of-fit measures for k discrete, mutually-exclusive categories were described and permutation methods were utilized to obtain exact probability values. A measure of effect size for the chi-squared goodness-of-fit test was presented and illustrated.

The second section illustrated the use of permutation statistical methods for analyzing contingency tables in which two nominal-level variables have been cross-classified. Three well-known and widely-used measures of nominal-nominal association were introduced and analyzed with permutation methods: Cramér’s symmetric V  measure, based on Pearson’s chi-squared test statistic, and Goodman and Kruskal’s t _a and t _b asymmetric measures, based on the differences between concordant and discordant pairs of observations. The relationships between Pearson’s χ ² test statistic and Goodman and Kruskal’s t _a and t _b measures were described.

The third section illustrated the use of permutation statistical methods for analyzing contingency tables in which two ordinal-level variables have been cross-classified. Three popular measures of ordinal-ordinal association were introduced and analyzed with permutation methods: Goodman and Kruskal’s G symmetric measure of ordinal-ordinal association and Somers’ d _yx and d _xy asymmetric measures of ordinal-ordinal association.

The fourth section illustrated the use of permutation statistical methods for analyzing contingency tables in which a nominal-level variable was cross-classified with an ordinal-level variable. Freeman’s θ measure of association for a nominal-level independent variable and an ordinal-level dependent variable was described and illustrated with exact permutation statistical methods.

The fifth section illustrated the use of permutation statistical methods for analyzing contingency tables in which a nominal-level variable was cross-classified with an interval-level variable. Pearson’s point-biserial correlation coefficient for a dichotomous nominal-level variable and a continuous interval-level variable was described and analyzed with exact permutation statistical methods.

The sixth section illustrated the use of permutation statistical methods for analyzing contingency tables in which an ordinal-level variable was cross-classified with an interval-level variable. Jaspen’s multi-serial correlation coefficient for ordinal-interval association was described and analyzed with Monte Carlo permutation methods.