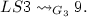Abstract
Fast reachability detection is one of the key problems in graph applications. Most of the existing works focus on creating an index and answering reachability based on that index. For these approaches, the index construction time and index size can become a concern for large graphs. More recently query-preserving graph compression has been proposed and searching reachability over the compressed graph has been shown to be able to significantly improve query performance as well as reducing the index size. In this paper, we introduce a multilevel compression scheme for DAGs, which builds on existing compression schemes, but can further reduce the graph size for many real-world graphs. We propose an algorithm to answer reachability queries using the compressed graph. Extensive experiments with two existing state-of-the-art reachability algorithms and 10 real-world datasets demonstrate that our approach outperforms the existing methods.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The reachability query, which asks whether there exists a path from one vertex to another in a directed graph, finds numerous applications in graph and network analysis. Such queries can be answered by graph traversal using either breadth-first or depth-first search in time \(O(|E|+|V|)\) without pre-processing (where V and E are the vertex set and edge set respectively), or in constant time if we pre-compute and store the transitive closure of each vertex, which takes O(|V||E|) time and \(O(|V|^2)\) space. Unfortunately, neither of these approaches is feasible for applications that need to process large graphs with limited memory. Over the last decades, the problem has been extensively studied and many advanced algorithms have been proposed, with most of them relying on building smart indexes that can strike a balance between online query processing time and offline index construction time (and index size).
More recently, researchers recognized that it is possible to reduce the graph size by graph compression without loosing reachability information, and the compressed graph can help speedup query processing as well as reduce index size and index construction time. Specially, Fan et al. [6] define equivalence classes of vertices with respect to reachability queries, and compress a graph by merging all vertices in an equivalence class into a single vertex. However, finding all equivalence classes is very time-consuming. Zhou et al. [21] propose an efficient algorithm to do a transitive reduction which turns a directed acyclic graph (DAG) into a DAG without redundant edges, after that the equivalence reduction of [6] can be done much more efficiently. The resulting graph \(G^\epsilon \) after transitive reduction and equivalence reduction over the original graph G can be a much smaller graph that retains all reachability information, and it was experimentally verified that for many real-world graphs, searching for reachability over \(G^\epsilon \) can be much faster than searching over G using state-of-the-art algorithms.
This paper builds on the work of [21]. We observe that after the removal of redundant edges many linear chains will be generated. Based on this, we propose a multi-level reachability - preserving compression method that can further reduce the size of the graph obtained by the method in [21]. Our compression utilizes a slightly modified concept of module [13], and constructs a modular decomposition tree. We show how to use the decomposition tree to answer reachability queries over the original graph efficiently. Furthermore, the decomposition tree usually takes very small space. We make the following contributions:
-
1.
We define a new concept of module, based on which we propose a multilevel graph compression scheme that compresses graphs into a smaller graph \(G_c\).
-
2.
We organize the modules into a hierarchical structure called modular decomposition tree, and propose an efficient algorithm to utilize the tree to answer reachability queries.
-
3.
We conduct extensive experiments with real-world graphs that demonstrate the advantages of our proposed approach.
The remainder of this paper is organized as follows. We first discuss related works in Sect. 2 and present the preliminaries in Sect. 3. Then we give an overview of our approach and provide the theoretical foundations in Sect. 4, followed by the detailed algorithms in Sect. 5. Our experimental results are given in Sect. 6. We conclude our paper in Sect. 7.
2 Related Work
As briefly mentioned in Sect. 1, existing approaches for answering reachability queries can be classified into index-based and compression-based.
Index-Based Approach: The index-based algorithms create labels for the vertices, such labels contain the reachability information. These algorithms can be divided into Label-only and Label+G methods [18]. The label-only [1, 3, 4, 7, 9,10,11,12, 19] methods use the labels of source and destination vertices only to answer reachability. Agrawal [1] proposed tree cover approach that creates an optimal spanning tree to create index. Here, an interval for each vertex is created. A reachability query is answered as true if the interval of target is contained in the interval of source vertex. The index construction time and index size both are high in this approach. A chain cover approach is first proposed in [7] where the entire graph is divided into a number of pairwise disjoint chains to create the index. The label of each vertex contains a minimal successor list containing their chain number and position in the chain. A vertex u will be reachable to v if label of u contains a pair (k, j) and v has an index pair (i, j) such that \(i \ge k\). This chain cover approach is later improved in [3]. Path tree [9] uses the similar concept of chain cover that uses paths to create index and has smaller index size than chain cover. The recent approaches DL [10], PLL [19] and TF [4] use the concept of 2-hop labeling proposed in [5]. In 2-hop labeling, a label is created for each vertex containing the subset of vertices that it can reach (\(L_{out}\)) as well as the subset of vertices that can reach it (\(L_{in}\)). Vertex u can reach vertex v if \(L_{out}(u) \cap L_{in}(v) \ne \emptyset \). [11] uses the concept of chain cover to improve 2-hop and proposes a 3-hop labeling that creates a transitive closure contour (Con(G)) of graph G using chain decomposition, and then applies 2-hop techniques. Path-hop [2] improves 3-hop by replacing the chain decomposition with a spanning tree. TF [4] proposes a topological folding approach for 2-hop labeling that can significantly reduce the index size as well as the query time.
The Label+G approaches include [14,15,16,17,18, 20] which require online searching of data graph G if the query can not be answered from labels. [16] uses interval labeling over a spanning tree and performs DFS online if needed. Grail [20] and Ferrari [14] use multiple interval instead of single interval label for each vertex over the spanning tree. Feline [17] creates coordinates \(i(u) = (X_u, Y_u)\) for a vertex u and answers reachability from u to v as true if the area of i(v) is contained in that of i(u). Feline also uses interval labeling over spanning tree and compares topological levels of u and v as additional pruning strategy to reduce DFS search. IP\(^+\) [18] uses independent permutation numbering to label each vertex. Feline and IP\(^+\) show significant improvement on query time and require less index construction time and smaller index size. BFL [15] proposes a Bloom-Filter Labeling to further improve the performance of IP\(^+\).
Compression-Based Approach: Graph compression based works include Scarab [8], Equivalence reduction [6] and DAG reduction [21]. Scarab [8] compresses the original graph by creating a reachability backbone that carries the major reachability information. To find reachability from vertex u to vertex v the algorithm needs access to a list of local outgoing backbone vertices of u and local incoming backbone vertices of v. The algorithm then performs a forward BFS for u and backward BFS for v on the original graph to answer reachability from u to v. If the answer is false then it checks whether any outgoing backbone vertex of u can reach any incoming backbone vertex of v in the reachability backbone, if yes, then u can reach v. Scarab requires large index size with high time complexity. Equivalence reduction [6] reduces the graph by merging equivalent vertices into a single vertex. Two vertices are equivalent if they have the same ancestors and same descendants. The algorithm requires high equivalence class construction time. DAG reduction [21] improves the construction time of equivalence classes by doing a transitive reduction of graph first.
Our work is different from the previous works in that we not only consider equivalent classes, but also linear chains, when compressing the graph, and to the best of our knowledge, none of the previous works uses multi-level compression and modular decomposition tree in reachability queries.
3 Preliminaries
We consider directed graphs in this paper. For any directed graph G, we will use \(V_G\) and \(E_G\) to denote the vertex set and the edge set of G, respectively. Given two vertices u and v in G, if there is a path from u to v, we say v is reachable from u, or equivalently, u can reach v. We use  to denote u can reach v in graph G. Given directed graph G and vertices u and v in G, a reachability query from u to v, denoted
to denote u can reach v in graph G. Given directed graph G and vertices u and v in G, a reachability query from u to v, denoted  , asks whether v is reachable from u in G.
, asks whether v is reachable from u in G.
A directed acyclic graph (DAG) is a directed graph without cycles. In the literature, most works on reachability queries assume the graph G is a DAG, because if it is not, it can be converted into a DAG by merging all vertices in a strongly connected component into a single vertex, and vertices in a strongly connected component can all reach each other. In this work, we also assume the graph G is a DAG.
If (u, v) is an edge in DAG G, we say u is a parent of v, and v is a child of u. For any vertex \(u\in V_G\), we will use parent(u, G) and child(u, G), respectively, to denote the set of parents of u and the set of children of u in G. We will also use anc(u, G) and des(u, G) to denote the set of ancestors of u and the set of descendents of u in G, respectively. When G is clear from the context, we will use the abbreviations parent(u), child(u), anc(u), and des(u) for parent(u, G), child(u, G), anc(u, G), and des(u, G) respectively.
Let M be a subset of vertices in G. For any vertex \(u\in M\) and a parent vertex \(u'\) of u, we say \(u'\) is an external parent of u (with respect to M) if \(u'\in parent(u)-M\). Similarly, we define an external child (resp. ancestor, descendent) of u with respect to M as a vertex in \(child(u)-M\) (resp. \(anc(u)-M\), \(des(u)-M\)).
Redundant Edges. Suppose (u, v) is an edge in G. If there is a path of length greater than 1 from u to v, then (u, v) is redundant for reachability queries, that is, removing (u, v) from G will not affect the answer to any reachability queries.
The redundant edges can be efficiently identified and removed by a transitive reduction algorithm proposed in [21]. The following lemma is shown in [21]:
Lemma 1
Suppose G is a DAG without redundant edges, then for any two vertices u and v in G, \(parent(u) = parent(v)\) if and only if \(anc(u) = anc(v)\); \(child(u) = child(v)\) if and only if \(des(u) = des(v)\).
Equivalence Class. Two vertices u and v are said to be equivalent if they have the same ancestors and the same descendants, that is, \(anc(u) = anc(v)\), \(des(u) = des(v)\) [6]. Because of Lemma 1, if G does not have redundant edges, then u and v are equivalent if and only if they have the same parents and same children. The equivalent vertices form an equivalence class. It is easy to see that all vertices in the same equivalence class have the same reachability properties, that is, if u is in an equivalence class, then for any other vertex \(u'\), u can reach \(u'\) (resp. u is reachable from \(u'\)) if and only if every vertex v in the same equivalence class can reach \(u'\) (resp. is reachable from \(u'\)).
Also as observed in [21], if G has no redundant edges, then all vertices in an equivalence class form an independent set, that is, there are no edges between the vertices in the same equivalence class.
Lemma 2
Suppose G is a DAG without redundant edges, then every equivalent class is an independent set.
Modular Decomposition. The modular decomposition [13] of a directed graph G partitions the vertex set into a hierarchy of modules, where a module is conventionally defined as follows.
Definition 1
Let M be a set of vertices in G. We call M a module of G if all vertices in M share the same external parents and the same external children. In other words, for any \(u,v\in M\), \(parent(u)-M =parent(v)-M\) and \(child(u)-M =child(v)-M\).
It is easy to see that a singleton set is a module and the set of all vertices in G is also a module. These modules are called trivial modules. Let G be a DAG that has no redundant edges. By Lemma 1, an equivalent class is also a module, and by Lemma 2, such a modules is an independent set. In the literature, modules that are independent sets are referred to as parallel modules.
4 Overview of Our Approach
The basic idea of our method is to compress the graph without loosing reachability information. We use modular decomposition, however the definition of modules has been slightly modified from that found in the literature, in order to help with reachability queries.
Definition 2
A module in a DAG G is a set of vertices \(M\subseteq V_G\) that have identical external ancestors and identical external descendants. In other words, for any two vertices \(u,v\in M\), \(anc(u)-M\) = \(anc(v)-M\), and \(des(u)-M\) = \(des(v)-M\).
Our module is an extension of the conventional module defined in Definition 1, that is, conventional modules are also modules by our definition. This is because vertices that share the same external parents also share the same external ancestors, and vertices that share the same external children also share the same external descendants. However, the converse is not true. For example, in the graph shown in Fig. 1, the set of vertices \(\{1, 2, 3, 4\}\) is a module by our definition. However, it is not a module according to the conventional definition. In what follows, when we say a module, we mean a module by Definition 2, unless explicitly stated otherwise.
In this work, we are interested in two special types of modules, referred to as parallel modules and linear modules respectively. A parallel module is a module that is an independent set, and a linear module is one that consists of a chain of vertices \(v_1, \ldots , v_k\) such that there is an edge \((v_i, v_{i+1})\) for all \(i\in [1,k-1]\). These modules have the following properties.
Lemma 3
Suppose G is a DAG that does not have redundant edges. (1) If M is a parallel module of G, then all vertices in M have the same parents and same children. (2) If M is a linear module consisting of the chain \(v_1, \ldots , v_k\), then for each \(i\in [2,k]\), \(v_{i-1}\) is the only parent of \(v_i\), and \(v_i\) is the only child of \(v_{i-1}\).
Proof
(1) Let M be a parallel module. By definition M is an independent set, and all the vertices have the same external ancestors and the same external descendants. Since M is an independent set, it is impossible for any vertex in M to have an ancestor or descendent in M, therefore, all the vertices have the same ancestors and the same descendants (both external and internal). By Lemma 1, all vertices in M have the same parents and the same children.
(2) Let M be a linear module consisting of the chain \(v_1, \ldots , v_k\). For any \(i\in [2,k]\), if \(v_i\) has a parent u that is not \(v_{i-1}\), then there are two possible cases. The first case is that u is also in M, that is u is one of \(v_{i+1}, \ldots , v_k\). This contradict the assumption that G is a DAG since there will be a cycle. The second case is that u is not in M. In this case, by the definition of a module, u must be an ancestor of \(v_1\), that is, there will be a path from u to \(v_i\) with length at least 2. Hence the edge \((u, v_i)\) would be redundant, contradicting the assumption that there are no redundant edges in G. This proves \(v_{i-1}\) is the only parent of \(v_i\). Similarly we can prove \(v_i\) is the only child of \(v_{i-1}\).
In Fig. 2(a), the vertices v1, v2, v3 form a parallel module. In Fig. 2(b), the vertices v1, v2, v3 form a linear module. Note, however, the set \(\{v4,v1,v2,v3,\) \(v6\}\) in Fig. 2(b) is not a linear module.
It is worth noting that each single vertex forms a parallel module as well as a linear module. These modules are referred to as trivial modules, along with the module that consists of all of the vertices in G. According to Lemma 3, a parallel module is an equivalence class, if G is a DAG that has no redundant edges.
Note that if two vertices are in the same linear module, then their reachability depends on their relative positions in the chain. If they are in the same parallel module, then they cannot reach each other, as shown in the lemma below.
Lemma 4
Let G be a DAG without redundant edges, and u, v be vertices in the same parallel module of G, then u cannot reach v in G.
Proof
Let the parallel module that contains u and v be M. If the lemma is not true, there will be a path \(u, v_1, \ldots , v_s, v\) from u to v. Since M is an independent set, \(v_1\) and \(v_s\) cannot be in M. Hence \(v_1\) is an external child of u, and \(v_s\) is an external parent of v. By Lemma 3 and the definition of modules, \(v_1\) must be a child of v and \(v_s\) must be a parent of u. Therefore there will be a cycle, contradicting the assumption that G is a DAG. Hence the proof.
A set of vertices may be in multiple parallel (or linear) modules, e.g., in the graph shown in Fig. 2(a), \(\{v1,v2\}\) and \(\{v1,v2,v3\}\) are both parallel modules. However, we are only interested in the maximal modules as defined below.
Definition 3
A parallel (resp. linear) module M is said to be maximal if there is no other parallel (resp. linear) module \(M'\) such that \(M\subset M'\).
For example, \(\{v1,v2, v3\}\) is a maximal parallel module in Fig. 2(a), and it is a maximal linear module in Fig. 2(b).
Note that two different maximal parallel modules of G cannot have overlaps, and two different maximal linear modules cannot have overlaps. Furthermore, there cannot exist a non-trivial parallel module and a non-trivial linear module such that they have a common vertex. In other words, each vertex can belong to at most one non-trivial parallel or linear module.
Multi-level Compression and Modular Decomposition Tree. To utilize parallel and linear modules in reachability search, we perform a multi-level compression of the original graph G. First, we identify the maximal linear modules and parallel modules, and merge the vertices in each module into a single super-vertex. We add an edge from super-vertex \(s_1\) to super-vertex \(s_2\) if and only if there exists \(u\in s_1\), and \(v\in s_2\) such that (u, v) is an edge in G. In this way, we obtain the first level compressed graph \(G_1 = Compress(G)\). Clearly, \(G_1\) is also a DAG without redundant edges. Then we apply the same compression process to \(G_1\) to obtain the next level compressed graph \(G_2=Compress(G_1)\), and this process is repeated until we obtain a graph \(G_c\) which can no longer be compressed, i.e., \(G_c\) does not have singleton-set parallel or linear modules.
Example 1
Consider the DAG G of Fig. 3(a), which consists of ten vertices numbered 1 to 10. The graph is reduced to \(\tilde{G}\) in Fig. 3(b) after transitive reduction. We will apply our compression to graph \(\tilde{G}\).
There are no parallel modules in \(\tilde{G}\). However, vertices 2, 3 and 4 can form a maximal linear module. Another maximal linear module exists in \(\tilde{G}\) that consists of vertices 5, 6 and 7. So, vertices 2, 3, 4 and vertices 5, 6, 7 are compressed into two single nodes, and they are reduced into nodes LS1 and LS2 respectively in graph \(G_1\) shown in Fig. 4(a) after the first level compression. Then \(G_1\) is compressed again to obtain \(G_2\) as shown in Fig. 4(b), where the nodes LS1, LS2 and 8 in \(G_1\) are merged as they form an equivalent set in \(G_1\). The third level compression creates graph \(G_3\) in Fig. 4(c) by merging nodes 1 and IS1 in \(G_2\) which form a linear module. The graph \(G_3\) does not contain any parallel or linear modules thus cannot be compressed further. So, \(G_3\) is the final compressed graph of data graph G.
We organize the modules in all levels of the compressed graphs into a tree structure, called the modular decomposition tree, or decomposition tree for brevity, as follows: The root of the tree is the final compressed graph \(G_c\). Each module in the previous-level compressed graph \(G_{c-1}\) is a child node of the root; Each child node of the root that corresponds to a non-trivial module of \(G_{c-1}\), in turn, has its own children, representing modules in the previous level graph \(G_{c-2}\). This continues until we reach the nodes representing modules in the first-level compressed graph, where each non-trivial module points to their children, which are individual vertices in the original graph G. Note that the leaf nodes of the tree are individual vertices in the original graph G. Also, to help reachability detection, we keep a record of the vertex positions in the chain of each linear module in a compressed graph \(G_i\), where if the starting vertex has position 1, the next vertex will have position 2, and so on. We will use pos(v, LS) to denote the position of node v in the chain of LS. Obviously, for \(u,v\in LS\),  if and only if \(pos(u,LS) < pos(v, LS)\).
if and only if \(pos(u,LS) < pos(v, LS)\).
Figure 5 shows the modular decomposition tree, T, of graph \(\tilde{G}\) in Fig. 3(b). Let M be a non-leaf node in the decomposition tree of G. By definition, M is either a parallel or linear module in some compressed graph \(G_i\) \((i<c)\), or it is the final compressed graph \(G_c\). M can be regarded as a set of the original vertices of G in the obvious way. Put in another way, we say vertex \(v\in G\) belongs to (or is in) M if v is a descendant of M in the decomposition tree. For example, the vertices 2, 3, 4, 5, 6, 7, 8 belong to the module IS1 in Fig. 5.
We have the following observations about modules in the decomposition tree:
Lemma 5
The vertices of G that belong to each parallel or linear module M in \(G_i\) \((i<c)\) form a module of G. In other words, all vertices in M have the same external ancestors, as well as the same external descendants in G.
The above lemma can be easily proved by induction on the compression level i. Using Lemma 5, we can easily see:
Lemma 6
Given two distinct nodes \(N_1\) and \(N_2\) in \(G_{i}\) (\(i\le c\)),  iff \(u\rightsquigarrow _{G} v\) for every pair of vertices \(u\in N_1\), \(v\in N_2\).
iff \(u\rightsquigarrow _{G} v\) for every pair of vertices \(u\in N_1\), \(v\in N_2\).
Answering Reachability Queries Using Modular Decomposition Tree. Suppose we have the decomposition tree T of G. For ease of presentation, let us use \(G_0\) to denote the graph G. For any pair of vertices u, v in the original graph G, we use LCA(u, v) to denote the lowest common ancestor of u and v in T. Note that LCA(u, v) corresponds either to a module in some compressed graph \(G_i\) \((i\in [1, c-1])\), or to the final compressed graph \(G_c\) (i.e., the root of T). We have the following result.
Theorem 1
Given two vertices \(u,v\in V_G\), if LCA(u, v) corresponds to a parallel module of some graph \(G_i\) \((i\in [1,c-1])\), then u cannot reach v in G.
Proof
If LCA(u, v) corresponds to a parallel module M of \(G_i\), then suppose \(N_1\) and \(N_2\) are the two vertices of \(G_i\) that contain u and v respectively. By Lemma 4, we know \(N_1\) cannot reach \(N_2\) in \(G_i\). Then by Lemma 6, we know u cannot reach v in G.
With the above discussion, we are ready to present the method for answering reachability queries using the decomposition tree and the final compressed graph \(G_c\). Given two vertices \(u,v\in V_G\), to find whether  , we can find the lowest common ancestor LCA(u, v) of u and v, and check the following:
, we can find the lowest common ancestor LCA(u, v) of u and v, and check the following:
-
1.
If LCA(u, v) is a parallel module, then u cannot reach v in G, by Theorem 1.
-
2.
If LCA(u, v) is a linear module, say M, then we check the positions of \(N_1\) and \(N_2\) in the corresponding chain of vertices in M, where \(N_1\) is the child of LCA(u, v) in the decomposition tree that contains u, and \(N_2\) is the child of LCA(u, v) that contains v, and u can reach v in G if and only if \(pos(N_1,M)< pos(N_2,M)\).
-
3.
If LCA(u, v) is the root of T, namely \(G_c\), then suppose \(N_1,N_2\) are the children of LCA(u, v) that contain u and v respectively. Then
 if and only if
if and only if  . Thus we only need to check whether
. Thus we only need to check whether  . We can do it using any existing reachability algorithms. Since \(G_c\) is usually much smaller than G, checking
. We can do it using any existing reachability algorithms. Since \(G_c\) is usually much smaller than G, checking  in \(G_c\) is likely to be faster than checking
in \(G_c\) is likely to be faster than checking  in G.
in G.
Example 2
Consider the decomposition tree T shown in Fig. 5.
-
(1)
For the query
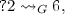 we find lowest common ancestor of vertices 2 and 6 is a parallel module, therefore, we know vertex 2 cannot reach vertex 6.
we find lowest common ancestor of vertices 2 and 6 is a parallel module, therefore, we know vertex 2 cannot reach vertex 6. -
(2)
For the query
 we find LCA(2, 4) is a linear module, and the position of vertex 2 is before that of vertex 4. Therefore we conclude that
we find LCA(2, 4) is a linear module, and the position of vertex 2 is before that of vertex 4. Therefore we conclude that 
-
(3)
For the query
 Since 2 and 9 are in different children of the root, i.e., LS3 and 9 respectively, we only need to check whether
Since 2 and 9 are in different children of the root, i.e., LS3 and 9 respectively, we only need to check whether 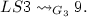
5 Algorithms
The previous section provides the main ideas of our approach. This section presents the detailed algorithms.
5.1 Building Modular Decomposition Tree
Algorithm 1 shows the process of creating the modular decomposition tree along with the final compressed graph. The algorithm takes a DAG that has no redundant edges G as input and returns the modular decomposition tree and the final compressed graph. The algorithm first creates a tree with a root node r. Starting with a random vertex v, the algorithm first tries to find all other vertices that can form a linear module with v (Line 7). If no such module is found then it will search for a maximal parallel module for v (Line 14). If such a module cannot be found, then v will be added as a child of r (Line 21), otherwise the found module M will be added as child of r, and each vertex in the module will be added as a child of M (Lines 8–12, 16–19). We record all such modules in S (Lines 9,16), and use them to compress the graph into a new graph (Line 24). Then we recursively call the algorithm to compress the new graph (Line 27). If no non-single-vertex module is found in the current graph, the current tree T will be returned, and the current graph will be returned as \(G_c\).
The functions FindParallelModule() and FindLinearModule() used in Algorithm 1 are shown in Algorithms 2 and 3 respectively. These algorithms try to find a relevant module based on Lemma 3.
Algorithm 2 takes a vertex v and DAG G as input, and it finds the set of vertices, M, that share the same parents and same children with v. To do that, it first finds the set of vertices, \(M_1\), that share the same parents with v, and then finds the set of vertices, \(M_2\), that share the same children with v. Then M is the intersection of \(M_1\) and \(M_2\).

Algorithms 3 takes a vertex v and DAG G as input, and it first searches for a possible chain of ancestors of v (Lines 2–12), and then searches for a chain of descendants of v (Lines 13–26). Both parts are via an iterative process. Specifically, Lines 2 and 4 check whether v has a sole parent \(v'\), and \(v'\) has a sole child v, if so \(v'\) is the parent of v in a linear module. After that lines 7–12 try to find a parent of the first vertex in the chain, one by one. In the process, it also provides a position number for each vertex found (Line 10). Note that the position does not have to be a positive number, as long as it can provide an appropriate order of the vertices in the chain, it will be fine. Lines 13–26 work similarly.
Complexity. Algorithm 3 takes L steps to find the linear module that contains v (checking the \(|parent(|v|)=1\) is just checking the in-degree of v), where L is the size of the linear module that contains v. Algorithm 2 takes \(\varSigma _{u\in parent(v)} |child(u)|\) + \(\varSigma _{u\in child(v)} |parent(u)|\) steps to find vertices that share the same parents and same children with v. If we use \(I_{max}\) and \(O_{max}\) to denote the maximum in-degree and maximum out-degree respectively, then Algorithm 2 takes \(O(I_{max}\times O_{max})\) time. In Algorithm 1, for the first level compression, we visit each vertex in \(V_G\) that has not been put in a module, and once the vertex is visited or put into a module, it will no longer be visited. In the worst case, no non-trivial module exists, so that every vertex will be visited. Therefore, the first level compression takes \(O(|V|\times I_{max} \times O_{max})\). Each next level compression will take no more than that of the previous level. Therefore, Algorithm 1 takes \(O(|V|\times I_{max} \times O_{max}\times h)\), where h is the height of the decomposition tree.

5.2 Finding Reachability Using the Decomposition Tree
As discussed in the previous subsection, to answer reachability query  using the decomposition tree, we only need to find LCA(u, v) and then take appropriate actions depending on the type of LCA(u, v). To save time for finding the LCA, we design a slightly modified algorithms as shown in Algorithm 4. Given vertices u and v, we first find the children of the root that u and v belong to respectively, let us suppose \(u\in N_1\), \(v\in N_2\), if they are different (this is equivalent to say LCA(u, v) is the root), we will use some existing algorithm to check
using the decomposition tree, we only need to find LCA(u, v) and then take appropriate actions depending on the type of LCA(u, v). To save time for finding the LCA, we design a slightly modified algorithms as shown in Algorithm 4. Given vertices u and v, we first find the children of the root that u and v belong to respectively, let us suppose \(u\in N_1\), \(v\in N_2\), if they are different (this is equivalent to say LCA(u, v) is the root), we will use some existing algorithm to check  . Otherwise we will find the lowest linear LCA of u, v (note that to do so we only need to record the linear module ancestors of the vertices), if no such LCA exists, then u cannot reach v. Otherwise, suppose the linear LCA is M, we will check the relative positions of u and v in M to determine whether u can reach v. Here the position of u is defined to be same as the position of the child of M that contains u. If LCA(u, v) is a parallel module then that module will be a child of M. So, u and v will have the same position in M thus u cannot reach v. It is easy to see that the algorithm is equivalent to the process described in Sect. 4, hence its correctness is guaranteed.
. Otherwise we will find the lowest linear LCA of u, v (note that to do so we only need to record the linear module ancestors of the vertices), if no such LCA exists, then u cannot reach v. Otherwise, suppose the linear LCA is M, we will check the relative positions of u and v in M to determine whether u can reach v. Here the position of u is defined to be same as the position of the child of M that contains u. If LCA(u, v) is a parallel module then that module will be a child of M. So, u and v will have the same position in M thus u cannot reach v. It is easy to see that the algorithm is equivalent to the process described in Sect. 4, hence its correctness is guaranteed.
Size of the Decomposition Tree. To answer reachability queries in the original graph G, we only need to store the final compressed graph \(G_c\) and the decomposition tree T. The total number of nodes in the tree is \(|V|+m+1\), where m denotes the number of non-trivial modules. The number of edges in T is \(|V|+m\).
6 Experiments
Setup: We obtained the source code of DAG reduction, IP\(^+\) and Feline from the authors which are written in C++, and compiled thm using G++ 7.3.0. We implemented our multilevel compression and reachability query processing algorithms in C# using Visual Studio 2017. We created the index of IP\(^+\) and Feline for each graph using the original code from the authors. Then we used that index to process the reachability queries. The experiments were run on a PC with Intel Core i7-7700 with 3.60 GHz CPU, 32 GB memory and Windows 10 operating system. We tested our approach with 10 real data sets. First we applied the transitive reduction of [21] to find  , which is a DAG without redundant edges. Then we applied our multilevel compression algorithm to get \(G_c\). We used two state-of-the-art reachability algorithms IP\(^+\) [18] and Feline [17] to process reachability queries over \(G_c\) and over the graph \(G^\epsilon \) which is obtained by DAG reduction. We compared our method with DAG reduction [21] which is the most recent graph compression method for reachability queries. We randomly generated 100,000 reachability queries for each graph.
, which is a DAG without redundant edges. Then we applied our multilevel compression algorithm to get \(G_c\). We used two state-of-the-art reachability algorithms IP\(^+\) [18] and Feline [17] to process reachability queries over \(G_c\) and over the graph \(G^\epsilon \) which is obtained by DAG reduction. We compared our method with DAG reduction [21] which is the most recent graph compression method for reachability queries. We randomly generated 100,000 reachability queries for each graph.


 , \(G^\epsilon \) and \(G_c\)
, \(G^\epsilon \) and \(G_c\)Datasets: We used 10 real datasets KeggFootnote 1, XMark (see footnote 1), Patent (see footnote 1), Citeseerx (see footnote 1), soc-EpinionsFootnote 2, Web (see footnote 2), LJ (see footnote 2), 05PatentFootnote 3, 05Citeseerx (see footnote 3) and DBpediaFootnote 4. Among the datasets Kegg and XMark are very small graphs. Datasets soc-Epinions, Web and LJ are comparatively larger whereas other 5 graphs can be considered as large graphs. Here Kegg is a metabolic network and XMark is an XML document. Datasets soc-Epinions and LJ are the online social networks. Web is the web graph from Google. Patent, 05Patent, 05Citeseerx and Citeseerx are the citation networks and DBpedia is a knowledge graph. The statistics of these datasets are shown in the first two columns of Table 1.
6.1 Comparison of Compression Ratio
The compression ratios of transitive reduction, DAG reduction (i.e., transitive reduction and equivalence reduction), and our modular decomposition are shown in Table 1. From the table we can see that our approach has more compression for every graph than DAG Reduction. The dataset XMark has the best result with 30.1% more compression of vertex and 26% more compression of edges than DAG Reduction. For larger graphs, DBpedia shows best compression with 6.6% more compression of nodes and 2.8% more compression of edges. On the other hand, our compression scheme does not show much better compression ratio than DAG reduction over the Citeseerx and the Patent data sets. This could be because these data sets do not contain many linear modules. Generally, the reduction ratio depends on the structure of the graph.
Note however, a small percentage of compression for a large graph can also have great impact on query processing since even a small percentage of compression means reduction of lots of vertices and edges in large graphs (see the Patent dataset in Table 6 for example).
Table 2 shows the size of G, \(G^\epsilon \) and \(G_c\). Here, we calculated the size of the graph as the sum of the number of vertices and the number of edges. For \(G^\epsilon \) we have also added the number of equivalent classes as we need them for reachability detection. For the same reason, we have added the number of modules to the size of graph \(G_c\). Table 3 shows the time required for building the decomposition tree using our algorithms which are implemented in C#, where the dataset Dbpedia has taken the most time and is comparable that of dataset Citeseerx. As the indexing is done offline, we consider these timings as viable in practice.
6.2 Performance on Reachability Query Processing
Table 4 shows the comparison of index construction time for IP\(^+\) and Feline algorithms over \(G^\epsilon \) and \(G_c\). The better results are highlighted in bold font in the table. Here, multilevel compression requires less index construction time for every graph for creating index for IP\(^+\). For Feline, we also have better result for each graph except 05Patent and 05Citeseerx. The index size of IP\(^+\) and Feline, for \(G^\epsilon \) and \(G_c\), are shown in Table 5. From the table we can see that the index sizes of \(G_c\) are smaller for every graph than \(G^\epsilon \) for both IP\(^+\) and Feline, although for the Citeseerx and Patent datasets the difference is very small. This is not surprising because the sizes of \(G_c\) and \(G^\epsilon \) are very close for these data sets.
Table 6 shows the comparison of the query time for both IP\(^+\) and Feline. We run each query 10 times and the time shown is the average of the 10 runs. We can see that our compression outperforms DAG reduction in query processing for almost every graph. Surprisingly, the best improvement is over the Patent dataset, where our approach is much faster than DAG reduction in both IP\(^+\) and Feline. It is also surprising that \(IP^+\) is lower using our approach than using DAG reduction in Kegg dataset.
7 Conclusion
We presented a method to compress a DAG that has no redundant edges, using two types of modules, to obtain a decomposition tree. We showed how to use the decomposition tree to answer reachability queries over the original graph. Experiments show that for many real-world graphs, our method can compress the graph to much smaller graphs than DAG reduction, and reachability queries can be answered faster, and the index size can be smaller as well.
References
Agrawal, R., Borgida, A., Jagadish, H.V.: Efficient management of transitive relationships in large data and knowledge bases. In: SIGMOD, pp. 253–262 (1989)
Cai, J., Poon, C.K.: Path-hop: efficiently indexing large graphs for reachability queries. In: CIKM, pp. 119–128 (2010)
Chen, Y., Chen, Y.: An efficient algorithm for answering graph reachability queries. In: ICDE, pp. 893–902 (2008)
Cheng, J., Huang, S., Wu, H., Chen, Z., Fu, A.W.: TF-label: a topological-folding labeling scheme for reachability querying in a large graph. In: SIGMOD (2013)
Cohen, E., Halperin, E., Kaplan, H., Zwick, U.: Reachability and distance queries via 2-hop labels. In: SIAM, pp. 937–946 (2002)
Fan, W., Li, J., Wang, X., Wu, Y.: Query preserving graph compression. In: SIGMOD, pp. 157–168 (2012)
Jagadish, H.V.: A compression technique to materialize transitive closure. TODS 15, 558–598 (1990)
Jin, R., Ruan, N., Dey, S., Yu, J.X.: SCARAB: scaling reachability computation on large graphs. In: SIGMOD, pp. 169–180 (2012)
Jin, R., Ruan, N., Xiang, Y., Wang, H.: Path-tree: an efficient reachability indexing scheme for large directed graphs. TODS 36, 7 (2011)
Jin, R., Wang, G.: Simple, fast, and scalable reachability oracle. PVLDB 6, 1978–1989 (2013)
Jin, R., Xiang, Y., Ruan, N., Fuhry, D.: 3-HOP: a high-compression indexing scheme for reachability query. In: SIGMOD, pp. 813–826 (2009)
Jin, R., Xiang, Y., Ruan, N., Wang, H.: Efficiently answering reachability queries on very large directed graphs. In: SIGMOD, pp. 595–608 (2008)
McConnell, R.M., de Montgolfier, F.: Linear-time modular decomposition of directed graphs. Discret. Appl. Math. 145(2), 198–209 (2005)
Seufert, S., Anand, A., Bedathur, S.J., Weikum, G.: Ferrari: Flexible and efficient reachability range assignment for graph indexing. In: ICDE, pp. 1009–1020 (2013)
Su, J., Zhu, Q., Wei, H., Yu, J.X.: Reachability querying: can it be even faster? TKDE 29, 683–697 (2017)
Trißl, S., Leser, U.: Fast and practical indexing and querying of very large graphs. In: SIGMOD, pp. 845–856 (2007)
Veloso, R.R., Cerf, L., Junior, W.M., Zaki, M.J.: Reachability queries in very large graphs: a fast refined online search approach. In: EDBT, pp. 511–522 (2014)
Wei, H., Yu, J.X., Lu, C., Jin, R.: Reachability querying: an independent permutation labeling approach. PVLDB 7, 1191–1202 (2014)
Yano, Y., Akiba, T., Iwata, Y., Yoshida, Y.: Fast and scalable reachability queries on graphs by pruned labeling with landmarks and paths. In: CIKM (2013)
Yildirim, H., Chaoji, V., Zaki, M.J.: GRAIL: a scalable index for reachability queries in very large graphs. VLDBJ 21, 509–534 (2012)
Zhou, J., Zhou, S., Yu, J.X., Wei, H., Chen, Z., Tang, X.: DAG reduction: fast answering reachability queries. In: SIGMOD, pp. 375–390 (2017)
Acknowledgement
This work is supported by Australian Research Council discovery grant DP130103051.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Anirban, S., Wang, J., Saiful Islam, M. (2019). Multi-level Graph Compression for Fast Reachability Detection. In: Li, G., Yang, J., Gama, J., Natwichai, J., Tong, Y. (eds) Database Systems for Advanced Applications. DASFAA 2019. Lecture Notes in Computer Science(), vol 11447. Springer, Cham. https://doi.org/10.1007/978-3-030-18579-4_14
Download citation
DOI: https://doi.org/10.1007/978-3-030-18579-4_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-18578-7
Online ISBN: 978-3-030-18579-4
eBook Packages: Computer ScienceComputer Science (R0)










 if and only if
if and only if  . Thus we only need to check whether
. Thus we only need to check whether  . We can do it using any existing reachability algorithms. Since
. We can do it using any existing reachability algorithms. Since  in
in  in G.
in G.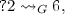 we find lowest common ancestor of vertices 2 and 6 is a parallel module, therefore, we know vertex 2 cannot reach vertex 6.
we find lowest common ancestor of vertices 2 and 6 is a parallel module, therefore, we know vertex 2 cannot reach vertex 6. we find LCA(2, 4) is a linear module, and the position of vertex 2 is before that of vertex 4. Therefore we conclude that
we find LCA(2, 4) is a linear module, and the position of vertex 2 is before that of vertex 4. Therefore we conclude that 
 Since 2 and 9 are in different children of the root, i.e., LS3 and 9 respectively, we only need to check whether
Since 2 and 9 are in different children of the root, i.e., LS3 and 9 respectively, we only need to check whether