Efficient Local Search for Minimum Dominating Sets in Large Graphs

Abstract

The Minimum Dominating Set (MinDS) problem is an NP-hard problem of great importance in both theories and applications. In this paper, we propose a new local search algorithm ScBppw (Score Checking and Best-picking with Probabilistic Walk) to solve the MinDS problem in large graphs. For diversifying the search, our algorithm exploits a tabu strategy, called Score Checking (SC), which forbids a vertex to be added into the current candidate solution if the vertex’s score has not been changed since the last time it was removed out of the candidate solution. Also, to keep a good balance between intensification and diversification during the search, we propose a strategy that combines, in a novel way, best-picking with probabilistic walk at removing stages. At this stage, the algorithm selects a vertex with the minimum loss, or other vertices in the candidate solution with a probability proportional to the their degrees, depending on how repeatedly the area has been visited. Experimental results show that our solver significantly outperforms state-of-the-art MinDS solvers. Also we conducted several experiments to show the individual impacts of our novelties.

Supported by the Natural Science Foundation of China (61672441, 61872154), the Shenzhen Basic Research Program (JCYJ20170818141325209), and the NSF grants (IIS-1814745, IIS-1302164).

1 Introduction

Given a simple undirected graph $G = (V, E)$, a dominating set is a subset $D \subseteq V$ s.t. every vertex outside D has at least one neighbor in D. The Minimum Dominating Set (MinDS) problem is to find a dominating set of the minimum size. MinDS arises in many application areas, $\textit{e.g.}$, biological networks [20], metro networks [1], power networks [13], computer vision [21, 26], multi-document summarization [23], and wireless communication [22]. Among various algorithms, $\textit{e.g.}$ [6, 10], local search is an effective approach and it is powerful on difficult graphs.

1.1 Local Search Techniques

Local search often suffers from the cycling problem, $\textit{i.e.}$, the search may spend too much time visiting a small part of the search space, thus various tabu strategies have been proposed to deal with this problem. Recently [5] proposed the so-called configuration checking (CC) strategy, and after that numerous variants of the CC strategy have been adopted to solve a wide range of combinatorial problems $\textit{e.g.}$, [11, 24, 25]. The idea of the CC strategy can be described as follows. If a vertex is removed out of the candidate solution, then it is forbidden to be added back until its configuration is changed, $\textit{i.e.}$, some neighboring vertex is added or removed out of the candidate solution.

The forbidding strength of CC can be too weak, which may lead a CC-based local search being stuck in a cycle. To escape from such a cycle, a CC-based local search usually needs some other diversifying strategies like constraint weighting [15], which is unfortunately time-consuming and impractical for large graphs. For diversifying the search, we exploit a strong CC-like tabu strategy, called Score Checking (SC), which forbids a vertex to be added into the current candidate solution if its score has not been changed since the last time it was removed out of the candidate solution. In this strategy, when a vertex is added or removed, some vertices in the neighborhood are released, while some others are still forbidden. This is different from usual CC variants.

To keep a good balance between intensification and diversification, we propose a strategy that combines, in a novel way, best-picking with probabilistic walk at removing stages. Best-picking with random walk has proved to be effective in solving the minimum vertex cover problem in large graphs [18]. More specifically, in greedy mode it chooses small-degree vertices while in random mode it selects a vertex from a uniform distribution. However, the strategy may still focus too much on small-degree vertices, in other words, there may not be enough chances to select a big-degree vertex. Therefore we adopt a probabilistic distribution to remove vertices in random mode. To be specific, a vertex is selected to be removed with a probability proportional to its degree. Evidently, this strategy gives more chances to big-degree vertices.

Also, when we are doing local search in large instances, the complexity becomes a big issue. In each step there can be millions of possible moves, and thus it is difficult to obtain a local move which maximizes certain kinds of benefits. Since most real-world graphs are sparse [3, 8, 10], it is beneficial to develop data structures so that the complexity of a single search step relies on the average degree rather than the number of vertices. For instance, a local search solver LMY-GRS [11] follows this idea and finds good solutions for the maximum weight clique problem. Inspired by this, we propose an efficient data structure named score-based partition to implement best-picking. The score-based partition effectively cuts off the average complexity of exchanging vertices in the local search algorithm.

1.2 Our Contributions

In this paper, we develop a local search solver named ScBppw (Score Checking and Best-picking with Probabilistic Walk) based on the strategies above. For showing the effectiveness, we compare ScBppw with FastWMDS [24] on large graphs¹. Experimental results show that (1) our solver ScBppw significantly outperforms FastWMDS on large graphs; (2) our proposed strategies play an important role in our solver.

2 Preliminaries

2.1 Basic Notations

We use N(v) = $\{u \in V | \{u, v\} \in E\}$ to denote the set of v’s neighbours, and we use N[v] to denote $N(v) \cup \{v\}$. The degree of a vertex v, denoted by d(v), is defined as |N(v)|. We use

$$\begin{aligned} N^2(v) = (N(v) \cup \{u | \{u, w\} \in E\,\text {and}\, w \in N(v)\}) \backslash \{v\} \end{aligned}$$

to denote the set of vertices whose distance from v is at most 2. Also we use $\bar{d}_2(G)$ to denote the average size of $N^2(v)$ over all the vertices, $\textit{i.e.}$, $\bar{d}_2(G) = \frac{1}{|V|}\sum _{v \in V}|N^2(v)|$, suppressing G if understood from the context. In graph theory, we have the following proposition that is useful in implementing our solver.

Proposition 1

$\sum _{v \in V}d(v) = 2|E|$.

A vertex is said to be covered by a set D if it is in D or at least one of its neighbors is in D. Otherwise it is said to be uncovered by D. If u’s removal from D makes v become uncovered, we also say that u’s removal uncovers v. Likely if u’s addition into D makes v become covered, we also say that u’s addition covers v. For a vertex $v \in D$, the loss of v, denoted as $loss (v)$, is defined as the number of covered vertices that will become uncovered by removing v from D. For a vertex $v \not \in D$, the gain of v, denoted as $gain (v)$, is defined as the number of uncovered vertices that will become covered by adding v into D. Both gain and loss are scoring properties. Obviously we have

Proposition 2

For all $v\in V$, $gain (v)\in [0, d(v) + 1]$, $loss (v)\in [0, d(v) + 1]$.

In MinDS solving, we have a proposition below which shows the set of vertices whose score needs to be updated.

Proposition 3

• 1. When a vertex u is added or removed, for any vertex $v \not \in N^2(u)$, $gain (v)$/$loss (v)$ remains unchanged.

• 2. If $gain (v)$ or $loss (v)$ is changed, then at least one vertex $u \in N^2(v)$ has been added or removed.

In any step, a vertex v has two possible states: inside D and outside D. We use age(v) to denote the number of steps that have been performed since last time v’s state was changed.

2.2 An Iterative Local Search Framework

Algorithm 1 presents a local search framework for MinDS. It consists of the construction phase (Line 1) and the local search phase (Lines 2 to 8).

In our algorithm, we will adopt a simple greedy strategy to implement InitDS(G), which works as follows. Given an empty set D, repeat the following operations until D becomes a dominating set: select a vertex $v \not \in D$ with the maximum gain and add v into D, breaking ties randomly. Actually we can use the data reduction rules in [2] to generate better initial solutions and more importantly simplify the input graph. Yet currently we do not do so, because our main concern in this paper is to develop an efficient local search algorithm.

In the local search phase, each time a k-sized dominating set is found (Line 3), the algorithm removes a vertex from D (Line 5) and proceeds to search for a $(k-1)$-sized dominating set, until a certain time limit is reached (Line 2). A local move consists of exchanging a pair of vertices (Line 8): a vertex $u \in D$ is removed from D, and a vertex $v \not \in D$ is added into D. Such an exchanging procedure is also called a step or an iteration by convention. In our algorithm, we also employ a predicate $lastStepImproved$ s.t. $lastStepImproved = true$ iff the number of uncovered vertices was decreased in the last step. This predicate will be used in the best-picking with probabilistic walk strategy we propose. Lastly, when the algorithm terminates, it outputs the smallest dominating set that has been found.

2.3 A Fast Hashing Function

In order to detect revisiting, we will use the hash function in [12] which is shown below.

Definition 1

Given a candidate set D and a prime number p, we define the hash value of D, denoted by $hash (D)$, as $(\sum _{v_i \in D}{2^i}) \mod p$, which maps a candidate set D to its hash entry hash(D).

Also, they showed that each time a vertex is added or removed, the hash value can be updated in O(1) complexity.

2.4 Geometric Distribution

To analyze the complexity of our algorithm, we first introduce Geometric Distribution which depicts the probability that the first success occurs in a particular trial.

Definition 2

A random variable X has a geometric distribution if the probability that the $k^{th}$ trial (out of k trials) is the first success is $Pr(X=k) = (1-p)^{k-1}p$, where k is a positive integer and p denotes the probability of success in a single trial.

Then the average number of trials needed for the first success is $\frac{1}{p}$ according to the following theorem [19].

Theorem 1

If X is a geometric random variable with parameter p, then the expected value E(X) is given by $\frac{1}{p}$.

2.5 Sorting Vertices wrt. Degrees

Our algorithm implementation requires sorting vertices into non-decreasing order wrt. their degrees in advance, so we introduce an efficient sorting algorithm as follows. Considering that $0 \le d(v) \le |V|$ for any $v \in V$, this satisfies the assumption of counting sort which runs in linear time [9]. So we have

Proposition 4

Sorting the vertices into non-decreasing order wrt. their degrees can be done in O(|V|) complexity.

2.6 Configuration Checking

In MinDS solving, there are three different CC strategies, $\textit{i.e.}$, neighboring vertices based CC (NVCC) [5], two-level CC (CC$^2$) [25] and three-valued two-level CC (CC$^2$V3). In NVCC, the configuration of a vertex v refers to the state of the vertices in N(v). On the other hand, in CC$^2$, the configuration of a vertex v refers to the state of the vertices in $N^2(v)$.

We use $V_{NVCC}$ to denote the set of vertices whose configuration is changed according to the NVCC strategy, and use $V_{CC^2}$ to denote the set of vertices whose configuration is changed according to the CC$^2$ strategy. [25] presented the proposition below which shows that the forbidding strength of NVCC is stronger than that of CC$^2$.

Proposition 5

If $V_{NVCC} = V_{CC^2}$ in some step, then $V_{NVCC} \subseteq V_{CC^2}$ in the next step.

3 Score Checking

We first define the notion of reversing operations and then propose a tabu strategy which is based on score change.

Effects of a Local Move. Given a vertex v, there are two possible operations: removing v from D and adding v into D, and we call them a pair of reversing operations. Adding a vertex into D has two types of effects: (1) turning some vertices from being uncovered to being covered by 1 vertex; (2) turning some vertices from being covered by $c (c \ge 1)$ vertices to being covered by $(c+1)$ vertices. Likely, a removing operation has analogous effects. Given a pair of reversing operations in a sequence of local search steps, we say that their effects are neutralized if and only if they have completely opposite effects.

Obviously if a pair of reversing operations occur consecutively, their effects will be neutralized. This is the worst case and any tabu strategy prevents such cases from happening. However, even though two reversing operations are not consecutive, their effects may still be neutralized. So the question is in under what condition their effects will not be neutralized.

Our Tabu Strategy. In fact it is impractical to record all the effects of an operation, since it requires much space and time for checking. To make it practicable, a compromising method is to memorize some important effects like the set of vertices which become covered (or uncovered). Then we avoid any two reversing operations which cover and uncover the same set of vertices.

However, maintaining these sets and checking equality relation still consumes too much time. Therefore we choose to consider the score (gain or loss) of the operations. Then we attempt to avoid any pair of reversing operations if their scores are opposite. Now we give an example to describe our motivation.

Example 1

Suppose a vertex v is removed from the candidate solution at Step i with $loss_i(v)$, and then added back at Step j with $gain_j(v)$. We observe that

• 1. if $loss _i(v) \ne gain _j(v)$, then the effects of these two operations will not be neutralized;

• 2. even though $loss _i(v) = gain _j(v)$, their effects are not necessarily neutralized, since they may cover and uncover different sets of vertices respectively;

• 3. if $gain (v)$ keeps unchanged after v’s removal, then v’s removal and later addition will uncover and cover the same set of vertices respectively.

Based on these observations, we propose a tabu strategy which is based on score change: After a vertex is removed from the candidate solution, it cannot be added back until its score has been changed. Throughout this paper, this strategy will be called Score Checking (SC).

Our strategy is implemented with a Boolean array named $free$ s.t. $free (v)=1$ means v is allowed to be added into the candidate solution, and $free (v)=0$ otherwise. Then we maintain the $free$ array as follows:

• 1. initially $free (v)$ is set to 1 for all $v \in V$;

• 2. when v is removed from D, $free (v)$ is set to 0;

• 3. when $gain (v)$ is changed, $free (v)$ is set to 1.

We notice that there is a concept called promising variable in SAT [17], which allows a variable to be flipped if its score becomes positive because of the flips of its neighboring variables. This concept is in some sense similar to the score checking strategy here.

3.1 Comparing SC to NVCC

Example 2 shows that SC has stronger forbidding strength than NVCC, while Example 3 shows the opposite.

Example 2

Suppose that we have a graph $G_2$ as below, the current candidate solution $D = \{v_2, v_5\}$, $free (v_3) = 1$ and $free (v_4) = 0$.

Now we add $v_3$ into D. According to NVCC, $free (v_4)$ will become 1, because one of its neighbors, $v_3$, has changed its state. However, according to SC, $free (v_4)$ will still be 0, because $gain (v_4)$ has not changed. So the forbidding strength of SC is stronger than that of NVCC in this case.

Example 3

Suppose that we have a graph $G_3$ as below, the current candidate solution $D = \{v_2, v_6\}$, $free (v_3) = 1$ and $free (v_4) = free (v_5) = 0$.

Now we add $v_3$ into D. According to NVCC, $free (v_5)$ will still be 0, because none of its neighbors has changed its state. However, according to SC, $free (v_5)$ will become 1, because $gain (v_5)$ is decreased by 1. So the forbidding strength of NVCC is stronger than that of SC in this case.

Based on the examples above, we have

Proposition 6

There exists a case in which the forbidding strength of SC is stronger than that of NVCC, and there also exists a case in which the forbidding strength of NVCC is stronger than that of SC.

3.2 Comparing SC to CC$^2$

By Item 2 in Proposition 3, if a vertex’s score is changed, then it must be that its configuration is changed according to CC$^2$ strategy. Therefore if a vertex is released by SC, it must also be released by CC$^2$. So the forbidding strength of SC is at least as strong as that of CC$^2$. On the other hand, Example 2 shows that the forbidding strength of SC can sometimes be stronger than that of NVCC, and thus also stronger than that of CC$^2$ by Proposition 5. Therefore we have a proposition below which shows that the forbidding strength of SC is strictly stronger than that of CC$^2$.

Proposition 7

Let $V_{SC}$ be the set of vertices which are free according to SC, then we have (1) $V_{SC} \subseteq V_{CC^2}$ always hold; (2) $V_{CC^2} \subseteq V_{SC}$ does not always hold.

4 Our Algorithm for Exchanging Vertices

Here, we present the ExchangeVertices(G, D) procedure in Algorithm 2, which adopts our new tabu strategy. In this algorithm, we use $uncov\_v\_num _1$ and $uncov\_v\_num _2$ to denote the number of uncovered vertices before and after exchanging vertices respectively. Furthermore, it adopts the two-stage exchange strategy in NuMVC [4].

4.1 Removing Stage

In the removing stage (Lines 2 to 12), we propose a heuristic called best-picking with probabilistic walk. The intuition is as follows: if the local search has spent only a little time in the current area, we prefer greedy mode to find a good solution; otherwise we favor random mode to leave.

To be specific, we exploit the hash function in the preliminary section to approximately detect revisiting. Like [12], we set the prime number to be 10$^9$ + 7 and do not resolve collisions. Since in our experiments, our solver performs less than $5 \times 10^8$ steps in any run, given the 10$^9$ + 7 hash entries, the number of collisions is negligible. Notice that we mark and detect the hash table only when $lastStepImproved = true$. The intuition is that if a solution is revisited together with the same $lastStepImproved$ value as before, then the current area has been visited to a significant extent. In this situation, a vertex is removed from the candidate solution with a probability proportional to its degree. We tend to remove large-degree vertices, because we rarely remove them in the greedy mode, and this will further strengthen the diversification in our algorithm.

To implement probabilistic selections, we employ an array with length 2|E|, where |E| is the number of edges, to store copies of the vertices. Before doing local search, given any vertex, say u, we put d(u) copies of u into the array. According to Proposition 1, there are exactly 2|E| copies of the vertices in the array. When we perform the probabilistic selection, we do the following: Randomly select an item in the array and if the result is in D, then return; otherwise repeat the random selection.

Now we analyze the complexity of this procedure. Each time we obtain an item, the probability that it is in D, denoted by p, is at least $\frac{|D|}{2|E|}$ (we use “at least” because usually a vertex in D has more than one copy in the array). Then by Theorem 1, the averaged number of trials needed for the first success is $\frac{1}{p} \le \frac{2|E|}{|D|}$. Moreover, we find that $\frac{2|E|}{|D|} \le 500$ in most graphs. So the time complexity is $O(\frac{2|E|}{|D|}) = O(1)$.

4.2 Adding Stage

In the adding stage (Lines 13 to 16), our algorithm chooses a random uncovered vertex and selects a vertex in its neighborhood to add into D. By the following proposition we ensure that Line 14 in Algorithm 2 always returns a valid vertex outside D².

Proposition 8

• 1. If v is uncovered, then $N[v] \cap D = \emptyset$;

• 2. For any uncovered vertex v s.t. $d(v) \ne 0$, there exists at least one vertex $n \in N[v]$ s.t. $free (n) = 1$.

The proof follows the arguments in [4].

5 Speeding up of Best-Picking

In this section we present the details of our data structure that achieves the average complexity of ExchangeVertices(G, D) (Algorithm 2) of $O(\bar{d}_2)$.

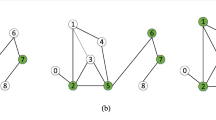
Score-Based Partition. The idea is to partition the vertices wrt. their scores, $\textit{i.e.}$, two vertices are in the same partition if they have the same score, otherwise they are in different partitions (see Fig. 1). Given a graph $G = (V, E)$ and a candidate solution D, we implement the score-based partition on an array where each position holds a vertex. Besides, we maintain two types of pointers, $\textit{i.e.}$, $P_{gain}$ and $P_{loss}$, each of which points to the beginning of a specific partition.

Fig. 1.

Initial state before adding $v_{68}$ into D

Algorithms and Implementations. We use loss-k (resp. gain-k) partition to denote the partition that contains vertices whose loss (resp. gain) is k. All the loss-k partitions are shown as dark regions, and all the gain-k partitions are shown as light ones. Then we use Algorithm 3 to find those vertices with the minimum loss.

Since $loss (v) \le d(v)+1$ for any $v\in V$, we have

Proposition 9

If Algorithm 3 returns a vertex v, then the complexity of its execution is O(d(v)).

Fig. 2.

Swapping vertex $v_{68}$ and $v_{91}$

Fig. 3.

Moving pointer $P_{gain-52}$

At the beginning when D is empty, there are no dark regions in our data structure, so initializing the partitions is equivalent to sorting the vertices into a non-decreasing order wrt. their gain. Notice that at this time, $gain (v) = d(v)+1$ for all $v \in V$. By Proposition 4, we have

Proposition 10

The complexity of initializing the partitions is O(|V|).

In both construction and local search phases, our algorithm will repeatedly add vertices into D or remove vertices from D, until some cutoff arrives. When a vertex v is added or removed, we have to maintain the gain or loss wrt. the vertices in $N^2(v)$. There are two cases in which a particular vertex, say v, has to be moved from one partition to another: (1) adding (resp. removing) v into (resp. from) D; (2) increasing/decreasing $gain (v)$/$loss (v)$. Thus the core operation is to move a vertex v to an adjacent partition.

Now we show how to do this with an example (See Figs. 1, 2 and 3). In this example, we are to add $v_{68}$ into D. Before $v_{91}$ and $v_{68}$ are in the gain-52 partition and thus their gain is 52 (Fig. 1). Notice that after being added, $v_{68}$’s loss will become 52, $\textit{i.e.}$, it should be in the loss-52 partition. Thus the operation is like this: (1) $v_{68}$ is swapped with $v_{91}$ (Fig. 2); (2) P$_{\textsf {\tiny gain-52}}$ is moved (Fig. 3).

We define placeVertexIntoD(v) as the procedure that moves v from some gain-k partition to the respective loss-k partition. Also we define to be the procedure that moves v from some gain-k partition to the respective gain-(k-1) partition. Likely we define , , and placeVertexOutFromD(v). Then we have

Proposition 11

All the procedures above are of O(1) complexity.

Complexity Analysis. When a vertex v is added or removed, we simply need to maintain the gain or loss wrt. the vertices in $N^2(v)$. Hence we have

Theorem 2

Suppose that each vertex has equal probability to be added or removed, then the average complexity of ExchangeVertices(G, D) (Algorithm 2) is $O(\bar{d}_2)$.

Table 1. Results on large graphs where FastWMDS and ScBppw found different $D_{min}$ or $D_{avg}$

6 Experimental Evaluations

We compared the overall performances of our solver ScBppw to FastWMDS on the benchmark instances in [24] and [16] which contain more than $5 \times 10^5$ vertices. Notice that large graphs are the main challenge of current solvers, and their size will keep growing due to the amount of data available. There are some other MinDS solvers like SAMDS [14], CC$^2$FS [25] and RLS-DS [7], but they do not materially change our conclusions below, because our preliminary experiments show that FastWMDS significantly outperforms them. Also we conducted experiments to evaluate the individual impacts.

6.1 Experimental Setup

FastWMDS was compiled by g++ 5.4.0 with O3 option while ScBppw was compiled by g++ 4.7.3 with O3 option. The experiments were conducted on a cluster equipped with Intel Xeon E5-2670 v3 2.3 GHz with 64 GB RAM, running CentOS6. Each solver was executed on each instance with seeds from 1 to 10. The cutoff was set to 1,000s. For each algorithm on each instance, we report the minimum size (“$D_{min}$”) and averaged size (“$D_{avg}$”) of the dominating sets found by the algorithm over the 10 runs. To make the comparisons clearer, we also report the difference (“$\delta _{min}$”) between the minimum size returned by ScBppw and that returned by other solvers. Similarly $\delta _{avg}$ represents the difference between the averaged sizes. A positive difference indicates that ScBppw performs better, while a negative value indicates the opposite. For the sake of space, we do not report results on those graphs where all solvers found the same $D_{min}$ and $D_{avg}$. The best $D_{min}$ and $D_{avg}$ values are shown in bold font. For the sake of space, in each table we will write bn-human-BNU_1 in short for bn-human-BNU_1_0025865_session_1-bg, channel-500 in short for channel-500x100x100-b050, and soc-groups in short for soc-livejournal-user-groups.

6.2 Main Results

Table 1 compares the overall performances of FastWMDS and ScBppw. From this table, we observe that:

• 1. ScBppw outperforms FastWMDS on most instances in terms of $D_{min}$ and $D_{avg}$.

• 2. Further observations show that there are 11 graphs which contain more than $10^7$ vertices. Among these graphs, ScBppw outperforms FastWMDS on 9 graphs (marked with * in the table) in terms of both $D_{min}$ and $D_{avg}$. On the other 2 graphs, $\textit{i.e.}$, soc-sinaweibo and socfb-uci-uni, both solvers found the same $D_{min}$ and $D_{avg}$. So ScBppw is more scalable than FastWMDS.

We also did similar experiments on those graphs in [24] and [16] whose vertex number lies between 2 $\times$ 10$^4$ and 5 $\times$ 10$^5$. Experimental results show that ScBppw is comparable and complementary with FastWMDS. More specifically, they have different performances, and the number of graphs on which ScBppw performs better is roughly equal to the number of graphs on which FastWMDS performs better. In addition, both solvers outperforms the other MinDS solvers.

Notice that FastWMDS exploits a list of reduction rules to simplify the input graphs before doing local search, while our solver only adopts a simple greedy heuristic. Therefore we can conclude that pure local search is also competitive.

6.3 Individual Impacts

In what follows, we first modify our algorithm and develop several variants. Then we redo the experiments above and compare them in terms of average solution quality.

Table 2. Results on large graphs where NVCCBppw and ScBppw found different $D_{min}$ or $D_{avg}$

Effectiveness of Score Checking. We replace the SC strategy in ScBppw with the NVCC, CC$^2$ and CC$^2$V3 strategies, and develop three variants named NVCCBppw, CC$^2$Bppw and CC$^2$V3Bppw respectively.

When comparing NVCCBppw with ScBppw, we find that

• 1. ScBppw performs better on 19 instances;

• 2. NVCCBppw performs better on 14 instances.

This means that the SC strategy is more suitable than the NVCC strategy in our solver. The detailed results are shown in Table 2.

Furthermore, when comparing CC$^2$Bppw, CC$^2$V3Bppw with ScBppw, we find that

• 1. CC$^2$Bppw outperforms the other solvers on 0 instances;

• 2. CC$^2$V3Bppw outperforms the others on 6 instances;

• 3. ScBppw outperforms the others on 32 instances.

This indicates that the SC strategy is more effective than the CC$^2$ and CC$^2$V3 strategies. For the sake of space, we omit the detailed results here. Overall, the SC strategy plays an essential role in our solver.

Now we analyzes the performances. (1) Apart from the tabu strategy, we find that there are two powerful diversification strategies in FastWMDS: a frequency based scoring function and a best-from-multiple-selection heuristic with some random walks. In contrast, besides the tabu strategy, ScBppw only exploits two weak diversification strategies: (i) best-picking with probabilistic walk; (ii) randomly selecting an uncovered vertex. Since (i) and (ii) are weak diversification strategies, an effective tabu strategy in our solver should be stronger than the CC$^2$V3 strategy in FastWMDS. Indeed, NVCC and SC greatly outperform CC$^2$ and CC$^2$V3 in our solver. (2) When a vertex v is added or removed, SC can release some vertices whose distance from v is 2. However, NVCC tends to release more vertices whose distance from v is 1. Thus SC is more likely to search in a bigger area while NVCC is more cautious in current areas. Therefore their performances are quite different.

Effectiveness of Best-Picking with Probabilistic Walk. We modify this strategy and develop two variants, ScBprw (Score Checking and Best-picking with Random Walk) and ScBppw-nlsp (ScBppw with no lastStepImproved) as follows. To develop ScBprw, we replace the probability selection in ScBppw with random walk, which means every vertex in D has equal probability to be removed. On the other hand, to develop ScBppw-nlsp, we remove the $lastStepImproved$ predicate from ScBppw so that our algorithm will mark and check the hash table regardless of the $lastStepImproved$ value. More specifically, we remove lines 1, 2, 8, 9, and 17 to 21, so as to develop ScBppw-nlsp. Then we compare these two variants with ScBppw. Experimental results show that

• 1. ScBprw outperforms the other solvers on 7 instances;

• 2. ScBppw-nlsp outperforms the others on 7 instances;

• 3. ScBppw outperforms the others on 21 instances.

Moreover, we remove the probabilistic selection component and develop a variant called ScDS, which will always do best-picking in the removing stage. Experimental results show ScBppw significantly outperforms ScDS as well.

Overall, we conclude that the probabilistic selection as well as the $lastStepImproved$ predicate play an important role in ScBppw. For the sake of space, we omit the detailed results here.

7 Conclusions

In this paper, we have developed a local search MinDS solver named ScBppw. Experimental results show that our solver outperforms state-of-the-art on large graphs. In particular, it makes a substantial improvement on those graphs that contain more than 10$^7$ vertices. The main contributions include: (1) a tabu strategy based on score change; (2) a best-picking with probabilistic walk strategy; (3) a data structure to accelerate best-picking.

For future works, we will develop efficient heuristics to solve the MinDS problem on massive graphs which are too large to be stored in the main memory and has to be accessed through disk IOs.