SIRCS: Slope-intercept-residual Compression by Correlation Sequencing for Multi-stream High Variation Data

Abstract

Multi-stream data with high variation is ubiquitous in the modern network systems. With the development of telecommunication technologies, robust data compression techniques are urged to be developed. In this paper, we humbly introduce a novel technique specifically for high variation signal data: SIRCS, which applies linear regression model for slope, intercept and residual decomposition of the multi data stream and combines the advanced tree mapping techniques. SIRCS inherits the advantages from the existing grouping compression algorithms, like GAMPS. With the newly invented correlation sorting techniques: the correlation tree mapping, SIRCS can practically improve the compression ratio by 13% from the traditional clustering mapping scheme. The application of the linear model decomposition can further facilitate the improvement of the algorithm performance from the state-of-art algorithms, with the RMSE decrease 4% and the compression time dramatically drop compared to the GAMPS. With the wide range of the error tolerance from 1% to 27%, SIRCS performs consistently better than all evaluated state-of-art algorithms regarding compression efficiency and accuracy.

1 Introduction

Multi-stream data is ubiquitous in the modern network systems [13]. With the development of telecommunication technologies, information is usually generated as a collective and multi-dimensional data stream from different sources. As the popularisation of the Internet of Things [17], the time-series group data compression is becoming more popular and important than ever before in both industry and academia. Meanwhile, in today’s critical network systems, information with high variation is also frequently generated, such as in the stock trade, traffic systems, massively distributed solar systems, etc. Such data usually preserves ambiguous variation pattern, big data range and high variance, and hence becomes a challenging data type to compress in the communication network. Therefore, current research needs to be widely extended to optimally encode and reconstruct the high variation data in a highly correlated multi-signal network system.

Previous work has been conducted for single-stream time-series data compression, such as APCA [2] and SF [6], to name a few. In a multi-signal environment, however, if we apply these methods directly to compress each single stream one by one without considering their correlation, it is highly possible to result in a small compression ratio.

To simultaneously handle all streaming data, multi-signal compression algorithms, such as GAMPS [7], are developed based on the data correlation information. Particularly, GAMPS first groups signals within spatial proximity into a cluster, and determines the best base signal in the cluster by iteratively checking the compression performance of using each stream as the base signal. For each data other than the base signal, it then constructs a ratio signal based on its difference with the base signal, called “cluster mapping”. Finally, it applies APCA to compress both base signal and ratio signals. However, such methods still have some drawbacks especially when dealing with high variation data: (1) The brute-force search for the base signal is extremely time-consuming; (2) The correlation information is never fully utilised when we transform each signal only according to the base signal in the cluster mapping; (3) Ratio signal cannot comprehensively capture complex patterns in high variation data, leading to relatively large reconstruction error.

To address the above issues, we propose a novel algorithm, SIRCS (Slope-Intercept-Residual compression by Correlation Sequencing), for multi-stream compression with high variation data. We introduce decomposition-based compression and tree mapping techniques in this work, and SIRCS is a condign combination of these techniques, which demonstrates an overall improvement over current state-of-the-art compression methods in both efficiency and precision. Our major contributions can be summarised as follows:

• 1. We study the problem of multi-signal compression which has important applications in modern network systems. The problem is challenging due to various correlation levels, and variation patterns existed in the streaming signals.

• 2. We introduce the correlation tree mapping technique for data grouping to fully utilise the correlation information between signals efficiently. The mapping can efficiently configure a tree index with a selected base signal, and meanwhile, maximise the preservation of the highest correlation information in the index. We theoretically prove the improvability of the tree mapping technique over traditional cluster mapping.

• 3. We propose a regression-based decomposition technique for data-variation reduction, which results in smaller fluctuation in the residual signals and hence better compression performance.

• 4. We propose a new idea of residual compression with the guarantee of the worst-case maximum $L_\infty$ error derived from the base signal error bound. This assures all signals to be perfectly reconstructed with a maximum error guarantee.

• 5. We empirically compare SIRCS with several state-of-the-art compression algorithms on a real-world dataset, and the experimental result demonstrates better performance achieved by SIRCS regarding compression ratio, reconstruction precision, and compression speed.

For the rest of the paper, we review the work of data compression in Sect. 2, then formulate the problem of multi-stream high variation data compression in Sect. 3. In Sect. 4, the SIRCS algorithm is introduced to solve the problem in Sect. 3 by integrating the tree mapping, regression-based decomposition, and residual compression. We report our empirical results in Sect. 5, followed by a brief conclusion in Sect. 6.

2 Related Work

Numerous state-of-art algorithms exist in the computing systems, usually classified into lossless and lossy compression schemes. Prevalent application of the lossless algorithms, such as Adaptive and Non-adaptive Huffman Coding [19], LZ77 [22], LZ78 [23], LZW [16], BWT [14] and PPM [4], remain robust and functional even in most of the modern operating systems. BWT-based compression reaches the optimised performance at $O(\frac{log(n)}{n})$, improving from $O(\frac{log(log(n))}{log(n)})$ from LZ77 [21] and $O(\frac{1}{log(n)})$ from LZ78 [12]. However, the compression ratio cannot be dramatically increased from a lossless algorithm, therefore, lossy compression is introduced for a better trade-off of the compression efficiency.

In lossy compression for single data, the piecewise approximation algorithms, in particular, are the most fundamental and can be furthermore classified into: piecewise constant approximation (eg., PCA [11], APCA [2], PAA [8], etc.), linear approximation (eg., SF [6], PWLH [1], PLA [3], etc.), and polynomial approximation (eg., CHEB [20], etc.). Another lossy compression type is the decomposition based algorithms, such as DWT [15], DCT [9], DFT [10], etc. Those compression algorithms usually preserves high compression ratio but longer compression time. However, in modern network systems, the correlation between multiple signals should also be considered to improve compression performance further.

Group data compression algorithms are introduced in the lossy compression domain. GAMPS is the first application using the data correlation. In GAMPS, ratio signals are introduced by dividing one signal value with the selected base signal value. Due to the signals similarity, the ratio signal from two highly correlated signals is much flatter than its original data, thus largely reducing the variation level. Compressing the low variation data by APCA, in turn, increases the total compression ratio. To select the proper base signal, GAMPS computes the compression ratio in every scenario with different signals as the base signal. Thorough iteration occurs to estimate the consumptions by summing the size of all compressed signals. The algorithm then picks the base signal leading to the smallest compressed file size. Consequently, GAMPS can lead to an excellent compression ratio but relatively large precision error and long compression time. Our work, on the contrary, aims to optimise all the three performance criteria in multi-stream compression.

3 Problem Definition

Definition 1

(High Variation Time Series Data) The time-series data with high variation D is defined as a stream of data points $(t_i, v_i)$ with a consecutive time index $t_i$ (i.e., $D = [(t_1, v_1),(t_2, v_2),\dots ,(t_n, v_n)]$), where the standard deviation $\sigma {D}$ and the range $D_{max}-D_{min}$ are much higher than regular time-series data. The time index follows monotonicity: $\forall {i<j, t_i<t_j}$.

We use $S = \{D_1, D_2, \dots , D_n\}$ to denote a multi-signal time series dataset, i.e., a set of time-series data D which share the same time index with the length n (i.e., $D_i = [(t_1, v_1^i),(t_2, v_2^i),\dots ,(t_n, v_n^i)]$). The problem studied in this paper can be formulated as follows.

Definition 2

(Group Compression of High Correlation Data with Max-error Precision) A dataset S formed by the high variation time-series data $D_i$, where $i \in {[1,n]}$, and an error bound $\epsilon$ are given. The problem is to compress all $D_i$ in the dataset S so that the reconstructed signal $D'_i$ suffice the equation: $\forall {D_i}\in {S}, (D'_i(t))-D_i(t))\le {\epsilon }$.

Intuitively, the hypothesis can be made that the higher the correlation, the higher the compression ratio will be obtained. We conduct an empirical evaluation to test the relationship between the correlation of a paired signal and their compression ratio, along with the precision. Assume two randomly picked signals from the signal network are $D_i , D_j$, and their correlation is $R^2_{i,j}$. In this two signals compression, we link the $R^2$ values to the CR and NRMSE from the compression between $D_i , D_j$. The result of the evaluation shows the statistical significance in the positively associated relationship between the correlation and the compression ratio. The detailed information of the empirical evaluation will be reported in Sect. 5. This result validates the hypothesis that a high correlation between two signals can improve the compression performance. Therefore, we focus our study of multi-stream data compression in a highly correlated network system as defined below.

Definition 3

(Correlated Multi-signal Network) The correlated multi-signal network is a system where any two randomly selected signals, $D_i(t)$ and $D_j(t)$, are correlated, thus similar in variation pattern, with a mathematical relation as a function of F, denoted as $D_i(t)=F(D_j(t))+\delta _j(t)$.

4 SIRCS: Slope-intercept-residual Compression by Correlation Sequencing

4.1 Overview

The algorithm consists of three main components: correlation tree sequencing, regression-based decomposition and the residual data compression. First, given the time-series dataset $S = \{D_1, D_2, \dots , D_n\}$, the correlation tree sequencing is to create a compressing index $I_{tree}$ and select the base signal $D_{base}$. Second, following $I_{tree}$ and $D_{base}$, the regression-based decomposition dissemble $D_i$ into its residual $R_i$ and the regression coefficients. Finally, the residual data is compressed with a newly estimated error bound. This residual error bound assures that the recovered residuals and the regression coefficients can reconstruct the raw signal under the original maximum error guarantee. We will elaborate on the technical details of these three components in the following sections, respectively.

4.2 Correlation Sequencing Mechanism

According to our hypothesis, data correlation can effectively minimise the memory consumption of multi-stream data. In this section, we will introduce our method of correlation tree mapping and meanwhile theoretically prove the improvability of the tree mapping over the cluster mapping.

Technique 1. (Correlation Tree Mapping) The cluster mapping is based on a unique base signal, so its information index, $I_{cluster}$, processes only one pass to each of the child signal ($D_{base}\rightarrow {D_{i}}$, where $0\le {i}\le {n-1}$). Replacing the cluster to tree mapping, whose information index, $I_{tree}$, processes multiple passes from one child signal to another child signal ($D_{base}\rightarrow {D_{i}}\rightarrow \dots \rightarrow {D_{j}}$, where $0\le {i,j}\le {n-1}$), we always have the compression ratio compared as

$$\begin{aligned} {(CR)}_{tree}(\sum _{i=0}^{n} D_i(t))\ge {{(CR)}_{cluster}(\sum _{i=0}^{n} D_i(t))}. \end{aligned}$$

(1)

Tree Components Formation

Definition 4

Correlation pairs are the signal link between two signals; correlation branches are the signal link with multiple signals sharing one head node and; correlation twigs are the branch components which are different in length but share the same head node with their branch.

Tree components formation aims to extract the high correlation pairs from signals m and n and arrange them in an ordered sequence. Considering the non-repetitive collection: if $r_{(m,n)}$ is chosen, the system will check if either m and n is already collected, and if not, the system will register $r_{(m,n)}$. Such correlation collection will not end until all signals are contained. During the signal collection, there will be three scenarios:

• 1. $r_{(m,n)}$ where m is in the list, and n is in the list. In this case, there will be no collecting operation occurred.

• 2. $r_{(m,n)}$ where m is in the list, but n is not in the list. In this case, only the signal n is collected. It further implies the node m is an intermediate connection between a collected signal and n.

• 3. $r_{(m,n)}$ where both m and n are not in the list. In this case, both signal ID m and n will be collected. It implies that the connecting pair m and n are isolated from the other signal nodes.

These three possibilities will impact on the branch creation in the later procedure: if there’s a node acting as an intermediate connection with two other nodes, a branch will be created. Then the high correlation pairs obtained previously will be connected to several branches with longer connections in each segment. The connection starts with connecting one pair’s head with the other pair’s tail if the head and tail have the same signal index. To achieve the repetitive seeking for the same heads and tails, the recursion algorithm is implemented to keep connecting the previously and newly generated segments until no same heads and tails occur in the segments. As a special case of the branch, several twigs may be included in one branch. In this case, they will be encapsulated in one branch.

Example 1

In Fig. 1, $r_{11,12}\rightarrow {r_{11,0}}\rightarrow {r_{1,2}}\rightarrow {\dots }\rightarrow {r_{7,6}}$ is sorted and there are 14 elements in total. All the 18 signals are just recovered from those 14 paired segments, where the signal 6 is the last selected element. The rest of the correlation pairs after $r_{7,6}$ will be ignored. In the left figure of Fig. 2, we find the repetition of the signals in the parental and child node position, such as the pairs $3\leftrightarrow {15}$ against $15\leftrightarrow {17}$ and $15\leftrightarrow {7}$. The connection will be ended with the segment $3\leftrightarrow {15}\leftrightarrow {17}$ and $3\leftrightarrow {15}\leftrightarrow {7}\leftrightarrow {6}$. After the connections, the branch with only one twig is 1 : [[2, 0]], and the branch with multiple twigs is 11 : [[0, 8], [12]], 3 : [[15, 7, 6], [15, 17], [9]], and 5 : [[13], [4, 16], [14]].

Fig. 1.

(a) Shows the example of the correlation sequencing: the system will arrange those collected signal pair into a structure similar to: $D_{r^2}=r_{11,12}:[11,12],r_{11,0}:[11,0],\dots {},r_{7,6}:[7,6]$. (b) demonstrates the example of connecting same ID of different pairs to branches.

Base Signal Selection. In this step, we aim to find a common based signal for all branches by seeking the highest correlation pair between one branch’s head node and any elements in the other branches. To assure the result of iteration is the highest correlation among all possibilities, the connecting candidates will not be defined until all the head nodes of the branches go through every element of the other branches and estimate their correlation level. The highest pair will be given the priority to connect and for each loop. As the plantation of branches is accomplished, there will be only one head node in the tree, which will be nominated as the base signal $D_{base}(t)$.

Example 2

Right figure in Fig. 2(a) demonstrates four branches with the head-node 3, 5, 1, and 11. The first highest correlation searching ends up with connecting the signal 12 with the head node 3 at $R^2 = 0.88$. The second searching follows up with the connection between signals 5 and 7 at $R^2 = 0.81$. The last searching ends up with connecting signals 1 and 10 at $R^2 = 0.78$. Finally, the tree index is constructed and $D_{base}(t)$ is $D_{11}(t)$, shown in Fig. 2(b).

Fig. 2.

(a) Demonstrates searching for the highest correlated pair: the searching process iterates three times in total, indicating the optimal connecting index among the branches, after which the correlation tree is eventually created. The whole steps guarantee that for each connection, the chosen correlation level remains the highest from the rest. (b) shows the result of the correlation tree mapping, the index of the signals is encoded in digital numbers as the header of the compressed file.

Proof of Improvability. The following theorem highlights the superiority of our proposed tree mapping over traditional cluster mapping.

Theorem 1

If the information of the total correlation level from an index is given by I, the sum of correlation level from the cluster mapping is always less equal than the sum of correlation level from the tree mapping, denoted as $I_{cluster}\le {I_{tree}}$.

Proof

Assume the branch number of the index is m, and within a branch, if the connecting nodes number is greater than 2, assume the node connection number as n. The formulas of the total correlation level from both cluster index mapping and tree index mapping can be written as

$$\begin{aligned} I_{cluster}=\sum _{i=1}^{m} {Cor(D_{base, 0}(t), D_{i, 1}(t))}, \end{aligned}$$

(2)

$$\begin{aligned} I_{tree}=\sum _{i=1}^{m} {\sum _{j=1}^{n} {Cor(D_{i,j}(t), D_{i, j + 1}(t))}}. \end{aligned}$$

(3)

In the cluster mapping formula, it is known there are only two signals in one branch: the base signal as $D_{base, 0}(t)$ and child signal as $D_{i, 1}(t)$, where the base signal is fixed once the index is created. Suppose the first component in the correlation calculation is a set of the possible parental signals, denoted as P, the set of the parental signals in the cluster mapping will then be $P_{cluster}=D_{base, 0}(t)$. It can be observed that the total number of elements in the cluster mapping is unique, while in the tree mapping, multiple parental signals including that in the cluster mapping case can concurrently exist, denoted as $D_{base, 0}(t)\in {P_{tree}}$. Therefore, the relation between the parental set from cluster and tree mapping will be $P_{cluster}\subset {P_{tree}}$. Since the parental-signal selection in the tree mapping has greater flexibility, a wider range of the correlation selection exists in the tree mapping than the cluster mapping, denoted as

$$\begin{aligned} Set(Cor(D_{base, 0}(t), D_{i, 1}(t)))\subset {Set(Cor(D_{i,j}(t), D_{i, j + 1}(t)))}. \end{aligned}$$

(4)

More correlation selection in the tree mapping further implies the tree index can cover higher correlation information. After all, cluster mapping only manifests the correlation between the base signal and its child signals, while the in tree mapping, both correlation between two child signals are also free to choose. With a wider range of selection, total correlation from tree mapping is no less than that from cluster mapping, denoted as $I_{tree}\ge {I_{cluster}}$.

4.3 Regression-Based Decomposition Mechanism

The essential reason for using regression-based decomposition is to reduce the data variation from raw to residual signal compression. With one base signal $D_{base}$ selected from the dataset S, other signals can be decomposed via the base signal and the correlation coefficients into another signal with a much smaller size $\hat{D}$. In this paper, $\hat{D}$ is the residual data $\hat{D_i}=R_i$, whose validity will be affirmed by proving $\sigma {(R_i)}<\sigma {(D)}$ in this section. Reversely, based on $D_{base}$, correlation coefficients and $\hat{D_i}$, the signals can be reconstructed with a given normalised error tolerance of $\epsilon$. The problem can be formulated as follow.

Technique 2. (Reduction of Data Variation) Based on the preceding assumptions, if a child signal is given by $D_i(t)$ and its residual signal is denoted as $R_i(t)$, for the variation level represented by standard deviation of $\sigma$, they are always satisfying the following relation: $\sigma (R_i(t)) < \sigma (D_i(t))$.

We recall the definition of the correlated signal network that $D_i(t)=F(D_j(t))+\delta _j(t)$, while we also assume the time lag between two randomly selected signals in the network cannot be too large compared to the signal period: $\varDelta _i\ll {T}$. Then we configure the linear model (LM) as $\hat{y} = \beta _0\hat{x}+\beta _1$. To minimise the mean square error of the regression line from the real data: $E_{i}^{k}=\sum _{i=0}^{n} (y-\hat{y})^2$, the coefficients are adjusted to the least square estimates [18] as

$$\begin{aligned} \beta _0=\frac{\sum _{i=0}^{N} (y_i-\hat{y_i})(x_i-\hat{x_i})}{\sum _{i=0}^{N} (x_i-\hat{x_i})^2}, \end{aligned}$$

(5)

$$\begin{aligned} \beta _1=\frac{\sum _{i=0}^{N} (y_i-\bar{y})(x_i-\bar{x})}{\sum _{i=0}^{N} (x_i-\bar{x})^2}. \end{aligned}$$

(6)

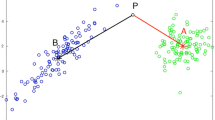
Such regression model can extract the coefficient of slope, intercept, and the residual data with zero mean and lower variation level. This theorem of data variation reduction can be proved bellow and visually shown in Fig. 3.

Fig. 3.

(a) Shows an example of three raw signals from the solar panel in St Lucia Campus. (b) Indicates the residual signals from the left figure have been visually reduced in data variation.

Theorem 2

Assume the original data has high range and standard deviation, while their variation patterns are also similar. Given the child signal $S_i(t)$ and its parental signal $S_{j}(t)=\beta _0S_{i}(t+\varDelta )+\beta _1+\delta _{i}(t)$ where $S_i(t), S_{j}(t)\ge {0}$ , we define $S_\varDelta (t)=S_i(t)-S_{j}(t)$. If $\sigma$ represent the standard deviation, we can always have $\sigma ({S_\varDelta (t))}\le {\sigma {(S_{i}(t))}}.$

Proof

If the coefficient of variation is defined as $\sigma (S(t)) = \sqrt{\frac{\sum _{i=0}^{n} (S(t)-\bar{S})^2}{n-1}}$. Taking $S_\varDelta (t)$, we have

$$\begin{aligned} \sigma (S_\varDelta (t)) = \sqrt{\frac{\sum _{i=0}^{n} (S_\varDelta (t)-\bar{S}_\varDelta )^2}{n-1}}. \end{aligned}$$

(7)

Since $S_\varDelta (t)=S_i(t)-S_{j}(t)$, we can deduce

$$\begin{aligned} \sigma (S_\varDelta (t)) = \sqrt{\frac{\sum _{i=0}^{n} ((S_i(t)-(\beta _0S_{i}(t+\varDelta )+\beta _1+\delta _{i}(t)))-\bar{S}_\varDelta )^2}{n-1}}. \end{aligned}$$

(8)

As $S_i(t)$ is periodic, and apparently $\beta _0S_{i}(t+\varDelta )+\beta _1$ is also periodic, according to the linearity of Fourier Transform, $S_T(t) = S_i(t) - (\beta _0S_{i}(t+\varDelta )+\beta _1)$ is a periodic signal. Since $\bar{S}_\varDelta =E(S_T(t))+E(\delta _{i}(t))$ and from the linear regression model, we know $E(\delta _{i}(t))=0$, then $\bar{S}_\varDelta =E(S_T(t))$. The formula can be rewritten as

$$\begin{aligned} \sigma (S_\varDelta (t)) = \sqrt{\frac{\sum _{i=0}^{n} (S_T(t) -\delta _{i}(t)-\bar{S}_T)^2}{n-1}}. \end{aligned}$$

(9)

Since the assumption of the distributed signals network is geographically closed, while the time latency $\varDelta$ should be small enough for the similarity detection, which is formulated as $S_{i}(t)\approx {S_{i}(t+\varDelta )}$.

We assume that the order of magnitude in delta signal and the error signal is much smaller than that of the original signal. This is normal to expect since $Power(S_i(t))\approx {\beta _0S_{i}(t+\varDelta )+\beta _1}$ and, without bad leverages and outliers, $Power(\delta _{i}(t))\ll {S_i(t)}$. Therefore, we have $S_T(t),\delta _{i}(t)\ll {S_i(t))}$.

Now that we want to compare the between $\sigma (S_i(t))$ and $sigma(S_\varDelta (t))$. In the course, we can rely on the aforementioned assumptions to approximate $\sum _{i=0}^{n}(S_T(t) - \bar{S}_T)^2\approx {0}$, compared to the much larger value of $S_i(t)$. Therefore we have

$$\begin{aligned} \sigma (S_\varDelta (t))\approx {\sqrt{\frac{\sum _{i=0}^{n} (\delta _{i}(t))^2}{n-1}}}. \end{aligned}$$

(10)

As one of the assumptions, $Var(S_{i}(t))=\sigma ^2(S_{i}(t))\gg {\sigma ^2(S_{\varDelta }(t)})$, we can deduce

$$\begin{aligned} \sigma (S_i(t))\ge {\sqrt{\frac{\sum _{i=0}^{n} (\delta _{i}(t))^2}{n-1}}=\sigma (S_\varDelta (t))}. \end{aligned}$$

(11)

4.4 Residual Data Compression

This section is proposed to compressed the $R_i(t)$ decomposed from the signals $D_i(t)$ based on the linear regression model with $D_{base}(t)$. The problem of the residual compression is shown as follow.

Technique 3. (Error Bound of Residual Compression) If the error precision of the raw signal is given by $\epsilon _{raw}$ and the corresponding error precision of the residual signal is given by $\epsilon _{res}$, the algorithm needs to assure for any signal reconstruction from its residual data with $\epsilon _{res}$, the precision of the reconstructed signal should fall in the range of $\epsilon _{raw}$.

The problem is solved by the theorem of the residual error bound, in which the signals D(t) are divided into direct parent signal P(t) and its child signals C(t). It implies that the error precision of the residual signal is equal to the error precision of the child signal, which we assumed to be the maximum error guarantee as $\epsilon _{raw}$.

Theorem 3

Suppose the error precision of the raw signal is given by $\epsilon _{raw}$ and the reconstructed parental and child signal is denoted as $P_{rec}(t)$ and $C_{rec}(t)$. If the linear regression model gives

$$\begin{aligned} C_{raw}(t) = \beta _0{P_{rec}(t)}+\beta _1, \end{aligned}$$

(12)

the maximum error tolerance of the residual signal will be equal to that of its raw signal, denoted as $\epsilon _{res} = \epsilon _{raw}$.

Proof

The relationship between the raw signal data and the residual data can be denoted as

$$\begin{aligned} C_{raw}(t)=\beta _{0}P_{raw}(t)+\beta _1+R_{raw}(t). \end{aligned}$$

(13)

Symbol C means the child signal, P means the parental signal, and R means the residual signal. We also recall the relation between the raw and reconstructed signal as $Rec(t)=Raw(t)+ \delta (t)$. We can deduce that the coefficients $\beta _0$ and $\beta _1$ are from the raw child signal and raw parental signal. Let us redesign the linear model between the raw child signal and the recovered parental signal. The equation is reformatted:

$$\begin{aligned} C_{raw}(t)=\beta _0P_{rec}(t)+\beta _1+R_{raw}(t). \end{aligned}$$

(14)

Let us assume that $P_{rec}(t)$ has high similarity with $P_{raw}(t)$. In decompression side, what are known are the values of $\beta _0$ and $\beta _1$, two reconstructed signals $P_{rec}(t)$ and $R_{raw}(t)$. The reconstructed child signal will be

$$\begin{aligned} C_{rec}(t)=\beta _0P_{rec}(t)+\beta _1+R_{rec}(t). \end{aligned}$$

(15)

Taking the residual signal to the linear model, we have

$$\begin{aligned} C_{rec}(t)-C_{raw}(t)=\beta _0P_{rec}(t)+\beta _1+R_{rec}(t)-\beta _0P_{rec}(t)-\beta _1-R_{raw}(t). \end{aligned}$$

(16)

Eventually, the formula can be rewritten as $\delta _R(t)=\delta _C(t)\le {\epsilon _{raw}}$.

The theorem finalises the estimation of the residual data error bound, therefore, the final design of the SIRCS algorithm can be integrated in Algorithm 1. Here we assume the group dataset as S, single data stream as D, lists for signal collection as L, and encapsulate the tree index creation in the starting procedure of pseudo code.

5 Experiment and Results

5.1 Experiment Setup

In the experiment, we use the real world dataset of the solar network system of the University of Queensland. 26 historical solar data are used from three different campuses: St Lucia Campus (18 signals), Gatton Campus (6 signals), and Herston Campus (2 signals). The time range of the data is 20 days from $10^{th}$ to $29^{th}$ in November in 2017, with the data sampling period of 60 s.

The performance evaluation is mainly based on traditional compression benchmarks, including compression ratio, normalised root-mean-square error, and computational time. They are formulated as follow:

$$\begin{aligned} CR = \frac{Size(F_{raw}(t))}{Size(F_{compressed}(t))} \end{aligned}$$

(17)

$$\begin{aligned} NRMSE = \frac{1}{norm}\sqrt{\frac{\sum _{i=0}^{N} (\hat{y}-y)^2}{N}} \end{aligned}$$

(18)

Additional evaluation, nominated as the precision test, is introduced in RIDA [5]. The test demonstrates the compression precision in a given compression ratio, regardless of the error tolerance selection.

State-of-art algorithms are realised under Python Environment (3.6.4) in the operating system with a 2.2 GHz Intel Core i7 processor and a 16 GB 1600 MHz DDR3 memory. Particularly, APCA, SF and GAMPS are selected for the performance comparison against the SIRCS. Their algorithm realisation is slightly customised in favour of the maximum performance: we adjust the floating precision to 5 digits and the coefficient c as 0.4 in GAMPS.

5.2 Effect of Correlation Level

The linear model test shows that a positive association exists between compression ratio and the signal pairs correlation, with the p-value approaching zero. From LM test in Fig. 4(a), p-value approaches to 0. For every unit increase of the correlation, the compression ratio rises 1.42856. The linear model test also shows that a positive association exists between NRMSE and the signal pairs correlation, with the p-value approaching zero. From LM test in Fig. 4(b), p-value also approaches to 0. The outcome implies the higher correlation grouping between two data streams will statistically lead to a higher compression ratio, therefore we validate the statement that picking high correlation signal pairs can improve the total compression performance.

Fig. 4.

(a) Implies that higher the correlation level, smaller the file will be compressed and (b) Implies that higher the correlation level, greater the compression error will be generated. (c) Shows the box plot of the two-sample t-test of the one-day dataset, and (d) shows that of twenty-day dataset, both of which manifests the improvement of the residual data compression.

5.3 Effect of Regression-Based Decomposition

We conduct two-sample t-tests between using and not using residual data compression for both the twenty days dataset and a one-day dataset on $21^{st}$ of January 2018. In Fig. 4(c), practically significant increase can be observed in SIR algorithm with the corresponding state-of-art algorithms: SIR application on Swing Filter has average 0.27 increase in compression ratio, while on APCA also has average 0.42 increase. To consolidate the persuasiveness of the result, Fig. 4(d) shows the outcome of the compression ratio comparison over a one-day dataset and the improvement is similar to the twenty-day dataset scenario. Two-sample t-tests imply a strong evidence that using SIR algorithm can significantly improve the compression ratio based on the corresponding state-of-art algorithms.

5.4 Effect of Tree Mapping

First, we demonstrate the difference between the cluster mapping and the tree mapping in Fig. 5(a). The bar chart in Fig. 5 shows practical improvement, from 0.04 to 0.18, for all eighteen tested signals in both APCA and Swing Filter. The improvement in compression ratio in APCA is averagely 0.026 higher than the improvement in Swing Filter. From this outcome, the improvement of the tree mapping is practically significant. The increased level varies with the base signal selection, but the improvement applies in all circumstances. Therefore, from the empirical evaluation, the improvement from the tree mapping is practically significant over the cluster mapping.

Fig. 5.

Shows the compression ratio with or without the tree mapping in different base signal selection. In all situations, tree mapping improves the compression efficiency in various extent.

5.5 Effect of Error Tolerance

From the outcome of the evaluation, we estimate the percentage improvement of SIRCS based on the state-of-art algorithms. In the compression ratio performance, the SIRCS has averagely 15% of the increase from the compression ratio of APCA, shown in Fig. 6 (a). It can shoot up to 30% of increase with the error tolerance equal to 1% and also go up to 11% when the error tolerance is equal to 13%. The swing filter algorithm applying SIRCS can increase its compression ratio up to 14%, and averagely increase 5% for any error level, shown in Fig. 6(b). The compression time shows in the similar level except that of GAMPS, which shoots up to 103.67 s to compress the whole datasets, according to Fig. 6(c). The rest has similar computational time varying from 1.05 to 4.72 s. In the precision test, SIRCS also has the noticeable improvement in reducing the NRMSE-compression ratio trade-off, shown in Fig. 6(d). In the APCA scheme, the SIRCS can decrease almost 75% of NRMSE when the compression ratio is 1.11, and it can also reduce 15% more in most of the compression ratio level. The swing-filter-based algorithm can reduce its NRMSE by using SIRCS up to 50%. Even though such improvement differs from applying different error tolerance, the improvement is proved to be practically significant.

Fig. 6.

Comparison of the performance between SIRCS and the other three state-of-art algorithms in terms of compression ratio in (a), NRMSE in (b), compression time in (c), and the precision level against a given compression ratio in (d).

6 Conclusion

In this paper, we have demonstrated the impact of data correlation level on the group compression performance. We proposed a new correlation grouping techniques: correlation tree mapping and developed a novel compression technique SIRCS for high variation data in the multi-signal network under a certain error bound. Conspicuous features of SIRCS include: (i) For high variation data, it improves the original algorithm’s performance in both compression ratio and NRMSE. (ii) Tree index provides optimal solutions of preserving the highest correlation level of the signal network, taking less compression time than the traditional grouping techniques. In summary, SIRCS is the first algorithm providing maximum correlation preservation and effectively compressed the high variation data. The evaluation of SIRCS from the real world dataset shows the practical improvement from its existing counterparts.