Abstract
The notion of symmetry in Quantum Theory is quite abstract. There are at least three distinct ideas, respectively due to Wigner, Kadison and Segal.
Access provided by Autonomous University of Puebla. Download chapter PDF
The notion of symmetry in Quantum Theory is quite abstract. There are at least three distinct ideas, respectively due to Wigner, Kadison and Segal [Sim76]. We shall focus on the first two only, plus a fourth type which crops up naturally from our formulation of the quantum theory. The exhaustive discussion of [Lan17] introduces six different definitions of quantum symmetry and discusses their equivalence.
7.1 Quantum Symmetries According to Kadison and Wigner
Generally speaking, symmetries are supposed to describe mathematically certain concrete transformations acting either on the physical system or on the instruments used to analyze the system. From a very general standing a symmetry is an active transformation of either the quantum system or, by duality, the observables representing physical instruments. It is further required that
-
(1)
the transformation is bijective, in the sense that
-
(a)
every state of the system or observable representing devices (according to the notion employed) can be reached by transforming the initial state or observable;
-
(b)
every symmetry admits an inverse;
-
(a)
-
(2)
the transformation should preserve some mathematical structure of the space of the states or the space of observables. This is what distinguishes between the various notions of symmetry.
Alas, there exists in the literature an intrinsically different notion of gauge symmetry . A gauge symmetry is not a symmetry in the above sense. A symmetry acts on the physical system by explicitly changing its state or the (observables representing the) instruments, whereas a gauge symmetry is a mathematical transformation that does not change anything that is directly related to measurements, hence it does not affect the system’s states nor the instruments. An example for a system with algebra of observables \({\mathfrak R}\) is the action of elements U of commutant group \( {\mathfrak G}_{\mathfrak R}\) (the group of unitary operators in \({\mathfrak R}'\)) on quantum probability measures on \(\mathcal {L}_{\mathfrak R}({\mathsf H})\) describing the states of a quantum system, see Sect. 6.3.2. Quantum states associated to two measures ρ and ρ(U ⋅ U −1) cannot be distinguished by acting on \(\mathcal {L}_{{\mathfrak R}}({\mathsf H})\) because UPU −1 = P for every \(P\in \mathcal {L}_{{\mathfrak R}}({\mathsf H})\), as we observed in Sect. 6.3.4 from a slightly different perspective.
Nevertheless the idea of gauge symmetry is technically very useful. In some fundamental theories the initial relevant algebra of operators \({\mathfrak F}\) is larger (in the von Neumann algebra framework it is \({\mathfrak B}({\mathsf H})\) itself) than the algebra of observables \({\mathfrak R}\). The latter is defined as the von Neumann algebra made of the operators in \({\mathfrak F}\) commuting with a suitable faithful and strongly-continuous representation U of a certain compact group G named the global gauge group of internal symmetries: \({\mathfrak R} = U'\). (As a consequence \(U \subset {\mathfrak G}_{\mathfrak R}\) and \(U' = {\mathfrak G}_{\mathfrak R}^{\prime }= {\mathfrak R}\).) We have already seen this procedure at work in the first part of Sect. 6.3.2. When we deal with spinor fields, for instance, there are operators, in particular spinor field operators, that cannot be interpreted as observables (or complex combinations of observables) because they violate some fundamental physical requisite (typically causality relations) ascribed to meaningful observables. However, other operators constructed out of spinor field operators (typically currents) are observables. One way to select the observables inside the larger algebra \({\mathfrak F}\), thus defining the von Neumann algebra \({\mathfrak R}\), is to require that operators representing (linear combinations of) observables are fixed under the action of a suitable compact group G—in this case the Abelian group U(1)—of unitary operators belonging in the commutant \( {\mathfrak G}_{\mathfrak R}\) of \({\mathfrak R}\), as in Sect. 6.3.2. Then \({\mathfrak R}\) turns out to be a sum of irreducible von Neumann algebras \({\mathfrak R}_k ={\mathfrak B}({\mathsf H}_k)\) on an orthogonal sum of sectors H k decomposing H. The procedure is general and works also when the commutant is non-Abelian, as in chromodynamics where G = SU(3) (colour). Our \({\mathfrak R}\) is a sum of factors \({\mathfrak R}_k\) defined on an orthogonal sum of G-invariant sectors H k. In this sense internal symmetries (distinct from those of the spacetime’s geometry) are not symmetries at all, since they do not act on observables (see [Haa96] for further discussions related to locality and the so-called DHR analysis of superselection rules in the algebraic formulation).
7.1.1 Wigner Symmetries, Kadison Symmetries and Ortho-Automorphisms
We henceforth consider a quantum system described on the Hilbert space H. We assume that H is either the whole Hilbert space in the absence of superselection charges, or it denotes a single coherent sector when Abelian superselection rules are on. Let \(\mathcal {S}({\mathsf H})\) indicate the convex body of quantum-state operators on \({\mathfrak B}({\mathsf H})\): these are positive trace-class operators of trace one representing normal states on \({\mathfrak B}({\mathsf H})\) (see Sect. 6.3.4), and call \(\mathcal {S}_p({\mathsf H})\) the subset of operators representing pure normal states (orthogonal projectors onto one-dimensional subspaces). Everything refers to one sector if need be.
Two notions of symmetry can be defined when we look at the space of normal states. Since on separable Hilbert spaces states are actually better described in terms of σ-additive probability measures on \(\mathcal {L}({\mathsf H})\), the definitions above make totally sense in physics when the aforementioned measures are faithfully described by quantum-state operators under Gleason’s theorem. This is the case when H is separable with dimension ≠ 2. (As we said, separability can be dropped, but then normal states correspond to the smaller subset of completely-additive probability measures.)
Definition 7.1
If H is a Hilbert space, we have the following types of symmetries.
-
(a)
A Wigner symmetry is a bijective map
$$\displaystyle \begin{aligned} s_W : {\mathcal{S}}_p({\mathsf H}) \ni \langle \psi| \:\: \rangle \psi \to \langle \psi'| \:\: \rangle \psi' \in {\mathcal{S}}_p({\mathsf H})\end{aligned} $$that preserves transition probabilities:
$$\displaystyle \begin{aligned} |\langle\psi_1|\psi_2\rangle|{}^2 = |\langle\psi_1^{\prime}|\psi_2^{\prime}\rangle|{}^2 \quad \mbox{if}\quad \psi_1 \:,\psi_2 \in {\mathsf H}\:\:\: \mbox{with}\:\: ||\psi_1||=||\psi_2||=1\:.\end{aligned} $$ -
(b)
A Kadison symmetry is a bijection
$$\displaystyle \begin{aligned} s_K : {\mathcal{S}}({\mathsf H}) \ni T \to T' \in {\mathcal{S}}({\mathsf H})\end{aligned} $$that preserves linear convexity in the space of the states:
$$\displaystyle \begin{aligned} (pT_1 + q T_2)^{\prime} = pT_1^{\prime} + qT_2^{\prime}\quad \mbox{if}\quad T_1,T_2 \in {\mathcal{S}}({\mathsf H}) \quad \mbox{and\:\: }p,q\geq 0\mbox{ with }p+q=1.\end{aligned} $$
\(\blacksquare \)
Remark 7.2
Wigner symmetries are well defined even if unit vectors define pure states just up to phase, as the reader can immediately prove, because transition probabilities are not affected by the phase ambiguity. \(\blacksquare \)
There is an apparently different approach to define symmetries that focuses on elementary observables in \(\mathcal {L}({\mathsf H})\) instead of normal states in \(\mathcal {S}({\mathsf H})\). Symmetries are viewed as active transformations preserving the lattice structure of elementary observables. From a practical viewpoint, these symmetries are interpreted as some sort of reversible active transformations on the measuring instruments. These transformations must preserve the logical connectives between elementary propositions.
Definition 7.3
If H is a Hilbert space, a symmetry of elementary observables is a map \(h: \mathcal {L}({\mathsf H}) \to \mathcal {L}({\mathsf H})\) such that
-
(i)
h is bijective,
-
(ii)
h(P) ≥ h(Q) if \(P,Q \in \mathcal {L}({\mathsf H})\) and P ≥ Q,
-
(iii)
h(I − P) = I − h(P) if \(P \in \mathcal {L}({\mathsf H})\).
Another name is ortho-automorphism of \(\mathcal {L}({\mathsf H})\). \(\blacksquare \)
Remark 7.4
-
(a)
It is easy to prove that an ortho-automorphism \(h : \mathcal {L}({\mathsf H}) \to \mathcal {L}({\mathsf H})\) preserves the entire complete orthocomplemented lattice structure. In particular
-
(i)
h(0) = 0 and h(I) = I,
-
(ii)
h(∨j ∈ J P j) = ∨j ∈ J h(P j), h(∧j ∈ J P j) = ∧j ∈ J h(P j) for every family \(\{P_j\}_{j\in J} \subset \mathcal {L}({\mathsf H})\).
Furthermore, \(h^{-1} : \mathcal {L}({\mathsf H}) \to \mathcal {L}({\mathsf H})\) is evidently an ortho-automorphism.
-
(i)
-
(b)
As the reader can straightforwardly prove, a symmetry of elementary observables induces a Kadison symmetry by duality, if we assume Gleason’s theorem 4.47 holds. In fact, if \(T\in \mathcal {S}({\mathsf H})\) and h is an ortho-automorphism, then
$$\displaystyle \begin{aligned}\rho_{T,h} : \mathcal{L}({\mathsf H}) \ni P \mapsto tr(Th(P))\in [0,1]\end{aligned}$$is a probability measure on \(\mathcal {L}({\mathsf H})\). The proof is trivial and relies on the fact that h preserves the lattice structures. Therefore there exists exactly one \(T^{\prime }_h \in \mathcal {S}({\mathsf H})\) such that
$$\displaystyle \begin{aligned}\rho_{T,h}(P)= tr(T^{\prime}_hP)\quad \mbox{ for every }P \in \mathcal{L}({\mathsf H}). \end{aligned}$$By construction, \(s^{(h)}_K: T \mapsto T^{\prime }_h \) preserves the convex structure of \(\mathcal {S}({\mathsf H})\). Indeed,
$$\displaystyle \begin{aligned} \left(s^{(h)}_K ( pT_1+qT_2)\right)(P) = tr \left( (pT_1 + qT_2)h(P)\right)= \left(ps^{(h)}_K ( pT_1) +qs^{(h)}_K(T_2)\right)(P) \:. \end{aligned}$$Since \(P\in \mathcal {L}({\mathsf H})\) is arbitrary,
$$\displaystyle \begin{aligned}s^{(h)}_K ( pT_1+qT_2) = ps^{(h)}_K ( pT_1) +qs^{(h)}_K(T_2)\:,\end{aligned}$$so \(\left (s^{(h)}_K\right )^{-1}= s^{(h^{-1})}_K\).
-
(c)
Symmetries of all three types do exist. If U : H →H is a unitary operator, the maps
$$\displaystyle \begin{aligned}s^{(U)}_W : \mathcal{S}_p({\mathsf H})\ni \langle \psi| \:\:\rangle \psi \mapsto \langle U\psi| \:\:\rangle U\psi \in \mathcal{S}_p({\mathsf H})\:,\end{aligned}$$$$\displaystyle \begin{aligned}s^{(U)}_K : \mathcal{S}({\mathsf H}) \ni T \to UTU^{-1}\in \mathcal{S}({\mathsf H})\end{aligned}$$and
$$\displaystyle \begin{aligned}h^{(U)}: \mathcal{L}({\mathsf H}) \ni P \mapsto U^{-1}PU \in \mathcal{L}({\mathsf H})\end{aligned}$$are respectively a Wigner symmetry, a Kadison symmetry and an ortho-automorphism of \(\mathcal {L}({\mathsf H})\). If Gleason’s theorem holds, furthermore, \(s^{(U)}_K\) is induced by h (U) by Remark (b).
-
(d)
When Abelian superselection rules occur, a more general notion of symmetry exist that is defined between different superselection sectors. An example would be a bijection from \(\mathcal {L}({\mathsf H}_k)\) to \(\mathcal {L}({\mathsf H}_h)\), k ≠ h, preserving the orthocomplemented lattice structure, or similar maps between normal states \(\mathcal {S}({\mathsf H}_k)\) and \(\mathcal {S}({\mathsf H}_h)\) that preserve the convex structure. Or even a bijective map between \(\mathcal {S}_p({\mathsf H}_k)\) and \(\mathcal {S}_p({\mathsf H}_h)\) preserving transition probabilities. A typical example of symmetry that swaps superselection sectors is the charge conjugation. We shall not discuss this sort of symmetries (see [Mor18]), but the reader can easily extend the theory developed below to these cases. \(\blacksquare \)
7.1.2 The Theorems of Wigner, Kadison and Dye
Although the previous three definitions are evidently different in nature, characterizations are in place (Theorem 7.6) to guarantee they lead to the same mathematical object. We need a preliminary definition first.
Definition 7.5
Let H, H ′ be Hilbert spaces. A map U : H →H ′ is called an anti-unitary operator if it is surjective, isometric and
when x, y ∈H and \(a,b \in {\mathbb C}\). \(\blacksquare \)
If U : H →H ′ is anti-unitary, then \(\langle Ux|Uy\rangle = \overline {\langle x|y\rangle '}\) for x, y ∈H, by polarization.
We come to the announced theorem.
Theorem 7.6
Let H ≠ {0} be a Hilbert space.
-
(a)
[Wigner’s theorem] For every Wigner symmetry s W there exists an operator U : H →H such that
$$\displaystyle \begin{aligned} \begin{array}{rcl} s_W : \langle \psi| \:\: \rangle \psi \mapsto \langle U\psi| \:\: \rangle U\psi\:, \quad \forall \langle \psi| \:\: \rangle \psi \in {\mathcal{S}}_p({\mathsf H})\:.{}\end{array} \end{aligned} $$(7.1)U can be unitary or anti-unitary, but when \(\dim ({\mathsf H}) \neq 1\) the choice is fixed by s W.
If \(\dim {\mathsf H} >1\) , U and U′ are associated to the same s W if and only if U′ = e ia U for \(a \in {\mathbb R}\).
-
(b)
[Kadison’s Theorem] For every Kadison symmetry s K there exists an operator U : H →H such that
$$\displaystyle \begin{aligned} \begin{array}{rcl} s_K : T \mapsto UT U^{-1} \:,\quad \forall T \in {\mathcal{S}}({\mathsf H})\:. {}\end{array} \end{aligned} $$(7.2)U can be unitary or anti-unitary, but when \(\dim ({\mathsf H}) \neq 1\) the choice is fixed by s K.
If \(\dim {\mathsf H} >1\) , U and U′ are associated to the same s K if and only if U′ = e ia U for \(a \in {\mathbb R}\).
-
(c)
[Dye’s Theorem (Simplest Version)] If H is separable and \(\dim ({\mathsf H}) \neq 2\) , for every ortho-automorphism \(h: \mathcal {L}({\mathsf H}) \to \mathcal {L}({\mathsf H})\) there exists an operator U : H →H such that
$$\displaystyle \begin{aligned} \begin{array}{rcl} h : P \mapsto U^{-1}P U \:,\quad \forall P \in \mathcal{L}({\mathsf H})\:. {}\end{array} \end{aligned} $$(7.3)U is unitary or anti-unitary, but for \(\dim ({\mathsf H}) \neq 1\) the choice is fixed by h.
For \(\dim {\mathsf H} >1\) , U and U′ are associated to the same h if and only if U′ = e ia U for \(a \in {\mathbb R}\).
-
(d)
Conversely, a unitary or anti-unitary map U : H →H simultaneously defines a Wigner symmetry (the same one defined by e ia U for any \(a\in {\mathbb R}\) ), a Kadison symmetry and an ortho-automorphism by recipes (7.1)–(7.3), respectively.
Proof
Statement (d) is trivial. The existence of U in (a) is difficult and can be found, e.g., in [Sim76, Var07, Lan17, Mor18]. The existence in case (b) comes from (a) and can be read in [Sim76, Lan17, Mor18]. As for (c) it is an immediate consequence of case (b) and Remark 7.4 (b).
Let us address the issue of uniqueness. If \(\dim {\mathsf H} =1\), the U map corresponding to a given symmetry can be taken unitary or anti-unitary as one pleases. The proof is direct and can be obtained by identifying H with \({\mathbb C}\). The fact that, for \(\dim {\mathsf H} >1\), U is fixed up to phase goes as follows. Suppose U and V are both unitary or both anti-unitary and define the same symmetry (any kind). Then UPU −1 = V PV −1, for some orthogonal projector P = 〈ψ| 〉ψ onto a one-dimensional subspace. This P can be viewed simultaneously as an element of \(\mathcal {S}_p({\mathsf H})\), \(\mathcal {S}({\mathsf H})\), and \(\mathcal {L}({\mathsf H})\). As V −1 UP = PV −1 U, then V −1 Uψ = a ψ ψ for some complex vector a ψ ∈H. If \(\dim {\mathsf H} >1\), we consider two orthogonal elements ψ, ψ′∈H with unit norm. Hence
Consequently \(\left (a_{ \frac {\psi +\psi '}{\sqrt {2}}} - a_{\psi '}\right ) \psi '= -\left (a_{ \frac {\psi +\psi '}{\sqrt {2}}} - a_{\psi }\right ) \psi \:. \) Since the vectors are orthonormal, the only possibility is that the coefficients vanish. In particular \(a_{\psi '}=a_\psi \). If N ⊂H is a Hilbert basis, we therefore have V −1 Uψu = au for every u ∈ N and for a unique constant \(a\in {\mathbb C}\). Therefore
But V −1 U is unitary so |a| = 1 and U = aV .
An analogous argument proves that, for \(\dim {\mathsf H} >1\), U and V must be both unitary or both anti-unitary. In fact, if that were not the case, the above reasoning would prove that the anti-unitary operator V −1 U, for every Hilbert basis N, acted as V −1 Uu = a N u with u ∈ N and \(a_N \in {\mathbb C}\). Define a new Hilbert basis N′ whose elements are those of N plus an extra element \(u^{\prime }_0:= iu_0\). Then the contradiction ensues: if u ≠ u 0 we would have \(a_{N'}u = V^{-1}U u = a_{N}u\), but also \(i a_{N'}u_0 = a_{N'}u^{\prime }_0 = V^{-1}U u^{\prime }_0 = V^{-1}U iu_0 = -i V^{-1}U u_0 = -i a_N u_0\). Hence \(a_{N'}= a_{N}= - a_{N}\) implying a N = 0 and therefore that V −1 U is the zero operator. This is not possible because V −1 U is isometric by hypothesis and H ≠ {0}. □
Remark 7.7
If Abelian superselection rules are present, quantum symmetries are similarly described using unitary or anti-unitary operators either acting on a single coherent sector or swapping different sectors [Mor18]. \(\blacksquare \)
7.1.3 Action of Symmetries on Observables and Physical Interpretation
If a unitary or anti-unitary operator V represents a (Kadison or Wigner) symmetry s, it defines an action on observables, too. If A is an observable (a selfadjoint operator on H), we define the transformed observable under the action of s as
Obviously D(s ∗(A)) = V (D(A)). This is the dual action on an observable of a Kadison/Wigner symmetry. There is another similar action, the inverse dual action
Again D(s ∗−1(A)) = V (D(A)). It is evident that these definitions are not affected by the phase ambiguity in the choice of V when s is given. Moreover, by Proposition 3.60 (j), the spectral measure of s ∗(A) is
as expected, and this is nothing but the ortho-automorphism induced by the unitary operator U (s ∗−1 is the inverse ortho-automorphism.) The punchline is that a symmetry’s action on an observable A is completely equivalent to the same action on the elementary observables of the PVM P (A). This fact is in perfect agreement with the physical idea, mathematically supported by the spectral theorem, that an observable (a selfadjoint operator) contains the same physical information as its PVM.
The meaning of the inverse dual action s ∗−1 on observables should be evident. The probability that the observable s ∗−1(A) produces outcome E when the state is s(T) (namely \(tr\left (P_E^{(s^{*-1}(A))}s(T)\right )\) ) equals the probability that the observable A produces outcome E when the normal state is \(T\in \mathcal {S}({\mathsf H})\) (that is \(tr(P_E^{(A)} T)\)). In other words, changing observables and states simultaneously and coherently does not alter a thing. Indeed
So, the inverse dual action of a Kadison/Wigner symmetry on observables is the transformation that reverses the symmetry’s action on states. As an example think of an isolated quantum system in an inertial frame: a translation along the z-axis can be annulled by a z-translation of the origin.
The meaning of the dual action s ∗ on observables is similarly clear. This operation on observables (whilst keeping states fixed) produces the same result as the action of s on states (keeping observables fixed).
Again on an isolated quantum system in an inertial frame: as far as measurements of the position are concerned, translating along the z-axis is equivalent to displacing the origin in the opposite direction.
Example 7.8
-
(1)
Fixing an inertial reference frame, the pure state of a quantum particle is defined, up to phase, as a unit element ψ of \(L^2({\mathbb R}^3, d^3x)\), where \({\mathbb R}^3\) stands for the rest three-space of the reference frame. The group of isometries IO(3) of the standard (Euclidean) \({\mathbb R}^3\) acts on states by Wigner and Kadison symmetries. If
$$\displaystyle \begin{aligned}(R,t) : {\mathbb R}^3 \ni x \mapsto Rx+t\in {\mathbb R}^3\end{aligned}$$indicates the action of the generic element (R, t) ∈ IO(3) on \(x\in {\mathbb R}^3\), where R ∈ O(3) and \(t \in {\mathbb R}^3\), the associated quantum (Wigner) symmetry s (R,t)(〈ψ| 〉ψ) = 〈U (R,t) ψ| 〉U (R,t) ψ is completely determined by the unitary operators
$$\displaystyle \begin{aligned} (U_{(R,t)}\psi)(x) &:= \psi((R,t)^{-1}x)\\ &= \psi(R^{-1}(x-t))\:, \quad x \in {\mathbb R}^3\:, \psi \in L^2({\mathbb R}^3, d^3x)\:, \quad ||\psi||=1\:. \end{aligned} $$As the Lebesgue measure is IO(3)-invariant, U (R,t) is isometric and also unitary because it is surjective, as it admits \(U_{(R,t)^{-1}}\) as right inverse.
It is furthermore easy to prove that
$$\displaystyle \begin{aligned} \begin{array}{rcl} U_{(I,0)} = I \:, \quad U_{(R,t)}U_{(R',t')}=U_{(R,t)\circ (R',t')} \:, \quad \forall (R,t), (R',t') \in IO(3)\:.\qquad {} \end{array} \end{aligned} $$(7.6) -
(2)
The transformation called time reversal corresponds classically to inverting the sign of all the velocities of the physical system. It is possible to prove [Mor18] (see also Exercise 7.33 (4) below) that in QM and systems whose energy is bounded below but not above, the time-reversal symmetry cannot be represented by unitary transformations, only anti-unitary ones. In the simplest situation, such as (1), time reversal is defined (up to phase) by the anti-unitary operator
$$\displaystyle \begin{aligned}(T\psi)(x) := \overline{\psi(x)} \:, \quad x \in {\mathbb R}^3\:, \psi \in L^2({\mathbb R}^3, d^3x)\:, \quad ||\psi||=1\:.\end{aligned}$$ -
(3)
In relationship to example (1), let us focus on the group of displacements along x 1. These elements \({\mathbb R}^3 \ni x \mapsto x + u{\mathbf {e}}_1\) of IO(3) are parametrised by \(u\in {\mathbb R}\), where e 1 denotes the unit vector in \({\mathbb R}^3\) along x 1. For every value of the parameter u, let s u indicate the (Wigner) quantum symmetry s u(〈ψ| 〉ψ) = 〈U u ψ| 〉U u ψ with
$$\displaystyle \begin{aligned}(U_{u}\psi)(x) = \psi(x - u\mathbf{e_1})\:, \quad u \in {\mathbb R}\:.\end{aligned}$$The inverse dual action of this symmetry on the observable X k turns out to be
$$\displaystyle \begin{aligned}s^{*-1}_u(X_k) = U_u X_k U^{-1}_u= X_k - u\delta_{k1} I\:, \quad u \in {\mathbb R} \:.\end{aligned}$$\(\blacksquare \)
7.2 Groups of Quantum Symmetries
As in example (1) above, in physics one deals very often with groups of symmetries. In other words, there is a certain group G, with neutral element e and product ⋅, and one associates to each element g ∈ G a symmetry s g (whether Kadison or Wigner is immaterial here, in view of Theorem 7.6). In turn, s g is related to an operator U g, unitary or anti-unitary. This correspondence however is ambiguous, because we are free to modify operators by arbitrary phases. This section is devoted to the study of this sort of representations.
7.2.1 Unitary(-Projective) Representations of Groups of Quantum Symmetries
Let G be a group, which is supposed to represent a group of symmetries of a quantum system described on the Hilbert space H, with \(\dim {\mathsf H} >1\). The action is in practice implemented by unitary operators \(U_g \in {\mathfrak B}({\mathsf H})\), which gives us a map G ∋ g↦U g. We know that multiplying U g by a phase preserves the symmetry associated to it. It would be nice to fix U g, though still allowing for arbitrary phase changes, in such a way that the map G ∋ g↦U g became a unitary representation of G on H.
Definition 7.9
A homomorphism G ∋ g↦U g from a group G to the group of unitary operators on the Hilbert space H is called a unitary representation of G on H.
Equivalently, a unitary representation G ∋ g↦U g is a map satisfying
\(\blacksquare \)
Formulas (7.6) from Example 7.8 (1) show that unitary representations of group of symmetries do exist. Generally speaking, however, requirement (7.7) does not hold. If G is a group of quantum symmetries the only thing guaranteed in physics is that every U g is unitary (or anti-unitary, but here we shall stick to the former only) and that \(U_{g\cdot g'}\) equals \(U_gU_{g'}\) only up to phase:
(As usual, \({\mathbb T} := \{z\in {\mathbb C} \:|\: |z|=1\}\).) For g = g′ = e this gives in particular
The numbers ω(g, g′) are called multipliers. They cannot be completely arbitrary, since associativity (\((U_{g_1}U_{g_2})U_{g_3}= U_{g_1}(U_{g_2}U_{g_3})\)) yields
which also implies, for suitable choices of g 1, g 2, g 3 (the reader should prove it),
All that leads us to the following important definition.
Definition 7.10
If G is a group, a map G ∋ g↦U g—where the U g are unitary operators on the Hilbert space H—is called a unitary-projective representation of G on H if (7.8) holds for some function \(\omega : G \times G \to {\mathbb T}\) satisfying (7.9) and (7.10). Moreover,
-
(i)
two unitary-projective representation \(G\ni g \mapsto U_g \in {\mathfrak B}({\mathsf H})\) and \(G\ni g \mapsto U^{\prime }_g\in {\mathfrak B}({\mathsf H})\) are said equivalent if \(U^{\prime }_g= \chi _g U_g\), where χ g ∈ U(1) for every g ∈ G. This is the same as requiring that there exist numbers χ g ∈ U(1) such that
$$\displaystyle \begin{aligned} \begin{array}{rcl} \omega'(g,g') = \frac{\chi_{g\cdot g'}}{\chi_g\chi_{g'}} \:\omega(g,g')\quad \forall g,g' \in G\:,{} \end{array} \end{aligned} $$(7.12)where \(\omega (g,g') I = U_gU_{g'}U_{g\cdot g'}^{-1}\) and \(\omega '(g,g') I =U^{\prime }_gU^{\prime }_{g'}{U'}^{-1}_{g\cdot g'}\);
-
(ii)
a unitary-projective representation with ω(e, e) = ω(g, e) = ω(e, g) = 1 for every g ∈ G is said to be normalized.
\(\blacksquare \)
A unitary-projective representation \(G \ni g \mapsto U_g \in {\mathfrak B}({\mathsf H})\) acts both on normal states (quantum-state operators) \(T \in {\mathcal {S}}({\mathsf H})\) and on elementary observables \(P\in \mathcal {L}({\mathsf H})\) (and also on observables, as already discussed). The action on states reads
We have two possible actions on elementary observables: the dual action
or the inverse dual action
Note that changing the phase of U g does not affect the action on states and observables. Hence these actions are invariant under equivalences of unitary-projective representations. Both actions on elementary observables have a physical meaning, as discussed in Sect. 7.1.3, and the choice between dual or inverse dual depends on physical convenience. However, from a pure mathematical viewpoint, the maps G ∋ g↦h g and \(G \ni g \mapsto h^{\prime }_g\) have different properties. As the reader can prove, the following facts hold.
-
(1)
The inverse dual action G ∋ g↦h g is a representation of G by ortho-automorphisms of \(\mathcal {L}({\mathsf H})\). In other words, every h g is an ortho-automorphisms of \(\mathcal {L}({\mathsf H})\) such that
$$\displaystyle \begin{aligned}h_e= id\:, \quad h_gh_{g'}= h_{g\cdot g'}\:.\end{aligned}$$ -
(2)
The dual action \(G \ni g \mapsto h^{\prime }_g\) is, instead, a left representation of G by ortho-automorphisms of \(\mathcal {L}({\mathsf H})\). That is to say, every h g is an ortho-automorphisms of \(\mathcal {L}({\mathsf H})\) satisfying
$$\displaystyle \begin{aligned}h^{\prime}_e= id \:, \quad h^{\prime}_gh^{\prime}_{g'}= h^{\prime}_{g'\cdot g}\:\end{aligned}$$(notice the reversed order of g and g′.)
Evidently, if G is Abelian the dual action is an ‘ordinary’ representation (in the sense of Definition 7.9).
Remark 7.11
-
(a)
It is easily proved that every unitary-projective representation g↦U g is always equivalent to a normalized representation. It is sufficient to redefine \(U_g^{\prime } := \chi _g U_g\) with χ g = 1 for g ≠ e and χ e = ω(e, e)−1, and remember the general formula ω′(g, e) = ω′(e, g) = ω′(g′, e).
-
(b)
Being equivalent is evidently an equivalence relation among unitary-projective representations. It is clear that two projective unitary representations are equivalent if and only if they are made of the same Wigner (or Kadison) symmetries, since the latter disregard the phases multiplying the unitary operators describing them. \(\blacksquare \)
7.2.2 Representations Comprising Anti-Unitary Operators
Up to now, we have only considered the case where the operators V g of a unitary-projective representation are unitary. We may however wonder if it is possible to construct a map G ∋ g↦V g where the V g, which we assumed represent quantum symmetries on the Hilbert space H with \(\dim {\mathsf H} >1\), are all anti-unitary, or even some unitary and some anti-unitary, and the group operations are preserved up to phase as in (7.7). Notice that the unitary or anti-unitary nature of V g is fixed by the corresponding g (since it defines the quantum symmetry) and Theorem 7.6 holds. If every g ∈ G can be written as g = h ⋅ h for some h depending on g, or more generally every g ∈ G can be written as a finite product of elements g 1, …, g n where each is a square g k = h k ⋅ h k, then the U g must be unitary. In fact, V g = ω(h, h)−1 V h V h is necessarily linear no matter whether U h is linear or anti-linear.
The argument above is valid in particular if G is a connected Lie group,Footnote 1 because: (a) there exists a sufficiently small neighbourhood O of the neutral element such that any g ∈ O has the form \(g= \exp (t_g T_g)\) for some \(T_g \in {\mathfrak g}\) (the Lie algebra of G) and \(t_g\in {\mathbb R}\), so that \(h= \exp ((t_g/2) T_g)\); furthermore, (b) every g ∈ G can be written as a finite product of elements g 1, …, g n ∈ O. As a matter of fact, there exist generalized unitary-projective representations where anti-unitary operators show up. These representations can be treated as particular cases. For instance, when representing the complete (non-connected) Poincaré group \(\mathcal {P}\) for quantum systems with non-negative squared mass and non-negative energy, the time-reversal symmetry is necessarily anti-unitary. Observe that time reversal does not belong to the connected component in \(\mathcal {P}\) of the identity.
When talking about unitary-projective representations of groups of quantum symmetries in this work, we shall stick to unitary operators only.
7.2.3 Unitary-Projective Representations of Lie Groups and Bargmann’s Theorem
As stressed above, a technical problem is to check whether a given unitary-projective representation is equivalent to a unitary representation. The point is that unitary representations are much simpler to handle. This is a difficult problem [Var07, Mor18], that has been addressed especially when G is a topological group or even better a Lie group (see [NaSt82] and [Var84] for classical treatises emphasizing the analytic structure of Lie groups, and [HiNe13] for a complete, up-to-date and modern report on the smooth structure). In these cases the representation satisfies the following, physically natural, continuity property. It refers to the transition probability of two pure states, which is a physically measurable quantity.
Definition 7.12
A unitary-projective representation G ∋ g↦U g of the topological group G on the Hilbert space H is called continuous if the map
is continuous for every ψ, ϕ ∈H. \(\blacksquare \)
Remark 7.13
In presence of superselection rules, continuous symmetries representing a connected topological group cannot swap coherent sectors when acting on pure states, for topological reasons [Mor18]. \(\blacksquare \)
A well-known cohomological condition ensuring that every unitary-projective representation of a Lie group is equivalent to a unitary one is due to Bargmann [BaRa84, Mor18].
Theorem 7.14 (Bargmann’s Criterion)
Let G be a (real, finite-dimensional) connected and simply connected Lie group with Lie algebra \({\mathfrak g}\) . Every continuous unitary-projective representation of G on a Hilbert space H is equivalent to a strongly-continuous unitary representation of G on H if, for every bilinear skew-symmetric map \(\Theta : {\mathfrak g}\times {\mathfrak g} \to {\mathbb R}\) such that
there exists a linear map \(\alpha : {\mathfrak g} \to {\mathbb R}\) such that
Remark 7.15
The condition is equivalent to demanding that the second real cohomology group \(H^2({\mathfrak g},{\mathbb R})\) be trivial. \(\blacksquare \)
Example 7.16
Let us prove that the group SU(2) satisfies Bargmann’s Theorem 7.14. As is well known (e.g., see [HiNe13]), SU(2) is connected and simply connected. We must prove that condition (7.17) holds. The Lie algebra su(2) of SU(2) is made by all skew-Hermitian 2 × 2 matrices. As a real vector space, it is three-dimensional and, in particular, it admits a basis T 1, T 2, T 3 of skew-Hermitian matrices given by \(T_k := - \frac {i}{2} \sigma _k\). Therefore \([T_a, T_b]= \sum _{c=1}^3\epsilon _{abc} T_c\), where \(\epsilon _{abc}\in {\mathbb R}\) is totally skew-symmetric in a, b, c ∈{1, 2, 3} and 𝜖 123 = 1. Now consider a skew-symmetric bilinear map \(\Theta : su(2) \times su(2) \to {\mathbb R}\). It is completely determined by the numbers Θab := Θ(T a, T b) = − Θba. In fact, considering generic vectors \(u= \sum _{a=1}^3 t_aT_a\) and \(v= \sum _{b=1}^3 s_bT_b\), we have
By direct inspection one sees that, as Θab = − Θba, we also have \(\Theta _{ab} = \sum _{c=1}^3 \alpha _c \epsilon _{cab}\), where α 1 = Θ23, α 2 := Θ31, α 3 := Θ12. Finally observe that, letting \(\alpha : su(2) \to {\mathbb R}\) be
we have
Now, notice that \( \sum _{c=1}^3\epsilon _{abc} \alpha _c= \sum _{c=1}^3 \epsilon _{cab} \alpha _c\), so that
We have proved that (7.17) for all u, v ∈ su(2). We stress that we have not even imposed constraint (7.16),
since this is automatically true in our case, as the reader can prove. \(\blacksquare \)
Remark 7.17
The hypothesis of simply connectedness in Bargmann’s theorem is not that fundamental. If the connected Lie group G is not simply connected, every continuous unitary-projective representation G ∋ g↦V g can be viewed as a continuous unitary-projective representation of the universal covering \(\widetilde {G}\) (which has the same Lie algebra as G). One must use the covering map \(\pi : \widetilde {G} \to G\) (which is a surjective Lie-group homomorphism and a local Lie-group isomorphism) to define
Notice also that if V is irreducible, U is irreducible as well, since irreducibility depends on the images of U and V which are identical. By definition \(\widetilde {G}\) is connected and simply connected, so if the remaining assumptions in Bargmann’s theorem are true, U can be made unitary. In this case, by knowing all (irreducible) strongly-continuous unitary representations of \(\widetilde {G}\) we also know up to equivalence all (irreducible) continuous unitary-projective representations of G. \(\blacksquare \)
Example 7.18
Recall that the Lie group SO(3) is connected but not simply connected. Besides, not all irreducible continuous unitary-projective of SO(3) can be made unitary, and annoying phases show up. The discussion above contains the reason why they can nevertheless be obtained as irreducible strongly-continuous unitary representations of the universal covering SU(2) (which satisfies Bargmann’s hypotheses, see Example 7.16).
Let us briefly analyse the structure of the representations arising thus. Since (e.g., see [HiNe13]) the universal covering map π : SU(2) → SO(3) has ker(π) = {±I}, two cases are possible for a given irreducible unitary representation SU(2) ∋ g↦U g. Starting from U −I U g = U −I⋅g = U g⋅(−I) = U g U −I for every g ∈ SU(2), since the representation is irreducible Schur’s lemma (Theorem 6.19) implies \(U_{-I}= \chi I_{{\mathfrak B}({\mathsf H})}\) for some \(\chi \in {\mathbb T}\). As \(I_{{\mathfrak B}({\mathsf H})}= U_{I}=U_{-I\cdot (-I)} = \chi ^2 I_{{\mathfrak B}({\mathsf H})}\) we conclude that either \(U_{-I}=I_{{\mathfrak B}({\mathsf H})}\) or \(U_{-I}=-I_{{\mathfrak B}({\mathsf H})}\). Now let us consider irreducible strongly-continuous unitary representations \(U: SU(2) \to {\mathfrak B}({\mathsf H})\).
-
(1)
If \(U_{-I} =I_{{\mathfrak B}({\mathsf H})}\), then SU(2) ∋ g↦U g can be seen as irreducible unitary representation SO(3) ∋ R↦V R as well, where \(V_R := U_{\pi ^{-1}(R)}\). This is well defined since π −1(R) = {±g R}, but \(U_{-g_R}= U_{-I g_R} = U_{-I}U_{g_R}= U_{g_R}\). Note that \(SO(3) \ni R \mapsto U_{\pi ^{-1}(R)}\) is also strongly-continuous if U is, because SO(3) is homeomorphic to the quotient Footnote 2 SU(2)∕ker(π), and V ∘ π = U. These unitary representations of SU(2) are called integer spin representations.
-
(2)
If \(U_{- I} =- I_{{\mathfrak B}({\mathsf H})}\) the picture is different. In this case, \(V_R := U_{\pi ^{-1}(R)}\) would be ill-defined because π −1(R) = {±g R}, but \(U_{g_R}= -U_{-g_R}\). However, by choosing one between ± g R for every given R, we obtain a unitary-projective representation of SO(3) whose multipliers take values in {±1}. The ensuing map \(V: SO(3) \to {\mathfrak B}({\mathsf H})\) satisfies |〈ψ|V π(g) ϕ〉| = |〈ψ|U g ϕ〉|, and the latter is continuous as g ∈ SU(2) varies. By definition of quotient topology, as SO(3) is homeomorphic to SU(2)∕ker(π) the map SO(3) ∋ R↦|〈ψ|V R ϕ〉| is continuous. Hence, \(V: SO(3) \to {\mathfrak B}({\mathsf H})\) is continuous as a unitary-projective representation. These irreducible representations of SU(2) are called half-integer spin representations.
Due to Remark 7.17, all irreducible continuous unitary-projective representation of SO(3) are constructed in this way up to equivalence, and necessarily belong in one of the two classes defined above. The (half-integer spin) unitary-projective representations of SO(3) are often interpreted as multi-valued unitary representations.
As observed in Sect. 7.3.1, the Peter-Weyl theorem says that all strongly-continuous unitary representations of SU(2) are direct sums of irreducible strongly-continuous and finite-dimensional unitary representations of SU(2). Therefore considering irreducible representations is not restrictive.
It is finally important to stress that the use of unitary representations of SU(2) is only based on mathematical convenience, but there is no physical reason to prefer them over unitary-projective representations of SO(3) where multipliers show up. The group of symmetries in physics is SO(3), not SU(2), and the action of SO(3) on states and observables is not affected by multipliers, as is evident from (7.13)–(7.15). \(\blacksquare \)
Back to the general case, there exist unitary-projective representations of a connected and simply connected Lie group G that cannot be made unitary, and one has to deal with them. There is nonetheless an overall way to circumvent this (merely technical) problem, which consists in viewing them as unitary representations of another group. Given a unitary-projective representation G ∋ g↦U g with multiplier ω, let us put on U(1) × G the product
and indicate by \(\hat {G}_\omega \) this group. The map \(\hat {G}_\omega \ni (\chi , g) \mapsto \chi U_g =: V_{(\chi ,g)}\) is a unitary representation of \(\hat {G}_\omega \). If the initial representation is normalized, \(\hat {G}_\omega \) is a central extension of G by \(U(1) (= {\mathbb T})\) [Var07, Mor18]. Indeed, its elements (χ, e) commute with everything in \(\hat {G}_\omega \) and thus they belong to the centre of the group. It is possible to prove that, with a suitable topology (different from the product topology in general), \(\hat {G}_\omega \) turns into a topological/Lie group if G is a topological/Lie group [Var07, Mor18].
Unitary representations of U(1)-central extensions play a remarkable role in physics. With a particular choice of ω, \(\hat {G}_\omega \) is sometimes viewed as the true group of symmetries at the quantum level, whereas G is the classical group of symmetries.
7.2.4 Inequivalent Unitary-Projective Representations and Superselection Rules
The notion of equivalence given in (7.12) can be extended to pairs of unitary-projective representations \(G \ni g \mapsto U_g \in {\mathfrak B}({\mathsf H})\) and \(G \ni g \mapsto U^{\prime }_g \in {\mathfrak B}({\mathsf H}')\) defined on different Hilbert spaces H and H ′. Again, two such representations are said to be equivalent if there is an assignment \(G\ni g \mapsto \chi _g \in {\mathbb T}\) such that multipliers obey (7.12).
Such a pair of unitary-projective representations, once the multipliers have been redefined to become identical, can be added together giving rise to a unitary-projective representation on the Hilbert space K := H ⊕H ′,
This map is a well-behaved unitary-projective representation: if the multipliers ω and ω′ of U and U′ are equal, then for any g, h ∈ G,
If, conversely, the representations are not equivalent, it is impossible to arrange phases in order to define a unitary-projective representation on the sum K, and G cannot be interpreted as symmetry group for a quantum system described on K (through a unitary-projective representation which reduces to U and U′ on the subspaces H and H ′).
There is however a way out when suitable Abelian superselection rules occur (Sect. 6.3.1).
Sometimes it happens that the system’s Hilbert space is an orthogonal sum H =⊕j ∈ J H j of closed subspaces which are invariant under respective unitary-projective representations \(G \ni g \mapsto U^{(j)}_g \in {\mathfrak B}({\mathsf H}_j)\) of a common group G of quantum symmetries. If some pairs of representations are not equivalent, the group does not act (as sum of the representations) on the entire Hilbert space, since as already observed this sum cannot define a unitary-projective representation. So, if H is the Hilbert space of the system, i.e. every orthogonal projector \(P \in \mathcal {L}({\mathsf H})\) represents an elementary observable of the system, G cannot be interpreted directly as a group of symmetries. But if each H j is a superselection sector or, more weakly, the Hilbert sum of superselection sectors, then the orthogonal projectors representing observables belong to the lattice \(\mathcal {L}_{\mathfrak R}({\mathsf H})\) of the system’s von Neumann algebra of observables \({\mathfrak R}\) (see Sect. 6.3.1), and hence P = ⊕j ∈ J P j, where \(P_j \in \mathcal {L}({\mathsf H}_j)\). In this case, the global action of G given by
is legit. This action is not induced by a unitary-projective representation of G on H, but it works well anyway as a representation of G made of automorphisms of \(\mathcal {L}_{\mathfrak R}({\mathsf H})\). In fact, the different phases arising when composing the representations of different elements g, g′ cancel each other:
Here are two important examples of this situation to do with continuous unitary-projective representations.
Example 7.19
-
(1)
A superselection rule arises as soon as we represent the group of spatial rotations SO(3). According to Example 7.18 these representations can be seen as continuous unitary-projective representations of SU(2), and the irreducible ones are divided in two equivalence classes in accordance with the value of an observable of the quantum system, the total angular momentum squared J 2. Its spectrum is a point spectrum and its eigenvalues are ħj(j + 1), where j = 0, 1∕2, 1, 3∕2, 2, … Every eigenspace of J 2 is invariant and irreducible (or a direct sum of irreducible closed subspaces where J 2 has the same value) for the action of a suitable unitary-projective representation of SO(3). All irreducible representations associated with j = 0, 1, 2, … are equivalent (also with different values of j of said type); they are also proper strongly-continuous unitary representations of SO(3), being integer spin representations by Example 7.18. All irreducible representations associated with j = 1∕2, 3∕2, 5∕2, … are similarly equivalent, but the representations of the first type are not equivalent to those of the second type, which is made of half-integer spin representations (Example 7.18). A superselection rule occurs if we split the Hilbert space in two sectors, which are sums of irreducible closed subspaces associated to integer or half-integer values of j. Following the discussion of Sect. 6.3.1 we may associate a superselection charge to this structure. For instance, eigenvalue 0 to the space of half-integer j and eigenvalue 1 to the integer j space. Obviously, this superselection rule may be accompanied by further compatible rules (e.g., the electrical charge superselection rule), thus producing a finer structure of sectors.
-
(2)
Another important case of superselection rule is related to inequivalent unitary-projective representations of the (universal covering of the) Galilean group G—the group of coordinate transformations between inertial reference frames in classical physics, viewed as active transformations. As clarified by Bargmann (see, e.g.,[Mor18]), the only physically relevant continuous unitary-projective representations of G in QM are those not equivalent to unitary representations! Furthermore there are infinitely many non-equivalent classes of such representations. The multipliers encapsulate the information about the mass m of the system: they take the form \(\omega _m(g,g') = e^{i m f(g,g')}\) with \(f: G\times G \to {\mathbb R}\) a universal smooth function. Different values m ∈ (0, +∞) produce inequivalent continuous unitary-projective representations. This phenomenon, according to the discussion above, gives rise to a famous superselection structure on the Hilbert space of quantum systems admitting the Galilean group as a symmetry group, known as Bargmann’s superselection rule (see [Mor18] for a summary). The superselection charge can be defined as the mass of the system provided the values are discrete. In other words, superselection sectors are labelled by distinct eigenvalues m of the mass, whereby we think of the mass as a proper quantum observable, a selfadjoint operator M. Differently from the electric charge, however, the eigenvalues of the mass are not proportional to a given elementary mass m 0. Therefore, if we intend to use the mass operator M (divided by some unit of mass) as the superselection charge Q appearing in the exponent of (6.13), no compact global gauge group will describe this Abelian superselection rule (Sect. 6.3.2). Still, we may employ a representation \({\mathbb R} \ni r \mapsto e^{irM}\) of the non-compact Abelian group \({\mathbb R}\), see the beginning of Sect. 6.3.2. Further compatible superselection rules, if present, would refine the sector decomposition. \(\blacksquare \)
7.2.5 Continuous Unitary-Projective and Unitary Representations of \({\mathbb R}\)
An important consequence of Bargmann’s theorem is the following crucial result, which describes strongly-continuous one-parameter unitary groups as a central tool in Quantum Theory. This theorem could be proved independently of Bargmann’s theorem [Mor18], but the proof is quite technical.
Theorem 7.20
Let \(\gamma : {\mathbb R} \ni r \mapsto U_r\) be a continuous unitary-projective representation of the additive group \({\mathbb R}\) on the Hilbert space H . Then
-
(a)
γ is equivalent to a strongly-continuous unitary representation \({\mathbb R} \ni r \mapsto V_r\) of \({\mathbb R}\) on H.
-
(b)
A strongly continuous unitary representation \({\mathbb R} \ni r \mapsto V^{\prime }_r\) is equivalent to γ if and only if
$$\displaystyle \begin{aligned}V^{\prime}_r = e^{icr}V_r\quad \mathit{\mbox{ for some constant }}c \in{\mathbb R}\mathit{\mbox{ and all }}r\in {\mathbb R}.\end{aligned}$$
Proof
-
(a)
Let us embed the connected, simply connected group \(({\mathbb R},+)\) in \(GL(2,{\mathbb R})\) as a Lie group: for this we represent with \(r\in {\mathbb R}\) by the 2 × 2 matrix
$$\displaystyle \begin{aligned}A_r := \left[\begin{matrix} 1\: \: r\\ 0 \:\: 1 \end{matrix}\right]. \end{aligned}$$Observe that
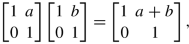
making \({\mathbb R} \ni r \mapsto A_r \in GL(2,{\mathbb R})\) a continuous, injective homomorphism and a homeomorphism on its image. The two groups are therefore isomorphic as topological groups. As the set of matrices A r is a closed subgroup of \(GL(2,{\mathbb R})\), by a theorem of Cartan it is a Lie subgroup of \(GL(2,{\mathbb R})\). In this picture, the Lie algebra of \({\mathbb R}\) is \({\mathbb R}\) itself, represented as one-dimensional subspace of the Lie algebra \(\mathfrak {gl}(2,{\mathbb R})\) with elements
$$\displaystyle \begin{aligned}T_a := \left[\begin{matrix} 0\: \: a\\ 0 \: \: 0 \end{matrix}\right] \end{aligned}$$for \(a\in {\mathbb R}\). In fact this is the vector space of derivatives at the origin of differentiable curves r↦A r such that A 0 = I. The commutator in the Lie algebra \({\mathbb R}\) is the restriction of the Lie bracket of \(GL(2,{\mathbb R})\), [T a, T b] = T a T b − T b T a = 0. As the Lie algebra is one-dimensional (it coincides with \({\mathbb R}\) itself as a vector space), any skew-symmetric map \(\Theta : {\mathbb R} \times {\mathbb R} \to {\mathbb R}\) is zero, so Bargmann’s condition is satisfied trivially for the Lie group \({\mathbb R}\).
-
(b)
If \({\mathbb R} \ni t \mapsto V_t\) is strongly-continuous and \(c\in {\mathbb R}\), evidently \({\mathbb R} \ni t \mapsto V^{\prime }_t := e^{ict}V_t\) is still strongly-continuous, and equivalent to the same unitary-projective representation of V . Let us prove the converse. Suppose that V ′ and V are strongly-continuous unitary representation obtained from the continuous unitary-projective representation U of \({\mathbb R}\). Then \(V^{\prime }_t = \chi (t) V_t\) for some map \(\chi : {\mathbb R} \to {\mathbb T} = \{z \in {\mathbb C} \:|\: |z|=1\}\). If x, y ∈H with 〈x|y〉≠ 0, we also have \(\chi (t) \langle x|y \rangle = \langle x| V_{-t}V^{\prime }_ty \rangle = \langle V_tx|V^{\prime }_ty \rangle \), and therefore χ is continuous. Now (a) and (b) in Theorem 7.25 (which is independent of the present proposition) prove that there exists a dense domain of vectors x such that \({\mathbb R} \ni t \mapsto V_tx\) is differentiable at t = 0 in the topology of H. The same happens for \(V^{\prime }_{t}y\). Choosing a pair of such vectors with 〈x|y〉≠ 0 (possible in view of density), \(\chi (t) \langle x|y \rangle = \langle V_tx|V^{\prime }_ty \rangle \) also implies that χ(t) admits derivative at t = 0. From \(V^{\prime }_t V^{\prime }_{t'}= \chi (t)\chi (t') V_t V_{t'}\) we deduce \(V^{\prime }_{t+t'} = \chi (t)\chi (t') V_{t+t'}\), that is \(\chi (t+t') V_{t+t'} = \chi (t)\chi (t') V_{t+t'}\), and then χ(t + t′) = χ(t)χ(t′) since \(V_{t+t'}\) is invertible. As the reader can easily prove, then, \(\frac {d\chi }{dt} = \frac {d\chi }{dt}|{ }_{t=0} \chi (t)\). This differential equation has the unique solution χ(t) = e at, where \(a= \frac {d\chi }{dt}|{ }_{t=0}\). But |χ(t)| = 1 forces a = ic for some \(c\in {\mathbb R}\), and χ(t) = e ict.
□
The above unitary representations of \({\mathbb R}\) include the strongly-continuous one-parameter unitary groups encountered in Propositions 3.61–3.62, where we treated what appeared to be a particular case.
Definition 7.21
If H is a Hilbert space, a representation \(V : {\mathbb R} \ni r \mapsto V_r \in {\mathfrak B}({\mathsf H})\) such that
-
(i)
V r is unitary for every \(r\in {\mathbb R}\)
-
(ii)
V 0 = I and V r V s = V r+s for all \(r,s \in {\mathbb R}\),
is a one-parameter unitary group. It is called a strongly-continuous one-parameter unitary group if, in addition,
-
(iii)
V is strongly continuous: \(V_r\psi \to V_{r_0}\psi \) for r → r 0 and every \(r_0 \in {\mathbb R}\) and ψ ∈H. \(\blacksquare \)
An elementary but important proposition holds.
Proposition 7.22
For a one-parameter unitary group \(U: {\mathbb R} \ni r \mapsto U_r \in {\mathfrak B}({\mathsf H})\) , strong continuity is equivalent to each of the conditions below:
-
(a)
U is weakly continuous;
-
(b)
U is strongly continuous at r = 0;
-
(c)
U is weakly continuous at r = 0;
-
(d)
〈ψ|U r ψ〉→〈ψ|ψ〉 as r → 0 for every given \(\psi \in \mathcal { D}\) , where \(\mathcal {D}\subset {\mathsf H}\) is a set such that \(\overline {\mathit{\mbox{span}}(\mathcal {D})}={\mathsf H}\).
Proof
Evidently, strong continuity implies (a), (b), (c), (d). The fact that (b) implies strong continuity follows from ||U r ψ − U s ψ|| = ||U −s(U r ψ − U s ψ)|| = ||U r−s ψ − ψ||, since r → s implies r − s → 0. (c) implies strong continuity because
when r → 0, and (b) implies strong continuity. (a) implies (c) which in turn forces strong continuity. Let us finally prove that (d) implies strong continuity. If ϕ ∈H, then
Using the density of \(\mbox{span} \mathcal {D}\), we can fix \(N \in {\mathbb N}\), the numbers \(c_k \in {\mathbb C}\) and the vectors \(\psi _k \in \mathcal {D}\) so that \(||U_r \sum _{k=1}^N c_k\psi _k -U_r\phi || = ||\sum _{k=1}^N c_k\psi _k - \phi || < \epsilon /2\). The formula used for part (c) now gives
for \(C= \max \{|c_1|,\ldots , |c_N|\}\), |r| < δ and δ > 0 small enough. Hence ||U r ϕ − ϕ|| < 𝜖 if |r| < δ, proving (b) and hence the claim. □
7.2.6 Strongly Continuous One-Parameter Unitary Groups: Stone’s Theorem
Theorem 7.20 certifies that when we deal with continuous unitary-projective representations of \({\mathbb R}\) we can always restrict to strongly-continuous one-parameter unitary groups. On a separable Hilbert space there are very few one-parameter unitary groups that are not strongly continuous, by the following result of von Neumann (for a proof see, e.g., [Sim76, Mor18]).
Theorem 7.23
On a separable complex Hilbert space H , a one-parameter unitary groups \(V : {\mathbb R} \ni r \mapsto V_r \in {\mathfrak B}({\mathsf H})\) is strongly continuous if and only if the maps \({\mathbb R} \ni r \mapsto \langle \psi |V_r \phi \rangle \) are Borel measurable for all ψ, ϕ ∈H.
Let us come to Stone’s celebrated characterization of strongly-continuous one-parameter unitary groups (and we stress again that strong continuity is here equivalent to weak continuity, by Proposition 7.22), whereby these groups always correspond to observables. We already know that if A is a selfadjoint operator on a Hilbert space, U t := e itA, for \(t \in {\mathbb R}\), defines a strongly-continuous one-parameter unitary group (Propositions 3.62 and 3.63). The main content of Stone’s remarkable achievement is that the result can be turned the other way around: for every strongly continuous one-parameter unitary group \(\{U_t\}_{t\in {\mathbb R}}\) there exists exactly one selfadjoint operator A such that U t = e itA, for \(t \in {\mathbb R}\).
Before we take the plunge let us prove a general result on uniformly bounded, weakly continuous maps \({\mathbb R} \ni t \mapsto V_t \in {\mathfrak B}({\mathsf H})\). C c(X) henceforth denotes the space of complex-valued continuous maps on a topological space X with compact support.
Proposition 7.24
Let H be a Hilbert space, take \(f\in C_c({\mathbb R})\) and ψ ∈H . If \({\mathbb R} \ni t \mapsto V_t \in {\mathfrak B}({\mathsf H})\) is a weakly continuous map such that ||V t|| < K for all \(t \in {\mathbb R}\) and some K < +∞, then the following facts hold.
-
(a)
There exists a unique vector, denoted by \(\int _{\mathbb R} f(t)V_t \psi dt\) , such that
$$\displaystyle \begin{aligned}\left\langle \phi \left| \int_{\mathbb R} f(t)V_t \right.\psi dt\right\rangle= \int_{{\mathbb R}}f(t) \langle \phi|V_t\psi\rangle dt\quad \mathit{\mbox{for all }}\phi \in {\mathsf H}. \end{aligned}$$ -
(b)
For every \(B\in {\mathfrak B}({\mathsf H})\) ,
$$\displaystyle \begin{aligned}B\int_{\mathbb R} f(t)V_t \psi dt= \int_{\mathbb R} f(t)BV_{t} \psi dt\:.\end{aligned}$$ -
(c)
We have the estimate
$$\displaystyle \begin{aligned}\left|\left| \int_{\mathbb R} f(t)V_t \psi dt\right|\right|\leq \int_{{\mathbb R}}|f(t)| ||V_t\psi|| dt\:.\end{aligned}$$ -
(d)
If \(g \in C_c({\mathbb R})\) and \(a,b\in {\mathbb C}\) , then
$$\displaystyle \begin{aligned}\int_{\mathbb R} (a f(t)+ b g(t))V_t \psi dt = a\int_{\mathbb R} f(t)V_t \psi dt + b\int_{\mathbb R} g(t)V_t \psi dt\:.\end{aligned}$$
Proof
-
(a)
By hypothesis, \({\mathsf H} \ni \phi \mapsto \int _{{\mathbb R}}f(t) \langle \phi |V_t\psi \rangle dt\) is well defined as the integrand function is continuous and compactly supported. This map is anti-linear in ϕ and also continuous because, by the Cauchy-Schwartz inequality, \(|\int _{{\mathbb R}}f(t) \langle \phi |V_t\psi \rangle dt| \leq \int _{{\mathbb R}}|f(t)| |\langle \phi |V_t\psi \rangle | dt \leq ||\phi || ||\psi || K \int _{{\mathbb R}}|f(t)| dt\). Riesz’s lemma therefore implies that it can be written as H ∋ ϕ↦〈ϕ|ψ V,f,t〉 for a unique ψ V,f,t ∈H. By definition, \(\int _{\mathbb R} f(t)V_t \psi dt:= \psi _{V,f,t}\).
-
(b)
Observe that \({\mathbb R} \ni t \mapsto BV_t \in {\mathfrak B}({\mathsf H})\) is weakly continuous and ||BV t||≤||B||K, so \(\int _{\mathbb R} f(t)BV_{t} \psi dt\) is well defined. From (a)
$$\displaystyle \begin{aligned} \left\langle \phi\left| B\int_{\mathbb R} f(t)V_t \right.\psi dt\right\rangle&= \left\langle B^*\phi\left| \int_{\mathbb R} f(t)V_t \right.\psi dt\right\rangle =\int_{{\mathbb R}}f(t) \langle B^*\phi|V_t\psi\rangle dt\\ &= \int_{{\mathbb R}}f(t) \langle\phi| BV_t\psi\rangle dt\:. \end{aligned} $$Using (a) again, we conclude \(B\int _{\mathbb R} f(t)V_t \psi dt= \int _{\mathbb R} f(t)BV_{t} \psi dt\).
-
(c)
Using (a) twice and the Cauchy-Schwartz inequality in the penultimate passage,
$$\displaystyle \begin{aligned} \left|\left| \int_{\mathbb R} f(t)V_t \psi dt\right|\right|{}^2 &= \left|\left\langle \int_{\mathbb R} f(s)V_s \psi ds \left| \int_{\mathbb R} f(t)V_t \right.\psi dt\right\rangle\right|\\ &= \left|\int_{{\mathbb R}} f(t)\left\langle \left.\int_{\mathbb R} f(s)V_s \psi ds \right| V_t\psi \right\rangle dt \right|\\ &= \left|\int_{{\mathbb R}} \int_{{\mathbb R}} \overline{f(s)}f(t) \langle V_s\psi |V_t \psi \rangle dsdt\right|\\ &\quad \leq \int_{{\mathbb R}} \int_{{\mathbb R}} |\overline{f(s)}||f(t)| || V_s\psi || ||V_t \psi|| dsdt\\ &= \left( \int_{{\mathbb R}} |f(t)| ||V_t \psi||dt\right)^2\:. \end{aligned} $$The proof of (d) is evident from (a) and the inner product’s linearity.
□
And here is Stone’s theorem.
Theorem 7.25 (Stone’s Theorem)
Let \({\mathbb R} \ni t \mapsto U_t \in {\mathfrak B}({\mathsf H})\) be a strongly continuous one-parameter unitary group on the Hilbert space H.
-
(a)
There exists a selfadjoint operator A on H , defined on a dense domain D(A), such that
$$\displaystyle \begin{aligned} \begin{array}{rcl} U_t= e^{itA}\:,\quad \forall t \in {\mathbb R}\:.{} \end{array} \end{aligned} $$(7.18) -
(b)
If (7.18) holds for some selfadjoint operator A, then
$$\displaystyle \begin{aligned} \begin{array}{rcl} D(A) = \left\{\psi \in {\mathsf H} \:\left|\: \exists \lim_{t \to 0} \frac{1}{t}(U_t -I)\psi \right.\in {\mathsf H}\right\}\: \quad \mathit{\text{and}}\quad A\psi = -i\lim_{t \to 0} \frac{1}{t}(U_t -I)\psi \:.\qquad {} \end{array} \end{aligned} $$(7.19) -
(c)
The operator A, called the selfadjoint (infinitesimal) generator of U, is unique.
-
(d)
U t(D(A)) = D(A) for all \(t\in {\mathbb R}\) and
$$\displaystyle \begin{aligned}AU_t\psi =U_tA\psi \quad \mathit{\mbox{if }}\psi \in D(A)\mathit{\mbox{ and }}t\in {\mathbb R}.\end{aligned}$$
Proof
We have to prove (a), (b) and (c), since (d) was established in Propositions 3.62 and 3.63.
-
(a)
We first construct a candidate generator for U on a special dense subspace D. By Proposition 7.24 we define D to contain all finite linear combinations of functions \(\psi _f := \int _{{\mathbb R}} f(t) U_t \psi dt\) for every \(f \in C_c^\infty ({\mathbb R})\) and ψ ∈H. In view of part (d) of the Proposition D coincides with the set of the ψ f. We claim this subspace is dense in H. To prove it, observe that by takingV t := U t − I in Proposition 7.24,
$$\displaystyle \begin{aligned} ||\psi_f-\psi|| &= \left|\left|\int_{\mathbb R} f(t) (U_t-I) \psi dt \right|\right| \leq \int_{\mathbb R} |f(t)| ||(U_t-I) \psi|| dt \\ &\quad \leq \int_{\mathbb R} |f(t)| dt \sup_{t \in \mbox{supp}(f)} ||(U_t-I) \psi||\:. \end{aligned} $$For every 𝜖 > 0, we can now define \(f_\epsilon (x) := \frac {1}{\epsilon }g(x/\epsilon )\) where \(g \in C_c^\infty ({\mathbb R})\) satisfies supp(g) ⊂ [−1, 1] and \(\int _{\mathbb R} gdt =1\), so that \(\int _{\mathbb R} f_\epsilon dt =1\) and supp(f 𝜖) ⊂ [−𝜖, 𝜖]. Inserting this choice in the inequality,
$$\displaystyle \begin{aligned}0 \leq ||\psi_{f_\epsilon}-\psi|| \leq \sup_{t \in [-\epsilon,\epsilon]} ||(U_t-I) \psi||\:.\end{aligned}$$As \({\mathbb R} \ni t \mapsto U_t\) is strongly continuous and U 0 = I, we obtain that \(\psi _{f_\epsilon }\to \psi \) as 𝜖 → 0 for every ψ ∈H. Hence D is dense in H.
Next we prove that the strong derivative of U at t = 0 can be computed on D. Let us assume s ∈ [−𝜖, 𝜖] for some 𝜖 > 0. With ψ f as above and K = [−a, a] such that supp(f) ⊂ [−a, a] for a sufficiently large a > 0, plus Proposition 7.24,
$$\displaystyle \begin{aligned} \frac{1}{s}\left(U_s-I \right)\psi_f = \frac{1}{s}\left(U_s-I \right)\int_K f(t) U_t\psi dt = \frac{1}{s}\int_{K} f(t) U_{t+s}\psi dt - \frac{1}{s}\int_K f(t) U_t\psi dt \end{aligned}$$$$\displaystyle \begin{aligned} = \frac{1}{s}\int_{K_\epsilon} f(t-s) U_t\psi dt - \frac{1}{s}\int_{K} f(t) U_t\psi dt = \frac{1}{s}\int_{K_\epsilon} f(t-s) U_t\psi dt - \frac{1}{s}\int_{K_\epsilon} f(t) U_t\psi dt\end{aligned} $$$$\displaystyle \begin{aligned} \begin{array}{rcl} = \int_{K_\epsilon} \frac{f(t-s)- f(t)}{s}U_t\psi dt\:,{} \end{array} \end{aligned} $$(7.20)where K 𝜖 := [−a − 𝜖, a + 𝜖] ⊃ K. Now, assuming that f is real, the mean value theorem implies that \(\left |\frac {f(t-s)- f(t)}{s}\right |= |f'(\xi _{t,s})|< C <+\infty \) where ξ t,s ∈ K 𝜖, and C does not depend on t, s since the continuous map f′ is bounded on the compact set K 𝜖. The result trivially extends to f complex by looking at its real and imaginary parts. Dominated convergence proves that, for s → 0,
$$\displaystyle \begin{aligned} \left|\left| \frac{1}{s}\left(U_s-I \right)\psi_f - \psi_{-f'}\right|\right|= \left|\left| \int_{K_\epsilon} \left(\frac{f(t-s)-f(t)}{s} + f'(t)\right) U_t\psi dt\right|\right| \end{aligned}$$$$\displaystyle \begin{aligned} \leq \int_{K_\epsilon} \left|\frac{f(t-s)-f(t)}{s} + f'(t)\right| ||U_t\psi|| dt =||\psi|| \int_{K_\epsilon} \left|\frac{f(t-s)-f(t)}{s} + f'(t)\right| dt \to 0\:. \end{aligned}$$We can therefore define the operator \(\widetilde {A} : D \to D \subset {\mathsf H}\) by means of
$$\displaystyle \begin{aligned} \begin{array}{rcl} \widetilde{A} \psi_f := -i\lim_{s\to 0}\frac{1}{s}\left(U_s-I \right)\psi_f = -i \psi_{-f'}\:,{}\end{array} \end{aligned} $$(7.21)and extend linearly to finite combinations of ψ f. Observe that
$$\displaystyle \begin{aligned} \begin{array}{rcl} U_u(D) = D \quad \mbox{and}\quad U_u \widetilde{A} =\widetilde{A}U_u \quad \forall u\in {\mathbb R}\:.{} \end{array} \end{aligned} $$(7.22)The first relation comes from the definition of D and Proposition 7.24 (b), alongside \(U_u^{-1}= U_{-u}\). The second formula is an immediate consequence of the first, the definition of \(\widetilde {A}\) in (7.21), the continuity of U u and Proposition 7.24(b) once more.
Let us now show that \(\widetilde {A}\) is essentially selfadjoint. First observe that it is symmetric because it is densely defined and Hermitian:
$$\displaystyle \begin{aligned} \langle \psi_g | \widetilde{A} \psi_f \rangle &= \left\langle \psi_g \left| -i\lim_{s\to 0}\frac{1}{s}\left(U_s-I \right)\psi_f\right.\right\rangle = \lim_{s\to 0} \left\langle\left. i\frac{1}{s}\left(U^*_s-I \right)\psi_g \right| \psi_f\right\rangle\\ &= \lim_{s\to 0} \left\langle\left. i\frac{1}{s}\left(U_{-s}-I \right)\psi_g \right| \psi_f\right\rangle = \lim_{s\to 0} \left\langle\left. -i\frac{1}{-s}\left(U_{-s}-I \right)\psi_g \right| \psi_f\right\rangle\\ &= \left\langle\left.-i\lim_{s\to 0} \frac{1}{s}\left(U_{s}-I \right)\psi_g \right| \psi_f\right\rangle =\langle \widetilde{A}\psi_g | \psi_f \rangle \:. \end{aligned} $$Concerning essentially selfadjointness, we employ Proposition 2.47 (b) directly. Suppose there exist \(\phi _\pm \in D(\widetilde {A}^*)\) such that \(\widetilde {A}^*\phi _\pm = \pm i\phi _\pm \). As a consequence, using (7.22) and (7.21), if \(\psi \in D = D(\widetilde {A})\)
$$\displaystyle \begin{aligned} \frac{d}{dt} \langle U_t \psi| \phi_\pm \rangle &= \lim_{s\to 0} \left\langle \left. \frac{1}{s} (U_s-I)U_t \psi \right| \phi_\pm\right\rangle = \langle i\widetilde{A}U_t\psi| \phi_\pm\rangle = \langle iU_t\psi| \widetilde{A}^*\phi_\pm\rangle\\ &= \pm \langle U_t\psi| \phi_\pm\rangle\:. \end{aligned} $$Hence \({\mathbb R} \ni t \mapsto \langle U_t \psi | \phi _\pm \rangle \) is continuously differentiable and satisfies the differential equation, so
$$\displaystyle \begin{aligned}\langle U_t \psi| \phi_\pm \rangle = \langle U_0 \psi| \phi_\pm \rangle e^{\pm t} = \langle \psi| \phi_\pm \rangle e^{\pm t}\quad \forall t \in {\mathbb R}\:.\end{aligned}$$The left-most side is bounded as |〈U t ψ|ϕ ±〉|≤||ψ||||ϕ ±||||U t|| = ||ψ||||ϕ ±||, whereas the right-most term is unbounded unless 〈ψ|ϕ ±〉 = 0. But the formula must be true for every ψ ∈ D, and since D is dense, we conclude that ϕ ± = 0. Therefore \(\widetilde {A}\) is essentially selfadjoint on D by Proposition 2.47 (b), and we denote by A its unique selfadjoint extension.
To conclude, we can define the strongly continuous one-parameter group of unitary operators \({\mathbb R} \ni t \mapsto e^{it A}\) according to Proposition 3.62. We want to prove that, if ψ, ϕ ∈ D, then 〈ϕ|U −t e itA ψ〉 = 〈ϕ|ψ〉. To this end it is sufficient to show
$$\displaystyle \begin{aligned}\frac{d}{dt}\langle \phi| U_{-t}e^{itA} \psi\rangle= \frac{d}{dt}\langle U_t\phi|e^{itA} \psi \rangle = 0\:.\end{aligned}$$Set V t := e itA. The domain D is U t-invariant, and also V t-invariant by Proposition 3.62 (since D ⊂ D(A)), so the second derivative is
$$\displaystyle \begin{aligned} &\lim_{h\to 0} \frac{1}{h} \left( \left\langle \left. U_{t+h} \phi\right|V_{t+h} \psi\right\rangle -\left\langle \left. U_t \phi\right| V_t \psi\right\rangle\right)\\ &\quad = \lim_{h\to 0} \frac{1}{h} \left( \left\langle \left.U_hU_t \phi\right| V_hV_t \psi\right\rangle -\left\langle \left. U_t \phi\right| V_t \psi\right\rangle\right)\\ &\quad =\lim_{h\to 0} \left\langle U_hU_t \phi\left| \frac{1}{h}(V_h -I)V_t\right. \psi\right\rangle + \lim_{h\to 0} \left\langle \left.\frac{1}{h}(U_h -I)U_t \phi\right| V_t \psi\right\rangle\\ &\quad = \langle U_t\phi| iAV_t \psi\rangle + \langle iAU_t\phi| V_t \psi\rangle i\langle AU_t\phi| V_t \psi\rangle -i \langle AU_t\phi| V_t \psi\rangle =0\:. \end{aligned} $$We exploited the fact that A is selfadjoint and Proposition 3.63. All-in-all, 〈ϕ|(U −t e itA − I)ψ〉 = 0 for all \(t\in {\mathbb R}\), so U −t e itA = I because ϕ, ψ ∈ D which is dense. In summary, we have proved that U t = e itA for every \(t\in {\mathbb R}\) and a selfadjoint operator A, concluding the proof of existence.
-
(b)
Consider a strongly continuous one-parameter group of unitary operators U t = e itA, where A is some selfadjoint operator. We known that if ψ ∈ D(A), then \(-i\lim _{t \to 0} \frac {1}{t}(U_t -I)\psi = A\psi \) by Proposition 3.63. We intend to prove that, if \(\lim _{t \to 0} \frac {1}{t}(U_t -I)\psi \) exists, then ψ ∈ D(A) and the limit coincides with iAψ. Let us define \(B\psi := \lim _{t \to 0} \frac {1}{t}(U_t -I)\psi \) for all ψ ∈H such that the right-hand side exists. It is easy to see that B is linear and D(B) is a dense subspace, for it contains D(A). Furthermore, exactly as we did for \(\widetilde {A}\), we immediately obtain that B is Hermitian. So B is a symmetric extension of the selfadjoint operator A, and Proposition 2.39 (a) tells B = A, concluding the proof.
-
(c)
Suppose that U t = e itB = e itA for all \(t\in {\mathbb R}\) and a pair of selfadjoint operators A and B. Applying (7.19) we have D(A) = D(B) and Aψ = Bψ for every ψ ∈ D(A) = D(B). The proof is over.
□
Corollary 7.26
Let A : D(A) →H be a selfadjoint operator on the Hilbert space H ⊃ D(A). Suppose that S ⊂ D(A) is a dense subspace such that e
itA
S ⊂ S for every \(t\in {\mathbb R}\)
. Then A↾S is essentially selfadjoint and its unique selfadjoint extension  is A itself. In other words, S is a core for A.
is A itself. In other words, S is a core for A.
Proof
Along the lines of Stone’s proof we replace the dense e
itA-invariant domain D ⊂ D(A) by the dense e
itA-invariant domain S ⊂ D(A), and \(\widetilde {A}\) by  (strong derivative). Then
(strong derivative). Then  is essentially selfadjoint on S. Since A ⊃ A↾S is selfadjoint, necessarily
is essentially selfadjoint on S. Since A ⊃ A↾S is selfadjoint, necessarily  . □
. □
7.2.7 Time Evolution, Heisenberg Picture and Quantum Noether Theorem
The perspective of quantum symmetries allows us to settle certain issues raised in Sect. 3.4.3 and justify more firmly several notions.
Consider a quantum system described on the Hilbert space H in some inertial reference frame. Suppose that, physically speaking, the system is either isolated or interacts with some external stationary environment. These hypotheses guarantee temporal homogeneity, and the time evolution of states is axiomatically described by a continuous symmetry: more precisely, a continuous unitary-projective representation \({\mathbb R} \ni t \mapsto V_t\).
In view of Theorems 7.20 and 7.25, this group is equivalent to a strongly continuous one-parameter group of unitary operators \({\mathbb R} \ni t \mapsto U_t\), and there is a selfadjoint operator H, called the Hamiltonian operator, such that (notice the sign in the exponent)
where for once we have included the constant ħ. By Theorems 7.20 and 7.25 V determines H up to additive real constants: the selfadjoint operator H + cI defines the same continuous symmetry V . H is usually thought of as the energy of the system in the reference frame, and \(c\in {\mathbb R}\) can be fixed using some physical case-by-case argument.
Within this picture, if \(T \in {\mathcal {S}}({\mathsf H})\) is the state of the system at t = 0, the state at time t is
If the initial state is pure and represented by the unit vector ψ ∈H, the state at time t is ψ t := U t ψ. As mentioned in Sect. 3.4.3, ψ ∈ D(H) implies ψ t ∈ D(H) for every \(t\in {\mathbb R}\) by Theorem 7.25 (b)–(d):
where the derivative is computed in the topology of H. One recognizes in Equation (7.24) the general form of Schödinger’s equation. From now on shall set ħ = 1.
Remark 7.27
It is possible to study quantum systems interacting with a non-stationary external system. In this case the Hamiltonian observable depends parametrically on time, see Sect. 1.2.1. A Schrödinger-type equation is supposed to describe the time evolution of the system, giving rise to a groupoid of unitary operators [Mor18]. We shall not tackle this technical issue here. \(\blacksquare \)
In this framework, called Schrödinger picture, observables do not evolve whereas states do. There is another approach to describe time evolution, called Heisenberg picture. In that representation, states do not evolve in time, but observables evolve under the dual action (7.4) of the symmetries induced by U t. In this sense, if A is an observable at t = 0, its evolution at time t is the observable
Obviously \(D(A_t)= U^{-1}_t(D(A))= U_{-t}(D(A))= U_t^*(D(A))\). As already observed in the case general case, by Proposition 3.60 (j) the spectral measure of A t is
as expected. The probability that, at time t, the observable A produces the outcome E, when the normal state is represented by the quantum-state operator \(T\in \mathcal {S}({\mathsf H})\) at t = 0, can be computed using either the standard (Schrödinger) picture, where states evolve as \(tr(P_E^{(A)}T_t)\), or the Heisenberg picture where observables evolve as \(tr(P_E^{(A_t)} T)\). Indeed
The two pictures are completely equivalent for the purpose of describing non-relativistic quantum physics. In relativistic quantum physics and QFT in particular, though, Heisenberg’s picture (extended covariantly to include spatial translations) is preferable, due to the existence of a plethora of different notions of time evolution. The Heisenberg picture grants us the following important definition, see also Sect. 3.4.3.
Definition 7.28
Let H be a the Hilbert space and \({\mathbb R} \ni t \mapsto U_t\) a strongly-continuous unitary one-parameter group representing time evolution. An observable A is said to be a constant of motion with respect to U if \(A_t := U^{-1}_tA U_t\) does not depend on t, i.e. A t = A 0 for every \(t\in {\mathbb R}\). \(\blacksquare \)
The definition can be further improved by considering a possible temporal dependence already in Schrödinger’s picture.
Definition 7.29
Let H be a the Hilbert space and \({\mathbb R} \ni t \mapsto U_t\) a strongly-continuous unitary one-parameter group representing time evolution. A family of observables \(\{A(t)\}_{t \in {\mathbb R}}\), parametrized by and also depending on time, is called a parametrically time-dependent constant of motion with respect to U if \(A_t := U^{-1}_tA(t) U_t\) does not depend on t, i.e. A t = A 0 for every \(t\in {\mathbb R}\). \(\blacksquare \)
The meaning of the two definitions should be clear: even if the state evolves, the probability to obtain an outcome E, when measuring a constant of motion, remains stationary. Expectation values and standard deviations do not change in time either.
We are now ready to state the analogue of Noether’s theorem in QM.
Theorem 7.30 (Quantum Noether Theorem I)
Consider a quantum system described on the Hilbert space H and a strongly continuous unitary one-parameter group \({\mathbb R} \ni t \mapsto U_t\) representing time evolution. If A is an observable represented by a (generally unbounded) selfadjoint operator A on H , the following facts are equivalent.
-
(a)
A is a constant of motion: A t = A 0 for all \(t \in {\mathbb R}\).
-
(b)
The one-parameter group of symmetries generated by A, \({\mathbb R} \ni s \mapsto e^{-isA}\) , is a group of dynamical (quantum) symmetries , i.e. it commutes with time evolution:
$$\displaystyle \begin{aligned} \begin{array}{rcl} e^{-isA} U_t = U_t e^{-isA}\quad \mathit{\mbox{ for all }}s,t \in {\mathbb R} {} \:.\end{array} \end{aligned} $$(7.25)In particular, it transforms the time evolution of a pure state into the evolution of (another) pure state, i.e. e −isA U t ψ = U t e −isA ψ.
-
(c)
The dual action on observables (7.4) (or equivalently the inverse dual action (7.5)) of the one-parameter group of symmetries \({\mathbb R} \ni s \mapsto e^{-isA}\) generated by A, leaves H invariant:
$$\displaystyle \begin{aligned}e^{-isA} H e^{isA} = H\:, \quad \mathit{\mbox{ for all }}s\in {\mathbb R} \:.\end{aligned}$$
Proof
Suppose that (a) holds. By definition \(U^{-1}_tAU_t =A\). From Proposition 3.69 we have \(U^{-1}_te^{-isA} U_t =e^{-isA}\) which is equivalent to (b). If (b) is true, we have e −isA e −itH e isA = e −itH. Proposition 3.69 yields e −isA He isA = H. Finally, suppose that (c) is valid. Again Proposition 3.69 produces e −isA U t e isA = U t, which can be written \(U^{-1}_te^{-isA} U_t =e^{-isA}\). Eventually, Proposition 3.69 leads to \(U^{-1}_tAU_t =A\) which is (a), concluding the proof. □
It is possible to define dynamical (quantum) symmetries , as of Exercise 7.33 (2), in agreement with the notion introduced above. The theorem can be extended to parametrically time-dependent observables \(\{A(t)\}_{t{\mathbb R}}\).
Theorem 7.31 (Quantum Noether Theorem II)
Consider a quantum system described on the Hilbert space H equipped with a strongly continuous unitary one-parameter group representing time evolution \({\mathbb R} \ni t \mapsto U_t\) . If \(\{A(t)\}_{t\in {\mathbb R}}\) is a family of observables represented by a (generally unbounded) selfadjoint operator depending on t, the following facts are equivalent.
-
(a)
\(\{A(t)\}_{t\in {\mathbb R}}\) is a parametrically time-dependent constant of motion: A t = A 0 for all \(t \in {\mathbb R}\).
-
(b)
The one-parameter group of symmetries generated by every A(t), \({\mathbb R} \ni s \mapsto e^{-isA(t)}\) , defines a group of dynamical symmetries depending parametrically on time :
$$\displaystyle \begin{aligned} \begin{array}{rcl} e^{-isA(t)} U_t = U_t e^{-isA(0)}\quad \mathit{\mbox{ for all }}s,t \in {\mathbb R}{}\:.\end{array} \end{aligned} $$(7.26)In particular it transforms the evolution of a pure state into the evolution of (another) pure state, i.e. e −isA(t) U t ψ = U t e −isA(0) ψ.
Proof
The proof is trivial by Proposition 3.69: A t = A 0 means \( U^{-1}_t A(t) U_t = A(0)\) which, in turn, implies \(U^{-1}_t e^{-isA(t)} U_t = e^{-isA(0)}\), namely e −isA(t) U t = U t e −isA(0). So (a) implies (b). But all implications are reversible, and from the last equation we obtain \( U^{-1}_t A(t) U_t = A(0)\), hence (b) implies (a). □
There is a suitable version of Theorem 7.30 (c) for observables depending parametrically on time. But exactly as in classical Hamiltonian mechanics, it has a more complicated interpretation [Mor18].
In physics’ textbooks the above statements are almost inevitably stated using time derivatives and commutators. This approach is cumbersome, useless and it involves all the subtleties concerning the domains of the operators. \(\blacksquare \)
Example 7.32
-
(1)
As we explained in Example 3.76, for the free particle in the rest space \({\mathbb R}^3\) of an inertial reference frame, the momentum along x 1 is a constant of motion, as a consequence of translational invariance along that axis. Let {U u} be the unitary group representing x 1-translations, (U u ψ)(x) = ψ(x − u e 1) if \(\psi \in L^2({\mathbb R}^3, d^3x)\). The Hamiltonian \(H= \frac {1}{2m}\sum _{j=1}^3 P_j^2\) commutes with U u, because the group is generated by P 1 itself: \(U_u := e^{-iu P_1}\). Theorem 7.30 yields the thesis.
-
(2)
An example of a parametrically time-dependent constant of motion is the generator of the boost along the axis n, i.e. the one-parameter subgroup \({\mathbb R}^3 \ni x \mapsto x+ tv \mathbf {n}\in {\mathbb R}^3\) of the Galilean group, where the speed \(v\in {\mathbb R}\) is the group’s parameter. The generator is [Mor18] the unique selfadjoint extension of
$$\displaystyle \begin{aligned} \begin{array}{rcl} K_{\mathbf{n}}(t)= \sum_{j=1}^3 n_j (m X_j|{}_D - tP_j|{}_{D})\:,{}\end{array} \end{aligned} $$(7.27)where m > 0 is the system’s mass and D is the Gårding or Nelson domain of the representation of the (central extension of the) Galilean group. The details will appear later in the book.
-
(3)
In QM there exist symmetries described by operators which are simultaneously selfadjoint and unitary, meaning they are observables and they can be measured. Among them we have the parity inversion, or spatial reflection: \((\mathcal {P}\psi )(x) := \eta \psi (-x)\) for any particle described on \(L^2({\mathbb R}^3, d^3x)\), where η = ±1 does not depend on ψ. They are constants of motion (\(U^{-1}_t \mathcal {P} U_t = \mathcal {P}\)) if and only if they are dynamical symmetries (\(\mathcal {P} U_t = U_t\mathcal {P}\)). This phenomenon has no classical correspondent.
-
(4)
The time-reversal symmetry, described by an anti-unitary operator \(\mathcal {T}\), is supposed to satisfy \(\mathcal {T}H\mathcal {T}^{-1} = H\). (See Exercise 7.33 (3) for the definition). Its anti-linearity implies (exercise) \(\mathcal {T}e^{-itH}\mathcal {T}^{-1} = e^{+it\mathcal {T}H\mathcal {T}^{-1}}\), so \(\mathcal {T}U_t = U_{-t}\mathcal {T}\), as expected physically. We stress that \(\mathcal {T}\) is a symmetry, but not a dynamical symmetry. There is no conserved quantity associated with this operator (it is not selfadjoint, nor linear!). \(\blacksquare \)
Exercise 7.33
-
(1)
Prove that a Hamiltonian observable that does not depend on time is a constant of motion.
Solution The time translation is described by U t = e itH and, trivially, it commutes with U s. Noether’s theorem allows to conclude. □
-
(2)
If U t = e −itH is the time time-evolution operator of a quantum system, a dynamical quantum symmetry (if any) is a Wigner symmetry represented by a unitary or anti-unitary operator V : H →H such that, recalling that pure states are unit vectors up to phase,
$$\displaystyle \begin{aligned}\chi^{(\psi)}_tVU_t \psi = U_{t}V\psi\end{aligned}$$for all \(t \in {\mathbb R}\) and every unit ψ ∈H, where \(\chi ^{(\psi )}_t \in {\mathbb C}\) with \(|\chi ^{(\psi )}_t|=1\).
Prove that \(\chi ^{(\psi )}_t\) does not depend on ψ and has the form χ t = e ict for some \(c\in {\mathbb R}\). Furthermore, if σ(H) is bounded below but not above, show that \(\chi ^{(\psi )}_t =1\), V is unitary and V HV −1 = H.
Solution By the same argument of the proof of Theorem 7.6 it is not hard to see that \(\chi ^{(\psi )}_t\) does not depend on ψ. Next observe that χ t U t = V U t V −1, the right-hand side being a strongly-continuous one-parameter group of unitary operators. Mimicking the proof of Theorem 7.20 (b) we find χ t = e ict for some \(c\in {\mathbb R}\). If the operator V is anti-unitary, e ict U t = V U t V −1 implies − V HV −1 = H − cI and therefore, with obvious notation, σ(V HV −1) = −σ(H) + c. Proposition 3.4 immediately yields σ(H) = −σ(H) + c, which contradicts the boundedness. Hence V must be unitary, and σ(H) = σ(H) − c. Since σ(H) is bounded below, c = 0. □
-
(3)
If U t = e −itH is the time time-evolution operator of a quantum system, time reversal (if present) is a Wigner symmetry represented by a unitary or anti-unitary operator \(\mathcal {T} : {\mathsf H} \to {\mathsf H}\) such that, according to the fact that pure states are unit vectors up to phase,
$$\displaystyle \begin{aligned}\chi^{(\psi)}_t\mathcal{T}U_t \psi = U_{-t}\mathcal{T}\psi\end{aligned}$$for all \(t \in {\mathbb R}\) and every unit ψ ∈H, where \(\chi ^{(\psi )}_t \in {\mathbb C}\) with \(|\chi ^{(\psi )}_t|=1\).
Prove that, \(\chi ^{(\psi )}_t\) does not depend on ψ and has the form χ t = e ict for some \(c\in {\mathbb R}\). Furthermore, if σ(H) is bounded below but not above, show that \(\chi ^{(\psi )}_t =1\), \(\mathcal {T}\) is anti-unitary, and \(\mathcal {T} H \mathcal {T}^{-1} = H\).
Solution With the same argument of Theorem 7.6, \(\chi ^{(\psi )}_t\) does not depend on ψ. In \(\chi _t U_t = \mathcal {T}U_{-t}\mathcal {T}^{-1}\) the right-hand side is a strongly-continuous one-parameter group of unitary operators. Inspired by the proof of Theorem 7.20 (b), we obtain χ t = e ict for some \(c\in {\mathbb R}\). If the operator \(\mathcal {T}\) is unitary, \(e^{ict} U_t = \mathcal {T}U_{-t}\mathcal {T}^{-1}\) implies \(\mathcal {T}H\mathcal {T}^{-1} = -H + cI\) and therefore, with obvious notation, \(\sigma (\mathcal {T}H\mathcal {T}^{-1}) = -\sigma (H) + c\). Proposition 3.4 immediately yields σ(H) = −σ(H) + c, which is false if σ(H) is bounded below but not above. Hence \(\mathcal {T}\) is anti-unitary and σ(H) = σ(H) + c. Since σ(H) is bounded below, c = 0. □
-
(4)
Consider the spinless particle, and prove that if \(V: L^2({\mathbb R}^3, d^3x)\to L^2({\mathbb R}^3, d^3x)\) is unitary, selfadjoint, and satisfies V X k V −1 = −X k , V P k V −1 = −P k for k = 1, 2, 3, then \(V = \mathcal {P}\), with \(\mathcal {P}\) defined in Example 7.32 (3).
Solution If V and V ′ satisfy the given conditions, then V −1 V ′ commutes with X k and P k for k = 1, 2, 3. According to Example 6.28 (3), V −1 V ′ = cI for some \(c \in {\mathbb C}\). That V and V ′ are selfadjoint and unitary respectively implies \(c\in {\mathbb R}\) and \(c \in {\mathbb T}\), hence c = ±1. To conclude, observe that the \(\mathcal {P}\) of Example 7.32 (3) satisfies the hypothesis. □
-
(5)
With reference to the spinless particle, suppose \(\mathcal {T}: L^2({\mathbb R}^3, d^3x)\to L^2({\mathbb R}^3, d^3x)\) is anti-unitary and satisfies
$$\displaystyle \begin{aligned}\mathcal{T} X_k \mathcal{T}^{-1} = X_k\:,\quad \mathcal{T} P_k \mathcal{T}^{-1} = -P_k\quad \mbox{for }k=1,2,3.\end{aligned}$$Show that \((\mathcal {T} \psi )(x) := \eta \overline {\psi (x)}\) for every \(\psi \in L^2({\mathbb R}^3, d^3x)\), and where η is a phase independent of ψ.
Solution Observe that \((V \psi )(x) := \overline {\psi (x)}\) and ηV satisfy the hypotheses, for every fixed \(\eta \in {\mathbb T}\). If \(\mathcal {T}\) is another anti-unitary operator satisfying the hypotheses then \(\mathcal {T} V^{-1}\) is unitary and commutes with X k and P k for k = 1, 2, 3. Exactly as for the previous exercise, necessarily \(\mathcal {T} V^{-1}= \eta I\) for some \(\eta \in {\mathbb T}\), proving the assertion. □
7.3 More on Strongly Continuous Unitary Representations of Lie Groups
Symmetry Lie groups arise naturally in physics when one considers the whole group of symmetries for a given quantum system [BaRa84]. For instance, in classical physics the (proper orthochronous) Galilean group (where SU(2) is used in place of SO(3)) is taken to be the group of continuous symmetries of every isolated quantum system studied in an inertial reference frame. Actually every strongly-continuous unitary representation of the Galilean group is trivial, and not accidentally those used in quantum physics are strongly-continuous unitary representations of a central extension of the Galilean group. This happens for reasons of physical and mathematical nature: the mass of the system is necessary to describe the action of the boost in quantum physics, and this piece of information is not retained by the Galilean group (but it can be encoded in the multipliers when constructing central extensions). Mathematically speaking, the Galilean group violates the cohomological obstruction of Bargmann’s theorem. The (proper orthochronous) Poincaré group (with SU(2) instead of SO(3)) replaces the Galilean group in the relativistic realm, and its continuous unitary-projective representations can always be made unitary because Bargmann’s constraint is satisfied [BaRa84].
From an abstract point of view, the groups of symmetries of a quantum system—excluding discrete symmetries if any—are by definition topological groups. We can always suppose that the group is connected by looking at the connected component of the identity. There are a bunch of assumptions of physical significance in addition to the continuity of the group operations, namely that the topology is (1) Hausdorff,Footnote 3 (2) second countable, and (3) locally Euclidean (every element of the group has compatible local coordinate charts, which create a local identification with \({\mathbb R}^n\)). If all of this happens, the celebrated Gleason-Montgomery-Zippin theorem (see [Mor18] for a concise discussion) implies that the topological group is actually a Lie group [HiNe13], whose unique smooth (analytic) structure underlies the C 0 structure.
It is worth stressing that the general group of continuous symmetries of a quantum system in particular contains time evolution as a subgroup. (Even different notions of time evolution, corresponding to different choices of the reference frame in the relativistic context.)
Sometimes these Lie groups can be represented in terms of proper unitary representations, in particular when Bargmann’s theorem holds. When not, the central extensions that have the structure of Lie groups can be represented unitarily and strongly continuously [Var07, Mor18]. Therefore it is not too restrictive to limit ourselves to strongly-continuous unitary representations of Lie groups only.
General reference texts on unitary and projective-unitary representations of topological and Lie groups with relevance in physics include: [BaRa84] (albeit not always rigorously written), [Var07], and for a concise summary on some topics [Mor18]. A fairly complete mathematical treatise on continuous representations (also of algebras) is [Schm90].
7.3.1 Strongly Continuous Unitary Representations
Before we examine Lie groups, let us tackle strongly-continuous representations of general topological groups. Sometimes strongly-continuous representations are simply called continuous representations. This is due to the following elementary result.
Proposition 7.34
If G is a topological group with neutral element e and \(U: G \ni g \mapsto U_g\in {\mathfrak B}({\mathsf H})\) is a unitary representation on the Hilbert space H , each of the following facts is equivalent to the strong continuity of U.
-
(a)
U is weakly continuous;
-
(b)
U is strongly continuous at e;
-
(c)
U is weakly continuous at e;
-
(d)
〈ψ|U g ψ〉→〈ψ|ψ〉 as g → e for every \(\psi \in \mathcal {D}\) , where \(\mathcal {D} \subset {\mathsf H}\) satisfies \(\overline {\mathit{\mbox{span}}(\mathcal { D})}= {\mathsf H}\).
Proof
Observing that \(||U_gx-U_fx||= ||U_{f^{-1}\cdot g}x -Ix||\) and f −1 ⋅ g → e if g → f, the proof is identical to that of Proposition 7.22. □
The theory of strongly-continuous unitary representations of topological groups is an important part of Representation Theory (see in particular [NaSt82] for a classical treatise on the subject and [BaRa84] for physical applications). An important result due to Peter and Weyl concerns compact Hausdorff groups (see [Mor18] for the full statement and proof).
Theorem 7.35 (Peter-Weyl’s Basic Statement)
Let G be a compact Hausdorff group—a compact Lie group in particular—and \(G \ni g \mapsto U_g \in {\mathfrak B}({\mathsf H})\) a strongly-continuous unitary representation on the Hilbert space H ≠ {0}.
-
(a)
If U is irreducible, then H is finite-dimensional.
-
(b)
If U is not irreducible, then the orthogonal Hilbert decomposition H =⊕k ∈ K H k holds, where H k are pairwise-orthogonal and non-trivial closed subspaces of finite dimension, all invariant under U. Furthermore every map
 is an irreducible representation of G.
is an irreducible representation of G.
This result applies in particular to compact Lie groups like SU(n) and SO(n), whose irreducible strongly-continuous unitary representations are therefore always finite-dimensional. The theory of the spin deals with strongly-continuous unitary irreducible representations of SU(2) which, as physicists know very well, are finite-dimensional by the Peter-Weyl theorem.
Another technical general result is the following one, that links a representation’s irreducibility to the Hilbert space’s separability. As before, we state it in a more general fashion which includes Lie groups.
Proposition 7.36
Let \(G\ni g \mapsto U_g\in {\mathfrak B}({\mathsf H})\) be a strongly-continuous unitary representation of a separable topological group G—a Lie group in particular—on the Hilbert space H . If the representation is irreducible, then H is separable.
Proof
As G is separable, let V ⊂ G be a dense countable set. Pick ψ ∈H ∖{0}. Since every U g : H →H is continuous, the closure H 0 of the set of finite combinations of elements U g ψ for g ∈ G is invariant under the action of U. The representation is irreducible and H 0 ≠ {0}, so H 0 = H. By the strong continuity of G ∋ g↦U g, every element in H 0 is the limit of finite linear combinations with rational (complex) coefficients of elements U h ψ where h ∈ V .
If G is a Lie group, in particular it is a second-countable and therefore separable. Given a topological basis \(\{B_n\}_{n\in {\mathbb N}}\) of G—where we assume \(B_n \neq \varnothing \)—choose b n ∈ B n for every \(n \in {\mathbb N}\). Then \(C:=\{b_n\:|\: n \in {\mathbb N}\}\) is countable and dense, because every open neighbourhood O g of g ∈ G necessarily contains some B p, so O g ∋ b p ∈ C. □
7.3.2 From the Gårding Space to Nelson’s Theorem
We henceforth restrict our study to Lie groups.
Remark 7.37
In the rest of the chapter we consider only finite-dimensional real Lie groups G, with Lie algebra \({\mathfrak g}\) and Lie bracket { , }. \(\blacksquare \)
A fundamental technical fact is that strongly-continuous unitary representations of (connected) Lie groups are associated with representations of the Lie algebras in terms of (anti-)selfadjoint operators. These operators are often interpreted physically as constants of motion (in general depending parametrically on time) when the Hamiltonian of the system belongs to the representation of the Lie algebra. We want to study the relationship between representations of G and representations of \({\mathfrak g}\). First of all, we define the operators representing the Lie algebra.
Definition 7.38
Let G be a Lie group and consider a strongly continuous unitary representation U of G on the Hilbert space H. Let \({\mathbb R} \ni s \mapsto \exp (s{\mathsf A}) \in G\) be the one-parameter Lie subgroup generated by \({\mathsf A} \in {\mathfrak g}\). The selfadjoint generator associated with A,
is the generator of the strongly continuous one-parameter unitary group
in the sense of Theorem 7.25.\(\blacksquare \)
The expectation is that these generators (with a factor − i) define a representation of the Lie algebra of the group. The major reason is that they are associated with unitary one-parameter subgroups exactly as the elements of the Lie algebra are associated with one-parameter Lie subgroups. In particular, we expect the Lie bracket to correspond to the commutator of operators. The problem is that the generators A may have different domains. We therefore seek a common invariant domain (the commutator must be defined on it), where all generators make simultaneous sense. This domain should retain all information on the operators A, disregarding the fact that they may be defined on larger domains. In other words, we would like each generator’s domain to be a core (Definition 2.30 (3)). There are several candidates for this space, and one of the most appealing is the Gårding space.
Definition 7.39
Let G be a Lie group and consider a strongly continuous unitary representation U of G on the Hilbert space H. If \(f \in C_c^\infty (G)\) (compactly-supported smooth complex functions on G) and x ∈H, define
where dg is the left-invariant Haar measure on G and integration is defined in a weak sense via Riesz’s lemma: since the anti-linear map H ∋ y↦∫G f(g)〈y|U g x〉dg is continuous, x[f] is the unique vector in H such that
The finite span of vectors x[f] ∈H with \(f \in C_c^\infty (G)\) and x ∈H is called the Gårding space of the representation, and we indicate by \(D^{(U)}_G\). \(\blacksquare \)
The subspace \(D^{(U)}_G\) enjoys very remarkable properties that we list in the next theorem. In the following \(L_g : C_c^\infty (G) \to C_c^\infty (G)\) denotes the standard left action of g ∈ G:
and, if \({\mathsf A} \in {\mathfrak g}\), \(X_{{\mathsf A}} : C_c^\infty (G) \to C_c^\infty (G)\) is the smooth vector field on G (smooth differential operator):
Thus
defines a representation of \({\mathfrak g}\) on \(C_c^\infty (G)\) by vector fields (differential operators). We conclude with the following theorem [Schm90, Mor18], whereby the Gårding space has all the expected properties.
Theorem 7.40
Referring to Definitions 7.38 and 7.39 , \(D^{(U)}_G\) satisfies the following properties.
-
(a)
\(D^{(U)}_G\) is dense in H.
-
(b)
\(U_g(D^{(U)}_G) \subset D^{(U)}_G\) for every g ∈ G. More precisely, if \(f \in C_c^\infty (G)\) , x ∈H , g ∈ G, then
$$\displaystyle \begin{aligned} \begin{array}{rcl} U_gx[f] = x[L_gf]\:.{} \end{array} \end{aligned} $$(7.32) -
(c)
If \({\mathsf A} \in {\mathfrak g}\) , then \(D^{(U)}_G\subset D(A)\) and \(A(D^{(U)}_G) \subset D^{(U)}_G\) . More precisely
$$\displaystyle \begin{aligned} \begin{array}{rcl} -iA x[f] = x[X_{{\mathsf A}}(f)] \end{array} \end{aligned} $$(7.33) -
(d)
The map
$$\displaystyle \begin{aligned} \begin{array}{rcl} {\mathfrak g} \ni {\mathsf A} \mapsto -iA|{}_{D^{(U)}_G} =: u({\mathsf A})\end{array} \end{aligned} $$(7.34)is a Lie algebra representation by skew-symmetric operators defined on the common dense and invariant domain \(D^{(U)}_G\) . In other words, the map is \({\mathbb R}\) -linear and
$$\displaystyle \begin{aligned}{}[u({\mathsf A}), u({\mathsf A}')] = u(\{{\mathsf A}, {\mathsf A}'\}) \quad \mathit{\mbox{if }}{\mathsf A}, {\mathsf A}'\in{\mathfrak g}.\end{aligned}$$ -
(e)
\(D^{(U)}_G\) is a core for every selfadjoint generator A with \({\mathsf A} \in {\mathfrak g}\) , that is
$$\displaystyle \begin{aligned} \begin{array}{rcl} A = \overline{A|{}_{D^{(U)}_G}}\:,\quad \forall {\mathsf A} \in {\mathfrak g}\:. \end{array} \end{aligned} $$(7.35)
Now we wish to address the converse problem. Suppose we are given a representation of a Lie algebra \({\mathfrak g}\) in terms of skew-symmetric operators defined on common invariant subspace of a Hilbert space H. We wonder whether or not it is possible to lift the representation to a unitary strongly-continuous representation of the unique simply connected Lie group G with Lie algebra \({\mathfrak g}\). This is a much more difficult problem. It was solved by Nelson [Nel69], who introduced a special domain in the Hilbert space of the representation.
Given a strongly continuous representation U of a Lie group G, there is another space \(D^{(U)}_N\) with similar features to \(D^{(U)}_G\) (see, e.g., [Mor18]). This space ends up being more useful than the Gårding space to build the representation U by exponentiating the Lie algebra representation. The domain \(D^{(U)}_N\) consists of vectors ψ ∈H such that G ∋ g↦U g ψ is analytic in g, i.e. expandable in power series of (real) analytic coordinates around any point of G. The elements of \(D^{(U)}_N\) are called analytic vectors of the representation U and \(D^{(U)}_N\) is the space of analytic vectors of the representation U. It turns out that \(D^{(U)}_N\) is invariant under every U g and that \(D^{(U)}_N \subset D^{(U)}_G\) (this is by no means trivial and follows from the deep Dixmier-Mallievin theorem [Mor18], whereby \(\psi \in D_G^{(U)}\) if and only if G ∋ g↦U g ψ is smooth).
There is a remarkable relationship between \(D^{(U)}_N\) and Definition 2.52. Nelson proved the following important result [Schm90, Mor18], which implies that \(D^{(U)}_N\) is dense in H, because analytic vectors for a selfadjoint operator are dense (Exercise 3.78). An operator crops up that we call Nelson operator.
Proposition 7.41
Let G be a Lie group and G ∋ g↦U g a strongly-continuous unitary representation on the Hilbert space H . Take a basis \({\mathsf A}_1,\ldots , {\mathsf A}_n \in {\mathfrak g}\) and define the Nelson operator on \(D^{(U)}_G\) by
where, as earlier, iu(A k) are the selfadjoint generators A k restricted to the Gårding domain \(D^{(U)}_G\) . Then
-
(a)
Δ N is essentially selfadjoint on \(D^{(U)}_G\).
-
(b)
Every analytic vector of the selfadjoint operator \(\overline {\Delta _N}\) is analytic and belongs in \(D^{(U)}_N\) . In particular \(D^{(U)}_N\) is dense.
-
(c)
Every vector in \(D^{(U)}_N\) is analytic for every selfadjoint operator \(i\overline {u({\mathsf A}_k)}\) , which is therefore essentially selfadjoint in \(D^{(U)}_N\) by Nelson’s criterion (Theorem 2.53 )
Now that we possess the necessary notions, we can eventually state the well-known theorem of Nelson that associates representations of the only simply connected Lie group with a given Lie algebra to representations of that Lie algebra.
Theorem 7.42 (Nelson’s Theorem)
Consider a real n-dimensional Lie algebra V of operators − iS, where each S is symmetric on the Hilbert space H , defined on a common invariant and dense subspace \(\mathcal {D}\subset {\mathsf H}\) , with the usual commutator as Lie bracket.
Let − iS 1, ⋯ , −iS n ∈ V be a basis of V and define Nelson’s operator with domain \(\mathcal {D}\) :
If Δ N is essentially selfadjoint, there exists a strongly-continuous unitary representation
on H of the unique connected, simply-connected Lie group G V with Lie algebra V .
U is uniquely determined by the fact that the closures \(\overline {S}\) , for every − iS ∈ V , are the selfadjoint generators of the representations of the one-parameter subgroups of G V in the sense of Definition 7.38 . In particular, the symmetric operators S are essentially selfadjoint on \(\mathcal {D}\).
Our version is slightly more than what is necessary, for it is known that the hypotheses can be relaxed (see [Mor18], also for further results on Nelson’s theory).
Exercise 7.43
Let H be a Hilbert space and A, B selfadjoint operators with common invariant dense domain D ⊂H where they are symmetric and commute. Prove that if A 2 + B 2 is essentially selfadjoint on D, then the spectral measures of A and B commute.
Solution
Exploit Nelson’s theorem after noticing that A, B define the Lie algebra of the Abelian Lie group \(({\mathbb R}^2, +)\) (which is connected and simply-connected) and that D is a core for A and B, since they are essentially selfadjoint on D by Nelson’s theorem. 
Example 7.44
-
(1)
Using polar coordinates, the Hilbert space \(L^2({\mathbb R}^3, d^3x)\) factorizes as
$$\displaystyle \begin{aligned}L^2([0,+\infty), r^2dr) \otimes L^2({\mathbb S}^2, d\Omega)\:,\end{aligned}$$where d Ω is the standard rotationally-invariant Borel measure on the unit sphere \({\mathbb S}^2\) in \({\mathbb R}^3\) normalized by \(\int _{{\mathbb S}^2} 1 d\Omega =4\pi \). In particular a Hilbert basis of \(L^2({\mathbb R}^3, d^3x)\) is made of the products \(\psi _n(r) Y^l_{m}(\theta ,\phi )\) where \(\{\psi _n\}_{n\in {\mathbb N}}\) is any Hilbert basis in L 2([0, +∞), r 2 dr) and \(\{Y^l_m\:|\: l=0,1,2,\ldots \:, m=0,\pm 1,\pm 2, \ldots \pm l \}\) is the standard Hilbert basis of spherical harmonics of \(L^2({\mathbb S}^2, d\Omega )\) [BaRa84]. The ψ n are smooth functions with compact support, whose derivatives at 0 vanish at every order. Since the \(Y^l_m\) are smooth on \({\mathbb S}^2\), the ψ n can be chosen so that \({\mathbb R}^3 \ni x \mapsto (\psi _n \cdot Y^l_{m})(x)\) are elements of \(C^\infty ({\mathbb R}^n)\) (and therefore also of \({\mathcal {S}}({\mathbb R}^3)\)). Now consider the three symmetric operators, defined on the common dense invariant domain \({\mathcal {S}}({\mathbb R}^3)\),
$$\displaystyle \begin{aligned}{\mathcal{L}}_k = \sum_{i,j=1}^3\epsilon_{kij} X_iP_j|{}_{{\mathcal{S}}({\mathbb R}^3)}\:,\end{aligned}$$where 𝜖 ijk is totally skew-symmetric in ijk and 𝜖 123 = 1. By direct inspection one sees that
$$\displaystyle \begin{aligned}{}[-i {\mathcal{L}}_k, -i{\mathcal{L}}_h] = \sum_{r=1}^3 \epsilon_{khr} (-i {\mathcal{L}}_r)\end{aligned}$$so that the real span of the operators \(-i{\mathcal {L}}_k\) is a representation of the Lie algebra of the simply connected real Lie group SU(2) (the universal covering of SO(3)). Define the Nelson operator \({\mathcal {L}}^2 := \sum _{k=1}^3 {\mathcal {L}}_k^2\) on \({\mathcal {S}}({\mathbb R}^3)\). Obviously this is a symmetric operator. A well-known computation proves that
$$\displaystyle \begin{aligned}{\mathcal{L}}^2 \: \psi_n(r) Y^l_{m} = l(l+1) \: \psi_n(r) Y^l_{m}\:.\end{aligned}$$We conclude that \({\mathcal {L}}^2\) admits a Hilbert basis of eigenvectors. Corollary 2.54 implies \({\mathcal {L}}^2\) is essentially selfadjoint. Therefore we can apply Theorem 7.42, and define a strongly continuous unitary representation SU(2) ∋ M↦U M (an SO(3)-representation actually, since U −I = I). The three selfadjoint operators \(L_k := \overline {{\mathcal {L}}_k}\) are the generators of the one-parameter group of rotations around the orthogonal Cartesian axes x k, k = 1, 2, 3. The one-parameter subgroup of rotations around the generic unit vector n, with components n k, has selfadjoint generator \(L_{\mathbf {n}} = \overline {\sum _{k=1}^3 n_k{\mathcal {L}}_k }\). The observable L n has the physical meaning of the n-component of the angular momentum of the particle described on \(L^2({\mathbb R}^3,d^3x)\). It turns out that, for \(\psi \in L^2({\mathbb R}^3, d^3x)\),
$$\displaystyle \begin{aligned} \begin{array}{rcl} (U_{M}\psi)(x) = \psi(\pi(M)^{-1} x)\:,\quad M \in SU(2) \:, x \in {\mathbb R}^3 {}\end{array} \end{aligned} $$(7.36)where π : SU(2) → SO(3) is the covering map. Equation (7.36) describes the action of the 3D rotation group on pure states in terms of quantum symmetries. This representation is, in fact, a subrepresentation of the unitary IO(3)-representation of Example 7.8 (1).
-
(2)
Given a quantum system, a quite general situation is that where the quantum symmetries of the systems are described by a strongly continuous representation V : G ∋ g↦V g on the Hilbert space H of the system, and time evolution is the representation of a one-parameter Lie subgroup with generator \({\mathsf H} \in {\mathfrak g}\):
$$\displaystyle \begin{aligned}V_{\exp(t{\mathsf H})}= e^{-itH} =: U_t\:.\end{aligned}$$This is the case, for instance, of relativistic quantum particles, where G is the special orthochronous Poincaré group, i.e. the semi-direct product \(SO(1,3)_+\ltimes {\mathbb R}^4\) (or its universal covering \(SL(2,{\mathbb C})\ltimes {\mathbb R}^4\)). To describe non-relativistic quantum particles, the relevant group G is a U(1)-central extension of the universal covering of the (connected, orthochronous) Galilean group.
In this situation, every element of \({\mathfrak g}\) determines a constant of motion. There are actually two cases.
-
(i)
If \({\mathsf A} \in {\mathfrak g}\) and {H, A} = 0, the Lie subgroups \(\exp (t{\mathsf H})\) and \(\exp (s{\mathsf A})\) commute by the Baker-Campbell-Hausdorff formula (see [NaSt82, Mor18], for instance). Consequently A is a constant of motion because \(V_{\exp (t{\mathsf H})} =e^{-itH}\) and \(V_{\exp (s{\mathsf A})} = e^{-isA}\) commute as well and Theorem 7.30 holds. In this case e −isA defines a dynamical symmetry by Noether’s theorem. This picture applies, for a free particle, to A = J n, the observable describing the total angular momentum along the unit vector n in an inertial frame.
-
(ii)
If \({\mathsf A} \in {\mathfrak g}\) but {H, A}≠ 0 the situation is slightly more complicated, and we exploit Theorem 7.31. A defines a constant of motion in terms of selfadjoint operators (observables) belonging to the representation of \({\mathfrak g}\). The difference with the previous case is that now the constant of motion depends parametrically on time. We therefore have a collection of observables \(\{A(t)\}_{t\in {\mathbb R}}\) in the Schrödinger picture, such that \(A_t := U^{-1}_t A(t) U_t\) are the corresponding observables in the Heisenberg picture. The equation of the constant of motion is therefore A t = A 0.
By exploiting the natural action of the one-parameter Lie subgroups on \({\mathfrak g}\) we define elements
$$\displaystyle \begin{aligned}{\mathsf A}(t) := \exp(t{\mathsf H}){\mathsf A}\exp(-t{\mathsf H}) \in {\mathfrak g}\:,\quad t \in {\mathbb R}\:\end{aligned}$$parametrised by time. If {A k}k=1,…,n is a basis of \({\mathfrak g}\),
$$\displaystyle \begin{aligned} \begin{array}{rcl} {\mathsf A}(t) = \sum_{k=1}^n a_k(t) {\mathsf A}_k{}\end{array} \end{aligned} $$(7.37)for some real-valued smooth maps a k = a k(t). By construction, the corresponding selfadjoint generators A(t), \(t\in {\mathbb R}\), define a parametrically time-dependent constant of motion. Indeed, since (exercise)
$$\displaystyle \begin{aligned}\exp(s\exp(t{\mathsf H}){\mathsf A}\exp(-t{\mathsf H})) = \exp(t{\mathsf H}) \exp(s{\mathsf A})\exp(-t{\mathsf H})\:,\end{aligned}$$we have
$$\displaystyle \begin{aligned}-iA(t) = \frac{d}{ds}|{}_{s=0}V_{\exp(s\exp(t{\mathsf H}){\mathsf A}\exp(-t{\mathsf H}))}= \frac{d}{ds}|{}_{s=0} V_{\exp(t{\mathsf H}) \exp(s{\mathsf A})\exp(-t{\mathsf H})}\end{aligned}$$$$\displaystyle \begin{aligned}= \frac{d}{ds}|{}_{s=0} V_{\exp(t{\mathsf H})} V_{\exp(s{\mathsf A})}V_{\exp(-t{\mathsf H})} = -i U_t A U^{-1}_t\:.\end{aligned}$$Therefore, as claimed, we end up with a constant of motion that depends parametrically upon time,
$$\displaystyle \begin{aligned}A_t = U^{-1}_t A(t) U_t = U^{-1}_t U_t A U^{-1}_tU_t = A = A_0\:.\end{aligned}$$By Theorem 7.40, as the map \({\mathfrak g} \ni A \mapsto A|{ }_{D_G^{(V)}}\) is a Lie algebra isomorphism, we can recast (7.37) for selfadjoint generators
$$\displaystyle \begin{aligned} \begin{array}{rcl} A(t)|{}_{D_G^{(V)}} = \sum_{k=1}^n a_k(t) A_k|{}_{D_G^{(V)}} \end{array} \end{aligned} $$(7.38)(where \(D_G^{(V)}\) could be replaced by \(D_N^{(V)}\) as the reader can easily establish, using Proposition 7.41 and Theorem 7.42). Since \(D_G^{(V)}\) (resp. \(D_N^{(V)}\)) is a core for A(t),
$$\displaystyle \begin{aligned} \begin{array}{rcl} A(t) = \overline{\sum_{k=1}^n a_k(t) A_k|{}_{D_G^{(V)}}}\:, \end{array} \end{aligned} $$(7.39)the bar denoting the closure of an operator, as usual. (The same is valid with \(D_N^{(V)}\) in place of \(D_G^{(V)}\).)
A relevant case, both for the non-relativistic and the relativistic framework is the selfadjoint generator K n(t) associated with the Galilean boost transformation along the unit vector n in \({\mathbb R}^3\) (the rest space of the inertial frame where the boost is viewed as an active transformation). Indeed, consider the generators of the connected orthochronous Galilean group (or a (U(1)-central extension of its universal covering). Then
$$\displaystyle \begin{aligned}\{h, k_{\mathbf{n}}\} = - p_{\mathbf{n}} \neq 0\:,\end{aligned}$$where p n is the generator of spatial translations along n, corresponding to the momentum observable along the axis n when passing to selfadjoint generators. The non-relativistic expression of K n(t), for a single particle, appears in (7.27). For an extended discussion on the non-relativistic case consult [Mor18]. A pleasant and physically exhaustive discussion encompassing the relativistic case appears in [BaRa84]. \(\hfill \blacksquare \)
Theorem 7.45 (Stone-von Neumann-Mackey Theorem)
Let H be a Hilbert space and suppose that there are 2n symmetric operators Q 1, …, Q n and M 1, …, M n on H satisfying the following requirements.
-
(1)
There is a common, dense, invariant subspace D ⊂H where the CCRs
$$\displaystyle \begin{aligned}{}[Q_h, M_k]\psi = i\hbar \delta_{hk} \psi \:,\quad [Q_h, Q_k]\psi =0\:, \quad [M_h, M_k]\psi = 0\:, {} \end{aligned} $$(7.40)with ψ ∈ D, h, k = 1, …, n, hold.
-
(2)
The representation is irreducible in the sense that there is no proper non-zero closed subspace K ⊂H such that \(P_{\mathsf K}\overline {Q_k}\subset \overline {Q_k}P_{\mathsf K}\) and \(P_{\mathsf K}\overline {M_k}\subset \overline {M_k}P_{\mathsf K}\) where P K : H →H is the orthogonal projector onto K.
-
(3)
The operator \(\sum _{k=1}^n Q_k^2|{ }_D + M_k^2|{ }_D\) is essentially selfadjoint.
Under these conditions, Q k and M k are essentially selfadjoint on D, which turns out to be a common core, and there exists a Hilbert-space isomorphism (a surjective linear isometry) \(U: {\mathsf H} \to L^2({\mathbb R}^n, d^nx)\) such that
where X k and P k are the standard position ( 2.22 ) and momentum ( 2.23 ) selfadjoint operators on \(L^2({\mathbb R}^n,d^nx)\) . In particular H is separable.
If only (1) and (3) are valid, then H decomposes as an orthogonal Hilbert sum H = ⊕r ∈ R H r where R is finite, or countable if H is separable, the H r ⊂H are closed with
where \(P_{{\mathsf H}_r} : {\mathsf H} \rightarrow {\mathsf H}\) is the orthogonal projector onto H r, k = 1, …, n and the restrictions of \(\overline {Q_k}\) and \(\overline {M_k}\) to each H r satisfy (7.41) for suitable surjective linear isometries \(U_r: {\mathsf H}_r \to L^2({\mathbb R}^n, d^nx)\).
Proof
If (1) holds, the restrictions to D of Q k, M k define symmetric operators (since they are symmetric and D is dense and contained in their domains), and also their squares are symmetric, since D is invariant. Adding (3), Nelson’s theorem (the symmetric operator \(I|{ }_D^2 + \sum _{k=1}^n Q_k^2|{ }_D + M_k^2|{ }_D\) is essentially selfadjoint if \(\sum _{k=1}^n Q_k^2|{ }_D + M_k^2|{ }_D\) is), says there is a strongly continuous unitary representation \(W \ni g \mapsto V_g \in {\mathfrak B}({\mathsf H})\) of the simply connected (2n + 1)-dimensional Lie group W whose Lie algebra is spanned by − iI, −iQ k, −iM k subject to (7.40) and [−iQ h, −iI] = [−iM k, −iI] = 0, where − iI is restricted to D. W is the Weyl-Heisenberg group [Mor18]. Due to Theorem 7.42, the selfadjoint generators of this representation are just the selfadjoint operators \(\overline {Q_k|{ }_{D}}\) and \(\overline {P_k|{ }_{D}}\) (and I). Since \(\overline {Q_k|{ }_D} \subset \overline {Q_k}\), where the former is selfadjoint and the latter symmetric, necessarily \(\overline {Q_k|{ }_D} = \overline {Q_k}\) and \(\overline {M_k|{ }_D} = \overline {M_k}\). D is therefore a common core. If, furthermore, the Lie algebra representation is irreducible (as in (2)), the unitary representation is irreducible, too: if K ⊂H were invariant under the unitary operators, by Stone’s theorem it would be invariant (again, as in (2)) under the selfadjoint generators \(\overline {Q_k}, \overline {P_k}\) of the one-parameter Lie groups associated to each Q k and P k. This is impossible if the representation is irreducible, as we are assuming. The standard version of the Stone-von Neumann theorem [Mor18] implies that there exists an isometric surjective operator \(U : {\mathsf H} \to L^2({\mathbb R}^n, d^nx)\) such that \(W \ni g \mapsto UV_gU^{-1}\in {\mathfrak B}(L^2({\mathbb R}^n,d^nx))\) is the standard unitary representation of W on \( L^2({\mathbb R}^n, d^nx)\), generated by X k and P k (and I). Stone’s theorem immediately yields (7.41). The last statement follows easily from the standard form of Mackey’s theorem, which completes the Stone-von Neumann result [Mor18]. □
With hindsight the result furnishes a strong justification for requiring the Hilbert space of an elementary quantum system, like a particle in non-relativistic quantum mechanics, must be separable. Separability also arises from Proposition 7.36 in the relativistic case when, following Wigner’s ideas, we think of elementary particles as described by irreducible strongly-continuous unitary representations of the (universal covering of the special orthochronous) Poincaré group.
7.3.3 Pauli’s Theorem
Physically meaningful Hamiltonian operators have lower-bounded spectrum to avoid thermodynamical instability. This fact prevents the existence of a “time operator” canonically conjugated to H. This result is sometimes quoted as Pauli’s theorem. As a consequence, the meaning of Heisenberg’s inequality ΔE ΔT ≥ħ∕2 differs from the meaning of the analogous relationship of position and momentum. Yet it is possible to define a sort of time observable simply by passing from PVMs to POVMs (positive-operator valued measures) [Mor18]. POVMs are employed to describe concrete physical phenomena related to measurement procedures, especially in quantum information theory [Bus03, BGL95].
Theorem 7.46 (Pauli’s Theorem)
If the spectrum of the (selfadjoint) Hamiltonian operator H of a quantum system described on the Hilbert space H is bounded below, there is no selfadjoint operator T satisfying
where D ⊂H is dense, invariant and such that \(H|{ }_D^2+T|{ }_D^2\) is essentially selfadjoint.
Proof
The pair H, T should be mapped to corresponding P, X in \(L^2({\mathbb R}, dx)\), or a direct sum of such spaces, by a Hilbert space isomorphism due to Theorem 7.45. In either case the spectrum of H should coincide with the spectrum of P, namely \({\mathbb R}\). But this is forbidden right from the start. □
Notes
- 1.
A Lie group is a second-countable Hausdorff real-analytic manifold, locally homeomorphic to \({\mathbb R}^n\), and equipped with smooth group operations. Real analyticity can be replaced by smoothness.
- 2.
A set A ⊂ SU(2)∕ker(π) = SO(3) is open if and only if π −1(A) ⊂ SU(2) is open.
- 3.
From the experimental point of view, a Hausdorff topology means that we can distinguish different elements of the group even if our knowledge is affected by experimental errors.
References
A.O. Barut, R. Raczka, Theory of Group Representations and Applications (World Scientific, Singapore, 1984)
P. Busch, M. Grabowski, P.J. Lahti, Operational Quantum Physics (Springer, Berlin, 1995)
P. Busch, Quantum states and generalized observables: a simple proof of Gleason’s theorem. Phys. Rev. Lett. 91, 120403 (2003)
R. Haag, Local Quantum Physics (Second Revised and Enlarged Edition) (Springer, Berlin, 1996)
J. Hilgert, K.-H. Neeb, Structure and Geometry of Lie Groups (Springer, Dordrecht, 2013)
K. Landsman, Foundations of Quantum Theory (Springer, New York, 2017)
V. Moretti, Spectral Theory and Quantum Mechanics, 2nd edn. (Springer, Cham, 2018)
M.A. Naimark, A.I. Stern, Theory of Group Representations (Springer, New York, 1982)
E. Nelson, Analytical vectors. Ann. Math. 70, 572–615 (1969)
K. Schmüdgen, Unbounded Operator Algebras and Representation Theory (Springer, Berlin, 1990)
B. Simon, Quantum Dynamics: From Automorphism to Hamiltonian. Studies in Mathematical Physics, Essays in Honor of Valentine Bargmann, ed. by E.H. Lieb, B. Simon, A.S. Wightman (Princeton University Press, Princeton, 1976), pp. 327–349
V.S. Varadarajan, Lie Groups, Lie Algebras, and Their Representations (Springer, Berlin, 1984)
V.S. Varadarajan, Geometry of Quantum Theory, 2nd edn. (Springer, Berlin, 2007)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Moretti, V. (2019). Quantum Symmetries. In: Fundamental Mathematical Structures of Quantum Theory. Springer, Cham. https://doi.org/10.1007/978-3-030-18346-2_7
Download citation
DOI: https://doi.org/10.1007/978-3-030-18346-2_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-18345-5
Online ISBN: 978-3-030-18346-2
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


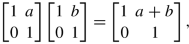
 is an irreducible representation of G.
is an irreducible representation of G.