Abstract
The overall goal of this chapter is to extend the elementary decomposition of a Hermitian operator (1.4) on a finite-dimensional Hilbert space seen in Chap. 1 to a formula valid in the infinite-dimensional case. We do this to make rigorous sense of the spectral decompositions of (generally unbounded) selfadjoint operators representing observables, such as momentum and position. What we need is called Spectral Theory on Hilbert spaces, which will be the subject of this chapter. After stating and proving the theory’s major theorems, we shall apply them to the elementary presentation of quantum theory introduced in the first chapter to produce a mathematically sound formulation. The proofs to certain technical results are relegated to the last section.
Access provided by Autonomous University of Puebla. Download chapter PDF
The overall goal of this chapter is to extend the elementary decomposition of a Hermitian operator (1.4) on a finite-dimensional Hilbert space seen in Chap. 1 to a formula valid in the infinite-dimensional case. We do this to make rigorous sense of the spectral decompositions of (generally unbounded) selfadjoint operators representing observables, such as momentum and position. What we need is called Spectral Theory on Hilbert spaces, which will be the subject of this chapter. After stating and proving the theory’s major theorems, we shall apply them to the elementary presentation of quantum theory introduced in the first chapter to produce a mathematically sound formulation. The proofs to certain technical results are relegated to the last section. Reference books are [Ped89, Rud91, Schm12, Tes14, Mor18].
3.1 Basics on Spectral Theory
As we shall see in a short while, when we pass to infinite dimensions sums are replaced by integrals and σ(A) must be enlarged to encompass more than just the eigenvalues of A. This is because, as already noticed in the first chapter, there exist operators playing crucial roles in QM that should be decomposed as prescribed by (1.4) yet do not have eigenvalues.
Notation 3.1
If A : D(A) →H is injective, A −1 indicates its inverse when the codomain of A is restricted to Ran(A). In other words, A −1 : Ran(A) → D(A). \(\blacksquare \)
3.1.1 Resolvent and Spectrum
The definition of spectrum of the operator A : D(A) →H extends the notion eigenvalue. The eigenvalues of A are numbers \(\lambda \in {\mathbb C}\) such that (A − λI)−1 is not defined. A naive generalization to infinite dimensions is not viable due to a number of topological issues. As a matter of fact, even if (A − λI)−1 does exist it may be bounded or unbounded, and its domain Ran(A − λI) may or not be dense. These features permit us to define a suitable extension of the notion of eigenvalue.
Definition 3.2
Let A be an operator on the Hilbert space H. The resolvent set of A is the subset of \({\mathbb C}\)
The spectrum of A is the complement \(\sigma (A):=\mathbb {C}\setminus \rho (A)\) and consists of the union of the following pairwise-disjoint three parts:
-
(i)
the point spectrum, σ p(A), for which A − λI is not injective (its elements are the eigenvalues of A),
-
(ii)
the continuous spectrum, σ c(A), for which A − λI is injective, \(\overline {Ran(A-\lambda I)} = {\mathsf H}\) and (A − λI)−1 is not bounded,
-
(iii)
the residual spectrum, σ r(A), where A − λI is injective and \(\overline {Ran(A-\lambda I)} \neq {\mathsf H}\).
If λ ∈ ρ(A), the operator
is called the resolvent operator of A. \(\blacksquare \)
The following technically elementary fact defines approximate eigenvector an element of the continuous spectrum. Even if proper eigenvectors do not exist, they can be approximated arbitrarily well.
Proposition 3.3
Let A : D(A) →H be an operator on the Hilbert space H and take λ ∈ σ c(A). For every 𝜖 > 0 there exists x 𝜖 ∈ D(A) with ||x 𝜖|| = 1 such that ||Ax 𝜖 − λx 𝜖|| < 𝜖.
Proof
Since λ ∈ σ c(A), we have that (A − λI)−1 : Ran(A − λI) → D(A) is not bounded. Therefore, for every 𝜖 > 0 there is y 𝜖 ∈ Ran(A − λI) with y 𝜖 ≠ 0 such that
By construction, we may write y 𝜖 = (A − λI)z 𝜖 for some z 𝜖 ∈ D(A) ∖{0}, so that
In other words, 𝜖||z 𝜖|| > ||Az 𝜖 − λz 𝜖||. It is now evident that x 𝜖 := ||z 𝜖||−1 z 𝜖 fulfils the claim. □
The property is also valid (a) if λ ∈ σ p(A), simply by choosing x 𝜖 as a λ-eigenvector irrespective of 𝜖, and also (b) if λ ∈ σ r(A) in case (A − λI)−1 is not bounded. For this reason, it is sometimes convenient to decompose σ(A) in a different way when we deal with operators admitting residual spectrum (this is not the case for normal operators, as we shall see shortly). The approximate point spectrum σ ap(A) consists of λ ∈ σ(A) such that, for every 𝜖 > 0, there exists x 𝜖 ∈ D(A) with ||Ax 𝜖 − λx 𝜖|| < 𝜖 and ||x 𝜖|| = 1 (including the case Ker(A − λI) = {0}). The residual pure spectrum σ rp(A) is just σ(A) ∖ σ ap(A).
In Hilbert spaces the spectrum and the resolvent are invariant under unitary operators and, more generally, under isomorphisms or anti-isomorphisms. The following elementary result, proven by using basic properties of surjective linear isometries, confirms this.
Proposition 3.4
If U : H →H ′ is an isometric surjective linear (or anti-linear) map between Hilbert spaces and A is any operator on H , then σ(UAU −1) = σ(A). In particular,
The next technically important proposition is concerned with resolvents and spectra of closed operators, where things simplify quite a lot.
Proposition 3.5
Let A : D(A) →H be a closed operator on the Hilbert space H (for instance \(A \in {\mathfrak B}({\mathsf H})\) ). Then λ ∈ ρ(A) if and only if the inverse to A − λI exists and belongs in \({\mathfrak B}({\mathsf H})\) . In particular Ran(A − λI) = H.
Proof
If \((A-\lambda I)^{-1} \in {\mathfrak B}({\mathsf H})\), then \(\overline {Ran(A-\lambda I)}= Ran(A-\lambda I) = {\mathsf H}\) and (A − λI)−1 is bounded, so that λ ∈ ρ(A) by definition. Let us prove the converse, and suppose that λ ∈ ρ(A). We know that (A − λI)−1 is defined on the dense domain Ran(A − λI) and is bounded. To conclude, it is therefore enough to prove that y ∈H implies y ∈ Ran(A − λI). To this end, notice that if \(y \in {\mathsf H} = \overline {Ran(A-\lambda I)}\), then y =limn→+∞(A − λI)x n for some x n ∈ D(A − λI). The sequence of elements x n converges. Indeed, H is complete and \(\{x_n\}_{n\in {\mathbb N}}\) is Cauchy because (1) x n = (A − λI)−1 y n, (2) ||x n − x m||≤||(A − λI)−1|| ||y n − y m||, and (3) y n → y. To finish the proof, we observe that A − λI is closed since A is closed (Remark 2.31 (b)). Consequently (Remark 2.31 (c)) x =limn→+∞ x n ∈ D(A − λI) and y = (A − λI)x ∈ Ran(A − λI). □
Remark 3.6
-
(a)
As a consequence of this result, if A : D(A) →H is closed or \(A\in {\mathfrak B}({\mathsf H})\) the definition of resolvent simplifies:
$$\displaystyle \begin{aligned}\rho(A) := \{\lambda \in {\mathbb C} \:|\: \exists (A-\lambda I)^{-1} \in {\mathfrak B}({\mathsf H})\}\:.\end{aligned}$$Some textbooks give this definition from the very beginning. In these cases, since the operators (A − λI)−1 have the same domain H when λ ∈ ρ(A), R μ(A) − R λ(A) is defined everywhere.
-
(b)
The conclusion of Proposition 3.5 can actually be stated in an even stronger form. Since A is closed, A − λI and its inverse (A − λI)−1 are closed as well (they have the same graph). So if A is defined everywhere on H, it is automatically bounded by the closed graph theorem. So we have an alternative version of Proposition 3.5. \(\blacksquare \)
Proposition 3.7
Let A : D(A) →H be a closed operator on the Hilbert space H (for example, \(A \in {\mathfrak B}({\mathsf H})\) ). Then λ ∈ ρ(A) if and only if A − λI : D(A) →H is a bijection.
The definitions of resolvent and spectrum can be extended as they stand to the case where H is replaced by a complex Banach space [Rud91, Mor18]. Even more generally, they adapt to abstract unital Banach algebras if we interpret operators as elements of the algebra.
Definition 3.8
If \(\mathcal {A}\) is a unital Banach algebra, the resolvent of an element \(a \in {\mathfrak A}\) is made of all \(\lambda \in {\mathbb C}\) such that  admits inverse, written R
λ(a), in \({\mathfrak A}\). The spectrum of \(a\in {\mathfrak A}\)
is \(\sigma (a):= {\mathbb C} \setminus \rho (a)\). \(\blacksquare \)
admits inverse, written R
λ(a), in \({\mathfrak A}\). The spectrum of \(a\in {\mathfrak A}\)
is \(\sigma (a):= {\mathbb C} \setminus \rho (a)\). \(\blacksquare \)
No finer spectral decompositions are made in this context.
A closed operator A satisfies the resolvent identity, which is evidently valid also for unital Banach algebras (replacing R z(A) by R z(a)).
Proposition 3.9
Let A : D(A) →H be a closed operator (or, more strongly, \(A\in {\mathfrak B}({\mathsf H})\) ) on the Hilbert space H and take μ, λ ∈ ρ(A). Then
called the resolvent identity.
Proof
First of all  and (A − μI)R
μ(A) = I. As a consequence, R
λ(A)(A − λI)R
μ(A) = R
μ(A) and R
λ(A)(A − μI)R
μ(A) = R
λ(A). Taking the difference produces (3.2). □
and (A − μI)R
μ(A) = I. As a consequence, R
λ(A)(A − λI)R
μ(A) = R
μ(A) and R
λ(A)(A − μI)R
μ(A) = R
λ(A). Taking the difference produces (3.2). □
We shall prove that if \(A\in {\mathfrak B}({\mathsf H})\) then \(\rho (A) \neq \varnothing \). The same applies to unital Banach algebras.
Proposition 3.10
Let H be a Hilbert space and \(A\in {\mathfrak B}({\mathsf H})\) . Then λ ∈ ρ(A) if |λ| > ||A||, so σ(A) is bounded by ||A||.
Proof
The series \(S_\lambda :=-\sum _{n=0}^{+\infty }\lambda ^{-(n+1)}A^n\) (where A 0 := I) converges in the operator norm of \({\mathfrak B}({\mathsf H})\) when |λ| > ||A|| since it is dominated by the complex series \(\sum _{n=0}^{+\infty }|\lambda |{ }^{-(n+1)}||A||{ }^n\) and \({\mathfrak B}({\mathsf H})\) is a Banach space. Furthermore
so S λ = R λ(A) and λ ∈ ρ(A). □
A few general properties of the spectrum and the resolvent set deserve special attention because they crop up in QM. The most important are encapsulated in the following proposition.
Proposition 3.11
Let A : D(A) →H be a closed operator on the Hilbert space H . Then
-
(a)
ρ(A) is open , σ(A) is closed and \(\rho (A) \ni \lambda \mapsto \langle x|R_\lambda (A) y\rangle \in {\mathbb C}\) is holomorphic for every x, y ∈H if \(\rho (A) \neq \varnothing \).
-
(b)
If \(A\in {\mathfrak B}({\mathsf H})\) , then
-
(i)
\(\sigma (A)\neq \varnothing \) ,
-
(ii)
\(\rho (A) \neq \varnothing \).
-
(iii)
σ(A) is compact.
-
(i)
If \({\mathfrak A}\) is a unital Banach algebra and \(a\in {\mathfrak A}\) , then ρ(a) is open, σ(a) is closed and part (b) holds with a replacing A.
Proof
Let us start from (b). Statement (ii) has already been proved in Proposition 3.10, and this proves (iii) provided (i) holds. (i) is established by studying the function \(\rho (A) \ni \lambda \mapsto f_{xy}(\lambda ) := \langle y| (A-\lambda I)^{-1}x\rangle \in {\mathbb C}\) for every given x, y ∈H. Using the expansion in the proof of Proposition 3.10, we have \(f_{xy}(\lambda ) = -\sum _{n=0}^{+\infty }\lambda ^{-(n+1)}\langle y|A^nx\rangle \). The series, for |λ| > |λ 0|, is dominated by the numerical series \(\sum _{n=0}^{+\infty }\lambda _0^{-(n+1)}||A||{ }^n||x||||y||\), which converges as |λ 0| > ||A||. Therefore the series of f xy converges absolutely and uniformly on \(\{\lambda \in {\mathbb C} \:|\: |\lambda |>|\lambda _0|\}\). Exploiting the dominated convergence theorem we conclude that f xy(λ) → 0 as |λ|→ +∞. But f xy is holomorphic because it is a uniform limit of holomorphic maps (use Morera’s theorem). Now, if \(\rho (A)= {\mathbb C}\) Liouville’s theorem would imply that f xy is constant for every y, x ∈H, so f xy(λ) = 0 everywhere because of the limit we computed. It would follow (A − λI)−1 = 0, a contradiction. We conclude that \(\rho (A) \neq {\mathbb C}\), so \(\sigma (A) \neq \varnothing \).
If we look at the Banach algebra picture and take \(a\in {\mathfrak A}\), the function f
xy has to be replaced by  for every element f of the topological dual \({\mathfrak A}^*\), but the proof proceeds similarly.
for every element f of the topological dual \({\mathfrak A}^*\), but the proof proceeds similarly.
-
(a)
Assume λ 0 ∈ ρ(A) and consider \(\lambda \in {\mathbb C}\) with \(|\lambda -\lambda _0|< ||R_{\lambda _0}(A)||{ }^{-1}\). We therefore have
$$\displaystyle \begin{aligned} \begin{aligned}A-\lambda I &= [(\lambda_0 -\lambda)I + (A-\lambda_0I)] = (A-\lambda_0I)[(\lambda-\lambda_0)R_{\lambda_0}(A) + I]\\ &= R_{\lambda_0}(A)^{-1}[(\lambda-\lambda_0)R_{\lambda_0}(A) + I]\:,\end{aligned}\end{aligned}$$so that
$$\displaystyle \begin{aligned}(A-\lambda I)^{-1} = [(\lambda-\lambda_0)R_{\lambda_0}(A) + I]^{-1} R_{\lambda_0}(A)\end{aligned}$$provided \( [(\lambda -\lambda _0 I)R_{\lambda _0}(A) + I]^{-1} \) exists. With the same argument used for Proposition 3.10, when \(|\lambda -\lambda _0|< ||R_{\lambda _0}(A)||{ }^{-1}\) we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} [(\lambda-\lambda_0)R_{\lambda_0}(A) + I]^{-1} = \sum_{n=0}^{+\infty} (\lambda_0-\lambda)^nR_{\lambda_0}(A)^n\:. {}\end{array} \end{aligned} $$(3.3)We have demonstrated that every point λ 0 ∈ ρ(A) admits an open neighbourhood where R λ(A) exists. We can therefore say that \(\rho (A)\subset {\mathbb C}\) is open and its complement σ(A) is closed. If \(\rho (A) \neq \varnothing \) the map ρ(A) ∋ λ↦〈x|(A − λI)−1 y〉 admits Taylor expansion around every λ ∈ ρ(A), constructed trivially out of (3.3). Hence the function is holomorphic.
The same proof works for unital Banach algebras \({\mathfrak A}\), by simply replacing 〈x|R λ(A)y〉 with f(R λ(a)), where \(f\in {\mathfrak A}^*\).
□
Remark 3.12
-
(a)
If \(A \in {\mathfrak B}({\mathsf H})\) is normal, the spectral radius formula holds
$$\displaystyle \begin{aligned} \begin{array}{rcl} \sup\{ |\lambda| \:|\: \lambda \in \sigma(A)\} = ||A||\:.{}\end{array} \end{aligned} $$(3.4)The spectral radius of A is the expression on left. We shall derive this formula for selfadjoint operators as an immediate consequence of the spectral theorem. However, Proposition 3.80 provides a general version for normal operators whose proof is independent of the spectral theorem. This formula holds also in abstract unital C ∗-algebras: replacing A is a normal element a: a ∗ a = aa ∗.
-
(b)
Item (i) in Proposition 3.11 (b) for unital Banach algebras implies the well-known Gelfand–Mazur theorem, whereby a Banach algebra whose every non-zero element is invertible is isomorphic to \({\mathbb C}\). Indeed
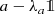 must be non-invertible for some \(\lambda _a\in \sigma (a)\subset {\mathbb C}\), and hence
must be non-invertible for some \(\lambda _a\in \sigma (a)\subset {\mathbb C}\), and hence 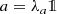 . \(\blacksquare \)
. \(\blacksquare \)
3.1.2 Spectra of Special Operator Types
We are ready to state and prove general properties of the spectra of selfadjoint and unitary operators.
Proposition 3.13
Let A : D(A) →H be a densely-defined operator on the Hilbert space H . Then
-
(a)
if A is selfadjoint, then \(\sigma (A) \subset {\mathbb R}\).
-
(b)
If A is unitary, then \(\sigma (A) \subset {\mathbb T} := \{z \in {\mathbb C} \:|\: |z|=1\}\).
-
(c)
If A is normal, in particular selfadjoint or unitary, the following hold (where the bar denotes complex conjugation of the single elements):
-
(i)
\(\sigma _r(A)= \sigma _r(A^*) =\varnothing \) ,
-
(ii)
\(\sigma _p(A) = \overline {\sigma _p(A^*)}\) ; in particular if x ≠ 0, Ax = λx if and only if \(A^*x= \overline {\lambda }x\) ,
-
(iii)
\(\sigma _c(A) = \overline {\sigma _c(A^*)}\).
-
(i)
-
(d)
If A is normal (in particular selfadjoint or unitary), then eigenvectors with distinct eigenvalues are orthogonal.
Proof
-
(a)
Suppose λ = μ + iν with ν ≠ 0 and let us prove λ ∈ ρ(A). If x ∈ D(A),
$$\displaystyle \begin{aligned}\langle (A -\lambda I)x | (A -\lambda I)x\rangle = \langle(A -\mu I)x | (A -\mu I)x \rangle + \nu^2 \langle x|x\rangle + i\nu [\langle Ax|x\rangle - \langle x|Ax\rangle]\:. \end{aligned}$$The last summand vanishes as A is selfadjoint. Hence ||(A − λI)x||≥|ν| ||x||. With a similar argument we obtain \(||(A-\overline {\lambda } I)x|| \geq |\nu |\: ||x||\). The operators A − λI and \(A-\overline {\lambda }I\) are injective, and ||(A − λI)−1||≤|ν|−1, where (A − λI)−1 : Ran(A − λI) → D(A). Notice that, from (2.21),
$$\displaystyle \begin{aligned}\overline{Ran(A-\lambda I)}^\perp = [Ran(A-\lambda I)]^\perp = Ker(A^* - \overline{\lambda}I) = Ker(A- \overline{\lambda}I) =\{0\}\:,\end{aligned}$$where the last equality makes use of the injectivity of \(A-\overline {\lambda }I\). Summarising: A − λI in injective, (A − λI)−1 bounded and \(\overline {Ran(A-\lambda I)}^\perp = \{0\}\), i.e. Ran(A − λI) is dense in H; therefore λ ∈ ρ(A), by definition of resolvent set.
-
(b)
Suppose that \(\lambda \in {\mathbb C}\) and |λ|≠ 1, and we want to prove λ ∈ ρ(A). If x ∈H = D(A) we have
$$\displaystyle \begin{aligned}\langle (A -\lambda I)x | (A -\lambda I)x\rangle = \langle A x | Ax \rangle + |\lambda|{}^2 \langle x| x\rangle - 2Re(\overline{\lambda}\langle Ax|x\rangle)\:. \end{aligned}$$In other words, using 〈Ax|Ax〉 = 〈x|x〉 = ||x||2 and |〈Ax|x〉|≤||x||2||A|| = ||x||2,
$$\displaystyle \begin{aligned}||(A-\lambda I)x||{}^2 \geq (1+|\lambda|{}^2)||x||{}^2 - 2|\lambda| ||x||{}^2 = (1+|\lambda|{}^2- 2|\lambda|)||x||{}^2\:.\end{aligned}$$Summing up, we have proved that ||(A − λI)x||2 ≥ (1 −|λ|)2||x||2.
As in (a), since (1 −|λ|)2 ≠ 0, the previous inequality implies that Ker(A − λI) = {0}, that ||(A − λI)−1||≤ (1 −|λ|)−1, and that Ran(A − λI) is dense because \(\overline {Ran(A-\lambda I)}^\perp = Ker(A^*-\overline {\lambda }I)=\{0\}\) (A ∗ is unitary as A is unitary and \(|\overline {\lambda }|= |\lambda | \neq 1\), so the previous argument applies).
-
(c)
First of all observe that A normal implies Ker(A) = Ker(A ∗). Indeed, if x ∈ Ker(A), then Ax = 0 and hence A ∗ Ax = A ∗0 = 0, so by definition of normal operator AA ∗ x = A ∗ Ax = 0. In particular x ∈ D(A ∗) and therefore 〈x|AA ∗ x〉 = 0. As a consequence, ||A ∗ x||2 = 〈A ∗ x|A ∗ x〉 = 〈x|AA ∗ x〉 = 0 and then x ∈ Ker(A ∗). Suppose, conversely, that x ∈ Ker(A ∗). Then A ∗ x = 0 and AA ∗ x = A0 = 0. Using normality, A ∗ Ax = AA ∗ x = 0. In particular, since normal operators are closed by definition, \(x\in D(A)=D(\overline {A})= D((A^*)^*)\) and therefore 〈x|A ∗ Ax〉 = 0 means 〈(A ∗)∗ x|Ax〉 = 〈Ax|Ax〉 = 0, which is nothing but ||Ax||2 = 0, i.e. x ∈ Ker(A).
Let us prove (i) \(\sigma _r(A)=\varnothing \). Suppose λ ∈ σ(A), but λ∉σ p(A). Then A − λI must be injective, that is Ker(A − λI) = {0}. Since A − λI is normal if A is normal (in particular closed Remark 2.31 (b)), we conclude that \(Ker(A^*-\overline {\lambda } I) =Ker(A-\lambda I) = \{0\}\). Therefore \([Ran(A -\lambda I)]^\perp = Ker(A^*-\overline {\lambda } I)= \{0\}\) due to (2.21), and \(\overline {Ran(A -{\lambda } I)} ={\mathsf H}\). Consequently λ ∈ σ c(A) and no complex number in σ(A) is allowed to belong in σ r(A). Observing that A ∗ is normal if A is normal, we conclude that \(\sigma _r(A^*)= \varnothing \) as well. Statement (ii) \(\sigma _p(A)= \overline {\sigma _p(A^*)}\) immediately descends from \(Ker(A-\lambda I)= Ker(A^* - \overline {\lambda } I)\), using (2.20) and noticing that the operators are closed. Let us apply the argument used above to show that Ker(A) = Ker(A ∗) on A − λI and \(A^*- \overline {\lambda }I\): then ||(A − λI)x|| = 0 if and only if \(||(A^*- \overline {\lambda }I)x||=0\), furnishing (ii). The proof of (iii) \(\sigma _c(A)= \overline {\sigma _c(A^*)}\) is more involved. Suppose λ ∈ σ c(A), so Ker(A − λI) is trivial—also \(Ker(A^*-\overline {\lambda } I)\) is trivial and \((A^*-\overline {\lambda }I)^{-1}\) exists—and the inverse (A − λI)−1 is an element of \({\mathfrak B}({\mathsf H})\) due to Proposition 3.5 since normal operators are closed by definition. From (A − λI)−1(A − λI) = I|D(A), using (2.8), we have \((A^*-\overline {\lambda } I) (A-\lambda I)^{-1*} = I|{ }^*_{D(A)} = I\). In particular \((A^*-\overline {\lambda } I) (A-\lambda I)^{-1*}|{ }_{Ran(A^*-\overline {\lambda } I)} = I|{ }_{Ran(A^*-\overline {\lambda } I)}\). Since we know that \((A^*-\overline {\lambda } I)\) is a bijection from D(A ∗) to \(Ran(A^*-\overline {\lambda } I)\), we conclude
$$\displaystyle \begin{aligned}(A-\lambda I)^{-1*}|{}_{Ran(A^*-\overline{\lambda} I)} = (A^*-\overline{\lambda} I)^{-1}\end{aligned}$$because inverses are unique. In particular, the right-hand side is bounded since the left-hand side is bounded. Hence λ ∈ σ c(A) implies \(\overline {\lambda } \in \sigma _c(A^*)\). We may replicate the argument starting from A ∗ and observe that \((A^*-\overline {\lambda }I)^*= A-\lambda I\) to conclude that \(\overline {\lambda } \in \sigma _c(A^*)\) implies \(\lambda = \overline {\overline {\lambda }} \in \sigma _c(A)\). This ends the proof of (iii).
-
(d)
If λ ≠ μ and Au = λu, Av = μv, then μ〈u|v〉 = 〈u|Av〉 = 〈A ∗ u|v〉 = λ〈u|v〉, so (μ − λ)〈u|v〉 = 0. The latter is only possible for 〈u|v〉 = 0 because μ − λ ≠ 0.
□
Example 3.14
The m-axis position operator X m on \(L^2({\mathbb R}^n, d^nx)\), introduced in Example 2.59 (1), satisfies
The arguments is as follows. First observe that \(\sigma (X_m) \subset {\mathbb R}\) since the operator is selfadjoint (Proposition 3.13). However we saw in Sect. 1.3 that \(\sigma _p(X_m) = \varnothing \), and \(\sigma _r(X_m)= \varnothing \) again by selfadjointness (Proposition 3.13). Let us examine when a number \(r\in {\mathbb R}\) belongs to ρ(X m). If no \(r\in {\mathbb R}\) belongs to ρ(X m), we must conclude that \(\sigma (X_m)=\sigma _c(X_m)= {\mathbb R}\).
Suppose that, for some \(r\in {\mathbb R}\), (X m − rI)−1 exists and is bounded. If ψ ∈ D(X m − rI) = D(X m) with ||ψ|| = 1 then ||ψ|| = ||(X m − rI)−1(X m − rI)ψ||, and hence ||ψ||≤||(X m − rI)−1|| ||(X m − rI)ψ||. Therefore ||(X m − rI)−1||≥||(X m − rI)ψ||−1. For every given 𝜖 > 0, it is easy to manufacture ψ ∈ D(X m) with ||ψ|| = 1 and ||(X m − rI)ψ|| < 𝜖. Assuming m = 1, it suffices to consider sets of the form \([r-1/k, r+1/k] \times {\mathbb R}^{n-1}\) and functions \(\psi _k \in C_c^\infty ({\mathbb R}^n, {\mathbb C})\) such that \(\mbox{supp}(\psi _k) \subset [r-1/k, r+1/k] \times {\mathbb R}^{n-1}\) and \(\int _{{\mathbb R}^n} |\psi _k|{ }^2 d^nx =1\). As k → +∞
Therefore (X m − rI)−1 cannot be bounded and r ∈ σ(X m). More precisely r ∈ σ c(X m), since no other possibility is allowed.
By Proposition 3.4 we also conclude that
simply because the momentum operator P m is related to the position operator by means of a unitary operator, namely the Fourier-Plancherel operator \(\hat {\mathcal {F}}\) of Example 2.59 (2). \(\blacksquare \)
3.2 Integration of Projector-Valued Measures
We introduce in this section the most important technical tool in spectral theory, the notion of projector-valued measure, whose repercussions in the interpretation of quantum theories are paramount. Before we do it, let us prove a few important and elementary facts concerning orthogonal projectors.
3.2.1 Orthogonal Projectors
Definition 3.15
Let H be a Hilbert space. An operator \(P \in {\mathfrak B}({\mathsf H})\) is called an orthogonal projector when PP = P and P ∗ = P. The set of orthogonal projectors of H is denoted by \({\mathcal {L}}({\mathsf H})\). \(\blacksquare \)
A well-known relation exists between orthogonal projectors and closed subspaces.
Proposition 3.16
Let H be a Hilbert space with orthogonal projectors \(\mathcal {L}({\mathsf H})\) . Then
-
(a)
if \(P \in {\mathcal {L}}({\mathsf H})\) , then P(H) is a closed subspace.
-
(b)
If \(P \in {\mathcal {L}}({\mathsf H})\) , then \(Q:= I-P \in \mathcal {L}({\mathsf H})\) and Q(H) = P(H)⊥.
-
(c)
There is an orthogonal sum H = P(H) ⊕ Q(H), so any z ∈H decomposes uniquely as z = x + y with x = P(z) ∈ P(H), y = Q(z) ∈ Q(H).
-
(d)
If H 0 ⊂H is a closed subspace, there exists exactly one \(P \in {\mathcal {L}}({\mathsf H})\) that projects H onto H 0 , i.e. P(H) = H 0.
Proof
-
(a)
It is clear that P(H) is a subspace. It is also closed because, if x =limn→+∞ Px n, then x = Px. Indeed, Px = Plimn→+∞ P(x n) =limn→+∞ PPx n =limn→+∞ Px n = x since P is continuous.
-
(b)
We have (I − P)∗ = I ∗− P ∗ = I − P and (I − P)(I − P) = I − 2P + PP = I − 2P + P = I − P, so \(Q:= I-P \in \mathcal {L}({\mathsf H})\). Let us prove that Q(H) = P(H)⊥. First of all, observe that y ∈ Q(H) and x ∈ P(H) yield 〈y|x〉 = 〈(I−P)y|Px〉 = 〈y|(I−P)Px〉 = 〈y|(P−PP)x〉 = 〈y|(P−P)x〉 = 0. Therefore Q(H) ⊂ P(H)⊥. To conclude, we have to prove that Q(H) ⊃ P(H)⊥. If y ∈ P(H)⊥ we have 〈Py|u〉 = 〈y|Pu〉 = 0 for u ∈H and therefore Py = 0. As a consequence, if we define z = y + x with x ∈ P(H), we obtain Qz = (I−P)y+(I−P)x = x+y−Py−Px = z−Py−Px = z−0−x = y. In other words, if y ∈ P(H)⊥, then y ∈ Q(H), proving Q(H) ⊃ P(H)⊥.
(d) and (c). Consider a closed subspace H 0. It is a Hilbert space in its own right since it contains the limits of its Cauchy sequences (which converge in H since H is Hilbert). Therefore H 0 admits a Hilbert basis N. It is easy to prove that if N′ is a Hilbert basis of \({\mathsf H}_0^\perp \), then N ∪ N′ is a Hilbert basis of H. By taking M = H 0, so that \(\overline {\mbox{span}\: M}= {\mathsf H}_0\), in (2.3) we obtain the orthogonal sum \({\mathsf H} = {\mathsf H}_0 \oplus {\mathsf H}_0^\perp \). Consider the operator Px :=∑z ∈ N〈z|x〉z for x ∈H. Using the Hilbert decomposition \(u = \sum _{z\in N\cup N'} \langle z|u \rangle z\), one immediately proves that ||P||≤ 1, PP = P, 〈Px|y〉 = 〈x|Py〉 and hence P = P ∗, so \(P\in \mathcal {L}({\mathsf H})\). Finally, P(H) = H 0 since N is a Hilbert basis of H 0.
Let us demonstrate that the orthogonal projector P satisfying P(H) = H 0 is uniquely determined by H 0. The same proof also establishes (c). Since P(H) ∩ Q(H) = {0}, because the subspaces are mutually orthogonal and I = P + Q, we conclude that z ∈H can be decomposed uniquely as z = x + y with x ∈ P(H) and y ∈ Q(H) and x = Pz, y = Qz. This fact proves that a P with P(H) = H 0 is unique: if P′(H) = H 0, we would have that Q′ := I − P′ projects onto \({\mathsf H}_0^\perp \) and z ∈H is uniquely decomposed as z = x + y with x ∈H 0, \(y\in {\mathsf H}_0^\perp \) where x = Pz = P′z and y = Qz = Q′z. Hence P′z = Pz for all z ∈H.
□
If \(P\in \mathcal {L}({\mathsf H})\), then P and Q := I − P project onto mutually orthogonal subspaces, and PQ = QP = 0. This fact is rather general, according to the next elementary result.
Proposition 3.17
Let H be a Hilbert space. Two projectors \(P,Q \in \mathcal {L}({\mathsf H})\) project onto orthogonal subspaces if and only if PQ = 0. In this case QP = 0 as well.
Proof
If P(H) ⊥ Q(H) then for every x, y ∈H we have 0 = 〈Px|Qy〉 = 〈x|PQy〉. Therefore PQ = 0. Taking adjoints we obtain QP = 0. If conversely PQ = 0, from the identity above we have 〈Px|Qy〉 = 0 for every x, y ∈H, so that P(H) ⊥ Q(H). □
Let us prove further properties of orthogonal projectors related with a natural order relation, which will play a crucial role in the next chapter.
Notation 3.18
Referring to Proposition 3.16, if \(P,Q \in {\mathcal {L}}({\mathsf H})\) we write P ≥ Q whenever P(H) ⊃ Q(H). \(\blacksquare \)
Proposition 3.19
If H is a Hilbert space and \(P,Q \in \mathcal {L}({\mathsf H})\) ,
-
(a)
P ≥ Q is equivalent to PQ = Q. In this case QP = Q too.
-
(b)
P ≥ Q is equivalent to 〈x|Px〉≥〈x|Qx〉 for every x ∈H.
Proof
-
(a)
If P(H) ⊃ Q(H), there exists a Hilbert basis \(N_P = N_Q\cup N^{\prime }_Q\) of P(H) where \(N_Q, N^{\prime }_Q\) are a Hilbert bases of \(Q({\mathsf H}), Q({\mathsf H})^{\perp _P}\) (orthogonality referring to P(H)). From \(Q= \sum _{z \in N_Q} \langle z|\cdot \rangle z\) and \(P= Q+\sum _{z \in N^{\prime }_Q} \langle z|\cdot \rangle z\) we have PQ = Q. The converse implication is obvious. Assume PQ = Q. If x ∈ Q(H) then Qx = x. Therefore Px = PQx = Qx = x, hence x ∈ P(H) and then Q(H) ⊂ P(H) as wanted. Finally, taking adjoints on PQ = Q we obtain QP = Q since P and Q are selfadjoint.
-
(b)
Assume P ≥ Q, i.e. Q(H) ⊂ P(H). If x ∈H, the vector Px ∈ P(H) decomposes as y + z where y := QPx ∈ Q(H) and z ∈ P(H) is orthogonal to y. Therefore ||Px||2 = ||QPx||2 + ||z||2. From (a), ||Px||2 = ||Qx||2 + ||z||2 which implies ||Px||2 ≥||Qx||2, namely 〈x|Px〉≥〈x|Qx〉 for every x ∈H. Conversely, if 〈x|Px〉≥〈x|Qx〉 for every x ∈H, then ||Px||2 ≥||Qx||2 for every x ∈H, so that Px = 0 implies Qx = 0 for every x ∈H. In other words P(H)⊥⊂ Q(H)⊥. Applying ⊥ again, we eventually get P(H) ⊃ Q(H).
□
Proposition 3.20
If H is a Hilbert space and \(\{P_n\}_{n\in {\mathbb N}} \in \mathcal {L}({\mathsf H})\) is a sequence such that either (i) P n ≤ P n+1 for all \(n \in {\mathbb N}\) or (ii) P n ≥ P n+1 for all \(n \in {\mathbb N}\) , then P n x → Px, for every x ∈H and some \(P \in \mathcal {L}({\mathsf H})\) , as n → +∞.
Proof
Assume P n ≤ P n+1 for all \(n \in {\mathbb N}\). For any x ∈H, the sequence \(\{P_nx\}_{n\in {\mathbb N}}\) is Cauchy. Indeed, for n > m and using Proposition 3.19 (a) alongside the selfadjointness and idempotence of orthogonal projectors, ||P n x − P m x||2 equals
Since the sequence of numbers ||P n x||2 = 〈x|P n x〉 is non-decreasing and bounded by ||x||2, it converges to some real number and hence it is a Cauchy sequence. This implies that \(\{P_nx\}_{n\in {\mathbb N}}\) is Cauchy as well. The map P : H ∋ x↦limn→+∞ P n x ∈H is linear by construction. Furthermore, 〈Px|y〉 = 〈x|Py〉 for every x, y ∈H by continuity of the inner product, so P = P ∗. Finally, for every x, y ∈H we also have 〈Px|Py〉 =limn→+∞〈P n x|P n y〉 =limn→+∞〈x|P n y〉 = 〈x|Py〉, so that PP = P and therefore \(P\in \mathcal {L}({\mathsf H})\). The other case’s proof is identical up to trivial changes. □
3.2.2 Projector-Valued Measures (PVMs)
At this juncture we can state one of the most important definitions in spectral theory.
Definition 3.21
Let H be a Hilbert space and Σ(X) a σ-algebra on X. A projector-valued measure (PVM) on X is a map \(P: \Sigma (X) \ni E \mapsto P_E \in {\mathcal {L}}({\mathsf H})\) such that
-
(i)
P X = I,
-
(ii)
P E P F = P E∩F,
-
(iii)
if \(N \subset {\mathbb N}\) and {E k}k ∈ N ⊂ Σ(X) satisfies \(E_j \cap E_k = \varnothing \) for k ≠ j, then
$$\displaystyle \begin{aligned}\sum_{j \in N} P_{E_j}x= P_{\cup_{j\in N}E_j}x \quad \mbox{for every}\ x\in {\mathsf H}.\end{aligned} $$
We say that P is concentrated on S ∈ σ(X) if P E = P E∩S for every E ∈ Σ(X). \(\blacksquare \)
Remark 3.22
-
(a)
Taking N = {1, 2} in (i) and (iii) tells that \(P_\varnothing =0\), using E 1 = X and \(E_2 = \varnothing \). Property (ii) entails that P E P F = 0 if \(E\cap F=\varnothing \) from Proposition 3.17. In particular, the vectors \(P_{E_j}x\) in (iii) are orthogonal. Therefore a series (for \(N={\mathbb N}\))
$$\displaystyle \begin{aligned} \begin{array}{rcl} \sum_{j \in {\mathbb N}} P_{E_j}x \:, {}\vspace{-3pt}\end{array} \end{aligned} $$(3.7)where \(E_j \cap E_k = \varnothing \) for k ≠ j, always converges. An alternative argument for convergence is to invoke Proposition 3.20, since the operators \(\sum _{j=0}^n P_{E_j}\) are orthogonal projectors and \(\sum _{j=0}^n P_{E_j} \leq \sum _{j=0}^{n+1} P_{E_j}\). (Series (3.7) can be rearranged because by Bessel’s inequality (2.1.2) we have
$$\displaystyle \begin{aligned}\sum_{j \in {\mathbb N}} ||P_{E_j}x||{}^2 \leq \sum_{j \in N} \sum_{u\in M_j} |\langle u| x\rangle|{}^2 < +\infty,\end{aligned}$$where \(M_j \subset P_{E_j}({\mathsf H})\) is a Hilbert basis of \(P_{E_j}({\mathsf H})\). Now Lemma 2.8 guarantees (3.7) converges and can be rearranged.) Proving explicitly that the series converges is nonetheless a useful exercise. For a given 𝜖 > 0, we use the inner product’s continuity and the fact that \( P_{E_j}x \perp P_{E_k}x\) if j ≠ k, to compute, for m > n > N 𝜖,
$$\displaystyle \begin{aligned}\begin{aligned}\left|\left|\sum_{j=0}^m P_{E_j}x- \sum_{j=0}^{n-1} P_{E_j}x\right|\right|{}^2 &= \left|\left| \sum_{j=n}^{j=m} P_{E_j}x \right|\right|{}^2= \left\langle \sum_{j=n}^{j=m} P_{E_j}x\left| \sum_{k=n}^{k=m} P_{E_k}x\right. \right\rangle\\ &= \sum_{j=n}^{j=m}\left\langle P_{E_j}x\left| \sum_{k=n}^{k=m} P_{E_k}x\right. \right\rangle \end{aligned}\end{aligned}$$$$\displaystyle \begin{aligned}=\sum_{j=n}^{j=m}\left\langle x\left| P_{E_j}\sum_{k=n}^{k=m} P_{E_k}x\right. \right\rangle =\sum_{j=n}^{j=m}\left\langle x\left| \sum_{k=n}^{k=m} P_{E_j}P_{E_k}x\right. \right\rangle = \sum_{j=n}^{j=m}\left\langle x\left| \sum_{k=n}^{k=m} \delta_{jk} P_{E_k}x\right. \right\rangle\end{aligned}$$$$\displaystyle \begin{aligned}= \sum_{j=n}^{j=m}\left\langle x\left| P_{E_j}x\right. \right\rangle = \sum_{j=n}^{j=m}\left\langle x\left| P_{E_j} P_{E_j}x\right. \right\rangle = \sum_{j=n}^{j=m}\left\langle P_{E_j} x\left| P_{E_j}x\right. \right\rangle =\sum_{j=n}^{j=m} ||P_{E_j}x ||{}^2 <\epsilon.\end{aligned}$$Hence (3.7) converges, as truncated sums form a Cauchy sequence.
In summary, (iii) can be viewed as a condition on the value of the sum of the series and not an assumption about its convergence.
-
(b)
If x, y ∈H, \(\Sigma (X) \ni E \mapsto \langle x|P_Ey\rangle =: \mu ^{(P)}_{xy}(E)\) is a complex measure whose (finite) total variation [Rud91] will be denoted by \(|\mu ^{(P)}_{xy}|\). This follows from the definition of PVM, in particular the inner product’s continuity implying σ-additivity: if the sets E n ⊂ Σ(X), \(n\in N \subset {\mathbb N}\), are pairwise disjoint (\(E_n\cap E_m= \varnothing \) for n ≠ m),
$$\displaystyle \begin{aligned}\mu^{(P)}_{xy}\left( \cup_{n\in N} E_n\right) = \left\langle x \left| P_{\cup_{n\in N}E_n} y \right. \right\rangle = \left\langle x \left| \sum_{n\in N}P_{E_n} y \right. \right\rangle =\sum_{n\in N} \left\langle x \left| P_{E_n} y \right. \right\rangle = \sum_{n\in N} \mu^{(P)}_{xy}(E_n)\:.\end{aligned}$$The definition of μ xy gives us immediately three important facts.
-
(i)
\(\mu ^{(P)}_{xy}(X)= \langle x| y \rangle \).
-
(ii)
\(\mu ^{(P)}_{xx}\) is always positive and finite, and \(\mu ^{(P)}_{xx}(X)= ||x||{ }^2\).
-
(iii)
Consider a simple function [Rud91] \(s = \sum _{k=1}^n s_k \chi _{E_k}\), where \(s_k \in {\mathbb C}\) and the sets E k ∈ Σ(X), k = 1, …, n, are pairwise disjoint, and χ E is the characteristic function of the set E, i.e. the map χ E(x) = 0 if x∉E and χ E(x) = 1 if x ∈ E. If h denotes the Radon–Nikodym derivative of μ xy with respect to its total variation |μ xy| (see, e.g., [Mor18]), we have
$$\displaystyle \begin{aligned}\begin{aligned} \int_X s d\mu_{xy} &= \int_X s h d|\mu_{xy}| = \sum_{k=1}^n s_k \int_{E_k} h d|\mu_{xy}| = \sum_{k=1}^n s_k \mu_{xy}(E_k)\\ &= \left\langle x\left| \sum_{k=1}^n s_k P_{E_k} y\right.\right\rangle\:. \end{aligned}\end{aligned}$$If we define
$$\displaystyle \begin{aligned} \int_X s(\lambda) dP(\lambda) := \sum_{k=1}^n s_k P_{E_k}\:\end{aligned}$$we may then write
$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_X s d\mu_{xy} = \left\langle x\left| \int_X s(\lambda) dP(\lambda)\right. y\right\rangle\:.{}\end{array} \end{aligned} $$(3.8)
The entire machinery of Spectral Theory and Measurable Functional Calculus is contingent on formula (3.8) (extended from simple functions s to general measurable functions f). \(\blacksquare \)
-
(i)
Example 3.23
-
(1)
The simplest example of a PVM arises from a Hilbert basis N in a Hilbert space H. Let Σ(N) be the power set of N. For E ∈ Σ(N) and z ∈H we define
$$\displaystyle \begin{aligned}P_{E}z := \sum_{x\in E} \langle x| z\rangle x\end{aligned}$$and \(P_{\varnothing }:=0\). It is easy to prove that the collection of P E thus defined forms a PVM on N. (This definition works even if H is not separable and N is uncountable, since for every y ∈H at most countably many elements x ∈ E satisfy 〈x|y〉≠ 0). Observe that P N x =∑u ∈ N〈u|x〉u = x for every x ∈H, so that P N = I as required.
In particular \(\mu ^{(P)}_{xy}(E) = \langle x|P_Ey \rangle = \sum _{z\in E} \langle x|z\rangle \langle z | y \rangle \) and \(\mu ^{(P)}_{xx}(E) = \sum _{z\in E}|\langle x| z \rangle |{ }^2\).
-
(2)
A more sophisticated version of (1) is built out of the Hilbert sum of a family of non-trivial, pairwise-orthogonal closed subspaces {H j}j ∈ J of a Hilbert space H =⊕j ∈ J H j. Defining once again Σ(J) as the family of subsets of J, for E ∈ Σ(J) and z ∈H we set \(P_\varnothing = 0\) and
$$\displaystyle \begin{aligned}P_{E}z := \sum_{j\in E} Q_jz\:,\end{aligned}$$where Q j is the orthogonal projector onto H j. It is easy to prove that the P E form a PVM on \({\mathbb N}\). Since ⊕j ∈ J H j = H we have ∑j ∈ J Q j x = x for every x ∈H, so P J = I as requested.
In particular \(\mu ^{(P)}_{xy}(E) = \langle x|P_Ey \rangle = \sum _{j\in E} \langle x|Q_j y \rangle \) and \(\mu ^{(P)}_{xx}(E) = \sum _{j\in E}||Q_j x||{ }^2\).
The reader can prove without difficulty that
$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_{J}f(j) d\mu_{xx}(j) =\sum_{j\in J} f(j) ||Q_j x||{}^2 {} \end{array} \end{aligned} $$(3.9)if f is μ xx-integrable. This formula is trivial for simple functions, and extends easily to general maps using dominated convergence.
-
(3)
Here is a PVM of a completely different sort, this time on \(L^2(\mathbb R^n, d^nx)\). To every E in the Borel σ-algebra \({\mathcal {B}}({\mathbb R}^n)\) associate the orthonormal projector
$$\displaystyle \begin{aligned}(P_E\psi)(x) := \chi_E(x)\psi(x)\quad \forall \psi \in L^2({\mathbb R}^n, d^nx)\:.\end{aligned}$$Note \(P_{\varnothing }:=0\). It is easy to prove that the collection of P E is a PVM. In particular \(\mu ^{(P)}_{fg}(E) = \langle f|P_Eg \rangle = \int _{E}\overline {f(x)}g(x) d^nx\) and \(\mu ^{(P)}_{ff}(E) = \int _E |f(x)|{ }^2 d^nx\).
The reader can easily check that
$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_{{\mathbb R}^n} f(x) d\mu_{gg}(x) = \int_{{\mathbb R}^n} f(x) |g(x)|{}^2 d^nx {} \end{array} \end{aligned} $$(3.10)if f is μ gg-integrable. This is trivial for simple functions, and can be generalized easily to measurable functions using the theorem of dominated convergence. \(\blacksquare \)
The following pivotal result [Rud91, Mor18, Schm12] generalizes (3.8) from simple functions to measurable functions of a suitable type.
Theorem 3.24
Let H be a Hilbert space, \(P: \Sigma (X) \to {\mathcal {L}}({\mathsf H})\) a PVM, and \(f: X \to {\mathbb C}\) a measurable function. Define
The following facts hold.
-
(a)
Δ f is a dense subspace in H and there exists a unique operator
$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_X f(\lambda) dP(\lambda) : \Delta_f \to {\mathsf H} \: {}\end{array} \end{aligned} $$(3.11)such that
$$\displaystyle \begin{aligned} \begin{array}{rcl} \left\langle x \left| \int_X f(\lambda) dP(\lambda) y \right.\right\rangle = \int_{X} f(\lambda) d\mu^{(P)}_{xy}(\lambda)\quad \forall x \in {\mathsf H} \:, \forall y \in \Delta_f {}\:.\end{array} \end{aligned} $$(3.12) -
(b)
The operator in (3.11) is closed and normal.
-
(c)
The adjoint operator to (3.11) satisfies
$$\displaystyle \begin{aligned} \begin{array}{rcl} \left(\int_X f(\lambda)\: d P(\lambda)\right)^* = \int_X \overline{f(\lambda)}\: d P(\lambda) {}\:. \end{array} \end{aligned} $$(3.13) -
(d)
The operator in (3.11) satisfies
$$\displaystyle \begin{aligned} \begin{array}{rcl} \left|\left| \int_X f(\lambda)\: d P(\lambda) x\right|\right|{}^2 = \int_X |f(\lambda)|{}^2 d \mu^{(P)}_{xx}(\lambda) \quad \forall x \in \Delta_f \:.{}\end{array} \end{aligned} $$(3.14)
Proof (I. Existence and Uniqueness)
We start by proving that if Δf is subspace of H, then there is a unique operator denoted by ∫X f(λ)dP(λ) satisfying (3.12). The proof of this fact relies on this preliminary lemma.
Lemma 3.25
If \(f: X \to {\mathbb C}\) is measurable, then
Proof
We henceforth write μ xy in place of \(\mu ^{(P)}_{xy}\) for the sake of shortness. The idea is initially to establish the inequality for simple functions and then pass to arbitrary functions. Take x ∈H and y ∈ Δf. Let \(s: X \to {\mathbb C}\) be a simple function, \(h: X \to {\mathbb C}\) the Radon–Nikodym derivative of μ xy with respect to |μ xy|, so that |h(x)| = 1 and μ xy(E) =∫E hd|μ xy|. For an increasing sequence of simple functions z n such that z n → h −1 pointwise, with |z n|≤|h −1| = 1, by the dominated convergence theorem we have
In the last step we used part (iii) in Remark 3.22 (b) for the simple function
and we have supposed that, for fixed n, the sets E n,k are disjoint from one another. The Cauchy–Schwartz inequality immediately yields
where, in computing the norm, we used \(P_{E_{n,k}}^*P_{E_{n,k'}} = P_{E_{n,k}}P_{E_{n,k'}}= \delta _{kk'}P_{E_{n,k}}\) since \(E_{n,k} \cap E_{n,k'}= \varnothing \) for k ≠ k′. Next observe that as |sz n|2 →|sh −1|2 = |s|2, dominated convergence yields
At last, replace s above by a sequence of simple functions s n → f ∈ L 2(X, dμ yy) pointwise, with |s n|≤|s n+1|≤|f|. The monotone convergence theorem and the dominated convergence theorem, applied respectively to the left- and right-hand side of the previous inequality, eventually produce (3.15). □
To proceed with the main proof we notice that inequality (3.15) also proves that \(f \in L^2(X, d\mu ^{(P)}_{yy})\) implies \(f \in L^1(X, d|\mu ^{(P)}_{xy}|)\) for x ∈H, hence the right-hand side of (3.12) makes sense. General measure theory guarantees that
whence (3.15) implies that \({\mathsf H} \ni x \mapsto \int _X f(\lambda )\: d \mu ^{(P)}_{xy}(\lambda )\) is continuous at x = 0. This map is also anti-linear if f is simple, as follows from the definition of μ xy and the left anti-linearity of the inner product. Anti-linearity extends to measurable functions f via the usual approximation procedure of measurable functions by simple functions. We conclude that, for y ∈ Δf, the map
is linear and continuous. Riesz’s Lemma guarantees the existence of a unique vector, indicated by ∫X f(λ)dP(λ)y, satisfying
Conjugating both sides we obtain (3.12). As we have assumed Δf is a subspace, the map
is linear when f is simple, as immediately follows from the definition of \(\mu ^{(P)}_{xy}\) and the right linearity of the inner product. As before, linearity extends to measurable functions f by approximating measurable functions with simple maps. As a consequence of (3.12)
is linear as well. The uniqueness of this operator is an immediate consequence of the uniqueness in Riesz’s Lemma.
(II. Δf is a Dense Subspace)
Let us show that Δf is a subspace first. It contains 0 so it is not empty. Moreover, directly by definition of Δf, it is clear that if x ∈ Δf, then ax ∈ Δf for every \(a\in {\mathbb C}\), because \(\mu ^{(P)}_{ax,ax}(E)= |a|{ }^2 \mu ^{(P)}_{xx}(E)\) independently of E and so
Next suppose that x, y ∈ Δf. We therefore have ||P E(x + y)||2 ≤ (||P E x|| + ||P E y||)2 ≤ 2||P E x||2 + 2||P E y||2. As a consequence \(\mu ^{(P)}_{x+y,x+y}(E) = ||P_E(x+y)||{ }^2 \leq 2\mu ^{(P)}_{xx}(E) + 2 \mu ^{(P)}_{yy}(E)\). Therefore
and hence x + y ∈ Δf. Let us pass to the density of Δf. Consider the countable partition of X made by measurable sets F n := {λ ∈ X | n ≤|f(λ)|2 < n + 1}, for n = 0, 1, 2, …. By the σ-additivity of P, if z ∈ H then \(z =P_Xz = \sum _{n=0}^{+\infty } P_{F_n}z\). Therefore the span of the unions of closed subspaces \({\mathsf H}_n := P_{F_n}({\mathsf H})\) is dense in H. If we prove that H n ⊂ Δf for every n, since Δf is a subspace, we immediately infer that it is dense. Let us prove it. If x ∈ H n, then \(x=P_{F_n}x\) and therefore \(\mu ^{(P)}_{xx}(E)= \langle P_{F_n}x|P_E P_{F_n}x\rangle = \langle x| P_{E\cap F_n}x \rangle = \mu ^{(P)}_{xx}(E\cap F_n)\). Since
we have x ∈ Δf, as wanted.
(III. Proof of Eq. (3.14))
For x ∈ Δf, using (3.12), we obtain
where
Since \(\mu ^{(P)}_{P_Ex,x}(F) = \langle P_Ex|P_F x \rangle = \langle x|P_{E\cap F}x \rangle \), we have
Using the definition of integral (of a complex measure), it immediately follows
for a simple function s. A standard argument based of dominated convergence (take a sequence of simple maps s n tending to f pointwise, with |s n|≤|f|) allows to establish
as |f|2 is μ xx-integrable. Inserting this result in (3.16) we obtain (3.14), as claimed.
(IV. Proof of Eq. (3.13) and the Closure of ∫XfdP)
Since the adjoint is always closed, Eq. (3.13) and \(\int _X fdP = (\int _X \overline {f}dP)^*\) would imply ∫X fdP is closed. So let us prove Eq. (3.13). From (3.12) it is easy to see that \(\int _X \overline {f} dP \subset (\int _X \overline {f} dP )^*\): noticing that \(\mu ^{(P)}_{yx}(E) = \overline {\mu ^{(P)}_{xy}(E)}\), namely, if x, y ∈ Δf then
Therefore we only have to prove that \(\int _X \overline {f} dP \supset (\int _X \overline {f} dP )^*\). This is equivalent to show that if \(y\in D( (\int _X \overline {f} dP )^*)\) then \(y\in \Delta _{\overline {f}}= \Delta _f\). So let us prove this then, for which we need an intermediate result.
Lemma 3.26
Under the assumptions of Theorem 3.24
-
(i)
∫X χ E dP = P E for every E ∈ Σ(X)
-
(ii)
∫X fdPP E =∫X f ⋅ χ E dP for every E ∈ Σ(X)
-
(iii)
if f is bounded on E ∈ Σ(X) then \((\int _X f \cdot \chi _E dP)^*= \int _X \overline {f} \cdot \chi _E dP\).
Proof (i) is true since \(\langle x|P_Ey \rangle = \mu _{xy}(E) = \int _E1 d\mu _{xy}^{(P)}\), and so (3.12) holds and uniquely determines ∫X χ E dP.
Concerning (ii), the domain of ∫X fdPP E consists of the x ∈H such that P E x ∈ Δf, that is \(\int _X |f|{ }^2 d\mu ^{(P)}_{P_Ex,P_Ex}<+\infty \). Since \(\mu ^{(P)}_{P_Ex,P_Ex}(F) = \langle P_Ex|P_FP_Ex\rangle = \langle x|P_{E\cap F}x\rangle = \mu ^{(P)}_{xx}(E\cap F)\), the condition can be rephrased as \(\int _X \chi _E \cdot |f|{ }^2 d\mu ^{(P)}_{xx}<+\infty \), or \(\int _X |\chi _E \cdot f|{ }^2 d\mu ^{(P)}_{xx}<+\infty \). Therefore ∫X fdPP E and ∫X χ E ⋅ fdP have the same domain. If x ∈H and y ∈ Δχ⋅f, \(\langle x| \int _XfdP P_E y \rangle = \int _X f d\mu ^{(P)}_{x,P_Ey} = \int _X f d\mu ^{(P)}_{P_Ex,P_Ey} = \int _E f d\mu ^{(P)}_{x,y} = \int _E f\cdot \chi _E d\mu ^{(P)}_{x,y}\), which implies ∫X fdPP E =∫X f ⋅ χ E dP again by (3.12).
(iii) is true because \(\Delta _{f\cdot \chi _E}={\mathsf H}\) and \(\int _X \overline {f} \cdot \chi _E dP\in {\mathfrak B}({\mathsf H})\) from (3.14). Hence replacing f with f ⋅ χ E in (3.17) ensures that \(\int _X \overline {f \cdot \chi _E} dP =\int _X \overline {f} \cdot \chi _E dP\) is the adjoint of ∫X f ⋅ χ E dP. □ To resume part IV of the main theorem, we claim (i), (ii), and (iii) imply \(y\in \Delta _{\overline {f}}\) if \(y\in D( (\int _X \overline {f} dP )^*)\). We start by defining E n := {λ ∈ X | |f(λ)| < n}. Then from (i)–(iii) we have
Hence if \(y\in D( (\int _X \overline {f} dP )^*)\) we infer
and so
Using (3.14),
Since \(|\overline {f} \cdot \chi _{E_n}|{ }^2\leq |\overline {f} \cdot \chi _{E_{n+1}}|{ }^2 \to |\overline {f}|{ }^2\) as n → +∞, the monotone convergence theorem implies
that is to say \(y\in \Delta _{\overline {f}}\), as wanted.
(V. Proof that ∫XfdP is Normal)
The same argument used in the previous lemma to establish (ii) gives P E∫X fdPx =∫X χ E ⋅ fdPx if x ∈ Δf. Consider the domain of \(\int _X \overline {f}dP\int _X fdP\). It consists of vectors x ∈ Δf such that
Let us write this condition in a simpler way. First observe that
Starting from simple functions and generalizing to measurable functions, it is therefore easy to prove that
In summary, (3.18) reads
Now replace f by |f|2 in the first statement of the theorem we are proving: that domain is dense and \(D(\int _X \overline {f}dP\int _X fdP)=D(\int _X fdP\int _X \overline {f}dP)\). To finish the proof consider \(x \in D(\int _X \overline {f}dP\int _X fdP)=D(\int _X fdP\int _X \overline {f}dP)\). We have
In other words
By polarization we finally obtain
for every \(x,y \in D(\int _X \overline {f}dP\int _X fdP)=D(\int _X fdP\int _X \overline {f}dP)\). Since this domain is dense, \(\int _X fdP\int _X \overline {f}dP - \int _X \overline {f}dP\int _X fdP=0\), and the proof ends.
□
The theorem just proved has technically important consequences, which we list in the following corollary and the subsequent proposition.
Corollary 3.27
Under the hypotheses of Theorem 3.24 , the following hold.
-
(a)
If \(f : X \to {\mathbb C}\) only assumes non-negative real values, then
$$\displaystyle \begin{aligned}\left\langle x\left|\int_X f dP x \right. \right\rangle \geq 0 \quad \forall x \in \Delta_f\:.\end{aligned}$$ -
(b)
If T is an operator on H with D(T) = Δ f such that
$$\displaystyle \begin{aligned} \begin{array}{rcl} \left\langle x \left|T x \right.\right\rangle = \int_{X} f(\lambda) \: d\mu^{(P)}_{xx}(\lambda)\quad \forall x \in \Delta_f \:, {}\end{array} \end{aligned} $$(3.19)then
$$\displaystyle \begin{aligned}T= \int_{X} f(\lambda) dP(\lambda)\:.\end{aligned}$$
Proof
-
(a)
The proof is evident from (3.12), taking y = x and noticing that \(\mu _{xx}^{(P)}\) is positive.
-
(b)
From the definition of μ xy we easily have (for simplicity we omit the superscript (P))
$$\displaystyle \begin{aligned}4\mu_{xy}(E) = \mu_{x+y,x+y}(E) - \mu_{x-y,x-y}(E) -i \mu_{x+iy,x+iy}(E) +i \mu_{x-iy,x-iy}(E) \:.\end{aligned}$$This identity implies, by the definition of integral, that for a simple function
$$\displaystyle \begin{aligned} 4\int_X s d\mu_{xy} = \int_X s d\mu_{x+y,x+y} -\int_X s d\mu_{x-y,x-y} -i \int_X s d\mu_{x+iy.x+iy} +i\int_X s d\mu_{x-iy,x-iy}\end{aligned}$$if x, y ∈ Δs. The customary approximation of measurable functions f by simple functions (via dominated convergence) gives
$$\displaystyle \begin{aligned}\begin{aligned} 4\int_X f d\mu_{xy} &= \int_X f d\mu_{x+y,x+y} -\int_X f d\mu_{x-y,x-y} -i \int_X f d\mu_{x+iy.x+iy}\\ &+i\int_X f d\mu_{x-iy,x-iy} \end{aligned}\end{aligned}$$for x, y ∈ Δf. Similarly, by the elementary properties of the inner product
$$\displaystyle \begin{aligned}4\langle x|T y\rangle = \langle x+y|T(x+y)\rangle - \langle x-y|T(x-y)\rangle -i \langle x+iy|T(x+iy)\rangle +i \langle x-iy|T(x-iy)\rangle\:\end{aligned}$$when x, y ∈ D(T). Collecting everything, it is now obvious that (3.19) implies
$$\displaystyle \begin{aligned} \left\langle x \left|T y \right.\right\rangle = \int_{X} f(\lambda) \mu^{(P)}_{xy}(\lambda)\quad \forall x, y \in \Delta_f\:, \end{aligned}$$so
$$\displaystyle \begin{aligned}\left\langle x \left| \left( T- \int_{X} f(\lambda) dP(\lambda)\right)\right. y\right\rangle = 0 \quad \forall x, y \in \Delta_f\:.\end{aligned} $$Since x varies in a dense set Δf, we have that Ty −∫X f(λ)dP(λ)y = 0 for every y ∈ Δf, which is the claim.
□
Example 3.28
-
(1)
Consider the PVM of Example 3.23 (2). Using Corollary 3.27 (b) and (3.9) we have
$$\displaystyle \begin{aligned}\int_J f(\lambda) dP(\lambda)z = \sum_{n\in J} f(j) Q_jz \end{aligned} $$for every \(f: J \to {\mathbb C}\) (which is necessarily measurable with our definition of Σ(J)). Correspondingly, the domain of ∫J f(λ)dP(λ) is
$$\displaystyle \begin{aligned}\Delta_f := \left\{ z \in {\mathsf H} \:\left|\: \sum_{j\in J} |f(j)|{}^2 ||Q_jz||{}^2 < +\infty \right.\right\}\:.\end{aligned}$$According to Corollary 3.27 (b) in fact, from (3.10) we have
$$\displaystyle \begin{aligned}\left\langle z \left|\int_J f(j) dP(j) z\right. \right\rangle = \sum_{j\in J} f(j) ||Q_jz||{}^2= \int_{\mathbb R} f(j) d\mu_{zz} \:\end{aligned} $$for every z ∈ Δf.
-
(2)
Now take to PVM in Example 3.23 (3). By Corollary 3.27 (b) and (3.10)
$$\displaystyle \begin{aligned}\left(\int_{{\mathbb R}^n} f(\lambda) dP(\lambda) \psi\right)(x) = f(x) \psi(x)\:, \quad x \in {{\mathbb R}^n}\:.\end{aligned}$$Correspondingly, the domain of \(\int _{{\mathbb R}^n} f(\lambda ) dP(\lambda )\) turns out to be
$$\displaystyle \begin{aligned}\Delta_f := \left\{ \psi \in L^2({\mathbb R}^n, d^nx) \:\left|\: \int_{{\mathbb R}^n} |f(x)|{}^2 |\psi(x)|{}^2 d^nx < +\infty \right.\right\}\:.\end{aligned}$$In fact, for every ψ ∈ Δf, Corollary 3.27 (b) and (3.10) give
$$\displaystyle \begin{aligned}\left\langle \psi \left|\int_{{\mathbb R}^n} f(\lambda) dP(\lambda) \psi \right. \right\rangle =\int_{{\mathbb R}^n} f(x) |\psi(x)|{}^2 d^nx = \int_{{\mathbb R}^n} f d\mu_{\psi\psi} \:.\end{aligned}$$\(\blacksquare \)
3.2.3 PVM-Integration of Bounded Functions
We now state and prove a proposition about the most important properties of ∫X fdP when \(f: X \to {\mathbb C}\) is bounded or, more weakly, P-essentially bounded. Some of these have already been exploited in the proof of Theorem 3.24; however, they turn out to be so useful in the practice that they deserve a separate presentation.
If μ is a σ-additive positive measure on a σ-algebra Σ(X),
Since the integral sees only non-zero measure sets in Σ(X), for instance,
The same definition can be extended to PVMs:
and f is said to be P -essentially bounded if \(||f||{ }_\infty ^{(P)} < +\infty \).
Note that if P E = 0, then \(\mu _{xy}^{(P)}(E)=0\) for E ∈ Σ(X). Therefore a P-essentially bounded map f is also \(\mu _{xx}^{(P)}\)-essentially bounded for every x ∈ Δf. In particular, since zero-measure sets for P evidently have zero measure for \(\mu ^{(P)}_{xx}\) as well,
A seminorm \(p : X \to {\mathbb R}\) on a complex vector space X by definition satisfies p(x) ≥ 0, p(ax) = |a|p(x) and p(x + y) ≤ p(x) + p(y) for all x, y ∈ X and \(a \in {\mathbb C}\).
It is easy to prove that \(||\:||{ }_\infty ^{(P)}\) is a seminorm on the vector space of P-essentially bounded, measurable, complex-valued functions on X. Moreover, |f|≤|g| pointwise implies \(||f||{ }_\infty ^{(P)} \leq ||g||{ }_\infty ^{(P)}\) and \(||f\cdot g||{ }_\infty ^{(P)} \leq ||f||{ }_\infty ^{(P)}||g||{ }_\infty ^{(P)}\), where f ⋅ g is the pointwise product (f ⋅ g)(x) = f(x)g(x) for x ∈ X.
Proposition 3.29
Let \(P: \Sigma (X) \to \mathcal {L}({\mathsf H})\) be a PVM.
-
(a)
A map f is P-essentially bounded if and only if
$$\displaystyle \begin{aligned}\int_X f(\lambda)\: d P(\lambda) \in {\mathfrak B}({\mathsf H})\:.\end{aligned}$$In this case
$$\displaystyle \begin{aligned} \begin{array}{rcl} \left|\left|\int_X f(\lambda)\: d P(\lambda)\right|\right| \leq ||f||{}^{(P)}_\infty\leq ||f||{}_\infty\:.{}\end{array} \end{aligned} $$(3.21) -
(b)
We have
$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_X \chi_E\: d P= P_E \:, \quad \mathit{\mbox{if}}\ E \in \Sigma(X).{} \end{array} \end{aligned} $$(3.22)In particular,
$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_X 1 \: d P = I\:.{} \end{array} \end{aligned} $$(3.23)For a simple function \(s= \sum _{k=1}^n s_k \chi _{E_k}\) , where \(s_k \in {\mathbb C}\) and E k ∈ Σ(X), k = 1, …, n,
$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_X \sum_{k=1}^n s_k \chi_{E_k} d P = \sum_{k=1}^n s_k P_{E_k}\:.{} \end{array} \end{aligned} $$(3.24) -
(c)
Let \(f, f_n :X \to {\mathbb R}\) be measurable functions such that \(||f||{ }^{(P)}_\infty , ||f_n||{ }^{(P)}_\infty \leq K<+\infty \) for some \(K\in {\mathbb R}\) and every \(n\in {\mathbb N}\) . If f n → f pointwise as n → +∞, then
$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_X f_n dPx \to \int_X f dPx\quad \mathit{\mbox{as}}\ n \to +\infty,\ \mathit{\mbox{for every}}\ x\in {\mathsf H} {}\:. \end{array} \end{aligned} $$(3.25) -
(d)
If \(f,g : X \to {\mathbb C}\) are P-essentially bounded and \(a,b \in {\mathbb C}\) , then
$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_X (af + bg)\: dP = a\int_X f dP + b \int_X g dP\:, {}\end{array} \end{aligned} $$(3.26)$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_X f dP \int_X g dP = \int_X f\cdot g \:dP\:.{}\end{array} \end{aligned} $$(3.27)
Proof
-
(a)
Assume f is P-essentially bounded. Since μ xx(X) = ||x||2 < +∞ for every x ∈H,
$$\displaystyle \begin{aligned} \int_X |f(\lambda)|{}^2 d \mu^{(P)}_{xx}(\lambda) \leq (||f||{}_\infty^{(\mu^{(P)}_{xx})})^2 \int_X 1 d \mu^{(P)}_{xx} \leq (||f||{}_\infty^{(P)})^2 \int_X 1 d \mu^{(P)}_{xx} = ||x||{}^2\:(|f||{}_\infty^{(P)})^2\:,\end{aligned}$$so that Δf = H. Next, dividing by ||x||2 and taking the \(\sup \) over the elements x ≠ 0, (3.14) implies (3.21). If, instead, f is not P-essentially bounded, then for every \(n\in {\mathbb N}\), there is E n ∈ Σ(X) with \(P_{E_n} \neq 0\) and |f(λ)|≥ n if λ ∈ E n. Pick \(x_n \in P_{E_n}({\mathsf H})\) with ||x n|| = 1 for every \(n \in {\mathbb N}\). If x n∉ Δf for some n, then \(\int _X fdP\not \in {\mathfrak B}({\mathsf H})\) because the domain of the operator is smaller than the entire H and the proof ends. If x n ∈ Δf for every \(n\in {\mathbb N}\), from Theorem 3.24 (d), we have \(||\int _X fdPx_n||{ }^2= \int _{X} |f|{ }^2 d\mu ^{(P)}_{x_nx_n} = \int _{E_n} |f|{ }^2 d\mu ^{(P)}_{x_nx_n}\), where we have used that \(\mu ^{(P)}_{x_nx_n}(F)= \langle x_n|P_Fx_n\rangle = \langle P_{E_n}x_n|P_F P_{E_n}x_n\rangle = \langle x_n| P_{F \cap E_n} x_n \rangle = \mu ^{(P)}_{x_nx_n}(F\cap E_n)\). Therefore \(||\int _X fdPx_n||{ }^2 \geq \int _{E_n} n^2 d\mu ^{(P)}_{x_n x_n}= n^2\int _{E_n} 1 d\mu _{x_n x_n}= n^2\int _{X} 1 d\mu ^{(P)}_{x_n x_n} = n^2||x_n||{ }^2=n^2\). Hence ||∫X fdP|| cannot be finite and \(\int _X fdP \not \in {\mathfrak B}({\mathsf H})\).
-
(b)
By direct inspection
$$\displaystyle \begin{aligned}\left\langle y \left| P_E x \right.\right\rangle = \mu^{(P)}_{yx}(E) = \int_{E} 1 d\mu^{(P)}_{yx}(\lambda)= \int_{X} \chi_E(\lambda) d\mu^{(P)}_{yx}(\lambda)\quad \forall x,y \in \Delta_{\chi_E}= {\mathsf H}\:.\end{aligned}$$This proves (3.22), which also implies (3.23) for E = X, since P X = I. The proof of (3.24) is a trivial extension of this argument by linearity of the integral in \(\mu ^{(P)}_{yx}\) and linearity of the inner product.
-
(c)
Under the given hypotheses,
$$\displaystyle \begin{aligned}\left|\left| \left(\int_X f dP -\int_X f_n dP\right)x\right|\right|{}^2= \left|\left| \int_X f -f_n \:dP x\right|\right|{}^2 = \int_X |f-f_n|{}^2 d\mu^{(P)}_{xx}\:.\end{aligned}$$The first equality comes from (3.26), whose proof is independent of the present argument. Note that |f − f n|2 ≤ 4K 2 almost everywhere with respect to P, and hence also with respect to \(\mu ^{(P)}_{xx}\). In addition, \(\int |K^2| d\mu ^{(P)}_{xx} =||x||{ }^2K^2< +\infty \), so the dominated convergence theorem implies \(\int _X |f-f_n|{ }^2 d\mu ^{(P)}_{xx} \to 0\) as n → +∞, proving our assertion.
-
(d)
(i) First observe that Δaf+bg, Δf, Δg = H because f, g, af + bg are P-essentially bounded (\(||af+bg||{ }^{(P)}_\infty \leq |a|||f||{ }^{(P)}_\infty + |b|||g||{ }^{(P)}_\infty \)), so both sides of (c)(i) are defined everywhere. Next, from standard properties of the integral, for every x ∈H
$$\displaystyle \begin{aligned}\int_X af + bg \: d\mu^{(P)}_{yx} = a\int_X f d\mu^{(P)}_{yx} + b\int_X g d\mu^{(P)}_{yx}\:. \end{aligned}$$Using (3.12) we find
$$\displaystyle \begin{aligned}\begin{aligned}\left\langle y \left|\int_X af + bg \:dP x \right. \right\rangle &= a\left\langle y \left|\int_X f \:dP x \right. \right\rangle + b\left\langle y\left|\int_X g \:dP x \right. \right\rangle\\ &=\left\langle y \left|\left(a\int_X fdP +b\int_X g \:dP \right) x\right. \right\rangle\:.\end{aligned}\end{aligned}$$The proof ends since x, y ∈H are arbitrary.
Let us prove (3.27). First consider a pair of simple functions \(s = \sum _{k=1}^n s_k\chi _{E_k}\) and \(t = \sum _{h=1}^m t_h\chi _{F_h}\). The pointwise product s ⋅ t is simple. Indeed,
$$\displaystyle \begin{aligned}\begin{aligned}s\cdot t &= \sum_{k=1}^n s_k\chi_{E_k}\sum_{h=1}^m t_h\chi_{F_h}= \sum_{k,h} s_k t_h \chi_{E_k}\chi_{F_h} = \sum_{(k,h) \in I_n\times I_m} s_k t_h \chi_{E_k\cap F_h}\\ &= \sum_{(k,h) \in I_{n}\times I_m} (s\cdot t)_{(k,h)} P_{G_{(k,h)}}\:,\end{aligned}\end{aligned}$$where I l := {1, 2, …, l} and G (k,h) := E k ∩ F h. Exploiting (3.24), we immediately find
$$\displaystyle \begin{aligned}\int_X sdP \int_XtdP = \sum_{k=1}^n s_kP_{E_k}\sum_{h=1}^m t_hP_{F_h}= \sum_{h,k} s_k t_h P_{E_k}P_{F_h}\end{aligned}$$$$\displaystyle \begin{aligned}= \sum_{(k,h) \in I_n\times I_m} s_k t_h P_{E_k\cap F_h} = \sum_{(k,h) \in I_n\times I_m} (s\cdot t)_{(k,h)} P_{G_{(k,h)}} = \int_X s\cdot t dP\:.\end{aligned}$$We have proved the claim for simple functions f, g. Taking arbitrary P-essentially bounded functions f, g, consider two sequences of simple maps s n → f and t n → g pointwise, such that |s n|≤|s n+1|≤|f| and |t n|≤|t n+1|≤|g| for all \(n \in {\mathbb N}\). Evidently s n ⋅ t n → f ⋅ g, |s n ⋅ t n|≤|s n+1 ⋅ t n+1|≤|f ⋅ g| plus \(||s_n||{ }^{(P)}_\infty \leq ||f||{ }^{(P)}_\infty \), \(||t_n||{ }^{(P)}_\infty \leq ||g||{ }^{(P)}_\infty \) and \(||s_n\cdot t_n||{ }^{(P)}_\infty \leq ||f\cdot g||{ }^{(P)}_\infty \leq ||f||{ }^{(P)}_\infty ||g||{ }^{(P)}_\infty \). We can apply (c) to obtain, for every x, y ∈H,
$$\displaystyle \begin{aligned}\begin{aligned}\left\langle \int_X \overline{s_n} dP x \left| \int_X t_n dP y\right. \right\rangle &= \left\langle x \left|\int_X s_n dP \int_X t_n dPy \right. \right\rangle\\ &= \left\langle x \left|\int_X s_n\cdot t_n dP y \right. \right\rangle \to \left\langle x \left| \int_X f\cdot g dPy \right. \right\rangle \end{aligned}\end{aligned}$$as n → +∞. On the other hand, using (c) again and exploiting the inner product’s continuity, we also have
$$\displaystyle \begin{aligned}\left\langle \int_X \overline{s_n} dP x \left| \int_X t_n dP y\right. \right\rangle \to \left\langle \int_X \overline{f}dP x \left| \int_X g dPy \right. \right\rangle\:\end{aligned}$$as n → +∞. Summarizing,
$$\displaystyle \begin{aligned}\left\langle \int_X \overline{f}dP x \left| \int_X g dPy \right. \right\rangle= \left\langle x \left| \int_X f\cdot g dPy \right. \right\rangle\:,\end{aligned}$$which, from (3.13) and using that the domain of ∫X fdP is H, implies
$$\displaystyle \begin{aligned}\left\langle x \left| \int_X fdP \int_X g dPy \right. \right\rangle= \left\langle x \left| \int_X f\cdot g\: dPy \right. \right\rangle\:.\end{aligned}$$Since x, y ∈H are arbitrary, (3.27) indeed holds.
□
Remark 3.30
-
(a)
Consider \(f: X \to {\mathbb C}\) measurable and P-essentially bounded. We may redefine it so that it maps complex numbers \(z\in {\mathbb C}\) with \(|z|> ||f||{ }_\infty ^{(P)}\) to 0. We thus obtain a measurable function f′∈ M b(X) such that ∫X f′dP =∫X fdP. With regard to the integration of measurable functions in a PVM, therefore, bounded functions carry the same information as P-essentially bounded functions.
-
(b)
The first inequality in Proposition 3.29 (a) is actually an equality [Rud91, Mor18],
$$\displaystyle \begin{aligned} \begin{array}{rcl} \left|\left|\int_X f(\lambda)\: d P(\lambda)\right|\right| = ||f||{}^{(P)}_\infty\:.{}\end{array} \end{aligned} $$(3.28)See the solution of Exercise 3.35 for a proof.
-
(c)
Consider a set X equipped with a σ-algebra Σ(X). The set
$$\displaystyle \begin{aligned}M_b(X) := \left\{ f : X \to {\mathbb C} \:|\: f \: \mbox{is measurable and}\ ||f||{}_\infty <+\infty\right\}\end{aligned}$$is a commutative C ∗ -algebra with unit. The norm making M b(X) a complete vector space is ||⋅||∞, the involution the standard complex conjugation of functions \(f^*(x)= \overline {f(x)}\) for x ∈ X, the algebra multiplication is the commutative pointwise product of maps (f ⋅ g)(x) = f(x)g(x), and the complex vector space structure is the standard one: (af + bg)(x) := af(x) + bg(x) if x ∈ X, \(a,b \in {\mathbb C}\), and f, g ∈ M b(X). The algebra’s unit is the constant map
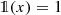 if x ∈ X. The C
∗-property ||f
∗⋅ f||2 = ||f||2 is nothing but \(|||f|{ }^2||{ }_\infty = ||f||{ }_\infty ^2\).
if x ∈ X. The C
∗-property ||f
∗⋅ f||2 = ||f||2 is nothing but \(|||f|{ }^2||{ }_\infty = ||f||{ }_\infty ^2\).Suppose now a PVM \(P: \Sigma (X) \to \mathcal {L}({\mathsf H})\) is also given. The map
$$\displaystyle \begin{aligned}\pi_P : M_b(X) \ni f \mapsto \int_X f dP \in {\mathfrak B}({\mathsf H})\end{aligned}$$preserves the structure of ∗-algebra and the unit, and hence is a representation. It is further continuous and norm-decreasing because of (3.21). This representation is neither injective nor isometric in general; however it enjoys a topological property unrelated to the continuity in the norms of M b(X) and \({\mathfrak B}({\mathsf H})\). The feature descends immediately from (3.14), by using \(\mu ^{(P)}_{xx}(X)<+\infty \).
Proposition 3.31 Retaining the above notation, if M b(X) ∋ f n → f pointwise as n → +∞, and there is a constant K ≥ 0 such that |f n|≤ K, then π P(f n)x → π P(f)x for every x ∈H.
-
(d)
Consider a topological space X and take its Borel σ-algebra \(\mathcal {B}(X)\) as Σ(X). Then the observation made in (c) holds provided we replace M b(X) with the commutative unital C ∗-algebra \(C_b(X) := \{ f : X \to {\mathbb C} \:|\: f \: \mbox{is continuous and} \ ||f||{ }_\infty <+\infty \}\). Recall that if X is compact, then \(C_b(X)=C(X):= \left \{ f : X \to {\mathbb C} \:|\: f \: \mbox{is continuous}\right \}\). An important result in the theory of C ∗-algebras (see [Mor18]) establishes that
Theorem 3.32 (Commutative Gelfand–Najmark Theorem) A commutative unital C ∗ -algebra is isometrically ∗ -isomorphic to the unital C ∗ -algebra C(X) for some compact Hausdorff space X. \(\blacksquare \)
3.2.4 PVM-Integration of Unbounded Functions
To conclude, we state a proposition concerning the most important and general properties of the integral in a PVM of a measurable, possibly unbounded, function.
Proposition 3.33
Consider a PVM P : Σ(X) →H , measurable functions \(f, g : X \to {\mathbb C}\) and let af, f ⋅ g, and f + g, with \(a\in {\mathbb C}\) , indicate the pointwise operations. Then
-
(a)
For \(a\in {\mathbb C}\)
$$\displaystyle \begin{aligned}a \int_Xf dP = \int_X af dP\:.\end{aligned}$$ -
(b)
D(∫X fdP +∫X gdP) = Δ f ∩ Δ g and
$$\displaystyle \begin{aligned}\int_Xf dP+\int_Xg dP \subset \int_X(f+g) dP\:,\end{aligned}$$with equality if and only if Δ f+g = Δ f ∩ Δ g.
-
(c)
D(∫X fdP∫X gdP) = Δ f⋅g ∩ Δ g and
$$\displaystyle \begin{aligned}\int_Xf dP\int_Xg dP \subset \int_X (f\cdot g)dP\end{aligned}$$with equality if and only if Δ f⋅g ⊂ Δ g.
-
(d)
\(D\left ((\int _Xf dP)^*\int _Xf dP \right )= D\left (\int _Xf dP(\int _Xf dP)^*\right ) = \Delta _{|f|{ }^2}\) and
$$\displaystyle \begin{aligned}\left(\int_Xf dP\right)^*\int_Xf dP = \int_X|f|{}^2 dP =\int_Xf dP\:\left(\int_Xf dP\right)^*\:.\end{aligned}$$ -
(e)
If U : H →H ′ is a surjective linear (or anti-linear) isometry, \(\Sigma (X) \ni E \mapsto P^{\prime }_E := UP_EU^{-1}\) is a PVM on H ′ and
$$\displaystyle \begin{aligned}U\left(\int_Xf dP\right) U^{-1} = \int_Xf dP'\:.\end{aligned} $$In particular, \(D\left (\int _Xf dP'\right ) = UD(\int _Xf dP) = U(\Delta _f)\).
-
(f)
If ϕ : X → X′ is measurable for the σ-algebras Σ(X), Σ′(X′) and \(f : X' \to {\mathbb C}\) is measurable, then
-
(i)
Σ′(X′) ∋ E′↦P′(E′) := P(ϕ −1(E′)) is a PVM on X′.
-
(ii)
we have
$$\displaystyle \begin{aligned}\int_{X'} f \:dP'= \int_X f \circ \phi \:dP \:.\end{aligned} $$Furthermore
$$\displaystyle \begin{aligned}\Delta^{\prime}_f = \Delta_{f\circ \phi}\:,\end{aligned} $$where \(\Delta ^{\prime }_f\) is the domain of \(\int _{X'} f \:dP'\).
-
(i)
Proof
Items (a), (e), and (f) are proved straightforwardly by checking the definitions. (d) is a trivial consequence of (c) and Theorem 3.24 (b)–(c). Part (b) can be proved in Δf ∩ Δg with the same argument used for the first identity in Proposition 3.29 (d). Besides, D(∫X fdP +∫X gdP) = Δf ∩ Δg is the very definition of domain of a sum of operators A + B. By this relation the last statement is obvious. Similarly, (c) can be proved as the second identity in Proposition 3.29 (d), by working in D(∫X fdP∫X gdP) and using D(∫X fdP∫X gdP) = Δf⋅g ∩ Δg. The latter is established as follows. D(∫X fdP∫X gdP) is made of vectors x ∈H such that both x ∈ Δg and
By the definition of \(\mu ^{(P)}_{zz}\) it is easy to prove that
hence D(∫X fdP∫X gdP) = Δf⋅g ∩ Δg. With this the last statement is now obvious. □
Remark 3.34
It is moreover possible to prove [Mor18] that if P : Σ(X) →H is a PVM and \(f, g : X \to {\mathbb C}\) are measurable functions, then
and
the bar denoting the closure.
Exercise 3.35
Prove formula (3.28) when \(f:X \to {\mathbb C}\) is measurable and P-essentially bounded.
Solution
We already know that \(||\int _X fdP|| \leq ||f||{ }^{(P)}_\infty \). In particular if \(||f||{ }^{(P)}_\infty =0\) the claim is obvious. Assume then \(||f||{ }^{(P)}_\infty >0\). Exactly as in the proof of Proposition 3.29 (a), for n > 0 there exists E n ∈ Σ(X) such that P E ≠ 0 and \(|f(\lambda )|\geq ||f||{ }_\infty ^{(P)}-1/n>0\) if λ ∈ E n and n is sufficiently large. Choosing \(x_n \in P_{E_n}({\mathsf H})\) with ||x n|| = 1, we have
that is
Since we know that \(||\int _X fdPx_n|| \leq ||f||{ }^{(P)}_\infty \) (note ||x n|| = 1), this proves that there is a sequence of unit vectors x n such that \(||\int _X fdPx_n|| \to ||f||{ }_\infty ^{(P)}\) as n → +∞, demonstrating the assertion.
Exercise 3.36
Suppose f n → f pointiwise as n → +∞, where \(f_n : X \to {\mathbb C}\) are measurable and |f n|≤|f|. Show that
Solution
Evidently \(\Delta _{f_n} \subset \Delta _f\), so \(x\in \Delta _{f_n}\) if x ∈ Δf. Next, using Proposition 3.33 (b) and (3.14), dominated convergence implies directly \(||\int _X f_ndPx -\int _X f \: dPx||{ }^2 = \int _X |f-f_n|{ }^2 d\mu ^{(P)}_{xx} \to 0\) as n → +∞. 
3.3 Spectral Decomposition of Selfadjoint Operators
We are ready to state the fundamental result in the spectral theory of selfadjoint operators, which extends expansion (1.4) to an integral formula befitting infinite dimensions. The eigenvalue set is replaced by the full spectrum of the selfadjoint operator. After this we shall focus on some relevant consequences in quantum physics.
Notation 3.37
From now on \({\mathcal {B}}(T)\) will denote the Borel σ-algebra of the topological space T. \(\blacksquare \)
Definition 3.38
Given a PVM \(P : \mathcal {B}(X) \to \mathcal {L}({\mathsf H})\) on the Borel σ-algebra of a topological space X, the support supp(P) of P is the complement in X of the union of all open sets O ⊂ X with P O = 0. \(\blacksquare \)
Remark 3.39
If X is second countable, P is necessarily concentrated on supp(P), i.e.,
In fact, D := X ∖supp(P) is the union of a number of open sets O with P O = 0. As the topology is second countable, we can extract a countable subcovering. By subadditivity of \(\mu ^{(P)}_{xx}\) we have \(\mu ^{(P)}_{xx}(D)=0\) for every x ∈H. This can be rephrased as ||P D x|| = 0 for every x ∈H. Hence P D = 0. If \(E \in \mathcal {B}(X)\), we therefore have P E = P E∩supp(P) + P E∩D = P E∩supp(P). \(\blacksquare \)
3.3.1 Spectral Theorem for Selfadjoint, Possibly Unbounded, Operators
Prior to stating the theorem, note that (3.13) implies \(\int f(\lambda ) dP(\lambda )\) is selfadjoint when f is real. The idea of the theorem is that every selfadjoint operator looks like that for a certain map f and a PVM on \({\mathbb R}\) associated with the operator itself.
Theorem 3.40 (Spectral Theorem for Selfadjoint Operators)
Let A be a selfadjoint operator on the complex Hilbert space H.
-
(a)
There exists a unique PVM \(P^{(A)} : {\mathcal {B}}({\mathbb R}) \to {\mathcal {L}}({\mathsf H})\) , called the spectral measure of A, such that
$$\displaystyle \begin{aligned}A = \int_{{\mathbb R}} \lambda dP^{(A)}(\lambda)\:.\end{aligned}$$In particular D(A) = Δ ı , where \(\imath : {\mathbb R} \ni \lambda \mapsto \lambda \).
-
(b)
We have
$$\displaystyle \begin{aligned}\mathit{\mbox{supp}}(P^{(A)}) = \sigma(A)\end{aligned}$$so that P (A) is concentrated on σ(A) (as the standard \({\mathbb R}\) is second countable):
$$\displaystyle \begin{aligned} \begin{array}{rcl} P^{(A)}(E) = P^{(A)}(E \cap \sigma(A))\:, \quad \forall E \in {\mathcal{B}}({\mathbb R}) {}\:.\end{array} \end{aligned} $$(3.29) -
(c)
λ ∈ σ p(A) if and only if P (A)({λ}) ≠ 0. This happens in particular when λ is an isolated point of σ(A). At last, \(P^{(A)}_{\{\lambda \}}\) is the orthogonal projector onto the λ-eigenspace.
-
(d)
λ ∈ σ c(A) if and only if P (A)({λ}) = 0, but P (A)(E) ≠ 0 if E ∋ λ is an open set in \({\mathbb R}\).
Proof
-
(a)
The existence part of the proof is involved and we postpone it to Sect. 3.6: Theorem 3.84 for the bounded case and Theorem 3.86 for the unbounded case (see also [Rud91, Mor18, Schm12]). Let us pass to the issue of uniqueness. Suppose there are two PVMs P 1 and P 2 on \(\mathcal {B}({\mathbb R})\) satisfying
$$\displaystyle \begin{aligned}A = \int_{{\mathbb R}} \lambda dP_k(\lambda)\quad k=1,2\:.\end{aligned}$$Consider the bounded normal operators
$$\displaystyle \begin{aligned}T_k:= \int_{{\mathbb R}} \frac{1}{r -i} dP_k(r)\:.\end{aligned}$$As we shall see below, either T k coincides with the resolvent operator R i(A) of A for λ = i, so these operators are actually identical and we shall write simply T.
Using Proposition 3.33 (f) we define new PVMs on the image \(\Gamma ' \subset {\mathbb C}\) of the continuous, injective map \(\phi : {\mathbb R} \ni r \mapsto \frac {1}{r -i} \in \Gamma \) (which turns out to be a homeomorphism on the image equipped with the topology induced by \({\mathbb C}\)). We also assume \(\Sigma (\Gamma ') := \mathcal {B}(\Gamma )\) so that \(\phi : {\mathbb R} \to \Gamma '\) is measurable. So we set
$$\displaystyle \begin{aligned}Q^{\prime}_k (E) := P_k(\phi^{-1}(E))\:, \quad E \in \mathcal{B}(\Gamma')\:, k=1,2\:.\end{aligned}$$With this choices,
$$\displaystyle \begin{aligned}T = \int_{\Gamma'} z dQ^{\prime}_k(z,\overline{z})\:,\quad k=1,2\:.\end{aligned}$$In Cartesian coordinates,
$$\displaystyle \begin{aligned}\Gamma = \left\{x+iy \in {\mathbb C}\setminus \{0\}\:\left|\: x^2 + \left(y-\frac{1}{2}\right)^2 = \frac{1}{4}\right. \right\}\end{aligned}$$is a circle—centred at i∕2 with radius 1∕2—without a point (the origin). If oriented in anti-clockwise manner, the ‘initial’ point 0− formally corresponds to r = −∞, and the ‘end’ point 0+ is reached when r = +∞.
It is certainly more practical to consider its compactification \(\Gamma := \overline {\Gamma '}= \Gamma \cup \{0\}\), again assuming \(\Sigma (\Gamma ) = \mathcal {B}(\Gamma )\), and extend the PVMs in a trivial way
$$\displaystyle \begin{aligned}Q_k(F) := Q^{\prime}_k(F\setminus\{0\})\:, \quad F \in \mathcal{B}(\Gamma)\:,\quad k=1,2\:.\end{aligned}$$The reader can easily prove that this extension does define well-behaved PVMs on \( \mathcal {B}(\Gamma )\). In this way the added point satisfies Q k({0}) = 0, even if it belongs to the supports of the measures (defined as we did for P (A)). For this reason we also have
$$\displaystyle \begin{aligned}T = \int_{\Gamma} z dQ_k(z,\overline{z})\:,\quad k=1,2\:.\end{aligned}$$It is also convenient to have at hand the adjoint of T,
$$\displaystyle \begin{aligned}T^* = \int_{\Gamma} \overline{z} dQ_k(z,\overline{z})\:,\quad k=1,2\:.\end{aligned}$$These operators are bounded and therefore we can apply Proposition 3.29 (d) to obtain that, for \(p\in {\mathbb C}[z,\overline {z}]\),
$$\displaystyle \begin{aligned}p(T,T^*) = \int_{\Gamma} p(z,\overline{z}) dQ_k(z,\overline{z})\:,\end{aligned}$$where the polynomial on the left is defined thinking of the product of operators as their composition. We also have, for x, y ∈H,
$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_\Gamma p(z,\overline{z}) d\mu^{(Q_1)}_{xy} =\langle x| p(T,T^*) y\rangle = \int_\Gamma p(z,\overline{z}) d\mu^{(Q_2)}_{xy}{}\:.\end{array} \end{aligned} $$(3.30)Since Γ is Hausdorff and compact, and \({\mathbb C}[z,\overline {z}]\) (i) contains the constant polynomial 1, (ii) is closed under complex conjugation and (iii) separates points in \({\mathbb C}\) and hence in Γ (i.e. if γ ≠ γ′∈ Γ there exists a polynomial p with p(γ) ≠ p(γ′)), the Stone–Weierstrass theorem implies that these polynomials are ||⋅||∞-dense in the Banach space C( Γ) of continuous complex-valued functions on Γ. Using a continuity argument coming from (3.21) and approximating continuous functions on Γ in terms of the above polynomials, Eq. (3.30) implies
$$\displaystyle \begin{aligned}\int_\Gamma f(z,\overline{z}) d\mu^{(Q_1)}_{xx} = \int_\Gamma f(z,\overline{z}) d\mu^{(Q_2)}_{xx}\quad \mbox{for every}\ f\in C(\Gamma).\end{aligned}$$Since in the locally compact Hausdorff space Γ an open set is a countable union of compact sets with finite \(\mu ^{(Q_2)}_{xx}\)-measure, these Borel measures are regular [Rud86]. Hence, the uniqueness in Riesz’s theorem for positive Borel measures [Rud86] implies that \(\mu ^{(Q_1)}_{xx}(E) =\mu ^{(Q_2)}_{xx}(E)\) for every \(E\in \mathcal {B}(\Gamma )\). In particular, for every \(E\in \mathcal {B}(\Gamma )\) and every x ∈H,
$$\displaystyle \begin{aligned}\langle x | (Q_1(E)- Q_2(E)) x\rangle = \int_\Gamma \chi_E d\mu^{(Q_1)}_{xx} - \int_\Gamma \chi_E d\mu^{(Q_2)}_{xx} =0\:,\end{aligned}$$proving that Q 1(E) = Q 2(E) for every \(E\in \mathcal {B}(\Gamma )\). Let us return to the initial PVMs: noting that \(\phi : {\mathbb R} \to \Gamma '\) is a homeomorphism, so \(\phi ^{-1} : \Gamma ' \to {\mathbb R}\) is measurable and \(\phi (F) \in \mathcal {B}(\Gamma ')\) if \(F\in \mathcal {B}({\mathbb R})\), we have
$$\displaystyle \begin{aligned}P_1(F) = Q^{\prime}_1(\phi(F)) = Q_1(\phi(F)) = Q_2(\phi(F))= Q^{\prime}_2(\phi(F)) = P_2(F)\:, \quad F\in \mathcal{B}({\mathbb R})\:.\end{aligned}$$We have established that P (A) is uniquely determined by A.
-
(b)
If λ∉supp(P (A)), the map \({\mathbb C} \ni r \mapsto \frac {1}{r -\lambda } = g(r)\) is P-essentially bounded, so \(\int _{\mathbb R} \frac {1}{r -\lambda } dP(r)\in {\mathfrak B}({\mathsf H})\) and Δg = H. According to Proposition 3.33 (c),
$$\displaystyle \begin{aligned} (A-\lambda I) \int_{\mathbb R} \frac{1}{r -\lambda} dP(r) =\int_{\mathbb R} \frac{r-\lambda}{r -\lambda} dP^{(A)}(r) =\int_{\mathbb R} 1 dP^{(A)}(r) = I\end{aligned}$$and
$$\displaystyle \begin{aligned} \int_{\mathbb R} \frac{1}{r -\lambda} dP(r)(A-\lambda I) x =\int_{\mathbb R} \frac{r-\lambda}{r -\lambda} dP^{(A)}(r) x = \int_{\mathbb R} 1 dP^{(A)}x =x \quad \mbox{if}\ x\in D(A) \:.\end{aligned}$$We conclude that \(\int _{\mathbb R} \frac {1}{r -\lambda } dP(r)= R_{\lambda }(A)\) and λ∉σ(A). Suppose conversely that λ∉σ(A), and so \(R_\lambda (A) := (A-\lambda I)^{-1}\in {\mathfrak B}({\mathsf H})\) exists. Then for x ∈ D(A) we have x = R λ(A)(A − λI)x and ||x||≤||R λ(A)|| ||(A − λ)x||, so ||(A − λ)x||2 ≥||x||2∕||R λ(A)||2. According to (3.14), taking ||x|| = 1,
$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_{{\mathbb R}} |r-\lambda|{}^2 d\mu^{(P^{(A)})}_{xx}(r) \geq \frac{1}{||R_\lambda(A)||{}^2}>0\:.{}\end{array} \end{aligned} $$(3.31)If λ ∈supp(P (A)), we would have \(P^{(A)}_{(\lambda -1/n, \lambda +1/n)} \neq 0\) and consequently we would be able to pick out a sequence \(x_n \in P^{(A)}_{(\lambda -1/n, \lambda +1/n)}({\mathsf H})\) with ||x n|| = 1, finding \(\int _{{\mathbb R}} |r-\lambda |{ }^2 d\mu ^{(P^{(A)})}_{xx}(r) \leq 4||x_n||/n^2 = 4/n^2\to 0\) as n → +∞. As (3.31) prevents this from happening, λ∉supp(P (A)). This concludes the proof of (b).
-
(c)
If \(P^{(A)}_{\{\lambda \}}\neq 0\), let \(0\neq x \in P^{(A)}_{\{\lambda \}}({\mathsf H})\). We have, from (3.22) and Proposition 3.33 (c),
$$\displaystyle \begin{aligned}Ax = AP_{\{\lambda\}}^{(A)}x =\int_{\mathbb R} r dP^{(A)}(r) \int_{\mathbb R} \chi_{\{\lambda\}}(r) dP(r)x = \int_{{\mathbb R} }r\chi_{\{\lambda\}}(r) dP^{(A)}x\end{aligned}$$$$\displaystyle \begin{aligned}\hspace{-7pt}= \int_{{\mathbb R} }\lambda\chi_{\{\lambda\}}(r) dP^{(A)}x = \lambda P^{(A)}_{\{\lambda\}}x = \lambda x\:. \end{aligned}$$Hence λ ∈ σ p(A). If conversely λ ∈ σ p(A), then Ax = λx for some eigenvector x ∈ D(A) with ||x|| = 1, so that (A − iI)x = (1 − i)x and (A − iI)−1 x = (λ − i)−1 x. Similarly, (A + iI)−1 x = (λ + i)−1 x. Exploiting the same argument we used in proving the uniqueness of P (A), and writing Q in place of Q 1 = Q 2, the relations found read
$$\displaystyle \begin{aligned}Tx = \int_{\Gamma} z dQ(z,\overline{z}) x = \frac{1}{\lambda-i}x\quad \mbox{and}\quad T^*x = \int_{\Gamma} \overline{z} dQ(z,\overline{z}) x = \frac{1}{\lambda +i}x\:.\end{aligned}$$By considering polynomial compositions of the operators T and T ∗ these relations can be extended: for instance
$$\displaystyle \begin{aligned}\begin{aligned}\int_{\Gamma} (a\overline{z} + bzz) dQ(z,\overline{z}) x &= aT^* +bTTx = a\frac{1}{\lambda -i}x + b\frac{1}{\lambda +i}Tx\\ &= \left[a\frac{1}{\lambda -i}+ b\left(\frac{1}{\lambda +i}\right)^2\right] x\:,\end{aligned}\end{aligned}$$and so on. In complete generality, defining \(t:=\frac {1}{\lambda -i}\), we have
$$\displaystyle \begin{aligned}\int_{\Gamma} p(z,\overline{z}) dQ(z,\overline{z}) x = p(T,T^*)x = p(t, \overline{t})x\end{aligned}$$for every polynomial p in the variables z and \(\overline {z}\). As before, we can extend to continuous functions \(f: \Gamma \to {\mathbb C}\) via the Stone–Weierstrass theorem and uniformly approximating a continuous functions \(f=f(z,\overline {z})\) on the compact set Γ by means of a sequence of polynomials \(p_n=p_n(z,\overline {z})\) restricted to Γ. As ||f − p n ↾Γ||∞→ 0 as n → +∞, (3.21) implies in particular
$$\displaystyle \begin{aligned}p_n(t,\overline{t})x =\int_{\Gamma} p_n(z,\overline{z}) dQ(z,\overline{z})x \to \int_{\Gamma} f(z,\overline{z}) dQ(z,\overline{z})x\quad \mbox{if}\ n \to +\infty\:.\end{aligned}$$Since \(p_n(t,\overline {t}) \to f(t,\overline {t})\), we eventually obtain
$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_{\Gamma} f(z,\overline{z}) dQ(z,\overline{z}) x = f(t, \overline{t})x\:.{}\end{array} \end{aligned} $$(3.32)Now it is not hard to construct a sequence of continuous maps on Γ such that f n → χ {t} pointwise on Γ as n → +∞ and \(|f_n(z,\overline {z})|< K <+\infty \) for some K > 0 and every \((z,\overline {z}) \in \Gamma \). (c) and (b) in Proposition 3.29 imply, from (3.32),
$$\displaystyle \begin{aligned}\begin{aligned}Q_{\{t\}}x &= \int_{\Gamma} \chi_{\{t\}}(z,\overline{z}) dQ(z,\overline{z}) x =\lim_{n\to +\infty}\int_{\Gamma} f_n(z,\overline{z}) dQ(z,\overline{z}) x\\ &= \lim_{n\to +\infty}f_n(t, \overline{t})x=\chi_{\{t\}}(t, \overline{t}) x =x\:.\end{aligned}\end{aligned}$$Since t ∈ Γ′ by construction, \(Q_{\{t\}} = Q^{\prime }_{\{t\}} = P^{(A)}_{\{\phi ^{-1}(t)\}} = P^{(A)}_{\{\lambda \}}\). We have discovered that \(P^{(A)}_{\{\lambda \}}x =x\). Since x ≠ 0, we also have \(P^{(A)}_{\{\lambda \}} \neq 0\), which concludes the proof.
It is clear that if λ ∈ σ(A) = supp(P (A)) is isolated, so that there is an open set O ∋ λ such that O ∖{λ} is contained in \({\mathbb R} \setminus \mbox{supp}(P^{(A)})\), then \(P^{(A)}_{\{\lambda \}}\neq 0\). For otherwise by additivity we would have \(P^{(A)}_{O}=0\) for some open set O ∋ λ, forbidding λ ∈supp(P (A)). Let us prove the last statement in (c): \(P^{(A)}_{\{\lambda \}}({\mathsf H}) = {\mathsf H}_\lambda \), where H λ is the eigenspace of λ ∈ σ p(A). We established that if \(P^{(A)}_{\{\lambda \}} \neq 0\) (or equivalently, λ ∈ σ p(A)), \(x \in P^{(A)}_{\{\lambda \}}({\mathsf H})\) satisfies Ax = λx. Therefore \(P^{(A)}_{\{\lambda \}}({\mathsf H}) \subset {\mathsf H}_\lambda \). We have also proved that x ∈H λ implies \(P^{(A)}_{\{\lambda \}}x=x\), that is \({\mathsf H}_\lambda \subset P^{(A)}_{\{\lambda \}}({\mathsf H})\). In summary, \(P^{(A)}_{\{\lambda \}}({\mathsf H}) = {\mathsf H}_\lambda \).
-
(d)
Assuming λ ∈ σ c(A), due to (c), necessarily \(P^{(A)}_{\{\lambda \}}=0\), because otherwise λ ∈ σ p(A), which is disjoint from σ c(A). On the other hand, since λ ∈supp(P (A)), for every open set O containing λ, \(P_O^{(A)}\neq 0\). Suppose \(P_O^{(A)}\neq 0\) for every open neighbourhood O of λ. This fact forces λ ∈supp(P (A)) = σ(A), and the further requirement \(P^{(A)}_{\{\lambda \}}=0\) yields λ ∈ σ c(A) due to (c).
□
Remark 3.41
-
(a)
If P is a PVM on \({\mathbb R}\) and \(f: {\mathbb R} \to {\mathbb C}\) is measurable, we can always write
$$\displaystyle \begin{aligned}\int_{{\mathbb R}} f(\lambda) dP(\lambda) = f(A),\end{aligned}$$for the selfadjoint operator A obtained as
$$\displaystyle \begin{aligned} \begin{array}{rcl} A= \int_{{\mathbb R}} \imath(\lambda) dP(\lambda)\:, \end{array} \end{aligned} $$(3.33)due to (3.13), where \(\imath : {\mathbb R} \ni \lambda \to \lambda \). By virtue of the uniqueness statement in the spectral theorem P (A) = P, which leads us to the conclusion that on a Hilbert space H, projector-valued measures on \(\mathcal {B}({\mathbb R})\) correspond one-to-one to selfadjoint operators on H.
-
(b)
Theorem 3.40 is a particular case of a more general theorem (see [Rud91, Mor18] and especially [Schm12]) that is valid when A is a (densely-defined closed) normal operator. The statement is identical, with the proviso of replacing \({\mathbb R}\) with \({\mathbb C}\). A special case is that in which A is unitary. The spectral theorem for normal operators on \({\mathfrak B}({\mathsf H})\) will show up in Sect. 3.6 disguised as Theorem 3.85.
\(\blacksquare \)
Notation 3.42
Suppose \(f: \sigma (A) \to {\mathbb C}\) is measurable for the σ-algebra obtained by restricting the elements of \({\mathcal {B}}({\mathbb R})\) to σ(A), which coincides with \(\mathcal {B}(\sigma (A))\) when σ(A) has the induced topology. In view of Theorem 3.40, part (b) in particular, we will indifferently use the notations
where \(g : {\mathbb R} \to {\mathbb C}\) is the extension of f to zero outside σ(A), or any other measurable function equal to f on supp(P (A)) = σ(A). Obviously g(A) = g′(A) if \(g,g' : {\mathbb R} \to {\mathbb C}\) coincide on supp(P (A)) = σ(A). \(\blacksquare \)
Example 3.43
-
(1)
Consider the m-axis position operator X m on \(L^2({\mathbb R}^n, d^nx)\) introduced in Example 2.59 (1). We know that \(\sigma (X_m)= \sigma _c(X_m)= {\mathbb R}\) from Example 3.14. We are interested in the PVM \(P^{(X_m)}\) of X m defined on \({\mathbb R}= \sigma (X_m)\). Let us fix m = 1, for the other cases are analogous. The PVM associated to X 1 is
$$\displaystyle \begin{aligned} \begin{array}{rcl} (P^{(X_1)}_E \psi)(x) = \chi_{E \times {\mathbb R}^{n-1}}(x) \psi(x) \quad \psi \in L^2({\mathbb R}^n , d^nx)\:,{}\end{array} \end{aligned} $$(3.35)where \(E \in {\mathcal {B}}({\mathbb R})\) is a subset of the first factor of \({\mathbb R} \times {\mathbb R}^{n-1} = {\mathbb R}^n\). Indeed, indicating by Pψ the right-hand side of (3.35), one easily verifies that \(\Delta _{x_1} = D(X_1)\). Furthermore, approximating the function \({\mathbb R}^n \ni x \mapsto x_1\in {\mathbb R}\) with simple maps,Footnote 1
$$\displaystyle \begin{aligned}\int_{{\mathbb R}^n} x_1 |\psi(x)|{}^2 d^nx = \int_{{\mathbb R}} x_1 \mu^{(P)}_{\psi,\psi}(x_1) =\int_{{\mathbb R}} \lambda \mu^{(P)}_{\psi,\psi}(\lambda)\quad \forall \psi \in D(X_1)= \Delta_{x_1}\end{aligned}$$where \(\mu ^{(P)}_{\psi ,\psi }(E) = \langle \psi | P_E \psi \rangle = \int _{E \times {\mathbb R}^{n-1}} |\psi (x)|{ }^2 d^nx\). Since the left-hand side is nothing but 〈ψ|X 1 ψ〉, Corollary 3.27 (b) confirms (3.35) holds.
-
(2)
Take the m-axis momentum operator P m on \(L^2({\mathbb R}^n, d^nx)\), introduced in Example 2.59(2). Taking (2.23) into account, where \(\hat {\mathcal {F}}\) (and thus \(\hat {\mathcal {F}}^*\)) is unitary, by Proposition 3.60 (i) the PVM of P m is
$$\displaystyle \begin{aligned}Q^{(P_m)}_E := \hat{\mathcal{F}}^* P^{(K_m)}_E \hat{\mathcal{F}}\:.\end{aligned}$$The operator K m is X m represented in \(L^2({\mathbb R}^n, d^nk)\), see Example 2.59 (1).
-
(3)
By a similar argument the PVM of the operator \(H= \overline {H_0}\) relative to the harmonic oscillator of Example (2.59) (4) is, for \(E \in \mathcal {B}({\mathbb R})\),
$$\displaystyle \begin{aligned}P_{E} = \sum_{\lambda \in E \cap \hbar\omega ({\mathbb N}+1/2)} \langle \psi_\lambda | \cdot \rangle \psi_\lambda\end{aligned}$$where
$$\displaystyle \begin{aligned} \begin{array}{rcl} H = \sum_{\lambda \in \hbar \omega ({\mathbb N}+1/2)} \lambda \langle \psi_\lambda | \cdot \rangle \psi_\lambda=\sum_{n\in {\mathbb N}} \hbar \omega(n+1/2) \langle \psi_n | \cdot \rangle \psi_n \:.{}\end{array} \end{aligned} $$(3.36)has domain
$$\displaystyle \begin{aligned}D(H) = \left\{\psi \in L^2({\mathbb R}, dx)\:\left|\: \sum_{n=0}^{+\infty} (n+1/2)^2|\langle \psi_n |\psi \rangle|{}^2 <+\infty\right. \right\}\:.\end{aligned}$$Indeed, since \(\{\psi _n\}_{n \in {\mathbb N}}\) is a Hilbert basis of \(L^2({\mathbb R},dx)\), the right-hand side of (3.36) is selfadjoint as integral of the (real) function \(\imath :{\mathbb R} \ni \lambda \mapsto \lambda \in {\mathbb R}\) of the said PVM (notice that D(H) = Δı). Therefore the right-hand side of (3.36) is a selfadjoint extension of the H 0 in Example (2.59) (4), which is essentially selfadjoint, so \(H= \overline {H_0}\). We will show that the spectrum of the Hamiltonian H of the harmonic oscillator is
$$\displaystyle \begin{aligned}\sigma(H) = \sigma_p(H) = \{\hbar \omega(n+1/2)\:|\: n=0,1,\ldots \}\:.\end{aligned}$$Evidently σ(H) contains the closed set of eigenvalues ħω(n + 1∕2). We claim it cannot contain any point λ other than these numbers. Indeed, suppose that there is a further λ in σ p(H), so that \(P^{(H)}_{\{\lambda \}}\neq 0\). If \(x\in P^{(H)}_{\{\lambda \}}({\mathsf H})\), we would have \(\langle x |\psi _n\rangle = \langle P^{(H)}_{\{\lambda \}}x |P^{(H)}_{\{\hbar \omega (n+1/2)\}}\psi _n\rangle = \langle x |P^{(H)}_{\{\lambda \}\cap \{\hbar \omega (n+1/2)\}}\psi _n\rangle = \langle x |P^{(H)}_{\varnothing }\psi _n\rangle =0\). Therefore x must vanish because it is orthogonal to a Hilbert basis, and \(P^{(H)}_{\{\lambda \}}=0\) contrarily to the hypothesis. There only remains the possibility that λ ∈ σ c(H). Since {ħω(n + 1∕2) | n = 0, 1, …} is closed and λ does not belong to that set, it cannot be an accumulation point. We can therefore find δ > 0 such that \((\lambda -\delta , \lambda + \delta ) \cap \{\hbar \omega (n+1/2)\:|\: n=0,1,\ldots \}= \varnothing \). With the same argument as before we can prove that \(x \in P^{(H)}_{(\lambda -\delta , \lambda + \delta )}({\mathsf H})\) forces x = 0, and thus \(P^{(H)}_{(\lambda -\delta , \lambda + \delta )}=0\). This violates Theorem 3.40 (d), so we conclude that σ(H) = σ p(H) = {ħω(n + 1∕2) | n = 0, 1, …}.
-
(4)
An argument similar to that of (2) and (3) applies to the symmetric momentum operator in a box P′, introduced in Example (2.59) (5). The selfadjoint extensions P α, α ∈ [0, 2π) of P′ are
$$\displaystyle \begin{aligned}P_\alpha = \sum_{n\in {\mathbb Z}} (\alpha + 2n\pi) \langle u_{\alpha, n}| \null\cdot\null \rangle\: u_{\alpha, n}\:,\end{aligned}$$so in particular
$$\displaystyle \begin{aligned}\sigma(P_\alpha) = \sigma_p(P_\alpha) = \{\alpha + 2\pi n\:|\: n\in {\mathbb Z} \}\:.\end{aligned}$$Replacing α with α + 2kπ, \(k\in {\mathbb Z}\), leaves P α invariant since it merely relabels the same eigenvectors coherently with their eigenvalues.
-
(5)
In general it is false that if a selfadjoint operator A admits a Hilbert basis of eigenvectors then its spectrum only contains eigenvalues. Since σ(A) is closed, but σ p(A) is not always closed, points of σ p(A) might accumulate in the continuous spectrum.
Using the Hilbert basis \(\{\psi _n\}_{n \in {\mathbb N}}\) of the previous example, consider the selfadjoint bounded operator
$$\displaystyle \begin{aligned}A = \sum_{\lambda \in {\mathbb Q} \cap [0,1]} \lambda \langle \psi_{n_\lambda}| \cdot \rangle \psi_{n_\lambda} : L^2({\mathbb R}, dx) \to L^2({\mathbb R}, dx)\end{aligned}$$where \({\mathbb Q} \cap [0,1] \ni q \mapsto n_q \in {\mathbb N}\) a bijection. We may define A equivalently as
$$\displaystyle \begin{aligned}A = \int_{\mathbb R} \lambda dP(\lambda)\end{aligned}$$where, for every \(E \in \mathcal {B}({\mathbb R})\),
$$\displaystyle \begin{aligned}P_E = \sum_{\lambda \in E\cap {\mathbb Q} \cap [0,1]} \lambda \langle \psi_{n_\lambda}| \cdot \rangle \psi_{n_\lambda}\:.\end{aligned}$$The operator A is evidently bounded and it is easy to prove that ||A|| = 1. The domain of A is therefore the whole \(L^2({\mathbb R}, dx)= \Delta _{\imath }\). By the same argument of the previous example, \({\mathbb Q} \cap [0,1] = \sigma _p(A)\) because \(\{\psi _n\}_{n \in {\mathbb N}}\) is a Hilbert basis of \(L^2({\mathbb R}, dx)\). As \(\sigma _p(A) \subset \sigma (A)=\overline {\sigma (A)}\), we have \(\overline {{\mathbb Q} \cap [0,1]} =[0,1] = \overline {\sigma _p(A)} \subset \sigma (A)\). It is easy to prove from (3.37) that σ(A) ⊂ [0, 1] because ||A|| = 1. We conclude that σ(A) = [0, 1] and \([0,1]\setminus {\mathbb Q}\) must lie in σ c(A).
-
(6)
More complicated situations exist. Consider an operator of Schrödinger form
$$\displaystyle \begin{aligned}H := \frac{1}{2m}\sum_{k=1}^nP_k^2 + U(x) = -\frac{1}{2m} \Delta + U(x)\end{aligned}$$where Δ is the Laplacian on \({\mathbb R}^n\), P k is the momentum operator on \(L^2({\mathbb R}^k, d^kx)\) associated to the k-th coordinate, m > 0 is a constant and U is a real-valued function on \({\mathbb R}\) acting as multiplication operator. Suppose U = U 1 + U 2 where \(U_1 \in L^2({\mathbb R}^k, d^kx)\) and \(U_2 \in L^\infty ({\mathbb R}^k, d^kx)\), k = 1, 2, 3, are real-valued and \(D(H) = C^\infty ({\mathbb R})\). Then H turns out to be (trivially) symmetric but also essentially selfadjoint [ReSi80, Mor18] as a consequence of a well-known result (the Kato–Rellich theorem). The unique selfadjoint extension \(\overline {H}=(H^*)^*\) of H physically represents the Hamiltonian operator of a quantum particle living in \({\mathbb R}^n\) with potential energy described by U. (This in particular applies to the Hamiltonian of an electron with attractive Coulomb potential: this is proportional to − 1∕||x|| in \({\mathbb R}^3\) and decomposes as a sum of functions exactly as above.) In general \(\sigma (\overline {H})\) has both point and continuous parts. If P λ denotes the orthogonal projector onto the λ-eigenspace of \(\overline {H}\), then \(\int _{\sigma _p(\overline {H})} \lambda dP^{(\overline {H})}(\lambda )\) takes this form
$$\displaystyle \begin{aligned}\int_{\sigma_p(\overline{H})} \lambda dP^{(\overline{H})}(\lambda) = \sum_{\lambda \in \sigma_p(\overline{H})} \lambda P^{(\overline{H})}_{\lambda}\:.\end{aligned}$$On the contrary, \(\int _{\sigma _c(\overline {H})} \lambda dP^{(\overline {H})}(\lambda )\) has a much more complicated expression. Under a unitary transformation, \(\int _{\sigma _c(\overline {H})} \lambda dP^{(\overline {H})}(\lambda )\) decomposes spectrally in analogy to the position operator X, which acts by multiplication on \(L^2({\mathbb R},dx)\); the difference is that now several copies of L 2-spaces may appear. If \({\mathsf H}_p := P^{(\overline {H})}_{\sigma _p(\overline {H})}({\mathsf H})\) is the closed subspace spanned by the eigenspaces of \(\overline {H}\) and \({\mathsf H}_c := P^{(\overline {H})}_{\sigma _c(\overline {H})}({\mathsf H})\), we have an orthogonal decomposition H = H c ⊕H p. The operator \(H_p := \int _{\sigma _p(\overline {H})} \lambda dP^{(\overline {H})}(\lambda )\) leaves invariant the subspace
$$\displaystyle \begin{aligned}D(H_p) := \left\{\psi \in H_p \:\left|\: \sum_{E \in \sigma_p(\overline{H})} E^2 ||P^{(\overline{H})}_E \psi||{}^2 <+\infty \right.\right\}\;,\end{aligned}$$whereas \(H_c := \int _{\sigma _c(\overline {H})} \lambda dP^{(\overline {H})}(\lambda )\) fixes
$$\displaystyle \begin{aligned}D(H_c) := \left\{\psi \in H_p \:\left|\: \int_{\sigma_c(\overline{H})} E^2 d\mu^{P^{(\overline{H})}}_{\psi,\psi}(E) <+\infty \right.\right\}\:.\end{aligned}$$In this sense, \(\overline {H} = H_c\oplus H_p\). A possible situation (not the only one) is that H c is isomorphic to a direct sum \(\oplus _{n=1}^N L^2( \sigma _c(\overline {H}), dE)\), and H c : (ψ 1, …, ψ N)↦(ı ⋅ ψ 1, …, ı ⋅ ψ N) acts as a multiple of the identity in each slot: (ı ⋅ ψ k)(E) := Eψ k(E) . \(\blacksquare \)
Definition 3.44
Selfadjoint operators admitting a Hilbert basis of eigenvectors are said to have a pure point spectrum. \(\blacksquare \)
Remark 3.45
Having a pure point spectrum does not automatically mean that σ p(A) = σ(A), as illustrated in example (4) above. However it implies that σ c(A) cannot have interior points (this is forbidden by Theorem 3.40 (d)). \(\blacksquare \)
3.3.2 Some Technically Relevant Consequences of the Spectral Theorem
The spectral theorem has repercussions pointing in several directions. We shall mention just a few which have a relevant impact on quantum theory. The first result concerns the positivity of selfadjoint operators.
Proposition 3.46
If A is a selfadjoint operator on the Hilbert space H , A is positive, that is 〈x|Ax〉≥ 0 for every x ∈ D(A) (also written A ≥ 0) if and only if σ(A) ⊂ [0, +∞).
Proof
Suppose σ(A) ⊂ [0, +∞). If x ∈ D(A) we have 〈x|Ax〉 =∫σ(A) λdμ x,x ≥ 0 by (3.12) (where μ stands for \(\mu ^{(P^{(A)})}\)), since μ x,x is a positive measure ad σ(A) ∈ [0, +∞).
Conversely, we shall prove that A is not positive if σ(A) contains a λ 0 < 0. Using parts (c) and (d) of Theorem 3.40, one finds an interval [a, b] ⊂ σ(A) with [a, b] ⊂ (−∞, 0) and \(P^{(A)}_{[a,b]} \neq 0\) (possibly a = b = λ 0). If \(x \in P^{(A)}_{[a,b]} ({\mathsf H})\) with x ≠ 0, then \(\mu _{xx}(E) = \langle x|P_E x\rangle = \langle x|P^*_{[a,b]}P_E x P_{[a,b]}\rangle = \langle x|P_{[a,b]}P_E P_{[a,b]}x \rangle = \langle x|P_{[a,b]\cap E}x\rangle =0\) if \([a,b]\cap E= \varnothing \). Therefore, 〈x|Ax〉 =∫σ(A) λdμ x,x =∫[a,b] λdμ x,x ≤∫[a,b] bμ x,x < b||x||2 < 0. □
Another remarkable result, about bounds on the extended spectrum, holds for normal operators as well, and is independent of the spectral theorem (it can be used to prove the spectral theorem, actually). We shall follow a much more elementary route in Proposition 3.80.
Proposition 3.47
A selfadjoint operator is bounded (and its domain is the entire H ) if and only if σ(A) is bounded. In this case
Proof
From Proposition 3.10 we have that if \(A \in {\mathfrak B}({\mathsf H})\) then \(||A|| \geq \sup \{|\lambda | \:|\: \lambda \in \sigma (A) \}\). If, conversely, σ(A) is bounded and hence compact (it is closed), by restricting the integration domain to X = σ(A) the continuous map ı : σ(A) ∋ λ → λ is bounded. Then (3.14) implies that A =∫σ(A) ıdP (A) is bounded and the following inequality holds
Hence \(||A|| \leq \sup \{|\lambda | \:|\: \lambda \in \sigma (A)\}\), so
In this case, furthermore, D(A) = Δı = H. □
Remark 3.48
Proposition 3.47 explains the reason why observables A in QM are very often represented by unbounded selfadjoint operators. The spectrum σ(A) is the set of values of the observable A. When, as it frequently happens, an observable is allowed to take arbitrarily large values (think of X or P), it cannot be represented by a bounded selfadjoint operator simply because its spectrum is not bounded.\(\blacksquare \)
Concerning the covariance of a selfadjoint operator and its PVM under unitary transformations (or surjective linear isometries), another simple yet technically important result is the following.
Proposition 3.49
Let A : D(A) →H be a selfadjoint operator on the Hilbert space H and U : H →H ′ an isometric, surjective linear (or anti-linear) map. Then UAU −1 , with domain D(UAU −1) = U(D(A)), is selfadjoint as well (Proposition 2.41 and the subsequent remark) and
Proof
If x ∈ D(A),
In the last passage we used
Applying Corollary 3.27 (b), we conclude that
The uniqueness of the PVM of A implies
which is the claim we wanted to prove. □
The notion of function of a selfadjoint operator (3.34) is just a generalization of the analogous (1.7) that was introduced for the finite-dimensional case, and may be used in QM applications. In finite dimensions the eigenvalue set of f(A) is the image under f of the eigenvalue set of A: σ(f(A)) = f(σ(A)). But what about the infinite-dimensional case?
If \(f :{\mathbb R} \to {\mathbb C}\) is Borel measurable (we could equivalently use an \(f: \sigma (A) \to {\mathbb C}\) Borel measurable for \(\mathcal {B}(\sigma (A))\)) and A : D(A) →H is selfadjoint, it is quite evident that
In fact, if λ ∈ σ p(A) there is \(x =P^{(A)}_{\{\lambda \}} x \neq 0\) by the spectral theorem. Therefore
hence f(λ) ∈ σ p(f(A)). In the infinite-dimensional case there exist simple counterexamples disproving the converse inclusion f(σ p(A)) ⊃ σ p(f(A)). The simples instance is \(\chi _E(A)= P^{(A)}_E\). This operator is an orthogonal projector and as such it only has point spectrum, given by a non-empty subset of {0, 1}, even in case σ(A) = σ c(A) so \(\chi _E(\sigma _p(A)) = \varnothing \).
Pressing on, let us introduce a new notion to the purpose.
Definition 3.50
Let \(P: \mathcal {B}(X) \to \mathcal {L}({\mathsf H})\) be a PVM on a topological space X. If \(f : X \to {\mathbb C}\) is measurable, we call P-essential rank the set
\(\blacksquare \)
Since f is Borel measurable and O (open) belongs to \(\mathcal {B}({\mathbb C})\), \(f^{-1}(O) \in \mathcal {B}(X)\) and therefore the essential rank is well defined. Here is an almost immediate consequence of the definition.
Proposition 3.51
Let \(P: \mathcal {B}(X) \to \mathcal {L}({\mathsf H})\) be a PVM on a topological space X. If \(f: X \to {\mathbb C}\) is measurable, then
Proof
If z∉essrank(f) there exists an open set B ∋ z in \({\mathbb C}\) with \(P_{f^{-1}(B)} = 0\). If B r(z) is an open ball of radius r centred at z and contained in B, by additivity \(P_{f^{-1}(B_r(z))} = 0\) (and \(P_{f^{-1}(B\setminus B_r(z))} = 0\)). The map \(X\ni \lambda \mapsto g(\lambda ):= \frac {1}{f(\lambda ) - z}\) is therefore P-essentially bounded with \(||g||{ }^{(P)}_\infty \leq 1/r\), since P {λ ∈ X | |g(λ)|>1∕r} = 0. Hence \(\int _X \frac {1} {f(\lambda ) - z} dP(\lambda ) \in {\mathfrak B}({\mathsf H})\) from Proposition 3.29 (a). In addition, by Propositions 3.33 (c) and 3.29 (a)
so that \(z\in \rho \left ( \int _X f dP \right )\), i.e. \(z \not \in \sigma \left ( \int _X f dP \right )\).
If z ∈ essrank(f), then \(P_{f^{-1} (O)} \neq 0\) for every open set O containing z. This holds for every ball B 1∕n(z) of radius 1∕n, n = 1, 2, …, centred at z. (In particular \(f^{-1}(B_{1/2}(z)) \neq \varnothing \), otherwise \(P_{f^{-1}(B_{1/2}(z))}= 0\).) We claim that if R := (∫X(f − zI)dP)−1 exists it cannot be bounded, and hence \(z\in \sigma _c\left ( \int _X f dP \right )\). Indeed, ||x|| = ||R∫X(f − zI)dPx|| would imply, taking ||x|| = 1,
which is not bounded as n = 1, 2, …. If R := (∫X(f − zI)dP)−1 is not defined, then \(z\in \sigma _p\left ( \int _X f dP \right )\). Since the residual spectrum is empty, as ∫X(f − zI)dP is normal, we have established that z ∈ essrank(f) implies \(z\in \sigma \left ( \int _X f dP \right )\), concluding the proof. □
Remark 3.52
A subtler argument [Rud91, Mor18] proves that z ∈ essrank(f) belongs to \(\sigma _p\left ( \int _X f dP \right )\) if and only if \(P_{f^{-1}(\{z\})} \neq 0\). \(\blacksquare \)
The relevant corollary of Proposition 3.51 and the spectral theorem is the following one.
Corollary 3.53
Let A be a selfadjoint operator on the Hilbert space H and \(f: \sigma (A) \to {\mathbb C}\) a continuous map. Then
The closure above is unnecessary if A is bounded.
Proof
In view of Proposition 3.51 and Theorem 3.40, we just need to prove \(essrank(f) = \overline {f(\mbox{supp}(P^{(A)}))}\). If z = f(r) for some r ∈supp(P (A)) and O ∋ z is open, then f −1(O) is open since f is continuous and it contains r. Hence \(P_{f^{-1}(O)}\neq 0\) by the very definition of support. This proves essrank(f) ⊂ f(supp(P (A))). As essrank(f) is closed by definition (its complement is open), we have \(essrank(f) = \overline {essrank(f)}\subset \overline {f(\mbox{supp}(P^{(A)}))}\). To conclude, suppose \(z\in \overline {f(\mbox{supp}(P^{(A)}))}\). If O ∋ z is open, it must have non-empty intersection with f(supp(P (A)). Hence f −1(O) is open, non-empty and \(f^{-1}(O) \cap \mbox{supp}(P^{(A)}) \neq \varnothing \). From the definition of support, \(P^{(A)}_{f^{-1}(O)} \neq 0\). By definition z ∈ essrank(f). We established that \(essrank(f) \supset \overline {f(\mbox{supp}(P^{(A)}))}\) and hence concluded the proof. Regarding the last statement, if A is bounded σ(A) is compact by Proposition 3.11 (b). Since f is continuous, f(σ(A)) is compact, and closed because \({\mathbb C}\) is Hausdorff, so that \(f(\sigma (A))= \overline {f(\sigma (A))}\). □
Remark 3.54
It is fundamental to stress that in QM (3.39) permits us to adopt the standard operational approach to interpret the observable f(A): it is the observable whose set of possible values is (the closure of) the set of real numbers f(a) where a is a value of A. \(\blacksquare \)
A final result which will be useful later in many contexts is the following proposition.
Proposition 3.55
If H is a Hilbert space and \(B\in {\mathfrak B}({\mathsf H})\) , then B is a linear combination of unitary operators.
Proof
As we know, B can be written as complex linear combination of selfadjoint operators \(B= \frac {1}{2}(B+B^*) + i \frac {1}{2i}(B-B^*)\), so it is sufficient to prove the claim for selfadjoint operators. Consider \(A^*=A \in {\mathfrak B}({\mathsf H})\). If ||A|| = 0 the thesis is trivial, so we assume ||A|| > 0. Then \(A' :=\frac {1}{||A||} A\) satisfies ||A′||≤ 1, so σ(A′) ⊂ [−1, 1] by Proposition 3.47. Moreover, \(A^{\prime }_\pm := A' \pm i \sqrt {I-A^{\prime 2}} \in {\mathfrak B}({\mathsf H})\) are well defined via spectral theory (integrating the corresponding functions on σ(A′)). It is easy to prove that \(A^{\prime }_\pm \) are unitary, for Theorem 3.24 and Proposition 3.29 guarantee \({A^{\prime }_\pm }^*A^{\prime }_\pm =A^{\prime }_\pm {A^{\prime }_\pm }^*=I\). By construction, \(A' = \frac {1}{2}A_+ + \frac {1}{2}A_-\). □
3.3.3 Joint Spectral Measures
The last spectral tool we need to introduce are joint spectral measures (see, e.g., [ReSi80, Mor18]). Everything is stated in the following theorem, whose proof is long and technical in most books. In Sect. 3.6 we shall present an original argument, which by character befits our presentation of the spectral machinery.
Theorem 3.56 (Joint Spectral Measure)
Let \({\mathfrak A} :=\{A_1,A_2,\ldots , A_n\}\) be a set of selfadjoint operators on the Hilbert space H . Suppose that their spectral measures commute:
Then there exists a unique PV M \(P^{({\mathfrak A})}\) on \({\mathbb R}^n\) such that
For every \(f : {\mathbb R} \to {\mathbb C}\) measurable,
where x = (x 1, …, x k, …, x n) and \(f(A_k) := \int _{\mathbb R} f(\lambda ) dP^{(A_k)}\).
Finally, \(B\in {\mathfrak B}({\mathsf H})\) commutes with \(P^{({\mathfrak A})}\) if and only if it commutes with all \(P^{(A_k)}\) , k = 1, 2, …, n.
Proof
See Sect. 3.6. □
Definition 3.57
The PVM \(P^{({\mathfrak A})}\) in Theorem 3.56 is called the joint spectral measure of A 1, A 2, …, A n, and its support \(\mbox{supp}(P^{({\mathfrak A})})\), i.e. the complement in \({\mathbb R}^n\) of the largest open set O with \(P^{({\mathfrak A})}_O=0\), is called the joint spectrum of A 1, A 2, …, A n. \(\blacksquare \)
Example 3.58
The simplest example is provided by considering the n position operators X m on \(L^2({\mathbb R}^n, d^nx)\). It should be clear that the n spectral measures commute because the operator \(P^{(X_k)}_E\), for \(E\in {\mathcal {B}}({\mathbb R})\), acts as multiplication by \(\chi _{{\mathbb R}\times \cdots \times {\mathbb R} \times E \times {\mathbb R}\times \cdots \times {\mathbb R}}\), where E is in the k-th position. The joint spectrum of the n operators X m coincides with \({\mathbb R}^n\) itself.
A completely analogous situation holds for the n momentum operators P k, since they are related to the position operators by means of the unitary Fourier-Plancherel operator, as already seen several times. Again, the joint spectrum of the n operators P m coincides with \({\mathbb R}^n\) itself. \(\blacksquare \)
Here is a useful fact proved by von Neumann (see [RiNa90] for a proof).
Theorem 3.59
Let A, B be (possibly unbounded) selfadjoint operators on the Hilbert space H . If the spectral measures of A and B commute, then there is a third (possibly unbounded) selfadjoint operator C on H such that A = f(C) and B = g(C) for some Borel measurable functions \(f, g : {\mathbb R} \to {\mathbb R}\).
3.3.4 Measurable Functional Calculus
The following proposition provides useful features of f(A), where A is selfadjoint and \(f: {\mathbb R} \to {\mathbb C}\) is Borel measurable. These properties constitute the so-called measurable functional calculus. We suppose here that A = A ∗, but statements can be reformulated for normal operators too [Mor18].
Proposition 3.60
Let A be a selfadjoint operator on the complex Hilbert space H and let \(f, g : \sigma (A) \to {\mathbb C}\) be measurable functions. Let af, f ⋅ g, f + g indicate the pointwise operations ( \(a\in {\mathbb C}\) ). The following facts hold.
-
(a)
If \(f(\lambda )= p_n(\lambda ) := \sum _{k=0}^n a_k \lambda ^k\) with a n ≠ 0, then
$$\displaystyle \begin{aligned}p_n(A) = \sum_{k=0}^n a_k A^k \quad \mathit{\mbox{with}}\ D(p_n(A))= \Delta_{p_n} = D(A^n),\end{aligned}$$where the right-hand side is defined on its standard domain, and A 0 := I, A 1 := A, A 2 := AA, and so forth.
-
(b)
If f = χ E is the characteristic function of \(E \in {\mathcal {B}}(\sigma (A))\) , then
$$\displaystyle \begin{aligned}f(A) = P^{(A)}(E)\:.\end{aligned}$$ -
(c)
Using bar to denote complex conjugation,
$$\displaystyle \begin{aligned}f(A)^* = \overline{f}(A)\:.\end{aligned}$$ -
(d)
For \(a\in {\mathbb C}\) ,
$$\displaystyle \begin{aligned}a f(A) = (af)(A)\:.\end{aligned}$$ -
(e)
D(f(A) + g(A)) = Δ f ∩ Δ g and
$$\displaystyle \begin{aligned}f(A)+g(A) \subset (f+g)(A)\:.\end{aligned}$$There is equality above if and only if Δ f+g = Δ f ∩ Δ g.
-
(f)
D(f(A)g(A)) = Δ f⋅g ∩ Δ g and
$$\displaystyle \begin{aligned}f(A)g(A) \subset (f\cdot g)(A)\:,\end{aligned}$$with equality if and only if Δ f⋅g ⊂ Δ g.
-
(g)
We have \(D(f(A)^*f(A))= \Delta _{|f|{ }^2}\) and
$$\displaystyle \begin{aligned}f(A)^*f(A) = |f|{}^2 (A)\:.\end{aligned}$$ -
(h)
If f ≥ 0 then
$$\displaystyle \begin{aligned}\langle x |f(A) x \rangle \geq 0 \quad \mathit{\mbox{for}}\ x \in \Delta_f.\end{aligned}$$ -
(i)
If x ∈ Δ f ,
$$\displaystyle \begin{aligned}||f(A)x||{}^2 = \int_{\sigma(A)} |f(\lambda)|{}^2 d\mu^{(P^{(A)})}_{xx}(\lambda)\:.\end{aligned}$$In particular, if f is bounded or P (A) -essentially bounded on σ(A), \(f(A) \in {\mathfrak B}({\mathsf H})\) and
$$\displaystyle \begin{aligned}||f(A)|| \leq ||f||{}^{(P^{(A)})}_{\infty} \leq ||f||{}_{\infty}\:.\end{aligned}$$ -
(j)
If U : H →H ′ is a linear (or anti-linear) surjective isometry, then
$$\displaystyle \begin{aligned}Uf(A)U^{-1}= f(UAU^{-1})\end{aligned}$$and, in particular, D(f(UAU −1)) = UD(f(A)) = U( Δ f).
-
(k)
If \(\phi : {\mathbb R} \to {\mathbb R}\) is measurable, then \({\mathcal {B}}({\mathbb R}) \ni E \mapsto P'(E):= P^{(A)}(\phi ^{-1}(E))\) is a PVM on \({\mathbb R}\) . Defining the selfadjoint operator
$$\displaystyle \begin{aligned}A' = \int_{{\mathbb R}} \lambda' dP'(\lambda') \end{aligned}$$such that \(P^{(A')}= P'\) , we have
$$\displaystyle \begin{aligned}A' = \phi(A)\end{aligned}$$and
$$\displaystyle \begin{aligned}f(A') = (f \circ \phi)(A) \quad \mathit{\mbox{and}} \quad \Delta^{\prime}_f = \Delta_{f\circ \phi}\end{aligned}$$for every \(f : {\mathbb R} \to {\mathbb C}\) measurable.
Proof
Everything but (a), (b), (c) and (i) are trivial reformulations of the corresponding statements in Proposition 3.33. As a matter of fact, (b), (c), (h) and (i) are nothing but (3.22), (3.13), (a) in Corollary 3.27 and (3.14) respectively. Item (a) is easy to prove. Let us initially focus on the case p n(λ) = λ n. Observe that A =∫σ(A) λdP (A) λ = p 1(A). Let us prove claim for a given n knowing it is true for n − 1: \(A^n = A A^{n-1} = \int _{\mathbb R} \lambda dP^{(A)}(\lambda ) \int _{\mathbb R} \lambda ^{n-1} dP^{(A)}(\lambda ) = \int _{\mathbb R} \lambda ^n dP^{(A)}(\lambda )=p_n(A)\). In the penultimate equality we used Proposition 3.33 (c): the condition Δf⋅g ⊂ Δg is satisfied for f = ı and g = ı n−1 because the measure \(\mu ^{(P)}_{xx}\) is finite and hence \(\int _{\mathbb R} |\lambda |{ }^{2n} d\mu _{xx}(\lambda )<+\infty \) implies \(\int _{\mathbb R} |\lambda |{ }^{2(n-1)} d\mu _{xx}(\lambda )<+\infty \).
Let us pass to polynomials. For every polynomial \(p_m(\lambda )= \sum _{k=0}^m a_k \lambda ^k\) of degree m (i.e. a m ≠ 0) set \(p_m(A):= \sum _{k=0}^m a_k A^k\). For m = 0 it is clear that \(p_1(A) = \int a_0 dP^{(A)}(\lambda ) = a_0I\). Suppose inductively that p n−1(A) =∫σ(A) p n−1(λ)dP (A)(λ). From Proposition 3.33 (b), if a n ≠ 0 then \(a_nA^n + p_{n-1}(A) = \int _{\mathbb R} a_n\lambda ^n +p_{n-1}(\lambda ) dP^{(A)}(\lambda )\). This is because the condition Δf+g = Δf ∩ Δg in Proposition 3.33 (b) is satisfied for f = a n ı n and g = p n−1 since \(\Delta _{a_n\:\imath ^n+p_{n-1}}= \Delta _{\imath ^n}\), again from the finiteness of \(\mu ^{(P)}_{xx}\). Putting everything together, we have \(\sum _{k=0}^n a_k A^k = \int _{\sigma (A)} p(\lambda ) d\lambda \) for every polynomial \(p(\lambda )= \sum _{k=0}^n a_k \lambda ^k\) of degree n. It is obvious that D(p n(A)) = D(A n) (if a n ≠ 0) by the definition of standard domain. □
3.3.5 A First Glance at One-Parameter Groups of Unitary Operators
Let us start with an elementary result based on Proposition 3.60.
Proposition 3.61
If A : D(A) → H is a selfadjoint operator on the Hilbert space H , then
is a one-parameter group of unitary operators, i.e.
-
(i)
U t is unitary for \(t\in {\mathbb R}\) ,
-
(ii)
U 0 = I and U t U s = U t+s for every \(t,s \in {\mathbb R}\).
As a consequence of (i) and (ii), \(U^*_t=(U_t)^{-1}= U_{-t}\) for \(t \in {\mathbb R}\).
Proof
\(U_t = \int _{{\mathbb R}} e^{it\lambda } dP^{(A)}(\lambda )\) is an element of \({\mathfrak B}({\mathsf H})\) because the function in the integral is bounded due to Proposition 3.60 (i). Then the conclusion follows immediately from (b), (c) and (f) in Proposition 3.60, since e i0 = 1, e itλ e isλ = e i(t+s)λ and \(\overline {e^{it\lambda }}= e^{-it\lambda }\). □
We have a pair of important technical facts about the one-parameter group of unitary operators introduced above.
Proposition 3.62
If A : D(A) → H is a selfadjoint operator on the Hilbert space H , the one-parameter group of unitary operators
is strongly continuous , i.e. U t x → U s x if t → s for every fixed x ∈H . Furthermore
Proof
Since U u is isometric, ||U t x − U s x|| = ||U s(U t−s x − x)|| = ||U t−s x − x||. Therefore continuity at any \(s\in {\mathbb R}\) is equivalent to continuity at 0. Next, Proposition 3.60 (i) entails that
where we used dominated convergence theorem and noticed that \(\mu ^{(P^{(A)})}_{xx}\) is finite and |e itλ − 1|2 ≤ 4. Regarding the second statement, observe that
by (i), (b) and (f) in Proposition 3.60. As a consequence, \(\mu ^{(P^{(A)})}_{U_tx,U_tx}(E) = ||P^{(A)}_EU_tx||{ }^2 = ||U_tP^{(A)}_Ex||{ }^2= ||P^{(A)}_Ex||{ }^2= \mu ^{(P^{(A)})}_{xx}(E)\). Therefore \(\int _{\mathbb R} |\lambda |{ }^2 d\mu _{xx}^{(P^{(A)})}= \int _{\mathbb R} |\lambda |{ }^2 d\mu _{U_tx,U_tx}^{(P^{(A)})}\), meaning U t(D(A)) = D(A). Now Proposition 3.60 (f) proves that \(U_tA= \int _{\mathbb R} e^{it\lambda } \lambda dP^{(A)} = AU_t\) if we write these operators in terms of integrals and observing that the condition on the domains necessary and sufficient to write = in place of ⊂ is here satisfied. □
Proposition 3.63
If A : D(A) → H is a selfadjoint operator on the Hilbert space H and x ∈ D(A), then
Proof
Let us start with s = 0. Notice that if x ∈ D(A), Proposition 3.60 (i) yields
The integrand tends to 0 pointwise as h → 0. On the other hand the mean value theorem, applied to real and imaginary parts of the argument of the absolute value, says that
for some \(h_0, h_0^{\prime } \in [-|H|,|H|]\). The map \({\mathbb R} \ni r \mapsto r^2\) is \(\mu ^{(P^{(A)})}_{xx}\)-integrable since \(x\in D(A)= \Delta _{\imath ^2}\). Finally, dominated convergence theorem proves that the limit of the left-hand side of (3.41) vanishes when h → 0. This establishes the claim for s = 0. The case s ≠ 0 can be proved by observing that
and applying the previous proposition. □
Exercise 3.64
Prove that if \(A \in {\mathfrak B}(H)\) is selfadjoint on the Hilbert space H, then
for every \(t\in {\mathbb R}\), where the series converges in operator norm.
Solution
By Proposition 3.60 (i), using the fact that \(e^{itA} - \sum _{n=0}^{N} \frac {(it)^n}{n!}A^n\) is bounded,
For a fixed \(t \in {\mathbb R}\), the limit as N → +∞ of the right-most term vanishes, proving the thesis. This is because the power series \(e^{z} = \sum _{n=0}^{+\infty } \frac {z^n}{n!}\) has convergence radius + ∞, hence it converges uniformly in every closed disc centred at the origin with finite radius. Therefore the convergence is uniform on any compact set of \({\mathbb C}\). In particular on σ(A), which is compact by Proposition 3.47) since A is bounded.  .
.
3.4 Elementary Quantum Formalism: A Rigorous Approach
We return to the discussion started in the introduction to show how, in practice, the physical hypotheses on quantum systems (1)–(3) must be interpreted mathematically on infinite-dimensional Hilbert spaces. (For convenience we reversed the order of (2) and (3).)
3.4.1 Elementary Formalism for the Infinite-Dimensional Case
Let us begin by listing the general assumptions for a mathematical description of quantum systems.
-
1.
A quantum mechanical system S is always associated to a Hilbert space H, either finite- or infinite-dimensional;
-
2.
observables are represented in terms of (generally unbounded) selfadjoint operators A on H,
-
3.
states are equivalence classes
$$\displaystyle \begin{aligned}{}[\psi] = \{e^{i\alpha} \psi \:|\: \alpha \in {\mathbb R}\}\end{aligned}$$of unit vectors ψ ∈H (the equivalence relation being ψ ∼ ψ′ iff ψ = e ia ψ′ for some \(a\in \mathbb R\)).
We set out to show how the above mathematical assumptions enable us to set the physical properties of quantum systems (1)–(3) of Sect. 1.1.2 in a mathematically nice form for infinite-dimensional Hilbert spaces H.
(1) Randomness
The Borel subset E ⊂ σ(A) represents the outcomes of measurement procedures of the observable associated with the selfadjoint operator A. (In case of continuous spectrum the outcome of a measurement is at least an interval in view of the experimental errors.) Given a state represented by the unit vector ψ ∈H, the probability to obtain outcome E ⊂ σ(A) when measuring A is
where we have used the PVM P (A) of the operator A.
Pursuing this interpretation, the expectation value 〈A〉ψ of A, when the state is represented by the unit vector ψ ∈H, turns out to be
This relation makes sense provided ı : σ(A) ∋ λ → λ belongs to \(L^1(\sigma (A), \mu ^{(P^{(A)})}_{\psi ,\psi })\) (which is equivalent to say that \(\psi \in \Delta _{|\imath |{ }^{1/2}}\) and, in turn, ψ ∈ D(|A|1∕2)). Otherwise the expectation value is not defined. Since
because \(\mu ^{(P^{(A)})}_{\psi ,\psi }\) is finite, we have the popular formula, derived from (3.12):
The associated standard deviation ΔA ψ is
This definition makes sense provided \(\imath \in L^2(\sigma (A), \mu ^{(P^{(A)})}_{\psi ,\psi })\) (i.e. ψ ∈ Δı, or ψ ∈ D(A)).
As before, functional calculus permits us to write the other famed formula
We stress that the Heisenberg inequalities, established in Exercise 1.11(1), are now completely justified, as the reader can easily check.
(3) Collapse of the State
If the Borel set E ⊂ σ(A) is the outcome of an (idealized) measurement of A when the state is represented by the unit vector ψ ∈H, the new state immediately after the measurement is represented by the unit vector
Remark 3.65
Lo and behold this formula does not make sense if \(\mu ^{(P^{(A)})}_{\psi ,\psi }(E)=0\). Moreover the arbitrary phase affecting ψ does not really matter due to the linearity of \(P^{(A)}_E\). \(\blacksquare \)
(2) Compatible and Incompatible Observables
Two observables A, B are compatible—i.e. they can be measured simultaneously—if and only if their spectral measures commute, which means
In this case
where P (A, B) is the joint spectral measure of A and B, has the natural interpretation of the probability to obtain outcomes E and F for a simultaneous measurement of A and B. If instead A and B are incompatible, it may happen that
Sticking to A, B incompatible, (3.47) gives
The meaning is the probability of obtaining first F and then E in subsequent measurements of B and A.
Remark 3.66
It is worth stressing that the notion of probability we are using here cannot be the classical one, because of the presence of incompatible observables. The theory of conditional probability cannot follow the standard rules. The probability \({\mathbb P}_\psi (E_A|F_B)\), that (in a state defined by a unit vector ψ) a certain observable A takes value E A when the observable B has value F B, cannot be computed by the standard procedure
if A and B are incompatible: in general, there is nothing which can be interpreted as the event “E A AND F B” if \(P^{(A)}_E\) and \(P^{(B)}_F\) do not commute! The correct formula is
which leads to well-known properties that depart from the classical theory, the so-called combination of “probability amplitudes” in particular. As a matter of fact, to the day we still do not have a clear notion of (quantum) probability. This issue will be clarified in the next chapter. \(\blacksquare \)
3.4.2 Commuting Spectral Measures
The reason to pass from operators to their spectral measures to define compatible observables is that, if A ad B are selfadjoint and defined on distinct domains, AB = BA does not make sense in general. Moreover, there are counterexamples (due to Nelson) where the commutativity of selfadjoint operators A and B on a common dense invariant subspace, which is a core for A and B, does not imply that their spectral measures commute. Nevertheless, general results again due to Nelson give us the following nice result, which we shall prove later (see Exercise 7.43).
Proposition 3.67
If selfadjoint operators A and B on a Hilbert space H commute on a common dense invariant domain D where A 2 + B 2 is essentially selfadjoint, then the spectral measures of A and B commute.
Definition 3.68
When the spectral measures of two selfadjoint operators A, B commute, i.e., (3.48) holds, one says that A and B commute strongly . \(\blacksquare \)
In addition to the aforementioned direct result by Nelson, there are several other technical facts providing necessary and sufficient conditions for the commutativity of the spectral measures of pairs of selfadjoint operators. The most elementary and perhaps useful is the following one.
Proposition 3.69
Let A, B be selfadjoint operators on the complex Hilbert space H . The following facts are equivalent:
-
(i)
A and B strongly commute,
-
(ii)
e itA e isB = e isB e itA for every \(s,t \in {\mathbb R}\) ,
-
(iii)
\(e^{itA} P^{(B)}_E = P^{(B)}_E e^{itA}\) for every \(t \in {\mathbb R}\) and \(E \in \mathcal {B}({\mathbb R})\) ,
-
(iv)
e itA B ⊂ Be itA for all \(t\in {\mathbb R}\) , or equivalently e itA B = Be itA for all \(t\in {\mathbb R}\).
Under any of the above statements: e itA(D(B)) = D(B) for all \(t\in {\mathbb R}\).
Proof
Evidently (i) implies (ii) since \(\int _{\mathbb R} s dP^{(A)}\int _{\mathbb R} t dP^{(B)}= \int _{\mathbb R} t dP^{(B)}\int _{\mathbb R} s dP^{(A)}\) if s and t are complex simple functions, due to (3.24); the result extends to the exponentials by Proposition (3.29) (c) with suitable sequences of bounded simple functions tending to the exponential functions. Let us prove that (ii) implies (iii). From (ii) and for x, y ∈H, we have 〈x|e −itA e isB e itA y〉 = 〈x|e isB y〉, which may be rephrased as
where U t := e itA. If \(f \in \mathcal {S}({\mathbb R})\), since both \(\mu ^{(P^{(B)})}_{xy}\) and \(\mu ^{(P^{(B)})}_{U_tx,U_ty}\) are complex measures (so their absolute variations are finite measures) we have
The very definition of integral in a complex measure and the Fubini-Tonelli theorem imply that
Since the Fourier transform is a bijection from \(\mathcal {S}({\mathbb R})\) onto \(\mathcal {S}({\mathbb R})\), the previous relation reads
for every \(g \in \mathcal {S}({\mathbb R})\). Using the Stone–Weierstrass theorem and a smoothing procedure, it is possible to prove that if f is a complex, continuous map with compact support in \({\mathbb R}\), say supp(f) ∈ [−a, a], there exists a sequence of smooth functions f n with compact support contained in [−2a, 2a] (obtained by approximating truncated polynomials outside [−2a, 2a], and then smoothing), such that ||f − f n||∞→ 0 when n → +∞. Since the measures in (3.50) are finite, this fact immediately implies that (3.50) holds also when g is continuous and compactly supported. Both Borel measures are regular because, being finite, open sets are countable unions of compact sets with finite measure [Rud86]. Riesz’s theorem for positive (regular) Borel measures [Rud86] implies that \(\mu ^{(P^{(B)})}_{xy}(E)= \mu ^{(P^{(B)})}_{U_tx,U_ty}(E)\) for every Borel set \(E\in \mathcal {B}({\mathbb R})\). In other words \(\langle x| (U^*_tP^{(B)}_EU_t - P^{(B)}_E )y\rangle = 0\) for every x, y ∈H, which in turn means \(U_tP^{(B)}_E = P^{(B)}_EU_t\), namely (iii). In order to prove that (iii) implies the measures P (A), P (B) commute, we proceed as above. Begin by observing that for x, y ∈H we have \(\langle x| e^{itA} P^{(B)}_E y \rangle =\langle x|P^{(B)}_E e^{itA} y\rangle \). The argument used earlier leads to \(\mu ^{(A)}_{P^{(B)}_E x, y}(F)= \mu ^{(A)}_{x, P^{(B)}_Ey}(F)\), namely \(\langle x| P^{(B)}_E P^{(A)}_F y \rangle = \langle x| P^{(A)}_F P^{(B)}_Ey \rangle \) for all x, y ∈H and \(E,F \in \mathcal {B}({\mathbb R})\). This is equivalent to (i).
Finally, assuming e itA B ⊂ Be itA for all \(t\in {\mathbb R}\), applying e −itA to the right of both sides and using the fact that t is arbitrary, proves Be itA ⊂ e itA B for all \(t\in {\mathbb R}\), so e itA B = Be itA \(t\in {\mathbb R}\). This fact is equivalent to e itA Be −itA = B. In turn, the latter is the same as saying that (iii) holds, \(e^{itA} P^{(B)}_Ee^{-itA} = P^{(B)}_E\) for all \(t\in {\mathbb R}\) and \(E\in \mathcal {B}({\mathbb R})\), in view of Proposition 3.49. The last statement is immediate from the second assertion in (iv), by the fact that e itA is bijective. □
With similar arguments one can proved straightforwardly the following proposition regarding a special case \(A\in {\mathfrak B}({\mathsf H})\).
Proposition 3.70
Let A, B be selfadjoint operators on the complex Hilbert space H . If \(A\in {\mathfrak B}({\mathsf H})\) the following facts are equivalent:
-
(i)
A and B strongly commute,
-
(ii)
AB ⊂ BA (with equality if, additionally, \(B\in {\mathfrak B}({\mathsf H})\) ) ,
-
(iii)
Af(B) ⊂ f(B)A if \(f: \sigma (B) \to {\mathbb R}\) is Borel measurable ,
-
(iv)
\(P_E^{(B)}A=AP_E^{(B)}\) if \(E \in {\mathcal {B}}(\sigma (B))\) .
Proof
(i) implies (iv) just using the definition of integral in a PVM that integrates the function ı with respect to P (A). Integrating again f with respect to P (B) we obtain (iii) from (iv): observe that \(\mu ^{(P^{(B)})}_{Ax,Ax}(E) \leq ||A||{ }^2 \mu ^{(P^{(B)})}_{x,x}(E)\) (since P (B) and A commute), so Ax ∈ D(f(B)) if x ∈ D(f(B)). The special choice f = ı produces (ii) from (iii). Finally (ii) implies A n B ⊂ BA n and also, by Exercise 3.64 and because our B is closed as selfadjoint, we have e itA B ⊂ Be itA for every \(t\in {\mathbb R}\). Proposition 3.69 now gives (i). □
Another useful result directed toward the converse statement is the following.
Proposition 3.71
Let A, B be selfadjoint operators on the complex Hilbert space H whose spectral measures commute. Then
-
(a)
ABx = BAx if x ∈ D(AB) ∩ D(BA) .
-
(b)
〈Ax|By〉 = 〈Bx|Ay〉 if x, y ∈ D(A) ∩ D(B).
Proof
-
(a)
Take y ∈ D(B) and x ∈ D(AB). Since e itB e isA = e isA e itB, we have 〈e −itB y|e isA x〉 = 〈y|e isA e itB x〉. Computing the t-derivative at t = 0 with Proposition 3.63 and using the continuity of e isA, we obtain 〈By|e isA x〉 = 〈y|e isA Bx〉. By the definition of adjoint we have e isA x ∈ D(B ∗) = D(B) and e isA Bx = B ∗ e isA x = Be isA x. Assuming x ∈ D(BA) and exploiting Proposition 3.63 once more, we can finally differentiate e isA Bx = Be isA x in s and evaluate at s = 0, using the fact that B is closed. This produces ABx = BAx.
-
(b)
It suffices to differentiate 〈e −itB y|e isA x〉 = 〈e −isA y|e itB x〉 and use Proposition 3.63.
□
3.4.3 A First Look at the Time Evolution of Quantum States
We have already mentioned that for quantum systems in an inertial frame subject to temporal homogeneity, the time evolution of states is described in terms of a strongly continuous one-parameter group of unitary operators of the form \(U_t := e^{-\frac {it}{\hbar } H}\), \(t\in {\mathbb R}\), where the selfadjoint operator H is called the Hamiltonian operator of the quantum system (it depends on the reference frame). The observable H has the physical meaning of the energy of the quantum system in the frame of reference considered. If a quantum state is represented at time t = 0 by the unit vector ψ ∈H, where H is the Hilbert space of the system, the evolved state ψ t at a generic time instant t is therefore
We shall not discuss here the motivations of this description of time evolution, but only make a few observations.
Remark 3.72
-
(a)
If we represent the state ψ at t = 0 by another vector ψ′ := e iα ψ, the evolved state is represented, coherently, by \(\psi ^{\prime }_t = U_t \psi ' = e^{i\alpha } U_t\psi \) in view of linearity of U t. This ensures that the description of time evolution is phase-independent as expected: it preserves equivalence classes
$$\displaystyle \begin{aligned}{}[\psi] = \{e^{i\alpha} \psi \:|\: \alpha \in {\mathbb R}\}\end{aligned}$$of unit vectors, i.e. states. As a consequence, we can define an action of time evolution on states unambiguously: U t[ψ] := [U t ψ].
-
(b)
Since U t is isometric, the unit normalization of ψ t is preserved by time evolution, in agreement with the interpretation of the measures \(\mu ^{(P^{(A)})}_{\psi _t,\psi _t}\), whereby \(\mu ^{(P^{(A)})}_{\psi _t,\psi _t}({\mathbb R}) =1\) (they are probability measures). \(\blacksquare \)
According to Propositions 3.62 and 3.63, if ψ ∈ D(H), from (3.51) we have
We have thus recovered the celebrated Schrödinger equation:
It is worth stressing that the correct topology to calculate the derivative is the topology of the Hilbert space. In other words, the Schrödinger equation is not a standard PDE in the simplest situation in standard QM, namely \({\mathsf H}= L^2({\mathbb R}^3, d^3x)\): there
for some real function \(V : {\mathbb R}^n \to {\mathbb R}\), and H 0 is defined on a suitable dense linear domain D(H 0) ⊂H of smooth functions, where furthermore it is essentially selfadjoint. Nevertheless, it is possible to prove that under suitable hypotheses jointly regular solutions \(\psi : {\mathbb R} \times {\mathbb R}^3 \to {\mathbb C}\) of the PDE interpretation of (3.52),
define proper solutions of (3.52).
A very particular class of physically interesting solutions are the so-called stationary states of a given Hamiltonian operator H. They are defined when \(\sigma _p(H) \neq \varnothing \). If E ∈ σ p(H) and ψ E ∈ D(H) is a corresponding eigenstate, so that Hψ E = Eψ E, its time evolution is trivial
The quantum state [ψ E] associated to ψ E is a stationary state with energy E. Notice that this state is fixed under time evolution, since states are (normalized) vectors up to phase, and \(e^{-i\frac {t}{\hbar } E}\) is such.
Consider a non-relativistic spinless particle described on \({\mathsf H}= L^2({\mathbb R}^3, d^3x)\), where the position operators along the Cartesian axes of the inertial reference frame are the multiplication operators X j of Example 2.59. For a stationary state \(\psi _E \in L^2({\mathbb R}^3,dx)\) the probability density |ψ Et(x)|2 = |ψ E(x)|2 of finding the particle at \(x\in {\mathbb R}^3\) is constant. For example, look at the electron in the hydrogen atom (with mass m and electrical charge e, and assuming the proton is located at the origin and generates the Coulomb force as a geometric point of the matter). Stationary states with energy levels corresponding to the spectrum of the Coulomb Hamiltonian \(\overline {H_0}\), where
define the orbitals of the atom.
Remark 3.73
Roughly speaking stationary states are stable states of matter, and all relatively stable structures of physical objects are described in terms of stationary quantum states of the Hamiltonian operator of the system. These states may cease to be stable when the Hamiltonian changes because of interactions with some external quantum system. For instance, the stationary states of the electron of the hydrogen atom are stationary as soon as the system is kept isolated. When interacting with other systems (especially photons), these states become non-stationary because they are not represented by eigenvectors of the complete Hamiltonian operator of the overall system. Even in an isolated hydrogen atom the proton should be treated quantistically, and the complete system is made of a pair of quantum particles described on an overall Hilbert space \(L^2({\mathbb R}_e^3 \times {\mathbb R}_p^3, d^3x_e\otimes d^3x_p)\). Usually the motion of the proton is neglected and is treated classically. This is because its mass is around 2000 times that of the electron, and in many applications where one is essentially interested in the motion of the electron, it may as well be considered as a fixed classical particle. \(\blacksquare \)
Example 3.74
Let us consider a free spinless particle of mass m > 0. In orthonormal Cartesian coordinates of an inertial reference frame, its Hilbert space is \(L^2({\mathbb R}^3, d^3x)\). This explicit representation of the Hilbert space of a non-relativistic particle, where the position operators are multiplication operators, is called position picture (or position representation). The Hamiltonian operator H is the unique selfadjoint extension of the essentially selfadjoint operator
It is evident that it includes only the kinetic part of the energy. In this sense the particle is free. Now, it is easier to represent the Hilbert space as an L 2 space where the momentum operators are described by multiplication operators. As we know from the content of Example 2.59 (2) (use Eq. (2.24) in particular), this realisation of the Hilbert space is related to the position representation by means of the Fourier-Plancherel operator
This Hilbert space isomorphism reduces to the standard integral Fourier transform on \(\mathcal {S}({\mathbb R}^3)\), and transforms this subspace into itself bijectively (changing the variable of the functions from x to k). The representation \(L^2({\mathbb R}^3, d^3k)\) of the Hilbert space, where momenta are multiplication operators, is popularly known as the momentum picture (or momentum representation). The corresponding Hamiltonian operator \(H = \overline {H_0}\) is represented by the selfadjoint operator
Since it is the square of the momentum operator up to the constant factor (2m)−1, it must act as
where \(k^2 := \sum _{j=1}^3 k^2_j\), and
The spectrum of H is continuous and it is not difficult to prove that σ(H) = σ c(H) = [0, +∞) as a byproduct of (3.53). This is expected from physical considerations, since the energy is purely kinetic.
Time evolution has a direct representation here:
Notice that the right-hand side belongs to \(\mathcal {S}({\mathbb R}^3)\) at every time t if it does at t = 0.
Time evolution has a corresponding representation in the space \(L^2({\mathbb R}^3, d^3x)\), obtained through the action of the Fourier-Plancherel isomorphism
If \(\psi \in \mathcal {S}({\mathbb R}^3)\), we can use the standard integral Fourier transform
Composing these transformations with (3.54) we find
Note in particular that the time evolution leaves fixed the space \(\mathcal {S}({\mathbb R}^3)\). \(\blacksquare \)
3.4.4 A First Look at (Continuous) Symmetries and Conserved Quantities
As we shall discuss better later, physical operations changing the states of a given quantum system are pictured in terms of either unitary or anti-unitary transformations U : H →H, called (quantum) symmetries.
Symmetries U transform vectors ψ↦ψ U := Uψ but preserve norms (U is isometric by hypothesis) and do not depend on the phase (e iα ψ maps to e iα ψ U). We may therefore pass to the quotient, to the effect that the action of a symmetry is well defined on equivalence classes of vectors, i.e., on pure states: U[ψ] := [Uψ].
A particular subclass of symmetries are continuous symmetries. These are strongly continuous one-parameter groups of unitary operators \(\{e^{isA}\}_{s\in {\mathbb R}}\) generated by some selfadjoint operator A : D(A) →H. This A is interpreted as an observable somehow related to the continuous symmetry, and is called the generator of the symmetry.
When a continuous symmetry commutes with time evolution, i.e. (always assuming ħ = 1)
the symmetry is said to be a dynamical symmetry. This feature has a fundamental consequence. The generator B becomes a constant of motion, in the sense that all statistical properties of the outcomes of measurements of B on a given state ψ ∈H turn out to be independent of the time evolution of ψ. Applying Proposition 3.69, if \(E \in \mathcal {B}({\mathbb R})\) the probability that the outcome of measuring B at time t belongs to E is
which coincides to the probability of obtaining E at time t = 0 when measuring B. The crucial passage above is the swap \(P^{(B)}_E U_t=U_t P^{(B)}_E\), which is consequence of (3.56) and Proposition 3.69 for A = H.
Remark 3.75
If B is a constant of motion as defined above, the expectation value of B and its standard deviation are constant in time, just by definition of expectation value and standard deviation.
These two facts, albeit immediate from the definition of expectation value and standard deviation, are usually derived by physicists using Eqs. (3.44) and (3.45) (when the requirements on the domains are fulfilled) and Proposition 3.69:
and
\(\blacksquare \)
Example 3.76
Consider the momentum operator P j along the j-th axis in \({\mathbb R}^3\). We want to examine the strongly continuous one-parameter group of unitary operators \(V_a := e^{-iaP_j}\) with \(a\in {\mathbb R}\). It is convenient to deal with the momentum representation. As we know, here P j is nothing but the multiplication operator \(\left (P^{\prime }_j \widehat {\psi }\right )(k) = k_j\widehat {\psi }(k)\), for every \(\psi \in L^2({\mathbb R}^3, d^3k)\). As in Example 3.74, we adopt the notation \(A':= \hat {\mathcal {F}} A \hat {\mathcal {F}}^{-1}\) to write down the momentum representation A′ of operators given by A in position representation. It is easy to prove that
Using (3.55), if \(\psi \in \mathcal {S}({\mathbb R}^3)\) then \(\widehat {\psi } \in \mathcal {S}({\mathbb R}^3)\) and vice versa, so
In other words, V a shift wavefunctions in \(\mathcal {S}({\mathbb R}^3)\) along the coordinate unit vector e j by the length a. Note that \(\mathcal {S}({\mathbb R}^3)\) is dense in \(L^2({\mathbb R}^3, d^3x)\) and V a is continuous. Moreover, if \(\mathcal {S}({\mathbb R}^3) \ni \psi _n \to \psi \in L^2({\mathbb R}^3, d^3x)\) as n → +∞, then \(\mathcal {S}({\mathbb R}^3) \ni \psi _n(\cdot -ae_j) \to \psi (\cdot -ae_j) \in L^2({\mathbb R}^3, d^3x)\) as n → +∞ by the translational invariance of the Lebesgue measure d 3 x. Summing up,
In other words,
In the language of physicists, the momentum along the j-th direction is the generator of physical spatial translations of the quantum system along the j-th axis.
This is not the whole story if we also assume that the Hamiltonian of the particle is the free Hamiltonian (3.53) in momentum representation. If so, time evolution is represented by (3.54) again in momentum representation. It is therefore evident that
We conclude that with the above free Hamiltonian the momentum operator along the j-th direction is a constant of motion. Therefore the statistical features of the measurements of P j are invariant along the temporal evolution of the state of the system. \(\blacksquare \)
3.5 Round-Up of Operator Topologies
There are at least 7 to 9 relevant topologies [KaRi97, BrRo02] in Quantum Theory which enter the game when one discusses sequences of operators. We shall limit ourselves to illustrate quickly a few of the most important ones [Mor18]. We shall work in a Hilbert space H, even though some of our examples adapt to more general ambient spaces.
-
(a)
The finest (strongest) topology of all is the uniform operator topology on \({\mathfrak B}({\mathsf H})\). It is the Hausdorff topology induced by the operator norm || || defined in (2.8).
As a consequence of the definition, a sequence of elements \(A_n \in {\mathfrak B}({\mathsf H})\) is said to converge uniformly to \(A\in {\mathfrak B}({\mathsf H})\) when ||A n − A||→ 0 as n → +∞.
We already know that \({\mathfrak B}({\mathsf H})\) is a Banach algebra for that norm, and a unital C ∗-algebra too.
-
(b)
Take a subspace D ⊂H and the complex vector space \({{\mathfrak L}}(D; {\mathsf H})\) of operators A : D →H. The strong operator topology on \({\mathfrak L}(D; {\mathsf H})\) is the Hausdorff topology induced by the seminorms p x where x ∈ D and p x(A) := ||Ax|| for \(A \in {\mathfrak L}(D;{\mathsf H})\). By definition of topology induced by a family of seminorms, the open sets are the empty set and (arbitrary) unions of intersections of a finite number n of open balls \(B^{(x_1,\ldots ,x_n)}_{r_1,\ldots ,r_n}(A_0)\) associated to the seminorms \(p_{x_i}\) with x i ∈ D distinct, of arbitrary finite radii r i > 0 and common fixed centre \(A_0\in {\mathfrak L}(D; {\mathsf H})\):
$$\displaystyle \begin{aligned}B^{(x_1,\ldots,x_n)}_{r_1,\ldots,r_n}(A_0) :=\{A \in {\mathfrak L}(D; {\mathsf H}) \:|\: p_{x_i}(A-A_0) \leq r_i \:, i=1,\ldots, n\}\:.\end{aligned}$$Therefore a sequence of elements \(A_n \in {\mathfrak L}(D; {\mathsf H})\) converges strongly to \(A\in {\mathfrak L}(D;{\mathsf H})\) when ||(A n − A)x||→ 0 as n → +∞ for every x ∈ D.
It should be evident that, if we restrict ourselves to work in \({\mathfrak B}({\mathsf H})\), the uniform operator topology is finer (larger) than the strong operator topology.
-
(c)
The weak operator topology on \({\mathfrak L}(D;{\mathsf H})\) is the Hausdorff topology induced by the seminorms p x,y with x ∈H, y ∈ D and p x,y(A) := |〈x|Ay〉| if \(A \in {\mathfrak L}(D; {\mathsf H})\). In other words, its open sets are the empty set and (arbitrary) unions of intersections of a finite number n of open balls \(B^{(x_1,y_1,\ldots ,x_n,y_n)}_{r_1,\ldots ,r_n}(A_0)\) associated to the seminorms \(p_{x_i,y_i}\) with x i ∈H and y i ∈ D distinct, of arbitrary finite radii r i > 0 and a common fixed centre \(A_0\in {\mathfrak L}(D; {\mathsf H})\):
$$\displaystyle \begin{aligned}B^{(x_1,y_1,\ldots,x_n,y_n)}_{r_1,\ldots,r_n}(A_0) :=\{A \in {\mathfrak L}(D; {\mathsf H}) \:|\: p_{x_i, y_i}(A-A_0) \leq r_i \:, i=1,\ldots, n\}\:.\end{aligned}$$A sequence of elements \(A_n \in {\mathfrak L}(D;{\mathsf H})\) is said to converge weakly to \(A\in {\mathfrak L}(D;{\mathsf H})\) when |〈x|(A n − A)y〉||→ 0 as n → +∞ for every x ∈H and y ∈ D. The weak operator topology lies at the opposite end to the uniform operator topology, for it is the coarsest (smallest) of all.
We present two more intermediate topologies which depend on the space \({\mathfrak B}_1({\mathsf H})\) of trace-class operators we will discuss later.
-
(d)
The ultrastrong topology (also known as σ -strong topology) on \({\mathfrak B}({\mathsf H})\) is the Hausdorff topology associated as above to seminorms p T, with \(T\in {\mathfrak B}_1({\mathsf H})\) and T ≥ 0, where \(p_{T}(A) := \sqrt {tr(TA^*A)}\) if \(A \in {\mathfrak B}({\mathsf H})\). In spite of the name, it is weaker than the uniform operator topology.
-
(e)
The ultraweak topology (or σ -weak topology) on \({\mathfrak B}({\mathsf H})\) is the Hausdorff topology induced as above by seminorms q T, \(T\in {\mathfrak B}_1({\mathsf H})\), defined as \(q_{T}(A) := |\sqrt {tr(TA)}|\) if \(A \in {\mathfrak B}({\mathsf H})\). It is finer than the weak operator topology.
The topological dual of \({\mathfrak B}({\mathsf H})\) possesses a special topology of its own.
-
(f)
Any normed space \({\mathfrak B}({\mathsf H})\) induces a significant weak topology on its topological dual
$$\displaystyle \begin{aligned}{\mathfrak B}({\mathsf H})^*:= \{f: {\mathfrak B}({\mathsf H}) \to {\mathbb C}\:| \: f\ \mbox{linear and continuous}\}\:.\end{aligned}$$The ∗ -weak topology on \({\mathfrak B}({\mathsf H})^*\) is associated as above to the family of seminorms \(\{p_A\}_{A\in {\mathfrak B}({\mathsf H})}\) defined as p A(f) := |f(A)| for every \(f\in {\mathfrak B}({\mathsf H})'\). The definition is general, and valid for normed spaces \({\mathfrak B}\) and their duals \({\mathfrak B}^*\) (replacing \({\mathfrak B}({\mathsf H})\) and \({\mathfrak B}({\mathsf H})^*\)). The Hahn–Banach theorem says that the ∗-weak topology is Hausdorff because the functionals in \({\mathfrak B}'\) separate the elements of \({\mathfrak B}\). Notice that \({\mathfrak B}'\) is also a normed Banach space for the standard operator norm
$$\displaystyle \begin{aligned}||f|| = \sup_{0\neq A\in {\mathfrak B}} \frac{|f(A)|}{||A||{}_{\mathfrak B}}\:.\end{aligned}$$This topology is stronger than the ∗-weak one. The relevance of the ∗-weak topology is due in particular to the Banach–Alaoglu theorem, whereby the closed unit ball in \({\mathfrak B}({\mathsf H})^*\) is compact in the ∗-weak topology.
Example 3.77
-
(1)
If \(f: {\mathbb R} \to {\mathbb C}\) is Borel measurable, and A a selfadjoint operator on H, consider the sets
$$\displaystyle \begin{aligned}R_n := \{r \in {\mathbb R} \:|\: |f(r)|< n\}\quad \mbox{ for}\ n \in {\mathbb N}\:.\end{aligned}$$It is clear that \(\chi _{R_n}f \to f\) pointwise as n → +∞ and \(|\chi _{R_n}f|{ }^2\leq |f|{ }^2\). As a consequence, if we restrict to Δf the operators appearing below on the left,
$$\displaystyle \begin{aligned}\left.\int_{\sigma(A)} \chi_{R_n}f dP^{(A)}\right|{}_{\Delta_f}\to f(A) \quad \mbox{strongly, as}\ n\to +\infty,\end{aligned}$$as an immediate consequence of Lebesgue’s dominated convergence theorem and the first part of Proposition 3.60 (i). (See also exercise 3.36.)
-
(2)
If in the previous example f is bounded on σ(A), and f n → f uniformly on σ(A) (or \(||f-f_n||{ }^{(P^{(A)})}_\infty \to 0\) P-essentially uniformly), then
$$\displaystyle \begin{aligned}f_n(A) \to f(A)\quad \mbox{uniformly, as}\ n\to+ \infty,\end{aligned}$$again by the second part of Proposition 3.60 (i). \(\blacksquare \)
Exercise 3.78
Prove that a selfadjoint operator A on the Hilbert H admits a dense set of analytic vectors in its domain.
Solution
Consider the family of functions f n = χ [−n,n] where \(n\in {\mathbb N}\). As in Example 3.77 (1), we have \(\psi _n := f_n(A)\psi = \int _{[-n,n]} 1 dP^{(A)}\psi \to \int _{\mathbb R} 1 dP^{(A)}\psi = P^{(A)}_{{\mathbb R}}\psi = \psi \) when n → +∞. Therefore the set \(D:= \{\psi _n\:|\: \psi \in {\mathsf H}\:, n \in {\mathbb N}\}\) is dense in H. The elements of D are analytic vectors for A as we go on to prove. Clearly ψ n ∈ D(A k) since \(\mu ^{(P^{(A)})}_{\psi _n,\psi _n}(E) = \mu ^{(P^{(A)})}_{\psi ,\psi }(E\cap [-n,n])\) by definition of \(\mu ^{(P^{(A)})}_{x,y}\). Therefore \(\int _{{\mathbb R}} |\lambda ^k|{ }^2 d \mu ^{(P^{(A)})}_{\psi _n,\psi _n}(\lambda ) = \int _{[-n,n]} |\lambda |{ }^{2k} d \mu ^{(P^{(A)})}_{\psi ,\psi }(\lambda ) \leq \int _{[-n,n]}|n|{ }^{2k} d \mu ^{(P^{(A)})}_{\psi ,\psi }(\lambda ) \leq |n| ^{2k} \int _{{\mathbb R}} d \mu ^{(P^{(A)})}_{\psi ,\psi }(\lambda ) = |n|{ }^{2k} ||\psi ||{ }^2 < +\infty \). Similarly \(||A^k\psi _n||{ }^2 = \langle A^k\psi _n | A^k \psi _n\rangle = \langle \psi _n | A^{2k} \psi _n\rangle = \int _{{\mathbb R}} \lambda ^{2k} d \mu ^{(P^{(A)})}_{\psi _n,\psi _n}(\lambda ) \leq |n|{ }^{2k} ||\psi ||{ }^2\). We conclude that \(\sum _{k=0}^{+\infty } \frac {(it)^k}{k!} ||A^k\psi _n||\) converges for every \(t\in {\mathbb C}\) because it is dominated by \(\sum _{k=0}^{+\infty } \frac {|t|{ }^k}{k!} |n|{ }^{2k} ||\psi ||{ }^2 = e^{|t|\:|n|{ }^2} ||\psi ||{ }^2\). \(\blacksquare \)
3.6 Existence Theorems of Spectral Measures
This final section is devoted to proving the existence of a PVM \(P^{(A)} : \mathcal {B}({\mathbb R}) \to \mathcal {L}({\mathsf H})\) for a selfadjoint operator A : D(A) →H on a Hilbert space H, which was announced in Theorem 3.40 (a). The remaining statements of that theorem have been already established. As an intermediate result we shall demonstrate the spectral theorem for normal operators on \({\mathfrak B}({\mathsf H})\). We will furnish a proof of Theorem 3.56 on joint spectral measures.
3.6.1 Continuous Functional Calculus
Let us start by establishing general properties of the spectral theory of bounded operators and unital C ∗-algebras.
Proposition 3.79
Take \(A\in {\mathfrak B}({\mathsf H})\) for some Hilbert space H and let \(p: {\mathbb C} \to {\mathbb C}\) be a complex polynomial of fixed degree n = 0, 1, …. Then
where p(A) is understood as in Proposition 3.60 (a). Furthermore
All this holds also if we replace \(A\in {\mathfrak B}({\mathsf H})\) by \(a\in {\mathfrak A}\) , where \({\mathfrak A}\) is any unital C ∗ -algebra.
Proof
We use explicitly Proposition 3.7: for any \(A\in {\mathfrak B}({\mathsf H})\), λ ∈ σ(A) iff A − λI : H →H is bijective.
First of all we factor polynomials irreducibly with help of the fundamental theorem of algebra: \(p(z) = c(z-\lambda _1)^{n_1}\cdots (z-\lambda _k)^{n_r}\), where the complex roots λ 1, …, λ r have multiplicity n 1, …, n r > 0, ∑l n k = n and c ≠ 0. A corresponding decomposition holds for \(p(A) = c(A-\lambda _1I)^{n_1}\cdots (A-\lambda _kI)^{n_k}\). Define μ := p(λ). As the polynomial \({\mathbb C} \ni z \mapsto p'(z) := p(z)-\mu \) has a zero at z = λ, its factorization contains the term (z − λ), whence p(A) − μI has (A − λI) as a factor. If λ ∈ σ(A), the operator (A − λI) is not bijective and therefore p′(A) := p(A) − μI (factored as \((A-\lambda ^{\prime }_k I)^{n^{\prime }_k}\)) cannot be a bijection from H to H: indeed, if (A − λI) is not injective, we can swap it over to the end in the product p′(A) (factors commute), whence p′(A) cannot be injective. If (A − λI) is not surjective, we can move it in front of p′(A) (as first factor), so p′(A) cannot be surjective. All in all, λ ∈ σ(A) implies μ = p(λ) ∈ σ(p(A)), i.e. p(σ(A)) ⊂ σ(p(A)). Let us prove the opposite inclusion. Suppose μ ∈ σ(p(A)). We know that \(p(z)-\mu = c (z-\alpha _1)^{n^{\prime }_1}\cdots (z-\alpha _{k'})^{n^{\prime }_{r'}}\). If all \(\alpha _{k'}\) belonged to ρ(A), the operator p(A) : H →H would be bijective with left and right inverse \(c^{-1} (A-\alpha _1 I)^{-n^{\prime }_1}\cdots (A-\alpha _{k'}I)^{-n^{\prime }_{r'}}\), an absurd. So at least one of the \(\alpha _{k'}\) must belong to σ(A), and \(p(\alpha _{k'})-\mu =0\). In other words μ ∈ p(σ(A)), which proves σ(p(A)) ⊂ p(σ(A)).
The second statement is quite obvious by observing that if \(T \in {\mathfrak B}({\mathsf H})\), then T ∗ is bijective if and only if T is (Exercise 2.29). In this case (T ∗)−1 = (T −1)∗. Applying this to A − λI proves the claim. With obvious modifications the argument still holds when \({\mathfrak B}({\mathsf H})\) is replaced by a unital C ∗-algebra \({\mathfrak A}\). □
We pass now to an important consequence, whose proof holds for any unital C ∗-algebra in place of \({\mathfrak B}({\mathsf H})\). The first assertion extends Proposition 3.47 and proves that it is actually independent of the spectral theorem.
Proposition 3.80
If \(A \in {\mathfrak B}({\mathsf H})\) is normal (A ∗ A = AA ∗ ) then
If A = A ∗ and \(p: {\mathbb R} \to {\mathbb C}\) is a polynomial, then

The results are valid also by replacing A with a in a unital C ∗ -algebra \({\mathfrak A}\).
Proof
Let us prove (3.59). We need a preliminary, and quite interesting, lemma.
Lemma 3.81 (Gelfand’s Formula for the Spectral Radius)
If \(A \in {\mathfrak B}({\mathsf H})\) for some Hilbert space H , then
The formula is valid for elements \(a\in {\mathfrak A}\) in a unital C ∗ -algebra as well.
Proof Define \(r_A := \sup \{ |\lambda | \:|\: \lambda \in \sigma (A)\}\). If |λ| > r A, then the resolvent R λ(A) is well defined. The Banach-space-valued map ρ(A) ∋ λ↦R λ(A) is holomorphic, and its Taylor expansion reads
where ζ = 1∕λ. It converges at least for |ζ| < 1∕||A|| (Proposition 3.10). The renowned Hadamard theorem (very easily generalizable to holomorphic maps with values in Banach spaces) guarantees that the convergence radius is determined by the first singularity, which necessarily belongs to σ(A). The series \(-\sum _{n=0}^{+\infty }{\zeta ^{n+1}}T^n\) therefore converges for |ζ| < 1∕r A and has convergence radius R ≥ 1∕r A. Hadamard’s formula for R then reads
On the other hand (3.58) implies σ(A n) = {μ n | μ ∈ σ(A)}, so by Proposition 3.10 we have
and hence r A ≤liminfn||A n||1∕n. In summary r A ≤liminfn||A n||1∕n ≤limsupn||A n||1∕n = r A, which is what we claimed. □ Let us take up the proof of Proposition 3.80 and suppose A = A ∗. Then ||A 2|| = ||A ∗ A|| = ||A||2 and, similarly, ||(A 2)2|| = ||A 2||2 = ||A||4, ||(A 4)2|| = ||A 4||2 = ||A||8 and so on. In general \(||A^{2^n}||=||A||{ }^{2^n}\). Applying (3.61), we find
Now consider \(A\in {\mathfrak B}({\mathsf H})\), so ||A n|| = ||(A n)∗ A n||1∕2 = ||(A ∗)n A n||1∕2. If A is normal, all operators commute and ||A n|| = ||(A ∗ A)n||1∕2. Since A ∗ A is selfadjoint, we can implement the result above:
At last, let us prove (3.60). Since A is selfadjoint, p(A) is normal. Therefore

where we exploited (3.58) in the last passage. □
The utmost consequence of these propositions is the following theorem, which establishes the existence and continuity of the so-called continuous functional calculus for bounded selfadjoint operators. The theorem holds as it stands for unital C ∗-algebras.
Theorem 3.82
Let \(A \in {\mathfrak B}({\mathsf H})\) be a selfadjoint operator on the Hilbert space H . There exists a unique representation of unital ∗ -algebras (Definition 2.27 ), called continuous functional calculus ,
that is continuous (with respect to ||⋅||∞ on the domain and the operator norm on the codomain) and such that Ψ(ı) = A (where \(\imath : \sigma (A) \ni x \mapsto x \in {\mathbb R}\) ). Furthermore
-
(a)
Ψ is isometric and hence injective,
-
(b)
\(B\in {\mathfrak B}({\mathsf H})\) commutes with every f(A) if B commutes with A.
The theorem holds replacing \({\mathfrak B}({\mathsf H})\) by a unital C ∗ -algebra \({\mathfrak A}\) and A by a selfadjoint element \(a \in {\mathfrak A}\).
Proof
If f ∈ C(σ(A)), there exist complex polynomials p
n → f uniformly on σ(A) as n → +∞ by the Stone–Weierstrass theorem. Define f(A) :=limn→+∞
p
n(A). Due to (3.60), the sequence p
n(A) is Cauchy. Hence there is a limit element in \({\mathfrak B}({\mathsf H})\) because this space is complete (Theorem 2.20). It is evident that the limit point does not depend on the sequence, since a different sequence would satisfy  . The map f↦f(A) is evidently isometric. Next observe that, if we only consider polynomials, f↦f(A) is linear, it preserves the product, and \(\overline {f}\mapsto f(A)^*\). These features are preserved under the limiting process when f ∈ C(σ(A)) is a general map. By construction f(1) = I and f(ı) = A. If B commutes with A, it commutes with all polynomials p(A). Hence
. The map f↦f(A) is evidently isometric. Next observe that, if we only consider polynomials, f↦f(A) is linear, it preserves the product, and \(\overline {f}\mapsto f(A)^*\). These features are preserved under the limiting process when f ∈ C(σ(A)) is a general map. By construction f(1) = I and f(ı) = A. If B commutes with A, it commutes with all polynomials p(A). Hence
To conclude, we prove that a continuous representation of unital ∗-algebras \(\Phi : C(\sigma (A)) \to {\mathfrak B}({\mathsf H})\) coincides with Ψ if we impose Φ(ı) = A. In fact, Ψ(ı) = Φ(ı) = A and Ψ(1) = Φ(1) = I, therefore Ψ(p) = Φ(p) for every polynomial p. By continuity, if p n → f as n → +∞ in the norm ||⋅||∞ on σ(A), we have Ψ(f) = Φ(f). All arguments carry through if we take a unital C ∗-algebra \({\mathfrak A}\) instead of \({\mathfrak B}({\mathsf H})\) and an element \(a=a^* \in {\mathfrak A}\) instead of A. □
3.6.2 Existence of Spectral Measures for Bounded Selfadjoint Operators
A cardinal consequence of Theorem 3.82 is the following proposition, which goes in the direction of the spectral theorem. Recall that M b(σ(A)) indicates the unital C ∗-algebra of complex, bounded and Borel-measurable functions on σ(A), with norm ||⋅||∞. We point out that in order to formulate this result the Hilbert structure is essential, so no straightforward generalizations exist for abstract C ∗-algebras.
Proposition 3.83
Let \(A \in {\mathfrak B}({\mathsf H})\) be a bounded selfadjoint operator on the Hilbert space H . There exists a norm-decreasing (hence continuous) representation of unital ∗ -algebras (Definition 2.27 ) \(\Psi ': M_b(\sigma (A)) \to {\mathfrak B}({\mathsf H})\) such that Ψ′(ı) = A . The representation also satisfies:
-
(a)
 ,
,
-
(b)
\(B\in {\mathfrak B}({\mathsf H})\) commutes with Ψ′(f) for every f ∈ M b(σ(A)) if B commutes with A,
-
(c)
Suppose M b(σ(A)) ∋ f n → f pointwise as n → +∞ and |f n|≤ K for some K ∈ [0, +∞) and all n. Then
$$\displaystyle \begin{aligned}\Psi'(f_n)x \to \Psi'(f)x \quad \mathit{\mbox{for every}}\ x\in {\mathsf H}.\end{aligned}$$
Proof
Taking x, y ∈H, the linear map C(σ(A)) ∋ f↦F x,y(f) := 〈x| Ψ(A)y〉 satisfies |F x,y(f)|≤||x|| ||y|| ||f||∞. Riesz’s theorem for complex measures [Rud91] implies that there exists a unique complex, regular Borel measure \(\mu _{xy} : \mathcal {B}(\sigma (A)) \to {\mathbb C}\) such that
and also ||F xy|| = |μ xy|(σ(A)) ≤||x|| ||y||. Actually, all complex Borel measures on \(\mathcal {B}(\sigma (A))\) are regular since the open sets of σ(A) are unions of countably many compact sets [Rud91]. Since \(\Psi (\overline {f})= \Psi (f)^*\) and by standard inner product properties the complex measures \(\mu _{xy}(E), \overline {\mu _{yx}(E)}\) produce the same result when we integrate continuous functions. In view of uniqueness, therefore, \(\mu _{xy}(E) = \overline {\mu _{yx}(E)}\). Using Riesz’s Lemma, if f ∈ M b(σ(A)) there exists a unique operator \(\Psi '(f) \in {\mathfrak B}({\mathsf H})\) such that
and |〈x| Ψ′(f)y〉|≤||f||∞|μ xy|(σ(A)) ≤||f||∞||x|| ||y||, so || Ψ′(f)||≤||f||∞. By construction Ψ′(1) = I and Ψ′(ı) = A. Furthermore M b(σ(A)) ∋ f↦ Ψ′(f) is linear and therefore it coincides with Ψ on polynomials. Continuity implies that it coincides with Ψ on C(σ(A)), proving (a). Ψ′ satisfies \(\Psi '(f)^* = \Psi '(\overline {f})\) as a consequence of (3.63), the fact that the inner product is Hermitian, and \(\mu _{xy}(E) = \overline {\mu _{yx}(E)}\). To conclude the proof of the first statement it is enough to prove Ψ′(f) Ψ′(g) = Ψ′(f ⋅ g). Take f, g ∈ C(σ(A)). Since Ψ(f ⋅ g) = Ψ(f) Ψ(g) and Ψ′ extends Ψ:
Riesz’s theorem implies that \(\mu _{x,\Psi '(g)y}\) equals the complex, regular Borel measure λ such that
Therefore
As a consequence
for x, y ∈H, f ∈ M b(σ(A)), g ∈ C(σ(A)). By a similar reasoning
must hold also if g ∈ M b(σ(A)). Summing up, for x, y ∈H, f, g ∈ M b(σ(A)), we have
whence Ψ′(f ⋅ g) = Ψ′(f) Ψ′(g) as required.
The proof of (b) is analogous: if \(B\in {\mathfrak B}({\mathsf H})\) commutes with A, it also commutes with every polynomial p(A) and hence with every Ψ′(f) with f ∈ C(σ(A)) by continuity. Therefore, for every f ∈ C(σ(A)).
Riesz’s theorem implies that μ x,By = μ Bx,y. The definition of Ψ′ immediately entails that 〈x| Ψ′(f)By〉 = 〈B ∗ x| Ψ′(f)y〉 = 〈x|B Ψ′(f)y〉 for every f ∈ M b(σ(A)). But this is the thesis, since x, y ∈H are arbitrary.
Let us prove (c). Since Ψ′ is a representation of unital ∗-algebras we immediately have
By (3.63)
when n → +∞ by dominated convergence, since |μ xy| is finite. □
We are ready to prove the existence claim in the Spectral Theorem (Theorem 3.40) for bounded selfadjoint operators.
Theorem 3.84
If \(A\in {\mathfrak B}({\mathsf H})\) is selfadjoint on the Hilbert space H , there exists a PVM \(P^{(A)}: \mathcal {B}({\mathbb R}) \to \mathcal {L}({\mathsf H})\) such that
More generally, if \(\Psi ': M_b(\sigma (A)) \to {\mathfrak B}({\mathsf H})\) is defined as in Proposition 3.83 ,
for every f ∈ M b(σ(A)).
Proof
Refer to Proposition 3.83. The required PVM is nothing but \(P^{(A)}_E := \Psi '(\chi _{E\cap \sigma (A)})\) for every \(E \in \mathcal {B}({\mathbb R})\), \(P^{(A)}_\varnothing :=0\). Indeed, suppose P (A) is a PVM. If \(s= \sum _{j=1}^N s_j \chi _{E_j}\) is a simple function, the linearity of Ψ′ immediately shows \(\Psi '(s) = \sum _{j=1}^N s_j \Psi '(\chi _{E_j}) = \int _{\mathbb R} s\: dP^{(A)}\). Now consider a sequence of simple functions s n such that |s n|≤|s n+1|≤|ı| on the compact set σ(A), vanishing outside σ(A), and converging pointwise to ı on σ(A). As the PVM is concentrated on σ(A) by construction, Propositions 3.83 (a)–(c) and 3.29 (c) imply
Since x ∈H is arbitrary, we get \(A= \int _{\mathbb R} \imath \: dP^{(A)}\), as we wanted. The same argument (using a sequence of simple functions s n converging to f ∈ M b(σ(A)) pointwise and such that |s n|≤|s n+1|≤|f|) returns the second claim.
To end the proof, there remains to prove that \(P^{(A)}_E := \Psi '(\chi _{E\cap \sigma (A)})\) with \(E\in \mathcal {B}({\mathbb R})\) (and obviously \(P^{(A)}_\varnothing :=0\)) defines a PVM. But \(P^{(A)}_{\mathbb R} =I\), \(P^{(A)}_{E}P^{(A)}_{F}= P^{(A)}_{E\cap F}\), \((P^{(A)}_E)^*=P^{(A)}_E\) (in particular \(P^{(A)}_E \in \mathcal {L}({\mathsf H})\)) are immediate consequences of the fact that Ψ′ is a representation of unital ∗-algebras, together with trivial properties of characteristic functions χ E, plus Ψ′(1) = Ψ′(χ σ(A)) = I. Finally, σ-additivity follows from Proposition 3.83 (c): taking a countable collection of disjoint sets \(E_k \in \mathcal {B}({\mathbb R})\), we have
(all functions are bounded by the constant 1). □
3.6.3 Spectral Theorem for Normal Operators in \({\mathfrak B}({\mathsf H})\)
The functional calculus developed in the previous section permits us to prove the spectral theorem for normal operators on \({\mathfrak B}({\mathsf H})\). In particular it handles selfadjoint operators on \(\mathcal {B}({\mathsf H})\) and unitary operators.
Theorem 3.85 (Spectral Theorem for Normal Operators on \({\mathfrak B}({\mathsf H})\))
Let \(T\in {\mathfrak B}({\mathsf H}) \) be a normal operator on the complex Hilbert space H.
-
(a)
There exists a unique PVM \(P^{(A)} : {\mathcal {B}}({\mathbb C}) \to {\mathcal {L}}({\mathsf H})\) , called the spectral measure of T, such that
$$\displaystyle \begin{aligned}T = \int_{{\mathbb C}} z dP^{(T)}(z, \overline{z})\:.\end{aligned}$$In particular D(T) = Δ ı , where \(\imath : {\mathbb C} \ni z \mapsto z\).
-
(b)
We have
$$\displaystyle \begin{aligned}\mathit{\mbox{supp}}(P^{(T)}) = \sigma(T).\end{aligned}$$As the standard topology of \({\mathbb C}\) is second-countable, P (T) is concentrated on σ(T):
$$\displaystyle \begin{aligned} \begin{array}{rcl} P^{(T)}(E) = P^{(T)}(E \cap \sigma(T))\:, \quad \forall E \in {\mathcal{B}}({\mathbb C}) {}\:.\vspace{-3pt}\end{array} \end{aligned} $$(3.64) -
(c)
z ∈ σ p(T) if and only if P (T)({z}) ≠ 0; in particular this happens if z is an isolated point of σ(T). Finally \(P^{(T)}_{\{z\}}\) is the orthogonal projector onto the eigenspace of z ∈ σ p(A).
-
(d)
z ∈ σ c(T) if and only if P (T)({λ}) = 0, but P (T)(E) ≠ 0 if E ∋ λ is an open set of \({\mathbb C}\).
Proof
(a) Let us prove that there exists a PVM on \({\mathbb C}\) with \(T = \int _{{\mathbb C}} z dP^{(T)}(z)\). Decompose T = A + iB where \(A=\frac {1}{2}(T+T^*)\) and \(A=\frac {1}{2i}(T-T^*)\) are selfadjoint, belong to \({\mathfrak B}({\mathsf H})\), and commute because T and T ∗ commute by hypothesis. Notice that, as a consequence of Proposition 3.83 (b) the spectral measure P (A) of A, which exists by Theorem 3.84 and satisfies \(P^{(A)}_E= \Psi _A^{\prime }(\chi _E)\), commutes with B. By the same argument the spectral measure P (B) of B commutes with the spectral measure of A.
Next consider step functions on the compact set \(K = [-||A||,||A||] \times [-||B||, ||B||] \subset {\mathbb R}^2 \equiv {\mathbb C}\). A step function is a simple function of the form
where \(s_{ij}\in {\mathbb C}\) are fixed numbers, I 1 := [−||A||, a 2], J 1 := [−||B||, b 2], I i := (a i, a i+1], J j := (b j, b j+1] for i, j > 1, and a N+1 = ||A||, b n+1 = ||B||. The decomposition of s ∈ S(K) in (3.65) is not unique, since every such expression can be refined by adding points a i or b j. It is easy to prove that the set S(K) of step functions on K is closed under linear combinations and products. Since it evidently contains the constant function 1 and it is invariant under conjugation, S(K) is a unital ∗-subalgebra of M b(K). Referring to (3.65), let us define \(\Phi _0 : S(K) \to {\mathfrak B}({\mathsf H})\) by
The definition is well-posed irrespective of the various expansions (3.65) that s possesses. By direct inspection, one sees that Φ0 is a homomorphism of unital ∗-algebras and also that
using that the sets I i × J j are pairwise disjoint and \(\sum _{i,j} P^{(A)}_{I_i} P^{(B)}_{J_j}=I\) because ∪i.j I i × J j = K . As a consequence
Since S(K) is dense in C(K) in norm ||⋅||∞ (a continuous function on a compact set is uniformly continuous), the same proof as for Theorem 3.82 ensures that the continuous unital ∗-homomorphism Φ0 generates a norm-decreasing unital ∗-homomorphism \(\Phi : C(K) \to {\mathfrak B}({\mathsf H})\). Notice that Φ is not an extension of Φ0, since its domain contains continuous maps only, whereas the domain of Φ0 contains discontinuous functions as well. By definition Φ(1) = I, and by setting ı 1 : K ∋ (x, y)↦x and ı 2 : K ∋ (x, y)↦y we have
Indeed, let \(s_n :[-||A||,||A||] \times [-||B||, ||B||]\to {\mathbb R}\) be a sequence of step functions, constant in the variable y ∈ [−||B||, ||B||] and converging uniformly to the map ı 1. Applying (3.66) gives, with obvious notation,
where we exploited (3.21). The story for ı 2 is identical.
As last step, and proceeding as in the proof of Proposition 3.83, we may extend Φ to a unital ∗-algebra homomorphism \(\Phi ': M_b(K) \to {\mathfrak B}({\mathsf H})\) completely determined by the requirement
where \(\nu _{\psi .\phi } : \mathcal {B}(K) \to {\mathbb C}\) is the unique complex regular Borel measure satisfying the above relation for f ∈ C(K). An argument that essentially replicates Proposition 3.83 shows that the homomorphism of unital ∗-algebras \(\Phi ': M_b(K) \to {\mathfrak B}({\mathsf H})\) is norm-decreasing (|| Φ′(f)||≤||f||∞), satisfies
and finally
if M b(K) ∋ f n → f pointwise as n → +∞ and |f n|≤ M for some M ∈ [0, +∞) and all n.
The last convergence property in particular implies, along the same lines of Theorem 3.84, that \(P^{(T)}_E := \Phi '(\chi _{E\cap K})\) (with \(P^{(T)}_\varnothing := 0\)) is a PVM on \({\mathbb C} \equiv {\mathbb R}^2\) when E varies in \(\mathcal {B}({\mathbb C})\). By (3.67) moreover,
Since T = A + iB and T ∗ = A − iB, these relations read
Let us pass to the uniqueness issue. First of all observe that if \(T= \int _{\mathbb C} z dP(z,\overline {z})\) then P must have bounded support: if not, for every \(n \in {\mathbb N}\), we could find \(E_n\in \mathcal {B}({\mathbb C})\) outside the disc of radius n at the origin of \({\mathbb C}\) such that \(P_{E_n}\neq 0\). Hence we could pick \(x_n\in P_{E_n}({\mathsf H})\) with ||x n|| = 1. As a consequence \(||Tx_n||{ }^2 \geq |n|{ }^2 \int _{{\mathbb C}} 1 d\mu ^{(P)}_{x_nx_n}= |n|{ }^2 \to +\infty \) as n → +∞, contradicting ||T|| < +∞. We conclude that there exists a sufficiently large compact rectangle \(K:= [a,b]\times [c,d] \subset {\mathbb R}^2 \equiv {\mathbb C}\) (we can always assume it to be larger than [−||A||, ||A||] × [−||B||, ||B||]), so that supp(P) ⊂ K. Hence it suffices to work in K. Taking adjoints of \(\int _K z dP(z,\overline {z})=T= \int _K z dP^{(T)}(z,\overline {z})\) produces \(\int _K \overline {z} dP(z,\overline {z})=T^*= \int _K \overline {z} dP^{(T)}(z,\overline {z})\). Using standard properties of bounded PVMs, we immediately have that \(\int _K p(z,\overline {z}) dP(z,\overline {z})= \int _K p(z,\overline {z}) dP^{(T)}(z,\overline {z})\) for every polynomial p defined on K. But polynomials are ||⋅||∞-dense in C(K) (Stone–Weierstrass theorem), so (3.21) implies \(\int _K f(z,\overline {z}) dP(z,\overline {z})= \int _K f(z,\overline {z}) dP^{(T)}(z,\overline {z})\) for every f ∈ C(K). Applying now the Riesz theorem for positive Borel measures to
we conclude \(\mu ^{(P^{(T)})}_{\psi \psi }(E) = \mu ^{(P)}_{\psi \psi }(E) \) for every \(E\in \mathcal {B}(K)\). Since the supports of the two measures stay in K, the relation we have found reads \(\mu ^{(P^{(T)})}_{\psi \psi }(E) = \mu ^{(P)}_{\psi \psi }(E) \) for every \(E\in \mathcal {B}({\mathbb C})\), i.e. \(\langle \psi | (P^{(T)}_E - P_E) \psi \rangle =0\) for every ψ ∈H. This result immediately leads to the thesis, \(P^{(T)}_E = P_E\) for every \(E\in \mathcal {B}({\mathbb C})\).
The proofs of (b), (c) and (d) are identical to those of the corresponding statements in Theorem 3.40, up to trivial changes (\({\mathbb R}\) becomes \({\mathbb C}\) and λ becomes z). □
3.6.4 Existence of Spectral Measures for Unbounded Selfadjoint Operators
At the end of this long detour, we are finally ready to justify the existence of PVMs for unbounded selfadjoint operators (the Spectral Theorem, 3.40).
Theorem 3.86
If A is a (generally unbounded) selfadjoint operator on the Hilbert space H , there exists a PVM \(P^{(A)}: \mathcal {B}({\mathbb R}) \to \mathcal {L}({\mathsf H})\) such that
Proof
First of all observe that, if A is normal, its resolvent satisfies \(R_\lambda (A)^*= R_{\overline {\lambda }}(A^*)\). Indeed, we know that λ ∈ ρ(A) iff \(\overline {\lambda } \in \rho (A^*)\) by Proposition 3.13 (c). In this case  implies
implies  , namely (A
∗ + iλI)R
λ(A)∗ = I. Since we also have \((A^*+i\lambda I)R_{\overline {\lambda }}(A^*) =I\) and the inverse is unique, necessarily \(R_\lambda (A)^*= R_{\overline {\lambda }}(A^*)\). This results is in particular true when A = A
∗. Next, assuming A = A
∗, consider the operator
, namely (A
∗ + iλI)R
λ(A)∗ = I. Since we also have \((A^*+i\lambda I)R_{\overline {\lambda }}(A^*) =I\) and the inverse is unique, necessarily \(R_\lambda (A)^*= R_{\overline {\lambda }}(A^*)\). This results is in particular true when A = A
∗. Next, assuming A = A
∗, consider the operator
called the Cayley transform of A. By the resolvent identity (3.2) and \(R_\lambda (A)^*= R_{\overline {\lambda }}(A)\), one immediately proves that UU ∗ = U ∗ U = I. Hence U is unitary and σ(U) is a closed subset of \({\mathbb T} = \{z \in {\mathbb C} \:|\: |z|=1\}\) in the topology induced by \({\mathbb C}\) due to Proposition 3.13. Finally,
by Theorem 3.85. We claim that the statement’s selfadjoint operator A coincides with the selfadjoint operator
(the integrand is real since \(\overline {z}= 1/z\) as \(z\in {\mathbb T}\)). In fact, since \(R_{-i}(A)= \frac {i}{2}(U-I)\) and taking Proposition 3.33 (c) into account,
We conclude that A′ + iI is defined on a domain that contains Ran(R −i A) = D(A), on which it coincides with the unique left inverse of R −i(A). In other words A′ + iI is an extension of A + iI, so A′⊃ A. Since A′ and A are selfadjoint, A′ = A by Proposition 2.39 (b). To conclude, we shall prove that (3.71) can be decomposed spectrally on \({\mathbb R}\). As
is a homeomorphism (\({\mathbb R} \cup \{\infty \}\) is the standard 1-point compactification), then
where we have defined the PVM \(P_E = P^{(T)}_{\phi ^{-1}(E)}\) for \(E \in \mathcal {B}({\mathbb R} \cup \{+\infty \})\) following Proposition 3.33 (f). Let us explain why ∞ is reached by ϕ only for z = 1 and \(P^{(U)}_{\{1\}}=0\). If \(P^{(U)}_{\{1\}}\neq 0\) we would have Ux = x for some \(x\in P^{(U)}_{\{1\}}({\mathsf H}) \setminus \{0\}\). Since U := I − 2iR −i(A), then R −i(A)x = 0, contradicting the fact that R −i(A) is invertible since A is selfadjoint and so − i ∈ ρ(A). We can rewrite the equation as
It is easy to check that the restriction P′ of P to \(\mathcal {B}({\mathbb R})\) is still a PVM on \({\mathbb R}\) and the integral above can be thought of as
The proof is over once we take P (A) := P′. □
3.6.5 Existence of Joint Spectral Measures
We shall provide a proof for Theorem 3.56. The argument differs from that appearing in [Mor18] in view of the distinct presentation of the spectral technology we have chosen here. In particular, the current proof does not require that the Hilbert space be separable.
Theorem 3.56 (Joint Spectral Measure)
Let \({\mathfrak A} :=\{A_1,A_2,\ldots , A_n\}\) be a set of selfadjoint operators on the Hilbert space H with commuting spectral measures:
Then there exists a unique PV M \(P^{({\mathfrak A})}\) on \({\mathbb R}^n\) such that
For every \(f : {\mathbb R} \to {\mathbb C}\) measurable, furthermore,
where x = (x 1, …, x k, …, x n) and \(f(A_k) := \int _{\mathbb R} f(\lambda ) dP^{(A_k)}\).
Finally, \(B\in {\mathfrak B}({\mathsf H})\) commutes with \(P^{({\mathfrak A})}\) if and only if it commutes with all \(P^{(A_k)}\) , k = 1, 2, …, n.
Proof (Existence)
We start by assuming \(A_k \in {\mathfrak B}({\mathsf H})\) for k = 1, …, n. Then we may replicate the initial part of the proof of Theorem 3.85, only replacing the two commuting selfadjoint operators in \(A,B \in {\mathfrak B}({\mathsf H})\) by n commuting selfadjoint operators \(A_k \in {\mathfrak B}({\mathsf H})\). In this way if \(K := [-a,a]^n\subset {\mathbb R}^n\) is sufficiently large and \(K \supset \times _{k=1}^n \sigma (A_k)\), there exists a map \(\Phi ': M_b(K) \to {\mathfrak B}({\mathsf H})\) with the following features. It is a norm-decreasing ∗-homomorphism of unital ∗-algebras, it satisfies
where \(\imath _k : {\mathbb R}^n \ni (x_1,\dots , x_n) \mapsto x_k \in {\mathbb R}\), and finally
if M b(K) ∋ f n → f pointwise as n → +∞ and |f n|≤ M for some M ∈ [0, +∞) and all n.
Invoking the proof of Theorem 3.84, the last convergence property implies that
(with \(P^{({\mathfrak A})}_\varnothing := 0\)) defines a PVM on \({\mathbb R}^n\) when E varies in \(\mathcal {B}({\mathbb R}^n)\) and
by (3.74). Now observe that as \(E \in \mathcal {B}({\mathbb R})\) varies, the family of orthogonal projectors \(P_{E} := P^{({\mathfrak A})}_{E \times {\mathbb R}^{n-1}}\) defines a PVM on \({\mathbb R}\). Take a sequence of simple functions s n on K, constant in the variables x 2, …, x n and such that s n → ı 1 pointwise with |s n|≤|ı 1| (which is bounded on K). Equation (3.75) and Proposition 3.29 (c) allow to rephrase (3.77) for k = 1 as
The uniqueness of the spectral measure of A 1 (Theorem 3.40) implies that
By the same argument,
This relation implies, together with (3.76) and the fact that Φ′ preserves products,
Hence (3.72) is true. Let us pass to unbounded selfadjoint operators A k. We shall reduce this to the case of bounded operators. To this end, define a family \({\mathfrak B} := \{ B_1,\ldots , B_n\}\),
for every k = 1, 2, …, n. It is clear that \(B_k^*=B_k \in {\mathfrak B}({\mathsf H})\) due to Theorem 3.24 (c) and Proposition 3.29 (a). Moreover, by Corollary 3.53 σ(B k) ⊂ [−1, 1], but ± 1∉σ p(B k). By contradiction, in fact, if ± 1 ∈ σ p(B k) and ψ ±∈H were a corresponding eigenvector, then (B k ± I)ψ ± = 0, and so
Since the positive measure \(\mu ^{(P_k)}_{\psi _\pm \psi _\pm }\) does not vanish (ψ ±≠ 0 because it is an eigenvector), the integrand would be zero almost everywhere. This is not possible because
Let us now focus on the map
where \(\overline {{\mathbb R}}= {\mathbb R} \cup \{\pm \infty \}\) is the compactification and [−1, 1] is standard. Note that \(\phi ({\mathbb R}) = (-1,1)\) and ϕ(±∞) = ±1. It is easy to see that ϕ is an homeomorphism, so ϕ and ϕ −1 are Borel measurable.
In view of these properties of ϕ it is preferable to extend the spectral measures \(P^{(A_k)}\) to new PVMs \(\widetilde {P}^{(A_k)}\) defined on the Borel algebra \(\mathcal {B}(\overline {R})\), by simply declaring that \(\widetilde {P}^{(A_k)}_{+\infty }=\widetilde {P}^{(A_k)}_{-\infty }=0\) and \(\widetilde {P}^{(A_k)}_{E}={P}^{(A_k)}_{E}\) when \(E\cap \{+\infty \}= E\cap \{-\infty \} =\varnothing \) for \(E\in \mathcal {B}(\overline {R})\). Now it is safe to write
Using the extension, Proposition 3.33 (f) tells
where
We could extend \(P^{(B_k)}\) to the whole \(\mathcal {B}({\mathbb R})\) by setting \(P_1^{(B_k)}(F) := P_1^{(B_k)}(F\cap [-1,1])\) for \(F\in \mathcal {B}({\mathbb R})\) trivially; we shall however stick to the first choice for the sake of simplicity, and allow ourselves to interpret the relevant PVM as their extensions where necessary.
Observe that the spectral measures \(P^{(B_k)}\) commute with each other due to (3.79) and the fact that the PVMs \(\widetilde {P}^{(A_k)}\) do (the added points ±∞ are harmless). We can therefore apply the previous proof, construct a PV M \(P^{({\mathfrak B})}\) on \(\mathcal {B}({\mathbb R}^n)\), with support in [−1, 1]n, which satisfies
Let us go back to the unbounded operators A k, define the homeomorphism
and the PVM on \(\overline {{\mathbb R}}^n\)
This is allowed by Proposition 3.33 (f) (Φ = ( Φ−1)−1 and Φ−1 is Borel measurable since Φ is an homeomorphism). With this definition, (3.80) implies
To conclude the proof of existence, it is enough to rid ourselves of the ‘annoying’ points ±∞. The boundary of \(\overline {{\mathbb R}}^n\) is the union of the 2n sets
Every such set has zero P-measure: exploiting (3.81), in fact,
because \(\widetilde {P}^{(A_1)}_{\{+\infty \}}=P^{(B_1)}_{+1}=0\) since + 1∉σ p(B 1) and by Theorem 3.40 (c)–(d). Hence the boundary of \(\overline {{\mathbb R}}^n\) has zero measure for P. This means that, restricting to the interior \({\mathbb R}^n\) of \(\overline {{\mathbb R}}^n\), the map \(P^{({\mathfrak A})}_{E}:= P_{E}\) with \(E \in \mathcal {B}({\mathbb R}^n)\), still defines a PVM, in particular \(P^{({\mathfrak A})}_{{\mathbb R}^n}=I\). By construction, \(P^{({\mathfrak A})}\) satisfies (3.73) since (3.80) holds, and that ends the existence part of the proof.
(Uniqueness)
Let us show uniqueness. We have the following known result of general measure theory [Coh80, Corollary 1.6.3].
Lemma 3.57
Let Σ(X) be a σ-algebra on X and \(\mathcal {P}\subset \Sigma (X)\) such that
-
(i)
\(\mathcal {P}\) is closed under finite intersections;
-
(ii)
the σ-algebra generated by P is Σ(X) itself;
-
(iii)
there is an increasing sequence \(\{C_m\}_{m\in {\mathbb N}}\subset \mathcal {P}\) such that \(\cup _{m\in {\mathbb N}} C_m= X\).
If μ and ν are positive σ-additive measures on Σ(X) such that μ(C m) = ν(C m) < +∞ for every \(m \in {\mathbb N}\) , then μ = ν.
Returning to our proof, define \(\Sigma (X):= \mathcal {B}({\mathbb R}^n)\) and let \(\mathcal {P}\) be the collection of sets E 1 ×⋯ × E n for \(E_k \in \mathcal {B}({\mathbb R})\). It it known that (\({\mathbb R}\) is a separable metric space) the σ-algebra generated by \(\mathcal {P}\) is just \(\mathcal {B}({\mathbb R}^n)\). Now set C m = (−r, r)m with \(m \in {\mathbb N}\). Finally, fix x ∈H and define μ(F) := 〈x|P F x〉 and \(\nu (F):= \langle x| P^{\prime }_F x\rangle \) for \(F \in \mathcal {B}({\mathbb R}^n)\), where both P and P′ satisfy (3.72) in place of \(P^{({\mathfrak A})}\). These measures are finite, as μ(F) = ν(F) = ||x||2 by definition of PVM, and satisfy μ(C n) = ν(C n) < +∞ because of (3.72). Lemma 3.57 proves that \( \langle x| P_F x\rangle = \langle x| P^{\prime }_F x\rangle \), so that \(\langle x| (P_F-P^{\prime }_F) x\rangle =0\). The arbitrariness of x ∈H and the usual polarization formula imply \(P_F=P_F^{\prime }\) for every \(F\in \mathcal {B}({\mathbb R})\).
(Equation (3.73))
The proof is easy. Consider k = 1 for instance. There exists a sequence of simple functions s m on \({\mathbb R}\) converging pointwise to the measurable function \(f :{\mathbb R} \to {\mathbb C}\), as m → +∞, and such that |s m|≤|s m+1|≤|f|. Let us write \(s_m(x_1) := \sum _{r=1}^N c_r \chi _{E_r}\) and define \(s^{\prime }_m(x_1,\ldots ,x_n):= \sum _{r=1}^N c_r \chi _{E_r\times {\mathbb R}^{n-1}}(x_1,\ldots ,x_n)\) (so that \(s^{\prime }_m\) is constant in x 1, …, x n and equals s m in the remaining variable). If \(\psi \in \Delta ^{(A_1)}_f\), by Theorem 3.24 (d) and dominated convergence we have
where the penultimate equality is justified by (3.72). The same argument, using monotone convergence and the identity \(\int _{{\mathbb R}} |s_m|{ }^2 d\mu ^{(P^{(A_1)})}_{\psi \psi }= \int _{{\mathbb R}} |s^{\prime }_m|{ }^2 d\mu ^{(P^{({\mathfrak A})})}_{\psi \psi }\), also proves that \(\psi \in \Delta ^{({\mathfrak A})}_f\) with obvious notation. Therefore \(\int _{{\mathbb R}^n} f(x_1) dP^{({\mathfrak A})}\psi \) is well defined.
(Last Statement)
If \(B\in {\mathfrak B}({\mathsf H})\) commutes with \(P^{({\mathfrak A})}\) it evidently commutes with every \(P^{(A_k)}\), k = 1, 2, …, n due to (3.72) by just taking all \(E_k = {\mathbb R}\) but one. Suppose conversely that \(U \in {\mathfrak B}({\mathsf H})\) is unitary and commutes with every \(P^{(A_k)}\). The PVM defined by the projectors \(UP^{({\mathfrak A})}_EU^{-1}\), for \(E \in \mathcal {B}({\mathbb R}^n)\), therefore coincides with \(P^{({\mathfrak A})}\) when E = E 1 ×⋯ × E n with \(E_k \in \mathcal {B}({\mathbb R})\). By the established uniqueness property, we immediately have \(UP^{({\mathfrak A})}_EU^{-1} = P^{({\mathfrak A})}_E\) for every \(E \in \mathcal {B}({\mathbb R}^n)\). In other words \(UP^{({\mathfrak A})}_E = P^{({\mathfrak A})}_EU\) for every \(E \in \mathcal {B}({\mathbb R}^n)\). In order to pass from U to a general \(B\in {\mathfrak B}({\mathsf H})\), it suffices to invoke Proposition 3.55 (whose proof relies only upon the spectral theorem of selfadjoint operators), write B = aU + bU′ as complex linear combination of unitary operators, and finally use the composition’s linearity in the relation above.
□
Notes
- 1.
More generally: \(\int _{{\mathbb R}}\int _{{\mathbb R}^{n-1}} g(x_1) |\psi (x)|{ }^2dx d^{n-1}x= \int _{{\mathbb R}} g(x_1) d\mu ^{(P)}_{\psi ,\psi }(x_1)\) is patently valid for simple functions. It extends to arbitrary measurable functions, provided both sides make sense, in view of, for instance, Lebesgue’s dominated convergence theorem for positive measures.
References
O. Bratteli, D.W. Robinson, Operator Algebras and Quantum Statistical Mechanics, vols. I, II, 2nd edn. (Springer, Berlin, 2002)
D. Cohn, Measure Theory (Birkhäuser, Basel, 1980)
R. Kadison, J.R. Ringrose, Fundamentals of the Theory of Operator Algebras. Graduate Studies in Mathematics, vols. I,II,III,IV (AMS, Providence, 1997)
V. Moretti, Spectral Theory and Quantum Mechanics, 2nd edn. (Springer, Cham, 2018)
G.K. Pedersen, Analysis Now. Graduate Texts in Mathematics, vol. 118 (Springer, New York, 1989)
M. Reed, B. Simon, Methods of Modern Mathematical Physics I: Functional Analysis. Revised and Enlarged Edition (Academic, New York, 1980)
F. Riesz, B. Nagy, Functional Analysis, 2nd edn. (Mc Graw Hill, New Delhi, 1991)
W. Rudin, Real and Complex Analysis, 3rd edn. (McGraw-Hill, New Delhi, 1986)
W. Rudin, Functional Analysis, reprinted edition (Dover, Mineola, 1990)
K. Schmüdgen, Unbounded Self-Adjoint Operators on Hilbert Space (Springer, Dordrecht, 2012)
G. Teschl, Mathematical Methods in Quantum Mechanics with Applications to Schrödinger Operators. Graduate Studies in Mathematics, 2nd edn. (AMS, Providence, 2014)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Moretti, V. (2019). Observables and States in General Hilbert Spaces: Spectral Theory. In: Fundamental Mathematical Structures of Quantum Theory. Springer, Cham. https://doi.org/10.1007/978-3-030-18346-2_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-18346-2_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-18345-5
Online ISBN: 978-3-030-18346-2
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


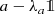 must be non-invertible for some
must be non-invertible for some 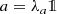 .
. 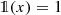 if x ∈ X. The C
∗-property ||f
∗⋅ f||2 = ||f||2 is nothing but
if x ∈ X. The C
∗-property ||f
∗⋅ f||2 = ||f||2 is nothing but 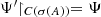 ,
,