Variational Deep Collaborative Matrix Factorization for Social Recommendation

Abstract

In this paper, we propose a Variational Deep Collaborative Matrix Factorization (VDCMF) algorithm for social recommendation that infers latent factors more effectively than existing methods by incorporating users’ social trust information and items’ content information into a unified generative framework. Unlike neural network-based algorithms, our model is not only effective in capturing the non-linearity among correlated variables but also powerful in predicting missing values under the robust collaborative inference. Specifically, we use variational auto-encoder to extract the latent representations of content and then incorporate them into traditional social trust factorization. We propose an efficient expectation-maximization inference algorithm to learn the model’s parameters and approximate the posteriors of latent factors. Experiments on two sparse datasets show that our VDCMF significantly outperforms major state-of-the-art CF methods for recommendation accuracy on common metrics.

1 Introduction

Recommender System (RS) has been attracting great interests recently. The most commonly used technology for RS is Collaborative Filtering (CF). The goal of CF is to learn user preference from historical user-item interactions, which can be recorded by a user-item feedback matrix. Among CF-based methods, matrix factorization (MF) [17] is the most commonly used one. The purpose of MF is to find the latent factors for users and items by decomposing the user-item feedback matrix. However, the feedback matrix is usually sparse, which would result in the poor performance of MF. To track this problem, many hybrid methods such as those in [12, 21,22,23,24, 26], called content MF methods, incorporate auxiliary information, e.g., content of items, into MF . The content of items can be their tags and descriptions etc. These methods all first utilize some models (e.g., Latent Dirichlet Allocation (LDA) [1], Stack Denoising AutoEncoders (SDAE) [20] or marginal Denoising AutoEncoders (mDAE) [3]) to extract items’ content latent representations and then input them into probabilistic matrix factorization [17] framework. However, these methods demonstrate a number of major drawbacks: (a) They assume that users are independent and identically distributed, and neglect the social information of users, which can be used to improve recommendation performance [15, 16]. (b) those methods [21, 22] which are based on LDA only can handle text content information which is very limited in current multimedia scenario in real world. The learned latent representations by LDA are often not effective enough especially when the auxiliary information is very sparse [24] (c) For those methods [12, 23, 24, 26] which utilize SDAE or aSDAE. The SDAE and mDAE are in fact not probabilistic models, which limits them to effectively combine probabilistic matrix factorization into a unified framework. They first corrupt the input content, and then use neural networks to reconstruct the original input. So those model also need manually choose various noise (masking noise, Gaussian noise, salt-and-peper noise, etc), which hinders them to expand to different datasets. Although some hybrid recommendation methods [2, 10, 18, 25] that consider user social information have been proposed, they still suffer from problem (b) and (c) mentioned above. Recently, the deep generative model such Variational AutoEncoder (VAE) [11] has been utilized to the recommendation task and achieve promising performance due to it’s full Bayesian nature and non-linearity power. Liang et al. proposed VAE-CF [14] which directly utilize VAE to the CF task. To incorporate item content information into VAE-CF, chen et al. proposed a collective VAE model [4] and Li et al. proposed Collaborative Variational Autoencoder [13]. However those methods all don’t consider users’ social information. To tackle the above problems, we propose a Variational Deep Collaborative Matrix Factorization algorithm for social recommendation, abbreviated as VDCMF, for social recommendation, which integrates item contents and user social information into a unified generative process, and jointly learns latent representations of users and items. Specifically, we first use VAE to extract items’ latent representation and consider users’ preferences effect by the personal tastes and their friends’ tastes. We then combine these information into probabilistic matrix factorization framework. Unlike SDAE based methods, our model needs not to corrupt the input content, but instead to directly model the content’s generative process. Due to the full Bayesian nature and non-linearity of deep neural networks, our model can learn more effective and better latent representations of users and items than LDA-based and SDAE-based methods and can capture the uncertainty of latent space [11]. In addition, with both item content and social information, VDCMF can effectively tackle the matrix sparsity problem. In our VDCMF, to infer latent factors of users and items, we propose a EM-algorithm to learn model parameters. To sum up, our main contributions are: (1) We propose a novel recommendation model called VDCMF for recommendation, which incorporates rich item content and user social information into MF. VDCMF can effectively learn latent factors of users and items in matrix sparsity cases. (2) Due to the full Bayesian nature and non-linearity of deep neural networks, our VDCMF is able to capture more effective latent representations of users and items than state-of-the-art methods and can capture the uncertainty of latent content representation. (3) We derive an efficient parallel variational EM-style algorithm to infer latent factors of users and items. (4) Comprehensive experiments conducted on two large real-world datasets show VDCMF can significantly outperform state-of-the-art hybrid MF methods for CF.

2 Notations and Problem Definition

Let $\varvec{R}\in \left\{ 0,1\right\} ^{N\times M}$ be a user-item matrix, where N and M are the number of users and items, respectively. $R_{ij}=1$ denotes the implicit feedback from user i over item j is observed and $R_{ij}=0$ otherwise. Let $\mathcal {G}=(\mathcal {U},\mathcal {E})$ denote a trust network graph, where the vertex set $\mathcal {U}$ represents users and $\mathcal {E}$ represents the relations among them. Let $\varvec{T}=\left\{ T_{ik}\right\} ^{N\times N}$ denote the trust matrix of a social network graph $\mathcal {G}$. We also use $N_i$ to represent user i’s direct friends and $U_{N_i}$ as their latent representations. Let $\varvec{X}=[\varvec{x}_1,\varvec{x}_2,\ldots , \varvec{x}_M]\in \mathbb {R}^{L\times M}$ represent item content matrix, where L denotes the dimension of content vector $\varvec{x}_j$, and $x_j$ be the content information of item j. For example, if item j is a product or a music, the content $x_j$ can be bag-of-words of its tags. We use $\varvec{U}=[\varvec{u}_1,\varvec{u}_2,\ldots , \varvec{u}_N]\in \mathbb {R}^{D\times N}$ and $\varvec{V}=[\varvec{v}_1,\varvec{v}_2,\ldots , \varvec{v}_M]\in \mathbb {R}^{D\times M}$ to denote user and item latent matrices, respectively, where D denotes the dimension. $\varvec{I}_D$ represents identity matrix with dimension D.

3 Variational Deep Collaborative Matrix Factorization

In this section, we propose a Variational Deep Collaborative Matrix Factorization for social recommendation, the goal of which is to infer user latent matrix $\varvec{U}$ and item latent matrix $\varvec{V}$ given item content matrix $\varvec{X}$, user trust matrix $\varvec{T}$ and user-item rating matrix $\varvec{R}$.

3.1 The Proposed Model

To incorporate users’ social information and item content information in to probabilistic matrix, we consider a users’ feedback or rating on items are a balance between item content, user’s taste and friend’s taste. For example, users’s rating on movies is effected by the movie’s content information (e.g., the genre and the actors) and his friend advices from their tastes. For items’ content information, since it can be very complex and various, we do not know its real distribution. However, we know any distribution can be generated by mapping simple Gaussian through a sufficiently complicated function [7]. In our proposed model, we consider item contents to be generated by their latent content vectors through a generative network. The generative process of VDCMF is as follows:

• 1. For each user i, draw user latent vector $\varvec{u}_i\sim \mathcal {N}(0,\lambda _u^{-1})\prod _{f \in N_i} \mathcal {N}(\varvec{u}_f,\lambda _f^{-1} T_{if}^{-1}\varvec{I}_{D})$.

• 2. For each item j:

  • (a) Draw item content latent vector $\varvec{z}_j\sim \mathcal {N}(0,\varvec{I}_{D})$.

  • (b) Draw item content vector $p_{\varvec{\theta }}(\varvec{x}_j|\varvec{z}_j)$.

  • (c) Draw item latent offset $\varvec{k}_j\sim \mathcal {N}(0,\lambda _v\varvec{I}_{D})$ and set the item latent vector as $\varvec{v}_j=\varvec{z}_j+\varvec{k}_j$.

• 3. For each user-item pair (i, j) in $\varvec{R}$, draw $R_{ij}$:

  $$\begin{aligned} R_{ij}\sim \mathcal {N}(\varvec{u}^\top _i \varvec{v}_j,c_{ij}^{-1}). \end{aligned}$$

  (1)

Fig. 1.

Graphical model of VDCMF: generative network (left) and inference network (right), where solid and dashed lines represent generative and inference process, shaded nodes are observed variables.

In the process, $\lambda _v, \lambda _u$ and $\lambda _g$ are the free parameters, respectively. Similar to [21, 24], $c_{ij}$ in Eq. 1 serves as confident parameters for $R_{ij}$ and $S_{ik}$, respectively:

$$\begin{aligned} c_{ij}=\left\{ \begin{array}{lr} \varphi _1 \quad \text {if} \quad R_{ij}=1,&{}\\ \varphi _2 \quad \text {if} \quad R_{ij}=0,&{} \end{array} \right. \end{aligned}$$

(2)

where $\varphi _1> \varphi _2 >0$ is the free parameters. In our model, we follow [18, 24] to set $\varphi _1=1$ and $\varphi _2=0.1$. $p_{\varvec{\theta }}(\varvec{x}_j|\varvec{z}_j)$ represents item content information and $\varvec{x}_j$ is generated from latent content vector $\varvec{z}_i$ through a generative neural network parameterized by $\theta$. It should be noted that the specific form of the probability $p_{\varvec{\theta }}(\varvec{x}_j|\varvec{z}_j)$ depends on the type of the item content vector. For instance, if $\varvec{x}_{j}$ is binary vector, $p_{\varvec{\theta }}(\varvec{x}_j|\varvec{z}_j)$ can be a multivariate Bernoulli distribution $\mathrm {Ber}(F_{\varvec{\theta }}(\varvec{z}_j))$ with $F_{\varvec{\theta }}(\varvec{z}_j)$ being the highly no-linear function parameterized by $\varvec{\theta }$.

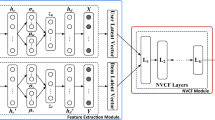
According to the graphic model in Fig. 1, the joint probability of $\varvec{R},\varvec{X},\varvec{U},\varvec{V}$, $\varvec{Z}$ and $\varvec{T}$ can be represented as:

$$\begin{aligned} p(\mathcal {O},&\mathcal {Z})=\prod \nolimits _{i=1}^{N}\prod \nolimits _{j=1}^{M}\prod \nolimits _{k=1}^{N}p(\mathcal {O}_{ijk},\mathcal {Z}_{ijk})= \prod \nolimits _{i=1}^{N}\prod \nolimits _{j=1}^{M}\nonumber \\&\prod \nolimits _{k=1}^{N}p(\varvec{z}_j)p(\varvec{u}_i|\varvec{U}_{N_i},\varvec{T})p_{\varvec{\theta }}(\varvec{x}_j|\varvec{z}_j) p(\varvec{v}_j|\varvec{z}_j)p(R_{ij}|\varvec{u}_i,\varvec{v}_j), \end{aligned}$$

(3)

where $\mathcal {O}= \left\{ \varvec{R},\varvec{S},\varvec{X}\right\}$ is the set of all observed variables, $\mathcal {Z}=\left\{ \varvec{U},\varvec{V},\varvec{Z}\right\}$ is the set of all latent variables needed to be inferred, and $\mathcal {O}_{ijk}=\left\{ R_{ij},T_{ik}, \varvec{x}_j \right\}$ and $\mathcal {Z}_{ijk}=\left\{ \varvec{u}_i,\varvec{v}_j,\varvec{z}_j \right\}$ for short.

3.2 Inference

Previous work [21, 24] has shown that using an expectation-maximization (EM) algorithm enables recommendation methods that integrate them to obtain high-quality latent vectors (in our case, $\varvec{U}$ and $\varvec{V}$). Inspired by these work, in this section, we derive an EM algorithm called VDCMF from the view of Bayesian point estimation. The marginal log likelihood can be given by:

$$\begin{aligned}&\log p(\mathcal {O})=\log \int p(\mathcal {O},\mathcal {Z})\mathrm {d}\mathcal {Z} \ge \int q(\mathcal {Z})\log \frac{p(\mathcal {O},\mathcal {Z})}{q(\mathcal {Z})} \mathrm {d}\mathcal {Z} \nonumber \\&=\int q(\mathcal {Z})\log p(\mathcal {O},\mathcal {Z})- \int q(\mathcal {Z}) \log q(\mathcal {Z}) \equiv \mathcal {L}(q), \end{aligned}$$

(4)

where we apply Jensen’s inequality, and $q(\mathcal {Z})$ and $\mathcal {F}(q)$ are variational distribution and the evidence lower bound (ELBO), respectively. For variational distribution $q(\mathcal {Z})$, we consider variational distributions in it to be matrix-wise independent:

$$\begin{aligned}&q(\mathcal {Z})=q(\varvec{U})q(\varvec{V})q(\varvec{Z}) \\&\,\,\,\, =\prod \nolimits _{i=1}^{N} q(\varvec{u}_i) \prod \nolimits _{j=1}^{M} q(\varvec{v}_j) \prod \nolimits _{j=1}^{M}q(\varvec{z}_j). \nonumber \end{aligned}$$

(5)

For Bayesian point estimation, we assume the variational distribution of $\varvec{u}_i$ is:

$$\begin{aligned} q(\varvec{u}_i)=\prod \nolimits _{d=1}^{D}\delta (U_{id}- \hat{U}_{id}). \end{aligned}$$

(6)

$$\begin{aligned} q(\varvec{v}_j)=\prod \nolimits _{d=1}^{D}\delta (V_{jd}- \hat{V}_{jd}). \end{aligned}$$

(7)

where $\{\hat{U}_{id}\}_{d=1}^D$ are variational parameters and $\delta$ is a Dirac delta function. Variational distributions of $\varvec{v}_j$ and $\varvec{g}_k$ are defined similarly. When $U_{id}$ are discrete, the entropy of $\varvec{u}_i$ is:

$$\begin{aligned} H(\varvec{u}_i)=-\int q(\varvec{u_i})\log q(\varvec{u}_i) =\sum \nolimits _{d=1}^{D}\sum \nolimits _{U_{id}}\delta (U_{id}-\hat{U}_{id})\log \delta (U_{id}-\hat{U}_{id})=0. \end{aligned}$$

(8)

Similarly, $H(\varvec{v}_j)$ is 0 when the elements are discrete. Then the evidence lower bound $\mathcal {L}(q)$ (Eq. 4) can be written as:

$$\begin{aligned}&\mathcal {L}_\text {point}(\hat{\varvec{U}},\hat{\varvec{V}},\varvec{\theta },\varvec{\phi })= \langle \log p(\varvec{U}|\varvec{T},\varvec{U}_{N_i})p(\varvec{V}|\varvec{Z}) \\&p(\varvec{X}|\varvec{Z})p(\varvec{R}|\varvec{U},\varvec{V}) \rangle _q- \text {KL}(q_{\varvec{\phi }}(\varvec{Z}|\varvec{X})||p(\varvec{Z})),\nonumber \end{aligned}$$

(9)

where $\langle \cdot \rangle$ is the statistical expectation with respect to the corresponding variational distribution. $\hat{\varvec{U}}=\left\{ \hat{U}_{id}\right\}$ and $\hat{\varvec{V}}=\left\{ \hat{V}_{jd}\right\}$ are variational parameters corresponding to the variational distribution $q(\varvec{U})$ and $q(\varvec{V})$, respectively.

For latent variables $\varvec{Z}$, However, it is intractable to infer $\varvec{Z}$ by using traditional mean-field approximation since we do not have any conjugate probability distribution in our model which requires by traditional mean-field approaches. To track this problem, we use amortized inference [6, 8], it consider a shared structure for every variational distributions, instead. Consequently, similar to VAE [11], we also introduce a variational distribution $q_{\varvec{\phi }}(\varvec{Z}|\varvec{X})$ to approximate the true posterior distribution $p(\varvec{Z}|\mathcal {O})$. $q_{\varvec{\phi }}(\varvec{Z}|\varvec{X})$ is implemented by a inference neural network parameterized by $\varvec{\phi }$ (see Fig. 1). Specifically, for $\varvec{z}_j$ we have:

$$\begin{aligned} q(\varvec{z}_j)=q_{\varvec{\phi }}(\varvec{z}_j|\varvec{x}_j)=\mathcal {N}(\varvec{\mu }_{j},\text {diag}(\varvec{\delta }_{j}^2)), \end{aligned}$$

(10)

where the mean $\varvec{\mu }_{j}$ and variance $\varvec{\delta }_{j}$ are the outputs of the inference neural network.

Directly maximizing the ELBO (Eq. 9) involves solving parameters $\hat{\varvec{U}}$, $\hat{\varvec{V}}$, $\varvec{\theta }$ and $\varvec{\phi }$, which is intractable. Thus, we derive an iterative variational-EM (VEM) algorithm to maximize $\mathcal {L}_\text {point}(\hat{\varvec{U}},\hat{\varvec{V}},\varvec{\theta },\varvec{\phi })$ , abbreviated $\mathcal {L}_\text {point}$.

Variational E-step. We first keep $\varvec{\theta }$ and $\varvec{\phi }$ fixed, then optimize evidence lower bound $\mathcal {L}_\text {point}$ with respect to $\hat{\varvec{U}}$ and $\hat{\varvec{V}}$. We take the gradient of $\mathcal {L}$ with respect to $\varvec{u}_i$ and $\varvec{v}_j$ and set it to zero. We will get the updating rules of $\hat{\varvec{u}}_i$ and $\hat{\varvec{v}}_j$:

$$\begin{aligned}&\hat{\varvec{u}}_i \leftarrow (\varvec{V}\varvec{C}_i\varvec{V}^{\top }+\lambda _u\varvec{I}_D+\lambda _f\varvec{T}_{i}\varvec{1}_{I}\varvec{I}_{D})^{-1} (\lambda _f\varvec{U}\varvec{T}_i^{\top }+\varvec{V}\varvec{C}_{i}\varvec{R}_i), \end{aligned}$$

(11)

$$\begin{aligned}&\hat{\varvec{v}}_j \leftarrow (\hat{\varvec{U}}\varvec{C}_j\hat{\varvec{U}}^\top +\lambda _v \varvec{I}_D)^{-1} (\hat{\varvec{U}}\varvec{C}_j\varvec{R}_j+\lambda _v \langle \varvec{z}_j \rangle ), \end{aligned}$$

(12)

where $\varvec{C}_i=\text {diag}(c_{i1},...c_{iM})$, $\varvec{T}_i=\text {diag}(T_{i1},...T_{iM})$, $\varvec{R}_i=[R_{i1},...R_{iM}]$. $\varvec{I}_{N}$ is a N dimensional column vector with all elements elements to 1. For item latent vector $\varvec{v}_j$, $\varvec{C}_j$ and $\varvec{R}_j$are defined similarly. $\hat{\varvec{u}}_i=[\hat{U}_{i1},...\hat{U}_{iD}]$ and $\hat{\varvec{v}}_j=[\hat{V}_{j1},...\hat{V}_{jD}]$. For $\varvec{z}_j$, its expectation is $\langle \varvec{z}_j\rangle =\varvec{\mu }_{j}$, which is the output of the inference network.

It can be observed that $\lambda _v$ governs how much the latent item vector $\varvec{z}_j$ affects item latent vector $\varvec{v}_j$. For example, if $\lambda _v= \infty$, it indicate we direct use latent item vector to represent item latent vector $\varvec{v}_j$; if $\lambda _v=0$, it means we do not embed any item content information into item latent vector. $\lambda _f$ serves as a balance parameter between social trust matrix and user-item matrix on user latent vector $\varvec{u}_i$. For example, if $\lambda _f=\infty$, it means we only use the social network information to model user’s preference; if $\lambda _f=0$, we only use user-item matrix and item content information for prediction. So $\lambda _v$ and $\lambda _f$ are regarded as collaborative parameters for item content, user-item matrix and social matrix.

Variational M-step. Keep $\hat{\varvec{U}}$ and $\hat{\varvec{V}}$ fixed, we optimize $\mathcal {L}_\text {point}$ w.r.t. $\varvec{\phi }$ and $\varvec{\theta }$ (we only focus on terms containing $\varvec{\phi }$ and $\varvec{\theta }$).

$$\begin{aligned}&\mathcal {L}_{\text {point}}= \text {constant}+ \sum \nolimits _{j=1}^{M}\mathcal {L}(\varvec{\theta },\varvec{\phi };\varvec{x}_j,\varvec{v}_j )=\text {constant} +\sum \nolimits _{j=1}^{M}\\&-\frac{\lambda _v}{2}\langle (\varvec{v}_j-\varvec{z}_j)^\top (\varvec{v}_j-\varvec{z}_j)\rangle _{q(\mathcal {Z})}+\langle \log p_{\varvec{\theta }}(\varvec{x}_j|\varvec{z}_j) \rangle _{q_{\varvec{\phi }}(\varvec{z}_j|\varvec{x}_j)}-\text {KL}(q_{\varvec{\phi }}(\varvec{z}_j|\varvec{x}_j)||p(\varvec{z}_j)),\nonumber \end{aligned}$$

(13)

where M is the number of items and the constant term represents terms which don’t contain $\varvec{\theta }$ and $\varvec{\phi }$. For the expectation term $\langle p_{\varvec{\theta }}(\varvec{x}_j|\varvec{z}_j) \rangle _{q_{\varvec{\phi }}(\varvec{z}_j|\varvec{x}_j)}$, we can not solve it analytically. To handle this problem, we approximate it by the Monte Carlo sampling as follows:

$$\begin{aligned} \langle \log p_{\varvec{\theta }}(\varvec{x}_j|\varvec{z}_j) \rangle _{q_{\varvec{\phi }}(\varvec{z}_j|\varvec{x}_j)}= \frac{1}{L} \sum \nolimits _{l=1}^{L}p_{\varvec{\theta }}(\varvec{x}_j|\varvec{z}_j^l), \end{aligned}$$

(14)

where L is the size of samplings, and $\varvec{z}_j^l$ denotes the l-th sample, which is reparameterized to $\varvec{z}_j^l=\varvec{\epsilon }_j^l\odot \text {diag}(\varvec{\delta }_{j}^2)+\varvec{\mu }_{j}$. Here $\varvec{\epsilon }_j^{l}$ is drawn from $\mathcal {N}(0,\varvec{I}_D)$ and $\odot$ is an element-wise multiplication. By using this reparameterization trick and Eq. 10, $\mathcal {L}(\varvec{\theta },\varvec{\phi };\varvec{x}_j,\varvec{v}_j)$ in Eq. 13 can be estimated by:

$$\begin{aligned}&\mathcal {L}(\varvec{\theta },\varvec{\phi };\varvec{x}_j,\varvec{v}_j)\simeq \tilde{\mathcal {L}}^j(\varvec{\theta ,\phi })=- \frac{\lambda _v}{2}(-2\varvec{\mu }_{j}^\top \hat{\varvec{v}}_j+\varvec{\mu }_{j}^\top \varvec{\mu }_{j} \nonumber \\&+ \mathrm {tr}(\text {diag}(\varvec{\delta }_{j}^2)))+\frac{1}{L} \sum \nolimits _{l=1}^{L}p_{\varvec{\theta }}(\varvec{x}_j|\varvec{z}_j^l) -\text {KL}(q_{\varvec{\phi }}(\varvec{z}_j|\varvec{x}_j)||p(\varvec{z}_j))+\text {constant}. \end{aligned}$$

(15)

We can construct an estimator of $\mathcal {L}_{\text {point}}(\varvec{\phi },\varvec{\theta };\varvec{X},\varvec{V})$, based on minibatches:

$$\begin{aligned} \mathcal {L}_{\text {point}}(\varvec{\theta },\varvec{\phi })\simeq \tilde{\mathcal {L}}^P(\varvec{\theta },\varvec{\phi })= \frac{M}{P}\sum \nolimits _{j=1}^{P}\tilde{\mathcal {L}}^j(\varvec{\theta },\varvec{\phi }). \end{aligned}$$

(16)

As discussed in [11], the number of samplings L per item j can be set to 1 as long as the minibatch size P is large enough, e.g., $P=128$. We can update $\varvec{\theta }$ and $\varvec{\phi }$ by using the gradient $\nabla _{\varvec{\theta },\varvec{\phi }} \tilde{\mathcal {L}}^P(\varvec{\theta },\varvec{\phi })$.

We iteratively update $\varvec{U}, \varvec{V}, \varvec{G}, \varvec{\theta }, \text {and} ~ \varvec{\phi }$ until it converges.

3.3 Prediction

After we get the approximate posteriors of $\varvec{u}_i$ and $\varvec{v}_j$. We predict the missing value $R_{ij}$ in $\varvec{R}$ by using the learned latent features $\varvec{u}_i$ and $\varvec{v}_j$:

$$\begin{aligned} R_{ij}^*=\langle R_{ij} \rangle&=(\langle \varvec{z}_j\rangle + \langle \varvec{k}_j\rangle )^\top \langle \varvec{u}_i\rangle = \langle \varvec{v}_j\rangle ^ {\top } \langle \varvec{u}_i\rangle \end{aligned}$$

(17)

For a new item that is not rated by any other users, the offset $\varvec{\epsilon }_j$ is zero, and we can predict $R_{ij}$ by:

$$\begin{aligned} R_{ij}^*=\langle R_{ij} \rangle = \langle \varvec{z}_j\rangle ^\top \langle \varvec{u}_i\rangle \end{aligned}$$

(18)

4 Experiments

4.1 Experimental Setup

Datasets. In order to evaluate performance of our model, we conduct experiments on two real-world datasets from Lastfm¹ (lastfm-2k) and Epinions² (Epinions) datasets:

Lastfm. This dataset contains user-item, user-user, and user-tag-item relations. We first transform this dataset as implicit feedback. For Lastfm dataset, we consider the user-item feedback is 1 if the user has listened to the artist (item); otherwise, it is 0. Lastfm only contains 0.27% observed feedbacks. We use items bag-of-word tag representations as their items content information. We direct use user social matrix as trust matrix.

Epinions. This dataset contains rating , user trust and review information. We transform this dataset as implicit feedback. For those ${>}3$ ratings, we transform it as ‘1’; otherwise, it is 0. We use item’s review as its content information. Epinions contains 0.08% observed feedbacks.

Baselines. For fair comparisons, like that in our VDCMF, the baselines we used also incorporate user social information or item content information into matrix factorization. (1) PMF. This model [17] is a famous MF method, and only uses user-item feedback matrix. (2) SoRec. This model [15] jointly decomposes user-user social matrix and user-item feedback matrix to learn user and item latent representations. (3) Collaborative topic regression (CTR). This model [21] utilizes topic model and matrix factorization to learn latent representations of users and items. (4) Collaborative deep learning (CDL). This model [24] utilizes stack denoising autoencoder to learn latent items’ content representations, and incorporates them into probabilistic matrix factorization. (5) CTR-SMF. This model [18] incorporates topic modeling and probabilistic MF of social networks. (6) PoissonMF-CS. This model [19], jointly models use social trust, item content and users preference using Poisson matrix factorization framework. It is a state-of-the-art MF method for Top-N recommendation on the Lastfm dataset. (7)Neural Matrix Factorization (NeuMF). This model is a state-of-the-art collaborative filtering method, which utilizes neural network to model the interaction between user model [9] is a state-of-the-art collaborative filtering method, which utilizes neural network to model the interaction between users and items.

Settings. For fair comparisons, We first set the parameters for PMF, SoRec, CTR, CTR-SMF, CDL, NeuMF via five-fold cross validation. For our model, we set $\lambda _u=0.1$, D = 25 for Lastfm and D = 50 for Epinions. Without special mention, we set $\lambda _v=0.1$ and $\lambda _f=0.1$. We will further study the impact of the key hyper-parameters for the recommendation performance.

Evaluation Metrics. The metrics we used are Recall@K, NDCG@K and MAP@K [5] which are common metrics for recommendation.

4.2 Experimental Results and Discussions

Overall Performance. To evaluate our model in top-K recommendation task, we evaluate our model and baselines in two datasets in terms of Recall@20, Recall@50, ND CG@20 and MAP@20. Table 1 shows the performance of our VDCMF and the baselines using the two datasets. According to Table 1, we have following findings: (a) VDCMF outperforms the baselines in terms of all matrices on Lastfm and Epinions, which demonstrates the effectiveness of our method of inferring the latent factors of users and items, and leading to better recommendation performance. (b) For more sparse dataset, Epinions, VDCMF also achieves the best performance, which demonstrates our model can effectively handle matrix sparsity problem. We attribute this improvement to the incorporated item content and social trust information. (c) We can see methods which both utilizes content and social information (VDCMF, NeuMF and PoissonMF-CS) outperform others (CDL,CTR, CTR-SMF, SoRec and PMF), which demonstrates incorporating content and social information can effectively alleviate matrix sparse problem. (d) Our VDCMF outperforms the strong baseline PoissonMF-CS, though they are both Bayesian generative model. The reason VDCMF is that our VDCMF incorporates neural network into Bayesian generative model, which makes it have powerful non-linearity to model item content’s latent representation. To further evaluate our VDCMF robustness, we evaluate the empirical performance of large recommendation list for our VDCMF on Lastfm and report results in Fig. 2. We can find our VDCMF significantly and consistently outperforms other baselines. This, again, demonstrates the effectiveness of our model. All of these findings demonstrates that our VDCMF is robust and it is able to achieve significant improvements of top-k recommendation over the state-of-the-art.

Table 1. Recommendation performance of VDCMF and baselines. The best baseline method is highlighted with underline.

Fig. 2.

Evaluation of Top-K item recommendation where K ranges from 50 to 250 on Lastfm

Fig. 3.

The effect of $\lambda _v$ and $\lambda _f$ of the proposed VDCMF with Recall@50 on Lastfm and Epinions.

Impact of Parameters. In this section, we study the effect of the key hyper-parameters of the proposed model. We first study the parameters of $\lambda _f$ and $\lambda _v$. We use Recall@50 as an example, the plot the contours on Lastfm and Epinions datasets. Figure 3(a) and (b) show the contour of Recall@50. As we can see, VDCMF achieves the best recommendation performance when $\lambda _v=\,$0.1 and $\lambda _f$ = 0.1 on Lastfm, and $\lambda _v$ = 1 and $\lambda _f=0.1$ on Epinions. From Fig. 3(a) and (b), we can find our model is sensitive to $\lambda _v$ and $\lambda _f$. The reason is that $\lambda _v$ can control how much item content information is incorporated into item latent vector, $\lambda _q$ can control how much social information is incorporated into user latent vector. Figure 3(a) and (b) show that we can balance the content information and social information by varying $\lambda _v$ and $\lambda _q$, leading to better recommendation performance.

5 Conclusion

In this paper, we studied the problem of inferring effective latent factors of users and items for social recommendation. We have proposed a novel Variational Deep Collaborative Matrix Factorization algorithm, VDCMF, which incorporates rich item content and user social trust information into a full Bayesian deep generative framework. Due to the full Bayesian nature and non-linearity of deep neural networks, our proposed model is able to learn more effective latent representations of users and items than those generated by state-of-the-art neural networks based recommendation algorithms. To effectively infer latent factors of users and items, we derived an efficient expectation-maximization algorithm. We have conducted experiments on two publicly available datasets. We evaluated the performance of our VDCMF and baselines methods based on Recall, NDCG and MAP metrics. Experimental results demonstrate that our VDCMF can effectively infer latent factors of users and items.