Computational Study of Emergency Service System Reengineering Under Generalized Disutility

Abstract

Emergency medical service system structure is determined by deployment of limited number of the service providing centers. The objective of the designer is to minimize the total discomfort of all system users. Thus, the problem often takes the form of the weighted p-median problem. Since population and demands for service change in time and space, current service center deployment may not meet the requirements of the users and service providers neither. We suggest and discuss a mathematical model for system reengineering under the generalized disutility. Formulation of the generalized disutility follows from the idea that the individual user’s disutility is caused by positions of more than one located service center. Generalized disutility enables to model the system performance more realistically. It enables to take into account also such situations in which the nearest service center may be temporarily unavailable due to satisfying another demand. This approach represents an extension of our previous research, in which only the nearest center was taken as a source of individual user’s demand satisfaction.

1 Introduction

An emergency service system as the medical emergency system, system of fire brigades and system of police stations are designed for given geographical area to satisfy the demand of population living in the area for more secure life. Associate service is provided from a given number of service centers and the overwhelming objective used for the design evaluation is the average time necessary to deliver service from a service center to the user location, in which a demand for service has occurred.

Host of models assume that serviced population is concentrated to a finite number of dwelling places of the considered area. Frequency of the demand occurrence at a given place is proportional to the number of inhabitants of the given town or village. A finite set of possible service center locations is assumed and also the assumption is made that a user demand is serviced from the nearest located service center. This way, the weighted p-median problem formulation is used to the emergency service system design and solving the underlying problem to optimality [2, 3, 6, 10]. The original way of modelling was based on the location-allocation decision variables and constraints [2], where an occurring demand is assigned to exactly one possible center location. As concerns usage of a general IP-solver, the size of the solved integer programming problem must be taken into account. In real problems, the number of serviced users takes the value of several thousands, and the number of possible service center locations can take this value as well [1]. The number of possible service center locations seriously impacts the computational time and the memory of computer due to used branch-and-bound method, which stores the unfathomed nodes of the inspected searching tree for the further processing. Therefore, the direct attempt at solving the problem described by a location-allocation model often fails, when larger instances are solved by a commercial IP-solver. Then, another approach using so-called radial formulation was developed to avoid the particular assignment of user’s locations to the located service centers. The radial approach successfulness is based on the fact that there is only finite set of radii, which must be taken into account [4, 5, 7]. To accelerate the p-median problem solving process performed by commercial IP-solvers, an approximate approach has been developed [8]. This approach uses an approximation of a common time distance between a service center location and a user by some pre-determined time distances and gives near to optimal results in the case of integer time distances. Accuracy of the resulting solution can be arbitrarily improved by usage of smaller units for the time-distance evaluation.

A bit different situation occurs, when reengineering of a current emergency service system is performed. The necessity of system updating usually follows from the fact that distribution of demands for service has been developing in time and space and thus, the originally determined center locations do not suit both serviced public and providers operating the service centers. Contrary to the original system design, the current service providers suggest changes in the center deployment and their suggestion may be in a conflict with public interests. That is why the system administrator permits system reengineering only subject to some formal rules, which are intended to prevent worsening the service accessibility. The considered formal rules are quantified by a maximal number of provider’s centers, which are allowed to change their locations and by the maximal distance between a current center location and a possible new location. Generally, addition of constraints may significantly spoil the computational time necessary to obtain the optimal solution of the problem. The study [12] showed, that they do not impact the computational time, when a user demand is serviced from the nearest located center.

In this paper, we deal with more general model of the emergency medical system design under reengineering. We assume that service of a user demand is provided from the nearest center only in the case, when the center is not occupied by servicing a former demand. Otherwise, the user’s demand is serviced from the nearest unoccupied center. Initial emergency system design considering the failing centers was studied in [14] and the associated radial formulation was presented in [11]. Nevertheless, the reengineering of service system with failing centers has not been studied yet. Therefore, we focus on the influence of the formal rule constraints on best possible service availability in the service system and on the associated computational process convergence.

We provide a reader with a radial model of emergency service system reengineering with failing centers under rules imposed by the system administrator. We perform a computational study to find whether real-sized instances of the problem are solvable using a common IP-solver.

The remainder of the paper is organized as follows. The next section is devoted to the radial model formulation, in which temporarily failing centers are considered. In Sect. 3, administrator’s auxiliary rules are introduced and various ways of their implementation in the associated models are discussed. Section 4 consists of numerical experiments focused on three goals. The first one is connected with optimization of model parameters, which influence both model size and the result accuracy. The second goal consists in answering the question: How do the individual parameters of the administrator’s rules influence the resulting average response time of the emergency service? The third portion of the numerical experiments aims at investigation of mutual impact of the observed formal rules parameters. The conclusion summarizes obtained findings and contains possible directions of a further research.

2 Reengineering of a Service System with Failing Centers

The emergency system reengineering was originally studied in [12], where the radial model of the problem was introduced. The basic idea follows from the analysis of current service center deployment, which may not be optimal due to changing demands and development of the underlying transportation network. To explain the problem in more details, consider the simple example depicted in Fig. 1. We assume that the left graph represents current deployment of four service centers marked by blue color. All the vertices represent possible demand points. To evaluate the current center deployment, the sum of distances from each network node to the nearest located center was used as the quality criterion. Here, it takes the value of 66. If we allowed changes in current service center locations and moved a service center from the node 2 to the node 6, we would perform system reengineering and we could achieve better value of the criterion. The new system design is depicted on the right graph and its evaluation is 64. By this small example we demonstrated the principle and goal of system reengineering.

Fig. 1.

Simple example of emergency service system reengineering [12].

In this paper, we study the reengineering problem under generalized disutility with the assumption that the service is provided by more than one provider. We also extend the research published in [13]. To describe the problem of the users’ disutility minimization by changing the deployment of centers belonging to one considered provider, we introduce several necessary notations. Let us denote J as a finite set of all users (dwelling places), where b_j denotes a volume of expected demand of user j ∈ J. Let I be a finite set of all possible center locations. We use the symbol d_ij to denote the integer network time distance between locations i and j, where i, j ∈ I ∪ J. The maximal considered distance is m. The current emergency service center deployment is described by union of two disjoint sets of located centers I_L and I_F, where I_L contains p centers of the considered provider and I_F is the set of centers belonging to the other providers. The considered provider performs updating of his part of the system by changing locations of the centers from I_L. The center locations from I_L can be relocated within the set I_R = I – I_F. Locations of centers from I_F stay unchanged.

Let value q_k represent probability of the case that the k-1 nearest centers are occupied and the k-th nearest center is the first one, which is available [9, 14].

The probabilities q_k for k = 1, …, r are positive real values, which meet the following inequalities q₁ ≥ q₂ ≥ … ≥ q_r and depend only on the order of distances from the user to the r nearest centers. In this paper, the generalized disutility perceived by a user is modelled by a sum of weighted time distances from the r nearest located centers. Mentioned concept of generalized disutility is depicted in the following Fig. 2.

Fig. 2.

Concept of generalized disutility, where the distances to the service centers are weighted by probability coefficients q_k. The shortest distance is weighted by the highest coefficient.

To complete the following radial model, we introduce coefficients $a_{ij}^{s}$ for each pair i, j of possible center location and location of the user j. We define $a_{ij}^{s} \, = \, 1$ if and only if d_ij ≤ s and $a_{ij}^{s} \, = \,0$ otherwise for each s = 0, 1, …, m – 1.

To describe decisions on new center deployment, we introduce location zero-one variables y_i defined for each i ∈ I_R. The variable y_i takes the value of one, if a service center is to be located at i and it takes the value of zero otherwise. To express the total distance necessary for user demand satisfaction in the radial manner, we introduce auxiliary zero-one variables x_jsk for j ∈ J, s ∈ 0 … m – 1, k ∈ 1 … r to model the disutility contribution value of the k-th nearest service center to the user j. The variable x_jsk takes the value of 1 if the k-th smallest disutility contribution for the user j ∈ J is greater than s and it takes the value of 0 otherwise. Then the expression x_j0k + x_j1k+ … + x_jm–1k constitutes the k-th smallest distance from the user j to a located center. If this k-th smallest distance is denoted by d_ik(j), then the expression of d_ik(j) by the auxiliary 0-1 variables x_jsk is clearly shown in the following Fig. 3.

Fig. 3.

Expression of the k-th smallest distance from the user j to a located center by the auxiliary 0-1 variables x_jsk for s ∈ 0 … m – 1 [13].

Using the above introduced coefficients, ranges and decision variables, we suggest the following model [13].

$$ Minimize\,\,\sum\limits_{j \in J} {b_{j} \sum\limits_{s = 0}^{m - 1} {\sum\limits_{k = 1}^{r} {q_{k} x_{jsk} } } } $$

(1)

$$ Subject\,\,to\,\,\sum\limits_{{i \in I_{R} }} {y_{i} } = p $$

(2)

$$ \sum\limits_{k = 1}^{r} {} x_{jsk} + \sum\limits_{{i \in I_{R} }} {a_{ij}^{s} y_{i} } + \sum\limits_{{i \in I_{F} }} {a_{ij}^{s} } \ge r\,\quad \quad for\,\,j \in J,\,\,s = 0\, \ldots \,m - 1 $$

(3)

$$ y_{i} \in \{ 0,\,\,1\} \,\quad \quad for\,\,i \in I_{R} $$

(4)

$$ x_{jsk} \in \{ 0,\,\,1\} \quad \quad for\,\,\,\,j \in J,\,\,s = 0\,\, \ldots \,\,m - 1,\,\,k = 1\,\, \ldots \,\,r $$

(5)

The objective function (1) expresses the expected volume of generalized disutility. Constraint (2) ensures that the number of centers belonging to the considered part of the emergency service system under reengineering will be constant. For given pair of user j and a distance value s, the constraint (3) expresses relation between the set of location variables y_i, i ∈ I_R and the sum of auxiliary variables x_jsk over range 1 … r of subscript k. If no center is located in the radius s, then the sum of auxiliary variables x_jsk equals to r. If exactly k  ≤  r centers are located in the radius s, then the sum of variables equals to r – k due to minimization process, which presses down the values of the variables x_jsk. If the sum of variables x_jsk equals to k < r, then the variables x_js1, …, x_jsr–k, equal to zero and remaining variables equal to one due to the used optimization process and decreasing values of the coefficients q₁, …, q_r.

Then, the objective function value of the optimal solution of the problem (1)–(5) gives expected total length or time of trips from the service centers to the demand locations necessary for satisfaction of all demands for service. This holds subject to assumptions that the coefficients q₁ … q_r correspond to the probability values expressing that the k-th nearest center is the first available (unoccupied) service center and that demand volume b_j is proportional to the number of trips necessary for the demand satisfaction. The model (1)–(5) is much more realistic than the original approach based on the simple weighted p-median problem, which corresponds to the case of r = 1. The bigger accuracy of the model (1)–(5) is paid for by higher complexity of the solved problem, which may issue to enormous increase of computational time. We want to find, what limit of accuracy presented by the value of r pays off regarding the increase of computational time. As a solution of the problem (1)–(5) is discrete and the values of probabilities q_k sharply decrease, we think that influence of increasing value of r may appear negligible behind some limiting value r*.

3 Reengineering Under Auxiliary Constraints

As mentioned in Sect. 1 and in [12, 13], the administrator of the system sets up parameters of rules to prevent a designer of new center deployment from increasing provider’s benefit at the expense of the system users. The rules must have a simple form to be easy to evaluated and checked. The first rule limits the total number w of the provider’s centers, which locations can be changed. The second rule limits the distance between current and newly suggested location of a service center.

To be able to formulate the rules in a concise way, we derive several auxiliary structures using Fig. 4. We assume that all points 1–11 represent system users and the black points 2, 3, 9 and 11 represent current service center locations.

Fig. 4.

Simple example of reengineering restrictions [13].

Let N_t = {i ∈ I_R: d_ti ≤ D} denote the set of all possible center locations, to which the center t ∈ I_L can be moved subject to limited length of the move. If we consider the example depicted in Fig. 4, we can observe that the center located at the point 9 can be moved to 6, 8, 10 and 13 or stay unchanged. Thus, the set N₉ = {6, 8, 9, 10, 13}. Similarly, N₃ = {3, 4, 6}. Additionally, let S_i = {t ∈ I_L: i ∈ N_t} denote a set of all centers of the considered provider, which can be moved to i ∈ I_R subject to the mentioned limitation. Here S₆ = {3, 9}. Realize that t ∈ N_t and i ∈ S_i for t ∈ I_L and i ∈ I_R and thus I_L ⊂ I_R.

Now, we introduce series of decision reallocation variables, which model the decisions on moving centers from their original positions to new ones. The variable

u_ti ∈ {0, 1} for t ∈ I_L and i ∈ N_t takes the value of one, if the service center at t is to be moved to i and it takes the value of zero otherwise. Using the above introduced structures and variables we suggest the following model extension.

$$ \sum\limits_{{i \in I_{L} }} {y_{i} } \ge p - w $$

(6)

$$ \sum\limits_{{i \in N_{t} }} {u_{ti} } = 1\quad \quad for\,\,t \in I_{L} $$

(7)

$$ \sum\limits_{{t \in S_{i} }} {u_{ti} } \le y_{i} \quad \quad for\,\,i \in I_{R} $$

(8)

$$ u_{ti} \in \{ 0,\,\,1\} \quad \quad for\,\,t \in I_{L} ,\,\,i \in N_{t} $$

(9)

Constraint (6) limits the number of changed center locations by the constant w. Constraints (7) allow moving the center from the current location t to at most one other possible location in the radius D. Constraints (8) enable to bring at most one center to a location i subject to condition that the original location of the brought center lies in the radius D. These constraints also assure consistency among the decisions on move and decisions on center location.

Another simpler modelling approach to the formal rules implementation consists in relaxation of the parameter D and associated constraints (7)–(9). Parameter D is used to limit the radius, within which an existing service center can be relocated. The idea introduced in [12] assumes that this limitation may represent too strict constraint. This simplified approach enables us to exclude the variables u_ti ∈ {0, 1} from the model. The relaxation consists in the fact that the system reengineering is performed in such a way that there must be at least one center located in the radius D from each existing service center and the center relocation will not limited by any distance. Based on these preliminaries, the constraints (7)–(9) may be replaced by the following expression (10), which guarantees that there will be at least one service center located in radius D from each currently located center. Then the associated simplified radial model takes the form of (1)–(6) and (10).

$$ \sum\limits_{{i \in N_{t} }} {y_{i} } \ge 1\quad for\;t \in I_{L} $$

(10)

The advantage of this simplified model consists in less number of decision variables and structural constraints. Thus, the problem is expected to be easily solvable due to lower model complexity. Furthermore, this model allows such center relocation that is shown in Fig. 5. Consider a transportation network, in which we have two centers (see the left part of the figure). If the optimal solution of the reengineering model places one of the current centers (the green one) to the red node, all the structural constraints stay met and the other center (the blue one) may be relocated anywhere without additional restrictions. Such solution would not be feasible in the original approach described by the model (1)–(9).

Fig. 5.

Reengineering of current emergency system using the simplified model [12]. (Color figure online)

The simplified model (1)–(6), (9) provides bigger variety from the point of possible center location changes in comparison to the original model (1)–(9) and thus it is expected that it could bring better results concerning the optimization criterion. On the other hand, even if this approach may bring better results concerning optimization, the obtained system design can be bad from the point of real system performance. If too many system users are assigned to the same service center, then it is obvious that the service center will be mostly unavailable due to its limited capacity. Therefore, we do not deal with this simplified model in our computational study and we take into account the original formal rules given by parameters w and D.

We want to answer the question about technical solvability of the formulated problem (1)–(9). We ask whether a common commercial integer programming solver based on the branch-and-bound technique is able to find the exact solution of a real-sized problem in acceptable time. Addition of new structural constraints to the original radial model is always questionable from the point of problem solvability. It may directly influence the computational process convergence. Furthermore, we have to realize that even if the administrator’s rules are established to defend users’ interests, they may represent a reduction of the set of feasible solutions. This phenomenon may lead to a less possible benefit (higher disutility) for the average user. That is why, the dependence of the optimal objective function value on setting of parameters w and D is worth to study.

4 Numerical Experiments

4.1 Benchmarks and Preliminaries

The numerical experiments in this section were performed in the optimization software FICO Xpress 8.3, 64-bit. The experiments were run on a PC equipped with the Intel® Core™ i7 5500U 2.4 GHz processor and 16 GB RAM.

Used benchmarks were derived from real emergency health care system, which was implemented in eight regions of Slovak Republic. For each self-governing region, i.e. Bratislava (BA), Banská Bystrica (BB), Košice (KE), Nitra (NR), Prešov (PO), Trenčín (TN), Trnava (TT) and Žilina (ZA), all cities and villages with corresponding number of inhabitants b_j were taken into account. The coefficients b_j were rounded to hundreds. The set of communities represents both the set J of users’ locations and the set I of possible center locations as well. The cardinalities of these sets vary from 87 to 664 locations. The total number of possible service center locations for the individual self-governing region is reported in Table 1 in the column denoted by |I|. Each self-governing region emergency sub-system provides its user with emergency service from the given number of service centers currently located at some of the possible locations from I. The number of service centers of the individual region is reported in Table 1 in the column denoted by TNC (the Total Number of located Centers). In all solved instances, we consider that disutility perceived by a system user is represented by response time and this response time is proportional to the network distance, which must be traversed from the servicing center to the user locations. As the generalized disutility according to the model in Sect. 2 is studied in this paper, associated parameters r and q_k for k = 1 … r must be established. For these numerical experiments, the value of r was set to 7 and the associated coefficients q_k for k = 1 … r were set in percentage in the following way: q₁ = 77.063, q₂ = 16.476, q₃ = 4.254, q₄= 1.593, q₅ = 0.47, q₆ = 0.126, and q₇ = 0.018. These values were obtained from a simulation model of existing emergency medical service system in Slovakia [9].

Table 1. Average results of numerical experiments for each self-governing region. The value of r was set to 7 [13].

To enrich the pool of benchmarks, we created ten instances for each self-governing region so that they differ in the list of located service centers operated by the considered provider. The average percentage rate of the provider’s centers is reported in Table 1 in the column denoted by “Prov. [%]”.

5 Basic Experiments

The basic experiments reported in this sub-section were originally published in [13]. An individual experiment was organized so that the optimal solution of the problem (1)–(5) was obtained first. The solution does not represent reengineering subject to auxiliary rules specified in Sect. 3, but it represents the best possible solution of the emergency system design problem without any restrictions. The average results are summarized in Table 1, where the right part of the table contains the average computational times in seconds across the ten instances solved for each region. The average computational times are reported in the column denoted by “CT [s]”. The last column “ObjF” contains the average values of the objective function (1).

The results indicate that the reengineering of the emergency service system under generalized disutility for r = 7 from the point of service provider does not represent a hard solvable problem. It can be observed that the radial formulation enables to get the optimal solution within 1 min.

In spite of this useful feature, the following portion of experiments was performed to find out, whether a lower value of r will have significant influence on the resulting objective function value. As mentioned in Sect. 2, we assume that the influence of increasing value of r may appear negligible behind some limiting value r*. To confirm this hypothesis and to find a suitable value of r*, we have solved all instances with different values of r. For bigger comfort of computation, we expressed the probabilities q_k in percentage, i.e. their sum equals to one hundred. If r < 7, then the coefficient q_r was computed according to (11) as a complement of the coefficients q_k for k = 1 … r – 1 to the value of 100, i.e. the sum of q_k for k = 1 … r must equal 100.

$$ q_{r} = 100 - \sum\limits_{k = 1}^{r - 1} {q_{k} } $$

(11)

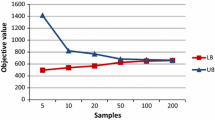
The dependency of average computational time on the value of r was studied first. We assume that the computational time increases with growing value of r, because the value of r affects the number of variables and the model size as well. Our expectation has been confirmed by the results summarized in Table 2. Each row of the table represents the average results of the ten instances for each region and the columns are used for different setting of parameter r. The last row contains the average values of all instances. The dependency of average computational time on the value of r is also shown in Fig. 6.

Table 2. Average computational time in seconds of the solving process depending on r for each region [13].

Fig. 6.

Dependency of average computational time in seconds on the number r [13].

When we studied the impact of the number r of considered centers on the resulting system design, we have evaluated Hamming distance of the vectors of resulting location variables obtained for various values of the parameter r. The Hamming distance of two 0-1 vectors y and z is defined by the expression (12). The average results are reported in Table 3.

Table 3. Average Hamming distance from the optimal solution obtained for r = 7 computed for each region [13].

$$ HD(\varvec{y},\varvec{z}) = \sum\limits_{i \in I} {\left( {y_{i} - z_{i} } \right)}^{2} $$

(12)

The dependency of average Hamming distance from the optimal solution obtained for r = 7 on the number r of service providing centers for each system user is also shown in Fig. 7.

Fig. 7.

Dependency of Hamming distance from the optimal solution obtained for r = 7 on the number r of service providing centers for each system user [13].

The reported results show that the suitable value of r* is 3. Thus, we proved that three nearest located service centers are enough to be taken into account, when emergency system reengineering under generalized disutility is performed. As shown in Table 3 and Fig. 7, the service center deployment for r = 3 differs from the service center deployment obtained for r = 7 only in one center on the average. The difference in one service center corresponds to Hamming distance equal to the value of two.

The last characteristics studied in this portion of experiments is the objective function value. For each system design obtained for particular value of r = 1, …, 6, the objective function (1) with r = 7 and the full set of coefficients q_k was computed. This value was compared to the objective function value obtained for r = 7 and the gap between the objective values was evaluated. The gap is defined as a percentage difference of the two objective function values, where the objective function value for r = 7 was taken as the base. The average values of gaps of the ten instances computed for each self-governing region are reported in Table 4, which is organized in the same manner as the previous tables. To enable finding a suitable value of r*, the gaps lower than 0.1% are marked by grey color.

Table 4. Average gap from the optimal solution obtained for r = 7 [13].

The dependency of average gap from the optimal solution obtained for r = 7 on the number r of service providing centers for each system user is shown also in Fig. 8.

Fig. 8.

Dependency of average gap from the optimal solution obtained for r = 7 on the number r of service providing centers for each system user [13].

The detailed analysis of presented results shows that usage of the three nearest service providing centers instead of the nearest seven centers leads to very similar results and saves more than one half of computational time. That is why, the next experiments were performed with the setting of r = 3.

The following table contains the final comparison of current service center deployment to the results of suggested reengineering model, which was configured as follows. Based on the above presented results, the parameter r was set to 1 (simple disutility) and 3 (generalized disutility). In the experiments with the generalized disutility, the associated probability coefficients q₁ = 77.063, q₂ = 16.476 and q₃ = 6.461 were used. The objective function values reported in the table was recomputed for setting r = 7 and the original seven probability values. The maximal number w of centers operated by the considered service provider, which are allowed to change their current location, was set to the cardinality of the set I_L, i.e. locations of all considered provider’s centers could be changed. The value 15 limited the radius D, in which a center could be relocated. This initial value of D corresponds to the rule applied in the emergency health care system of the Slovak Republic [12]. Table 5 contains the average results of the ten instances solved for each self-governing region. The objective function value of the current service center deployment is reported in the column denoted by “Current ObjF”. The right part of the table is dedicated to the results of suggested reengineering problems. The abbreviation “ObjF” denotes the objective function value of the emergency system design obtained by solving the reengineering model. Finally, the value of Imp was computed to show possible improvement of the objective function value expressed by the generalized disutility, which can be achieved by relocating w = |I_L| service centers. The value of possible improvement was computed as a percentage difference between objective function values of the current service center deployment and the new system design resulting from optimal solution of the problem described by the associated model. The objective function value of current deployment was taken as the base.

Table 5. Comparison of current service center deployment to the results of reengineering model for r = 1 (simple disutility) and r = 3 (generalized disutility). The reengineering parameters were set at w = p and D = 15 [13].

The reported results show that the emergency system reengineering can cause a considerable improvement of service accessibility for system users expressed by general disutility. The average values of the improvement (Imp) indicate that the objective function value corresponding to the system design can be reduced up to 6%. The achieved results also confirm the usefulness of suggested reengineering model, because it enables us to obtain better system design from the point of service accessibility. It is obvious from the comparison of the cases with r = 1 and r = 3 that the usage of generalized disutility (r = 3) leads to such solutions, which are approximately by 2% better than those, which can be obtained by usage of simple disutility model (r = 1).

5.1 Extended Experiments

This portion of experiments was devoted to observation of impact of the additional constraints (6)–(9) on the solving process. We concentrated on the three parameters, which may play role both in reengineering effectiveness and computational time. This set of experiments was organized so that two of the parameters were fixed and the third one was changed across a given range. The studied parameters were: p – the number of centers supervised by the considered provider, w – the total number of provider’s centers, which can be moved, and D – the maximal radius, in which a center can be moved.

In the first part of this portion of experiments, the parameter p was set at the value reported at the beginning of this section, i.e. p = |I|/2 and the experiments were performed either with fixed parameter D or parameter w. This portion of experiments was originally published in [13].

First, the maximal radius D was fixed at the value of 15 and the maximal number w of centers allowed to change their locations was set to p/4, p/2, 3p/4, and p respectively. Dependency of average computational time in seconds computed for the ten instances of each region is reported in Table 6. Each row of the table represents one region and the columns are devoted to different settings of w.

Table 6. Average computational time in seconds for each region and different values of w. Parameter D was 15 [13].

The reported results show that different settings of w do not significantly affect the computational process, because the value of w limits only the number of possible service center location changes and thus, the number of variables and constraints is independent on w.

The objective function values can be studied in Table 7. Even if parameter r was set to 3 in all solved models, the objective function values were computed for r = 7 based on the resulting service center deployment.

Table 7. Average objective function values for each region and different values of w. Parameter D was 15. The objective function value was recomputed for r = 7 and the whole set of probability coefficients q_k [13].

Second, we fixed the parameter w to its maximal value p, i.e. all centers operated by the provider could change their current locations. Then, we explored the impact of the parameter D on the solving process complexity.

The average computational times in seconds computed for each self-governing region and given values of D across the range of 5, 10, 15, 20, and 25 are reported in Table 8.

Table 8. Average computational time in seconds for each region and different values of D. Parameter w was set to its maximal value, i.e. w = p [13].

The results reported in Table 8 have confirmed our expectation that the parameter D has a direct impact on the computational process. As it can be observed, the average computational time grows with increasing value of D, i.e. with increasing radius, in which current center can be removed. This phenomenon has a simple explanation. The bigger is the radius for center location change, the higher is the number of its possible new locations. As we can notice, this parameter defines the number of decision variables and it directly affects the model size. Therefore, the solving process takes longer time for higher distance D. Finally, the dependency of objective function value on the parameter D is shown in Table 9.

Table 9. Average objective function values for each region and different values of D. Parameter w = p. The objective function value was recomputed for r = 7 and the whole set of probability coefficients q_k [13].

As far as the objective function value expressed by generalized disutility is concerned, the achieved results indicate that the higher value of D is, the better solution can be obtained. As the radius D defines the set of new possible center locations, its setting affects the possibility for obtaining better results. More elements in the set N_t for each t ∈ I_L causes more candidates for new center locations and bigger possible change of current center deployment, which can be followed by better service accessibility for system users.

To verify obtained results and to confirm observed dependences, another portion of numerical experiments was suggested. This new set of experiments was performed for a new set of benchmarks. The new instances were generated from the same transportation networks as before, but these instances differ in the percentage of service centers operated by the considered provider. While in the preliminary experiments, the considered provider owned approximately half of all located centers, in these new benchmarks the ratio is 25 and 75% respectively. The reported results represent the average values of 10 problem instances. Since the self-governing region of Bratislava (BA) is too small for such a study, it was excluded from this portion of experiments.

The main goal of these experiments was to study the impact of formal parameters w and D on the computational time and the resulting system design quality measured by the value of generalized disutility. The obtained results are summarized in the following eight tables. Tables 10, 11, 12 and 13 contain the results aimed at studying the impact of individual parameters w and D on the average computational time. The structure of the tables is the same as used in Tables 6 and 8.

Table 10. Average computational time in seconds for each region and different values of w. Parameter D was 15. The considered provider operated 25% of all located service centers.

Table 11. Average computational time in seconds for each region and different values of w. Parameter D was 15. The considered provider operated 75% of all located service centers.

Table 12. Average computational time in seconds for each region and different values of D. Parameter w = p. The considered provider operated 25% of all located service centers.

Table 13. Average computational time in seconds for each region and different values of D. Parameter w = p. The considered provider operated 75% of all located service centers.

Finally, the last set of tables reports the studied impact of individual parameters w and D on the optimization criterion, which consists in generalized disutility perceived by an average system user. The obtained results are summarized in Table 14, Table 15, Table 16 and Table 17, which follow the structure of Table 7 and Table 9 respectively.

Table 14. Average objective function values for each region and different values of w. Parameter D was 15. The objective function value was recomputed for r = 7 and the whole set of probability coefficients q_k. The considered provider operated 25% of all located service centers.

Table 15. Average objective function values for each region and different values of w. Parameter D was 15. The objective function value was recomputed for r = 7 and the whole set of probability coefficients q_k. The considered provider operated 75% of all located service centers.

Table 16. Average objective function values for each region and different values of D. Parameter w = p. The objective function value was recomputed for r = 7 and the whole set of probability coefficients q_k. The considered provider operated 25% of all located service centers.

Table 17. Average objective function values for each region and different values of D. Parameter w = p. The objective function value was recomputed for r = 7 and the whole set of probability coefficients q_k. The considered provider operated 75% of all located service centers.

5.2 Mutual Relation of the Formal Rules

All the experiments presented above were aimed primarily at studying the model solvability and the sensitivity of the associated computational process on different model parameters. Besides some interesting findings and suitable settings of parameters, we focused also on mutual combinations of the administrator’s rules and their impact on the computational time and the quality of resulting solution given by generalized disutility. The considered rules are that at most given number of center locations can be changed and each center location can be moved only in a given radius from its original position. For these experiments, the self-governing region of Žilina was used. Here, it was assumed that the considered provider operates half of all service centers.

An individual experiment was organized so that the reengineering was performed using the model (1)–(9) for different values of parameters w and D. The parameter w expresses the number of service centers, which can change their current location. Parameter D limits the radius, in which the service center can be relocated. This way, 20 problems for all combinations of mentioned parameters were solved for each problem instance. The results obtained for the individual self-governing regions are presented in Table 18 and Table 19 respectively. The first table contains the average computational time in seconds. It must be noted that ten different instances were generated randomly for each self-governing region as described in previous sections. These instances differ in the list of located service centers operated by the considered provider. The parameter w was set to 25, 50, 75 and 100% of the total number of centers operated by the considered provider. The parameter D took the value 5, 10, 15, 20 and 25.

Table 18. Average computational times in seconds for different settings of parameters w and D in the self-governing region of Žilina (ZA), in which the considered provider operates approximately half of all located service centers.

Table 19. Average objective function values for different settings of parameters w and D in the self-governing region of Žilina (ZA), in which the considered provider operates approximately half of all located service centers. The objective function value was recomputed for r = 7 and the whole set of probability coefficients q_k.

The results reported in Tables 18 and 19 have proved our expectations and confirmed previously observed trends. This new portion of experiments was focused on studying the efficiency of the administrator’s rules imposed on provider’s changes. It was found that the parameters w and D may directly influence the resulting system design, because they affect possible changes in current service center deployment. As far as computational time is concerned, parameter w does not have significant impact. It is used as the right side of the constraint (6) and thus, its value does not change the model size. On the other hand, parameter D considerably affects the solving process. It must be noted that the radius D defines the set of all new possible locations of a service center and thus, it affects the number of decision variables and structural constraints as well. More elements in the set N_t for each t ∈ I_L mean more candidates for new center locations and higher computation time.

6 Conclusions

This paper deals with emergency medical system reengineering under consideration of generalized disutility, which follows the idea that the associated service can be provided from given number of the nearest located centers. Application of the generalized disutility makes the model more realistic by taking into account possible temporarily unavailability of service centers. In our computational study we have found, that three nearest located centers are enough to be considered in the objective function value, because the accuracy of the result is satisfactory.

The next part of experiments was aimed at exploration of impact of additional constraints imposing new restrictions on service center location changes. The additional constraints regulate extent of the permitted reengineering and the reported results give deeper insight into their influence upon computational time of the solving process and quality of the resulting service system design. Based on the results and obtained experience, we can conclude that we have constructed a very useful tool for emergency medical system reengineering under generalized disutility performed by the system administrator with service centers of a considered provider. Designed and investigated model is easy to be implemented and solved in common optimization environment equipped with the branch-and-bound method or other technique destined for integer programming problems.

Future research in this field may be aimed at such system reengineering, which takes into account uncertainty following from randomly occurring failures in the underlying transportation network.