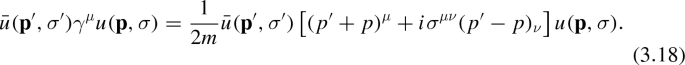From perturbative QFT it is clear that a generic quantum filed \(\phi _i(x)\) contains both the annihilation operators of a type of particles and the creation operators of the corresponding antiparticles [4]. The former term is multiplied by the space-time factor \(\exp (-ipx)\) while the latter is so by \(\exp (ipx)\). To get the basic idea involved in crossing let us consider that the field has spin zero. Therefore, the same vertices in a given scattering process can be associated with a particle of four-momentum p or with an antiparticle with four-momentum \(-p\) and viceversa. This implies that if we have a scattering amplitude of the form

$$\begin{aligned} a_1(p_1)+a_2(p_2)+\cdots \rightarrow b_1(p'_1)+b_2(p'_2)+\cdots \end{aligned}$$
(3.1)

the same scattering amplitude governs any other process in which one or several particles are changed from initial/final to final/initial and at the same time there is a flip in the global sign of the four-momenta. For instance, for the previous reaction we could have many others related by crossing, in particular

$$\begin{aligned} a_1(p_1)+a_2(p_2)+\cdots +\bar{b}(-p'_1) \rightarrow b_2(p'_2)+\cdots \end{aligned}$$
(3.2)

where the bar indicates the corresponding antiparticle. This is the basic content of crossing.

Let us particularize crossing to the two-body scattering \(a+b\rightarrow c+d\). We can then distinguish the following related processes:

$$\begin{aligned} a(p_1)+b(p_2)&\rightarrow c(p_3)+d(p_4),\end{aligned}$$
(3.3)
$$\begin{aligned} a(p_1)+\bar{c}(-p_3)&\rightarrow \bar{b}(-p_2)+d(p_4),\end{aligned}$$
(3.4)
$$\begin{aligned} a(p_1)+\bar{d}(-p_4)&\rightarrow c(p_3)+\bar{b}(-p_2). \end{aligned}$$
(3.5)

From top to bottom, these processes are referred to as s-channel, t-channel and u-channel, in order. We also denote the s-channel as the direct one while the t- and u-channels are also called crossed channels. Apart from the processes indicated in Eqs. (3.3)–(3.5), there are other three processes in which instead of exchanging \(b(p_2)\rightarrow \bar{b}(-p2)\) from the initial to the final state, we could also exchange \(a(p_1)\rightarrow \bar{a}(-p_1)\). These processes can also be obtained by CPT invariance from the ones shown in these equations.

Under the exchange of signs in the four-momenta, the s, t and u variables for every channel are related. Let us designate with a subscript t and u the Mandelstam variables for the t- and u-channels, respectively. Then we have for the t-channel:

$$\begin{aligned} s_t&=(p_1-p_3)^2=t,\end{aligned}$$
(3.6)
$$\begin{aligned} t_t&=(p_1+p_2)^2=s,\nonumber \\ u_t&=(p_1-p_4)^2=u, \end{aligned}$$
(3.7)

and for the u-channel the relations are

$$\begin{aligned} s_u&=(p_1-p_4)^2=u,\end{aligned}$$
(3.8)
$$\begin{aligned} t_u&=(p_1-p_3)^2=t,\nonumber \\ u_u&=(p_1+p_2)^2=s. \end{aligned}$$
(3.9)

The physical regions for these processes are disjoint. To simplify the discussion let us take that the four particles have the same mass m, e.g., this is the case of \(\pi \pi \) scattering. The s, t and u variables are given in the CM by

$$\begin{aligned} s&=4(m^2+\mathbf {p}^2),\\ t&=-2(s/4-m^2)(1-\cos \theta ),\nonumber \\ u&=-2(s/4-m^2)(1+\cos \theta ),\nonumber \end{aligned}$$
(3.10)

with \(\theta \) the scattering angle. From here we see that the physical region for the s-channel comprises the domain

$$\begin{aligned} s&\ge 4m^2,\\ t&\le 0,\nonumber \\ u&\le 0.\nonumber \end{aligned}$$
(3.11)

For the other channels the same values take place in terms of the variables with the subscripts. Thus, for the t-channel

$$\begin{aligned} t&=s_t\ge 4m^2,\\ s&=t_t\le 0,\nonumber \\ u&=u_t\le 0.\nonumber \end{aligned}$$
(3.12)

In turn for the u-channel,

$$\begin{aligned} u&=s_u\ge 4m^2,\\ s&=u_u\le 0,\nonumber \\ t&=t_u\le 0.\nonumber \end{aligned}$$
(3.13)

For the equal-mass case we have the relation, cf. Eq. (2.4),

$$\begin{aligned} s+t+u&=4m^2. \end{aligned}$$
(3.14)

Therefore, only two of the three variables are independent.

Analyticity assumes that the scattering amplitudes in the three disjoint physical regions for the s-, t- and u-channels are given by the same analytical function A(s, t, u) of s and t [u is then given by Eq. (3.14)]. The physical values for the different channels correspond to boundary values of this analytic function.

In particular, if we take a constant value of t the unitarity cut associated with the normal cuts in the u-channel, cf. Eq. (2.5), gives rise to a new cut in the complex s plane apart from the s-channel unitary cut. This is a simple example of a crossed-channel cut (also called unphysical cut, because it involves unphysical values of the Mandelstam variables in the s-channel) arising from a branch point singularity attached to a two-body threshold. In particular, this cut runs for \(u\ge 4m^2\) so that it correspond to the s values

$$\begin{aligned} s&=4m^2-t-u\le -t, \end{aligned}$$
(3.15)

and for \(s\ge 4m^2\) we have the s-channel unitary cut.

For particles with spin the analytical continuation of the scattering amplitude in the complex s and t planes is more involved due to the presence of kinematical singularities, whose origin is not dynamical, like the unitarity cuts in the s or crossed channels. They have to do with the solutions of the relativistic equations for the particles with spins, like the spinors for spin 1/2. For a general account on kinematical singularities we refer to [12, 13].

A possible way to deal with the kinematics singularities is to isolate Lorentz invariant functions out of the scattering amplitudes. For instance, let us consider the process \(\pi ^a(q)N(p,\sigma ;\alpha )\rightarrow \pi ^{a'}(q')N(p',\sigma ';\alpha ')\), where a and \(a'\) denote the Cartesian coordinates in the isospin space. In terms of them the charged pions correspond to the combination

$$\begin{aligned} \sum _a \frac{\pi ^a\tau ^a}{\sqrt{2}}=\left( \begin{array}{cc} \frac{\pi ^0}{\sqrt{2}} &{} \pi ^+\\ \pi ^- &{} -\frac{\pi ^0}{\sqrt{2}} \end{array} \right) . \end{aligned}$$
(3.16)

First, the scattering amplitude contains two invariant isospin amplitudes corresponding to \(I=1/2\) and 3/2, because the pions are isospin 1 particles and the nucleons have isospin 1/2. Any matrix in the isospin 1/2 space of nucleons can be expressed as a superposition of Pauli matrices \(\tau ^a\) and the 2\(\times \)2 identity matrix. Given two pions with indices a and \(a'\) the tensors with good properties under isospin rotations at our disposition are \(\delta _{aa'}\) and \([\tau _a,\tau _{a'}]\).Footnote 1 In this way we write,

$$\begin{aligned} T_{aa'}&=\delta _{a'a} T^+ + \frac{1}{2}[\tau _a,\tau _{a'}]T^-. \end{aligned}$$
(3.17)

In turn the two amplitudes \(T^{\pm }\) are operators acting in the space of the Dirac spinors and can be written as a linear combination of the 16 linearly independent matrices I, \(\gamma ^\mu \), \(\sigma ^{\mu \nu }\), \(\gamma _5\) and \(\gamma _5\gamma ^\mu \) with the Lorentz indices contracted with four-momenta. The matrices \(\gamma _5\) and \(\gamma _5\gamma ^\mu \) would violate parity and they do not appear. The set \(\sigma ^{\mu \nu }\) does not appear either because of the Gordon identity,Footnote 2 which implies that it does not give rise to any independent structure apart from the ones already accounted for by the identity matrix and \(\gamma ^\mu \). Taking also into account that and , we arrive to the standard form [12]

(3.19)

The analytical properties of the Lorentz invariant functions \(A^\pm \) and \(B^\pm \) are essentially the same as those of the scattering amplitude for scalar particles. The other factors in Eq. (3.19) have to be taken into account in establishing relations between analyticity and experimental results.

The crossed-channel poles, corresponding to poles in the crossed t- and u-channels for certain real values of t or u, in order, give rise to crossed cuts in the complex s plane of partial-wave amplitudes. For instance, consider the u-channel proton pole in \(\pi ^- n\rightarrow \pi ^- n\) scattering (in this sense these poles are called “bound states”, even though they could be elementary states or composite of other degrees of freedom [14]). Such a pole gives rise to a crossed cut in a given partial wave. For pion–nucleon scattering in the CM the u variable is given by (m and \(m_\pi \) are the nucleon and pion masses)

$$\begin{aligned} u&=m^2+m_\pi ^2-2\omega E-2\mathbf {p}^2\cos \theta . \end{aligned}$$
(3.20)

In this equation E and \(\omega \) are the nucleon and pion CM energies, respectively. When performing the partial-wave projection the scattering angle is integrated and \(\cos \theta \in [-1,1]\). Thus, setting \(u=m^2\) in Eq. (3.20) and expressing \(\omega \), E and \(\mathbf {p}^2\) in terms of s,

$$\begin{aligned} \omega&=\frac{s+m_\pi ^2-m^2}{2\sqrt{s}},\\ E&=\frac{s+m^2-m_\pi ^2}{2\sqrt{s}},\nonumber \\ \mathbf {p}^2&=\frac{\lambda (s, m^2,m_\pi ^2)}{4s},\nonumber \\ \lambda (s, m_1^2,m_2^2)&=(s-(m_1+m_2)^2)(s-(m_1-m_2)^2),\nonumber \end{aligned}$$
(3.21)

with \(\lambda (s, m_1^2,m_2^2)\) the Källén triangle function, we have the following solutions for s as a function of \(x=\cos \theta \),

$$\begin{aligned} s_1(x)=\frac{m^2 x + m_\pi ^2(1+x)-\sqrt{m^4+2m_\pi ^4(1+x)+2m^2m_\pi ^2(-1+x+2x^2)}}{1+x},\\ s_2(x)=\frac{m^2 x + m_\pi ^2(1+x)+\sqrt{m^4+2m_\pi ^4(1+x)+2m^2m_\pi ^2(-1+x+2x^2)}}{1+x}.\nonumber \end{aligned}$$
(3.22)

The first solution \(s_1(x)\) gives always a cut along the negative real axis because the radicand is larger than the squared of the the terms in the numerator before the square root [their difference is \((1-x^2)(m^2-m_\pi ^2)^2\)]. Incidentally this also shows that the radicand is always positive for any values of the masses and \(x\in [-1,1]\). Its upper limit happens for \(x=1\) and it is zero, while its lower limit is \(-\infty \) because \((1+x)\) in the denominator tends to zero for \(x\rightarrow -1\). This is a clear example of a left-hand cut (LHC). Regarding \(s_2(x)\), this implies a finite cut which ranges along the positive real axis with values from \((m^2-m_\pi ^2)^2/m^2\) up to \(m^2+2m_\pi ^2\).

The analysis for \(\pi \pi \) scattering is simpler because the two-pion cut along the t-channel and u-channel happens for \(t=-2(s/4-m_\pi ^2)(1-x)\ge 4m_\pi ^2\) and \(u=-2(s/4-m_\pi ^2)(1+x)\ge 4m_\pi ^2\). Solving s in terms of x we find that both cases give rise to LHCs with \(s\in ]-\infty , 0]\) when x moves along \([-1,1]\).

In the case of a nonrelativistic theory, the quantum fields only involve annihilation operators (or creation ones for the Hermitian conjugate field, Chap. 5 of Ref. [3]) and crossing does not operate. Nonetheless, there is still a LHC in this case due to the particles exchanged that give rise to the potential. For instance, let us consider a Yukawa potential

$$\begin{aligned} V(r)&=\alpha \frac{ e^{-r m_\pi }}{r}. \end{aligned}$$
(3.23)

Its Fourier transform is

$$\begin{aligned} V(\mathbf {q}^2)&=\alpha \int d^3 r e^{-i\mathbf {q}\mathbf {r}}\frac{e^{-r m_\pi }}{r}=\frac{4\pi \alpha }{\mathbf {q}^2+m_\pi ^2}, \end{aligned}$$
(3.24)

where \(\mathbf {q}=\mathbf {p}'-\mathbf {p}\) is the three-momentum transfer. Its angular projection for particles without spin is simply

$$\begin{aligned} V_J(p, p')&=\frac{1}{2}\int _{-1}^{+1}d\cos \theta \, V(\mathbf {q}^2)\, P_J(\cos \theta )\\&=-\frac{\pi \alpha }{pp'}\int _{-1}^{+1}d\cos \theta \frac{P_J(\cos \theta )}{\cos \theta -(p^2+{p'}^2+m_\pi ^2)/(2pp')}. \nonumber \end{aligned}$$
(3.25)

The LHC results by the vanishing of the denominator. Thus, in order to study its appearance we isolate the term that produces it by proceeding as follows:

$$\begin{aligned} V_J(p, p')&=-\frac{\pi \alpha }{pp'}\int _{-1}^{+1}d\cos \theta \frac{P_J(\cos \theta )}{\cos \theta -\xi } =-\frac{\pi \alpha }{pp'}\int _{-1}^{+1}d\cos \theta \frac{P_J(\cos \theta )-P_J(\xi )}{\cos \theta -\xi }\\&-\frac{\pi \alpha }{pp'}P_J(\xi )\int _{-1}^{+1} \frac{d\cos \theta }{\cos \theta -\xi },\nonumber \end{aligned}$$
(3.26)

with

$$\begin{aligned} \xi&=\frac{p^2+{p'}^2+m_\pi ^2}{2pp'}. \end{aligned}$$
(3.27)

The term before the last one in Eq. (3.26) does not give rise to the LHC because when the denominator vanishes the numerator also does. Therefore, the last term is the only one responsible for the LHC and the integration over \(\cos \theta \) can be done explicitly with the result

$$\begin{aligned} -\frac{\pi \alpha }{pp'}P_J(\xi )\int _{-1}^{+1} \frac{d\cos \theta }{\cos \theta -\xi }&=-\frac{\pi \alpha }{pp'}P_J(\xi )\left[ \log (1-\xi )-\log (-1-\xi ) \right] . \end{aligned}$$
(3.28)

Now for real and positive p and \(p'\) we can rewrite the difference of logarithms in the last term as

$$\begin{aligned} \frac{\pi \alpha }{pp'}P_J(\xi )\left[ \log ((p+p')^2+m_\pi ^2)-\log ((p-p')^2+m_\pi ^2) \right] . \end{aligned}$$
(3.29)

This expression is specially suitable for performing the analytical continuation to complex values of p and \(p'\) and so determine the position of the cuts, as fully exploited in Ref. [7]. The point is that the cuts in the p variable for given \(p'\) occurs when \((p+p')^2+m_\pi ^2<0\) (first logarithm) or \((p-p')^2+m_\pi ^2<0\) (second logarithm). This implies the vertical cuts

$$\begin{aligned} p=(\pm )p'\pm i \sqrt{m_\pi ^2+x^2},~x\in \mathbb {R}, \end{aligned}$$
(3.30)

with the first ± symbol uncorrelated with the second one. An analogous reciprocal relation exists for the cuts in the variable \(p'\) for a given p. The cuts for on-shell scattering, \(p=p'\), result from the only meaningful equation then, by taking the minus sign between brackets in Eq. (3.30),

$$\begin{aligned} p=-p\pm i\sqrt{m_\pi ^2+x^2}. \end{aligned}$$
(3.31)

Its solution gives

$$\begin{aligned} p=\pm \frac{i}{2}\sqrt{m_\pi ^2+x^2}, \end{aligned}$$
(3.32)

and for the variable \(p^2\) we have a cut for the values

$$\begin{aligned} p^2\le -\frac{m_\pi ^2}{4}. \end{aligned}$$
(3.33)

This is the LHC that occurs in nonrelativistic nucleon–nucleon (NN) scattering [7]. The NN partial waves are function of the variable \(p^2\) because by imposing parity invariance of the T matrix,

$$\begin{aligned} P T P&=T, \end{aligned}$$
(3.34)

in the equation that gives the projection onto the partial waves, Eq. (2.46), one easily deduces that

$$\begin{aligned} T_{ij}(-p)=\eta ^2 (-1)^{\ell _i+\ell _j} T_{ij}(p)=T_{ij}(p),\nonumber \\ \end{aligned}$$
(3.35)

because \(Y_\ell ^m(-\hat{\mathbf {p}})=(-1)^\ell Y_\ell ^m(\mathbf {p})\) and \(P|\mathbf {p},\sigma _1\sigma _2,\alpha _1\alpha _2\rangle = \eta |-\mathbf {p},\sigma _1\sigma _2,\alpha _1\alpha _2\rangle \), with \(\eta \) the intrinsic parity. We can write \(\eta ^2 (-1)^{\ell _i+\ell _j}=+1\) because parity is a good quantum number and partial-wave states with different parity are not connected by time evolution.