Suppression of Zeroth-Order Diffraction in Phase-Only Spatial Light Modulator

Abstract

A correction beam is created using a spatial light modulator (SLM) to suppress the zeroth-order diffraction (ZOD) that is produced by the unmodulated light coming from the dead areas of the said SLM. The correction beam is designed to interfere destructively with the undesirable ZOD that degrades the overall quality of the propagated SLM signal. Two possible techniques are developed and tested for correction-beam generation: aperture division and field addition. With a properly-calibrated SLM, ZOD suppression is demonstrated numerically and experimentally at sufficiently high area factor (AF) values where suitable matching is achieved between the correction beam and the ZOD profiles to result in a $39\%$ reduction of the ZOD intensity via angular aperture division, $32\%$ reduction via annular aperture division, and $24\%$ reduction via vertical aperture division. At low AF values however, meaningful ZOD suppression is not obtained. With the field addition method, a ZOD reduction as high as $99\%$ is gained numerically which was not realized experimentally using an SLM with a fill factor of 0.81 due to limitations posed by an iterative phase-recovery algorithm (ghost image) as well as unwanted signal contributions from the SLM anti-reflection coating, SLM surface variations, optical misalignment and aberrations.

1.1 Introduction

Manipulating the amplitude and phase of light had been extensively studied to achieve desired complex light distribution in different practical applications [1,2,3,4,5,6]. Controlling the amplitude or the phase, or both at the same time can be done as necessary. Phase modulation has become more popular than amplitude modulation due to its higher efficiency, avoiding light loss due to spatial filtering [7]. Phase modulation is done using lenses, prisms, and in the past decade, the spatial light modulator (SLM).

The SLM is a device that allows control over the phase of the incident light via a computer generated hologram (CGH) in its input giving it pixel by pixel control. Because of this versatility, the SLM is used in many different applications such as optical trapping  [8, 9], microfabrication  [5, 10], microscopy  [11, 12] and astronomy  [13].

Each SLM pixel has an active and inactive area. The ratio of the active area to the whole area of a pixel in an SLM is called the fill factor. Due to the electronic addressing of the SLM, the fill factor is typically less than one, which results to an inactive area that does not modulate incident light [14]. In a Fourier reconstruction set-up, where a lens is used to reconstruct the desired light configuration, this unmodulated light gets focused, and manifests as a high intensity spot called the zeroth order diffraction (ZOD).

The ZOD disrupts the complex light distribution due to its localized high intensity. It is usually removed in applications by shifting the desired light pattern away from the optical axis or placing a physical beam block [2]. Both of these techniques limit the functional area and decreases the diffraction efficiency. Another way is to create a correction beam together within the desired area [3]. The correction beam interferes with the ZOD, thereby lessening the intensity of the focused spot. This technique becomes slow in cases where multiple variable targets are to be shown in succession since recalculation of the target with the correction beam is necessary.

In this paper, we suppress the unwanted ZOD intensity with a correction beam that is generated via the SLM without the introduction of a physical block or grating. The final phase input to the SLM is calculated using the aperture division method or the field addition method as discussed by Hilario et al. [6]. We calculate the hologram input to SLM that contains the phase information needed for constructing the correction beam and the desired target. The field addition and the aperture division method are described and evaluated in the next Section.

1.2 The Spatial Light Modulator

The SLM is a device that allows versatile and dynamic light manipulation due to its pixel by pixel control capability and fast refresh rate [9]. The SLM can be used for amplitude modulation, phase modulation or both simultaneously. Newer SLMs can also control the polarization of incident light [15] thus allowing for a high degree of freedom control on the incident light. When using the SLM for phase modulation, a hologram is programmed to display on the SLM through a computer. This changes the phase of the incident light without changing the intensity. The corresponding desired pattern is then reconstructed using a Fourier lens.

In this work, we use a programmable phase modulator (PPM, Hamamatsu X8267) as our SLM. The structure is shown in Fig. 1.1 [16]. The PPM is an electrically addressed phase modulator, which uses an optical image transmitting element to couple an optically-addressed PAL-SLM (Parallel Aligned Nematic Liquid Crystal Spatial Light Modulator) with an electrically addressed intensity modulator. From the figure, the electrically addressed intensity modulator is an LCD controlled via an external computer. The LCD is coupled to the PAL-SLM using a fiber optic plate (FOP) as the optical image transmitting element to remove the diffraction noise from the pixel structure of the LCD. The photoconductive layer of the PAL-SLM will then be modulated with electric fields by the image from the FOP. This in turn changes the optical path of the incident light thereby modulating the phase in a pixel by pixel manner. Ideally, the SLM will be able to impose the exact phase to the incident light and all of the incident light is modulated. However, limitations in the SLM exists that affect the phase input itself, and limits the area of the incident light that can be controlled. We will discuss some of the limitations in the next section.

Fig. 1.1

Structure of the SLM [16]

1.2.1 Limitations of the SLM

Spatial Phase Variation. Many factors affect the phase that is input to the SLM. An example is the distortion of the phase caused by variation in ambient temperature [17]. Due to the thermal expansion of the SLM, the phase response maybe different for different ambient temperature and thus it becomes necessary to compensate for the change in phase response. Another is the effect of the imperfect flatness of the surface of the SLM. This results to a different phase response per pixel since there is variation in the thickness of the SLM [18]. These kinds of spatial variation in phase response is static, which means these have the same effect for different holograms. Therefore by calibrating the SLM, the effect of these variations in phase can be compensated [19].

Pixel Crosstalk. Phase retardation of the SLM comes from the reaction of the photoconductive layer of the PAL-SLM to the image brought by the FOP from the LCD. Thus, if the working areas of each pixel are in close proximity, gradual voltage changes (known as fringing fields) occur across the border of neighboring pixels [20,21,22]. This effect is called pixel crosstalk, and studies have shown that it low-pass filters the desired phase pattern. Pixel crosstalk changes the effective phase imposed to the incident light and is modelled as a convolution of the ideal phase with a point-spread-function given by the SLM [20, 21].

Fig. 1.2

Pixel crosstalk between two neighboring pixels. The closer the working areas, the stronger the crosstalk

Figure 1.2 shows the crosstalk in a schematic between two pixels of an SLM. If the working areas of two neighboring pixels are near to each other, the effect of fringing fields is greater than if the working areas are farther. In a multiple spot reconstruction, pixel crosstalk causes non-uniformity of the intensities of the spots. The effect of pixel crosstalk varies from hologram to hologram since it depends on the fields between adjacent pixels which is different for each hologram. Pixel crosstalk is describe as a non-linear dynamic phase response [19, 22].

Persson et al. [20] solved this problem by modifying the phase retrieval algorithm, specifically the GS algorithm, used to calculate the hologram that is programmed to the SLM. The calculated hologram compensates for the effect of the low-pass filtering thus producing the desired reconstruction. In their modified algorithm, the hologram is oversampled to a higher resolution before being convolved with the point-spread function that represents the pixel crosstalk. The field is then propagated. After which, the output field is undersampled to the original matrix size. The amplitude is then replaced by a weighted sum between the desired amplitude and the obtained amplitude before being back propagated to the SLM plane. They tested the algorithm using multiple spots usually used in optical trapping. Using this modified GS algorithm resulted in the increased uniformity of the diffraction spots and increased diffraction efficiency.

Fill Factor. In order to lessen the effect of the pixel crosstalk, there must be a separation between the working area of one pixel to another. The outcome of this separation is that the fill factor (F), or the ratio of the working area of a pixel to the whole pixel area is not equal to one [3, 14, 23], which results to areas that do not modulate light. As F decreases, the effect of pixel crosstalk also decreases, but the area that does not modulate light increases.

It is assumed that F is the same for all pixels over the PAL-SLM area. If the length of one side of a pixel is D and the length of one side of the working area is d, then $F=\frac{d^2}{D^2}$. These non-modulating areas result to unmodulated light that, when propagated using a lens, results to the zeroth order diffraction (ZOD). The ZOD will be discussed in the next section.

1.2.2 The Zeroth Order Diffraction

The non-unity F results to areas that do not modulate the incident light. The consequence of this unmodulated light is a highly localized bright spot in the reconstruction known as the zeroth order diffraction (ZOD) pattern [14]. The ZOD can be described by calculating the propagation of the nonmodulating areas of the SLM. We start with the transmission function of the SLM with $F<1$, given by [14]:

$$\begin{aligned} \begin{aligned} t(\eta ,\chi )= a(\eta ,\chi )\left\{ \mathrm{rect} \left( \frac{\eta }{d},\frac{\chi }{d} \right) \otimes q(\eta ,\chi ) + \left[ \mathrm{rect} \left( \frac{\eta }{D},\frac{\chi }{D} \right) - \mathrm{rect} \left( \frac{\eta }{d},\frac{\chi }{d}\right) \right] \otimes p(\eta ,\chi )\right\} \end{aligned} \end{aligned}$$

(1.1)

where $\otimes$ denote the convolution operation, $\eta$ and $\chi$ are the field coordinates, $\mathrm{rect}$ is the rectangular function, $a(\eta ,\chi )$ is the aperture function, and $q(\eta ,\chi )$ and $p(\eta ,\chi )$ are given by:

$$\begin{aligned} q(\eta ,\chi ) = \sum \limits _{m,n=0}^{M-1} \delta (\eta -mD,\chi -nD)\mathrm{exp}(i\phi _{mn}) \end{aligned}$$

(1.2)

$$\begin{aligned} p(\eta ,\chi ) = \sum \limits _{m,n=0}^{M-1} \delta (\eta -mD,\chi -nD)\mathrm{exp}(i\phi _{c}) \end{aligned}$$

(1.3)

$\phi _{mn}$ describes the input hologram to reconstruct the desired target while $\phi _{c}$ describes the phase imposed by the nonmodulating areas of the SLM. In this work, $\phi _{c}$ is assumed to be the same for all non-working areas and that, all working areas are strictly square-shaped [14].

Equation (1.1) can then be rewritten in terms of fields incident to the SLM:

$$\begin{aligned} U_\mathrm{SLM}(\eta ,\chi )= U_{w}(\eta ,\chi ) + U_{nw}(\eta ,\chi ) \end{aligned}$$

(1.4)

where $U_{w}$ is the field due to the working areas of the SLM and $U_{nw}$ is the field due to the non-working areas. In relation to the transmission function, we have:

$$\begin{aligned} U_{w}(\eta ,\chi )= a(\eta ,\chi ) \times \left( \mathrm{rect} \left( \frac{\eta }{d},\frac{\chi }{d} \right) \otimes q(\eta ,\chi )\right) \end{aligned}$$

(1.5)

$$\begin{aligned} \begin{aligned} U_{nw}(\eta ,\chi )= a(\eta ,\chi ) \times \left\{ \left[ \mathrm{rect} \left( \frac{\eta }{D},\frac{\chi }{D} \right) - \mathrm{rect} \left( \frac{\eta }{d},\frac{\chi }{d}\right) \right] \otimes p(\eta ,\chi )\right\} \end{aligned} \end{aligned}$$

(1.6)

Propagating (1.4) forward using Fourier transform, we have:

$$\begin{aligned} \begin{aligned} \mathscr {F}\{U_\mathrm{SLM}(\eta ,\chi )\} = \mathscr {U}_\mathrm{recon}(x,y) = \mathscr {U}_\mathrm{target} (x,y) + \mathscr {U}_\mathrm{ZOD} (x,y) \end{aligned} \end{aligned}$$

(1.7)

where (x, y) are the field coordinates in the Fourier reconstruction, $\mathscr {U}_\mathrm{target}$ and $\mathscr {U}_\mathrm{ZOD}$ are the field of the desired target and ZOD, respectively, with the following correspondence:

$$\begin{aligned} \mathscr {F}\{U_{w}(x,y)\} = \mathscr {U}_\mathrm{target} \end{aligned}$$

(1.8)

$$\begin{aligned} \mathscr {F}\{U_{nw}(x,y)\} = \mathscr {U}_\mathrm{ZOD} \end{aligned}$$

(1.9)

inserting (1.5)–(1.8) and (1.6)–(1.9), we obtain the expressions for both the desired reconstruction and the ZOD, given by:

$$\begin{aligned} \mathscr {U}_\mathrm{target} = \mathscr {A}(x,y) \otimes \{d^2 \mathrm{sinc}(xd,yd)Q(x,y)\} \end{aligned}$$

(1.10)

$$\begin{aligned} \begin{aligned} \mathscr {U}_\mathrm{ZOD} = \mathscr {A}(x,y) \otimes \{(\mathrm{sinc}(xD,yD) - F \mathrm{sinc}(xd, yd))D^2 P(x,y) \end{aligned} \end{aligned}$$

(1.11)

where:

$$\begin{aligned} \mathrm{sinc}(\zeta _x,\zeta _y) = \frac{\mathrm{sin}(\pi \zeta _x)}{\pi \zeta _x} \frac{\mathrm{sin}(\pi \zeta _y)}{\pi \zeta _y} \end{aligned}$$

(1.12)

and P(x, y) and Q(x, y) are Fourier transforms of (1.2) and (1.3), respectively. $\mathscr {U}_\mathrm{ZOD}$ is the result of propagating the nonmodulating areas of the SLM and describes the ZOD. It distorts the reconstruction in the low spatial frequencies and as such reduces the functionality of the reconstructed pattern [3]. It also introduces unnecessary illumination that will saturate the camera due to its high intensity. In applications involving microscopy, the ZOD may introduce heating in the sample. The ZOD also affects the diffraction efficiency of the SLM [14].

One common way to remove the ZOD is by placing a physical beam block in an intermediate plane [2]. The physical beam block will fully block the ZOD, and remove it from the final reconstruction. However, a non-accessible area in the final reconstruction arises, since any part of the reconstruction that is near the ZOD will be blocked by the physical beam block. Thus reconstructing holographic traps near the center will entail moving the whole set-up physically so that the non-accessible area will also move.

Ronzitti et al. [24] characterized the SLM by using binary gratings and checkerboards with different modulation depths as holograms. By comparing it with the theoretical output, they solved for the correcting function in the calculation of the hologram, and were able to reduce the power of the ZOD by about 90%. However, the main cause of the ZOD for their SLM is the pixel crosstalk due to high fill factor of their SLM.

Liang et al. [25] proposed phase compression method to lessen the ZOD intensity. Phase compression is applied to the hologram, making recalculation of the hologram unnecessary. However, the signal to noise ratio of the resulting reconstruction decreased.

One way to remove the ZOD is by introducing a correction beam in the location of the ZOD. Daria and Palima [14] constructed the correction beam by deriving the field at $(x,y) = (0,0)$, given by:

$$\begin{aligned} \mathscr {U}_\mathrm{recon} (0,0) = d^2 Q(0,0) + (1 - F)D^2 \mathrm{exp}(i\phi _c) \end{aligned}$$

(1.13)

The field given by (1.13) is then combined with the desired target. A phase retrieval algorithm is then used to obtain the phase $\phi _{mn}$ that will reconstruct both the desired target and the correction beam, with a constraint that the phase of the correction beam must be equal to $\phi _c + \pi$. Using this, they were able to show that the ZOD can be totally removed.

However, the main limitation with this method is that, if the desired target is changed to a new one, then the phase must be recalculated so that the correction beam is combined with the new desired target. This takes longer computation time. Normally, this is not an issue, but in applications where the change in the desired target depends on an external factor then the recalculation of the phase greatly hinders the experiment. An example is in optical trapping. If the traps are moving and the configuration depends on the experimental particles to be trapped, then recalculation of the phase to construct both of the traps and the correction beam makes it hard to control the traps.

In this work, the objective is to create a suppression method that calculates the field for the correction beam separate from the calculation of the desired target so that if there is a change in the desired target, then there is no recalculation needed for the correction beam. It is assumed that only the non-modulating areas of the SLM contributes to the ZOD. Methods to independently calculate the desired target and correction beam is discussed in the next section.

1.3 Suppression of the Zeroth Order Diffraction

In order to suppress the ZOD, we construct a correction beam in the location of the ZOD, independent of the construction of the desired target. Essentially, the field from the SLM given by (1.7) becomes:

$$\begin{aligned} \mathscr {U}_\mathrm{recon} (x,y) = \mathscr {U}_\mathrm{target}(x,y) + \mathscr {U}_\mathrm{corr}(x,y) + \mathscr {U}_\mathrm{ZOD}(x,y) \end{aligned}$$

(1.14)

where $\mathscr {U}_\mathrm{corr}$ is the correction beam that will be used to destructively interfere with the ZOD by adding the correct phase to this field.

Thus, (1.8) becomes:

$$\begin{aligned} \mathscr {F}\{U_{w} (\eta ,\chi )\} = \mathscr {U}_\mathrm{target}(x,y) + \mathscr {U}_\mathrm{corr}(x,y) \end{aligned}$$

(1.15)

Obtaining $U_w$ so that both the desired target and correction beam employs the use of a phase retrieval algorithm. Here, we discuss the construction of the correction beam.

1.3.1 The ZOD Suppression Method

Creating the Correction Beam. We suppress the ZOD by inducing a destructive interference between the ZOD and a correction beam. This correction beam will be created either using aperture division, or by addition of fields, as discussed by Hilario et al. [6]. Using the GS algorithm, the phase that is needed to construct the correction beam is calculated, given by $\phi _\mathrm{corr} (\eta , \chi )$. We then add a constant phase $\phi _\mathrm{shift}$ to the whole field until total destructive interference occurs.

The inputs to the GS algorithm are the amplitude of the source and the amplitude of the ZOD. The amplitude of the source is a part of the aperture, as is the case in aperture division, or the whole aperture, as the case in addition of fields. Both methods of constructing the correction beam needs the ZOD amplitude as target to the phase retrieval algorithm.

In order to have the ZOD amplitude, we obtain the light distribution of the non-modulating areas, $U_{nw}(\eta ,\chi )$. This is from oversampling the light distribution that is incident to the SLM. The distribution is then obtained by separating the non-modulating areas, $U_{nw}(\eta ,\chi )$, from the modulating areas, $U_{w}(\eta ,\chi )$. Due to oversampling, the size of the matrix becomes $15360 \times 15360$ from $768 \times 768$. Fourier transform is then performed to $U_{nw}(\eta ,\chi )$. The ZOD is then obtained from the middle $768 \times 768$ of the reconstruction. From this, we obtain the ZOD amplitude from an SLM with $F = 0.81$. The SLM to be used in the experiment, Hamamatsu PPM X8267, has $F = 0.8$. In our method, we also create a desired target. In order to properly describe the effectiveness of suppressing the ZOD, the desired target does not have intensity in $(x,y) = (0,0)$ and surrounding area. This desired target represents the application that will be done using the SLM, whether it be optical trapping, lithography or others. In our case, we are focused on suppressing the ZOD beam, therefore we need to observe the behaviour of the intensity of the ZOD itself. To do this, the field due to the desired application must be separated from the location of the ZOD so that only the ZOD and the correction beam will interact. In this case, reconstructing the target will suffice. We use GS algorithm to obtain the phase needed to construct the desired target, $\phi _\mathrm{target} (\eta , \chi )$.

After calculating $\phi _\mathrm{corr}$ and $\phi _\mathrm{target}$, we combine the fields in order to obtain the phase input to the SLM, $\phi _\mathrm{SLM}$. From this, we can obtain the field of the incident light to the SLM, given by:

$$\begin{aligned} U_\mathrm{SLM}(\eta ,\chi ) = A_\mathrm{SLM} (\eta ,\chi ) e^{i\phi _\mathrm{SLM}(\eta ,\chi )} \end{aligned}$$

(1.16)

We use two methods in constructing the correction beam. First is the aperture division, and the second is addition of fields, to be discussed below.

Aperture Division. In this method, we divide the aperture into two parts, $A_\mathrm{corr}(\eta ,\chi )$ and $A_\mathrm{target}(\eta ,\chi )$. $A_\mathrm{corr}(\eta ,\chi )$ is used as source to calculate for $\phi _\mathrm{corr}(\eta ,\chi )$ while $A_\mathrm{target}(\eta ,\chi )$ is used to calculate for $\phi _\mathrm{target}(\eta ,\chi )$. The aperture division is shown in Fig. 1.3. The relationship between $A_\mathrm{corr}$ and $A_\mathrm{target}$ is given by following:

$$\begin{aligned} A_\mathrm{SLM}(\eta ,\chi ) = A_\mathrm{corr}(\eta ,\chi ) + A_\mathrm{target}(\eta ,\chi ) \end{aligned}$$

(1.17)

where $A_\mathrm{SLM}(\eta ,\chi )$ is the aperture function of the SLM. Since $A_\mathrm{corr}$ and $A_\mathrm{target}$ are independent spatially, their intensities are simply added together.

We divide the aperture three ways: (1) annular aperture division, where the aperture is divided into an inner circle and an annulus; (2) angular aperture division, where the aperture is divided in an angular fashion; and (3) vertical aperture division, where the aperture is divided vertically.

Fig. 1.3

Three aperture division to be employed in creating the correction beam. a Annular aperture division. b Angular aperture division. c Vertical aperture division

In the three aperture divisions, a factor that determines the total area used in constructing the correction beam is applied. This factor is called the area factor (AF), given by:

(1.18)

In each aperture divisions, we calculate $\phi _\mathrm{corr}(\eta ,\chi )$ using $A_\mathrm{corr}(\eta ,\chi )$ as source input and ZOD as target input to the GS algorithm. We then calculate $\phi _\mathrm{target}(\eta ,\chi )$ using $A_\mathrm{target}(\eta ,\chi )$ as source input and the desired target as input to the GS algorithm. This is to simulate the application where the SLM is to be used. Another reason is to move the area used to construct the desired target away from the location where the ZOD and correction beam are located so that when measuring the change in the total intensity of the ZOD, it is only the ZOD and the correction beam that contributes to the total intensity. In order to induce destructive interference, we add a spatially constant phase shift $\phi _\mathrm{shift}$ to $\phi _\mathrm{corr}$ Since $A_\mathrm{corr}(\eta ,\chi )$ and $A_\mathrm{target}(\eta ,\chi )$ are spatially independent, the final phase input to the SLM is given by:

$$\begin{aligned} \phi _\mathrm{SLM}(\eta ,\chi ) = \phi _\mathrm{target}(\eta ,\chi ) + \phi _\mathrm{corr}(\eta ,\chi ) + \phi _\mathrm{shift} \end{aligned}$$

(1.19)

We add $\phi _\mathrm{shift}$ to $\phi _\mathrm{SLM}$ in order to induce destructive interference between correction beam and the ZOD. From (1.1), the non modulating areas give phase shift $\phi _c$ to the incident light. However, this $\phi _c$ is not known. Thus, $\phi _\mathrm{shift}$ is added so that the correct phase shift is obtained and destructive interference is induced.

For this method, we obtain the optimal AF which controls the total energy and the information used to create the correction beam. The optimal AF gives the maximum energy to the desired target and creates a correction beam that is most similar to the ZOD in terms of total energy and profile. Therefore, we scan the AF from 0 to 1 in order to obtain the optimal value. The procedure in obtaining $\phi _\mathrm{SLM}$ is shown in Fig. 1.4.

Fig. 1.4

Calculation of the necessary phase to reconstruct both the desired target and the correction beam for the aperture division

Addition of Fields. The second method in creating the correction beam and the desired target is the addition of fields, as discussed by Hilario et al. [6, 26, 27]. $\phi _\mathrm{target}$ and $\phi _\mathrm{corr}$ are calculated separately. The source input for the GS algorithm for each phase is the whole aperture. We have:

$$\begin{aligned} A_\mathrm{target}(\eta ,\chi ) = A_\mathrm{corr}(\eta , \chi ) = A_\mathrm{SLM}(\eta ,\chi ) \end{aligned}$$

(1.20)

where $A_\mathrm{SLM}(\eta ,\chi )$ is the aperture function of the SLM. The amplitudes and phase give us the fields needed to reconstruct the correction beam and target separately:

$$\begin{aligned} U_\mathrm{target}(\eta ,\chi ) = A_\mathrm{SLM}(\eta ,\chi )e^{i\phi _\mathrm{target}(\eta ,\chi )} \end{aligned}$$

(1.21)

$$\begin{aligned} U_\mathrm{corr}(\eta ,\chi ) = A_\mathrm{SLM} (\eta ,\chi )e^{i\phi _\mathrm{corr}(\eta ,\chi )} \end{aligned}$$

(1.22)

where $U_\mathrm{target}$ is the field of the SLM when only the target is to be reconstructed, and $U_\mathrm{corr}$ is the field when only the correction beam is to be reconstructed. If the fields $U_\mathrm{target}$ and $U_\mathrm{corr}$ are propagated independently, we have:

$$\begin{aligned} \mathscr {F}\{U_\mathrm{target}(\eta ,\chi )\} = \mathscr {U}_\mathrm{target}(x,y) \end{aligned}$$

(1.23)

$$\begin{aligned} \mathscr {F}\{U_\mathrm{corr} (\eta ,\chi )\} = \mathscr {U}_\mathrm{corr}(x,y) \end{aligned}$$

(1.24)

The phase to construct both target and correction beam is given by calculating:

$$\begin{aligned} \phi _\mathrm{inp} (\eta ,\chi ) =\mathrm{arg}\big ( c_\mathrm{corr}U_\mathrm{corr}(\eta ,\chi ) + c_\mathrm{target}U_\mathrm{target}(\eta ,\chi )\big ) \end{aligned}$$

(1.25)

$c_\mathrm{corr}$ and $c_\mathrm{target}$ are the constants used in order to control the total energy that goes to the corresponding reconstructions of each field. The field that hits the SLM is then given by:

$$\begin{aligned} U_\mathrm{SLM}(\eta ,\chi ) =A_\mathrm{SLM}(\eta ,\chi )e^{(i\phi _\mathrm{inp}(\eta ,\chi ) + \phi _\mathrm{shift})} \end{aligned}$$

(1.26)

If we calculate the amplitude and phase of the added field (inside the parenthesis in (1.25)), we obtain:

$$\begin{aligned} \begin{aligned} U_\mathrm{sum}(\eta ,\chi )&= c_\mathrm{corr}U_\mathrm{corr}(\eta ,\chi )+c_\mathrm{target}U_\mathrm{target}(\eta ,\chi )\\&=c_\mathrm{corr}A_\mathrm{SLM}(\eta ,\chi )e^{i\phi _\mathrm{corr}(\eta ,\chi )} + c_\mathrm{target}A_\mathrm{SLM}(\eta ,\chi )e^{i\phi _\mathrm{target}(\eta ,\chi )} \end{aligned} \end{aligned}$$

(1.27)

$U_\mathrm{sum}(\eta ,\chi )$ has the same phase profile as $U_\mathrm{SLM}$ since:

$$\begin{aligned} \phi _\mathrm{SLM} (\eta ,\chi )&=\mathrm{arg}\big ( c_\mathrm{corr}U_\mathrm{corr}(\eta ,\chi ) + c_\mathrm{target}U_\mathrm{target}(\eta ,\chi )\big ) + \phi _\mathrm{shift}\\&=\mathrm{arg}(U_\mathrm{sum}) + \phi _\mathrm{shift} \end{aligned}$$

and $\phi _\mathrm{shift}$ is constant for the whole field. However, the amplitude of $U_\mathrm{sum}$ is different. We have:

$$\begin{aligned} |U_\mathrm{SLM}(\eta ,\chi )|&=|U_\mathrm{corr}+U_\mathrm{target}|\\&=A_\mathrm{SLM}(\eta ,\chi ) \times \\&\sqrt{(c^2_\mathrm{corr} + c^2_\mathrm{target} + 2c_\mathrm{corr}c_\mathrm{target}\mathrm{cos}(\phi _\mathrm{corr}(\eta ,\chi ) - \phi _\mathrm{target}(\eta ,\chi ))} \end{aligned}$$

If we set

$$\begin{aligned} A_\mathrm{cross}(\eta ,\chi ) = \sqrt{(c^2_\mathrm{corr} + c^2_\mathrm{target} + 2c_\mathrm{corr}c_\mathrm{target}\mathrm{cos}(\phi _\mathrm{corr}(\eta ,\chi ) - \phi _\mathrm{target}(\eta ,\chi ))}, \end{aligned}$$

then we have the following:

$$\begin{aligned} U_\mathrm{SLM} (\eta ,\chi ) = \frac{U_\mathrm{sum}(\eta ,\chi )}{A_\mathrm{cross}(\eta ,\chi )} \end{aligned}$$

(1.28)

If $U_\mathrm{SLM}$ is propagated forward using Fourier transform, we obtain the following:

$$\begin{aligned} \mathscr {F}\{U_\mathrm{SLM}(\eta ,\chi )\} = \mathscr {F}\left\{ \frac{1}{A_\mathrm{cross}(\eta ,\chi )}\right\} *\mathscr {F}\{U_\mathrm{sum}(\eta ,\chi )\} \end{aligned}$$

(1.29)

invoking the convolution theorem of the Fourier transform. Then finally, the reconstruction is given by:

$$\begin{aligned} \begin{aligned} \mathscr {F}\{U_\mathrm{SLM}(\eta ,\chi )\} = \mathscr {F}\left\{ \frac{1}{A_\mathrm{cross}(\eta ,\chi )}\right\} *\{\mathscr {U}_\mathrm{corr}(x,y) + \mathscr {U}_\mathrm{target}(x,y)\} \end{aligned} \end{aligned}$$

(1.30)

The cross term in the amplitude of $U_\mathrm{SLM}$, $A_\mathrm{cross}(\eta ,\chi )$, is not constant and thus, we cannot analytically isolate the total intensities of $\mathscr {U}_\mathrm{corr}(x,y)$ and $\mathscr {U}_\mathrm{target}(x,y)$ without explicit knowledge of $\phi _\mathrm{corr} (\eta ,\chi )$ and $\phi _\mathrm{target}(\eta ,\chi )$. Because of this, the exact relationship between $c_\mathrm{corr}$ and $c_\mathrm{target}$ cannot be determined analytically. In this case, we set $c_\mathrm{corr} + c_\mathrm{target} = 1$.

The cross term in (1.30) results to the presence of ghost orders [24] due to the cross terms between the added field. The ghost orders are undesired reconstructions that make a symmetry with the reconstructed target. When constructing a correction beam using the field addition method, the location of its ghost order is at the same spot, which can affect the suppression of the ZOD. Since the ghost order has the conjugate phase of the correction beam, it lessens the total intensity of the correction beam itself.

The procedure in calculating for $\phi _\mathrm{SLM}$ is summarized in Fig. 1.5.

Fig. 1.5

Calculation of the phase required to reconstruct both the desired target and correction beam in field addition. First the fields for reconstructing the desired target and correction beam are calculated separately, with the amplitude being the aperture function of the SLM. Then the fields are added. The phase of the output field is then $\phi _\mathrm{SLM}$

1.3.2 Suppression of the ZOD

The constant phase shift $\phi _\mathrm{shift}$ is varied from 0 to $3\pi$. For the aperture division method, AF is changed from 0 to 1 to achieve the maximum AF with maximum suppression while still reconstructing the desired target. For the field addition method, $c_\mathrm{corr}$ is changed from 0 to 1.

To measure the effect of the method, we calculate the relative intensity R, given by the following:

$$\begin{aligned} R = \frac{I_\mathrm{method} - I_\mathrm{ZOD}}{I_\mathrm{ZOD}} \times 100\% \end{aligned}$$

(1.31)

where $I_\mathrm{ZOD}$ is the total intensity of the ZOD before the suppression method is applied. This is when $U_\mathrm{mod}$ is used entirely to create the desired pattern. $I_\mathrm{method}$ is the total intensity after application of the suppression method.

If R is greater than zero, this means the intensity of the ZOD increased, which indicates that either constructive interference occurred between the correction beam and the ZOD, or the total energy of the correction beam overshoots that of the ZOD, that even if full destructive interference was induced, there was still enough energy from the correction beam to create another ZOD. If R is equal to zero, this means nothing changed. If R is less than zero, the total intensity of the ZOD decreased. The ideal result is that $I_\mathrm{method}$ equals zero, which means R is equal to $-100\%$.

1.4 Experiment

1.4.1 Suppression of the ZOD Experiment

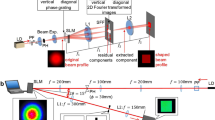
We input the hologram which reconstructs the desired target without the correction beam to the SLM. From this, we add or remove NDF until the image captured by camera is unsaturated (Fig. 1.6). We capture this image and extract the total intensity of the ZOD by summing the intensities of the pixels around the ZOD. This total intensity is then our $I_\mathrm{ZOD}$. We then input holograms that reconstruct both the desired target and the phase shifted correction beam. For each hologram, we capture the image without changing the NDF and obtain the total intensity of the ZOD. This is then $I_\mathrm{method}$.

Fig. 1.6

Optical set-up used to verify the suppression of the ZOD

Aperture Division. Sample holograms for different AF with different $\phi _\mathrm{shift}$ is shown in Fig. 1.7 for angular, annular and vertical aperture division. These holograms are input to the SLM. In the experiment, the number of $\phi _\mathrm{shift}$ added is 128 ranging from 0 to $3\pi$ for 32 values of AF from 0 to 1. Images are captured for each hologram. Three trials are done per AF. For the capture images, we obtain $I_\mathrm{method}$ by summing the total intensity of a $15\times 15$ box around the ZOD. This size is the smallest box to capture the whole ZOD while avoiding the intensity due to ambient light capture by the camera. We plot R versus $\phi _\mathrm{shift}$ in Fig. 1.8.

Fig. 1.7

Sample $\phi _\mathrm{SLM}$ for different AF and different $\phi _c$ for the angular aperture division (top left), annular aperture division (top right) and vertical aperture division (bottom)

Fig. 1.8

Relative intensity versus $\phi _\mathrm{shift}$ for different AF. a Angular aperture division, b Annular aperture division and c vertical aperture division

Fig. 1.9

Top left: Sample reconstruction of desired target and ZOD. Image is saturated so that the desired target is observed; Top right, bottom row: ZOD with minimum R for each AF for annular, angular and vertical aperture division

Figure 1.8 shows that for the three aperture divisions, the minimum relative intensity is found when $\phi _\mathrm{shift}$ is equal to 0 or $2\pi$. At $\phi _\mathrm{shift}$ = 0, R is negative. But when a small $\phi _\mathrm{shift}$ is added, R shoots up to a positive value, at around $20{-}30\%$. Then as $\phi _{shift}$ increases, R steadily decreases until $\phi _\mathrm{shift}$ is equal to $2\pi$, where it reaches a small value of R, comparable to when $\phi _\mathrm{shift}$ is equal to 0. However, when it increases again, a sudden jump is again observed. This can be attributed to the fact that, when saving the holograms, it is ensured that the phase range is from 0 to $2\pi$, which means that the hologram when $\phi _\mathrm{shift}$ = $2\pi + \theta$ is the same as the hologram when $\phi _\mathrm{shift} = \theta$.

We shown in Fig. 1.9 a sample reconstruction of the desired target with the ZOD. This is to show that in each aperture division, we are still constructing a desired target together with the correction beam. We also show sample intensities of the ZOD for annular, angular and vertical aperture division when R is minimum for an AF. The intensities are visually lower as AF becomes higher. We plot the minimum R for each AF versus AF in Fig. 1.10.

Fig. 1.10

Minimum R versus AF for annular, angular and vertical aperture divisions

Maximum suppression versus AF is plotted in Fig. 1.10 for the three different aperture divisions. For the angular aperture division, $-39\%$ of the ZOD is suppressed at $AF = 0.94$. For the annular aperture division, $-32\%$ of the ZOD intensity is suppressed at $AF = 0.97$. Finally, for the vertical aperture division, $-24\%$ of ZOD is suppressed at $AF = 0.88$. For the three aperture divisions, there is no clear trend between the maximum suppression and AF. However, it is observed that as higher suppression occurs at high AF for the three aperture divisions.

Field Addition Method. We plot R versus phase shift in Fig. 1.11 for different $c_\mathrm{corr}$. Similar to the Fig. 1.8 in the aperture division, maximum suppression is at phase shift equal to 0 or $2\pi$. For higher values of $c_\mathrm{corr}$, the discontinuity is evident to phase shift below $2\pi$ and after. For lower values of $c_\mathrm{corr}$, the plot approaches a sinusoid-like behavior.

Fig. 1.11

Relative intensity versus $\phi _\mathrm{shift}$ for different $c_\mathrm{corr}$

Fig. 1.12

Top image: ZOD with minimum R for each $c_\mathrm{corr}$. Bottom image: Maximum suppression versus $c_\mathrm{corr}$ for the field addition method

We show the ZOD when maximum suppression occurs per $c_\mathrm{corr}$ in Fig. 1.12a [27]. It is observed that the change in the ZOD intensity is gradual as $c_\mathrm{corr}$ increases. This is attributed to the fact that $c_\mathrm{corr}$ only changes the total energy that goes into reconstructing the correction beam, as opposed to the aperture division where AF dictates both the energy and the information used to construct the correction beam.

We plot the maximum suppression versus $c_\mathrm{corr}$ in Fig. 1.12b. The minimum R is steady for low values of $c_\mathrm{corr}$ (up to $c_\mathrm{corr}$ equal to 0.3). Then its value decreases until $c_\mathrm{corr}$ is equal to 0.82, where ZOD is suppressed up to $-32\%$ of its original value. It does not change significantly for $c_\mathrm{corr}$ greater than 0.82.

1.4.2 Discussion of Results

To separate the contribution of the correction beam from the two methods mentioned above, we calculate the effect of the correction beam numerically. We simulate the suppression method with the assumption that only dead areas contribute to the ZOD. Moreover, the SLM used in the simulation has no limitation other than its F value being less than one. We also assume that the phase input to the SLM is imposed without error.

The simulation of the SLM with $F < 1$ is done by oversampling the hologram where every pixel is sampled at higher resolution. In our case, each pixel is represented by 400 sampled points to form a $20 \times 20$ image. To simulate the non-working areas, the outer pixels of the $20 \times 20$ image are assigned non-modulating zero phase shift values.

The oversampled holograms with F constraint are then used as phase with an oversampled aperture size. Hence the fields that are originally represented as $768 \times 768$ pixel image sizes now become $15360 \times 15360$ pixel images. These oversampled fields are then propagated via Fourier transform and a reconstruction is obtained at higher frequencies.

We choose the middle reconstruction, in the zeroth order, and take the total intensity of the ZOD in a $40 \times 40$ square area that is used so that the ZOD intensity is obtained without the desired target while avoiding ambient noise (see Fig. 1.13).

Fig. 1.13

Representation of SLM operation. Each hologram is oversampled and F is imposed. The resulting hologram is used as phase and propagated using Fourier transform. Reconstruction by Fourier transformation is shown in log scale. Middle reconstruction is then obtained from the result and the total intensity of the ZOD is given by the sum of all the intensities inside the $40 \times 40$ area

1.4.3 Result of Numerical Simulation

The introduction of the correction beam suppresses the ZOD intensity by destructive interference. We first evaluate the profile of the correction beam by comparing it with the ZOD profile using the Linfoots criteria of merit [28]: Fidelity (F), Correlation quality (Q) and Structural content (C), which measure the overall similarity of two signals, alignment of peaks and the relative sharpness of peak profiles, respectively. If the ZOD and correction beam profiles are identical then: $F = C = Q = 1$. In general, $2Q-C = F$.

We find the dependence of R with $\phi _\mathrm{shift}$ and locate the ZOD when R is minimum for different AF and $c_\mathrm{corr}$ values when using the aperture division and field addition method, respectively. The minimum R values are then plotted as a function of AF and $c_\mathrm{corr}$.

Aperture Division. Figure 1.14 presents the ZOD and correction beam profiles for different AF when only the modulating areas are propagated via Fourier transform. Each image is normalized to its maximum thereby observing only the profile and the effect of AF while not observing the the total energy to the correction beam.

Fig. 1.14

Left column: The ZOD and correction beam intensities for angular aperture division (top), annular aperture division (middle) and vertical aperture division. Right column: Cross section profile of each beam and the ZOD

We also show the corresponding cross-sections of the ZOD profiles. At low AF values, the correction beam and the ZOD profiles do not match with each other because only a part of the aperture is utilized to construct the correction beam thereby limiting its bandwidth. On the other hand, the ZOD is produced by the contributions of all the dead areas present in the entire SLM. Because the correction-beam bandwidth increases with AF a matching of the correction beam and ZOD profiles is eventually achieved at sufficiently high AF values. We note that the profile matching is reached without taking into account the total energy that is used to construct the correction beam since it is the AF that dictates how much energy is used.

Figure 1.15 plots the values of F, C and Q as a function of AF. With the angular and annular aperture division, both F and C reach the value of unity when AF equals 0.8 while Q remains equal to one all throughout. For the vertical aperture division, $F = C = Q = 1$ only when AF reaches 0.9. Note that the total intensity of the correction beam for a given AF value and that of the ZOD are held equal because we are only concerned with the beam profiles and not with the total energy in the correction beam.

Fig. 1.15

Linfoot’s criteria of merit plot for the three aperture divisions

Fig. 1.16

R versus $\phi _\mathrm{shift}$ for sample values of AF for the angular, annular and vertical aperture division

Figure 1.16 plots the values of R versus $\phi _\mathrm{shift}$ for the angular, annular and vertical aperture division, respectively. A sinusoidal trend is observed for R as a function of phase shift since the interference intensity depends on the individual intensities of the interfering beams and the cosine of the phase difference between them. Thus the ZOD intensity after suppression would depend on the ZOD and the correction beam intensities as well as on the value of the phase shift $\phi _\mathrm{shift}$. The minimum R is found when $\phi _\mathrm{shift}$ becomes equal to 0 or $2\pi$ since a phase shift of $\pi$ is produced when light is reflected. A $\pi$-phase difference already exists between the correction beam and the ZOD even when no phase shift is inputted into the SLM itself. Figure 1.17 shows the original ZOD and the ZOD intensities at different AF values when R is minimum for three different methods of aperture division. Instead of suppressing the ZOD, the correction beam only alters the profile and increases the total intensity of the ZOD due to a significant mismatch between the ZOD and the correction beam profiles that occurs at low AF and high correction beam energy at high AF values.

Fig. 1.17

Sample ZOD intensities when R is minimum

Fig. 1.18

Minimum R versus AF for the angular, annular and vertical aperture division

Figure 1.18 plots maximum suppression (minimum R) versus AF. It can be seen that maximum suppression per AF increases as AF increases—at low AF values, limited information is employed to construct the correction beam and the profiles of the correction beam and the ZOD do not match. As the AF increases, more information becomes available for constructing the correction beam at the expense of additional beam energy that exceeds that of the ZOD (beam imbalance). Even when the two profiles are now matched with each other, the excess energy from the correction beam would contribute to the generation of a new ZOD.

Fig. 1.19

R versus $\phi _\mathrm{shift}$ for different values of $c_\mathrm{corr}$

Field Addition Method. The profile of the correction beam matches that of the ZOD using the field addition method since the entire aperture is used to construct the correction beam for all $c_\mathrm{corr}$ values and full information is available for the construction of the correction beam [27]. As a result, $F = C = Q = 1$ for all $c_\mathrm{corr}$ values. Figure 1.19 plots R as a function of $\phi _\mathrm{shift}$ for different $c_\mathrm{corr}$ values. The minimum R is found when $\phi _\mathrm{shift}$ is equal to 0 and $2\pi$, similar to the aperture division method simulation results. Here however, negative values of R are observed.

We show the plot of R versus $\phi _\mathrm{shift}$ for different $c_\mathrm{corr}$ in Fig. 1.19. The minimum R is found when $\phi _\mathrm{shift}$ is equal to 0 and $2\pi$, similar to the aperture division method simulation results. Here however, negative values of R is observed.

Fig. 1.20

Left: The ZOD and the correction beam for different values of $c_\mathrm{corr}$. Middle: Cross section profile of each beam and the ZOD. Right: Linfoot’s criteria of merit versus $c_\mathrm{corr}$

Figure 1.20 presents sample images of the ZOD for different $c_\mathrm{corr}$ values as well as the plot of minimum R versus $c_\mathrm{corr}$. The minimum R plot reveals that the ZOD intensity is reduced to near zero i.e. $99\%$ suppression, at $c_\mathrm{corr} = 0.3125$, which happens when the correction beam and ZOD profiles are totally matched. The only remaining problem is in balancing the energies of the two beams. We determine the total energy of the correction beam including its ghost order by changing $c_\mathrm{corr}$. The possible suppression that is attainable numerically higher than that achieved experimentally.

Figure 1.10 shows experimental plots for the minimum R versus AF for the three methods of aperture division, which are unlike their corresponding simulation plots at high AF. The difference is explained as follows: at low AF values, the correction beam profile is wider than that of the ZOD (see Fig. 1.14) while at high AF values, the profiles become narrower and more similar making the beams more sensitive to relative misalignment. Slight misalignments are sufficient to significantly reduce the effectivity of two-beam interference in suppressing the ZOD. Figure 1.18 shows that numerical results do not predict any suppression with the intensity of the ZOD increasing linearly with AF because at low AF values, correction beam and the ZOD profiles do no match does not match while at high AF, the total energies of correction beam and the ZOD are unequal. Instead of full destructive interference, a ZOD is created by the excess energy from the correction beam.

For the field addition method, the experiment yields negative values for minimum R at all $c_\mathrm{corr}$. The minimum R-value decreases with increasing $c_\mathrm{corr}$ until $c_\mathrm{corr} = 0.82$, (see Fig. 1.11). The numerical results reveal a minimum R-value that decreases with increasing $c_\mathrm{corr}$ until $c_{corr} = 0.3125$ where minimum R achieves its lowest value of $R = -99\%$ (see Fig. 1.20). For $c_\mathrm{corr} > 0.3125$, minimum R increases with $c_\mathrm{corr}$. At low $c_\mathrm{corr}$ values, the simulation and the experiment results are in agreement and they result from low energy of the correction beam that limits its effectivity to suppress the ZOD. However the two results start to deviate from each other as $c_\mathrm{corr}$ increases due in part to the presence of a ghost image that strengthens with the correction beam energy. The undesirable ghost image which reduces the R value, is an artifact that arises from the iterative nature of the GS algorithm [29] which could not distinguish between the mirror/ghost image from the primary image. The ghost or twin image may be removed using various methods [24, 30].

Three reasons may be cited to cause the difference between the numerical and the experimental results. First, we have simply assumed that only the non-modulating areas of the SLM contribute to the ZOD in the construction of the correction beam in the numerical simulations. In practice other factors might affect the total intensity and profile of the ZOD. For example, minute imperfections in the anti-reflection coating of the SLM could result in a fraction of the incident beam being left unmodulated [24]. The presence of random phase fluctuations [31] can also alter the ZOD intensity profile.

Second is the presence of spatial phase variations caused by uneven illumination and imperfect SLM surface flatness that may be caused by manufacturing and variations in the ambient temperature. Spatial phase variations contribute to the effective phase of the correction beam changing its profile and lessening its ability to suppress the ZOD. The presence of pixel cross-talk also changes the input phase and the ZOD profile. The effect of pixel crosstalk on the hologram also depends on the type of hologram since it is caused by fringing fields that exist between pixels.

The third reason is imperfect alignment of the optical system. If aberration is induced by misalignment, or if the hologram is not correctly inputted to the SLM, the degree of interference between the ZOD and the correction beam is seriously affected. In general aberration differently affects ZOD and the correction beam since it is location dependent.

For the correction beam to completely suppress the ZOD, the above mentioned issues must be addressed satisfactorily. The experimental ZOD profile can be determined accurately and then used to match with the profile of the correction beam. By properly calibrating the SLM, the effect of the spatial phase variation can be taken into account and the correction beam profile may be designed to match to that of the ZOD. Accurate alignment of the different elements comprising the optical set-up can reduce significantly the degree of aberration present. Satisfying the aforementioned conditions will lead to full ZOD suppression.

1.5 Summary and Conclusions

We have suppressed the unwanted ZOD by inducing a destructive interference between the ZOD and a correction beam. Two methods were tested to create the correction beam—aperture division and addition of fields [6]. We have calculated the fields necessary to create the desired target and correction beam separately—the input source to the GS algorithm serving as the aperture amplitude of the SLM. The final phase input to the SLM is obtained by calculating the phase of the sum of the two fields. The energy that is given to the correction beam is controlled using multiplicative constants $c_\mathrm{corr}$ and $c_\mathrm{target}$.

We have observed a discontinuity in the dependence of R with $\phi _\mathrm{shift}$, which could be attributed to the algorithm used to generate the hologram input to the SLM. The phase maps were wrapped from 0 to $2\pi$, which greatly limits the number gray levels that are possible for the hologram. In the experiments, we were able to suppress the ZOD up to: $39\%$ at $AF = 0.94$ with the angular aperture division method, $32\%$ at $AF = 0.97$ with the annular aperture division method and $24\%$ at $AF = 0.88$ with the vertical aperture division method. At lower AF values, the correction beam and the ZOD profiles do not match thus limiting the effectivity of the correction beam to suppress the ZOD. At higher AF, the correction beam becomes narrower and more sensitive to misalignment. For the field addition method, we have been able to suppress the ZOD up to $32\%$ at $c_\mathrm{corr} = 0.82$.

For the field addition method, simulations show that ZOD suppression is possible up to $99\%$ of its original total intensity since the whole aperture is used to construct the correction beam allowing maximum similarity between the ZOD and correction beam. Suitable choice of the multiplicative constants allowed us to match the total energy of the correction beam to that of the ZOD and making full destructive interference between the two profiles nearly possible.

To fully suppress the ZOD and improve the quality of reconstruction using the SLM, we have cited a number of experimental issues that needed to be addressed by calibrating the SLM in order to neutralize the effect of spatial phase variations in the SLM surface. By obtaining a more accurate ZOD profile, the profile of the correction beam can be matched with the ZOD profile. The degree of ZOD suppression is highly sensitive to aberrations that may be caused by minute misalignments among the different optical elements in the set-up and has to be seriously taken into consideration.