Keywords

38.1 Introduction

Accurate simulations of a complex systems require high number of Degrees of Freedoms (DoFs) and therefore high computational cost. Computational effort further increases when the system requires the use of nonlinear models to describe its behaviour. In recent years, efforts have been made reduce the number of model DoFs, with a marginal loss of accuracy. Methods resulting from such activities are generically called Model Order Reduction (MOR) methods. These methods have been applied to several engineering fields, as summarized in [1, 2]. Examples of their application can be found in structural dynamics [3,4,5,6], systems and control [7, 8] and mathematics [9,10,11].

Two classes of MOR methods can be identified: Data-based and Model-based. The first class is based on a database of previous simulations of the full original nonlinear system. Proper Orthogonal Decomposition method (POD) [12, 13] is one of the examples of MOR method for nonlinear systems: a base of orthogonal modes is built to describe the system. The second class is based on the full nonlinear model itself and no preliminary simulations are required. The model is generically projected into a sub-manifold, whose definition depends on the method used. The reduced system has a lower computational cost and it is therefore useful for simulations, both in time or frequency domain. Methods of this class and aimed to nonlinear systems have been proposed, both retaining the nonlinearities [14, 15] and linearising them. Two interesting methods belonging to this last subclass are the Trajectory Piecewise Linear Approximation (TPWL) [16,17,18] and the Global Modal Parametrization (GMP) [19, 20].

In [21,22,23] the important topic of how to select a base is considered. Recently, classical model reduction techniques have been applied to contact problems [24], implementing linearised event-driven simulations that also address the problem of changing the reduced base.

Multi-Phi, the method proposed in this paper, is a linearisation method based on the projection of the original nonlinear system into the configuration space. Theoretically, it is possible to use any other space as long as it is possible to determine a univocal linear representation for each linearisation point. Since the span of the possible system states must be known before the simulation itself, the configuration space is the most predictable space and it is the one used in this paper. The nonlinear system is described by means of a set of linear systems (linearisation), and each one could be reduced by using a subset of its mode shapes.

Multi-Phi uses each base separately from the others, differently from TPWL: the bases are not orthonormal between each other, but they result to be orthonormal within themselves. With respect to GMP, the aim is not to transform Differential Algebraic Equations (DAEs) into nonlinear Ordinary Differential Equations (ODEs), but to build piecewise linear ODEs. In the proposed method, the off-line computation consists just in a series of linear modal analysis.

Nonlinearities in Multi-Phi are implied in the differences between the different bases. Non-holonomic constraints, such as contacts, or continuous nonlinear effects can be handled similarly. In the following, the proposed method is introduced and a simple application is provided.

Multhi-Phi methodology was presented in [25, 26], where it is applied to numerical nonlinear systems with localised nonlinearity. The method seems to be quite robust when the nonlinearities are both discrete or continuous. The potentiality in terms of accuracy and computational time reduction are shown through numerical simulations compared to classical integration. The aim of this work is to predict the time domain response of a non-smooth nonlinear system with a discrete nonlinearity and compare it to experimental results of the real system.

The paper is organised as follow: in Sect. 38.2 the experimental test-rig is shown with attention to the system equipment, in Sect. 38.3 the methodology for discrete system is explained. In Sect. 38.4 the results of a non-null initial condition case study are analysed and compared to the experimental results. Finally, some comments on this work are discussed in the conclusion.

38.2 Experimental Set-Up

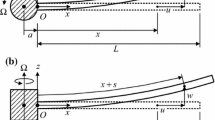
The experimental laboratory test-rig is shown in Fig. 38.1. The nonlinear system is a flexible aluminium cantilever beam with an additional steel mass of 213 g in the free tip. The dimensions of the beam are shown in Fig. 38.2. A non-smooth nonlinearity is obtained though the addiction of an ideally rigid support at 400 mm from the constraint, called Support constraint in Fig. 38.1, with a gap of 1.35 mm from the beam in its undeformed configuration. This is a non-holonomic constraint; therefore, the system is nonlinear because of the change of boundary conditions/stiffness matrix when the gap is closed. Three points of interest are selected along the beam: node 1 distant 95 mm from the clamped constraint and used for the excitation, node 2 that is the contact point of the non-smooth nonlinearity, and node 3 that is the free tip of the beam. A shaker is used to excite the system in node 1 during preliminary modal analysis tests. The response of the nonlinear beam is measured though three displacement laser sensors, monitoring node 1 (Keyence LK-H052), 2 (Keyence LK-H082) and 3 (Keyence LK-H152). The data are acquired using a LMS Scadas Mobile and Test.Lab software.

Fig. 38.1
figure 1

Laboratory test-rig and experimental setup

Full size image
Fig. 38.2
figure 2

Sketch of the non-linear system, relevant dimensions are in millimeters

Full size image

The characterisation of the beam natural frequencies and damping ratios is performed by sweeps from 2 to 250 Hz on the linear structure, i.e. with the support constraint removed. Only the bending modes in x–z plane are investigated. The natural frequencies of the bending modes inside the spanned frequency range are listed in Table 38.1.

Table 38.1 Experimental bending modes in x–z plane
Full size table

A finite element model, shown in Fig. 38.3, is implemented to represent the beam. The model is made of one-dimensional Timoshenko beam with a total of 348 DoFs. The model was tuned on the experimental data; the resulting density ρ and Young Modulus E are respectively ρ = 2700 kg/m3 and E = 43.5 GPa. The steel mass is modelled as a punctual mass in the DoF at 529 mm from the constraint, with the actual mass and inertia tensor of the steel cylinder.

Fig. 38.3
figure 3

One-dimensional finite element model

Full size image

Several different tests are performed on the beam with non-null initial conditions. The initial conditions are obtained by the application of a static force in the three holes highlighted in Fig. 38.2, in both directions ±z: the application of the force in different positions let to have different deformed initial conditions. If the force is applied in −z, the beam is in contact with the support constraint. The force is applied with a hanged weight linked to the beam by mean of a cable, which is cut to observe the free oscillations of the system.

38.3 Multi-Phi Method

Linear modal analysis allows to rewrite the equations of a linear dynamic system by means of diagonal matrices only, so uncoupling the problem. The proposal of Multi-Phi is to describe the nonlinearities through a limited number of parameters and to decompose the nonlinear system into a series of linear systems, each one characterised by a reference value of each parameter. In the following, the assumption of a single parameter α is made. It is considered a set of lv linearised models characterised by a reference values α l.

Linear modal analysis is performed on each linear system l, obtaining r l modes, used to build a collection of lv linear models. Each linear model can represent with a good approximation the system behaviour for α ≈ α l.

Considering a generic l linear system, the equations of motion are described by Eq. (38.1).

$$ {\mathbf{M}}^{(l)}\ddot{\mathbf{x}}+{\mathbf{C}}^{(l)}\dot{\mathbf{x}}+{\mathbf{K}}^{(l)}\mathbf{x}=\mathbf{f}(t) $$
(38.1)

where \( \mathbf{x},\dot{\mathbf{x}},\ddot{\mathbf{x}}\in {\Re}^{n\times 1} \) are respectively displacements, velocities and accelerations of the system, M (l), C (l), K (l) are respectively mass, damping and stiffness matrices of the l linear system and f(t) is the time depending external forcing function applied to the system.

Assuming a proportional damping matrix, the modal superposition results:

$$ \mathbf{x}={\boldsymbol{\Phi}}^{(l)}{\boldsymbol{\upeta}}^{(l)} $$
(38.2)

where \( {\boldsymbol{\Phi}}^{(l)}\in {\Re}^{n\times {r}_l} \) and \( {\boldsymbol{\upeta}}^{(l)}\in {\Re}^{r_l\times 1} \).

In Eqs. (38.1) and (38.2) the superscript (l) is referred to the modal coordinates of the l th linear model.

If the eigenvectors are unitary modal mass normalised, Eq. (38.1) can be then expressed by means of modal coordinates as Eq. (38.3).

$$ \mathbf{I}\;{\ddot{\boldsymbol{\upeta}}}^{(l)}+\mathit{\operatorname{diag}}\left(2{\boldsymbol{\upzeta}}_l{\boldsymbol{\upomega}}_l\right)\;{\dot{\boldsymbol{\upeta}}}^{(l)}+\mathit{\operatorname{diag}}\left({\boldsymbol{\upomega}}_l^2\right)\;{\boldsymbol{\upeta}}^{(l)}={\boldsymbol{\Phi}}^{(l)T}\mathbf{f}(t) $$
(38.3)

where ω l and ζ l are the vector of natural frequencies and corresponding damping ratios vectors of the l th linear model.

The state in terms of physical coordinates can be obtained using Eq. (38.4):

$$ \left\{\begin{array}{l}\mathbf{x}(t)=\boldsymbol{\Phi} (t)\kern0.24em \boldsymbol{\upeta} (t)+{\mathbf{x}}_{\infty }(t)\\ {}\dot{\mathbf{x}}(t)=\boldsymbol{\Phi} (t)\kern0.24em \dot{\boldsymbol{\upeta}}(t)\\ {}\ddot{\mathbf{x}}(t)=\boldsymbol{\Phi} (t)\kern0.24em \ddot{\boldsymbol{\upeta}}(t)\end{array}\right. $$
(38.4)

In Eq. (38.4) the addition of x ∞, called asymptotic configuration, is necessary whenever the set of mode shapes used to simulate the system evolution cannot describe the system state because of non-null boundary conditions. It is considered function of time because it depends on the linearised system considered at each time instant.

To determine \( {\mathbf{x}}_{\infty}^{(l)} \), the Guyan reduction is applied, by means of Eq. (38.5). In such equation, x k represents the boundary conditions (known DoFs) while x u represents the not constrained DoFs (unknown).

$$ \left\{\begin{array}{l}{\mathbf{x}}_{\infty }=\left[\begin{array}{c}-{\left({\mathbf{K}}_{uu}^{(l)}\right)}^{-1}{\mathbf{K}}_{uk}^{(l)}\\ {}\mathbf{I}\end{array}\right]\;{\mathbf{x}}_k\\ {}{\dot{\mathbf{x}}}_{\infty }=\mathbf{0}\end{array}\right. $$
(38.5)

The matrix Φ(t) is varying in time as a consequence of the transition between the linearised system: it is composed by the succession in time of the matrices Φ l, with l = 1, … , L if a number of linearised systems equal to L is considered.

In the following it will be referred to each linearised system as to a “level”, so that at the level l it is associated the linearised system characterised by α = α l, the set of reduced matrices \( \hbox{diag}{\left(2\boldsymbol{\upzeta} \boldsymbol{\upomega} \right)}_l,\ \hbox{diag}({\boldsymbol{\upomega}}_l^2) \), Φ l and the asymptotic configuration x ∞, l.

When the nonlinearity is discrete, it is supposed that the parameter α can assume only discrete values. Therefore, during the simulation only one level at the time is considered, depending on the value of α. The evolution of the full system, during the span of time in which α = α l, depends only by the linearised system l and the transition to another level m occurs whenever α = α m.

The transition is governed by Eq. (38.6), in which the initial conditions of the modal coordinates of the level m are described by means of the final conditions of modal coordinates of the level l:

$$ \left\{\begin{array}{l}{\boldsymbol{\upeta}}_{m,0}={\boldsymbol{\Phi}}_m^{-1}\left({\boldsymbol{\Phi}}_l{\boldsymbol{\upeta}}_{l, end}+{\mathbf{x}}_{\infty, l}-{\mathbf{x}}_{\infty, m}\right)\\ {}{\dot{\boldsymbol{\upeta}}}_{m,0}={\boldsymbol{\Phi}}_m^{-1}{\boldsymbol{\Phi}}_l{\dot{\boldsymbol{\upeta}}}_{l, end}\end{array}\right. $$
(38.6)

The class of problem targeted is the one in which: (1) the external actions are potentially non-periodic; (2) the interest lies in the transient solution as well as in the steady state.

38.4 Comparison Between Prediction and Experimental Data

The case study discussed in this paragraph is the free oscillations of the system described in Sect. 38.2 due to non-null initial conditions. A force is applied in the hole closest to the free tip in +z direction, as shown in Fig. 38.4, producing a deformation of the beam. The imposed deformation represents the displacement initial conditions of the free vibrations, while the velocity initial conditions are null. The observation of the free vibrations starts when the force is suddenly removed.

Fig. 38.4
figure 4

Non-null initial condition imposed displacements (undeformed state is overlapped in transparency)

Full size image

The evolution starts with a series of impacts of the beam on the support constraint, until the displacement oscillations of the beam contact point decreases under the gap level.

Time-frequency analysis of the evolution of the three measured points is shown in Fig. 38.5, through Wavelet [27] transformation. The time domain evolution presents 3–4 harmonics clearly identified related to the system natural frequencies when it is in contact with the support or not and some other natural frequencies that are the linear combination of those. The natural frequencies have an unexpected trend, in fact they are higher in the first second of oscillations and then they smoothly converge to the expected natural frequencies. This experimental behaviour is under further investigations, due to possible related geometric nonlinearity when the system presents large oscillations or non-ideal behaviour of the constraint.

Fig. 38.5
figure 5

Time-frequency analysis of the measured points: node 1 (left), node 2 (middle) and node 3 (right)

Full size image

The numerical model of the system has a discrete nonlinearity, the parameter is in this case the displacement of the contact point, α = x 2. Two levels (L = 2) are used for the numerical prediction through Multi-Phi method. In particular, when the displacement of the contact point x 2 >  − g the corresponding linear system, shown in Fig. 38.6 (left), is a clamped free beam. On the other end when x 2 <  − g the boundary condition of the system changes and the displacement of the contact point along z is constrained, as shown in Fig. 38.6 (right). The modal properties used in the simulation are therefore related to these to linearised system. The natural frequencies of the bending modes of the two configurations are shown in Table 38.2.

Fig. 38.6
figure 6

Discrete levels used in the simulation: clamped-free (left) and clamped-pinned (right)

Full size image
Table 38.2 Natural frequencies of each level
Full size table

The initial condition of all the degrees of freedom of the system is required for the numerical simulation. The initial conditions are obtained by imposing a static load in the same node on which it was applied in the experimental test (Fig. 38.7), in order to have the displacement of the contact point as in the experimental case.

Fig. 38.7
figure 7

Imposed non-null initial condition in the numerical model (undeformed state is overlapped in transparency)

Full size image

The comparison of the free vibrations in terms of displacement for the three measured points is shown in Figs. 38.8, 38.9, and 38.10.

Fig. 38.8
figure 8

Displacement of node 1: comparison between experimental data and numerical prediction

Full size image
Fig. 38.9
figure 9

Displacement of node 2: comparison between experimental data and numerical prediction

Full size image
Fig. 38.10
figure 10

Displacement of node 3: comparison between experimental data and numerical prediction

Full size image

The time span in which the system is in the “free–free” level have white background, while the grey background indicates a contact condition between the beam and the support constraint.

The behaviour of node 1 in Fig. 38.8 is well predicted by the simulations. Both low frequency oscillations and high frequency excitations compare very well. The high frequency oscillations of the measured data have larger amplitude. This difference can be related to the non-ideal behaviour, with some degree of flexibility, of the constraint, with respect to the perfectly fixed boundary condition of the model. The initial condition of this point is significantly less than the experimental one, this is another prove of the non-perfectly rigid constraint that influence more the closest analysed point.

The comparison of the contact point displacement in Fig. 38.9 is much more interesting. The displacement is bounded in the lower part to the gap value in both the experimental and numerical simulation. The duration of the contact is very well predicted from the numerical method, even if it is visible a small flexibility of the experimental constraint that is not taken into account in the model. The time domain behaviour is very well predicted from the simulation, except the change of frequency of the experimental result already discussed for Fig. 38.5. It is very interesting to observe that both lower and higher frequency and amplitude of oscillations are almost coincident between experimental and numerical result. Moreover, the behaviour of the system during the first contact is really surprising: some oscillations can be seen in the experimental curves, with bouncing of the beam on the support; the same behaviour is also numerically found, with the beam that loss the contact with the support two times inside the first contact in correspondence of the experimental bouncing.

In Fig. 38.10 the experimental measured data of the beam tip are compared with the numerical ones. This point is useful to understand the excited natural frequency of this system. The numerical initial condition in this case is really close to the experimental one. Also in this case the simulation results are almost coincident with the experimental one, except the phase shift starting from 6 s. The detailed view on the first oscillations gives an idea of the level of accuracy of the simulation, which is very high.

38.5 Conclusion

The Multi-Phi method has been successfully applied to a non-smooth nonlinear system to predict the response in time domain. The basic theory of the method is evident: it lets to reduce the computational cost of a non-linear system integration by using only linearised discrete levels of the considered nonlinear system. The method has been valuated against experimental results of the free vibrations of a laboratory test-rig. The predicted time domain displacements agree very well with the measured ones, even if the model could be substantially improved. Some aspects requires further investigations, in particular the flexibility of the clamp. Moreover support constraints are not actually considered and the hardening effect of the experimental system when the amplitude of oscillation is larger should be deeper investigated and eventually included in the numerical model.