1 Introduction

Feedback stabilization by means of static state-feedback, dynamic output-feedback and input-output feedback linearization for nonlinear retarded systems has been extensively studied in the literature (see, for instance, [1,2,3,4,5, 9,10,11, 16, 26,27,29, 43]). Nevertheless, though many approaches are available, the stabilization problem for general nonlinear systems, with an arbitrary number of discrete and distributed time-delays, is still far from being fully solved. The technique of control Lyapunov functions has been exploited to practically or asymptotically stabilize a large class of time-invariant retarded systems in affine form in [16], using Lyapunov Razumikhin functions. The domination redesign control methodology is employed (see [39]). Results concerning the use of control Lyapunov-Krasovskii functionals (instead of control Lyapunov-Razumikhin functions) for the design of stabilizing control laws for retarded systems can be found in [7, 15, 21, 33, 34, 38]. In [15] a fixed type of control Lyapunov-Krasovskii functionals is exploited. For this type of control Lyapunov-Krasovskii functionals, remarkable results are achieved for a broad class of retarded systems. For instance, it is shown that both Sontag’s (see [41]) and Freeman’s (see [8]) formulas can be successfully used for global stabilization purposes. If the small control property holds (see [15, 41]), the proposed feedback control laws are, at least, locally Lipschitz outside the origin and continuous at the origin. In [7] the authors propose a predictive control scheme with guaranteed closed-loop stability for nonlinear retarded systems, utilizing the same fixed type of control Lyapunov-Krasovskii functionals as in [15]. In [21] the authors prove the equivalence of the existence of a completely locally Lipschitz control Lyapunov-Krasovskii functional satisfying the small control property (see [41] and references therein), and the stabilizability property by means of completely locally Lipschitz control laws, for fully nonlinear, retarded systems. Moreover, stabilizability is intended robust with respect to vanishing disturbances. In [38] the inverse optimality approach for delay-free nonlinear systems is extended to time-delay systems, by the use of complete quadratic control Lyapunov-Krasvoskii functionals. In the paper [33] it is shown how invariantly differentiable functionals (see [24, 25]) can play an important role for the input-to-state practical stabilization (see Definition 2.1 in [17]) of retarded systems, by using the Sontag’s universal formula with a slight modification. The hypotheses introduced in [33] do not guarantee that the state feedback law obtained by the Sontag’s formula, as proposed in [15], is locally Lipschitz. Therefore, the Sontag’s formula extended to retarded systems is modified in the critical subsets of the infinite dimensional state space where the Lipschitz property of the related feedback control law may be lost. By this modification, the problem of non Lipschitz feedback control law is solved. Then, an input-to-state stabilizing term (see [32, 35, 40]) is added to the control law, thus achieving the twofold result of attenuation of the actuator disturbance and attenuation of the bounded error due to the above modification of the Sontag’s formula. Sontag’s stabilizer is studied in [34] also for neutral systems in Hale’s form, which include retarded systems as a special case. Sufficient conditions for both the global asymptotic stabilization and for the global practical stabilization, by Sontag’s and modified Sontag’s formula, are provided. A robustifying controller for retarded interconnected systems is studied in [12]. It is shown that, under a suitable small-gain condition (see [14]), decentralized controllers can be found in order to achieve actuator disturbance attenuation, in the sense of input-to-state stability, for interconnected systems stabilizable by means of decentralized state feedback control laws. The interested reader can refer to the recent monograph [20] for an extensive presentation of Lyapunov-based stabilization methods for nonlinear systems, in both the finite dimensional and the retarded cases, in the continuous-time as well as in the discrete-time. It is well known that finding control Lyapunov-Krasovskii functionals is in general a not easy task, as well as that small-gain methods (see [18]) can provide an important tool in order to simplify the construction of suitable Lyapunov functions and Lyapunov-Krasovskii functionals (see [13, 14, 17]). For this reason, we propose here a constructive methodology for the design of controllers for a class of interconnected systems, which makes use of control Lyapunov-Krasovskii functionals for each subsystem, aimed at simplifying the search of these functionals. Then, for each subsystem, the locally Lipschitz control law proposed in [33] is found. By means of a small-gain condition for retarded systems developed in [14], it is proved that the resulting overall closed-loop system is input-to-state practically stable with respect to actuator disturbances. If the disturbances are bounded, it is proved that, by suitably tuning a control parameter, the system state can be driven to an arbitrarily small neighborhood of the origin. The easier search of control Lyapunov-Krasovskii functionals is evident in the special case when delays appear on the communication channels only. In this case, it is possible to look for just control Lyapunov functions in Euclidean spaces, and transfer to the small-gain condition the problem of dealing with interconnection delays (see (17) in [14]). Moreover, the provided conditions do not include the small control property, which may well be not satisfied, as shown in [33]. Actually, the small control property may be an additional property hard to be satisfied for retarded systems (see examples in [33] and, in the neutral case, in [34]). The proposed control law is locally Lipschitz in the infinite dimensional state space of the systems described by retarded functional differential equations here considered. Moreover, the control law is decentralized, that is, each control law depends only on the state of each sub-system, which may be an interesting property for the practical situation where subsystems are located far away each other, and each subsystem is provided with a controller. A numerical example is studied in details, in order to show the effectiveness of the proposed methodology.

A preliminary version of this chapter has been published in [36].

Notation \(\mathcal {R}\) denotes the set of real numbers, \(\mathcal {R}^{\star }\) denotes the extended real line \([-\infty ,+\infty ]\), \(\mathcal {R}^+\) denotes the set of non-negative reals \([0,+\infty )\). The symbol \(\vert \cdot \vert \) stands for the Euclidean norm of a real vector. The essential supremum norm of an essentially bounded function is indicated with the symbol \(\Vert \cdot \Vert _{\infty }\). A function \(v:\mathcal {R}^+\rightarrow \mathcal {R}^m\), m positive integer, is said to be essentially bounded if \(ess\sup _{t\ge 0}\vert v(t) \vert <+\infty \). For given times \(0\le T_1<T_2\), with \(v_{[T_1,T_2)}:\mathcal {R}^+\rightarrow \mathcal {R}^m\) we mean the function given by \( v_{[T_1,T_2)}(t)= v(t) \) for all \(t \in [T_1,T_2)\) and \(=0\) elsewhere. An input v is said to be locally essentially bounded if, for any \(T>0\), \(v_{[0,T)}\) is essentially bounded. For a positive integer n, for a positive real \(\Delta \) (maximum involved time delay), \({\mathcal {C}}_n\) and \({\mathcal {Q}}_n\) denote the space of the continuous functions mapping \([-\Delta ,0]\) into \(R^n\) and the space of the bounded, continuous except at a finite number of points with jump discontinuities, and right-continuous functions mapping \([-\Delta ,0)\) into \(\mathcal {R}^n\), respectively. For \(\phi \in {\mathcal {C}}_n\), \(\phi _{[-\Delta ,0)}\) is the function in \({\mathcal {Q}}_n\) defined as \(\phi _{[-\Delta ,0)}(\tau )=\phi (\tau )\), \(\tau \in [-\Delta ,0)\). For a continuous function \(x:[-\Delta , c)\rightarrow \mathcal {R}^n\), with \(0<c\le +\infty \), for any real \(t\in [0,c)\), \(x_t\) is the function in \({\mathcal {C}}_n\) defined as \(x_{t}(\tau )=x(t+\tau )\), \(\tau \in [-\Delta ,0]\). For a positive real \(\delta \), \(\phi \in {\mathcal {C}}_n\), \(I_{\delta }(\phi )=\{\psi \in {\mathcal {C}}_n: \Vert \psi -\phi \Vert _{\infty }\le \delta \}\). For given positive integers n, m, a map \(f: \mathcal {C}_n\rightarrow \mathcal {R}^{n\times m}\) is said to be: completely continuous if it is continuous and takes bounded subsets of \({\mathcal {C}}_n\) into bounded subsets of \(\mathcal {R}^{n\times m}\); locally Lipschitz in \({\mathcal {C}}_n\) if, for any \(\phi \in {\mathcal {C}}_n\), there exist positive reals \(\delta , \eta \) such that, for any \(\phi _1, \phi _2 \in I_{\delta }(\phi )\), the inequality \(\vert f(\phi _1)-f(\phi _2)\vert \le \eta \Vert \phi _1-\phi _2\Vert _{\infty }\) holds. Let us here recall that a function \(\gamma :\mathcal {R}^+\rightarrow \mathcal {R}^+\) is: of class \({\mathcal {P}}\) if it is continuous, zero at zero, and positive at any positive real; of class \({\mathcal {K}}\) if it is of class \({\mathcal {P}}\) and strictly increasing; of class \({\mathcal {K}}_{\infty }\) if it is of class \({\mathcal {K}}\) and it is unbounded; of class \({\mathcal {L}}\) if it is continuous and it monotonically decreases to zero as its argument tends to \(+\infty \). A function \(\beta :\mathcal {R}^+\times \mathcal {R}^+\rightarrow \mathcal {R}^+\) is of class \(\mathcal {KL}\) if \(\beta (\cdot , t)\) is of class \({\mathcal {K}}\) for each \(t\ge 0\) and \(\beta (s,\cdot )\) is of class \({\mathcal {L}}\) for each \(s\ge 0\). The symbol \(\circ \) denotes composition of functions. With the symbol \(M_a\) is indicated any functional mapping \(\mathcal {C}_n\) into \(\mathcal {R}^+\) (see [32]), such that, for some \({\mathcal {K}}_{\infty }\) functions \(\gamma _{a}, \overline{\gamma }_{a}\), the inequalities \(\gamma _{a}(\vert \phi (0) \vert ) \le M_a(\phi ) \le \overline{\gamma }_{a}(\Vert \phi \Vert _{\infty })\) hold for any \(\phi \in {\mathcal {C}}_n\). Throughout the chapter, RFDE stands for retarded functional differential equation, ISS stands for input-to-state stability or input-to-state stable, ISpS stands for input-to-state practical stability or input-to-state practically stable, GAS stands for global asymptotic stability or globally asymptotically stable. A system with an equilibrium at zero is said to be 0-GAS if the zero solution is GAS. CLF stands for control Lyapunov function, CLRF stands for control Lyapunov-Razumikhin function, CLKF stands for control Lyapunov-Krasovskii functional.

2 Preliminaries

Let us consider the system described by the following RFDE

$$\begin{aligned}&\dot{x}(t)=f(x_t)+g(x_t)u(t), \qquad t\ge 0, \qquad a.e., \nonumber \\&x(\tau )=\xi _0(\tau ),\quad \,\,\,\,\,\, \tau \in [-\Delta ,0], \qquad \xi _0\in {\mathcal {C}}_n, \end{aligned}$$
(1)

where: \(x(t)\in \mathcal {R}^n\), n is a positive integer; \(\Delta >0\) is the maximum involved time delay; the maps \(f:{\mathcal {C}}_n\rightarrow \mathcal {R}^n\) and \(g:{\mathcal {C}}_n\rightarrow R^{n\times m}\) are completely continuous and locally Lipschitz in \({\mathcal {C}}_n\), \(f(0)=0\); m is a positive integer; \(u(t)\in \mathcal {R}^m\) is the input signal, assumed to be Lebesgue measurable and locally essentially bounded.

Given a locally Lipschitz continuous functional \(V:{\mathcal {C}}_n\rightarrow \mathcal {R}^+\), the upper right-hand derivative \(D^+ V: {\mathcal {C}}_n\times \mathcal {R}^m\rightarrow \mathcal {R}^{\star }\) of the functional V, in the Driver’s form (see [6, 19, 37]), is defined, for \(\phi \in \mathcal {C}_n\), \(v\in \mathcal {R}^m\), as

$$\begin{aligned} D^+ V(\phi ,v)= \limsup _{h\rightarrow 0^+} {1\over h} \left( V(\phi _{h})-V(\phi ) \right) ,\end{aligned}$$
(2)

where \(\phi _h \in {\mathcal {C}}_n\) is given, for \(h\in [0,\Delta )\), by

$$\begin{aligned}&\phi _h (\theta ) = \left\{ \begin{array}{cc} \phi (\theta +h), &{} \theta \in [-\Delta ,-h), \\ \phi (0)+(f(\phi )+g(\phi )v)(\theta +h), &{} \theta \in [-h,0] \end{array} \right. \end{aligned}$$
(3)

Remark 1

It is proved in [30] that, for locally Lipschitz continuous functionals V, the following equality holds

$$\begin{aligned}&\limsup _{h\rightarrow 0^+}\frac{V(x_{t+h})-V(x_t)}{h}= D^+V(x_t,u(t)), \qquad t\in [0,b), \qquad a.e., \end{aligned}$$
(4)

where \(x_t\) is the solution of (1) in a maximal time interval [0, b), \(0<b\le +\infty \). It is proved in [31] that, for locally Lipschitz functionals V, the problem of the local absolute continuity of the function \(t\rightarrow V(x_t)\) is overcome.

The following definition of invariant differentiable functionals is taken from [25], see Definitions 2.2.1, 2.5.2 in Chap. 2. The formalism used in [25] is here slightly modified for the purpose of formalism uniformity over the chapter. For any given \(x\in \mathcal {R}^n\), \(\phi \in {\mathcal {Q}}_n\) and for any given continuous function \({\mathcal {Y}}:[0,\Delta ]\rightarrow \mathcal {R}^n\) with \({\mathcal {Y}}(0)=x\), let \(\psi ^{(x,\phi ,{\mathcal {Y}})}_h \in {\mathcal {Q}}_n\), \(h\in [0,\Delta )\), be defined as

$$\begin{aligned}&\psi ^{(x,\phi ,{\mathcal {Y}})}_h(s)= \left\{ \begin{array}{cc} \phi (s), \qquad \, s\in [-\Delta , 0), &{} h=0, \\ \\ \left\{ \begin{array}{cc} \phi (s+h), &{} s\in [-\Delta ,-h), \\ {\mathcal {Y}}(s+h), &{} s\in [-h,0),\end{array}\right\} ,&\ h\in (0,\Delta ) \end{array} \right. \end{aligned}$$
(5)

For \(\phi \in {\mathcal {C}}_n\), \(h\in [0,\Delta )\), let \(\phi ^h\in {\mathcal {C}}_n\) be defined as follows

$$\begin{aligned} \phi ^h(s)=\left\{ \begin{array}{cc}\phi (s+h), &{} s\in [-\Delta ,-h)\\ \phi (0), &{} s\in [-h,0]\end{array}\right. \end{aligned}$$
(6)

Definition 1

(see [25]) A functional \(V:\mathcal {R}^n\times {\mathcal {Q}}_n\rightarrow \mathcal {R}^+\) is said to be invariantly differentiable if, at any point \((x,\phi )\in R^n\times {\mathcal {Q}}_n\), the following conditions hold:

  1. (i)

    for any continuous function \({\mathcal {Y}}:[0,\Delta ]\rightarrow R^n\) with \({\mathcal {Y}}(0)=x\), the right-hand derivative \(\left. \frac{\partial V\left( x, \psi ^{(x,\phi ,{\mathcal {Y}})}_h\right) }{\partial h}\right| _{h=0}\) exists and such derivative is invariant with respect to the function \({\mathcal {Y}}\);

  2. (ii)

    the derivative \( \frac{\partial V(x,\phi )}{\partial x}\) exists;

  3. (iii)

    for any given continuous function \({\mathcal {Y}}:[0,\Delta ]\rightarrow R^n\) with \({\mathcal {Y}}(0)=x\), the following limit holds (involved \(z\in R^n\) and \(h\in [0,\Delta )\)),

    $$\begin{aligned}&\lim _{z\rightarrow 0,\ h\rightarrow 0^+}\frac{1}{\sqrt{\vert z\vert ^2+h^2}}\cdot \nonumber \\&\left( V\left( x+z,\psi ^{(x,\phi ,{\mathcal {Y}})}_{h}\right) -V(x,\phi )- \frac{\partial V(x,\phi )}{\partial x}z - \left. \frac{\partial V\left( x, \psi ^{(x,\phi ,{\mathcal {Y}})}_{\ell }\right) }{\partial \ell }\right| _{\ell =0}h\right) =0 \nonumber \\&\end{aligned}$$
    (7)

For a given locally Lipschitz and invariantly differentiable functional \(V:\mathcal {R}^n\times {\mathcal {Q}}_n\rightarrow \mathcal {R}^+\), let \(V_0:\mathcal {C}_n\rightarrow \mathcal {R}^+\) be the locally Lipschitz continuous functional defined, for \(\phi \in {\mathcal {C}}_n\), as \(V_0(\phi )=V(\phi (0),\phi _{[-\Delta ,0)})\). Then, the following result holds, for any \(\phi \in {\mathcal {C}}_n\) and any \(v\in \mathcal {R}^m\),

$$\begin{aligned}&D^+V_0(\phi ,v)=\left. \frac{\partial V(x,\phi _{[-\Delta ,0)})}{\partial x}\right| _{x=\phi (0)}\left( f(\phi )+g(\phi )v\right) +\left. \frac{\partial V\left( \phi (0), \phi ^h_{[-\Delta ,0)}\right) }{\partial h}\right| _{h=0},\nonumber \\&\end{aligned}$$
(8)

where the second term of the right-hand side of (8) is a right-hand derivative (see point (i) in Definition 1 and (6)).

In the following, for given positive integer n, \({\mathcal {V}}_n\) is the class of functionals \(V:\mathcal {R}^n\times {\mathcal {Q}}_n\rightarrow \mathcal {R}^+\) which have the following properties: i) V is locally Lipschitz in \(\mathcal {R}^n\times {\mathcal {Q}}_n\) and invariantly differentiable; ii) the maps (\(\phi \in {\mathcal {C}}_n\), involved \(x\in \mathcal {R}^n\), \(h\in [0,\Delta )\))

$$\begin{aligned}&\phi \rightarrow \left. \frac{\partial V\left( \phi (0), \phi ^h_{[-\Delta ,0)}\right) }{\partial h}\right| _{h=0}, \qquad \phi \rightarrow \left. \frac{\partial V(x,\phi _{[-\Delta ,0)})}{\partial x}\right| _{x=\phi (0)} \end{aligned}$$
(9)

are completely continuous and locally Lipschitz in \({\mathcal {C}}_n\).

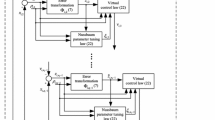
3 Interconnected Retarded Systems

Consider an interconnected system \(\Sigma \) described by the following RFDEs

$$\begin{aligned} &\Sigma \left\{ \begin{array}{ll} \Sigma _1 : &{} \dot{x}_1(t)=f_1(x_{1,t})+H_1(x_{1,t},x_{2,t}) +g_1(x_{1,t})(u_1(t)+d_1(t)) \\ \Sigma _2 : &{} \dot{x}_2(t)=f_2(x_{2,t})+H_2(x_{2,t},x_{1,t}) +g_2(x_{2,t})(u_2(t)+d_2(t)) \end{array}\right. \\ &\qquad \qquad x_{1,0}=\xi _{1,0}, \quad x_{2,0}=\xi _{2,0}, \nonumber \end{aligned}$$
(10)

where, for \(i=1,2\): \(x_i(t)\in \mathcal {R}^{n_i}\); \(d_i(t) \in \mathcal {R}^{m_i}\) is a disturbance adding to the control input (measurable, locally essentially bounded); \(n_i\) and \(m_i\) are positive integers; for \(t\in \mathcal {R}^+\), \(x_{i,t}:[-\Delta ,0]\rightarrow \mathcal {R}^{n_i}\) denotes (see Notation section) the function \(x_{i,t}(\tau )=x_i(t+\tau )\), \(\tau \in [-\Delta ,0]\), where \(\Delta >0\) is the maximum involved delay; \(\xi _{i,0}\in {\mathcal {C}}_{n_i}\). The maps \(f_i: {\mathcal {C}}_{n_i}\rightarrow \mathcal {R}^{n_i}\), \(H_i: {\mathcal {C}}_{n_i}\times {\mathcal {C}}_{n_{3-i}} \rightarrow \mathcal {R}^{n_i}\), \(g_i: {\mathcal {C}}_{n_i}\rightarrow \mathcal {R}^{n_i\times m_i}\) are locally Lipschitz and completely continuous. We combine vectors as \(x(t)=[x_1(t)^T, x_2(t)^T]^T\in \mathcal {R}^n\), \(n = n_1 +n_2\), \(u(t)=[u_1(t)^T, u_2(t)^T]^T\in \mathcal {R}^m\), \(d(t)=[d_1(t)^T, d_2(t)^T]^T\in \mathcal {R}^m\), \(m = m_1 +m_2\), \(\xi _0=[\xi _{1,0}^T, \xi _{2,0}^T]^T\in {\mathcal {C}}_n\), \(f(\cdot )=[f_1(\cdot )^T, f_2(\cdot )^T]^T\), \(H(\cdot )=[H_1(\cdot )^T, H_2(\cdot )^T]^T\) and \(g(\cdot )=[g_1(\cdot )^T, g_2(\cdot )^T]^T\). The element \(x_t\in \mathcal {C}_n\) is defined as for its i-th component \(x_{i,t}\) (see Notations section). It is assumed that \(f_i(0)=H_i(0,0)=0\), \(i=1,2\). We use functionals \(M_{a,i}:{\mathcal {C}}_{n_i}\rightarrow \mathcal {R}^+\) for which there exist class \(\mathcal {K}_\infty \) functions \(\underline{\gamma }_{a,i}\), \(\overline{\gamma }_{a,i}\), such that

$$\begin{aligned}&\underline{\gamma }_{a,i}(\vert \phi _i(0)\vert ) \le M_{a,i}(\phi _i) \le \overline{\gamma }_{a,i}(\Vert \phi _i\Vert _{\infty }), \forall \phi _i\in \mathcal {C}_{n_i}\nonumber \\&\end{aligned}$$
(11)

For functionals \(V_i:\mathcal {R}^{n_i}\times \mathcal {Q}_{n_i}\rightarrow \mathcal {R}^+\) in the class \(\mathcal {V}_{n_i}\), \(i=1,2\), let the maps \(a_i:\mathcal {C}_{n_i}\rightarrow \mathcal {R}\), \(b_i:\mathcal {C}_{n_i}\rightarrow \mathcal {R}^{m_i}\) (row vectors), \(c_i:\mathcal {C}_{n_i}\times \mathcal {C}_{n_{3-i}}\rightarrow \mathcal {R}\), and \(\rho _i :\mathcal {C}_{n_i}\times \mathcal {C}_{n_{3-i}}\rightarrow \mathcal {R}\) be defined, for \(\phi _i\in \mathcal {C}_{n_i}\), as follows:

$$\begin{aligned}&a_i(\phi _i)= \left. \frac{\partial V_i(x_i,\phi _{i_{[-\Delta ,0)}})}{\partial x_i}\right| _{x_i=\phi _i(0)}f_i(\phi _i) + \left. \frac{\partial V_i\left( \phi _i(0), \phi ^{\ell }_{i_{[-\Delta ,0)}}\right) }{\partial \ell }\right| _{\ell =0}, \nonumber \\&b_i(\phi _i)= \left. \frac{\partial V_i(x_i,\phi _{i_{[-\Delta ,0)}})}{\partial x_i}\right| _{x_i=\phi _i(0)}g_i(\phi _i), \nonumber \\&c_i(\phi _i,\phi _{3-i})= \left. \frac{\partial V_i(x_i,\phi _{i_{[-\Delta ,0)}})}{\partial x_i}\right| _{x_i=\phi _i(0)}H_i(\phi _i,\phi _{3-i}), \nonumber \\&\rho _i(\phi _i,\phi _{3-i})=-\sqrt{ a_i^2(\phi _i) +\vert b_i(\phi _i)\vert ^4} +c_i(\phi _i,\phi _{3-i}) \end{aligned}$$
(12)

Moreover, for a positive real r, let \(k_{i,r}:{\mathcal {C}}_{n_i}\rightarrow R^{m_i}\) be defined as follows, for \(\phi _i\in {\mathcal {C}}_{n_i}\),

$$\begin{aligned}&k_{i,r}(\phi _i)= \left\{ \begin{array}{c}-\frac{a_i(\phi _i)+\sqrt{a_i^2(\phi _i)+\vert b_i(\phi _i)\vert ^4}}{\vert b_i(\phi _i)\vert ^2}b_i^T(\phi _i), \ \vert b_i(\phi _i)\vert > r, \\ \\ -\frac{a_i(\phi _i)+\sqrt{a_i^2(\phi _i)+\vert b_i(\phi _i)\vert ^4}}{r^2}b_i^T(\phi _i), \ \vert b_i(\phi _i)\vert \le r \end{array} \right. \end{aligned}$$
(13)

The following assumption will be used in the forthcoming theorem (see Assumption 6 in [14], Hypothesis 4 in [33], Hypothesis 18 in [34]).

Assumption 1

There exist functionals \(V_i: \mathcal {R}^{n_i}\times {\mathcal {Q}}_{n_i}\rightarrow \mathcal {R}^+\), \(i=1,2\), in the class \({\mathcal {V}}_{n_i}\), with corresponding maps \(a_i\), \(b_i\), \(c_i\), \(\rho _i\), positive reals r, p, non-negative integers h, \(h_d\), functions \(\underline{\alpha }_{i}\), \(\overline{\alpha }_{i}\), \(\alpha _{i}\) of class \({\mathcal {K}}_{\infty }\), integers \(S_{i,j}\in \{0,1\}\), functions \(\sigma _{i,j}\) of class \({\mathcal {K}}\) and positive reals \(\Delta _{j}\in (0,\Delta ]\), \(j=0, 1, \dots , h+h_d\), such that, \(\forall \ \phi _i\in {\mathcal {C}}_{n_i}\), the following conditions hold, for \(i=1,2\):

  1. (i)

    \(\underline{\alpha }_{i}(M_{a,i} (\phi _i))\le V_i(\phi _i(0),\phi _{i_{[-\Delta ,0)}})\le \overline{\alpha }_i(M_{a,i}(\phi _i))\);

  2. (ii)

    \(\left( b_i(\phi _i)=0\right) \ \Rightarrow \ \left( a_i(\phi _i)\le 0\right) \);

  3. (iii)
    $$\begin{aligned}&\rho _i(\phi _i,\phi _{3-i})\le -\alpha _{i}(M_{a,i}(\phi _i) ) + S_{i,0}\sigma _{i,0}(M_{a,3-i}(\phi _{3-i})) \nonumber \\&+\sum _{j=1}^{h}S_{i,j}\sigma _{i,j}\left( \underline{\gamma }_{a,3-i}(\vert \phi _{3-i}(-\Delta _{j})\vert )\right) +\sum _{j=h+1}^{h+h_d}S_{i,j}\int _{-\Delta _j}^0 \sigma _{i,j} \left( \underline{\gamma }_{a,3-i}(\vert \phi _{3-i}(\tau ))\vert \right) d\tau ; \nonumber \\&\end{aligned}$$
    (14)
  4. (iv)

    \(\sup _{\{\psi _i\in {\mathcal {C}}_i,\ 0<\vert b_i(\psi _i)\vert \le r\}}\ \frac{a_i(\psi _i)}{\vert b_i(\psi _i)\vert }\le p\).

Remark 2

By \(h=0\) (resp., \(h_d=0\)), it is meant that the first (resp., second) sum in (14) vanishes. As well, when \(h_d=0\), the maximum term involving \(h_d\) in forthcoming equality (15) is meant to be zero.

Theorem 1

Let Assumption 1 hold. Let \(\sigma _i:\mathcal {R}^+\rightarrow \mathcal {R}^+\), \(i=1,2\), be the functions defined, for \(s\in \mathcal {R}^+\), as

$$\begin{aligned}&\sigma _i(s) =\left( \sum _{k=0}^{h+h_d}S_{i,k}\right) \max \left\{ \max _{j=0,1,\dots ,h}S_{i,j}\sigma _{i,j}(s),\right. \left. \max _{j=h+1,\dots ,h+h_d}S_{i,j}\Delta _j\sigma _{i,j}(s) \right\} \end{aligned}$$
(15)

Assume also there exist reals \(c_i>1\), \(i=1,2\), such that, \(\forall s\in \mathcal {R}^+\), the small-gain inequality holds (see (17) in [14])

$$\begin{aligned} c_1\sigma _{1}\circ \underline{\alpha }_2^{-1}\circ \overline{\alpha }_2\circ \alpha _2^{-1}\circ c_2\sigma _2(s) \le \alpha _{1}\circ \overline{\alpha }_{1}^{-1}\circ \underline{\alpha }_{1}(s) \end{aligned}$$
(16)

Then:

  1. (1)

    the maps \(k_{i,r}:{\mathcal {C}}_{n_i}\rightarrow \mathcal {R}^{m_i}\), \(i=1,2\), are completely continuous and locally Lipschitz in \({\mathcal {C}}_{n_i}\);

  2. (2)

    there exist a function \(\beta \) of class \({\mathcal {KL}}\) and a function \(\gamma \) of class \({\mathcal {K}}\) such that, chosen any positive real q, for any initial state \(\xi _0\) and any measurable, locally essentially bounded disturbance d(t), the corresponding solution x(t) of the closed loop system (10) with decentralized control laws

    $$\begin{aligned} u_i(t)=k_{i,r}(x_{i,t})-qb_i^T(x_{i,t}), \qquad i=1,2, \end{aligned}$$
    (17)

    exists for all \(t\ge 0\) and, furthermore, satisfies the following inequality

    $$\begin{aligned}&\vert x(t)\vert \le \beta (\Vert x_0\Vert _{\infty },t) +\gamma \left( \frac{\Vert d_{[0,t)}\Vert _{\infty }+2p+r}{\sqrt{q}}\right) \end{aligned}$$
    (18)

Proof

Let the map \(k_i: \mathcal {C}_{n_i}\rightarrow R^{m_i}\), \(i=1,2\), be defined, for \(\phi _i \in \mathcal {C}_{n_i}\), as (Sontag’s universal stabilizer, see [33, 34, 41])

$$\begin{aligned}&k_{i}(\phi _i)= \left\{ \begin{array}{cc}-\frac{a_i(\phi _i)+\sqrt{a_i^2(\phi _i)+\vert b_i(\phi _i)\vert ^4}}{\vert b_i(\phi _i)\vert ^2}b_i^T(\phi _i), &{} b_i(\phi _i)\ne 0 \\ \\ 0, &{} b_i(\phi _i)=0 \end{array} \right. \end{aligned}$$
(19)

Under Assumption 1, it is proved in [33] that the maps \(k_{i,r}\) are completely continuous and locally Lipschitz in \(\mathcal {C}_{n_i}\) and satisfy the inequality

$$\begin{aligned} \vert k_{i,r}(\phi _i)-k_i(\phi _i)\vert \le 2p+r, \ \forall \phi _i \in \mathcal {C}_{n_i} \end{aligned}$$
(20)

Let \(W_i:\mathcal {C}_{n_i}\rightarrow \mathcal {R}^+\) be defined, for \(\phi _i \in \mathcal {C}_{n_i}\) as \(W_i(\phi _i)=V_i(\phi _i(0),\phi _{i_{[-\Delta ,0)}})\), \(i=1,2\). Then, the following inequalities hold for the functional \(D^+W_i:\mathcal {C}_{n_i}\times \mathcal {C}_{n_{3-i}}\times \mathcal {R}^{m_i}\rightarrow \mathcal {R}^{\star }\), for any \(\phi _i\in \mathcal {C}_{n_i}\), \(d_i\in \mathcal {R}^{m_i}\), \(i=1,2\),

$$\begin{aligned}&D^+W_i(\phi _i,\phi _{3-i},d_i)= \nonumber \\&a_i(\phi _i)+b_i(\phi _i)k_{i,r}(\phi _i) -q b_i(\phi _i)b_i^T(\phi _i)+c_i(\phi _i,\phi _{3-i})+ b_i(\phi _i)d_i=\nonumber \\&a_i(\phi _i)+b_i(\phi _i)k_i(\phi _i)+b_i(\phi _i)(k_{i,r}(\phi _i)-k_i(\phi _i)) -q \vert b_i(\phi _i)\vert ^2+c_i(\phi _i,\phi _{3-i})+b_i(\phi _i)d_i \nonumber \\&\end{aligned}$$
(21)

By definition of the maps \(k_i\), it is obtained

$$\begin{aligned}&a_i(\phi _i)+b_i(\phi _i)k_i(\phi _i)= \left\{ \begin{array}{cc} -\sqrt{a_i^2(\phi _i)+\vert b_i(\phi _i)\vert ^4}, &{} b_i(\phi _i)\ne 0,\\ a_i(\phi _i), &{} b_i(\phi _i)=0\end{array}\right. \end{aligned}$$
(22)

Therefore, by the point (ii) in Assumption 1, taking into account of the definition of the map \(\rho _i\) in (12), it follows that

$$\begin{aligned} a_i(\phi _i)+b_i(\phi _i)k_i(\phi _i)+c_i(\phi _i,\phi _{3-i})=\rho _i(\phi _i,\phi _{3-i}) \end{aligned}$$
(23)

From (20), (21), (23), by Young’s inequality, it is obtained

$$\begin{aligned}&D^+W_i(\phi _i,\phi _{3-i},d_i)\le \vert b_i(\phi _i)\vert (2p+r) -q\vert b_i(\phi _i)\vert ^2+b_i(\phi _i)d_i +\rho _i(\phi _i,\phi _{3-i})\le \nonumber \\&-q\vert b_i(\phi _i)\vert ^2+\vert b_i(\phi _i)\vert (\vert d_i\vert +2p+r) +\rho _i(\phi _i,\phi _{3-i})\le \nonumber \\&-q\vert b_i(\phi _i)\vert ^2+q\vert b_i(\phi _i)\vert ^2+\frac{(\vert d_i\vert +2p+r)^2}{4q} +\rho _i(\phi _i,\phi _{3-i})= \nonumber \\&\rho _i(\phi _i,\phi _{3-i})+\sigma _{Ri}\circ \eta (\vert d_i\vert ), \end{aligned}$$
(24)

where \(\eta :\mathcal {R}^+\rightarrow \mathcal {R}^+\) is the function defined, for \(s\in \mathcal {R}^+\), as \(\eta (s)=\frac{s +2p+r}{\sqrt{q}},\) and \(\sigma _{Ri}\), \(i=1,2\), is the function of class \(\mathcal {K}_{\infty }\) defined, for \(s\in \mathcal {R}^+\), as \(\sigma _{Ri}(s)=\frac{1}{4}s^2\). We now remark that Lemmas 21, 23 in [14] hold as well if the argument \(s\in \mathcal {R}^+\) of the functions \(\sigma _{Ri}\), \(i=1,2\), as defined in (14) in [14], is replaced by a continuous, increasing function mapping \(\mathcal {R}^+\) to \(\mathcal {R}^+\), as, for instance, \(\eta \). Then, from point (iii) in Assumption 1, from Theorem 8 in [14] (taking into account of the above remark), it follows that there exist a locally Lipschitz functional \(W_{cl}:\mathcal {C}_n\rightarrow \mathcal {R}^+\) (see (18) in [14]), a functional \(M_a:\mathcal {C}_n\rightarrow \mathcal {R}^+\), functions \(\underline{\gamma }_a\), \(\overline{\gamma }_a\), \(\underline{\alpha }\), \(\overline{\alpha }\) and \(\alpha _{cl}\) of class \(\mathcal {K}_{\infty }\), and a function \(\sigma _{cl}\) of class \(\mathcal {K}\), such that, for any \(\phi \in \mathcal {C}_n\), \(d\in \mathcal {R}^{m}\), the inequalities hold (see (18) and D.4 in [14]),

$$\begin{aligned}&\underline{\alpha }(M_a(\phi ))\le W_{cl}(\phi )\le \overline{\alpha }(M_a(\phi )), \qquad \underline{\gamma }_a(\vert \phi (0)\vert )\le M_a(\phi )\le \overline{\gamma }_a(\Vert \phi \Vert _{\infty }), \end{aligned}$$
(25)
$$\begin{aligned}&D^+W_{cl}(\phi ,d)\le -\alpha _{cl}(M_{a}(\phi )) +\sigma _{cl}\circ \eta (\vert d\vert ) \end{aligned}$$
(26)

From (25), (26), it follows that the solution exists \(\forall t\ge 0\) and that the inequality (18) holds. The same reasoning used in the proof of Theorem 3.1 in [37] can be used here in order to obtain the ISpS result (see Definition 2.1 in [17]) described by the inequality (18).

Remark 3

We provide here a discussion on Assumption 1. The point (i) in Assumption 1 is standard in the 0-GAS, ISS theory for systems described by RFDEs (see [14, 37, 44], see in particular Lemma 4 in [14] as far as the lower bound is concerned). The point (ii) is the standard key property for a function V to be referred as a CLF (see [16, 20, 41]) and, for a functional V, to be referred as a CLKF (see, for instance, [15, 20, 21]). Notice that, in this case, it is allowed, for non-zero \(\phi _i\in \mathcal {C}_i\) satisfying \(b_i(\phi _i)=0\), that \(a_i(\phi )=0\) (see related discussions in [33, 34]). The point (iii) allows that, if the control input were equal to the state feedback obtained with Sontag’s universal formula, then the derivative in Driver’s form of the functionals \(V_i\) would satisfy a very general dissipative inequality with supply rates which may cope with both discrete and distributed time delays, in both subsystems and interconnections (see (13), (14) and Remark 10 in [14]). Notice that, in each dissipative inequality, only the map describing the dynamics of the related lower dimension subsystem is involved. This lower dimension may significantly simplify the analysis (namely, the computation of involved functions of class \(\mathcal {K}\) and \(\mathcal {K}_{\infty }\)). The condition (14) incorporates the fact that, if the interconnection terms were zero (i.e., \(H_i(\phi _i, \phi _{3-i})=0\), \(i=1,2\), \(\forall \phi _j\in \mathcal {C}_{n,j}\), \(j=1,2\), and \(S_{i,j}=0\), \(i=1,2\), \(j=0,1,\dots , h+h_d\)), each resulting subsystem would satisfy a standard inequality for 0-GAS, ISS concerns (see [14, 20, 22, 23, 37, 44]). The point (iv) is a key condition by which, using the methodology presented in [33], the problems related to non locally Lipschitz maps \(k_i\), \(i=1,2\), in (19) (i.e., the Sontag’s universal stabilizers for subsystems), can be overcome. A similar condition was introduced in [16] in the framework of CLRFs (see Assumption 1 in [16]), and in [15] in the framework of CLKFs, for exploiting the domination redesign formula (see [39]).

Remark 4

Because of the inequality (18), the closed-loop system (10), (17) is ISpS (see Definition 2.1 in [17]) with respect to the disturbance d(t). Notice in (18) that, if the disturbance is bounded, the solution can achieve an arbitrarily small neighborhood of the origin by increasing the control tuning parameter q.

4 Illustrative Numerical Example

Consider the interconnected system described by the following RFDE

$$\begin{aligned}&\dot{x}_1(t)=x_1^3(t)+\omega _1x_1(t)x_2(t-\Delta )+u_1(t)+d_1(t), \nonumber \\&\dot{x}_2(t)=x_2(t)+\omega _2x^2_1(t-\Delta )+x_2(t)\left( u_2(t)+d_2(t)\right) , \end{aligned}$$
(27)

where \(x_i, u_i, d_i\in \mathcal {R}\), \(i=1,2\), \(\Delta \) is a positive unknown real, \(\omega _i\in (-2,2)\), \(i=1,2\). Let \(V_i:\mathcal {R}\times \mathcal {Q}_1\rightarrow \mathcal {R}^+\), \(i=1,2\), be defined, for \(x_i\in \mathcal {R}\), \(\psi _i\in \mathcal {Q}_1\), as \(V_i(x_i,\psi _i)=\frac{1}{2}x^2_i\). Let \(M_{a,i}:\mathcal {C}_1\rightarrow \mathcal {R}^+\), \(i=1,2\), be defined, for \(\phi _i\in \mathcal {C}_1\), as \(M_{a,i}(\phi _i)=\vert \phi _i(0)\vert \). As far as (11) and point (i) in Assumption 1 are concerned, they are satisfied by the functions \(\underline{\gamma }_{a,i}\), \(\overline{\gamma }_{a,i}\), \(\underline{\alpha }_{a,i}\), \(\overline{\alpha }_{a,i}\) of class \(\mathcal {K}_{\infty }\), \(i=1,2\), defined, for \(s\in R^+\), as

$$\begin{aligned}&\underline{\gamma }_{a,i}(s)=\overline{\gamma }_{a,i}(s)=s; \qquad \underline{\alpha }_i(s)=\overline{\alpha }_i(s)=\frac{1}{2}s^2. \end{aligned}$$
(28)

As far as the functions \(a_i\), \(b_i\), \(\rho _i\), \(i=1,2\), defined in (12) are concerned, we have, for \(\phi _i\in \mathcal {C}_1\), \(i=1,2\),

$$\begin{aligned}&a_1(\phi _1)=\phi ^4_1(0); \qquad b_1(\phi _1)=\phi _1(0); \qquad c_1(\phi _1,\phi _2)=\omega _1\phi ^2_1(0)\phi _2(-\Delta );\nonumber \\&\rho _1(\phi _1,\phi _2)=-\phi _1^2(0)\sqrt{1+\phi ^4_1(0)}+\omega _1\phi ^2_1(0)\phi _2(-\Delta ); \nonumber \\&a_2(\phi _2)=\phi ^2_2(0); \qquad b_2(\phi _2)=\phi ^2_2(0); \qquad c_2(\phi _2,\phi _1)=\omega _2\phi _2(0)\phi ^2_1(-\Delta ); \nonumber \\&\rho _2(\phi _2,\phi _1)=-\phi ^2_2(0)\sqrt{1+\phi _2^4(0)}+\omega _2\phi _2(0)\phi ^2_1(-\Delta )\nonumber \\&\end{aligned}$$
(29)

Point (ii) in Assumption 1 is satisfied. As far as the point (iv) in Assumption 1 is concerned, it is satisfied and, in particular, for any positive real r, we obtain \(p=\max \{r^3, 1\}\). As far as the point (iii) in Assumption 1 is concerned, the following inequalities hold, for any \(\phi _i\in \mathcal {C}_1\), \(i=1,2\),

$$\begin{aligned}&\rho _1(\phi _1,\phi _2)\le -\left( M_{a,1}(\phi _1)\right) ^4+\frac{1}{2}\vert \omega _1\vert \left( M_{a,1}(\phi _1)\right) ^4+\frac{1}{2}\vert \omega _1\vert \phi _2^2(-\Delta ); \nonumber \\&\rho _2(\phi _2,\phi _1)\le -\left( M_{a,2}(\phi _2)\right) ^2+\frac{1}{2}\vert \omega _2\vert \left( M_{a,2}(\phi _2)\right) ^2+\frac{1}{2}\vert \omega _2 \vert \phi ^4_1(-\Delta )\nonumber \\&\end{aligned}$$
(30)

Therefore, the point (iii) in Assumption 1 is satisfied with \(h=1\), \(h_d=0\) \(S_{1,0}=S_{2,0}=0\), \(S_{1,1}=S_{2,1}=1\), and the functions \(\alpha _i\), \(\sigma _{i,1}\), \(i=1,2\), of class \(\mathcal {K}_{\infty }\) defined, for \(s\in R^+\), as

$$\begin{aligned}&\alpha _1(s)=\left( 1-\frac{1}{2}\vert \omega _1\vert \right) s^4; \qquad \sigma _{1,1}(s)=\frac{1}{2}\vert \omega _1\vert s^2; \nonumber \\&\alpha _2(s)=\left( 1-\frac{1}{2}\vert \omega _2\vert \right) s^2; \qquad \sigma _{2,1}(s)=\frac{1}{2}\vert \omega _2\vert s^4 \end{aligned}$$
(31)

Let \(\sigma _i\), \(i=1,2\), be the functions of class \(\mathcal {K}_{\infty }\) defined, for \(s\ge 0\), as \(\sigma _i(s)=\sigma _{i,1}(s)\), according to (15). If the inequality holds

$$\begin{aligned} \vert \omega _1\vert +\vert \omega _2\vert <2, \end{aligned}$$
(32)

then the small-gain inequality (16) is satisfied for this example. All the hypotheses of Theorem 1 are satisfied for this example, provided that (32) holds. By Theorem 1, the feedback control law, for any chosen positive real q (see (13), (17)),

$$\begin{aligned}&u_1(t)=\left\{ \begin{array}{cc} -x_1(t)\left( x_1^2(t)+\sqrt{1+x_1^4(t)}\right) -qx_1(t), &{} \vert x_1(t)\vert>r \\ -\frac{1}{r^2}x^3_1(t)\left( x_1^2(t)+\sqrt{1+x_1^4(t)}\right) -qx_1(t), &{} \vert x_1(t)\vert \le r, \end{array} \right. \nonumber \\&\nonumber \\&u_2(t)=\left\{ \begin{array}{cc} -1-\sqrt{1+x^4_2(t)}-qx^2_2(t), &{} x^2_2(t) >r, \\ -\frac{1}{r^2}x^4_2(t)\left( 1+\sqrt{1+x^4_2(t)}\right) -qx_2^2(t), &{} x^2_2(t) \le r, \end{array} \right. \end{aligned}$$
(33)

is such that the closed-loop system (27), (33) satisfies the inequality (18), provided that the inequality (32) is satisfied. The control law (33) is memoryless, decentralized. As can be seen, since the system (27) involves time delays only in interconnections, the CLKFs, used for each subsystem, are actually CLFs defined in \(\mathcal {R}\).

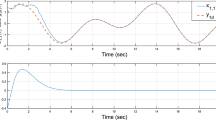
Finding controllers, by Sontag’s formula, for (27) directly with an overall CLKF would be, at least, much more complicated than the methodology here presented, since this overall CLKF should involve integral terms to cope with the time-delays. One could try, for instance, with the candidate CLKF \(V:\mathcal {R}^2\times \mathcal {Q}_2\rightarrow \mathcal {R}^+\) defined, for \(x\in \mathcal {R}^2\), \(\phi =\left[ \begin{array}{c}\phi _1\\ \phi _2\end{array} \right] \in \mathcal {Q}_2\), as \( V(x,\phi )=x^TPx+\int _{-\Delta }^0e^{\mu \theta }(\phi _1^4(\theta )+g\phi _2^2(\theta ))d\theta , \) with \(\mu ,g\) suitable positive reals and P a suitable positive definite symmetric matrix to be chosen. Then, one should prove that the points \((i)-(iv)\), Hypothesis 4, in [33], are satisfied. The analytical proof is not easy and, anyway, the resulting controller would be neither memoryless nor decentralized. Notice also that the small control property is not satisfied by subsystem 2 and \(V_2\). If one applied the Sontag’s universal formula for the controller in the subsystem 2, that controller would be not continuous whenever \(x_2(t)=0\). This would mean discontinuity of the overall feedback control law in the infinite dimensional subspace \(\left\{ \phi =\left[ \begin{array}{c}\phi _1\\ \phi _2\end{array} \right] \in \mathcal {C}_2, \ \phi _i\in \mathcal {C}_1,\ i=1,2, \ \phi _2(0)=0\right\} \). By the use of the results in [33] this discontinuity problem is overcome (the feedback control law (33) is locally Lipschitz in \(\mathcal {C}_2\)). If the disturbances \(d_i(t)\), \(i=1,2\), are bounded, then an arbitrarily small neighborhood of the origin can be reached, by increasing the control parameter q (see the inequality (18)). Simulations have been performed with \(r=1\), \(q=10\), \(\omega _1=\omega _2=0.9\), \(d_1=sin(2t)\), \(d_2(t)=cos(2t)\), \(t\ge 0\), \(x_0(\tau )=[\begin{array}{cc}1&-1\end{array}]^T\), \(\tau \in [-\Delta ,0]\), \(\Delta =1.2\). The state variables are reported in Fig. 1. As can be seen, the state variables are kept suitably bounded by the control law (33), thus validating the theoretical results. In Fig. 2 the control signals are reported. If \(u_1(t)=u_2(t)=0\), \(t\ge 0\), then simulations show divergence of the magnitude of the state variables to \(\infty \). As well, simulations show that, increasing the tuning parameter q, smaller neighborhoods of the origin are asymptotically reached. In Fig. 3, the state variables are reported with the tuning parameter choice \(q=100\). The better performance with the increased value of the parameter q is achieved at the price of an increased control effort (the control signals reach in this case a maximum absolute value close to 120).

Fig. 1
figure 1

State variables of (27), (33), with \(\Delta =1.2\), \(q=10\), \(r=1\), \(\omega _1=\omega _2=0.9\)

Full size image
Fig. 2
figure 2

Control signals (33), with \(\Delta =1.2\), \(q=10\), \(r=1\), \(\omega _1=\omega _2=0.9\)

Full size image
Fig. 3
figure 3

State variables of (27), (33), with \(\Delta =1.2\), \(q=100\), \(r=1\), \(\omega _1=\omega _2=0.9\)

Full size image

Remark 5

In general, when delays appear in the subsystems, CLKFs are involved for subsystems and checking Assumption 1 becomes more difficult, even in the linear case (the proposed control law is nonlinear also in this case), because of involved integral terms (see [14]). Numerical software tools may often be used to provide a sufficient confidence about satisfaction of inequalities involved in Assumption 1. Alternative conditions, which however require the satisfaction of the small control property, may be used in the disturbance-free case (see Hypothesis 8 in [34]). These alternative conditions avoid the use of the \(M_a\) functionals and may return to be easier to be checked, than the ones in Assumption 1, provided that the small control property holds. These alternative conditions will be topic of forthcoming investigation, as far as the control design by small-gain arguments is concerned.

5 Conclusions

Since finding a CLKF, and a related controller, for retarded systems, is in general not an easy task, this chapter has the aim to provide a constructive methodology for the design of controllers for a class of systems which are in the interconnection form. The approach makes use of a CLKF for each subsystem and of a suitably modified Sontag’s universal formula. By suitable hypotheses, the resulting closed-loop system is proved to be ISpS with respect to actuator disturbances, exploiting a small-gain condition which copes with time delays. Here time delays in both subsystems and interconnections are dealt with, and a significant simplification of the control design is achieved, with respect to the case of control design by an overall CLKF. For instance, when the delays affect only the interconnections, the CLKF for each subsystem becomes a CLF, defined on finite dimensional Euclidean spaces rather than on infinite dimensional Banach spaces, with evident improvement towards simplification. On the other hand, a small gain condition is required to be satisfied. A major goal of this work is to make it possible to exploit, in a unified framework, some existing results in the past literature, at the aim of the controller design. We still assume the strict matching condition (i.e., disturbance belonging to the input space and adding to the control law) in the chapter. This restrictive assumption may be removed through systematic use of backstepping and small-gain techniques. An interesting research topic may be the application of the methodology here shown to networked systems, for instance by the use of the small-gain results provided in [13, 42]. This would further simplify the design of decentralized, input-to-state practically stabilizing controllers, provided that a suitable network small-gain condition can be satisfied.