Linear Approximations of Turbulent Moments of Horizontal Velocity and Temperature Fluctuations Within a Forced Convection Sublayer of the Atmospheric Surface Layer

Abstract

In the convective surface layer a heavy forced convection sublayer is distinguished. The turbulent moments of this sublayer depend mainly on the buoyance flux. It is shown that “linear” approximations are effective for describing turbulent moments of this sublayer. These approximations correspond to truncated Taylor series expansions in a modified height, that include only two terms. The first-order expansion terms do not take into account the wind and represent the free convection limits of the Monin-Obukhov similarity theory. The second-order expansion terms take into account the wind and its effect on the convection. The proposed approximations are compared with the experimental data.

1 Introduction

The classical similarity theory of the atmospheric surface layer was first formulated in [1,2,3] for approximation of the first-order turbulent moments.

It is significant that the Monin-Obukhov similarity theory allows us to find turbulent moments of a higher order under no-wind conditions. In particular, second-order turbulent moments were calculated in [4,5,6,7]. Approximations of the turbulent moments of the surface layer, corresponding to no-wind conditions, are called free-convection limits. For them, the parameter $z/\left| {L_{ * } } \right| = \infty$, where $z$ is the height of the level above the underlying surface; $\left| {L_{ * } } \right| = 0$ is the Monin-Obukhov length parameter.

The free-convection limits of the convective surface layer can be used as a first-order approach in the construction of linear approximations of turbulent moments in a sufficiently heavy region $\upzeta_{0} \le z/\left| {L_{ * } } \right| < \infty$, where $\upzeta_{0} \approx 4 \cdot 10^{ - 2}$. Linear approximations of turbulent moments complement the free-convective limits by the components that take into account the presence of wind. Therefore, the region $\upzeta_{0} \le z/\left| {L_{ * } } \right| < \infty$ should be interpreted as a sublayer of forced convection.

In the present work, linear approximations are used to describe known observational data. A comparison with experimental data indicates the existence of a forced convection sublayer with a lower boundary $\upzeta_{0} \approx 4 \cdot 10^{ - 2}$.

2 Local Parameters of Friction Velocity and Buoyancy Flux

Let $t$ be time and $x$, $y$, $z$ be a Cartesian coordinate system placed at the underlying surface $z = 0$ so that the $z$ axis is opposite to gravitational acceleration $g$.

We assume that $u = u(x,y,z,t)$ and $w = w{\kern 1pt} {\kern 1pt} (x,y,z,t)$ are the velocity vector components along the horizontal and vertical axes; $\bar{u} = \bar{u}(z)$ is the mean value of the horizontal wind velocity vector along the $x$ axis; and $u^{{\prime }} (x,y,z,t) = u(x,y,z,t) - \bar{u}$ is the fluctuation of the horizontal velocity.

It is supposed that $\Theta =\Theta (x,y,z,t)$ is the potential air temperature and $\Theta _{0}$ is a constant mean value of the potential temperature at the upper boundary of the surface layer [8]. A potential temperature fluctuation $\Theta ^{{\prime }} (x,y,z,t) =\Theta (x,y,z,t) -\Theta _{0}$ and a dimensionless potential-temperature fluctuation $\uptheta(x,y,z,t) =\Theta ^{{\prime }} (x,y,z,t)/\Theta _{0}$ are introduced following [8]. The quantity $g\uptheta(x,y,z,t)$ denotes local buoyancy [9].

Let us assume that

$$ U_{ * } = \mathop {\lim }\limits_{z \to 0} \left( { - \overline{{u^{{\prime }} w^{{\prime }} }} } \right)^{1/2} > 0,\quad gS_{\uptheta} = \mathop {\lim }\limits_{z \to 0} \overline{{g\uptheta w}} > 0 $$

(1)

where $U_{ * }$ and $gS_{\uptheta}$ have dimensions $[U_{ * } ] = {\text{m}}/{\text{s}}$ and $\left[ {gS_{\uptheta} } \right] = {\text{m}}^{2} /{\text{s}}^{3}$.

For application of the similarity theory in the convective surface layer, we use three key parameters: $z$, $gS_{\uptheta}$ and $U_{ * }$. The parameter of height $z$ is a variable; the buoyancy flux $gS_{\uptheta}$ and friction velocity $U_{ * }$ parameters are constants.

The parameters $U_{ * } > 0$ and $gS_{\uptheta} > 0$ allow us to introduce constant parameters of length $L_{ * } < 0$ and buoyancy $g\Theta _{ * } > 0$ such that

$$ L_{ * } = - \frac{{U_{ * }^{3} }}{{k_{v} gS_{\uptheta} }},\quad g\Theta _{ * } = \frac{{gS_{\uptheta} }}{{U_{ * } }} $$

(2)

where $k_{v} = 0.4$ is the von Kármán constant.

We suppose that $H$ is the mean heat flux from the underlying surface, $\uprho_{ 0}$ is the mean air density at the underlying surface, $c_{P}$ is the specific heat capacity of dry air and $T_{ * }$ is the temperature parameter of the Monin-Obukhov theory.

Then, taking into account (2), it is found that

$$ gS_{\uptheta} = \left( {\frac{g}{{\Theta _{0} }}} \right)\frac{H}{{c_{P}\uprho_{0} }},\quad g\Theta _{ * } = - \left( {\frac{g}{{\Theta _{0} }}} \right)T_{ * } ,\quad T_{ * } = -\Theta _{ * }\Theta _{0} $$

(3)

Relationships (3) indicate the proportionality of the key parameters $gS_{\uptheta}$ and $g\Theta _{ * }$ to the conventional parameters $H$ and $T_{ * }$ of the Monin-Obukhov similarity theory.

3 Monin-Obukhov Similarity Theory and Free-Convection Limits of the Surface Layer

We examine a convective surface layer in conditions of free convection, $U_{ * } = 0$. In this case, only two key parameters $z$ and $gS_{\uptheta}$ are finite.

In accordance with [3, 6], the first and second moments of buoyancy and the second moment of horizontal velocity fluctuation have the forms

$$ \frac{\partial }{\partial z}\overline{{g\uptheta}} = -\uplambda_{\uptheta} z^{ - 4/3} (gS_{\uptheta} )^{2/3} $$

(4)

$$ \overline{{(g\uptheta)^{2} }} =\uplambda_{{\uptheta \uptheta }} (gS_{\uptheta} )^{4/3} z^{ - 2/3} ,\quad \overline{{(u^{{\prime }} )^{2} }} =\uplambda_{uu} (gS_{\uptheta} )^{2/3} z^{2/3} $$

(5)

where $\uplambda_{\uptheta} = 1$ from [6], $\uplambda_{{\uptheta \uptheta }} = 1.8$ from [10] and $\uplambda_{uu}$ is a positive constant.

According to [11,12,13], the second relationship of (5) is formed by a stochastic ensemble of convective jets.

It is supposed that that $K_{h}$ is the coefficient of turbulent heat transport. Under the free convection regime, the buoyance flux does not change with the height. In accordance with the Boussinesq gradient relationships and the similarity equality (4), we obtain

$$ - K_{h} \frac{\partial }{\partial z}g\overline{\uptheta} = \overline{{g\uptheta w}} = gS_{\uptheta} ,\quad K_{h} = \frac{1}{{\uplambda_{\uptheta} }}(gS_{\uptheta} )^{1/3} z^{4/3} $$

(6)

Let us consider the convective surface layer in forced convection with low winds $0 \ne U_{ * } < < 1$. In this case, all three key parameters $z$, $gS_{\uptheta}$ and $U_{ * }$ are finite.

To construct free-convection limits of the Monin-Obukhov similarity theory, it is suggested that the turbulent moments in low wind $0 \ne U_{ * } < < 1$ are the same as those when there is no wind, $U_{ * } = 0$.

Substituting (2) and (3) into the relationship for the first buoyancy moment (4) leads to the equality

$$ - \frac{{k_{v} z}}{{g\Theta _{ * } }}\frac{\partial }{\partial z}\overline{{g\uptheta}} = - \frac{{k_{v} z}}{{\Theta _{ * } }}\frac{\partial }{\partial z}\overline{\uptheta} = - \frac{{k_{v} z}}{{\left| {T_{ * } } \right|}}\frac{\partial }{\partial z}\overline{\Theta } =\upalpha_{\uptheta} \left( {z/\left| {L_{ * } } \right|} \right)^{ - 1/3} $$

(7)

where $\upalpha_{\uptheta} = k_{v}^{4/3}\uplambda_{\uptheta} \approx 0.3$ is a positive constant (see [5, 6, 14]).

The transformation of (6), with (2) and (3) taken into account, leads to the equality

$$ \frac{{K_{h} }}{{U_{ * } \left| {L_{ * } } \right|}} = \frac{1}{{\lambda_{\uptheta} k_{v}^{1/3} }}\;\left( {z/\left| {L_{ * } } \right|} \right)^{4/3} $$

(8)

The second moments of buoyance and horizontal velocity fluctuations (5) are transformed by taking into account (2) and (3). Thus

$$ \frac{{\overline{{(g\uptheta)^{2} }} }}{{(g\Theta _{ * } )^{2} }} = \frac{{\overline{{\uptheta^{2} }} }}{{\Theta _{ * }^{2} }} = \frac{{\overline{{(\Theta ^{{\prime }} )^{2} }} }}{{\left| {T_{*} } \right|^{2} }} =\upalpha_{{\uptheta \uptheta }}^{2} \left( {z/\left| {L_{ * } } \right|} \right)^{ - 2/3} $$

(9)

$$ \frac{{\overline{{(u^{{\prime }} )^{2} }} }}{{U_{ * }^{2} }} = \alpha_{uu}^{2} \left( {z/\left| {L_{ * } } \right|} \right)^{2/3} $$

(10)

where the constant coefficients $\upalpha_{{\uptheta \uptheta }}^{ 2} = k_{v}^{2/3}\uplambda_{{\uptheta \uptheta }} \approx 1$ from the data of [7, 14] and $\alpha_{uu} = 5.5$ from the data of [15].

It is assumed that $K_{m}$ is the coefficient of turbulent transport of horizontal momentum; $P_{t} = K_{m} /K_{h}$ is the turbulent Prandtl number. According to [16, 17], it is assumed that $P_{t} = 0.76$.

Within the surface layer, the buoyance and momentum fluxes do not change with the height. In accordance with the Boussinesq gradient relationships, the relationship for momentum flux can be written as

$$ K_{m} = K_{h} P_{t} ,\quad K_{m} \frac{\partial }{\partial z}\bar{u} = U_{ * }^{2} $$

(11)

Substituting (8) into the relationships (11), we find the relationship for the free convection limit of horizontal velocity

$$ - \frac{{k_{v} z}}{{\left| {U_{ * } } \right|}}\frac{\partial }{\partial z}\bar{u} =\upalpha_{u} \left( {z/\left| {L_{ * } } \right|} \right)^{ - 1/3} ,\quad\upalpha_{u} =\upalpha_{\uptheta} /P_{t} =\uplambda_{\uptheta} k_{v}^{4/3} /P_{t} $$

(12)

When $P_{t} = 0.76$ and $\upalpha_{\uptheta} = 0.3$, the relationship (12) gives $\upalpha_{u} = 0.4$.

The relationships (7), (9), (10) and (12) are the free convection limits of the bouyance and horizontal velocity.

4 Linear Approximations of the Monin-Obukhov Universal Similarity Functions, the First and Second Moments of the Surface Layer

Length parameter $L_{ * } \le 0$ is used to construct the dimensionless height $z/\left| {L_{ * } } \right|$. The region $\zeta_{0} < z/\left| {L_{ * } } \right| < \infty$ is denoted as a forced-convection sublayer with moderate wind. We suppose that $\upzeta_{0} \approx 4 \cdot 10^{ - 2}$. In the forced-convection sublayer a free-convection area $1 < < z/\left| {L_{ * } } \right|$ is also distinguished.

It can be assumed that the dimensionless forms of the equations for the first (7) and second (9) buoyancy moments in the forced-convection sublayer within $4 \cdot 10^{ - 2} < z/\left| {L_{ * } } \right| < \infty$ can be written as

$$ - \frac{{k_{v} z}}{{\left| {T_{ * } } \right|}}\frac{\partial }{\partial z}\overline{\Theta } =\upalpha_{\uptheta} \left( {z/\left| {L_{ * } } \right|} \right)^{ - 1/3} F_{\uptheta} \left( {z/\left| {L_{ * } } \right|} \right),\quad \mathop {\lim }\limits_{{z/\left| {L_{ * } } \right| \to \infty }} F_{\uptheta} \left( {z/\left| {L_{ * } } \right|} \right) = 1 $$

(13)

$$ \frac{{\overline{{(\Theta ^{{\prime }} )^{2} }} }}{{\left| {T_{*} } \right|^{2} }} =\upalpha_{{\uptheta \uptheta }}^{ 2} \left( {z/\left| {L_{ * } } \right|} \right)^{ - 2/3} F_{{\uptheta \uptheta }}^{ 2} \left( {z/\left| {L_{ * } } \right|} \right),\quad \,\mathop {\lim }\limits_{{z/\left| {L_{ * } } \right| \to \infty }} F_{{\uptheta \uptheta }}^{ 2} \left( {z/\left| {L_{ * } } \right|} \right) = 1 $$

(14)

It should be noted that the coefficient $\upalpha_{\uptheta} = k_{v}^{4/3}\uplambda_{\uptheta} \approx 0.3$ from the data of [5, 6, 14] and the coefficient $\upalpha_{{\uptheta \uptheta }}^{ 2} \approx 0.95$ from the data of [18,19,20].

The first and second moments of horizontal velocity can be defined as the forms that are similar to the first (13) and second (14) moments of buoyance:

$$ - \frac{{k_{v} z}}{{U_{ * } }}\frac{\partial }{\partial z}\bar{u} =\upalpha_{u} \left( {z/\left| {L_{ * } } \right|} \right)^{ - 1/3} F_{u} \left( {z/\left| {L_{ * } } \right|} \right),\quad \mathop {\lim }\limits_{{z/\left| {L_{ * } } \right| \to \infty }} F_{u} \left( {z/\left| {L_{ * } } \right|} \right) = 1 $$

(15)

$$ \frac{{\overline{{(u^{{\prime }} )^{2} }} }}{{\left| {U_{*} } \right|^{2} }} =\upalpha_{uu}^{ 2} \left( {z/\left| {L_{ * } } \right|} \right)^{2/3} F_{uu}^{ 2} \left( {z/\left| {L_{ * } } \right|} \right),\quad \,\mathop {\lim }\limits_{{z/\left| {L_{ * } } \right| \to \infty }} F_{uu}^{ 2} \left( {z/\left| {L_{ * } } \right|} \right) = 1 $$

(16)

Linear approximations of the moments of horizontal velocity and potential temperature fluctuations are constructed in the forced-convection sublayer. The first-order expansion terms of linear approximations are chosen according to the free convective limits of the Monin-Obukhov similarity theory under no-wind conditions, $U_{ * } = 0$. The second-order expansion terms of linear approximations will then describe profiles of turbulent moments with the presence of wind, $U_{ * } \ne 0$.

Limiting ourselves to a linear Taylor expansion of $F_{\uptheta} (z/\left| {L_{ * } } \right|)$, $F_{u} (z/\left| {L_{ * } } \right|)$, $F_{{\uptheta \uptheta }} \left( {z/\left| {L_{ * } } \right|} \right)$ and $F_{uu} \left( {z/\left| {L_{ * } } \right|} \right)$ in parameter $\left( {z/\left| {L_{ * } } \right|} \right)^{ - 2/3}$, we obtain

$$ - \frac{{k_{v} z}}{{\left| {T_{ * } } \right|}}\frac{{\partial }}{{{\partial }z}}\overline{\Theta } =\upalpha_{\uptheta} \left( {z/\left| {L_{ * } } \right|} \right)^{ - 1/3} \left\{ {1 -\upbeta_{\uptheta} \left( {z/\left| {L_{ * } } \right|} \right)^{ - 2/3} } \right\} $$

(17)

$$ - \frac{{k_{v} z}}{{U_{ * } }}\frac{{\partial }}{{{\partial }z}}\overline{u} =\upalpha_{u} \left( {z/\left| {L_{ * } } \right|} \right)^{ - 1/3} \left\{ {1 -\upbeta_{u} \left( {z/\left| {L_{ * } } \right|} \right)^{ - 2/3} } \right\} $$

(18)

$$ \frac{{\overline{{(\Theta ^{{\prime }} )^{2} }} }}{{\left| {T_{*} } \right|^{2} }} = \frac{{\upsigma_{\uptheta}^{ 2} }}{{\left| {T_{*} } \right|^{2} }} =\upalpha_{{\uptheta \uptheta }}^{ 2} \left( {z/\left| {L_{ * } } \right|} \right)^{ - 2/3} \left\{ {1 -\upbeta_{{\uptheta \uptheta }} \left( {z/\left| {L_{ * } } \right|} \right)^{ - 2/3} } \right\} $$

(19)

$$ \frac{{\overline{{(u^{{\prime }} )^{2} }} }}{{U_{ * }^{2} }} = \frac{{\upsigma_{u}^{ 2} }}{{U_{ * }^{2} }} =\upalpha_{uu}^{ 2} \left( {z/\left| {L_{ * } } \right|} \right)^{2/3} \left\{ {1 +\upbeta_{uu} \left( {z/\left| {L_{ * } } \right|} \right)^{ - 2/3} } \right\} $$

(20)

where $\upsigma_{\uptheta}$, $\upsigma_{u}$ are variances of potential-temperature fluctuation and horizontal velocity; $\upbeta_{\uptheta}$, $\upbeta_{u}$, $\upbeta_{{\uptheta \uptheta }}$, $\upbeta_{uu}$ are constant coefficients.

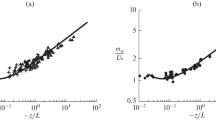
Figure 1a presents a comparison of the linear approximation of Monin-Obukhov similarity theory (17) at $\upalpha_{\uptheta} = 0.3$, $\upbeta_{\uptheta} = 3 \cdot 10^{ - 2}$ with the field data [21]. It shows that the approximation (17) slightly overestimates this field data within the free-convection sublayer.

Fig. 1.

Comparison of linear approximations (17) and (18) with empirical values of the function $- k_{v} z\left| {T_{*} } \right|^{ - 1} \partial \bar{\Theta}/{\partial }z$ and $- k_{v} z\left| {U_{*} } \right|^{ - 1} {\partial }\bar{u}/{\partial }z$ from [21]. The solid line (a) corresponds to approximation (17) with coefficients $\upalpha_{\uptheta} = 0.3$ and $\upbeta_{\uptheta} = 3 \cdot 10^{ - 2}$. The solid line (b) corresponds to approximation (18) with coefficients $\upalpha_{u} = 0.4$ and $\upbeta_{u} = 3 \cdot 10^{ - 2}$.

Figure 1b presents a comparison between the field data [21] and the linear approximation of Monin-Obukhov similarity theory (18) at $\upalpha_{u} = 0.4$ and $\upbeta_{u} = 3 \cdot 10^{ - 2}$.

A comparison between the field data [22] of the dimensionless potential temperature variance $\upsigma_{\uptheta} /\left| {T_{ * } } \right|$ and its linear approximation in the form of (19) with $\upalpha_{{\uptheta \uptheta }}^{ 2} = 0.95$, $\upbeta_{{\uptheta \uptheta }} = 0.06$ is shown in Fig. 2a.

Fig. 2.

Comparison of linear approximations (19) and (20) with empirical values of $\upsigma_{\uptheta} /\left| {T_{ * } } \right|$ from [22] and $\upsigma_{u} /\left| {U_{ * } } \right|$ from [20]. The solid line (a) corresponds to approximation (19) with coefficients $\upalpha_{{\uptheta \uptheta }}^{ 2} = 0.95$ and $\upbeta_{{\uptheta \uptheta }} = 0.06$. The solid line (b) corresponds to approximation (20) with coefficients $\upalpha_{uu} = 5.5$ and $\upbeta_{uu} = 0.06$.

A comparison between the field data [20] of the dimensionless horizontal velocity variance $\upsigma_{u} /\left| {U_{ * } } \right|$ and its linear approximation in the form of (20) with $\upalpha_{u} = 5.5$ and $\upbeta_{uu} = 0.06$ is shown in Fig. 2b.

The results, that are presented in Fig. 1, show that the linear approximations (17) and (18) are correct within the range of $2.7 \cdot 10^{ - 2} < z/\left| {L_{ * } } \right| < \infty$.

Figure 2 shows that the linear approximations (19) and (20) describe the empirical values within the range $4 \cdot 10^{ - 2} < z/\left| {L_{ * } } \right| < \infty$ fairly well.

We choose $\upzeta_{0} \approx 4 \cdot 10^{ - 2}$ as the lower boundary of the forced convection sublayer. Thus, the results of comparisons in Figs. 1 and 2 prove that the linear approximations (17)–(20) correspond to turbulent moments within the forced convection sublayer, $4 \cdot 10^{ - 2} < z/\left| {L_{ * } } \right| < \infty$.

Another expansion, which is similar to (17)–(20), and its comparison with experimental data sets are shown in [23].

Alternative global approaches that are using the local similarity theory are presented in [24,25,26,27].

Modern comprehensive field data of atmospheric surface layer parameters and techniques of its processing are described in [28, 29].

5 Conclusion

The analysis of the known experimental data shows that in the convective surface layer there is a heavy sublayer of forced convection, with a clearly defined lower boundary. For describing turbulent moments of this sublayer, the Monin-Obukhov similarity theory is used. The universal functions of the similarity theory are expanded to truncated Taylor series expansions, that include only two terms.

The first-order expansion terms correspond to the free-convection limits of the Monin-Obukhov theory in the static atmosphere. The second-order expansion terms take into account the presence of wind and its effect on convection. The presented results can be used as a basis for construction of a layered structure of the atmospheric surface layer.

This study was supported by the Russian Foundation for Basic Research, grant 17-05-01116.