INTRODUCTION

The surface layer of the atmosphere is a thin air layer about 100 m thick in contact with the underlying land of water surface. In the case when the air is warmed by heat flow entering into the atmosphere through its bottom boundary, the surface layer is called the surface convective layer.

The classical theory of the similarity of atmospheric surface layer was first presented in [4, 5] for the approximation of the first turbulent moments of velocity and temperature. Within the framework of the Monin–Obukhov theory, the height of the surface layer \(h\) is assumed infinite, because h is not among the parameters determining the similarity.

Let z be the height of the level over the underlying surface; \({{L}_{*}} < 0\) is Monin–Obukhov length parameter [6]. We introduce dimensionless height \({{\xi }} = {z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}}\). Now the vertical length of the convective surface layer satisfies the inequalities \(0 \leqslant {{\xi }} = {z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}} < \infty \).

Note that \(\left| {{{L}_{*}}} \right| = 0\) when there is no wind and the heat flow at the underlying surface is positive [6]. Therefore, the domain \(\xi \gg 1\) corresponds to free convection regime. The Monin–Obukhov similarity theory is known to allow one to find also turbulent moments of higher order in the domain \(\xi \gg 1\). In particular, approximations of second-order turbulent moments are given in [13, 21]. The approximations of turbulent moments of the surface layer for the case \(\xi = {z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}} = \infty \) are called free-convection limits.

In this study, in the convective atmospheric surface layer, the top part of the domain \({{\xi }_{0}} \leqslant \xi = {z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}} < \infty \) is identified with fixed bottom boundary \({{\xi }_{0}} \approx 6 \times {{10}^{{ - 2}}}\). Following the approach [3], the turbulent moments in the domain \({{\xi }_{0}} \leqslant \xi < \infty \) are approximated with the use of universal “linear” forms, consisting of two summands. The first summands of the “linear” approximations correspond to free-convection limits in the domain \(\xi \gg 1\). The second summands of the “linear” approximations are obtained by expansion of universal function into Taylor series with respect to parameter \({{\xi }^{{ - 1}}}\) and include wind. Therefore, the identified domain \({{\xi }_{0}} \leqslant \xi < \infty \) corresponds to the sublayer of forced convection.

Consider a family of turbulent moments in which subscript i characterizes the chosen turbulent moment. The proposed linear approximations can be used to determine the point of extremum \({{{{\xi }}}_{{0i}}}\) for the vertical profile of the ith turbulent moment. The existence of the sublayer of forced convection with a fixed bottom boundary means that the extreme points of all turbulent profiles coincide, i.e., \({{{{\xi }}}_{{0i}}} = {{{{\xi }}}_{0}}\). Note that in the domain \(0 < {{\xi }} < {{{{\xi }}}_{0}}\), “linear” approximations of the moments disagree with experimental data and have no physical sense. Therefore, the extreme point \({{{{\xi }}}_{0}}\) should be regarded as the bottom boundary of the forced convection sublayer.

The existence of parameter \({{{{\xi }}}_{0}}\), which is common for all turbulent profiles, considerably reduces the number of unknown coefficients in “linear” approximations. It can be shown that the a priori specification of extreme point \({{{{\xi }}}_{0}}\) allows one to calculate all unknown coefficients of “linear” approximations. In other words, the notion of a sublayer of forced convection with a fixed boundary leads to the construction of a one-parameter family of approximations, which depends on an unknown parameter \({{{{\xi }}}_{0}}\). The a priori value \({{{{\xi }}}_{0}}\) should be set in such a way as to meet the condition of acceptable agreement with the experimental data. The value \({{{{\xi }}}_{0}} \approx 6 \times {{10}^{{ - 2}}}\) implements this condition.

The analytical construction of a universal one-parameter family of “linear” approximations, corresponding to field measurements of second turbulent momenta of the sublayer of forced convection, is the main result of this study.

LOCAL PARAMETERS OF THE DYNAMIC VELOCITY, BUOYANCY FLOW

Let \(t\) be the time; \(x\), \(y\), \(z\) is a rectangular coordinate system on the underlying surface \(z = 0\), \(z\) axis is directed opposite to the gravity acceleration \(~{\text{g}}\).

Suppose that \(u = u\left( {x,y,z,t} \right)\), \({v} = {v}\left( {x,y,z,t} \right)\), and \(w = w\left( {x,y,z,t} \right)\) are components of velocity vector along x, y, and z, respectively. Suppose that \(\bar {u} = \bar {u}\left( z \right)\) is the mean value of the horizontal flow velocity along x axis; \({\bar {v}} = 0\) and \(\bar {w} = 0\) are the values of the horizontal and vertical velocities along y and z axes, respectively. The equality \(\bar {w} = 0\) follows from the continuity equation of the system of convection theory [1, 19] and the periodicity conditions on the vertical boundaries of the domain. Now \(u{\kern 1pt} '\left( {x,y,z,t} \right) = u\left( {x,y,z,t} \right) - \bar {u}\left( z \right)\), \({v}{\kern 1pt} ' = {v}\left( {x,y,z,t} \right)\), and \(w{\kern 1pt} ' = w\left( {x,y,z,t} \right)\) are perturbations of velocity along axes x, y, and z, respectively.

We assume that \(T = T\left( {x,y,z,t} \right)\) is air temperature; \(p = p\left( {x,y,z,t} \right)\) is pressure; p0 = 105 Pa is the standard air pressure on the underlying surface; \({{R}_{d}}\) and \({{c}_{P}}\) are the gas constant and the specific heat capacity of dry air, respectively. Let \({{\Theta }} = T{{({p \mathord{\left/ {\vphantom {p {{{p}_{0}}}}} \right. \kern-0em} {{{p}_{0}}}})}^{{ - {{{{R}_{d}}} \mathord{\left/ {\vphantom {{{{R}_{d}}} {{{c}_{P}}}}} \right. \kern-0em} {{{c}_{P}}}}}}}\) be the potential air temperature; \({{{{\Theta }}}_{0}} = {\text{const}}\) is the constant value of mean potential temperature at the upper boundary of the surface layer [19]. The pulsation of the potential temperature \({{\Theta }}_{a}^{'}\left( {x,y,z,t} \right) = {{\Theta }}\left( {x,y,z,t} \right) - {{{{\Theta }}}_{0}}\) and the dimensionless pulsation of the potential temperature \({{{{\theta }}}_{a}}\left( {x,y,z,t} \right) = {{{{\Theta }}_{a}^{'}\left( {x,y,z,t} \right)} \mathord{\left/ {\vphantom {{{{\Theta }}_{a}^{'}\left( {x,y,z,t} \right)} {{{{{\Theta }}}_{0}}}}} \right. \kern-0em} {{{{{\Theta }}}_{0}}}}\) are defined in accordance with [19]. These values are close to the fluctuations and dimensionless fluctuations of the temperature \(T\). The value \({\text{g}}{{{{\theta }}}_{a}}\left( {x,y,z,t} \right)\) will be referred to as local “adiabatic” buoyancy [22].

In the classical Monin–Obukhov theory, the velocity friction \({{U}_{*}} > 0\) is specified as

$${{U}_{*}} = \mathop {{\text{lim}}}\limits_{z{\kern 1pt} \to {\kern 1pt} 0} {{\left( { - \overline {u{\kern 1pt} 'w{\kern 1pt} '} } \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} > 0,$$
(1)

where the dimension of \({{U}_{*}}\) is \(\left[ {{{U}_{*}}} \right] = {{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. \kern-0em} {\text{s}}}\) . The definition (1) is in agreement with the equation of turbulent kinetic energy in a one-dimensional flow (e.g., [11]).

We introduce a parameter of “adiabatic” buoyancy flux on the underlying surface \({\text{g}}{{S}_{{{\theta }}}} > 0\) and a parameter of turbulent buoyancy \({\text{g}}{{{{\Theta }}}_{*}} < 0\), assuming that

$${\text{g}}{{S}_{{{\theta }}}} = \mathop {{\text{lim}}}\limits_{z \to 0} \overline {{\text{g}}{{{{\theta }}}_{a}}w} > 0,\,\,\,\,{\text{g}}{{{{\Theta }}}_{*}} = \frac{{{\text{g}}{{S}_{{{\theta }}}}}}{{{{U}_{*}}}} < 0,$$
(2)

\({\text{g}}{{S}_{{{\theta }}}}\) and \({\text{g}}{{{{\Theta }}}_{*}}\) have dimensions \(\left[ {{\text{g}}{{S}_{{{\theta }}}}} \right] = {{{{{\text{m}}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{{\text{m}}}^{{\text{2}}}}} {{{{\text{s}}}^{3}}}}} \right. \kern-0em} {{{{\text{s}}}^{3}}}}\) \(\left[ {{\text{g}}{{\Theta }_{*}}} \right] = {{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {{{{\text{s}}}^{2}}}}} \right. \kern-0em} {{{{\text{s}}}^{2}}}}\).

Let \(H\) be the mean heat flow entering into the atmosphere from the underlying surface; \({{{{\rho }}}_{0}}\) is the mean air density on the underlying surface; \({{T}_{*}} < 0\) is the temperature parameter in Monin–Obukhov theory. Now, considering (2), we have

$$\begin{gathered} {\text{g}}{{S}_{{{\theta }}}} = \left( {\frac{{\text{g}}}{{{{{{\Theta }}}_{0}}}}} \right)\frac{H}{{{{c}_{P}}{{{{\rho }}}_{0}}}},\,\,\,\,{\text{g}}{{{{\Theta }}}_{*}} = \left( {\frac{{\text{g}}}{{{{{{\Theta }}}_{0}}}}} \right){{T}_{*}}. \\ {{T}_{*}} = {{{{\Theta }}}_{*}}{{{{\Theta }}}_{0}}. \\ \end{gathered} $$
(3)

Equalities (3) indicate to the proportionality of the governing parameters \({\text{g}}{{S}_{{{\theta }}}}\) and \({\text{g}}{{{{\Theta }}}_{*}}\) to the conventional parameters of the Monin–Obukhov similarity theory \(H\) and \({{T}_{*}}\).

As shown in [3], the use of parameters \({\text{g}}{{S}_{{{\theta }}}}\) and \({\text{g}}{{{{\Theta }}}_{*}}\) instead of \(H\) and \({{T}_{*}}\) is more effective theoretically and does not influence the processing and use of experimental data. Therefore, the theory of similarity describes the surface layer of dry air with the use of three basic parameters: \(z\), \({\text{g}}{{S}_{{{\theta }}}}\), and \({{U}_{*}}\). The parameter of elevation \(z\) is variable, while the parameters of buoyancy flux \({\text{g}}{{S}_{{{\theta }}}}\) and dynamic velocity \({{U}_{*}}\) are constant.

Consider the surface layer of humid atmosphere. Let \(q = q\left( {x,y,z,t} \right)\) be air humidity and \(\bar {q} = \bar {q}\left( z \right)\) be the mean humidity. Following [5] and [18],   we    also     introduce humidity fluctuations: \(q{\kern 1pt} '\left( {x,y,z,t} \right) = q\left( {x,y,z,t} \right) - \bar {q}\left( z \right)\).

Based on an analogy with (1), (2), we introduce a parameter of modified humidity flux on the underlying surface \({\text{g}}{{S}_{q}}\) and a modified humidity parameter \({\text{g}}{{q}_{*}}\). Now we have:

$${\text{g}}{{S}_{q}} = \mathop {{\text{lim}}}\limits_{z \to 0} \overline {{\text{g}}qw} = \mathop {{\text{lim}}}\limits_{z \to 0} \overline {{\text{g}}q{\kern 1pt} 'w{\kern 1pt} '} > 0,\,\,\,\,{\text{g}}{{q}_{*}} = - \frac{{{\text{g}}{{S}_{q}}}}{{{{U}_{*}}}} < 0.$$
(4)

Here \({\text{g}}{{S}_{q}}\) and \({\text{g}}{{q}_{*}}\) have dimensions \(\left[ {{\text{g}}{{S}_{q}}} \right] = {{{{{\text{m}}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{{\text{m}}}^{{\text{2}}}}} {{{{\text{s}}}^{3}}}}} \right. \kern-0em} {{{{\text{s}}}^{3}}}}\) and \(\left[ {{\text{g}}{{q}_{*}}} \right] = {{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {{{{\text{s}}}^{2}}}}} \right. \kern-0em} {{{{\text{s}}}^{2}}}}\).

As follows from definition (4), the dimensionless parameter \({{q}_{*}}\) is identical to the humidity parameter in the classical Monin–Obukhov similarity theory, defined, e.g., according to [18].

The parameters \({\text{g}}{{S}_{{{\theta }}}} > 0\), \({\text{g}}{{S}_{q}} \geqslant 0\), and \({{U}_{*}} > 0\) allow us to introduce a constant parameter of length for humid atmosphere \(L_{*}^{{v}} < 0\). Now, following, e.g., [10] and [18], we have

$$L_{*}^{{v}} = - \frac{{U_{*}^{3}}}{{{{k}_{{v}}}\left( {{\text{g}}{{S}_{{{\theta }}}} + 0.61{\text{og}}{{S}_{q}}} \right)}},$$
(5)

\({{k}_{{v}}} = 0.4\) is Carman constant.

Hereafter, we will use the approximation of a small modified moisture flux \(0 \leqslant {\text{g}}{{S}_{q}} \ll 1.64{\text{g}}{{S}_{{{\theta }}}}\). This approximation is valid

(a) over dry enough land areas with intense convective heat flux and low evaporation;

(b) over water surfaces under the conditions in which the buoyancy flux is determined mostly by evaporation.

Indeed, let \({{L}_{W}} = 2260\) kJ/kg be the specific heat of water vaporization, \({{c}_{p}} = 1.005 \times {{10}^{3}}\) J/(kg K) is the specific heat of dry air, \({{\Theta }_{0}} \approx 300\,{\text{K}}\) is the mean value of potential temperature, then \({{{{L}_{W}}} \mathord{\left/ {\vphantom {{{{L}_{W}}} {\left( {{{c}_{P}}{{\Theta }_{0}}} \right)}}} \right. \kern-0em} {\left( {{{c}_{P}}{{\Theta }_{0}}} \right)}} \approx 7.5\). Therefore, we can assume that \(0 \leqslant {\text{g}}{{S}_{q}} \ll {{1.64~{{L}_{W}}} \mathord{\left/ {\vphantom {{1.64~{{L}_{W}}} {\left( {{{c}_{P}}{{{{\Theta }}}_{0}}} \right){\text{g}}{{S}_{q}}}}} \right. \kern-0em} {\left( {{{c}_{P}}{{{{\Theta }}}_{0}}} \right){\text{g}}{{S}_{q}}}} \approx 1.64{\text{ g}}{{S}_{{{\theta }}}}\). The obtained inequality proves the assumption made above.

In the approximation \(0 \leqslant {\text{g}}{{S}_{q}} \ll 1.64~{\text{g}}{{S}_{{{\theta }}}}\), the modified moisture flux \({\text{g}}{{S}_{q}}\) does not enter the definition of the length parameter (5), so \(L_{*}^{{v}} = {{L}_{*}}\), where

$${{L}_{*}} = - \frac{{U_{*}^{3}}}{{{{k}_{{v}}}{\text{g}}{{S}_{{{\theta }}}}}}.$$
(6)

The relationship (6) determines the classical Monin–Obukhov length parameter \({{L}_{*}}\) for the dry atmosphere.

Nevertheless, the approximation (6) for the description of the turbulence of humid atmosphere was used, for example, in [9].

The application of the similarity theory to describing the convective surface layer of humid air involves the use of four basic parameters: \(z\), \({\text{g}}{{S}_{{{\theta }}}}\), \({\text{g}}{{S}_{q}}\), and \({{U}_{*}}\). The parameter of height \(z\) is variable, and the parameters of the fluxes of buoyancy and moisture \({\text{g}}{{S}_{{{\theta }}}}\), \({\text{g}}{{S}_{q}}\), as well as the parameter of dynamic velocity \({{U}_{*}}\) are constant.

Importantly, in the approximation \(0 \leqslant {\text{g}}{{S}_{q}} \ll 1.64{\text{g}}{{S}_{{{\theta }}}}\), the moisture flux \({\text{g}}{{S}_{q}}\), as the basic similarity parameter, has no effect on the calculation of turbulent moments existing in dry atmosphere at \({\text{g}}{{S}_{q}} = 0\), and it needs to be taken into account only in the calculation of the turbulent moments of humidity \(q\).

MONIN–OBUKHOV SIMILARITY THEORY AND FREE CONVECTION LIMITS OF THE SURFACE LAYER

Consider a convective surface layer of dry atmosphere under the conditions of free convection \({\text{g}}{{S}_{{{\theta }}}} > 0\), \({{U}_{*}} = 0\). In this case, only two governing parameters exist: \({\text{g}}{{S}_{{{\theta }}}}\) and \(z\).

In accordance with [21], expressions for the second moments of the vertical velocity and buoyancy take the form:

$$\overline {{{w}^{2}}} = {{{{\lambda }}}_{{ww}}}{{({\text{g}}{{S}_{{{\theta }}}})}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}{{z}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}},\,\,\,\,\overline {{{{({\text{g}}{{{{\theta }}}_{a}})}}^{2}}} = {{{{\lambda }}}_{{{{\theta \theta }}}}}{{({\text{g}}{{S}_{{{\theta }}}})}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}{{z}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}},$$
(7)

where \({{{{\lambda }}}_{{ww}}}\) and \({{{{\lambda }}}_{{{{\theta \theta }}}}}\) are constant coefficients.

Over land surface with poor vegetation and water surface, we will use coefficients \({{{{\lambda }}}_{{ww}}} = 1.8\) and \({{{{\lambda }}}_{{{{\theta \theta }}}}} = 1.8\). These values were derived from measurements over both Minnesota prairies [14] and the East China Sea [16].

The development of relationships (7) with the use of a statistical model of the ensemble of spontaneous convective jets is given in [2, 23, 24].

Consider a convective surface layer of dry atmosphere at weak wind: \(0 \ne {{U}_{*}} \ll 1\). In this case, basic parameters \(z\), \({\text{g}}{{S}_{{{\theta }}}}\), and \({{U}_{*}}\) exist.

To calculate free convective limits of Monin–Obukhov theory, we assume that the moments of vertical velocity and buoyancy under weak wind \(0 \ne {{U}_{*}} \ll 1\) are the same as in the case of no wind \({{U}_{*}} = 0\).

Let \({{{{\sigma }}}_{w}}\), \({{{{\sigma }}}_{{{\theta }}}}\) be the variances of the vertical velocity and fluctuation of potential temperature. Then, transformation (7) considering (2), (6) leads to equalities

$$\left\{ \begin{gathered} \frac{{\overline {{{w}^{2}}} }}{{U_{*}^{2}}} = \frac{{{{\sigma }}_{w}^{2}}}{{U_{*}^{2}}} = {{\alpha }}_{{ww}}^{2}{{({z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}})}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} \hfill \\ \frac{{\overline {{{{({\text{g}}{{{{\theta }}}_{a}})}}^{2}}} }}{{{{{({\text{g}}{{{{\Theta }}}_{*}})}}^{2}}}} = \frac{{\overline {{{{({{{{\theta }}}_{a}})}}^{2}}} }}{{{{\Theta }}_{*}^{2}}} = \frac{{\overline {{{{({{\Theta }}_{{\text{a}}}^{'})}}^{2}}} }}{{{{{\left| {{{T}_{*}}} \right|}}^{2}}}} = {{\alpha }}_{{{{\theta \theta }}}}^{2}{{({z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}})}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}. \hfill \\ \end{gathered} \right.$$
(8)

Here \({{\alpha }}_{{ww}}^{2} = k_{{v}}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}{{{{\lambda }}}_{{ww}}}\), \({{\alpha }}_{{{{\theta \theta }}}}^{2} = k_{{v}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}{{{{\lambda }}}_{{{{\theta \theta }}}}}\) are positive constants [25].

Over land surface with weak vegetation and water surface, we have \({{{{\lambda }}}_{{ww}}} = 1.8\), \({{{{\lambda }}}_{{{{\theta \theta }}}}} = 1.8\) and \({{k}_{{v}}} = 0.4\); therefore, the values of the constants are \({{{{\alpha }}}_{{ww}}} = 1.82\) and \({{{{\alpha }}}_{{{{\theta \theta }}}}} = 0.99\), whatever the type of underlying surface.

Consider a convective surface layer of humid atmosphere. In this case, basic parameters \(z\), \({\text{g}}{{S}_{{{\theta }}}}\), \({\text{g}}{{S}_{q}}~\), and \({{U}_{*}}\) exist. Clearly, in the approximation \(0 \leqslant {\text{g}}{{S}_{q}} \ll 1.64{\text{g}}{{S}_{{{\theta }}}}\) the relationships for momenta (7), (8) hold true for humid air as well.

The transport of moisture and the transport of potential temperature are known to obey the same dynamic equation. This fact leads to an assumption that the profiles of momenta of potential temperature and humidity are similar [8]. Now, for the second turbulent moment of humidity fluctuation, we have a relationship similar to the approximation of buoyancy momentum (8):

$$\frac{{\overline {{{{({\text{g}}q{\kern 1pt} ')}}^{2}}} }}{{{{{({\text{g}}{{q}_{*}})}}^{2}}}} = \frac{{\overline {{{{(q{\kern 1pt} ')}}^{2}}} }}{{{{{\left| {{{q}_{*}}} \right|}}^{2}}}} = \frac{{{{\sigma }}_{q}^{2}}}{{{{{\left| {{{q}_{*}}} \right|}}^{2}}}} = {{\alpha }}_{{qq}}^{2}{{\left( {{z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}}} \right)}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}.$$
(9)

Here \({{{{\sigma }}}_{q}}\) is the variance of humidity fluctuations; \({{{{\alpha }}}_{{qq}}} \approx {{{{\alpha }}}_{{{{\theta \theta }}}}}~\) is a positive constant.

The relationships (8), (9) are free-advective limits of the vertical velocity, buoyancy, and humidity. Now, we assume that above water surface or land surface with poor vegetation, the values of constant parameters in asymptotic relationships (8), (9) are \({{{{\alpha }}}_{{ww}}} = 1.8\), \({{{{\alpha }}}_{{{{\theta \theta }}}}} = 1.0\), and \({{{{\alpha }}}_{{qq}}} = 1.2\).

LINEAR APPROXIMATIONS OF SECOND TURBULENT MOMENTA OF THE VELOCITY, TEMPERATURE FLUCTUATIONS, AND HUMIDITY FLUCTUATIONS IN THE SUBLAYER OF FORCED CONVECTION

We consider universal functions of turbulent momenta in the sublayer of forced convection: \({{{{\zeta }}}_{0}} \leqslant {z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}} < \infty \), \({{{{\xi }}}_{0}} \approx 6 \times {{10}^{{ - 2}}}.\)

Without loss of generality, we can assume that the equations for second momenta of the vertical velocity, “adiabatic” buoyance, and humidity in the layer of forced convection \({{{{\zeta }}}_{0}} \leqslant {z \mathord{\left/ {\vphantom {z {{{L}_{*}}}}} \right. \kern-0em} {{{L}_{*}}}} < \infty \), \({{{{\xi }}}_{0}} \approx 6 \times {{10}^{{ - 2}}}\) can be written as

$$\left\{ \begin{gathered} \frac{{\overline {{{w}^{2}}} }}{{U_{*}^{2}}} = \frac{{\sigma _{w}^{2}}}{{U_{*}^{2}}} = \alpha _{{ww}}^{2}{{\left( {{z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}}} \right)}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}F_{{ww}}^{2}\left( {{z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}}} \right),\,\,\,\,\mathop {{\text{lim}}}\limits_{{z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}}{\kern 1pt} \to {\kern 1pt} \infty } F_{{ww}}^{2}\left( {{z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}}} \right) = 1 \hfill \\ \frac{{\overline {{{{({{\Theta }}_{a}^{'})}}^{2}}} }}{{{{{\left| {{{T}_{*}}} \right|}}^{2}}}} = \frac{{\sigma _{\theta }^{2}}}{{{{{\left| {{{T}_{*}}} \right|}}^{2}}}} = \alpha _{{\theta \theta }}^{2}{{\left( {{z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}}} \right)}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}F_{{\theta \theta }}^{2}\left( {{z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}}} \right),\,\,\,\,\mathop {{\text{lim}}}\limits_{{z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}}{\kern 1pt} \to {\kern 1pt} \infty } F_{{\theta \theta }}^{2}\left( {{z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}}} \right) = 1 \hfill \\ \frac{{\overline {{{{(q{\kern 1pt} ')}}^{2}}} }}{{{{{\left| {{{q}_{*}}} \right|}}^{2}}}} = \frac{{\sigma _{q}^{2}}}{{{{{\left| {{{q}_{*}}} \right|}}^{2}}}} = \alpha _{{qq}}^{2}{{\left( {{z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}}} \right)}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}F_{{qq}}^{2}\left( {{z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}}} \right),\,\,\,\,\mathop {{\text{lim}}}\limits_{{z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}}{\kern 1pt} \to {\kern 1pt} \infty } F_{{qq}}^{2}\left( {{z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}}} \right) = 1. \hfill \\ \end{gathered} \right.$$
(10)

Here \(F_{{ww}}^{2}({z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}})\), \(F_{{{{\theta \theta }}}}^{2}({z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}})\), \(F_{{qq}}^{2}({z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}})\) are differentiable functions; \({{\alpha }}_{{ww}}^{2}\), \(\alpha _{{{{\theta \theta }}}}^{2}\), \({{\alpha }}_{{qq}}^{2}\) are constant coefficients.

Following [3], we will expand functions \({{F}_{{ww}}}({z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}})\), \({{F}_{{{{\theta \theta }}}}}\left( {{z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}}} \right)\) and \({{F}_{{qq}}}({z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}})\) in Taylor series in parameter \({{({z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}})}^{{ - 1}}}\). We restrict ourselves to the linear Taylor expansion of functions \({{F}_{{ww}}}({z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}})\), \({{F}_{{{{\theta \theta }}}}}({z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}})\), \({{F}_{{qq}}}({z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}})\) in \({{({z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}})}^{{ - 1}}}\). Then the variances \({{{{\sigma }}}_{w}}\), \({{{{\sigma }}}_{{{\theta }}}}\) и \({{{{\sigma }}}_{q}}\) take the form

$$\left\{ \begin{gathered} \frac{{{{\sigma }_{w}}}}{{{{U}_{*}}}} = {{\alpha }_{{ww}}}{{\left( {{z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}\left[ {1 + {{\beta }_{{ww}}}{{{\left( {{z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}}} \right)}}^{{ - 1}}}} \right],\,\,\,\,{{\zeta }_{{ww}}} \leqslant {z \mathord{\left/ {\vphantom {z {{{L}_{*}}}}} \right. \kern-0em} {{{L}_{*}}}} < \infty \hfill \\ \frac{{{{\sigma }_{\theta }}}}{{\left| {{{T}_{*}}} \right|}} = {{\alpha }_{{\theta \theta }}}{{\left( {{z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}}} \right)}^{{ - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}\left[ {1 - {{\beta }_{{\theta \theta }}}{{{\left( {{z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}}} \right)}}^{{ - 1}}}} \right],\,\,\,\,{{\zeta }_{{\theta \theta }}} \leqslant {z \mathord{\left/ {\vphantom {z {{{L}_{*}}}}} \right. \kern-0em} {{{L}_{*}}}} < \infty \hfill \\ \frac{{{{\sigma }_{q}}}}{{\left| {{{q}_{*}}} \right|}} = {{\alpha }_{{qq}}}{{\left( {{z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}}} \right)}^{{ - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}\left[ {1 - {{\beta }_{{qq}}}{{{\left( {{z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}}} \right)}}^{{ - 1}}}} \right],\,\,\,\,{{\zeta }_{{qq}}} \leqslant {z \mathord{\left/ {\vphantom {z {{{L}_{*}}}}} \right. \kern-0em} {{{L}_{*}}}} < \infty . \hfill \\ \end{gathered} \right.$$
(11)

The dimensionless parameters \({{{{\zeta }}}_{{ww}}}\), \({{{{\zeta }}}_{{{{\theta \theta }}}}}\), and \({{{{\zeta }}}_{{qq}}}\) denote the boundaries of forced convection for vertical velocity profiles, fluctuations of potential temperature and fluctuations of humidity. The dimensionless parameters \({{{{\alpha }}}_{{ww}}} > 0\), \({{{{\alpha }}}_{{{{\theta \theta }}}}} > 0\), and \({{{{\alpha }}}_{{qq}}} > 0\) correspond to limiting values at free convection and are assumed known. The dimensionless parameters \({{{{\beta }}}_{{ww}}} > 0\), \({{{{\beta }}}_{{{{\theta \theta }}}}} > 0\), and \({{{{\beta }}}_{{qq}}} > 0\) characterize linear expansions and are indefinite.

The existence of a sublayer of forced convection with a fixed boundary \({{\zeta }_{0}}\), corresponding to the extremum point of profiles, leads to the relationships

$$\left\{ \begin{gathered} {{{{\zeta }}}_{{ww}}} = {{{{\zeta }}}_{{{{\theta \theta }}}}} = {{{{\zeta }}}_{{qq}}} = {{{{\zeta }}}_{0}} \hfill \\ {{\left. {\frac{d}{{d{{\zeta }}}}{{{{\sigma }}}_{w}}} \right|}_{{{{\zeta }} = {{{{\zeta }}}_{0}}}}} = {{\left. {\frac{d}{{d{{\zeta }}}}{{{{\sigma }}}_{{{\theta }}}}} \right|}_{{{{\zeta }} = {{{{\zeta }}}_{0}}}}} = {{\left. {\frac{d}{{d{{\zeta }}}}{{{{\sigma }}}_{q}}} \right|}_{{{{\zeta }} = {{{{\zeta }}}_{0}}}}} = 0. \hfill \\ \end{gathered} \right.$$
(12)

With a priori specified parameter \({{{{\zeta }}}_{0}}\), the equations of the system (12) allow us to evaluate the coefficients \({{{{\zeta }}}_{{ww}}}\), \({{{{\zeta }}}_{{{{\theta \theta }}}}}\), \({{{{\zeta }}}_{{qq}}}\) and \({{{{\beta }}}_{{ww}}}\), \({{{{\beta }}}_{{{{\theta \theta }}}}}\), \({{{{\beta }}}_{{qq}}}\). Therefore, approximations (11), (12) form a one-parameter family of analytical approximations, depending on \({{{{\zeta }}}_{0}}\).

Hereafter, the coefficients for the domain above the land surface with weak vegetation and water surface will have the following values: \({{{{\alpha }}}_{{ww}}} = 1.8\), \({{{{\beta }}}_{{ww}}} = 0.03\);\({{{{\alpha }}}_{{{{\theta \theta }}}}} = 0.97\), \({{{{\beta }}}_{{{{\theta \theta }}}}} = 0.016\), and \({{{{\alpha }}}_{{qq}}} = 1.2\), \({{{{\beta }}}_{{qq}}} = 0.016\).

COMPARISON OF “LINEAR” APPROXIMATIONS OF THE VARIANCES OF VERTICAL VELOCITY, BUOYANCY, AND HUMIDITY WITH EXPERIMENTAL DATA

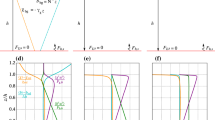
The “linear” approximation of the variance of the vertical velocity (11) with parameters \({{{{\alpha }}}_{{ww}}} = 1.8\), \({{{{\beta }}}_{{ww}}} = 0.03\) is compared with the data of measurements over the ocean [12, 15] in the domain \({{{{\zeta }}}_{0}} \leqslant {z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}} < \infty \), \({{{{\zeta }}}_{0}} = 6 \times {{10}^{{ - 2}}}\) in Fig. 1a. The “linear” approximation of the variance of the vertical velocity (11) with parameters \({{{{\alpha }}}_{{ww}}} = 1.8\), \({{{{\beta }}}_{{ww}}} = 0.03\) is compared with data of measurements over the land [7] in the domain \({{{{\zeta }}}_{0}} \leqslant {z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}} < \infty \), \({{{{\zeta }}}_{0}} = 6 \times {{10}^{{ - 2}}}\) is given in Fig. 1b.

Fig. 1.
figure 1

Comparison of the “linear” approximation of the similarity theory (11) with coefficients \({{{{\alpha }}}_{{ww}}} = 1.8\),\(~{{{{\beta }}}_{{ww}}} = 0.03\) and measurement data on the variance of the vertical velocity over (a) ocean and (b) land in the domain \({{{{\zeta }}}_{0}} \leqslant {z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}} < \infty \), \({{{{\zeta }}}_{0}} = 6 \times {{10}^{{ - 2}}}\). The full line corresponds to approximation (11). Triangles, crosses, and circles correspond to measurement data [7, 12, 15], respectively.

Full size image

The linear approximation of the dimensionless variance of pulsation of the potential temperature \({{{{{{\sigma }}}_{{{\theta }}}}} \mathord{\left/ {\vphantom {{{{{{\sigma }}}_{{{\theta }}}}} {{{T}_{*}}}}} \right. \kern-0em} {{{T}_{*}}}}\) in the form (11) at \({{\alpha }}_{{{{\theta \theta }}}}^{2} = 0.95\), \({{{{\beta }}}_{{{{\theta \theta }}}}} = 0.016\) is compared with field data [17] in Fig. 2.

Fig. 2.
figure 2

Comparison of linear approximation of similarity theory (11) with empirical values of buoyancy variance \({{{{{{\sigma }}}_{{{\theta }}}}} \mathord{\left/ {\vphantom {{{{{{\sigma }}}_{{{\theta }}}}} {{{T}_{*}}}}} \right. \kern-0em} {{{T}_{*}}}}\) according to measurements [17]. The full line corresponds to approximation (11) with coefficients \({{\alpha }}_{{{{\theta \theta }}}}^{2} = 0.97\), \({{{{\beta }}}_{{{{\theta \theta }}}}} = 0.016\).

Full size image

The “liner” approximation of the variance of humidity fluctuation (11) with parameters \({{{{\alpha }}}_{{qq}}} = 1.2\), \({{{{\beta }}}_{{qq}}} = 0.016\) is compared with data of measurements over the ocean [12, 15] in the domain \({{{{\zeta }}}_{0}} \leqslant {z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}} < \infty \) in Fig. 3a. The linear approximation of the variance of humidity fluctuations (11) with parameters \({{{{\alpha }}}_{{qq}}} = 1.2\), \({{{{\beta }}}_{{qq}}} = 0.016\) is compared with data of measurements over land [17, 20] in the domain \({{{{\zeta }}}_{0}} < {z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}} < \infty \), \({{{{\zeta }}}_{0}} = 6 \times {{10}^{{ - 2}}}~\)in Fig. 3b.

Fig. 3.
figure 3

Comparison of the “linear” approximation of similarity theory (11) with coefficients \({{{{\alpha }}}_{{qq}}} = 1.2\), \({{{{\beta }}}_{{qq}}} = 0.016\) and measurement data on fluctuations of humidity over (a) ocean and (b) land in the domain \({{{{\zeta }}}_{0}} \leqslant {z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}} < \infty \), \({{{{\zeta }}}_{0}} = 6 \times {{10}^{{ - 2}}}\). The full line corresponds to approximation (11). Triangles, crosses, circles, and squares correspond to measurement data [7, 12, 15, 20].

Full size image

The results of comparison, given in Figs. 1–3, suggest the existence of a thick sublayer of forced convection in the domain \({{\zeta }_{0}} \leqslant {z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}} < \infty \), \({{{{\zeta }}}_{0}} = 6 \times {{10}^{{ - 2}}}\).

“LINEAR” APPROXIMATION OF THE SECOND TURBULENT MOMENT OF THE FLUCTUATIONS OF NEUTRAL GAS CONCENTRATION IN A SUBLAYER OF FORCED CONVECTION

We assume that some neutral gas (for example, carbon dioxide) uniformly releases from the underlying surface into the atmospheric surface layer; this gas is supposed not to enter into chemical reactions with the air.

Based on the analogy with relationships (4), we introduce a parameter of modified concentration flux on the underlying surface \({\text{g}}{{S}_{c}}\) and a modified parameter of concentration \({\text{g}}{{c}_{*}}\). We obtain

$${\text{g}}{{S}_{c}} = \mathop {{\text{lim}}}\limits_{z \to 0} \overline {{\text{g}}cw} = \mathop {{\text{lim}}}\limits_{z \to 0} \overline {{\text{g}}csw{\kern 1pt} '} > 0,\,\,\,\,{\text{g}}{{c}_{*}} = - \frac{{{\text{g}}{{S}_{c}}}}{{{{U}_{*}}}} < 0.$$
(13)

Here the dimensions of \({\text{g}}{{S}_{c}}\) and \({\text{g}}{{c}_{*}}\) are \(\left[ {{\text{g}}{{S}_{c}}} \right] = {{{\text{m}}}^{2}}{\text{/}}{{{\text{s}}}^{3}}\) and \(\left[ {{\text{g}}{{c}_{*}}} \right] = {\text{m/}}{{{\text{s}}}^{2}}\).

Let \({{{{\sigma }}}_{c}}\) be the variance of the concentration of the neutral gas, then, by analogy with (11), we obtain

$$\begin{gathered} \frac{{{{{{\sigma }}}_{c}}}}{{{{c}_{*}}}} = {{{{\alpha }}}_{{cc}}}{{({z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}})}^{{ - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}\left[ {1 - {{{{\beta }}}_{{cc}}}{{{({z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}})}}^{{ - 1}}}} \right], \\ {{{{\zeta }}}_{{cc}}} \leqslant {z \mathord{\left/ {\vphantom {z {{{L}_{*}}}}} \right. \kern-0em} {{{L}_{*}}}} < \infty \\ \end{gathered} $$
(14)

The undetermined dimensionless parameter \({{{{\zeta }}}_{{cc}}}\) denotes the boundary of the sublayer of forced convection for the profile of fluctuations of carbon dioxide concentration. The dimensionless parameter \({{{{\alpha }}}_{{cc}}} > 0\) characterizes the free convective limit and is assumed known. The undetermined dimensionless parameter \({{{{\beta }}}_{{cc}}} > 0\) characterizes the linear expansion. The values of coefficients \({{{{\zeta }}}_{{cc}}}\) and \({{{{\beta }}}_{{cc}}}\) can be calculated from (12), from where it follows that \({{{{\zeta }}}_{{cc}}} = {{{{\zeta }}}_{0}}\) and \({{{{\beta }}}_{{cc}}} = {{{{\beta }}}_{{{{\theta \theta }}}}} = {{{{\beta }}}_{{qq}}}\).

We compare the “linear” approximation for the variance of fluctuations of carbon dioxide concentration (14) with available observation data. The comparison of (14) with parameters \({{{{\alpha }}}_{{cc}}} = {{{{\alpha }}}_{{qq}}} = 1.2\), \({{{{\beta }}}_{{cc}}} = {{{{\beta }}}_{{qq}}} = 0.016\) and measurement data [20] in the domain \({{{{\zeta }}}_{0}} \leqslant {z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}} < \infty \), \({{{{\zeta }}}_{0}} = 6 \times {{10}^{{ - 2}}}\) is given in Fig. 4.

Fig. 4.
figure 4

Comparison of linear approximation of similarity theory (14) with coefficients \(~{{{{\alpha }}}_{{ss}}} = 1.2\), \({{{{\beta }}}_{{cc}}} = 0.016\) and data of measurements of the variance of carbon-dioxide concentration fluctuations in the domain \({{{{\zeta }}}_{0}} \leqslant {z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}} < \infty \), \({{\zeta }_{0}} = 6 \times {{10}^{{ - 2}}}\). The full line corresponds to approximation (14). Triangles, crosses, circles, and squares correspond to measurement data [20].

Full size image

The results of comparison given in Fig. 4, indicate to the existence of a thick sublayer of forced convection in the domain \({{{{\zeta }}}_{0}} \leqslant {z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}} < \infty \), \({{{{\zeta }}}_{0}} = 6 \times {{10}^{{ - 2}}}\). Clearly, the approximation (14) supplements the one-parameter family of approximations (11), (12).

CONCLUSIONS

The analysis of experimental data [12, 15, 17] shows that a thick sublayer of forced convection with a fixed bottom boundary exists in the convective surface layer (above both the sea and the land).

The comparison of approximations with observation data shows that “linear” approximations (11), (12), (14) convincingly agree with available experimental data on the variances of the vertical velocity, fluctuations of potential temperature, humidity, and carbon dioxide concentration.

A sublayer of forced convection can be identified in the observed profiles of second turbulent moments of the vertical velocity, fluctuations of potential temperature, humidity, and carbon-dioxide concentration.

The profiles of the variations of fluctuations of the potential temperature, humidity, and carbon dioxide concentrations are similar.

The boundary of the sublayer of forced convection \({{{{\zeta }}}_{0}}\) does not depend on the choice of the turbulent moment, and it is the same for the moments of the vertical velocity, fluctuations of potential temperature, humidity, and carbon dioxide concentration. In addition, the value of \({{{{\zeta }}}_{0}}\) does not depend on the choice of the underlying surface, and it is the same over both land and water surface.