Spatio-Temporal and Spectral Transformation of Femtosecond Pulsed Beams with Phase Dislocation Propagating Under Conditions of Self-action in Transparent Solid-State Dielectrics

Abstract

Self-action of a femtosecond optical vortex in fused silica at a wavelength of 1900 nm is analyzed by means of numerical simulations. The formation of a multi-focus ring structure is demonstrated. We show that self-focusing in a ring of relatively large radius occurs without plasma generation. The frequency spectrum of the pulse is broadening mainly into the Stokes band.

1 Introduction

Self-focusing of femtosecond pulses may result in formation of extended filaments with high fluence [1]. The parameters of such structures are quite stable. In particular, stable peak intensity values of the order of magnitude $5\times 10^{13}\,\text {W/cm}^2$ can be observed in the femtosecond pulse at distances significantly greater than the length of the beam waist [2, 3].

Femtosecond filamentation has been widely studied for Gaussian and other beams with a smooth phase. In such beams, a single filament is usually formed on the axis. In media with anomalous group velocity dispersion self-focusing in space is accompanied by self-compression in time, which leads to the formation of localized in space and time “light bullets” [4, 5]. In fused silica samples, such conditions arise for IR radiation at wavelengths greater than $1.3\,\upmu \text {m}$ [6].

On the other hand, there are beams with phase singularity, in which the spiral phase dislocation prevents the appearance of the light field on the beam axis, retaining its ring structure. These donut shaped laser beams, which are often called spiral laser beams or optical vortices, can be promising for such applications as tubular refractive index micromodifications, electrons accelerations, etc. [7]. Self-focusing of spiral laser beams in a medium with cubic nonlinearity was considered theoretically in [7, 8], where the dependence of critical power on the optical vortex topological charge m was obtained. The presence of phase dislocation significantly increases the value of the critical power. For example, the critical power for an optical vortex with topological charge $m=1$ is four times higher than the critical power of a Gaussian beam. As the topological charge increases, the critical power becomes even higher.

The experimental observation of self-focusing of vortex beams, maintaining ring structure, was done in a water cell for 100 fs pulses at a wavelength of 800 nm [8, 9]. In studies of the self-action of femtosecond vortex beams, considerable attention is paid to the emergence of multiple filamentation. The fact is that the vortex beam is quite stable with respect to its radius, but in a nonlinear medium with cubic nonlinearity it undergoes azimuthal modulational instability. As far as we know, the first observation of the set of filaments in vortex beams was performed in [10]. The annular beam with phase singularity on the axis during self-focusing in sodium vapor formed a high-intensity ring, which then disintegrated into separate hot spots due to azimuthal instability. In [9] on the basis of experimental and theoretical studies, a formula was proposed for estimating the number of filaments arising after the collapse of a singular beam, depending on the excess of the peak power over the critical one and the value of the topological charge. The possibility of increasing the distance to the start of multiple filamentation of high-power femtosecond radiation in vortex beams was considered in [11]. It is shown numerically that in relatively wide beams propagating in atmosphere it is possible to transfer high fluence annular structure at a distance of hundreds of meters before it decays into a set of filaments. Improvement of longitudinal stability and reproducibility of filaments in vortex beams with energy of 2–30 mJ formed by special phase plates and propagating in atmosphere was demonstrated in [12]. Experimental studies of the behavior of optical vortices during filamentation in gases and numerical analysis in a stationary approximation without taking into account plasma generation showed the possibility of obtaining stable multiple filamentation regimes in beams with a lattice of optical vortices [13].

A detailed picture of the spatiotemporal dynamics of a femtosecond pulse in a vortex beam in fused silica at a wavelength of 800 nm was obtained in our paper [14]. It is shown that a tubular structure with a radius of 3–4 $\upmu$m can be formed in the nonlinear focus, and the length of this structure significantly exceeds the length of the beam waist under linear propagation.

A number of papers are devoted to the study of frequency spectrum transformation of femtosecond pulses in vortex beams. Experimental spectra of supercontinuum during filamentation of beams with phase singularity in a variety of media (BK7, silica, water, CaF$_2$) were obtained in [15]. It was registered that in the process of supercontinuum generation, the profile of the annular beam practically did not change, and the arising of a small number of filaments resulted in characteristic interference fringes in the supercontinuum radiation.

Transformation of optical vortices into newly emerging spectral components due to phase modulation and four-wave mixing was demonstrated in [16]. The influence of inertia of plasma formation on the propagation stability of optical vortices was studied numerically in [17] under filamentation of beams with phase singularity in fused silica. It is shown that it leads to a quasi-soliton regime of the beam propagation, which is stable to perturbations destroying symmetry, and the multi-focus behavior of optical vortices was revealed.

It should be noted that currently experimental and numerical studies of femtosecond filamentation in vortex beams are mainly performed at wavelengths corresponding to the normal group velocity dispersion in a medium considered. On the other hand, tunable parametric amplifiers allow obtaining high-intensity femtosecond pulses in the mid-IR range, where group velocity dispersion of many transparent solid-state dielectrics is anomalous and where there is a self-compression of pulses. Self-action of pulses with spiral phase dislocation qualitatively changes the manifestation of self-focusing in a nonlinear medium, provoking the formation of tubular filaments.

In this paper, we investigate numerically the spatiotemporal dynamics and spectral characteristics of femtosecond optical vortices under self-action in fused silica glass at a wavelength of 1900 nm. In the first part of the paper, the mathematical model based on the approximation of slowly varying wave [18] is discussed in detail. This allows describing self-steepening of the optical pulse and corresponding transformation of its frequency spectrum. No less important for the correct description of the spatiotemporal dynamics of the pulse is taking into account the delayed response of the Kerr medium, for the description of which a damped oscillator model can be used [19]. The features of the self-action of optical vortices are discussed in the second part of the paper. In particular, the possibility of nonlinear self-focusing into a narrow ring structure without the appearance of plasma is shown.

2 Mathematical Model for Numerical Simulations of Optical Vortex Self-action

2.1 Nonlinear Wave Equation

The numerical simulation of optical vortex propagation is based on nonlinear wave equation, which could be obtained starting with Maxwell’s system of equations.

Considering medium is dielectric ($\mathbf {\rho _f}(\mathbf {r}, t) = 0$) and nonmagnetic ($\mathbf {B}(\mathbf {r}, t) = \mu _0 \mathbf {H}(\mathbf {r}, t)$) we get:

$$\begin{aligned} \varDelta \mathbf {E}(\mathbf {r}, t) - \nabla (\nabla \cdot \mathbf {E}(\mathbf {r}, t)) = \frac{1}{\varepsilon _0 c^2} \frac{\partial \mathbf {j}(\mathbf {r}, t)}{\partial t} + \frac{1}{c^2} \frac{\partial ^2 \mathbf {E}(\mathbf {r}, t)}{\partial t^2} + \frac{1}{\varepsilon _0 c^2} \frac{\partial ^2 \mathbf {P}(\mathbf {r}, t)}{\partial t^2}, \end{aligned}$$

(3.1)

where $\mathbf {E}$ is electric field, $\mathbf {j}$ is current density and $\mathbf {P}$ is polarization, $c=1/\sqrt{\varepsilon _0 \mu _0}$. We examine each of (3.1) members one by one using several further approximations.

Assuming paraxiality, that is transverse wave number is much smaller than longitudinal one, $k_\perp \ll k_z$, and linear polarization of the electric field $\mathbf {E}$, we can use method of slowly varying amplitude $\mathbf {E}$ and current density $\mathbf {j}$:

$$\begin{aligned} \mathbf {E}(\mathbf {r}, t) = \frac{1}{2}\mathbf {e} A(\mathbf {r}, t) \exp \{i (\omega _0 t - k_0 z)\} + \text {c.c.} \end{aligned}$$

(3.2)

$$\begin{aligned} \mathbf {j}(\mathbf {r}, t) = \frac{1}{2}\mathbf {e} J(\mathbf {r}, t) \exp \{i (\omega _0 t - k_0 z)\} + \text {c.c.} \end{aligned}$$

(3.3)

where $A(\mathbf {r}, t)$ and $J(\mathbf {r}, t)$ are complex slowly varying amplitudes, $\mathbf {e}$ is a unit vector.

Using dipole approximation ($\chi ^{(i)}(\mathbf {r},t) = \chi ^{(i)}(t)$) we can write ($\otimes$ means convolution) polarization as:

$$\begin{aligned} \mathbf {P}(\mathbf {r}, t)&= \mathbf {P}^{(1)}(\mathbf {r}, t) + \mathbf {P}^{(2)}(\mathbf {r}, t) + \mathbf {P}^{(3)}(\mathbf {r}, t) + \cdots = \varepsilon _0 \chi ^{(1)}(t) \otimes \mathbf {E}(\mathbf {r}, t) + \nonumber \\&\quad + \varepsilon _0 \chi ^{(2)}(t) \otimes \mathbf {E}(\mathbf {r}, t) \mathbf {E}(\mathbf {r}, t) + \varepsilon _0 \chi ^{(3)}(t) \otimes \mathbf {E}(\mathbf {r}, t) \mathbf {E}(\mathbf {r}, t) \mathbf {E}(\mathbf {r}, t) + \cdots \end{aligned}$$

(3.4)

where $\chi ^{(i)}(t)$—permittivity tensor of i-th order. We consider isotropic medium ($\mathbf {P}^{(2 m)}(\mathbf {r}, t)=0, \ m \in \mathbb {N}$). Each $(n+2)$-th term of the polarization series (3.4) refers to n-th one as ${\sim }\bigl |I(\mathbf {r}, t) \bigr | \bigl / \bigl |I_{\text {a}} \bigr |$, where $I_{\text {a}} \sim 5 \times 10^{16}$ W/cm$^2$ is atomic intensity. Peak intensity inside the filament is about $5 \times 10^{13}$ W/cm$^2$, so the ratio is of the order of ${\sim }10^{-3}$. We can neglect nonlinearities of higher orders and write:

$$\begin{aligned} \mathbf {P}(\mathbf {r}, t) = \mathbf {P}^{(1)}(\mathbf {r}, t) + \mathbf {P}^{(3)}(\mathbf {r}, t). \end{aligned}$$

(3.5)

Therefore we will limit our consideration only to linear and cubic polarizations. Linear polarization can be written as

$$\begin{aligned} \mathbf {P}^{(1)}(\mathbf {r}, t)&= \varepsilon _0 \chi ^{(1)}(t) \otimes \mathbf {E}(\mathbf {r}, t) = \varepsilon _0 \int \limits _{-\infty }^{+\infty } \chi ^{(1)}(\tau ) \mathbf {E}(\mathbf {r}, t - \tau ) \text {d}\tau = \nonumber \\&= \frac{1}{2}\mathbf {e} \exp \{i (\omega _0 t - k_0 z)\} \varepsilon _0 \int \limits _{-\infty }^{+\infty } \chi ^{(1)}(\tau ) A(\mathbf {r}, t - \tau ) \exp \{-i \omega _0 \tau \} \text {d}\tau . \end{aligned}$$

(3.6)

Using inverse Fourier transform of slowly varying electric field amplitude

$$\begin{aligned} A(\mathbf {r}, t) = \frac{1}{2 \pi } \int \limits _{-\infty }^{+\infty } \tilde{A}(\mathbf {r}, \varOmega ) \exp \{ i \varOmega t \} \text {d}\varOmega , \end{aligned}$$

(3.7)

forward Fourier transform of electric susceptibility

$$\begin{aligned} \tilde{\chi }^{(1)}(\omega ) = \int \limits _{-\infty }^{+\infty } \chi ^{(1)}(t) \exp \{ -i \omega t \} \text {d}t \end{aligned}$$

(3.8)

and relation between susceptibility and wave vector $\tilde{\chi }^{(1)}(\omega ) = k^2(\omega ) c^2 / \omega ^2 - 1$, we obtain

$$\begin{aligned} \begin{aligned} \mathbf {P}^{(1)}(\mathbf {r}, t) = \frac{1}{2}\mathbf {e} \exp \{i (\omega _0 t - k_0 z)\} \varepsilon _0 c^2 \frac{1}{2 \pi } \int \limits _{-\infty }^{+\infty } \frac{k^2(\omega _0 + \varOmega )}{\omega _0^2 + 2 \omega _0 \varOmega + \varOmega ^2} \tilde{A}(\mathbf {r}, \varOmega ) \times \\ \times \exp \{ i \varOmega t \} \text {d}\varOmega - \varepsilon _0 \mathbf {E}(\mathbf {r}, t), \end{aligned} \end{aligned}$$

(3.9)

where $k(\omega ) = \omega n(\omega )/ c$, $n(\omega )$—index of refraction. The linear part of the last term in (3.1) takes the form:

$$\begin{aligned}&\frac{1}{\varepsilon _0 c^2} \frac{\partial ^2 \mathbf {P}^{(1)}(\mathbf {r}, t)}{\partial t^2} = -\frac{1}{2}\mathbf {e} \exp \{i (\omega _0 t - k_0 z)\} \times \nonumber \\&\qquad \qquad \qquad \times \frac{1}{2 \pi } \int \limits _{-\infty }^{+\infty } k^2(\omega _0 + \varOmega ) \tilde{A}(\mathbf {r}, \varOmega ) \exp \{ i \varOmega t \} \text {d}\varOmega - \frac{1}{c^2} \frac{\partial ^2 \mathbf {E}(\mathbf {r}, t)}{\partial t^2}. \end{aligned}$$

(3.10)

The expression for cubic polarization consists of two terms related to the first and third harmonics:

$$ \mathbf {P}^{(3)}(\mathbf {r}, t) = \varepsilon _0 \chi ^{(3)}(t) \otimes \mathbf {E}(\mathbf {r}, t) \mathbf {E}(\mathbf {r}, t) \mathbf {E}(\mathbf {r}, t) = $$

$$= \frac{1}{8} \mathbf {e} \exp \{ i (3 \omega _0 t - 3 k_0 z) \}\varepsilon _0 \iiint \chi ^{(3)}(\tau _1, \tau _2, \tau _3) A(\mathbf {r}, t - \tau _1) A(\mathbf {r}, t - \tau _2) A(\mathbf {r}, t - \tau _3) \times $$

$$ \times \exp \{-i \omega _0 (\tau _1 + \tau _2 + \tau _3) \} \text {d}\tau _1 \text {d}\tau _2 \text {d}\tau _3 + $$

$$ + \frac{3}{8} \mathbf {e} \exp \{ i (\omega _0 t - k_0 z) \} \varepsilon _0 \iiint \chi ^{(3)}(\tau _1, \tau _2, \tau _3) A(\mathbf {r}, t - \tau _1) A(\mathbf {r}, t - \tau _2) A^*(\mathbf {r}, t - \tau _3) \times $$

$$\begin{aligned} \times \exp \{-i \omega _0 (\tau _1 + \tau _2 - \tau _3) \} \text {d}\tau _1 \text {d}\tau _2 \text {d}\tau _3. \end{aligned}$$

(3.11)

Due to strong violation of wave synchronism, $\varDelta k = 3 k (\omega _0) - k(3 \omega _0) \ne 0$, we neglect the third harmonic generation. Fourier transform of 3-th order electric susceptibility (similarly to (3.8)) and well-known relation between intensity and electric field amplitude $I(\mathbf {r}, t) = c n_0 \varepsilon _0 |A(\mathbf {r}, t)|^2 \bigl / 2$ yield

$$\begin{aligned} \mathbf {P}^{(3)}(\mathbf {r}, t) = \frac{3}{4} \mathbf {e} \exp \{ i (\omega _0 t - k_0 z) \} \varepsilon _0 \frac{\tilde{\chi }^{(3)}}{c n_0 \epsilon _0} I(\mathbf {r}, t) A(\mathbf {r}, t). \end{aligned}$$

(3.12)

The second time derivative of nonlinear polarization in (3.1) takes the form

$$\begin{aligned} \frac{1}{\varepsilon _0 c^2} \frac{\partial ^2 \mathbf {P}^{(3)}(\mathbf {r}, t)}{\partial t^2} = -\frac{1}{2} \mathbf {e} \exp \{ i (\omega _0 t - k_0 z) \} \frac{2 k_0^2}{n_0} \hat{T}^2 \varDelta n_k(\mathbf {r}, t) A(\mathbf {r}, t), \end{aligned}$$

(3.13)

where

$$\begin{aligned} \hat{T} = 1 - \frac{i}{\omega _0} \frac{\partial }{\partial t} \end{aligned}$$

(3.14)

is the operator of wave-nonstationarity [18], which provides more accurate description of short pulse propagation compared to commonly used approximation of this operator by unit.

In case of instant response the nonlinear (Kerr) addition to the refractive index $\varDelta n_k(\mathbf {r}, t) = n_2 I(\mathbf {r}, t)$, where $n_2 = 3 \tilde{\chi }^{(3)} \bigl / 4 c n_0^2 \epsilon _0$.

Delayed (Raman) response can be taken into account by special convolution with oscillating kernel $H(\tau )$ [19]:

$$\begin{aligned} \varDelta n_k (\mathbf {r}, t) = (1 - g) n_2 I (\mathbf {r}, t) + g n_2 \int \limits _{0}^{+\infty } H(\tau ) I(\mathbf {r}, t - \tau ) \text {d}\tau , \end{aligned}$$

(3.15)

where

$$\begin{aligned} H(t) = \varTheta (t) \frac{1 + \varOmega _{\text {R}}^2 \tau _k^2}{\varOmega _{\text {R}} \tau _k^2} \sin (\varOmega _{\text {R}} t) \exp \{ -t/\tau _k \} \end{aligned}$$

(3.16)

and g—weighting factor, H(t)—convolution kernel, $\varTheta (t)$—Heaviside step function, $\varOmega _{\text {R}}$—rotating frequency of molecules, $\tau _k$—characteristic response time.

Conduction current density $\mathbf {j}$ depends on plasma appearing in filamentation regime. Using simple Drude’s model we can write motion equation for electron gas including elastic electron-ion interactions with collision frequency $\nu _{\text {ei}}$:

$$\begin{aligned} \frac{\text {d}\mathbf {j}(\mathbf {r},t)}{\text {d}t} = \frac{e^2}{m_{\text {e}}} \mathbf {E}(\mathbf {r}, t) N_{\text {e}}(\mathbf {r}, t) - \nu _{\text {ei}}\mathbf {j}_{\text {e}}(\mathbf {r},t), \end{aligned}$$

(3.17)

where $N_{\text {e}}$ is free electron concentration; e and $m_{\text {e}}$—charge and mass of electron. Substituting (3.3) into (3.17), we obtain:

$$\begin{aligned} J(\mathbf {r},t) \omega _0 \biggl ( i + \frac{\nu _{\text {ei}}}{\omega _0} + \frac{1}{\omega _0}\frac{\partial }{\partial t} \biggr ) = \frac{e^2}{m_{\text {e}}} N_{\text {e}}(\mathbf {r}, t) A(\mathbf {r}, t). \end{aligned}$$

(3.18)

Note that $i + \nu _{\text {ei}} \bigl / \omega _0 + \omega _0^{-1} \partial \bigl / \partial t = i \hat{T} + \nu _{\text {ei}} \bigl / \omega _0$. Factor $\nu _{\text {ei}} \bigl / \omega _0$ is small, because for dielectrics $\nu _{\text {ei}} \sim 10^{14}$ s$^{-1}$ and central frequency for near infrared radiation is about $\omega _0 \sim 5\times 10^{14}$ s$^{-1}$. After some algebra we obtain expressions for conduction current density:

$$\begin{aligned} \mathbf {j}(\mathbf {r},t) = \frac{1}{2} \mathbf {e} \frac{e^2}{m_{\text {e}}} \frac{1}{i \omega _0 + \frac{\partial }{\partial t} } \biggl ( 1 + i\frac{\nu _{\text {ei}}}{\omega _0} \hat{T}^{-1} \biggr ) N_{\text {e}}(\mathbf {r}, t) A(\mathbf {r}, t) \exp \{ i(\omega _0 t - k_0 z) \} \end{aligned}$$

(3.19)

and its derivative:

$$\begin{aligned} \frac{1}{\varepsilon _0 c^2} \frac{\partial \mathbf {j}(\mathbf {r},t)}{\partial t}&= \frac{1}{2}\mathbf {e} \exp \{ i(\omega _0 t - k_0 z) \} \times \nonumber \\&\qquad \qquad \qquad \times \biggl ( -\frac{2 k_0^2}{n_0} \varDelta n_{\text {pl}}(\mathbf {r}, t) - i \hat{T}^{-1} \sigma (\mathbf {r}, t) \biggr ) A(\mathbf {r}, t), \end{aligned}$$

(3.20)

where we denoted $\omega _{\text {pl}}^2(\mathbf {r}, t) = e^2 N_{\text {e}}(\mathbf {r}, t) \bigl / m_{\text {e}} \varepsilon _0$ as plasma frequency, $\varDelta n_{\text {pl}}(\mathbf {r}, t) = -\omega _{\text {pl}}^2(\mathbf {r}, t) \bigl / 2 n_0 \omega _0^2$ as nonlinear plasma addition to refractive index and $\sigma (\mathbf {r}, t) = -\omega _{\text {pl}}^2(\mathbf {r}, t) \bigl / c^2 \times \nu _{\text {ei}} \bigl / \omega _0$ as bremsstrahlung cross-section.

Substituting the expressions (3.10), (3.13) and (3.20) to (3.1), assuming $\nabla \cdot \mathbf {E}(\mathbf {r}, t) = 0$ and expanding the Laplace operator to transverse and longitudinal parts $\varDelta = \varDelta _\perp + \partial ^2/\partial z^2$ we obtain nonlinear wave equation, which can be written in retarded time $t'=t-k_1 z$ and $z'=z$ coordinates as

$$\begin{aligned}&\frac{\partial ^2 A (\mathbf {r}, t')}{\partial z'^2} - 2 i k_0 \biggl ( 1 - \frac{i k_1}{k_0} \frac{\partial }{\partial t'} \biggr ) \frac{\partial A (\mathbf {r}, t')}{\partial z'} + \varDelta _{\perp } A (\mathbf {r}, t') = \nonumber \\&\qquad \qquad \qquad = -\frac{2 k_0^2}{n_0} \varDelta n_{\text {pl}}(\mathbf {r}, t) A (\mathbf {r}, t') - i \hat{T}^{-1} \sigma (\mathbf {r}, t) A(\mathbf {r}, t') - \nonumber \\&\qquad -\frac{1}{2 \pi } \int \limits _{-\infty }^{+\infty } \Bigl ( k^2(\omega _0 + \varOmega ) - (k_0 + k_1 \varOmega )^2 \Bigr ) \tilde{A}(\mathbf {r}, \varOmega ) \exp \{ i \varOmega t' \} \text {d} \varOmega - \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad - \frac{2 k_0^2}{n_0} \hat{T}^2 \varDelta n_k(\mathbf {r}, t') A(\mathbf {r}, t'), \end{aligned}$$

(3.21)

where $k_1 = \text {d}k/\text {d}\omega |_{\omega =\omega _0}$. We neglect the second derivative of the field A on $z'$ due to slowly varying amplitude approximation, assume the factor $k_1/k_0$ in brackets approximately equals to $1/\omega _0$ and redesignate $t'$, $z'$ back to t, z.

Equation (3.21) lacks dissipation terms. We can account for the energy loss due to plasma generation by adding the following equation:

$$\begin{aligned} -\frac{\partial I(\mathbf {r}, t)}{\partial z} = \frac{\partial N_{\text {e}}(\mathbf {r}, t)}{\partial t} K \hbar \omega _0, \end{aligned}$$

(3.22)

where $K = \bigl \langle U_i \bigl / \hbar \omega _0 + 1 \bigr \rangle$—number of photons on frequency $\omega _0$ needed to put electron out from the ionization potential $U_i$.

Passing from intensity I to field amplitude A after some algebra we obtain:

$$\begin{aligned} 2 i k_0\frac{\partial A(\mathbf {r}, t)}{\partial z} = -i k_0 \frac{\frac{\partial N_{\text {e}}(\mathbf {r}, t)}{\partial t} K \hbar \omega _0}{I(\mathbf {r}, t)} A(\mathbf {r}, t). \end{aligned}$$

(3.23)

On the right-hand side of the (3.23) we can distinguish the nonlinear absorption coefficient as $\alpha (\mathbf {r}, t) = (\partial N_{\text {e}}(\mathbf {r},t)/ \partial t) K \hbar \omega _0 \bigl / I(\mathbf {r}, t)$. Adding linear extinction coefficient $\delta$ we finally obtain the nonlinear wave equation for simulation of optical vortex self-action:

$$\begin{aligned}&2 i k_0 \frac{\partial A(\mathbf {r}, t) }{\partial z} = \hat{T}^{-1}\varDelta _{\perp } A(\mathbf {r}, t) + \nonumber \\&\quad + \hat{T}^{-1} \frac{1}{2 \pi } \int \limits _{-\infty }^{+\infty } \Bigl (k^2(\omega _0 + \varOmega ) - (k_0 + k_1 \varOmega )^2 \Bigr ) \tilde{A}(\mathbf {r}, \varOmega )\exp \{ i \varOmega t \} \text {d}\varOmega + \nonumber \\&\quad \qquad + \frac{2 k_0^2}{n_0} \hat{T} \varDelta n_k A(\mathbf {r}, t) + \frac{2 k_0^2}{n_0} \hat{T}^{-1} \varDelta n_{\text {pl}} A(\mathbf {r}, t) + i \hat{T}^{-2} \sigma A(\mathbf {r}, t) - \nonumber \\&\quad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad - ik_0 (\alpha + \delta ) A(\mathbf {r}, t). \end{aligned}$$

(3.24)

Obtained wave equation contains several operators of wave nonstationarity $\hat{T}$ as in [18], but the important feature of this equation is the presence of terms responsible for medium ionization, depending on concentration of generated electrons. To calculate electron concentration $N_{\text {e}}$ we need cinetic equation for plasma electrons. The increment of electron concentration is proportional to difference between neutrals concentration $N_0$ and current electron concentration $N_{\text {e}}$ with ionization rate W(I):

$$\begin{aligned} \frac{\partial N_{\text {e}}(\mathbf {r},t)}{\partial t} = W(I) (N_0 - N_{\text {e}}(\mathbf {r},t)). \end{aligned}$$

(3.25)

Electrons generation may be enhanced by the avalanche with nonlinear coefficient $\nu _i$ [20]:

$$\begin{aligned} \nu _i(I) = \frac{1}{U_i}\frac{e^2 \nu _{\text {ei}}}{m_{\text {e}} (\omega _0^2 + \nu _{\text {ei}}^2)} \frac{I}{c n_0 \varepsilon _0}. \end{aligned}$$

(3.26)

Recombination of plasma electrons is taken into account as a negative term which is proportional to current electrons concentration with some constant coefficient $\beta$.

Finally we obtain the cinetic equation for plasma electrons:

$$\begin{aligned} \frac{\partial N_{\text {e}}(\mathbf {r},t)}{\partial t} = W(I) (N_0 - N_{\text {e}}(\mathbf {r},t)) + \nu _i(I) N_{\text {e}}(\mathbf {r},t) - \beta N_{\text {e}}(\mathbf {r},t). \end{aligned}$$

(3.27)

It should be noticed that ionization rate W(I) is calculated according to the Keldysh model [21].

2.2 Problem Statement and Initial Conditions

Numerical simulations of optical vortex self-action are connected with experimental setup shown in Fig. 3.1.

Fig. 3.1

Schematic experimental setup for numerical simulations of optical vortex self-action

Femtosecond laser system generates Gaussian beam, which travels through special vortex lens, providing annular beam with topological charge m at the focal plane, where the input face of the silica glass sample is at $z=0$. Femtosecond pulse with vortex beam propagates further in the bulk fused silica experiencing self-action.

General case of the problem is computationally complex. If we consider pulse propagation before it breaks up due to azimuthal instability, we can save computing resources using axial symmetry of the beam and introducing one spatial coordinate $r = \sqrt{x^2 + y^2}$ instead of two cartesian coordinates x and y. It should be noticed that described approach forbids initialization of asymmetric vortex phase. But we can make a substitution $A(\mathbf {r},z,t) = A'(r,z,t) \exp \{ i m \varphi \}$ in (3.24) and obtain a nonlinear wave equation for $A'(r,z,t)$. The only difference from (3.24) will be the new expression for the transverse laplacian:

$$\begin{aligned} \varDelta _\perp = \frac{\partial ^2}{\partial r^2} + \frac{1}{r} \frac{\partial }{\partial r} - \frac{m^2}{r^2}. \end{aligned}$$

(3.28)

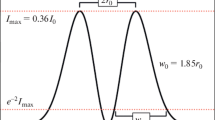
We suppose that at the focal plane of vortex lens there is an annular beam with topological charge m in a bandwidth-limited Gaussian pulse:

$$\begin{aligned} A_{\text {V}}(r,t) = A_0 \biggl (\frac{r}{r_0} \biggr )^2 \exp \biggl \{ -\frac{r^2}{2 r_0^2} \biggr \} \exp \biggl \{ -\frac{t^2}{2 t_0^2} \biggr \} \exp \biggl \{ i m \varphi \biggr \}, \end{aligned}$$

(3.29)

where $r_0 = 120$ $\upmu$m, $t_0 = 60$ fs, $\varphi =\arctan (y/x)$. Intensity and phase profiles of this vortex beam are shown in Fig. 3.2.

Fig. 3.2

Intensity (a) and phase (b) spatial distribution and spatiotemporal intensity distribution (c) for optical vortex with topological charge $m=1$ at $z=0$. Line profiles are shown by dashed lines

Self-action of optical vortex in fused silica is studied in the region of anomalous group velocity dispersion at the wavelength of 1900 nm, where $k_2=-80$ fs$^2$/mm. The critical power of self-focusing for vortex beam with topological charge m can be calculated by formula [9]:

$$\begin{aligned} P_{\text {V}}^{(m)} = \frac{2^{2m+1}\varGamma (m+1)\varGamma (m+2)}{2\varGamma (2m+1)} P_{\text {G}}, \end{aligned}$$

(3.30)

where $P_{\text {G}} = 3.77 \lambda ^2/8 \pi n_0 n_2$ is a critical power of self-focusing for Gaussian beam. We consider topological charge $m=1$ and $P_{\text {V}}^{(1)} = 4 P_{\text {G}}$. The peak power of the pulse was taken substantially higher than critical power, $P = 6 P_{\text {V}}^{(1)}$, which corresponds to the pulse energy of $E = 27$ $\upmu$J. For comparison reasons we also considered propagation of two other beams: annular $A_{\text {R}}(r,t)$ and Gaussian $A_{\text {G}}(r,t)$ pulsed beams with the same excess of peak power on respective critical power. They can be described by the following formulas:

$$\begin{aligned} A_{\text {R}}(r,t) = A_0 \biggl (\frac{r}{r_0} \biggr )^2 \exp \biggl \{ -\frac{r^2}{2 r_0^2} \biggr \} \exp \biggl \{ -\frac{t^2}{2 t_0^2} \biggr \}, \end{aligned}$$

(3.31)

$$\begin{aligned} A_{\text {G}}(r,t) = A_0 \exp \biggl \{ -\frac{r^2}{2 r_0^2} \biggr \} \exp \biggl \{ -\frac{t^2}{2 t_0^2} \biggr \}. \end{aligned}$$

(3.32)

Note that $A_{\text {R}}=A_{\text {G}}(r/r_0)^2$ and $A_{\text {V}}=A_{\text {R}} \exp \bigl \{ i m \varphi \bigr \}$. Spatiotemporal intensity distributions of annular and Gaussian beams are shown in Fig. 3.3.

Fig. 3.3

Spatiotemporal profiles for annular (a) and Gaussian (b) beams at $z=0$

3 Spatiotemporal Dynamics and Spectral Broadening of Optical Vortex in Fused Silica at 1900 nm

3.1 Evolution of Intensity Distribution in Vortex, Annular and Gaussian Beams

Figure 3.4 shows intensity distributions for different beams on the logarithmic scale with initial intensity $I_0 = 2.81 \times 10^{11}$ W/cm$^2$ at distances corresponding to local maxima along z axis.

Fig. 3.4

Spatiotemporal intensity distributions for vortex (a), annular (b) and Gaussian (c) beams

Fig. 3.5

Maximum intensity dependence on coordinate z along propagation distance for vortex, annular and Gaussian beams

In the initial stage of vortex beam propagation, the self-action yields narrowing ring of practically the same radius. This is clearly seen in Fig. 3.4a at $z = 1.41$ cm, when the first local maximum of intensity $1.5 \times 10^{13}$ W/cm$^2$ is reached, its localization in time domain being shifted to the pulse tail. Two mechanisms are responsible for the pulse delay. Both of them are connected with Kerr effect. These are delayed nonlinear response and operator of the wave-nonstationarity. The further propagation of the pulse is accompanied by a decrease in the radius of the ring structure containing the focusing part of the pulse energy. The next intensity maximum of almost the same value is reached at $z = 4.68$ cm (Fig. 3.5). The global maximum is reached in a few millimeters. It exceeds $5\times 10^{13}$ W/cm$^2$ and the radius of the ring structure is reduced to approximately 10 $\upmu$m. On the one hand, phase dislocation prevents energy localization on the optical axis. On the other hand, the achieved intensity values are sufficient for plasma generation, which defocuses pulse tail. Together these factors lead to the cessation of the emergence of high-intensity ring structures in the beam profile and widening of the pulse (Fig. 3.4a III). Note that a noticeable plasma concentration (Fig. 3.6) is achieved only in the last narrowest ring with maximum intensity. Defocusing of the two previous high-intensity rings occurs without plasma generation.

Fig. 3.6

Peak plasma concentration dependence on coordinate z along propagation distance for vortex, annular and Gaussian beams

The spatiotemporal dynamics of annular beam in the initial stage of self-action is qualitatively similar. Again we can see a narrowing ring in the cross section due to self-focusing (Fig. 3.4b I). However, because the critical power for the annular beam is significantly less than for the optical vortex (it is about 1.2 times higher than the critical power for the Gaussian beam), the absolute value of its peak power is also less. This leads to the fact that the maximum intensity in the narrowing ring is achieved at the significantly greater distance $z = 7.72$ cm. The absence of phase singularity ultimately leads to the appearance of the maximum intensity on the beam axis (Fig. 3.4b II). After that, the self-focusing of the annular beam becomes similar to the self-focusing of the Gaussian beam (Fig. 3.4c).

Intensity increases up to $5\times 10^{13}$ W/cm$^2$, plasma with concentration $0.6\times 10^{-3} N_0$ appears. Peak plasma concentration is 6 times higher than in the vortex beam, intensity maximum being on the level of optical vortex, but it remains on longer time interval. Parts of this high-intensive structure self-focus, deviding it to two light bullets, which start to compete for pulse energy. Light bullets’ life cycle is connected with movement towards pulse tail, so the last bullet finally extinguishes the first one, after which we can see approximately typical for gauss pulse evolution. Specified bullet dies at the tail of the pulse, background energy forms the new one at the front and the process repeats until there is enough power (Fig. 3.4b III).

Gaussian beam propagation starts with self-focusing at the optical axis at time slices slightly shifted to pulse tail due to delayed response of Kerr nonlinearity and influence of operator $\hat{T}$ (Fig. 3.4c I). The intensity reaches values $6 \times 10^{13}$ W/cm$^2$, plasma electrons appear at the trail of the pulse (Figs. 3.5 and 3.6). Ring structure in the pulse cross-section is formed due to interference of radiation moving towards and backwards the optical axis. Nonlinear focus drifts backwards on time coordinate while there is enough power and then disappears (Fig. 3.4c II). Such relatively stable in space and time domain structures are usually cited as a “light bullets”. Background energy gives the birth to new light bullet on the pulse front and the process repeats several times (Figs. 3.4c III and 3.7a). Anomalous group velocity dispersion keeps these spatiotemporal bullets from splitting into sub-pulses. The number of light bullets in the vortex beam is significantly less than in Gaussian one. They have an annular structure and quickly shift to the tail of the pulse (Fig. 3.7b).

Fig. 3.7

Spatiotemporal evolution of light bullets in Gaussian (a) and vortex (b) beams

Fig. 3.8

Maximum intensity dependence on coordinate z along propagation distance for vortex with topological charge $m=1$ (green line), $m=2$ (black line) and $m=2$ in the model without operator $\hat{T}$ in instant Kerr effect (dashed line)

Fig. 3.9

Peak plasma concentration dependence on coordinate z along propagation distance for vortex with topological charge $m=1$ (green line), $m=2$ (black line) and with $m=2$ in the model without operator $\hat{T}$ in instant Kerr effect (dashed line)

The propagation of an optical vortex with a higher topological charge ($m=2$) has the peculiarity that the maximum intensity along the propagation direction z is approximately twice less than that of a vortex with a charge $m=1$. This is clearly seen in Fig. 3.8, which shows the maximum intensity for beams with different topological charges. This is enough for the maximum plasma concentration in a beam with $m=2$ to be 30 times less than in a beam with $m=1$ (Fig. 3.9). This case can be considered as an ionization free mode of self-focusing of the optical vortex. The peak intensity and concentration of the plasma can be “returned” to the “ionization values”, if we cross out the operator of the wave-nonstationarity $\hat{T}$ from the mathematical model in the term describing Kerr nonlinearity (Figs. 3.8 and 3.9, dashed curve). This demonstrates the importance of this operator for the correct description of the self-action of a femtosecond optical vortex.

3.2 Fluence of Optical Vortex and Gaussian Beams

The spatial distribution of light energy is characterized by fluence

$$\begin{aligned} F(r,z) = \int \limits _{-\infty }^{+\infty } I(r,z,t) \text {d}t \end{aligned}$$

(3.33)

Fig. 3.10

Fluence distribution for optical vortex in case of linear propagation

Linear divergence of optical vortex beam is the same as Gaussian beam [22]. The diffraction length in fused silica glass for both beams is 6.8 cm. At smaller distances, the divergence of the optical vortex is weak (Fig. 3.10).

Fluence distributions for vortex and Gaussian beams in nonlinear medium are shown in Fig. 3.11.

Initial self-focusing of optical vortex taking place on $z=1.4$ cm is characterized by ring narrowing. Its radius doesn’t practically change, fluence inside the ring being increased. We can see the first nonlinear focus as a hot point in Fig. 3.11a at $z = 1.4$ cm. The intensity in this non-linear focus does not exceed $I = 1.5 \times 10^{13}$ W/cm$^2$, despite the fact that the plasma defocusing lens in this place is not formed. After passing the first nonlinear focus, most of the pulse energy flows to the beam axis. However, the pace of this flowing is different. Thus, two rings are formed in the cross section. The inner ring reaches the minimum radius in the vicinity of $z = 2$ cm. However, the energy in it is not enough to form pronounced hot spots. Then the radius of this inner ring begins to grow, and fluence inside it decreases. The outer fluence ring at the same distances continues to shrink at a gradually increasing rate. Ultimately, this ring is narrowed to the smallest radius up to 10 $\upmu$m, providing the nonlinear focus with the highest fluence $F = 0.31$ J/cm$^2$ at approximately $z = 5$ cm. The peak intensity in this location sufficient for plasma generation, which defocuses the tail of the pulse. Note that at a short distance before this point there is another local maximum of fluence in the ring of the intermediate radius. Thus, in the process of self-action of the optical vortex, a multi-focus structure is formed consisting of several rings of different radius arising at different distances z.

This multi-focus structure is significantly different from the self-focusing of a Gaussian beam in which a collapse occurs on the beam axis (Fig. 3.11b). In a Gaussian beam, moving foci and refocusing form a sequence of almost continuous hot spots with fluence $F = 0.48$ J/cm$^2$, in each of them a noticeable plasma concentration is reached. Note that the distance between the first and the last hot spots in both beams turns out to be the same. Recall that despite the significant energy difference, the excess over the critical power in both pulses is also the same.

Fig. 3.11

Fluence distribution for optical vortex (a) and Gaussian beam (b)

3.3 Evolution of Frequency Spectrum and Energy Transformation in Optical Vortex

Spectral dynamics as a function of the propagation distance z for vortex beam is shown in Fig. 3.12 in logarithmic scale. It is clearly seen as due to self-phase modulation the spectrum begins to gradually expand mainly into the Stokes region. Sharp broadening of the spectrum occurs when the beam reaches a nonlinear focus at $z = 1.4$ cm. At this point, an annular light bullet is formed, which implies strong pulse self-steepening, and a noticeable broadening of the spectrum in the anti-Stokes region is observed. With further propagation, this process is repeated when other nonlinear foci are reached in the vicinity $z = 5$ cm.

Fig. 3.12

Evolution of frequency spectrum for optical vortex in logarithmic scale

Fig. 3.13

Energy transformation from central spectral band (1745 – 2045 nm) towards anti-Stokes (${<}1745$ nm) and Stokes (${>}2045$ nm) regions

To describe pulse spectrum dynamics quantitatively, we devided spectrum with full energy $E_0$ to three bands: central ($\lambda = 1900 \pm 145$ nm with energy $E_{\text {c}}$), anti-Stokes ($\lambda < 1755$ nm with energy $E_{\text {a}}$) and Stokes ($\lambda > 2045$ nm with energy $E_{\text {s}}$). Thus, the width of the central band is 5 times greater than the width of the input pulse spectrum (1/e level). So, initially pulse energy $E_0$ is located entirely in the central band (Fig. 3.13).

First centimeters of propagation distance are characterized by energy transformation mostly from central to Stokes region. After the first nonlinear focus at $z = 1.4$ cm most of the pulse energy is in the Stokes region, 5–10% of the total energy being transformed into the anti-Stokes region. In the end more than 70% of the energy is converted into Stokes region and less than 10% into anti-Stokes region.

4 Conclusions

In this paper, we considered the self-action in fused silica glass at a wavelength of 1900 nm of a femtosecond optical vortex—annular beam with a phase singularity under conditions of preserving the axial symmetry of its intensity profile. In computer simulations, we used the model including slowly varying wave approximation for propagation equation with the operator of wave-nonstationarity $\hat{T}$ and delayed response of Kerr nonlinearity. This turns out to be critical for correct describing the multi-focus structure of an optical vortex in a nonlinear medium.

It is shown that for a six-fold excess of the pulse peak power over the critical one, rings with high fluence are formed sequentially in nonlinear foci along the optical axis. At the beginning of the propagation, these rings have a larger radius. The maximum intensity in these nonlinear foci is several times lower than in filament of Gaussian beam. This is not sufficient to produce appreciable plasma concentration that results in ionisation free propagation of the pulse through nonlinear focus. The frequency spectrum of the pulse is broadening mainly into the Stokes band. A relatively strong broadening of the spectrum into the anti-Stokes region is observed in nonlinear foci.

This research was supported by the Russian Foundation for Basic Research, grant 18-02-00624. Calculations were partly conducted using Supercomputer “Lomonosov” in MSU.