Relativistic Laser Plasma Atto-Physics

Abstract

Interaction of an ultrashort and ultraintense laser pulse with overdense/underdense plasmas is considered. Efficient conversion of fundamental laser radiation into sub-femtosecond XUV/X-ray radiation and its significant amplification in laser plasmas are obtained. The results of the simulations were compared with the experimental data and have shown a good coexistence.

1 Introduction

The interaction of high intensity laser pulses with matter (including plasma) is usually accompanied by some dynamical processes of a time scales in the range of femto (fs)- or even attoseconds (as). The study of these processes (attophysics) is possible only if the appropriate laser system with high enough (relativistic) intensity is available to initiate them. Recently the researchers direct substantial efforts to the development of coherent power attosecond light pulses because wide ranging applications [1, 2]. Several methods of generation of such pulses have been explored involving high-order harmonic generation (HHG) through the interaction of high-intensity fs laser pulses with gases [3, 4], including low density partly ionized plasma [5] and highly ionized overdense plasmas [6]. Materials start breaking down at relatively low laser intensity and plasma is the only medium that can be used for modern high-power fs lasers operating at relativistic intensities. Such a pulse focused on a solid target, instantly ionizes the surface in its leading edge triggering plasma that subsequently interacts with the rest of the pulse energy. The specific nature of the interaction depends strongly upon the driving laser properties, the interaction geometry and plasma characteristics. The ordinary laser plasma theory is considering processes with duration comparable or bigger than few fs (laser wave period). Recent experimental technique gives us an opportunity to operate with even smaller (as) time scales this demanding to revise some assumptions of standard models. One important example is the investigation of fast dynamical processes in overdense plasma because in the field of dense plasma physics, in particular plasmas close to solid densities originating from the sudden heating of solid matter, the time scale of all plasma oscillations is set by the plasma frequency ω_p = 2π/T_p. The period of these oscillations relative to the laser period is given by T_p/T_L = (n_c/n_e)^0.5 where the critical density n_c ~10²¹ cm⁻³ for laser light of period T_L ~ 3 fs and n_e is electron density ~10²⁴ cm⁻³. This implies oscillation periods of hundreds attoseconds, and thus time-resolved measurements will require pulses in (as) range. Under appropriate conditions such an interaction can lead to nonlinear specular reflection of light with generation of new frequencies through the surface high-harmonic generation process [7]. This approach is essential since it is important for interdisciplinary applications in the fields of laboratory astrophysics [8], high-energy density physics [9], fast particle generation [10] and has the potential to provide an intense (as) pulses with enough high conversion efficiencies [11, 12].

We start from plasma of high (solid) density because as it was mentioned above harmonic generated from such plasma is the most promising mechanism for future radiation sources based on reflecting plasmas, since the maximum generated frequency grows with laser intensity, and has been predicted to eventually reach multi-keV photon energies and pulse durations down to the zepto-second range for ultra-relativistic laser intensities [13, 14]. Interaction of intense laser pulses with solid surfaces has been intensively studied in the last two decades. Precise manufacturing and high power (~100 TW) laser systems allow physicists to investigate incoherent heating of electrons leading to ion acceleration in the sheath field generated at the target surfaces. If the laser pulse is compressed down to a few 10 s of femtoseconds the regime of coherent heating (acceleration) can be also explored, where the electron nano-bunching results in intense coherent radiation. The electrons move around the laser-plasma boundary at nearly the same trajectory and emit high frequency photons in form of atto-pulses [15]. The ultra-short laser pulses have the advantage in applications where high repetition rate is required. The lower is the energy contained in one pulse the higher the repetition rate can be.

At laser intensities higher than $10^{18} \,{\text{W}}/{\text{cm}}^{2}$ the electrons acquire relativistic velocity during a quarter laser cycle and get pushed into the plasma by the ponderomotive force. This is illustrated by the first step shown in Fig. 18.1. When this force changes its sign the electrons get accelerated towards the incident pulse and they are pulled also by the charge separation field, because the ions stay still during this short time period (step 2). In this phase the electron momentum is the highest. In the next quarter period the electrons are compressed by the counter acting ponderomotive force and emit coherent synchrotron radiation (step 3) until they are slowed down by the ions. This mechanism of attopulse generation is very general and often referred as ROM (Relativistic Oscillating Mirror) model [15] at close to normal incidence and it is interpreted as coherent synchrotron emission (CSE) [16] at large incident angles, which is described in the next section.

Fig. 18.1

The three major steps in the relativistic oscillating mirror model. In the upper picture the blue line represents the laser field, while the red line is the ponderomotive force

2 Attopulse Generation at Low Repetition Rates

In the case of nowadays high power laser systems, in which a few Joule can be pumped in one pulse leading to peak intensities about several 10²⁰ W/cm² and repetition rate is limited to maximum 10 Hz. At such high intensities intense attopulses can be generated with broad spectrum spanning up to the 100th harmonics of the fundamental laser wave. For the spectral intensity of reflected wave a universal model has been developed, the so called BGP model [15], where the $I\left( \omega \right) \sim \omega^{ - 8/3}$ scaling was obtained and a cut-off frequency $\omega_{\text{c}} \sim \gamma^{3}$, where $\gamma$ is the relativistic Lorentz factor of electrons. It has been quickly realized that this power scaling can be different in the case of oblique incidence [17], where the Brunel electrons escape from the plasma and get accelerated continuously by the laser field along the plasma surface having a long trajectory, not oscillating like in the previous case. The electrons are strongly bunched near the plasma surface and have more synchrotron-like trajectories, therefore this mechanism acquired the name coherent synchrotron emission (CSE), which has been proven to be highly efficient for atto-pulse generation [18]. A representative particle-in-cell simulation is shown in Fig. 18.2, where only the negative part of the electric field is shown by color code because this part is transformed into attopulse. In this scenario the ponderomotive force is responsible mostly for the longitudinal acceleration (along x direction), while the laser electric field drives directly the surface oscillation described in Fig. 18.1. The electron bunches extracted from the plasma experience a longitudinal and transversal acceleration simultaneously at the laser phase corresponding to the step 3 in Fig. 18.1. An observer placed near the plasma surface at some distance from the interaction zone would see the electric field plotted in Fig. 18.3, which contains strong narrow negative peaks, which are the signature of atto-pulses .

Fig. 18.2

Electric field (purple) and electron density (green) from the interaction of an intense laser pulse with a flat surface at 75 degrees incidence angle. The intensity is $5 \times 10^{19} \,{\text{W}}/{\text{cm}}^{2}$, the pulse duration is 30 fs and the plasma density is $50n_{\text{cr}}$

Fig. 18.3

Measured electric field at 1 µm away from the surface in Fig. 18.2

In order to analyse the near field we measure the current density along a line parallel with the plasma surface and use the following expression to obtain the electric field in time:

$$ E_{y} \left( {x_{0,} y_{0,} t} \right) = \frac{1}{{2\varepsilon_{0} }}\smallint_{{j_{y} }} \left( {y_{0,} x^{{\prime }} ,t^{{\prime }} } \right){\text{d}}t^{{\prime }} , $$

(18.1)

where the concept of retarded time has been used: $t^{{\prime }} = t - \left( {x^{{\prime }} - x_{0} } \right)/c$ and $\left( {x_{0,} y_{0} } \right)$ are the coordinates of the observer. In Fig. 18.2 one can see that the emitted attopulses have some angular spread and they are emitted at a small angle, comparable to the reflection angle. The angle of emission at each instance of time can be calculated by the following formula:

$$ \phi (x^{{\prime }} ,t^{{\prime }} ) = \arctan \left( {j_{x} t^{{\prime }} /\int {j_{y} } {\text{d}}t^{{\prime \prime }} } \right) $$

(18.2)

Using this it is possible to obtain the angular distribution of emission at any time-space coordinate:

$$ E_{y} \left( {x,t,\theta } \right) = \frac{1}{{2\varepsilon_{0} }}\smallint \delta \left( {\theta - \phi \left( {x^{{\prime }} ,t^{{\prime }} } \right)} \right)j_{y} \left( {x^{{\prime }} ,t^{{\prime }} } \right){\text{d}}t^{{\prime }} , $$

(18.3)

where $\theta$ is a chosen angular interval (cone angle) which defines the k vector of measurable radiation. By performing a Fourier transformation on $E_{y} \left( {x,t,\theta } \right)$ one obtains the angle resolved spectral intensity of the emitted radiation and from the phase information one can select the cone angle, where the coherency is the highest. Basically it is necessary to find the angular interval where the variation of ${\text{d}}\varphi /{\text{d}}\omega$ is the smallest, where $\varphi$ is the phase obtained from Fourier transform of the field. By doing so it is possible to obtain the temporal shape of the coherently emitted radiation, which is plotted in Fig. 18.4. It can be seen that the duration of the atto-pulse emitted within the 0.15 rad angle is less than 100 as and its amplitude is 10 times higher than the amplitude of the electric field in the laser pulse.

Fig. 18.4

Absolute value of the electric field emitted in a small cone angle, where the coherency is the highest. Obtained from the simulation shown in Figs. 18.2 and 18.3 and using (18.3)

The modeling of the attopulse emission can be done by directly calculating the electric field starting from the Lienard–Wiechert potential. We use the expression derived in [16]:

$$ E_{y} \left( t \right) = C\frac{{a_{y} \left( {t^{{\prime }} } \right)}}{{\left( {1 - v_{x} \left( {t^{{\prime }} } \right)/c} \right)^{2} }}, $$

(18.4)

where C is the constant and $a_{y} \left( t \right) = \exp \left( { - t^{2} } \right)$ is the approximated transversal acceleration which is a fit to the simulation results. In the extended version of the theory [17] the transversal velocity was approximated by the function $v_{y} \sim t^{n}$, where n = 1 and 2 were considered, which also results in similar acceleration around $t \approx 0$. In our work we have extended this model and we have shown that higher values of n are also possible. The longitudinal velocity is often approximated by a polinomial function of t around the zero point, which behaves very similarly to the electron velocity around the point where it reaches the maximum value. The velocity $v_{x} \approx c\left( {1 - \alpha_{1} t^{{{\prime }\,{2\nu }}} } \right)$ is derived in [19] which can be used to obtain the expression of retarded time:

$$ t^{{\prime }} = \frac{{t2\gamma^{2} }}{{1 + 2\alpha_{1} \gamma^{2} t^{{{\prime }\,{2\nu }}} /\left( {2n + 1} \right)}}, $$

(18.5)

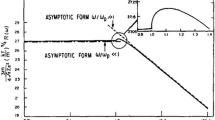
where $\alpha_{1} \approx 6/a_{0}^{3}$ and $a_{0} = eE_{L0} /cm_{e} \omega_{L}$ is the normalized laser field. Inserting (18.5) into (18.4) one obtains the electric field of a single unfiltered attopulse and its Fourier transform is shown in Fig. 18.5, which is in good agreement with the simulation for the given parameters. One can see that the spectrum has a plateau region where the intensity is almost constant and it is followed a sudden drop and exponential decay at higher frequencies. The harmonic order where the spectral intensity drops is approximately $N_{\text{dr}} \approx \left( {3/2} \right)a_{0}^{2} ,$ which is close to 32 in our case.

Fig. 18.5

Comparison between the spectrum of the field shown in Fig. 18.4 and the model described in the text [red curve, (18.4, 18.5)]

So far we have used only 2D geometry, but the same atto-pulse generation can be realized in 3D as well and it is more efficient if the interaction of circularly polarized laser pulse with cylindrical symmetric targets is considered. In this case the P-polarized interaction is ensured at each moment of time at one point of a cylinder (or cone) inner surface [20]. The iso-value surface of the generated radiation is shown in Fig. 18.6 for the case of cylinder (a) and cone (b) targets. The radius of the rotation symmetric targets is $0.8\;\upmu{\text{m}}$ and their axes coincide with the laser propagation axis. In the case of cone target the atto-spiral gets focused at the exit side (see Fig. 18.7), where the radius is 30% smaller, thus the intensity can be even higher than that of the incident pulse.

Fig. 18.6

The iso-surface of energy density of electromagnetic radiation produced in the case of cylinder (a) and cone (b) targets [6]

Fig. 18.7

Blue: initial shape of the target. Orange: ultra-relativistic electrons extracted and accelerated by the laser field. Purple: high energy density radiation, i.e. focused atto-spiral

Thus we can conclude in this section that high intensity laser pulses are capable of generating intense atto-pulses via the nano-bunching of electrons near the plasma surface. The process of coherent synchrotron emission results in not so steep spectral intensity scaling and peak amplitudes of attopulses larger than that of the incident pulse. The conversion efficiency from laser to attopulse is about 2–5%, depending on the filtering. The radiated fields presented here are near-fields, the far-field would have different distribution and it should be investigated in further studies. However, the repetition rate of these attopulses is quite low and other means should be found to generate similar pulses with higher repetition rates.

3 Atto-Pulse Generation and Amplification at High Repetition Rates

In the previous section high harmonic generation mechanisms up to the 100th harmonic of the laser pulse can be produced with high efficiency resulting in intense attopulses. The drawback if the high intensity pulses is the low repetition rate and the limited contrast ratio, which makes difficult to control the plasma surface before the main pulse arrives. It is possible to produce shorter and less intense laser pulses with high repetition rate (up to 100 kHz), which contain energy on the order of 10 mJ. In this case very high contrast ratio can be also maintained and the remaining challenge is ensuring the new and fresh plasma surfaces after each pulse, which requires rotating or moving target holder. One option for decreasing constrain on the target movement speed is to exploit the possibility of multiple reflection of the short pulse between two plasma surfaces, which was first proposed in [20].

Recently we have investigated the problem of multiple reflections at oblique incidence with the help of 1D (boosted frame) and 2D (lab-frame) simulations [21]. The basic setup is illustrated in Fig. 18.8. The distance between the two foils has to be large enough to ensure non-overlapping laser spots, i.e. after each reflection the laser pulse and its harmonics interacts with fresh surfaces. On the other hand this distance has to be much smaller than the Rayleigh length of the loosely focused pulse in order to avoid significant divergence during consecutive reflections. The intensity of individual harmonics increases after each reflection because the reflected pulse inherently contains the low-order harmonics with the right phase thus the waveform is modified such that in the next interaction the electron bunch motion is more optimal for the described process. We have considered S and P polarization separately and we found that the S-polarized interaction leads to stronger harmonic amplification. After 6–7 reflections the intensity of 10th–30th harmonics can be enhanced by 3 orders of magnitudes. A detailed numerical model is developed in [21], which models each reflection and includes the spectral change caused by the previous reflection. The spectral intensity distribution after the first reflection (obtained from the model) is shown in Fig. 18.9a while the enhancement of harmonics after 8 reflections is shown in Fig. 18.9b. In this idealized model, where laser energy absorption, i.e. electron heating, and dispersion effects are not included the maximum amplification factor can reach the value of $10^{5}$ for the harmonic numbers between 10 and 20. It is interesting to note that this strong amplification happens at low intensity, at higher intensities the enhancement is lower, but it spans over a broader spectral range.

Fig. 18.8

Schematics of the multiple reflection setup. The two foils are parallel and are moved perpendicular to the interaction plane with 100 cm/s velocity

Fig. 18.9

a Intensity distribution of harmonics (n_i) for different laser amplitudes. b Amplification factor of each harmonics after the 8th reflection

The agreement between the model and 1D simulations is good in [21], although the simulations show one order of magnitude lower amplification because of energy absorption effects. In 2D this difference is even higher, because of the non-uniform transversal intensity of the Gaussian beam, but the amplification factor is higher than $10^{3}$, which is already a good achievement. The change of spectral intensity during consecutive reflections in 2D simulation is shown in Fig. 18.9 for two laser field amplitudes. Due to the large focal spot area the beam divergence does not play a role in the amplitude evolution. There is another important parameter which influences the process, namely the similarity parameter: $S = n_{0} /\left( {a_{0} n_{\text{cr}} } \right)$, where $n_{0}$ is the plasma density and $n_{\text{cr}} = \omega_{L}^{2} m_{e} \varepsilon_{0} /e^{2}$ is the critical density defined by the laser wavelength. The general tendency is that for small S parameters (high intensity) the harmonics are strong already after the first reflection and enhancement in further reflections is small. For high values of S a single reflection does not provide high harmonic content, but after several reflections the harmonic intensity can be enhanced significantly.

Thus, we have presented a method to amplify the intensity of atto-pulses generated via the ROM mechanism at moderate or small incident angles and in the case of large focal spots. The mechanism is based on the multiple reflection of the same pulse between two metal foils and it is shown that the amplification saturates after 4–5 reflections for low harmonics ($\omega < \sqrt {n_{0} /n_{\text{cr}} } \omega_{L}$), but the amplification of higher harmonics continues aver more reflections. This technique can be applied at laser systems with above kHz repetition rate where the laser intensity is slightly above the relativistic threshold. From laser to higher harmonics energy conversion efficiency can reach 1% level. The amplification of relatively low number harmonics by using inhomogeneous plasma layer was considered in [22] with help the developed theory and was confirmed in the experiment.

4 Atto-Pulse Amplification in Low Density Plasmas

Another method, which permits to amplify a weak atto-pulse , is connected with nonlinear wave interaction in under-dense plasma . In particularly, it can be Backward Raman Amplification (BRA) scheme, which considers the resonant energy transfer from large energy pump pulse to short Raman down-shifted and counter propagating seed pulse via Langmuir plasma wave [23, 24]. The amplifying medium in this schema is plasma, which can tolerate much larger energy density than any standard grating. We used this schema in the amplifying of a low energy ultra-short pulses.

The BRA resonant condition in order to achieve significant amplification, using the conservation of momentum and energy can be written as: $\varvec{k}_{{\mathbf{0}}} - \varvec{k}_{{\mathbf{1}}} = \varvec{k}_{{\mathbf{2}}}$, $\omega_{0} = \omega_{1} + \omega_{2}$, where k_j and $\omega_{j} ( = 2\pi c/\lambda_{j} )$ are the wave vector and frequency associated with interacting waves, c is the speed of light, $\lambda_{j}$ indicates the wavelength; the subscripts j = 0,1,2 correspond to the pump, seed and plasma parameters respectively. BRA is a consequence of three wave decay process where the pump loses its energy to the counter propagating seed and the plasma wave. The Langmuir (plasma) wave is characterized by the dispersion relation $\omega_{2}^{2} = \omega_{\text{p}}^{2} + \upsilon_{\text{th}}^{2} k_{2}^{2}$, where $\upsilon_{\text{th}}$ is the electron thermal velocity and $\omega_{\text{p}}$ is the plasma frequency corresponding to plasma slab with electron density n_e. Considering the plasma is not too hot (i.e. $k_{2} \upsilon_{\text{th}} \ll \omega_{\text{p}} T_{\text{e}} \le 0.01m_{\text{e}} c^{2} \sim 5\;{\text{keV}}$), thus $\omega_{2} \approx \omega_{\text{p}} = (4\pi n_{\text{e}} e^{2} /m_{\text{e}} )^{1/2}$, where e and $m_{\text{e}}$ correspond to the electron charge and mass respectively. The propagation of pump and seed laser pulses in the plasma is specified by dispersion relation $\omega_{0,1}^{2} = \omega_{\text{p}}^{2} + c^{2} k_{0,1}^{2}$; in this configuration the critical plasma density corresponds to downshifted seed pulse and can be written as $n_{\text{cr}} = (m_{\text{e}} \omega_{1}^{2} /4\pi e^{2} )$. The propagation of em waves under resonant BRA condition immediately gives $\lambda_{1} \in (\lambda_{0} ,2\lambda_{0} )$ i.e., the seed wavelength should be smaller than twice of the pump wavelength and it is reasonable to keep them (seed/ pump) spectrally close as it reduces the required resonant plasma density. The resonant plasma density may be expressed as $n_{\text{e}} = (\pi mc^{2} /e^{2} )(\lambda_{0}^{ - 1} - \lambda_{1}^{ - 1} )^{2}$. This expression indicates that the resonant plasma density for an efficient BRA operation resembles with the order of the solid density in XUV range. It is well understood from the earlier investigations that the BRA process holds efficiently in the under critical plasma regime. To scale and estimate the features of output signal and necessary physical properties of the BRA; we use the analysis [23,24,25,26,27] for the amplification of short pulses, takes account of simple analytical estimates based on slowly varying envelope approximation (svea).

In three waves interaction process the excited Langmuir (L-) plasma wave procures the fraction $(\omega_{2} /\omega_{0} )$ of the energy from the laser pump. If any damping loss from the L-wave is ignored during the energy acquisition from the pump and its transfer to the seed pulse, the sustenance of L-wave is limited ideally by the wave breaking phenomenon, occurs when the electron gains quiver velocity larger than the phase velocity of the L-wave. Hence, the peak intensity of the pump corresponding to the L-wave breaking threshold can be given by $I_{\text{br}} = (n_{\text{e}} /n_{\text{cr}} )^{3/2} (4\omega_{1} \omega_{0} /c^{2} k_{2}^{2} )I_{\text{M}}$, where $I_{\text{M}} \approx (n_{\text{cr}} m_{\text{e}} c^{3} /16)$. The maximum achievable duration of the leading spike of the seed thus can be given by

$$ \Delta t_{1} \sim (\varLambda_{0} /\gamma_{0}^{2} t) > \Delta t_{1m} \approx (\omega_{0} /\omega_{1} )^{2} (4/\omega_{0} )[(2\Lambda _{0} I_{\text{M}} /3\delta_{o} I_{0} )(\omega_{1} /\omega_{0} )]^{1/3} . $$

This refers to the largest achievable intensity as

$$ I_{1} < I_{1m} \approx (w_{1m} /\Delta t_{1m} )\sim (\omega_{1} /\omega_{0} )^{2} (16I_{\text{M}} \omega_{0} /\omega_{2} )[(3\delta_{o} I_{0} /2\Lambda _{0} I_{\text{M}} )(\omega_{0} /\omega_{1} )]^{2/3} . $$

Using the above expressions which represents the optimal seed pulse parameters after its amplification, a parametric space between $(\lambda_{0} /\lambda_{1} )$ and $(\lambda_{{0,{\text{nm}}}} /I_{0,18} )$, defining the maximum compression and intensity in the resonant BRA operation has been identified in [27] (see Fig. 18.10; here λ_nm, I₁₈ and t_fs refer wavelength in nm, intensity in 10¹⁸ W cm⁻² and time in fs units.

Fig. 18.10

a Contour plot describing temporal width of the leading seed spike ($\Delta t_{{1,{\text{fs}}}}$) in terms of $(\lambda_{{0,{\text{nm}}}} /I_{0,18} )$ and $(\lambda_{0} /\lambda_{1} )$. b Contour plot describing optimum intensity of the leading seed spike ($I_{1,18}$) in terms of $(I_{0,18} /\lambda_{{0,{\text{nm}}}} )$ and $(\lambda_{0} /\lambda_{1} )$

As an illustrative case a contour plot demonstrating this region for $I_{1o} \Delta t_{1o} \sim 0.08\;{\text{J}}\,{\text{cm}}^{ - 2}$ having leading spike <1 fs, has been displayed in Fig. 18.10a; this seed parameter is consistent with I_1o ~ 10¹⁴ W cm⁻² and Δt_1o ~ 0.08 fs which has further been used for the numerical calculations. It may readily be seen that the pump with shorter wavelength and large intensity yield larger compression. Similar region has been specified for maximum intensity of the leading spike in Fig. 18.10b; the colored region in figure represents optimum intensity of the leading spike. This concludes that the maximum intensified seed pulse via resonant BRA could be achieved for a moderate plasma density and large intensity pump operating with the shorter wavelengths. These expressions and results (i.e. contour plots) are general in nature and are applicable to arbitrary system parameters for a given seed fluence. The largest seed intensity is achieved in the plasma of lowest possible density (wave-breaking density) i.e. $\omega_{2} \sim \omega_{1} (c^{2} k_{2}^{2} I_{0} /4\omega_{1} \omega_{0} I_{\text{M}} )^{1/3}$. Maximizing the above equations over the plasma density at wave breaking density, the maximum achievable seed intensity can be obtained as the following: $I_{ \hbox{max} } \approx 16(I_{\text{M}}^{2} I_{0} )^{1/3} (3\delta_{o} \omega_{1} /ck_{2}\Lambda _{0} )^{2/3}$.

From the above discussion one can conclude that a pump source could be a free electron laser (FEL) [28], which can be produced by using PW lasers, for electron bunch acceleration (I₀ ~ 10²¹ W/cm², $\lambda \approx 800\,{\text{nm}}$) up to energy ~10 meV. Such electron bunch can be used as electron source for preliminary injection to FEL. For example, FEL output pulse of Fermi light source [28] is specified by spectral range ~60 nm, peak power ~10 GW, pulse length ~50 fs, spot size ~200 µm, and intensity ~10¹³ W/cm². A system like [29] can be used to optimize the focal spot and pulse intensity, thus one can say that the anticipated FEL pump pulse can further be compressed spatially to a ~µm size spot and thus the intensities of the order of ~10¹⁸ W/cm² can be achieved. The schema of BRA setup, consistent with ELI-ALPS parameters is shown in Fig. 18.11.

Fig. 18.11

A schematic of the feasible BRA setup, relevant to ALPS infrastructure

The thickness of the amplified overdense plasma layer should be of the order of half of the pump pulse duration (~10’s µm). Such plasma layers can be generated via illuminating of target surface through the long duration intense laser pulses; for example ~100 µm width plasma of density (~10²² cm⁻³, 100 eV) has experimentally been obtained (see for example [30]). We will use quasi-FEL source and the pump may be specified with intensity $I_{0} \approx 10^{17} \,{\text{W}}/{\text{cm}}^{2}$ ($\lambda_{0} \approx 40\,{\text{nm}}$). The parameters for the ultra-short seed pulse ($\lambda_{1} \approx 60\,{\text{nm}}$) viz. the pulse length and energy has been taken from above. We take $\tau_{1} \le 1\,{\text{fs}}$ seed pulse into account to commence further parametric configuration. The plasma density, consistent with the resonant conditions is found to acquire a value ($n_{\text{e}} \le n_{\text{cr}} /4$). The pump intensity is taken below the L-wave breaking threshold intensity. For this case, the seed pulse may acquire the linear growth rate. For the initial seed pulse features consistent with parameter access ELI-ALPS facility, one gets the number of seed pulse exponent: $\Lambda _{0} \approx 8$. For the pump laser and plasma parameters one gets $T_{e} \sim 1.5\;{\text{keV}}$ and corresponds to plasma wave noise exponentiations $\Lambda _{p}$ is slightly higher than $\Lambda _{0}$ and consistent with the obligation to achieve prominent amplification. The maximum intensity achieved by the seed pulse after amplification is $I_{1m} \approx 10^{19} \,{\text{W}}/{\text{cm}}^{2}$. Subsequently, the shortest achievable duration of the output seed pulse is $\delta t_{\text{s}} \le 0.9\,{\text{fs}}$ (the pulse may be compressed to 400 as). The seed pulse evaluation leads to maximal possible amplification time $t_{\text{M}} \approx 160\,{\text{fs}}$, this certainly limits the maximum duration of pump pulse ($\tau_{0} \sim 2t_{\text{M}}$) and hence the plasma width ($l \le ct_{\text{M}} \approx 48\,\upmu{\text{m}}$). The criteria for the length of the plasma can be expressed as $l < c/\nu_{ib} \sim 700\,\upmu{\text{m}}$. The sterner one between the two limits should be preferred for plasma scaling. In this case $T_{\text{e}} \ll T_{\text{M}}$ and Landau damping of plasma waves during amplification can be ignored. The preliminary pump/seed laser pulse parameters exploring the possibility of seed pulse amplification/ compression, evaluated in this section has been summarized in [31] and listed in Table 18.1.

Table 18.1 Plausible parametric configuration for resonant BRA realization

The seed pulse amplification has been verified via the simulations with help of 1D relativistic electromagnetic particle in cell code. In order to simulate BRA, in the scheme we take into account of the interaction between the counter propagating harmonics of a reference fundamental frequency ($\omega_{\text{f}}$). To mimic laser and seed wavelengths we use $\omega_{\text{f}} { = 1} . 5 7\cdot 1 0^{ 1 6} \,{\text{s}}^{ - 1}$ and plasma parameters are established via the frequency matching between plasma, pump and seed frequencies, thus the pump and seed frequencies can be referred as $\omega_{0} = 3\omega_{\text{f}}$ and $\omega_{1} = 2\omega_{\text{f}}$. In the case $\omega_{2} = \omega_{0} - \omega_{1}$ this should be equal to the fundamental frequency and the resonant plasma density n_c = 7.82 × 10²² cm⁻³. The temporal profile of the pulse as $\sin^{2}$ is used. The duration of pump and seed pulses are chosen as ~10 and 1 fs respectively. For the simulation $a_{0} \sim 0.3$$(I_{0} \sim 10^{17} \,{\text{W}}/{\text{cm}}^{2} )$ and $a_{1} \sim 0.01(I_{1} \sim 10^{14} \,{\text{W}}/{\text{cm}}^{2} )$ corresponding to pump and seed pulses, are used as the normalized laser fields. In the simulations one can see that the peak electric field of the seed pulse is amplified by a large factor (say two orders of magnitude) due to resonant BRA and thus the intensity of the input seed is enhanced by four orders of magnitude. For the same set of data used for these simulations, we have made analytical amplification estimates [27]. The corresponding intensities of the amplified seed pulse for both the simulations and analytical model, are shown in Fig. 18.12.

Fig. 18.12

a The amplification factor ($I_{{1{\text{m}}}} /I_{1}$) of the amplified seed pulse as a function of pump intensity ($I_{0}$); the results refer to pump pulse $\lambda_{0} = 40\,{\text{nm}}$, $\tau_{0} = 10\,{\text{fs}}$, seed with $I_{1} \approx 0.1I_{15}$, $\lambda_{1} = 60\,{\text{nm}}$, $\tau_{1} = 1\,{\text{fs}}$ and the plasma density corresponds to the resonant condition $\lambda_{2} = 120\,{\text{nm}}$ ($\sim n_{\text{e}} \sim n_{\text{cr}} /4$). The black and red color marks refer to PIC and analytical results; b the amplification factor ($I_{{1{\text{m}}}} /I_{1}$) of the amplified seed pulse as a function of the seed duration ($\tau_{1}$); the results refer to $\lambda_{0} = 40\,{\text{nm}}$, $I_{0} \approx I_{18}$, $I_{1} \approx 0.1I_{15}$, $\lambda_{1} = 60\,{\text{nm}}$, $\tau_{0} = 10\,{\text{fs}}$ and $n_{\text{e}} \sim n_{\text{cr}} /4$ (resonant case); the curves refer to PIC results

From the above it is seen that the simulation results are in order of magnitude agreed with the calculations based on the analytical model. It is also seen that the analytical and simulation results are converging for the high intensity pump. For smaller amplitude seed pulses the decrease in the amplification can be attributed to the smaller energy transfer from the pump during amplification and some stretching of the seed pulse duration, which results in decrease of seed peak intensity. For the optimal choice of the system parameters, seed pulse can be intensified by ~four orders of magnitude, but the pulse compression is not so simple and in this case one need to operate pump at order of magnitude higher intensity. Nonetheless, based on the present analysis, it may be concluded that the resonant BRA operating in XUV regime may efficiently be utilized to amplify and compress the weak ultra-short pulses to Exawatt cm⁻² and sub fs time scale.