1 Introduction

The phenomenon of the self-focusing (SF) of electromagnetic waves was predicted by Askaryan in 1962 in general form, more than fifty years ago. In his paper devoted to this effect, he wrote [1] “The action of the light beam on the medium can become so strong, that the properties of the medium within the beam differ from those outside the beam. It causes waveguide propagation of light beam and cancels the divergence of the beam due to diffraction. This phenomenon can be named as the self-focusing of the electromagnetic beam”. SF is described by the system of nonlinear parabolic equations for the slowly varying amplitudes \( E_{ \pm } = (E_{x} \pm iE_{y} )/\sqrt 2 \) of the circularly polarized components of the electric field. The first efforts to analyze the spatial dynamics of the intensity and polarization distributions of the propagating laser light were taken in [2,3,4,5,6]. The system of equations for the dimensionless waist sizes \( f_{ \pm } \) of the circularly polarized partial beams was solved numerically in [5, 6] and the monotonic and non-monotonic regimes of \( f_{ \pm } \) behavior were found. The oscillation and other regimes of polarization ellipse’s ellipticity degree dependence on the propagation coordinate were derived in [7]. The self-focusing of an elliptically polarized light beam with the Gaussian profile in an isotropic medium with spatial nonlocality of nonlinear optical response is studied in [8, 9]. The examination of the system of equations for \( E_{ \pm } \) using the method of moments showed that the distribution of the intensity of an originally homogeneously elliptically polarized beam loses its Gaussian shape in the process of light propagation in nonlinear medium and its polarization distribution becomes non-uniform in the plane of the beam cross-section [8]. The obtained dependencies of the light intensity, the ellipticity degree of the polarization ellipse and the angle of orientation of the major axis of the polarization ellipse on the spatial coordinates were found to be in a reasonable accordance with numerical simulations data near the axis of the beam [9, 10].

More than forty years ago SF of laser pulses with duration of few tens picoseconds in isotropic phase of nematic liquid crystal (NLC) at temperature close to the temperature of nematic-isotropic phase transition (NIPT) was of a special interest due to peculiarities of the light propagation dynamics. Among them one can point out significant growth of nonlinear optical response (a few orders of magnitude higher compared to ordinary liquids) and the dramatic increase of its relaxation time when approaching the temperature of NIPT, the existence of low limit of focused beam waist size regardless of initial power of laser radiation, its unusual robustness—the beam did not split into separated filaments [11, 12], transformation of elliptical polarization of laser beam into linear during its propagation [13]. Theoretical research of elliptically polarized beam SF in isotropic phase of NLC at temperature close to NIPT demonstrated [14] that many of the above peculiarities are caused by strong nonlocality of nonlinear optical response in this specific temperature domain. The nonlocality itself is caused by inter-molecular correlations near NIPT and medium heating. The theory of optical response of liquid crystal was developed and comprehensively described in [15, 16]. Flexibility of liquid crystals makes them one of the most prominent media for changing and designing of phase and polarization profiles of propagating laser radiation.

The complicated spatial evolution of the intensity and polarization during light SF lets one to suppose the formation of the points of polarization singularity (C-points) in which the elliptical polarization of the propagating radiation degenerates into a circular one [17, 18]. C-points are differentiated by their topological charge and type. The topological charge is the variation of orientation angle of the major axis of the polarization ellipse calculated along a small closed loop surrounding the C-point and normalized on 2\( \pi \) (customarily, this quantity can be either 1/2 or −1/2) [17]. Each topological type of C-point corresponds to the qualitatively different distribution of the polarization ellipses near the point of singularity. In literature three topological types are known: lemon (topological charge 1/2), monstar (topological charge 1/2) and star (topological charge −1/2) [17]. In three dimensions, the loci of these points are the lines, which are called C-lines.

Liquid crystal optical elements are now widely used in experimental singular optics. The researches of last ten years have shown that optical vortices may appear when light propagates in NLC with topological defects—disclinations that spontaneously appear in films under degenerate planar anchoring [19], generated by external fields [20, 21], or even light-driven quasi-static electric field [22]. Recent paper [23] reports an effective way to generate optical vortices in wide spectrum range using Bragg reflection of the light from the layer of cholesteric liquid crystal with topological defect. Finally, optical vortices and polarization singularities can naturally arise as a result of optical anisotropy in LC without topological defects [24, 25].

Light singularities are of special interest in nonlinear optics. Structurally stable singularities formation was experimentally observed in several nonlinear optical processes in crystals: photorefraction [26, 27], Pockels effect [28,29,30], Faraday effect [31]. A number of theoretical researches discover the complicated dynamics of C-points generated on the surface and in the bulk of isotropic media with spatial dispersion of quadratic nonlinearity by the fundamental beams with polarization singularities in sum-frequency generation and second harmonic generation processes [32, 33]. Optical singularities behavior in filamentation and supercontinuum generation processes were studied in [34,35,36]. Until recently, the possibility of polarization singularities formation in Gaussian beam, self-focusing in isotropic medium with cubic nonlinearity, was not researched, except for [10]. However, the specific range of the nonlinear medium’s parameters considered in this paper did not allow polarization singularities to appear.

In the present work we study the possibility of C-points formation in the process of SF of an initially uniformly elliptically polarized Gaussian beam in an isotropic medium with cubic nonlinearity (without frequency and spatial dispersion) and in isotropic phase of NLC near the temperature of NIPT.

2 Basic Equations of the Self-focusing of Elliptically Polarized Laser Beam in an Isotropic Medium and in an Isotropic Phase of NLC

The propagation along z axis of an elliptically polarized light beam in an isotropic medium with cubic nonlinearity is described by the following system of equations [8, 9] for the slowly varying complex amplitude \( E_{ \pm } (x,y,z) \) of circularly polarized wave:

$$ \frac{{\partial E_{ \pm } }}{\partial z} + \frac{i}{2k}\Delta _{ \bot } E_{ \pm } = - i\sigma (|E_{ \pm } |^{2} + 2|E_{ \mp } |^{2} )E_{ \pm } . $$
(1.1)

Here \( \sigma = 2\pi \omega^{2} \chi_{xxyy}^{(3)} /kc^{2} \) is proportional to the component of the local nonlinear susceptibility tensor \( \hat{\chi }^{(3)} (\omega ;\omega ,\omega , - \omega ) \), \( k \)—is the wave number, the transversal Laplacian \( \Delta _{ \bot } = \partial^{2} /\partial r^{2} + r^{ - 1} \partial /\partial r \), where \( r = (x^{2} + y^{2} )^{1/2} \).

In isotropic phase of NLC the propagation of elliptically polarized light beam is described by two parabolic equations for \( E_{ \pm } (x,y,z) \):

$$ \frac{{\partial E_{ \pm } }}{\partial z} + \frac{i}{2k}\Delta _{ \bot } E_{ \pm } = - \frac{2\pi ik}{{3n^{2} }}\Delta \chi (QE_{ \pm } + q_{ \pm } E_{ \mp } ). $$
(1.2)

This system generalizes the equation used in [14] for describing the linearly polarized light. Here n is a linear refractive index of NLC in the isotropic phase, \( Q = Q_{xx} + Q_{yy} \), \( q_{ \pm } = Q_{xx} - Q_{yy} \pm 2iQ_{xy} \), where \( Q_{ij} \) is a traceless three-dimensional symmetrical real tensor of NLC ordering parameter [37], which determines the anisotropic term \( \Delta \chi \) of medium linear dielectric susceptibility tensor \( \hat{\chi } \), induced by electromagnetic field, \( \chi_{ij} = (\text{Tr} \{ \hat{\chi }\} \delta_{ij} + 2\Delta \chi Q_{ij} )/3 \). The equations for \( Q_{ij} \) in stationary case are obtained by varying the expression for free energy of NLC in isotropic phase close to NIPT in the presence of electromagnetic field [11, 12, 15, 16]. Following [37], we represent the density F of free energy as a Taylor series, including main terms up to the second power of \( Q_{ij} \) tensor invariants (and its spatial derivatives):

$$ F = F_{0} + \frac{1}{2}[a\Delta TQ_{ij}^{2} + L_{1} (\partial_{i} Q_{jk} )^{2} ] - \frac{1}{3}\Delta \chi Q_{ij} E_{i}^{ * } E_{j} . $$
(1.3)

In (1.3), \( F_{0} \) is free energy density of isotropic phase of NLC, \( L_{1} \) and a are parameters that do not depend on temperature \( T = {\text{const}} \), \( \Delta T = T - T^{ * } \), where \( T^{ * } \) is slightly below the actual NIPT temperature [37, 38]. Using the properties of the tensor of NLC ordering parameter \( \text{Tr} \{ \hat{Q}\} = 0 \), \( Q_{ij} = Q_{ji} \) and varying (1.3), we obtain the equations for \( Q \) and \( q_{ \pm } \):

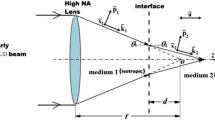
$$ \begin{aligned} (a\Delta T - L_{1}\Delta _{ \bot } )Q & = \frac{{\Delta \chi }}{18}(|E_{ + } |^{2} + |E_{ - } |^{2} ), \\ (a\Delta T - L_{1}\Delta _{ \bot } )q_{ \pm } & = \frac{{\Delta \chi }}{3}E_{ \pm } E_{ \mp }^{ * } . \\ \end{aligned} $$
(1.4)

Let an initially homogenously polarized beam with plane wavefront and Gaussian-like intensity profile fall normally on flat medium surface \( (z = 0) \). Its circularly polarized components are then given by the expressions:

$$ E_{ \pm } (x,y,z = 0) = I_{0}^{1/2} (1 \pm M_{0} )^{1/2} {\text{exp[}} - (x^{2} /b^{2} + y^{2} )/r_{0}^{2} ]. $$
(1.5)

Here \( r_{0} \) is beam waist size, \( I_{0} \) is maximum of normalized intensity \( I(x,y,z) = (|E_{ + } |^{2} + |E_{ - } |^{2} )/2 \) in plane \( z = 0 \). In (1.5), constant \( M_{0} = M(x,y,z = 0) \) where ellipticity degree of polarization ellipse \( M(x,y,z) = (|E_{ + } |^{2} - |E_{ - } |^{2} )/2I_{0} \). Varying \( M_{0} \) it is possible to obtain any polarization state of incident radiation: from right hand circularly polarized \( (M_{0} = - 1) \) through linearly polarized \( (M_{0} = 0) \) to left-hand circularly polarized \( (M_{0} = 1) \) light. Parameter \( M_{0} \) is actually the third normalized Stokes parameter. The real constant \( b \ge 1 \) characterizes stretching of the beam intensity profile along x-axis. It is readily shown that problems (1.1), (1.5) and (1.2), (1.4), (1.5) are symmetrical with respect to simultaneous substitutions: \( M_{0} \) to \( - M_{0} \), \( q_{ \pm } \) to \( q_{ \mp } \), and \( E_{ \pm } \) to \( E_{ \mp } \). For this reason, we will further assume that \( M_{0} \ge 0 \).

3 Polarization Singularities in the SF in an Isotropic Kerr Medium

It is natural to expect the C-lines formation with left-hand circular polarization when \( |E_{ - } (x,y,z)|^{2} \ll |E_{ + } (x,y,z)|^{2} \). The equation \( r_{m} (z_{m} ) \), determining the series of curves, can be easily obtained [39] from limiting condition \( E_{ - } (x,y,z) = 0 \) and the system (1.1) in the following form:

$$ r_{m} (z_{m} ) = - \left( {\frac{{\partial^{2} E_{ - } }}{{\partial r^{2} }}} \right)_{\begin{subarray}{l} r = r_{m} , \\ z = z_{m} \end{subarray} }^{ - 1} \left( {\frac{{\partial E_{ - } }}{\partial r}} \right)_{\begin{subarray}{l} r = r_{m} , \\ z = z_{m} \end{subarray} } , $$
(1.6)

where \( m = 1,2,3, \ldots \). In the case of axial symmetry \( (b = 1) \) separate C-line with number “\( m \)” has the shape of a circumference \( r_{m} (z_{m} ) \) with radius \( r_{m} \) that fully lies in the plane \( z = z_{m} \). The physical reasons of the C-line formation at distances \( z_{m} \) from the nonlinear medium border are discussed in detail in [39].

We illustrate the C-lines formation by the numerical simulations, when axially symmetric uniformly elliptically polarized incident beam has the normalized intensity \( I_{0} \sigma L_{d} = 1.7 \) \( (L_{d} = kr_{0}^{2} ) \) and ellipticity degree of polarization ellipse \( M_{0} = 0.85 \). The first C-line \( r_{1} (z_{1} ) \) appears at the distance \( z_{1} \) and lies in the interval \( 1.46L_{d} < z_{1} < 1.47L_{d} \). It is interesting that in this range of propagation coordinate the distribution of the transversal component of the electromagnetic energy flow (its general form can be found, for example, in [35]) changes significantly with increasing  \( z \). For \( z < z_{1} \) the beam cross-section is divided into four zones (Fig. 1.1a): “gray” center (I), “white” internal ring (II), “gray” external ring (III) and “white” peripheral zone (IV). The direction of transversal flow of energy is indicated by arrows. As the \( z \)-coordinate increases the distribution of the transversal component of the electromagnetic energy flow changes significantly (Fig. 1.1b): the zone II is expanding, consuming zone III. As a result for \( z > z_{1} \) only the central zone (I), in which the light energy flows toward the beam’s axis, and the peripheral zone (IV), where the energy flows away, are presented in laser beam cross-section.

Fig. 1.1
figure 1

Transversal distribution of electromagnetic energy flow in the plane \( z/L_{d} = 1.46 \) (a) and \( z/L_{d} = 1.47 \) (b)

Full size image

The appearance of C-line \( r_{1} (z_{1} ) \) takes place during SF of light with \( |M_{0} | \) close to 1. In [8] the SF was considered for the almost linearly polarized beams, and this is the reason why the C-lines did not appear. Figure 1.2 illustrates typical dependency \( z_{1} (M_{0} ) \) when the normalize intensity is set. The closer the state of polarization is to the circular one, the closer to the medium border the C-line arises.

Fig. 1.2
figure 2

Dependency of distance \( z_{1} /L_{d} \) between the medium’s border and the plane, containing C-line, on the initial ellipticity degree \( M_{0} \). The normalized intensity \( I_{0} \sigma L_{d} = 1.7 \)

Full size image

If the axial symmetry of an incident beam is broken \( (b > 1) \), C-line transform from the circumference that fully lies in the beam cross-sections into a three dimensional curve. It intersects a continuous set of the transversal cross-sections of the propagating beam, leading to the formation of C-points. Figure 1.3 shows the dependencies \( z_{n} (b) \) (squares) and \( z_{a} (b) \) (circles), where two pairs of C-points with opposite topological charges are nucleated and annihilated correspondingly. The length of the segment \( [z_{n} (b),\;z_{a} (b)] \) is increasing as the parameter \( b \) grows.

Fig. 1.3
figure 3

Dependency of nucleation coordinate \( z_{n} /L_{d} \) (squares) and annihilation coordinate \( z_{a} /L_{d} \) (circles) of C-points on the axes ratio of the incident beam elliptical intensity profile in the case of \( M_{0} = 0.85 \) and \( I_{0} \sigma L_{d} = 1.7 \)

Full size image

The generated C-points are marked by filled (charge 1/2) and empty (charge −1/2) circles in Fig. 1.4, where the distribution of transverse electromagnetic energy flow is shown for two values of the propagation coordinate from the segment \( [z_{n} (b),\;z_{a} (b)] \). C-points located near the sharp ends of the crescents and in the vicinity of the singularities the energy flow is vortex-like. As \( z \)-coordinate increases, zones IIIa and IIIb in Fig. 1.4a are getting smaller (Fig. 1.4b). When the zones IIIa and IIIb vanish, the C-points collide and annihilate each other.

Fig. 1.4
figure 4

Transversal distributions of energy flow in the cross-section of the propagating beam with the parameters \( b = 1.03 \), \( M_{0} = 0.85 \), \( I_{0} \sigma L_{d} = 1.7 \) at distance \( z/L_{d} = 1.57 \) (a) and \( z/L_{d} = 1.60 \) (b). Filled and empty circles mark the C-points with topological charge \( 1/2 \) and \( - 1/2 \) correspondingly

Full size image

Figure 1.5a shows the distribution of polarization ellipses for the same incident beam parameters for which Fig. 1.4a is represented. In Fig. 1.5a each ellipse has the same eccentricity and orientation as the polarization ellipse in the point in the laser beam cross-section, corresponding to the ellipse center and the black curve marks the e−1 intensity level. The distributions of the polarization lines, which are tangent in every point to the major axis of the corresponding polarization ellipse, are shown in the vicinity of the C-points with the coordinates \( x/r_{0} = 1.54 \), \( y/r_{0} = 0.89 \) (Fig. 1.5b) and \( x/r_{0} = 1.54 \), \( y/r_{0} = - 0.89 \) (Fig. 1.5c). The first C-point has the topological charge 1/2 and represents a monstar type (three polarization lines are meeting at the singularity point and they lie inside a straight angle). The second one has the topological charge −1/2 and is of a star type, because three polarization lines are meeting at the point, but they do not lie inside a straight angle.

Fig. 1.5
figure 5

Polarization ellipses distribution in the transversal cross section of the beam (a) and polarization lines close to the C-points in dashed squares (b and c) at the distance \( z/L_{d} = 1.57 \). Filled (empty) circles mark the C-points with topological charge 1/2 (−1/2). The beam’s parameters are the same as in Fig. 1.4a

Full size image

4 Polarization Singularities in the SF in an Isotropic Phase of NLC Near the Temperature of INPT

In the hypothetical limit case \( L_{1} = 0 \) (which is actually impossible for any liquid crystal), (1.2), (1.4), can be simplified to those describing the evolution of \( E_{ \pm } \) during SF in the isotropic medium with Kerr-like nonlinearity without spatial dispersion [8]. Even in this particular case, circularly polarized components \( E_{ \pm } \) can propagate in medium very differently (qualitatively different regimes of \( E_{ \pm } \) evolution are thoroughly described in [8]). Various criteria of SF collapse of propagating radiation lead to various expressions for the threshold intensity. The appearance of C-points is possible in certain cases [39] if the polarization of the incident beam is close to circular. The phenomena described in [39] are caused by the aberrations of the propagating beam in light-induced nonlinear Gaussian-like lens, which are studied in general in [40] and particularly in [41].

At sufficiently small \( L_{1} \), (1.4) have approximate solutions

$$ \begin{aligned} Q & \approx \frac{{\Delta \chi }}{{18a\Delta T}}\left( {1 + \frac{{L_{1} }}{{a\Delta T}}\Delta _{ \bot } } \right)\left( {|E_{ + } |^{2} + |E_{ - } |^{2} } \right), \\ q_{ \pm } & \approx \frac{{\Delta \chi }}{{3a\Delta T}}\left( {1 + \frac{{L_{1} }}{{a\Delta T}}\Delta _{ \bot } } \right)\left( {E_{ \pm } E_{ \mp }^{ * } } \right), \\ \end{aligned} $$
(1.7)

from which it is evident that intensity growth in the beam center and the collapse of the beam, caused by SF, lead to corresponding growth of absolute values of transversal derivatives of the electromagnetic field near the beam axis. Being negative, the summands with transversal derivatives slow down the growth of absolute values of \( Q \) and \( q_{ \pm } \), which is followed by their decrease, so the beam starts defocusing. This process can happen several times during beam propagation. As a result, a multi-focal structure is formed inside NLC [14]. If the nonlocality of NLC is strong enough, its defocusing impact is noticeable even at early stages of beam propagation and there is no sharp increase of beam intensity, which is typical to self-focusing. In this paper, we consider such values of dimensionless power \( P = \pi I_{0} (k\omega\Delta \chi )^{2} /(54n^{2} a\Delta T) \), \( \eta = L_{1} /(a\Delta Tr_{0}^{2} ) \) and \( M_{0} \), that provide the multi-focal structure formation in the bulk of NLC. We stress out that all three values are determined both by NLC properties and incident beam parameters, so one can easily control the self-focusing regime in a real experiment.

First of all, we consider axially symmetrical incident beams (\( b = 1 \) in (1.5)). Owing to the symmetry rules, lines of purely circular polarization (C-lines) can only be circles, the planes of which are perpendicular to the beam axis. Centers of the circles lie on the beam axis as well. In numerical simulations carried out in \( \{ r,z\} \) space, we looked for special points \( (r_{i} ,z_{i} ) \) (\( i = 1,2,3, \ldots \)) in which \( E_{ + } \) \( (E_{ - } ) \) equals zero and \( \text{Arg} \{ E_{ + } \} \) \( (\text{Arg} \{ E_{ - } \} ) \) is not determined. These points correspond to C-lines described above, as the polarization ellipse there degenerates into a circle.

When \( M_{0} \sim 1 \) the following inequality is valid \( |E_{ + } (r,0)| \gg |E_{ - } (r,0)| \) and the power of the right-hand circularly polarized component is much greater than that of the left-hand one at NLC border. Thus, the propagation dynamics of \( E_{ + } \) and \( E_{ - } \) are significantly different. The mean period of multi-focal structure (sequence of maxima and minima) of dependency \( |E_{ - } (0,z)| \) is much shorter than that of dependency \( |E_{ + } (0,z)| \). The SF of partial left-hand polarized beam \( E_{ - } \) is much weaker: its peak intensity variation is not so big compared to the right-hand circularly polarized component \( E_{ + } \). Due to the \( E_{ \pm } \) cross-interaction , there are short-period minor perturbations in \( |E_{ + } (0,z)| \) dependency as well that are caused by \( |E_{ - } (0,z)| \) fast oscillations.

Our numerical simulations show that ring-shaped C-lines with left-hand (right-hand) polarization appear close to the cross-sections, in which the peak intensity of left-hand (right-hand) circularly polarized component attains local maxima. The left column in Fig. 1.6 shows typical dependencies \( \arg \{ E_{ + } (r,z)\} \) (a), \( |E_{ \pm } (0,z)| \) (b) and \( \arg \{ E_{ - } (r,z)\} \) (c) in case \( M_{0} = 0.85 \). Two-dimensional gray-scale diagrams show the phase distributions of circularly polarized partial beams in \( r,z \) space. Circles mark the points where the phase is not determined. Each point is connected by a thin vertical line with the corresponding dependency of right-hand circularly polarized (solid line) or left-hand circularly polarized (dashed line) partial beam peak intensity on propagation coordinate  \( z \).

Fig. 1.6
figure 6

The dependencies of the field parameters of the beam in the bulk of NLC at \( P = 2 \), \( \eta = 0.009 \), and \( M_{0} = 0.85 \) (a–c) and \( \eta = 0.07 \) and \( M_{0} = 0.4 \) (d–f). Subfigures (a, d) show the evolution of phase radial distribution of the right-hand circularly polarized component and (c, f) show the same of the left-hand polarized one. The black color corresponds to the zero phase, and the white color corresponds to phase \( 2\pi \). Subfigures (b, e) show the peak intensities of the right-hand (solid line) and the left-hand (dashed line) circularly polarized components of the beam. Thin vertical lines designate cross-sections, containing C-lines. Their intersections with plane containing \( z \)-axis are marked by circles in (a, c, d, f)

Full size image

It can be derived from (1.2), (1.4) that in the extreme case of the right-hand circularly polarized incident radiation \( (M_{0} = 1) \) its polarization state remains constant during propagation. However, even in this case the circumferences on which the intensity of the beam is zero (phase singularities) appear in the cross-sections that are close to multi-focal structure maxima. Short-period perturbations of \( |E_{ + } (0,z)| \) dependency are absent in this particular case.

When the polarization state is not close neither to circular nor to linear one \( (0 < M_{0} < 1) \), the periods of multi-focal structure formed in NLC can be close enough (Fig. 1.6e). In this case, \( |E_{ + } (r,0)| > |E_{ - } (r,0)| \) and the left-hand polarization singularities (zeros of \( E_{ + } \)) are formed more rarely—only in the cross-sections that are close to \( |E_{ + } (0,z)| \) maxima, which is characteristic to the case \( M_{0} \sim 1 \). Right-hand polarization singularities (zeros of \( E_{ - } \)) are formed more often (Fig. 1.6f), but their \( z \)-coordinates are shifted away from positions of peak intensity maxima of \( E_{ - } \) component. As \( M_{0} \) increases and initial polarization of the beam is getting close to circular, the phase distributions \( \arg \{ E_{ \pm } (r,z)\} \) are getting more and more different (see right and left columns in Fig. 1.6). The distance between left-handed C-lines is getting shorter and eventually the singularities occupy the cross-sections close to peak intensity maxima of \( E_{ - } \) component (Fig. 1.6c).

Fig. 1.7
figure 7

Peak amplitude (a) and phase distribution (b) of the initially linearly polarized beam in NLC (\( P = 1.7 \), \( \eta = 0.06 \)). The black color corresponds to the zero phase, and the white color corresponds to phase \( 2\pi \). Thin vertical lines designate cross-sections, containing lines of phase singularities. Their intersections with the plane containing \( z \)-axis are marked by circles

Full size image

As the polarization state of the incident beam is getting close to linear, the phase and peak intensity dependencies in right column of Fig. 1.6 become more and more identical. Generated C-lines remain circles centered at the beam axis and they lie close to the corresponding peak intensity maxima. C-lines of opposite polarization handedness are getting closer to each other. However, a distinctively new family of C-lines appear in the beam when \( M_{0} \to 0 \). They have the same geometry as the “old” ones, but they are located close to local minima of \( |E_{ \pm } (0,z)| \) functions. The radii of these “new” C-lines are few times greater than those of the “old” ones. In the limit case of linearly polarized incident beam \( (M_{0} = 0) \), the equality \( |E_{ + } (r,z)| = |E_{ - } (r,z)| \) is valid in any point inside NLC. Thus, the complex amplitudes of circularly polarized components of the beam can attain zero values only simultaneously. In this case, phase singularities (points of zero intensity of light field) are formed. When \( M_{0} \) slightly deviates from zero, the phase distribution of more powerful right-hand polarized component \( \arg \{ E_{ + } (r,z)\} \) changes rapidly and the radii of left-hand polarized C-lines, located close to minima of multi-focal structure, dramatically increase. As a result, only these left-hand polarized C-lines, which lie close to maxima of \( |E_{ + } (0,z)| \approx |E_{ - } (0,z)| \), are left near the axis of the beam. The radii of right-hand polarized C-lines, on which \( E_{ - } = 0 \), change significantly slower, when \( M_{0} \) increased from zero. Figure 1.7 shows typical dependencies of peak amplitudes \( |E_{ \pm } (0,z)| \) (a) and phase distribution \( \arg \{ E_{ \pm } (r,z)\} \) (b) at \( P = 1.7 \), \( \eta = 0.06 \).

C-lines of both polarization handednesses emerging during SF of a light beam in the bulk of NLC are stable with respect to small disturbance of beam at medium border [42]. For example, stretching of beam transversal intensity profile along \( x \)-axis transforms initially planar ring-shaped C-lines into fully three-dimensional saddle-like curves. The examples of two of these C-lines with right-hand and left-hand circular polarization are shown in Fig. 1.8a, b. Each of the curves occupies a certain domain of transversal cross-sections \( z_{ni} - z_{ai} \) and form points of polarization singularities (C-points) at intersections. In cross-sections with coordinates \( z_{ni} \), pairwise nucleations of four C-points of opposite topological charges take place and in cross-sections with coordinates \( z_{ai} \) these C-points annihilate in pairs. The sum topological charge of nucleated C-points is zero. As the stretching parameter \( b \) in (1.5) increases and transversal intensity profile of the beam becomes more elliptical, C-lines get more deformed and domains of \( z \)-coordinate in which C-points exist are expanding (Fig. 1.8b, d). Since these C-lines are caused by wavefront aberrations of \( E_{ \pm } \) components, they look like the nodal lines that are discussed in [40, 41]. The expansion of the domain \( z_{ni} - z_{ai} \) was previously shown for the C-lines that are studied in [39].

Fig. 1.8
figure 8

Three-dimensional right-hand (a) and left-hand (b) C-lines at \( b = 1.05 \) and c, d dependencies of corresponding nucleation (squares) and annihilation (circles) \( z/L_{d} \)-coordinates on beam stretching parameter \( b \). Other beam and medium parameters are \( P = 2 \), \( \eta = 0.05 \), \( b = 1.05 \), \( M_{0} = 0.85 \). In (a, b), white stars show the points of singularities nucleation and black stars show the points of their annihilation

Full size image

Other kind of light singularities is three-dimensional surfaces on which the polarization is linear (L-surfaces) . The intersections of these surfaces with the cross-sections of the beam (L-lines) are separating the regions with right-hand and left-hand polarized light. In major part of space, the beam, which we consider in this paper, is right-hand polarized and does not contain L-lines. However, they inevitably appear in the vicinity of left-hand polarized C-lines, separating them from the rest of the beam. The thorough analysis of L-lines dynamics is more complicated compared to C-lines and should be the subject of a future investigation.

5 Conclusions

The possibility of generation of polarization singularities during SF of an initially uniformly elliptically polarized Gaussian beam in medium with cubic nonlinearity is shown by numerical simulations. If the incident beam’s intensity profile has no axial symmetry the C-lines generation is possible in separate planes, perpendicular to the beam’s axis. These lines have the shape of circumferences and the closer the initial beam polarization state is to the circular, the closer to the medium’s border the first C-line is. If the incident beam’s intensity profile has no axial symmetry, then there is a segment of propagation coordinate, in which two pairs of C-points exist and their total topological charge is zero. The growth of beam asymmetry leads to the expansion of this segment.

When initially homogenously polarized axially symmetric Gaussian light beam self-focuses in an isotropic phase of NLC at temperature close to the temperature of nematic-isotropic transition, C-lines with right-hand and left-hand circular polarization are formed in its cross-sections that are close to local extrema of peak intensities of corresponding circularly polarized components of the propagating field. These lines are circles centered at beam axis and they appear in wide range of NLC parameters and at any polarization ellipse initial ellipticity degree (except for \( M_{0} = 0 \)). They are also stable to small perturbations of incident beam transversal profile. If one stretches the intensity profile of the incident beam that way, it becomes elliptical, then C-lines become fully three dimensional curves. When intersecting with transversal cross-sections of the beam, they form four C-points, two of which having positive topological charge and two other having negative one.