Abstract
This chapter introduces to the theory of atomic population kinetics and radiative properties of atomic and ionic bound–bound transitions. Particular attention is devoted to the general problems related to an extremely large number of kinetic equations describing populations of Rydberg and autoionization atomic states in plasmas. A new method of reduced kinetics for autoionizing states, the virtual contour shape kinetic theory (VCSKT), is described in details. The method is based on a probability method for LTE- and non-LTE-level populations that allows effective level reduction while preserving all detailed atomic transitions. The representation employs effective relaxation constants that have analytical solutions. The comparison with detailed level-by-level calculations demonstrates high accuracy and large efficiency of the VCSKT. In order to solve many states’ kinetic problems for Rydberg atomic states, the quasi-classical representation of the system of kinetic equations is proposed. In particular, the two-dimensional radiative cascades between Rydberg atomic states are described by a purely classical motion of atomic electrons in a Coulomb field that lose energy and orbital momentum. The general collisional-radiative model for large principal quantum numbers is reduced to an effective diffusion in two-dimensional energy and orbital momentum space. The results of these new kinetic models are compared with standard collisional-radiative kinetics demonstrating an important reduction of computer times, the possibility to obtain scaling relations and to independently study the precision of complex quantum calculations for these many level kinetic problems.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
6.1 Generalized Atomic Kinetics of Non-Equilibrium Plasmas Containing Ions of Various Charge States
6.1.1 Principles of Atomic Line Emission: The Two-Level Atom
Let us consider a two-level atom to understand the basic principles of atomic line emission. Figure 6.1 depicts the two-level atom and the related atomic physics processes. For a two-level atom, the system of differential population equations takes the form:
n1 is the upper level density, n0 the lower level density, ne is the electron density, the C’s are the electron collisional rate coefficients and A is the spontaneous radiative decay rate. In stationary plasmas, d/dt = 0 and (6.1) can readily be solved for the upper-level density:
The intensity of the spectral line is then given by
In the high-density limit when neC10 ≫ A10 and Cd1 = Cd0 = 0 (due to the detailed balance of populating and depopulating collisions from and to levels not explicitly included in the two-level system), the intensity is proportional to the radiative decay rate:
In the low-density limit, however, when neC10 ≪ A10 (Corona model), the intensity is given by
Equation (6.5) shows that the intensity is independent of the spontaneous radiative decay rate. How to understand this result? Let us imagine that we fill a bottle with water that has a hole, see Fig. 6.2 left. The size of the hole (area A) corresponds to the radiative decay rate Arad, the water that flows out of the hole corresponds to the line intensity, and the water flow into the bottle corresponds to the excitation rate C. If the hole is small, the water mounts in the bottle because it cannot escape quickly enough through the small hole.
Let us now imagine that we fill the bottle only with a tiny rate. In this case, the water escapes immediately through the whole and the water is not mounting in the bottle. Under these circumstances, we could increase the size of the hole without changing the amount of water that is escaping from the hole because for the small hole already all water escapes. This regime is equivalent to the case where the intensity does not depend on the radiative decay rate and corresponds to the Corona model. Equation (6.2) shows that in the limit of low densities the upper state population is given by
If the radiative decay rate is small, the upper state population is large (so-called metastable level). This explains why we can observe in experimental spectra line emissions of forbidden transitions with intensities that are of the same order like those for resonance lines. Famous examples are the light emission from the Aurora Borealis (green and red emission from atomic oxygen), the observation of the forbidden lines X and Z of He-like impurity ions in tokamaks (see Sect. 1.2.3) as well as the observation of the intercombination line Y of He-like ions in many dense laser-produced plasmas.
6.1.2 The Principles of Ionic Charge State Distributions in Plasmas
Atomic radiation in plasmas is rather complex as line emission from several ionization stages of the atom contribute at the same time. We therefore start our investigation with the so-called ionic charge state distribution in plasmas. In order to get some insight in the relevant physics, we consider an atomic level with population density nZ and charge state “Z” that is linked to (Z + 1) and (Z − 1) via several elementary atomic processes, see Fig. 6.3: electron collisional ionization I, three-body recombination T, radiative recombination R, and dielectronic recombination D. These processes are defined as follows (see also Chap. 1 and Sect. 3.5):
- Ionization::
-
\({X}^{Z} + {e} \to {X}^{{{Z} + 1}} + {e} + {e}\)
- Three-body recombination::
-
\({X}^{Z} + {e} + {e} \to {X}^{{{Z} - 1}} + {e}\)
- Radiative recombination::
-
\({X}^{Z} + {e} \to {X}^{{{Z} - 1}} + \hbar \omega_{{\text{rad}.\text{recom}.}}\)
- Dielectronic recombination::
-
\({X}^{Z} + {e} \to {X}^{{{Z} - 1,**}} \to {X}^{{{Z} - 1,*}} + \hbar \omega_{\text{sat}} \to {X}^{{{Z} - 1}} + \hbar \omega_{\text{l}}\)
\({X}^{Z}\) characterizes an atom “X” in charge state “Z”, “e” is an electron in the continuum, \(\hbar \omega_{{\text{rad}.\text{recom}.}}\) is the continuum radiation of the radiative recombination. \({X}^{{{Z},*}}\) and \({X}^{{{Z},**}}\) characterize single- and double-excited ions, \(\hbar \omega_{\text{sat}}\) and \(\hbar \omega_{\text{l}}\) indicate bound–bound radiation from atomic and ionic lines. The dielectronic recombination describes a multistep process: it starts from the so-called dielectronic capture of a continuum electron that forms first a double-excited atom \({X}^{{{Z} - 1,**}}\) (means that the energy of the recombining originally free electron is used to excite another bound electron in the atom). De-excitation is via successive radiative decays between bound atomic levels, creating the photons \(\hbar \omega_{\text{sat}}\) and \(\hbar \omega_{\text{l}}\). The photon \(\hbar \omega_{\text{sat}}\) originates from a double-excited state and is called “dielectronic satellite”. As the atoms start from charge state “Z” and end up finally in charge state “Z − 1”, effective recombination has occurred.
The evolution of the atomic populations can be described by the following system of differential rate equations:
Let us now consider explicit solutions of the set of (6.7). The stationary solution is given by
Due to the \(n_{\text{e}}^{2}\)-dependence of the three-body recombination, radiative recombination and dielectronic recombination are negligible compared to three-body recombination at high densities:
The ionization rate coefficient \(I_{\text{Z,Z} + 1}\) is related to the three-body recombination rate coefficient \(T_{\text{Z}+ 1,\text{Z}}\) via the principle of microreversibility (see also Sects.7.7.2 and 10.6.5.4) that for a system containing Maxwellian electrons at temperature Te takes the form (\(E_{\text{Z,Z} + 1}\) is the ionization energy from the charge state “Z” to charge state “Z + 1”):
With the help of (6.10), (6.9) can be rewritten as:
Equation (6.11) is equivalent to the famous Saha–Boltzmann equation. Note that (6.11) connects only two levels in charge states “Z” and “Z + 1”, whereas the so-called Saha-equation connects all levels from charge state “Z” to all levels of charge state “Z + 1” with the help of their respective partition functions.
At low densities, three-body recombination is small compared to radiative and dielectronic recombinations:
As ionization rate coefficients, radiative recombination rate coefficients, and dielectronic recombination rate coefficients depend on the electron temperature, (6.12) does not depend on density and is a function of electron temperature only:
The low-density limit according to (6.13) is called “Corona distribution”. In the Corona limit, \(F_{\text{Z,Z} + 1} \left( {kT_{\text{e}} } \right)\) is a universal function of the electron temperature. As for every charge state a universal function can be obtained, the Corona limit describes a universal charge state distribution of all ions in a plasma. Even if the density changes by orders of magnitude, the charge state distribution does not change as long as for every charge state three-body recombination is negligible compared to the sum of radiative and dielectronic recombination.
Equation (6.8) demonstrates that the distribution of the ionic charge state populations is strongly dependent on elementary atomic processes. We therefore discuss in the following radiative recombination, dielectronic recombination, ionization, and three-body recombination in the context of their application for the calculation of the ionic charge state distribution.
In order to make practical use of the general solution of the charge state distribution according to (6.8), we need explicit expressions for the radiative recombination rate coefficient \({R}_{\text{Z,Z} + 1}\), the dielectronic recombination rate coefficient \({D}_{\text{Z,Z} + 1}\), the three-body recombination rate coefficient \({T}_{\text{Z,Z} + 1}\), and the ionization rate coefficient \({I}_{\text{Z,Z} + 1}\).
Let us begin with the Corona limit (6.13) and consider the schematic atomic level system depicted in Fig. 6.4. Radiative recombination takes place into the ground and all excited states:
After radiative recombination, the excited states \(X^{Z} \left( n \right)\) can decay via spontaneous radiative emission as indicated by the red flashes in Fig. 6.4. In the Corona limit, radiative decay Ann′ is much more important than collisional transfer processes between excited states Cnn′ because the electron density is low: Ann′ ≫ neCnn′. This implies that excited state population is low compared to the ground state and effective ionization from excited states is very small compared to the ionization from the ground states (an exception might be metastable levels: radiative decay is low and population might be very high). Therefore, all radiative recombination ends up finally into the ground state. The total radiative recombination is therefore the sum of all radiative recombination into the ground and excited states (Nmax is the largest principal quantum number to be taken into account):
In the optical electron model (hydrogenic approximation), the radiative recombination can be directly represented by a sum over the orbital l-quantum numbers
The rate coefficient \(R\left( n \right)\) can be estimated with the formulas from (5.61) while the sum \(R^{\text{tot}} \left( {n \ge n_{1} } \right)\) over the n-quantum numbers (n1 is the principal quantum number from which the sum is taken, i.e., overall higher-lying excited states with n > n1) can be directly approximated with (5.62).
In a similar manner, dielectronic recombination \(D_{\text{Z}+1,\text{Z}}(\alpha_0\rightarrow \alpha,nl)\) has to be summed over the excited state contribution to account for the total recombination due to cascading from excited levels:
The sums in (6.16) can considerably be simplified with the help of the Burgess formula (see also Sect. 5.6.2) where the sums over the quantum numbers “nl” of the spectator electrons are explicitly taken into account:
assuming that dielectronic recombination into the ground state is usually the most important one. In this case, the state α0 coincides with the atomic ground state and the sum over α0 can be suppressed (see also Sect. 5.6):
The factor Bd is a so-called branching factor: after dielectronic capture, a double-excited state is formed that can decay via autoionization or radiative decay. For the dielectronic recombination, only the radiative decays contribute finally to recombination as autoionization only returns the original state. In the one-channel approximation, (6.19) can be estimated with the help of the Burgess and Cowan formulas from (5.138–5.143).
Due to multichannel autoionization and radiative decay and the complex configurations involved numerical calculations of the dielectronic recombination turn out to be very complex and the precision of the Burgess formula is difficult to estimate. This is one of the major reasons that up to present-day different atomic population models to calculate the ionization charge state distribution differ largely from each other, in particular for high-Z elements (Rubiano et al. 2007; Chung et al. 2013; Colgan et al. 2015).
The ionization rates involved in (6.7) are the ionizations from the ground state that can be directly estimated from the formulas (5.49) while radiative recombination and dielectronic recombination rates are given by (6.14), (6.16) and its approximations discussed in this chapter and in the Annex A.1.
As it has been discussed above for the radiative recombination and dielectronic recombination processes, also the three-body recombination rate into excited states followed by radiative cascades has to be taken into account:
Summation over the orbital l-quantum numbers “l” provides:
The three-body recombination rate \(T_{\text{Z}+ 1,\text{Z}} \left( n \right)\,\,\) can be estimated from (5.50). The summations over principal quantum number “n” until Nmax in (6.21) have to be taken out with care and follow the methods described in Sect. 5.3.2 and corresponding approximation formulas from (5.51–5.58).
6.1.3 Characteristics of the Ionic Charge State Distribution
Figure 6.5 shows the charge state distribution of Argon obtained from the collisional–radiative code MARIA (Rosmej 1997; 2001, 2006, 2012). The dominance of the shell structure in the distribution of different charge states is clearly visible: a rather wide existence over temperature of the Ne-like and He-like ions densities.
The dominance of closed shell configurations is a general feature and almost independent of the atom and the electron density. The large “high-temperature wings” of the Na-like and Li-like charge states are related to the dielectronic recombination that proceeds from the closed shell configurations 1s22s22p6 and 1s2. As one can see from Fig. 6.5, in general, only about 3–6 charge states are highly populated for a given temperature. This is a typical feature of plasmas with Maxwellian electron energy distributions. We note that in non-Maxwellian plasma, however, qualitative changes appear (Rosmej 1997) that in turn witness the presence of suprathermal electrons.
6.1.4 Generalized Atomic Population Kinetics
In dense plasmas, collisional excitation results into an important population of excited states from which ionization processes may then proceed more efficiently. A particular important case is the ionization from a metastable state because radiative decay is low and population correspondingly high. At the same time, collisional and radiative processes are equally important. It is therefore desirable to consider ionic population and excited states on the same footing rather than calculating the ionic charge state distribution from a set of (6.7) and, separately from these, the corresponding excited states. A widely applied and very successful model (albeit only rates are considered) is the so-called collisional–radiative model (CRM) where all ionization states, ground states, and excited states are connected via elementary collisional radiative processes. The population equations are based on the rate equation principle (see Fig. 6.2) while the elementary processes are calculated with quantum mechanical, quasi-classical or classical methods. The CRM is also called the standard atomic kinetics. The time-dependent evolution of the atomic populations is given by a set of differential rate equations:
\(n_{{j_{\text{Z}} }}\) is the atomic population of level j in charge state Z, Zn is the nuclear charge, \(N_{\text{Z}^{\prime}}\) is the maximum number of atomic levels in charge state Z, and \(W_{{j_{\text{Z}} i_{{Z^{\prime}}} }}\) is the population matrix which contains the rates of all elementary processes from level j of charge state Z to level i of charge state Z′.
In general, (6.22) is a system of nonlinear differential equations because the population matrix might contain the populations by itself (e.g., when radiation transport is included). Only for special cases, the population matrix W does not depend on the atomic populations and the set of equations becomes linear. Equations (6.22) provide N differential equations where the number of levels N is given by:
Looking more carefully to the symmetry relations of (6.22), one finds that the system of equations contains only (N − 1) independent equations for the N atomic populations. We are therefore seeking for a supplementary equation. Let us consider atomic populations in terms of a probability (like in quantum mechanics). In this case, the probability to find the atom in any state is equal to 1:
Equation (6.24) is the desired Nth equation and is called the “boundary condition”. The population matrix is given by:
The matrix describing the radiative and autoionizing processes is given by
The collisional processes are described by
where \(W_{\text{ij}}^{\text{col-heavy}}\) describes the heavy-particle collisions, \(A_{\text{ij}}\) is the spontaneous radiative decay rate, \(\Gamma _{\text{ij}}\) the autoionization rate, \(P_{\text{ij}}^{\text{abs}}\) the stimulated photoabsorption, \(P_{\text{ij}}^{\text{em}}\) the stimulated photoemission, \(P_{\text{ij}}^{\text{rr}}\) the stimulated radiative emission, \(P_{\text{ij}}^{\text{iz}}\) the photoionization, \(C_{\text{ij}}\) the electron collisional excitation/de-excitation, \(I_{\text{ij}}\) the electron collisional ionization, \(T_{\text{ij}}\) the three-body recombination, \(R_{\text{ij}}\) the radiative recombination, \(D_{\text{ij}}\) the dielectronic capture, \(Cx_{\text{ij}}\) the charge exchange (see also Annex 1), \(C_{\text{ij}}^{\text{HP}}\) the excitation/de-excitation by heavy-particle collisions, and \(I_{\text{ij}}^{\text{HP}}\) the ionization by heavy-particle collisions.
In the framework of the general set of (6.22), the distribution of atomic populations over the various charge states is readily obtained from its detailed solution:
\(n_{\text{Z}}\) is the population for the charge state Z. Heavy-particle collisions are usually not very important in dense hot plasmas. However, there are a few important exceptions, e.g., the coupling of the H-like levels 2s1/2 and 2p1/2 via heavy-particle collisions that might change the line ratio of the Lyman-alpha doublet (Boiko et al. 1985) because the energy difference between the levels 2s1/2 and 2p1/2 is very small compared to the difference between the levels 2s1/2 and 2p3/2. Therefore, the coupling to the level 2p3/2 is inefficient. Another example is the proton collisional induced ionization of Rydberg levels in magnetic fusion plasmas (Rosmej and Lisitsa 1998).
6.1.5 Statistical Charge State Distribution Based on Average Occupation Numbers
It is evident from (6.22)–(6.29) that the calculation of the charge state distribution can be very complex, in particular, for mid-Z or more heavy elements. It is therefore of interest to develop simplified methods to estimate the charge state distribution over the various shells (in particular for the more complex shells L, M, N, O, P). For these purposes, a statistical model has been developed (Rosmej et al. 2002a) to calculate the probability of the charge state distribution based on an average occupation number:
\(f\left( {k_{\text{n}} } \right)\) is the probability to find \(k_{\text{n}}\)-electrons \(\left( {0 \le k_{\text{n}} \le 2n^{2} } \right)\) in quantum shell \(n\) (K-shell: n = 1, L-shell: n = 2, M-shell: n = 3 etc.) if the average non-integer population is \(P_{\text{n}}\). Figure 6.6 shows the charge state distribution for L-, M- and N-shell for various different averaged populations \(P_{\text{n}}\).
It can be seen from Fig. 6.6 that if the average occupation number is \(P_{\text{n}} = n^{2}\) the probabilities are centered around the maximum probability at \(k_{\text{n}} = P_{\text{n}}\) and that the maxima are far from 1, e.g., for the L-shell, we find a maximum at 0.273, M-shell at 0.185, and N-shell at 0.141. At the same time, the charge state distribution becomes more wider from L-shell to M-shell to N-shell. The calculations for \(P_{\text{n}} = 2n^{2} - 1\) show that even at such high-shell occupation, the maximum fraction for the corresponding charge state is much below 1, only for the case of almost complete shell occupation, fractions near 1 are encountered (see calculations for \(P_{\text{n}} = 2n^{2} - 0.5\)).
The charge state distribution can be visualized with the spectral distribution. This is demonstrated in Fig. 6.7 via the inner-shell X-ray transitions of type \(1s^{1} 2s^{n} 2p^{m} \to 1s^{2} 2s^{n} 2p^{m - 1} + \hbar {{\omega}}\) for copper. The spectral distribution \(I\left( \omega \right)\) has been calculated from
where \(g_{\text{j}}^{{(k_{\text{n}} )}}\) is the statistical weight of level j in charge state kn, \(A_{\text{ji}}^{{(k_{\text{n}} )}}\) is the transition probability from level j to level i in charge state kn and \(\hbar \omega_{\text{ji}}^{{(k_{\text{n}} )}}\) is the corresponding transition energy.
6.2 Characteristic Time Scales of Atomic and Ionic Systems
The development of short-pulse lasers (optical and free electron lasers) allows to study systems that are highly out of equilibrium and it is therefore of great interest to study the general properties of the radiating atoms and ions for time-dependent perturbations. It turns out that two principle time scales can be identified: the characteristic time scale to establish an ionization balance and the characteristic time scale of photon emission.
6.2.1 Characteristic Times to Establish Ionization Balance
The time-dependent response properties can be studied in the framework of a two-level atom considering the level “Z + 1” and “Z” of Fig. 6.3. Equation (6.7) then takes the form:
For the two-level atom, the normalization condition (closure relation) reads
which means that the probability to find the atom either in state “Z” or in state “Z + 1” is equal to one. Inserting (6.33) into (6.32), we obtain:
where
If the rate coefficients and the electron density do not depend explicitly on time, the differential equation (6.34) has an analytical solution:
Let us consider a rapid cooling process (e.g., a recombining plasma when the laser interaction is switched off) where all initial populations are in the state \(n_{\text{Z} + 1}\):
Inserting (6.37) into (6.34), we obtain for t = 0:
Inserting (6.38) into (6.37), it follows
An additional equation can be obtained remembering that at \(t \to \infty\) a physical solution must be finite. Inserting (6.37) into (6.34), we obtain:
In order to select finite solutions for \(t \to \infty\), we must request β < 0:
From (6.40), (6.41), (6.43), we obtain all further integration constants:
The final solution (6.37) is therefore:
Equation (6.46) shows that the cooling process which populates the level \(n_{\text{Z}}\) has a characteristic time scale:
A similar result can be obtained for rapid heating. Therefore, even sudden cooling/heating processes do not lead to a sudden response of the atomic level populations. It is important to note that the time scale for the ionization process (Z) → (Z+1) is not given by the inverse rate of ionization itself but rather by the inverse of the sum of the ionization and all recombination process. This has important numerical consequences for the time-dependent charge state evolution. The physical reason is that equilibrium requests not only the equilibrium of the atomic state that is ionized but also the equilibrium of those levels that are populated by ionization. From these levels, however, recombination processes originate which request to be in equilibrium with these processes too.
In order to obtain more insight in the meaning of (6.47), let us rewrite the equation in the following form:
If three-body recombination is negligible (Corona model), the characteristic time scale (6.48) is inversely proportional to the electron density:
Therefore, the characteristic time scale for low-density plasmas can be very long. Although each ionization stage and each element has, in principle, its own characteristic time scale according to (6.48), numerical calculations demonstrate, however, that rather general time constants can be identified (Rosmej 1997; 2001; 2006). For example, the characteristic time constant of the K-shell of highly charged ions is given by
that is rather insensitive of the temperature and the atomic element. This can be directly understood from (6.48) that contains the sum of the recombination and ionization processes: at high temperature ionization is dominating, whereas at low temperature recombination processes dominate so that the sum of all these processes is finally not strongly dependent on temperature.
6.2.2 Characteristic Times of Photon Emission
We consider now the transient evolution of photon emission according to Fig. 6.8. The relevant set of differential equations is given by
which means that the probability to find the atom either in state “i” or in state “j” is equal to one. Inserting (6.52) in (6.51), we obtain:
where
The analytical solution of the differential equation (6.53)–(6.54) is given by
Let us consider a rapid cooling process and an initial condition
The analytical solution of the differential equation (6.53)–(6.57) is then given by:
and the time-dependent upper-level density is given by
As can be seen from (6.61) the cooling process that populates the level \(n_{\text{j}}\) has a characteristic time scale:
Therefore, a sudden cooling does not lead to a sudden response of the atomic level populations and the radiative decay. At very low densities, the relaxation constant is given by
Equation (6.63) is principally different from (6.48). Even for low densities, the relaxation time can be very small due to the radiative decay rate. The relaxation constant of allowed transitions between principal quantum numbers can be estimated from the following expression (n, m are principal quantum numbers, m > n) (Cowan 1981):
Note that (6.64) is valid only for allowed dipole transitions without any change in spin quantum number. In a multilevel system, all radiative decay rates to the lower levels have to be considered for the relaxation constant (Sobelman and Vainshtein 2006):
6.2.3 Collisional Mixing of Relaxation Time Scales
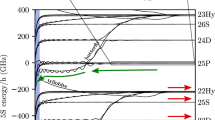
Equations (6.61), (6.62) show that the population of levels which decay radiatively is strongly density-dependent if the rates of collisional processes are of the order of the radiative decay rate. In this case, the characteristic time scales for photon emission are strongly density-dependent. Moreover, in a multilevel system, collisions might transfer population from levels with different relaxation constants, the so-called Mixing of Relaxation Times (Rosmej and Rosmej 1996; Rosmej 2012). This can have very important impact on the time-dependent radiative properties. For example, in a multilevel system, a metastable level can “feed” a resonance emission for a long time via collisions. This phenomenon is demonstrated in Fig. 6.9 for a rapidly cooled argon plasma. The multilevel collisional radiative simulations are carried out with the MARIA code (Rosmej 1997, 2001, 2006, 2012) for Zn = 18 at ne = 1021 cm−3 and rapid cooling from kTe = 2000 eV to kTe = 500 eV.
Collisional mixing of relaxation times of the He-like levels 1s2s 3S1, 1s2s 1S1, 1s2p 3P2, 1s2p 3P1, 1s2p 3P0, 1s2p 1P1. The simulations show the collisional mixing of the relaxation times for the He-like resonance line W = 1s2 1S0–1s2p 1P1 and the He-like intercombination line Y = 1s2 1S0–1s2p 3P1. Simulations are carried out with the MARIA code (Rosmej 1997, 2001, 2006, 2012) for argon, Zn = 18 at ne = 1021 cm−3 and rapid cooling from kTe = 2000 eV to kTe = 500 eV
The shortest relaxation time is those of the He-like resonance line τ(W) ≈ 9 × 10−15 s (indicated by the arrow at the first step in Fig. 6.9). The next step is due to a collisional coupling between the levels 1s2p 1P1 and 1s2s 1S0. The relaxation time of the 1s2s 1S0-level is determined by the two-photon decay τ(2E1) ≈ 3 × 10−9 s as well as by collisions. At an electron density of ne = 1021 cm−3, the relaxation time of the 1s2s 1S0-level is determined by collisions (rate coefficient C(1s2s 1S0–1s2p 1P1) ≈ 2 × 10−9 cm3 s−1). The effective relaxation time is therefore about τ(1s2s 1S0) ≈ 4 × 10−13 s as indicated by the arrow “1s2s 1S0” (giving rise to the second step at about t = 10−13–10−12 s). The last step is due to the establishment of ionization equilibrium: the recombination rate from the H-like to He-like ions at kTe = 500 eV is about R ≈ 4 × 10−12 cm3 s−1, giving a relaxation time of about τ(1s 2S1/2) ≈ 3 × 10−10 s. This is indicated by the arrow “1s 2S1/2”. Almost stationary conditions are achieved at times larger than 1 ns, providing τ(1s 2S1/2) ne ≈ 1 × 1012 cm−3 s. These numerical results are in good agreement with (6.50).
Due to the strong Z-scaling of intercombination and forbidden transitions (\(Z_{\text{eff}}^{8} \ldots ..Z_{\text{eff}}^{10}\), contrary to the Z-scaling of allowed dipole transitions with \(Z_{\text{eff}}^{4}\)), the relaxation steps depicted in Fig. 6.9 may change by many orders of magnitude for different elements. Therefore, in transient dense plasmas, collisional processes do not lead only to a transfer of population but also to a mixing of relaxation times. This can result in a considerable prolongation of the radiation emission. Let us, for example, consider the intercombination line of He-like argon ions as an example: the radiative relaxation time is τ(Y = 1s2–1s2p 3P1) ≈ 6 × 10−13 s, however, the fine structure 1s2l 3L is metastable and decays by magnetic multipole transitions with very long relaxation times: τ(Z = 1s2−1s2s 3S1) ≈ 2 × 10−7 s and τ(X = 1s2–1s2p 3P2) ≈ 3 × 10−9 s. It is therefore possible that the intercombination line emission has a collisionally enhanced relaxation time by about five orders of magnitude compared to the radiative relaxation time of the Y-line itself (indicated by the vertical arrow “1s2l 3L” in Fig. 6.9). This can lead to very long-lasting intercombination line emission in cooling plasmas like, e.g., in laser-produced plasmas and Z-pinch plasmas. This effect has been observed with X-ray streak camera measurements in a dense plasma focus experiment (Lebert et al. 1995): intercombination line emission over time scales of the order of some 0.1 ns are observed.
Figure 6.9 demonstrates, likewise, that the intercombination line intensity in the time interval of about 10−13 − 10−9 s is much stronger than those of the resonance line. This effect has likewise been observed in experiments (Lebert et al. 1995). It is important to note that inner-shell ionization (1s22l + e → 1s2l 1,3L + 2e) may explain at maximum three times larger intensities of the intercombination line compared to the resonance line (due to the ratio of the statistical weights of the singlet and triplet systems) but is practically limited to about a factor of 2 due to charge state distribution effects.
Therefore, collisional mixing of relaxation times explains simultaneously up to order of magnitude different intensities in certain time intervals and very long-lasting emission. Both effects have been simultaneously observed in experiments of a dense argon pinch during its transition from the column to the micropinch mode (Lebert et al. 1995). The time-dependent measurement has been performed with the help of an X-ray streak camera coupled to a X-ray Bragg crystal, and time-dependent observation of the spectral distribution containing the X-ray intercombination and resonance line emissions Y = 1s2−1s2p 3P1 and W = 1s2−1s2p 1P1.
6.3 Reduced Atomic Kinetics
6.3.1 Ground States, Single-Excited and Autoionizing Levels: General Considerations
The atomic structure of multielectron atoms is rather complex, and the large number of levels is often prohibitive for numerical solution of the population kinetic equations. This is essentially due to the large number of autoionizing states that have to be explicitly involved in dense plasmas in order to reasonably approximate the dielectronic recombination to get right the ionic charge state distribution. It is important to underline that the dielectronic recombination rates calculated by, e.g., the Burgess formula and other similar approaches (see Chap. 5) are strictly only applicable in Corona plasmas, where density effects do not play an important role. There are principally two different density effects:
-
I.
Due to collisional excitation also single-excited states are subjected to dielectronic capture (see Sect. 5.6.2.3 “Excited states driven dielectronic recombination”, comparison of Tables 5.5 and 5.6).
-
II.
In dense plasmas, electron collisions may redistribute population between the autoionizing levels, thereby changing the dielectronic recombination after dielectronic capture. This invalidates in general the assumption made for using branching factors [see (5.130)] that do not depend on density and therefore invalidates the use of the simple dielectronic recombination formulas. In order to take into account the density effects among the autoionizing states, all autoionizing levels have to be included explicitly in the population kinetics.
As the number of autoionizing levels is excessively larger than the number of ground and single-excited states, the numerical load to solve the population kinetic equations in dense hot plasmas is finally dominated by the number of the autoionizing states. Currently, there are essentially three different methods in use to handle a large number of levels (thousands up to millions of levels) in population kinetics:
-
(1)
Averaged models of the Fermi type and its various modifications. These models, however, are not very useful for high-resolution spectroscopy and related plasma diagnostics. They are usually employed for equation of state and opacity simulations (Lieb and Simon 1977; Piron and Blenski 2011). So-called plasma atomic models (Demura et al. 2013) have recently been proposed to extend statistical models to plasma diagnostic precision (to be discussed in Chap. 9).
-
(2)
The super-configuration methods where numerous levels are lumped together via to a certain coupling scheme (Bar-Shalom et al. 1995; Bauche et al. 2006; Abdallah and Sherrill 2008; Hansen et al. 2011). As details of the level structure are suppressed, high-resolution spectroscopic applications are very challenging (a discussion with respect to dielectronic satellite transitions can be found in (Petitdemange and Rosmej 2013).
-
(3)
The virtual contour shape kinetic theory (VCSKT) that is based on a probability formalism to account for collisional–radiative effects in complex autoionizing configurations (Rosmej 2006). VCSKT allows for a maximum reduction of autoionzing levels in population kinetics (in the limit to one autoionizing level for a certain configuration instead of all detailed autoionizing levels, e.g., the 274 LSJ-split autoionizing levels 1s3l5l′ are replaced by just one level) while maintaining the details of all transitions (e.g., means all detailed transitions originating from the 274 levels of the 1s3l5l′-configuration) with respect to their existence and to their distribution of oscillator strengths over frequency. This allows maximum simplification in the population kinetics while maintaining maximum information in the spectral distribution (e.g., necessary for diagnostic applications).
6.3.2 The Virtual Contour Shape Kinetic Theory (VCSKT)
6.3.2.1 Exact and Reduced Kinetics
Due to the important practical difference between autoionizing states and single-excited states, it is convenient to first reformulate the population kinetics and corresponding spectral distribution explicitly with respect to autoionizing states. Let us start with the general expression for the spectral distribution:
where the indexes \(i,j\) run over all ground, single, and autoionzing states from all charge states. \(N\) is the number of levels included in the model, \(n_{\text{j}}\) is the population of level \(j\), \({{\omega}}_{\text{ji}}\) is the frequency of the transition \(j \to i\), \(A_{\text{ji}}\) is the corresponding spontaneous transition probability (of any multipole order for electric and magnetic transitions), \({\varphi }_{\text{ji}}\) is the line profile, and \({\theta}\) specifies the ensemble of parameters for the line profile calculation (e.g., the ionic temperature, electron density, ion density, etc.). The population \(n_{\text{j}}\) of level j is determined from
with
\(W_{\text{ij}}\) are the transition matrix elements [see also (6.25)–(6.28)] connecting the discrete levels [\(i,j,k\) in (6.67)] in all ionization stages. If a particular transition \(j \to i\) cannot occur because of energy or symmetry considerations, \(W_{\text{ij}} = 0\). \(N_{\text{a}}\) and \(N_{\text{b}}\) are the total numbers of autoionizing-state and bound-state manifolds, respectively, and \(N_{{\text{a},{{\alpha}} }}\) and \(N_{{\text{b},{{\beta}} }}\) are the numbers of levels in the individual autoionizing-state and bound-state manifolds \(\left\{ {{\alpha}} \right\}\) and \(\left\{ {{\beta}} \right\}\), respectively. These manifolds may be defined to include states with the same principal quantum numbers but different angular-momentum combinations, e.g., \(\left\{ {{\alpha}} \right\} = \left\{ {1s3l5l^{\prime}} \right\}\), \(N_{{\text{a},{{\alpha}} }} = 274\), \(\left\{ {{\beta}} \right\} = \left\{ {1s3l} \right\}\), \(N_{{\text{b},{{\beta}} }} = 10\). The number of possible angular-momentum combinations \(N_{{\text{a},{{\alpha}} }}\) can be enormous. Consequently, it is necessary to consider many thousands, possibly millions of levels, even for combinations of only a few \(nl\)-configurations in the evaluation of the radiative emission \(I_{{{\alpha}} } \left( \omega \right)\) from the manifold \(\left\{ {{\alpha}} \right\}\) of the autoionizing states:
The difficulty associated with (6.66), (6.67) is that the retention of a reduced number of autoionizing levels \(N_{{\text{a},{{\alpha}} }} \to N_{{\text{a},{{\alpha}} }}^{r}\) in order that
in the atomic-state kinetics leads to the omission of many emission lines in the evaluation of (6.69). The multitude of original, detailed emission lines is thereby replaced by a reduced set of artificial lines (with averaged intensities, line center positions, and broadening parameters). Consequently, important spectral features and plasma-parameter sensitivities can be lost as a result of this reduction procedure.
We are therefore led to inquire, if (6.69) is the only possible form for the determination of the spectral distribution. This is not only a fundamental question but also one of great practical importance: the exact treatments of (6.67), (6.69) present a severe challenge for practical integrated calculations, which are needed to provide spectroscopic/diagnostic accuracy for the radiation field generated by inertial fusion and other dense plasmas. It is therefore highly desirable to develop alternative methods.
6.3.2.2 The Probability Method for Boltzmann-like Populations
For the purpose of a more transparent presentation of the principal ideas, let us consider the case
for which all autoionizing levels \({{\alpha}}\) are represented by only a single level in the population kinetics described by (6.67), with a density \(n_{{{{\alpha}} \,\Re }}\) and a statistical weight \(g_{{{{\alpha}} \,\Re }}\) \(\left( {i^{\prime} \in N} \right)\):
Note that in (6.72) we have used the index \(\left( {i^{\prime} \in N} \right)\) instead of \(\left( {i \in N} \right)\) because after level reduction the overall level identification changes. A generalization of (6.71) to several levels for the manifold \(\left\{ {{\alpha}} \right\}\) is straightforward. As one can see from the comparison of (6.69), (6.72), the dimensionless vector \(\Re_{\text{j}}\) transforms the averaged level \(n_{{{{\alpha}} \,\Re }}\) to non-statistical individual populations \(n_{\text{j}}\). Practically, we seek for a solution for \(\Re_{\text{j}}\) that continuously transforms the individual level populations from the Corona model to the Boltzmann case with increasing densities. For clarity of the physical meaning of \(\Re_{\text{j}}\), let us first consider the trivial solution of (6.72):
i.e., Equation (6.73) makes (6.72) equal to (6.69): in other words, \(\Re_{\text{j}}^{(T)}\) depends on the exact individual population vector \(n_{\text{j}}\). A non-trivial solution for \(\Re_{\text{j}}\) does not invoke the exact solution for all \(n_{\text{j}}\) (6.67), (6.68) but employs only the reduced kinetics according to (6.67), (6.70), i.e.,
from which the approximate individual populations are obtained according to
The upper index (n) for \(n_{\text{j}}^{(n)}\) and \(\Re_{\text{j}}^{(n)}\) indicates the approximate solutions of order “n”. Equation (6.75) has a clear physical meaning. The first term in (6.75) for \(n_{\text{j}}^{(n)}\) is an individual level population according to the statistical assumption (the total population is just divided by the total statistical weight), i.e., the population per statistical weight. The second term, namely \(\Re_{\text{j}}^{(n)}\) provides a correction to the statistical population.
A solution of (6.75) can be obtained recalling that the radiation emission from autoionizing states is primarily produced by four individual atomic mechanisms: dielectronic recombination (D), inner-shell collisional excitation (C), collisional coupling among the autoionizing levels \(\left\{ {{\alpha}} \right\}\) (B), and couplings to all other levels retained in the atomic kinetics (A). We therefore split \(\Re_{\text{j}}\) into the respective contributions \((j \in {{\alpha}}\), \(k,l,q,s,t,u \in\) reduced set of bound levels retained in the population kinetics pertaining to the various excitation channels):
Within the manifold \(\left\{ {{\alpha}} \right\}\) \(\Re_{\text{j}}^{(B)}\) describes collisions corresponding to no change in the principal quantum number n, whereas \(\Re_{\text{q,j}}^{(A)}\) pertains to transitions with changes in n:
\(\Delta E\) is the energy threshold, \(F\left( E \right)\) is the electron energy distribution function and \(\sigma\) the cross section. For the majority of relevant transitions
We therefore neglect detailed collisional processes between different n-quantum numbers from and to the manifold \(\left\{ {{\alpha}} \right\}\) and approximate \(\Re_{\text{q,j}}^{(A)}\) by
The symbol X denotes additional (to D and C type) processes, e.g., direct radiative recombination, three-body recombination, charge transfer, and ionization. Accordingly, (6.74) generalizes the standard processes of dielectronic recombination and inner-shell excitation (Gabriel 1972; Jacobs and Blaha 1980) to further excitation channels (X). Equations (6.74), (6.75) reduce the complex redistribution effects to collisional processes with the manifold \(\left\{ {{\alpha}} \right\}\) only. Processes (D), (C), and (X) are therefore decoupled from the detailed level populations according to (6.67), (6.70). This permits the derivation of an analytical solution for the elements \(\Re_{\text{j}}\) \(\left( {{{\gamma}} = D,C,X} \right)\):
In Maxwellian plasmas, \(b_{\text{j}}\) is the Boltzmann factor. \({{\rho}}_{\text{j}}\) describes the degree of collisionality over radiative and autoionization processes and is given by
where \(\nu_{\text{j}}^{({\text{redis}}) }\) is a characteristic collision frequency for level \(j\) and \({{\Gamma}}_{\text{k,j}}\) is the autoionization rate of level j via channel k. Taking into account all details of the atomic data via the index j in (6.72), (6.82) even metastable level features are recovered. The strengths \(R_{{\text{k}^{\prime},\text{j}}}^{{({{\gamma}} )}}\) from (6.81) can be derived by considering the low-density limit. In this limit, the spectral distribution, which is defined by (6.69), can be exactly evaluated as the sum of the contributions from all individual excitation channels as follows:
where \(n_{{\text{k}^{\prime}}}^{{({{\gamma}} )}}\) are the population densities of the initial states in various excitation channels (γ) and \(\left\langle {{\gamma}} \right\rangle_{{\text{k}^{\prime}\text{j}}}\) are the corresponding individual collisional excitation rate coefficients, \(k^{\prime} \in k,l,q\), i.e., \(k^{\prime}\) is an index in the reduced set of bound levels [see (6.76)]. The link of (6.83) to (6.72) can be accomplished via (6.76, 6.79) approximating \(n_{{{{\alpha}} ,\Re }}\) from (6.67), (6.70), (6.72) by
\(\bar{A}_{{{{\alpha}} \,\Re ,\,s}}\), \({\bar{{\Gamma}}}_{{{{\alpha}} \Re ,t}}\) and \(\overline{\left\langle X \right\rangle }_{{{{\alpha}} \Re ,u}}\) are effective depopulation rates that decrease the level density \(n_{{{{\alpha}} \Re }}\) due to radiative decay, autoionization (decay of level “\({{{{\alpha}} \Re }}\)” to level “t”), and processes (X), while \(\overline{{\left\langle {{\gamma}} \right\rangle }}_{{\text{k},{{\alpha}} \Re }}\) are effective population rates that increase the level density \(n_{{{{\alpha}} \Re }}\) due to the processes (γ):
As can be seen from (6.85), the effective population rate is given just by the sum of all detailed population rates. The depopulation rates are more complex as they request the knowledge of the individual populations that are expressed in terms of the vector \(\Re_{\text{j}}\) from (6.75). With the help of (6.86)–(6.88), we can now determine the strengths \(R_{{\text{k}^{\prime},\text{j}}}^{{({{\gamma}} )}}\) from (6.81). Inserting (6.81) and (6.84) into (6.72) and equating the result with (6.83) we obtain
The strength parameter \(R_{{\text{k}^{\prime},\text{j}}}^{{({{\gamma}} )}}\) has a clear physical meaning: it determines the strength to populate level j from level \(k^{\prime}\) via the elementary process (γ) in the Corona limit while the strength parameter \(\Re_{{\text{k}^{\prime},\text{j}}}^{{({{\gamma}} )}} = \left( {1 - {{\rho}}_{\text{j}} } \right)g_{\text{j}} R_{{\text{k}^{\prime},\text{j}}}^{{({{\gamma}} )}}\) from (6.81) determines this strength for arbitrary density.
According to (6.80)–(6.82), the intermediate densities and corresponding redistribution among the individual levels are determined via a probability method: \({{\rho}}_{\text{j}}\) is the probability for level \(j\) to be “Boltzmann-like” (see (6.80), while \(1 - {{\rho}}_{\text{j}}\) is the probability for level \(j\) to be “non-Boltzmann-like” [see (6.81)]. Therefore, the redistribution among the levels from the manifold \(\left\{ {{\alpha}} \right\}\) that is a complex interplay between collisional–radiative and autoionization processes is replaced by the individual probabilities from (6.82). The system of equations is closed, if the individual densities \(n_{\text{j}}\) from (6.86)–(6.88) are replaced by the approximate individual populations from (6.75).
6.3.2.3 Maximum Recovery Properties and Convergence Properties
In order to solve the system of (6.67), (6.70), the effective depopulation and population rates from (6.85)–(6.88) have to be specified. The system (6.67), (6.70) can be initially set up assuming \({{\rho}}_{\text{j}}^{(0)} = 1\) (the upper index specifies the iteration number). According to (6.76), (6.79), (6.80), (6.81), this corresponds to:
from which it follows [see (6.76)]
According to (6.75), this corresponds to an individual level population of
i.e., the Boltzmann population. The system of (6.67), (6.70) is therefore initially set up with statistical/Boltzmann averaged rate coefficients. The population densities \(n_{\text{k}}^{(\gamma ),(0)}\) are then used in (6.89) to calculate non-statistical vectors \(R_{\text{j}}^{(1)}\) from (6.81), (6.82) and non-statistical depopulations rates from (6.86)–(6.88) and so on. The numerical calculations show extremely rapid convergence, in fact, already the 0-iteration (mean no iteration in the set of (6.67), (6.70) providing the first non-statistical approximation \(R_{\text{j}}^{(1)}\)) provides a very good approximation to the spectral distribution.
In order to demonstrate the maximum efficiency of the virtual contours shape kinetic theory (VCSKT), let us consider the extreme case
for which all autoionizing levels \(\{ {{\alpha}} \}\) are represented by only a single level in the population kinetics described by (6.67), with a density \(n_{{{{\alpha}} \,\Re }}\) and a statistical weight \(g_{{{{\alpha}} \,\Re }}\) \(\left( {i^{\prime} \in N} \right)\). We consider also examples where (D) and (C) driven dielectronic satellite transitions are well separated: model inaccuracies are not masked by line overlapping and a stringent test for the accuracy of VCSKT is provided. We likewise chose parameter intervals so large that all experimental situations of interest are covered.
Figure 6.10 displays the spectral range of the He-like resonance line \(W = {{He}}_{{{\alpha}} } = 1s2p\,^{1}P_{1} \to 1s^{2} \,^{1} S_{0}\), intercombination line, \(Y = 1s2p\,^{3}P_{1} \to 1s^{2} \,^{1}S_{0}\) and Li-like dielectronic satellites \(1s2l2l^{\prime}\,LSJ \to 1s^{2} 2l\,L^{\prime}S^{\prime}J^{\prime}\). This spectral range is of particular interest for spectroscopic diagnostics (Gabriel 1972; Boiko et al. 1985; Rosmej 1997; Rosmej 2012; Glenzer et al. 1998). The agreement is found to be very good: first, although large temperature variations are considered, the relative intensity between the He-like resonance line W and the satellite transitions is very well described. This demonstrates the correct connection between the reduced atomic kinetics description of (6.67), (6.70), (6.85)–(6.88) and the recovered spectral distribution of (6.72). Second, in Fig. 6.10a, the plasma density is too low for titanium to couple the autoionizing levels via \(\Re_{\text{j}}^{(B)}\). Therefore, correct intensities driven by dielectronic recombination and inner-shell excitation show the correct distribution over excitation channels (6.76), (6.79), (6.81). Third, the intensity redistribution among the transitions due to collisions (Jacobs and Blaha 1980; Petitdemange and Rosmej 2013) is correct over many orders of magnitude. Therefore, the probability method for Boltzmann-like populations (6.80)–(6.82) provides a very satisfactory approximation.
Spectral distributions of the He-like resonance line W, intercombination line Y and Li-like 1s2l2l′-satellites of titanium for various temperatures and densities. The simulations with the VCSKT with maximum reduction, i.e., \(N_{\text{a}, \alpha}^{r} = 1\), show overall very good agreement with the exact solutions
Let us study the probability method for Boltzmann-like populations with another important example, namely the 1s2l3l′-satellites near \(He_{{\beta}} = W3 = 1s3p\,^{1}P_{1} \to 1s^{2} \,^{1}S_{0}\) that have been employed in gas-bag experiments to control the uniformity of the compression toward near-solid density (Woolsey et al. 1997) and in dense laser-produced plasmas to characterize non-Maxwellian effects (Rosmej et al. 2001). Figure 6.11a shows a near-solid density case, Fig. 6.11b an intermediate density case, and Fig. 6.11c shows a low-density (corona) case. The agreements between the results of the exact simulations and the predictions of VCSKT over many orders of magnitude in density are remarkable and demonstrate the efficiency of the probability method for Boltzmann-like populations.
6.3.2.4 Broadening Properties of Complex Emission Groups
Let us consider the broadening properties of the emission from the manifold \(\left\{ {{\alpha}} \right\}\). Unlike the broadening of a single line, the broadening of the total contour is determined by the broadening of a single transition from \(\left\{ {{\alpha}} \right\}\) and also by the number of transitions with their respective line center positions. In VCSKT, the last effect is treated exactly, because all transitions with their exact line center positions are retained in the summation, based on (6.83). In (Rosmej and Abdallah 1998), a Voigt profile representation was proposed for \({\varphi }_{\text{ij}}\) with a Lorentz width given by
The inelastic collision rates \(C_{\text{jk}}\) can be approximated by a unique frequency \(\nu_{\text{eff}}^{{({{\alpha}} )}}\), i.e.,
Figure 6.11 shows the results of simulations using width expression according to (6.95) (solid curves) and (6.96) (dashed curves): \(\nu_{\text{eff}}^{{({{\alpha}} )}}\) is found to provide a good agreement for the broadening of the total satellite contour. We note that the expression for the width according to (6.96) readily permits further sophistications via the introduction of additional effective width expression \(\nu_{\text{eff}}^{{({{\alpha}} )}} \to \nu_{\text{eff}}^{{({{\alpha}} )}} + \nu_{\text{eff},1}^{{({{\alpha}} )}} + \ldots\). We note that also Stark broadening effects could be incorporated in this approach (Rosmej et al. 2002b).
6.3.2.5 Response Properties of VCSKT to Hot Electrons
We consider now the response properties of the VCSKT with respect to hot electrons that have important impact on the radiative properties of matter, in particular, in inertial confinement fusion ICF and high-intensity laser-produced plasmas. The hot electron fraction is defined as follows (Rosmej 1997):
where \(T_{\text{hot}}\) and \(T_{\text{bulk}}\) are the “bulk” and “hot” electron temperature, respectively.
Figure 6.12 shows the Lyman-alpha satellite emission \(2l2l^{\prime} \to 1s2l + \hbar {{\omega}}_{\text{satellite}}\) of non-Maxwellian and optically thick argon plasmas. A group of transitions is appreciably populated by hot electrons via the inner-shell excitation process \(1s2l + e \to 2l2l^{\prime} + e\) (indicated by the arrow in Fig. 6.12). The results of exact and analytical non-Maxwellian VCSKT simulations are found to be in very good agreement. This indicates that preferential population via single channels (γ) (e.g., the inner-shell excitation driven by hot electrons) is very well described by (6.81).
Spectral distributions of the He-like 2l2l′-satellites (near Lyα) of argon for dense plasmas containing hot electrons for kTbulk = 500 eV, kThot = 20 keV, ne,tot = ne,bulk + ne,hot = 1023 cm−3, effective plasma size Leff = 10 μm. The simulations with the VCSKT with maximum reduction, i.e., \(N_{{\text{a},{{\alpha}} }}^{r} = 1\), show overall very good agreement with the exact solutions
Equations (6.80), (6.81) can be regarded as providing a virtual contour shape \(I_{{{{\alpha}} \,\Re }}\) and population kinetics description (VCSK): the strengths of channels (γ) are redistributed by the action of \(\Re_{\text{j}}^{(B)}\) and \(\Re_{{\text{k}^{\prime},\text{j}}}^{(\gamma )}\) from (6.80, 6.81). The levels \(\{{\alpha}\}\) are thereby decoupled from the atomic kinetics while retaining the details of all individual transitions according to (6.83).
An important property of the VCSKT is that (6.79)–(6.89) are exact in the high-density limit, as well as in the low-density limit. Consequently, VCSKT is applicable for all kinds of plasma conditions. Equation (6.83) together with (6.79)–(6.89) differs from the spectral distribution obtained from common reduction schemes, e.g., (Bar-Shalom et al. 1995; Bauche et al. 2006; Abdallah and Sherrill 2008; Hansen et al. 2011). In these schemes, the reduction of the atomic kinetics is also applied to the evaluation of (6.66), and therefore the reduced number of levels \(N_{{\text{a},{{\alpha}} }}^{(r)} = 1\) (e.g., the maximum reduction possible and applied for all examples of Figs. 6.10, 6.11, 6.12) would then result in the retention of only a single-line transition for each lower state \(i^{\prime}\). Practically, all information from the detailed spectral distribution would be lost. However, (6.83) together with (6.76)–(6.89) recovers all spectral details via the summation over the full manifold \(\left\{ {{\alpha}} \right\}\) from the reduced population \(n_{{{{\alpha}} \,\Re }}\) via \(\Re_{\text{j}} \left( {n_{{{{\alpha}} \Re }} } \right)\). VCSKT generates therefore a detailed, unreduced spectral distribution from a reduced description of atomic level population kinetics. This is of fundamental interest for the atomic radiative properties and also of great practical importance because VCSKT reduces the computational effort by orders of magnitude. VCSKT could therefore be especially promising for applications: fully integrated simulations with diagnostic accuracy for the most complex configurations (e.g., hollow atoms/ions) become feasible.
6.4 Two-Dimensional Radiative Cascades Between Rydberg Atomic States
Many physical applications require calculations of radiative cascade between highly excited atomic states. Examples include calculations of the level populations and line intensities of hydrogen and ionized He(II) in interstellar gas plasmas (nebulas) (Seaton 1959; Pengelly 1964; Summers 1977; Grin and Hirata 2010), spectral line calculations for highly stripped ions in hot rarefied plasmas whose levels are populated by the processes of charge transfer (Abramov et al. 1987), or dielectronic recombination (Sobelman and Vainshtein 2006) as well as natural lasing (Strelnitski et al. 1996; Messenger and Strelnitski 2010). Several analytical and numerical techniques for calculating the parameters of radiative cascades were developed and discussed (Seaton 1959; Pengelly 1964; Summers 1977; Biberman et al. 1982; Kukushkin and Lisitsa 1985; Flannery and Vrinceanu 2003; Sobelman and Vainshtein 2006; Grin and Hirata 2010).
Many works deal with one-dimensional radiative cascades, in which the populations \(f_{\text{nl}}\) of atomic states with different orbital quantum numbers \(l\) are assumed to be determined by their statistical weights: \(f_{\text{nl}} = f_{\text{n}} \cdot(2l + 1)/n^{2}\), where the function \(f_{\text{n}}\) depends only on the principal quantum number n and corresponds to the total (with respect to l) level population. The radiative transitions in such a consideration thus occur between levels with a definite n, and the corresponding probabilities \(W(n \to n^{\prime})\) are obtained by averaging the probabilities \(W(nl \to n^{\prime}l^{\prime})\) over \(l\) and \(l^{\prime}\) (this is called the \(n\)-method). Pengelly (Pengelly 1964) and Summers (1977) have carried out numerical calculations for two-dimensional cascades, i.e., dealing with the populations of the individual \(nl\)-levels (this is called the \(nl\)-method). In the work of (Summers 1977) also collisional transitions are considered making it difficult to trace the role of radiative cascades using his data.
The amount of data and the complexity of the numerical calculations in the \(nl\)-method clearly increase with the number of levels considered. Moreover, even in numerical calculations, one ought to treat levels with large principal quantum number up to about \(n \sim 10^{2}\) (cf., e.g., [Sobelman and Vainshtein 2006)]. For large principal and orbital momenta, scaling relations need to be invoked to calculate the cascade matrix and the error increases with the increase of \(n\) and \(l\) (Grin and Hirata 2010). It has been demonstrated (Pengelly 1964) that already for n = 5 considerable deviations are encountered. On the other hand, just for \(n \gg 1\) and \(l \gg 1\), the radiative transition probabilities could be accurately described by quasi-classical methods, and in particular by the Kramers Electrodynamics. This is realized due to the good agreement between quasi-classical results and quantum numerical calculations. We will show below that the description of radiative cascade based on the quasi-classical approach leads to manageable analytic solutions which are in good agreement with quantum numerical calculations. These solutions also allow identification of the parameters in terms of which the numerical data can be interpreted in a consistent, unified way without recourse to laborious numerical methods.
Apart from its practical significance, the study of radiative cascades between Rydberg states is of general physical interest: it can shed light on the relative importance of direct and cascade populations of atomic levels and on the interrelation between quantum mechanical and classical descriptions of electron motion along the atomic levels. Indeed, the problem can be solved in two extreme cases:
-
(1)
The \(nl\)-state may be assumed to be populated directly by a source \(q_{\text{nl}}\), after which it decays with a probability \(A_{\text{nl}}\) into all of the lower-lying states; the population will then be equal to \(q_{\text{nl}} /A_{\text{nl}}\) (this is the direct population model).
-
(2)
One may assume that the electron can reach a certain \(nl\)-level only by downward cascading through all of the upper-lying states (the cascade population model).
The latter approach is closely related to the classical concept of motion in \(nl\)-space, in which the electron motion is associated with a gradual loss of energy \(\left( {E = - {{Ry}}/n^{2} } \right)\) and angular momentum \(\left[ {M = \hbar (l + 1/2)} \right]\) at a rate which is determined by corresponding classical quantities (Landau and Lifschitz 2000). This classical description has been employed (Belyaev and Budker 1958) for the treatment of radiative cascades; this method is equivalent to using the equation of continuity in phase space for the population \(f(E,M)\). On the other hand, it was shown (Beigman and Gaisinsky 1982; Beigman 2001) that the classical “flow” description with respect to the energy variable \(E\) is invalid: the electron always moves in quantum-mechanical jumps. It is therefore of interest to examine the regions of \(nl\)-space within which the electron can be considered to move classically or by quantum jumps.
Of particular interest is the cascade population in the case of a photorecombination source of external population when the free electrons with an equilibrium (Maxwellian) energy distribution populate the bound atomic states, and the radiative transitions determine both the population source and the subsequent radiative cascade. It is noteworthy that the distribution of the atomic electrons with respect to the orbital quantum number l is by no means always proportional to statistical weights, even if the source of electrons populating the levels is in equilibrium (Pengelly 1964).
6.4.1 Classical Kinetic Equation
Following (Belayev and Budker 1958), we will use canonically conjugate action-angle variables to analyze the classical kinetic equation for the electron distribution function (DF) in an atom or ion. These variables are most convenient because the characteristic time of action variables variation for a radiating electron is appreciably larger than the period of electron motion (the latter is the characteristic time of the variation of the angles variables). That is why the DF may be regarded as independent of the angle variables. We shall take the initial kinetic equation to be the continuity equation in six-dimensional phase space. After averaging over the angle variables, this equation takes the form
where \(I_{\text{k}}\) are the action variables,
and the \(\dot{I}_{\text{k}}\) are the corresponding generalized momenta (averaged over the angle variables):
Here and below, \(E > 0\) is the modulus of the total energy of the bound electron. Equations (6.100), (6.101) give the rate at which a classically radiating electron losses energy \(\left( {I_{1} } \right)\), angular momentum \(\left( {I_{2} } \right)\), and its z-component \(\left( {I_{3} } \right)\) (Landau and Lifschitz 2000).
We shall consider only the stationary case in what follows. The spherical symmetry of the Coulomb field implies that the DF f must be independent of \(M_{\text{z}}\) (we also assume that the source \(q\) is independent of \(M_{\text{z}}\)). Equation (6.98) thus simplifies to
Here the superscript indicates the dimensionality of the space in which \(f\) is defined. We note that the variables \(E\), \(M\), and \(M_{\text{z}}\) satisfy the classical kinematic constraints
In deriving (6.102), we have used the important property
of the generalized momentum, which implies that the electron flux in the space \(E\), \(M\), \(M_{\text{z}}\) may be uniform (\(f^{(3)} = {{const}}.\) satisfies (6.98) if \(q = 0\)). Solving (6.102) by the method of characteristics, we find
where \(\varphi (M)\) is the boundary condition for (6.102) (we take the boundary to be the line \(E = E_{0}\); the generalization to the case of an arbitrary boundary is evident),
\(\varepsilon\) is the eccentricity of the electron orbit, and the dependence \(M({{\tau}} ,E)\) in (6.104) is determined by (6.105). Using (6.104), we can rewrite the Green function for (6.102) in the form
where \(\eta = 0\) for \(x < 0\) and \(\eta = 1\) for \(x > 0\). The \(\delta\)-function in (6.106) corresponds to the classical motion of the radiating electron in the two-dimensional \(\{ E,M\}\)-space; the trajectories coincide with the characteristic curves of (6.102) defined by the relation \(\tau (E,M) = {{const}}\). Since the energy loss rate exceeds the angular momentum loss, \(\varepsilon\) decreases during the radiation emission process so that the orbits eventually become “rounder”.
6.4.2 Quantum Kinetic Equation in the Quasi-classical Approximation
We will consider the quantum mechanical kinetic equation for the distribution function \(f^{(2)}\) in the two-dimensional space \(\{ I_{1} ,I_{2} \}\) and use the formulae
which relate the action variables to the quantum numbers \(n\), \(l\) and \(m_{\text{z}}\). Because \(f^{(3)}\) is independent of \(M_{\text{z}}\), \(f^{(2)}\) and \(f^{(3)}\) obey the simple relation
The kinetic equation has the standard form \(\left( {\Gamma = \{ nl\} } \right)\)
where we have allowed for cascades from all higher-lying states; \(W\) is the probability per unit time for a radiative transition \(\Gamma ^{\prime} \to\Gamma\), \(q\) is the external population source, and \(A\) is the total rate of radiative decay from the \(\Gamma\) level:
For \(n \gg 1\), we can replace the sum in (6.109) by an integral, and for \(l \gg 1\), \(f(\Gamma ^{\prime})\) can be expanded in l near the state \(\Gamma\). This leads to an integro-differential equation (we will henceforth write f in place of \(f^{(2)}\) where no confusion may arise)
where
The quasi-classical kinetic (6.111) reduces to a simpler one-dimensional integral or two-dimensional differential equation, depending on the specific region in \(nl\)-space, and the solutions can be joint uniquely because the corresponding regions overlap.
Indeed, consider (6.111) for the region \(l \ll n\), for which the Kramers approximation is valid for the radiative transition probabilities W. The radiative angular momentum loss \(\left( {\Delta l = \pm 1} \right)\) for \(l \ll n\) is slower than the energy loss, because transitions with \(\Delta n \gg 1\) (including those with \(\Delta n \simeq 1\)) are more likely to occur. If the DF is smooth enough we can therefore discard the differential term in (6.111), so that \(l\) appears to be merely a parameter of the resulting integral equation \((E = 1/2n^{2} ,\;M = \hbar (l + 1/2))\):
where \(x_{\text{m}} \equiv \displaystyle\frac{{(l + 1/2)^{3} }}{{6n^{2} }}\), \(E = 1/2n^{2}\) (in atomic units), \(M = \hbar (l + 1/2)\), and, as before \(f\) is normalized in \(\Gamma\) space. The function \({G} _{0}\) is related to the leading term in the expansion of the transition probability \(W(n^{\prime} \to nl)\) (6.112) with respect to \(\hbar\) for \(l \ll n\)
The function \(A(\Gamma )\) is the total radiative decay rate for the level \(\Gamma = \{ nl\}\)
The first (cascade) integral in (6.113) is negligible for small \(x_{\text{m}}\), so that the population of level \(\Gamma\) is determined by the external source q,
The cascade term becomes important as \(x_{\text{m}}\) increases.
Since the Kramers’ probability W depends only on the difference between the energies of the initial and final states, the integral (6.113) can be solved by taking Laplace transforms. The latter satisfy the equation
where \(s\) is the Laplace variable conjugate to \(x_{\text{m}}\),
We can approximate \(G _{2}\) to within 10% by the expression
where the function \(\alpha (s)\) is slowly varying, \(\alpha (s = 0) = \pi^{2} /6 = 1.64;\alpha (s = \infty ) = \pi \sqrt 3 = 1.81\). If we set \(\alpha = 1.7\), ensuring at most a 10% error in (6.120), (6.121), we obtain the approximate analytic expression
for an arbitrary source q; here, the quantity \(\hbar \dot{n} \equiv \dot{I}_{1}\) is the rate of energy loss [see \(E\) in (6.100)] in Kramers’ domain \(l \ll n\).
To illuminate the essence of the approximation (6.120), (6.121) it should be pointed out that the exact relation between \(G_{2}\) and \(G_{0}\) takes the form (with account of (6.118), (6.119))
The correction \(D(x)\) which is the “Bethe Rule Defect” is proportional to the Kramers’ transition probability for a transition with \(\Delta l = - {{sgn}}(\Delta n)\). Such transitions are suppressed (relative to the transitions with \(\Delta l = {{sgn}}(\Delta n)\)) the stronger the larger \(\Delta n\). In the Kramers’ domain, this leads to an approximate coincidence of the averaged \(\Delta l\) transition probability with the one corresponding to \(\Delta l = {{sgn}}(\Delta n)\) transitions only. The transition to the limit of a classical trajectory (in \(\Gamma\) space) corresponds to the motion with averaged (over \(\Delta l\)) probabilities. That is why the transitions with \(\Delta l = - {{sgn}}(\Delta n)\), in spite of their existence as an elementary, one-step transition, can, within the framework of the KrED, be neglected in multistep transitions.
The DF (6.122) satisfies (6.111) for \(x_{\text{m}} \le 1\) (including \(x_{\text{m}} \ll 1\)), where both integrals in (6.113) are of the same order of magnitude. The integrals cancel each other for \(x_{\text{m}} \gg 1\) that corresponds to the classical limit in (6.122). We can follow this limit by expanding \(f(\Gamma ^{\prime})\) in the integrand with respect to both n and l (not only with respect to l as in the derivation of (6.111)). This expansion, which is valid for \(x_{\text{m}} \gg 1\), leads to the two-dimensional differential equation
for \(f^{(2)} (\Gamma )\). Recalling (6.108), we see that (6.124) is equivalent to (6.102).
We note that since the classical limit is consistent with the inequality \(l \ll n\), it can be described in terms of Kramers transition probabilities. The contribution of the leading term in the \(\hbar\)-expansion for the transition probability, which is proportional to \(\hbar^{ - 1}\), vanishes due to the aforementioned cancellation between the contribution of cascades from all upper levels to the \(nl\)-level under consideration and the contribution of cascades from the \(nl\)-level to all lower levels. This cancellation takes place (in the two-dimensional consideration) only for the leading terms of the \(\hbar\)-expansion for the contributions mentioned. The calculation of these contributions, with account of the quantum corrections to the leading term of the \(\hbar\)-expansion for \(W\), gives the third term on the left-hand of (6.124). As \(\hbar \to 0\), a continuous classical flow of electrons described by (6.124) thus replaces the discrete quantum mechanical “jumps” specified by the non-local coupling in the integral (6.113).
We will now consider how the quasi-classical and classical distributions (6.104) and (6.122) are to be matched. Comparison in the Kramers’ domain \(l \ll n\) shows that the first term in (6.104) (the contribution from the boundary condition for a classical differential equation) must be replaced by the contribution from the direct population. The resulting distribution function is valid for the entire quasi-classical domain of n and l, including the non-Kramers region \(n \sim l\):
where \(l(\tau ,n)\) is given by (6.105) (note, that M = ℏ(l+1/2)). Indeed, the boundary condition contributes to the classical distribution function (6.104) mostly for large \(n\) and, respectively, small \(x_{\text{m}}\), for which the purely classical description breaks down. We will carry out calculations for a specific (photorecombination) source and explicitly piece the solutions together. The results will prove the correctness of the quasi-classical expression (6.125).
6.4.3 Relationship of the Quasi-classical Solution to the Quantum Cascade Matrix. The Solution in the General Quantum Case
We will interpret the above result (6.125) by using the quantum cascade matrix formalism, in which the cascade matrix \(\ C (\Gamma ^{\prime} \to\Gamma )\) plays the role of the Green function for the quantum mechanical equation (6.109). The DF obeying (6.109) can be expressed in the form (Sobelman and Vainshtein 2006; Seaton 1959; Pengelly 1964):
The matrix C can be regarded as the probability of a \(\Gamma ^{\prime} \to\Gamma\) transition via all possible cascades \(\left( {C(\Gamma \to\Gamma ) = 1} \right)\) and obeys the two equivalent recursion formulae:
Comparison of (6.126) with the quasi-classical function, (6.125) shows that the cascade population will be purely classical if f is smooth enough (so that \(f(\Gamma ^{\prime})\) can be expanded in (6.109) as a Taylor series near the point \(\Gamma ^{\prime} =\Gamma\)). In the classical limit, the matrix C takes the form
where the \(\delta\)-function of the argument \(\tau\) [cf. (6.105)] describes the classical trajectory. A similar expression for C also follows directly from (6.127) in the classical limit. If we let \(\hbar \to 0\) as in the derivation of (6.124), we find that
where the function \(F\) is arbitrary.We will now estimate the error in the classical description of cascades for an arbitrary source q \((\text{including a selective population source} \ q \propto \delta (\Gamma -\Gamma _{0} ))\) by substituting the approximate solution (6.122) for the Kramers’ domain \(l \ll n\) into the corresponding (6.113). The remaining term can be transformed into
The expression in square brackets in the integrand coincides with the above-defined “Bethe rule defect” to within 10%. Equation (6.130) implies that the terms in square brackets cancels only for those x for which the Bethe rule defect can be neglected. The distribution function f given by (6.125) cannot be used for sources q whose main contribution to the integral in (6.127) comes from small x, for which the terms in square brackets do not cancel.
Let us analyze the case of a \(\delta\)-function source. Equation (6.125) is clearly not applicable if direct transitions from the level \(\Gamma ^{\prime}\) populated by the source to the level \(\Gamma\) are important (this corresponds to the leading term in the Bethe rule defect as \(x \to 0\)). In any case, such direct transitions will be important for levels \(\Gamma\) close to \(\Gamma ^{\prime}\), as well as for more remote levels that are populated solely by Bethe rule defect transitions, i.e., by electrons lying far from the classical trajectory. Classical cascade may occur between the levels which lie close to the classical trajectory provided they are sufficiently far from the levels \(\Gamma ^{\prime}\) populated directly by the source \(\left( {\Delta x_{\text{m}} \ge 1} \right)\).
The situation depicted (i.e., transition from the quantum direct population, in the domain close to an externally populated level, to the classical cascade population) can be described in terms of a modified classical cascade. For example, in Kramers’ domain this gives [here x is the same as in (6.130)]:
However, there is an alternative, more systematic method for treating “the quantum mechanical properties” of the external source of population. This method exploits the fact that the form of the quantum mechanical kinetic equation remains unchanged if we subtract an arbitrary number of the leading terms in the expansion of the distribution function in powers of the number of the transitions in a cascade from the externally populated level \(\Gamma ^{\prime}\) to the investigated level \(\Gamma\). Indeed, (6.109) continues to hold for the function \(\left( {f - q/A} \right)\) if we replace q by
We thus arrive at the distribution function [compare with (6.125)]
The generalization of the result (6.125) in the case of an arbitrary number of averaging procedures for the source \(q\) gives the result
where the effective source \(\langle q \rangle_{\text{N}}\) describes the population of the level \(\Gamma\) by all possible \(N\)-step (i.e., \(N\)-photon) cascade transitions from all points of the source,
and the appropriate selection rules for the radiative transition probabilities must be used in calculating (6.135). Each additional summation in (6.135) further smoothens the effective source and thus decreases the error caused by summing the remainder terms in the series (6.126) “classically” to \(\simeq 10\%\). The error in the final result depends both on the specific form of the source q and on the values of quantum numbers n and l. The error will be small if the relative change of \(f(\Gamma )\) is small due to subtracting one more term (corresponding to \((N + 1)\)-step transitions) out of the classical cascade.
The above algorithm can be used to calculate the distribution function f for radiative electron cascades between Rydberg atomic or ionic states for arbitrary sources and quantum numbers (in particular, n and l may be of the order of unity).
Note that the extent to which the population source q is of essentially “quantum-mechanical” character depends partly on the sharpness of its distribution in \(\Gamma\)-space (6.127) and partly on the range of values of n, l within which the source is concentrated. For example, the distribution function (DF) is of essentially quantum character if a smoothly distributed (i.e., “classical”) source is concentrated in the “quantum” region \(x_{\text{m}} \ll 1\). On the other hand, the cascade population can be described quasi-classically even for a selective source if the latter is concentrated in the “classical” region \(l \sim n\). Thus, if the levels with \(l = n - 1\) are selectively populated by the external source, the population of the lower levels by cascades can be described purely classically and the result agrees with the exact quantum calculation. Specifically, if we use the quantum cascade matrix and recall the relations for this case \(\left( {l = n - 1} \right)\),
we find from (6.126) that
where \(\delta\) is the Kronecker symbol and \(k \ge 0\). The calculation using (6.125) leads to the same result.
6.4.4 Atomic Level Populations for a Photorecombination Source. Quasi-classical Scaling Laws
The general results of Sects. 6.4.2, 6.4.3 are now applied to the calculation of level population for a Rydberg atom externally populated by a photorecombination source which is of great interest for astrophysical applications. Since the source involves the same radiative transitions as the cascade between the atomic levels, the above approximations for the cascade can be also applied to the recombination source [see approximation (6.120), (6.121) for the error in the quasi-classical DF (6.125)] in a specific case.
The calculation of the DF (6.122) for the photorecombination source q provides (xm = EnM3/3 = (l+1/2)3/6n2, xT = 3/TM3 in a.u.)
and corresponds to including the Bethe rule defect contribution to the source q but neglecting it in the Green function for (6.113). It is worthwhile to express the result for the DF in terms of the equilibrium DF (as well as the corresponding ratio \(b(\Gamma )\))
where \(\psi\) and \(\alpha\) are given by (6.139) and (6.120), (6.121), respectively (remind, that we use \(E > 0\)).
For \(n,l \gg 1\), the second term in \(b_{\text{nl}}\) is of importance only for \(x_{\text{m}} \ll 1\), \(x_{\text{T}} \gg 1\); the DF is therefore independent on the energy E at the edge (\(l \sim n\), or \(x_{\text{m}} \ge 1\)) of the Kramers’ domain. This implies that the solution outside the Kramers’ domain could be found from the first term in (6.141), regarded simply as a classical boundary condition. Because this term is independent of E, the resulting DF will be the same regardless of which line in nl-space is chosen as the boundary. If we then use (6.104) and (6.105) to continue the DF (6.140, 6.141) along the characteristic curves, we obtain the final result
which is valid for all quasi-classical values of n and l. It is legitimate to continue the solution in this way because the source (6.138) is concentrated in the Kramers’ domain, so that there is no need to evaluate (6.125) directly (recall that A and dn/dt in (6.125) are the transition probabilities for an arbitrary ratio \(l/n\)). Indeed, a calculation using (6.125) for \((l/n - 1) \ll 1\) reveals that these states are populated solely by classical cascades; moreover, most of the contribution comes from the transitions whose initial state is far from the curve \(l \sim n\). The latter result corresponds precisely to the classical behavior, in which the states near the boundary \(M = M_{\max} (E)\) can be populated by a source concentrated within a region with an eccentricity \(\varepsilon \to 1\). For a recombination source, the Kramers’ domain shrinks along the n axis as l increases (as the edge of the continuum is approached) and thus is effectively transformed into a boundary condition.
We will now show that the use of the algorithm discussed in Sect. 6.4.3 permits to incorporate some additional Bethe rule defect contributions to the DF. For a singly averaged source \(\left( {N = 1} \right)\), (6.132) gives
Within 10% error (approximation of the coefficient \(\alpha\) in (6.120, 6.121)), this gives
for \(\langle f \rangle\) in (6.133); where \(f\) is defined by (6.125). The calculation of \(\langle f \rangle\) for the photorecombination source reveals that the corrections due to the Bethe rule defect contribution are smaller than the 10% error arising from the approximation (6.120), (6.121). Thus, if we include the linear correction to (6.141), in accordance with (6.144), we find that
Since the factor multiplying \(\psi\) in (6.145) is significant only for \(x_{\text{m}} \ll 1\), \(x_{\text{T}} \gg 1\), we conclude, as in Sect. 6.4.3, that the accuracy of the DF (6.141) is the same as for (6.120), (6.121).
The quasi-classical DF (6.140, 6.142) derived above reveals approximate scaling laws for the exact quantum-level populations, while these laws are unknown from the results of complex quantum numerical calculations. These laws are a consequence of the fact that the quasi-classical DF (6.140, 6.142) depends on a lower number of variables than in the case for the quantum DF. Indeed, \(f_{\text{nl}}\) depends only on \(x_{\text{m}}\) and \(x_{\text{T}}\) for \(x_{\text{m}} \ll 1\), \(x_{\text{T}} \gg 1\). If one of the parameters \(x_{\text{m}}\) or \(1/x_{\text{T}}\) becomes \(\sim 1\), the second term in (6.142) becomes much less than the first term and f depends only on \(x_{\text{T}}\). Elsewhere in \(nl\)-space, f depends on the parameter \(x_{\text{T}} \varepsilon^{2}\). We thus have a smooth transition between three scaling laws for \(n,l \gg 1\). Comparison of the quasi-classical DF (6.140, 6.142) with the results of numerical quantum calculations (Pengelly 1964) reveals that quasi-classical DF (6.142) can also be used for relatively small values of n and l. The validity of the scaling laws derived by the quasi-classical method can be verified by means of a corresponding transformation of quantum numerical data.
It is worthwhile to illustrate the relative importance of direct and cascade population in the Kramers’ domain \(l \ll n\) for a photorecombination source. We find from (6.122)
for the cascade \(\left( {f_{C} } \right)\) and direct \(\left( {f_{\text{D}} } \right)\) populations. The contribution from \(f_{\text{D}}\) clearly decreases as \(x_{\text{m}}\) increases while the sum \(\left( {f_{\text{C}} + f_{\text{D}} } \right)\) coincides with (6.141). The numerical values of the ratio \(f_{\text{D}} /(f_{\text{D}} + f_{\text{C}} )\) agree reasonably well with the data in (Pengelly 1964), e.g., for \(n = 6\) and \(T = 10^{4} \;K\), (6.146) implies that this ratio is equal to 96% for \(l = 1\) and 87% for \(l = 2\); the corresponding values from (Pengelly 1964) are 81% and 73%, respectively.
It is important to note that the dependence of the integral over l population differs from the one found by the n-method. The major contribution to \(f(n)\) comes from the first term in (6.142), which gives the following dependence on the parameter \(Tn^{3}\):
We note, that in the n-method the universal parameter is \(Tn^{2}\).
The quasi-classical method for an analytic description of radiative cascades developed in this section gives the possibility of an approximate (to within 10%) calculation of the contribution of multistep cascade transitions to the atomic level populations. This calculation is known to be the most difficult part of the corresponding numerical calculations. Indeed, the \(\delta\)-function properties of the cascade matrix that correspond to radiating electrons moving (in the \(nl\)-space) along the characteristics in the classical domain are difficult to reveal from the results of quantum numerical calculations. For example, the calculations in (Pengelly 1964) detected only the boundary characteristics corresponding to \(l = l_{\max} = n - 1\).
The algorithm in Sect. 6.4.3 for calculating populations in the general quantum case and for arbitrary sources can thus be used to correctly treat cascades through an arbitrary large number of Rydberg states. The number of quantum mechanical cascade transitions which cannot be described classically may be quite small in practice, particularly for the case of distributed sources. For example, the cascade population is purely classical (to within 10%) for a photorecombination source.
6.5 Two-Dimensional Collisional–Radiative Model of Highly Excited Atomic States
As outlined in the foregoing Sect. 6.4, the population of Rydberg atomic states determined by radiative–collisional cascades is the subject of many years’ investigations (Sobelman and Vainshtein 2006; Beigman 2001; Griem 2005; Strelnitski et al. 1996; Grin and Hirata 2010). As a rule, the one-dimensional (1D) kinetics is used for the modeling. When one makes a transition to 2D (in principle n and orbital momentum l quantum numbers) the number of kinetic equations grows sharply. Really if, for example, n = 100, one needs to take into account 100 * 100 = 104 equations for radiative–collisional transitions between two highly excited states multiplied by 100 transitions from the continuum to a specific atomic energy state which results in more than 106 kinetic equations with further account of cascade transitions to other Rydberg atomic states. Direct solution of such a large number of kinetic equations is a problem even for modern computers, but the most essential point is the estimation of the precision of such calculations.
The possible solution of the problem is the application of quasi-classical or pure classical model for description of highly excited atomic states. This was demonstrated above for radiative (R) cascade transitions. We generalize the model for general case of both radiative and collisional (RC) processes. For a specific application, we will use below experimental data for recombination radio lines of highly excited hydrogen atoms (n > 100) observed in astrophysical plasma with low electron density \(\left( {n_{\text{e}} \propto 10^{3}{-}10^{4} \,{\text{cm}}^{ - 3} } \right)\) and moderate temperatures \(\left( {T_{\text{e}} \propto 1\,{\text{eV}}} \right)\). One can apply the results for large densities in the case of highly charged ions with ion charge Z ≫ 1 using the scaling between radiative and collisional processes, proportional to Z7 [see also (5.53)].
6.5.1 Kinetic Model of Radiative–Collisional Cascades
Let us consider the transition from the quantum kinetic equation to the classical one. The structure of a quantum kinetic equation for a radiative–collisional (RC) cascade takes the form (Kadomtsev et al. 2007, 2008):
where \(\hat{L}_{\text{c}}\) is the collision transition operator, \(\hat{L}_{\text{r}}^{q}\) is radiation transition operator, \(f(nl)\) is population distribution function in two-dimensional space of principal n and orbital momentum l atomic quantum numbers, and \(q(nl)\) is the population source of atomic energy states. The action of these operators on population distribution function takes the form:
Here, \(W(n^{\prime},l^{\prime};nl)\) and \(A(n,l;n^{\prime},l^{\prime})\) are the rates of collisional and radiative transitions between atomic states with different quantum numbers, and \(A(n,l) = \mathop {\Sigma} \nolimits_{{n^{\prime},l^{\prime}}} A(n,l;n^{\prime},l^{\prime})\) is the total radiation decay rate to all lower atomic states. The sums in (6.149), (6.150) go over all values of quantum numbers with account for corresponding selection rules.
For the case of highly excited (Rydberg) atomic states, it is possible to simplify the collision operator by its transformation to a diffusion operator in the space of principle and orbital momentum quantum numbers. The situation is complex due to the non-local connection between atomic states via radiative transitions. In fact, the radiation operator (6.150) is in reality an integral operator describing the possibilities of large changes (jumps) of principle quantum numbers in radiative transitions. It is possible, however, to show that in the domain \(n > l \gg n^{2/3}\) the action of the radiation operator (6.150) can be reduced to a differential one describing the continuous motion (flux) of the electron in 2D space of quantum numbers with rates determined by the classical conservation laws with respect to energy and momentum:
Therefore, the quantum integral radiation operator \(\hat{L}_{\text{r}}\) reduces to the classical differential operator \(\hat{L}_{\text{r}}^{cl}\). However, this approach is only valid for population sources which are broad enough (for example, three-body recombination) so that the statistical weight of atomic states with small values of orbital momentum would be also small: \(l_{\text{eff}}^{2} \propto n^{4/3} \ll n^{2}\). However, this is not the case for many others recombination sources (for example, radiative or dielectronic ones).
We will use the iteration approach to account for the non-local connection of 2D distributions used above for a radiative cascade where the distribution function is presented by
The same iteration method can be developed accounting for the collision operator. The general scheme looks as follows. In the first step of the iteration procedure, we find \(f\) as the sum \(f = f_{0} + f_{1}\) where \(f_{0}\) satisfies the zero-order approximation determined by populations from external sources, collisional diffusion and radiation decay to lower atomic states:
After the substitution \(f = f_{0} + \delta f\) into (6.148), we obtain the equation for \(\delta f\):
or, in the operator form:
It can be seen that the function \(\delta f\) is determined from an equation that is of similar type as for f (6.148), where the modified source q1(n, l) enters instead of q(n ,l):
It corresponds to the population after the first quantum emission. Application of the same procedure like in (6.152) to the function \(\delta f\) we separate out the direct population \(f_{1} (n,l)\) by the source \(q_{1}\) (determined from (6.156)) and from the previous iteration for \(\delta f\) with f0. Applying the iteration procedure step-by-step to the initial (6.148), we find the solution of f in the form of a series \(f = f_{0} + f_{1} + f_{2} + \cdots + f_{\text{k}} + \cdots\) that corresponds to a step-by-step quanta emission where every term \(f_{\text{k}}\) is determined from the equation
using the function \(f_{\text{k} - 1}\) calculated at the previous step of (6.157), while f0 can be found from (6.153) with initial source. From the physical point of view, the contributions \(f_{\text{k}}\) are determined by a collision transition kinetics between the steps k and k + 1 with correspondingly emitted quanta. The convergence of the series is, in general, rather slow (logarithmic), so that higher-order contributions are of importance. From a mathematical point of view, the iterative solution corresponds to a von Neumann series for integral equations.
According to (6.157), the source qk in a specific state nl is determined by different transitions between the atomic states \(\left( {n^{\prime} > n} \right)\) after the emission of a k-th-quantum. At every further step, the quantum becomes more “continuous” and from a specific iteration number on it is possible to make a transition from the quantum operator \(\hat{L}_{\text{r}}\) to the classical differential operator \(\hat{L}_{\text{r}}^{cl}\) [see (6.151)]. This is realized by changing in the further iteration series terms the quantum for the classical distribution function \(f_{\text{n}}^{cl}:\)
As a result, the total distribution function is determined by the sum
The quasi-classical radiation operator has been discussed in the foregoing Sections and will be used in specific calculations below.
6.5.2 The Classical Collision Operator
The collision operator determining the diffusion in the space of principal and orbital momentum quantum numbers will be determined in a pure classical representation. For this purpose, the general kinetic equation was solved in the framework of a quasi-classical representation for radiation transitions and a pure classical collision integral. The specific form of the collision integral can be obtained by calculations of energy and orbital momentum transfer in classical Coulomb collision between an atomic electron on a Kepler orbit with a plasma particle. The diffusion coefficients in energy and orbital momentum space are then determined from the well-known averaged quadrates of energy and orbital momentum transfer. The general form of the kinetic equation is of Fokker–Planck-type (Belyaev and Budker 1958, Ecker 1972, Kadomtsev et al. 2008):
Here \(I_{\text{k,j}}\) are in general arbitrary motion integrals. For a Coulomb field, a natural choice is to choose the motion integrals as the energy and orbital momentum integrals. The average values in (6.160) represent an integration over the parameters of the plasma particles parameters and the motion phases of the Kepler atomic electron.
Let us consider the cases of fast (inelastic) and slow (elastic) collisions for plasma electrons and ions correspondently. In the case of fast collisions, the motion of a plasma particle can be taken as rectangular with an impact parameter \({{\rho}}\) and velocity \( \upsilon_{\text{e}}\):
This results in the squared energy change:
where \(\vec{ \upsilon}_{\text{a}}\) is the electron velocity on the Bohr orbit. After averaging over impact parameters, Maxwellian velocity distribution and multiplication by the perturbing particles’ density \(n_{\text{e}}\), one obtains the collision frequency \(\omega\) (or the time between collisions):
where T is the temperature of the perturber particles, L is the Coulomb logarithm. In order to obtain independent diffusion operators in 2D scheme, it is useful to introduce dimensionless variables:
Equation (6.165) corresponds to the electron energy, (6.166) to the ratio \(l/n\), and (6.167) is the orbital momentum projection (that is of no importance for spherically plasma electron distributions). The domains for changing of variables are: \(0 < \xi < \infty,\, 0<\eta<1, \, -1< \zeta <1\). The energy parameter \(E_{0}\) for the dimensionless energy variable in (6.167) is taken to be equal to one which corresponds to equal rates of classical collision and radiative decay rates:
It is obvious that such a choice corresponds to the transition of a collision cascade to a radiation one, if \(\xi \approx 1\). The average squared of the new variable is equal to
It is convenient also to introduce a dimensionless distribution function according
The collision operator expressed in terms of the new variables takes the form:
Such representation of the collision integral was obtained in (Belyaev and Budker 1958) by direct application of the Landau collision integral to the collisions between plasma and atomic electrons. The elastic collisions correspond to the diffusion in the orbital momentum quantum number space. Most contributions originate from ion-atom collisions due to relatively small ion’s velocity compared to the electron ones.
6.5.3 Numerical Solution for Delta-Function Source
The solution of the kinetic equation solution for a local (delta-function) source is of interest in order to demonstrate the effects of collisions on the radiative cascades. From the point of view of application, it is of interest for a selective (laser) population source. The calculation procedure includes the introduction of a point source and an iterative calculation procedure as described above.
The plasma parameters have been selected close to astrophysical experimental conditions (temperature of \(kT_{\text{e}} = 1\,{\text{eV}}\), density \(n_{\text{e}} = 2.5 \times 10^{3} \,{\text{cm}}^{ - 3}\)), and two pairs of quantum numbers n, l: (100,55) and (50,20). The first one corresponds to the values presented in (Strelnitski et al. 1996) in order to check the results with quantum calculations. The second pair corresponds to the decrease of quantum numbers approximately two times in order to demonstrate the sharp change between radiation and collision processes when quantum numbers are changed. Note that the collision operator scaling is close to \(\hat{L}_{\text{c}} \sim\,n_{\text{e}} \upsilon_{\text{e}} n^{4}\), whereas the radiation operator scaling is proportional to \(\hat{L}_{\text{r}} \sim\,n^{ - 3} l^{ - 2}\). This results in different distributions in 2D space of quantum numbers.
Figure 6.13 shows the 2D population distribution function for the pure radiation cascade for a delta-function source for a populated atomic state n, l = (50, 20). The radiation cascade follows the classical trajectory according to (6.151).
2D population distribution function for the radiation cascade from a delta-function source supporting the population \(\psi_{0} = 1\) for n, l = (50, 20) in the case when collisions are absent (note that the sharp maximum \(\psi_{0} = 1\) at n, l = (50, 20) is not shown for better demonstration of the overall features of the distribution function)
Figure 6.14 shows the 2D population distribution function for the collision–radiative cascade. Collisions result into an important distribution over principle and orbital momentum quantum numbers (compare with Fig. 6.13).
6.5.4 Radiation Recombination Population Source
Numerical calculations have been performed employing the general iteration scheme outlined above. It is of interest to compare 1D and 2D models. In order to do so, the total population function was averaged over orbital momentum quantum numbers \(l\), i.e.,
Figure 6.15 presents a comparison between 1D and averaged 2D population distribution functions. One can see that in the absence of collisions, the two models differ strongly. It is due to the simple circumstance: the 1D model deals with the ratio of averaged rates, whereas the 2D model deals with the averaged ratio of the rates; such difference in the averaging procedure results in different dependencies of populations on principle quantum numbers. When collision frequencies increase, the difference between 1D and 2D populations decreases. It is due to the strong mixing over orbital momentum states driving their populations to statistical equilibrium which is just the initial starting point for the 1D kinetics.
Populations of atomic levels in direct population by a photorecombination source: 1—averaged two-dimensional calculations without collisions, 2—one-dimensional calculations without collisions, 3—one-dimensional calculations with allowance for collisions, 4—averaged two-dimensional calculations with allowance for collisions. The plasma parameters correspond to astrophysical conditions: ne = 2500 cm−3, kTe = 1 eV
6.5.5 Intensities of Rydberg Spectral Lines
The intensities of Rydberg spectral lines are calculated from the equation:
where \(\hbar \omega_{{\text{nn}^{\prime}}}\) are the radiation transition energies, \(N_{\text{nl}}\) are populations of upper energy atomic levels calculated according to the scheme described above, \(A\left( {nl;n^{\prime}l^{\prime}} \right)\) are radiation transition probabilities. In experiments on radio-recombination lines (Biberman et al. 1982) the dependence of radiation transition intensities on the principle quantum number of the upper level is of interest for a fixed value of transition frequency \(\omega\). Figure 6.16 demonstrates the line intensities for the transitions from the energy levels n = 50–100 at the observed frequency near \(\omega = 8 \cdot10^{ - 6}\) a.u. The comparison between statistical equilibrium (large n) and non-equilibrium (low n) upper-level populations demonstrates the essential difference between the two curves in Fig. 6.16 (dashed curve show calculations for a statistical equilibrium, while the solid curve presents non-statistical equilibrium calculations). This is important for Rydberg spectra interpretation. The results allow also to judge the degree of non-equilibrium of the populations.
Intensities of Rydberg spectral lines for the transition \(n = 50 - 100\) at the observed frequency \(\omega = 8 \times 10^{ - 6} \,{\text{a.u}}.\), corresponding to the transition with \(\Delta n = 1\) between energy levels 50 and 49 for an electron density ne = 2500 cm−3 and temperature kTe = 1 eV
References
J. Abdallah Jr., M.E. Sherrill, The reduced detailed configuration accounting RDCA model for NLTE plasma calculations. HEDP 4, 124 (2008)
V.A. Abramov, F.F. Baryshnikov, A.I. Kazanskii, I.V. Komarov, V.S. Lisitsa, M.I. Chibisov, in Charge Exchange of Atoms on Multiply Charged Ions, Reviews of Plasma Physics, vol. 12, ed. by M.A. Leantovich, B.B. Kadomtsev (Consultants Bureau, New York, London, 1987)
A. Bar-Shalom, J. Oreg, W.H. Goldstein, D. Shvarts, A. Zigler, Super-transition-arrays: a model for the spectral analysis of hot, dense plasma. Phys. Rev. A 40, 6414 (1995)
J. Bauche, C. Bauche-Arnoult, O. Peyrusse, Effective temperatures in hot dense plasmas. JQSRT 99, 55 (2006)
I.L. Beigman, Analytical methods for highly excited level populations in hot plasma, in Astrophysics and Space Science Reviews, OPA (2001). ISBN-9789058232410
I.L. Beigman, I.M. Gaisinsky, An analytical description of populations of highly excited levels. JQSRT 28, 441 (1982)
S.T. Belyaev, G.I. Budker, Multiquantum recombination in ionized gases, in Plasma Physics and the Problem of Controlled Thermonuclear Reactions, ed. by M.A. Leontovich, vol. 3 (Pergamon Press, Oxford, 1958)
L.M. Biberman, V.S. Vorobiev, I.T. Yakubov, Kinetics of a non-equilibrium low-temperature plasma (Nauka, Moscow, 1982)
V.A. Boiko, A.V. Vinogradov, S.A. Pikuz, I.Y. Skobelev, A.Y. Faenov, X-ray spectroscopy of laser produced plasmas. J. Sov. Laser Res. 6, 82 (1985)
H.K. Chung, C. Bowen, C.J. Fontes, S.B. Hansen, Yu. Ralchenko, Comparison and analysis of collisional-radiative models at the NLTE-7 workshop. HEDP 9, 645 (2013)
J. Colgan, C.J. Fontes, H. Zhang, J. Abdallah Jr., Collisional-radiative modeling of tungsten at temperatures of 1200–2400 eV. Atoms 3, 76 (2015). https://doi.org/10.3390/atoms3020076
R.D. Cowan, The Theory of Atomic Structure and Spectra (University of California Press, Berkely, 1981)
A.V. Demura, M.B. Kadomtsev, V.S. Lisitsa, V.A. Shurygin, Statistical model of radiation losses for heavy ions in plasmas. JETP Lett. 98, 786 (2013)
G. Ecker, Theory of Fully Ionized Plasmas (Academic Press, New York 1972)
M.R. Flannery, D. Vrinceanu, Quantal and classical radiative cascade in Rydberg plasmas. Phys. Rev. A 68, 030502(R) (2003)
A.H. Gabriel, Dielectronic satellite spectra for highly-charged he-like ion lines. Mon. Not. R. Astro. Soc. 160, 99 (1972)
S.H. Glenzer, F.B. Rosmej, R.W. Lee, C.A. Back, K.G. Estabrook, B.J. MacCowan, T.D. Shepard, R.E. Turner, Measurements of suprathermal electrons in hohlraum plasmas with X-ray spectroscopy. Phys. Rev. Lett. 81, 365 (1998)
H.R. Griem, On the narrowing of radio recombination lines at high principal quantum numbers. Astrophys. J. 620, L133 (2005)
D. Grin, C.M. Hirata, Cosmological hydrogen recombination: the effect of extremely high-n states. Phys. Rev. D 81, 083005 (2010)
S.B. Hansen, J. Bauche, C. Bauche-Arnoult, Superconfiguration widths and their effects on atomic models. HEDP 7, 27 (2011)
V.L. Jacobs, M. Blaha, Effects of angular-momentum–changing collisions on dielectronic satellite spectra. Phys. Rev. A 21, 525 (1980)
M.B. Kadomtsev, M.G. Levashova, V.S. Lisitsa, Universal two-dimensional kinetics of the populations of Rydberg atoms in plasmas. JETP Lett. 85, 493 (2007)
M.B. Kadomtsev, M.G. Levashova, V.S. Lisitsa, Semiclassical theory of the radiative-collisional cascade in a Rydberg atom. JETP 106, 635 (2008)
A.B. Kukushkin, V.S. Lisitsa, Radiative cascades between Rydberg atomic states. Sov. Phys. JETP 61, 937 (1985)
L.D. Landau, E.M. Lifschitz, The Classical Theory of Fields, 4th edn. (Butterworth-Heineman, Oxford, 2000)
R. Lebert, A. Engel, W. Neff, Investigation on the transition between column and micropinch mode of plasma focus operation. J. Appl. Phys. 78, 6414 (1995)
E.H. Lieb, B. Simon, The Thomas-Fermi theory of atoms, molecules and solids. Adv. Math. 23, 22 (1977)
S.J. Messenger, V. Strelnitski, On the 1.7 mm FeII and other natural lasers. Mon. Not. R. Astron. Soc 404, 1545 (2010)
F. Petitdemange, F.B. Rosmej, Dielectronic satellites and Auger electron heating: irradiation of solids by intense XUV-free electron laser radiation, in New Trends in Atomic & Molecular Physics—Advanced Technological Applications, ed. by M. Mohan, vol. 76 (Springer, Heidelberg, 2013), pp. 91–114. ISBN 978-3-642-38166-9
R.M. Pengelly, Recombination spectra—I. calculations for hydrogenic ions in the limit of low densities. Mon. Not. R. Astron. Soc 127, 145 (1964)
R. Piron, T. Blenski, Variational-average-atom-in-quantum-plasmas VAAQP code and virial theorem: equation-of-state and shock-Hugoniot calculations for warm dense Al. Fe, Cu, and Pb, Phys. Rev. E 83, 026403 (2011)
F.B. Rosmej, Hot electron X-ray diagnostics, J. Phys. B. Lett. At. Mol. Opt. Phys. 30, L819 (1997)
F.B. Rosmej, A new type of analytical model for complex radiation emission of hollow ions in fusion and laser produced plasmas. Europhys. Lett. 55, 472 (2001)
F.B. Rosmej, An alternative method to determine atomic radiation. Europhys. Lett. 76, 1081 (2006)
F.B. Rosmej, X-ray emission spectroscopy and diagnostics of non-equilibrium fusion and laser produced plasmas, in Highly Charged Ion Spectroscopic Research, ed. by Y. Zou, R. Hutton, (Taylor and Francis, Abingdon, UK 2012), pp. 267–341. ISBN: 9781420079043. http://www.crcnetbase.com/isbn/9781420079050
F.B. Rosmej, O.N. Rosmej, Transient formation of forbidden lines, J. Phys. B Lett. At. Mol. Opt. Phys. 29, L359 (1996)
F.B. Rosmej, J. Abdallah Jr., Blue satellite structure near Heα and Heβ and redistribution of level populations. Phys. Lett. A 245, 548 (1998)
F.B. Rosmej, V.S. Lisitsa, A self-consistent method for the determination of neutral density from X-ray impurity spectra. Phys. Lett. A 244, 401 (1998)
F.B. Rosmej, A. Calisti, B. Talin, R. Stamm, D.H.H. Hoffmann, W. Süß, M. Geißel, A.Ya. Faenov, T.A. Pikuz, Observation of two-electron transitions in dense non-Maxwellian laser produced plasmas and their use as diagnostic reference lines. JQSRT 71, 639 (2001)
F.B. Rosmej, R. More, O.N. Rosmej, J. Wieser, N. Borisenko, V.P. Shevelko, M. Geißel, A. Blazevic, J. Jacoby, E. Dewald, M. Roth, E. Brambring, K. Weyrich, D.H.H. Hoffmann, A.A. Golubev, V. Turtikov, A. Fertman, BYu. Sharkov, A.Ya. Faenov, T.A. Pikuz, A.I. Magunov, IYu. Skobelev, Methods of charge state analysis of fast ions inside matter based on their X-ray spectral distribution. Laser Part. Beams 20, 479 (2002a)
F.B. Rosmej, H.R. Griem, R.C. Elton, V.L. Jacobs, J.A. Cobble, A.Ya. Faenov, T.A. Pikuz, M. Geißel, D.H.H. Hoffmann, W. Süß, D.B. Uskov, V.P. Shevelko, R.C. Mancini, Investigation of charge exchange induced formation of two electron satellite transitions in dense laser produced plasmas. Phys. Rev. E 66, 056402 (2002b)
J.G. Rubiano, R. Florido, C. Bowen, R.W. Lee, Y. Ralchenko, Review of the 4th NLTE code comparison workshop. HEDP 3, 225 (2007)
M.J. Seaton, The solution of capture-cascade equations for hydrogen. Mon. Not. R. Astron. Soc. 119, 90 (1959)
I.I. Sobelman, L.A. Vainshtein, Excitation of Atomic Spectra (Alpha Science International Ltd., Oxford, U.K., 2006)
V.S. Strelnitski, V.O. Ponomarev, H.A. Smith, Hydrogen masers. I. Theory and prospects. Astrophys. J. 470, 1118 (1996)
H.P. Summers, The recombination and level populations of ions—II; resolution of angular momentum states. Mon. Not. R. Astron. Soc. 178, 101 (1977)
N.C. Woolsey, B.A. Hammel, C.J. Keane, A. Asfaw, C.A. Back, J.C. Moreno, J.K. Nash, A. Calisti, C. Mossé, R. Stamm, B. Talin, L. Klein, R.W. Lee, Evolution of electron temperature and electron density in indirectly driven spherical implosions. Phys. Rev. E 56, 2314 (1997)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Rosmej, F.B., Astapenko, V.A., Lisitsa, V.S. (2021). Atomic Population Kinetics. In: Plasma Atomic Physics. Springer Series on Atomic, Optical, and Plasma Physics, vol 104. Springer, Cham. https://doi.org/10.1007/978-3-030-05968-2_6
Download citation
DOI: https://doi.org/10.1007/978-3-030-05968-2_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-05966-8
Online ISBN: 978-3-030-05968-2
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)