Impact of Direct Communications on the Performance of Cooperative Spectrum-Sharing with Two-Way Relays and Maximal Ratio Combining

Abstract

In this paper, we investigate a three-phase two-way (TW) amplify-and-forward (AF) relaying for cognitive radio networks. By utilizing the direct communications, the end user can employ maximal ratio combining to achieve the full diversity. We derive the closed-form and asymptotic expressions for user and system outage probabilities which allow us to highlight the advantage of cooperative cognitive communications. The numerical results, obtained through compact forms of these outage probabilities, yield that the cognitive TW AF relaying scheme can significantly enhance the reliability of unlicensed networks in which the transmit power at each secondary user is strictly governed.

1 Introduction

With a tremendous growth of wireless multimedia services and the number of customers, it has been an enormous pressure on available frequency bands and spectrum allocation policies. However, most of frequency bands are under-utilization according to the report of Federal Communication Commission (FCC). To get around this troublesome, cognitive radio (CR) technique has been proposed to allow the unlicensed user can utilize the licensed spectrum band [1]. The principal idea of CR networks is that the secondary users (SUs) are able to use the spectrum bands of primary users (PUs) provided that the quality of service (QoS) of licensed networks is not compromised. Several CR schemes have been introduced in the literature to implement the CR network. In particular, for interweave paradigm, the unlicensed users are not allowed to occupy the spectrum bands if PU activities are detected. As such, the transmission of CR network strictly relies on the primary system. On the other hand, the underlay spectrum-sharing paradigm allows SUs to transmit its information simultaneously with PUs as long as the maximal interference does not exceed the predefined threshold. For this approach, it ensures the stable transmission for SUs at an expense of limited coverage area and low QoS. One efficient way to alleviate the disadvantages of CR underlay scheme is to combine CR with relay networks [2, 3], where the latter is known as an efficient approach for combating the effect of fading channels and expanding the communication range through the assistance of the third party named relay. In particular, relay node helps source node to transmit its signal by adopting one of relaying techniques, i.e., amplify and forward (AF) [4] and decode and forward (DF) [5].

Although the one-way cognitive relay network can overcome both the impact of fading channels and the drawbacks of underlay scheme, the spectral efficiency of this system is still constrained by multiple time-slots owing to half-duplex relaying protocol [6]. More recently, two-way relaying (TWR) technique [7] has drawn a lot of attention due to fully compensating this loss by permitting two users concurrently transmit its signal to each other with the help of half-duplex relays [8]. Despite getting higher spectral efficiency than the traditional cognitive one-way relay networks, only several works investigated the performance of two-way counterpart [9,10,11,12,13,14]. The performance of two-way relaying with single and multiple relays has been reported in [9] and [10], respectively. In [10], the exact outage probability of opportunistic two-way relaying with spectrum-sharing has been presented. Moreover, it has been proved that system performance largely depends on the number of relay nodes and the location of relay nodes together with primary user. While the topic of energy harvesting in two-way networks has been investigated in [13, 14]. In [11], the tight lower bound of user outage performance in multiple primary users environment has been obtained in two cases, i.e., two users and two group of users. The optimal relay selection for two-way cognitive relay networks has been discussed in [12]. In addition, relay selection combined with power allocation for two-way relaying in the presence of imperfect channel state information (CSI) were studied in [15, 16]. Note that previous works have only considered DF relaying and neglected the impact of direct communication.

Different from the above works, in this paper, we investigate the two-way AF relaying for underlay spectrum-sharing with the existence of the direct link between two users. Generally, there are two distinct two-way relaying schemes depending on the number of required time-slots to complete the communication [17]: (i) time division broadcast (TDBC) or three-phase two-way relay (3P-TWR) and (ii) multiple access broadcast (MABC) or two-phase TWR (2P-TWR) [18]. For CR networks, the performance of SU is limited due to the fact that its transmit power is governed by the maximally allowable interference power constraint at PU. As such, in this paper, we exploit the direct link in 3P-TWR where the communication reliability is enhanced via diversity combining between the direct and relaying links. Our considered scheme can enhance both spectral efficiency for cognitive relay networks while keeping the desired QoS of secondary networks satisfactorily. Our main contribution in this paper is summarized as follows: We consider the cognitive two-way relay networks in the presence of direct communication under the peak interference power constraint impinged on the licensed user. We investigate the spatial diversity gain for cognitive two-way relay networks by employing MRC technique between relaying and direct links. We characterize the statistics for the end-to-end SNR of cognitive two-way AF relay networks with MRC by deriving the exact cumulative distribution function (CDF). Utilizing this result, the exact closed-form expressions for both user and system outage probability.

2 System Model

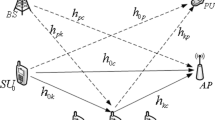
We consider a CR network in which two secondary users $\left( \mathrm{{S}}_1 \; \mathrm{{and}} \; \mathrm{{S}}_2 \right)$ exchange information with each other with the help of a non-regenerative relay R as shown in Fig. 1. The secondary network co-exists with the primary network that represents by one PU receiver. All nodes are operated in half-duplex mode and equipped with one antenna. In addition, all channels are assumed to be Rayleigh flat fading, time-invariant and reciprocal while exchanging data. Let us denote $h_m$ and $f_n$, with $\left( m \in \left\{ 0,1,2 \right\} , n \in \left\{ 1,2,r \right\} \right)$, as fading coefficients of data links and interference links. Particularly, $h_0$, $h_1$ and $h_2$ are data links between $\mathrm{{S}}_1 \leftrightarrow \mathrm{{S}}_2$, $\mathrm{{S}}_1 \leftrightarrow \mathrm{{R}}$ and $\mathrm{{S}}_2 \leftrightarrow \mathrm{{R}}$, respectively. Similarly, $f_1$, $f_2$ and $f_r$ are interference links between $\mathrm{{S}}_1 \leftrightarrow \mathrm{{PU}}$, $\mathrm{{S}}_2 \leftrightarrow \mathrm{{PU}}$ and $\mathrm{{R}} \leftrightarrow \mathrm{{PU}}$, successively. As a consequence, the channel gains, i.e., ${\left| {{h_m}} \right| ^2}$ and ${\left| {{f_n}} \right| ^2}$, are exponential random variables (RVs) with parameter $\lambda _m$ and $\omega _n$.

Fig. 1.

Two-way relaying in cognitive cooperative communications.

On the other hand, owing to adopting underlay approach, the transmit power of secondary users could not exceed the maximal tolerable interference level $\mathcal {I}_{\mathsf {p}}$. Mathematically, we have

$$\begin{aligned} {P_n} = \mathcal {I}_{\mathsf {p}}/\left| f_n \right| ^2. \end{aligned}$$

(1)

The communication between $\mathrm{{S}}_1$ and $\mathrm{{S}}_2$ is taken over three phase. In the first phase, user $\mathrm{{S}}_1$ transmits its modulated signal $x_1$ to user $\mathrm{{S}}_2$ and relay R. Followed by, $\mathrm{{S}}_2$ send its signal $x_2$ to user $\mathrm{{S}}_1$ and relay R in the second phase. The received signals at R and $\mathrm{{S}}_j$ in i-phase $\left( i,j \in \left\{ 1,2 \right\} , i \ne j \right)$ can be given by

$$\begin{aligned} y_{\mathrm{{R}},i} =&\sqrt{P_i} h_i x_i + n_{\mathrm{{R}},i} \nonumber \\ y_{\mathrm{{S}}_j,i} =&\sqrt{P_i} h_0 x_i + n_{\mathrm{{S}}_j,i}, \end{aligned}$$

(2)

where n is a circular symmetric complex Gaussian random variable with zero mean and variance $\mathcal {N}_0$. In the third phase, R broadcasts the scaling version of two previous received signals as

$$\begin{aligned} x_{\mathrm{{R}},3} = G \left( y_{\mathrm{{R}},1} + y_{\mathrm{{R}},2} \right) , \end{aligned}$$

(3)

where $G = \sqrt{\frac{P_r}{ {P_1} \left| h_1 \right| ^2 + P_2 \left| h_2 \right| ^2 + 2 \mathcal {N}_0} }$ is the amplifying gain. Signal is received by user $\mathrm{{S}}_j$ in the third phase after canceling self-interference term is given as follows:

$$\begin{aligned} y_{{\mathrm{{S}}_j},3} = G\sqrt{P_i} h_i h_j x_i + G h_j \left( n_{\mathrm{{R}},1} + n_{\mathrm{{R}},2} \right) + n_{\mathrm{{S}}_j,3}. \end{aligned}$$

(4)

3 Performance Analysis

3.1 Maximal Ratio Combining

For MRC technique, two end-users will combine two links, namely, direct and indirect link, linearly. The end to end signal to noise ratios (SNRs) at user $\mathrm{{S}}_j$ denoted as $\gamma _{ij}$ is obtained as

$$\begin{aligned} \gamma _{ij} = P_i \left| h_0 \right| ^2 + \tfrac{ P_r P_i \left| h_i \right| ^2 \left| h_j \right| ^2 }{ 2 P_r \left| h_j \right| ^2 + P_i \left| h_i \right| ^2 + P_j \left| h_j \right| ^2 + 2 }. \end{aligned}$$

(5)

The upper bound of Eq. (5) is given by

$$\begin{aligned} \gamma _{ij} \le P_i \left| h_0 \right| ^2 + \min \left( \frac{P_r P_i \left| h_i \right| ^2}{2} P_r + P_j, P_r \left| h_j \right| ^2 \right) . \end{aligned}$$

(6)

User Outage Probability (UOP). In this subsection, we study the outage probability (OP) of each user with MRC is used at the secondary users. OP at user $\mathrm{{S}}_j$ occurs when the information flow from node $i \rightarrow j$ is below the target rate $\mathcal {R}$. Mathematically, we have

$$\begin{aligned} \mathrm{{UOP}}_\mathrm{{MRC}}^j = \! \Pr \left[ \frac{1}{3} \log _2 \left( 1 + \gamma _{ij} \right)< \mathcal {R}\right] \!\! = \Pr \!\! \bigg [ \gamma _{ij} < \gamma _\text {th}\bigg ] \!, \end{aligned}$$

(7)

where $\gamma _\text {th}= 2^{3 \mathcal {R}}-1$. Due to sharing the same variable, i.e., $\left| f_i \right| ^2$ the direct and indirect link are not independent. As a result, (7) is rewritten as

$$\begin{aligned} \mathrm{{UOP}}_\mathrm{{MRC}}^j = \! \int \limits _0^\infty \!\! \int \limits _0^\gamma \!\! F_{\gamma _{\mathrm{{R}}\left| \left| f_i \right| ^2 \right. }} \! \left( \gamma - y \right) f_{\gamma _{0 \left| \left| f_i \right| ^2 \right. }} \! \left( y \right) f_{\left| f_i \right| ^2} \left( x \right) \! dydx. \end{aligned}$$

(8)

As can be observed in (8), we need to find out the cumulative distribution function (CDF) of two links before evaluating the user outage probability. The CDF of indirect link under condition $\left| f_i \right| ^2$ is given by $F_{\gamma _{\mathrm{{R}}} \left| x \right. } \left( \gamma \right) = 1 - \frac{{\overline{\gamma }}\lambda _j}{\gamma \omega _r + {\overline{\gamma }}\lambda _j} \exp \left( - 2 \frac{\gamma x}{\lambda _i {\overline{\gamma }}} \right) + x\frac{{\overline{\gamma }}\left( \lambda _j \right) ^2 \gamma \omega _r}{\lambda _i \omega _j \left( \gamma \omega _r + {\overline{\gamma }}\lambda _j \right) ^2} \exp \Bigg [ - x\left( \frac{ 2\gamma }{\lambda _i {\overline{\gamma }}} - \frac{\gamma \lambda _j \omega _r}{\lambda _i \omega _j\left( \gamma \omega _r + {\overline{\gamma }}\lambda _j \right) } \right) \Bigg ] \times E_1\left( x\frac{\gamma \lambda _j \omega _r}{\lambda _i \omega _j \left( \gamma \omega _r + {\overline{\gamma }}\lambda _j \right) } \right) .$ where $\overline{\gamma }= \frac{\mathcal {I}_{\mathsf {p}}}{\mathcal {N}_0}$ denotes as an average SNRs of system and $E_1 \left( x \right)$ is exponential integral function, defined in [19, Eq. 8.211].

The probability density function (PDF) of $\left| f_i \right| ^2$ and $\gamma _{0\left| \left| f_i \right| ^2 \right. }$ are given as $f_{\left| f_i \right| ^2} \left( x \right) = \omega _i^{-1} \exp \left( - x \omega _i^{-1} \right)$ and $f_{\gamma _0 \left| x \right. }\left( y \right) = x ({\overline{\gamma }}\lambda _0)^{-1} \exp \left( - yx ({\overline{\gamma }}\lambda _0)^{-1} \right) .$ Finally, the outage probability at $\mathrm{{S}}_j$ is given by

$$\begin{aligned} \mathrm{{UOP}}_\mathrm{{MRC}}^j =&J_1 \left( \omega _i, {\overline{\gamma }}\lambda _0, \gamma _\text {th}\right) - \tfrac{\lambda _j}{\lambda _0 \omega _i} J_2 \left( \gamma _\text {th}\omega _r + {\overline{\gamma }}\lambda _j, \omega _r, \tfrac{2 \gamma _\text {th}}{{\overline{\gamma }}\lambda _i} + \tfrac{1}{\omega _i}, \tfrac{2}{{\overline{\gamma }}\lambda _i} - \tfrac{1}{{\overline{\gamma }}\lambda _0}, \gamma _\text {th}\right) \nonumber \\&+ \tfrac{\left( \lambda _j \right) ^2}{\lambda _0 \lambda _i \omega _i \omega _j \omega _r} J_3 \left( \frac{2 \gamma }{{\overline{\gamma }}\lambda _i} + \frac{1}{\omega _i}, \tfrac{2}{{\overline{\gamma }}\lambda _i} - \tfrac{1}{ {\overline{\gamma }}\lambda _0}, \tfrac{\lambda _j}{\lambda _i \omega _j}, \gamma + \tfrac{{\overline{\gamma }}\lambda _j}{\omega _r}, \gamma \right) . \end{aligned}$$

(9)

where $J_1 \left( a,b,c \right) = \frac{ac}{b + ac}$, $J_2 \left( a,b,c,d,g \right) = A_1 \log \left( 1 - \frac{gb}{a} \right) + B_1 \log \left( 1 - \frac{gd}{c} \right) + \frac{g B_2 d^2}{c\left( c - dg \right) },$ $A_1 = - \frac{1}{b d^2 \left( \frac{a}{b} - \frac{c}{d} \right) ^2}$, $B_2 = - \frac{1}{b d^2 \left( \frac{c}{d} - \frac{a}{b} \right) }$ and $B_1 = \frac{1}{b d^2 \left( \frac{c}{d} - \frac{a}{b} \right) ^2}$. Besides, $J_3 \left( {a,b,c,d,g} \right) = - \frac{ 8 \sqrt{2} \pi \mathbf {a}_N \mathbf {a}_I }{b^3} \sum \limits _{n = 1}^{N + 1} \sum \limits _{i = 1}^{I + 1} \sum \limits _{o = 1}^3 \sqrt{b_n} \Bigg [ C_o J_4 \left( \gamma ,\frac{E + F}{2},o \right) + D_o J_4 \left( \gamma ,\frac{E - F}{2},o \right) \Bigg ]$, $J_4\left( a,b,n \right) = \left\{ \begin{array}{*{20}{c}} \log \left( 1 - \frac{a}{b} \right) \;\;\;\;\;\;\;\;\;\;\;\;\;;n = 1\\ \frac{\left( - b \right) ^{1 - n} - \left( a - b \right) ^{1 - n}}{\left( n - 1 \right) } \;\;\;\;\;;n \ne 1 \end{array} \right.$, $E = \frac{ a+bd-c \left( 1 - 4 b_n b_i \right) }{b}$, $F = ( E^2 - 4\left( \frac{ad}{b} - \frac{cg}{b} \left( 1 - 4 b_n b_i \right) \right) )^{1/2}$, $C_o = \frac{1}{\left( 3 - o \right) !} \frac{d^{\left( 3 - o \right) }}{dy} \left. \left[ \frac{\left( g - y \right) \left( y - d \right) }{\left( y - \frac{E + F}{2} \right) ^3} \right] \right| _{y = \frac{E - F}{2}}$, $D_o = \frac{1}{\left( 3 - o \right) !} \frac{d^{\left( 3 - o \right) }}{dy} \left. \left[ \frac{\left( g - y \right) \left( y - d \right) }{\left( y - \frac{E - F}{2} \right) ^3} \right] \right| _{y = \frac{E + F}{2}}.$

Here $\mathbf {a}_N$, $\mathbf {a}_I$, $b_n$ and $b_i$ are calculated similar in [20]. The remain UOP at $\mathrm{{S}}_i$ gets easily by applying the similar steps.

System Outage Probability (SOP). The system outage probability (SOP) appears when one of two user’s data is under the threshold, $\gamma _\text {th}$. Mathematically, we have

$$\begin{aligned} \mathrm{{SOP}_{MRC}} =&\underbrace{\Pr \left[ T_1 \le \gamma _\text {th},P_i \le P_j \right] }_{\varOmega _1} \! + \! \underbrace{\Pr \left[ T_2 \le \gamma _\text {th},P_j \le P_i \right] }_{\varOmega _2}, \nonumber \\ T_1 =&P_i \left| h_0 \right| ^2 + \frac{ P_r \min \left( P_i \left| h_i \right| ^2, P_j \left| h_j \right| ^2 \right) }{2 P_r + P_j}, \end{aligned}$$

(10)

$$\begin{aligned} T_2 =&P_j \left| h_0 \right| ^2 + \frac{P_r\min \left( P_i \left| h_i \right| ^2, P_j \left| h_j \right| ^2 \right) }{2 P_r + P_i}. \end{aligned}$$

(11)

By using the same approach as UOP, the CDF of indirect links of $\varOmega _i$ is given by

$$\begin{aligned}&F_{\gamma _\mathrm{{R}}^\mathrm{{sys}}\left| x \right. }\left( \gamma \right) \nonumber \\&= 1 - e^{ { - \tfrac{x}{\omega _j}} } - \tfrac{{\overline{\gamma }}\lambda _j}{{\overline{\gamma }}\lambda _j \omega _j + \gamma \omega _r \omega _j} e^{ - (x\tfrac{2 \gamma }{{\overline{\gamma }}\lambda _i}) } \Bigg \{ \frac{{\overline{\gamma }}\lambda _j \omega _j }{{\overline{\gamma }}\lambda _j + 2\gamma \omega _j} \left[ 1 - \exp \left( - x \frac{{\overline{\gamma }}\lambda _j + 2\gamma \omega _j}{{\overline{\gamma }}\lambda _j \omega _j} \right) \right] \Bigg . \nonumber \\&\left. - x \tfrac{\gamma \omega _r \lambda _j}{\lambda _i} \Big ( {\overline{\gamma }}\lambda _j + \gamma \omega _r \Big ) \exp \left( x \tfrac{\gamma \omega _r \left( {\overline{\gamma }}\lambda _j + 2\gamma \omega _j \right) }{{\overline{\gamma }}\omega _j \lambda _i \left( {\overline{\gamma }}\lambda _j + \gamma \omega _r \right) } \right) \right. \nonumber \\&\times \Bigg . \bigg \{ E_1 \left( x\tfrac{\gamma \omega _r \left( {\overline{\gamma }}\lambda _j + 2 \gamma \omega _j \right) }{{\overline{\gamma }}\omega _j \lambda _i \left( {\overline{\gamma }}\lambda _j + \gamma \omega _r \right) } \right) - E_1 \left[ x\left( \tfrac{{\overline{\gamma }}\lambda _j + 2 \gamma \omega _j}{{\overline{\gamma }}\lambda _j \omega _j} \right) \left( \tfrac{\gamma \omega _r \lambda _j + \lambda _i \left( {\overline{\gamma }}\lambda _j + \gamma \omega _r \right) }{ \lambda _i \left( {\overline{\gamma }}\lambda _j + \gamma \omega _r \right) } \right) \right] \bigg \} \Bigg \}. \end{aligned}$$

(12)

After that we get $\varOmega _i$ which is offer in Eq. (13).

$$\begin{aligned}&\varOmega _1 = J_1 \Big ( \omega _i, {\overline{\gamma }}\lambda _0, \gamma _\text {th}\Big ) - \left( 1+ \frac{\omega _j}{\omega _i} \right) J_1 \left( \left( \frac{1}{\omega _i} + \frac{1}{\omega _j} \right) ^{-1}, {\overline{\gamma }}\lambda _0, \gamma _\text {th}\right) \nonumber \\&+ \tfrac{{\overline{\gamma }}\left( \lambda _j \right) ^2}{2 \lambda _0 \omega _i \omega _j \omega _r} \Bigg [ J_5 \left( \tfrac{{\overline{\gamma }}\lambda _j \omega _j + \gamma \omega _r \omega _j}{\omega _r \omega _j}, \tfrac{{\overline{\gamma }}\lambda _j + 2 \gamma \omega _j}{2 \omega _j}, \tfrac{2\gamma }{{\overline{\gamma }}\lambda _i} + \tfrac{1}{\omega _i}, \tfrac{1}{{\overline{\gamma }}\lambda _0} - \tfrac{2}{{\overline{\gamma }}\lambda _i},\gamma _\text {th}\right) \Bigg . \nonumber \\&\Bigg . - J_5 \left( \tfrac{{\overline{\gamma }}\lambda _j \omega _j + \gamma \omega _r \omega _j }{ \omega _r \omega _j}, \tfrac{{\overline{\gamma }}\lambda _j + 2 \gamma \omega _j}{2 \omega _j}, \tfrac{2\gamma }{{\overline{\gamma }}\lambda _i} + \tfrac{1}{\omega _i} + \tfrac{2\gamma }{{\overline{\gamma }}\lambda _j} + \tfrac{1}{\omega _j}, \tfrac{1}{{\overline{\gamma }}\lambda _0} - \tfrac{2}{{\overline{\gamma }}\lambda _i} - \tfrac{2}{{\overline{\gamma }}\lambda _j},\gamma _\text {th}\right) \Bigg ] \nonumber \\&+ \tfrac{ \left( \lambda _j \right) ^2}{ \lambda _0 \lambda _i \omega _i \omega _j \omega _r } \Bigg [ J_6 \bigg ( \gamma + \tfrac{{\overline{\gamma }}\lambda _j}{ \omega _r}, \frac{1}{{\overline{\gamma }}\lambda _0} - \tfrac{2}{{\overline{\gamma }}\lambda _i}, \tfrac{1}{\omega _i} + \frac{2 \gamma }{{\overline{\gamma }}\lambda _i}, \tfrac{2}{{\overline{\gamma }}\lambda _i}, \gamma + \frac{{\overline{\gamma }}\lambda _j}{2 \omega _j}, \tfrac{2}{{\overline{\gamma }}\lambda _i},\gamma ,\gamma + \tfrac{{\overline{\gamma }}\lambda _j}{2 \omega _j},\gamma \bigg ) \Bigg . \nonumber \\&\Bigg . - J_6 \left( \gamma + \tfrac{{\overline{\gamma }}\lambda _j}{\omega _r}, \tfrac{1}{{\overline{\gamma }}\lambda _0} - \tfrac{2}{{\overline{\gamma }}\lambda _i}, \tfrac{1}{\omega _i} + \frac{2 \gamma }{{\overline{\gamma }}\lambda _i}, \tfrac{2}{{\overline{\gamma }}\lambda _i}, \gamma + \tfrac{{\overline{\gamma }}\lambda _j}{2 \omega _j}, \tfrac{2}{{\overline{\gamma }}\lambda _j} + \tfrac{2}{{\overline{\gamma }}\lambda _i}, \gamma + \tfrac{{\overline{\gamma }}\lambda _i \lambda _j}{\omega _r \left( \lambda _i + \lambda _j \right) }, \gamma + \tfrac{{\overline{\gamma }}\lambda _j}{2 \omega _j}, \gamma \right) \Bigg ]. \end{aligned}$$

(13)

Here, $J_5 \left( a,b,c,d,g \right) = \tfrac{1}{d^2} \bigg [ G_1 J_4\left( g,a,1 \right) + H_1 J_4 \left( g,b,1 \right) \bigg . \bigg . + K_1 J_4 \left( g, - \frac{c}{d},1 \right) + K_2 J_4 \left( g, - \frac{c}{d},2 \right) \bigg ],$ where $G_1 = \tfrac{1}{ \left( a - b \right) \left( a + \tfrac{c}{d} \right) ^2}$, $H_1 = \tfrac{1}{\left( b - a \right) \left( b + \frac{c}{d} \right) ^2}$, $K_2 = \frac{1}{\left( \tfrac{c}{d} + a \right) } \tfrac{1}{\left( \tfrac{c}{d} + b \right) }$ and $K_1 = \tfrac{a + b + \frac{2c}{d}}{\left( a + \frac{c}{d} \right) ^2 \left( b + \frac{c}{d} \right) ^2}$. While $J_6 \left( a,b,c,d,e,f,g,h,i \right) = \tfrac{1}{b^3} \sum \limits _{u = 1}^2 \sum \limits _{k = 1}^4 U_{n_k,u} J_4 \left( \gamma _\text {th},n_k,u \right) + \frac{2}{b^3} \sum \limits _{u = 1}^3 \sum \limits _{k = 3}^4 \left[ \sum \limits _{o = 3}^4 V_{n_k,u} J_7 \left( n_o,n_k,\gamma _\text {th},u \right) \right. \left. - \sum \limits _{o = 5}^6 V_{n_k,u} J_7 \left( n_o,n_k,\gamma _\text {th},u \right) \right]$ where $U_{n_k,u} = \frac{1}{\left( 2 - u \right) !} \frac{d^{\left( 2 - u \right) }}{dy} \left. \left[ \frac{ \left( y - n_k \right) ^2 \left( i - y \right) \left( a - y \right) \left( S - 3Q \right) }{ \left( y - n_1 \right) ^2 \left( y - n_2 \right) ^2 \left( y - n_3 \right) ^2 \left( y - n_4 \right) ^2} \right] \right| _{y = {n_k}}$, $V_{n_k,u} = \frac{1}{\left( 3 - u \right) !} \frac{d^{\left( 3 - u \right) }}{dy} \left. \left[ \frac{\left( y - n_k \right) ^3 \left( i - y \right) \left( a - y \right) }{\left( y - n_3 \right) ^3 \left( y - n_4 \right) ^3 } \right] \right| _{y = {n_k}}$, $Q = S + \left( a - y \right) \left( y + \frac{c}{b} \right) - \frac{d}{b} y^2 + \frac{d \left( i + e \right) }{b} y - \frac{edi}{b}$, $S = \frac{f}{b} y^2 - \frac{f}{b} \left( g + h \right) y + \frac{fgh}{b}$. Finally, $n_1$, $n_2$ are roots of $S-Q$, $n_3$, $n_4$ are roots of Q, $n_5$, $n_6$ are roots of S and $J_7 \left( a,b,c,n \right) \! = \!\! \int \limits _0^c \frac{\log \left( a - y \right) }{\left( y - b \right) ^n} dy \! = \! W \left( a \right) - W \left( a - c \right) .$ Here W is calculated with the support of [19, 2.727.1]. On the other hand, due to the symmetric between $\varOmega _1$ and $\varOmega _2$, we solely need to obtain $\varOmega _1$ then taking similar steps to find out $\varOmega _2$. Finally, the $\mathrm {SOP}_{MRC}$ is calculated as $\mathrm{{SOP}_{MRC}} = \varOmega _1 + \varOmega _2.$

Asymptotic System Outage Probability (ASOP). In this subsection, we derive the asymptotic system outage probability (ASOP) for discovering the system diversity. As this case, we assume that $\overline{\gamma }\rightarrow \infty$ and using the fact that

$$\begin{aligned} \mathrm{{ASOP_{MRC}}}&{\mathop = \limits ^{\overline{\gamma }\rightarrow \infty }} \mathrm{{AUOP}_{MRC}^1} + \mathrm{{AUOP}_{MRC}^2} - \mathrm{{AUOP}_{MRC}^1} \mathrm{{AUOP}_{MRC}^2} \nonumber \\ \mathrm{{ASOP_{MRC}}}&\;= \mathrm{{AUOP}_{MRC}^1} + \mathrm{{AUOP}_{MRC}^2}. \end{aligned}$$

(14)

Here ${\mathrm{{AUOP}}_\mathrm{{MRC}}^i}$, $i \in \left\{ 1,2 \right\}$, is the asymptotic of i-th user outage probability. By using binomial expansion [19, Eq. 1.110] and vanishing the second term, the asymptotic OP of $\mathrm{{S}}_i$ is given by

$$\begin{aligned} \mathrm{{AUOP}_{MRC}^i} \mathop = \limits ^{\overline{\gamma }\rightarrow \infty }&\mathcal {E}\left\{ \mathcal {G}- \frac{1}{ \overline{\gamma }} \left[ \mathcal {A}+ \mathcal {B}+ \mathcal {C}- \frac{\gamma _\text {th}\mathcal {H}}{ a_1 a_2^2} \right] - \frac{1}{ \overline{\gamma }^2} \left[ \tfrac{\gamma _\text {th}\left( \mathcal {A}+ \mathcal {C}\right) }{a_2} + \tfrac{2 \gamma _\text {th}\left( \mathcal {B}- \mathcal {A}\right) }{a_1} \right] \right\} \end{aligned}$$

(15)

where $\mathcal {E}= \sum \limits _{n = 1}^{N + 1} \sum \limits _{i = 1}^{I + 1} \frac{8 \sqrt{2 b_n} \pi a_\mathbf {N} a_\mathbf {I} \left( \lambda _i \lambda _j \lambda _0 \right) ^2}{ \omega _i \omega _j \omega _r \left( \lambda _i - 2 \lambda _0 \right) ^3},$ $\mathcal {C}= \frac{a_2 D \gamma _\text {th}}{a_1 a_2}$, $\mathcal {B}= \frac{3 \big ( 2 a_2 \omega _r + \left( \lambda _j - a_1 \omega _r \right) \big ) \gamma _\text {th}}{2 a_1 \omega _r \big [ a_2 \left( { a_1 - 4 a_2} \right) \big ]^2 }$, $a_1 = \frac{ - \lambda _0 \lambda _j \left( 4b_n b_i - 1 \right) }{ \omega _j \left( \lambda _i - 2 \lambda _0 \right) }$, $\mathcal {A}= \frac{ \gamma _\text {th}\left( \lambda _j - a_1 \omega _r \right) }{ 2 \omega _r \left( a_1 a_2 \right) ^2 \left( a_1 - 4 a_2 \right) }$, $\mathcal {F}= \frac{ - 2\big ( a_1 \left( a_1 - 4 a_2 \right) D + 1 \big )}{\root 3 \of { a_1 \left( a_1 - 4a_2 \right) }}$,

$\mathcal {D}= \tfrac{3 \left( \lambda _j - a_1 \omega _r \right) - 6 a_2 \omega _r + \omega _r \left( a_1 - 4 a_2 \right) }{\omega _r a_1 ( \left( a_1 - 4 a_2 \right) )^2}$, $\mathcal {G}= \mathcal {F}\big [ \tanh ^{-1} \left( a_6 \right) - \tanh ^{-1} \left( a_7 \right) \big ]$,

$a_6 = \frac{2 \gamma _\text {th}- a_1 \overline{\gamma }}{\overline{\gamma }\sqrt{a_1 \left( a_1 - 4a_2 \right) } }$, $\mathcal {H}= \frac{2 a_2 \left( \lambda _j - \omega _r a_1 \right) \left( \overline{\gamma }\right) ^2 + a_5 \left( \overline{\gamma }\right) + a_2 a_3 a_4\left( 2 \lambda _j - \omega _r a_1 \right) }{\left( \overline{\gamma }\right) ^2 \omega _r \left( a_2 + \frac{\gamma _\text {th}}{\overline{\gamma }} \right) }$, $a_2 = \frac{ \lambda _i \omega _j}{ \omega _i \omega _r \left( 4b_n b_i - 1 \right) }$, $a_3 = \frac{\gamma _\text {th}\left( \lambda _j - a_1 \omega _r \right) }{a_2 \left( 2 \lambda _j - a_1 \omega _r \right) }$, $a_5 = 2 a_2 \left( \lambda _j - \omega _r a_1 \right) \left( a_3 + a_4 \right) + \omega _r \left( a_2 a_3 + a_1 \gamma _\text {th}- a_2 \gamma _\text {th}\right)$, $a_4 = \frac{\gamma _\text {th}}{2a_2} - \frac{\gamma _\text {th}}{a_1}$, $a_7 = \sqrt{\frac{a_1}{a_1 - 4 a_2}}.$ The AUOP of $\mathrm{{S}}_j$ is obtained by applying the similar approach. Finally, the ASOP of MRC is obtained by substituting Eq. (15) into (14). As can be seen in (15), the diversity gain of the system with MRC technique is 2.

Fig. 2.

Outage probability of MRC vs ${\overline{\gamma }}$ with $\mathcal {R}= 1$ and $\eta = 3$.

4 Numerical Results

Let us consider our simulation model in two-dimensional plane in which user $\mathrm{{S}}_1$ and $\mathrm{{S}}_2$ locate at (0, 0) and (1, 0), respectively. Whereas, the position of relay and primary user are $\left( x_\mathrm{{R}}, y_\mathrm{{R}} \right)$ and $\left( x_\mathrm{{PU}}, y_\mathrm{{PU}} \right)$, successively. Furthermore, only the location of relay and PU is changeable when two users situation is fixed throughout this section. The channel gain $\lambda _m$ and $\omega _n$ are calculated by a simplified path loss model, i.e., $\lambda _1 = d_{\mathrm{{S}}_1\mathrm{{R}}}^\eta$, with $d_{ij}$ is distance from node i to j, $\eta$ is path loss exponent.

Figure 2 plots UOP and SOP of MRC combining with the location of relay and PU are (0.4, 0.2) and (0.8, 0.8), respectively. As can be seen in Fig. 2, our analyses absolutely match with simulation results. Moreover, the SOP curve is equal to the curve of UOP at user 2 especially in high SNRs region. It shows that the overall outage probability of the network completely depends on the weaker user’s rate. In addition, the ASOP also has the same value with exact curve in high SNRs regime. Figure 3 plots the OP versus $x_R$ where $y_R = 0$, and PU = (0.8, 0.8). As we can be seen that when $x_R$ is quite small or it is close to the $\mathrm{{S}}_1$, the UOP of $\mathrm{{S}}_1$ is outperform than $\mathrm{{S}}_2$ and vice versa. In addition, the SOP only leans on the weaker rate while the relative position between relay node and primary user is sufficient large, whereas it has a little gap with the weaker rate. Figure 4 illustrates the impact of PU position on the performance of consider system. Particularly, the location of PU is changing from (0, 1) to (1, 1), it means only the x-axis is vary. In this figure, we see that when the PU is proximity to $\mathrm{{S}}_1$ or $x_\mathrm{{PU}}$ is tiny, the SOP is limited by UOP1 curve and vice versa. It can be explained that the transmit power of a specific user is approach to zero when the PU is quite closely. Thereby, it easily go into outage events.

Fig. 3.

Outage probability versus the position of relay with $\overline{\gamma }$ = 30 dB, $\mathcal {R}= 1$ and $\eta = 3$.

Fig. 4.

Outage probability versus the position of primary user with $\overline{\gamma }$ = 30, PR = (0.4, 0.2), $\mathcal {R}= 1$ dB and $\eta = 3$.

5 Conclusions

In this paper, outage performance has been studied in TW cognitive spectrum sharing in the presence of the direct link. In particular, the closed-form and asymptotic expression for both user and system OP have been addressed in basically tractable functions. Furthermore, it is proven that full diversity is got by adopting MRC at two end users. The correctness of our analysis is verified through simulation.