Secure Cooperative Systems with Jamming and Unreliable Backhaul over Nakagami-m Fading Channels

Abstract

In this paper, the secrecy performance of cooperative networks with jamming signals of eavesdroppers are studied under the impacts of unreliable backhaul networks. By proposing a two-phase transmitter/relay selection scheme, the desired signal-to-noise ratio (SNR) of relays is maximized by selected the best transmitter, meanwhile, the jamming signal-to-interference-plus-noise ratio (SINR) of the eavesdroppers is minimized by selected the best relay. The secrecy outage probability is derived in closed-form expressions by following some useful lemmas and theorems. Furthermore, the analysis of asymptotic secrecy outage probability is also performed to explicitly reveal the impacts of unreliable backhaul links on the secrecy performance. By the impact of imperfect backhaul links, the diversity gain is limited as shown in our results.

Supported by the Newton Prize 2017 and by a Research Environment Links grant, ID 339568416, under the Newton Programme Vietnam partnership. The grant is funded by the UK Department of Business, Energy and Industrial Strategy (BEIS) and delivered by the British Council. For further information, please visit www.newtonfund.ac.uk/.

1 Introduction

Physical layer security (PLS) concept has become an emerging feature in wireless communication systems [14] with the serious effects of malicious eavesdroppers on the confidential transmission. In fact, the transmitted information might be vulnerable with the jamming interference by the existing of eavesdroppers [15] in the wireless communication systems. For preventing eavesdropping attacks, the message between the source and destination is encrypted/decrypted with sharing the specific secretly key. To this end, PLS performs the information-theoretical methods, which involve the cooperative relaying to secure received messages at the receiver by exploiting the impact of jamming signals, to utilise the benefits of physical characteristics by different upper layer security [3]. On the other hand, cooperative networks (CNs) have grown in network infrastructure for satisfying the excessing increase of data transmission [8]. However, by deploying higher density of small-cell numbers, e.g., relay nodes, one of the critical problems of CNs is unreliable backhaul links [11, 15, 20]. Besides the threats of jamming interference from eavesdropping, the issues of propagation, e.g., multipath fading, transmission delay and synchronization can impact the reliable backhaul network as well as the network performance in CNs [13, 16]. As a result, the unreliable backhaul transmissions significantly depreciate the performance of network [12, 20].

Many previous PLS works ensure the success of the private signals from source to the legitimate destination under the assumption of ideal reliability backhaul link. In these studies, the cooperative relay technique is investigated to minimize the jamming interference of the eavesdroppers [4, 9] under both decode-and-forward (DF) and amplify-and-forward (AF) relaying schemes [1, 3, 17]. However, in practice, the presence of unreliable backhaul cannot avoid since this issue strongly impacts the real network performance. Some researches have tackled the unreliable backhaul for enhancing the network performance [5, 11, 12, 20]. For instances, the cooperative frameworks are proposed to scale the performance under the impact of unreliable backhaul links in [5, 20] or the extension of spectrum sharing in backhaul communication with the limit interference of primary users [11, 12].

From the observations of PLS and unreliable backhaul in CNs, it is obvious that the investigation of PLS under unreliable backhaul links has been completely necessary. In this paper, we study the network performance of a CN with the impact of jamming interference in term of secrecy outage probability. By exploiting a CN scenario, the unreliable backhaul links between a macro-cell and relay nodes (e.g., small-cells) is considered. This scheme is to eliminate the inter-symbol interference (ISI) [6, 7]. On the other hand, the transmission information will be reflected by considering frequency selective fading channel [15, 17]. Very recently, the performance of physical layer security has been investigated with single carrier system under the impact of imperfect backhaul condition [10]. To the best of our knowledge, all of the previous works on the physical layer security performance under the impact of unreliable backhaul only considered the Rayleigh fading channels. Therefore, in this paper, we take a step further to extend this research into a more general fading channel, namely, Nakagami-m. For the transmission scheme, a two-phase transmitter/relay selection scheme is provided in density multi-relay networks. The best relay selection is obtained in the first phase for maximizing the desired SNR at the relays and minimizing the signal-to-interference-plus-noise ratio (SINR) at the eavesdroppers during the second phase simultaneously. We show that the backhaul reliability is an important factor in PLS system design, which strongly affects the achievable secrecy performance.

Notation: $\mathcal {CN}(\mu ,\sigma _n^2)$ denotes the complex Gaussian distribution with mean $\mu$ and variance $\sigma _n^2$; ${{\varvec{I}}}_{m}$ is an $m \times m$ identity matrix; $\mathbb {C}^{m \times n}$ is vector space of $m \times n$ complex matrices; $X \sim \chi ^2\left( {N_X},{\alpha _X}\right)$ denotes chi-square distribution with degree of freedom (DoF) $N_X$ and power normalizing constant $\alpha _X$; $X \sim \text {Ga}(\mu _X,\eta _X)$ denotes Gamma distribution with shape $\mu _X$ and rate $\eta _X$. $F_\lambda (\gamma )$ and $f_\lambda (\gamma )$ denote the cumulative distribution function (CDF) and probability density function (PDF) of the random variable (RV) $\lambda$, respectively; ${{\mathrm{\mathbb {E}}}}_{\lambda }\left\{ f(\gamma ) \right\}$ denotes the expectation of $f_{{}}\left( {\gamma }\right)$ with respect to the RV $\lambda$. In addition, $\left( {\begin{array}{c}\tau _1\\ \tau _2\end{array}}\right) = \dfrac{\tau _1!}{\tau _2!(\tau _1-\tau _2)}$ denotes the binomial coefficient.

2 Network and Channel Models

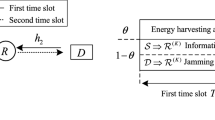
We consider a CN in where a macro-cell base station (Macro BS) connected to the core network as shown in Fig. 1. Meanwhile, K small-cell transmitters T$_{k}$, $k\in \{1,2,\cdots ,K\}$ connect to the Macro-BS via unreliable backhaul links and communicate with a destination (D) via M relays R$_{m}$, $m\in \{1,2,\cdots ,M\}$ applying DF scheme. Otherwise, a single jammer J and N eavesdroppers E$_{n}$, $n\in \{1,2,\cdots ,N\}$ exist in the network. Due to poor channel conditions, the direct link from T$_{k}$ to destination and between T$_{k}$ and E$_{n}$ $\forall k \in K, \forall n \in N$ are neglected. On the other hand, the interference at the eavesdroppers is caused by J while the eavesdroppers cooperate to overhear the transmissions between R$_{m}$ and D. In this work, we also assume that both of transmitters and receivers use half-duplex mode and exploit a single antenna.

Fig. 1.

System model.

For a cooperative system, we make the following assumptions for the channel model. Nakagami-m fading is considered in the channel model of the system. Therein, the channel between T$_{k}$ and R$_{m}, \; \forall k,m$ is denoted by $\textit{h}^{k,m}\sim \text {Ga}(\mu _k^m,\tilde{\eta }_k^m)$. Meanwhile, $\textit{g}^{m,n}\sim \text {Ga}(\mu _m^n,\tilde{\eta }_m^n)$ denotes the channel between R$_{m}$ and E$_{n}, \; \forall m,n$. The path loss component corresponding to $\textit{h}^{k,m}$ and $\textit{g}^{m,n}$ are denoted as $\alpha _T^{k,m}$ and $\alpha _E^{m,n}$, respectively. The channel between R$_{m}$ and D,$\; \forall m$ and the channel between J and E$_{n}$,$\; \forall n$ are defined by $\textit{f}^{\,m}\sim \text {Ga}(\mu _d^m,\tilde{\eta }_d^m) \; \text {and} \; \textit{q}^{n}\sim \text {Ga}(\mu _j^n,\tilde{\eta }_j^n)$. The path loss component corresponding to $\textit{f}^{\,m}$ and $\textit{q}^{n}$ are represented by $\alpha _D^{m}$ and $\alpha _J^{n}$, respectively. We also assume that ${{\mathrm{\mathbb {E}}}}[\textit{x} ] = {{\mathrm{\mathbb {E}}}}[\textit{v} ]= 0$.

For all active links, the channel state information (CSI) is common assumed to be perfectly known at the relays, J, and D in PLS literature [3, 15, 18]. Also, the information can be measured by J from the eavesdroppers in the network [2]. The transmit symbol block x, which is transmitted from the Macro-BS, must pass through the dedicated wireless backhaul links. The success/failure transmission represents the reception status at the K transmitters. Hence, a Bernoulli process $\mathbb {I}_k$ can be applied to the reliability of the wireless backhaul links, i.e., the message is successfully received at the receivers with a successful probability of $\lambda _k$. The failure probability is accordingly given by $1-\lambda _k$ [5, 12].

The received signal at R$_{m}$ from T$_{k}$ is expressed as

$$\begin{aligned}&\textit{y}_R^{k,m} = \sqrt{\mathcal {P}_{t}\alpha _T^{k,m}} \textit{h}^{k,m}\mathbb {I}_k\textit{x} + \textit{n}_R^{k,m} , \end{aligned}$$

(1)

where $\mathcal {P}_{t}$ is the transmit power and $\textit{n}_R^{k,m} \sim \mathcal {CN}\left( {0},{\sigma _n^2}\right)$ is an additive noise vector at R$_m$. $\mathbb {I}_k$ recalls the backhaul reliability which is modeled as a Bernoulli process. This model is common for the representation of the backhaul reliability with canonically success/failure transmission [5, 12, 15, 20]. In the first time slot, the instantaneous SNR between T$_{k}$ and R$_{m}$ from (1) can be expressed as

$$\begin{aligned} \gamma _{R}^{k,m}= \dfrac{\mathcal {P}_{t}\alpha _T^{k,m}||\textit{h}^{k,m}||^2 }{\sigma _n^2} \mathbb {I}_k= \widetilde{\alpha }_T^{k,m}||\textit{h}^{k,m}||^2 \mathbb {I}_k= \lambda ^{k,m} \mathbb {I}_k, \end{aligned}$$

(2)

where $\widetilde{\alpha }_T^{k,m}{\mathop {=}\limits ^{\triangle }}\dfrac{\mathcal {P}_{t}\alpha _T^{k,m}}{\sigma _n^2}, \lambda ^{k,m} \sim \text {Ga}(\mu _k^m,\eta _k^m)$ with $\eta _k^m = \dfrac{\widetilde{\alpha }_T^{k,m}{{\mathrm{\mathbb {E}}}}\left\{ {||\textit{h}^{k,m}||^2}\right\} }{\mu _k^m}$.

The received signals at E$_{n}$ and D from R$_{m}$ are given by

$$\begin{aligned}&\textit{y}_E^{m,n} = \sqrt{\mathcal {P}_{r}\alpha _E^{m,n}} \textit{g}^{m,n}\textit{x} + \sqrt{\mathcal {P}_{j}\alpha _J^{n}} \textit{q}^{n}\textit{v} +\textit{n}_E^{m,n} , \nonumber \\&\textit{y}_D^{m} = \sqrt{\mathcal {P}_{r}\alpha _D^{m}} \textit{f}^{\,m}\textit{x} + \textit{n}_D^{m} , \end{aligned}$$

(3)

where $\mathcal {P}_{r}$ and $\mathcal {P}_{j}$ are the transmit powers at the relays and J, respectively, $\textit{n}_E^{m,n} \sim \mathcal {CN}(0,\sigma _n^2)$ and $\textit{n}_D^{m} \sim \mathcal {CN}(0,\sigma _n^2)$ define the noise at E$_n$ and D.

Therefore, the instantaneous SINR between R$_{m}$ and E$_{n}$ can be formulated as

$$\begin{aligned} \gamma _{E}^{m,n}= \dfrac{\mathcal {P}_{r}\alpha _E^{m,n}||\textit{g}^{m,n}||^2 }{\sigma _n^2+ \mathcal {P}_{j}\alpha _J^{n}||\textit{q}^{n}||^2} = \dfrac{\widetilde{\alpha }_E^{m,n}||\textit{g}^{m,n}||^2}{1+ \widetilde{\alpha }_J^{n}||\textit{q}^{n}||^2} = \dfrac{\lambda ^{m,n}}{1+ \lambda _J^{n}} , \end{aligned}$$

(4)

where $\widetilde{\alpha }_E^{m,n}{\mathop {=}\limits ^{\triangle }}\dfrac{\mathcal {P}_{r}\alpha _E^{m,n}}{\sigma _n^2}, \widetilde{\alpha }_J^{n}{\mathop {=}\limits ^{\triangle }}\dfrac{\mathcal {P}_{j}\alpha _J^{n}}{\sigma _n^2}, \lambda ^{m,n} \sim \text {Ga}(\mu _m^n,\eta _m^n), \lambda _J^{n} \sim \text {Ga}(\mu _j^n,\eta _j^n)$ with $\eta _m^n = \dfrac{\widetilde{\alpha }_E^{m,n}{{\mathrm{\mathbb {E}}}}\left\{ {||\textit{g}^{m,n}||^2}\right\} }{\mu _m^n }, \eta _j^n = \dfrac{\widetilde{\alpha }_J^{n}{{\mathrm{\mathbb {E}}}}\left\{ {||\textit{q}^{n}||^2}\right\} }{\mu _j^n}$.

In the remaining time slot, the instantaneous SNR between R$_{m}$ and D can be expressed as

$$\begin{aligned} \gamma _{D}^{m}= \dfrac{\mathcal {P}_{r}\alpha _D^{m}||\textit{f}^{\,m}||^2 }{\sigma _n^2} = \widetilde{\alpha }_D^{m}||\textit{f}^{\,m}||^2 = \lambda _D^{m}, \end{aligned}$$

(5)

where $\widetilde{\alpha }_D^{m}{\mathop {=}\limits ^{\triangle }}\dfrac{\mathcal {P}_{r}\alpha _D^{m}}{\sigma _n^2}, \lambda _D^{m} \sim \text {Ga}(\mu _d^m,\eta _d^m)$ with $\eta _d^m = \dfrac{\widetilde{\alpha }_D^{m}{{\mathrm{\mathbb {E}}}}\left\{ {||\textit{f}^{\,m}||^2}\right\} }{\mu _d^m}$.

Moreover, the channels are distributed according to chi-square distribution since they are assumed to undergo Nakagami-m fading. Thus, the CDF and PDF of RV $\chi \sim \text {Ga}(\mu _\chi ,\eta _\chi )$, where $\chi \in \lbrace \textit{h}^{k,m}, \textit{g}^{m,n}, \textit{f}^{\,m}, \textit{q}^{n}\rbrace$ are given, respectively,

$$\begin{aligned}&f_\chi (x)=\dfrac{1}{(\mu _\chi -1)!(\eta _\chi )^{\mu _\chi }}x^{\mu _\chi -1} e^{\left( -x/\eta _\chi \right) },\nonumber \\&F_\chi (x)=1-e^{\left( -x/\eta _\chi \right) }\sum _{i=0}^{\mu _\chi -1} \dfrac{1}{i!} \left( x/\eta _\chi \right) ^i , \end{aligned}$$

(6)

respectively. We assume that the unreliable backhaul links are independent from the indices of the K transmitters, i.e., $\lambda _{k}= \lambda , \forall k$ and the positive fading severity parameter $\mu _\chi$ and $\eta _\chi$ are identically varied among the K transmitters, M relays and N eavesdroppers, i.e., $\mu _T=\mu _k^m, \mu _E=\mu _m^n, \mu _J=\mu _j^n, \mu _D=\mu _d^m,$ and $\eta _T=\eta _k^m, \eta _E=\eta _m^n, \eta _J=\eta _j^n, \eta _D=\eta _d^m, \forall k,m,n$.

3 Secrecy Performance Analysis

3.1 Two-Phase Transmitter/Relay Selection Scheme

By providing a two-phase selection scheme, our target is to achieve high PLS level. This scheme is to maximizes the achievable performance and minimizes the undesired performance at the eavesdroppers simultaneously. Following this intuition, in the first phase, each relay chooses the best transmitter among the K small-cells to maximize their achievable SNR. The selected scheme in the first phase can be mathematically expressed as

$$\begin{aligned} \text {Phase 1:} \quad k^* = \arg \max _{k=1,...,K} \gamma _{R}^{k,m}, \end{aligned}$$

(7)

where $\gamma _{R}^{k,m}$ recalls the instantaneous SNR at R$_{m}$ via T$_{k}$. From (7), the statistical property of the instantaneous SNR via the best transmitter T$_{k^*}$ is given in the following theorem.

Theorem 1

Given K independent and identical unreliable backhaul connections, the CDF of the received SNR at R$_{m}$ via the best transmitter is given as

$$\begin{aligned} F_{{\gamma _{R}^{k^*,m}}}\left( {x}\right)&= 1+ \sum _{k=1}^{K} \sum _{\omega _1,...,\omega _{\mu _R}}^{k} \left( {\begin{array}{c}K\\ k\end{array}}\right) \left( \dfrac{k!}{\omega _1!...\omega _{\mu _R}!} \right) \nonumber \\&\dfrac{ (-1)^k \lambda ^k }{\prod _{t=0}^{\mu _R-1} \left( t!(\eta _T)^t \right) ^{\omega _{t+1}}} x^{\sum _{t=0}^{\mu _R-1}t \omega _{t+1}} e^{-k x/\eta _T}. \end{aligned}$$

(8)

Proof

The proof will show in the journal version by the limit of conference version.

The relay selection will be implemented in the second phase, which is to minimize the SINR between the particular relay and N eavesdroppers. This scheme can be formulated as

$$\begin{aligned} \text {Phase 2:} \quad m^* = \arg \min _{m=1,...,M} \gamma _{E}^{m,n^*} \quad , \end{aligned}$$

(9)

where $\gamma _{E}^{m,n^*} = \max (\gamma _{E}^{m,1},...,\gamma _{E}^{m,N})$ is the maximum instantaneous SINR between R$_{m}$ and N eavesdroppers. The CDF of the RV $\gamma _{E}^{m,n^*}$ is given in the following lemma and theorems in [10].

3.2 Secrecy Outage Probability

In this subsection, we focus on the secrecy outage probability, where the eavesdroppers’s CSI is assumed unavailable in the considered network. In this case, the transmitters encode and send the confidential message with the constant secrecy rate of $\theta$. If the instantaneous secrecy capacity, denoted by $\mathcal {C}_{S}$ in bits/s/Hz, is greater than $\theta$, the secrecy gain is guaranteed. To study the asymptotic behavior, the asymptotic secrecy outage probability will be analysed in this work.

Following [19], the secrecy capacity $\mathcal {C}_{S}$ can be expressed as

$$\begin{aligned} \mathcal {C}_{S} = \dfrac{1}{2} \left[ \log _2 (1+ \widetilde{\gamma }_{DF}^{m^*}) -\log _2 (1+ \gamma _{E}^{m^*,n^*}) \right] ^+ , \end{aligned}$$

(10)

where $\log _2 (1+ \widetilde{\gamma }_{DF}^{m^*})$ is the instantaneous capacity at D respect to the $m^*$-th relay and $\log _2 (1+ \gamma _{E}^{m^*,n^*})$ is the instantaneous capacity of the $m^*$-th relay and $n^*$-th eavesdropper link.

Thus, the secrecy outage probability, i.e. the probability when the secrecy capacity (10) falls below the given rate threshold, can be expressed as [17]

$$\begin{aligned} \mathcal {P}_{out} (\theta )&= Pr(\mathcal {C}_{S} < \theta ) \nonumber \\&= \int _{0}^{\infty } F_{{\widetilde{\gamma }_{DF}^{m^*}}}\left( {2^{2 \theta }(1+x)-1}\right) f_{{\gamma _{E}^{m^*,n^*}}}\left( {x}\right) dx. \end{aligned}$$

(11)

The closed-from expression for the secrecy outage probability in (11) is given in the following theorem.

Theorem 2

For the CN with unreliable backhaul links, the secrecy outage probability with two-phase transmitter/relay selection scheme is given as in (12) at the top of next page.

Proof

The proof will be provided in the journal version by the limit of conference version.

To study the impacts of unreliable backhaul connections, the asymptotic expression for the secrecy outage probability is given in the following theorem.

Theorem 3

Given the fixed set $\lbrace \eta _T, \eta _E, \eta _J\rbrace$, the asymptotic expression for secrecy outage probability is given as (13) at the top of next page.

Proof

The proof will be provided in the journal version by the limit of conference version.

From (13), due to the unreliable backhaul links, the secrecy diversity gain is not achievable. Furthermore, the limitation on secrecy outage probability is determined as a constant since the asymptotic secrecy outage is independent of DoF of channels between relay and D.

4 Numerical Results

In this section, we validate our analysis and investigate the secrecy outage probability of the considered system model by providing the numerical results. In our simulation, we deploy the binary phase-shift keying (BPSK) modulation with transmission block size $S=64$ symbols. For convenience, we define Ex and An as the results of link-level simulations and the analytical results, respectively. In the following, we investigate the network performance with various parameters to examine the effects of the degrees of cooperative transmission, DoFs, and backhaul reliability.

4.1 Secrecy Outage Probability

Fig. 2 illustrates the secrecy outage probability for various M and N. The network parameters are set as $K=3, \lambda = 0.995, \lbrace \mu _R, \mu _E, \mu _J, \mu _D \rbrace = \lbrace 2,2,2,3 \rbrace ,$ and $\lbrace \eta _T, \eta _E, \eta _J\rbrace = \lbrace 10, 10, 10 \rbrace$ dB. It can be observed that the number of relays/eavesdroppers strongly affects the secrecy outage probability. For example, when $N=1$, the secrecy outage probability becomes lower when more relays help with the cooperative transmission. Differently, when $M=1$, the secrecy outage probability becomes higher when the number of eavesdroppers increases. This is due to the fact that when the number of relays increases, the secrecy rate becomes higher as a result of the reduction in the wiretap channel capacity. Similarly, the secrecy rate decreases proportionally to the increase in the number of eavesdroppers. We further see that our analysis precisely matches the simulations and our analysis approaches the asymptotic results, presented in Theorem 3, in the high SNR regime.

Fig. 2.

Secrecy outage probability for various M, N of the proposed network.

In Fig. 3, we investigate the effects of DoFs and $\lbrace \eta _T, \eta _E, \eta _J\rbrace$ on the secrecy outage probability. In the settings, we set $K=3, M=1, N=2, \lambda =0.98,$ and $\lbrace \mu _R, \mu _E, \mu _J \rbrace = \lbrace 2,2,4 \rbrace$. As $\mu _D$ increases, we observe that the lower secrecy outage probability is achieved. We also observe that as $\eta _T$ and $\eta _J$ increase, the secrecy outage probability becomes lower while the increase in $\eta _E$ results in high achievable secrecy outage. It is clearly to see that the increase in $\eta _T$ results in a high received power at the receiver while the increase in $\eta _J$ reduces the SINR of the eavesdroppers.

Fig. 3.

Secrecy outage probability for various DoFs and $\lbrace \eta _T, \eta _E, \eta _J\rbrace$ of the proposed network.

5 Conclusions

This work has studied the impacts of unreliable backhaul links on the secrecy performance of a CN. A two-phase transmitter/relay selection scheme was proposed to minimize the information overheard of the eavesdroppers with guaranteeing the requirement of the instantaneous SNR at the receiver. The secrecy outage probability is analysed and derived to the exact expressions. For high SNRs regime, the asymptotic expressions of secrecy outage probability were attained to investigate the network performance. The simulation results demonstrated that the impact of backhaul reliability is an important parameter for the improvement of the secrecy performance.