Abstract
In this work, we propose two IPE schemes achieving both adaptive security and full attribute-hiding in the prime-order bilinear group, which improve upon the unique existing result satisfying both features from Okamoto and Takashima [Eurocrypt ’12] in terms of efficiency.
-
Our first IPE scheme is based on the standard \(k\textsc {-lin}\) assumption and has shorter master public key and shorter secret keys than Okamoto and Takashima’s IPE under weaker \({\textsc {dlin} }=2\textsc {-lin}\) assumption.
-
Our second IPE scheme is adapted from the first one; the security is based on the \({\textsc {xdlin}}\) assumption (as Okamoto and Takashima’s IPE) but now it also enjoys shorter ciphertexts.
Technically, instead of starting from composite-order IPE and applying existing transformation, we start from an IPE scheme in a very restricted setting but already in the prime-order group, and then gradually upgrade it to our full-fledged IPE scheme. This method allows us to integrate Chen et al.’s framework [Eurocrypt ’15] with recent new techniques [TCC ’17, Eurocrypt ’18] in an optimized way.
J. Chen—School of Computer Science and Software Engineering. Supported by the National Natural Science Foundation of China (Nos. 61472142, 61632012, U1705264) and the Young Elite Scientists Sponsorship Program by CAST (2017QNRC001). Homepage: http://www.jchen.top.
J. Gong—Supported in part by the French ANR ALAMBIC Project (ANR-16-CE39-0006).
H. Wee—Supported in part by the European Union’s Horizon 2020 Research and Innovation Programme under grant agreement 780108 (FENTEC).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Attribute-based encryption (ABE) is an advanced public-key encryption system supporting fine-grained access control [20, 31]. In an ABE system, an authority publishes a master public key \({\textsf {mpk}}\) for encryption and issues secret keys to users for decryption; a ciphertext for message m is associated with an attribute x while a secret key is associated with a policy f, a boolean function over the set of all attributes; when \(f(x)=1\), the secret key can be used to recover message m. The basic security requirement for ABE is message-hiding: an adversary holding a secret key with \(f(x)=0\) cannot infer any information about m from the ciphertext; furthermore, this should be ensured when the adversary has more than one such secret key, which is called collusion resistance.
In some applications, an additional security notion attribute-hiding [10, 22] is desirable, which concerns the privacy of attribute x instead of message m. In the literature, there are two levels of attribute-hiding: (1) weak attribute-hiding is against an adversary who holds multiple secret keys with \(f(x)=0\); (2) full attribute-hiding is against an adversary holding any kind of secret keys including those with \(f(x)=1\). Nowadays we have seen many concrete ABE schemes [7, 9, 18,19,20,21, 24,25,26, 30, 33]. Based on the seminal dual system method [32], we even reached generic frameworks for constructing and analyzing ABE [2,3,4,5,6, 11, 12, 35] in bilinear groups. Many of them, including both concrete ABE schemes and generic frameworks, have already achieved weak attribute-hiding [9, 11, 12, 18, 19, 21].
However it is much harder to obtain ABE with the full attribute-hiding feature. In fact, all known schemes only support so-called inner-product encryption (IPE), in which both ciphertexts and secret keys are associated with vectors and the decryption procedure succeeds when the two vectors has zero inner-product. Furthermore, almost all of them are selectively or semi-adaptively secure which means the adversary has to choose the vectors associated with the challenge ciphertext (called challenge vector/attribute) before seeing \({\textsf {mpk}}\) or before seeing any secret keys [10, 22, 29, 36]. Both of them are much weaker than the standard adaptive security (i.e., the one we have mentioned in the prior paragraph) where the choice can be made at any time. (Note that Wee achieved simulation-based security in [36].) What’s worse, some schemes [10, 22] are built on the composite-order group, on which group operations are slower and more memory space is required to store group elements. The best result so far comes from Okamoto and Takashima [27]: the IPE scheme is adaptively secure and fully attribute-hiding based on external decisional linear assumptionFootnote 1 (\({\textsc {xdlin}}\)) in efficient prime-order bilinear groups.
1.1 Our Results
In this work, we propose two IPE schemes in prime-order bilinear groups achieving both adaptive security and full attribute-hiding, which improve upon Okamoto and Takashima’s IPE scheme [27] in terms of space efficiency:
-
Our first construction is proven secure under standard k-Linear (\(k\textsc {-lin}\)) assumption. When instantiating with \(k=2\) (i.e., \({\textsc {dlin} }\) assumption), it enjoys shorter master public key and secret keys under weaker assumption than Okamoto and Takashima’s IPE, but we have slightly larger ciphertexts. With parameter \(k=1\) (i.e., \({\textsc {sxdh}}\) assumption), we can also achieve shorter ciphertexts but at the cost of basing the security on a stronger assumption.
-
Our second construction is proven secure under the \({\textsc {xdlin}}\) assumption, which is stronger than \({\textsc {dlin} }\) assumption. This gives another balance point between (space) efficiency and assumption. Now we can get better efficiency than Okamoto and Takashima’s IPE in terms of master public key, ciphertext and secret keys without sacrificing anything — Okamoto and Takashima also worked with \({\textsc {xdlin}}\).
A detailed comparison is provided in Table 1.
1.2 Our Technique in Composite-Order Groups
As a warm-up, we present a scheme in asymmetric composite-order bilinear groups. Here, we will rely on composite-order groups whose order is the product of four primes; this is different from the settings of adaptively secure ABE schemes and selectively secure full attribute-hiding inner product encryption where it suffices to use two primes.
The Scheme. Assume an asymmetric composite-order bilinear group \({\mathbb {G}}= (N,G_N,\) \(H_N,G_T,e:G_N \times H_N \rightarrow G_T)\) where \(N = p_1p_2p_3p_4\). Let \(g_1,h_{14}\) be respective random generators of subgroups \(G_{p_1},H_{p_1p_4}\). Pick \(\alpha ,u,w_1,\ldots ,w_n\leftarrow {\mathbb {Z}}_N\). We describe an IPE scheme for n dimensional space over \({\mathbb {Z}}_N\) as follows.
where \({\mathbf {x}}= (x_1,\ldots ,x_n) \in {\mathbb {Z}}_N^n\) and \({\mathbf {y}}= (y_1,\ldots ,y_n) \in {\mathbb {Z}}_N^n\). The construction is adapted from Chen et al. IPE [11] (without attribute-hiding feature) by embedding it into groups with four subgroups. This allows us to carry out the proof strategy introduced by Okamoto and Takashima [27], which involves a non-trivial extension of the standard dual system method [32]. We only give a high-level sketch for the proof below but show the complete game sequence in Fig. 1 for reference.
As is the case for adaptively secure ABE [32, 35], we will rely on the following private-key one-ciphertext one-key fully attribute-hiding inner product encryption scheme in the proof of security. Here, \(g_3,h_3\) denote the respective generators for the subgroups of order \(p_3\).
Note that the scheme satisfies (simulation-based) information-theoretic security in the selective setting, which immediately yields (indistinguishability-based) adaptive security via complexity leveraging.
In the proof of security (outlined in Fig. 1), we will first switch the ciphertext to having just a \(p_2p_3p_4\)-component via the subgroup decision assumption. At the beginning of the proof, all the secret keys will have a \(p_4\)-component, and at the end, all the secret keys will have a \(p_2\)-component; throughout, the secret keys will also always have a \(p_1\)-component but no \(p_3\)-components at the beginning or the end. To carry out the change in the secret keys from \(p_4\)-components to \(p_2\)-components, we will switch the keys one by one. For the switch, we will introduce a \(p_3\)-component into one secret key and then invoke security of the above private-key one-ciphertext one-key scheme in the \(p_3\)-subgroup. It is important here that throughout the hybrids, at most one secret key has a \(p_3\)-component.
Game sequence for composite-order IPE. In the table, \({\mathbf {x}}_0 = (x_{1,0},\ldots ,x_{n,0})\) and \({\mathbf {x}}_1 = (x_{1,1},\ldots ,x_{n,1})\) are the challenge vectors; \(b \in \{0,1\}\) is the secret bit we hope to hide against the adversary. The gray background highlights the difference between adjacent games. The column “\({\mathsf {ct}}\)” shows the structure of the challenge ciphertext on four subgroups whose generators are \(g_1,g_2,g_3,g_4\), while the next column gives the subgroup where every secret keys lie in. In the last column, the notation “\(p_1 \mapsto p_2p_3p_4\) in G” is indicating the subgroup decision assumption stating that \(G_{p_1} \approx _c G_{p_2p_3p_4}\).
1.3 Our Technique in Prime-Order Groups
Assume a prime-order bilinear group \({\mathbb {G}}= (p,G_1,G_2,G_T,e:G_1 \times G_2 \rightarrow G_T)\) and let \([\cdot ]_1,[\cdot ]_2,[\cdot ]_T\) denote the entry-wise exponentiation on \(G_1,G_2,G_T\), respectively. Naively, we simulate a composite-order group whose order is the product of four primes using vectors of dimension 4k “in the exponent” under \(k\textsc {-lin}\) assumption. That is, we replace
where \({\mathbf {A}}_1 \leftarrow {\mathbb {Z}}_p^{4k \times k}, {\mathbf {B}}_{14} \leftarrow {\mathbb {Z}}_p^{4k \times 2k}\). However, the resulting IPE scheme is less efficient than Okamoto and Takashima’s scheme [27]. Instead, we will show that it suffices to use
Then, with the correspondence by Chen et al. [11, 13, 16]:
we have the following prime-order IPE scheme:
Note that, with matrices \({\mathbf {A}}_1 \in {\mathbb {Z}}_p^{(k+1) \times k}\) and \({\mathbf {B}}\in {\mathbb {Z}}_p^{(2k+1) \times k}\), we only simulate two and three subgroups, respectively, rather than four subgroups; meanwhile some of them are simulated as low-dimension subspaces. Although it has become a common optimization technique to adjust dimensions of subspaces, it is not direct to justify that we can work with less subspaces. In fact, these optimizations are based on elaborate investigations of the proof strategy sketched in Sect. 1.2. In the rest of this section, we explain our method leading to the optimized parameter shown in (3).
Our Translation. We start from an IPE scheme in a very restricted setting and then gradually upgrade it to our full-fledged IPE scheme in the prime-order group. In particular, we follow the roadmap

The private key one-key IPE corresponds to scheme (2) over \(p_3\)-subgroup (cf. \({\mathsf {Game}}_{2.j-1.2}\) in Fig. 1). In Step 1, we move from one-key to multi-key model using the technique from [13], which is related to the argument just after we change ciphertext in proof of scheme (1) (cf. \({\mathsf {Game}}_{2.0}\) to \({\mathsf {Game}}_{2.q}\) and \({\mathsf {Game}}_3\) in Fig. 1). In Step 2, we move from private-key to public-key setting with the compiler in [36], which is related to the change of ciphertext at the beginning of the proof (cf. \({\mathsf {Game}}_1\) in Fig. 1). By handling these proof techniques underlying the proof sketched in Sect. 1.2 (cf. Fig. 1) one by one as above, we are able to integrate Chen et al.’s framework [11] with recent new techniques [13, 36] in an optimized way.
Private-key IPE in One-key Setting. We start from a private-key IPE where the ciphertext is created from \({\textsf {msk}}\) rather than \({\textsf {mpk}}\). We also consider a weaker one-key model where the adversary can get only one secret key. Pick  and let message
and let message  . We give the following private-key IPE over \({\mathbb {Z}}_p\):
. We give the following private-key IPE over \({\mathbb {Z}}_p\):
Analogous to scheme (2), the scheme satisfies (simulation-based) information-theoretic security in the selective setting (cf. [36]). By the implication from simulation-based security to indistinguishability-based security and standard complexity leveraging technique, we have the following statement: For adaptively chosen \({\mathbf {x}}_0= (x_{1,0},\ldots ,x_{n,0})\in {\mathbb {Z}}_p^n\), \({\mathbf {x}}_1= (x_{1,1},\ldots ,x_{n,1})\in {\mathbb {Z}}_p^n\) and \({\mathbf {y}}= (y_1,\ldots ,y_n) \in {\mathbb {Z}}_p^n\) satisfying either \(\langle {\mathbf {x}}_0,{\mathbf {y}}\rangle \ne 0 \wedge \langle {\mathbf {x}}_1,{\mathbf {y}}\rangle \ne 0\) or \(\langle {\mathbf {x}}_0,{\mathbf {y}}\rangle = \langle {\mathbf {x}}_1,{\mathbf {y}}\rangle = 0\) and all \(b\in \{0,1\}\), we have
Note that the statement here is different from that used in Fig. 1 (where \(x_{i,0}\) is in the place of \(x_{i,1-b}\)). Looking ahead, this choice is made to employ the “change of basis” technique when moving from one-key to multi-key model (see the next paragraph).
Private-key IPE in Multi-key Setting. To handle multiple keys revealed to the adversary, we employ Chen et al.’s prime-order generic frameworkFootnote 2 [11] based on the dual system method [32] to scheme (6). The framework works with prime-order finite cyclic group G on which the \(k\textsc {-lin}\) assumption holds. Let \([\cdot ]\) denote the entry-wise exponentiation on G. In order to avoid collusion of multiple secret keys, we will re-randomize each secret key [8, 31, 34] using fresh vector \({\mathbf {d}}\leftarrow \mathsf {span}({\mathbf {B}}_1)\) where \({\mathbf {B}}_1 \leftarrow {\mathbb {Z}}_p^{(k+1) \times k}\), which supports standard dual system method [32] with a hidden subspace \({\mathbf {B}}_2 \leftarrow {\mathbb {Z}}_p^{k+1}\). For this purpose, we need to do the following “scalar to vector” substitutions:
Then the re-randomization is done by multiplying \({\mathbf {u}}\) and each \({\mathbf {w}}_i\) in secret keys by \({\mathbf {d}}\) and moving them from \({\mathbb {Z}}_p\) to G. This yields the following private-key IPE:
To carry out the non-trivial extension by Okamoto and Takashima [27] which involves three subgroups of \(H_N\) (cf. game sequence from \({\mathsf {Game}}_{2.0}\) to \({\mathsf {Game}}_{2.q}\)), we increase the dimension of vectors \({\mathbf {u}},{\mathbf {w}}_1,\ldots ,{\mathbf {w}}_n\), \({\mathbf {d}}\) in secret keys by k (i.e., from \(k+1\) to \(2k+1\)) as in [13] such that the support of \({\mathbf {d}}\) can accommodate three subspaces defined by
where \({\mathbf {B}}_1,{\mathbf {B}}_2,{\mathbf {B}}_3\) play the roles similar to \(p_4\), \(p_2\), \(p_3\)-subgroup respectively. Following the proof strategy in [13] and statement (7) for the one-key scheme (6), we can change secret keys and the challenge ciphertext revealed to the adversary into the form:
where \({\mathbf {u}}^{(1)}\) (resp. \({\mathbf {u}}^{(2)}\), \({\mathbf {u}}^{(3)}\)) is a random vector orthogonal to \(\mathsf {span}({\mathbf {B}}_2,{\mathbf {B}}_3)\) (resp. \(\mathsf {span}({\mathbf {B}}_1,{\mathbf {B}}_3)\), \(\mathsf {span}({\mathbf {B}}_1,{\mathbf {B}}_2)\)). Finally, by the “change of basis” commonly appeared in the proof with dual pairing vector space [23, 27] (and a simple statistical argument), we claim that \({\mathsf {ct}}^*\) has the same distribution as
where \({\mathbf {u}}_0,{\mathbf {u}}_1\leftarrow {\mathbb {Z}}_p^{1 \times (2k+1)}\). This means that \({\mathsf {ct}}^*\) hides b and scheme (8) is fully attribute-hiding.
Note that the support of randomness \({\mathbf {d}}\) (after the change) is \(\mathsf {span}({\mathbf {B}}_1,{\mathbf {B}}_2)\) rather than \(\mathsf {span}({\mathbf {B}}_2)\), which simulates \(p_2\)-subgroup in the composite-order scheme (1). This is crucial to derive more efficient IPE scheme but slightly complicates the final argument above where “change of basis” technique has to be used to deal with \(x_{i,b} \cdot {\mathbf {u}}^{(1)}\) interplaying with \({\mathbf {B}}_1\)-component in \(\mathsf {sk}_{\mathbf {y}}\).
(Public-key) IPE scheme. To upgrade our private-key IPE to public-key IPE, we will employ the “private-key to public-key” compiler in [36]. The compiler relies on bilinear groups \((p,G_1,G_2,G_T,e:G_1 \times G_2 \rightarrow G_T)\) in which the \(k\textsc {-lin}\) assumption holds. In detail, we do the following “vector to matrix”/“scalar to vector” substitution for entries in \({\textsf {msk}}\) and secret keys:
and publish them as parts of \({\textsf {mpk}}\) in the form of
In the ciphertext, we translate \({\mathbf {u}},{\mathbf {w}}_1,\ldots ,{\mathbf {w}}_n\) into \([{\mathbf {c}}^{\top }{\mathbf {U}}]_1,[{\mathbf {c}}^{\top }{\mathbf {W}}_1]_1,\ldots ,[{\mathbf {c}}^{\top }{\mathbf {W}}_n]_1\) where \({\mathbf {c}}\leftarrow \mathsf {span}({\mathbf {A}})\) and translate \([\alpha ]_2\) into \([{\mathbf {c}}^{\top }{\mathbf {k}}]_T\). Finally, secret keys are now moved to group \(G_2\). This results in the following IPE scheme:
Note that the translation does not involve \(({\mathbf {B}}_1,{\mathbf {B}}_2,{\mathbf {B}}_3)\) we just introduced.
To prove the security of the resulting public-key IPE scheme, we first show that we can change the support of \({\mathbf {c}}\) from \(\mathsf {span}({\mathbf {A}})\) to \({\mathbb {Z}}_p^{k+1}\) by the following statement implied by the \(k\textsc {-lin}\) assumption:

Since \(({\mathbf {A}}\mid {\mathbf {c}})\) is full-rank with overwhelming probability, we can see that
are distributed independently. Then the security of scheme (9) can be reduced to that of private-key scheme (8) by observations: (i) \(\widetilde{\textsf {msk}}\) is necessary for generating \({\textsf {mpk}}\) in scheme (9); (ii) we can view a ciphertext in scheme (9) as a ciphertext of our private-key IPE scheme under master secret key \({\textsf {msk}}^*\); (iii) a secret key in scheme (9) can be produced from a secret key of private-key IPE scheme (8) under master secret key \({\textsf {msk}}^*\) with the help of \(\widetilde{\textsf {msk}}\).
How to Shorten the Ciphertext. The ciphertext size of our IPE scheme (9) mainly depends on the width of matrix \({\mathbf {U}}\) and \({\mathbf {W}}_i\), which is further determined by the dimensions of subspaces defined by \({\mathbf {B}}_1,{\mathbf {B}}_2,{\mathbf {B}}_3\). Therefore, in order to reduce the ciphertext size, we employ the “dimension compress” technique used in [16]. The basic idea is to let \({\mathbf {B}}_1\) and \({\mathbf {B}}_3\) “share some dimensions” and finally decrease the width of \({\mathbf {U}}\) and \({\mathbf {W}}_i\), the cost is that we have to use the \({\textsc {xdlin}}\) assumption. Compared with our first scheme, a qualitative difference is that the private-key variant now works with bilinear maps. This is not needed when we work with the \(k\textsc {-lin}\) assumption in the first scheme.
Organization. The paper is organized as follows. In Sect. 2, we review some basic notions. The next two sections, Sects. 3 and 4, will be devoted to our two IPE schemes, respectively. In both sections, we will first develop a private-key scheme and then transform it to the public-key version as [36].
2 Preliminaries
Notation. Let \({\mathbf {A}}\) be a matrix over \({\mathbb {Z}}_p\). We use \(\mathsf {span}({\mathbf {A}})\) to denote the column span of \({\mathbf {A}}\), use \({\mathsf {basis}}({\mathbf {A}})\) to denote a basis of \(\mathsf {span}({\mathbf {A}})\), and use \(({\mathbf {A}}_1 | {\mathbf {A}}_2)\) to denote the concatenation of matrices \({\mathbf {A}}_1,{\mathbf {A}}_2\). By \(\mathsf {span}({\mathbf {A}}^{\top })\), we are indicating the row span of \({\mathbf {A}}^{\top }\). We let \({\mathbf {I}}_n\) be the n-by-n identity matrix and \({\mathbf {0}}\) be a zero matrix of proper size. Given an invertible matrix \({\mathbf {B}}\), we use \({\mathbf {B}}^*\) to denote its dual satisfying \({\mathbf {B}}^{\top }{\mathbf {B}}^*={\mathbf {I}}\).
2.1 Inner-Product Encryption
Algorithms. An inner-product encryption (IPE) scheme consists of four algorithms \((\mathsf {Setup},{\mathsf {KeyGen}},{\mathsf {Enc}},{\mathsf {Dec}})\):
-
\(\mathsf {Setup}(1^\lambda ,n) \rightarrow ({\textsf {mpk}}, {\textsf {msk}})\). The setup algorithm gets as input the security parameter \(\lambda \) and the dimension n of the vector space. It outputs the master public key \({\textsf {mpk}}\) and the master key \({\textsf {msk}}\).
-
\({\mathsf {KeyGen}}({\textsf {msk}},{\mathbf {y}})\rightarrow \mathsf {sk}_{\mathbf {y}}\). The key generation algorithm gets as input \({\textsf {msk}}\) and a vector \({\mathbf {y}}\). It outputs a secret key \(\mathsf {sk}_{\mathbf {y}}\) for vector \({\mathbf {y}}\).
-
\({\mathsf {Enc}}({\textsf {mpk}},{\mathbf {x}},m)\rightarrow {\mathsf {ct}}_{\mathbf {x}}\). The encryption algorithm gets as input \({\textsf {mpk}}\), a vector \({\mathbf {x}}\) and a message m. It outputs a ciphertext \({\mathsf {ct}}_{\mathbf {x}}\) for vector \({\mathbf {x}}\).
-
\({\mathsf {Dec}}({\mathsf {ct}}_{\mathbf {x}},\mathsf {sk}_{\mathbf {y}}) \rightarrow m\). The decryption algorithm gets as a ciphertext \({\mathsf {ct}}_{\mathbf {x}}\) for \({\mathbf {x}}\) and a secret key \(\mathsf {sk}_{\mathbf {y}}\) for vector \({\mathbf {y}}\) satisfying \(\langle {\mathbf {x}},{\mathbf {y}}\rangle = 0\). It outputs message m.
Correctness. For all vectors \({\mathbf {x}},{\mathbf {y}}\) satisfying \(\langle {\mathbf {x}},{\mathbf {y}}\rangle = 0\) and all m, it holds that
where \(({\textsf {mpk}},{\textsf {msk}}) \leftarrow \mathsf {Setup}(1^\lambda ,n)\), \({\mathsf {ct}}_{\mathbf {x}}\leftarrow {\mathsf {Enc}}({\textsf {mpk}},{\mathbf {x}},m)\), \(\mathsf {sk}_{\mathbf {y}}\leftarrow {\mathsf {KeyGen}}({\textsf {msk}},{\mathbf {y}})\).
Security. For a stateful adversary \({\mathcal {A}}\), we define the advantage function

with the following restrictions on all queries \({\mathbf {y}}\) that \({\mathcal {A}}\) submitted to \({\mathsf {KeyGen}}({\textsf {msk}},\cdot )\):
-
if \(m_0 \ne m_1\), we require that \(\langle {\mathbf {x}}_0,{\mathbf {y}}\rangle \ne 0 \wedge \langle {\mathbf {x}}_1,{\mathbf {y}}\rangle \ne 0\);
-
if \(m_0 = m_1\), we require that either \(\langle {\mathbf {x}}_0,{\mathbf {y}}\rangle \ne 0 \wedge \langle {\mathbf {x}}_1,{\mathbf {y}}\rangle \ne 0\) or \(\langle {\mathbf {x}}_0,{\mathbf {y}}\rangle = \langle {\mathbf {x}}_1,{\mathbf {y}}\rangle = 0\).
An IPE scheme is adaptively secure and fully attribute-hiding if for all PPT adversaries \({\mathcal {A}}\), the advantage \({\mathsf {Adv}}_{{\mathcal {A}}}^\textsc {ipe}(\lambda )\) is a negligible function in \(\lambda \).
Private-key IPE. In a private-key IPE, the \(\mathsf {Setup}\) algorithm does not output \({\textsf {mpk}}\); and the \({\mathsf {Enc}}\) algorithm takes \({\textsf {msk}}\) instead of \({\textsf {mpk}}\) as input. The adaptive security and full attribute-hiding can be defined analogously except that \({\mathcal {A}}\) only gets \({\mathsf {ct}}^*\) and has access to \({\mathsf {KeyGen}}({\textsf {msk}},\cdot )\). The advantage function is denoted by \({\mathsf {Adv}}_{{\mathcal {A}}}^\textsc {ipe*}(\lambda )\). Accordingly, we may call the standard IPE public-key IPE.
2.2 Prime-Order Groups and Matrix Diffie-Hellman Assumptions
A group generator \({\mathcal {G}}\) takes as input security parameter \(\lambda \) and outputs group description \({\mathbb {G}}= (p,G_1,G_2,G_T,e)\), where p is a prime of \(\varTheta (\lambda )\) bits, \(G_1\), \(G_2\) and \(G_T\) are cyclic groups of order p, and \(e : G_1 \times G_2 \rightarrow G_T\) is a non-degenerate bilinear map. We require that group operations in \(G_1\), \(G_2\) and \(G_T\) as well the bilinear map e are computable in deterministic polynomial time with respect to \(\lambda \). Let \(g_1 \in G_1\), \(g_2 \in G_2\) and \(g_T = e(g_1,g_2) \in G_T\) be the respective generators. We employ the implicit representation of group elements: for a matrix \({\mathbf {M}}\) over \({\mathbb {Z}}_p\), we define \([{\mathbf {M}}]_1=g_1^{{\mathbf {M}}},[{\mathbf {M}}]_2=g_2^{{\mathbf {M}}},[{\mathbf {M}}]_T=g_T^{{\mathbf {M}}}\), where exponentiations are carried out component-wise. Given \({\mathbf {A}}\) and \([{\mathbf {B}}]_2\), we let \({\mathbf {A}}\odot [{\mathbf {B}}]_2 = [{\mathbf {A}}{\mathbf {B}}]_2\); for \([{\mathbf {A}}]_1\) and \([{\mathbf {B}}]_2\), we let \(e([{\mathbf {A}}]_1,[{\mathbf {B}}]_2) = [{\mathbf {A}}{\mathbf {B}}]_T\).
We review the matrix Diffie-Hellman (MDDH) assumption on \(G_1\) [14]. The \(\textsc {mddh}_{k,\ell } \) assumption on \(G_2\) can be defined analogously and it is known that \(k\textsc {-lin}\Rightarrow \textsc {mddh}_{k,\ell } \) [14].
Assumption 1
( MDDH\(_{{k,\ell }}{}\) Assumption). Let \(\ell > k \ge 1\). We say that the \(\textsc {mddh}^{}_{k,\ell } \) assumption holds with respect to \({\mathcal {G}}\) if for all PPT adversaries \({\mathcal {A}}\), the following advantage function is negligible in \(\lambda \).

where \({\mathbb {G}}\leftarrow {\mathcal {G}}(1^\lambda )\), \({\mathbf {M}}\leftarrow {\mathbb {Z}}_p^{\ell \times k}\), \({\mathbf {s}}\leftarrow {\mathbb {Z}}_p^{k}\) and \({\mathbf {u}}\leftarrow {\mathbb {Z}}_p^{\ell }\).
We also use the external decisional linear (\({\textsc {xdlin}}\)) assumption on \(G_2\) [1]:
Assumption 2
( \({\textsc {xdlin}}\) Assumption). We say that the \({\textsc {xdlin}}\) assumption holds with respect to \({\mathcal {G}}\) if for all PPT adversaries \({\mathcal {A}}\), the following advantage function is negligible in \(\lambda \).

where \({\mathbb {G}}\leftarrow {\mathcal {G}}(1^\lambda )\) and \(D = (\,[a_1,a_2,a_3,a_1s_1,a_2s_2]_1,[a_1,a_2,a_3,a_1s_1,a_2s_2]_2\,)\) with \(a_1,a_2,a_3,s_1,s_2\leftarrow {\mathbb {Z}}_p\).
3 Construction from \(k\textsc {-lin}\) Assumption
3.1 Preparation
Fix parameters \(\ell _1,\ell _2,\ell _3 \ge 1\) and let \(\ell := \ell _1 + \ell _2 + \ell _3\). We use basis
and its dual basis \(({\mathbf {B}}^{\parallel }_1, {\mathbf {B}}^{\parallel }_2, {\mathbf {B}}^{\parallel }_3)\) such that \({\mathbf {B}}_i^{\top }{\mathbf {B}}^{\parallel }_i = {\mathbf {I}}\) (known as non-degeneracy) and \({\mathbf {B}}_i^{\top }{\mathbf {B}}_j = \mathbf {0}\) if \(i \ne j\) (known as orthogonality), as depicted in Fig. 2.
Assumption. We review the \(\textsc {sd}^{G_2}_{{\mathbf {B}}_{1} \mapsto {\mathbf {B}}_{1},{\mathbf {B}}_{2}}\) assumption [13, 15, 17] as follows. By symmetry, one may permute the indices for subspaces.
Lemma 1
( \(\textsc {mddh}_{\ell _1,\ell _1+\ell _2} \Rightarrow \textsc {sd}^{G_2}_{{\mathbf {B}}_{1} \mapsto {\mathbf {B}}_{1},{\mathbf {B}}_{2}}\)). Under the \(\textsc {mddh}_{\ell _1,\ell _1+\ell _2} \) assumption in \(G_2\), there exists an efficient sampler outputting random \(([{\mathbf {B}}_1]_2,[{\mathbf {B}}_2]_2,[{\mathbf {B}}_3]_2)\) (as described above) along with base \({\mathsf {basis}}({\mathbf {B}}^{\parallel }_3)\) and \({\mathsf {basis}}({\mathbf {B}}_1^{\parallel },{\mathbf {B}}_2^{\parallel })\) (of arbitrary choice) such that the following advantage function is negligible in \(\lambda \).
where
Facts. With basis \(({\mathbf {B}}_1,{\mathbf {B}}_2,{\mathbf {B}}_3)\), we can uniquely decompose \({\mathbf {w}}\in {\mathbb {Z}}_p^{1 \times \ell }\) as
In the paper, we use notation \({\mathbf {w}}^{(\beta )}\) to denote the projection of \({\mathbf {w}}\) onto \(\mathsf {span}({{\mathbf {B}}_\beta ^{\parallel }}^{\top })\) and define \( {\mathbf {w}}^{(\beta _1\beta _2)} = {\mathbf {w}}^{(\beta _1)} + {\mathbf {w}}^{(\beta _2)}\) for \(\beta _1,\beta _2 \in [3]\). Furthermore, we highlight two facts: (1) For \(\beta \in [3]\), it holds that  ; (2) For all \(\beta ^* \in [3]\), it holds that
; (2) For all \(\beta ^* \in [3]\), it holds that
when \({\mathbf {w}}\leftarrow {\mathbb {Z}}_p^{1 \times \ell }\) and \({\mathbf {w}}^* \leftarrow \mathsf {span}({{\mathbf {B}}_{\beta ^*}^{\parallel }}^{\top })\).
3.2 Step One: A Private-Key IPE in Prime-Order Groups
Our first prime-order private-key IPE is described as follows. We use the basis described in Sect. 3.1 with \((\ell _1,\ell _2,\ell _3)=(k,1,k)\). As mentioned in Sect. 1.2, we do not need bilinear map for this private-key IPE. However, for our future use in Sect. 3.4, we describe the IPE in bilinear groups and note that only one of source groups is used.
-
\(\mathsf {Setup}(1^\lambda ,n)\): Run \({\mathbb {G}}= (p,G_1,G_2,G_T,e) \leftarrow {\mathcal {G}}(1^\lambda )\). Sample \( {\mathbf {B}}_1 \leftarrow {\mathbb {Z}}_p^{(2k+1) \times k} \) and pick \( {\mathbf {u}},{\mathbf {w}}_1,\ldots ,{\mathbf {w}}_n \leftarrow {\mathbb {Z}}_p^{1 \times (2k+1)}\), \(\alpha \leftarrow {\mathbb {Z}}_p \). Output
$$\begin{aligned} {\textsf {msk}} = (\,{\mathbb {G}},\alpha ,{\mathbf {u}},{\mathbf {w}}_1,\ldots ,{\mathbf {w}}_n,{\mathbf {B}}_1\,). \end{aligned}$$ -
\({\mathsf {KeyGen}}({\textsf {msk}},{\mathbf {y}})\): Let \({\mathbf {y}}= (y_1,\ldots ,y_n) \in {\mathbb {Z}}_p^n\). Sample \({\mathbf {r}}\leftarrow {\mathbb {Z}}_p^k\) and output
$$\begin{aligned} \mathsf {sk}_{\mathbf {y}}=(\, K_0 = [\alpha + (y_1 \cdot {\mathbf {w}}_1 + \cdots + y_n \cdot {\mathbf {w}}_n) {\mathbf {B}}_1 {\mathbf {r}}]_2, \, K_1 = [{\mathbf {B}}_1 {\mathbf {r}}]_2 \,) \end{aligned}$$ -
\({\mathsf {Enc}}({\textsf {msk}},{\mathbf {x}},m)\): Let \({\mathbf {x}}= (x_1,\ldots ,x_n) \in {\mathbb {Z}}_p^n\) and \(m \in G_2\). Output
$$\begin{aligned} {\mathsf {ct}}_{\mathbf {x}}= (\, C_1 = x_1 \cdot {\mathbf {u}}+ {\mathbf {w}}_1,\,\ldots ,\,C_n = x_n \cdot {\mathbf {u}}+ {\mathbf {w}}_n,\, C = [\alpha ]_2 \cdot m \,) \end{aligned}$$ -
\({\mathsf {Dec}}({\mathsf {ct}}_{\mathbf {x}},\mathsf {sk}_{\mathbf {y}})\): Parse \({\mathsf {ct}}_{\mathbf {x}}= (C_1,\ldots ,C_n,C)\) and \(\mathsf {sk}_{\mathbf {y}}= (K_0,K_1)\) for \({\mathbf {y}}= (y_1,\ldots ,y_n) \in {\mathbb {Z}}_p^{n}\). Output
$$\begin{aligned} m' = C \cdot ((y_1 \cdot C_1 + \cdots + y_n \cdot C_n) \odot K_1) \cdot K_0^{-1}. \end{aligned}$$
The correctness is straightforward.
3.3 Security of Private-Key IPE
We will prove the following theorem.
Theorem 1
Under the \(k\textsc {-lin}\) assumption, the private-key IPE scheme described in Sect. 3.2 is adaptively secure and fully attribute-hiding (cf. Sect. 2.1).
Following [11, 35], we can reduce the case \(m_0 \ne m_1\) to the case \(m_0 = m_1\) by arguing that an encryption for \(m_b\) is indistinguishable with an encryption for \(m_0\). Therefore it is sufficient to prove the following lemma for \(m_0 = m_1\).
Lemma 2
For any adversary \({\mathcal {A}}\) that makes at most Q key queries and outputs \(m_0 = m_1\), there exists adversaries \({\mathcal {B}}_1,{\mathcal {B}}_2,{\mathcal {B}}_3\) such that
and \({\mathsf {Time}}({\mathcal {B}}_1),{\mathsf {Time}}({\mathcal {B}}_2),{\mathsf {Time}}({\mathcal {B}}_3) \approx {\mathsf {Time}}({\mathcal {A}})\).
Game sequence for private-key IPE based on \(k\textsc {-lin}\) assumption. The gray background highlights the difference between adjacent games. Here, \({\mathbf {B}}_1,{\mathbf {B}}_2,{\mathbf {B}}_3\) play a role similar to the \(p_4,p_2,p_3\)-subgroups in Fig. 1.
Game sequence. We prove Lemma 2 via the following game sequence, which is summarized in Fig. 3.
-
\({\mathsf {Game}}_0\) is the real game in which the challenge ciphertext for \({\mathbf {x}}_b = (x_{1,b},\ldots ,x_{n,b})\) is of the form
$$\begin{aligned} x_{1,b} \cdot {\mathbf {u}}+ {\mathbf {w}}_1,\ \ldots ,\ x_{n,b} \cdot {\mathbf {u}}+ {\mathbf {w}}_n,\ [\alpha ]_2 \cdot m_0. \end{aligned}$$Here \(b \leftarrow \{0,1\}\) is a secret bit.
-
\({\mathsf {Game}}_{1}\) is identical to \({\mathsf {Game}}_{0}\) except that the challenge ciphertext is
$$\begin{aligned} x_{1,b} \cdot {\mathbf {u}}^{(13)} + \boxed {x_{1,1-b} \cdot {\mathbf {u}}^{(2)}} + {\mathbf {w}}_1,\ \ldots ,\ x_{n,b} \cdot {\mathbf {u}}^{(13)} + \boxed {x_{n,1-b} \cdot {\mathbf {u}}^{(2)}} + {\mathbf {w}}_n,\ [\alpha ]_2 \cdot m_0. \end{aligned}$$We claim that \({\mathsf {Game}}_1 \equiv {\mathsf {Game}}_0\). This follows from facts that (1) secret keys will not reveal \({\mathbf {w}}_1^{(2)},\ldots ,{\mathbf {w}}_n^{(2)}\); (2) for all \({\mathbf {x}}_0,{\mathbf {x}}_1 \in {\mathbb {Z}}_p^n\) and \({\mathbf {u}}^{(2)} \in \mathsf {span}({{\mathbf {B}}_2^{\parallel }}^{\top })\), it holds
$$\begin{aligned} \{\,\boxed {x_{i,b} \cdot {\mathbf {u}}^{(2)}} + {\mathbf {w}}_i^{(2)} \,\}_{i \in [n]} \, \equiv \, \{\,\boxed {x_{i,1-b} \cdot {\mathbf {u}}^{(2)}} + {\mathbf {w}}_i^{(2)} \,\}_{i \in [n]} \end{aligned}$$when \({\mathbf {w}}_1^{(2)},\ldots ,{\mathbf {w}}_n^{(2)} \leftarrow \mathsf {span}({{\mathbf {B}}_2^{\parallel }}^{\top })\). See Lemma 4 for more details.
-
\({\mathsf {Game}}_{2.j}\) for \(j \in [0,q]\) is identical to \({\mathsf {Game}}_{1}\) except that the first j secret keys are
$$\begin{aligned}{}[\alpha + (y_1 \cdot {\mathbf {w}}_1 + \cdots + y_n \cdot {\mathbf {w}}_n) {\mathbf {d}}]_2,\ [{\mathbf {d}}]_2 \quad \text{ where } \quad \boxed {{\mathbf {d}}\leftarrow \mathsf {span}({\mathbf {B}}_1,{\mathbf {B}}_2)}. \end{aligned}$$We claim that
 for \(j \in [q]\) and give a proof sketch later.
for \(j \in [q]\) and give a proof sketch later. -
\({\mathsf {Game}}_3\) is identical to \({\mathsf {Game}}_{2.q}\) except that the challenge ciphertext is
$$\begin{aligned} \{\,\boxed {x_{i,0} \cdot {\mathbf {u}}_0^{(12)} + x_{i,1} \cdot {\mathbf {u}}_1^{(12)}} + x_{i,b} \cdot {\mathbf {u}}^{(3)} + {\mathbf {w}}_i\,\}_{i\in [n]}, [\alpha ]_2 \cdot m_0. \end{aligned}$$where \({\mathbf {u}}_0,{\mathbf {u}}_1 \leftarrow {\mathbb {Z}}_p^{1 \times (2k+1)}\). We claim that \({\mathsf {Game}}_{2.q} \equiv {\mathsf {Game}}_3\). This follows from the “change of basis” technique used in dual pairing vector spaces [23, 28]. In particular, we argue that
$$\begin{aligned} (\,\overbrace{{\mathbf {u}}^{(1)}}^{x_{i,b}},\overbrace{{\mathbf {u}}^{(2)}}^{x_{i,1-b}}\,) \equiv (\,{\mathbf {u}}_0^{(12)},{\mathbf {u}}_1^{(12)}\,) \end{aligned}$$when \({\mathbf {u}},{\mathbf {u}}_0,{\mathbf {u}}_1\) and basis \({\mathbf {B}}_1,{\mathbf {B}}_2\) are chosen at random. Here we use the fact that randomness \({\mathbf {d}}\) in secret keys reveals no information about the basis of \(\mathsf {span}({\mathbf {B}}_1,{\mathbf {B}}_2)\). See Lemma 5 for more details.
-
\({\mathsf {Game}}_4\) is identical to \({\mathsf {Game}}_3\) except that the challenge ciphertext is
$$\begin{aligned} \boxed {x_{1,0} \cdot {\mathbf {u}}_0 + x_{1,1} \cdot {\mathbf {u}}_1} + {\mathbf {w}}_1,\ \ldots ,\ \boxed {x_{n,0} \cdot {\mathbf {u}}_0 + x_{n,1} \cdot {\mathbf {u}}_1} + {\mathbf {w}}_n,\ [\alpha ]_2 \cdot m_0 \end{aligned}$$in which the adversary has no advantage in guessing b. We claim that \({\mathsf {Game}}_3 \equiv {\mathsf {Game}}_4\). The proof is similar to that for \({\mathsf {Game}}_1 \equiv {\mathsf {Game}}_0\). See Lemma 6 for details.
Proving  . We now prove
. We now prove  and thus complete the proof for Lemma 2. For all \(j \in [q]\), we employ the following game sequence, which has been included in Fig. 3.
and thus complete the proof for Lemma 2. For all \(j \in [q]\), we employ the following game sequence, which has been included in Fig. 3.
-
\({\mathsf {Game}}_{2.j-1.1}\) is identical to \({\mathsf {Game}}_{2.j-1}\) except that the jth secret key is
$$\begin{aligned}{}[\alpha + (y_1 \cdot {\mathbf {w}}_1 + \cdots + y_n \cdot {\mathbf {w}}_n) {\mathbf {d}}]_2,\ [{\mathbf {d}}]_2 \quad \text{ where } \quad \boxed {{\mathbf {d}}\leftarrow \mathsf {span}({\mathbf {B}}_1,{\mathbf {B}}_3)}. \end{aligned}$$We claim that
 . This follows from the \(\textsc {sd}^{G_2}_{{\mathbf {B}}_{1} \mapsto {\mathbf {B}}_{1},{\mathbf {B}}_{3}}\) assumption: given \([{\mathbf {B}}_1]_2,[{\mathbf {B}}_2]_2,[{\mathbf {B}}_3]_2,{\mathsf {basis}}({\mathbf {B}}_2^{\parallel }),{\mathsf {basis}}({\mathbf {B}}_1^{\parallel },{\mathbf {B}}_3^{\parallel })\), it holds that
. This follows from the \(\textsc {sd}^{G_2}_{{\mathbf {B}}_{1} \mapsto {\mathbf {B}}_{1},{\mathbf {B}}_{3}}\) assumption: given \([{\mathbf {B}}_1]_2,[{\mathbf {B}}_2]_2,[{\mathbf {B}}_3]_2,{\mathsf {basis}}({\mathbf {B}}_2^{\parallel }),{\mathsf {basis}}({\mathbf {B}}_1^{\parallel },{\mathbf {B}}_3^{\parallel })\), it holds that 
In the reduction, we sample \(\alpha \leftarrow {\mathbb {Z}}_p\), \({\mathbf {w}}_1,\ldots ,{\mathbf {w}}_n \leftarrow {\mathbb {Z}}_p^{1\times (2k+1)}\) and pick
$$\begin{aligned} {\mathbf {u}}^{(13)} \leftarrow \mathsf {span}(({\mathbf {B}}_1^{\parallel }|{\mathbf {B}}_3^{\parallel })^{\top }) \quad \text{ and }\quad {\mathbf {u}}^{(2)} \leftarrow \mathsf {span}({{\mathbf {B}}_2^{\parallel }}^{\top }) \end{aligned}$$using \({\mathsf {basis}}({\mathbf {B}}_1^{\parallel },{\mathbf {B}}_3^{\parallel })\) and \({\mathsf {basis}}({\mathbf {B}}_2^{\parallel })\), respectively. The challenge ciphertext is generated using
$$\begin{aligned} \{\, x_{i,b} \cdot {\mathbf {u}}^{(13)} + x_{i,1-b} \cdot {\mathbf {u}}^{(2)} + {\mathbf {w}}_i\, \}_{i\in [n]}; \end{aligned}$$the jth secret key is created from \({\mathbf {w}}_1,\ldots ,{\mathbf {w}}_n\) and \([{\mathbf {t}}]_2\) while the remaining keys can be generated using \([{\mathbf {B}}_1]_2\) and \([{\mathbf {B}}_2]_2\) along with \(\alpha ,{\mathbf {w}}_1,\ldots ,{\mathbf {w}}_n\). See Lemma 7 for more details.
-
\({\mathsf {Game}}_{2.j-1.2}\) is identical to \({\mathsf {Game}}_{2.j-1.1}\) except that the challenge ciphertext is
$$\begin{aligned} \{\,x_{i,b} \cdot {\mathbf {u}}^{(1)} + x_{i,1-b} \cdot {\mathbf {u}}^{(2)} + \boxed {x_{i,1-b} \cdot {\mathbf {u}}^{(3)}} + {\mathbf {w}}_i\,\}_{i\in [n]}, [\alpha ]_2 \cdot m_0. \end{aligned}$$We claim that \({\mathsf {Game}}_{2.j-1.2} \equiv {\mathsf {Game}}_{2.j-1.1}\). This follows from facts that: (1) \({\mathbf {u}}^{(3)}\) and \({\mathbf {w}}_i^{(3)}\) are only revealed from the challenge ciphertext and the jth secret key; (2) for all \({\mathbf {x}}_0\), \({\mathbf {x}}_1\) and \({\mathbf {y}}\) with the restriction that (a) \(\langle {\mathbf {x}}_0,{\mathbf {y}}\rangle = \langle {\mathbf {x}}_1,{\mathbf {y}}\rangle = 0\); or (b) \(\langle {\mathbf {x}}_0,{\mathbf {y}}\rangle \ne 0 \wedge \langle {\mathbf {x}}_1,{\mathbf {y}}\rangle \ne 0\), it holds that
$$\begin{aligned} \begin{array}{cl} &{} (\,\overbrace{x_{1,b} \cdot {\mathbf {u}}^{(3)} + {\mathbf {w}}_1^{(3)},\ldots ,x_{n,b} \cdot {\mathbf {u}}^{(3)} + {\mathbf {w}}_n^{(3)}}^{{\mathsf {ct}}},\,\overbrace{y_1 \cdot {\mathbf {w}}_1^{(3)} + \cdots + y_n \cdot {\mathbf {w}}_n^{(3)}}^{\mathsf {sk}}\,)\\ \equiv &{} (\boxed {x_{1,1-b} \cdot {\mathbf {u}}^{(3)}} + {\mathbf {w}}_1^{(3)},\ldots ,\boxed {x_{n,1-b} \cdot {\mathbf {u}}^{(3)}} + {\mathbf {w}}_n^{(3)},\,y_1 \cdot {\mathbf {w}}_1^{(3)} + \cdots + y_n \cdot {\mathbf {w}}_n^{(3)}).\\ \end{array} \end{aligned}$$See Lemma 8 for more details.
-
\({\mathsf {Game}}_{2.j-1.3}\) is identical to \({\mathsf {Game}}_{2.j-1.2}\) except that the jth secret key is
$$\begin{aligned}{}[\alpha + (y_1 \cdot {\mathbf {w}}_1 + \cdots + y_n \cdot {\mathbf {w}}_n) {\mathbf {d}}]_2,\ [{\mathbf {d}}]_2 \quad \text{ where } \quad \boxed {{\mathbf {d}}\leftarrow \mathsf {span}({\mathbf {B}}_1,{\mathbf {B}}_2,{\mathbf {B}}_3)}. \end{aligned}$$We claim that
 . This follows from the \(\textsc {sd}^{G_2}_{{\mathbf {B}}_{3} \mapsto {\mathbf {B}}_{3},{\mathbf {B}}_{2}}\) assumption: given \([{\mathbf {B}}_1]_2,[{\mathbf {B}}_2]_2,[{\mathbf {B}}_3]_2,{\mathsf {basis}}({\mathbf {B}}_1^{\parallel }),{\mathsf {basis}}({\mathbf {B}}_2^{\parallel },{\mathbf {B}}_3^{\parallel })\), it holds that
. This follows from the \(\textsc {sd}^{G_2}_{{\mathbf {B}}_{3} \mapsto {\mathbf {B}}_{3},{\mathbf {B}}_{2}}\) assumption: given \([{\mathbf {B}}_1]_2,[{\mathbf {B}}_2]_2,[{\mathbf {B}}_3]_2,{\mathsf {basis}}({\mathbf {B}}_1^{\parallel }),{\mathsf {basis}}({\mathbf {B}}_2^{\parallel },{\mathbf {B}}_3^{\parallel })\), it holds that 
In the reduction, we sample \(\alpha \leftarrow {\mathbb {Z}}_p\), \({\mathbf {w}}_1,\ldots ,{\mathbf {w}}_n\leftarrow {\mathbb {Z}}_p^{1\times (2k+1)}\) and pick
$$\begin{aligned} {\mathbf {u}}^{(1)} \leftarrow \mathsf {span}({{\mathbf {B}}_1^{\parallel }}^{\top }) \quad \text{ and }\quad {\mathbf {u}}^{(23)} \leftarrow \mathsf {span}(({\mathbf {B}}_2^{\parallel }|{\mathbf {B}}_3^{\parallel })^{\top }) \end{aligned}$$using \({\mathsf {basis}}({\mathbf {B}}_1^{\parallel })\) and \({\mathsf {basis}}({\mathbf {B}}_2^{\parallel },{\mathbf {B}}_3^{\parallel })\), respectively. The challenge ciphertext is generated using
$$\begin{aligned} \{\, x_{i,b} \cdot {\mathbf {u}}^{(1)} + x_{i,1-b} \cdot {\mathbf {u}}^{(23)} + {\mathbf {w}}_i \,\}_{i \in [n]} \end{aligned}$$the jth secret key is created from \(\alpha ,{\mathbf {w}}_1,\ldots ,{\mathbf {w}}_n\) and \([{\mathbf {B}}_1]\), \([{\mathbf {t}}]_2\) while the remaining keys can be generated using \([{\mathbf {B}}_1,{\mathbf {B}}_2]_2\) along with \(\alpha ,{\mathbf {w}}_1,\ldots ,{\mathbf {w}}_n\). See Lemma 9 for more details.
-
\({\mathsf {Game}}_{2.j-1.4}\) is identical to \({\mathsf {Game}}_{2.j-1.3}\) except that the challenge ciphertext is
$$\begin{aligned} \{\,x_{i,b} \cdot {\mathbf {u}}^{(1)} + x_{i,1-b} \cdot {\mathbf {u}}^{(2)} + \boxed {x_{i,b} \cdot {\mathbf {u}}^{(3)}} + {\mathbf {w}}_i\,\}_{i\in [n]}, [\alpha ]_2 \cdot m_0. \end{aligned}$$We claim that \({\mathsf {Game}}_{2.j-1.4} \equiv {\mathsf {Game}}_{2.j-1.3}\). The proof is identical to that for \({\mathsf {Game}}_{2.j-1.2} \equiv {\mathsf {Game}}_{2.j-1.1}\). See Lemma 10 for more details.
-
\({\mathsf {Game}}_{2.j-1.5}\) is identical to \({\mathsf {Game}}_{2.j-1.4}\) except that the jth secret key is
$$\begin{aligned}{}[\alpha + (y_1 \cdot {\mathbf {w}}_1 + \cdots + y_n \cdot {\mathbf {w}}_n) {\mathbf {d}}]_2,\ [{\mathbf {d}}]_2 \quad \text{ where } \quad \boxed {{\mathbf {d}}\leftarrow \mathsf {span}({\mathbf {B}}_1,{\mathbf {B}}_2)}. \end{aligned}$$We claim that
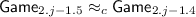 . The proof is identical to that for
. The proof is identical to that for  . See Lemma 11 for more details. Note that \({\mathsf {Game}}_{2.j-1.5} = {\mathsf {Game}}_{2.j}\).
. See Lemma 11 for more details. Note that \({\mathsf {Game}}_{2.j-1.5} = {\mathsf {Game}}_{2.j}\).
3.4 Step Two: From Private-Key to Public-Key
We describe our prime-order full-fledged IPE, which is derived from our private-key IPE in Sect. 3.2 via the “private-key to public-key” compiler [36].
-
\(\mathsf {Setup}(1^\lambda ,n)\): Run \({\mathbb {G}}= (p,G_1,G_2,G_T,e) \leftarrow {\mathcal {G}}(1^\lambda )\). Sample \( {\mathbf {A}}\leftarrow {\mathbb {Z}}_p^{(k+1) \times k}\), \({\mathbf {B}}_1 \leftarrow {\mathbb {Z}}_p^{(2k+1) \times k} \) and pick
$$\begin{aligned} {\mathbf {U}},{\mathbf {W}}_1,\ldots ,{\mathbf {W}}_n \leftarrow {\mathbb {Z}}_p^{(k+1) \times (2k+1)} \quad \text{ and }\quad {\mathbf {k}}\leftarrow {\mathbb {Z}}_p^{k+1}. \end{aligned}$$Output
$$\begin{aligned} \begin{array}{rcl} {\textsf {mpk}} &{} = &{} (\,{\mathbb {G}},[{\mathbf {A}}^{\top }]_1, [{\mathbf {A}}^{\top }{\mathbf {U}}]_1,[{\mathbf {A}}^{\top }{\mathbf {W}}_1]_1,\ldots ,[{\mathbf {A}}^{\top }{\mathbf {W}}_n]_1,[{\mathbf {A}}^{\top }{\mathbf {k}}]_T\,)\\ {\textsf {msk}} &{} = &{} (\,{\mathbf {k}},{\mathbf {W}}_1,\ldots ,{\mathbf {W}}_n,{\mathbf {B}}_1\,). \end{array} \end{aligned}$$ -
\({\mathsf {KeyGen}}({\textsf {msk}},{\mathbf {y}})\): Let \({\mathbf {y}}= (y_1,\ldots ,y_n) \in {\mathbb {Z}}_p^n\). Sample \({\mathbf {r}}\leftarrow {\mathbb {Z}}_p^k\) and output
$$\begin{aligned} \mathsf {sk}_{\mathbf {y}}=(\, K_0 = [{\mathbf {k}}+ (y_1 \cdot {\mathbf {W}}_1 + \cdots + y_n \cdot {\mathbf {W}}_n) {\mathbf {B}}_1{\mathbf {r}}]_2, K_1 = [{\mathbf {B}}_1{\mathbf {r}}]_2 \,) \end{aligned}$$ -
\({\mathsf {Enc}}({\textsf {mpk}},{\mathbf {x}},m)\): Let \({\mathbf {x}}= (x_1,\ldots ,x_n) \in {\mathbb {Z}}_p^n\) and \(m \in G_T\). Sample \({\mathbf {s}}\leftarrow {\mathbb {Z}}_p^k\) and output
$$\begin{aligned} {\mathsf {ct}}_{\mathbf {x}}= (\, C_0 = [{\mathbf {s}}^{\top }{\mathbf {A}}^{\top }]_1, \{\,C_i = [{\mathbf {s}}^{\top }{\mathbf {A}}^{\top }(x_i \cdot {\mathbf {U}}+ {\mathbf {W}}_i)]_1\,\}_{i\in [n]}, C = [{\mathbf {s}}^{\top }{\mathbf {A}}^{\top }{\mathbf {k}}]_T \cdot m \,) \end{aligned}$$ -
\({\mathsf {Dec}}({\mathsf {ct}}_{\mathbf {x}},\mathsf {sk}_{\mathbf {y}})\): Parse \({\mathsf {ct}}_{\mathbf {x}}= (C_0,C_1,\ldots ,C_n,C)\) and \(\mathsf {sk}_{\mathbf {y}}= (K_0,K_1)\) for \({\mathbf {y}}= (y_1,\ldots ,y_n)\). Output
$$\begin{aligned} m' = C \cdot e(y_1 \odot C_1 \cdots y_n \odot C_n ,K_1) \cdot e(C_0,K_0)^{-1}. \end{aligned}$$
The correctness is straightforward.
Security. We will prove the following theorem.
Theorem 2
Under the \(k\textsc {-lin}\) assumption, the IPE scheme described above is adaptively secure and fully attribute-hiding (cf. Sect. 2.1).
For the same reason as in Sect. 3.3, we prove the lemma for the \(m_0=m_1\), which shows that the security of the IPE described above is implied by that of our private-key IPE in Sect. 3.2 and the \(\textsc {mddh}_{k} \) assumption.
Lemma 3
For any adversary \({\mathcal {A}}\) that makes at most Q key queries and outputs \(m_0 = m_1\), there exists adversaries \({\mathcal {B}}_0,{\mathcal {B}}\) such that
and \({\mathsf {Time}}({\mathcal {B}}_0),{\mathsf {Time}}({\mathcal {B}}) \approx {\mathsf {Time}}({\mathcal {A}})\).
We prove Lemma 3 via the following game sequence.
-
\({\mathsf {Game}}_0\) is the real game in which the challenge ciphertext for \({\mathbf {x}}_b = (x_{1,b},\ldots ,x_{n,b})\) is of the form
$$\begin{aligned}{}[{\mathbf {c}}^{\top }]_1, [{\mathbf {c}}^{\top }(x_{1,b} \cdot {\mathbf {U}}+ {\mathbf {W}}_1)]_1,\,\ldots ,\, [{\mathbf {c}}^{\top }(x_{n,b} \cdot {\mathbf {U}}+ {\mathbf {W}}_n)]_1, e([{\mathbf {c}}^{\top }]_1,[{\mathbf {k}}]_2) \cdot m_0 \end{aligned}$$where \({\mathbf {c}}\leftarrow \mathsf {span}({\mathbf {A}})\). Here \(b \leftarrow \{0,1\}\) is a secret bit.
-
\({\mathsf {Game}}_1\) is identical to \({\mathsf {Game}}_0\) except that we pick \( {\mathbf {c}}\leftarrow {\mathbb {Z}}_p^{k+1}\) when generating the challenge ciphertext. We claim that
 . This follows from the \(\textsc {mddh}_{k} \) assumption:
. This follows from the \(\textsc {mddh}_{k} \) assumption: 
In the reduction, we sample \({\mathbf {k}},{\mathbf {U}},{\mathbf {W}}_1,\ldots ,{\mathbf {W}}_n\) and \({\mathbf {B}}_1\). The master public key \({\textsf {mpk}}\) and the challenge ciphertext are simulated using \({\mathbf {k}},{\mathbf {U}},{\mathbf {W}}_1,\ldots ,{\mathbf {W}}_n\) along with \([{\mathbf {A}}]_1\), \([{\mathbf {c}}]_1\); all secret keys can be created honestly. See Lemma 12 for details.
It remains to show that the advantage in guessing \(b \in \{0,1\}\) in \({\mathsf {Game}}_1\) is negligible. This follows from the security of our private-key IPE in Sect. 3.2. For \({\mathbf {A}}\) and \({\mathbf {c}}\), define

We can then rewrite \({\textsf {mpk}}\) as

the challenge ciphertext (in \({\mathsf {Game}}_1\)) becomes
Assume that \(({\mathbf {A}}|{\mathbf {c}})\) is full-rank which occurs with high probability and define  , we have
, we have  and
and  , a secret key can be rewritten as
, a secret key can be rewritten as
Observe that the underlined parts are exactly the ciphertext and secret keys of our private-key IPE in Sect. 3.2; and \((\widetilde{\mathbf {U}},\widetilde{\mathbf {W}}_i,\widetilde{\mathbf {k}})\), \(({\mathbf {u}},{\mathbf {w}}_i,\alpha )\) are distributed uniformly and independently. This means we can simulate \({\textsf {mpk}}\) honestly and transform a ciphertext/secret key from our private-key IPE to its public-key counterpart using \({\mathbf {A}}\), \({\mathbf {c}}\), \(\widetilde{\mathbf {U}}\), \(\widetilde{\mathbf {W}}_i\), \(\widetilde{\mathbf {k}}\). This is sufficient for the reduction from the public-key IPE to private-key IPE. See Lemma 13 for more details.
3.5 Lemmas for Private-Key IPE
Let \({\mathsf {Adv}}_x\) be the advantage function with respect to \({\mathcal {A}}\) in \({\mathsf {Game}}_x\). We prove the following lemma for the game sequence in Sect. 3.3.
Lemma 4
( \({\mathsf {Game}}_0 \equiv {\mathsf {Game}}_1\) ). \( {\mathsf {Adv}}_0(\lambda ) = {\mathsf {Adv}}_1(\lambda ). \)
Proof
It is sufficient to prove that, for all \({\mathbf {u}}\leftarrow {\mathbb {Z}}_p^{1 \times (2k+1)}\), it holds that
when \({\mathbf {w}}_1,\ldots ,{\mathbf {w}}_n \leftarrow {\mathbb {Z}}_p^{1 \times (2k+1)}\). By the facts shown in Sect. 3.1, it is implied by the statement that, for all \({\mathbf {u}}^{(2)} \in \mathsf {span}({{\mathbf {B}}_2^{\parallel }}^{\top })\), it holds that
when \({\mathbf {w}}_1^{(2)},\ldots ,{\mathbf {w}}_n^{(2)} \leftarrow \mathsf {span}({{\mathbf {B}}_2^{\parallel }}^{\top })\). This completes the proof. \(\square \)
Lemma 5
( \({\mathsf {Game}}_{2.q} \equiv {\mathsf {Game}}_3\) ). \( {\mathsf {Adv}}_{2.q}(\lambda ) = {\mathsf {Adv}}_3(\lambda ). \)
Proof
We simulate \({\mathsf {Game}}_{2.q}\) as follows:
-
Setup. We alternatively prepare basis \((\,{\mathbf {B}}_1,{\mathbf {B}}_2,{\mathbf {B}}_3\,)\) as follows: Sample \(\widetilde{\mathbf {B}}_1,{\mathbf {B}}_3\leftarrow {\mathbb {Z}}_p^{(2k+1) \times k},\widetilde{\mathbf {B}}_2\leftarrow {\mathbb {Z}}_p^{2k+1}\) and compute dual basis \(\widetilde{\mathbf {B}}_1^{\parallel },\widetilde{\mathbf {B}}_2^{\parallel },{\mathbf {B}}_3^{\parallel }\) as usual. Pick \({\mathbf {R}}\leftarrow \text {GL}_{k+1}({\mathbb {Z}}_p)\) and define
$$\begin{aligned} ({\mathbf {B}}_1|{\mathbf {B}}_2) = (\widetilde{\mathbf {B}}_1|\widetilde{\mathbf {B}}_2){\mathbf {R}}\quad \text{ and }\quad ({\mathbf {B}}_1^{\parallel }|{\mathbf {B}}_2^{\parallel }) = (\widetilde{\mathbf {B}}_1^{\parallel }|\widetilde{\mathbf {B}}_2^{\parallel }){\mathbf {R}}^*. \end{aligned}$$This does not change the distribution of basis. We then sample \(\alpha ,{\mathbf {u}},{\mathbf {w}}_1,\ldots ,{\mathbf {w}}_n\) honestly.
-
Key queries. On input \({\mathbf {y}}= (y_1,\ldots ,y_n)\), output
$$\begin{aligned}{}[\alpha + (y_1\cdot {\mathbf {w}}_1+\cdots +y_n\cdot {\mathbf {w}}_n) {\mathbf {d}}]_2,\,[{\mathbf {d}}]_2 \quad \text{ where } \quad {\mathbf {d}}\leftarrow \mathsf {span}(\widetilde{\mathbf {B}}_1,\widetilde{\mathbf {B}}_2). \end{aligned}$$Although we sample \({\mathbf {d}}\) using \(\widetilde{\mathbf {B}}_1,\widetilde{\mathbf {B}}_2\), the vector is uniformly distributed over \(\mathsf {span}({\mathbf {B}}_1,{\mathbf {B}}_2)\) as required and our simulation is perfect.
-
Ciphertext. On input \(({\mathbf {x}}_0,{\mathbf {x}}_1,m_0,m_1)\) with \(m_0=m_1\), we create the challenge ciphertext honestly using \(({\mathbf {B}}_1^{\parallel },{\mathbf {B}}_2^{\parallel },{\mathbf {B}}_3^{\parallel })\). That is, we pick \(b\leftarrow \{0,1\}\) and output
$$\begin{aligned} \{\,x_{i,b} \cdot {\mathbf {v}}_0 + x_{i,1-b} \cdot {\mathbf {v}}_1 + x_{i,b} \cdot {\mathbf {u}}^{(3)} + {\mathbf {w}}_i\,\}_{i \in [n]},\,[\alpha ]_2 \cdot m_0 \end{aligned}$$where \({\mathbf {u}}^{(3)} \leftarrow \mathsf {span}({{\mathbf {B}}_3^{\parallel }}^{\top })\) and
$$\begin{aligned} {\mathbf {v}}_0 = {\mathbf {u}}^{(1)} \leftarrow \mathsf {span}({{\mathbf {B}}^{\parallel }_1}^{\top }) \quad \text{ and }\quad {\mathbf {v}}_1 = {\mathbf {u}}^{(2)} \leftarrow \mathsf {span}({{\mathbf {B}}^{\parallel }_2}^{\top }). \end{aligned}$$
Observe that, we have a 2-by-\((k+1)\) matrix \({\mathbf {V}}\) of rank 2 such that

Since \({\mathbf {R}}\) is independent of other part of simulation, \({\mathbf {V}}{\mathbf {R}}^{-1}\) are uniformly distributed over \({\mathbb {Z}}_p^{2 \times (k+1)}\) and thus it is equivalent to sample \({\mathbf {v}}_0,{\mathbf {v}}_1 \leftarrow \mathsf {span}((\widetilde{\mathbf {B}}^{\parallel }_1|\widetilde{\mathbf {B}}^{\parallel }_2)^{\top })\) when creating the challenge ciphertext. This leads to the simulation of \({\mathsf {Game}}_3\) (with respect to \(\widetilde{\mathbf {B}}_1,\widetilde{\mathbf {B}}_2,{\mathbf {B}}_3\)). \(\square \)
Lemma 6
( \({\mathsf {Game}}_3 \equiv {\mathsf {Game}}_4\) ). \( {\mathsf {Adv}}_3(\lambda ) = {\mathsf {Adv}}_4(\lambda ). \)
Proof
The proof is similar to that for Lemma 4, except that we work with \({\mathbf {u}}^{(3)}\), \({\mathbf {u}}_0^{(3)}\), \({\mathbf {u}}_1^{(3)}\), \({\mathbf {w}}_i^{(3)}\) instead. \(\square \)
Lemma 7
(  ). There exists adversary \({\mathcal {B}}_1\) with \({\mathsf {Time}}({\mathcal {B}}_1)\approx {\mathsf {Time}}({\mathcal {A}})\) such that
). There exists adversary \({\mathcal {B}}_1\) with \({\mathsf {Time}}({\mathcal {B}}_1)\approx {\mathsf {Time}}({\mathcal {A}})\) such that
Proof
This follows from the \(\textsc {sd}^{G_2}_{{\mathbf {B}}_{1} \mapsto {\mathbf {B}}_{1},{\mathbf {B}}_{3}}\) assumption stating that, given \([{\mathbf {B}}_1]_2,[{\mathbf {B}}_2]_2\), \([{\mathbf {B}}_3]_2,{\mathsf {basis}}({\mathbf {B}}_2^{\parallel }),{\mathsf {basis}}({\mathbf {B}}_1^{\parallel },{\mathbf {B}}_3^{\parallel })\), it holds that

On input \([{\mathbf {B}}_1]_2,[{\mathbf {B}}_2]_2,[{\mathbf {B}}_3]_2,{\mathsf {basis}}({\mathbf {B}}_2^{\parallel }),{\mathsf {basis}}({\mathbf {B}}_1^{\parallel },{\mathbf {B}}_3^{\parallel })\) and \([{\mathbf {t}}]_2\), the adversary \({\mathcal {B}}_1\) works as follows:
-
Setup. Sample \(\alpha \leftarrow {\mathbb {Z}}_p\), \({\mathbf {w}}_1,\ldots ,{\mathbf {w}}_n \leftarrow {\mathbb {Z}}_p^{1\times (2k+1)}\). Implicitly sample \({\mathbf {u}}\) by picking
$$\begin{aligned} {\mathbf {u}}^{(13)} \leftarrow \mathsf {span}(({\mathbf {B}}_1^{\parallel }|{\mathbf {B}}_3^{\parallel })^{\top }) \quad \text{ and }\quad {\mathbf {u}}^{(2)} \leftarrow \mathsf {span}({{\mathbf {B}}_2^{\parallel }}^{\top }) \end{aligned}$$using \({\mathsf {basis}}({\mathbf {B}}_1^{\parallel },{\mathbf {B}}_3^{\parallel })\) and \({\mathsf {basis}}({\mathbf {B}}_2^{\parallel })\), respectively.
-
Key Queries. On the \(\kappa \)th query \({\mathbf {y}}= (y_1,\ldots ,y_n)\), output
$$\begin{aligned}{}[\alpha + (y_1 \cdot {\mathbf {w}}_1 + \cdots + y_n \cdot {\mathbf {w}}_n) {\mathbf {d}}]_2, [{\mathbf {d}}]_2 \quad \text{ where } \quad {\mathbf {d}}\leftarrow \left\{ \begin{array}{ll} \mathsf {span}({\mathbf {B}}_1,{\mathbf {B}}_2) &{} \kappa < j; \\ {\mathbf {t}}&{} \kappa = j; \\ \mathsf {span}({\mathbf {B}}_1) &{} \kappa > j; \\ \end{array} \right. \end{aligned}$$using \([{\mathbf {B}}_1]_2\), \([{\mathbf {B}}_2]_2\) and \([{\mathbf {t}}]_2\)
-
Ciphertext. On input \(({\mathbf {x}}_0,{\mathbf {x}}_1,m_0,m_1)\) with \(m_0 = m_1\), pick \(b \leftarrow \{0,1\}\) and output
$$\begin{aligned} x_{1,b} \cdot {\mathbf {u}}^{(13)} + x_{1,1-b} \cdot {\mathbf {u}}^{(2)} + {\mathbf {w}}_1,\,\ldots ,\, x_{n,b} \cdot {\mathbf {u}}^{(13)} + x_{n,1-b} \cdot {\mathbf {u}}^{(2)} + {\mathbf {w}}_n,\,[\alpha ]_2 \cdot m_0. \end{aligned}$$
Observe that, when \({\mathbf {t}}\) is uniformly distributed over \(\mathsf {span}({\mathbf {B}}_1)\), the simulation is identical to \({\mathsf {Game}}_{2.j-1}\); otherwise, when \({\mathbf {t}}\) is uniformly distributed over \(\mathsf {span}({\mathbf {B}}_1,{\mathbf {B}}_3)\), the simulation is identical to \({\mathsf {Game}}_{2.j-1.1}\). This proves the lemma. \(\square \)
Lemma 8
(\({\mathsf {Game}}_{2.j-1.1} \equiv {\mathsf {Game}}_{2.j-1.2}\)). \({\mathsf {Adv}}_{2.j-1.1} = {\mathsf {Adv}}_{2.j-1.2}\).
Proof
By complexity leveraging and the facts shown in Sect. 3.1, it is sufficient to prove the following statement: for all \({\mathbf {x}}_0\), \({\mathbf {x}}_1\) and \({\mathbf {y}}\) (corresponding to the jth key query) satisfying that (a) \(\langle {\mathbf {x}}_0,{\mathbf {y}}\rangle = \langle {\mathbf {x}}_1,{\mathbf {y}}\rangle = 0\); or (b) \(\langle {\mathbf {x}}_0,{\mathbf {y}}\rangle \ne 0 \wedge \langle {\mathbf {x}}_1,{\mathbf {y}}\rangle \ne 0\), it holds that
when \({\mathbf {u}}^{(3)}, {\mathbf {w}}_1^{(3)},\ldots ,{\mathbf {w}}_n^{(3)} \leftarrow \mathsf {span}({{\mathbf {B}}_3^{\parallel }}^{\top })\). By the linearity, it in turn follows from the following statement
where \(u,w_1,\ldots ,w_n \leftarrow {\mathbb {Z}}_p\). This follows from the statistical argument for all \({\mathbf {x}}= (x_1,\ldots ,x_n)\) which is implicitly used in the proof of Wee’s simulation-based selectively secure IPE [36]: by programming \(\tilde{w}_i = x_i \cdot u + w_i\) for all \(i \in [n]\), we have
which means that the left-hand side distributions for all vector \({\mathbf {x}}\) not orthogonal to \({\mathbf {y}}\) are identical (since u hides the information about the inner-product) and so do all vector \({\mathbf {x}}\) orthogonal to \({\mathbf {y}}\). This proves the above statement and thus proves the lemma. \(\square \)
Lemma 9
(  ). There exists adversary \({\mathcal {B}}_2\) with \({\mathsf {Time}}({\mathcal {B}}_2)\approx {\mathsf {Time}}({\mathcal {A}})\) such that
). There exists adversary \({\mathcal {B}}_2\) with \({\mathsf {Time}}({\mathcal {B}}_2)\approx {\mathsf {Time}}({\mathcal {A}})\) such that
Proof
The proof is analogous to that for Lemma 7 ( ). \(\square \)
). \(\square \)
Lemma 10
(\({\mathsf {Game}}_{2.j-1.3} \equiv {\mathsf {Game}}_{2.j-1.4}\)). \({\mathsf {Adv}}_{2.j-1.3} = {\mathsf {Adv}}_{2.j-1.4}\).
Proof
The proof is identical to that for Lemma 8 ( ). \(\square \)
). \(\square \)
Lemma 11
(  ). There exists adversary \({\mathcal {B}}_3\) with \({\mathsf {Time}}({\mathcal {B}}_3)\approx {\mathsf {Time}}({\mathcal {A}})\) such that
). There exists adversary \({\mathcal {B}}_3\) with \({\mathsf {Time}}({\mathcal {B}}_3)\approx {\mathsf {Time}}({\mathcal {A}})\) such that
Proof
The proof is analogous to that for Lemma 7 ( ). \(\square \)
). \(\square \)
3.6 Lemmas for Public-Key IPE
Let \({\mathsf {Adv}}_x\) be the advantage function with respect to \({\mathcal {A}}\) in \({\mathsf {Game}}_x\). We prove the following lemma for the game sequence in Sect. 3.4.
Lemma 12
(\({\mathsf {Game}}_0 \equiv {\mathsf {Game}}_1\)). There exists adversary \({\mathcal {B}}_0\) with \({\mathsf {Time}}({\mathcal {B}}_0)\approx {\mathsf {Time}}({\mathcal {A}})\) such that
Proof
The proof is direct, we omit it here and refer the reader to the full paper. \(\square \)
Lemma 13
(Advantage in \({\mathsf {Game}}_1\)). There exists adversary \({\mathcal {B}}\) with \({\mathsf {Time}}({\mathcal {B}})\approx {\mathsf {Time}}({\mathcal {A}})\) such that
Proof
We construct the adversary \({\mathcal {B}}\) as below:
-
Setup. Sample \(({\mathbf {A}},{\mathbf {c}}) \leftarrow {\mathbb {Z}}_p^{(k+1) \times k}\times {\mathbb {Z}}_p^{k+1}\) and compute \({\mathbf {T}}= \left( {\begin{matrix} {\mathbf {A}}^{\top }\\ {\mathbf {c}}^{\top }\end{matrix}}\right) ^{-1}\). Since \(({\mathbf {A}}|{\mathbf {c}})\) is full-rank which occurs with high probability, \({\mathbf {T}}\) is well-defined. Pick
$$\begin{aligned} \widetilde{\mathbf {U}},\widetilde{\mathbf {W}}_1,\ldots ,\widetilde{\mathbf {W}}_n \leftarrow {\mathbb {Z}}_p^{k \times (2k+1)} \quad \text{ and }\quad \widetilde{\mathbf {k}}\leftarrow {\mathbb {Z}}_p^{k} \end{aligned}$$and output
$$\begin{aligned} \textsf {mpk} = (\,[{\mathbf {A}}^{\top }]_1, [\widetilde{\mathbf {U}}]_1,[\widetilde{\mathbf {W}}_1]_1, \ldots , [\widetilde{\mathbf {W}}_n]_1, [\widetilde{\mathbf {k}}]_T\,). \end{aligned}$$ -
Key Queries. On input \({\mathbf {y}}\), adversary \({\mathcal {B}}\) forwards the query to its environment and receives \((K_0,K_1)\). Compute
$$\begin{aligned} \widetilde{K}_0 = [\widetilde{\mathbf {k}}]_2 \cdot ( (y_1 \cdot \widetilde{\mathbf {W}}_1 + \cdots + y_n \cdot \widetilde{\mathbf {W}}_n) \odot K_0 ) \end{aligned}$$and output

-
Ciphertext. On input \(({\mathbf {x}}_0,{\mathbf {x}}_1,m_0,m_1)\), adversary \({\mathcal {B}}\) sends query \(({\mathbf {x}}_0,{\mathbf {x}}_1,1,1)\) to its environment and receives \((C_1,\ldots ,C_n,C)\). Create the challenge ciphertext as
$$\begin{aligned}{}[{\mathbf {c}}^{\top }]_1, [C_1]_1,\,\ldots ,\, [C_n\,]_1, e([1]_1,C) \cdot m_0. \end{aligned}$$
The adversary \({\mathcal {B}}\) outputs \({\mathcal {A}}\)’s guess bit. By the observation in Sect. 3.4, \(\textsf {mpk}\) is simulated perfectly; if \((K_0,K_1)\) is a private-key IPE secret key, secret keys we computed is for our public-key IPE; if \((C_1,\ldots ,C_n,C)\) is a private-key IPE ciphertext for \(b=0\), the ciphertext we created is a public-key IPE ciphertext for \(b=0\); this also holds for \(b=1\). This readily proves the lemma. \(\square \)
4 Construction from \({\textsc {xdlin}}\) Assumption
In this section, we improve the IPE scheme presented in Sect. 3 by the optimization technique in [16]. As in Sect. 3, we will first develop a private-key IPE from that in Sect. 3.2 and then compile it into the public-key setting.
4.1 Correspondence
Applying the technique in [16] to our private-key IPE in Sect. 3.2, we basically overlap \(\mathsf {span}({\mathbf {B}}_1)\) and \(\mathsf {span}({\mathbf {B}}_3)\) so that the total dimension decreases. Technically, we work with basis
where \(\ell _1,\ell _2,\ell _3,\ell _4 \ge 1\) and \(\ell := \ell _1 + \ell _2 + \ell _3 + \ell _4\), and follow the correspondence:
saying that \({\mathbf {B}}_1\) and \({\mathbf {B}}_3\) used in Sect. 3 are replaced by \(({\mathbf {B}}_1|{\mathbf {B}}_4)\) and \(({\mathbf {B}}_3|{\mathbf {B}}_4)\), respectively, whose spans interact at \(\mathsf {span}({\mathbf {B}}_4)\). Analogous to Sect. 3.1, we can define its dual basis \(({\mathbf {B}}_1^{\parallel },{\mathbf {B}}_2^{\parallel },{\mathbf {B}}_3^{\parallel },{\mathbf {B}}_4^{\parallel })\) and decompose \({\mathbf {w}}\in {\mathbb {Z}}_p^{1\times \ell }\) as \({\mathbf {w}}^{(1)} + {\mathbf {w}}^{(2)} + {\mathbf {w}}^{(3)} + {\mathbf {w}}^{(4)}\).
Assumptions. With the correspondence (10), the assumption \(\textsc {sd}^{G_2}_{{\mathbf {B}}_{1} \mapsto {\mathbf {B}}_{1},{\mathbf {B}}_{3}}\) used in Sect. 3.3 will be replaced by \(\textsc {sd}^{G_2}_{{\mathbf {B}}_{1},{\mathbf {B}}_{4} \mapsto {\mathbf {B}}_{1},{\mathbf {B}}_{3},{\mathbf {B}}_{4}}\) defined as follows.
Lemma 14
(  ). Under \(\textsc {mddh}_{\ell _1+\ell _4,\ell _1+\ell _3+\ell _4} \) assumption in \(G_2\), there exists an efficient sampler outputting random \(([{\mathbf {B}}_1]_2,\,[{\mathbf {B}}_2]_2,\) \([{\mathbf {B}}_3]_2,\,[{\mathbf {B}}_4]_2)\) along with base \({\mathsf {basis}}({\mathbf {B}}^{\parallel }_2)\) and \({\mathsf {basis}}({\mathbf {B}}_1^{\parallel },{\mathbf {B}}_3^{\parallel },{\mathbf {B}}_4^{\parallel })\) (of arbitrary choice) such that the following advantage function is negligible in \(\lambda \).
). Under \(\textsc {mddh}_{\ell _1+\ell _4,\ell _1+\ell _3+\ell _4} \) assumption in \(G_2\), there exists an efficient sampler outputting random \(([{\mathbf {B}}_1]_2,\,[{\mathbf {B}}_2]_2,\) \([{\mathbf {B}}_3]_2,\,[{\mathbf {B}}_4]_2)\) along with base \({\mathsf {basis}}({\mathbf {B}}^{\parallel }_2)\) and \({\mathsf {basis}}({\mathbf {B}}_1^{\parallel },{\mathbf {B}}_3^{\parallel },{\mathbf {B}}_4^{\parallel })\) (of arbitrary choice) such that the following advantage function is negligible in \(\lambda \).

where
The proof is analogous to that for Lemma 1 (cf. [13]).
Also, we replace \({\textsc {sd}}^{G_2}_{{\mathbf {B}}_{3} \mapsto {\mathbf {B}}_{2},{\mathbf {B}}_{3}}\) assumption in Sect. 3.3 with external subspace decision assumption \(\textsc {xsd}^{G_2}_{{\mathbf {B}}_{3},{\mathbf {B}}_{4} \mapsto {\mathbf {B}}_{2},{\mathbf {B}}_{3},{\mathbf {B}}_{4}}\) defined as below.
Assumption 3
(  ). We say that \(\textsc {xsd}^{G_2}_{{\mathbf {B}}_{3}, {\mathbf {B}}_{4} \mapsto {\mathbf {B}}_{2},{\mathbf {B}}_{3},{\mathbf {B}}_{4}}\) assumption holds if there exists an efficient sampler outputting random \(([{\mathbf {B}}_1]_2,[{\mathbf {B}}_2]_2,[{\mathbf {B}}_3]_2,[{\mathbf {B}}_4]_2)\) along with base \({\mathsf {basis}}({\mathbf {B}}_1^{\parallel }), {\mathsf {basis}}({\mathbf {B}}^{\parallel }_4)\) and \([{\mathsf {basis}}({\mathbf {B}}_2^{\parallel },{\mathbf {B}}_3^{\parallel })]_1\) (of arbitrary choice) such that the following advantage function is negligible in \(\lambda \).
). We say that \(\textsc {xsd}^{G_2}_{{\mathbf {B}}_{3}, {\mathbf {B}}_{4} \mapsto {\mathbf {B}}_{2},{\mathbf {B}}_{3},{\mathbf {B}}_{4}}\) assumption holds if there exists an efficient sampler outputting random \(([{\mathbf {B}}_1]_2,[{\mathbf {B}}_2]_2,[{\mathbf {B}}_3]_2,[{\mathbf {B}}_4]_2)\) along with base \({\mathsf {basis}}({\mathbf {B}}_1^{\parallel }), {\mathsf {basis}}({\mathbf {B}}^{\parallel }_4)\) and \([{\mathsf {basis}}({\mathbf {B}}_2^{\parallel },{\mathbf {B}}_3^{\parallel })]_1\) (of arbitrary choice) such that the following advantage function is negligible in \(\lambda \).

where
We note that we do not give out \({\mathsf {basis}}({\mathbf {B}}_2^{\parallel },{\mathbf {B}}_3^{\parallel },{\mathbf {B}}_4^{\parallel })\) as usual; instead, \({\mathsf {basis}}({\mathbf {B}}_4^{\parallel })\) on \({\mathbb {Z}}_p\) and \([{\mathsf {basis}}({\mathbf {B}}_2^{\parallel },{\mathbf {B}}_3^{\parallel })]_1\) on \(G_1\) are provided. We then prove the following lemma saying that, for a specific set of parameters, the assumption is implied by xdlin assumption.
Lemma 15
(  ). Under the external decisional linear assumption (\({\textsc {xdlin}}\)) [1] (cf. Sect. 2.2), the \(\textsc {xsd}^{G_2}_{{\mathbf {B}}_{3},{\mathbf {B}}_{4} \mapsto {\mathbf {B}}_{2},{\mathbf {B}}_{3},{\mathbf {B}}_{4}}\) assumption holds for parameter \(\ell _2=\ell _3=\ell _4=1\).
). Under the external decisional linear assumption (\({\textsc {xdlin}}\)) [1] (cf. Sect. 2.2), the \(\textsc {xsd}^{G_2}_{{\mathbf {B}}_{3},{\mathbf {B}}_{4} \mapsto {\mathbf {B}}_{2},{\mathbf {B}}_{3},{\mathbf {B}}_{4}}\) assumption holds for parameter \(\ell _2=\ell _3=\ell _4=1\).
Proof
For any PPT adversary \({\mathcal {A}}\), we construct an algorithm \({\mathcal {B}}\) with \({\mathsf {Time}}({\mathcal {B}}) \approx {\mathsf {Time}}({\mathcal {A}})\) such that
On input \( (\,[a_1,a_2,a_3,a_1s_1,a_2s_2]_1, [a_1,a_2,a_3,a_1s_1,a_2s_2]_2, T\,) \) where \(a_1,a_2,a_3,s_1,s_2 \leftarrow {\mathbb {Z}}_p\) and T is either \([a_3(s_1+s_2)]_2\) or uniformly distributed over \(G_2\), algorithm \({\mathcal {B}}\) works as follows:
-
Programming \({\mathbf {B}}_1,{\mathbf {B}}_2,{\mathbf {B}}_3,{\mathbf {B}}_4\) and \({\mathbf {B}}_1^{\parallel },{\mathbf {B}}_2^{\parallel },{\mathbf {B}}_3^{\parallel },{\mathbf {B}}_4^{\parallel }\). Sample \(\widetilde{\mathbf {B}}\leftarrow \mathrm{GL}_{3+\ell _1}({\mathbb {Z}}_p)\) and define
$$\begin{aligned} \begin{array}{cl} &{} ({\mathbf {B}}_1,{\mathbf {B}}_2,{\mathbf {B}}_3,{\mathbf {B}}_4) = \widetilde{\mathbf {B}}\left( {\begin{matrix} \ {\mathbf {I}}_{\ell _1} &{}\ &{} &{} \\ &{} \ 1 &{}\ a_3\ &{}\ a_3\ \\ &{} &{}\ a_2 &{}\ \\ &{} &{} &{}\ a_1\ \\ \end{matrix}}\right) \\ \quad \text{ and }\quad \qquad &{} ({\mathbf {B}}_1^{\parallel },{\mathbf {B}}_2^{\parallel },{\mathbf {B}}_3^{\parallel },{\mathbf {B}}_4^{\parallel }) = \widetilde{\mathbf {B}}^* \left( {\begin{matrix} \ {\mathbf {I}}_{\ell _1} &{}\ \ &{} &{} \\ &{} \ 1\ &{} &{} \\ &{} - a_3 a_2^{-1} &{}\ a_2^{-1} &{}\ \\ &{} -a_3 a_1^{-1} &{} &{}\ a_1^{-1}\ \\ \end{matrix}}\right) \\ \end{array} \end{aligned}$$Algorithm \({\mathcal {B}}\) can simulate \([{\mathbf {B}}_1,{\mathbf {B}}_2,{\mathbf {B}}_3,{\mathbf {B}}_4]_2\) using \([a_1,a_2,a_3]_2\).
-
Simulating \({\mathsf {basis}}({\mathbf {B}}_1^{\parallel }),{\mathsf {basis}}({\mathbf {B}}_4^{\parallel })\). We define
$$\begin{aligned} {\mathsf {basis}}({\mathbf {B}}_1^{\parallel }) = \widetilde{\mathbf {B}}^* \left( {\begin{matrix} {\mathbf {I}}_{\ell _1}\\ {\mathbf {0}}\\ \end{matrix}}\right) \quad \text{ and }\quad {\mathsf {basis}}({\mathbf {B}}_4^{\parallel }) = \widetilde{\mathbf {B}}^* (a_1^{-1} {\mathbf {e}}_{3+\ell _1}) a_1 = \widetilde{\mathbf {B}}^* {\mathbf {e}}_{3+\ell _1}, \end{aligned}$$both of which can be simulated using \(\widetilde{\mathbf {B}}^*\).
-
Simulating \([{\mathsf {basis}}({\mathbf {B}}_2^{\parallel },{\mathbf {B}}_3^{\parallel })]_1\). We define
$$\begin{aligned} {\mathsf {basis}}({\mathbf {B}}_2^{\parallel },{\mathbf {B}}_3^{\parallel }) = \widetilde{\mathbf {B}}^* \left( {\begin{matrix} {\mathbf {0}}&{}\ \\ 1 &{} \\ -a_3 a_2^{-1} &{} a_2^{-1} \\ - a_3 a_1^{-1}&{} \\ \end{matrix}}\right) \left( {\begin{matrix} a_1 &{} \\ a_1 a_3 &{}\ a_2 \\ \end{matrix}}\right) = \widetilde{\mathbf {B}}^* \left( {\begin{matrix} {\mathbf {0}}&{} \\ a_1 &{} \\ &{} 1\\ -a_3&{} \\ \end{matrix}}\right) \end{aligned}$$such that \([{\mathsf {basis}}({\mathbf {B}}_2^{\parallel },{\mathbf {B}}_3^{\parallel })]_1\) (over \(G_1\)) can be simulated using \(\widetilde{\mathbf {B}}^*\) and \([a_1,a_3]_1\).
-
Simulating the challenge. Output the challenge
$$\begin{aligned} \left( {\begin{matrix} {[{\mathbf {0}}]_2}\\ T\\ [a_2 s_2]_2\\ {[a_1 s_1]_2} \\ \end{matrix}}\right) . \end{aligned}$$
Observe that if \(T = [a_3(s_1 + s_2)]_2\), the output challenge is uniformly distributed over \([\mathsf {span}({\mathbf {B}}_3,{\mathbf {B}}_4)]_2\); if T is uniformly distributed over \(G_2\), the output challenge is then uniformly distributed over \([\mathsf {span}({\mathbf {B}}_2,{\mathbf {B}}_3,{\mathbf {B}}_4)]_2\). This readily proves the lemma. \(\square \)
4.2 Step One: A Private-Key IPE from \({\textsc {xdlin}}\) Assumption
Our second private-key IPE is described as follows, which is translated from the private-key IPE in Sect. 3.2 with the correspondence (10). Here we employ the basis defined in Sect. 4.1 with parameter \((\ell _1,\ell _2,\ell _3,\ell _4) = (1,1,1,1)\).
-
\(\mathsf {Setup}(1^\lambda ,n)\): Run \({\mathbb {G}}= (p,G_1,G_2,G_T,e) \leftarrow {\mathcal {G}}(1^\lambda )\). Sample \( {\mathbf {B}}_{14} = ({\mathbf {B}}_1 | {\mathbf {B}}_4) \leftarrow {\mathbb {Z}}_p^{4 \times 2} \) and pick \({\mathbf {u}},{\mathbf {w}}_1,\ldots ,{\mathbf {w}}_n \leftarrow {\mathbb {Z}}_p^{1 \times 4}\), \(\alpha \leftarrow {\mathbb {Z}}_p\). Output
$$\begin{aligned} {\textsf {msk}} = (\,{\mathbb {G}},\alpha ,{\mathbf {u}},{\mathbf {w}}_1,\ldots ,{\mathbf {w}}_n,{\mathbf {B}}_{14}\,). \end{aligned}$$ -
\({\mathsf {KeyGen}}({\textsf {msk}},{\mathbf {y}})\): Let \({\mathbf {y}}= (y_1,\ldots ,y_n) \in {\mathbb {Z}}_p^n\). Sample \({\mathbf {r}}\leftarrow {\mathbb {Z}}_p^2\) and output
$$\begin{aligned} \mathsf {sk}_{\mathbf {y}}=(\, K_0 = [\alpha + (y_1 \cdot {\mathbf {w}}_1 + \cdots + y_n \cdot {\mathbf {w}}_n) {\mathbf {B}}_{14} {\mathbf {r}}]_2,\, K_1 = [{\mathbf {B}}_{14} {\mathbf {r}}]_2 \,) \end{aligned}$$ -
\({\mathsf {Enc}}({\textsf {msk}},{\mathbf {x}},m)\): Let \({\mathbf {x}}= (x_1,\ldots ,x_n) \in {\mathbb {Z}}_p^n\) and \(m \in G_T\). Output
$$\begin{aligned} {\mathsf {ct}}_{\mathbf {x}}= (\, C_1 = [x_1 \cdot {\mathbf {u}}+ {\mathbf {w}}_1]_1,\,\ldots ,\,C_n = [x_n \cdot {\mathbf {u}}+ {\mathbf {w}}_n]_1,\, C = [\alpha ]_T \cdot m \,) \end{aligned}$$ -
\({\mathsf {Dec}}({\mathsf {ct}}_{\mathbf {x}},\mathsf {sk}_{\mathbf {y}})\): Parse \({\mathsf {ct}}_{\mathbf {x}}= (C_1,\ldots ,C_n,C)\) and \(\mathsf {sk}_{\mathbf {y}}= (K_0,K_1)\) for \({\mathbf {y}}= (y_1,\ldots ,y_n) \in {\mathbb {Z}}_p^{n}\). Output
$$\begin{aligned} m' = C \cdot e(y_1 \odot C_1 \cdots y_n \odot C_n, K_1) \cdot e([1]_1,K_0)^{-1}. \end{aligned}$$
The correctness is straightforward. Compared with the construction in Sect. 3.2, we now have ciphertexts over \(G_1\) instead of \({\mathbb {Z}}_p\) and the bilinear map is required for decryption procedure. However the total dimension \(\ell =4\) is smaller than that in Sect. 3.1 when \(k=2\) (corresponding to \({\textsc {dlin} }\) assumption), which is \(\ell =5\).
4.3 Security
We will prove the following theorem.
Theorem 3
Under the xdlin assumption, the private-key IPE scheme described in Sect. 4.2 is adaptively secure and fully attribute-hiding (cf. Sect. 2.1).
As before, we only need to prove the following lemma for \(m_0 = m_1\).
Lemma 16
For any adversary \({\mathcal {A}}\) that makes at most Q key queries and outputs \(m_0 = m_1\), there exists adversaries \({\mathcal {B}}_1,{\mathcal {B}}_2,{\mathcal {B}}_3\) such that
and \({\mathsf {Time}}({\mathcal {B}}_1),{\mathsf {Time}}({\mathcal {B}}_2),{\mathsf {Time}}({\mathcal {B}}_3) \approx {\mathsf {Time}}({\mathcal {A}})\).
Game sequence. With the correspondence in Sect. 4.1, the proof for Lemma 16 is almost the same as that for Lemma 2 presented in Sect. 3. Here we only give the game sequence, summarized in Fig. 4.
-
\({\mathsf {Game}}_0\) is the real game in which the challenge ciphertext for \({\mathbf {x}}_b = (x_{1,b},\ldots ,x_{n,b})\) is of the form
$$\begin{aligned}{}[x_{1,b} \cdot {\mathbf {u}}+ {\mathbf {w}}_1]_1,\,\ldots ,\,[x_{n,b} \cdot {\mathbf {u}}+ {\mathbf {w}}_n]_1, [\alpha ]_T \cdot m_0. \end{aligned}$$Here \(b \leftarrow \{0,1\}\) is a secret bit.
-
\({\mathsf {Game}}_{1}\) is identical to \({\mathsf {Game}}_{0}\) except that the challenge ciphertext is
$$\begin{aligned} \{\,[x_{i,b} \cdot {\mathbf {u}}^{(134)} + \boxed {x_{i,1-b} \cdot {\mathbf {u}}^{(2)}} + {\mathbf {w}}_i]_1\,\}_{i\in [n]},\ [\alpha ]_T \cdot m_0. \end{aligned}$$We claim that \({\mathsf {Game}}_1 \equiv {\mathsf {Game}}_0\). The proof is analogous to that for \({\mathsf {Game}}_1 \equiv {\mathsf {Game}}_0\) in Sect. 3.3.
-
\({\mathsf {Game}}_{2.j}\) for \(j \in [0,q]\) is identical to \({\mathsf {Game}}_{1}\) except that the first j secret keys are
$$\begin{aligned}{}[\alpha + (y_1 \cdot {\mathbf {w}}_1 + \cdots + y_n \cdot {\mathbf {w}}_n) {\mathbf {d}}]_2,\ [{\mathbf {d}}]_2 \quad \text{ where } \quad \boxed {{\mathbf {d}}\leftarrow \mathsf {span}({\mathbf {B}}_1,{\mathbf {B}}_2,{\mathbf {B}}_4)}. \end{aligned}$$We claim that
 for \(j \in [q]\) and give a proof sketch later.
for \(j \in [q]\) and give a proof sketch later. -
\({\mathsf {Game}}_3\) is identical to \({\mathsf {Game}}_{2.q}\) except that the challenge ciphertext is
$$\begin{aligned} \{\,[\boxed {x_{i,0} \cdot {\mathbf {u}}_0^{(124)} + x_{i,1} \cdot {\mathbf {u}}_1^{(124)}} + x_{i,b} \cdot {\mathbf {u}}^{(3)} + {\mathbf {w}}_i]_1\,\}_{i \in [n]}, [\alpha ]_T \cdot m_0. \end{aligned}$$where \({\mathbf {u}}_0,{\mathbf {u}}_1\leftarrow {\mathbb {Z}}_p^{1 \times (k+1)}\). We claim that \({\mathsf {Game}}_{2.q} \equiv {\mathsf {Game}}_3\). The proof is analogous to that for \({\mathsf {Game}}_{2.q} \equiv {\mathsf {Game}}_3\) in Sect. 3.3 using “change of basis” technique [23, 28], except that we now work with subspace \(\mathsf {span}({\mathbf {B}}_1,{\mathbf {B}}_2,{\mathbf {B}}_4)\) corresponding to \(\mathsf {span}({\mathbf {B}}_1,{\mathbf {B}}_2)\) there (cf. Section 4.1).
-
\({\mathsf {Game}}_4\) is identical to \({\mathsf {Game}}_3\) except that the challenge ciphertext is
$$\begin{aligned}{}[ \boxed {x_{1,0} \cdot {\mathbf {u}}_0 + x_{1,1} \cdot {\mathbf {u}}_1} + {\mathbf {w}}_1]_1,\,\ldots ,\, [\boxed {x_{n,0} \cdot {\mathbf {u}}_0 + x_{n,1} \cdot {\mathbf {u}}_1 } + {\mathbf {w}}_n]_1,\, [\alpha ]_T \cdot m_0 \end{aligned}$$We claim that \({\mathsf {Game}}_3 \equiv {\mathsf {Game}}_4\) and the adversary has no advantage in guessing b in \({\mathsf {Game}}_4\). The proof for the former claim is similar to that for \({\mathsf {Game}}_1 \equiv {\mathsf {Game}}_0\).
Proving  . We now proves
. We now proves  which completes the proof for Lemma 16. For all \(j \in [q]\), we employ the following game sequence, which has been included in Fig. 4.
which completes the proof for Lemma 16. For all \(j \in [q]\), we employ the following game sequence, which has been included in Fig. 4.
-
\({\mathsf {Game}}_{2.j-1.1}\) is identical to \({\mathsf {Game}}_{2.j-1}\) except that the jth secret key is
$$\begin{aligned}{}[\alpha + (y_1 \cdot {\mathbf {w}}_1 + \cdots + y_n \cdot {\mathbf {w}}_n) {\mathbf {d}}]_2,\ [{\mathbf {d}}]_2 \quad \text{ where } \quad \boxed {{\mathbf {d}}\leftarrow \mathsf {span}({\mathbf {B}}_1,{\mathbf {B}}_3,{\mathbf {B}}_4)}. \end{aligned}$$We claim that
 . This follows from the \(\textsc {sd}^{G_2}_{{\mathbf {B}}_{1},{\mathbf {B}}_{4} \mapsto {\mathbf {B}}_{1},{\mathbf {B}}_{3},{\mathbf {B}}_{4}}\) assumption with a reduction analogous to that for
. This follows from the \(\textsc {sd}^{G_2}_{{\mathbf {B}}_{1},{\mathbf {B}}_{4} \mapsto {\mathbf {B}}_{1},{\mathbf {B}}_{3},{\mathbf {B}}_{4}}\) assumption with a reduction analogous to that for  in Sect. 3.3.
in Sect. 3.3. -
\({\mathsf {Game}}_{2.j-1.2}\) is identical to \({\mathsf {Game}}_{2.j-1.1}\) except that the challenge ciphertext is
$$\begin{aligned} \{\,[x_{i,b} \cdot {\mathbf {u}}^{(14)} + x_{i,1-b} \cdot {\mathbf {u}}^{(2)} + \boxed {x_{i,1-b} \cdot {\mathbf {u}}^{(3)}} + {\mathbf {w}}_i]_1\,\}_{i\in [n]}, [\alpha ]_T \cdot m_0. \end{aligned}$$We claim that \({\mathsf {Game}}_{2.j-1.2} \equiv {\mathsf {Game}}_{2.j-1.1}\). The proof is analogous to that for \({\mathsf {Game}}_{2.j-1.2} \equiv {\mathsf {Game}}_{2.j-1.1}\) in Sect. 3.3.
-
\({\mathsf {Game}}_{2.j-1.3}\) is identical to \({\mathsf {Game}}_{2.j-1.2}\) except that the j-th secret key is
$$\begin{aligned}{}[\alpha + (y_1 \cdot {\mathbf {w}}_1 + \cdots + y_n \cdot {\mathbf {w}}_n) {\mathbf {d}}]_2,\ [{\mathbf {d}}]_2 \quad \text{ where } \quad \boxed {{\mathbf {d}}\leftarrow \mathsf {span}({\mathbf {B}}_1,{\mathbf {B}}_2,{\mathbf {B}}_3,{\mathbf {B}}_4)}. \end{aligned}$$We claim that
 . This follows from \(\textsc {xsd}^{G_2}_{{\mathbf {B}}_{3}, {\mathbf {B}}_{4} \mapsto {\mathbf {B}}_{2},{\mathbf {B}}_{3},{\mathbf {B}}_{4}}\) assumption. The proof is analogous to that for \({\mathsf {Game}}_{2.j-1.3} \equiv {\mathsf {Game}}_{2.j-1.2}\) in Sect. 3.3. Note that, in the reduction, we simulate the challenge ciphertext over \(G_1\) using \([{\mathsf {basis}}({\mathbf {B}}_2^{\parallel },{\mathbf {B}}_3^{\parallel })]_1\).
. This follows from \(\textsc {xsd}^{G_2}_{{\mathbf {B}}_{3}, {\mathbf {B}}_{4} \mapsto {\mathbf {B}}_{2},{\mathbf {B}}_{3},{\mathbf {B}}_{4}}\) assumption. The proof is analogous to that for \({\mathsf {Game}}_{2.j-1.3} \equiv {\mathsf {Game}}_{2.j-1.2}\) in Sect. 3.3. Note that, in the reduction, we simulate the challenge ciphertext over \(G_1\) using \([{\mathsf {basis}}({\mathbf {B}}_2^{\parallel },{\mathbf {B}}_3^{\parallel })]_1\). -
\({\mathsf {Game}}_{2.j-1.4}\) is identical to \({\mathsf {Game}}_{2.j-1.3}\) except that the challenge ciphertext is
$$\begin{aligned} \{\,[ x_{i,b} \cdot {\mathbf {u}}^{(14)} + x_{i,1-b} \cdot {\mathbf {u}}^{(2)} + \boxed {x_{i,b} \cdot {\mathbf {u}}^{(3)}} + {\mathbf {w}}_i ]_1\}_{i\in [n]}, [\alpha ]_T \cdot m_0. \end{aligned}$$We claim that \({\mathsf {Game}}_{2.j-1.4} \equiv {\mathsf {Game}}_{2.j-1.3}\). The proof is identical to that for \({\mathsf {Game}}_{2.j-1.2} \equiv {\mathsf {Game}}_{2.j-1.1}\).
-
\({\mathsf {Game}}_{2.j-1.5}\) is identical to \({\mathsf {Game}}_{2.j-1.4}\) except that the jth secret key is
$$\begin{aligned}{}[\alpha + (y_1 \cdot {\mathbf {w}}_1 + \cdots + y_n \cdot {\mathbf {w}}_n) {\mathbf {d}}]_2,\ [{\mathbf {d}}]_2 \quad \text{ where } \quad \boxed {{\mathbf {d}}\leftarrow \mathsf {span}({\mathbf {B}}_1,{\mathbf {B}}_2,{\mathbf {B}}_4)}. \end{aligned}$$We claim that
 . The proof is identical to that for
. The proof is identical to that for  . Note that \({\mathsf {Game}}_{2.j-1.5} = {\mathsf {Game}}_{2.j}\).
. Note that \({\mathsf {Game}}_{2.j-1.5} = {\mathsf {Game}}_{2.j}\).
4.4 Step Two: From Private-Key to Public-Key
Following the “private-key to public-key” compiler [36], we transform the private-key IPE in Sect. 4.2 to the following public-key IPE:
-
\(\mathsf {Setup}(1^\lambda ,n)\): Run \({\mathbb {G}}= (p,G_1,G_2,G_T,e) \leftarrow {\mathcal {G}}(1^\lambda )\). Sample \( {\mathbf {A}}\leftarrow {\mathbb {Z}}_p^{3 \times 2}, {\mathbf {B}}_{14} \leftarrow {\mathbb {Z}}_p^{4 \times 2} \) and pick
$$\begin{aligned} {\mathbf {U}},{\mathbf {W}}_1,\ldots ,{\mathbf {W}}_n \leftarrow {\mathbb {Z}}_p^{3 \times 4} \quad \text{ and }\quad {\mathbf {k}}\leftarrow {\mathbb {Z}}_p^{3}. \end{aligned}$$Output
$$\begin{aligned} \begin{array}{rcl} {\textsf {mpk}} &{} = &{} (\,{\mathbb {G}},[{\mathbf {A}}^{\top }]_1, [{\mathbf {A}}^{\top }{\mathbf {U}}]_1,[{\mathbf {A}}^{\top }{\mathbf {W}}_1]_1,\ldots ,[{\mathbf {A}}^{\top }{\mathbf {W}}_n]_1, [{\mathbf {A}}^{\top }{\mathbf {k}}]_T\,) \\ {\textsf {msk}} &{} = &{} (\,{\mathbf {k}},{\mathbf {W}}_1,\ldots ,{\mathbf {W}}_n,{\mathbf {B}}_{14}\,). \end{array} \end{aligned}$$ -
\({\mathsf {KeyGen}}({\textsf {msk}},{\mathbf {y}})\): Let \({\mathbf {y}}= (y_1,\ldots ,y_n) \in {\mathbb {Z}}_p^n\). Sample \({\mathbf {r}}\leftarrow {\mathbb {Z}}_p^2\) and output
$$\begin{aligned} \mathsf {sk}_{\mathbf {y}}=(\, K_0 = [{\mathbf {k}}+ (y_1 \cdot {\mathbf {W}}_1 + \cdots + y_n \cdot {\mathbf {W}}_n) {\mathbf {B}}_{14}{\mathbf {r}}]_2, K_1 = [{\mathbf {B}}_{14}{\mathbf {r}}]_2 \,) \end{aligned}$$ -
\({\mathsf {Enc}}({\textsf {mpk}},{\mathbf {x}},m)\): Let \({\mathbf {x}}= (x_1,\ldots ,x_n) \in {\mathbb {Z}}_p^n\) and \(m \in G_T\). Sample \({\mathbf {s}}\leftarrow {\mathbb {Z}}_p^2\) and output
$$\begin{aligned} {\mathsf {ct}}_{\mathbf {x}}= (\, C_0 = [{\mathbf {s}}^{\top }{\mathbf {A}}^{\top }]_1, \{ C_i = [{\mathbf {s}}^{\top }{\mathbf {A}}^{\top }(x_i \cdot {\mathbf {U}}+ {\mathbf {W}}_i)]_1\}_{i \in [n]}, C = [{\mathbf {s}}^{\top }{\mathbf {A}}^{\top }{\mathbf {k}}]_T \cdot m \,) \end{aligned}$$ -
\({\mathsf {Dec}}({\mathsf {ct}}_{\mathbf {x}},\mathsf {sk}_{\mathbf {y}})\): Parse \({\mathsf {ct}}_{\mathbf {x}}= (C_0,C_1,\ldots ,C_n,C)\) and \(\mathsf {sk}_{\mathbf {y}}= (K_0,K_1)\) for \({\mathbf {y}}= (y_1,\ldots ,y_n)\). Output
$$\begin{aligned} m' = C \cdot e(y_1 \odot C_1 \cdots y_n \odot C_n, K_1) \cdot e(C_0,K_0)^{-1}. \end{aligned}$$
The correctness is straightforward.
Security. We will prove the following theorem.
Theorem 4
Under the xdlin assumption, the IPE scheme described above is adaptively secure and fully attribute-hiding (cf. Sect. 2.1).
Concretely, we prove the following lemma, showing that the security of the above IPE is implied by that of our private-key IPE in Sect. 4.2 and the \(\textsc {mddh}_{2} \) assumption.
Lemma 17
For any adversary \({\mathcal {A}}\) that makes at most Q key queries, there exists adversaries \({\mathcal {B}}_0,{\mathcal {B}}\) such that
and \({\mathsf {Time}}({\mathcal {B}}_0),{\mathsf {Time}}({\mathcal {B}}) \approx {\mathsf {Time}}({\mathcal {A}})\).
We prove Lemma 17 via the following game sequence, as in Sect. 3.4.
-
\({\mathsf {Game}}_0\) is the real game in which the challenge ciphertext for \({\mathbf {x}}_b = (x_{1,b},\ldots ,x_{n,b})\) is of the form
$$\begin{aligned}{}[{\mathbf {c}}^{\top }]_1, [{\mathbf {c}}^{\top }(x_{1,b} \cdot {\mathbf {U}}+ {\mathbf {W}}_1)]_1,\,\ldots ,\, [{\mathbf {c}}^{\top }(x_{n,b} \cdot {\mathbf {U}}+ {\mathbf {W}}_n)]_1, e([{\mathbf {c}}^{\top }]_1,[{\mathbf {k}}]_2) \cdot m_b \end{aligned}$$where \({\mathbf {c}}\leftarrow \mathsf {span}({\mathbf {A}})\). Here \(b \leftarrow \{0,1\}\) is a secret bit.
-
\({\mathsf {Game}}_1\) is identical to \({\mathsf {Game}}_0\) except that we sample \({\mathbf {c}}\leftarrow {\mathbb {Z}}_p^{k+1}\) when generating the challenge ciphertext. We claim that
 . This follows from \(\textsc {mddh}_{2} \) assumption and the proof is analogous to that for
. This follows from \(\textsc {mddh}_{2} \) assumption and the proof is analogous to that for  in Sect. 3.4.
in Sect. 3.4.
Analogous to Sect. 3.4 and Sect. 3.6, we can prove that adversary’s advantage in \({\mathsf {Game}}_1\) is bounded by that against our private-key IPE in Sect. 4.2.
Notes
- 1.
The construction is originally based on the decisional linear assumption in symmetric prime-order bilinear group. In this paper, we will work with asymmetric bilinear group where their proof will be translated into a proof based on the external decisional linear assumption. Note that \({\textsc {xdlin}}\) assumption is stronger than \({\textsc {dlin} }\) assumption.
- 2.
Note that, with their framework, we can work out a public key IPE directly, but we focus on the technique handling multiple secret keys at the moment.
References
Abe, M., Chase, M., David, B., Kohlweiss, M., Nishimaki, R., Ohkubo, M.: Constant-size structure-preserving signatures: generic constructions and simple assumptions. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 4–24. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34961-4_3
Agrawal, S., Chase, M.: A study of pair encodings: predicate encryption in prime order groups. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9563, pp. 259–288. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49099-0_10
Agrawal, S., Chase, M.: Simplifying design and analysis of complex predicate encryption schemes. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10210, pp. 627–656. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_22
Attrapadung, N.: Dual system encryption via doubly selective security: framework, fully secure functional encryption for regular languages, and more. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 557–577. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_31
Attrapadung, N.: Dual system encryption framework in prime-order groups via computational pair encodings. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10032, pp. 591–623. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_20
Attrapadung, N., Yamada, S.: Duality in ABE: converting attribute based encryption for dual predicate and dual policy via computational encodings. In: Nyberg, K. (ed.) CT-RSA 2015. LNCS, vol. 9048, pp. 87–105. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-16715-2_5
Bethencourt, J., Sahai, A., Waters, B.: Ciphertext-policy attribute-based encryption. In: 2007 IEEE Symposium on Security and Privacy, pp. 321–334. IEEE Computer Society Press, May 2007
Boneh, D., Boyen, X.: Efficient selective-ID secure identity-based encryption without random oracles. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 223–238. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24676-3_14
Boneh, D., et al.: Fully key-homomorphic encryption, arithmetic circuit ABE and compact garbled circuits. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 533–556. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_30
Boneh, D., Waters, B.: Conjunctive, subset, and range queries on encrypted data. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 535–554. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70936-7_29
Chen, J., Gay, R., Wee, H.: Improved dual system ABE in prime-order groups via predicate encodings. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 595–624. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_20
Chen, J., Gong, J.: ABE with tag made easy. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017. LNCS, vol. 10625, pp. 35–65. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70697-9_2
Chen, J., Gong, J., Kowalczyk, L., Wee, H.: Unbounded ABE via bilinear entropy expansion, revisited. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10820, pp. 503–534. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78381-9_19
Escala, A., Herold, G., Kiltz, E., Ràfols, C., Villar, J.: An algebraic framework for Diffie-Hellman assumptions. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 129–147. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_8
Gay, R., Hofheinz, D., Kiltz, E., Wee, H.: Tightly CCA-secure encryption without pairings. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9665, pp. 1–27. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49890-3_1
Gong, J., Chen, J., Dong, X., Cao, Z., Tang, S.: Extended nested dual system groups, revisited. In: Cheng, C.-M., Chung, K.-M., Persiano, G., Yang, B.-Y. (eds.) PKC 2016. LNCS, vol. 9614, pp. 133–163. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49384-7_6
Gong, J., Dong, X., Chen, J., Cao, Z.: Efficient IBE with tight reduction to standard assumption in the multi-challenge setting. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10032, pp. 624–654. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_21
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Attribute-based encryption for circuits. In: Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) 45th ACM STOC, pp. 545–554. ACM Press, June 2013
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Predicate encryption for circuits from LWE. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 503–523. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_25
Goyal, V., Pandey, O., Sahai, A., Waters, B.: Attribute-based encryption for fine-grained access control of encrypted data. In: Juels, A., Wright, R.N., Vimercati, S. (eds.) ACM CCS 2006, pp. 89–98. ACM Press, October/November 2006. Cryptology ePrint Archive Report 2006/309
Ishai, Y., Wee, H.: Partial garbling schemes and their applications. In: Esparza, J., Fraigniaud, P., Husfeldt, T., Koutsoupias, E. (eds.) ICALP 2014. LNCS, vol. 8572, pp. 650–662. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-43948-7_54
Katz, J., Sahai, A., Waters, B.: Predicate encryption supporting disjunctions, polynomial equations, and inner products. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 146–162. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_9
Lewko, A.: Tools for simulating features of composite order bilinear groups in the prime order setting. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 318–335. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_20
Lewko, A., Okamoto, T., Sahai, A., Takashima, K., Waters, B.: Fully secure functional encryption: attribute-based encryption and (hierarchical) inner product encryption. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 62–91. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_4
Lewko, A., Waters, B.: New proof methods for attribute-based encryption: achieving full security through selective techniques. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 180–198. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_12
Okamoto, T., Takashima, K.: Fully secure functional encryption with general relations from the decisional linear assumption. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 191–208. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_11
Okamoto, T., Takashima, K.: Adaptively attribute-hiding (hierarchical) inner product encryption. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 591–608. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_35
Okamoto, T., Takashima, K.: Fully secure unbounded inner-product and attribute-based encryption. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 349–366. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34961-4_22
Okamoto, T., Takashima, K.: Efficient (hierarchical) inner-product encryption tightly reduced from the decisional linear assumption. IEICE Trans. 96–A(1), 42–52 (2013)
Ostrovsky, R., Sahai, A., Waters, B.: Attribute-based encryption with non-monotonic access structures. In: Ning, P., di Vimercati, S.D.C., Syverson, P.F. (eds.) ACM CCS 07, pp. 195–203. ACM Press, October 2007
Sahai, A., Waters, B.: Fuzzy identity-based encryption. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 457–473. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_27
Waters, B.: Dual system encryption: realizing fully secure IBE and HIBE under simple assumptions. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 619–636. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_36
Waters, B.: Ciphertext-policy attribute-based encryption: an expressive, efficient, and provably secure realization. In: Catalano, D., Fazio, N., Gennaro, R., Nicolosi, A. (eds.) PKC 2011. LNCS, vol. 6571, pp. 53–70. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19379-8_4
Waters, B.: Efficient identity-based encryption without random oracles. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 114–127. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_7
Wee, H.: Dual system encryption via predicate encodings. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 616–637. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_26
Wee, H.: Attribute-hiding predicate encryption in bilinear groups, revisited. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10677, pp. 206–233. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_8
Acknowledgement
We thank the reviewers for their detailed and constructive feedback.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Chen, J., Gong, J., Wee, H. (2018). Improved Inner-Product Encryption with Adaptive Security and Full Attribute-Hiding. In: Peyrin, T., Galbraith, S. (eds) Advances in Cryptology – ASIACRYPT 2018. ASIACRYPT 2018. Lecture Notes in Computer Science(), vol 11273. Springer, Cham. https://doi.org/10.1007/978-3-030-03329-3_23
Download citation
DOI: https://doi.org/10.1007/978-3-030-03329-3_23
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-03328-6
Online ISBN: 978-3-030-03329-3
eBook Packages: Computer ScienceComputer Science (R0)








 for
for  . This follows from the
. This follows from the 
 . This follows from the
. This follows from the 
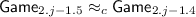 . The proof is identical to that for
. The proof is identical to that for  . See Lemma
. See Lemma  . This follows from the
. This follows from the 


 for
for  . This follows from the
. This follows from the  in Sect.
in Sect.  . This follows from
. This follows from  . The proof is identical to that for
. The proof is identical to that for  . Note that
. Note that  . This follows from
. This follows from  in Sect.
in Sect. 