A Secure and Efficient kNN Classification Algorithm Using Encrypted Index Search and Yao’s Garbled Circuit over Encrypted Databases

Abstract

Database outsourcing has been popular according to the development of cloud computing. Databases need to be encrypted before being outsourced to the cloud so that they can be protected from adversaries. However, the existing kNN classification scheme over encrypted databases in the cloud suffers from high computation overhead. So we proposed a secure and efficient kNN classification algorithm using encrypted index search and Yao’s garbled circuit over encrypted databases. Our algorithm not only preserves data privacy, query privacy, and data access pattern. We show that our algorithm achieves about 17x better performance on classification time than the existing scheme, while preserving high security level.

1 Introduction

Research on preserving data privacy in outsourced databases has been spotlighted with the development of a cloud computing. Since a data owner (DO) outsources his/her databases and allows a cloud to manage them, the DO can reduce the cost of data management by using the cloud’s resources. However, because the data are private assets of the DO and may include sensitive information, they should be protected against adversaries including a cloud server. Therefore, the databases should be encrypted before being outsourced to the cloud. A vital challenge in the cloud computing is to protect both data privacy and query privacy. Meanwhile, during query processing, the cloud can derive sensitive information from the actual data items and users by observing data access patterns even if the data and the query are encrypted [1].

Meanwhile, a classification has been widely adopted in various fields such as marketing and scientific applications. Among various classification methods, a kNN classification algorithm is used in various fields because it does not require a time consuming learning process while guaranteeing good performance with moderate k [2]. When a query is given, a kNN classification first retrieves the kNN results for the query. Then, it determines the majority class label (or category) among the labels of kNN results. However, since the intermediate kNN results and the resulting class label are closely related to the query, the queries should be more cautiously dealt to preserve the privacy of the users.

However, to the best of our knowledge, a kNN classification scheme proposed by Samanthula [3] is the only work that performs classification over the encrypted data in the cloud. The scheme preserves data privacy, query privacy, and intermediate results throughout the query processing. The scheme also hides data access pattern from the cloud. To achieve this, they adopt SkNN_m [4] scheme among various secure kNN schemes [4,5,6,7] when retrieving k relevant records to a query. However, the scheme suffers from high computation overhead because it considers all the encrypted data during the query processing.

To solve the problem, in this paper, we propose a secure and efficient kNN classification algorithm over encrypted databases. Our algorithm can preserve data privacy, query privacy, the resulting class labels, and data access patterns from the cloud. To enhance the performance of our algorithm, we adopt the encrypted index scheme proposed in our previous work [7]. For this, we also propose efficient and secure protocols based on the Yao’s garbled circuit [8] and a data packing technique.

The rest of the paper is organized as follows. Section 2 introduces the related work. Section 3 presents our overall system architecture and various secure protocols. Section 4 proposes our kNN classification algorithm over encrypted databases. Section 5 presents the performance analysis. Finally, Sect. 6 concludes this paper with some future research directions.

2 Background and Related Work

2.1 Background

Paillier Crypto System.

The Paillier cryptosystem [9] is an additive homomorphic and probabilistic asymmetric encryption scheme for public key cryptography. The public encryption key pk is given by (N, g), where N is a product of two large prime numbers p and q, and g is in $Z_{{N^{2} }}^{*}$. Here, $Z_{{N^{2} }}^{*}$ denotes an integer domain ranging from 0 to N². The secret decryption key sk is given by (p, q). Let E() and D() denote the encryption and decryption functions, respectively. The Paillier crypto system provides the following properties. (i) Homomorphic addition: The product of two ciphertexts $E\left( {m_{1} } \right)$ and $E\left( {m_{2} } \right)$ results in the encryption of the sum of their plaintexts m₁ and m₂. (ii) Homomorphic multiplication: The b^th power of ciphertext $E\left( {m_{1} } \right)$ results in the encryption of the product of b and m₁. (iii) Semantic security: Encrypting the same plaintexts using the same encryption key does not result in the identical ciphertexts. Therefore, an adversary cannot infer any information about the plaintexts.

Yao’s Garbled Circuit.

Yao’s garbled circuits [8] allows two parties holding inputs x and y, respectively, to evaluate a function f(x, y) without leaking any information about the inputs beyond what is implied by the function output. One party generates an encrypted version of a circuit to compute f. The other party obliviously evaluates the output of the circuit without learning any intermediate values. Therefore, the Yao’s garbled circuit provides high security level. Another benefit of using the Yao’s garbled circuit is that it can provide high efficiency if a function can be realized with a reasonably small circuit.

Adversarial Models.

There are two main types of adversarial models, semi-honest and malicious [10, 11]. In this paper, we assume that clouds act as insider adversaries with high capability. In the semi-honest adversarial model, the clouds honestly follow the protocol specification, but try to use the intermediate data in malicious way to learn forbidden information. In the malicious adversarial model, the clouds can arbitrarily deviate from the protocol specification. Protocols against malicious adversaries are too inefficient to be used in practice while protocols under the semi-honest adversaries are acceptable in practice. Therefore, by following the work done in [4, 10], we also consider the semi-honest adversarial model in this paper.

2.2 Secure kNN Classification Schemes

To the best of our knowledge, Samanthula proposed a kNN classification scheme (PPkNN) [3], which is the only work that performs classification over the encrypted data. The scheme performs SkNN_m [4] scheme to retrieve k relevant records to a query and determines the class label of the query. The scheme can preserve both data privacy and query privacy while hiding data access pattern. However, the scheme suffers from the high computation overhead because it directly adopts the SkNN_m scheme.

3 System Architecture and Secure Protocols

In this section, we explain our overall system architecture and present generic secure protocols used for our kNN classification algorithm.

3.1 System Architecture

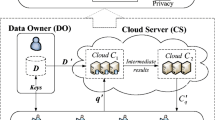
We provide the system architecture of our scheme, which is designed by adopting that of our previous work [7]. Our previous work has a disadvantage that comparison operations cause high overhead by using encrypted binary arrays [7]. To solve this problem, we propose an efficient query processing algorithm that performs comparison operations through yao’s garbled circuits [8]. Figure 1 shows the overall system architecture and Table 1 summarizes common notations used in this paper. The system consists of four components: data owner (DO), authorized user (AU), and two clouds (C_A and C_B). The DO stores the original database (T) consisting of n records. A record $t_{i} \left( {1 \le i \le n} \right)$ consists of $\left( {m + 1} \right)$ attributes and t_i,j denotes the j^th attribute value of t_i. A class label of t_i is stored in $\left( {m + 1} \right)^{\text{th}}$ attribute, i.e., $t_{i,m + 1}$. We do not consider $\left( {m + 1} \right)^{\text{th}}$ attribute when making an index using T. Therefore, the DO indexes on T by using a kd-tree, based on $t_{i,j} \left( {1 \le i \le n\;{\text{and}}\;1 \le j \le m} \right)$. The reason why we utilize a kd-tree (k-dimensional tree) as a space-partitioning data structure is that it not only can evenly partition data into each node, but also is useful for organizing points in a k-dimensional space [14]. When we visit the tree in a hierarchical manner, access patterns can be disclosed. Consequently, we only consider the leaf nodes of the kd-tree and all of the leaf nodes are retrieved once during the query processing step. Let h denote the level of the kd-tree and F be a fan-out which is the maximum number of data to be stored in each node. The total number of leaf nodes is 2 ^h−1. Henceforth, a node refers to a leaf node. The region information of each node is represented as both the lower bound lb_z,j and the upper bound $ub_{z,j} \left( {1 \le z \le 2^{h - 1} ,1 \le j \le m} \right)$. Each node stores the identifiers (id) of data located in the node region. Although we consider the kd-tree in this paper, another index structure whose nodes store region information can be applied to our scheme.

Fig. 1.

The overall system architecture

Table 1. Common notations

To preserve data privacy, the DO encrypts T attribute-wise by using the public key (pk) of the Paillier cryptosystem [9] before outsourcing the database. Thus, the DO generates $E (t_{i,j} )$ for $1 \le i \le n$ and $1 \le j \le m$. The DO also encrypts the region information of all kd-tree nodes to support efficient query processing. Specifically, ${\text{E(}}lb_{z,j} )$ and $E (ub_{z,j} )$ are generated with $1 \le z \le 2^{h - 1}$ and $1 \le j \le m$ by encrypting lb and ub of each node attribute-wise. Assuming that C_A and C_B are non-colluding and semi-honest (or honest-but-curious) clouds, they correctly execute the assigned protocols, but an adversary may try to obtain additional information from the intermediate data while executing the assigned protocol. This assumption is not new and has been considered in earlier work [4, 10]. Specifically, because most cloud services are provided by renowned IT companies, collusion between them that would blemish their reputations is improbable [4].

To process kNN classification algorithm over the encrypted database, we utilize a secure multiparty computation (SMC) between C_A and C_B. To do this, the DO outsources both the encrypted database and its encrypted index to a cloud with pk, C_A in this case, but it sends sk to a different cloud, C_B in this case. In addition, the DO outsources the list of encrypted class labels denoted by $E\left( {label_{i} } \right)$ for $1 \le i \le w$ to C_A. The encrypted index includes the region information of each node in cipher-text and the ids of data located in the node in plaintext. The DO also sends pk to AUs to allow them to encrypt a query. At query time, an AU encrypts a query attribute-wise. The encrypted query is denoted by E(q_j) for $1 \le j \le m$. C_A processes the query with the help of C_B and sends the query result to the AU.

As an example, assume that an AU has eight data instances as depicted in Fig. 2. Each data t_i is depicted with its class label (e.g., 3 in case of t₆). The data are partitioned into four nodes (e.g., node₁– node₄) for a kd-tree. The DO encrypts each data instance and the region of each node attribute-wise. For example, t₆ is encrypted as $E\left( {t_{6} } \right) = \left\{ {E\left( 8 \right),E\left( 5 \right),E\left( 3 \right)} \right\}$ because the values of x-axis and y-axis are 8 and 5, respectively, and the class label of t₆ is 3. Meanwhile, the node₁ is encrypted as $\left\{ {\left\{ {{\text{E}}\left( 0 \right),{\text{E}}\left( 0 \right)} \right\},\left\{ {{\text{E}}\left( 5 \right),{\text{E}}\left( 5 \right)} \right\},\left\{ {1,2} \right\}} \right\}$ because the lb and ub of node₁ are {0, 0} and {5, 5}, respectively, and the node₁ stores both t₁ and t₂.

Fig. 2.

An example in two-dimensional space

3.2 Secure Protocols

Our kNN classification algorithm is constructed using several secure protocols. In this section, all of the protocols except the SBN are performed with the SMC technique between C_A and C_B. The SBN can be solely executed by C_A. Due to space limitations, we briefly introduce five secure protocols found in the literature [3, 4, 7, 10]. (i) SM (Secure Multiplication) [4] computes the encryption of $a \times b$, i.e., $E\left( {a \times b} \right)$, when two encrypted data E(a) and E(b) are given as inputs. (ii) SBN (Secure Bit-Not) [7] performs a bit-not operation when an encrypted bit E(a) is given as an input. (iii) CMP-S [10] returns 1 if u < v, 0 otherwise, when −r₁ and −r₂ are given from C_A as well as u + r₁ and v + r₂ are given from C_B. (iv) SMS_n (Secure Minimum Selection) [10] returns the minimum value among the inputs by performing the CMP-S for n − 1 times when E(d_i) for $1 \le i \le n$ are given as inputs. (v) SF (Secure Frequency) [3] returns $E\left( {f\left( {label_{j} } \right)} \right)$, the number of occurrence of each $E\left( {label_{j} } \right)$ in E(c_i), when both E(c_j) for $1 \le i \le k$ and $E\left( {label_{j} } \right)$ for $1 \le j \le w$ are given as inputs.

Meanwhile, we propose new secure protocols, i.e., ESSED, GSCMP, and GSPE. Contrary to the existing protocols, the proposed protocols do not take the encrypted binary representation of the data, like E(0) or E(1), as inputs. Therefore, our protocols can provide a low computation cost. Next, we propose our new secure protocols.

ESSED Protocol.

ESSED (Enhanced Secure Squared Euclidean Distance) computes E(|X–Y|²) when two encrypted vectors E(X) and E(Y) are given as inputs, where X and Y consist of m attributes. To enhance the efficiency, we pack λ number of σ-bit data instances to generate a packed value. The overall procedure of ESSED is as follows. First, C_A generates random numbers r_j for $1 \le j \le m$ and packs them by computing $R = \mathop \sum \limits_{j = 1}^{m} r_{j} \times 2^{{\sigma \left( {m - j} \right)}}$. Then, C_A generates E(R) by encrypting R. Second, C_A calculates $E\left( {x_{j} {-}y_{j} } \right)$ attribute-wise and packs them by computing $E\left( v \right) = \mathop \prod \limits_{j - 1}^{m} E\left( {x_{j} - y_{j} } \right)^{{2^{{\sigma \left( {m - j} \right)}} }}$. Then, C_A computes $E\left( v \right) = E\left( v \right) \times E\left( R \right)$ and sends E(v) to C_B. Third, assuming that w_j denotes $x_{j} - y_{j} + r_{j} \left( {1 \le j \le m} \right)$, C_B acquires $v = \left[ {w_{1} \left| \ldots \right|w_{m} } \right]$ by decrypting E(v). C_B obtains w_j for $1 \le j \le m$ by unpacking v through $v \times 2^{{{-}\upsigma(m{-}j)}}$. Here, each instance of w_j represents the randomized distance of two input vectors for each attribute. C_B also calculates w ² _j attribute-wise and stores their sum into d. C_B encrypts d and sends E(d) to C_A. Finally, C_A obtains $E\left( {|X{-}Y|^{2} } \right)$ by eliminating randomized values using the following Eq. (1).

$$ E\left( {|X{-}Y|^{2} } \right) = E\left( d \right) \times \prod\nolimits_{j = 1}^{m} {\left( {E\left( {x_{j} - y_{j} } \right)^{ - 2rj} \times E(r_{j}^{2} )^{ - 1} } \right)} $$

(1)

Our ESSED achieves better performance than the existing distance computation protocol, DPSSED [10], in two aspects. First, our ESSED requires only one encryption operation on the C_B side while DPSSED needs m times. Second, our ESSED calculates the randomized distance in plaintext on the C_B side while DPSSED computes the sum of the squared Euclidean distances among all attributes over ciphertext on the C_A side. Therefore, the number of computations on encrypted data in our ESSED can be reduced greatly.

GSCMP Protocol.

When E(u) and E(v) are given as inputs, GSCMP (Garbled Circuit based Secure Compare) protocol returns 1 if u ≤ v, 0 otherwise. The main difference between GSCMP and CMP-S is that GSCMP receives encrypted data as inputs while CMP-S receives the randomized plaintext. The overall procedure of the GSCMP is as follows. First, C_A generates two random numbers r_u and r_v, and encrypts them. C_A computes $E\left( {m_{1} } \right) = E\left( u \right)^{2} \times E\left( {r_{u} } \right)$ and $E\left( {m_{2} } \right) = E\left( v \right)^{2} \times E\left( 1 \right) \times E\left( {r_{v} } \right)$. Second, C_A randomly selects one functionality between $F_{0} :u > v$ and $F_{1} :v > u$. The selected functionality is oblivious to C_B. Then, C_A sends data to C_B, depending on the selected functionality. If $F_{0} :u > v$ is chosen, C_A sends ${<}E\left( {m_{2} } \right),E\left( {m_{1} } \right){>}$ to C_B. If $F_{1} :u < v$ is chosen, C_A sends ${<}E\left( {m_{1} } \right),E\left( {m_{2} } \right){>}$ to C_B. Third, C_B obtains ${<}m_{2,} m_{1}{>}$ by decrypting ${<}E\left( {m_{2} } \right),E\left( {m_{1} } \right){>}$ if $F_{0} :u > v$ is chosen. If $F_{1} :u < v$ is chosen, C_B obtains ${<}m_{1,} m_{2}{>}$ by decrypting ${<}E\left( {m_{1} } \right),E\left( {m_{2} } \right){>}$. Fourth, C_A generates a garbled circuit consisting of two ADD circuits and one CMP circuit. Here, ADD circuit takes two integers u and v as input, and outputs u + v while CMP circuit takes two integers u and v as input, and outputs 1 if u < v, 0 otherwise. If $F_{0} :u > v$ is selected, C_A puts −r_v and −r_u into the 1^st and 2^nd ADD gates, respectively. If $F_{1} :u < v$ is selected, C_A puts −r_u and −r_v into the 1^st and 2^nd ADD gates. Fifth, if $F_{0} :u > v$ is selected, C_B puts m₂ and m₁ into the 1^st and 2^nd ADD gates, respectively. If $F_{1} :u < v$ is selected, C_B puts m₁ and m₂ into the 1^st and 2^nd ADD gates. Sixth, the 1^st ADD gate adds two input values and puts the output result₁ into CMP gate. Similarly, the 2^nd ADD gate puts the output result₂ into CMP gate. Seventh, CMP gate outputs α = 1 if $result_{1} < result_{2}$ is true, α = 0 otherwise. The output of the CMP is returned to the C_B. Then, C_B encrypts α and sends $E\left( \alpha \right)$ to C_A. Finally, only when the selected functionality is $F_{0} :u > v$, C_A computes $E\left( \alpha \right) = {\text{SBN}}\left( {E\left( \alpha \right)} \right)$ and returns the final $E\left( \alpha \right)$. If $E\left( \alpha \right)$ is E(1), u is less than v.

GSPE Protocol.

GSPE (Garbled circuit based Secure Point Enclosure) protocol returns E(1) when p is inside a range or on a boundary of the range, E(0) otherwise. GSPE takes an encrypted point E(p) and an encrypted range E(range) as inputs. Here, the range consists of the E(lb_j) and the E(ub_j) for $1 \le j \le m$. If $E\left( {p_{j} } \right) \le E\left( {range.ub_{j} } \right)$ and $E\left( {p_{j} } \right) \ge E\left( {range.lb_{j} } \right)$, the p is inside a range. The overall procedure of the GSPE is as follows. First, C_A generates two random numbers ra_j and rb_j for $1 \le j \le 2m$. C_A obtains packed values RA and RB by packing ra_j and rb_j, respectively, using the following Eq. (2) for $1 \le j \le 2m$.

$$ RA = \sum\nolimits_{j = 1}^{2m} {ra_{j} \times 2^{{\sigma \left( {2m - j} \right)}} } ,RB = \sum\nolimits_{j = 1}^{2m} {rb_{j} \times 2^{{\sigma \left( {2m - j} \right)}} } $$

(2)

Here, σ means the bit length to represent a data. Then, C_A generates E(RA) and E(RB) by encrypting RA and RB. Second, C_A computes $E(\mu_{j} ) = E\left( {p_{j} } \right)^{2}$ and $E(\omega_{j} ) = E\left( {range.lb_{j} } \right)^{2}$ for $1 \le j \le m$. C_A also computes $E(\delta_{j} ) = E\left( {p_{j} } \right)^{2} \times E\left( 1 \right)$ and $E(\rho_{j} ) = E\left( {range.ub_{j} } \right)^{2} \times E\left( 1 \right)$ for $1 \le j \le m$. Third, C_A randomly selects one functionality between $F_{0} :u > v$ and $F_{1} :v > u$. Then, C_A performs data packing by using the $E(\mu_{j} )$ and $E(\rho_{j} )$, depending on the selected functionality.

• If F₀: u > v is selected, compute

  $$ E\left( {RA} \right) = E\left( {RA} \right) \times E(\rho_{j} ) ^{{2^{{\sigma \left( {2m - j} \right)}} }} ,E\left( {RB} \right) = E\left( {RB} \right) \times E(\mu_{j} ) ^{{2^{{\sigma \left( {2m - j} \right)}} }} $$

• If F₁: v > u is selected, compute

  $$ E\left( {RA} \right) = E\left( {RA} \right) \times E(\mu_{j} ) ^{{2^{{\sigma \left( {2m - j} \right)}} }} ,E\left( {RB} \right) = E\left( {RB} \right) \times E(\rho_{j} ) ^{{2^{{\sigma \left( {2m - j} \right)}} }} $$

In addition, C_A performs data packing by using the $E(\omega_{j} )$ and $E(\delta_{j} )$, depending on the selected functionality. Then, C_A sends packed values E(RA) and E(RB) to C_B.

• If F₀: u > v is selected, compute

  $$ E\left( {RA} \right) = E\left( {RA} \right) \times E(\delta_{j} ) ^{{2^{{\sigma \left( {2m - j} \right)}} }} ,E\left( {RB} \right) = E\left( {RB} \right) \times E(\omega_{j} ) ^{{2^{{\sigma \left( {2m - j} \right)}} }} $$

• If F₁: v > u is selected, compute

  $$ E\left( {RA} \right) = E\left( {RA} \right) \times E(\omega_{j} ) ^{{2^{{\sigma \left( {2m - j} \right)}} }} ,E\left( {RB} \right) = E\left( {RB} \right) \times E(\delta_{j} ) ^{{2^{{\sigma \left( {2m - j} \right)}} }} $$

Fourth, C_B obtains RA and RB by decrypting E(RA) and E(RB). C_B computes $ra_{j} + u_{j}$←  $RA \times 2^{{ - \sigma \left( {2m - j} \right)}}$ and $rb_{j} + v_{j}$← $RB \times 2^{{ - \sigma \left( {2m - j} \right)}}$ for $1 \le j \le 2m$. Here, u_j (or v_j) is one of the $\mu_{j}$, ρ_j, ω_j, and δ_j. Fifth, C_A generates CMP-S circuit and puts −ra_j and −rb_j into CMP-S while C_B puts $ra_{j} + u_{j}$ and $rb_{j} + v_{j}$ into CMP-S for $1 \le j \le 2m$. Once four inputs (i.e., ${-}ra_{j} ,{-}rb_{j} ,ra_{j} + u_{j}$ and $rb_{j} + v_{j}$) are given to CMP-S, the output $\alpha_{j}^{\prime}$ is returned to C_B. Then, C_B encrypts α′ and sends E(α′) to C_A. Sixth, C_A performs $E\left( {\alpha_{j}^{{\prime }} } \right) = {\text{SBN}}\left( {E\left( {\alpha_{j}^{{\prime }} } \right)} \right)$ for $1 \le j \le 2m$ only when the selected functionality is $F_{0} :u > v$. Then, C_A computes $E\left( \alpha \right) = {\text{SM}}\left( {E\left( \alpha \right),E\left( {\alpha_{j}^{{\prime }} } \right)} \right)$ where the initial value of E(α) is E(1). Only when all of the $E\left( {\alpha_{j}^{{\prime }} } \right)$ for $1 \le j \le 2m$ are E(1), the value of E(α) remains E(1). Finally, GSPE outputs the final E(α). The p is inside the range if the final E(α) is E(1).

SXS_n Protocol.

SXS_n (Secure Maximum Selection) returns the maximum value among the inputs when E(d_i) for $1 \le i \le n$ are given as inputs. SXS_n can be realized by converting the logic of SMS_n in opposite way. Therefore, we omit the detailed procedure of SXS_n due to the space limitation.

4 KNN Classification Algorithm

In this section, we present our kNN classification algorithm (SkNNC_G) which uses the Yao’s garbled circuit. Our algorithm consists of four steps; encrypted kd-tree search step, kNN retrieval step, result verification step, and majority class selection step.

4.1 Step 1: Encrypted kd-Tree Search Step

In the encrypted kd-tree search phase, the C_A securely extracts all of the data from a node containing a query point while hiding the data access patterns. To obtain high efficiency, we redesign the index search scheme proposed in our previous work [7]. Specifically, our algorithm does not require operations related to the encrypted binary representation which causes high computation overhead. In addition, we utilize our newly proposed secure protocols based on Yao’s garbled circuit.

The procedure of the encrypted kd-tree search step is shown in Algorithm 1. First, C_A securely finds nodes which include a query by executing $E\left( {\alpha_{z} } \right)$ ← ${\text{GSPE}}\left( {E\left( q \right),E\left( {node_{z} } \right)} \right)$ for $1 \le z \le num_{node}$ where $num_{node}$ means the total number of kd-tree leaf nodes (lines 1–2). Note that the nodes with $E\left( {\alpha_{z} } \right) = E\left( 1 \right)$ are related to the query, but both C_A and C_B cannot know whether or not the value of each $E\left( {\alpha_{z} } \right)$ is E(1), because the Paillier encryption provides semantic security. Then, we partially perform the index search algorithm in [7]. Specifically, C_A generates ${\text{E}}\left( {\alpha^{{\prime }} } \right)$ by permuting E(α) using a random permutation function π and then sends ${\text{E}}\left( {\alpha^{{\prime }} } \right)$ to C_B (line 3). For example, the output of GSPE is $E\left( \alpha \right) = \left\{ {E\left( 1 \right),E\left( 0 \right),E\left( 0 \right),E\left( 0 \right)} \right\}$ in Fig. 2 because the q is given inside the node₁. Assuming that π permutes data in reverse way, C_A sends the $E\left( {\alpha^{{\prime }} } \right) = \left\{ {E\left( 0 \right),E\left( 0 \right),E\left( 0 \right),E\left( 1 \right)} \right\}$ to C_B.

Third, C_B obtains α′ by decrypting ${\text{E}}\left( {\alpha^{{\prime }} } \right)$ and counts the number of α′ = 1 and stores it into c. Here, c means the number of nodes that the query is related to (line 4). Fourth, C_B creates c number of node groups. Assuming that NG denotes a node group, C_B assigns to each NG both a node with $\alpha^{{\prime }} = 1$ and $num_{node} /c - 1$ nodes with $\alpha^{{\prime }} = 0$. Then, C_B obtains NG′ by randomly shuffling the ids of nodes in each NG and sends NG′ to C_A (lines 5–9). For example, C_B can obtain $\alpha^{{\prime }} = \left\{ {0,0,0,1} \right\}$ which contains one at the fourth position. Because one node group is required, C_B assigns all nodes to one node group and randomly shuffles the ids of the nodes, i.e., $NG_1^{\prime }$ = {2, 1, 3, 4}.

Fifth, C_A obtains NG^* by permuting the ids of nodes using π⁻¹ in each NG′ (line 11). Six, C_A gets access to one datum in a node for each NG^* and executes ${\text{E}}\left( {t_{i,j}^{{\prime }} } \right) = {\text{SM}}\left( {{\text{E}}\left( {node_{z} .t_{s,j} } \right),{\text{E}}\left( {\alpha_{z} } \right)} \right)$ for $1 \le s \le F$ and $1 \le j \le m + 1$ where ${\text{E}}\left( {\alpha_{z} } \right)$ is the result of GSPE corresponding to node_z (line 12–16). As a result, SM results in ${\text{E}}\left( {node_{z} .t_{s,j} } \right)$ only for the data inside the nodes related to the query because their $E\left( {\alpha_{z} } \right)$ values are E(1); otherwise SM results in E(0). If a node has the less number of data than F, it performs SM by using E(max), instead of using ${\text{E}}\left( {node_{z} .t_{s,j} } \right)$. Here, E(max) is the largest value in the domain. When C_A accesses one datum from every node in a NG^*, C_A performs $E\left( {cand_{cnt,j} } \right)$ ← $\mathop \prod \limits_{i = 1}^{num} E(t'_{i,j} )$ where num means the total number of nodes in the selected NG^* (line 17–18). As a result, a datum in the nodes related to the query is securely extracted without revealing the data access patterns because the searched nodes are not revealed. By repeating these steps, all of the data in the nodes are safely stored into the $E\left( {cand_{cnt,j} } \right)$ for $1 \le i \le cnt$ and $1 \le j \le m + 1$ where cnt means the total number of data extracted during the index search. For example, C_A obtains $NG_1^{*}$ = {3, 4, 2, 1} by permuting the $NG_1^{\prime }$ = {2, 1, 3, 4} using π⁻¹. C_A gains access to E(t₅) in node₃, E(t₇) in node₄, E(t₃) in node₂, and E(t₁) in node₁. The results of SM using E(t₅), E(t₇), and E(t₃) are E(0) for all attributes because E(α_z) for the corresponding nodes are E(0). The results are stored into $E\left( {t_{1}^{{\prime }} } \right),E\left( {t_{2}^{{\prime }} } \right)\;{\text{and}}\;E\left( {t_{3}^{{\prime }} } \right)$, respectively. However, the results of SM using E(t₁) become $\left\{ {E\left( 2 \right),E\left( 1 \right),{\text{E}}\left( 1 \right)} \right\}$ because the values of x-axis and y-axis are 2 and 1, respectively, and the class label of t₁ is 1. The results are stored into $E\left( {t_{4}^{{\prime }} } \right)$. Thus, the final attribute-wise homomorphic addition of E(t ^′ _i ) for 1 ≤ i ≤ 4 are {E(2), E(1), E(1)}. Accordingly, one datum E(t₁) in node₁ is securely extracted. By repeating this, the encrypted kd-tree search step can extract all of the data in node₁ (e.g., E(t₁) and E(t₂)) and finally stores them into $E\left( {cand} \right)$.

4.2 Step 2: kNN Retrieval Step

In the kNN retrieval phase, we retrieve the k closest data from the query by partially utilizing the SkNN_m scheme [4]. However, we only consider $E\left( {cand_{i} } \right)$ for $1 \le i \le cnt$, which are extracted in the index search phase, whereas the SkNN_m considers all the encrypted data. In addition, we utilize our efficient protocols which require relatively low computation costs, instead of using the existing expensive protocols. The procedure of the kNN retrieval step is shown in Algorithm 2.

First, using our proposed ESSED, C_A securely calculates the squared Euclidean distances $E\left( {d_{i} } \right)$ between a query and $E\left( {cand_{i} } \right)$ for $1 \le i \le cnt$ (lines 1–2). Then, instead of using the inefficient SMIN_n, C_A performs SMS_n to find the minimum value $E\left( {d_{min} } \right)$ among $E\left( {d_{i} } \right)$ for $1 \le i \le cnt$. Second, C_A calculates ${\text{E}}\left( {\tau_{i} } \right) = E\left( {d_{min} } \right) \times E\left( {d_{i} } \right)^{N - 1}$, i.e., the difference between the $E\left( {d_{min} } \right)$ and $E\left( {d_{i} } \right)$, for $1 \le i \le cnt$. Then, C_A computes ${\text{E}}\left( {\tau_{i}^{{\prime }} } \right) = {\text{E}}\left( {\tau_{i} } \right)^{{r_{i} }}$ (lines 3–6). Note that only the $E\left( {\tau_{i}^{{\prime }} } \right)$ corresponding to the $E\left( {d_{min} } \right)$ has a value of E(0). C_A obtains $E\left( \beta \right)$ by shuffling $E\left( {\tau^{{\prime }} } \right)$ using a random permutation function π and then sends $E\left( \beta \right)$ to the C_B (line 7). For example, because $E\left( {cand} \right) = \left\{ {E\left( {t_{1} } \right),{\text{E}}\left( {t_{2} } \right)} \right\}$ is given from the index search phase, $E\left( {d_{1} } \right) = E\left( 4 \right)$ and $E\left( {d_{2} } \right) = E\left( 5 \right)$. By performing SMS_n, $E\left( {d_{min} } \right)$ is set as E(4). Then, $E\left( {\tau^{{\prime }} } \right)$ is computed as $\left\{ {E\left( 0 \right),E\left( { - r} \right)} \right\}$. The $E\left( {\tau_{i}^{{\prime }} } \right)$ with E(0) corresponds to the $E\left( {d_{min} } \right)$, i.e., E(t₁). Assuming that π permutes data in reverse way, C_A sends the $E\left( \beta \right) = \left\{ {E\left( { - r} \right),E\left( 0 \right)} \right\}$ to C_B. Third, after decrypting $E\left( \beta \right)$, C_B sets $E\left( {U_{i} } \right) = E\left( 1 \right)$ if $E\left( {\beta_{i} } \right) = 0$, and sets $E\left( {U_{i} } \right) = E\left( 0 \right)$ otherwise. After C_B sends E(U) to C_A, C_A obtains E(V) by permuting E(U) using π⁻¹ (line 8–11). Then, C_A performs SM protocol by using E(V_i) and $E\left( {cand_{i,j} } \right)$ to obtain $E\left( {V_{i,j}^{{\prime }} } \right)$. By computing $E\left( {t_{s,j}^{{\prime }} } \right) = \mathop \prod \limits_{i = 1}^{cnt} E(V_{i,j}^{{\prime }} )$ for $1 \le j \le m + 1$, C_A can securely extract the datum corresponding to the $E\left( {d_{min} } \right)$ (line 12–14). For example, C_B sends $E\left( U \right) = \left\{ {E\left( 0 \right),E\left( 1 \right)} \right\}$ because the $\beta_{2} = 1$. Then, C_A obtains $E\left( V \right) = \left\{ {E\left( 1 \right),E\left( 0 \right)} \right\}$ by permuting E(U) using π⁻¹. For the x-attribute, C_A performs ${\text{SM}}({\text{E}}\left( {cand_{1,1} } \right)$, ${\text{E}}\left( {V_{1} } \right)) = {\text{E}}\left( 2 \right)$ and ${\text{SM}}({\text{E}}\left( {cand_{2,1} } \right)$, ${\text{E}}\left( {V_{2} } \right)) = {\text{E}}\left( 0 \right)$. By adding the two values, the x-attribute value of ${\text{E}}\left( {t_{1} } \right)$, i.e., E(2), is securely calculated. Similarly, we can compute E(1), the y-attribute value of ${\text{E}}\left( {t_{1} } \right)$. Therefore, we can store ${\text{E}}\left( {t_{1} } \right) = \left\{ {{\text{E}}\left( 2 \right),{\text{E}}\left( 1 \right)} \right\}$ into ${\text{E}}\left( {t_{1}^{{\prime }} } \right)$ without revealing data access patterns. Finally, to prevent the selected result from being selected in later phase, C_A securely updates the distance of the selected result as $E\left( {max} \right)$ by performing $E\left( {d_{i} } \right) = {\text{SM}}\left( {E\left( {V_{i} } \right),E\left( {max} \right)} \right) \times {\text{SM}}\left( {{\text{SBN}}\left( {E\left( {V_{i} } \right)} \right),E\left( {d_{i} } \right)} \right)$ (line 15-16). This procedure is repeated for k rounds to find the kNN result. For example, in the first round, $E\left( {t_{1} } \right)$ with distance E(4) is securely selected as the 1NN result and $E\left( {t_{2} } \right)$ with E(d₂) = E(5) is selected in the second round as the 2NN result.

4.3 Step 3: Result Verification Step

The result of the step 2 may not be accurate because they are retrieved over the partial data being extracted in the step 1. Therefore, the result verification is essential to confirm the correctness of the current query result. Specifically, assuming that dist_k denotes the squared Euclidean distance between the k^th closest result, i.e., $E\left( {t_{k}^{{\prime }} } \right)$, and the query, the neighboring nodes located within dist_k in the kd-tree need to be searched. For this reason, we use the concept of shortest point (sp) defined in [7]. The sp is a point in a given node whose distance is closest to a given point p as compared with the other points in the node. To find an sp in each node, we use the following properties. (i) If both the lower bound (lb) and the upper bound (ub) of the node are lesser than p, the ub is the sp. (ii) If both the lb and the ub of the region are greater than p, the lb is the sp. (iii) If p is between the lb and the ub of the region, p is the sp. To enhance the efficiency of the result verification algorithm in the previous work [7], we use our newly proposed protocols instead of using the existing expensive protocols.

The procedure of the result verification step is shown in Algorithm 3. First, C_A computes ${\text{E}}\left( {dist_{k} } \right) = {\text{ESSED}}\left( {{\text{E}}\left( q \right),E\left( {t_{k}^{{\prime }} } \right)} \right)$ to calculate the squared Euclidean distance between the query and the k^th closest result among E(t′), i.e., the output of the kNN retrieval step (line 1). Second, C_A performs GSCMP by using E(q_j) and E(node_z.lb_j) for $1 \le z \le num_{node}$ and $1 \le j \le m$ and then stores the result in $E\left( {\psi_{1} } \right)$. C_A also performs GSCMP by using E(q_j) and $E\left( {node_{z} .ub_{j} } \right)$ for $1 \le z \le num_{node}$ and $1 \le j \le m$ and then stores the result into $E\left( {\psi_{2} } \right)$. In addition, C_A calculates $E\left( {\psi_{3} } \right)$ by executing $E\left( {\psi_{1} } \right) \times E\left( {\psi_{2} } \right) \times {\text{SM}}(E\left( {\psi_{1} } \right),E\left( {\psi_{2} } \right))^{N - 2}$ to obtain the result of bit-xor operation between $E\left( {\psi_{1} } \right)$ and $E\left( {\psi_{2} } \right)$ (lines 3–6). Note that “−2” is equivalent to “N − 2” under Z_N. Third, C_A securely obtains the shortest point of each node, i.e., $E\left( {sp_{z,j} } \right)$, by executing ${\text{SM}}\left( {E\left( {\psi_{3} } \right),E\left( {q_{j} } \right)} \right) \times {\text{SM}}\left( {{\text{SBN}}\left( {E\left( {\psi_{3} } \right)} \right),f\left( {E\left( {lb_{z,j} } \right),E\left( {ub_{z,j} } \right)} \right)} \right)$ for $1 \le z \le num_{node}$ and $1 \le j \le m$, where $f\left( {E\left( {lb_{j} } \right),E\left( {ub_{j} } \right)} \right)$ means ${\text{SM}}\left( {E\left( {\psi_{1} } \right),E\left( {lb_{z,j} } \right)} \right) \times {\text{SM}}\left( {{\text{SBN}}\left( {E\left( {\psi_{1} } \right)} \right),E\left( {ub_{z,j} } \right)} \right)$ (lines 7–10). For example, assuming that the required k is 2, E(dist₂) = E(5) because E(t₂) is the current 2NN. Meanwhile, in Fig. 2, the shortest point of node₃ (i.e., sp₃) to the E(q) is computed as follows. Because the x-value of the q is less than the x-values of both lb and ub of node₃, the x-value of E(sp₃) is calculated by E(sp_3,1) = E(0) × E(4) + E(1) × (E(1) × E(5) + E(0) × E(10)) = E(5). Similarly, the y-value of E(sp₃) is computed as E(sp_3,2) = E(1).

Fourth, C_A calculates ${\text{E}}\left( {spdist_{z} } \right)$, the squared Euclidean distances between the query and E(sp_z) for $1 \le z \le num_{node}$ by using ESSED. In addition, C_A securely updates the E(spdist_z) of the retrieved nodes into E(max) by computing $E\left( {spdist_{z} } \right) = {\text{SM}}\left( {E\left( {\alpha_{z} } \right),E\left( {max} \right)} \right) \times {\text{SM}}\left( {{\text{SBN}}\left( {E\left( {\alpha_{z} } \right)} \right),E\left( {spdist_{z} } \right)} \right)$ (lines 11–12). Here, E(α_z) is the output of GSPE computed in index search step. Then, C_A performs $E\left( {\alpha_{z} } \right) = {\text{GSCMP}}\left( {E\left( {spdist_{z} } \right),E\left( {dist_{k} } \right)} \right)$ (line 13). The nodes with $E\left( {\upalpha_{z} } \right) = E\left( 1 \right)$ need to be retrieved for query result verification. For example, the initial value of E(spdist) is (E(0), E(16), E(1), E(26)) for each node in Fig. 2, and E(spdist) is updated as (E(max), E(16), E(1), E(26)). Therefore, the result of GSCMP becomes E(α) = (E(0), E(0), E(1), E(0)) because E(dist_k) = E(5). Fifth, C_A securely extracts the data stored in the nodes with E(α) = E(1) by performing the 4–20 lines of the Algorithm 1 and appends them to E(t′). Then, C_A executes the kNN retrieval step (Algorithm 2) based on E(t′) to obtain the E(result_i) for 1 ≤ i ≤ k (lines 14–16). Finally, C_A stores E(result_i,m+1) into E(c_i) for 1 ≤ i ≤ k to extract the class labels of the kNN results (line 18–19). For example, the final result becomes E(result) = {E(t₁), E(t₅)}. Because the class labels of both E(t₁) and E(t₅) are 1 in Fig. 2, the final E(c) becomes (E(1), E(1)).

4.4 Step 4: Majority Class Selection Step

We securely determine the majority class label among the output of the result verification step, i.e., E(label). The procedure of the result verification step is shown in Algorithm 4. First, C_A performs SF using E(label_j) for $1 \le j \le w$ and E(c_i) for $1 \le i \le k$ to obtain E(f(label_j)). Then, C_A finds the maximum value, i.e., E(f_max), among E(f(label_j)) for $1 \le j \le w$ by using SXS_n (line 1–2). Second, C_A securely obtains the class label E(output) corresponding to the E(f_max) by using the logic similar to 5–10 lines of Algorithm 2. Due to the space limitation, we briefly describe this procedure. C_A calculates ${\text{E}}\left( {\tau_{i} } \right) = E\left( {f_{max} } \right) \times E(f\left( {label_{j} } \right))^{N - 1}$ for $1 \le i \le w$. Then, C_A computes ${\text{E}}\left( {\tau_{i}^{{\prime }} } \right) = {\text{E}}(\tau_{i} )^{{r_{i} }}$ and obtains E(β) by shuffling E(τ′) by using π and then sends E(β) to the C_B (line 3–5). After decrypting E(β), C_B sets E(U_i) = E(1) if E(β_i) = 0, and sets E(U_i) = E(0) otherwise. After C_B sends E(U) to C_A, C_A obtains E(V) by permuting E(U) using π⁻¹ (line 6–9). Then, C_A performs $E(output) = \prod\nolimits_{j = 1}^{w} {{\text{SM(E(}}V_{j} ) , {\text{E(}}label_{j} ) )}$ for $1 \le j \le w$ to obtain the majority class label (line 10–12). For example, E(output) is E(1) because the class label ‘1’ has the maximum occurrence among E(f(label)) = (E(2), E(0), E(0)). Third, C_A returns the decrypted result to AU in cooperation with C_B to reduce the computation overhead at the AU side. To do this, C_A computes E(output) × E(r) by generating a random value r, and then sends the result of E(output + r) to C_B and r to AU (lines 14). C_B decrypts the data sent from C_A and sends the decrypted value (e.g., output + r) to AU (lines 15). Finally, AU computes the actual class label by computing (output + r) − r in plaintext (lines 16–17).

5 Performance Analysis

In this section, we compare our SkNNC_G (secure kNN classification algorithm using the Yao’s garbled circuit) with PPkNN [3] that is the only existing work to perform classification over encrypted databases in the cloud. To measure the performance gains of using our newly proposed protocols, we also compare our scheme with SkNNC_I (secure kNN classification algorithm with secure index) that performs classification based on the existing expensive secure protocols, instead of using our newly proposed protocols. Therefore, we can see that the performance gap between SkNNC_I and PPkNN comes from the use of secure index search scheme. We implemented three schemes by using C++ and evaluate their performances in terms of classification time under different parameters settings. The parameters used for our performance analysis are shown in Table 2. We used the Paillier cryptosystem to encrypt a database for all of the schemes. Our experiments were performed on a Linux machine running Ubuntu 14.04.2 with an Intel Xeon E3-1220v3 4-Core 3.10 GHz and 32 GB RAM. We conducted performance analysis by using the real Chess dataset because it is considered as an appropriate dataset for classification [15]. It consists of 28,056 records with six attributes and their class labels.

Table 2. Experimental parameters

In Fig. 3, we measure the performance of SkNNC_I and our SkNNC_G by varying the level of kd-tree because PPkNN does not use the secure index. The classification times of both schemes are decreased as h changes from 5 to 7 while the classification time increase as h changes from 7 to 9. This is because as h increases, the total number of leaf nodes grows, thus requiring more GSPE and SPE [7] executions for SkNNC_G and SkNNC_I, respectively. Whereas, as h increases, the number of data in the node decreases, thus requiring less computation cost for distance calculation. However, our SkNNC_G outperforms SkNNC_I because our scheme uses both efficient secure protocols based on the Yao’s garbled circuit and the data packing technique.

Fig. 3.

Performance of varying h

Figure 4(a) shows the performance of three schemes by varying the n. As the n becomes larger, the query processing time of PPkNN linearly increases because it considers all of the data. Although the overall query processing times of SkNNC_I and SkNNC_G are increased as the n increases, they are less affected by n than PPkNN. Overall, our SkNNC_G shows 17.1 and 4.7 times better performance than PPkNN and SkNNC_I, respectively. Due to the index-based data filtering, both SkNNC_G and SkNNC_I shows better performance than PPkNN. However, our SkNNC_G outperforms SkNNC_I because our algorithm can reduce the computation cost by using the Yao’s garbled circuit and the data packing technique.

Fig. 4.

Classification time for varying n

Figure 4(b) shows the performance of three schemes by varying the k. As the k becomes larger, the query processing times of three schemes increase because the larger k requires more executions of expensive protocols, e.g., SMS_n in case of our SkNNC_G and SMIN_n in case of both PPkNN and SkNNC_I, to retrieve the more kNN results. Overall, our SkNN_G shows 17.7 and 4.2 times better performance than PPkNN and SkNNC_I, respectively, due to the same reasons described for Fig. 3.

6 Conclusion

Databases need to be encrypted before being outsourced to the cloud, due to its privacy issues. However, the existing kNN classification scheme over encrypted databases in the cloud has a problem that it suffers from high computation overhead. Therefore, in this paper we proposed a new secure and efficient kNN classification algorithm over encrypted databases. Our algorithm not only preserves data privacy and query privacy, but also conceals resulting class labels and data access pattern. In addition, our algorithm can support efficient kNN classification by using an encrypted index search scheme, the Yao’s garbled circuit and a data packing technique. We showed from our performance analysis that the proposed algorithm showed about 17 times better performance on classification time than the existing PPkNN scheme, while preserving high security level.

As a future work, we plan to expand our algorithm to the distributed cloud computing environment. We also plan to study on data clustering and association rule mining over encrypted database for cloud computing.