Keywords

1 Introduction

Over the last years, many researchers have been seeking tools that can help with the diagnosis and prognosis of mental health problems. Research groups have used machine learning approaches in the analysis of fMRI data in order to build predictors that can diagnose, for example, attention deficit and hyperactivity disorders, mild cognitive impairment and Alzheimer’s disease, schizophrenia, or autism [2]. The reported accuracy of the different tasks varies from chance level to \({>}85\%\), depending on the task, dataset, features, and learning algorithm used for creating the classifier.

One of the main obstacles that limits the usability and generalization capabilities (to new instances) of machine learning approaches is the usually small number of instances (n) of the datasets used to train the models [2]. This is especially problematic when there are a large number of features (p), which might range from a few hundreds to millions depending on the approach, known as “small n, large p” [8]. This situation is undesirable because machine learning approaches assume that the training sample is a good approximation of the real distribution of the data, which might not be the case with only a few instances in a high dimensional space.

1.1 Multi-site Data and Batch Effects

In order to mitigate this problem, many researchers use a larger datasets, formed by aggregating fMRI scans obtained at different locations into a single dataset. Unfortunately, inter-scanner variability, possibly caused by field strength of the magnet, manufacturer and parameters of the MRI scanner or radio-frequency noise environments [7], creates a second problem known as batch effects [12], which is technical noise that might confound the real biological signal. The main consequence of batch effects in prediction studies is that researchers have observed a decrease in classification accuracy on multi-site studies compared with that obtained using a single site [3, 12, 16].

Fig. 1.
figure 1

(a) The dataset sampled from the scanning site 1 follows a different probability distribution than data scanned on site 2. (b) After applying g(X) to the data of site 1 both sites follow the same probability distribution.

Full size image

An underlying assumption of machine learning is that the training set and test set are sampled from the same probability distribution. Because of batch effects, data coming from different sites follow different probability distributions, which might cause the predictors to have a decrease in performance. These discrepancies between the training and test sets are known as dataset shift [14]. This paper focuses on a specific subcase: Let \(P_{A}(\, X,Y\,)\) be the joint distribution of the covariates X (the features extracted from the fMRI data) and the label Y (e.g., healthy control or schizophrenia) of scanning site A, and \(P_{B}(\, X,Y\,)\) be the corresponding probability distribution for a scanning site B, then \(P_{A}(\, Y\,|\,X\,) \ne P_{B}(\, Y\,|\,X\,)\), and \(P_{A}(\, X\,) \ne P_{B}(\, X\,)\), but there is a function g(X) such that \(P_{A}(\, Y\,|\,X\,) = P_{B}(\, Y\,|\,g(X)\,)\), and \(P_{A}(\, X\,) = P_{B}(\, g(X)\,)\). This concept is exemplified in Fig. 1.

The problem of removing batch effects is closely related to that of domain adaptation in the computer vision community [5]. Although some of these approaches have been tested on fMRI data, the performance of classifiers learned from multi-site datasets is in many cases lower than using a single site [16]. The objective of this paper is to analyze some techniques for removing batch effects and the situations where they can be effectively used.

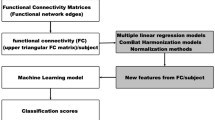
2 Machine Learning and Functional Connectivity Graphs

The standard approach for applying machine learning to fMRI data begins by parcellating the (properly preprocessed) brain volumes into m regions of interest. It then forms a symmetric \(m \times m\) pairwise connectivity matrix, whose (i, j) entry each correspond to some measure of statistical dependence between regions i and j, whose upper-triangle is vectorized into a vector of length \(p=\frac{1}{2}m(m-1)\).

The vectors corresponding to each of the n subjects in the training set are arranged into a matrix X of dimensions \(n \times p\). Similarly, a vector Y of length n, contains the labels of X. Finally, this labeled training data (X, Y) is given to a learning algorithm, that produces the final classifier. A detailed description of this procedure can be found elsewhere [15, 16].

A critical aspect in assessing the impact of batch effects in classification studies, as well as the effectiveness of the techniques applied to removed them, is the methodology used to measure the performance of the classifiers. Some studies pool together the data from the different sites and then randomly split the data into a training and test set, while others use the data from \((r-1)\) sites for training and the \(r^{th}\) site for testing [1, 6, 11, 12]. The first approach might mask the influence of batch effects because it artificially makes the distribution of the training set and test set more similar. This is an unrealistic scenario. In a real application, a clinician cares about the performance of the classifier on the patients that s/he is evaluating. The second approach is more realistic, but also more complicated. If there is indeed a function g(X) that makes \(P_{1}(\, Y\,|\,X\,)\ = \ P_{2}(\, Y\,|\,g(X)\,)\) then we need information from both scanning sites to learn it.

We propose a third evaluation scenario: Fix the test set to be a specific subset of the data from site A. Then consider two training sets: just the remaining instances from site-A versus those remaining site-A instances and also the instances from site B. This approach, illustrated in Fig. 2, has the advantage of identifying if there is a benefit of mixing data from different sites, or if it is better to train one classifier independently for every site. Note that this methodology requires having a labeled dataset from both scanning sites.

Fig. 2.
figure 2

Evaluating a classifier in single site (a) and multi-site (b) scenarios.

Full size image

3 Batch Effects Correction Techniques

3.1 Adding Site as Covariate

This technique involves augmenting each instance with its site information – encoded as a 1-hot-encoding. (That is, using r additional bit features, where the \(j^{th}\) feature is 1 if that instance comes from the \(j^{th}\) site, and the other features here are 0.)

When using a linear classifier, this method assumes that the only difference between sites is in the threshold that we use to classify an instance as belonging to one class, or another. If we assume that the decision function for one site is given by \(w^Tx = 0\), where the x vector represent the features and w is the vector of the coefficients (or weights) of the features, then the decision function for a second site is given by \(w^Tx + c = 0\). This method is effective when the batch effect is caused by a translation (adding a constant) to each instance of the dataset, but it will be ineffective otherwise. Figure 3(a) shows an illustration of this case. Note how the learned decision boundary is appropriate for one of the sites (red), but suboptimal for the other (blue). Note that this technique forces both decision boundaries to have the same slope, and only the bias changes.

3.2 Z-Score Normalization

This approach modifies the probability distribution of the features extracted from both sites, A and B, by making the values of each individual feature, for each site, zero-mean with unit variance – i.e., for each site, for the \(i^{th}\) feature, subject its mean (for that site), and divide by its empirical standard deviation (for that site). Using this technique, only the marginals are the same in both sites, but the covariance structure is not. Applying this “Z-score normalization” to the data from every scanning site independently, will effectively remove batch effects caused by translation and scaling of features (see Appendix A.1). However it fails with more complex transformations, such as rotations or linear transformations in general; see Fig. 3(b). Note that this scaling and translation is in the feature space, and so it is different to the affine transformations that are corrected during the preprocessing stage (which are applied in the coordinate space).

3.3 Whitening

Whitening is a linear transformation that can be viewed as a generalization of the z-score normalization. Besides making the mean of every feature equal to zero and its variance equal to one, it also removes the correlation between features by making the overall covariance matrix the identity matrix. One of the most common procedures to perform this process is PCA Whitening [10]. This transformation first rotates the data, in each site, by projecting it into its principal components, and then it scales the rotated data by the square root of its eigenvalues (which represent the variance of each new variable in the PCA space). Applying this whitening transformation to every dataset independently will remove the batch effects caused by a rotation and translation of the datasets, since in this cases the principal components of the different sites will be aligned; see Appendix A.2 for the mathematical derivation. However, since there is no guarantee that the principal components will be aligned in general, it might not work with other linear transformations; see Fig. 3(c).

Fig. 3.
figure 3

Examples of linear transformation where the methods fail. (a) Including site as covariate, (b) z-score normalization, (c) whitening. (Color figure online)

Full size image

3.4 Solving Linear Transformations

Note that z-score normalization and whitening solve specific cases of

$$\begin{aligned} X_B\ \ =\ \ \alpha X_A + \beta \quad \alpha \in \mathbb {R}^{p\times p},\ \ \beta \in \mathbb {R}^p \end{aligned}$$
(1)

(corresponding to Eq. 5 in Appendix A.2.) Z-score solves batch effects when the associated matrix \(\alpha \) is diagonal, while whitening solves them when \(\alpha \) is orthogonal with determinant 1. Nevertheless, both methods fail to solve batch effects for a general matrix \(\alpha \). Note also that the previous approaches did not explicitly compute \(\alpha \) and \(\beta \), but instead, applied a transformation that removed their effects under the specified circumstances. Of course, if we could compute \(\alpha \) and \(\beta \), or even a good approximation \(\hat{\alpha }\) and \(\hat{\beta }\), we could then solve for any batch effect corresponding to an arbitrary linear transformation.

For any two random vectors \(X_A\) and \(X_B\), such that \(X_B = \alpha X_A + \beta \):

$$\begin{aligned} {\begin{matrix} \mu _B\ &{} =\quad E[X_B]\quad =\quad E[\alpha X_A + \beta ]\quad =\quad \alpha E[X_A] + \beta \quad =\ \alpha \mu _A + \beta \\ \varSigma _B\ &{} =\ COV[X_B]\ =\ COV[\alpha X_A + \beta ]\ =\ \alpha COV[X_A] \alpha ^T\ =\ \alpha \varSigma _A \alpha ^T \end{matrix}} \end{aligned}$$
(2)

Although we can obtain empirical estimates of \(\mu _A,\ \mu _B,\ \varSigma _A,\ \varSigma _B\) from the dataset, the problem is in general ill-defined – i.e., there is an infinite number of solutions. Now note that every site includes (at least) two different subpopulations – e.g., healthy controls versus cases (perhaps people with schizophrenia). Each subpopulation has its own mean vector and covariance matrix (\(\mu _A^{HC}, \mu _A^{SCZ}\), \(\mu _B^{HC}, \mu _B^{SCZ}\), and \(\varSigma _A^{HC}, \varSigma _A^{SCZ}, \varSigma _B^{HC}, \varSigma _B^{SCZ})\). A reasonable assumption is that the batch effects affect both populations in the same way, but by computing the mean and covariance matrix of every population and site independently we are effectively increasing the number of equations available. We can then get an estimate for \(\alpha \) and \(\beta \) as follows:

(3)

where p is the dimensionality of the feature set, and \(||\cdot ||_F\) is the Frobenius norm of a matrix. Note that it is possible to combine data from more than two datasets by finding a linear transformation for every pair of sites.

4 Experiments and Results

4.1 Dataset

We applied the four aforementioned methods to the task of classifying healthy controls and people with schizophrenia using the data corresponding to the Auditory Oddball task to the FBIRN phase II dataset, which is a multisite study developed by the Function Biomedical Informatics Research Network (FBIRN). Keator et al. provides a complete description of the study [9].

After preprocessing the data, we eliminated the subjects who presented head movement greater than the size of one voxel at any point in time in any of the axis, a rotation displacement greater than 0.06 radians, or that did not pass a visual quality control assessment. The original released data contains scans extracted from 6 different scanning sites; however, we only used 4 of them. One of the sites was discarded because it lacked T1-weighted images, which were required as part of our preprocessing pipeline. The second discarded site contained only 6 subjects (5 with schizophrenia) after the quality control assessment, so it was not suitable for our analysis. In summary, we have 21 participants from Site 1, 22 from Site 2, 23 from Site 3 and 23 from Site 4. In all cases, the proportion of healthy controls vs people with schizophrenia is \({\sim }50\%\).

4.2 Experiments and Results

To obtain the feature vector of every fMRI scan, we used the subset corresponding to the Fronto-Parietal Network for a total of \(k=25\) out of the 264 regions of interest defined by Power et al. [13]. The time series corresponding to every region was simply the average time series of all the voxels inside the region. In order to obtain the functional connectivity matrix, we computed the Pearson’s correlation between the time series of all \(k \atopwithdelims ()2\) pairs of regions.

We produced classifiers using a support vector machine (SVM) with linear kernel using the SVMLIB library [4]. The parameters of the SVM were set using cross validation. We applied the batch effect correction techniques previous to merging the datasets into a single training set, and repeated the experiment 15 times with different train/test splits. All the parameters required for the batch effects correction techniques were obtained using only the training sets. Table 1 reports the average accuracy over the 15 rounds.

Table 1. Average accuracy after correcting batch effects. The number in entry (i, j) is the accuracy, over instances from the target site i, of the classifier learned by adding all of site j to the training subset of site i. The colored cells indicate results whose difference improves (green) or decrease (red) relative to the single site classification.
Full size table

5 Discussion

In each of the sub-tables in Table 1, the (i, j) entry represent the average accuracy when the training set has instances from the ith and jth site, and the test set has instances only from the ith site. Ideally, all the off-diagonal values should be higher than the diagonal ones; however, this is not the case. In most of the cases we have mixed and inconsistent results. The only method that consistently improves the performance of the classifiers is the one that solves for arbitrary linear transformations (Table 1e). Note that site S3 is an exception, where we do not see any improvement; however, this particular site has a low performance even in the single site scenario. It is likely that the signal in this particular site is too low and cannot be properly detected by the used methods.

These results reinforce the idea that batch effects play predominant role in classification studies, and motivate the need to develop techniques that address them in order to be able to effectively combine multi-site datasets. We can additionally conclude that whitening, z-score normalization and adding the site as covariate are insufficient to solve batch effects in fMRI data. Our method for solving linear transformations is the one who consistently improves the results in a multi-site scenario, indicating that it is a step in the right direction.