Abstract
Even though players in a game optimize their goals by playing an equilibrium, the perceived payoff per round may (and in most cases will) deviate from the expected average payoff. For the example of loss minimization, an undercut of the expected loss is unproblematic, while suffering more than the expected loss may disappoint the player and lead it to believe that the played strategy is not optimal. In the worst case, this may subsequently cause deviations towards seemingly better strategies, even though the equilibrium cannot be improved in general. Such deviations from the utility maximization principle are subject of bounded rationality research, and this work is a step towards more accurate game theoretic models that include disappointment aversion as an additional incentive. This incentive necessarily creates discontinuities in the payoff functionals, so that Nash’s classical equilibrium theorem is no longer applicable. For games with disappointment aversion (defined in this work) the existence of equilibria can nonetheless be shown, i.e., we are able to find Nash equilibria that comply with disappointment aversion.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Consider a standard security game as being a competition between a defender and an attacker, where the defender aims to minimize losses caused by the attacker. If the model is incomplete in the sense that the defender knows the attacker’s action space but is unaware of the attacker’s payoff structure, we may substitute this information by assuming the attacker’s intentions to be exactly opposite to the defender’s aims. Formally, we define the attacker’s utility \(u_2\) as \(u_2:=-u_1\), where \(u_1\) is the defender’s payoff function, and thus create a zero-sum game in this setting of incomplete information. It is easy to show that the value of the so-constructed zero-sum game bounds the outcome of the actual bi-matrix game (with unknown payoff to the attacker), provided that the defender plays a zero-sum Nash equilibrium strategy. Thus, such strategies are called security strategies [17], and we shall call the respective game a security game in our context (though the term has a much wider meaning including many further game models with security applications).
A typical use-case for a security game is to estimate the amount of preparation against worst-case scenarios. In risk management, experienced disappointments can influence preparedness for expected incident scenarios. Consider a critical infrastructure (CI) which is known to potentially fall victim to certain attacks or experience natural disasters (fire, floods, etc.). If the CI risk management’s employs an optimized control of defensive resources, which can be described through a game theoretic model (e.g., [1, 2, 13, 14, 18] to name only a few), then the expected impact is what the CI provider will prepare for. This optimal, yet worst-case expected impact can be obtained from a game theoretic model which sets the bar for the preparations to be undertaken. Disappointment occurs when the actual damage suffered, despite optimal (equilibrium) control measures, exceeds the expected damage we were prepared for. Since the infrastructure is “critical”, it is a natural requirement to minimize the chances of such an event, i.e., the case that despite all preparation, the damage is still such that we CI cannot recover any more. Practically, this is exactly what insurances are for, where the amount is set sufficiently high to cover the worst among the expected scenarios. If this is too low (manifesting itself as the event of a disappointment in the game), the insurance client may suffer irrecoverable losses.
In playing a security strategy, the defender is assured to never suffer more damage than measured by the value of the zero-sum security game. Thus, the residual damage under this best worst-case defense is what we would take out an insurance for. However, when considering repeated games, the saddle-point value is only an average value, and we will necessarily encounter rounds with higher and lower payoffs than the expected value. For security games about minimizing losses, this means that a security strategy can only bound the average loss; we will henceforth call the event of losing more than expected disappointment. Hence, when we conclude an insurance contract covering the expected maximal damage under worst-case attack scenarios, disappointment is the event where the insurance lot would be insufficient to cover the damage. Suffering from such not fully recoverable damage too often, the defender may not “survive” on the long run. For many utility provisioning infrastructures, such as water supply or power networks, the matter is even more crucial, by definition of the infrastructure as critical.
Therefore, in addition to minimizing the losses themselves, the likelihood of disappointment, the disappointment rate, should be minimized too. Obviously, solely minimizing the disappointment rate itself does not make sense, since avoiding disappointment is trivially done by preparing for maximal damage in first place (i.e. no scenario can ever cause more damage in the game model). Hence, disappointment aversion is always connected to some “primary” goal, and equilibria with disappointment aversion are always a matter of multi-criteria optimization.
The main obstacle, which we will expose later, lies in the possible discontinuities that incorporating disappointment in the game payoff functions may introduce; these discontinuities render classical results inapplicable to study the existence of equilibria. This is the technical difficulty explored in this work, for which we propose several solutions.
1.1 Related Work
Several approaches exist to describe disappointment when playing games. In a well-known classical example, Kahneman and Tversky [9] observed that in a one-shot game (lottery), a majority of players prefer 3, 000$ for sure over an 80% chance of receiving 4, 000$ (and a 20% chance at nothing), whereas a majority prefer a 20% chance at 4, 000$ over a 25% chance at 3, 000$. Bell [4] was the first to explain this phenomenon using the term disappointment. In his Bernoulli model, the player wins \(x\$\) with probability p and \(y\$\) with probability \((1 - p)\). The expectation is \(px + (1 - p)y\) and the disappointment in receiving \(y\$\) is modelled via \(Disappointment = d(px + (1 - p)y - y) = dp(x - y)\), i.e. it is directly proportional (with constant \(d>0\)) to the discrepancy between actual and anticipated performance and the relation between economic payoff and disappointment is linear and additive. Inman, Dyer and Jia [8] generalized this concept to decision problems with more than two outcomes. The significance of Kahneman and Tversky’s lottery for security is its similarity to choice situations about security precautions to be implemented: if “protection A” is weaker than “protection B” but A comes with deterministic guarantees over the mere probabilistic assurances of B, then the practical choice may be guided by anticipated disappointment. In applications of game theory for optimized resource planning (e.g., [14]), practical choices may be more accurately be reflected by considering disappointment aversion.
Decision making in the context of disappointment (aversion) has also been investigated in [5], where disappointment is measured as a strictly increasing function in the difference to the expected utility. In [6], a disappointment metric is used to evaluate expert algorithms that quickly learn effective strategies in repeated games. In this setting, minimizing disappointment is equivalent to maximizing payoffs.
2 Preliminaries and Definitions
In the following we will use the notation \(\varGamma = (\mathcal {I}, (S_i)_{i\in \mathcal {I}},(u_i)_{i \in \mathcal {I}})\) for a game where \(\mathcal {I} = \{1, \dots , n\}\),  denotes a finite index set representing players 1 to n, \((S_i)_{i\in \mathcal {I}}\) is the strategy space and \((u_i)_{i \in \mathcal {I}}\) is the set of utility functions.
denotes a finite index set representing players 1 to n, \((S_i)_{i\in \mathcal {I}}\) is the strategy space and \((u_i)_{i \in \mathcal {I}}\) is the set of utility functions.
We let players have finite sets of strategies denoted as \(PS_i\) (pure strategies) for the i-th player. Mixed strategies are probability distributions supported on a finite set \(PS_i\), all of which constitute the set, i.e., simplex, \(S_i:=\varDelta (PS_i)\) for the i-th player. Using the standard notation \(PS_{-i}, S_{-i}\) to denote the pure, resp. mixed, strategies of player i’s opponents (all embodied within a single large vector), we let the utility functions \({\varvec{u}}_i\) be vector-valued mappings from \(S_i\times S_{-i}\) to  , with \(d\ge 1\) and the j-th coordinate in \({\varvec{u}}_i\) be denoted as
, with \(d\ge 1\) and the j-th coordinate in \({\varvec{u}}_i\) be denoted as  . Accordingly, vectors will hereafter appear in bold lower-case letters, sets and random variables will be uppercase normal font letters. If the utilities are all scalar-valued \((d=1)\), we simply speak about a game, as opposed to a multi-objective game (MOG) having at least one player with at least two goals to optimize. In the case of vectors
. Accordingly, vectors will hereafter appear in bold lower-case letters, sets and random variables will be uppercase normal font letters. If the utilities are all scalar-valued \((d=1)\), we simply speak about a game, as opposed to a multi-objective game (MOG) having at least one player with at least two goals to optimize. In the case of vectors  , we write \({\varvec{u}}<{\varvec{v}}\) to mean \(u_i<v_i\) for all \(i=1,2,\ldots ,d\). The complement relation \({\varvec{u}}\ge _1{\varvec{v}}\) means the existence of at least one index \(i_0\) for which \(u_{i_0}\ge v_{i_0}\), no matter what the other components do. The usual Nash equilibrium condition, rephrased in terms of \(\ge _1\) for minimizing players, then reads as: for each player i,
, we write \({\varvec{u}}<{\varvec{v}}\) to mean \(u_i<v_i\) for all \(i=1,2,\ldots ,d\). The complement relation \({\varvec{u}}\ge _1{\varvec{v}}\) means the existence of at least one index \(i_0\) for which \(u_{i_0}\ge v_{i_0}\), no matter what the other components do. The usual Nash equilibrium condition, rephrased in terms of \(\ge _1\) for minimizing players, then reads as: for each player i,
As usual, this expresses that any unilateral deviation from the equilibrium \({\varvec{x}}_i^*\) for the i-th player would cause a suboptimal payoff in at least one of its goals (by the \(\ge _1\)-relation), even though other payoffs may be improved (in the sense of decreased, since the player is minimizing). It is easy to see that (1) boils down to the standard condition if the payoff is scalar-valued. Any mixed strategy profile satisfying condition (1) is called a Pareto-Nash equilibrium.
For the sake of generality we shall consider games with a finite number of players yet allow each to have an infinitude (up to a compact continuum) of strategies. Nash’s classical result has been extended towards this direction by I. Glicksberg [7]:
Theorem 1
(Glicksberg’s theorem). If for a game in normal form, the strategy spaces are nonempty compact subsets of a metric space, and the utility-functions are continuous w.r.t the metric, then at least one Nash equilibrium in mixed strategies exists.
Remark 1
The requirement of continuous w.r.t the metric was later extended by Dasgupta and Maskin [11], who generalized Glicksberg’s theorem to some classes of semi-continuous utility functions, where the discontinuities are restricted to occur only in subsets of the strategy space, in which all components of the (mixed) strategy vector of player i can be expressed via a finite number of 1-to-1 invertible functions of a single component of another players strategy vector. Furthermore, the sum of utility functions of all players must be upper-semicontinuous and the individual utilities needs to be weakly-lower continuous over the set of discontinuities.
It is not difficult to lift Glicksberg’s result to multi-goal equilibria, which will become relevant once we include disappointment as an explicit goal to minimize on its own:
Corollary 1
Let \(\varGamma \) be a (MOG) that satisfies the hypothesis of Glicksberg’s Theorem for each payoff function of each player. Then, \(\varGamma \) has a Pareto-Nash equilibrium in mixed strategies.
Proof
Let \(1\le i\le n\) be an arbitrary among n maximizing players with \(d_i\ge 1\) payoff functions \(u_i^{(1)},\ldots ,u_i^{(d_i)}\). Let player i pick constants \(\alpha _{i,1},\ldots ,\alpha _{i,d_i}>0\), and define the (scalarized) function \(f_i := \sum _j \alpha _{i,j}\cdot u_i^{(j)}\). Repeating this for each player, call the game with the payoff functions \(f_1,\ldots ,f_n\) game \(\varGamma _{sc}\). So, Glicksberg’s theorem gives an equilibrium \({\varvec{x}}^*=({\varvec{x}}_1^*,\ldots ,{\varvec{x}}_n^*)\) in mixed strategies in \(\varGamma _{sc}\). We show that this a Pareto-Nash equilibrium in the original game \(\varGamma \): adopt an arbitrary player i’s perspective and let it unilaterally deviate from \({\varvec{x}}^*\) by playing an arbitrary mixed strategy \({\varvec{x}}'=({\varvec{x}}_1^*,{\varvec{ x}}_2^*,{\varvec{x}}_{i-1}^*,{\varvec{x}}_i',{\varvec{x}}_{i+1}^*,\) \(\ldots ,{\varvec{x}}_n^*) \ne {\varvec{x}}^*\) Since \({\varvec{x}}^*\) is an equilibrium in \(\varGamma _{sc}\), we have \(f_i({\varvec{x}}')\le f_i({\varvec{x}}^*)\). Towards a contradiction, suppose that \({\varvec{x}}'\) were chosen to outperform the strategy \({\varvec{x}}^*\) in \(\varGamma \), meaning that
Because the constants \(\alpha _{i,j}\) are all by definition \({>}\,0\), we have \(f_i({\varvec{x}}')>f_i({\varvec{x}}^*)\), contradicting the fact that \({\varvec{x}}^*\) is an equilibrium. Thus, (2) cannot hold and there must be an index \(j_0\) for which \(u_i^{(j_0)}({\varvec{x}}')\le u_i^{(j)}({\varvec{x}}^*)\) and hence \({\varvec{u}}_i({\varvec{x}}')\le _1{\varvec{u}}_i({\varvec{x}}^*)\). Since i was arbitrary, \({\varvec{x}}^*\) is, as an equilibrium, Pareto-optimal. \(\square \)
Remark 2
Some authors [10] additionally assume the constants to add up to 1. This has the geometric appeal of exhibiting parts of the convex hull’s border as the Pareto front containing all optimal among the admissible strategies. Formally, the requirement merely amounts to a scaling of the scalarized payoffs by a positive factor, which just creates another strategically equivalent set of payoff functions.
Since the strategy spaces that our players use in the following are just stated to be compact (yet not necessarily discrete), we shall henceforth describe their mixed strategies as measures supported on a strategy space (which practically amount to certain distribution functions that help choosing a randomized action in the concrete game’s instance). For the average (\(=\) expected) payoff \({\varvec{u}}_i\) (possibly vector-valued) for the i-th player under a strategy profile \(\varvec{\mu }=(\mu _1,\ldots ,\mu _n)\) for all players, we shall use the abbreviated notation
where the integral is taken per coordinate function of \({\varvec{u}}_i\). We shall write out the vector of measures more explicitly whenever it aids the explanation.
3 The Main Results
Let us consider a conventional static and repeated game as the simplest model to start with. Whenever there is an equilibrium in pure strategies, the payoff in the game will be constant over all repetitions. However, when the optimum exists in mixed strategies only, the equilibrium optimizes the long-run average over a hypothetical infinitude of independent instances of the game. This may create an unwanted side-effect for the player, such as temporary losses, since the actual payoff per round can be larger or lower than the average payoff that the equilibrium promises. Suppose that the player is minimizing, say, it strives for the least losses due to security breaches. Let \(({\varvec{x}}^*,{\varvec{ y}}^*)\) be an equilibrium in the game, and let u(X, Y) be the payoff (loss) obtained from the game upon a random choice \(X\sim {\varvec{x}}^*, Y\sim {\varvec{y}}^*\).
Calling \(Z=u(X,Y)\) the random variable describing the loss incurred by the game play, then a conventional equilibrium optimizes the first moment \(\overline{z}=\mathrm {E}_{({\varvec{x}}^*,{\varvec{y}}^*)}(Z)=({\varvec{x}}^*)^T{\varvec{A}}{\varvec{y}}^*\) only. This optimization, however, does not extend to higher moments (such as variance). Thus, among a sequence of repetitions of the game, amounting to a set of samples \(z_1,z_2,z_3,\ldots \) from Z, we call the event \(z_i>\overline{z}\) a disappointing round. We shall confine ourself to disappointment aversion hereafter, noting that the definitions and treatment based on the opposite event \(z_i\le \overline{z}\) follows mutatis mutandis.
Let us further confine our study to finite (matrix) games, so that \(\overline{z}=({\varvec{x}})^T\cdot {\varvec{A}}\cdot {\varvec{y}}\) for randomized actions \({\varvec{ x}},{\varvec{y}}\).
Definition 1
Let \(\varGamma \) be an n-person game and let \(\mu =({\varvec{x}}_1^*,\ldots ,{\varvec{ x}}_n^*)\) be an equilibrium. Depending on the nature of the i-th player we define the disappointment rate as
Remark 3
As mentioned in Sect. 1.1, there exist numerous definitions and concepts of disappointment. We chose this simple definition as an easy-to-understand example and stress the fact that the following results also apply for other disappointment concepts, such as [4,5,6, 8].
From here onwards, and w.l.o.g., let us assume a finite two-person game and a minimizing first player whose perspective we are going to adopt (the upcoming results will be formulated to hold for more general games). It is straightforward to take the disappointment rate as a goal to optimize in the game, but obviously, this goal makes no sense by itself unless we combine it with at least one other goal. Otherwise, in case of a zero-sum game, we could just play towards maximal losses, in order to avoid being disappointed, but this is trivially against the purpose of the game at all.
As the nontrivial cases occur when the optimization is on multiple goals we shall coin the disappointment rate a weak goal, to express that the goal is not meaningful on its own. This is opposed to the “actual” goals in the game that we will call strong. The existence of goals whose optimization is only useful relative to other aims is not a new discovery, as the switching cost (i.e., the cost incurred when an instance of a mixed strategy is changed between repetitions of a game) [14] is another example of such a weak goal.
Definition 2
(Game with Disappointment Aversion). Let any game \(\varGamma \) be given which optimizes one (or more) goals for the players. If we add the disappointment rate as an additional payoff to be minimized, we call the resulting game a game with disappointment aversion.
Formally, let the primary payoff be described by a payoff matrix  , whose average is \(u_1({\varvec{x}},{\varvec{y}})={\varvec{ x}}^T\cdot {\varvec{A}}\cdot {\varvec{y}}\). The disappointment rate can, by the law of large numbers, be written as a long-run average of payoffs, where a loss given by \(u_1\) is counted into the sum if and only if it exceeds the average loss \(u_1\). Thus, the disappointment rate \(d_1\) is
, whose average is \(u_1({\varvec{x}},{\varvec{y}})={\varvec{ x}}^T\cdot {\varvec{A}}\cdot {\varvec{y}}\). The disappointment rate can, by the law of large numbers, be written as a long-run average of payoffs, where a loss given by \(u_1\) is counted into the sum if and only if it exceeds the average loss \(u_1\). Thus, the disappointment rate \(d_1\) is

where the random indices r, s are sampled from the distributions \({\varvec{x}} = (x_1, \) \(\ldots , x_n)\), \({\varvec{y}}=(y_1,\ldots ,y_m)\), and  is the indicator function (returning 1 if and only if the inner condition is satisfied and 0 otherwise).
is the indicator function (returning 1 if and only if the inner condition is satisfied and 0 otherwise).
Remark 4
Obviously, yet not discussed in more depth hereafter, the magnitudes of the disappointment rate, being bounded within [0, 1] should be relatively equal to the magnitudes of the other payoffs, in order to avoid the disappointment rate becoming a “negligible” loss or gain throughout the game play. We can assume this without loss of generality for any magnitude and number of payoffs, since it is a simple matter of scaling to equalize the magnitudes of all payoffs accordingly without strategically changing the game. For multi-objective games, this can be done along the scalarization algorithm as described in [10].
Thus, in a finite game with disappointment aversion the resulting utility for player 1 with disappointment aversion, denoted here as \(u_1^d\), takes the form
where \({\varvec{U}}^d ({\varvec{x}},{\varvec{y}}) = (u_{ij}^d({\varvec{x}},{\varvec{y}}))_{ij }\) with  and \(\alpha >0\) is a scalarization factor (for the multi-objective optimization).
and \(\alpha >0\) is a scalarization factor (for the multi-objective optimization).
Observe that the individual utility function \(u_1^d\) in a game with disappointment aversion need not be a continuous function, so neither Glicksberg’s nor Nash’s theorems are applicable to assure the existence of equilibria. As shown by an earlier example due to Sion and Wolfe [16], games with discontinuous payoff functions may in general even lack any equilibria at all. In addition, even though Dasgupta and Maskin have proven the existence of equilibria for some classes of discontinuous utility functions (see Sect. 2), \(u_1^d\) may not fall into this classes for several reasons: First, we observe that for given \({\varvec{y}}\) the discontinuity set of \(u_1({\varvec{x}}, \cdot )\) is in fact the set of all hyperplanes \(a_{ij} = {\varvec{x}}^T\cdot {\varvec{A}}\cdot {\varvec{y}}\) of dimension \(n-1\) (in \({\varvec{x}}\)). The set of discontinuities over \(S_1 \times S_2\) is \(\{ ({\varvec{x}}, {\varvec{y}}),~x_i, y_i \ge 0,~\sum _{i \in \mathcal {I}_1} x_i = 1, \sum _{i \in \mathcal {I}_2} y_i =1 \mid ~ \exists i \in \mathcal {I}_1,~ \exists j \in \mathcal {I}_1:~a_{ij} = {\varvec{x}}^T\cdot {\varvec{A}}\cdot {\varvec{y}} \}\). By definition of the disappointment rate, it is in general not possible to express the components of player 1’s strategy vector \({\varvec{x}}\) in the discontinuity set by a finite number of functions  as Dasgupta and Maskin assume [11]. Second, even if it is possible to do so, \(u_1^d\) is by construction a piecewise continuous function, but it neither has to be upper semi-continuous, nor weakly lower continuous on the set of discontinuities. Therefore, disappointment averse games as in Definition 2, despite their decision theoretical value, are impractical and therefore ineffective in applications.
as Dasgupta and Maskin assume [11]. Second, even if it is possible to do so, \(u_1^d\) is by construction a piecewise continuous function, but it neither has to be upper semi-continuous, nor weakly lower continuous on the set of discontinuities. Therefore, disappointment averse games as in Definition 2, despite their decision theoretical value, are impractical and therefore ineffective in applications.
To fix the theoretical aspects and to ensure the existence of equilibria, we adopt Simon and Zame’s concept of games with endogenous-sharing rules [15] that has also been used in [3]. In the following we will write S for \((S_i)_{i\in \mathcal {I}}\) to improve readability. We stress that the results of [15] applies to scalar-valued utility functions only, so, w.l.o.g., we assume our multi-criteria games to be scalarized (according to [10, 12] or also Corollary 1) before computing equilibria. The resulting equilibria are then exactly the sought Pareto-Nash equilibria (optimizing the disappointment rate besides the primary utility).
Definition 3
(Game with endogenous-sharing). A game with endogenous-sharing rule, or an endogenous-sharing game is any \(\varGamma _s = (\mathcal {I}, S,U)\), where \(\mathcal {I}, S\) are as in Sect. 2, and  is a correspondence that specifies a set of utility payoff allocations for every combination of player’s strategies.
is a correspondence that specifies a set of utility payoff allocations for every combination of player’s strategies.
Thus, U is a multivalued function, and for any \(\varvec{\mu }\) in S the correspondence U allocates a set of utility payoff allocations to each player. Thus, \(U(\varvec{\mu }) = (U_i)_{i \in \mathcal {I}}\) where each  is a (not necessarily countable) set of utilities for player i that could all occur, if strategy \(\varvec{\mu }\) is chosen.
is a (not necessarily countable) set of utilities for player i that could all occur, if strategy \(\varvec{\mu }\) is chosen.
Definition 4
(Upper Hemicontinuity). A correspondence  with closed valuesFootnote 1 is upper hemicontinuous, if for all \(\varvec{\mu } \in S\) and for all sequences
with closed valuesFootnote 1 is upper hemicontinuous, if for all \(\varvec{\mu } \in S\) and for all sequences  and for all \({\varvec{u}} \in U(S)\) and
and for all \({\varvec{u}} \in U(S)\) and  we have \( \lim _{n\rightarrow \infty }\varvec{\mu }_{n} = \varvec{\mu },\) \(\lim _{n\rightarrow \infty } {\varvec{u}}_{n} = {\varvec{u}} \implies {\varvec{u}}\in U (\varvec{\mu })\).
we have \( \lim _{n\rightarrow \infty }\varvec{\mu }_{n} = \varvec{\mu },\) \(\lim _{n\rightarrow \infty } {\varvec{u}}_{n} = {\varvec{u}} \implies {\varvec{u}}\in U (\varvec{\mu })\).
In other words, a correspondence U is upper hemicontinuous if the following holds: for every convergent sequence  in S which maps to a sequence of sets
in S which maps to a sequence of sets  in the range of U that contains a convergent sequence
in the range of U that contains a convergent sequence  , the image of limiting point in the domain must contain the limit of the sequence in the range. I.e.
, the image of limiting point in the domain must contain the limit of the sequence in the range. I.e.  whenever the limits of
whenever the limits of  and
and  exist.
exist.
Definition 5
A correspondence U is bounded, if there exists a constant K such that for all strategies \(\varvec{\mu } \in S\), for all \(i \in \mathcal {I}\) and every \(u_i^j(\varvec{\mu }) \in U_i(\varvec{\mu })\) it holds: \(|u^j_i(\varvec{\mu })|<K\).
Theorem 2
(Simon and Zame [15]). Let \(\varGamma _s\) be an endogenous-sharing game as in Definition 3. Let S be a compact set within some metric space. Assume U is an upper-hemicontinuous and bounded correspondence. Furthermore, assume for each \(\varvec{\mu } \in S\) the image \(U(\varvec{\mu })\) is a nonempty convex subset of  . Then there exists some profile of utility functions \((\hat{u}_i(\varvec{\mu }))_{i \in \mathcal {I}} \in U(\varvec{\mu })\) such that \(\hat{u}_i\) is a measurable function for every \(\varvec{\mu }\) and the resulting game has at least one Nash equilibrium in S.
. Then there exists some profile of utility functions \((\hat{u}_i(\varvec{\mu }))_{i \in \mathcal {I}} \in U(\varvec{\mu })\) such that \(\hat{u}_i\) is a measurable function for every \(\varvec{\mu }\) and the resulting game has at least one Nash equilibrium in S.
Following this approach, we do not consider disappointment averse utility functions \({\varvec{u}}^d = (u_1^d, u_2^d)\), but we define a correspondence U, for which \(U(\varvec{\mu }) = {\varvec{u}}^d( \varvec{\mu })\) at points of continuity, and at the discontinuity points U maps \(\varvec{\mu }\) to the convex hull of all limiting values of \({\varvec{u}}^d\). This can be interpreted as follows: in any discontinuity point \(\varvec{\mu }\) we define the correspondence \(U(\varvec{\mu })\) as set of all limits of expected utility allocations that can be achieved by randomizing over strategy profiles which are arbitrarily close to \(\varvec{\mu }\). It can be shown that the resulting U is the coarsest upper hemicontinuous correspondence that only maps to convex sets [15]. We call this resulting mapping a minimal correspondence.
By Theorem 2 we can now ensure that there exists some profile of utility functions \(\hat{u}\) such that \({\varvec{u}}^d\) and only differs from \(\hat{u}\) at points of discontinuity and an equilibrium of the resulting game \(\hat{\varGamma } = (\mathcal {I},S,(\hat{u}_i)_{i \in \mathcal {I}})\) exists.
Remark 5
At this point, it can easily be verified that the above results does not only apply disappointment as defined in Definition 1, but also to disappointment as defined in [4, 8] or [5]. We can in fact use all kinds of disappointment functions as long as it can be ensured that a minimal correspondence U exists.
Another possibility to incorporate disappointment is to consider a smoothed version of \(\hat{\varGamma } = (\mathcal {I},S,(\hat{u}_i)_{i \in \mathcal {I}})\). Let \(S_1,S_2,\ldots ,S_n\) be the strategy sets of all players. W.l.o.g., let player 1 be minimizing its disappointment relative to a goal  . Let \(\mu _1, \mu _{-1}\) be the probability measures (practically represented by distribution or density functions if the latter exist) from which player 1 and its opponents choose their strategies, denoted as \(X_1,{\varvec{X}}_{-1}\). Recall the disappointment rate as
. Let \(\mu _1, \mu _{-1}\) be the probability measures (practically represented by distribution or density functions if the latter exist) from which player 1 and its opponents choose their strategies, denoted as \(X_1,{\varvec{X}}_{-1}\). Recall the disappointment rate as
Choose a mollifier  of bandwidth \(h>0\) and so that \(\delta _h\in C(\prod _i S_i)\), i.e., the function should be continuous w.r.t. the common metric of the host spaces covering the \(S_i\)’s. Define \(\tilde{d}_h:=d*\delta _h\) and observe that \(\tilde{d}_h\) is now a continuous payoff function. A simple admissible choice for a mollifier is the n-fold tensor product of a univariate mollifier such as \(\delta _k(x) := \frac{k}{c}g(|kx|)\) with the \(C^\infty \)-function
of bandwidth \(h>0\) and so that \(\delta _h\in C(\prod _i S_i)\), i.e., the function should be continuous w.r.t. the common metric of the host spaces covering the \(S_i\)’s. Define \(\tilde{d}_h:=d*\delta _h\) and observe that \(\tilde{d}_h\) is now a continuous payoff function. A simple admissible choice for a mollifier is the n-fold tensor product of a univariate mollifier such as \(\delta _k(x) := \frac{k}{c}g(|kx|)\) with the \(C^\infty \)-function
and the normalization constant  . The support of the tensor product \(\delta _k(x_1,\ldots ,x_n)=\prod _j \delta _k(x_j)\) is then the compact hypercube \([-1/k,1/k]^n\).
. The support of the tensor product \(\delta _k(x_1,\ldots ,x_n)=\prod _j \delta _k(x_j)\) is then the compact hypercube \([-1/k,1/k]^n\).
Definition 6
Let \(\varGamma \) be an n-person game, and let \(\mu =({\varvec{x}}_1^*,\ldots ,{\varvec{ x}}_n^*)\) be an equilibrium. Depending on the nature of the i-th player, the smooth disappointment rate with bandwidth h is defined as \(\tilde{d^i}_h:=d_i*\delta _h\).
Analogously to 2 we can now define games with smooth disappointment aversion if we replace the disappointment rate by the smooth disappointment rate.
This corresponds to allowing not only a 0 / 1 formalism of disappointment but to specify some kind of degree of disappointment at points close to the expected value. This enables a more distinct perspective on disappointment and also helps in computing the equilibrium. It follows:
Theorem 3
Let the game \(\varGamma \) have compact strategy sets within some metric space U, and let the initial payoff functions each be continuous let there be a player in \(\varGamma \) who is minimizing the smoothed disappointment rate w.r.t. at least one other goal. Then \(\varGamma \) has at least one Pareto-Nash equilibrium (in mixed strategies).
Proof
Follows directly from Glicksbergs’s Theorem via Corollary 1. \(\square \)
Figure 1 sums up the three concepts of disappointment discussed in this paper. Note that both (b) and (c) can be applied when dealing with games and display two different notions: When considering disappointment as an endogenous sharing rule (see (b)), we are disappointed whenever the utility exceeds the expected value, yet whenever it equals the mean we are – just like Schrödinger’s cat – both disappointed and not. The smooth disappointment rate allows for a continuous view of disappointment. One may argue that smoothing may falsely incorporate some notion disappointment, even when the encountered loss does not exceed the expected damage, but is somewhat below it. Indeed, insurances naturally do not cover damages that are higher than the maximum liability amount, which causes disappointment. Yet, there always remains the risk of not receiving the full amount from an insurance company, but only partial compensation. The higher the damage, the more insurance companies try to lower the sum they have to come up for. Hence, smooth disappointment rates can incorporate this additional phenomenon. If this is not desired, we advice to shift the of the disappointment rate to the right, such that a positive disappointment value may only occur when the expected value is exceeded.
4 Conclusion and Future Work
We have shown that disappointment aversion can be accounted for in the computation of Nash equilibria in repeated games. In this being work in progress, we close with a couple of directions that may merit exploration along future work, including Stackelberg equilibria (where the problem is essentially one of optimizing a discontinuous functional for the leading player), or the difference between equilibria with and without disappointment aversion (in the latter regard, Remark 4 is a first insight). We stress that the meaning of disappointment for individuals and for companies may be different, and our concept of disappointment aversion was basically motivated by critical infrastructure protection applications. In a follow-up work, we shall explore an application of disappointment aversion to individual’s decision making in more detail, specifically the lottery mentioned Sect. 1.1, where we study the disappointment aversion as one possible explanation for the empirically observed deviation of individuals from the prediction of the Nash equilibrium.
A combination of different concepts of disappointment, e.g., [5, 6], may be interesting to look at when further modelling the insurance example from the introduction, since the disappointment of the individual (customer) and the disappointment event for the insurance may be conceptually different things, and thus lead to different payoff functionals in the resulting security games (then no longer being zero-sum or even repeated). From the insurance company’s perspective, thinking about retained amounts, a disappointment with an insurance may occur if the bar for the deductibles is set so high that the customers would have to pay for most of the incidents. In turn, they will soon look for other insurances with better service. Conversely, if the bar is set too low, the insurance will not be profitable while the customer is never disappointed. The resulting game can thus be seen as one with disappointment aversion (on both sides even).
Notes
- 1.
A correspondence
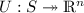 has closed values, if all \(U(\varvec{\mu })\) \(\varvec{\mu } \in S\) are closed subsets of
has closed values, if all \(U(\varvec{\mu })\) \(\varvec{\mu } \in S\) are closed subsets of 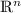 .
.
References
Al-Shaer, E., Duan, Q., Jafarian, J.H.: Random host mutation for moving target defense. In: Keromytis, A.D., Di Pietro, R. (eds.) SecureComm 2012. LNICSSITE, vol. 106, pp. 310–327. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36883-7_19
Alpcan, T., Başar, T.: Network Security: A Decision and Game Theoretic Approach. Cambridge University Press, Cambridge (2010)
Balder, E.J.: An equilibrium closure result for discontinuous games. Econ. Theory 48(1), 47–65 (2010)
Bell, D.E.: Disappointment in decision making under uncertainty. Oper. Res. 33(1), 1–27 (1985)
Chauveau, T., Nalpas, N.: A theory of disappointment (2005)
Crandall, J.W.: Towards minimizing disappointment in repeated games. J. Artif. Int. Res. 49(1), 111–142 (2014)
Glicksberg, I.L.: A further generalization of the kakutani fixed point theorem, with application to nash equilibrium points. Proc. Am. Math. Soc. 3, 170–174 (1952)
Inman, J.J., Dyer, J.S., Jia, J.: A generalized utility model of disappointment and regret effects on post-choice valuation. Mark. Sci. 16(2), 97–111 (1997)
Kahneman, D., Tversky, A.: Prospect theory: an analysis of decision under risk. Econometrica 47, 263–291 (1979)
Lozovanu, D., Solomon, D., Zelikovsky, A.: Multiobjective games and determining pareto-nash equilibria. Buletinul Academiei de Stiinte a Republicii Moldova Matematica 3(49), 115–122 (2005)
Maskin, E., Dasgupta, P.: The existence of equilibrium in discontinuous economic games, part i (theory). Rev. Econ. Stud. 53(1), 1–26 (1986). Reprinted in K. Binmore and P. Dasgupta (eds.), Economic Organizations as Games, Oxford: Basil Blackwell, 1986, pp. 48–82
Rass, S.: On game-theoretic network security provisioning. Springer J. Netw. Syst. Manag. 21(1), 47–64 (2013)
Rass, S., König, S., Schauer, S.: Defending against advanced persistent threats using game-theory. PLoS One 12(1), e0168675 (2017)
Rass, S., König, S., Schauer, S.: On the cost of game playing: how to control the expenses in mixed strategies. In: Rass, S., An, B., Kiekintveld, C., Fang, F., Schauer, S. (eds.) GameSec 2017. LNCS, vol. 10575, pp. 494–505. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-68711-7_26
Simon, L.K., Zame, W.R.: Discontinuous games and endogenous sharing rules. Econometrica 58(4), 861–872 (1990)
Sion, M., Wolfe, P.: On a Game without a Value, pp. 299–306. Princeton University Press, Princeton (1957)
Voorneveld, M.: Pareto-optimal security strategies as minimax strategies of a standard matrix game. J. Optim. Theory Appl. 102(1), 203–210 (1999)
Zhu, Q., Rass, S.: On multi-phase and multi-stage game-theoretic modeling of advanced persistent threats. IEEE Access 6(1), 13958–13971 (2018)
Acknowledgment
This work was done in the context of the project “Cross Sectoral Risk Management for Object Protection of Critical Infrastructures (CERBERUS)”, supported by the Austrian Research Promotion Agency under grant no. 854766. We thank the anonymous reviewers for their valuable suggestions that helped to improve this work.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this paper
Cite this paper
Wachter, J., Rass, S., König, S., Schauer, S. (2018). Disappointment-Aversion in Security Games. In: Bushnell, L., Poovendran, R., Başar, T. (eds) Decision and Game Theory for Security. GameSec 2018. Lecture Notes in Computer Science(), vol 11199. Springer, Cham. https://doi.org/10.1007/978-3-030-01554-1_18
Download citation
DOI: https://doi.org/10.1007/978-3-030-01554-1_18
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-01553-4
Online ISBN: 978-3-030-01554-1
eBook Packages: Computer ScienceComputer Science (R0)






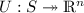 has closed values, if all
has closed values, if all 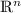 .
.