Analysis and Computation of Adaptive Defense Strategies Against Advanced Persistent Threats for Cyber-Physical Systems

Abstract

Cyber-physical systems are facing new security challenges from Advanced Persistent Threats (APTs) due to the stealthy, dynamic and adaptive nature of the attack. The multi-stage Bayesian game captures the incomplete information of the players’ type, and enables an adaptive belief update according to the observable history of the other player’s actions. The solution concept of perfect Bayesian Nash equilibrium (PBNE) under the proactive and reactive information structures of the players provides an important analytical tool to predict and design the players’ behavior. To capture the learning process and enable fast computation of PBNE, we use conjugate priors to update the beliefs of the players parametrically, which is assimilated into backward dynamic programming with an expanded state space. We use a mathematical programming approach to compute the PBNE of the dynamic bi-matrix game of incomplete information. In the case study, we analyze and study two PBNEs under complete and one-sided incomplete information. The results reveal the benefit of deception of the private attackers’ types and motivate defender’s use of deception techniques to tilt the information asymmetry. Numerical results have been used to corroborate the analytical findings of our framework and show the effectiveness of defense design to deter the attackers and mitigate the APTs strategically.

1 Introduction

The integration of cyber-physical systems increases the operating efficiency and promotes the cross-layer communication. However, the interconnections also turn the industrial control systems (ICS) from the previous safe area to a hard-hit of emerging advanced cyber attacks such as Petya and Stuxnet. After the Aurora generator test in 2007 warns us of the possibilities of physically destroying power generators with merely 21 lines of malicious codes, Petya has attacked the Ukrainian power plant in December 2015. Petya is the first known successful attack on the power grid and causes a power cut to more than 80,000 people. It takes a long time to recover, and the recovery under a similar attack would be worse in the United States in 2018 because of the increasing degree of automation and integration. Similarly, Stuxnet discovered in 2010, have infected over 200,000 computers all over the world and caused over 1,000 centrifuges out of operation. Stuxnet starts its initial infection through the USB driver of the hardware provider. These USB drives are stealthily compromised by Stuxnet when the hardware provider serves other less secure clients. Thus, Stuxnet manages to compromise the air gap even though the nuclear system is carefully isolated from the Internet. These attacks form the Advanced Persistent Threats (APTs) to the ICS security and indicate the urgency of effective defensive mechanisms to respond to the new threats.

APTs have the following three features distinct from the traditional attacks. First, they use customized incursion techniques and have specific targets, such as private organizations, state government, and critical infrastructures, with the goal to gather intelligence and sabotage facilities [4]. Second, they adopt persistent and stealthy attacking strategies to cause more permanent, significant, and irreversible damages. Stuxnet persists in alternating the rotor speed for years to increase the failure probability of the centrifuge. However, Stuxnet launches this attack only once a month to remain stealthy, i.e., human operators do not relate the increase in the number of inoperative centrifuges to an attack. Third, they are methodically designed. For example, Stuxnet replays a 21-s pre-recorded normal sensory data to deceive the monitor when the attack has begun to change the rotor speed.

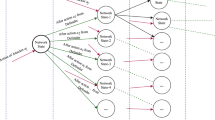
Recent works on secure control systems [9] and intrusion detection systems (IDS) [3] have provided prevalent methods for malware prevention and detection, yet they can be insufficient for human-expert operated APTs that adopt advanced techniques and learn the detection rule during their lengthy stay in the system to evade the detection. To protect infrastructures from APTs, defenders need to design strategic and proactive policies that can learn, anticipate, and adapt the defense strategies over time. To this end, a game theory approach provides a natural framework to develop strategic and adaptive security solutions to harden the cyber-physical security [10, 15]. Starting from the initial infection, APTs establish the foothold and escalate privilege by exploiting zero-day vulnerabilities to sign malware with the private key from stolen certificates. Then, they create tunnels and utilize the backdoor to control the Command and Control (C&C) server to receive additional instructions and malicious codes. Next, APTs establish additional points of entries and propagate stealthily and laterally in the cyber network until they reach the target computer. Finally, they can either collect data in the cyber layer or launch attacks on physical plants. The attack path of APTs, as shown in Fig. 1, can be represented by a tree network without loops and jumps. Thus, a multi-stage dynamic game [7] is a befitting framework to study the lateral movement and privilege escalation of the attack.

Flip-IT game [13], as one example of the dynamic game framework, has successfully analyzed the scenario of the key leakage under APTs so that system defender and APTs stealthily take over the system alternately. However, Flip-IT is a complete-information game, and it cannot be sufficient to capture the deceptive nature of the attack and the information asymmetry of the game. In the example of Stuxnet, it is hard to conclude from the observation of the alternating of the rotor’s speed whether the system is under attack or what kind of attacks. One way to model the incomplete information caused by deceptions in games is to introduce the notion of types [5], which reflects the uncertainties of one player about the other player’s motivation and objectives. Signaling game, a two-stage game with the one-sided type has been applied to study the deception in cyber-physical systems [14]. As a countermeasure for the deceptive attackers, [11] surveys defensive deceptions including perturbation, moving target defense, obfuscation, mixing, honey-x and attacker engagement. For example, cyber denial and deception (D&D) proposed in [12] aims to create sufficient amount of uncertainties so that adversaries would waste time and resources on ‘honey files.’ The authors in [6] show how the defender can manipulate the attacker’s belief to deter attacks and minimize the damage inflicted to the network.

In our framework, we consider that attackers and defenders can adopt adversarial and defensive deceptions, respectively, in the dynamic game of cyber-physical systems. Each player has a type that characterizes his/her private information. Hence we model the scenario with a two-sided dynamic Bayesian game to uniformly capture the three characteristics of APTs, i.e., strategic adversaries, multiple stages, and incomplete information. The history of both players’ actions is fully observable. The private type represents the uncertainty of the two-sided deception so that both players have to strategically gauge the other’s type to respond optimally to their type-related utility functions. The solution concept for this dynamic game is the perfect Bayesian Nash equilibrium (PBNE) in which the players form a consistent belief and policy pair such that no player can gain via unilateral policy deviation with the belief that supports the actions. The computation of PBNE is challenging when the utility is a function of continuous type space. We propose an equivalent mathematical program with infinite-dimensional constraints to solve the dynamic Bayesian game and approximate it by sampling the type space. In particular, for the one-sided incomplete information bi-matrix game, we obtain two necessary conditions for the existence of the equilibrium.

1.1 Organization of the Paper

The rest of the paper is organized as follows. Section 2 introduces the system model and the Bayesian belief update. The solution concept of PBNE under proactive and reactive information structures is introduced in Sect. 3. In Sect. 4, we adopt the conjugate prior assumption for parametric update of the belief and form an expanded-state dynamic programming to unify the forward and backward processes. A case study of one-sided information is presented in Sect. 5, and Sect. 6 concludes the paper.

Fig. 1.

The multi-stage life cycle of APTs forms a tree network. The threat actor starts the infection by exploiting the human weakness (social engineering) or cyber attacks. Then, APTs gain the foothold, escalate privilege, propagate laterally in the cyber network and finally either cause physical damages or collect confidential data. APTs use each stage as a stepping stone for the next and cannot jump directly to the final stage. Attackers also have no incentives to go back to stages that they has already compromised because their ultimate goal is to compromise the specific target at the final stage.

2 System Model

This section introduces a multi-stage dynamic game of incomplete information to model the strategic behaviors of APTs and defenders. Consider two players, a system defender $P_1$ (pronoun ‘she’) who holds different security levels and a user $P_2$ (pronoun ‘he’) of different threat levels to the system. The security or threat level of player $i\in \{1,2\}$ is private information unknown to the other player and is characterized by a continuous type $\theta _i\in \varTheta _i:=[0,1]$. For any finite set $\mathcal {A}$, define $\bigtriangleup \mathcal {A}:=\{p:\mathcal {A} \mapsto R_{+} | \sum _{a\in \mathcal {A}} p(a)=1\}$ while for any infinite set ${\varTheta }$, define $\bigtriangleup \varTheta :=\{p:\varTheta \mapsto R_{+} | \int _{\theta \in \varTheta } p(\theta )d\theta =1\}$. Mathematically, type $\theta _i$ is the realization of $\tilde{\theta }_i$, a random variable with an underlying probability space $(\varOmega , \mathcal {F}, P)$. The prior probability distribution $B_i^0\in \bigtriangleup \varTheta _i$ is common knowledge. User $P_2$’s type $\theta _2$ indicates the strength of the user in terms of damages that he can inflict on the system. A user with a large type value indicates a higher threat level to the system. A user with $\theta _2$ less than a pre-defined threshold $\bar{\theta }_2\in (0,1)$ is treated as legitimate. Similarly, the type of defender $P_1$ indicates the defense strength and the resource she has for security. For example, defenders can use deception techniques (e.g., honeypots and honeyfiles) to detect the attackers and cut links to isolate the attacker. The existence of honeypot can reduce the number of attacks because an attacker cannot be sure whether it is a trap or not when observing network vulnerability. In this case, a defender with a higher type value $\theta _1$ indicates that she possesses a larger number of honeypots to deploy. Since APTs move stage by stage from the initial infection to reach the final target, we model the transition of APTs as a multi-stage game with a finite horizon T.

At each stage $t\in \{0,1,\cdots ,T\}$, each player $P_i$ chooses an action $a_i^t$ from his/her feasible action set $\mathcal {A}_i^t$. The user’s actions $a_2^t\in \mathcal {A}_2^t$ are the behaviors that are directly observable from activity log files, e.g., a privilege escalation request and sensor access. Sine both legitimate and adversarial users can take these activities, a defender cannot identify the user’s type directly from observing these actions. The user’s type, however, determines the real actions and the corresponding payoff, e.g., a legitimate user’s access to the sensor benefit the system while a pernicious user’s access can cost a considerable loss. On the other hand, the defender’s action $a_1^t$ will be mitigation or proactive actions such as restricting the escalation request or monitoring the sensor access. These proactive actions also do not directly disclose the system type. The action set $\mathcal {A}_i^t$ is stage-variant and has a stage-dependent cardinality $|\mathcal {A}_i^t|$. For example, at the early stage of the attack on a nuclear plant, the defender can choose to shut down the reactor, while in a later stage, the defender switches from automatic to manual mode to control the feedwater flow. Each player cannot observe the current-stage t action of the other player until the action appears in the log file at the next stage. The perfect recall assumption leads to a fully observable history $\mathbf {h}^t:=\{a_1^0,\cdots ,a_1^{t-1},a_2^0,\cdots ,a_2^{t-1}\} \in \mathcal {H}^t$ to both players. State $x^t\in \mathcal {X}^t$ representing the status of the system at stage t is the sufficient statistic of history $\mathbf {h}^t$ because a Markov state transition $x^{t+1}=f^t(x^t,a_1^t,a_2^t)$ contains all the information of the history update $\mathbf {h}^t=\mathbf {h}^{t-1} \cup \{a_1^t,a_2^t\}$. The function $f^t$ is deterministic and may also be stage-dependent. In the example of nuclear power plant, at the early stage, attacker and defender actions will determine whether the reactor can be shut down successfully, while in a later stage of the attack, the actions will determine whether the feedwater flow can be controlled appropriately to maintain the steam generator with an adequate water level.

Information structure $I_i^t\in \mathcal {I}_i^t$ is a set that contains the information available to player $P_i$ at stage t. The behavioral strategy $\sigma ^t_i: \mathcal {I}_i^t \mapsto \bigtriangleup \mathcal {A}_i^t$ for player $P_i$ maps his/her information structure set into a distribution over $P_i$’s action space. All the potential behavioral strategies constitute the feasible set $\varSigma _i^t$. Let $\sigma ^t_i(a_i^t|{I}_i^t)$ be the probability of taking action $a_i^t$ under the information structure $I_i^t$, i.e., $\sum _{a_i^t \in \mathcal {A}_i^t}\sigma ^t_i(a_i^t|{I}_i^t)=1, \forall I_i^t\in \mathcal {I}_i^t$. An action $a_i^t$ is the realization of the behavioral strategy $\sigma _i^t$. In this work, we study the reactive information structure $\mathcal {I}_i^t:=\mathcal {H}^t \times \varTheta _i$ for outsider threats and the proactive information structure $\mathcal {I}_i^t:=\sigma _{-i}^t \times \mathcal {H}^t \times \varTheta _i$ for insider threats as introduced in Sect. 3. For $i\in \mathcal {I}$, notation $-i$ means $\mathcal {I}\setminus \{i\}$. For example, if $\mathcal {I}:=\{1,2\}$ and $i=1$, then $-i=2$. At stage $t\in \{1,\cdots ,T\}$, $P_i$ forms a belief $B^t_i: \mathcal {H}^t \mapsto \bigtriangleup \varTheta _{-i}$ of the other player’s type according to the history $\mathbf {h}^t$. Similarly, $B^t_i(\theta _{-i}|\mathbf {h}^t)$ at stage t is the conditional probability density function (PDF) of the other player’s type $\theta _{-i}$ and $\int _0^1 B^t_i(\theta _{-i}|\mathbf {h}^t)d\theta _{-i}=1, \forall t, \mathbf {h}^t, i\in \{1,2\}$. The belief of the type is updated according to the Bayesian rule upon the arrival of the observations of actions ${a}_i^t,{a}_{-i}^t$ with the boundary condition $B_i^0$:

$$\begin{aligned} B^{t+1}_i(\theta _{-i}|[\mathbf {h}^t,{a}_i^t,{a}^t_{-i}])=\frac{B^t_i(\theta _{-i}|\mathbf {h}^t)\sigma ^t_{-i}({a}_{-i}^t|\mathbf {h}^t,\theta _{-i})}{\int _0^1 B^t_i(\hat{\theta }_{{-i}}|\mathbf {h}^t)\sigma ^t_{-i}({a}_{-i}^t|\mathbf {h}^t,\hat{\theta }_{-i})d\hat{\theta }_{-i}},i\in \{1,2\}, \end{aligned}$$

(1)

where we write $\sigma _{-i}^t(a_{-i}^t|{I}_i^t)$ as $\sigma _{-i}^t(a_{-i}^t|\mathbf {h}^t, \theta _{-i})$ for both information structures because the belief $B_i^t$ depends only on the history $\mathbf {h}^t$.

At each stage t, $\bar{J}_i^t$ is the stage utility that depends on both types $\theta _i,\theta _{-i}$, both actions $a_i^t,a_{-i}^t$, the current state $x^t$, and an external random noise $w_i^t$ with a known distribution. We introduce the external random noise to model other unknown factors that could affect the value of the stage utility. The existence of the external noise makes it impossible for each player i to directly acquire the value of the other’s type based on the combined observation of input parameters $x^t,a_1^t,a_2^t,\theta _i$ plus the output value of the utility function $\bar{J}_i^t$. In this work, we consider any additive noise with the 0 mean $\bar{J}_i^t(x^t,a_1^t,a_2^t, \theta _{i},\theta _{-i}, w_i^t)={J}_i^t(x^t,a_1^t,a_2^t, \theta _{i},\theta _{-i})+w_i^t$, which leads to an equivalent utility over the expectation of the external noise $E_{w_i^t}\bar{J}_i^t={J}_i^t, \forall x^t,a_1^t,a_2^t, \theta _{i},\theta _{-i}$. The expected payoff of a player is taken with respect to his/her time-varying belief $B_i^t$ over the type of the other player and their policy pair ${\sigma _i^t,\sigma _{-i}^t}$. Define a sequence of policies from $t'$ to T, i.e., $\sigma _i^{t':T}:=\{\sigma ^t_i \in \varSigma _i^t\}_{t=t',\cdots ,T}\in \varSigma _i^{t':T}$, then for player $i\in \{1,2\}$ with $t'$ as the initial stage, the expected accumulated utility is as follows.

$$\begin{aligned} \begin{aligned} U^{t':T}_i(\sigma _i^{t':T},\sigma _{-i}^{t':T}, \mathbf {h}^{T+1},\theta _i):=\sum _{t=t'}^{T} E_{\theta _{-i}\sim B_i^t, a_i^t\sim \sigma _i^t,a_{-i}^t\sim \sigma _{-i}^t,w_i^t} \bar{J}_i^t(x^t,a_1^t,a_{2}^t,\theta _1,\theta _{2}, w_i^t)\\ =\sum _{t=t'}^{T} \int _0^1 B^t_i(\theta _{-i} |\mathbf {h}^t) \sum _{a_{i}^t \in \mathcal {A}_i^t} \sigma _{i}^t(a_{i}^t |{I}_{i}^t) \sum _{a_{-i}^t \in \mathcal {A}_{-i}^t}\sigma _{-i}^t(a_{-i}^t |{I}_{-i}^t) J_i^t(x^t,a_1^t,a_{2}^t,\theta _1,\theta _{2}) d\theta _{-i}. \end{aligned} \end{aligned}$$

(2)

In the scenario of APTs, both players consider cumulative utility of T stages because APTs have to move stage by stage to finish the entire life circle shown in Fig. 1.

3 Solution Concepts

In this section, we investigate the perfect Bayesian Nash equilibrium (PBNE) under two different information structures. The proactive PBNE (P-PBNE) corresponds to an insider threat, i.e, agent $P_2$ can observe the policy of the principal $P_1$ at each stage. On the other hand, the reactive PBNE (R-PBNE) corresponds to the outsider threat where both players cannot observe the other’s policy at any stages. The PBNE under both information structures can be solved using dynamic programming that is consistent with a type belief update in (1).

3.1 P-PBNE

We model the scenario of APTs as a dynamic principal-agent problem as shown in Fig. 2. Attacker $P_2$ acts as an insider who knows policy $\sigma _1^t$ and determines his policy $\sigma _2^t$ as a best response to $\sigma _1^t$ that maximizes his expected cumulative utility $U_2^{t:T}$. On the defender’s side, a sophisticated defender is aware of the potential policy leakage through insider threats and anticipates the strategic response of the attacker using the attack tree analysis or proactive defenses (e.g., honeypots and honeyfiles). The described scenario leads to Definition 2 of P-PBNE. The P-PBNE may not exist or be unique. A counterexample in the static setting is shown in Remark 4.

Fig. 2.

Example of sequential plays under the proactive information structure.

Definition 1

In the two-person dynamic game with the cumulative utility function $U_i^{t':T}$ in (2) and a sequence of beliefs $B_i^t, t\in \{t',\cdots ,T\}$ in (1), define the set

$$R_2(\sigma _1^{t':T}):=\{\gamma \in \varSigma _2^{t':T}: U_2^{t':T}(\sigma _1^{t':T},\gamma )\ge U_2^{t':T}(\sigma _1^{t':T},\sigma _2^{t':T}), \forall \sigma _2^{t':T}\in \varSigma _2^{t':T}\}$$

as the best-response set of $P_2$ to $P_1$’s policy $\sigma _1^{t':T} \in \varSigma _1^{t':T}$.    $\square$

Definition 2

In the two-person dynamic Bayesian game with $P_1$ as the principal, the cumulative utility function $U_i^{t':T}$ in (2), a sequence of beliefs $B_i^t, t\in \{t',\cdots ,T\}$ in (1) and proactive information structure $\mathcal {I}_1^t:= \mathcal {H}^t \times \varTheta _1, \mathcal {I}_2^t:=\sigma _{1}^t \times \mathcal {H}^t \times \varTheta _2, t\in \{t',\cdots ,T\}$ , a sequence of strategies $\sigma _1^{*,t':T}\in \varSigma _1^{t':T}$ is called a proactive perfect Bayesian Nash equilibrium (P-PBNE) for the principal, if

$$\begin{aligned} \begin{aligned} U_1^{*,t':T}:=&\inf _{\sigma _2^{t':T}\in R_2(\sigma _1^{*,t':T})} U_1^{t':T}(\sigma _1^{*,t':T},\sigma _{2}^{t':T})\\ =&\sup _{\sigma _1^{t':T}\in \varSigma _1^{t':T}}\inf _{\sigma _2^{t':T} \in R_2(\sigma _1^{t':T})} U_1^{t':T}(\sigma _1^{t':T},\sigma _{2}^{t':T}). \end{aligned} \end{aligned}$$

(3)

A strategy $\sigma _2^{*,t':T}\in arg\max _{\sigma _2^{t':T}\in \varSigma _2^{t':T}} U_2^{t':T}(\sigma _1^{*,t':T},\sigma _{2}^{t':T}):=U_2^{*,t':T}$ is called a P-PBNE for the agent $P_2$.    $\square$

Remark 1

Since the agent’s polices in the best-response set may not be unique, principal $P_1$ in (3) considers the worst-case policy among the best-response set $R_2(\sigma _1^{*,t':T})$. If the best-response set $R_2(\sigma _1^{t':T})=\{\sigma _2^{*,t':T}\}$ is a singleton, we have $U_1^{*,t':T}=\sup _{\sigma _1^{t':T}\in \varSigma _1^{t':T}} U_1^{t':T}(\sigma _1^{t':T},\sigma _{2}^{*,t':T})$ in (3).    $\square$

3.2 R-PBNE

If each player does not know the policy of the other player at every stage, then $P_i$ chooses a sequence of behavioral strategies $\sigma ^{*,t}_i(a_i^t|\mathcal {I}_i^t)=\sigma ^{*,t}_i(a_i^t|\mathbf {h}^{t},\theta _i), t\in \{t',\cdots ,T\}$ so that she/he cannot gain if deviating unilaterally at any stage of the game, which leads to Definition 3 of R-PBNE.

Definition 3

In the two-person dynamic Bayesian game with the cumulative utility function $U_i^{t':T}$ in (2), a sequence of beliefs $B_i^t, t\in \{t',\cdots ,T\}$ in (1) and reactive information structure $\mathcal {I}_i^t:= \mathcal {H}^t \times \varTheta _i, t\in \{t',\cdots ,T\}$ for player $P_i, i \in \{1,2\}$, a sequence of strategies $\sigma _i^{*,t':T}\in \varSigma _i^{t':T}$ is called the $\varepsilon$-reactive perfect Bayesian Nash equilibrium for player $P_i$ if, for a given $\varepsilon \ge 0$, $i\in \{1,2\}$ and $\forall \theta _i\in \varTheta _i$,

$$\begin{aligned} U_i^{t':T}(\sigma _i^{*,t':T},\sigma _{-i}^{*,t':T}, \mathbf {h}^{T+1},\theta _i)\ge U_i^{t':T}(\sigma _i^{t':T},\sigma _{-i}^{*,t':T}, \mathbf {h}^{T+1},\theta _i)-\varepsilon , \forall \sigma _i^{t':T} \in \varSigma _i^{t':T}. \end{aligned}$$

If $\varepsilon =0$, we have a reactive perfect Bayesian Nash equilibrium (R-PBNE).    $\square$

Remark 2

The belief update (1) is strongly consistent as it applies to all possible histories from stage t to $t+1$: even when history $\mathbf {h}^t$ has probability 0. In other word, belief update (1) is valid starting from all states, even if the equilibrium trajectory does not contain that state. The strong time consistency indicates perfectness, i.e., even some trembling hand mistakes happen at stage $\hat{t}$ and an unexpected state is reached, the player can still achieve optimality from that new state on by applying $\sigma _{-i}^{*, \hat{t} :T}$. Thus, PBNE strategies can adapt to unexpected changes.    $\square$

3.3 Dynamic Programming

Given the type belief at every stage, we can use dynamic programming to find the PBNE in a backward fashion because of the tree structure and the finite horizon. Define the value function $V_i^{t}(\mathbf {h}^{t},\theta _i):=U_i^{t: T}(\sigma _i^{*,t:T},\sigma _{-i}^{*, t:T}, \mathbf {h}^{t+1},\theta _i)$ as the optimal utility-to-go function at stage t. Let $V_i^{T+1}(\mathbf {h}^{T+1},\theta _i):=0$ be the boundary condition of the value function, we have the following recursive system equations involving both players’ policies:

$$\begin{aligned} \begin{aligned}&V_1^{t}(\mathbf {h}^{t},\theta _1)= \sup _{\sigma _1^{t}} E_{\theta _{2} \sim B_1^{t}, a_1^{t}\sim \sigma _1^{t},a_2^{t}\sim \sigma _{2}^{*,t}} [ V_1^{t+1}(\{\mathbf {h}^{t},a_1^{t},a_{2}^{t}\},\theta _1) + J_1^{t}(x^{t}, a_1^{t},a_{2}^{t},\theta _1,\theta _{2})]; \\&V_2^{t}(\mathbf {h}^{t},\theta _2)= \sup _{\sigma _2^{t}} E_{\theta _{1}\sim B_2^{t},a_2^{t}\sim \sigma _2^{t},a_1^{t}\sim \sigma _{1}^{*,t}} [ V_2^{t+1}(\{\mathbf {h}^{t},a_1^{t},a_{2}^{t}\},\theta _2) + J_2^{t}(x^{t}, a_1^{t},a_{2}^{t},\theta _1,\theta _{2})], \end{aligned} \end{aligned}$$

(4)

where $\sigma _1^{*,t},\sigma _2^{*,t}, t\in \{0,\cdots ,T\}$ are the PBNE policy pair. Figure 3 summarizes the forward update of the history $\mathbf {h}^t$, belief $B_i^t$, and policy $\sigma _i^t$ from stage $t-1$ to t. The challenge is that the type belief is not directly known at each stage. The forward belief update in (1) depends on the PBNE strategy. However, the backward computation of PBNE strategy in (4) also couples with the belief as shown in Fig. 4. Hence, we need to find the PBNE strategy consistent with the belief at each stage.

Fig. 3.

A two-player stage transition from stage $t-1$ to stage t. The transition loop iterates from stage $t=0$ to the terminal stage $t=T-1$, which constitutes the entire multi-stage dynamic game. Both players’ history of actions are fully observable yet their types are private information to the other player. Each player $P_i$ learns to update his/her belief $B_i^t \in \bigtriangleup \varTheta _{-i}$ of the other’s private type $\theta _{-i}$ based on the policy of the other player $\sigma _{-i}^t$ at stage t.

4 Conjugate Prior Learning

If we assume that $B^{t}_i$ is of the beta distribution and the strategy $\sigma _{-i}^t$ of the other player corresponds to a binomial distribution, then $B^{t+1}_i$ is also a beta distribution with updated hyperparameters. Figure 5 illustrates how a defender can learn the type of the attacker to decrease the probability of attacks. An expanded state includes the parameters of the distribution, and we can form one backward dynamic program with a larger dimension to unify the forward and backward processes. Finally, as the type-related policy makes it challenging to compute the PBNE for the expanded-state dynamic programming, we use a mathematical programming approach to compute R-PBNE. The P-PBNE can be analyzed likewise.

Fig. 4.

The backward policy computation and the forward belief update are coupled.

Table 1. Stage utility of two players. Player $P_2$ takes action $a^T_2=1$ with probability $q(\theta _2)$.

4.1 State Independent Belief Formation

At each stage t, player $-i$ divides the action space of the other player $P_i$ into $K_{i}+1$ time-invariant set of categories $\mathcal {C}^i_j$, i.e., $\mathcal {A}_i^t=\{\cup \mathcal {C}^i_j\}_{j=0,1, \cdots , K_i},\forall t, i=1,2$ and mutual exclusive $\mathcal {C}^i_j\,\cap \,\mathcal {C}^i_l = \emptyset , \forall j\ne l, i=1,2$. Then, each $a_{-i}^t$ uniquely corresponds to one category and we can transform $\sigma ^t_{-i}(a_{-i}^t|\mathbf {h}^t,\theta _{-i})$, the distribution of $a_{-i}^t$, into a distribution of the corresponding category $k_{-i}^t\in \{0,1,\cdots , K_i\}$.

After changing the history of actions $\mathbf {h}^t=\{a_1^0,\cdots ,a_1^{t-1},a_2^0,\cdots ,a_2^{t-1}\}$ into the history of corresponding categories $\tilde{\mathbf {h}}^t:=\{k_1^0,\cdots ,k_1^{t-1},k_2^0,\cdots ,k_2^{t-1}\}$, we rewrite the Bayesian update of the belief with respect to the category.

$$\begin{aligned} B^{t+1}_i(\theta _{-i}|[\mathbf {\tilde{h}}^t,{k}_i^t,{k}^t_{-i}])=\frac{B^t_i(\theta _{-i}|\mathbf {\tilde{h}}^t)\sigma ^t_{-i}({k}_{-i}^t|\mathbf {\tilde{h}}^t,\theta _{-i})}{\int _{0}^1 B^t_i(\hat{\theta }_{{-i}}|\mathbf {\tilde{h}}^t)\sigma ^t_{-i}({k}_{-i}^t|\mathbf {\tilde{h}}^t,\hat{\theta }_{-i}) d\hat{\theta }_{-i}},i=1,2. \end{aligned}$$

(5)

The distribution of $\sigma _{-i}^t$ is assumed to be a binomial distribution with the parameter $q=\theta _{-i}$ and $N=K_{-i}$. The probability mass function (PMF) of category k is $\Pr (k)=\left( {\begin{array}{c}N\\ k\end{array}}\right) q^k (1-q)^{N-k}.$ The prior belief $B_i^t$ over the other player’s private type $\theta _{-i} \in [0,1]$ is assumed to be a beta distribution with hyperparameters $\alpha$ and $\beta$. With gamma function $\varGamma (n)=(n-1)!$ and $Be(\alpha , \beta )=\frac{\varGamma (\alpha )\varGamma (\beta )}{\varGamma (\alpha +\beta )}$, the probability density function (PDF) of the type is$Beta^{\alpha ,\beta }(q)=\frac{q^{\alpha -1}(1-q)^{\beta -1}}{Be(\alpha , \beta )}.$ Since binomial and Beta distributions are conjugate, the posterior belief conserves to be a Beta distributed with updated hyperparameters $(\alpha _i^{t+1},\beta _i^{t+1})=(\alpha _i^t+k_i^t,\beta _i^t+K_i-k_i^t), i=1,2$, where $k_i^t$ is the category that the action of player $P_i$ at stage t falls into. Moreover, we can express in the closed form for player $P_i$’s belief of the other player $-i$’s type at any stage t with parameters $\alpha _{-i}^t=\alpha _{-i}^0+\sum _{t'=1}^t k_{-i}^{t'}$ and $\beta _{-i}^t=\beta _{-i}^0+t K_i-\sum _{t'=1}^t k_{-i}^{t'}$, where $(\alpha _{-i}^0,\beta _{-i}^0)$ is the prior distribution. Thus, every node just needs to count the frequency of categories of the other player’s action at each stage t. Finally, we transform the type belief conditioned on the categories back to the belief conditioned on the corresponding actions using the hard de-aggregation, i.e., $B_i^{t+1}(\theta _{-i}|\mathbf {\tilde{h}}^t,a_i^t,a_{-i}^t)=B_i^{t+1}(\theta _{-i}|\mathbf {\tilde{h}}^t,{a}_i^t,\bar{a}_{-i}^t)=B_i^{t+1}(\theta _{-i}|\mathbf {\tilde{h}}^t,k_i^t,k_{-i}^t), \forall a_{i}^t\in \mathcal {C}^{i}_{k_i^t}, \forall {a}_{-i}^t,\bar{a}_{-i}^t \in \mathcal {C}^{-i}_{k_{-i}^t}$. Here, hard de-aggregation means that actions $a_{-i}^t, \bar{a}_{-i}^t$ correspond to the same category $k_{-i}^t$ share the same belief distribution of the type and approximate the true type belief distribution.

Example 1

Consider a one-sided, incomplete information case where the system type is known to the user who has a private continuous type satisfying beta distribution $(\alpha ,\beta )$. $P_1$ classifies all possible actions of $P_2$ into $K+1$ categories, and a larger category index means a higher threat level. For example, a low occupancy of system resources is in the category 1, yet a frequent and longtime resource occupancy belongs to the category K because of its potential intention to block the system. Note that the category of action observation in one-shot does not reveal the type because a legitimate user may sometimes also occupy the resource for a long time and an attacker can behave legitimately to evade detection. However, since the payoff function is type-related, neither the legitimate user will always have longtime occupancy, nor the attacker can always hide. Thus, the belief will approach the truth after the multi-stage belief update based on the action observations.    $\square$

4.2 State-Dependent Belief Formation

Since the same action can lead to different payoffs at different states, we generalize our results to classify the action according to the state and the action at stage t. We divide a composed set $\mathcal {D}^t_i:=\mathcal {X}^t\times \mathcal {A}_i^t$ into $K_i+1$ mutual exclusive partitions $\mathcal {\bar{C}}^i_j$, i.e., $\mathcal {D}_i^t=\{\cup \mathcal {\bar{C}}^i_j\}_{j=0,1, \cdots , K_i},\forall t, i=1,2$ and $\mathcal {\bar{C}}^i_j \cap \mathcal {\bar{C}}^i_l = \emptyset , \forall j\ne l, i=1,2$.

Example 2

Let the set of nodes of stage t in Fig. 6 be the possible states $x^t\in \mathcal {X}^t$. The state represents the value of the reactor pressure. The defender tries to stabilize the pressure at the reference value to guarantee the product quality and process safety in chemical plants. Reference values $n_3^0, \cdots , n_3^T$ and the possible pressure state $x^t$ could be stage-varying. The attacker aims to change the pressure. A substantial deviation from the standard pressure brings a considerable reward to attackers. The state transition is Markov, i.e., the current pressure $x^t$ and the both players’ actions determine the pressure at stage $t+1$. It could be challenging to determine the legitimacy of the actions based merely on whether the user increases or decreases the pressure. The state of the pressure can provide additional information to determine the criticality of operations. For example, it is clearly more dangerous when a user aims to increase the pressure when the current pressure value already far exceeds the standard pressure.    $\square$

Fig. 5.

The multi-stage learning scheme of attacker’s type mitigates the probability of attacks.

Fig. 6.

A multi-stage game with a finite horizons T and a Markov state transition $x^{t+1}=f^t(x^t,a_1^t,a_2^t)$.

4.3 Expanded State and Sufficient Statistic

At each stage t, an expanded state $y^t=\{x^t,\alpha _i^t,\beta _i^t,\alpha _{-i}^t,\beta _{-i}^t\}$ contains the original cyber state $x^t$ plus the belief state $B_i^t, B_{-i}^t$ represented by the hyperparameters from the beta distribution. Define new state transition function $y^{t+1}=\tilde{f}^t(y^t,a_1^t,a_2^t)$ where $x^{t+1}={f}^t(x^t,a_1^t,a_2^t)$ and $(\alpha _i^{t+1},\beta _i^{t+1})=(\alpha _i^t+k_i^t,\beta _i^t+K_i-k_i^t), i=1,2$. Because of $\alpha _{i}^t+\beta _i^t=\alpha _{i}^0+\beta _i^0+tK_i$, we only need $\alpha _{i}^t$ (or $\beta _i^t$) to uniquely determine the $\beta _i^t$ (or $\alpha _{i}^t$). We choose $\alpha _{i}^0=\beta _i^0=1$ as the prior belief, then $\alpha _i^t,\beta _i^t\in [1,\cdots ,1+tK_i]$, and the dimension of the expanded state $y^t$ is $|\mathcal {X}_i|^t \times (1+tK_i)$. Define ${\tilde{I}}_i^t=\{y^t,\theta _i\}$ for reactive information structure (${\tilde{I}}_i^t=\{\sigma _{-i}^t, y^t,\theta _i\}$ for reactive information structure), $\tilde{I}_i^t$ is the sufficient statistic of ${I}_i^t$ because the history $\mathbf {h}^t$ uniquely determines the cyber state $x^t$ as well as the belief state. With the Markov assumption that $\tilde{\sigma }_i^t(a_i^t|{\tilde{I}}_i^t)=\sigma _i^t(a_i^t|{{I}}_i^t)$, the new value function $\tilde{V}_i^t(y^t,\theta _i)$ is sufficient to determine the original value function $V_i^{t}(\mathbf {h}^{t},\theta _i)$. Unlike the entire history, the carnality of state space does not increase with the number of stages, which greatly reduces the computation complexity. By letting $\tilde{V}_i^{T+1}(y^{T+1},\theta _i):=0$, we have the following recursive form for $t=0,\cdots ,T$, i.e.,

$$\begin{aligned} \begin{aligned} \tilde{V}_1^{t}(y^{t},\theta _1)=&\sup _{\tilde{\sigma }_1^{t}} E_{\theta _{2} \sim \beta _1^{t}, a_1^{t}\sim \tilde{\sigma }_1^{t},a_2^{t}\sim \tilde{\sigma }_{2}^{*,t}} [ \tilde{V}_1^{t+1}(\tilde{f}^t(y^t,a_1^t,a_2^t),\theta _1) + J_1^{t}(x^{t}, a_1^{t},a_{2}^{t},\theta _1,\theta _{2})]; \\ \tilde{V}_2^{t}(y^{t},\theta _2)=&\sup _{\tilde{\sigma }_2^{t}} E_{\theta _{1}\sim \beta _2^{t},a_2^{t}\sim \tilde{\sigma }_2^{t},a_1^{t}\sim \tilde{\sigma }_{1}^{*,t}} [ \tilde{V}_2^{t+1}(\tilde{f}^t(y^t,a_1^t,a_2^t),\theta _2) + J_2^{t}(x^{t}, a_1^{t},a_{2}^{t},\theta _1,\theta _{2})],\\ \end{aligned} \end{aligned}$$

Since the expanded state transition incorporates the parameter of the belief update, we can compute the optimal utility-to-go function from stage T back to 0 w.r.t. the expanded state space to obtain a consistent belief-PBNE pair at each stage.

4.4 Computations of Static and Dynamic Bayesian Games

In this section, we formulate a mathematical program to compute the equilibrium for both static and multi-stage Bayesian bi-matrix games. The computation of static Bayesian games serves as a building block for the computation of the PBNE for the multi-stage games. The stage-varying belief leads to a nonzero-sum utility function. We also investigate the class of two-by-two matrices and provide further analytical insights. In the static setting, i.e., $T=0$, the P-PBNE degenerates to be the Bayesian Stackelberg equilibrium (BSE) with leader $P_1$ and follower $P_2$. The R-PBNE degenerates to be a Bayesian Nash equilibrium (BNE). In this section, we focus on the analysis of BNE and the analysis of BSE can be done similarly. Define $m_i^t:=|\mathcal {A}_i^t|$ as the total number of alternatives $P_i$ can take at stage t. Let vector $p^t(\theta _1)=[p^t_1(\theta _1),\cdots ,p^t_{m_2^t}(\theta _1)]' \in \mathbb {R}^{m_2^t \times 1}$ and $q^t(\theta _2)=[q^t_1(\theta _2),\cdots ,q^t_{m_1^t}(\theta _2)]' \in \mathbb {R}^{m_1^t \times 1}$ be the outcome vector of the behavioral strategy $\sigma ^t_1$ and $\sigma ^t_2$, respectively. For example, $p_l^t(\theta _1)$ is the probability of $P_1$ taking the l-th action (i.e., $a_1^t=l, l \in \{1,\cdots ,m_1^t\}$) when her type is $\theta _1$ at stage t. Notation ‘$'$’ is the transpose of a vector and $l_{m^t_i }:=[1,1,\cdots ,1]'\in \mathbb {R}^{m^t_i \times 1}$. Player i’s utility matrix $\mathcal {J}_i (x^t,\theta _1,\theta _2), i\in \{1,2\}$ is a $m_1^t \times m_2^t$ matrix where the element (k, l) is the value of $J_i^t(x^t, a_1^t=k,a_2^t=l, \theta _1, \theta _2)$. $P_1$ is the row player while $P_2$ is the column player. Both players are rational and aim at maximizing their own utilities.

Final Stage/Static Case. The computation starting from the final stage T with a given belief $B_i^T$ is the same as a static Bayesian game. Thus, we suppress the superscript of T, i.e., $m_i:=m_i^T, p(\theta _1):=p^T(\theta _1),q(\theta _2):=q^T(\theta _2)$. Also, we write $\mathcal {J}_i (x^T,\theta _1,\theta _2)$ as $\mathcal {J}_i (\theta _1,\theta _2)$ because the state $x^T$ is known.

Theorem 1

A strategy pair $(p^*(\theta _1),q^*(\theta _2))$ constitutes a mixed-strategy Bayesian Nash equilibrium to the bi-matrix Bayesian game $(\mathcal {J}_1(\theta _1,\theta _2), \mathcal {J}_2(\theta _1,\theta _2))$ under continuous private type $\theta _i\in \varTheta _i$ and a public belief $B_i, i\in \{1,2\}$, if and only if, there exists a scalar function pair $(s^*(\theta _1),w^*(\theta _2))$ such that $(p^*(\theta _1),q^*(\theta _2),s^*(\theta _1),w^*(\theta _2))$ is a solution to the following mathematical program:

$$\begin{aligned} \begin{aligned} \sup _{q,p,s,w}\quad&E_{\theta _1}s(\theta _1) +E_{\theta _2}w(\theta _2)+ E_{\theta _1} E_{\theta _2}\{p(\theta _1)'[\mathcal {J}_1(\theta _1,\theta _2)+\mathcal {J}_2(\theta _1,\theta _2)]q(\theta _2)\}\\ s.t.\quad&E_{\theta _1}[\mathcal {J}_2'(\theta _1,\theta _2)p(\theta _1)]\le -w(\theta _2)l_{m_2} , \forall \theta _2, \ \ q(\theta _2)'l_{m_2}=1,q(\theta _2)\ge 0, \forall \theta _2,\\&E_{\theta _2}[\mathcal {J}_1(\theta _1,\theta _2)q(\theta _2)]\le -s(\theta _1) l_{m_1}, \ \forall \theta _1, \ \ \ p(\theta _1)'l_{m_1}=1, p(\theta _1)\ge 0, \forall \theta _1. \end{aligned} \end{aligned}$$

(6)

The computation challenge of the continuous Bayesian bi-matrix program (6) is the infinite-dimensional constraints induced by the continuous type space. We can obtain approximate solutions by sampling the bounded type space $\varTheta _i:=[0,1]$ and solve a high-dimensional bilinear program. The bias between the value of the objective function and value 0 measures the approximation accuracy.

Proof

Define the simplex set $\varGamma :=\{p\in \mathcal {R}^{m_1\times 1} |p 'l_{m_1}=1, p \ge 0\}$. We first prove that the mixed-strategy is the solution to the bilinear program. The constraints imply a non-positive objective function. If $p^*(\theta _1)\in \varGamma ,q^*(\theta _2)\in \varGamma$ is a Bayesian Nash equilibrium pair, i.e.,

$$\begin{aligned}&q(\theta _2)' E_{\theta _1}[\mathcal {J}_2'(\theta _1,\theta _2)p^*(\theta _1)]\le (q^*(\theta _2))' E_{\theta _1}[\mathcal {J}_2'(\theta _1,\theta _2)p^*(\theta _1)] , \forall \theta _2, \forall q(\theta _2)\in \varGamma , \\&p(\theta _1)'E_{\theta _2}[\mathcal {J}_1(\theta _1,\theta _2)q^*(\theta _2)]\le (p^*(\theta _1))'E_{\theta _2}[\mathcal {J}_1(\theta _1,\theta _2)q^*(\theta _2)], \forall \theta _1, \forall p(\theta _1)\in \varGamma . \\ \end{aligned}$$

Then the quadruple $p^*(\theta _1),q^*(\theta _2), w^*(\theta _2)=-E_{\theta _1}[p^*(\theta _1)'\mathcal {J}_2(\theta _1,\theta _2)q^*(\theta _2)], s^*(\theta _1)=-E_{\theta _2}[p^*(\theta _1)'\mathcal {J}_1(\theta _1,\theta _2)q^*(\theta _2)]$ is a feasible solution to the program (because it satisfies all the constraints) and the value of the objective function is 0, which is the maximum solution to the non-positive objective function and provides the value function ${V}_2(\theta _2)=\max _{q(\theta _2)}E_{\theta _1}[p^*(\theta _1)'\mathcal {J}_2(\theta _1,\theta _2)q(\theta _2)]=-w^*(\theta _2), \forall \theta _2$ and ${V}_1(\theta _1)=\max _{p(\theta _1)}E_{\theta _2}[p(\theta _1)'\mathcal {J}_1(\theta _1,\theta _2)q^*(\theta _2)]=-s^*(\theta _1), \forall \theta _1.$ Conversely, if the program has an optimal solution $p^*(\theta _1),q^*(\theta _2), w^*(\theta _2),s^*(\theta _1)$, then

$$\begin{aligned} E_{\theta _1}s(\theta _1) +E_{\theta _2}w(\theta _2)+ E_{\theta _1} E_{\theta _2}\{p(\theta _1)'[\mathcal {J}_1(\theta _1,\theta _2)+\mathcal {J}_2(\theta _1,\theta _2)]q(\theta _2)\}=0. \end{aligned}$$

(7)

and

$$\begin{aligned} \begin{aligned}&q(\theta _2)' E_{\theta _1}[\mathcal {J}_2'(\theta _1,\theta _2)p^*(\theta _1)]\le -w^*(\theta _2), \forall \theta _2, \forall q(\theta _2)\in \varGamma \\&p(\theta _1)'E_{\theta _2}[\mathcal {J}_1(\theta _1,\theta _2)q^*(\theta _2)]\le -s^*(\theta _1), \forall \theta _1, \forall p(\theta _1)\in \varGamma . \end{aligned} \end{aligned}$$

(8)

In particular, we pick $p(\theta _1)=p^*(\theta _1), q(\theta _2)=q^*(\theta _2)$ to arrive at

$$\begin{aligned} \begin{aligned} (q^*(\theta _2))' E_{\theta _1}[\mathcal {J}_2'(\theta _1,\theta _2)p^*(\theta _1)]\le -w^*(\theta _2), \forall \theta _2,\\ (p^*(\theta _1))'E_{\theta _2}[\mathcal {J}_1(\theta _1,\theta _2)q^*(\theta _2)]\le -s^*(\theta _1), \forall \theta _1. \end{aligned} \end{aligned}$$

(9)

Combined with (7), the inequality in (9) turns out to be an equality and equation (8) becomes

$$\begin{aligned}&q(\theta _2)' E_{\theta _1}[\mathcal {J}_2'(\theta _1,\theta _2)p^*(\theta _1)]\le (q^*(\theta _2))' E_{\theta _1}[\mathcal {J}_2'(\theta _1,\theta _2)p^*(\theta _1)], \forall \theta _2,\\&p(\theta _1)'E_{\theta _2}[\mathcal {J}_1(\theta _1,\theta _2)q^*(\theta _2)]\le (p^*(\theta _1))'E_{\theta _2}[\mathcal {J}_1(\theta _1,\theta _2)q^*(\theta _2)], \forall \theta _1, \end{aligned}$$

which verifies that $(p^*(\theta _1),q^*(\theta _2))$ is a BNE.    $\square$

For the one-sided information, the information-superior player $P_2$ knows the type of $P_1$ and the information-inferior player $P_1$ does not know the type of $P_2$. Since the $P_1$’s type is known, we can suppress writing $\mathcal {J}_i,p,s$ as a function of $\theta _1$. Following similar proof steps, we have Corollary 1.

Corollary 1

A strategy vector pair $(p^*,q^*(\theta _2))$ constitutes a Bayesian Nash equilibrium to the bi-matrix Bayesian game $(\mathcal {J}_1(\theta _2), \mathcal {J}_2(\theta _2))$ under private type $\theta _2$ and the public type belief $B_2$, if and only if, there exists a scalar function pair $(s^* ,w^*( \theta _2))$ such that $(p^*,q^*(\theta _2),s^*,w^*(\theta _2))$ is a solution to the mathematical program:

$$\begin{aligned} \sup _{q,p,s,w} \quad&E_{\theta _2}\{ p'[\mathcal {J}_1(\theta _2)+\mathcal {J}_2(\theta _2)]q(\theta _2)+w(\theta _2)\}+s\\ s.t \quad&\mathcal {J}_2'(\theta _2)p \le -w(\theta _2)l_{m_2} , \forall \theta _2, \quad q(\theta _2)'l_{m_2}=1,q(\theta _2)\ge 0, \forall \theta _2, \\&E_{\theta _2}[\mathcal {J}_1(\theta _2)q(\theta _2)]\le -s l_{m_1}, \quad p'l_{m_1}=1, p\ge 0. \end{aligned}$$

Two-by-Two Matrix. We specify $m_1=2,m_2=2$ with utility functions of one-sided information as shown in Table 1. Let $V_1=E_{\theta _2\sim B_2}[\hat{V}_1]=\sup _p E_{\theta _2}[R_{21}^1-R_{11}^1+q^*(\theta _2)(R_{22}^1-R_{12}^1-R_{21}^1+R_{11}^1)]p+E_{\theta _2}[R_{11}^1+(R_{12}^1-R_{11}^1)q^*(\theta _2)]$ be the expected value function under the belief $B_2$ of private type $\theta _2$ and $\hat{V}_2=\sup _{q(\theta _2)} [R_{21}^2-R_{11}^2+p^*(R_{22}^2-R_{12}^2-R_{21}^2+R_{11}^2)]q(\theta _2)+R_{11}^2+(R_{12}^2-R_{11}^2)p^*$ be the value function of complete information. The best response of $P_1$ is $p^*=\mathbf {1}_{\{E[R_{21}^1-R_{11}^1+q^*(\theta _2)(R_{22}^1-R_{12}^1-R_{21}^1+R_{11}^1)]>0\}}$ and the best response of $P_2$ is $q^*(\theta _2)=\mathbf {1}_{\{R_{21}^2-R_{11}^2+p^*(R_{22}^2-R_{12}^2-R_{21}^2+R_{11}^2)>0\}}$. The BNE is the result of the intersection of two best-response functions. Since $p^*$ is not a function of type, $p^*=0$ or 1 is the only stable value¹. Then, $P_2$ as a function of type is a threshold policy, which leads to Lemma 1.

Lemma 1

For the one-sided information bi-matrix Bayesian game with utility functions in Table 1 under the BNE solution concept, the information-inferior player adopts a pure policy, and the information-superior player adopts a threshold policy.    $\square$

In particular, if $p^*=1$, we have $q^*(\theta _2)=\mathbf {1}_{\{R_{21}^2-R_{11}^2+(R_{22}^2-R_{12}^2-R_{21}^2+R_{11}^2)>0\}}=\mathbf {1}_{\{R_{22}^2(\theta _2)>R_{12}^2(\theta _2)\}}$, which should be consistent with the corresponding condition $E[R_{21}^1-R_{11}^1+q(\theta _2)(R_{22}^1-R_{12}^1-R_{21}^1+R_{11}^1)]>0$. Likewise, we have a consistent condition for $p^*=0$. Theorem 2 summarizes these two necessary conditions for $B_2$.

Theorem 2

There exists at most two mixed-strategy Bayesian Nash equilibriums for the one-sided information bi-matrix game with utility functions shown in Table 1, private type $\theta _2\in \varTheta _2$, and public type belief $B_2(\theta _2)$. First, the policy pair $p^*=1,q^*(\theta _2)=\mathbf {1}_{\{R_{22}^2(\theta _2)>R_{12}^2(\theta _2)\}}$ is a BNE if

$$\begin{aligned}&\int _{\theta _2\in \varTheta _2} (R_{21}^1(\theta _2)-R_{11}^1(\theta _2))\mathbf {1}_{\{R_{22}^2(\theta _2)<R_{12}^2(\theta _2)\}}B_2(\theta _2)d\theta _2+\\&\int _{\theta _2\in \varTheta _2} (R_{22}^1(\theta _2)-R_{12}^1(\theta _2))\mathbf {1}_{\{R_{22}^2(\theta _2)>R_{12}^2(\theta _2)\}}B_2(\theta _2)d\theta _2 >0, \end{aligned}$$

Second, the policy pair $p^*=0,q^*(\theta _2)=\mathbf {1}_{\{R_{21}^2(\theta _2)>R_{11}^2(\theta _2)\}}$ is a BNE if

$$\begin{aligned}&\int _{\theta _2\in \varTheta _2} (R_{21}^1(\theta _2)-R_{11}^1(\theta _2))\mathbf {1}_{\{R_{21}^2(\theta _2)<R_{11}^2(\theta _2)\}}B_2(\theta _2)d\theta _2+\\&\int _{\theta _2\in \theta _2} (R_{22}^1(\theta _2)-R_{12}^1(\theta _2))\mathbf {1}_{\{R_{21}^2(\theta _2)>R_{11}^2(\theta _2)\}}B_2(\theta _2)d\theta _2<0. \end{aligned}$$

Remark 3

We cannot apply the indifference principle as in Sect. 5.2 to compute the equilibrium under incomplete information because the information-inferior player unknown the type $\theta _2$ is incapable of making decision p as a function of $\theta _2$.    $\square$

Dynamic Case. Recall the dynamic programming equation in Sect. 4.3:

$$\begin{aligned} \tilde{V}_i^{t}(y^{t},\theta _i)= \sup _{\tilde{\sigma }_i^{t}} E_{\theta _{-i} \sim \beta _i^{t}, a_1^{t}\sim \tilde{\sigma }_1^{t},a_2^{t}\sim \tilde{\sigma }_{2}^{*,t}} [ \tilde{V}_i^{t+1}(y^{t+1},\theta _i) + J_i^{t}(x^{t}, a_1^{t},a_{2}^{t},\theta _1,\theta _{2})]. \end{aligned}$$

The computation of the static BNE serves as building blocks to the computation of dynamic R-PBNE via the following procedures. At the last stage T with a known boundary condition $\tilde{V}_i^{T+1}$, the value function $\tilde{V}_i^{T+1}+J_i^T$ is the same as the static objective function $J_i$ and we can compute the equilibrium policy as well as the value function $\tilde{V}_i^{T}$ via Theorem 1. At the second last stage $T-1$, since both $\tilde{V}_i^{T}$ and $J_i^{T-1}$ are known, we can treat $\tilde{V}_i^{T}+ J_i^{T-1}$ as the new static objective function $J_i$ and repeat the analysis in the static setting. In a backward fashion, it is clear that at stage $t\in \{0,1,\cdots ,T-1\}$, we only need to replace the static objective function $J_i$ to the dynamic objective function $\tilde{V}_i^{t}+ J_i^{t-1}$ to obtain the R-PBNE policy $\tilde{\sigma }_i^{t-1}$ at each stage $t-1$ for each player $P_i$.

5 Case Study

Similar to our previous work [8], we consider a four-stage Bayesian game with one-sided incomplete information, i.e., the information-inferior player $P_1$ forms a belief of attacker $P_2$’s type $\theta _2$ via a beta distribution with parameters $\alpha _2^t,\beta _2^t$. The first three stages model the cyber network transition while the last stage model the sensor compromise of a physical plant, i.e., the benchmark Tennessee Eastman (TE) chemical process [2]. Since APTs benefit mainly from their specific targets, i.e., sabotage the TE process, we assume a negligible utility for the intermediate stage $t=0,1,\cdots ,T-1$ in this case study. However, the scenario is still multi-stage rather than static because APTs have to go through the intermediate stages stealthily to reach their final targets. Their actions at the intermediate stages will affect the belief and the state at the final stage. The state $x^T\in \mathcal {X}^T:=\{0,1,2\}$ represents which sensors the attacker can control in the TE process. If the attacker changes the sensor reading, the system states such as the pressure and the temperature may deviate from the desired value, which degrades the product quality and even causes the shutdown of the entire process if the deviation exceeds the safety threshold. To reach a favorable state at the final stage, e.g., control the essential sensors of the TE process, the attacker has to behave aggressively at the intermediate stages, e.g., escalates the privilege, which thus increases the risk of being identified as malicious. Both players have a binary action set $\mathcal {A}_i^t=\{0,1\}$ where $a_i^t=1$ means taking either aggressive or defensive actions and $a_i^t=0$ means no special operation performed. As stated in the Sect. 2, the action is observable, yet the one-shot observation does not directly reveal the type. Let $K_2=1$, the secure category $k=0$ includes $a_2^t=0$ and $k=1$ includes $a_2^t=1$, respectively. The utility at the last stage is shown in Table 1 and defined as follows. The operation time under state $x^T$ is the output of the mapping $C: \mathcal {X}^T \mapsto \mathbb {R}^+$, which can be determined using numerical experiments of the TE process under different sensor-compromise scenarios. Since the defender’s stage utility should be proportional to the operation time $C(x^T)$, the normalized defender’s stage reward is $R_{11}^1=C(x^T),R_{12}^1=0.5C(x^T)(1-\theta _2),R_{21}^1=0.9C(x^T),R_{22}^1=0.9C(x^T)$, which satisfies two conditions. First, $R_{21}^1=R_{22}^1$, $R_{11}^1\ge R_{21}^1$: The defensive action prevents attacking loss while incurs a cost to deploy. Second, $R_{12}^1\le R_{21}^1$: Attacks cause a loss in lack of active defenses. Moreover, the loss is proportional to the type, i.e., $R_{12}^1$ is a monotonically decreasing function in type $\theta _2$. On the other hand, we assign utility $R_{11}^2=2,R_{12}^2=10\theta _2,R_{21}^2=4\theta _2,R_{22}^2=0$ to attackers according to the following reasonable conditions.

• 1. Attackers obtain $R_{12}^2$ when attacks happen without defenses and $R_{21}^2$ when $P_2$ does not attack yet wastes system resources by deceiving defenders to defend. Both cases benefit attackers proportionally to their type, i.e., $R_{21}^2$ and $R_{12}^2$ are monotonically increasing functions in type $\theta _2$. Moreover, the latter scenario brings more attacking rewards for the same type, i.e., $R_{21}^2(\theta _2)\ge R_{12}^2(\theta _2), \forall \theta _2$.

• 2. Attackers $\theta _2\ge \bar{\theta }_2$ benefit from inflicting damages and deceiving defenders to defend, i.e., $R_{12}^2(\theta _2)\ge R_{11}^2(\theta _2), R_{21}^2(\theta _2)\ge R_{11}^2(\theta _2), \forall \theta _2\ge \bar{\theta }_2$. However, benign users $\theta _2<\bar{\theta }_2$ benefit from a normal operation of the system, i.e., $R_{12}^2(\theta _2)\le R_{11}^2(\theta _2), R_{21}^2(\theta _2)\le R_{11}^2(\theta _2), \forall \theta _2<\bar{\theta }_2$.

• 3. The no-attack-no-defense scenario outweighs the scenario when $P_2$ attacks yet $P_1$ defends because no damages are incurred and the defender obtains extra information about the attacker. Thus, $R_{11}^2(\theta _2)\ge R_{22}^2(\theta _2), \forall \theta _2$.

5.1 The Final Stage with One-Sided Incomplete Information

At the terminal stage T, we need to solve the static Bayesian game for each possible expanded state $y^T$. Suppose that defender takes action $a_1^T=1$ with probability $p(y^T)$ and attacker takes action $a_2^T=1$ with probability $q(y^T,\theta _2)$. At the last stage, the accumulated utility function is the same as the stage utility function. Since all elements $R^1_{ij}, i,j\in \{1,2\}$ of the utility matrix is linear in $C(x^T)\ne 0$, both players’ policies are not a function of $C(x^T)$ and we can consider a normalized value function ${\hat{V}_1^T(y^T, \theta _2)}/{ C(x^T)}= \max _{p(y^t)} [0.5 q^*(y^T,\theta _2) (1+\theta _2)-0.1]p(y^T) +1-0.5( 1+\theta _2) q^*(y^T,\theta _2),$ where $p^*,q^*$ is the PBNE policy pair. Since defender does not know the type value, she can only form an expected value function ${V}_1^T(y^T) = \max _{p(y^T)} \int _0^1Beta^{\alpha _2^T,\beta _2^T}(\theta _{2})[ \hat{V}_1^T(y^T, \theta _2)]d\theta _2.$ The attacker as the information-superior player knows the type, and thus his objective function $\hat{V}_2^T(y^T,\theta _2)$ is

$$\begin{aligned} \max _{q(y^T,\theta _2)} [2p^*(y^T)-2+10\theta _2-14p^*(y^T)\theta _2]q(y^T,\theta _2)+2(1-p^*(y^T))+4\theta _2p^*(y^T). \end{aligned}$$

Bayesian Nash Equilibrium. Bayesian Nash equilibrium corresponds to the intersection of two best-response curves $p^*$ and $q^*$, as stated in Sect. 4.4. We use Theorem 2 to show the existence and uniqueness of the BNE, i.e., $q^*=\mathbf {1}_{\{\theta _2>0.2\}}, p^*=0$ when the condition $\int _{0.2}^1Beta^{\alpha _2^T,\beta _2^T}(\theta _2) (1+\theta _2)d\theta _2<0.2$ is true. Small $\alpha _2$ and large $\beta _2$, e.g., (1, 10), satisfy the condition as the probability density is focused on the low $\theta _2$ value. The BNE does not exist when the condition is not met.

Bayesian Stackelberg Equilibrium. After plugging in the attacker’s best response to the value function $V_1$, we need to maximize a function of p:

$$\begin{aligned} \max _p E[R_{21}^1\!-\!R_{11}^1\!+\!\mathbf {1}_{\{R_{21}^2-R_{11}^2+p(R_{22}^2-R_{12}^2-R_{21}^2+R_{11}^2)>0\}}(R_{22}^1-R_{12}^1-R_{21}^1+R_{11}^1)]p. \end{aligned}$$

Since we assume that $R_{ij}^2(\theta _2)$ is linear in $\theta _2$, the follower $P_2$’s best response $q^*(y^T, \theta _2)=R_2(p(y^T), \theta _2)=\mathbf {1}_{\{R_{21}^2-R_{11}^2+p(R_{22}^2-R_{12}^2-R_{21}^2+R_{11}^2)>0\}}=\mathbf {1}_{\{ \theta _2>\bar{\theta }_2(p)\}}$ can be represented as an indicator function of a threshold type $\bar{\theta }_2=\frac{1-p(y^T)}{5-7p(y^T)}$, which simplifies the computation of the leader’s optimal policy $p^*$. The existence of equilibrium depends on the type value classified as follows. First, $\bar{\theta }_2\ge 1$, $p^*(y^T)\in [\frac{2}{3},\frac{5}{7})$ is not consistent with $p^*(y^T)=0$ via the optimization of the defender’s value function. Second, $\bar{\theta }_2\le 0$ leads to $p^*(y^T)\in (\frac{5}{7},1], q^*(y^T,\theta _2)=\mathbf {1}_{\{\theta _2<\bar{\theta }_2\}}=0$. Then, $p^*=0$ is not consistent with $p^*\in (\frac{5}{7},1]$. Third, if $p^*=5/7$, $q^*=0$, then the optimization of defender’s value function returns $p^*=0$, which is not consistent with $p^*=5/7$. Finally, $0< \bar{\theta }_2< 1$ leads to the feasible region $p^*(y^T)\in [0,\frac{2}{3})$ and the value function ${{V}_1^T(y^T)}/{C(x^T)}= \max _{p(y^T)\in [0,\frac{2}{3})} [\int _{\bar{\theta }_2}^1Beta^{\alpha _2^T,\beta _2^T}(\theta _2) [0.5 (1+\theta _2)]d\theta _2 -0.1]p(y^T) +1-0.5\int _{\bar{\theta }_2}^1Beta^{\alpha _2^T,\beta _2^T}(\theta _{2})( 1+\theta _2) d\theta _2.$

Remark 4

The BSE may not always exist. Take state $\{0,4,1\}$ as an example, the function is increasing during the interval [0, 2 / 3), with supreme value of ${V}^T_1=0.56, \hat{V}^T_2 =2/3 + (8 \theta _2)/3$ under the limiting BSE (LBSE) policy $p^*\rightarrow 2/3,q^*=\mathbf {1}_{\{\theta _2>\bar{\theta }_2\}}$ with $\bar{\theta }_2 \rightarrow 1$. The BSE does not exist because the feasible region of policy does not include 2 / 3 as analyzed above. However, we can use the supreme value under LBSE as an upper bound of the value function, which serves as a good approximation in practice.    $\square$

5.2 Final Stage with Complete Information

For the complete information, the type value $\theta _2$ is a common knowledge, thus defender can respond to the threat by considering objective $\hat{V}_1^T, \hat{V}_2^T$ rather than expected objective $V_1^T=\max _{p(y^T)} \int _0^1Beta^{\alpha _2^T,\beta _2^T}(\theta _{2})[ \hat{V}_1^T(y^T, \theta _2)]d\theta _2, \hat{V}_2^T$ in Sect. 5.1.

Nash Equilibrium. Since both player’s policies are functions of type $\theta _2$ in the complete information case, we can use the indifference principle for the following three type classifications. First, when $\theta _2\in [0.2,1]$, we obtain NE policy $p^*=\frac{1-5\theta _2}{1-7\theta _2} \in [0,2/3], q^*=\frac{1}{5(1+\theta _2)}\in [\frac{1}{10}, \frac{1}{5}]$ and value function $\hat{V}^T_1=0.9C(x^T)$, $\hat{V}_2^T=2 + ((1 - 5 \theta _2) (-2 + 4 \theta _2))/(1 - 7 \theta _2)=\frac{20 \theta ^2_2}{-1 + 7 \theta _2}\in [1.63265,\frac{10}{3}]$. Second, if $\theta _2=1/7$, no NE exists and both players’ behaviors would be uncertain. Third, for other $\theta _2\in [0,1]$, NE policy $q^*=0, p^*=0$ leads to $(C(x^T),2)$. Figure 7(b) shows that both defender and attacker’s policies are functions of their types. On the one hand, $P_1$ defends with a higher probability when the type value increases because an attack with a larger type value incurs more loss once he succeeds. On the other hand, the increasing probability of defensive actions reduces the probability of attacks to a relatively low level. For benign users who do not attack and inflict damages, which is known by the defender in the complete information case, the defender will not take defensive actions and the system will operate normally.

Stackelberg Game. Following a similar analysis as the NE, we can see that the SE policy also depends on the realization of the type. If $\theta _2\in [0,1/5)$, then SE $p^*=0,q^*=0$ leads to the defender value $(C(x^T),2)$; if $\theta _2\in (1/5,1]$, then $p^*=2/3$ and $q^*=0$ is the SE with value functions $(2.8/3C(x^T),(2+8\theta _2)/3)$; if $\theta _2=1/5$, then $q^*=0, p^*\rightarrow 0$ is the limiting SE.

5.3 Comparison of Value Functions

For the complete information case, the best response set of the attacker $R_2(p, \theta _2)$ exists and is a singleton for each $p\in [0,1]$ for all given $\theta _2\in [0,1]$ except for $\theta _2=1/5$. Thus, the leader player never does worse under SE than under NE policy as stated in Theorem 3, which is also illustrated in Fig. 7(a). The proof is similar to the proof of Proposition 3.16 in [1].

Theorem 3

For the finite two-person game defined in Sect. 2 and two solution concepts defined in Sect. 3, let $\hat{V}_1^S$ and $\hat{V}_1^N$ be the value function of $P_1$ under SE and NE policy, respectively. If $R_2(\sigma _1^T)$ is a singleton for each $\sigma _1^T \in \varSigma _1^T$, then $\hat{V}_1^S\ge \hat{V}_1^N$.    $\square$

In the incomplete information case, the best-response set of the attacker $R_2(p, \theta _2)$ is also a singleton for each $p\in [0,1]$ for all given $\theta _2$. Thus, we further obtain that the defender’s value function under BSE is better than that under BNE when the belief is the same, which is supported by the numerical results in Fig. 7(c). The above comparison of the proactive and reactive information structures, i.e., BSE/SE with BNE/NE demonstrates that acquiring the best response set of the attacker via attack tree analysis can effectively confront the insider threat of APTs.

Fig. 7.

Comparisons of value functions at the terminal stage.

Comparisons of defender’s value function between the NE and BNE in Fig. 8(a) and between SE, BSE in Fig. 8(b) show that the value function of the defender $P_1$ under incomplete information is always no better than that under complete information, which is true for the PBNE under both proactive and reactive information structures. The numerical result corroborates the current unfavorable situation of systems that the deception of APTs creates uncertainties for defenders and decreases defenders’ utilities.

Fig. 8.

The private type of APTs creates uncertainties for defenders and decreases defenders’ value function under both outsider and insider threats.

The comparison of attacker’s value function $\hat{V}_2^T$ under BNE, NE, SE, and LBSE is shown in Fig. 7(d). We observe that $\hat{V}_2^T$ under the LBSE as the upper bound of BSE coincides with $\hat{V}_2^T$ under SE. We also notice that the attacker’s value function under BNE is always no worse than NE, which validates the advantage of concealing a private type to increase the uncertainty of defenders.

5.4 Insights from Multi-stage Analysis

The main insight from the multi-stage analysis is the tradeoff between taking adversary actions to obtain instant attacking reward and hiding to arrive at a more favorable expanded state $y^t=\{x^t,\alpha _2^t, \beta _2^t\}$ in the future stages as shown in Fig. 5. The system state $x^t$ and the belief parameter $\alpha _2^t, \beta _2^t$ comprise the expanded state $y^t$. Thus, on the one hand, a desirable $y^t$ for attacker is to turn the system to a fragile state $x^t$. On the other hand, attacks try to deceive the defender into a Pollyanna. The more the defender belief in $P_2$ as a legitimate user, the less probability she will act defensively and the attacker can bear a smaller threshold $\bar{\theta }_2$ to launch the attack. Other results and insights are summarized as follows. First, the healthy system state $x^t$ at the terminal stage dominates defender’s utility, while at the same time, a belief of a legitimate user increases the defender’s utility. Second, due to the petty stage cost assumption, the attacker chooses to hide at the initial stage to deceive defender to form wrong beliefs. However, since attackers move at the intermediate stages to reach their final target, the defender can gradually form the right belief based on the observable footprints of the adversary.

6 Conclusion

In this work, we propose a multi-stage game of incomplete information to model the interactions between defenders and Advanced Persistent Threats (APTs). The dynamic Bayesian game has captured the stealthy and persistent nature of the APTs. Types are used to represent the private information of the players. A defender forms a belief on the uncertainties of an attacker and updates it using Bayesian rules with observations of attack footprints. We have adopted conjugate priors to enable parametric and large-scale learning of the players and extended the dynamic programming principles with an expanded state space. We have developed mathematical programs to compute the perfect Bayesian Nash equilibrium and studied the existence of Bayesian Nash equilibrium under bi-matrix game. A case study of one-sided information has illustrated the disadvantage to the defender as well as the advantage to the attacker when the attack manages to conceal his private type. It also motivates a further comparison of our framework under two-sided incomplete information in the future so that the defender can also use counter-deception to increase the attacking cost and tilt the current information asymmetry caused by the attacker. We have compared the PBNE under two different information structures and shown that disclosing the best response set of the attacker via attack tree analysis or proactive defenses such as honeypots and honey files can effectively confront the insider threat of APTs. A preliminary multi-stage analysis has shown that although APTs hide at the initial stages, yet the adaptive formation of the belief reveals the attacker at intermediate stages.