Keywords

1 Introduction

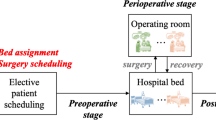
Patient admission scheduling problems (PASPs) concern with deciding which patient to admit and at what time. These problems can be very complex, mainly when different subproblems are tackled at the same time, like patient-to-bed assignment and surgery scheduling problems. The patient bed assignment problem (PBAP) is a sub-task of the PASP and concerns the choose of a suitable room to be assigned to patients by considering medical requirements, patient needs, and hospital resource availability. Despite PBAPs were usually addressed only as bed capacity problems [1, 2] formalized them as an offline and combinatorial optimization problem. Interesting problem extensions were based on it [3, 4]. New realistic situations, like patients with a risk of overstay and postponed admission date were introduced to PASPs in [4]. The goal consists on defining patient admission dates, assigning patients to suitable bed-room-wards, and reduce overcrowded rooms. These problems were named as PASU. The reader is referred to [4] for more details about PASU problems. More complex is the PASU with surgery scheduling problem [5], referred hereafter as PASU-OR problem.

The PBAP of [2] is NP-hard [6], as well as all other similar problems based on it, and heuristic approaches to solve benchmark instances for the aforementioned problems were designed in the literature.

The contribution of this study is twofold. First, it fills the gap in the literature by introducing a mixed integer programming (MIP) model for the PASU-OR problem. It is an extension of that proposed for PASU problems in [7] and an improvement of those proposed in [4, 8] because reduces at minimum the number of decision variables. Second, this study tests an efficient matheuristic procedure and improves the results on a set of benchmark instances available in the literature. The matheuristic was originally designed for PBAPs in [9].

The paper is organized as follows. Section 2 presents the PASU-OR and the MIP model. Section 3 reports computational results on a set of the benchmarks of PASU-OR. The results are compared with those reported in [5] and discussed. Conclusions are drawn in Sect. 4.

2 Problem Statement and an Optimization Model

In the following, we introduce the problem statement and the used notation. The PASU-OR problem is characterized by patient admission date, patient-to-room assignment and surgery scheduling decisions. Patients are characterised by mandatory and preferred medical equipment, gender, admission date (which can be postponed up to a defined date), fixed length of the stay (LOS), medical specialty, room preference. Rooms, located in wards, differ for medical equipment, number of beds, and high/or medium levels of expertise in treating certain pathologies. All patients have to be admitted to the hospital in a defined planning horizon and assigned to suitable hospital rooms in correspondence with their characteristics for a fixed number of consecutive nights.

Let H be a planning horizon, and P be the set of elective patients, indexed by h and p, respectively. \(L_p\) denotes the length of stay (LOS), which could be extended by one night for some patients with a risk of overstay. For each patient is known the range of admission dates AD, and \({H}_p\) that is the range of days between the first possible admission date and the last day of hospitalization. Some patients have to undergo a surgery and exactly \(\delta _p\) days after their admission. Surgeries are scheduled by considering an already defined master surgical schedule (MSS). In addition, some patients were already assigned to rooms before the current planning phase. Let \({P_0}\) be this set of patients. A transfer in a different room is allowed only for them, even if is penalised in order to reduce patient discomfort. Let R, S and SS, be the set of rooms, medical and surgical specialties, indexed by r and s, respectively. The main attributes of patients, rooms and ORs are reported in Table 1.

Table 1 Patient and room attributes
Full size table

To simplify the readability of the model formulation, we define \({H}^{ov}_p=\left\{ z_p, \ldots , z^{'}_p\right\} \) as the range of possible overstay nights, and the following subsets of patients and rooms: \({P}_F\), \({P}_M\), PS, and \({P}^{ov}\) are the sets of woman, men, patients who have to undergo surgery, and patients with a risk of overstay, respectively. Let \({\bar{R}}^{dgp}= \left\{ r \in {R}{\mid }gp_{r}=3\right\} \), be the set of rooms with DGP. Let \({\bar{R}}_p=\left\{ r \in { R}: sp_p \notin \bar{S}_r, ME_p\subseteq E_r\right\} \), and \({\bar{R}}^{dgp}_p= \left\{ r \in {\bar{R}}_p{\mid }gp_{r}=3\right\} \), be the subsets of rooms feasible for patient p and those with DGP, respectively.

Hard constraints are on room capacity, mandatory equipment, patient specialty, and patient stay as consecutive nights. A surgery has to be performed in a defined date and scheduled in those OR blocks assigned to the related surgical specialty, as defined by the MSS. Requirements related to preferred equipment, room capacity preference, gender policies, department specialism, delayed admissions, transfers, and overcrowded rooms due to overstay patients, OR underutilization, and OR overtime express desired properties. They are tackled as soft constraints since do not influence the validity of a schedule but impact on its quality. Violated soft constraints are penalised in objective function.

2.1 An Optimization Model for Offline Patient Admission, Rooms and Surgery Scheduling Problems

Before to introduce our optimization model, we define the decision variables and their meaning as follows. \(ad_{prh}=1\) and \(x_{prh}=1\), if patient \(p\in {P}\) is admitted on day \(h\in {AD}_p\) and then assigned to room \(r \in \bar{R}_p\) over \({H}_p\); \(os_{prh}=1\) if \(p\in {P}^{ov}\) is in room \(r \in {R}\) on day \(d\in {H}^{ov}_p\); \(t_{p}=1\), if \(p\in {P_0}\) is not assigned to the already occupied room \(\bar{r}_p\); \(m_{rh}=1\) if male patients are in room \(r \in {\bar{R}}^{dgp}\) on day \(d \in H\), and \(bg_{rh}=1\) if there are both male and female patients. The above binary decision variables take value 0 otherwise. Delayed admission (in days) is denoted by \(del_p \ge 0\). A room r is overcrowded on day \(h \in H\) if \(oc_{rh} > 0\). Finally, variables related to surgeries scheduling are: \(sd_{ph}=1\) if patient p undergoes surgery on day \(h \in SD_p\); auxiliary variables are \(sov_{hs}\), \(tov_h\), and \(u_h\) denoting daily OR overtime per surgical specialty, overall OR overtime and OR underutilization, respectively. The overall OR time underutilization is computed as deviation of utilised OR time from a constant \(k_u\), defined as \(k_u=min\left\{ reqOR, avOR \right\} \), where reqOR and avOR are the overall requested OR time and the overall available OR time. The objective function is a weighted sum of eight terms. The costs are listed in Table 2.

Table 2 Violations of the soft constraints and related penalty costs
Full size table
$$\begin{aligned} \min&\sum \limits _{p\in {P}} \sum \limits _{r\in \bar{ R}_p} \sum \limits _{h\in {H}_p} w_{pr} x_{prh} + \sum \limits _{r\in \bar{ R}^{dgp}} \sum \limits _{h\in H} w_{g} bg_{rh} + w_t \sum \limits _{p\in {P_0}} {t_{p}} + \sum \limits _{p\in {P}} (w_{del}del_p) + \nonumber \\ +&\sum \limits _{r\in {R}} \sum \limits _{h\in H} w_{oc} oc_{rh} + \sum \limits _{h\in H} \sum \limits _{s\in {SS}} w_{sov} sov_{hs} + \sum \limits _{h\in H} w_{tov} tov_{h} + w_{u}(k_{u}-\sum \limits _{h\in H}u_{h}) \end{aligned}$$
(1)
$$\begin{aligned}&\sum \limits _{r\in {\bar{R}}_p} \sum \limits _{h\in {AD}_p} ad_{prh} =1&\forall p \in { P} \end{aligned}$$
(2)
$$\begin{aligned}&del_{p}= \sum \limits _{r\in {\bar{R}}_p} \sum \limits _{h\in {AD}_p}ad_{prh}(h-a_p)&\qquad \qquad \qquad \forall p \in { P} \end{aligned}$$
(3)
$$\begin{aligned}&\sum \limits _{k=h}^{h+L_p-1} x_{prk}\ge ad_{prh} L_p&\qquad \qquad \qquad \forall p \in {P}, r\in \bar{ R}_p, h \in {AD}_p \end{aligned}$$
(4)
$$\begin{aligned}&\sum \limits _{h \in H_p} x_{prh}= L_p ad_{prh}&\qquad \qquad \qquad \forall p \in {P}, r\in {\bar{R}}_p \end{aligned}$$
(5)
$$\begin{aligned}&C_r \ge \sum _{\begin{array}{c} p \in {P} \\ h \in H_p, r \in \bar{ R}_p \end{array}} x_{prh}&\qquad \qquad \qquad \qquad \forall r \in {R}, h \in H \end{aligned}$$
(6)
$$\begin{aligned}&m_{rh}\ge x_{prh}&\qquad \qquad \qquad \qquad \forall r \in \bar{ R}^{dgp}_p, p \in {P}_M, h\in H \end{aligned}$$
(7)
$$\begin{aligned}&bg_{rh}+1 \ge m_{rh}+ x_{prd}&\qquad \qquad \qquad \qquad \forall r \in \bar{ R}^{dgp}, p \in {P_F}, h\in H_p \end{aligned}$$
(8)
$$\begin{aligned}&t_{p}= \sum \limits _{r\in {R}\setminus \bar{r}_p} x_{pr1}&\qquad \qquad \qquad \qquad \forall p \in { P_0} \end{aligned}$$
(9)
$$\begin{aligned}&os_{prk} = ad_{pr,k-L_p}&\qquad \qquad \qquad \qquad \forall {p\in {P^{ov}}}, r \in \bar{ R}_{p}, k \in {H}^{ov}_p \end{aligned}$$
(10)
$$\begin{aligned}&C_r +oc_{rh}\ge \sum _{\begin{array}{c} p \in {P}| \\ h \in H_p, r \in \bar{ R}_p \end{array}} x_{prh} + \sum _{\begin{array}{c} p\in {P^{ov}}| \\ h \in H^{ov}_p, r \in \bar{ R}_p \end{array}} os_{prh}&\forall r \in {R}, h \in H \end{aligned}$$
(11)
$$\begin{aligned}&sd_{p, h+\delta _p}= \sum \limits _{r\in {\bar{R}}_p} ad_{prh}&\qquad \qquad \qquad \forall p \in PS, h\in {AD_p} \end{aligned}$$
(12)
$$\begin{aligned}&sd_{ph} \le b_{h,sp_{p}}&\qquad \qquad \qquad \qquad \forall p \in {PS}, h\in {SD_p} \end{aligned}$$
(13)
$$\begin{aligned}&b_{hs} + sov_{hs} \ge \sum \limits _{p\in {PS_{\mid sp_{p}=s, h \in SD_p}}}ls_{p}sd_{ph}&\qquad \qquad \qquad \qquad \forall h \in H, s \in {SS} \end{aligned}$$
(14)
$$\begin{aligned}&\sum \limits _{s \in SS} b_{hs} + tov_h \ge \sum \limits _{p\in {PS}\mid h \in SD_p}ls_{p}sd_{ph}&\forall h \in H \end{aligned}$$
(15)
$$\begin{aligned}&u_h = \sum \limits _{p\in {PS}\mid h \in SD_p}ls_{p}sd_{ph} - \sum \limits _{s\in {SS}}sov_{hs}&\forall h \in H \end{aligned}$$
(16)
$$\begin{aligned}&sov_{hs} \le uv^{sov}_s&\qquad \qquad \qquad \qquad \forall h \in { H}, s \in { S} \end{aligned}$$
(17)
$$\begin{aligned}&tov_{h} \le uv^{tov}&\qquad \qquad \qquad \qquad \forall h \in H \end{aligned}$$
(18)

Objective function (1) plans patient admissions, assigns patients to rooms according to quality of care and patient preferences, and schedules surgeries. The first term considers violations \(v_1-v_4\): patient-to-room assignments are penalised per night by \(w_{pr}\), which is the sum of the first four costs. The subsequent four terms penalise \(v_5-v_8\), respectively; the last three terms penalise overall OR overtime computed per all specialties, OR under-utilization and overall OR under-utilization, respectively. Constraints (2) ensure that each patient is admitted only once in \({AD}_p\) and has to be assigned only one room among those feasible. Constraints (3) evaluate delayed admissions and Constraints (4)–(5) ensure patient stay as consecutive \(L_p\) nights. Constraints (6) state that the number of patients assigned to a room cannot be greater than the number of beds. Constraints (7)–(8) capture the presence of male patients and DGP violation if there both male and female patients on the same day, respectively. Constraints (9) evaluate transfers, and Constraints (10)–(11) consider overstays and overcrowded rooms. Constraints (12) and (13) ensure that each patient \(p\in PS\) undergoes surgery \(\delta _p\) days after admission, only once, and on day in which his/her specialty has allotted OR time in the MSS. Constraints (14)–(16) are on surgical specialty overtime, overall OR overtime per day, and OR under-utilization, respectively. Finally, Constraints (17)–(18) impose an upper value to OR overtime. The above defined decision variables complete the MIP model formulation.

3 Computational Results

In this section we present computational results carried out on the small short family [5] for assessing the quality of the matheuristic solution and found good schedules in reasonable times. This family consists of three sets and 15 instances. Main features are summarised in Table 3.

The PASU-OR benchmark are infeasible instances owing a greater demand than resource. To overcome this, the planning horizon is doubled with respect to the original, and room underutilization related to the H is minimized. This term is defined as deviation of the overall room utilization from a constant. The constant is \(k_{bed}=min \left\{ reqB, avB \right\} \), where reqB and avB are the overall bed requests and the overall number of beds, respectively. The term \((k_{bed}-\sum \nolimits _{h\in H} bu_{h})\), denoted by \(\bar{v}_{12}\) in Table 4, is penalised and added to objective function (1).

Table 3 Main features of the short family instances
Full size table
Table 4 Results on the small family instances
Full size table

As already stated in Sect. 1, PASU-OR problems are NP-hard and heuristic approaches were devised to find good solutions in a reasonable time because exact solvers are not effective to explore the solution space mainly of large instances. The solution approach here implemented is based on the matheuristic FiNeMath, developed to solve PBAPs in [9]. Metaheuristic algorithms are generic solution procedures based on exploring the solution space by considering an incumbent solution and iteratively changing it in favour of a new solution. FiNeMath exploits complementarity among fix-relax methods, neighbourhood-based searches, and exact solvers. Let \(s_0\) be an initial feasible schedule, and \(F_0\) its objective function value. Some patient-to-room assignments are selected from \(s_0\) randomly and added to the MIP model as constraints. They are thus fixed components, while the remaining ones are repaired by an exact solver in the defined neighbourhood. The procedure is iterated until a stopping criterion is reached. The objective function value is thus improved iteratively by destroying a current schedule and repairing it by an exact solver. A high level pseudocode is provided below, named as Algorithm 1. For more details, the reader is referred to [9].

figure a

The number of patient-to-room assignments added as constraints to the MIP model influences both improvements in the objective function value and computational times [9]. The percentage range of fixed assignments was set in the range 10–40%; each MIP problem was solved with a gap of 3%, that decreases up to 1% in the latest iterations; the number of iterations was set to 32. The computational experiments were performed using IBM ILOG CPLEX V12.7.1, Academic license. We used the cost values reported in [5]. We evaluated the improvement/worsening of our results with respect to the best-known mean values \(R_{CS}\), found by a simulated annealing approach in [5]. All the best-known values \(R_{CS}\) were improved. Table 4 lists the results in terms of mean values per set of instances, and reports the single components of the objective function. In the last column there are the percentage improvement values, which were evaluated by \(\varDelta F=\frac{(R_{CS} \ value - our \ value)}{({R_{CS} \ value})} \times 100\). Observe that they are in the range 4.7–10.5%.

4 Conclusion

In this paper, we formulated an optimization model to manage patients admissions, hospital rooms, and surgeries. Schedules with planned patient admissions, patient-to-room assignments and planned surgeries are developed using the matheuristic FiNeMath, which is based on solving the optimization formulation. Preliminary results achieved on a set of benchmark instances, point out that our approach is promising. Currently, we are working on improving the FiNeMath efficiency by developing suitable solution destroying phases to reduce computational times.