Exploiting Local Persistency for Reduced State Space Generation

Abstract

This paper deals with the partial order techniques of Petri nets, based on persistent sets and step graphs. To take advantage of the strengths of each method, it proposes the persistent step sets as a parametric combination of the both methods. The persistent step sets method allows to fix, for each marking, the set of transitions to be covered by the selected steps and then to control their maximal length and number. Moreover, this persistent step selective search preserves, at least, deadlocks of Petri nets.

This paper also provides two practical computation procedures of the persistent step sets based on the strong-persistent sets [5, 10] and the persistent sets, respectively.

1 Introduction

The state explosion problem is the main obstacle for the verification of concurrent systems, as they are generally based on an interleaving semantics, where all possible firing orders of concurrent actions are exhaustively explored. Different techniques for fighting this problem have been proposed such as structural analysis, symmetries and partial orders.

The structural analysis attempts to find a relationship between the behaviour of the net and its structure. Its results are of particular importance since initial marking is considered as a parameter. The net structure can be studied through its associated incidence matrix and the corresponding net state equation leading mainly to the concept of place invariants [4] or through topological properties of the interplay between conflict and synchronisation of remarkable substructures of the net such siphons and traps leading to necessary and/or sufficient structural conditions to check general behavioural properties such as liveness [3, 7] for large subclasses of place/transition nets [1, 2].

The second well-accepted technique to tackle combinatorial explosion in model-checking consists into exploitation of symmetries over states and the transition relation [6] leading to the building of a quotient graph of equivalence classes of states, that may be exponentially smaller than the full state graph and preserving many behavioural properties of interest.

The partial order techniques have been proven to be the most successful in practice. We distinguish two classes of partial order techniques: partial order reduction [5, 8, 9, 11,12,13] and step graph [14]. Partial order reduction techniques, such as the ample sets [8, 9], the stubborn sets [11,12,13] and the persistent sets [5], deal with the state explosion problem by avoiding as much as possible to explore firing sequences that are equivalent w.r.t. the properties of interest (deadlock freeness, reachability, liveness, or linear properties)¹. The step graph methods explore all the transitions of the state space but some of them are fired together in atomic steps. The common characteristics of all these methods is to reduce the state space to be explored, by selecting the actions or sets of actions (steps) to be executed from each state. The selection procedure of actions or steps relies on the notion of independent actions. Two actions are said to be independent, if whenever they are enabled, they can be fired in both orders and the firing of one of them does not inhibit the occurrence of the other. Moreover, their firing in both orders leads to the same state. Both of these conditions constitute the well known diamond property.

Each of the partial order reduction methods above provides sufficient conditions that ensure, at least, preservation of deadlocks. Thus, the set ST of the selected transitions or steps is only empty for the deadlock markings (i.e., markings with no enabled transitions). The other sufficient conditions are generally based on the structure of the model, the property to be verified and the current marking. Their aim is to ensure independency between transitions of ST and the others. Indeed, for the ample sets method [8, 9], there is no transition outside ST that is firable before all transitions of ST and, at the same time, is dependent of at least a transition of ST. For the stubborn sets method [11,12,13], ST contains at least an enabled transition that cannot be disabled by the transitions outside ST and each of its transitions t is independent of all transitions outside ST that are firable before t. The persistent sets method [5] is considered a particular case of the stubborn sets method, where all transitions of ST are enabled. For the covering-steps graph method [14], the set of steps to be fired from each marking must cover the set of enabled transitions.

To achieve more reductions, in [10], the authors have combined this technique with the persistent sets method. This combination consists to firstly compute a persistent set for the current marking and then look for firing steps within this persistent set. For these approaches, the transitions within the same step are neither in weak-conflict nor in structural conflict with the partially enabled transitions.

This paper is interested in the persistent sets and the step graphs. To take advantage of the strengths of each method, it investigates their combination and proposes persistent step sets method. Persistent-step sets method is a parametric combination of persistent sets with step graphs that allows to fix, for each marking, the set of transitions to be covered by the selected steps and then to control their maximal length and number.

The rest of the paper is organized as follows. Section 2 fixes some classical definitions and notations used throughout the paper. Section 3 presents the strong-persistent sets [5, 10], the persistent sets (a weaker version of the strong-persistent sets) and the step graph methods, while pointing out their weaknesses. Section 4 provides a formal definition of persistent step sets and proves that they yield graphs preserving deadlocks of Petri nets. Section 5 establishes two computation procedures of persistent step sets that are based on strong-persistent sets and persistent sets, respectively. Conclusions are presented in Sect. 6.

2 Preliminaries

Let $P$ be a nonempty set. A multi-set over $P$ is a function $M: P \longrightarrow \mathbb {N}$, $\mathbb {N}$ being the set of natural numbers, defined also by the linear combination over P: $\underset{ p\in P}{\sum }M(p)\times p$. We denote by $P_{MS}$ and 0 the set of all multi-sets over $P$ and the empty multi-set, respectively. Operations on multi-sets are defined as usual. Notice that any subset $X \subseteq P$ can be defined as a multi-set over P: $X= \underset{ p\in X}{\sum }1\,\times \, p.$

An ordinary Petri net (PN in short) is a tuple $PN=(P, T, pre, post)$ where:

• P and T are finite and nonempty sets of places and transitions with $P\, \cap \, T = \emptyset$,

• pre and post are the backward and forward incidence functions over the set of transitions T ($pre, post: T \longrightarrow 2^P$).

For $t \in T,$ pre(t) and post(t) are the sets of input and output places of t, denoted also by ${^{\bullet }t}$ and $t^{\bullet }$, respectively. Similarly, the sets of input and output transitions of a place $p \in P$ are defined by $^{\bullet }p = \{t \in T \ | \ p \in t^{\bullet }\}$ and $p^{\bullet } = \{t \in T \ | \ p \in {^{\bullet }t} \}$, respectively.

Two transitions t and $t'$ are in structural conflict, denoted by $t \perp t'$ iff $pre(t) \cap pre(t') \ne \emptyset$. We denote by $CFS(t) =\{t' \in T | t \perp t'\} = (^{\bullet } t)^{\bullet }$ the set of transitions in structural conflict with t. They are in weak conflict iff $t \perp ^* t'$, where $\perp ^*$ is the transitive closure of $\perp$. We denote by $CFS^*(t) =\{t' \in T | t \perp ^* t'\}$ the set of transitions in weak conflict with t. Notice that $t \in CFS(t)$ and $CFS(t) \subseteq CFS^*(t)$.

A marking of an ordinary Petri net indicates the distribution of tokens over its places. It is defined as a multi-set over places. A marked PN is a pair $\mathcal {N}=(PN, M_0)$, where PN is an ordinary Petri net and $M_0 \in P_{MS}$ is its initial marking. Starting from its initial marking, PN evolves by firing enabled transitions. For the following, we fix a marked PN $\mathcal {N}$, a marking $M \in P_{MS}$ and a transition $t \in T$ of $\mathcal {N}$.

The transition t is enabled at M, denoted $M[t\rangle$ iff all the required tokens for firing t are present in M, i.e., $M\ge pre(t)$. The transition t is partially enabled in M iff t is not enabled in M and, at least, one of its input places is marked. In case t is enabled at M, its firing leads to the marking $M'=M - pre(t) + post(t)$. The notation $M[t\rangle M'$ means that t is enabled at M and $M'$ is the marking reached from M by t. We denote by En(M) the set of transitions enabled at M, i.e., $En(M) =\{t \in T \ | \ M \ge pre(t)\}$. The marking M is a deadlock iff $En(M)=\emptyset$.

For any sequence of transitions $\omega = t_1t_2...t_n \in T^+$ of $\mathcal {N}$, the usual notation $M{[t_1t_2...t_n\rangle }$ means that there exist markings $M_1,..., M_{n}$ such that $M_1=M$ and $M_i{[t_i\rangle } M_{i+1}$, for $i\in [1,n-1]$ and $M_n{[t_n\rangle }$. The sequence $\omega$ is said to be a firing sequence of M. The notation $M{[t_1t_2...t_n\rangle } M'$ gives, in addition, the marking reached by the sequence ($M'$ is reachable from M by $\omega$). By convention, we have $M[\epsilon \rangle M$. We denote by $\overrightarrow{M}$ the set of markings reachable from M, i.e., $\overrightarrow{M}=\{M' \in P_{MS} | \exists \omega \in T^*, M[\omega \rangle M'\}$.

A firing sequence $\omega$ of M is maximal iff it is infinite (i.e., $\omega \in T^\infty$) or it is finite and leads to a deadlock marking. The transition t is potentially firable from M if there exists a sequence $\omega \in T^*$ s.t. $M{[\omega t\rangle }$. Two sequences of transitions $\omega$ and $\omega '$ are equivalent, denoted by $\omega \equiv \omega '$ iff they are identical or each one can be obtained from the other by a series of permutations of transitions. If $\omega \equiv \omega '$ then $\forall M', M'' \in P_{MS}, (M[\omega \rangle M' \wedge M[\omega '\rangle M'') \Rightarrow M'=M''$. We denote by $[\omega ]$ the set of transitions in $\omega$. The firing sequences of $\mathcal {N}$ are the firing sequences of its initial marking.

The different possible evolutions of $\mathcal {N}$ are represented in a marking graph MG defined by the structure $MG=(\overrightarrow{M}_0, [\rangle , M_0)$. Let n be a natural number. The marked PN $\mathcal {N}$ is n-bounded iff for every reachable marking of $M_0$, the number of tokens in each place does not exceed n. It is safe iff it is 1-bounded. It is bounded iff it is k-bounded for some natural number k.

A firing step $\tau$ of $\mathcal {N}$ is a non-empty subset of transitions ($\tau \subseteq T$) fired simultaneously and atomically from a marking of $\mathcal {N}$. From an interleaving semantic point of view, it represents an abstraction of all firing orders of its transitions. For instance, $\tau = \{t_1,t_2,t_3\}$ represents the following six sequences: $t_1t_2t_3$, $t_1t_3t_2$, $t_2t_1t_3$, $t_2t_3t_1$, $t_3t_1t_2$ and $t_3t_2t_1$. The intermediate markings are abstracted to keep only the markings before and after the firing step.

Let $M \in P_{MS}$ be a marking and $\tau$ a firing step of $\mathcal {N}$. The firing step $\tau$ is enabled in M, denoted by $M[\tau \rangle$ iff $M \ge \underset{t \in \tau }{\sum }pre(t),$ which means that there are enough tokens to fire concurrently all the transitions within the step. If $\tau$ is enabled in M, its firing leads to the marking $M' = M + \underset{t \in \tau }{\sum }(post(t) - pre(t))$. The notation $M[\tau \rangle M'$ means that $\tau$ is enabled at M and $M'$ is the marking reached from M by $\tau$. We denote by EnS(M) the set of all enabled steps in M, i.e., $EnS(M) = \{\tau \subseteq T \ | \ \tau \ne \emptyset \wedge M \ge \underset{t \in \tau }{\sum }pre(t)\}$. The firing step $\tau$ is maximal in M iff it is maximal for the inclusion in EnS(M),  i.e., $M \ge \underset{t \in \tau }{\sum }pre(t)$ and $\forall t' \in En(M) - \tau , M \not \ge pre(t') + \underset{t \in \tau }{\sum }pre(t)$.

A step graph of $\mathcal {N}$ is a structure $SG=(MM, R, M_0)$, where $MM \subseteq \overrightarrow{M}_0$ is a subset of reachable markings, $M_0$ is the initial marking and $R \subseteq MM\, \times \, 2^T\, \times \, MM$ is relation defined by $(M,\tau ,M') \in R \Rightarrow M[\tau \rangle M'.$

For the rest of paper, we fix an ordinary Petri net $\mathcal {N}=(P,T, pre, post, M_0)$.

3 Persistent Sets and Step Graphs

3.1 Persistent Sets

Let M be a marking. Informally, a persistent set of M is a subset $\mu$ of enabled transitions such that no transition of $\mu$ can be disabled, as long as no transition of $\mu$ is fired [5, 10]. A persistent graph is obtained by recursively firing from each marking a persistent set. Persistent graphs preserve deadlocks of Petri nets [10].

However, this strong definition of persistent sets can be weakened while preserving deadlocks of Petri nets. The idea comes from the stubborn sets [13]. But unlike the stubborn sets, all the transitions inside a persistent set are enabled. To distinguish between the two definitions of persistent sets, the persistent sets of [5, 10] are referred to as strong-persistent sets.

Definition 1

Let M be a marking and $\mu \subseteq En(M)$ a subset of enabled transitions.

Formally, the subset $\mu$ is a strong-persistent set of M, if all the following conditions are satisfied:

• $En(M)\ne \emptyset \ \Leftrightarrow \ \mu \ne \emptyset$.

• $\forall t \in \mu , \forall \omega \in (T - \mu )^+, M[\omega \rangle \ \Rightarrow \ M[\omega t \rangle$.

• $\forall t \in \mu , \forall \omega \in (T - \mu )^+, M[\omega t \rangle \ \Rightarrow \ M[t \omega \rangle$.

The subset $\mu$ is a persistent set of M, if it satisfies all the following conditions:

• D0: $En(M)\ne \emptyset \ \Leftrightarrow \ \mu \ne \emptyset$.

• D1: $\exists t \in \mu , \forall \omega \in (T - \mu )^+, M[\omega \rangle \ \Rightarrow \ M[\omega t \rangle$.

• D2: $\forall t \in \mu , \forall \omega \in (T - \mu )^+, M[\omega t \rangle \ \Rightarrow \ M[t \omega \rangle$.

Intuitively, Condition D0 ensures that the persistent set of M is empty only if M is a deadlock. Conditions D1 means that there is at least a transition inside $\mu$ such that no transition outside $\mu$ can disable it. Condition D2 means that if some sequence $\omega$ with no transition from $\mu$ is firable before any transition t of $\mu$, then it is also firable after t.

The transitions of $\mu$ that satisfy D1 are called the key-transitions of $\mu$ [13]. Note that in strong-persistent sets, all their transitions are key-transitions.

In the following, we investigate the combination of the persistent sets with the step graphs, in order to achieve more reduction.

Fig. 1.

Model PN1

Fig. 2.

Step graph of PN1

Fig. 3.

A persistent set graph of PN1

Fig. 4.

A persistent step graph of PN1

3.2 Step Graphs

The aim of the step graph methods is to represent by a single path a largest possible set of equivalent maximal firing sequences of the model, by choosing appropriately, from each marking, the transitions to be fired together in steps. All transitions of the equivalent sequences are represented in the path but the concurrent ones are grouped together in steps. Step graphs allow to reduce the path depths.

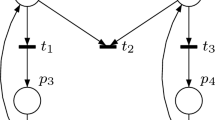
However, in case there are several sets of transitions that are independent from each other, the number of steps and their lengths may be very large. For example, consider the model PN1 at Fig. 1. Its marking graph consists of 27 nodes and 54 arcs. Its initial marking $M_0$ has 3 persistent sets that are independent from each other: $\{t_1, t_2\}$, $\{t_3, t_4\}$ and $\{t_5, t_6\}$. A persistent graph of PN1 is shown in Fig. 3. Note that there are different persistent graphs but they have all the same size ($2^4 -1=15$ nodes and $15 -1=14$ arcs). Using the 3 independent persistent sets of $M_0$, steps can be built by picking a transition from each persistent set. Its step graph is shown in Fig. 2 and consists of $9=2^3 +1$ nodes, $8=2^3$ arcs and $2^3$ maximal steps. It is a covering-step graph, as the set of steps selected from each marking covers all its enabled transitions. But, the number of successors of the initial marking exceeds the number of enabled transitions and is exponential with the number of independent persistent sets. Even if the covering-step graph is smaller than the persistent graph, the number of maximal steps and their lengths may be very large, which limits the usefulness of the step graph method.

To take advantage of the strengths of each method, the persistent sets and step graphs are combined in [10]. The idea is to compute a strong-persistent set and then determine the transitions within this set to be fired together in steps. As an example, for the strong-persistent set $\{t_1, t_2, t_3, t_4\}$ of the initial marking $M_0$, we can build 4 steps: $\{t_1, t_3\}$, $\{t_1, t_4\}$, $\{t_2, t_3\}$ and $\{t_2, t_4\}$. The resulting reduced graph is reported in Fig. 4 and consists of 13 nodes and 12 arcs. This combination allows to control the number and the length of the steps to be considered from each marking, while yielding a graph that is larger than the step graph but smaller than the persistent graph.

4 Persistent Step Sets

We first define the notion of persistent step sets. Then, we show that the resulting graphs preserve deadlock markings of Petri nets.

Definition 2

Let M be a marking and $SS= \{\tau _1, ..., \tau _n\}$ a set of n enabled steps in M with $n>0$. The set SS is a persistent step set in M if it satisfies all the following conditions: Let $\mu = \underset{i \in [1,n]}{\bigcup }\tau _i$.

• DS0: $\ En(M) \ne \emptyset \Leftrightarrow \mu \ \ne \emptyset .$

• DS1: $\ \forall (t_1,...t_n) \in \tau _1 \times ... \times \tau _n, \forall \omega \in (T- \underset{j \in [1,n]}{\bigcup }\{t_j\})^+,$ $(M[\omega \rangle \ \Rightarrow \exists i \in [1,n], \exists t \in \tau _i, M[\omega t \rangle ) \wedge$ $(\forall i \in [1,n], M[\omega t_i \rangle \ \Rightarrow M[t_i\omega \rangle )$

Condition DS0 is identical to D0. Intuitively, Condition DS1 means that as long as a sequence does not contain all transitions of, at least, a step (even scattered), there is always a possibility to extend this sequence with a missed transition of a step. Moreover, if a missed transition is firable after $\omega$ then it can be shifted to the front of the sequence of $\omega$ to, at the end, constitute a firing step. Note that if SS is a persistent step set of M such that all its steps are singletons, then $\mu$ is a persistent set of M. Indeed, in this case $\mu = \{t_1, ...,t_n\}$ and then $DS0 \wedge DS1$ implies $D0 \wedge D1 \wedge D2$.

Example 1

Consider the model PN1 at Fig. 1.

• The set $\mu = \{t_1,t_2,t_3\}$ is a persistent set but is not a strong-persistent set of the initial marking $M_0=p_1+p_2+p_3$, as it satisfies conditions D0 and D1 (for only $t_1$ and $t_2$). There are two key-transitions in $\mu$: $t_1$ and $t_2$.

• The step set $SS = \{ \{t_1,t_3\},\{t_2,t_3\}\}$ is not a persistent step set of $M_0$, as it does not satisfy Condition DS1. Indeed, we have $M_0[t_4t_1\rangle$ and $\lnot M_0[t_4t_1t_3\}\rangle$.

Theorem 1

Let M be a marking reached in a persistent step selective search from $M_0$ and D a deadlock marking reachable from M in the Petri net. Then D will also be reached by the persistent step selective search from $M_0$.

Proof

The marking M is reachable in the Petri net. Let $\omega$ be a firing sequence leading to the marking D from M in the Petri net. The proof is by induction on the length of $\omega$.

• (a) If $\omega =\epsilon$ then $M=D$.

• (b) If $\omega =t$ and $\{t\} \in SS$ then D is reached by the persistent step selective search.

• (c) If $\omega =t$ and $\{t\} \notin SS$ then, by DS1, D is not a deadlock marking as there is, at least, a transition from $\mu$ that is firable after t, which is in contradiction with the fact that D is a deadlock.

Suppose that Theorem 1 holds for any marking $M'$ (reachable in a persistent step set selective search) and D reachable from $M'$ by a sequence $\omega '$ such that $|\omega '| < |\omega |$.

• If there is no step of SS (scattered or not) in $\omega$, then, by DS1, there is, at least, a missed transition of a step that is firable after $\omega$. It means that D has, at least, a successor, which is in contradiction with the fact that D is a deadlock.

• If there is, at least a step $\tau$ of SS, scattered or not, in $\omega$, then these transitions of this step can be shifted to the front to constitute a step firable from M. Firing this step from M leads to some marking $M'$ that is reachable by the persistent step selective search. Moreover, D is reachable from $M'$, in the Petri net, by a sequence $\omega '$ s.t. $|\omega '| < |\omega |$. Therefore, D is reachable by the persistent step selective search from $M_0$. $\square$

5 Parametric Combination of Persistent Sets with Step Graphs

From a practical point of view, the above definition of persistent step sets is not useful. We propose, in the following, two parametric selection algorithms of persistent step sets, based on strong-persistent sets and persistent sets, respectively.

For a given marking M and a subset S of transitions enabled in M ($S \subseteq En(M)$), the idea is to compute a persistent step set that covers, at least, the transitions of S. Unlike, the approach proposed in [10], the set S is not necessarily a strong-persistent set. As we will show, according to the parameter S, the provided persistent step set is either a (strong) persistent set, a covering-step set or a set of steps that covers partially the enabled transitions in M.

We suppose that there are two available computation procedures PS and $PS^+$ of strong-persistent sets and persistent sets, respectively. For a given marking M and a transition t enabled in M, PS(t, M) returns a persistent set of M, where at least t is a key-transition. This set can be computed from $\{t\}$ by adding recursively the enabled transitions that prevent it to satisfy D1 and D2, until reaching a fixed point. For $PS^+(t,M)$, the set returned is a strong-persistent set of M calculated from PS(t, M) by adding recursively $PS(t',M)$, for each non key-transition $t'$ within the set, until reaching a fixed point. Thus, the transitions of $PS^+(t,M)$ are all key-transitions.

5.1 Computing Strong-Persistent Step Sets

A computation procedure of strong-persistent step sets is provided in Algorithm 1. For a given marking M and a set of enabled transitions $S \subseteq En(M)$, Algorithm 1 returns a set of steps firable from M. The parameter S allows to specify the set of enabled transitions that must be, at least, covered by the set of steps. The computed set of steps is a sort of product of some disjoint strong-persistent sets ($PS^+(t,M)$, for t chosen from the input set S). The first term of the product is $R=PS^+(t,M)$, where t is chosen randomly in $S'$ (a copy of S). Then, the transitions of R are deleted from $S'$, to ensure that the next terms are disjoints from those computed so far. If the resulting $S'$ is not empty, then the same process is repeated to compute the next term of the product, and so on. Theorem 2 establishes that the returned set of steps is a persistent step set.

Example 2

Consider the initial marking $M_0$ of the model PN1 at Fig. 1.

• For $S= \{t_1,t_2,t_3\}$, Algorithm 1 computes SS as follows. It starts by setting SS and $S'$ to $\emptyset$ and $\{t_1,t_2,t_3\}$, respectively. If $t_1$ of $S'$ is the first transition selected in the loop while, then $R=\{t_1,t_2\}$, $S'=\{t_3\}$ and $SS= \emptyset \otimes R = \{\{t_1\}, \{t_2\}\}$. For the second iteration, $t_3$ is selected, then $R=\{t_3,t_4\}$, $S'=\emptyset$ and $SS = SS \otimes \{t_3,t_4\} = \{\{t_1,t_3\}, \{t_1,t_4\}, \{t_2,t_3\}, \{t_2,t_4\} \}$. Algorithm 1 returns SS.

• For $M_0$ and $S= En(M_0)$, Algorithm 1 returns the set:

  $SS = (\{\{t_1\},\{t_2\}\} \otimes \{\{t_3,t_4\}\}) \otimes \{\{t_5,t_6\} \}$.

  Indeed, initially, we have $S'=S=En(M_0)$. The loop while will perform successively the following updates of R, $S'$ and SS, for the case where the selected transitions are successively $t_1, t_3$ and $t_5$:

  For $t_1$: $R=\{t_1,t_2\}$, $S'=\{t_3,t_4,t_5,t_6\}$ and $SS = \{\{t_1\}, \{t_2\}\}$.

  For $t_3$: $R=\{t_3,t_4\}$, $S'=\{t_5,t_6\}$ and $SS=SS \times R$.

  For $t_5$: $R=\{t_5,t_6\}$, $S'=\emptyset$ and then

  Then, $SS= (\{\{t_1\},\{t_2\}\} \otimes \{t_3,t_4\}) \otimes \{t_5,t_6\}$. Note that in this case, SS is a covering-step set.

• For $M_0$ and $S= \{t_1,t_2\}$, Algorithm 1 returns $SS=\{\{t_1\},\{t_2\}\}$, as the transitions of S are all key-transitions. If $t_1$ (or $t_2$) is selected first then $R=S'$, $S' = \emptyset$ and $SS=\{\{t_1\},\{t_2\}\}$.

Theorem 2

Algorithm 1 returns a persistent step set of M.

Proof

It suffices to show that the returned set SS by Algorithm 1 satisfies DS0 and DS1 (presented in Definition 2). It is obvious that SS satisfies DS0.

DS1? Suppose that n ($n>0$) iterations are needed to complete the loop while of the algorithm. During the $i^{th}$ iteration ($i\in [1,n]$, a transition $t^i$ is selected from $S'^i$ and $R^i=PS^+(t^i,M)$. The set $R^i$ is a strong-persistent set where all its transitions are keys. Therefore, it holds that:

$$\begin{aligned} \forall i\in [1,n], \forall t^i \in R^i, \forall \omega \in (T-R^i)^+, M[\omega \rangle \ \Rightarrow \ M[\omega t^i\rangle \wedge M[t^i\omega \rangle . \end{aligned}$$

Each step of SS contains one and only one transition from each $R^i$, for $i\in [1,n]$. Therefore, all sequences where, at least, a transition from each step is missing, is given by the union of sets $(T- R^i)^+$, for $i \in [1,n]$. Consequently, SS satisfies DS1. $\square$

5.2 Computing Persistent Step Sets

The set of steps returned by Algorithm 1 is a product of some pairwise disjunct strong-persistent sets of the marking M. To achieve further reductions, Algorithm 2 computes, in SS, a product of some pairwise disjunct persistent sets, instead of strong-persistent sets. However, unlike disjunct strong-persistent sets, the product of disjunct persistent sets may contain some non enabled steps. These steps must be deleted from SS to keep only the enabled ones. According to Theorem 3, SS is a persistent step set.

Fig. 5.

Model PN2

Fig. 6.

CSG of PN2

Fig. 7.

MSPG of PN2 (using Algorithm 2)

Example 3

Consider the model PN2 at Fig. 5 and its initial marking $M_0$.

For $S= \{t_0,t_1,t_2,t_3\}$, Algorithm 2 first sets SS, $S'$ and $R'$ to $\emptyset$, $\{t_0,t_1,t_2,t_3\}$ and $\emptyset$, respectively. Then, if $t_0$ of $S'$ is the first transition selected in the loop while on $S'$, then $R=\{t_0,t_1\}$, $S'=\{t_2,t_3\}$, $SS= \emptyset \otimes R = \{\{t_0\}, \{t_1\}\}$ and $R'=\{t_0,t_1\}$. For the second iteration, $t_3$ is selected, as: $PS(t_2,M_0) \cap R' = \{t_1\}$ and $PS(t_3,M_0) \cap R' = \emptyset$. Therefore, $R=\{t_2,t_3\}$, $S'=\emptyset$ and

$$\begin{aligned} SS = SS \otimes \{t_2,t_3\} = \{\{t_0,t_2\}, \{t_0,t_3\}, \{t_1,t_2\}, \{t_1,t_3\} \}. \end{aligned}$$

Finally, Algorithm 2 returns $SS \cap EnS(M_0)$, i.e., $\{\{t_0,t_2\}, \{t_0,t_3\}, \{t_1,t_3\}\}$.

Theorem 3

Algorithm 2 returns a persistent step set of M.

Proof

It is obvious that the set SS returned by Algorithm 2 satisfies DS0. DS1? SS is a product of some pairwise disjunct persistent sets. Suppose that $SS = R^1 \otimes R^2 .... \otimes R^n$ with ($n>0$).

Then, (i) $\forall i \in [1,n], \exists t^i \in R^i, \forall \omega \in (T-R^i)^+, M[\omega \rangle \ \Rightarrow \ M[\omega t^i\rangle$ and (ii) $\forall i \in [1,n], \forall t^i \in R^i, \forall \omega \in (T-R^i)^+, M[\omega t^i\rangle \ \Rightarrow \ M[t^i\omega \rangle$.

By construction, sets $R^i$, for $i \in [1,n]$ are pairwise disjunct and each step of SS contains one and only one transition from each $R^i$, for $i \in [1,n]$. Condition (i) states that there is at least a transition $t^i$ in $R^i$ that is firable after each firable sequence of $(T- R^i)^+$. As the sets $R^i$, for $i \in [1,n]$, are pairwise disjunct, it follows that $R^j \subseteq (T-R^i)$ for $i, j \in [1,n]$ s.t. $i\ne j$.

Condition (ii) means that whenever a first transition from $R^i$ is fired (after some sequence), it can be shifted to the front without disabling the sequence.

Let $\omega \in T^+$ be a sequence firable from M. We distinguish 3 main cases (a) $\omega$ contains no transition from $R^1 \cup ... \cup R^n$, (b) $\omega$ contains at least a transition from $R^1 \cup ... \cup R^n$ and $\omega$ contains at least a transition from each $R^i$ for $i \in [1,n]$. For $n=2$, the different cases are shown in Fig. 8: (a) $\omega$ has no transition from $R^{1} \cup R^{2}$; (b1) $\omega$ has at least a transition from $R^{1}$ but no transition from $R^{2}$; (b2) $\omega$ has at least a transition from $R^{2}$ but no transition from $R^{1}$, and (c) $\omega$ has at least a transition from $R^{1}$ and from $R^{2}$.

• Case a: According to Condition (i) above, $\forall i \in [1,n], \exists t^i \in R^i, M[\omega \{t^{1}, ..., t^{n}\}\rangle$ and by Condition (ii), $M[\{t^{1}, ..., t^{n}\}\omega \rangle .$ Note that $\{t^{1}, ..., t^{n}\}$ is eventually a firing step of M as each $t^i$ is a key-transition of $R^i$ and $R^i$ for $i\in [1,n]$ are pairwise disjunct.

• Case b: If $\omega$ contains no transition from $R^{j_1} \cup ... \cup R^{j_k}$ but contains some transitions of $R^{l_1}, ...,$ and $R^{l_m}$, for some m and n such that $0<m, 0<k$ and $m+k=n$, then according to Condition (i), $\exists t^{j_1} \in R^{j_1}, ..., \exists t^{j_k} \in R^{j_k}, M[\omega \{t^{j_1}, ..., t^{j_k}\}\rangle$ and by Condition (ii), $M[\{t^{j_1}, ..., t^{j_k}\}\omega \rangle .$

  Let $t^{l_1}, ..., t^{l_m}$ be the first transitions of $R^{l_1}, ..., R^{l_m}$, respectively, appearing in $\omega$. By Condition (ii), all these transitions can be shifted to the front of $\omega$ without disabling the other transitions of $\omega$. Therefore, there is a firable sequence from M equivalent to $\omega t^{j_1}... t^{j_k}$ that starts with a sequence of the step $\{t^{j_1}, ..., t^{j_k}, t^{l_1}, ..., t^{l_m}\}$. Note that this case is not possible, if $\{t^{j_1}, ..., t^{j_k}, t^{l_1}, ..., t^{l_m}\}$ is not a firable step of M.

• Case c: Let $t^{l_1}, ..., t^{l_n}$ be the first transitions of $R^{l_1}, ..., R^{l_n}$, respectively, appearing in $\omega$. By Condition (ii), all these transitions can be shifted to the front of $\omega$ without disabling the other transitions of $\omega$. Therefore, there is a firable sequence from M equivalent to $\omega$ that starts with a sequence of the step $\{t^{l_1}, ..., t^{l_n}\}$. Note that this case is not possible, if $\{t^{l_1}, ..., t^{l_n}\}$ is not a firable step of M.

Consequently, $SS \cap EnS(M)$ satisfies DS1. $\square$

Fig. 8.

Proof of DS1, case $n=2$ and $M[\omega \rangle$

Fig. 9.

Model PN3: Parallel composition of n instances of PN2 ($\parallel _n PN2$)

Table 1. Parallel composition of instances of PN2

Example 4

For the model PN2 at Fig. 5, the graphs depicted at Figs. 6 and 7 are obtained using the selection Algorithms 1 and 2, respectively, for the case where all the enabled transitions are covered from each marking. Let us apply, Algorithm 1 to the initial marking $M_0$ for $S=En(M_0)$. It starts by $SS=\emptyset , S'=S= \{t_0, t_1,t_2,t_3\}$. If $t_0$ of $S'$ is the first transition selected in the loop while on $S'$, then R is set to $PS^+(t_0,M_0)=\{t_0,t_1,t_2,t_3\}$ and $S'$ to $\emptyset$. Then, Algorithm 1 returns $SS= \emptyset \otimes R = \{\{t_0\}, \{t_1\}, \{t_2\}, \{t_3\} \}$. Note that for $M_0$ and $S=En(M_0)$, Algorithm 2 returns $SS =\{\{t_0,t_2\}, \{t_0,t_3\}, \{t_1,t_3\}\}$ (see Example 3).

Unlike the method in [14], which is based, as Algorithm 1, on the strong-persistent sets, the firing steps obtained by Algorithm 2 may contain some transitions that are in weak-conflict. Indeed, for the previous example, the transitions within each step of SS, returned by Algorithm 2, are not in conflict but they are in weak-conflict. The following examples shows the effectiveness of Algorithm 2 over Algorithm 1 for models where concurrency and weak-conflicts are combined.

Example 5

Consider now the model PN3 at Fig. 9 a parallel composition of PN2. We report in Table 1 for the model in Fig. 9, sizes of MG, CSG, PO, PO combined with CSG, and MPSG. The CSG, PO, PO combined with CSG are provided by the tool TINA². The MPSG is computed based on Algorithm 2 for the case where all the enabled transitions are covered from each marking. For this model, PO provides better results than CSG. Also, even if it is combined with CSG, it never gives better reduction than MPSG. One can easily check that the number of markings of the state space is of order of $3^n$ for MPSG while it is of order of $4^{n+1}$ for PO, CSG, and their combination. It stems from the fact that the selection Algorithm 2 handles in better way the weak-conflicts. For this model, the application of the selection Algorithm 2 shows an effectiveness relatively to the selection Algorithm 1, which is based, as the approach developed in [14], on the strong-persistent sets. Thus, it is not exaggerated to say that the persistent step sets method, based on persistent sets, is very promising to fight the state explosion and to address the verification of very large asynchronous concurrent systems, where the interplay between concurrency and conflict is expanded.

6 Conclusion

Although, partial order methods gained some success in coping with the state space explosion in concurrent systems with asynchronous components, the applicability of verification by state-space exploration of large systems remains as a challenge.

In this work, we have proposed a new parametric combination of the persistent sets with step graphs, based on a better understanding of the intricacy of the interplay between concurrency and conflict, revealing local persistency and leading to a significant reduction. The proposed approach takes into account, in a finer way, the structure of the net, while preserving deadlocks of Petri Nets. Indeed, unlike the method in [14], persistent steps may contain some transitions that are in weak-conflict. Moreover, it allows choosing the transitions to be covered while controlling the length and the number of steps to be selected from each marking.

Finally, the performed tests show the effectiveness of the proposed approach in terms of state space reduction and time execution, relatively to the covering-steps, strong-persistent sets methods or their combination implemented in the tool TINA. They also suggest that combining step graphs with any partial order technique is of very great interest for model-checking.