Small Spiking Neural P Systems with Structural Plasticity

Abstract

Spiking neural P systems or SN P systems are computing models inspired by spiking neurons. The SN P systems variant we focus on are SN P systems with structural plasticity or SNPSP systems. Unlike SN P systems, SNPSP systems have a dynamic topology for creating or removing synapses among neurons. In this work we construct small universal SNPSP systems: 62 and 61 neurons for computing functions and generating numbers, respectively. We then provide some new directions, e.g. parameters to consider, in the search for such small systems.

1 Introduction

In this work we continue the search for small universal systems concerning variants of spiking neural P systems (in short, SN P systems) as in [5, 10, 13, 17] to name a few. Investigations on the power, efficiency, and applications of SN P systems and variants is a very active area, with a recent survey in [12]. The specific class of SN P systems we focus here are spiking neural P systems with structural plasticity (or SNPSP systems) from [3] with further works in [1, 2, 14] to name a few. SNPSP systems are inspired by the ability of neurons to add or delete synapses (the edges) among neurons (the nodes in the graph). Computations in SNPSP systems proceed with a dynamic topology in contrast with SN P systems and their many variants with static topologies. This way, even with simplified types of rules, SNPSP systems can be “useful” by controlling the flow of information (in the form of spikes) in the system by using rules to create or remove synapses. This work is structured as follows: Sect. 2 provides preliminaries for our results; Sects. 3 and 4 provide our results with SNPSP systems having 62 and 61 neurons for computing functions and generating numbers, respectively. In Sect. 5 we discuss why such numbers of neurons are “small enough” and provide ideas, e.g. parameters, for future research on small universal systems.

2 Preliminaries

We assume that the reader has basic knowledge in formal language and automata theory, and membrane computing. We only briefly mention notations and definitions relevant to what follows. More information can be found in various monographs, e.g. [11].

A register machine is a construct of the form ${M}=(m, H, l_{0}, l_{f}, I)$ where m is the number of registers, H is a finite set of instruction labels, $l_0$ and $l_f$ are the start and final (or halt) labels, respectively, and I is a finite set of instructions bijectively labelled by H. Instructions have the following forms:

• $l_{i}: (ADD(r), l_{j}, l_{k})$, add 1 to register r, then nondeterministically apply either instruction labelled by $l_{j}$ or by $l_{k}$,

• $l_{i}: (SUB(r), l_{j}, l_{k})$, if register r is nonempty then subtract 1 from r and apply $l_{j}$, otherwise apply $l_{k}$,

• $l_{f}: FIN$, halts the computation of M.

A register machine is deterministic if all ADD instructions are of the form $l_{i}:(ADD(r),l_{j})$. To generate numbers, M starts with all registers empty, i.e. storing the number zero. The computation of M starts by applying $l_{0}$ and proceeds to apply instructions as indicated by the labels. If $l_f$ is applied, the number n stored in a specified register is said to be computed by M. If computation does not halt, no number is generated. It is known that register machines are computationally universal, i.e. able to generate all sets of numbers that are Turing computable. To compute Turing computable functions, introduce arguments $n_{1}, n_{2}, \ldots , n_{k}$ in specified registers $r_{1}, r_{2}, \ldots , r_{k}$, respectively. The computation of M starts by applying $l_{0}$. If $l_f$ is applied, the value of the function is placed in a specified register $r_{t}$, with all registers different from $r_{t}$ being empty. In this way, the partial function computed is denoted by $M(n_{1}, n_{2}, \ldots , n_{k})$.

The universality of register machines that compute functions is define as follows [10, 15]: Let $\varphi _{0},\varphi _{1}, \ldots$ be a fixed and admissible enumeration of all unary partial recursive functions. A register machine $M_{u}$ is (strongly) universal if there is a recursive function g such that for all natural numbers x, y we have $\varphi _{x}(y)=M_{u}(g(x),y)$. The numbers g(x) and y are introduced in registers 1 and 2 as inputs, respectively, with the result obtained in a specified output register.

Fig. 1.

The universal register machine from [6]

As in [10], we use the universal register machine $M_{u}=(8,H,l_{0},l_{f},I)$ from [6] with the 23 instructions in I and respective labels in H given in Fig. 1. The machine from [6] which contains a separate instruction that checks for zero in register 6 is replaced in [10] with $l_{8}:(SUB(6),l_{9},l_{0})$, $l_{9}:(ADD(6),l_{10})$. It is important to note that as in [10], and without loss of generality, a modification is made in $M_{u}$ because SUB instructions on the output register 0 are not allowed in the construction from [4]. A new register 8 is added and we obtain register machine $M'_{u}$ by replacing $l_f$ of $M_{u}$ with the following instructions: $l_{f}: (SUB(0),l_{22},l^{'}_f)$, $l_{22}: (ADD(8),l_{f})$, $l^{'}_f: FIN$.

A spiking neural P system with structural plasticity or SNPSP system $\varPi$ of degree $m \ge 1$ is a construct $\varPi =(O, \sigma _1,\ldots$, $\sigma _m, syn, in, out)$, where $O = \{a\}$ is the alphabet containing the spike symbol a, and $\sigma _1, \ldots , \sigma _m$ are neurons of $\varPi$. A neuron $\sigma _i = (n_i, R_i)$, $1 \le i \le m$, where $n_i \in \mathbb {N}$ indicates the initial number of spikes in $\sigma _i$ written as string $a^{n_i}$ over O; $R_i$ is a finite set of rules with the following forms:

• 1. Spiking Rule: $E/a^c \rightarrow a$ where E is a regular expression over O and $c \ge 1$.

• 2. Plasticity Rule: $E/a^c \rightarrow \alpha k(i,N)$ where $c \ge 1$, $\alpha \in \{+,-,\pm ,\mp \}$, $N \subset \{1,\ldots ,m\}$, and $k \ge 1$.

The set of initial synapses between neurons is $syn \subset \{1,\ldots ,m\} \times \{1,\ldots ,m\}$, with $(i,i) \not \in syn$, and in, out are neuron labels that indicate the input and output neurons, respectively. When $L(E)=\{a^c\}$, rules can be written with only $a^c$ on their left-hand sides. The semantics of SNPSP systems are as follows. For every time step, each neuron of $\varPi$ checks if any of their rules can be applied. Activation requirements of a rule are specified as $E/a^c$ at the left-hand side of every rule. A rule $r \in R_i$ of $\sigma _i$ is applied if the following conditions are met: the $a^n$ spikes in $\sigma _i$ is described by E of r, i.e. $a^n \in L(E)$, and $n \ge c$. When r is applied, $n - c$ spikes remain in $\sigma _i$. If $\sigma _i$ can apply more than one rule at a given time, exactly one rule is nondeterministically chosen to be applied. When a spiking rule is applied in neuron $\sigma _i$ at time t, all neurons $\sigma _j$ such that $(i,j) \in syn$ receive a spike from $\sigma _i$ at the same step t.

When a plasticity rule $E/a^c \rightarrow \alpha k(i, {N})$ is applied in $\sigma _i$, the neuron performs one of the following actions depending on $\alpha$ and k: For $\alpha = +$, add at most k synapses from $\sigma _i$ to k neurons whose labels are specified in N. For $\alpha = -$, delete at most k synapses that connect $\sigma _i$ to neurons whose labels are specified in N. For $\alpha = \pm$ (resp., $\alpha = \mp$), at time step t perform the actions for $\alpha = +$ (resp., $\alpha = -$), then in step $t+1$ perform the actions for $\alpha = -$ (resp., $\alpha = +$).

Let $P(i) = \{j \mid (i,j)\in syn\}$, be the set of neuron labels such that $(i,j) \in syn$. If a plasticity rule is applied and is specified to add k synapses, there are cases when $\sigma _i$ can only add less than k synapses: when most of the neurons in N already have synapses from $\sigma _i$, i.e. $| {N}- P(i)| < k$. A synapse is added from $\sigma _i$ to each of the remaining neurons specified in N that are not in P(i). If $| {N}-P(i)| = 0$ then there are no more synapses to add. If $| {N}-P(i)| = k$ then there are exactly k synapses to add. When $| {N}-P(i)| > k$ then nondeterministically select k neurons from ${N}-P(i)$ and add a synapse from $\sigma _i$ to the selected neurons.

We note the following important semantic of plasticity rules: when synapse (i, j) is added at step t then $\sigma _j$ receives one spike from $\sigma _i$ also at step t.

Similar cases can occur when deleting synapses. If $|P(i)| < k$, then only less than k synapses are deleted from $\sigma _i$ to neurons specified in N that are also in P(i). If $|P(i)| = 0$, then there are no synapses to delete. If $|P(i) \cap {N}|=k$ then exactly k synapses are deleted from $\sigma _i$ to neurons specified in N. When $|P(i) \cap {N}| > k$, nondeterministically select k synapses from $\sigma _i$ to neurons in N and delete the selected synapses. A plasticity rule with $\alpha \in \{\pm ,\mp \}$ activated at step t is applied until step ${t+1}$: during these steps, no other rules can be applied but the neuron can still receive spikes.

$\varPi$ is synchronous, i.e. at each step if a neuron can apply a rule then it must do so. Neurons are locally sequential, i.e. they apply at most one rule each step, but $\varPi$ is globally parallel, i.e. all neurons can apply rules at each step. A configuration of $\varPi$ indicates the distribution of spikes among the neurons, as well as the synapse dictionary syn. The initial configuration is described by $n_1, n_2, \ldots , n_m$ for each of the m neurons, and the initial syn. A transition is a change from one configuration to another following the semantics of rule application. A sequence of transitions from the initial configuration to a halting configuration, i.e. where no more rules can be applied, is referred to as a computation.

At each computation, if $\sigma _{out}$ fires at steps $t_1$ and $t_2$ for the first and second time, respectively, then a number $n = t_2 - t_1$ is said to be computed by the system. When the system receives or sends a spike to the environment, denote with “1” or “0” each step when the system sends or does not send (resp., receives or does not receive) a spike, respectively. This way, the spike train $10^{n-1}1$ denotes the system receiving or sending 2 spikes with interval n between the spikes.

3 A Small SNPSP System for Computing Functions

In this section we provide a small and universal SNPSP system that can compute functions. The system will follow the same design as in [10] for simulating $M'_u$: the system takes in the input spike train $10^{g(x)-1}10^{y-1}1$, where the numbers g(x) and y are the inputs of $M'_u$. After taking in the input spike train, simulation of $M'_u$ begins by simulating instruction $l_0$ until instruction $l_f$ is encountered which ends the computation of $M'_u$. Finally, the system output is a spike train $10^{\varphi _x(y)-1}1$ corresponding to the output of $\varphi _x(y)$ of $M'_u$. Each neuron is associated with either a register or a label of an instruction of $M'_u$. If register r contains number n, the corresponding $\sigma _r$ has 2n spikes. Simulation of $M'_{u}$ starts when two spikes are introduced to $\sigma _{l_0}$, after $\sigma _{1}$ and $\sigma _{2}$ are loaded with 2g(x) and 2y spikes, respectively. If $M'_u$ halts with $r_8$ containing $\varphi _{x}(y)$ then $\sigma _{8}$ has $2\varphi _{x}(y)$ spikes. Figures 2 and 3 are the modules associated with the ADD and SUB instructions, respectively. These modules have $\sigma _{l^{'}_i}$ and $\sigma _{l^{''}_i}$ referred to as auxiliary neurons, and such neurons do not correspond to registers or instructions. Instead of using rules of the form $a^s \rightarrow \lambda$, i.e. forgetting rules of standard SN P systems in [4], our systems only use plasticity rules of the form $a \rightarrow -1(l_{i}, \emptyset )$. In this way, deleting a non-existing synapse simply consumes spikes and nothing else, hence simulating a forgetting rule.

Fig. 2.

ADD module

Fig. 3.

SUB module

Module ADD in Fig. 2 simulates the instruction $l_{i}: (ADD(r), l_{j})$. The first instruction of M is an ADD instruction and is labeled $l_{0}$. Let us assume that the simulation of the module starts at time t. Initially, $l_{i}$ contains 2 spikes and all other neurons are empty. At time t, neuron $l_{i}$ uses the rule $a^{2} \rightarrow a$ to send one spike each to $l^{'}_i$ and $l^{''}_i$. At time $t+1$, neurons $l^{'}_i$ and $l^{''}_i$ each fire a spike, and both r and $l_{j}$ each receive 2 spikes. At the next step, neuron $l_{j}$ activates in order to simulate the next instruction.

Module SUB in Fig. 3 simulates the instruction $l_{i}: (SUB(r), l_{j}, l_{k})$. Initially, $l_{i}$ contains 2 spikes and all other neurons are empty. When the simulation starts at time t, neuron $l_{i}$ uses the rule $a^{2} \rightarrow a$ to send one spike each to $l^{'}_i$, $l^{''}_i$, and r. At time $t+1$, neuron $l^{'}_i$ fires a spike to $l_{j}$. At the same time, neuron $l^{''}_i$ deletes its synapse to $l_{k}$ and waits until time $t+2$ to add the same synapse, thus sending one spike to $l_{k}$.

In the case $\sigma _r$ was not empty before it received a spike from $l_{i}$, neuron r now contains at least three spikes which corresponds to register $\sigma _r$ containing the value of at least 1. Neuron r in this case uses the rule $(a^{2})^{+}a/a^{3} \rightarrow \pm |S_{j} | (r, S_{j})$, where $S_{j} = \{j \mid j$ is the second element of the triple in a SUB instruction on register $r\}$. If this rule was used, neuron $l_{j}$ receives a total of 2 spikes at time $t+1$. At $t+2$, neuron ${l_{j}}$ is activated and continues the simulation of the next instruction. At the same time, neuron $l^{''}_i$ sends a spike to $\sigma _{l_{k}}$ which $\sigma _{l_k}$ removes at $t+3$ using its rule $a \rightarrow -1(l_k, \emptyset )$.

In the case where $\sigma _r$ was empty before receiving a spike from $\sigma _{l_{i}}$, this corresponds to register r containing the value 0. Neuron r uses the rule $a \rightarrow \mp | S_{k} | (r, S_{k})$, where $S_{k} = \{k \mid k$ is the third element of the triple in a SUB instruction on register $r\}$. At $t+1$, neuron r deletes its synapse to $\sigma _{l_{k}}$. At $t+2$, neuron ${l_{k}}$ receives 2 spikes in total – one from $\sigma _r$ and from $\sigma _{l^{''}_i}$ – and is activated in the next step in order to simulate the next instruction. Also at $t+2$, neuron $l_{j}$ removes the spike it received from $\sigma _{l^{'}_i}$ using its rule $a \rightarrow -1(l_j, \emptyset )$.

Fig. 4.

INPUT module

Module INPUT as seen in Fig. 4 loads 2g(x) and 2y spikes to $\sigma _{1}$ and $\sigma _{2}$, respectively. The module begins its computation after $\sigma _{in}$ receives the first spike from the input spike train $10^{g(x)-1}10^{y-1}1$. We assume that the simulation of the INPUT module starts at time t when $\sigma _{in}$ sends spikes to $\sigma _{c_{1}}$ and $\sigma _{c_{2}}$. At this point, both $\sigma _{c_{1}}$ and $\sigma _{c_{2}}$ have 5 spikes and each use the rule $a^{5}/a \rightarrow a$. At $t+1$, $\sigma _{1}$ receives 2 spikes, so $\sigma _{c_{1}}$ and $\sigma _{c_{2}}$ receive a spike from each other. Since $\sigma _{c_{1}}$ and $\sigma _{c_{2}}$ each have 5 spikes again, they use the same rules again. Neurons $c_{1}$ and $c_{2}$ continue to send spikes to $\sigma _{1}$ and to each other in a loop. This loop continues until both neurons receive a spike again from $\sigma _{in}$, at this point they have 6 spikes each. Note that this spike from $\sigma _{in}$ is from the second spike in the input spike train.

In the next step, $\sigma _{c_{1}}$ and $\sigma _{c_{2}}$ use rules $a^6/a^3 \rightarrow -2(c_1, \{1, c_2\} )$ and $a^6/a^3 \rightarrow -2(c_2, \{ 1, c_1 \} )$, respectively, to delete their synapses to each other and to $\sigma _{1}$. Neurons $c_1$ and $c_2$ each have 3 spikes now, so they create synapses and send one spike to each other and $\sigma _{2}$. Both neurons have one spike each so they use rule $a \rightarrow a$ to send a spike to $\sigma _2$ and each other in a loop similar to the previous one. Once both neurons receive a spike from $\sigma _{in}$ for the third and last time, the loop is broken. Neurons $c_{1}$ and $c_{2}$ each have 2 spikes now so they use rules $a^2 \rightarrow +1(c_1, \{ l_0 \})$ and $a^2 \rightarrow +1(c_2, \{ l_0 \})$ to create a synapse and send a spike to $\sigma _{l_{0}}$. At the next step, $\sigma _{l_{0}}$ activates and the simulation of $M'_u$ begins.

Fig. 5.

OUTPUT module.

Fig. 6.

ADD-ADD module to simulate $l_{17}: (ADD(2), l_{21})$ and $l_{21}: (ADD(3), l_{18})$.

Module OUTPUT in Fig. 5 is activated when instruction $l_{f}$ is executed by $M'_{u}$. Recall that $M'_u$ stores its result in output register 8. We assume that at some time t, instruction $l_{f}$ is executed so $M'_{u}$ halts. Also at t, and for simplicity, $\sigma _{8}$ contains 2n spikes corresponding to the value n stored in register 8 of $M'_{u}$. Actually, and as mentioned at the beginning of this section, register 8 stores the number $\varphi _x(y)$ and hence $\sigma _8$ stores $2\varphi _x(y)$ spikes.

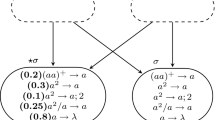
Neuron $l_{f}$ sends a spike to $\sigma _{8}$ and $\sigma _{out}$. At $t+1$, neuron out applies rule $a \rightarrow a$ and sends the first of two spikes to the environment. Neuron 8 now with $2n + 1$ spikes applies rule $a(aa)^{+}/a^{2} \rightarrow -1(8, \emptyset )$ to consume 2 spikes. Neuron 8 continues to use this rule until only 1 spike remains, then uses the rule $a \rightarrow \pm {1}(8, {out})$ to send a spike to $\sigma _{out}$. At the next step, $\sigma _{8}$ deletes its synapse to $\sigma _{out}$, while $\sigma _{out}$ sends a spike to the environment for the second and last time. In this way, the system produces an output spike train of the form $10^{2n-1}1$ corresponding to the output of $M'_u$. The breakdown of the 86 neurons in the system are as follows:

• 9 neurons for registers 0 to 8,

• 25 neurons for 25 instruction labels $l_0$ to $l_{22}$ with $l_f$ and $l'_f$,

• 48 neurons for 24 ADD and SUB instructions,

• 3 neurons in the INPUT module, 1 neuron in the OUTPUT module.

This number can be reduced by some “code optimizations”, exploiting some particularities of $M'_{u}$ similar to what was done in [10]. We observe the case of two consecutive ADD instructions. In $M'_{u}$, there is one pair of consecutive ADD instructions, i.e. $l_{17}: (ADD(2), l_{21})$ and $l_{21}: (ADD(3), l_{18})$. By using the module in Fig. 6 to simulate the sequence of two consecutive ADD instructions, we save the neuron associated with $l_{21}$ and 2 auxiliary neurons.

A module for the sequence of ADD-SUB instructions is in Fig. 7. We save the neurons associated with $l_{6}$, $l_{10}$, and one auxiliary neuron for each pair. There are two sequences of ADD-SUB instructions, i.e. $l_{5}: (ADD(5), l_{6})$, $l_{6}: (SUB(7), l_{7}, l_{8})$, $l_{9}: (ADD(6), l_{10})$ and $l_{10}: (SUB(4), l_{0}, l_{11})$.

Fig. 7.

ADD-SUB module to simulate $l_{5}: (ADD(5), l_{6})$ and $l_{6}: (SUB(7), l_{7}, l_{8})$.

Fig. 8.

SUB-SUB module

To further reduce the number of neurons, we use similar techniques as in [17] to decrease neurons by sharing one or two auxiliary neurons among modules. Consider the case of two ADD modules: As shown in Proposition 3.1 in [17], $l_{2}: (ADD(6), l_{3})$ and $l_{9}: (ADD(6), l_{10})$ can share one auxiliary neuron without producing “wrong” simulations. Now consider the case of two SUB instructions: We follow the same grouping using Proposition 3.2 in [17] to make sure that two SUB modules follow only the “correct” simulations of $M'_u$. All modules associated with the instructions in each of the following groups can share 2 auxiliary neurons:

• 1. $l_{0}: (SUB(1), l_{1}, l_{2})$, $l_{4}:(SUB(6), l_{5}, l_{3})$, $l_{6}:(SUB(7), l_{7}, l_{8})$,

  $l_{10}: (SUB(4), l_{0}, l_{11})$, $l_{11}:(SUB(5), l_{12}, l_{13})$, $l_{13}:(SUB(2), l_{18}, l_{19})$,

  $l_{15}: (SUB(3), l_{18}, l_{20})$.

• 2. $l_{3}: (SUB(5), l_{2}, l_{4})$, $l_{8}:(SUB(6), l_{9}, l_{0})$, $l_{f}:(SUB(0), l_{22}, l'_{f})$.

• 3. $l_{14}: (SUB(5), l_{16}, l_{17})$, $l_{18}:(SUB(4), l_{0}, l_{22})$, $l_{19}:(SUB(0), l_{0}, l_{18})$.

• 4. $l_{12}: (SUB(5), l_{14}, l_{15})$.

In order to allow the sharing of auxiliary neurons between SUB modules in the system, the rules of auxiliary neurons must be changed as shown in Fig. 8. The rule in $l'_{i}$ auxiliary neurons is changed to $a \rightarrow \pm |G_{j} | (r, G_{j})$, where $G_{j} = \{j \mid j$ is the second element of the triple in a SUB instruction within the same group$\}$. Similarly, the rule in $l''_{i}$ auxiliary neurons is changed to $a \rightarrow \mp | G_{k} | (r, G_{k})$, where $G_{k} = \{k \mid k$ is the third element of the triple in a SUB instruction within the same group$\}$. As such, in the first group we have $G_{j}$ as $\{l_{0}, l_{1}, l_{5}, l_{7}, l_{12}, l_{18}\}$ and $G_{k}$ as $\{l_{2}, l_{3}, l_{8}, l_{11}, l_{13}, l_{19}, l_{20}\}$.

These groupings allow the saving of 20 neurons, however only 16 neurons are saved since $l_{6}:(SUB(7), l_{7}, l_{8})$ and $l_{10}: (SUB(4), l_{0}, l_{11})$ are already used in the ADD-SUB module in Fig. 7. This gives a total decrease of 17 neurons. Together with the 3 neurons saved by the module in Fig. 6, as well as the 4 neurons saved by the module in Fig. 7, an improvement is achieved from 86 to 62 neurons which we summarize as follows.

Theorem 1

There is a universal SNPSP system for computing functions having 62 neurons.

4 A Small SNPSP System for Generating Numbers

In this section, an SNPSP system $\varPi$ is said to be universal as a generator of a set of numbers as in [10], according to the following framework: Let $\varphi _0, \varphi _1, \ldots$ be a fixed and admissible enumeration of partial recursive functions in unary. Encode the xth partial recursive function $\varphi _x$ as a number given by g(x) for some recursive function g. We then introduce from the environment the sequence $1 0^{g(x) -1} 1$ into $\varPi$. The set of numbers generated by $\varPi$ is $\{m \in \mathbb {N} \mid \varphi _x(m) \text { is defined}\}$.

We consider the same strategy from [10]. First, from the environment we introduce the spike train $10^{g(x)-1}1$ and load 2g(x) spikes in $\sigma _{1}$. Second, nondeterministically load a natural number m into $\sigma _{2}$ by introducing 2m spikes in $\sigma _{2}$, and send the spike train $10^{m-1}1$ out to the environment to generate the number m. Third and lastly, to verify if $\varphi _x$ is defined for m we start the register machine $M_u$ in Fig. 1 with the values g(x) and m in registers 1 and 2, respectively. If $M_u$ halts then so does $\varPi$, thus $\varphi _x(m)$ is defined. Note the main difference between generating numbers and computing functions: we do not require a separate OUTPUT module but we need to nondeterministically generate the number m. Since no OUTPUT module is needed we can omit register 8, and computation simply halts after $l_{18}: (SUB(4), l_0, l_f)$. The combined INPUT-OUTPUT module is given in Fig. 9.

Fig. 9.

INPUT-OUTPUT module

Module INPUT-OUTPUT loads 2g(x) and 2m spikes to $\sigma _{1}$ and $\sigma _{2}$, respectively. The module is activated when $\sigma _{in}$ receives a spike from the environment. Neurons $c_{1}$, $c_{2}$, and $c_{3}$ initially contain 4, 4, and 3 spikes respectively. Assume the module is activated at t and $\sigma _{in}$ sends one spike each to $\sigma _{c_{1}}$, $\sigma _{c_{2}}$, and $\sigma _{c_{3}}$. At this point, both $c_{1}$ and $c_{2}$ have 5 spikes and they use the rule $a^{5}/a \rightarrow a$. At $t+1$, neuron 1 receives 2 spikes, and $c_{1}$ and $c_{2}$ will receive a spike from each other. Neurons $c_{1}$ and $c_{2}$ continue to spike at $\sigma _{1}$ and to each other in a loop until they receive a spike again from in. When $\sigma _{in}$ fires a spike for the second and last time at some $t+x$, neurons $c_{1}$, $c_{2}$, and $c_3$ now have 6, 6, and 5 spikes, respectively. At $t+x+1$, neurons $c_{1}$ and $c_{2}$ use rules $a^{6}/a^{3} \rightarrow -2(c_{1}, \{1,c_{2}\})$ and $a^{6}/a^{3} \rightarrow -2(c_{2}, \{1,c_{1}\})$, respectively. They each delete their synapses to $\sigma _{1}$ and consume 3 spikes so 3 spikes remain. At the same time $\sigma _{c_{3}}$ uses the rule $a^{5}/a^{3} \rightarrow -1(c_{3}, \{in\})$ and consumes 3 spikes. Now $\sigma _{c_{3}}$ has 2 spikes and nondeterministically chooses between two rules.

If $\sigma _{c_{3}}$ applies $a^{2}/a \rightarrow a$ at $t+x+2$, it sends one spike each to $\sigma _{c_{1}}$ and $\sigma _{c_{2}}$. At the same time, $\sigma _{c_{1}}$ applies $a^{3} \rightarrow +2(c_{1}, \{2, c_{2}\})$ to create synapses and send spikes to $\sigma _{2}$ and $\sigma _{c_{2}}$. Neuron $c_{2}$ applies $a^{3} \rightarrow +5(c_{2}, \{2, c_{1}, c_{3}, c_{4}, out\})$ to create synapses and send spikes to $\sigma _{2}$, $\sigma _{c_{1}}$, $\sigma _{c_{3}}$, $\sigma _{c_{4}}$, and $\sigma _{out}$. Since $\sigma _{c_1}$ and $\sigma _{c_2}$ received one spike from each other and one spike from $\sigma _{c_{3}}$, they both apply $a^{2} \rightarrow a$ at $t+x+3$. If $\sigma _{c_{3}}$ continues to apply $a^{2}/a \rightarrow a$, neurons $c_{1}$ and $c_{2}$ continue to send one spike to each other, $\sigma _{c_4}$, and $\sigma _{out}$, as well as load $\sigma _{2}$ with 2 spikes. If $\sigma _{c_{3}}$ applies $a^{2} \rightarrow \mp 2(c_{3}, \{c_{1}, c_{2}\})$ instead then it ends the loop between $\sigma _{c_{1}}$ and $\sigma _{c_{2}}$. Neurons $c_{1}$ and $c_{2}$ receive a spike from each other but do not receive a spike from $\sigma _{c_{3}}$. At the next step both neurons do not fire a spike and instead apply $a \rightarrow -1(c_{1}, \{in\})$ to simply consume their spikes.

Now we verify the operation of the remainder of the module. When $\sigma _{c_{2}}$ applies $a^{3} \rightarrow +5(c_{2}, \{2, c_{1}, c_{3}, c_{4}, out\})$ at $t+x+2$, it sends a spike each to $\sigma _{c_{4}}$ and $\sigma _{out}$ for the first time. At $t+x+3$, neuron $c_{4}$ sends a spike to $\sigma _{out}$, followed by the sending of a spike of $\sigma _{out}$ to the environment for the first time. Note that $\sigma _{c_{4}}$ and $\sigma _{out}$ also receive one spike each from $\sigma _{c_{2}}$ at $t+x+3$ due to $a^{2} \rightarrow a$. At the next step, $\sigma _{c_{4}}$ and $\sigma _{out}$ have 1 and 2 spikes, respectively. If $\sigma _{c_{3}}$ continues to apply $a^{2}/a \rightarrow a$ then $\sigma _{c_{2}}$ continues to fire spikes to $\sigma _{c_4}$ and $\sigma _{out}$. Neuron out does not fire since it accumulates an even number of spikes from $\sigma _{c_{2}}$ and $\sigma _{c_{4}}$.

Once $\sigma _{c_3}$ applies $a^{2} \rightarrow \mp {2}(c_{3},\{c_{1}, c_{2}\})$ to end the loop between $\sigma _{c_1}$ and $\sigma _{c_2}$, neurons $c_{4}$ and out do not receive a spike from $\sigma _{c_{2}}$. Neuron $c_{4}$ fires a spike to $\sigma _{out}$ so now $\sigma _{out}$ has an odd number of spikes. At the next step, $\sigma _{out}$ fires a spike to the environment for the second and last time. Neuron out also sends a total of two spikes each to $\sigma _{c_{5}}$ and $\sigma _{c_{6}}$. Once $\sigma _{c_{5}}$ and $\sigma _{c_{6}}$ collect two spikes each they fire a spike to $\sigma _{l_{0}}$ to start the simulation of $M_u$. The modified module for halting and simulating $l_{18}$, since register 8 is not required, is in Fig. 10. The following is the breakdown of the 81 neurons in the system:

• 8 neurons for 8 registers (the additional register 8 is omitted),

• 22 neurons for 22 labels ($l_{f}$ is omitted), 42 neurons for 21 ADD and SUB instructions, 1 neuron for the special SUB instruction (Fig. 10),

• 8 neurons in the INPUT-OUTPUT module.

Fig. 10.

Module for simulating $l_{18}: (SUB(4), l_{0}, l_{f})$ without $l_f$.

As in Sect. 3, we can decrease by 7 the number of neurons by using the optimizations in Figs. 6 and 7. We can also use the method in [17] and the module shown in Fig. 8 to share auxiliary neurons. A neuron is saved in two ADD modules, and we follow a similar grouping for the 12 SUB instructions where we save 12 neurons. A total of 20 neurons are saved. Using the results above, an improvement is made from 81 to 61 neurons. The breakdown is as follows, and the result summarized afterwards.

• 8 neurons for 8 registers, 19 neurons for 19 labels ($l_{6}$, $l_{10}$, and $l_{21}$ are saved),

• 25 neurons for ADD and SUB instructions, 1 neuron for the special SUB instruction, and 8 neurons in the INPUT-OUTPUT module.

Theorem 2

There is a universal number generating SNPSP system having 61 neurons.

5 Discussions and Final Remarks

We report our preliminary work on small universal SNPSP systems with 62 and 61 neurons for computing functions and generating numbers, respectively. Of course these numbers can still be reduced but here we note some observations on results for small SN P systems and their variants. While the numbers obtained in this work are still “large”, we argue that the technique used in this work and as in [10, 17] and more recently in [5, 13], which here we denote as the Korec simulation technique, seems closer to biological reality: each neuron is associated either with an instruction or a register only. In this technique, neurons also have “fewer” rules making them more similar to the systems in [16] as compared to smaller systems in [7,8,9] with “super neurons”, i.e. neurons having a fixed but “large” number of rules. The Korec simulation can also bee seen as a normal form, i.e. observing a simplifying set of restrictions. While it is interesting to pursue the search for systems with the smallest number of neurons, we think it is also interesting to search for systems with a small number of neurons and rules in the neurons. Korec simulation can also be extended to other register machines given in [6].

The smallest systems due to Korec simulation must have $m+n$ neurons as mentioned in [8]. In this work as in others using Korec simulation, simulating $M_u$ or $M'_u$ means having 34 and 30 neurons, respectively. Hence, results in this work and in [5, 10, 13, 17] are approximately double these numbers but it is still open how to further reduce them without violating the Korec simulation. Perhaps including a parameter k where each neuron has no more than k rules could be considered in future works. In our results, all neurons in our modules have $k = 2$ except for the $c_i$ neurons in the INPUT module. Such neurons can be replaced with neurons having at most 2 rules, but it remains open how to do this in our systems and in others without increasing the number of neurons “significantly”.

Lastly, this work is only concerned with SNPSP systems having neurons that produce at most one spike each step. It remains to be seen how small the system can become if neurons produce more than one spike each step, e.g. using synapse weights as in [1] and extended spiking rules as in [7, 8, 13].