On the Use of Optimal Transport Distances for a PDE-Constrained Optimization Problem in Seismic Imaging

Abstract

Full waveform inversion is a PDE-constrained nonlinear least-squares problem dedicated to the estimation of the mechanical subsurface properties with high resolution. Since its introduction in the early 80s, a limitation of this method is related to the non-convexity of the misfit function which is minimized when the method is applied to the estimation of the subsurface wave velocities. Recently, the definition of an alternative misfit function based on an optimal transport distance has been proposed to mitigate this difficulty. In this study, we review the difficulties for exploiting standard optimal transport techniques for the comparison of seismic data. The main difficulty is related to the oscillatory nature of the seismic data, which requires to extend optimal transport to the transport of signed measures. We review three standard possible extensions relying on a decomposition of the data into its positive and negative part. We show how the two first might not be adapted for full waveform inversion and focus on the third one. We present a numerical strategy based on the dual formulation of a particular optimal transport distance yielding an efficient implementation. The interest of this approach is illustrated on the 2D benchmark Marmousi model.

1 Full Waveform Inversion as a PDE-Constrained Nonlinear Optimization Problem

Full waveform inversion (FWI) is a high resolution seismic imaging technique which aims at reconstructing subsurface mechanical properties such as wave velocities, density, attenuation, or anisotropy parameters, from the recording of seismic waves at the surface. Compared to conventional tomography strategies, based on the interpretation of arrival times only, FWI should exploit the totality of the seismic signal, which is expected to provide higher resolution estimates of the subsurface parameters, in the limit of half the shortest wavelength of the propagated signal following the theory of diffraction tomography [12]. A recent review of FWI is proposed by Virieux et al. [43]. FWI is usually formulated as the minimization over the space of the subsurface parameters of the misfit between predicted and observed data. The predicted data is computed through the solution of partial differential equations (PDE) describing the seismic waves propagation. In the simplest settings, which we consider in this study, the acoustic approximation is adopted. Using this formalism, the problem is cast as the following PDE-constrained nonlinear optimization problem [18, 40]

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} \displaystyle \min_{v_P} J(v_P)=g(d_{cal},d_{obs}) + \alpha R(v_P), \; v_P(x) \in \mathcal{C}^{p}(\varOmega), \;\; \varOmega \subset \mathcal{R}^{d} \\ \displaystyle \frac{1}{\rho v_P(x)^2}\partial_{tt} u(x,t) - \mathrm{ div} \left(\frac{1}{\rho(x)} \nabla u(x,t)\right) =s(x,t), \; (x,t) \in \varOmega \times [0,T], \\ \displaystyle d_{cal}(x_r,t)=H(u)(x_r,t), \, (x_r,t) \in \varGamma \times [0,T]. \end{array} \right.\end{aligned} $$

(1)

In the system (1), the spatial domain Ω is a subset of $\mathcal {R}^{d}$, where d = 2 or d = 3, while Γ denotes a subset of the border ∂Ω. The time interval is defined by [0, T], where T > 0. The control variable is denoted by v_P(x): this is the pressure wave (P-wave) velocity, which is supposed to be smooth up to a certain level of regularity $p \in \mathcal {N}$. The P-wave velocity is generally the main parameter to be reconstructed, even if the density ρ(x) can also be included in the inverse problem yielding a so-called multiparameter problem (see [32] for a review on multiparameter FWI). The functional J(v_P) measures the misfit between predicted data d_cal(x_r, t) and observed data d_obs(x_r, t) through a misfit measurement function g which is often taken as the least-squares norm

$$\displaystyle \begin{aligned} g(d_{cal},d_{obs})=\frac{1}{2}\|d_{cal}-d_{obs}\|{}^2_{L^2}. \end{aligned} $$

(2)

It shall be noted that this least-squares distance measure is local: each sample of the observed data is compared with its synthetic counterpart at the same position in the data space, neglecting any information which could come from the neighboring samples. As a result, the least-squares distance is unable to detect shifted patterns between two datasets.

A regularization term R(v_p), weighted by a positive coefficient α, is also generally added to the misfit measurement to reduce the null space of the underlying inverse problem. Usual choices for R(v_P) include prior information regularization, or penalization of the first-order spatial derivatives (Tikhonov regularization)

$$\displaystyle \begin{aligned} R(v_P)=\frac{1}{2}\|v_{P}-v_{P,0}\|{}^2_{L^2}, \;\; R(v_P)=\sum_{i=1}^{d}\frac{1}{2}\|\partial x_i v_{P}\|{}^2_{L^2}. \end{aligned} $$

(3)

The calculated data d_cal(x_r, t) is computed from the solution u(x, t) of the acoustic wave equation through the observation operator H(u). In practice, this observation operator simply extracts the value of the wavefield u(x, t) at the receivers’ locations.

A Lagrangian function associated with the PDE-constrained problem (1) is

$$\displaystyle \begin{aligned} \begin{array}{ll} \displaystyle L(v_{P},d_{cal},u,\lambda_1,\lambda_2)& \displaystyle =g(d_{cal},d_{obs})+\alpha R(v_P) \\ & \displaystyle + \int_{x_r \in \varGamma}\int_{0}^{T}\left(d_{cal}(x_r,t)-Hu(x_r,t)\right)\lambda_2(x_r,t) dx_r dt \\ & \displaystyle +\int_{x \in \varOmega}\int_{0}^{T}\left(\frac{1}{\rho v_P^2}\partial_{tt} u(x,t) \right.\\&\left.\displaystyle - \mathrm{ div} \left(\frac{1}{\rho} \nabla u(x,t)\right) -s(x,t) \right)\lambda_1(x,t) dx dt \end{array}\end{aligned} $$

(4)

First-order Karush-Kuhn-Tucker conditions give necessary conditions to characterize the solution of (1). They are obtained by canceling the first-order partial derivatives of the Lagrangian operator.

Instead of solving the Karush-Kuhn-Tucker system iteratively through a Newton algorithm, a “reduced space” method is preferred [31] for efficiency. The misfit function J(v_P) is minimized following iterative local optimization methods for smooth nonlinear functions, which rely on the ability to compute its gradient ∇J(v_P). This gradient is computed from the equation

$$\displaystyle \begin{aligned} \nabla J(v_P)=-\frac{2}{\rho v_P^3}\int_{0}^{T}\partial_{tt} \overline{u}(x,t)\overline{\lambda}_1(x,t) dt+ \alpha \nabla R(v_P), \end{aligned} $$

(10)

where fields $\overline {u}(x,t)$ and $\overline {\lambda }_1(x,t)$ are obtained through the solution of the Equations from (6) to (9). In particular, using the L² norm for the definition of the misfit measurement function g yields the simple expression

$$\displaystyle \begin{aligned} \lambda_2=-(d_{cal}-d_{obs}). \end{aligned} $$

(11)

The reduced space method thus yields an efficient strategy to compute the gradient ∇J(v_P). This technique, also introduced as the adjoint-state method within the optimal control theory [21], has been known for a long time in seismic imaging [9] and in weather forecasting [19]. A review of the adjoint-state method and its application in seismic imaging has been proposed by Plessix [34].

Among different minimization strategies, the nonlinear conjugate gradient method, the quasi-Newton l-BFGS [30], or the truncated Newton approach [29] are used to solve the FWI problem (see [25] for a review of standard minimization algorithms used in FWI).

Since its introduction in the 80’s, one of the main challenges for FWI is related to the non-convexity of the P-wave velocity reconstruction problem. For practical applications, the size of the discrete problem prevents the use of global or semi-global optimization strategies (Monte-Carlo or genetic algorithms, for instance): in 2D, the number of unknowns easily reaches O(10⁶), in 3D this number grows up to O(10⁹). The use of local optimization strategies thus requires to start the iterative process from a v_P model close enough from the solution, otherwise the method converges to a local minimum. Wave physics analysis provides useful information to better assess what are the requirements that an initial model should satisfy to ensure the convergence toward the global minimum.

The non-convexity of the misfit function with respect to the P-wave velocity is related to the choice of the function g(d_cal, d_obs) to measure the discrepancy between observed and calculated data. Seismic observations are in essence oscillatory signals. Macroscale P-wave velocity perturbation mainly affects the seismic data by modifying the propagation time rather than the amplitude of the seismic events [16]. As a result, observed and calculated data mainly differ through time-shifts of the different seismic arrivals. The function g(d_cal, d_obs) should thus be convex with respect to these time-shifts. This is not the case for the L² distance which is used in practice. This is illustrated in Figure 1 where the seismic data is schematically represented as a periodic sinusoidal signal. When the signals are shifted by a multiple of one period of the signal, the L² differences between the signals reach a local minimum: this is what is referred to a cycle skipping, or phase ambiguity problem, in the FWI community. Avoiding these local minima thus requires to start the minimization from less than half-a-phase shift. In other words, the initial velocity model should be sufficiently accurate to predict the kinematic of the wave propagation up to half-a-phase shift.

Fig. 1

Schematic example of the cycle skipping/phase ambiguity issue on sinusoidal signals. As soon as the initial shift is larger than half a period of the signal, the fit of the signal using a least-squares distance is performed up to one or several phase shifts. One may try to fit the n + 1 dashed wriggle of the top signal with the n continuous wriggle of the middle signal moving to the wrong direction. The bottom dashed signal predicts the n wriggle in less than half-period leading to a correct updating direction (figure from [44])

Mitigating this non-convexity has been the aim of numerous methods proposed during the past decades. Three main lines of investigation have been followed. The first one relies on the design of hierarchical schemes. The data is interpreted through a sequence of FWI problems, the estimation obtained from the problem i being used as an initial guess for the problem i + 1. For each FWI problem, only a subset of the data is interpreted. The usual data decomposition is performed in the frequency domain: the data is interpreted from low-to-high frequencies. Low frequency components of the signal have a larger period, therefore the requirement on the initial model to fit the observed data within half-a-period of the signal is partially relaxed. Additional level of hierarchy can also be applied (time-windowing and offset selection, for instance) following layer stripping approaches [8, 35, 37]. The second line of investigation is based on the modification of the misfit measurement function g(d_cal, d_obs). Cross-correlation functions have been first investigated [23], and later on warping techniques [15], deconvolution approaches [22, 45] as well as envelope and phase separation [6, 14]. The third line of investigation relies on probing the consistency of the velocity model by building reflectivity images using different subset of the data. The velocity is updated such that the different reflectivity images become similar (see [39] and references therein for a review). These methods are known as (extended) image-domain techniques.

None of these approaches has completely overcome the cycle skipping or phase ambiguity problem. Hierarchical approaches relax the constraint on the accuracy of the initial velocity model by working first at low frequencies; however, this strategy is limited by the lowest available frequency, which is most of the time not low enough to sufficiently constrain the model. The different modifications of the misfit function proposed so far also enables to start from an initial velocity model further away from the solution; however, this is often at the expense of the resolution of the final estimation. Image-domain techniques also exhibit interesting properties in terms of convexity of the misfit function; however, the computation cost associated with the repeated computation of reflectivity images seems to preclude their use to large-scale datasets, especially in 3D configuration.

In this study, we discuss how optimal transport distances could be used to define an alternative misfit function measurement g in the framework of FWI. In particular, these distances provide natural tools to go beyond the point-to-point comparison underlaid by the least-squares distance by performing global comparison. The field of optimal transport has been very active in the last years, as testified by the number of textbooks published on this topic recently [2, 36, 41, 42]. Recent applications in image processing demonstrate the interest of optimal transport distance to compare images, notably for its ability to detect shifted patterns from one image to another [20]. We discuss what are the main difficulties when applying optimal transport distance for the comparison of seismic data. In particular, we show that the oscillatory nature of the seismic data requires to extend optimal transport to the comparison of signed measures, which is a nontrivial problem. We review three different propositions found in the literature relying on the decomposition of the data in its positive and negative part. We show how the two first options might not be adapted for full waveform inversion. We thus focus on the third possibility and show how an efficient implementation can be obtained, as we have presented it in previous studies [26, 28]. We present numerical results obtained on the 2D Marmousi case study, a benchmark in the seismic imaging community, which illustrate the interest of this approach.

In Section 2, we discuss the optimal transport problem formulation for positive measures and present a state-of-the-art for its extension to the comparison of signed measures. In Section 3, we present the alternative strategy we have promoted in previous studies and its application to the 2D Marmousi case study. Conclusion and perspectives are given in Section 4.

2 Optimal Transport for Full Waveform Inversion

2.1 Basics on Optimal Transport

Optimal transport has its roots in the work of a French scientist named Gaspard Monge, in an attempt to devise the best strategy to move piles of sand to a building site. The aim was to minimize the volume of the sand to be displaced as well as the distance on which it had to be displaced. In modern mathematics, an expression of this problem is the following. Consider two probability measures $\mu \in \mathcal {P}(X)$ and $\nu \in \mathcal {P}(Y)$ (μ would represent the initial configuration of sand and ν the targeted one). We consider the mapping T(x) from X to Y  such that

$$\displaystyle \begin{aligned} \left\{ \begin{array}{ccc} \displaystyle X&\longrightarrow& Y \\ T : x &\longrightarrow& T(x), \end{array} \right. \end{aligned} $$

(12)

The push forward distribution of μ through the mapping T is denoted by T_#μ, such that for any measurable subset A ⊂ Y , we have

$$\displaystyle \begin{aligned} \left(T_{\#}\mu\right)(A)\equiv \mu\left(T^{-1}(A)\right)=\nu(A). \end{aligned} $$

(13)

In this framework, the original Monge problem is formulated as

$$\displaystyle \begin{aligned} \inf_{T} \; \left\{\int_{X} ||x-T(x)|| d\mu(x), \;\; T_{\#}\mu=\nu\right\}. \end{aligned} $$

(14)

This problem has not necessarily a solution, and when the solution exists, it is difficult to compute because of the nonlinear constraint T_#μ = ν.

A relaxation of this problem has been proposed by Kantorovich [17], under the form

$$\displaystyle \begin{aligned} \inf_{\gamma} \; \left\{\int_{X\times Y} c(x,y) d\gamma (x,y), \;\; \gamma\in \varPi(\mu,\nu) \right\}, \end{aligned} $$

(15)

where the ensemble of transport plans Π(μ, ν) is defined by

$$\displaystyle \begin{aligned} \varPi(\mu,\nu)= \left\{ \gamma \in \mathcal{P}(X\times Y),\;\; \left(\pi_{X}\right)_{\#}\gamma=\mu, \;\: \left(\pi_{Y}\right)_{\#}\gamma=\nu \right\}. \end{aligned} $$

(16)

The operators π_X and π_Y are the projectors on X and Y , respectively. This relaxation is the cornerstone of modern application of optimal transport as the problem (15) has always a solution which coincides with the one of the original Monge problems when this one exists. The problem (15) generalizes (14) in the sense that, instead of considering a mapping T transporting each particle of the distribution μ to the distribution ν, it considers all pairs (x, y) of the space X × Y  and for each pair defines how many particles of μ go from x to y.

In discrete form, the Kantorovich problem becomes a linear programming problem of the form

$$\displaystyle \begin{aligned} \min_{\gamma_{ij}} \sum_{ij} \gamma_{ij}c_{ij}, \;\; \gamma \in \varPi(\mu,\nu) \end{aligned} $$

(17)

where

$$\displaystyle \begin{aligned} \varPi(\mu,\nu)=\{\gamma \geq 0, \sum_{j=1} \gamma_{ij}=\mu_i, \;\;\sum_{i=1} \gamma_{ij}=\nu_j\} \end{aligned} $$

(18)

The entry γ_ij represents how much mass should be moved from x_i to y_j while c_ij measures the distance between x_i to y_j. The constraint ensures that the initial distribution is equal to μ while the transported distribution through the transport plan γ is equal to ν.

Of particular interest, optimal transport induces distances between distribution, named as Wasserstein distances or earth mover’s distances (EMD). They are defined by

$$\displaystyle \begin{aligned} W_{p} (\mu,\nu)= \left(\min_{\gamma_{ij}} \sum_{ij} \gamma_{ij}\|x_i-y_j\|{}^p, \;\; \gamma \in \varPi(\mu,\nu)\right)^{1/p} \end{aligned} $$

(19)

One interest for using such distance for signal processing applications is their ability to detect shifted pattern from one signal to another. This property is also referred to in the literature as the fact that W_p distances should be seen as “horizontal distances” while L^p distances should be seen as “vertical distances” [36]. The W_p distance between two shifted probability distributions is convex with respect to this shift, while the L^p distance is insensitive to this shift.

2.2 Applying Optimal Transport for the Comparison of Seismic Data: The Difficulty of Transporting Signed Measures

The existence of a solution to the optimal transport problem (16) depends on two assumptions that shall be satisfied by the measures μ and ν

• 1. μ and ν shall be positive

• 2. μ and ν shall have the same total mass

  $$\displaystyle \begin{aligned} \int_{X} d\mu(x)=\int_{X} d\nu(x). \end{aligned} $$

  (20)

In this section, for the sake of simplicity, we assume that the two measures μ and ν are defined on the same space X . This is the case when μ and ν represent seismic data. Seismic data do not satisfy the positivity requirement due to its oscillatory nature. However, the zero frequency component of each seismic trace is zero

$$\displaystyle \begin{aligned} \forall x_r, \;\; \int_{0}^{T}d_{cal}(x_r,t)dt=\int_{0}^{T}d_{obs}(x_r,t)dt=0. \end{aligned} $$

(21)

Therefore, we have

$$\displaystyle \begin{aligned} \int_{x_r} \int_{0}^{T}d_{cal}(x_r,t)dt dx_r=\int_{x_r} \int_{0}^{T}d_{obs}(x_r,t)dt dx_r=0. \end{aligned} $$

(22)

Thus, interpreting seismic data as density functions, Equation (22) shows that the seismic data satisfy the second assumption: observed and calculated data have the same total mass, which is zero.

The main difficulty to apply optimal transport to the comparison of seismic data thus relies on the non-positivity of the seismic data. This is a well-identified issue in the optimal transport community. The question how to extend optimal transport to signed measures is investigated in particular by Ambrosio et al. [2] and Mainini [24]. Mainini makes use of the following Jordan-Hahn decomposition,

$$\displaystyle \begin{aligned} \mu=\mu^{+}-\mu^{-}, \end{aligned} $$

(23)

where μ⁺ (respectively, μ⁻) is the positive part of μ (respectively, the negative part of μ). Three strategies are reviewed in [24] to extend optimal transport to signed measures. The corresponding extension of the W_p distances to signed measures is introduced as W_p,i(μ, ν), i = 1, 2, 3 in the following. The three strategies proposed by Mainini are

• 1. Transport separately the positive and negative part of the measures

  $$\displaystyle \begin{aligned} W_{p,1}(\mu,\nu)=W_{p}(\mu^{+},\nu^{+})+W_{p}(\mu^{-},\nu^{-}) \end{aligned} $$

  (24)

• 2. Transport the absolute value of the measures

  $$\displaystyle \begin{aligned} W_{p,2}(\mu,\nu)=W_{p}(|\mu|,|\nu|) \end{aligned} $$

  (25)

• 3. Perform the decomposition

  $$\displaystyle \begin{aligned} W_{p,3}(\mu,\nu)=W_{p}(\mu^{+}+\nu^{-},\nu^{+}+\mu^{-}) \end{aligned} $$

  (26)

The first strategy, which might appear as the more intuitive, is the one proposed originally by Engquist and Froese [13]. It is successfully applied to the comparison of two time-shifted Ricker functions. The function $W_{2,1}^2(\mu ,\nu )$ exhibits a quadratic convexity with respect to the time-shift between the two Ricker functions (Figure 2). Two drawbacks can nonetheless be identified. First, the mass conservation between positive and negative parts of the measure is not ensured. Second, there is no obvious reason that the positive and negative parts of the seismic data should be uncorrelated. For realistic application, the source wavelet s(x, t) is not known, and a prior source estimation is required to perform FWI. Hence, we can expect this decomposition to be strongly sensitive to errors in this source wavelet estimation.

Fig. 2

Computation of the misfit function between two time-shifted Ricker signals depending on the time-shift, using a least-squares distance and an optimal transport distance. While the least-squares distance yields a non-convex misfit function with two local minima aside the global minimum at zero time-shift, the optimal transport distance yields a perfectly convex misfit function [13]

The second strategy is straightforward to apply; however, the mass conservation between |μ| and |ν| is also not ensured. In addition, FWI misfit functions relying on the absolute value of the data lose the sensitivity to the polarity of the signal. As a result, positive or negative impedance contrasts cannot be distinguished. This prevents from the correct interpretation of reflected waves.

The third strategy comes from the decomposition

$$\displaystyle \begin{aligned} \mu-\nu=\left(\mu^{+}+\nu^{-}\right) -\left(\nu^{+}+\mu^{-}\right).\end{aligned} $$

(27)

This method seems appealing as, for any μ and ν satisfying the mass conservation assumption, one has

$$\displaystyle \begin{aligned} \int_{X} d\mu^{+}- d\mu^{-}(x)=\int_{X} d\nu^{+}(x)- d\nu^{-}(x),\end{aligned} $$

(28)

therefore

$$\displaystyle \begin{aligned} \int_{X} d\mu^{+}+ d\nu^{-}(x)=\int_{X} d\nu^{+}(x)+ d\mu^{-}(x),\end{aligned} $$

(29)

and the mass conservation is ensured for the distance W_p,3.

We thus see that the mass conservation assumption is not satisfied in the definition of W_p,1, W_p,2. This might not be a shortcoming as severe as the one associated with the transport of signed measures as several possibilities exist to extend optimal transport to situation where the mass conservation is not ensured, known as partial optimal transport. However, the correlation between the negative and positive part of the seismic data is not accounted for using W_p,1. The sensitivity to the polarity of the seismic data is lost using W_p,2. These two drawbacks are severe. On the other hand, W_p,3 is based on a formulation for which the mass conservation is ensured and only positive measures are compared. For this reason, we are interested in investigating the use of this strategy for FWI.

2.3 A Strategy Using the W₁ Distance in Its Dual Form

2.3.1 Link Between the Dual W₁ Distance and the Mainini Decomposition

As the size of seismic data easily reaches several millions of discrete parameters for realistic FWI applications, we need to design a numerical strategy for large-scale optimal transport problem with at most quasi-linear complexity.

Standard approaches for fast optimal transport computation encompass

• the direct solution of the Monge-Ampère equations [33]

• the solution of a fluid dynamic problem following the Benamou-Brenier formulation [3]

• the solution of a regularized optimal transport problem following an entropic regularization strategy [4, 11]

The last of this strategy can be applied for the computation of general W_p distances, while the two first strategies are dedicated to the computation of the W₂ distance.

Instead of relying on these developments, we rather propose another fast optimal transport computation technique, dedicated to a particular instance of the W₁ distance. The reason we focus on the W₁ distance is related to the Mainini technique, described in the previous paragraph, we want to apply. We explain it in the following.

The very important duality result due to [17] states that the Kantorovich optimal transport problem (16) is equivalent to the maximization problem

$$\displaystyle \begin{aligned} \max_{\varphi,\psi} \int_X \varphi(x) d\mu(x) + \int_X \psi(x) d\nu(x), \;\; \varphi(x)+\psi(x^\prime) \leq c(x,x^\prime). \end{aligned} $$

(30)

In the particular case of the W₁ distance, the dual problem (30) can be expressed using a single potential function φ(x) as

$$\displaystyle \begin{aligned} \max_{\varphi \in \mathrm{Lip}_1(X)} \int_{X} \varphi(x) d(\mu-\nu)(x), \end{aligned} $$

(31)

where the space of 1-Lipschitz function over X is denoted by Lip₁(X). This simplification comes from the fact that for W₁, we have

$$\displaystyle \begin{aligned} c(x,y)=|x-y| \end{aligned} $$

(32)

which is itself a distance over X × X (see [36] for a complete proof). Note that this is not the case for W_p distances with p > 1.

Interestingly, using this duality result, we see that

$$\displaystyle \begin{aligned} \begin{array}{lll} W_{1,3}(\mu,\nu)&=&W_{1}(\mu^{+}+\nu^{-},\nu^{+}+\mu^{-}) \\ &=& \displaystyle \max_{\varphi \in \mathrm{Lip}_1(X)} \int_{X} \varphi(x) d(\mu^{+}+\nu^{-}-\nu^{+}+\mu^{-})(x), \\ &=& \displaystyle \max_{\varphi \in \mathrm{Lip}_1(X)} \int_{X} \varphi(x) d(\mu-\nu)(x) \\ &=& \displaystyle W_{1}(\mu,\nu) \end{array} \end{aligned} $$

(33)

This equality is important, as it reveals that through its particular dual formulation, the distance W₁ (31) can be computed for signed measures satisfying the mass conservation assumption (22). Indeed, as it is mentioned in [20] and [5, 8.10.viii], the problem

$$\displaystyle \begin{aligned} \max_{\varphi \in Lip(X)} \int_{X} \varphi_x d\mu(x), \end{aligned} $$

(34)

defines the norm $\|\mu \|{ }_{KR}^{*}$ on the space of signed measures with first-order moment equal to zero

$$\displaystyle \begin{aligned} \int_{X} d\mu(x)=0. \end{aligned} $$

(35)

We have mentioned that for seismic data, the measure μ − ν satisfies (35), therefore we have

$$\displaystyle \begin{aligned} \left\{\max_{\varphi \in Lip_1(X) } \int_{X} \varphi(x) d(\mu-\nu)(x), \right\}=\|\mu-\nu\|{}_{KR}^{*} \end{aligned} $$

(36)

In addition, this shows that the Mainini decomposition is directly embedded in the dual formulation of W₁ as soon as signed measures are involved.

This has the following important advantage for our application: there is no need to numerically perform the Jordan-Han decomposition into positive and negative part of the data to compute our misfit function. This could be problematic as we minimize this misfit function through local optimization strategies for differentiable functions, relying on the gradient and the Hessian of this function. As the Jordan-Han decomposition is not differentiable (by definition), the resulting misfit function would not be differentiable, and we would need to use optimization strategies for non-smooth misfit functions.

Note that in the case the mass conservation assumption is not satisfied, the norm $\|.\|{ }_{KR}^{*}$ can be easily extended to the Kantorovich-Rubinstein norm, defined by

$$\displaystyle \begin{aligned} \|\mu-\nu\|{}_{KR}= \left\{\max_{\varphi} \int_{X} \varphi(x) d(\mu-\nu)(x), \;\; \varphi(x) \in Lip_1(X), \|\varphi\|{}_{\infty}<1\right\}\end{aligned} $$

(37)

This problem admits a solution even in the case μ − ν does not satisfy (35). It might be more flexible to use for realistic application as the mass conservation is satisfied only at machine precision, which might occur instabilities when using the formulation (31).

In a series of articles [26,27,28], we have investigated the use of this Kantorovich-Rubinstein norm for realistic FWI applications. In the following, we summarize the numerical method developed in these studies to compute this norm.

2.3.2 Numerical Method

We consider in the following the computation of the Kantorovich-Rubinstein norm for d_obs(x_r, t) − d_cal(x_r, t). In discrete form, this is equivalent to the solution of the problem

$$\displaystyle \begin{aligned} \begin{array}{l} \displaystyle \max_{\varphi_{rn}} \sum_{r=1}^{N_r}\sum_{n=1}^{N_t} \varphi_{rn}\left((d_{obs})_{rn}-(d_{cal})_{rn}\right), \\ \\ \displaystyle \forall r,n,r',n' \;\; |\varphi_{rn}-\varphi_{r'n'}| \leq \|(x_r,t_n)-(x_r^{\prime},t_n^{\prime})\|, \\ \\ \displaystyle \forall r,n,\;\; |\varphi_{rn}| \leq 1 \end{array}\end{aligned} $$

(38)

where the integer r is the index associated with the receiver coordinate x_r and the integer n is the index associated with the time coordinate t.

We denote by N = N_r × N_t the total number of discrete samples associated with one dataset. In this framework, the computation of the Kantorovich-Rubinstein norm is a linear programming problem with O(N) unknowns and O(N²) constraints. For realistic application, N easily reaches O(10⁶), already for 2D problems. It is therefore important to reduce the number of constraints of the problem to reach feasible complexity algorithms.

With this purpose, we focus on the particular case where, instead of the Euclidean distance ∥.∥, we use the ℓ₁ distance we denote by |.| to measure the distance between (x_r, t_n) and $(x_r^{\prime },t_n^{\prime })$. In [28], we show that satisfying the N² constraints

$$\displaystyle \begin{aligned} \forall r,n,r',n' \;\; |\varphi_{rn}-\varphi_{r'n'}| \leq |(x_r,t_n)-(x_r^{\prime},t_n^{\prime})|=|x_r-x_r^{\prime}|+|t_n-t_n^{\prime}|\end{aligned} $$

(39)

is equivalent to satisfying the 2N constraints

$$\displaystyle \begin{aligned} \forall r,n \;\; |\varphi_{rn}-\varphi_{r+1,n}| \leq |x_r-x_{r+1}|\;\; |\varphi_{rn}-\varphi_{r,n+1}| \leq |t_n-t_{n+1}|\;\; \end{aligned} $$

(40)

This is simply due to the “Manhattan” property of the ℓ₁ norm. This yields the following ℓ₁ Kantorovich-Rubinstein problem

$$\displaystyle \begin{aligned} \begin{array}{l} \displaystyle \max_{\varphi_{rn}} \sum_{r=1}^{N_r}\sum_{n=1}^{N_t}\varphi_{rn}\left((d_{obs})_{rn}-(d_{cal})_{rn}\right), \;\; \forall r,n \\ \\ \displaystyle |\varphi_{rn}-\varphi_{r+1,n}| \leq |x_r-x_{r+1}|\\ \\ \displaystyle |\varphi_{rn}-\varphi_{r,n+1}| \leq |t_n-t_{n+1}|\\ \\ |\varphi_{rn}| \leq 1 \end{array} \end{aligned} $$

(41)

which is a linear programming problem with O(N) unknowns and O(N) constraints.

In [28], we have detailed how this problem can be recast as the convex non-smooth optimization problem

$$\displaystyle \begin{aligned} \max_{\varphi} f_1(\varphi)+f_2(A\varphi), \end{aligned} $$

(42)

where

$$\displaystyle \begin{aligned} f_1(\varphi)=\sum_{r=1}^{N_r}\sum_{n=1}^{N_t}\varphi_{rn}\left((d_{obs})_{rn}-(d_{cal})_{rn}\right),\;\; f_2(\psi)=i_{K}(\psi). \end{aligned} $$

(43)

The function i_K is the indicator function on the unit hypercube K such that

$$\displaystyle \begin{aligned} i_{K}(x)= \left| \begin{array}{lll} 0 &\;\;\mathrm{if} \;\;& x \in K \\ +\infty &\;\;\mathrm{if} \;\;& x \notin K, \end{array} \right. \end{aligned} $$

(44)

The operator A is the rectangular real matrix

$$\displaystyle \begin{aligned} A=\left[D_{x_r}\;\; D_{t} \;\; I_N \right]^{T}, \end{aligned} $$

(45)

where I_N is the real identity matrix of size N and $D_{x_r},\;\; D_{t}$ are the forward finite-difference operators

$$\displaystyle \begin{aligned} \left\{ \begin{array}{c} \displaystyle \left(D_{x_r}\varphi\right)_{rn}= \displaystyle \frac{\varphi_{r+1,n}-\varphi_{rn}}{\varDelta x_r}, \\ \displaystyle \left(D_{t}\varphi\right )_{rn}= \displaystyle \frac{\varphi_{r,n+1}-\varphi_{rn}}{\varDelta t}, \end{array} \right. \end{aligned} $$

(46)

Efficient strategies based on proximal splitting can be used to solve problems such as (42), where the functions f_i might not be differentiable. Among several possibilities, we choose the simultaneous direction method of multipliers (SDMM), which is well described in [10], for its good convergence properties. The method can be summarized as the Algorithm 1.

Algorithm 1 SDMM method for the solution of the problem (42)

The proximity operator can be seen as the generalization of the convex projection operator. For a given function f, it is defined as

$$\displaystyle \begin{aligned} \mathrm{prox}_f(x)=\mathrm{arg}\min_{y} f(y) + \frac{1}{2}\|x-y\|{}_2^2, \end{aligned} $$

(47)

For the particular case of the function f₁ and f₂, closed-form formulations exist

$$\displaystyle \begin{aligned} \mathrm{prox}_{\gamma f_1}(\varphi)=\varphi- \gamma(d_{obs}-d_{cal}), \end{aligned} $$

(48)

$$\displaystyle \begin{aligned} \forall i=1,\dots,P, \;\; \left(\mathrm{prox}_{\gamma f_{2}}(x)\right)_i=\left(\mathrm{prox}_{i_{K}}(x)\right)_i= \left| \begin{array}{cll} x_i &\mathrm{if}& -1\leq x_i\leq 1 \\ 1 &\mathrm{if}& x_i> 1 \\ -1&\mathrm{if}& x_i<- 1. \end{array} \right. \end{aligned} $$

(49)

The closed-form formulations (48) and (49) are inexpensive to compute with an overall complexity in O(N) operations. However, the SDMM algorithm requires the solution of a linear system involving the matrix I + A^TA. In [28], we show that the matrix A^TA is a second-order finite-difference discretization of the Laplacian operator with homogeneous Neumann boundary conditions. Therefore, these linear systems can be solved in O(NlogN) complexity using fast Fourier transform-based algorithms [38], or in O(N) complexity using multigrid strategies [1, 7]. The combination of the reduction of the number of constraints using the property of the ℓ₁ distance and the observation that the matrix I + A^TA appearing in the SDMM strategy actually corresponds to the discretization of the Poisson’s equation offers the possibility to design an efficient numerical method to compute the ℓ₁ Kantorovich-Rubinstein norm for large-scale problems.

Following the notations used in Section 1, the use of the ℓ₁ Kantorovich-Rubinstein as the misfit measurement function for FWI implies that

$$\displaystyle \begin{aligned} g(d_{obs},d_{cal})=\|d_{cal}-d_{obs}\|{}_{KR} \end{aligned} $$

(50)

The computation of the gradient of the resulting misfit function only requires the definition of the source of the adjoint field λ₁(x, t) through

$$\displaystyle \begin{aligned} \frac{\partial \|d_{cal}-d_{obs}\|{}_{KR}} {\partial d_{cal}} \end{aligned} $$

(51)

Interestingly, following the definition of ∥d_cal − d_obs∥_KR, if we denote by $\overline {\varphi }$ the solution of the maximization problem (42), we have

$$\displaystyle \begin{aligned} \frac{\partial \|d_{cal}-d_{obs}\|{}_{KR}} {\partial d_{cal}}=\overline{\varphi} \end{aligned} $$

(52)

As a consequence, the computation of the solution to the problem (42) yields simultaneously the value of the misfit function, through the value of the criterion at the maximum, as well as the quantity $\overline {\varphi }$ required to compute the gradient of the misfit function through the adjoint-state approach. The solution of a single optimal transport problem per seismic source is thus required at each iteration of FWI.

3 Example of Application of the Kantorovich-Rubinstein Norm to FWI

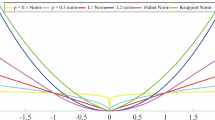
In order to illustrate the property of the Kantorovich-Rubinstein norm for the interpretation of seismic data, we first reproduce the experiment proposed in [13] where the distance between shifted in time Ricker signal is computed using the L² distance and the W₂ distance applied to the positive and negative part of the Ricker separately. Here, instead of the W₂ distance, we compute directly the Kantorovich-Rubinstein distance without separating positive and negative parts of the signal. The results are presented in Figure 3. Compared to the least-squares distance, a single minimum is recovered. However, the convexity of the misfit function with respect to the time-shift is lost. The loss of convexity is due to the signed nature of the Ricker signal (presence of negative values). One could expect optimal transport to be able to detect that the same pattern is shifted when comparing the Ricker, and that the W₁ distance would be proportional to this shift. This is not the case, which results from the presence of negative values. However, an important feature is preserved, with respect to the L² distance: a single minimum is obtained, while the L² distance displays two local minima aside the global minimum. This prompts us to test the use of the Kantorovich-Rubinstein norm to a more realistic case study.

Fig. 3

Computation of the misfit function between two time-shifted Ricker signals depending on the time-shift, using a least-squares distance (black) and the Kantorovich-Rubinstein distance (red). We recover a single minimum; however, compared to the optimal transport distance used by Engquist and Froese [13], the convexity of the misfit function is lost

To this purpose, we consider the Marmousi model presented in Figure 4(a). A synthetic dataset is computed in the 2D acoustic constant-density approximation. A fixed-spread surface acquisition is used, with 128 sources each 125 m and 168 receivers each 100 m, at 50 m depth. A Ricker source function centered on 5 Hz is used to generate the synthetic dataset. The frequency content of the source is high-pass filtered below 3 Hz to mimic realistic seismic data. In practical application, this frequency band is contaminated by noise, and therefore filtered out before inversion. Two initial P-wave velocity models are considered: the first contains the main features of the exact model, only with smoother interfaces (Figure 4(b)). The second is a strongly smoothed version of the exact model with very weak lateral variations and underestimated growth of the velocity in depth (Figure 4(c)). Starting from these two initial models, we compare the FWI results obtained using a least-squares distance and the ℓ₁ Kantorovich-Rubinstein distance. The minimization is performed using the l-BFGS algorithm [30] implemented in the SEISCOPE optimization toolbox [25].

Fig. 4

Marmousi model case study. Exact model (a), initial model 1 (b), initial model 2 (c), results obtained with the L² distance starting from model 1 (d), from model 2 (e), results obtained with the ℓ₁ Kantorovich-Rubinstein distance starting from model 1 (f), from model 2 (g)

These results are presented in Figure 4(d–g). Starting from the first initial model, a correct estimation of the P-wave velocity model is obtained, using both the L² distance (Figure 4(d)) and the ℓ₁ Kantorovich-Rubinstein distance (Figure 4(f)). The estimation of the low velocity zone at x = 11 km, z = 2.5 km is slightly improved using the ℓ₁ Kantorovich-Rubinstein distance, as a high velocity artifact located in this zone is computed using the L² estimation. Starting from the second initial model, only the results obtained using ℓ₁ Kantorovich-Rubinstein distance are meaningful (Figure 4(g)). The poor initial approximation of the P-wave velocity is responsible for the cycle skipping effect and the L² estimation corresponds to a local minimum of the misfit function (Figure 4(f)). The estimation obtained with the ℓ₁ Kantorovich-Rubinstein distance is significantly closer from the true model, despite low velocity artifacts in the shallow part at x = 1.5 km, z = 1 km and in depth at x = 12 km, z = 3.4 km. This example illustrates the potential of optimal transport for FWI: starting from a very crude approximation of the P-wave velocity, a meaningful estimation is computed. In the same configuration, FWI based on the least-squares distance fails and produces a heavily cycle skipped estimation.

4 Conclusion and Perspectives

The use of optimal transport distances for seismic imaging is promising. Comparing seismic data through these distances should yield more convex misfit functions with respect to the P-wave velocity parameter. However, the application of optimal transport to the comparison of seismic data requires the extension of the standard optimal transport problem to the transport of signed measures, which is not straightforward. Standard decomposition techniques proposed in [24], which are based on the negative and the positive part of the data, either are not adapted to FWI (separate transport of the positive and negative part, transport of the absolute value of the data) or lose the convexity property with respect to time-shifts which is one of the key properties one would like to satisfy for FWI.

Nonetheless, in the particular case of the dual formulation of the W₁ distance, the optimal transport distance can be related to a norm in the space of signed measure, the Kantorovich-Rubinstein norm. Hence, it can be directly use to compare seismic data. This is the strategy we have followed in previous works and which is summarized in this study. The results are encouraging. The resulting misfit function is not convex with respect to time-shifts, however, it already allows to start the FWI process from more crude initial velocity model, which denotes a wider valley of attraction of the misfit function. This method has been already successfully applied to 2D synthetic datasets in the context of deep water salt structures imaging (BP 2004 case study) and reflection dominated data (Chevron 2014 case study) [27] as well as to a 3D synthetic dataset (SEG/EAGE overthrust model) [28]. The method should now be applied to 2D and 3D real datasets to further investigate the interest of this strategy for FWI.

Despite the interesting results provided by the Kantorovich-Rubinstein norm, the convexity property of the optimal transport distance with respect to shifted patterns on the data one could expect is lost. Further investigations are thus required to assess the feasibility of the design of a misfit function, based on optimal transport, adapted to the comparison of seismic data, which would benefit from this convexity property. Among different possibilities, one could think of the construction of positive observable from the seismic data, such as its envelope, which could thus be compared through W_p distances.