Abstract
In this chapter, we review fuzzy multi-criteria optimization focusing on possibilistic treatments of objective functions with fuzzy coefficients and on interactive fuzzy stochastic multiple objective programming approaches. In the first part, treatments of objective functions with fuzzy coefficients dividing into single objective function case and multiple objective function case. In single objective function case, multi-criteria treatments, possibly and necessarily optimal solutions, and minimax regret solutions are described showing the relations to multi-criteria optimization. In multiple objective function case, possibly and necessarily efficient solutions are investigated. Their properties and possible and necessary efficiency tests are shown. As one of interactive fuzzy stochastic programming approaches, multiple objective programming problems with fuzzy random parameters are discussed. Possibilistic expectation and variance models are proposed through incorporation of possibilistic and stochastic programming approaches. Interactive algorithms for deriving a satisficing solution of a decision maker are shown.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
- Fuzzy programming
- Possibility measure
- Necessity measure
- Minimax regret
- Possible efficiency
- Necessary efficiency
- Fuzzy random variable
- Random fuzzy variable
- Interactive algorithm
1 Introduction
In mathematical programming problems, parameters such as coefficients and right-hand side values of constraints have been assumed to be given as real numbers. However, in real world problems, there are cases that those parameters cannot be given precisely by lack of knowledge or by uncertain nature of coefficients. For example, rate of return of investment, demands for products, and so on are known as uncertain parameters. Moreover, time for manual assembly operation and the cost of a taxi ride can also be ambiguous and depend on the worker’s skill and the degree of traffic congestion, respectively. Those uncertain parameters have been treated as random variables so that the mathematical programming problems become stochastic programming problems [85, 86].
To formulate a stochastic programming problem, we should estimate a proper probability distribution which parameters obey. However, the estimation is not always a simple task because of the following reasons: (1) historical data of some parameters cannot be obtained easily especially when we face a new uncertain variable, and (2) subjective probabilities cannot be specified easily when many parameters exist. Moreover, even if we succeeded to estimate the probability distribution from historical data, there is no guarantee that the current parameters obey the distribution actually.
We may often come across that we can estimate the possible ranges of the uncertain parameters. For example, we may find out a possible range of cost of taxi ride through experience if we almost know the distance and the traffic quantity. Then, it is conceivable that we represent the possible ranges by fuzzy sets and formulate the mathematical programming problems as fuzzy programming problems [10, 25, 31, 59, 66, 78, 80, 83, 85].
In this paper, we introduce approaches to mathematical programming problems with fuzzy parameters dividing into two parts. In the first part, we review treatments of objective functions with fuzzy coefficients dividing into single objective function case and multiple objective function case. In both cases, the solutions are studied first in problems with interval coefficients and then in the problems with fuzzy coefficients.
In the single objective function case, we show that multi-criteria treatments of an objective function with coefficients using lower and upper bounds do not always produce good solutions. Then possibly and necessarily optimal solutions are introduced. The relations of those solution concepts with solution concepts in multi-criteria optimization are described. A necessarily optimal solution is the most reasonable solution but it does not exist in many cases while a possibly optimal solution always exists when the feasible region is bounded and nonempty but it is only one of least reasonable solutions. Then minimax regret and maximin achievement solutions are introduced as a possibly optimal solution minimizing the deviation from the necessary optimality. Those solutions can be seen as robust suboptimal solutions.
In the multiple objective function case, possibly and necessarily efficient solutions are introduced as the extensions of possibly and necessarily optimal solutions. Because many efficient solutions exist usually in the conventional multiple objective programming problem, it is highly possible that necessarily optimal solutions exist. The properties of possibly and necessarily efficient solutions are investigated. Moreover the possible and necessary efficient tests are described.
In the second part, we consider a case where a part of uncertain parameters can be expressed by random variables but the other part can be expressed by fuzzy numbers. In order to take into consideration not only fuzziness but also randomness of the coefficients in objective functions, multiple objective programming problems with fuzzy random coefficients are discussed. By incorporating possibilistic and stochastic programming approaches, possibilistic expectation and variance models are proposed. It is shown that multiple objective programming problems with fuzzy random coefficients can be deterministic linear or nonlinear multiple objective fractional programming problems. Interactive algorithms for deriving a satisficing solution of a decision maker are provided.
2 Problem Statement and Preliminaries
Multiple objective linear programming (MOLP) problems can be written as
where \(\boldsymbol{c}_{k} = (c_{k1},c_{k2},\ldots,c_{kn})^{\mathrm{T}}\), k = 1, 2, …, p and \(\boldsymbol{a}_{i} = (a_{i1},a_{i2},\ldots,a_{in})^{\mathrm{T}}\), i = 1, 2, …, m are constant vectors and b i , i = 1, 2, …, m constants. \(\boldsymbol{x} = (x_{1},x_{2},\ldots,x_{n})^{\mathrm{T}}\) is the decision variable vector.
In MOLP problems, many solution concepts are considered (see [13]). In this chapter, we describe only the following three solution concepts:
- Complete optimality: :
-
A feasible solution \(\hat{\boldsymbol{x}}\) is said to be completely optimal if and only if we have \(\boldsymbol{c}_{k}^{\mathrm{T}}\hat{\boldsymbol{x}} \geq \boldsymbol{c}_{k}^{\mathrm{T}}\boldsymbol{x}\), k = 1, 2, …, p for all feasible solution \(\boldsymbol{x}\).
- Efficiency: :
-
A feasible solution \(\hat{\boldsymbol{x}}\) is said to be efficient if and only if there is no feasible solution \(\boldsymbol{x}\) such that \(\boldsymbol{c}_{k}^{\mathrm{T}}\boldsymbol{x} \geq \boldsymbol{c}_{k}^{\mathrm{T}}\hat{\boldsymbol{x}}\), k = 1, 2, …, p with at least one strict inequality.
- Weak efficiency: :
-
A feasible solution \(\hat{\boldsymbol{x}}\) is said to be weakly efficient if and only if there is no feasible solution \(\boldsymbol{x}\) such that \(\boldsymbol{c}_{k}^{\mathrm{T}}\boldsymbol{x}> \boldsymbol{c}_{k}^{\mathrm{T}}\hat{\boldsymbol{x}}\), k = 1, 2, …, p.
In the conventional MOLP problem (20.1), the coefficients and right-hand side values are assumed to be specified as real numbers. However, in the real world applications, we may face situations where coefficients and right-hand side values cannot be specified as real numbers by the lack of exact knowledge or by their fluctuations. Even in those situations there are cases when ranges of possible values for coefficients and right-hand side values can be specified by experts’ vague knowledge. In the first part of this paper, we assume that those ranges are expressed by fuzzy sets and consider the MOLP problem with fuzzy coefficients. Because we focus on the treatments of objective functions with fuzzy coefficients, we assume the constraints are crisp so that they do not include any fuzzy parameters. However, the constraints with fuzzy parameters are often reduced to the crisp constraints in fuzzy/possibilistic programming approaches [10, 25, 31].
MOLP problems with fuzzy numbers treated in the first part of this chapter can be represented as
where we define
\(\tilde{\boldsymbol{c}}_{k} = (\tilde{c}_{k1},\tilde{c}_{k2},\ldots,\tilde{c}_{kn})^{\mathrm{T}}\), k = 1, 2, …, p is a vector of fuzzy coefficients. \(\tilde{c}_{kj}\), j = 1, 2, …, n, k = 1, 2, …, p are fuzzy numbers. A fuzzy number \(\tilde{c}\) is a fuzzy set on a real line whose membership function \(\mu _{\tilde{c}}: \mathbf{R} \rightarrow [0,1]\) satisfies (see, for example, [11])
-
(i)
\(\tilde{c}\) is normal, i.e., there exists r ∈ R such that \(\mu _{\tilde{c}}(r) = 1\).
-
(ii)
\(\mu _{\tilde{c}}\) is upper semi-continuous, i.e., the h-level set \([\tilde{c}]_{h} =\{ r \in \mathbf{R}\mid \mu _{\tilde{c}}(r) \geq h\}\) is a closed set for any h ∈ (0, 1].
-
(iii)
\(\tilde{c}\) is a convex fuzzy set. Namely, \(\mu _{\tilde{c}}\) is a quasi-concave function, i.e., for any r 1, r 2 ∈ R, for any \(\lambda \in [0,1]\), \(\mu _{\tilde{c}}(\lambda r_{1} + (1-\lambda )r_{2}) \geq \min (\mu _{\tilde{c}}(r_{1}),\mu _{\tilde{c}}(r_{2}))\). In other words, h-level set \([\tilde{c}]_{h}\) is a convex set for any h ∈ (0, 1].
-
(iv)
\(\tilde{c}\) is bounded, i.e., \(\lim _{r\rightarrow +\infty }\mu _{\tilde{c}}(r) =\lim _{r\rightarrow -\infty }\mu _{\tilde{c}}(r) = 0\). In other words, the h-level set \([\tilde{c}]_{h}\) is bounded for any h ∈ (0, 1].
From (ii) to (iv), an h-level set \([\tilde{c}]_{h}\) is a bounded closed interval for any h ∈ (0, 1] when \(\tilde{c}\) is a fuzzy number. L-R fuzzy numbers are often used in literature. An L-R fuzzy number \(\tilde{c}\) is a fuzzy number defined by the following membership function:
where L and \(R: [0,+\infty ) \rightarrow [0,1]\) are reference functions, i.e., L(0) = R(0) = 1, \(\lim _{r\rightarrow +\infty }L(r) =\lim _{r\rightarrow +\infty }R(r) = 0\) and L and R are upper semi-continuous non-increasing functions. α and β are assumed to be non-negative.
An example of L-R fuzzy number \(\tilde{c}\) is illustrated in Fig. 20.1. As shown in Fig. 20.1, c L and c R are lower and upper bounds of the core of \(\tilde{c}\), i.e., \(\mbox{ Core}(\tilde{c}) =\{ r\mid \mu _{\tilde{c}}(r) = 1\}\). α and β show the left and right spreads of \(\tilde{c}\). Functions L and R specify the left and right shapes. Using those parameters and functions, fuzzy number \(\tilde{c}\) is represented as \(\tilde{c} = (c^{\mathrm{L}},c^{\mathrm{R}},\alpha,\beta )_{LR}\). A membership degree \(\mu _{\tilde{c}}(r)\) of fuzzy coefficient \(\tilde{c}\) shows the possibility degree of an event ‘the coefficient value is r’.
Problem (20.2) has fuzzy coefficients only in the objective functions. In Problem (20.2), we should calculate fuzzy linear function values \(\tilde{\boldsymbol{c}}_{k}^{\mathrm{T}}\boldsymbol{x}\), k = 1, 2, …, p. Those function values can be fuzzy quantities since the coefficients are fuzzy numbers. The extension principle [11] defines the fuzzy quantity of function values of fuzzy numbers. Let \(g: \mathbf{R}^{q} \rightarrow \mathbf{R}\) be a function. A function value of \((\tilde{c}_{1},\tilde{c}_{2},\ldots,\tilde{c}_{q})\), i.e., \(g(\tilde{c}_{1},\tilde{c}_{2},\ldots,\tilde{c}_{q})\) is a fuzzy quantity \(\tilde{Y }\) with the following membership function:
Since \(\tilde{\boldsymbol{c}}\) is a vector of fuzzy numbers \(\tilde{c}_{i}\) whose h-level set is a bounded closed interval for any h ∈ (0, 1], we have the following equation (see [11]) when g is a continuous function;
where \([\tilde{\boldsymbol{c}}]_{h} = ([\tilde{c}_{1}]_{h},[\tilde{c}_{2}]_{h},\ldots,[\tilde{c}_{q}]_{h})\). Note that \([\tilde{c}_{j}]_{h}\) is a closed interval since \(\tilde{c}_{j}\) is a fuzzy number. Equation (20.6) implies that h-level set of function value \(\tilde{Y }\) can be obtained by interval calculations. Moreover, since g is continuous, from (20.6), we know that \([\tilde{Y }]_{h}\) is also a closed interval and \([\tilde{Y }]_{1}\neq \emptyset\). Therefore, \(\tilde{Y }\) is also a fuzzy number.
Let \(g(\boldsymbol{r}) = \boldsymbol{r}^{\mathrm{T}}\boldsymbol{x}\), where we define \(\boldsymbol{r} = (r_{1},r_{2},\ldots,r_{n})^{\mathrm{T}}\). We obtain the fuzzy linear function value \(\tilde{\boldsymbol{c}}_{k}^{\mathrm{T}}\boldsymbol{x}\) as a fuzzy number \(g(\tilde{\boldsymbol{c}}_{k})\). For \(\boldsymbol{x} \geq \mathbf{0}\), we have
where c kj L(h) and c kj R(h) are lower and upper bounds of h-level set \([\tilde{c}_{kj}]_{h}\), i.e., \(c_{kj}^{\mathrm{L}}(h) =\inf [\tilde{c}_{kj}]_{h}\) and \(c_{kj}^{\mathrm{R}}(h) =\sup [\tilde{c}_{kj}]_{h}\). Note that when \(\tilde{c}_{kj}\) is an L-R fuzzy number (c kj L, c kj R, \(\gamma _{kj}^{\mathrm{L}},\gamma _{kj}^{\mathrm{R}})_{L_{kj}R_{kj}}\), we have
where L kj (−1) and R kj (−1) are pseudo-inverse functions of L kj and R kj defined by \(L_{kj}^{(-1)}(h) =\sup \{ r\mid L_{kj}(r) \geq h\}\) and \(R_{kj}^{(-1)}(h) =\sup \{ r\mid R_{kj}(r) \geq h\}\).
In Problem (20.2), each objective function value \(\tilde{\boldsymbol{c}}_{k}^{\mathrm{T}}\boldsymbol{x}\) is obtained as a fuzzy number. Minimizing a fuzzy number \(\tilde{\boldsymbol{c}}_{k}^{\mathrm{T}}\boldsymbol{x}\) cannot be clearly understood. Therefore, Problem (20.2) is an ill-posed problem. We should introduce an interpretation of Problem (20.2) so that we can transform the problem to a well-posed problem. Many interpretations have been proposed. In the first part of this paper, we describe the interpretations from the viewpoint of optimization. For the other interpretations from viewpoint of satisficing, see, for example, [10, 25].
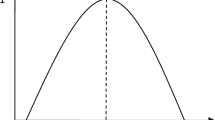
Possibility and necessity measures of a fuzzy set \(\tilde{B}\) under a fuzzy set \(\tilde{A}\) are defined as follows (see [12]):
Those possibility and necessity measures are depicted in Fig. 20.2.
When fuzzy sets \(\tilde{A}\) and \(\tilde{B} \subseteq \mathbf{R}^{q}\) have upper semi-continuous membership functions and \(\tilde{A}\) is bounded, we have, for any h ∈ (0, 1],
where \(\tilde{A}\) is said to be bounded when \([\tilde{A}]_{h}\) is bounded for any h ∈ (0, 1]. \((\tilde{A})_{1-h}\) is a strong (1 − h)-level set of \(\tilde{A}\) defined by \((\tilde{A})_{1-h} =\{ r\mid \mu _{\tilde{A}}(r)> 1 - h\}\). In (20.11) and (20.12), we may understand that the possibility measure shows to what extent \(\tilde{A}\) intersects with \(\tilde{B}\) while the necessity measure shows to what extent \(\tilde{A}\) is included in \(\tilde{B}\). This interpretation is true even for other conjunction and implication functions T and I.
3 Single Objective Function Case
In this section, we treat Problem (20.2) with p = 1, i.e., single objective function case. In the single objective function case, there are many approaches (see for example, [15, 32, 40, 79, 90]). These approaches can be divided into two classes: satisficing approach and optimizing approach. The satisficing approach use a goal, the objective function value with which the decision maker is satisfied, while the optimizing approach does not use such a goal but generalizes the optimality concept to the case with uncertain coefficients. We describe the optimizing approaches to Problem (20.2) with p = 1 in this section. We demonstrate that even in the single objective function case, Problem (20.2) with p = 1 has a deep connection to multi-criteria optimization.
When p = 1, Problem (20.2) is reduced to
3.1 Optimization of Upper and Lower Bounds
When fuzzy coefficients \(\tilde{c}_{1j}\), j = 1, 2, …, n degenerate to intervals \([c_{1j}^{\mathrm{L}},c_{1j}^{\mathrm{R}}]\), j = 1, 2, …, n, Problem (20.13) becomes an interval programming problem. In this case, Problem (20.13) is formulated as the following bi-objective linear programming problem in many papers [15, 40, 79, 91]:
where \(\boldsymbol{c}_{1}^{\mathrm{L}} = (c_{11}^{\mathrm{L}},c_{12}^{\mathrm{L}},\ldots,c_{1n}^{\mathrm{L}})^{\mathrm{T}}\) and \(\boldsymbol{c}_{1}^{\mathrm{R}} = (c_{11}^{\mathrm{R}},c_{12}^{\mathrm{R}},\ldots,c_{1n}^{\mathrm{R}})^{\mathrm{T}}\).
The inequality relation between two interval A = [a L, a R] and \(B = [b^{\mathrm{L}},b^{\mathrm{R}}]\) is frequently defined by
Problem (20.14) would be understood as a problem inspired from this inequality relation. Moreover, because Problem (20.14) maximizes the lower and upper bounds of objective function value simultaneously, it can be also seen as a problem maximizing the worst objective function value and the best objective function value. Namely, it is a model applied simultaneously the maximin criterion and the maximax criterion proposed for decision making under strict uncertainty. An efficient solution to Problem (20.14) is considered as a reasonable solution in this approach.
Extending this idea to general fuzzy coefficient case, we may have the following linear programming (LP) problem with infinitely many objective functions [91]:
where \(\boldsymbol{c}_{1}^{\mathrm{L}}(h) = (c_{11}^{\mathrm{L}}(h),c_{12}^{\mathrm{L}}(h),\ldots,c_{1n}^{\mathrm{L}}(h))^{\mathrm{T}}\) and \(\boldsymbol{c}_{1}^{\mathrm{R}}(h) = (c_{11}^{\mathrm{R}}(h),c_{12}^{\mathrm{R}}(h),\ldots,c_{1n}^{\mathrm{R}}(h))^{\mathrm{T}}\).
This formulation is also related to the following inequality relation between fuzzy numbers \(\tilde{A}\) and \(\tilde{B}\) (see [75, 91]):
where we define for h ∈ (0, 1], \(a^{\mathrm{L}}(h) =\inf [\tilde{A}]_{h}\), \(b^{\mathrm{L}}(h) =\inf [\tilde{B}]_{h}\), \(a^{\mathrm{R}}(h) =\sup [\tilde{A}]_{h}\) and \(b^{\mathrm{R}}(h) =\sup [\tilde{B}]_{h}\).
When all fuzzy coefficients \(\tilde{c}_{1j}\) are assumed to be L-R fuzzy numbers \((c_{1j}^{\mathrm{L}},c_{1j}^{\mathrm{R}},\) \(\gamma _{1j}^{\mathrm{L}},\gamma _{1j}^{\mathrm{R}})_{LR}\) with same left and right reference functions L and R such that L(1) = R(1) = 0 and \(\forall r \in [0,1)\), L(r) > 0, R(r) > 0, the following LP problem with four objective functions are considered:
where \(\boldsymbol{c}_{1}^{\mathrm{L}} = (c_{11}^{\mathrm{L}},c_{12}^{\mathrm{L}},\ldots,c_{1n}^{\mathrm{L}})^{\mathrm{T}}\), \(\boldsymbol{c}_{1}^{\mathrm{R}} = (c_{11}^{\mathrm{R}},c_{12}^{\mathrm{R}},\ldots,c_{1n}^{\mathrm{R}})^{\mathrm{T}}\), \(\boldsymbol{\gamma }_{1}^{\mathrm{L}} = (\gamma _{11}^{\mathrm{L}},\gamma _{12}^{\mathrm{L}},\ldots,\gamma _{1n}^{\mathrm{L}})^{\mathrm{T}}\), \(\boldsymbol{\gamma }_{1}^{\mathrm{R}} = (\gamma _{11}^{\mathrm{R}},\gamma _{12}^{\mathrm{R}},\ldots,\gamma _{1n}^{\mathrm{R}})^{\mathrm{T}}\).
The following theorem shows the equivalence between Problems (20.16) and (20.18).
Theorem 1.
The efficient solution set \(\mathit{Eff }_{\mathrm{many}}\) of Problem (20.16) coincides with the efficient solution set \(\mathit{Eff }_{\mathrm{four}}\) of Problem (20.18).
Proof.
Let \(\boldsymbol{x}\not\in \mathit{Eff }_{\mathrm{four}}\). Then there exists \(\bar{\boldsymbol{x}} \in X\) such that
with at least one strict inequality. For L-R fuzzy numbers \((c_{1j}^{\mathrm{L}},c_{1j}^{\mathrm{R}},\gamma _{1j}^{\mathrm{L}},\gamma _{1j}^{\mathrm{R}})_{LR}\), as in (20.8), we have
for any h ∈ (0, 1]. From L(1) = R(1) = 0 and \(\forall r \in (0,1]\), L(r) > 1 and R(r) > 1, we have \(\forall h \in (0,1]\), L (−1)(h) ∈ [0, 1] and R (−1)(h) ∈ [0, 1]. From (∗), we obtain
with at least one strict inequality. Then we obtain \(\boldsymbol{x}\not\in \mathit{Eff }_{\mathrm{many}}\).
On the contrary, let \(\boldsymbol{x}\not\in \mathit{Eff }_{\mathrm{many}}\). Then there exists \(\bar{\boldsymbol{x}} \in X\) such that (∗∗) with at least one strict inequality holds. Because (∗∗) holds, we have (∗). Then we shall show that (∗) holds with at least one strict inequality. We can prove this dividing into two cases: (a) \(\exists \bar{h} \in (0,1]\), \(\boldsymbol{c}_{1}^{\mathrm{L}}(h)^{\mathrm{T}}\bar{\boldsymbol{x}}> \boldsymbol{c}_{1}^{\mathrm{L}}(h)^{\mathrm{T}}\boldsymbol{x}\) and (b) \(\exists \bar{h} \in (0,1]\), \(\boldsymbol{c}_{1}^{\mathrm{R}}(h)^{\mathrm{T}}\bar{\boldsymbol{x}}> \boldsymbol{c}_{1}^{\mathrm{R}}(h)^{\mathrm{T}}\boldsymbol{x}\). In case (a), if \(L^{(-1)}(\bar{h}) = 0\), we obtain \(\boldsymbol{c}_{1}^{\mathrm{L}}{}^{\mathrm{T}}\bar{\boldsymbol{x}}> \boldsymbol{c}_{1}^{\mathrm{L}}{}^{\mathrm{T}}\boldsymbol{x}\) and this directly implies that (∗) holds with at least one strict inequality. Then we assume \(L^{(-1)}(\bar{h})\neq 0\) and \(\boldsymbol{c}_{1}^{\mathrm{L}}{}^{\mathrm{T}}\bar{\boldsymbol{x}} = \boldsymbol{c}_{1}^{\mathrm{L}}{}^{\mathrm{T}}\boldsymbol{x}\). This and condition for (a) imply \(-L^{(-1)}(\bar{h})(\boldsymbol{\gamma }_{1}^{\mathrm{L}}{}^{\mathrm{T}}\bar{\boldsymbol{x}})> -L^{(-1)}(\bar{h})(\boldsymbol{\gamma }_{1}^{\mathrm{L}}{}^{\mathrm{T}}\boldsymbol{x})\). Because we have \(L^{(-1)}(\bar{h})\neq 0\) and \(L^{(-1)}(\bar{h}) \in [0,1]\), we obtain \((\boldsymbol{c}_{1}^{\mathrm{L}} -\boldsymbol{\gamma }_{1}^{\mathrm{L}})^{\mathrm{T}}\bar{\boldsymbol{x}}> (\boldsymbol{c}_{1}^{\mathrm{L}} -\boldsymbol{\gamma }_{1}^{\mathrm{L}})^{\mathrm{T}}\boldsymbol{x}\), i.e., (∗) holds with at least one strict inequality. In case (b), we can prove in the same way. Then (∗) holds with at least one strict inequality, i.e., \(\boldsymbol{x}\not\in \mathit{Eff }_{\mathrm{four}}\). □
In this approach, an efficient solution to the reduced multiple objective programming problems is considered as a reasonable solution [15, 40, 79]. If the complete optimal solution exists, it is considered as the best solution. Furukawa [15] proposed an efficient enumeration method of efficient solutions of Problem (20.16).
The following example given in [33] shows the limitation of this approach.
Example 1.
Consider the following LP problem with interval objective function:
In this case, the following bi-objective problem corresponds to Problem (20.16):
The efficient optimal solution to Problem (20.20) is unique it is (x 1, x 2)T = (4, 7)T. In other words, \((x_{1},x_{2})^{\mathrm{T}} = (4,7)^{\mathrm{T}}\) is the complete optimal solution. This solution on the feasible region is depicted in Fig. 20.3.
In Fig. 20.3, a box on c 1-c 2 coordinate shows all possible realizations of the objective function coefficient vector. Area G 1 shows the possible realizations of the objective function coefficient vector to which solution (x 1, x 2)T = (4, 7)T is optimal. Similarly, Area G 2 and G 3 show the possible realizations of the objective function coefficient vector to which solutions \((x_{1},x_{2})^{\mathrm{T}} = (8,2.55556)^{\mathrm{T}}\) and \((x_{1},x_{2})^{\mathrm{T}} = (2.8889,8)^{\mathrm{T}}\) are optimal, respectively. Although solution (x 1, x 2)T = (4, 7)T is the unique efficient solution to Problem (20.20), Area G 1 is much smaller than Areas G 2 and G 3. If all possible realizations of the objective function coefficient vector are equally probable, the probability that (x 1, x 2)T = (4, 7)T is not the optimal solution is rather high. From this point of view, the validity of selecting solution \((x_{1},x_{2})^{\mathrm{T}} = (4,7)^{\mathrm{T}}\) may be controversial.
3.2 Possibly and Necessarily Optimal Solutions
Let \(S(\boldsymbol{c})\) be a set of optimal solutions to an LP problem with objective function \(\boldsymbol{c}^{\mathrm{T}}\boldsymbol{x}\),
Consider Problem (20.13) when \(\tilde{c}_{1j}\), j = 1, 2, …, n degenerate to intervals \([c_{1j}^{\mathrm{L}},c_{1j}^{\mathrm{R}}]\), j = 1, 2, …, n and define \(\varGamma =\prod _{ j=1}^{n}[c_{1j}^{\mathrm{L}},c_{1j}^{\mathrm{R}}] =\{ (c_{1},c_{2},\ldots,c_{n})^{\mathrm{T}}\mid c_{1j}^{\mathrm{L}} \leq c_{j} \leq c_{1j}^{\mathrm{R}},\ j = 1,2,\ldots,n\}\). Then we define the following two optimal solution sets:
An element of Π S is a solution optimal for at least one \(\boldsymbol{c} = (c_{1},c_{2},\ldots,c_{n})^{\mathrm{T}}\) such that \(c_{1j}^{\mathrm{L}} \leq c_{j} \leq c_{1j}^{\mathrm{R}}\), j = 1, 2, …, n. Since \([c_{1j}^{\mathrm{L}},c_{1j}^{\mathrm{R}}]\), j = 1, 2, …, n show the possible ranges of objective function coefficients c 1j , j = 1, 2, …, n, an element of Π S is called a “possibly optimal solution”. On the other hand, an element of NS is a solution optimal for all \(\boldsymbol{c} = (c_{1},c_{2},\ldots,c_{n})^{\mathrm{T}}\) such that \(c_{1j}^{\mathrm{L}} \leq c_{j} \leq c_{1j}^{\mathrm{R}}\), j = 1, 2, …, n and called a “necessarily optimal solution”. Solution set Π S was originally considered by Steuer [88] for a little different purpose while the concept of solution set NS was proposed by Bitran [4] in the setting of MOLP problems. Luhandjula [65] introduced those concepts into MOLP problem with fuzzy objective function coefficients. However, his definition was a little different from the one we described in what follows. Inuiguchi and Kume [30] and Inuiguchi and Sakawa [34] connected those concepts to possibility theory [12, 98] and termed Π S and NS ‘possibly optimal solution set’ and ‘necessarily optimal solution set’.
Consider the following MOLP problem:
where \(\bar{\boldsymbol{c}}_{j},\ j = 1,2,\ldots,q\) are all extreme points of box set \(\varGamma =\prod _{ j=1}^{n}[c_{1j}^{\mathrm{L}},c_{1j}^{\mathrm{R}}]\). Accordingly, we have q = 2n when \(c_{1j}^{\mathrm{L}} <c_{1j}^{\mathrm{R}}\), j = 1, 2, …, n and q < 2n when there exists at least one j ∈ { 1, 2, …, n} such that \(c_{1j}^{\mathrm{L}} = c_{1j}^{\mathrm{R}}\). We have \(NS \subseteq \varPi S\), i.e., a necessarily optimal solution is a possibly optimal solution. The following theorem given by Inuiguchi and Kume [30] connects possibly and necessarily optimal solutions to weakly efficient and completely optimal solutions, respectively.
Theorem 2.
A solution is possibly optimal to Problem (20.13) with \(\tilde{c}_{1j} = [c_{1j}^{\mathrm{L}},c_{1j}^{\mathrm{R}}]\) , j = 1,2,…,n if and only if it is weakly efficient to Problem (20.24) . A solution is necessarily optimal to Problem (20.13) when \(\tilde{c}_{1j} = [c_{1j}^{\mathrm{L}},c_{1j}^{\mathrm{R}}]\) , j = 1,2,…,n if and only if it is completely optimal to Problem (20.24).
Proof.
Suppose \(\hat{\boldsymbol{x}}\) is a weakly efficient solution to Problem (20.24). There are no feasible solutions such that \(\bar{\boldsymbol{c}}_{j}^{\mathrm{T}}\boldsymbol{x}> \bar{\boldsymbol{c}}_{j}^{\mathrm{T}}\hat{\boldsymbol{x}}\), j = 1, 2, …, q. As is well known in the literature, there is a vector \(\boldsymbol{\lambda } = (\lambda _{1},\lambda _{2},\ldots,\lambda _{q})^{\mathrm{T}}\) such that \(\sum _{j=1}^{q}\lambda _{j} = 1\), \(\lambda _{j} \geq 0\), j = 1, 2, …, q and \(\hat{\boldsymbol{x}}\) is an optimal solution to the following LP problem:
Thus, we have \(\hat{\boldsymbol{x}} \in S\left (\sum _{j=1}^{q}\lambda _{j}\bar{\boldsymbol{c}}_{j}\right )\). By the definition of \(\bar{\boldsymbol{c}}_{j}\)’s, \(\sum _{j=1}^{q}\lambda _{j}\bar{\boldsymbol{c}}_{j} \in \varGamma\). Hence, \(\hat{\boldsymbol{x}}\) is a possibly optimal solution to Problem (20.13) with \(\tilde{c}_{1j} = [c_{1j}^{\mathrm{L}},c_{1j}^{\mathrm{R}}]\), j = 1, 2, …, n. Conversely, suppose \(\hat{\boldsymbol{x}}\) is a possibly optimal solution to Problem (20.13) with \(\tilde{c}_{1j} = [c_{1j}^{\mathrm{L}},c_{1j}^{\mathrm{R}}]\), j = 1, 2, …, n, there is a vector \(\boldsymbol{c} \in \varGamma\) such that \(\hat{\boldsymbol{x}} \in S(\boldsymbol{c})\). By the definition of \(\boldsymbol{c}^{j}\)’s, there is a vector \(\boldsymbol{\lambda } = (\lambda _{1},\lambda _{2},\ldots,\lambda _{q})^{\mathrm{T}}\) such that \(\sum _{j=1}^{q}\lambda _{j} = 1\), \(\lambda _{j} \geq 0\), j = 1, 2, …, q and \(\boldsymbol{c} =\sum _{ j=1}^{q}\lambda _{j}\bar{\boldsymbol{c}}_{j}\). Thus, \(\hat{\boldsymbol{x}}\) is an optimal solution to the problem (∗) and from this fact, it is a weakly efficient solution to problem (20.24). Hence, the first assertion is proved.
The second assertion can be proved similarly. □
Possibly and necessarily optimal solutions are exemplified in the following example.
Example 2.
Let us consider the following LP problems with interval objective function:
For this problem, we obtain \(\varGamma =\{ (c_{1},c_{2})^{\mathrm{T}}\mid 2 \leq c_{1} \leq 3,\ 1.5 \leq c_{2} \leq 2.5\}\) and \(X =\{ (x_{1},x_{2})^{\mathrm{T}}\mid 3x_{1} + 4x_{2} \leq 42,\ 3x_{1} + x_{2} \leq 24,\ x_{1} \geq 0,\ 0 \leq x_{2} \leq 9\}\) at (6, 6)T. Consider solution (x 1, x 2)T = (6, 6)T and the normal cone to X at this solution, i.e., a set of vectors (c 1, c 2)T such that \((x_{1} - 6,x_{2} - 6)^{\mathrm{T}}(c_{1},c_{2}) \leq 0\). The normal cone to X at (6, 6)T is obtained as
As shown in Fig. 20.4, we obtain \(\varGamma \subseteq P((6,6)^{\mathrm{T}})\). This implies that solution (6, 6)T is optimal for all \((c_{1},c_{2})^{\mathrm{T}} \in \varGamma\). Therefore, solution (6, 6)T is a necessarily optimal solution.
Problem (20.25)
On the other hand, when the objective function of Problem (20.25) is changed to
Γ is updated to \(\varGamma = \left \{(c_{1},c_{2})^{\mathrm{T}}\mid 1 \leq c_{1} \leq 3,\ 1.5 \leq c_{2} \leq 3\right \}\). As shown in Fig. 20.5, \(\varGamma \subseteq P((6,6)^{\mathrm{T}})\) is no longer valid. In this case, \(\varGamma \subseteq P((2,9)^{\mathrm{T}}) \cup P((6,6)^{\mathrm{T}})\) is obtained and solutions on the line segment between (2, 9)T and (6, 6)T are all possibly optimal solutions. As shown in this example, there are infinitely many possibly optimal solutions. However, the number of possibly optimal basic solutions (extreme points) is finite.
Problem (20.25) with the updated objective function
As shown in this example, a necessarily optimal solution does not exist in many cases but if it exists it is the most reasonable solution. On the other hand, a possibly optimal solution always exist whenever X is bounded and nonempty but it is often non-unique. If a possibly optimal solution is unique, it is a necessarily optimal solution. Moreover, as is conjectured from this example, we can prove the following equivalences for a given \(\boldsymbol{x} \in X\):
where \(P(\boldsymbol{x})\) is the normal cone to X at solution \(\boldsymbol{x}\).
The possibly and necessarily optimal solutions are extended to the case where \(\tilde{c}_{1j}\), j = 1, 2, …, n are fuzzy numbers. In this case, the possible range Γ 1 of coefficient vectors \(\boldsymbol{c}\) becomes a fuzzy set defined by the following membership function:
where \(\boldsymbol{c} = (c_{1},c_{2},\ldots,c_{n})^{\mathrm{T}}\) and \(\mu _{\tilde{c}_{1j}}\) is the membership function of \(\tilde{c}_{1j}\). Accordingly the possibility optimal solution set Π S and the necessarily optimal solution set NS become fuzzy sets defined by the following membership functions:
where μ Π S and μ NS are membership functions of the possibility optimal solution set Π S and the necessarily optimal solution set NS. Because \(\tilde{c}_{1j}\) has membership function, each solution \(\boldsymbol{x} \in X\) has possible optimality degree \(\mu _{\varPi S}(\boldsymbol{x})\) and necessary optimality degree \(\mu _{NS}(\boldsymbol{x})\). Because \(\tilde{c}_{1j}\), j = 1, 2, …, n are fuzzy numbers, from (20.11) and (20.12), we have the following properties for any h ∈ (0, 1]:
As shown in those properties, the chance that a necessarily optimal solution exists increases by defining [Γ]1 smaller. Especially, if we define Γ with a continuous membership function such that [Γ]1 is a singleton composed of the most plausible objective function coefficient vector and (Γ)0 shows the largest possible range, we can analyze the degree of robust optimality of a solution \(\boldsymbol{x}\) by \(\mu _{NS}(\boldsymbol{x})\).
Computation methods for the degree of possible optimality and the degree of necessary optimality of a given feasible solution are investigated by Inuiguchi and Sakawa [32]. They showed that the former can be done by solving an LP problem while the latter by solving many LP problems. On the other hand, Steuer [88] investigated enumeration methods of all possibly optimal basic solutions of Problem (20.13) when \(\tilde{c}_{j}\)’s are closed intervals. Inuiguchi and Tanino [38] proposed an enumeration method of all possibly optimal basic solutions of Problem (20.13) with possible optimality degree \(\mu _{\varPi S}(\boldsymbol{x})\).
Remark 1.
Consider a MOLP problem,
and solve it by weighting method. If the weight \(\boldsymbol{w} \geq \mathbf{0}\) cannot be specified uniquely but by a fuzzy set \(\tilde{\boldsymbol{w}}\), the possible and necessary optimalities are useful to find candidate solutions.
3.3 Minimax Regret Solutions and the Related Solution Concepts
As seen in the previous subsection, a necessarily optimal solution is the most reasonable solution to Problem (20.13) but its existence is not guaranteed. On the other hand, possibly optimal solutions are the least reasonable solutions to Problem (20.13) but there are usually many possibly optimal solutions. Therefore, these solution concepts are two extremes.
In this subsection, we consider intermediate solution concepts such that
-
1.
the solution is a possibly optimal solution,
-
2.
it coincides with the necessarily optimal solution when the necessarily optimal solution exists, and
-
3.
it minimizes the deviation from the necessary optimality, or it maximizes the proximity to the necessity optimality.
For the sake of ease, we first consider cases where Γ is a crisp set. To measure the deviation from the necessary optimality and the proximity to the necessity optimality, the following two functions \(R: X \rightarrow [0,\infty )\) and \(WA: X \rightarrow (-\infty,1]\) have been considered so far (see Inuiguchi and Kume [30], Inuiguchi and Sakawa [33, 35]):
where \(R(\boldsymbol{x})\) is known as the maximum regret. \(R(\boldsymbol{x})\) takes its minimum value zero if and only if \(\boldsymbol{x}\) is a necessarily optimal solution. On the other hand, \(WA(\boldsymbol{x})\) shows the worst achievement rate and is defined only when \(\max _{\boldsymbol{y}\in X}\boldsymbol{c}^{\mathrm{T}}\boldsymbol{y}> 0\). \(WA(\boldsymbol{x})\) takes its maximum value one if and only if \(\boldsymbol{x}\) is a necessarily optimal solution.
Hence, we obtain the following programming problems:
The former problem is the minimax regret problem and the latter problem is the maximin achievement rate problem. Optimal solutions to those problems are called ‘a minimax regret solution’ and ‘a maximin achievement rate solution’, respectively. The possible optimalities of minimax regret solutions and maximin achievement rate solutions are proved by using Theorem 2 as shown in the following theorem (Inuiguchi and Kume [30] and Inuiguchi and Sakawa [35]).
Theorem 3.
Minimax regret solutions as well as maximin achievement rate solutions are possibly optimal solutions to the problem (20.13).
Proof.
We prove the possible optimality of a minimax regret solution because that of a maximin achievement rate solution can be proved in the same way. Let \(\hat{\boldsymbol{x}}\) be a minimax regret solution. Assume it does not a possibly optimal solution. Then it does not a weakly efficient solution to MOLP problem (20.24) from Theorem 2. Thus, there exists a feasible solution \(\boldsymbol{x}\) such that \(\bar{\boldsymbol{c}}_{j}^{\mathrm{T}}\boldsymbol{x}>\bar{ \boldsymbol{c}}_{j}^{\mathrm{T}}\hat{\boldsymbol{x}},j = 1,2,\ldots,q\). Namely,
holds for all \(\boldsymbol{\lambda } = (\lambda _{1},\lambda _{2},\ldots,\lambda _{p})\) such that \(\sum _{j=1}^{q}\lambda _{j} = 1\) and \(\lambda _{j} \geq 0,\ j = 1,2,\ldots,q\). Since \(\bar{\boldsymbol{c}}_{j}\), j = 1, 2, …, q are all extreme points of Γ, this inequality can be rewritten as
Thus we have
This contradicts the fact that \(\hat{\boldsymbol{x}}\) is a minimax regret solution. Hence, a minimax regret solution is a possibly optimal solution. □
Example 3.
Consider Problem (20.19) again. The minimax regret solution is obtained as point (5. 34211, 5. 50877)T in Fig. 20.3. As shown in Fig. 20.3, this solution is on the polygonal line segment composed of (2. 8889, 8)T, (4, 7)T and (8, 2. 55556)T. The polygonal line segment shows the possibly optimal solution set. Then we know that the minimax regret solution is a possibly optimal solution. Moreover, from Fig. 20.3, we observe the solution (5. 34211, 5. 50877)T is located at a well-balanced place on the polygonal line segment.
Now we consider cases where Γ is a fuzzy set. In this case, by the extension principle, we define fuzzy regret \(\tilde{r}(\boldsymbol{x})\) and fuzzy achievement rate \(\widetilde{ac}(\boldsymbol{x})\) for a feasible solution \(\boldsymbol{x} \in X\) by the following membership functions:
Moreover, we specify fuzzy goal G r having an upper semi-continuous non-increasing membership function \(\mu _{G_{r}}: [0,+\infty ) \rightarrow [0,1]\) such that \(\mu _{G_{r}}(0) = 1\) on the regret, and fuzzy goal G ac having an upper semi-continuous non-decreasing membership function \(\mu _{G_{ac}}: (-\infty,1] \rightarrow [0,1]\) such that \(\mu _{G_{ac}}(1) = 1\) on the achievement rate. Then, using necessity measure, the problem is formulated as
We note that optimal solutions to these problem can be seen as relaxations of necessarily optimal solutions. Let us define two kinds of suboptimal solution sets to LP problem (20.13) with objective function \(\boldsymbol{c}^{\mathrm{T}}\boldsymbol{x}\) as fuzzy sets \(S_{dif}(\boldsymbol{c})\) and \(S_{rat}(\boldsymbol{c})\) by the following membership functions:
where χ X is the characteristic function of feasible region X, i.e., \(\chi _{X}(\boldsymbol{x}) = 1\) for \(\boldsymbol{x} \in X\) and \(\chi _{X}(\boldsymbol{x}) = 0\) for \(\boldsymbol{x}\not\in X\).
Based on these, we define two kinds of necessarily suboptimal solution sets NS dif and NS rat by the following membership functions:
We obtain \(\mu _{NS_{dif}}(\boldsymbol{x}) = N_{\tilde{r}(\boldsymbol{x})}(G_{r})\) and \(\mu _{NS_{rat}}(\boldsymbol{x}) = N_{\widetilde{ac}(\boldsymbol{x})}(G_{r})\) for \(\boldsymbol{x} \in X\). Therefore, problems in (20.40) are understood optimization problems of necessary suboptimality degrees.
The minimax regret problem was considered by Inuiguchi and Kume [30] and Inuiguchi and Sakawa [33]. Inuiguchi and Sakawa [33] proposed a solution method based on the relaxation procedure when all possibly optimal basic solutions are known. Mausser and Laguna [71] proposed a mixed integer programming approach to the minimax regret problem. Inuiguchi and Tanino [37] proposed a solution approach based on outer approximation and cutting hyperplane. The maximin achievement rate approach was proposed by Inuiguchi and Sakawa [35] and a relaxation procedure for a maximin achievement rate solution was proposed when all possibly optimal basic solutions are known. The necessarily suboptimal solution set is originally proposed by Inuiguchi and Sakawa [36]. They treated the regret case and proposed a solution algorithm based on the relaxation procedure and the bisection method. Inuiguchi et al. [39] further investigated a solution algorithm for both problems in (20.40). In those solution algorithms, the relaxation procedure and bisection method converges at the same time. The reduced problems described in this subsection are non-convex optimization problems. The recent global optimization techniques [21] would work well for those problems. The minimax regret solution concept is applied to discrete optimization problems [41] and MOLP problems [76]. The minimax regret solution to a MOLP problem minimizes the deviation from the complete optimality. The computational complexity of minimax regret solution is investigated in [1].
4 Multiple Objective Function Case
Now we describe the approaches to Problem (20.2) with p > 1, i.e., multiple objective function case.
4.1 Possibly and Necessarily Efficient Solutions
The concepts of possibly and necessarily optimal solutions can be extended to the case of multiple objective functions. In this case, the corresponding solution concepts are possibly and necessarily efficient solutions.
Before giving the definitions of possibly and necessarily efficient solutions, we define a set of efficient solutions, E(C) to the following MOLP problem:
where we define p × n matrix C by \(C = (\boldsymbol{c}_{1}\ \boldsymbol{c}_{2}\ \cdots \ \boldsymbol{c}_{p})^{\mathrm{T}}\).
First, we describe the case where \(\tilde{c}_{kj}\), k = 1, 2, …, p, j = 1, 2, …, n degenerate to intervals \([c_{kj}^{\mathrm{L}},c_{kj}^{\mathrm{R}}]\), k = 1, 2, …, p, j = 1, 2, …, n and define \(\varTheta =\prod _{ k=1}^{p}\varGamma _{k}\) and \(\varGamma _{k} =\prod _{ j=1}^{n}[c_{kj}^{\mathrm{L}},c_{kj}^{\mathrm{R}}] =\{ (c_{1},c_{2},\ldots,c_{n})^{\mathrm{T}}\mid c_{kj}^{\mathrm{L}} \leq c_{j} \leq c_{kj}^{\mathrm{R}},\ j = 1,2,\ldots,n\}\), k = 1, 2, …, p. Namely, \(\varTheta\) is a box set of p × n matrices. Then, in the analogy, we obtain the possibly efficient solution set Π E and the necessarily efficient solution set NE by
Elements of Π E and NE are interpreted in the same way as those of Π S and NS, respectively. Namely, an element of Π E is a solution efficient for at least one \(C\,\in \,\varTheta\). Because \(\varTheta\) shows the possible range of objective function coefficient matrix, an element of Π E is called a “possibly efficient solution”. On the other hand, an element of NE is a solution efficient for all \(C \in \varTheta\) and called a “necessarily efficient solution”.
Let \(K(C) =\{ \boldsymbol{s}\mid C\boldsymbol{s} \geq \mathbf{0}\ \mathrm{and}\ C\boldsymbol{s}\neq \mathbf{0}\}\) and \(R(C) =\{ C^{\mathrm{T}}\boldsymbol{z}\mid \boldsymbol{z}> \mathbf{0}\}\). Namely, K(C) shows the set of improving directions while R(C) is the set of positively weighted sum of objective coefficient vectors. Using K(C) and R(C), we define the following sets:
Let \(T(\boldsymbol{x})\) be the tangent cone of feasible region X at point \(\boldsymbol{x} \in X\), i.e., \(T(\boldsymbol{x}) = \mathrm{cl}\{r(\boldsymbol{y} -\boldsymbol{x})\mid \boldsymbol{y} \in X,\ r \geq 0\}\), where clK is the closure of a set K. Let \(P(\boldsymbol{x})\) be the normal cone of X at \(\boldsymbol{x} \in X\), in other words, \(P(\boldsymbol{x}) =\{ \boldsymbol{c}\mid \boldsymbol{c}^{\mathrm{T}}(\boldsymbol{y} -\boldsymbol{x}) \leq 0,\ \forall \boldsymbol{y} \in X\} = \left \{\boldsymbol{c}\ \Big\vert \ \boldsymbol{c}^{\mathrm{T}}\boldsymbol{x} =\max _{\boldsymbol{y}\in X}\boldsymbol{c}^{\mathrm{T}}\boldsymbol{y}\right \}\).
Because the following equivalence for \(\boldsymbol{x} \in X\) is known in MOLP Problem (see, for example, Steuer [89]):
Then, for \(\boldsymbol{x} \in X\), we have
Let Φ be the subset of matrices of \(\varTheta\) having all elements of each column at the upper bound or at the lower bound. Namely, C ∈ Φ implies C ⋅ j = L ⋅ j or \(C_{\cdot j} = U_{\cdot j}\) for j = 1, 2, …, p, where L = (c ij L), \(U = (c_{ij}^{\mathrm{R}})\) and C ⋅ j is the j-th column of matrix C. We have the following proposition (see Bitran [4]).
Proposition 1.
We have the following equations:
Proof.
We prove (20.58) and (20.59). Equation (20.60) is obtained from (20.59) in a straightforward manner.
\(KN(\varPhi ) \subseteq KN(\varTheta )\) is obvious. Then we prove the reverse inclusion relation. Assume \(\boldsymbol{s} \in KN(\varTheta )\), Then there exists \(C \in \varTheta\) such that \(C\boldsymbol{s} \geq \mathbf{0}\) and \(C\boldsymbol{s}\neq \mathbf{0}\). Consider \(\bar{C}\) defined by \(\bar{C}_{\cdot j} = L_{\cdot j}\) if s j < 0 and \(\bar{C}_{\cdot j} = U_{\cdot j}\) otherwise, for j = 1, 2, …, p. Then \(\bar{C} \in \varPhi\). We have \(\bar{C}\boldsymbol{s} \geq C\boldsymbol{s} \geq \mathbf{0}\) and \(\bar{C}\boldsymbol{s}\neq \mathbf{0}\). This implies \(\boldsymbol{s} \in K(\bar{C}) \subseteq KN(\varPhi )\). Hence, \(KN(\varPhi ) \supseteq KN(\varTheta )\).
Now let use prove (20.59). By definition, we have \(NE =\bigcap \{ E(C)\mid C \in \varTheta \}\subseteq \bigcap \{ E(C)\mid C \in \varPhi \}\). Then we prove the reverse inclusion relation. Assume \(\boldsymbol{x}\not\in NE\). Thus, from (20.55), we have \((KN(\varTheta ) \cup \{\mathbf{0}\}) \cap T(\boldsymbol{x})\neq \{\mathbf{0}\}\). From (20.58), we obtain \((KN(\varPhi ) \cup \{\mathbf{0}\}) \cap T(\boldsymbol{x})\neq \{\mathbf{0}\}\). Namely, \(\boldsymbol{x}\not\in E(C)\) for some C ∈ Φ. Consequently, \(\boldsymbol{x}\not\in \bigcap \{E(C)\mid C \in \varPhi \}\). Hence, \(NE =\bigcap \{ E(C)\mid C \in \varTheta \}\supseteq \bigcap \{ E(C)\mid C \in \varPhi \}\). □
As is known in the literature, we have
where D ∗ stands for the polar cone of a set D, i.e., \(D^{{\ast}} =\{ \boldsymbol{y}\mid \boldsymbol{x}^{\mathrm{T}}\boldsymbol{y} \leq 0,\forall \boldsymbol{x} \in D\}\). We obtain the following proposition.
Lemma 1.
The following are true:
where int D is the interior of set \(D \subset \mathbf{R}^{n}\).
Proof.
From definition, we obtain (20.62). Equations (20.63) and (20.64) are obtained from (20.62) in a straight forward manner. □
We obtain the following theorem (Inuiguchi [27]).
Theorem 4.
If \(RN(\varTheta )\) is not empty, we have
Proof.
We prove that \(RN(\varTheta ) \cap P(\boldsymbol{x})\neq \emptyset\) implies \(\boldsymbol{x} \in NE\) because the reverse implication is obtained from (20.57).
Assume \(\boldsymbol{x}\not\in NE\). Then, from (20.55) and \(\mathbf{0} \in T(\boldsymbol{x})\), \(KN(\varTheta ) \cap T(\boldsymbol{x})\neq \emptyset\). Let \(\hat{\boldsymbol{s}} \in KN(\varTheta ) \cap T(\boldsymbol{x})\). There exists \(C \in \varTheta\) such that \(\hat{\boldsymbol{s}} \in K(C) \cap T(\boldsymbol{x})\). Considering \(\{\hat{\boldsymbol{s}}\}^{{\ast}} =\{ \boldsymbol{c} \in \mathbf{R}^{n}\mid \boldsymbol{c}^{\mathrm{T}}\hat{\boldsymbol{s}} \leq 0\}\), we have
From (20.61), the second inclusion relation implies \(P(\boldsymbol{x}) \subseteq \{\hat{\boldsymbol{s}}\}^{{\ast}}\), i.e.,
On the other hand, from (20.63), we have \(-R(C) \subseteq \{\hat{\boldsymbol{s}}\}^{{\ast}}\). From \(\hat{\boldsymbol{s}} \in K(C)\) and (20.64), we obtain \(-R(C) \subseteq \mathrm{int}\{\hat{\boldsymbol{s}}\}^{{\ast}}\). This means
From (∗) and (∗∗), we find that \(\{\boldsymbol{y}\mid \hat{\boldsymbol{s}}^{\mathrm{T}}\boldsymbol{y} = 0\}\) is a separating hyperplane of \(P(\boldsymbol{x})\) and R(C). Therefore, we obtain \(R(C) \cap P(\boldsymbol{x}) =\emptyset\). By definition of \(RN(\varTheta )\), this implies
Hence, we have \(RN(\varTheta ) \cap P(\boldsymbol{x})\neq \emptyset \Rightarrow \boldsymbol{x} \in NE\). □
Let us consider the following set of objective function coefficients:
When \(\varLambda (\varTheta )\) is not empty, from the definition, we have
Let \(\mathit{Uni} =\{ \boldsymbol{c} = (c_{1},c_{2},\ldots,c_{n})^{\mathrm{T}}\mid \sum _{j=1}^{n}\vert c_{j}\vert = 1\}\). We find the following strong relations between \(RN(\varTheta )\) and \(\varLambda (\varTheta )\):
-
\(RN(\varTheta )\) is empty if and only if \(\varLambda (\varTheta ) \cap \mathit{Uni}\) is neither an empty set nor a singleton.
-
\(RN(\varTheta ) \cap \mathit{Uni}\) is neither an empty set nor a singleton if and only if \(\varLambda (\varTheta ) =\emptyset\).
-
\(RN(\varTheta ) \cap \mathit{Uni}\) is a singleton if and only if \(\varLambda (\varTheta ) \cap \mathit{Uni}\) is a singleton, and moreover we have \(\varLambda (\varTheta ) = RN(\varTheta )\).
We note \(RN(\varTheta ) \subseteq R\varPi (\varTheta )\) and \(\varLambda (\varTheta ) \subseteq R\varPi (\varTheta )\).
Moreover, comparing (20.65) and (20.67) with (20.29) and (20.28), respectively, we found the following relations:
where we note that we apply possible and necessary optimality concepts even when Γ is not a box set. Namely, when \(RN(\varTheta )\) is not empty, the necessary efficiency can be tested by the possible optimality with objective coefficient vector set \(RN(\varTheta )\). On the contrary, when \(RN(\varTheta )\) is empty, the necessary efficiency can be tested by the necessary optimality with objective coefficient vector set \(\varLambda (\varTheta )\). Moreover, cones \(RN(\varTheta )\) and \(\varLambda (\varTheta )\) can be replaced with bounded sets \(RN(\varTheta ) \cap \mathit{Uni}\) and \(\varLambda (\varTheta ) \cap \mathit{Uni}\), respectively. We may apply the techniques in single objective function case including minimax regret solution concepts to multiple objective function case if we obtain \(RN(\varTheta )\) and \(\varLambda (\varTheta )\).
When \(\tilde{c}_{kj}\), k = 1, 2, …, p, j = 1, 2, …, n degenerate to intervals \([c_{kj}^{\mathrm{L}},c_{kj}^{\mathrm{R}}]\), k = 1, 2, …, p, j = 1, 2, …, n, possibility efficient solutions and necessarily efficient solutions are illustrated in the following example.
Example 4.
Let us consider the following LP problem with multiple interval objective functions (Inuiguchi and Sakawa [34]):
To this problem, from Fig. 20.6, we obtain
while \(\varLambda (\varTheta ) =\emptyset\). Consider a solution \(\boldsymbol{x} = (x_{1},x_{2})^{\mathrm{T}} = (6,6)^{\mathrm{T}}\). The normal cone of the feasible region at (6, 6)T is obtained as
We obtain \(RN(\varTheta ) \cap P((6,6)^{\mathrm{T}})\neq \emptyset\). From Theorem 4, this implies that (6, 6)T is a necessarily efficient solution. Moreover, any solution (x 1, x 2)T on the line segment from (6, 6)T to (8, 0)T includes \(\{k(3,0.8)\mid k \geq 0\} \subset RN(\varTheta )\) in its normal cone P((x 1, x 2)T), and therefore, it is also a necessarily efficient solution. Thus there are many necessarily efficient solutions.
On the other hand, we obtain
and \(R\varPi (\varTheta ) \cap P((6,6)^{\mathrm{T}})\neq \emptyset\). Thus, (6, 6)T is also a possibly efficient solution. Moreover solutions on the line segment from (6, 6)T to (8, 0)T are all possibly efficient solutions because we have \(R\varPi (\varTheta ) \cap P((x_{1},x_{2})^{\mathrm{T}})\neq \emptyset\). There are no other possibly efficient solutions because other feasible solutions (x 1, x 2)T satisfy \(R\varPi (\varTheta ) \cap P((x_{1},x_{2})^{\mathrm{T}}) =\emptyset\). Thus, in this example, we have Π E = NE.
Next, let us consider the following LP problem with multiple interval objective functions:
For this problem, we obtain \(RN(\varTheta ) =\emptyset\) while
Because the constraints are same as the previous problem, the normal cone of the feasible region at (6, 6)T is same as P((6, 6)T). As shown in Fig. 20.7, we have \(\varLambda (\varTheta )\not\subseteq P((6,6)^{\mathrm{T}})\). Then (6, 6)T is not a necessarily efficient solution. However, as shown in Fig. 20.7, we have \(\varLambda (\varTheta ) \cap P((6,6)^{\mathrm{T}})\neq \emptyset\) and this implies \(R\varPi (\varTheta ) \cap P((6,6)^{\mathrm{T}})\neq \emptyset\). Namely, (6, 6)T is a possibly optimal solution. In this case, we obtain
Then solutions (x 1, x 2) on the polygon passing (2, 9)T, (6, 6)T and (8, 0)T are all possibly optimal solutions because they satisfy \(R\varPi (\varTheta ) \cap P((x_{1},x_{2})^{\mathrm{T}})\neq \emptyset\). No other solutions are possibly optimal.
Finally, let us consider the following LP problem with multiple interval objective functions:
For this problem, we obtain \(RN(\varTheta ) =\emptyset\) and \(\varLambda (\varTheta ) = \mathbf{R}^{2}\). Because \(P((x_{1},x_{2})^{\mathrm{T}}) \subset \mathbf{R}^{2}\) for any (x 1, x 2)T ∈ X, there is no necessarily optimal solution. Moreover, \(R\varPi (\varTheta ) = \mathbf{R}^{2}\) and thus, all feasible solutions are possibly efficient.
The possibly efficient solution set Π E and the necessarily efficient solution set NE are extended to the case where \(\varTheta\) is fuzzy set. Namely, they are defined by the following membership functions:
Similar to possibly and necessarily optimal solution sets, we have
where \([\varTheta ]_{h}\) and \((\varTheta )_{1-h}\) are h-level set and strong (1 − h)-level set of \(\varTheta\). From those we have
Therefore, the h-level sets of possibly and necessarily efficient solution sets with fuzzy objective function coefficients are treated almost in the same way as possibly and necessarily efficient solution sets with interval objective function coefficients.
The examples of possibly and necessarily efficient solutions in fuzzy coefficient case can be found in Inuiguchi and Sakawa [34].
Remark 2.
By taking a positively weighted sum of objective functions of Problem (20.2), we obtain an LP problem with a single objective function. To this single objective LP problem, we obtain possibly and necessarily optimal solution sets. Let \(\varPi S(\boldsymbol{w})\) and \(NS(\boldsymbol{w})\) be possibly and necessarily optimal solution sets of the single objective LP problem with weight vector \(\boldsymbol{w}\), respectively. We have the following relations to possibly and necessarily efficient solution sets of Problem (20.2) (see Inuiguchi [27]):
Remark 3.
Luhandjula [64] and Sakawa and Yano [81, 82] earlier defined similar but different optimal and efficient solutions to Problems (20.13) and (20.2), respectively. Those pioneering definitions are based on the inequality relations between objective function values of solutions. However the interactions between objective function values are discarded. The omission of the interaction between fuzzy objective function values are not always reasonable as shown by Inuiguchi [26]. On the other hand, Inuiguchi and Kume [29] proposed several extensions of efficient solutions based on the extended dominance relations between solutions. They showed the relations of the proposed extensions of efficient solutions including possibly and necessarily efficient solutions.
4.2 Efficiency Test and Possible Efficiency Test
In this subsection, we describe a method to confirm the possible and necessary efficiency of a given feasible solution. To confirm this, we solve mathematical programming problems called Possible and necessary efficiency test problems. The test problems are often investigated for given basic feasible solutions while Inuiguchi and Sakawa [34] investigated the possible efficiency test problem of any feasible solution.
First let us consider a basic feasible solution \(\boldsymbol{x}^{0} \in X\). Let C B and C N be the submatrices of objective function coefficient matrix C corresponding to the basic matrix B and the non-basic matrix N which are submatrices of \(A = (\boldsymbol{a}_{1}\ \boldsymbol{a}_{2}\ \ldots \ \boldsymbol{a}_{m})^{\mathrm{T}}\). We define a vector function \(V: \mathbf{R}^{p\times n} \rightarrow \mathbf{R}^{p\times (n-m)}\) by
Let J B and J N be the index sets of basic and non-basic variables, respectively, i.e., J B = { j∣x j is a basic variable} and \(J_{\mathrm{N}} =\{ j\mid x_{j}\mbox{ is a non-basic variable}\}\). A solution \(\boldsymbol{s}\) satisfying the following system of linear inequalities shows an improvement direction of objective function without violation of constraints from \(\boldsymbol{x}^{0}\):
where we note that D is an index set of basic variables which degenerate at \(\boldsymbol{x}^{0}\). Then D is empty if \(\boldsymbol{x}^{0}\) is nondegenerate. Then the necessary and sufficient condition that \(\boldsymbol{x}^{0}\) is efficient solution with respect to objective function coefficient matrix C is given by the inconsistency of (20.77) (see Evans and Steuer [14]).
Using Tucker’ theorem of alternatives [70], the inconsistency of (20.77) is equivalent to the consistency of
or equivalently,
where 1 = (1, 1, …, 1)T.
The necessary and sufficient conditions described above are applicable to basic solutions. Now let us consider a feasible solution \(\boldsymbol{x}^{0}\) which is not always a basic solution. Because an efficient solution is a proper efficient solution [16], an optimal solution to an LP problem with objective function \(\boldsymbol{u}_{2}^{\mathrm{T}}C\boldsymbol{x}\) for some \(\boldsymbol{u}_{2}> \mathbf{0}\) is an efficient solution of Problem (20.45) and vice versa. Then, the necessary and sufficient condition that \(\boldsymbol{x}^{0}\) is efficient solution with respect to objective function coefficient matrix C is given by the consistency of the following system of linear inequalities [34]:
In Problem (20.2), the objective function coefficient matrix is not clearly given by a matrix but by a set of matrices, \(\varTheta =\{ C\mid L \leq C \leq U\}\). The necessary and sufficient condition that \(\boldsymbol{x}^{0}\) is possibly efficient solution to Problem (20.2) is given by the consistency of the following system of linear inequalities [34]:
Moreover, if \(\boldsymbol{x}^{0}\) is a basic solution, the necessary and sufficient condition that \(\boldsymbol{x}^{0}\) is a possibly efficient solution to Problem (20.2) is given also by the consistency of the following system of linear inequalities [28]:
Inuiguchi and Kume [28] showed that, for i ∈ D, the i-th row of C B can be fixed at the i-th row of L B as we fixed C N at L N by the consideration of (20.77).
As shown above the possible efficiency of a given feasible solution can be checked easily by the consistency of a system of linear inequalities.
Let us consider a case where the (k, j)-component c kj of C is given by L-R fuzzy number \(\tilde{c}_{kj} = (c_{kj}^{\mathrm{L}},c_{kj}^{\mathrm{R}},\gamma _{kj}^{\mathrm{L}},\gamma _{kj}^{\mathrm{R}})_{L_{kj}R_{kj}}\). Define matrices with parameter h, \(\varDelta ^{\mathrm{L}}(h) = (\gamma _{kj}^{\mathrm{L}}L_{kj}^{(-1)}(h))\) and \(\varDelta ^{\mathrm{R}}(h) = (\gamma _{kj}^{\mathrm{R}}R_{kj}^{(-1)}(h))\). Then \([\varTheta ]_{h}\) is obtained by
Then, from (20.81), the degree of possible optimality of a given feasible solution \(\boldsymbol{x}^{0}\) is obtained as (see Inuiguchi and Sakawa [32])
For a fixed h, the conditions in the set of the right-hand side in (20.84) become a system of linear inequalities. Then the supremum can be obtained approximately by a bisection method of h ∈ [0, 1] and LP for finding a solution satisfying the system of linear inequalities.
Moreover, when \(\boldsymbol{x}^{0}\) is a basic solution, from (20.82), we obtain
where Δ B L and \(\varDelta _{\mathrm{B}}^{\mathrm{R}}\) are submatrices of Δ L and Δ R corresponding to basic variables while \(\varDelta _{\mathrm{N}}^{\mathrm{L}}\) and \(\varDelta _{\mathrm{N}}^{\mathrm{R}}\) are submatrices of Δ L and Δ R corresponding to non-basic variables. Similar to (20.84), for a fixed h, the conditions in the set of the right-hand side in (20.85) become a system of linear inequalities. Then the supremum can be obtained approximately by a bisection method of h ∈ [0, 1] and LP for finding a solution satisfying the system of linear inequalities.
As shown above, even in fuzzy coefficient case, the possible efficiency degree of a given feasible solution can be calculated rather easily by a bisection method and an LP technique.
4.3 Necessary Efficiency Test
The necessary efficiency test is much more difficult than the possible efficiency test. Bitran [4] proposed an enumeration procedure for the necessary efficiency test of a non-degenerate basic solution when \(\varTheta\) is a crisp set. In this paper, we describe the implicit enumeration algorithm for the necessary efficiency test of a basic solution based on (20.77) when \(\varTheta\) is a crisp set. The difference from the Bitran’s approach is only that we have additional constraints \(B_{i\cdot }^{-1}N\boldsymbol{s} \leq \mathbf{0}\), \(i \in D =\{ i\mid x_{i}^{0} = 0,i \in J_{\mathrm{B}}\}\).
Because the necessary and sufficient condition for a basic feasible solution \(\boldsymbol{x}^{0}\) to be an efficient solution with respect to objective coefficient matrix C is given as the inconsistency of (20.77), from Proposition 1, we check the inconsistency of (20.77) for all \(C \in \varPhi \subseteq \varTheta\). To do this, we consider the following non-linear programming problem:
If the optimal value of Problem (20.86) is zero, the given basic solution \(\boldsymbol{x}^{0}\) is a necessarily optimal solution. Otherwise, \(\boldsymbol{x}^{0}\) is not a necessarily optimal solution.
We obtain the following Proposition.
Proposition 2.
In Problem (20.86) , there is always an optimal solution \((C_{\mathrm{B}}^{{\ast}},C_{\mathrm{N}}^{{\ast}},\boldsymbol{s}^{{\ast}},\boldsymbol{y}^{{\ast}})\) with \(C_{\mathrm{N}}^{{\ast}} = U_{\mathrm{N}}\) and \(C_{\mathrm{B}}{}_{\cdot i}^{{\ast}} = U_{\mathrm{B}}{}_{\cdot i}\) , i ∈ D.
Proof.
It is trivial from \(\boldsymbol{s} \geq \mathbf{0}\) and \(B_{i\cdot }^{-1}N\boldsymbol{s} \leq \mathbf{0}\), i ∈ D. □
From Proposition 2, some part of C = (C B C N) can be fixed to solve Problem (20.86). For each non-basic variable x j , let C B(j) be the p × n matrix with columns C B(j)⋅ k defined by
We obviously have \(C_{\mathrm{B}}(j)B^{-1}N_{\cdot j}\boldsymbol{s} \leq C_{\mathrm{B}}B^{-1}N_{\cdot j}\boldsymbol{s}\) for L B ≤ C B ≤ U B and \(\boldsymbol{s} \geq \mathbf{0}\). We have the following proposition.
Proposition 3.
If Problem (20.86) has a feasible solution \((C_{\mathrm{B}}^{{\ast}},C_{\mathrm{N}}^{{\ast}},\boldsymbol{s}^{{\ast}},\boldsymbol{y}^{{\ast}})\) such that \(\mathbf{1}^{\mathrm{T}}\boldsymbol{s}^{{\ast}}> 0\) then the following problem with an arbitrary index set \(M_{1} \subseteq J_{\mathrm{B}}\setminus D\) has a feasible solution \(\mathbf{1}^{\mathrm{T}}\boldsymbol{s}> 0\).
Proof.
We have \(U_{\mathrm{N}}{}_{\cdot j} \geq C_{\mathrm{N}}{}_{\cdot j}\), \(j \in J_{\mathrm{N}}\) and \(C_{\mathrm{B}}(j)_{\cdot k}B_{\cdot k}^{-1}N_{\cdot j} \leq C_{\mathrm{B}}{}_{\cdot k}B_{\cdot k}^{-1}N_{\cdot j}\), j ∈ J N, \(C_{\mathrm{B}}{}_{\cdot k} \in \{ L_{\mathrm{B}}{}_{\cdot k},\ U_{\mathrm{B}}{}_{\cdot k}\}\). Moreover, for s j ≥ 0 such that \(B_{i\cdot }^{-1}N_{\cdot j}s_{j} \leq 0,\ j \in J_{\mathrm{N}},\ i \in D\), we have \(U_{\mathrm{B}}{}_{\cdot k}B_{\cdot k}^{-1}N_{\cdot j}s_{j} \leq C_{\mathrm{B}}{}_{\cdot k}B_{\cdot k}^{-1}N_{\cdot j}s_{j}\). Then the constraints of Problem (20.88) is a relaxation of those of Problem (20.86). Hence, we obtain this proposition. □
This proposition enables us to apply an implicit enumeration algorithm. We explain the procedure following Bitran’s explanation [4]. However, the description in this paper is different from Bitran’s because Bitran proposed the method when the basic solution is not degenerate.
Let \(w = \vert J_{\mathrm{B}}\setminus D\vert\) and \(J_{\mathrm{B}}\setminus D =\{ k_{1},k_{2},\ldots,k_{w}\}\). If w = 0, the necessary efficiency can be checked by solving Problem (20.88) with M 1 = ∅. Then, we assume w ≠ 0 in what follows. We consider \(M_{1} =\{ k_{1},k_{2},\ldots,k_{m_{1}}\}\) with m 1 ≤ k w . For convenience, let \(P(\boldsymbol{x}^{0},m_{1} = 0)\) be Problem (20.88) with M 1 = ∅. Then the implicit enumeration algorithm is described as follows.
Implicit Enumeration Algorithm [4]
Start by solving \(P(\boldsymbol{x}^{0},m_{1} = 0)\). If the optimal value is zero, terminate the algorithm and \(\boldsymbol{x}^{0}\) is necessarily efficient. Otherwise, let m 1 = 1 and generate the following two problems:
and
Where in the notation \(P(\boldsymbol{x}^{0},m_{1} = 1,z)\), z = 1 (z = 0) indicates that the column, in C B corresponding to m 1 = 1 has all its elements at the upper (lower) bound. If the optimal value of \(P(\boldsymbol{x}^{0},m_{1} = 1,1)\) is zero, by Proposition 3, there is no optimal matrix C B in Problem (20.86), with \(\mathbf{1}^{\mathrm{T}}\boldsymbol{y}> 0\) and having \(C_{\mathrm{B}}{}_{\cdot k_{1}} = U_{\mathrm{B}}{}_{\cdot k_{1}}\). In this case we do not need to consider any descendent of \(P(\boldsymbol{x}^{0},m_{1} = 1,1)\) and the branch is fathomed. If the optimal value of \(P(\boldsymbol{x}^{0},m_{1} = 1,1)\) is positive we generate two new problems \(P(\boldsymbol{x}^{0},m_{1} = 2,1,1)\) and \(P(\boldsymbol{x}^{0},m_{1} = 2,1,0)\). These two problems are obtained by substituting \(U_{\mathrm{B}}{}_{\cdot k_{2}}\) and \(L_{\mathrm{B}}{}_{\cdot k_{2}}\), respectively, for \(C_{\mathrm{B}}(j)_{\cdot k_{2}}\) in \(P(\boldsymbol{x}^{0},m_{1} = 1,1)\). We proceed in the same way, i.e., branching on problems with optimal value positive and fathoming those with optimal value zero until, we either conclude that \(\boldsymbol{x}^{0}\) is necessarily efficient or obtain a C B such that \(L_{\mathrm{B}} \leq C_{\mathrm{B}} \leq U_{\mathrm{B}}\) and the optimal value of Problem (20.86) is positive. An example of a tree generated by the implicit enumeration algorithm is given in Fig. 20.8. In this figure, \(P(\boldsymbol{x}^{0},m_{1} = 2,0,1,0)\) is the problem,
The convergence of the algorithm, after solving a finite number of LP problems, follows from Proposition 3 and the fact that the number of matrices C B that can possibly be enumerated is finite.
The implicit enumeration algorithm may be terminated earlier when \(\boldsymbol{x}^{0}\) is necessarily efficient because we can fathom the branches only when the optimal value is zero. As Ida [22] pointed out, we may build the implicit enumeration algorithm which may be terminated earlier when \(\boldsymbol{x}^{0}\) is not necessarily optimal. To this end, we define
and problem \(\check{P}(\boldsymbol{x}^{0},m_{1} = l,z_{1},z_{2},\ldots,z_{l})\) as the problem \(P(\boldsymbol{x}^{0},m_{1} = l,z_{1},z_{2},\ldots,z_{l})\) with substitution of \(\check{C}_{\mathrm{B}}(j)_{\cdot k}\) for \(C_{\mathrm{B}}(j)_{\cdot k}\), where 0 ≤ l ≤ w and z i ∈ { 0, 1}, i = 1, 2, …, l. We obtain the following proposition.
Proposition 4.
If the optimal value of \(\check{P}(\boldsymbol{x}^{0},m_{1} = l,\bar{z}_{1},\bar{z}_{2},\ldots,\bar{z}_{l})\) is positive for some \(\bar{z}_{i} \in \{ 0,1\}\) , i = 1,2,…,l, so is the optimal value of \(Q(\boldsymbol{x}^{0},m_{1} = l + 1,\bar{z}_{1},\bar{z}_{2},\ldots,\bar{z}_{l},z_{l+1})\).
Proof.
The proposition can be obtained easily. □
From Proposition 4, at the each node of the tree generated by the implicit enumeration, we solve \(Q(\boldsymbol{x}^{0},m_{1} = l,\bar{z}_{1},\bar{z}_{2},\ldots,\bar{z}_{l})\) as well as \(P(\boldsymbol{x}^{0},m_{1} = l,\bar{z}_{1},\bar{z}_{2},\ldots,\bar{z}_{l})\). If the optimal value of \(Q(\boldsymbol{x}^{0},m_{1} = l,\bar{z}_{1},\bar{z}_{2},\ldots,\bar{z}_{l})\) is positive, from the applications of Proposition 4, we know the optimal value of \(Q(\boldsymbol{x}^{0},m_{1} = w,\bar{z}_{1},\bar{z}_{2},\ldots,\bar{z}_{l},z_{l+1},\ldots,z_{w})\) is positive for any z i ∈ { 0, 1}, i = l + 1, l + 2, …, w. This implies that (20.77) is consistent with \(C \in \varPhi \subseteq \varTheta\) specified by \((\bar{z}_{1},\bar{z}_{2},\ldots,\bar{z}_{l},z_{l+1},\ldots,z_{w})\). Namely, we know that \(\boldsymbol{x}^{0}\) is not necessarily efficient. Therefore, if the optimal value of \(Q(\boldsymbol{x}^{0},m_{1} = l,\bar{z}_{1},\bar{z}_{2},\ldots,\bar{z}_{l})\) is positive, we terminate the algorithm with telling that \(\boldsymbol{x}^{0}\) is not necessarily efficient.
An example of a tree generated by this extended enumeration algorithm is shown in Fig. 20.9. While Fig. 20.8 illustrates a tree generated by the original enumeration algorithm when \(\boldsymbol{x}^{0}\) is necessarily efficient, Fig. 20.9 illustrates a tree generated by the extended enumeration algorithm when \(\boldsymbol{x}^{0}\) is not necessarily efficient. Even if the optimal value of \(P(\boldsymbol{x}^{0},m_{1} = l,\bar{z}_{1},\bar{z}_{2},\ldots,\bar{z}_{l})\) is zero, we do not terminate the algorithm but fathom the subproblem. On the contrary, if the optimal value of \(Q(\boldsymbol{x}^{0},m_{1} = l,\bar{z}_{1},\bar{z}_{2},\ldots,\bar{z}_{l})\) is positive, we know that \(\boldsymbol{x}^{0}\) is not necessarily efficient and terminate the algorithm.
As Ida [22] proposed, we may build the implicit enumeration algorithm only with solving \(Q(\boldsymbol{x}^{0},m_{1} = l,\bar{z}_{1},\bar{z}_{2},\ldots,\bar{z}_{l})\). Moreover, Ida [22, 23] proposed a modification of extreme ray generation method [7] suitable for the problem. In either way, the necessary efficiency test requires a lot of computational cost. Recently, Hladík [20] showed that the necessary efficiency test problem is co-NP-complete even for the case of only one objective and Hladík [19] gives a necessary condition for necessary efficiency which can solve easily. An overview of MOLP models with interval coefficients is also done by Oliveira and Antunes [72]. The necessity efficiency test of a given non-basic feasible solution can be done based on the consistency of (20.80) for all \(C \in \varPhi \subseteq \varTheta\). However, it is not easy to build an implicit enumeration algorithm as we described above in basic feasible solution case because we cannot easily obtain a proposition corresponding to Proposition 3. The necessity efficiency test of a given basic feasible solution in fuzzy coefficient case can be done by the introduction of a bisection method to the implicit enumeration method. However, this becomes a complex algorithm. The studies on effective methods for necessity efficiency tests in non-basic solution case as well as necessity efficiency tests in fuzzy coefficient case are a part of future topics.
5 Interactive Fuzzy Stochastic Multiple Objective Programming
One of the traditional tools for taking into consideration uncertainty of parameters involved in mathematical programming problems is stochastic programming [3, 9, 24], in which the coefficients in objective functions and/or constraints are represented with random variables. Stochastic programming with multiple objective functions were first introduced by Contini [8] as a goal programming approach to multiobjective stochastic programming, and further studied by Stancu-Minasian [86]. For deriving a compromise or satisficing solution for the DM in multiobjective stochastic decision making situations, an interactive programming method for multiobjective stochastic programming with Gaussian random variables were first presented by Goicoecha et al. [18] as a natural extension of the so-called STEP method [2] which is an interactive method for deterministic problems. An interactive method for multiobjective stochastic programming with discrete random variables, called STRANGE, was proposed by Teghem et al. [92] and Słowiński and Teghem [84]. The subsequent works on interactive multiobjective stochastic programming have been accumulated [57, 93, 94]. There seems to be no explicit definitions of the extended Pareto optimality concepts for multiobjective stochastic programming, until White [97] defined the Pareto optimal solutions for the expectation optimization model and the variance minimization model. More comprehensive discussions were provided by Stancu-Minasian [86] and Caballero et al. [6] through the introduction of extended Pareto optimal solution concepts for the probability maximization model and the fractile criterion optimization model. An overview of models and solution techniques for multiobjective stochastic programming problems were summarized in the context of Stancu-Minasian [87].
When decision makers formulate stochastic programming problems as representations of decision making situations, it is implicitly assumed that uncertain parameters or coefficients involved in multiobjective programming problems can be expressed as random variables. This means that the realized values of random parameters under the occurrence of some event are assumed to be definitely represented with real values. However, it is natural to consider that the possible realized values of these random parameters are often only ambiguously known to the experts. In this case, it may be more appropriate to interpret the experts’ ambiguous understanding of the realized values of random parameters as fuzzy numbers. From such a practical point of view, this subsection introduces multiobjective linear programming problems where the coefficients of the objective function are expressed as fuzzy random variables.
5.1 Fuzzy Random Variable
A fuzzy random variable was first introduced by Kwakernaak [58], and its mathematical basis was constructed by Puri and Ralescu [73]. An overview of the developments of fuzzy random variables was found in the recent article of Gil et al. [17].
In general, fuzzy random variables can be defined in an n dimensional Euclidian space \(\mathbb{R}^{n}\) [73]. From a practical viewpoint, as a special case of the definition by Puri and Ralescu, following the definition by Wang and Zhang [96], we present the definition of a fuzzy random variable in a single dimensional Euclidian space \(\mathbb{R}\).
Definition 1 (Fuzzy Random Variable).
Let \((\varOmega,\mathfrak{A},P)\) be a probability space , where Ω is a sample space , \(\mathfrak{A}\) is a \(\sigma\)-field and P is a probability measure . Let F N be the set of all fuzzy numbers and \(\mathfrak{B}\) a Borel \(\sigma\)-field of \(\mathbb{R}\). Then, a map \(\tilde{\bar{C}}:\varOmega \rightarrow F_{N}\) is called a fuzzy random variable if it holds that
where \(\tilde{\bar{C}}_{\alpha }(\omega ) = \left [\tilde{\bar{C}}_{\alpha }^{-}(\omega ),\tilde{\bar{C}}_{\alpha }^{+}(\omega )\right ] = \left \{\tau \in \mathbb{R}\ \big\vert \ \mu _{\tilde{\bar{C}}(\omega )}(\tau ) \geq \alpha \right \}\) is an α-level set of the fuzzy number \(\tilde{\bar{C}}(\omega )\) for ω ∈ Ω.
Intuitively, fuzzy random variables are considered to be random variables whose realized values are not real values but fuzzy numbers or fuzzy sets.
In Definition 1, \(\tilde{\bar{C}}(\omega )\) is a fuzzy number corresponding to the realized value of fuzzy random variable \(\tilde{\bar{C}}\) under the occurrence of each elementary event ω in the sample space Ω. For each elementary event ω, \(\tilde{\bar{C}}_{\alpha }^{-}(\omega )\) and \(\tilde{\bar{C}}_{\alpha }^{+}(\omega )\) are the left and right end-points of the closed interval \(\left [\tilde{\bar{C}}_{\alpha }^{-}(\omega ),\tilde{\bar{C}}_{\alpha }^{+}(\omega )\right ]\) which is an α-level set of the fuzzy number \(\tilde{\bar{C}}(\omega )\) characterized by the membership function \(\mu _{\tilde{\bar{C}}(\omega )}(\tau )\). Observe that the values of \(\tilde{\bar{C}}_{\alpha }^{-}(\omega )\) and \(\tilde{\bar{C}}_{\alpha }^{+}(\omega )\) are real values which vary randomly due to the random occurrence of elementary events ω. With this observation in mind, realizing that \(\tilde{\bar{C}}_{\alpha }^{-}\) and \(\tilde{\bar{C}}_{\alpha }^{+}\) can be regarded as random variables, it is evident that fuzzy random variables can be viewed as an extension of ordinary random variables.
In general, if the sample space Ω is uncountable, positive probabilities cannot be always assigned to all the sets of events in the sample space due to the limitation that the sum of the probabilities is equal to one. Realizing such situations, it is significant to introduce the concept of \(\sigma\)-field which is a set of subsets of the sample space.
To understand the concept of fuzzy random variables, consider discrete fuzzy random variables. To be more specific, when a sample space Ω is countable, the discrete fuzzy random variable can be defined by setting the \(\sigma\)-field \(\mathfrak{A}\) as the power set 2Ω or some other smaller set, together with the probability measure P associated with the probability mass function p satisfying
Consider a simple example: Let a sample space be Ω = {ω 1, ω 2, ω 3}, a \(\sigma\)-field \(\mathfrak{A} = 2^{\varOmega }\), and a probability measure \(P(A) =\sum _{\omega \in A}p(\omega )\) for all \(A \in \mathfrak{A}\). Then, Fig. 20.10 illustrates a discrete fuzzy random variable where fuzzy numbers \(\tilde{\bar{C}}(\omega _{1})\), \(\tilde{\bar{C}}(\omega _{2})\) and \(\tilde{\bar{C}}(\omega _{3})\) are randomly realized at probabilities p(ω 1), p(ω 2) and p(ω 3), respectively, satisfying \(\sum _{j=1}^{3}p(\omega _{j}) = 1\).
5.2 Brief Survey of Fuzzy Random Multiple Objective Programming
Studies on linear programming problems with fuzzy random variable coefficients, called fuzzy random linear programming problems, were initiated by Wang and Qiao [95] and Qiao et al. [74] as a so-called distribution problem of which goal is to seek the probability distribution of the optimal solution and optimal value. Optimization models of fuzzy random linear programming were first developed by Luhandjula et al. [67, 69], and further studied by Liu [60, 61] and Rommelfanger [77]. A brief survey of major fuzzy stochastic programming models including fuzzy random programming was found in the paper by Luhandjula [68].
On the basis of possibility theory, Katagiri et al. firstly introduced possibilistic programming approaches to fuzzy random linear programming problems [42, 44] where only the right-hand side of an equality constraint involves a fuzzy random variable, and considered more general cases where both sides of inequality constraints involve fuzzy random variables [45]. They also tackled the problem where the coefficients of the objective functions are fuzzy random variables [43]. Through the combination of a stochastic programming model and a possibilistic programming model, Katagiri et al. introduced a possibilistic programming approach to fuzzy random programming model [50] and proposed several multiobjective fuzzy random programming models using different optimization criteria such as possibility expectation optimization [46], possibility variance minimization [48], possibility-based probability maximization [53] and possibility-based fractile optimization [51].
Extensions to multiobjective 0-1 programming problems with fuzzy random variables were provided by incorporating the branch-and-bound method into the interactive methods [49].
Along this line, this section devotes to discussing the optimization models for multiobjective fuzzy random programming problems where each of coefficients in the objective functions are represented with fuzzy random variables.
5.3 Problem Formulation
Assuming that the coefficients of the objective functions are expressed as fuzzy random variables, we consider a multiobjective fuzzy random programming problem
where \(\boldsymbol{x}\) is an n dimensional decision variable column vector, A is an m × n coefficient matrix, \(\boldsymbol{b}\) is an m dimensional column vector and \(\tilde{\bar{\boldsymbol{C}}}_{l} = (\tilde{\bar{C}}_{l1},\ldots,\tilde{\bar{C}}_{ln}),\ l = 1,\ldots,k\) are n dimensional coefficient row vectors of fuzzy random variables.
For notational convenience, let F denote the feasible region of (20.91), namely
Considering a simple but practical fuzzy random variables satisfying the conditions in Definition 1, suppose that each element \(\tilde{\bar{C}}_{lj}\) of the vector \(\tilde{\bar{\boldsymbol{C}}}_{l} = (\tilde{\bar{C}}_{l1},\ldots,\tilde{\bar{C}}_{ln})\) is a fuzzy random variable whose realized value is a fuzzy number \(\tilde{C}_{ljs_{l}}\) depending on a scenario \(s_{l} \in \{ 1,\ldots,S_{l}\}\) which occurs with a probability \(p_{ls_{l}}\), where \(\sum _{s_{l}=1}^{S_{l}}p_{ ls_{l}} = 1\).
The sample space is defined as Ω = { 1, …, S l }, and the corresponding \(\sigma\)-field is \(\mathfrak{A} = 2^{\varOmega }\). Unfortunately, however, if the shapes of \(\tilde{C}_{ljs_{l}}\), s l = 1, …, S l are not the same as shown in Fig. 20.10, it is quite difficult to calculate the fuzzy random variable representing the objective function involving fuzzy random variables in problem (20.91). Realizing such difficulty, Katagiri et al. [43, 46, 48, 49] considered a discrete fuzzy random variable as an extended concept of the discrete random variable. Along this line, in this section, we restrict ourselves to considering the case where the realized values \(\tilde{C}_{ljs_{l}}\), s l = 1, …, S l are triangular fuzzy numbers with the membership function defined as
where the value of \(d_{ljs_{l}}\) varies depending on which scenario \(s_{l} \in \{ 1,\ldots,S_{l}\}\) occurs, and β lj and γ lj are not random parameters but constants. Figure 20.11 illustrates an example of the membership function \(\mu _{\tilde{C}_{ljs_{ l}}}(\tau )\). Formally, the membership function of the fuzzy random variable \(\tilde{\bar{C}}_{lj}\) is represented by
Through the Zadeh’s extension principle, each objective function \(\tilde{\bar{\boldsymbol{C}}}_{l}\boldsymbol{x}\) is represented by a single fuzzy random variable of which realized value for scenario s l is a triangular fuzzy number \(\tilde{\boldsymbol{C}}_{ls_{l}}\boldsymbol{x}\) characterized by the membership function
where \(\boldsymbol{d}_{ls_{l}}\) is an n dimensional column vector which is different from the other \(\boldsymbol{d}_{l\hat{s}_{l}}\), \(\hat{s}_{l} \in \{ 1,\ldots,S_{l}\}\), \(\hat{s}_{l}\not =s_{l}\), and \(\boldsymbol{\beta }_{l}\) and \(\boldsymbol{\gamma }_{l}\) are n dimensional constant column vectors. Figure 20.12 illustrates an example of the membership function \(\mu _{\tilde{\boldsymbol{C}}_{ ls_{l}}\boldsymbol{x}}(\upsilon )\). Also for the lth objective function \(\tilde{\bar{\boldsymbol{C}}}_{l}\boldsymbol{x}\), its membership function is formally expressed as
Considering the imprecise nature of human judgments, it is quite natural to assume that the decision maker (DM) may have a fuzzy goal for each of the objective functions \(z_{l}(\boldsymbol{x}) =\tilde{\bar{ \boldsymbol{C}}}_{l}\boldsymbol{x}\), and in a minimization problem, the DM specifies the fuzzy goal such that “the objective function value should be substantially less than or equal to some value.” Such a fuzzy goal can be quantified by eliciting the corresponding membership functions through some interaction process from the DM. In this subsection, for simplicity, the linear membership function expressed as the following is assumed:
where z l 0 and z l 1 are parameters determined by decision makers so as to represent the DM’s degree of satisfaction of the objective function values
It should be noted here that z l 0 and z l 1 are obtained by solving linear programming problems. Figure 20.13 illustrates an example of the membership function \(\mu _{\tilde{G}_{l}}\) of a fuzzy goal \(\tilde{G}_{l}\).
Recalling that the membership function is regarded as a possibility distribution, the degree of possibility that the objective function value \(\tilde{\bar{\boldsymbol{C}}}_{ls_{l}}\boldsymbol{x}\) for a given scenario s l ∈ { 1, …, S l } attains the fuzzy goal \(\tilde{G}_{l}\) is expressed as
Figure 20.14 illustrates the degree of possibility that the fuzzy goal \(\tilde{G}_{l}\) is fulfilled under the possibility distribution \(\mu _{\tilde{C}_{ls_{ l}}\boldsymbol{x}}\).
A possibility measure is useful to a decision maker who observes decision making situations from an optimistic point of view. However, when a decision maker is pessimistic about the situation, it is reasonable to use a necessity measure rather than a possibility measure. Then, the degree of necessity that the objective function value \(\tilde{\bar{\boldsymbol{C}}}_{ls_{l}}\boldsymbol{x}\) for a given scenario s l ∈ { 1, …, S l } attains the fuzzy goal \(\tilde{G}_{l}\) is expressed as
Observing that the degrees of possibility vary randomly depending on which scenario occurs, it should be noted here that conventional possibilistic programming approaches cannot be directly applied to (20.91). With this observation in mind, realizing that (20.91) involves not only fuzziness but also randomness, Katagiri et al. considered fuzzy random decision making models such as possibilistic expectation model [43, 46, 49] and possibilistic variance model [48] by incorporating the possibility theory into stochastic programming models.
5.4 Possibilistic Expectation Model
One of the natural solution approaches to such decision making situations as discussed in the previous subsection is to maximize expectation of the degree of possibility and/or necessity. Katagiri et al. [43, 46, 49] introduced possibilistic expectation models under the assumption that a DM intends to maximize the expected degree of possibility and/or necessity that each of the original objective functions involving fuzzy random variable coefficients attains the fuzzy goals. On the basis of possibilistic expectation models the original multiobjective fuzzy random programming problem (20.91) can be reformulated as the following problem:
where E[⋅ ] denotes the expectation operator. \(\mathcal{L}_{pos}\) and \(\mathcal{L}_{nec}\) are index sets satisfying \(\mathcal{L}_{pos} \cup \mathcal{L}_{nec} =\{ 1,2,\ldots,k\}\) and \(\mathcal{L}_{pos} \cap \mathcal{L}_{nec} =\emptyset\).
When the triangular fuzzy random variable (20.94) and the linear fuzzy goal (20.96) are given, the degree of possibility (20.98) is explicitly represented by
On the other hand, the degree of necessity (20.99) is explicitly expressed as
Recalling that the occurrence probability of scenario s l is \(p_{ls_{l}}\), the expectation of the degree of possibility or necessity is calculated as
Let \(Z_{l}^{E}(\boldsymbol{x})\) denote
To calculate a candidate for the satisficing solution which is also Pareto optimal, in interactive multiobjective programming, the DM is asked to specify reference levels \(\hat{z}_{l}^{E}\), l = 1, …, k of the objective function values of (20.105), and it is called the reference (expected possibility) levels. For the DM’s reference levels \(\hat{z}_{l}^{E},\ l = 1,\ldots,k\), an Pareto optimal solution, which is the nearest to a vector of the reference levels or better than it if the reference levels are attainable in a sense of minimax, is obtained by solving the minimax problem
Following the preceding discussion, we can now present an interactive algorithm for deriving a satisficing solution for the DM from among the Pareto optimal solution set.
5.4.1 Interactive Satisficing Method for the Possibilistic Expectation Model
- Step 1: :
-
Determine the linear membership functions \(\mu _{\tilde{G}_{l}}\), l = 1, …, k defined as (20.96) by calculating z l 0 and z l 1, l = 1, …, k.
- Step 2: :
-
Set the initial reference levels at 1s, which can be viewed as the ideal values, i.e., \(\hat{z}_{l}^{E} = 1,\ l = 1,\ldots,k\).
- Step 3: :
-
For the current reference levels \(\hat{z}_{l}^{E}\), l = 1, …, k, solve the minimax problem (20.106).
- Step 4: :
-
The DM is supplied with the corresponding Pareto optimal solution \(\boldsymbol{x}^{{\ast}}\). If the DM is satisfied with the current objective function values \(Z_{l}^{E}(\boldsymbol{x}^{{\ast}}),\ l = 1,\ldots,k\), then stop the algorithm. Otherwise, ask the DM to update the reference levels \(\hat{z}_{l}^{E}\), l = 1, …, k by considering the current objective function values, and return to step 3.
Here it should be stressed for the DM that any improvement of one expectation of the degree of possibility can be achieved only at the expense of at least one of other expected possibilities or expected necessities.
5.5 Possibilistic Variance Model
As discussed in the previous subsection, the possibilistic expectation model would be appropriate if the DM intends to simply maximize the expected degrees of possibility without concerning about those fluctuations.
However, when the DM prefers to decrease the fluctuation of the objective function values, the possibilistic expectation model is not relevant because some scenario yielding a very low possibility of good performance may occur even with a small probability.
To avoid such risk, from the risk-averse point of view, by minimizing the variance of the degree of possibility under the constraints of feasibility together with the conditions for the expected degrees of possibility, Katagiri et al. [48] considered a possibilistic variance model for fuzzy random multiobjective programming problems. Along this line, in this section, we consider the following problem as a risk-aversion approach to the original problem (20.91):
where Var[⋅ ] denotes the variance operator, and \(\xi _{l},\ l = 1,\ldots,k\) are permissible expectation levels for the expected degrees of possibility specified by the DM.
For notational convenience, let \(F(\boldsymbol{\xi })\) be the feasible region of (20.107), namely
Recalling (20.98) and (20.99), each of the objective functions in (20.107) is calculated as
where V l is the variance-covariance matrix of \(\bar{\boldsymbol{d}}_{l}\) expressed by
and
Furthermore, from (20.103) and (20.104), the constraint of the expected degree of possibility \(E\left [\varPi _{\tilde{\bar{\boldsymbol{C}}}_{l}\boldsymbol{x}}(\tilde{G}_{l})\right ] \geq \xi _{l}\) and that of necessity \(E\left [N_{\tilde{\bar{\boldsymbol{C}}}_{l}\boldsymbol{x}}(\tilde{G}_{l})\right ] \geq \xi _{l}\) are explicitly represented as
and
By substituting (20.109), (20.110) and (20.111) into (20.107), (20.107) is equivalently transformed as
From the fact that it holds
and \(\boldsymbol{x}^{T}V _{l}\boldsymbol{x} \geq 0\) due to the positive-semidefinite property of V l , by computing the square root of the objective functions of (20.112), (20.112) is equivalently rewritten as
where each of the objective functions represents the standard deviation of the degree of possibility or necessity.
It should be noted here that the minimization of the variance is equivalent to the minimization of the standard deviation.
To calculate a candidate for the satisficing solution, the DM is asked to specify the reference levels \(\hat{z}_{l}^{D}\), i = 1, …, k of the objective function values of (20.113).
Let \(Z_{l}^{D}(\boldsymbol{x})\) denote
Then, for the DM’s reference levels \(\hat{z}_{l}^{D}\), i = 1, …, k, a (weakly) Pareto optimal solution is obtained by solving the minimax problem
For notational convenience, we introduce \(N_{l}(\boldsymbol{x})\) and \(D_{l}(\boldsymbol{x})\) such that
where
Since the numerator \(N_{l}(\boldsymbol{x})\) is a convex function and the denominator \(D_{l}(\boldsymbol{x})\) is an affine function, it follows that \(N_{l}(\boldsymbol{x})/D_{l}(\boldsymbol{x})\) is a quasi-convex function. Using this property, we can solve (20.114) by using the following extended Dinkelbach-type algorithm [5]:
5.5.1 Extended Dinkelbach-Type Algorithm for Solving (20.114)
- Step 1: :
-
Set r: = 0 and find a feasible solution \(\boldsymbol{x}^{r} \in F(\boldsymbol{\xi })\).
- Step 2: :
-
For a q r calculated by
$$\displaystyle{ q^{r} =\max _{ 1\leq l\leq k}\left \{\frac{N_{l}(\boldsymbol{x}^{r})} {D_{l}(\boldsymbol{x}^{r})}\right \}, }$$find an optimal solution \(\boldsymbol{x}^{c}\) to the convex programming problem
$$\displaystyle{ \left.\begin{array}{rl} \mathop{\mbox{ minimize}}\ &v \\ \mbox{ subject to}\ & \frac{1} {D_{l}(\boldsymbol{x}^{r})}\left \{D_{l}(\boldsymbol{x}) - q^{r}N_{ l}(\boldsymbol{x})\right \} \leq v,\ l = 1,\ldots,k \\ &\sum _{j=1}^{n}\left \{\sum _{ s_{l}=1}^{S_{l} }p_{ls_{l}}d_{ljs_{l}} - (1 -\xi _{l})\beta _{lj}\right \}x_{j} \leq z_{l}^{0} -\xi _{ l}(z_{l}^{0} - z_{ l}^{1}),\ l \in \mathcal{L}_{ pos} \\ &\sum _{j=1}^{n}\left \{\sum _{ s_{l}=1}^{S_{l} }p_{ls_{l}}d_{ljs_{l}} +\xi _{l}\gamma _{lj}\right \}x_{j} \leq z_{l}^{0} -\xi _{ l}(z_{l}^{0} - z_{ l}^{1}),\ l \in \mathcal{L}_{ nec} \\ &\boldsymbol{x} \in F.\end{array} \right \} }$$(20.116) - Step 3: :
-
For a sufficiently small positive number \(\varepsilon\), if \(v <\varepsilon\), stop the algorithm. Otherwise, set \(\boldsymbol{x}^{r}:= \boldsymbol{x}^{c}\), r: = r + 1, and return to step 2.
Now we are ready to summarize an interactive algorithm for deriving a satisficing solution for the DM from among the Pareto optimal solution set.
5.5.2 Interactive Satisficing Method for the Possibilistic Variance Model
- Step 1: :
-
Determine the linear membership functions \(\mu _{\tilde{G}_{l}},\ l = 1,\ldots,k\) with z l 0 and z l 1, l = 1, …, k obtained by solving linear programming problems (20.97).
- Step 2: :
-
Calculate the individual minima and maxima of \(Z_{l}^{E}(\boldsymbol{x})\), l = 1, …, k.
- Step 3: :
-
Ask the DM to specify the permissible levels \(\xi _{l}\), l = 1, …, k taking into account the individual minima and maxima obtained in step 2.
- Step 4: :
-
Set the initial reference levels at 0s, which can be viewed as the ideal values, i.e., \(\hat{z}_{l}^{D} = 0,\ l = 1,\ldots,k\).
- Step 5: :
-
For the current reference levels \(\hat{z}_{l}^{D},\ l = 1,\ldots,k\), solve the minimax problem (20.114) by using the extended Dinkelbach-type algorithm.
- Step 6: :
-
The DM is supplied with the obtained Pareto optimal solution \(\boldsymbol{x}^{{\ast}}\). If the DM is satisfied with the current objective function values \(Z_{l}^{D}(\boldsymbol{x}^{{\ast}})\), l = 1, …, k, then stop. Otherwise, ask the DM to update the reference levels \(\hat{z}_{l}^{D}\), l = 1, …, k, and return to step 5.
5.6 Recent Topics: Random Fuzzy Multiple Objective Programming
When a random variable is used to express an uncertain parameter related to a stochastic factor of real systems, it is implicitly assumed that there exists a single random variable as a proper representation of the uncertain parameter. However, in some cases, experts may consider that it is suitable to employ a set of random variables, rather than a single one, in order to more precisely express the uncertain parameter. In this case, depending on the degree to which experts convince that each element (random variable) in the set is compatible with the uncertain parameter, it would be quite natural to assign different values (different degrees of possibility) to the elements in the set. For handling such real-world decision making situations, a random fuzzy variable was introduced by Liu [62] and explicitly defined [63] as a function from a possibility space to a collection of random variables.
Recently, by considering the experts’ ambiguous understanding of mean and variance of random variables, Katagiri et al. [47] introduced a linear programming problem where an objective function contains random fuzzy parameters and discussed the problem in the framework of random fuzzy variables. They focused on the case where the mean of each random variable is represented with a fuzzy number and constructed a novel decision making model on the basis of possibility theory. Their model was extended to a multiobjective case [52] where only the coefficients of the objective functions are given as random fuzzy variables. A more general type of random fuzzy programming problems, in which not only objective functions but also constraints involve random fuzzy variables, was developed [56]. In these models, it is shown that the original problems can be transformed into deterministic nonlinear programming problems, and that the obtained deterministic problems can be exactly solved using conventional nonlinear programming techniques under some assumptions. These random fuzzy programming models are extended to other decision making problems such as two-level (bilevel) programming problems [54] and minimum spanning tree problems [55].
References
Averbakh, I., Lebedev, V.: On the complexity of minmax regret linear programming. Eur. J. Oper. Res. 160, 227–231 (2005)
Benayoun, R., de Montgolfier, J., Tergny, J., Larichev, O.I.: Linear programming with multiple objective functions: STEP Method (STEM). Math. Program. 1, 366–375 (1971)
Birge, J.R., Louveaux, F.: Introduction to Stochastic Programming, 2nd edn. Springer, New York/Dordrecht/Heidelberg/London (2011)
Bitran, G.R.: Linear multiple objective problems with interval coefficients. Manag. Sci. 26, 694–706 (1980)
Borde, J., Crouzeix, J.P.: Convergence of a Dinkelbach-type algorithm in generalized fractional programming. Z. Oper. Res. 31, 31–54 (1987)
Caballero, R., Cerdá, E., Muñoz, M.M., Rey, L., Stancu-Minasian, I.M.: Efficient solution concepts and their relations in stochastic multiobjective programming. J. Optim. Theory Appl. 110, 53–74 (2001)
Chernikova, N.V.: Algorithm for finding a general formula for the nonnegative solutions of a system of linear inequalities. USSR Comput. Math. Math. Phys. 5, 228–233 (1965)
Contini, B.: A stochastic approach to goal programming. Oper. Res. 16, 576–586 (1968)
Dantzig, G.B.: Linear programming under uncertainty. Manag. Sci. 1, 197–206 (1955)
Dubois, D.: Linear programming with fuzzy data. In: Bezdek, J.C. (ed.) Analysis of Fuzzy Information. Application in Engineering and Science, vol. III, pp. 241–263. CRC Press, Boca Raton (1987)
Dubois, D., Prade, H.: Fuzzy numbers: an overview. In: Bezdek, J.C. (ed.) Analysis of Fuzzy Information. Mathematics and Logic, vol. I, pp. 3–39. CRC Press, Boca Raton (1987)
Dubois, D., Prade, H.: Possibility Theory: An Approach to Computerized Processing of Uncertainty. Plenum Press, New York (1988)
Ehrgott, M., Gandibleux, X. (eds.): Multiple Criteria Optimization: State of the Art Annotated Bibliographic Surveys. Kluwer Academic Publishers, Boston (2002)
Evans, J.P., Steuer, R.E.: A revised simplex method for linear multiple objective programs. Math. Program. 5, 54–72 (1973)
Furukawa, N.: Parametric orders on fuzzy numbers and their roles in fuzzy optimization problems. Optimization 40, 171–192 (1997)
Geoffrion, A.M.: Proper efficiency and the theory of vector maximization. J. Math. Anal. Appl. 22, 618–630 (1968)
Gil, M.A., Lopez-Diaz, M., Ralescu, D.A.: Overview on the development of fuzzy random variables. Fuzzy Sets Syst. 157, 2546–2557 (2006)
Goicoecha, A., Hansen, D.R., Duckstein, L.: Multiobjective Decision Analysis with Engineering and Business Applications. Wiley, New York (1982)
Hladík, M.: On necessary efficient solutions in interval multiobjective linear programming. In: CD-ROM Proceedings of the 25th Mini-EURO Conference Uncertainty and Robustness in Planning and Decision Making URPDM 2010, pp. 1–10 (2010)
Hladík, M.: Complexity of necessary efficiency in interval linear programming and multiobjective linear programming. Optim. Lett. 6, 893–899 (2012)
Horst, R., Tuy, H.: Global Optimization: Deterministic Approaches, 3rd Revised and Enlarged Edition. Springer, Berlin (1995)
Ida, M.: Necessary efficient test in interval multiobjective linear programming. In: Proceedings of the Eighth International Fuzzy Systems Association World Congress, pp. 500–504 (1999)
Ida, M.: Efficient solution generation for multiple objective linear programming and uncertain coefficients. In: Proceedings of the 8th Bellman Continuum, pp. 132–136 (2000)
Infanger, G. (eds.): Stochastic Programming. Springer, New York/Dorderecht/Heidelberg/ London (2011)
Inuiguchi, M.: Multiple objective linear programming with fuzzy coefficients. In: Figueira, J., Greco, S., Ehrgott, M. (eds.) Multiple Criteria Decision Analysis: State of the Art Surveys, pp.723–760. Kluwer Academic Publishers, Boston (2002)
Inuiguchi, M.: On possibilistic/fuzzy optimization. In: Melin, P., Castillo, O., Aguilar, L.T., Kacprzyk, J., Pedrycz, W. (eds.) Foundations of Fuzzy Logic and Soft Computing. Proceedings of 12th International Fuzzy Systems Association World Congress, IFSA 2007, Cancun, June 2007. Lecture Notes in Artificial Intelligence, vol. 4529, pp. 351–360. Springer, Berlin (2007)
Inuiguchi, M.: Necessary efficiency is partitioned into possible and necessary optimalities. In: Proceedings of 15th International Fuzzy Systems Association World Congress, IFSA-NAFIPS 2013 (2013)
Inuiguchi, M., Kume, Y.: A discrimination method of possibly efficient extreme points for interval multiobjective linear programming problems (in Japanese). Trans. SICE 25, 824–826 (1989)
Inuiguchi, M., Kume, Y.: Solution concepts for fuzzy multiple objective programming problems. Jpn. J. Fuzzy Theory Syst. 2, 1–22 (1990)
Inuiguchi, M., Kume, Y.: Minimax regret in linear programming problems with an interval objective function. In: Tzeng, G.H., Wang, H.F., Wen, U.P., Yu, P.L. (eds.) Multiple Criteria Decision Making, pp. 65–74. Springer, New York (1994)
Inuiguchi, M., Ramík, J.: Possibilistic linear programming: a brief review of fuzzy mathematical programming and a comparison with stochastic programming in portfolio selection problem. Fuzzy Sets Syst. 111, 3–28 (2000)
Inuiguchi, M., Sakawa, M.: Possible and necessary optimality tests in possibilistic linear programming problems. Fuzzy Sets Syst. 67, 29–46 (1994)
Inuiguchi, M., Sakawa, M.: Minimax regret solutions to linear programming problems with an interval objective function. Eur. J. Oper. Res. 86, 526–536 (1995)
Inuiguchi, M., Sakawa, M.: Possible and necessary efficiency in possibilistic multiobjective linear programming problems and possible efficiency test. Fuzzy Sets Syst. 78, 231–241 (1996)
Inuiguchi, M., Sakawa, M.: An achievement rate approach to linear programming problems with an interval objective function. J. Oper. Res. Soc. 48, 25–33 (1997)
Inuiguchi, M., Sakawa, M.: Robust optimization under softness in a fuzzy linear programming problem. Int. J. Approx. Reason. 18, 21–34 (1998)
Inuiguchi, M., Tanino, T.: On computation methods for a minimax regret solution based on outer approximation and cutting hyperplanes. Int. J. Fuzzy Syst. 3, 548–557 (2001)
Inuiguchi, M., Tanino, T.: Enumeration of all possibly optimal vertices with possible optimality degrees in linear programming problems with a possibilistic objective function. Fuzzy Optim. Decis. Making 3, 311–326 (2004)
Inuiguchi, M., Tanino, T., Tanaka, H.: Optimization approaches to possibilistic linear programming problems. In: Proceedings of Joint 9th IFSA World Congress and 20th NAFIPS International Conference, pp. 2724–2729 (2001)
Ishibuchi, H., Tanaka, H.: Multiobjective programming in optimization of the interval objective function. Eur. J. Oper. Res. 48, 219–225 (1990)
Kasperski, A.: Discrete Optimization with Interval Data: Minimax Regret and Fuzzy Approach. Springer, Berlin (2008)
Katagiri, H., Ishii, H.: Linear programming problem with fuzzy random constraint. Math. Jpn. 52, 123–129 (2000)
Katagiri, H., Sakawa, M.: A study on fuzzy random linear programming problems based on possibility and necessity. In: Bilgic, T., DeBaets, B., Kaynak, O. (eds.) Fuzzy Sets and Systems, IFSA 2003: 10th International Fuzzy Systems Association World Congress, Istanbul. Lecture Notes in Computer Science, pp. 725–732. Springer, Berlin (2003)
Katagiri, H., Ishii, H., Itoh, T.: Fuzzy random linear programming problem. In: Proceedings of Second European Workshop on Fuzzy Decision Analysis and Neural Networks for Management, Planning and Optimization, Dortmund, pp. 107–115 (1997)
Katagiri, H., Ishii, H., Sakawa, M.: Linear programming problem under fuzziness and randomness. In: Proceedings of International Conference on Applied Stochastic System Modeling, Kyoto, pp. 97–106 (2000)
Katagiri, H., Sakawa, M., Ishii, H.: Multiobjective fuzzy random linear programming using E-model and possibility measure. In: Joint 9th IFSA World Congress and 20th NAFIPS International Conference, Vancouver, pp. 2295–2300 (2001)
Katagiri, H., Ishii, H., Sakawa, M.: Linear programming problems with random fuzzy variable coefficients. In: Proceedings of 5th Czech-Japan Seminar on Data Analysis and Decision Making under Uncertainty, Koyasan, vol. 1, pp. 55–58 (2002)
Katagiri, H., Sakawa, M., Ohsaki, S.: An interactive satisficing method through the variance minimization model for fuzzy random linear programming problems. In: Tanino, T., Tamaki, T., Inuiguchi, M. (eds.) Multi-Objective Programming and Goal-Programming: Theory and Applications. Advances in Soft Computing, pp.171–176. Springer, Berlin (2003)
Katagiri, H., Sakawa, M., Kato, K., Nishizaki, I.: A fuzzy random multiobjective 0-1 programming based on the expectation optimization model using possibility and necessity measures. Math. Comput. Model. 40, 411–421 (2004)
Katagiri, H., Sakawa, M., Ishii, H.: Studies of stochastic programming models using possibility and necessity measures for linear programming problems with fuzzy random variable coefficients. Electron. Commun. Jpn. Part III-Fundam. Electron. Sci. 88, 68–75 (2005)
Katagiri, H., Sakawa, M., Kato, K., Ohsaki, S.: An interactive fuzzy satisficing method based on the fractile optimization model using possibility and necessity measures for a fuzzy random multiobjective linear programming problem. Electron. Commun. Jpn. Part III-Fundam. Electron. Sci. 88, 20–28 (2005)
Katagiri, H., Hasuike, T., Ishii, H., Nishizaki, I.: Interactive multiobjective programming under random fuzzy environments. In: Proceedings of the 11th Czech-Japan Seminar on Data Analysis and Decision Making Under Uncertainty, Sendai, pp. 33–38 (2008)
Katagiri, H., Sakawa, M., Kato, K., Nishizaki, I.: Interactive multiobjective fuzzy random linear programming: maximization of possibility and probability. Eur. J. Oper. Res. 188, 530–539 (2008)
Katagiri, H., Niwa, K., Kubo, D., Hasuike, T.: Interactive random fuzzy two-level programming through possibility-based fractile criterion optimality. In: Proceedings of The International MultiConference of Engineers and Computer Scientists 2010, vol. 3, pp. 2113–2118 (2010)
Katagiri, H., Kato, K., Hasuike, T.: A random fuzzy minimum spanning tree problem through a possibility-based value at risk model. Expert Syst. Appl. 39, 205–220 (2012)
Katagiri, H., Uno, T., Kato, K., Tsuda, H., Tsubaki, H.: Random fuzzy multiobjective programming: optimization of possibilistic value at risk (pVaR). Expert Syst. Appl. 40, 563–574 (2013)
Klein, G., Moskowitz, H., Ravindran, A.: Interactive multiobjective optimization under uncertainty. Manag. Sci. 36, 58–75 (1990)
Kwakernaak, H.: Fuzzy random variable-1. Inf. Sci. 15, 1–29 (1978)
Lai, Y.-J., Hwang, C.L.: Fuzzy Mathematical Programming. Springer, Berlin (1992)
Liu, B.: Fuzzy random chance-constrained programming. IEEE Trans. Fuzzy Syst. 9, 713–720 (2001)
Liu, B.: Fuzzy random dependent-chance programming. IEEE Trans. Fuzzy Syst. 9, 721–726 (2001)
Liu, B.: Random fuzzy dependent-chance programming and its hybrid intelligent algorithm. Inf. Sci. 141, 259–271 (2002)
Liu, B.: Uncertainty Theory. Springer, Berlin/Heidelberg/New York (2004)
Luhandjula, M.K.: On possibilistic linear programming. Fuzzy Sets Syst. 18, 15–30 (1986)
Luhandjula, M.K.: Multiple objective programming problems with possibilistic coefficients. Fuzzy Sets Syst. 21, 135–145 (1987)
Luhandjula, M.K.: Fuzzy optimization: an appraisal. Fuzzy Sets Syst. 30, 257–282 (1989)
Luhandjula, M.K.: Fuzziness and randomness in an optimization framework. Fuzzy Sets Syst. 77, 291–297 (1996)
Luhandjula, M.K.: Fuzzy stochastic linear programming: survey and future research directions. Eur. J. Oper. Res. 174, 1353–1367 (2006)
Luhandjula, M.K., Gupta, M.M.: On fuzzy stochastic optimization. Fuzzy Sets Syst. 81, 47–55 (1996)
Mangasarian, O.L.: Nonlinear Programming. McGraw-Hill, New York (1969)
Mausser, H.E., Laguna, M.: A new mixed integer formulation for the maximum regret problem. Int. Trans. Oper. Res. 5, 389–403 (1998)
Oliveira, C., Antunes, C.H.: Multiple objective linear programming models with interval coefficients—an illustrated overview. Eur. J. Oper. Res. 181, 1434–1463 (2007)
Puri, M.L., Ralescu, D.A.: Fuzzy random variables. J. Math. Anal. Appl. 14, 409–422 (1986)
Qiao, Z., Zhang, Y., Wang, G.-Y.: On fuzzy random linear programming. Fuzzy Sets Syst. 65, 31–49 (1994)
Ramík, J., Římánek, J.: Inequality relation between fuzzy numbers and its use in fuzzy optimization. Fuzzy Sets Syst. 16, 123–138 (1985)
Rivaz, S., Yaghoobi, M.A.: Minimax regret solution to multiobjective linear programming problems with interval objective functions coefficients. Cent. Eur. J. Oper. Res. 21, 625–649 (2013)
Rommelfanger, H.: A general concept for solving linear multicriteria programming problems with crisp, fuzzy or stochastic variables. Fuzzy Sets Syst. 158, 1892–1904 (2007)
Rommelfanger, H., Słowiński, R.: Fuzzy linear programming with single or multiple objective functions. In: Słowiński, R. (ed.) Fuzzy Sets in Decision Analysis. Operations Research and Statistics. Kluwer Academic Publishers, Boston (1998)
Rommelfanger, H., Hanuscheck, R., Wolf, J.: Linear programming with fuzzy objective. Fuzzy Sets Syst. 29, 31–48 (1989)
Sakawa, M.: Fuzzy Sets and Interactive Multiobjective Optimization. Plenum Press, New York (1993)
Sakawa, M., Yano, H.: Feasibility and Pareto optimality for multiobjective nonlinear programming problems with fuzzy parameters. Fuzzy Sets Syst. 43, 1–15 (1991)
Sakawa, M., Takahashi, J., Yano, H.: Extended Pareto optimality concept for multiobjective linear programming problems with fuzzy parameters and its properties. Electron. Commun. Jpn. Part III-Fundam. Electron. Sci. 73, 1–9 (1990)
Słowiński, R.: Fuzzy multi-objective linear programming. Belg. J. Oper. Res. Stat. Comput. Sci. 37, 83–98 (1997)
Słowiński, R., Teghem, J.: Fuzzy vs. stochastic approaches to multicriteria linear programming under uncertainty. Nav. Res. Logist. 35, 673–695 (1988)
Słowiński, R., Teghem, J. (eds.): Stochastic Versus Fuzzy Approaches to Multiobjective Mathematical Programming Under Uncertainty. Kluwer Academic Publishers, Dordrecht (1990)
Stancu-Minasian, I.M.: Stochastic Programming with Multiple Objective Functions. D. Reidel Publishing Company, Dordrecht (1984)
Stancu-Minasian, I.M.: Overview of different approaches for solving stochastic programming problems with multiple objective functions. In: Słowiński, R., Teghem, J. (eds.) Stochastic Versus Fuzzy Approaches to Multiobjective Mathematical Programming Under Uncertainty, pp.71–101. Kluwer Academic Publishers, Dordrecht/Boston/London (1990)
Steuer, R.E.: Algorithms for linear programming problems with interval objective function coefficients. Math. Oper. Res. 6, 333–348 (1981)
Steuer, R.E.: Multiple Criteria Optimization: Theory, Computation, and Application. Wiley, New York (1986)
Tanaka, H., Asai, K.: Fuzzy linear programming problems with fuzzy numbers. Fuzzy Sets Syst. 13, 1–10 (1984)
Tanaka, H., Ichihashi, H., Asai, K.: A formulation of fuzzy linear programming problem based on comparison of fuzzy numbers. Control Cybern. 13, 185–194 (1984)
Teghem, J., Dufrane, D., Thauvoye, M., Kunsch, P.: STRANGE: an interactive method for multi-objective linear programming under uncertainty. Eur. J. Oper. Res. 26, 65–82 (1986)
Urli, B., Nadeau, R.: Stochastic MOLP with incomplete information: an interactive approach with recourse. J. Oper. Res. Soc. 41, 1143–1152 (1990)
Urli, B., Nadeau, R.: PROMISE/scenarios: an interactive method for multiobjective stochastic linear programming under partial uncertainty. Eur. J. Oper. Res. 155, 361–372 (2004)
Wang, G.-Y., Qiao, Z.: Linear programming with fuzzy random variable coefficients. Fuzzy Sets Syst. 57, 295–311 (1993)
Wang, G., Zhang, Y.: The theory of fuzzy stochastic processes. Fuzzy Sets Syst. 51, 161–178 (1992)
White, D.J.: Optimality and Efficiency. Wiley, New York (1982)
Zadeh, L.A.: Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets Syst. 1, 3–28 (1978)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer Science+Business Media New York
About this chapter
Cite this chapter
Inuiguchi, M., Kato, K., Katagiri, H. (2016). Fuzzy Multi-Criteria Optimization: Possibilistic and Fuzzy/Stochastic Approaches. In: Greco, S., Ehrgott, M., Figueira, J. (eds) Multiple Criteria Decision Analysis. International Series in Operations Research & Management Science, vol 233. Springer, New York, NY. https://doi.org/10.1007/978-1-4939-3094-4_20
Download citation
DOI: https://doi.org/10.1007/978-1-4939-3094-4_20
Publisher Name: Springer, New York, NY
Print ISBN: 978-1-4939-3093-7
Online ISBN: 978-1-4939-3094-4
eBook Packages: Business and ManagementBusiness and Management (R0)