Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Chronic myeloid leukemia (CML) is a myeloproliferative disorder that represents about 20 % of leukemias in adults [1]. A majority of cases of CML is initiated by the formation of the Philadelphia chromosome (Ph), which results in the production of the BCR-ABL gene, coding for a constitutively active tyrosine kinase. The tyrosine kinase inhibitor imatinib (IM) has significantly improved CML patient outlook. Treatment with IM results in complete hematological remission in most patients [16] and cytogenetic remission in 75 % of patients [4]. Moreover, in many patients, IM induces a major molecular response (MMR), or a 3-log decrease in BCR-ABL ratio [9]. Still, in most cases, even after several years of therapy, a small population of Ph+ cells persists, and cessation of treatment will generally lead to a rapid relapse [4].

Several mathematical models have been developed and applied to CML and its treatment. Modeling approaches include ordinary differential equations (ODEs) [19, 21, 22, 27], delay differential equations (DDEs) [3, 10], branching processes [15, 28], and birth–death processes [13, 14]. These tools have been applied to studying cancer genesis, therapy, combination therapy, and drug resistance. Additionally, in [10, 22], the immune system is incorporated, and in [10], a combination therapy is proposed that combines IM with cancer vaccines, whose dose and timing are adjusted to the profile of the immune response in individual patients.

Roeder et al. [24] develop a stochastic agent-based model (ABM) for the interaction between IM and CML. This model considers the differentiation of cells through three stages: stem cells, proliferating precursor cells, and non-proliferating precursor and mature cells. The stem cells are divided into two compartments: proliferating and non-proliferating stem cells. Individual stem cells circulate continually between the two compartments and are affected by IM only while proliferating.

Applications of the Roeder et al. ABM can be found in several papers. In [7], interferon-α (IFN-α) is considered in combination with IM, in order to stimulate quiescent cancer cells to enter the cell cycle, where they are more likely to be affected by IM. In considering drug schedules, it is shown in [24] that pulsed IFN-α with continuous IM leads to the greatest clinical benefits while still limiting side effects. Using patient-specific data, the Roeder model is used in [8] to predict which patients can be safely taken off IM without relapsing.

Although ABMs are able to capture cell dynamics and interactions, simulations with a large number of agents can be computationally prohibitive. To address this difficulty, Kim et al. reformulate the Roeder model as a system of difference equations [12] and as a system of partial differential equations (PDEs) [11]. A simplified version of the PDE model is later studied in [5]. An alternative approach to obtaining a continuum limit of the ABM is proposed by Roeder et al. in [25]. By using these reduced systems, computation time no longer depends on cell population sizes, and simulations with realistic numbers of cells are made possible.

In this chapter, we propose several modifications to the Roeder model [24], constructing a model that more closely represents hematopoiesis. Specifically, we incorporate asymmetric division of stem cells and precursors, allow precursors to live a variable amount of time before maturing, and introduce feedback inhibition from mature cells to stem cells and precursors. These modifications result in more accurate simulations of cancer genesis and treatment.

The rest of the chapter is organized as follows. In Sect. 2, we provide a brief overview of the Roeder model. The derivation of the corresponding system of difference equations is given in Sect. 3. We present our modifications to the Roeder model in Sect. 4. Parametrization of the model and numerical simulations are discussed in Sect. 5. The final section “Conclusion” concludes with a discussion and insight about how CML therapy can be potentially improved.

2 The Roeder Model

In this section we provide a brief overview of the Roeder model [24]. This model is an ABM that considers hematopoietic cells in three compartments: stem cells (STC), proliferating precursor cells (P), and mature cells (M). Stem cells are either quiescent, denoted by A, or cycling, denoted by Ω. Let A(t) and Ω(t) represent the total number of quiescent and cycling stem cells at time t. Each individual stem cell is characterized by an affinity variable a(t) ∈ [a min , a max ] which determines the probability that the cell will be quiescent or cycling. At each time step, which represents 1 h, a quiescent stem cell will enter the cell cycle with probability ω, and a cycling stem cell will become quiescent with probability α, where

$$\displaystyle\begin{array}{rcl} \omega (\varOmega (t),a(t))& =& \frac{a_{min}} {a(t)} f_{\omega }(\varOmega (t)),{}\end{array}$$
(1)
$$\displaystyle\begin{array}{rcl} \alpha (A(t),a(t))& =& \frac{a(t)} {a_{max}}f_{\alpha }(A(t)).{}\end{array}$$
(2)

Thus, cells with affinity a(t) close to a max tend to remain or become quiescent, while cells with a(t) close to a min tend to remain or become cycling. The functions f ω and f α are defined by

$$\displaystyle\begin{array}{rcl} f_{\omega }(\varOmega (t))& =& \frac{1} {\nu _{1} +\nu _{2}\exp \left(\nu _{3}\frac{\varOmega (t)} {N_{\omega }} \right)} +\nu _{4},{}\end{array}$$
(3)
$$\displaystyle\begin{array}{rcl} f_{\alpha }(A(t))& =& \frac{1} {\mu _{1} +\mu _{2}\exp \left(\mu _{3}\frac{A(t)} {N_{\alpha }} \right)} +\mu _{4}.{}\end{array}$$
(4)

Both functions, f ω and f α , are decreasing sigmoidal functions whose shapes depend on the parameters ν i and μ i . The parameters N ω and N α are scaling factors for Ω(t) and A(t). Given the values of f ω at Ω(t) = 0, N ω ∕2, N ω , and ∞, we can compute the coefficients ν i as follows:

$$\displaystyle\begin{array}{rcl} \nu _{1}& =& (h_{1}h_{3} - h_{2}^{2})/(h_{ 1} + h_{3} - 2h_{2}), {}\\ \nu _{2}& =& h_{1} -\nu _{1}, {}\\ \nu _{3}& =& \log ((h_{3} -\nu _{1})/\nu _{2}), {}\\ \nu _{4}& =& f_{\omega }(\infty ), {}\\ \end{array}$$

where

$$\displaystyle\begin{array}{rcl} h_{1}& =& 1/(f_{\omega }(0) - f_{\omega }(\infty )), {}\\ h_{2}& =& 1/(f_{\omega }(N_{\omega }/2) - f_{\omega }(\infty )), {}\\ h_{3}& =& 1/(f_{\omega }(N_{\omega }) - f_{\omega }(\infty )). {}\\ \end{array}$$

A similar set of formulas can be used to determine the parameters μ i of f α . These functions are constructed so that the cells that are in the less-populated compartment are less likely to move.

Quiescent cells that remain quiescent during a time step increase their affinity by a factor of r, until they reach the maximum affinity a max . Cycling cells that continue to cycle during a time step decrease their affinity by a factor of d, until they reach the minimum affinity a min . In other words, cells that remain in A or Ω become more likely to stay in A or Ω in the future.

Cycling cells are also characterized by a cell cycle counter c(t), which represents their place in the cell cycle. In [24], the cell cycle lasts 49 h, so c(t) ∈ { 0, 1, …, 48}. The first 32 h represent the G1 phase, where cells grow and can transition to quiescence. Cells that reach c(t) = 32 commit to division and must go through the S, G2, and M stages of the cell cycle. After the cell divides (c(t) = 48), each daughter cell reenters G1 (c(t) = 0) and becomes an uncommitted cycling cell that may transition to quiescence. Quiescent cells that enter the cell cycle have their cell cycle counter initialized to c(t) = 32, which means that they commit to at least one division.

Stem cells that reach affinity a(t) = a min differentiate into precursor cells. Precursors (P) live for a fixed amount of time and undergo a fixed number of divisions. They then differentiate into mature cells (M), which do not divide and die after a fixed amount of time. Figure 1 summarizes the Roeder model.

Fig. 1
figure 1

A diagram for the Roeder model. (1) At each time step, quiescent stem cells enter the cell cycle with probability ω, while cycling cells in G1 become quiescent with probability α. Quiescent stem cells that remain quiescent during a time step increase their affinity by a factor of r, up to a maximum value of a max . Cycling stem cells that continue to cycle decrease their affinity by a factor of d. (2) Cycling stem cells progress through G1, S, G2, and M. The cell cycle counter c(t) ∈ { 0, 1, …, 48} indicates the cell’s phase in the cell cycle. Stem cells enter the cell cycle at hour c(t) = 32. At hour c(t) = 48, the cell divides, and its daughter cells reset their cell cycle counters to c(t) = 0. (3) A cycling stem cell whose affinity reaches a min differentiates into a precursor cell, which lives for 20 days and divides once per day. (4) In the last division, precursor cells differentiate into mature cells, which do not divide and die after 8 days

Full size image

Both healthy (Ph−) and cancer (Ph+) cells differentiate through the maturity stages discussed above. Ph− cells and Ph+ cells compete at the stem cell level through the functions f ω and f α , whose inputs are the total number of cycling cells and quiescent cells, respectively. Ph+ cells differ from Ph− cells in their transition functions f ω and f α . It is assumed that Ph+ stem cells are more likely to transition between quiescence and cycling and that the probability of a quiescent Ph+ stem cell transitioning to cycling is only slightly affected by the current number of cycling stem cells. Cancer genesis is characterized by a long latency period of 5–7 years, in which Ph+ and Ph− populations coexist. Without treatment, Ph+ cells are eventually able to out-compete Ph− cells and take over the system.

Treatment with IM is assumed to have two effects on Ph+ stem cells while not directly affecting Ph− cells. First, all cycling Ph+ stem cells are killed at a rate r deg . In addition, all cycling Ph+ stem cells become IM-affected with probability r inh . Once a Ph+ stem cell becomes IM-affected, its transition function f ω is decreased significantly, making it much less likely for quiescent Ph+ stem cells to enter the cell cycle. Note that there is no direct action of IM on quiescent Ph+ stem cells.

The effect of the treatment is evaluated by monitoring levels of BCR-ABL fusion transcript in the blood. These levels are reported relative to an endogenous control transcript, BCR or ABL, in order to normalize the BCR-ABL measurements. This relative value, known as the BCR-ABL ratio, is estimated in [24] by

$$\displaystyle\begin{array}{rcl} \text{BCR-ABL ratio} = \frac{100 \times (\sharp \textrm{of mature Ph}+ \textrm{cells})} {2 \times ({\sharp \textrm{of mature Ph}- \textrm{cells}}) + (\sharp \textrm{of mature Ph}+ \textrm{cells})}.\end{array}$$
(5)

The contributions of stem cells and precursors to this ratio are negligible because these populations are small relative to the mature cells, and the mature cells are the dominant population in the blood. In each healthy Ph− cell, there are two copies of the control gene, while Ph+ cells are assumed to possess one copy of the BCR-ABL fusion gene and one copy of the control gene. Thus, BCR-ABL transcript levels should be proportional to the number of mature Ph+ cells, while the control transcript levels should be proportional to twice the number of mature Ph− cells plus the number of mature Ph+ cells. This quantity is multiplied by 100 so that it represents a percentage.

In simulations, long-term treatment leads to a biphasic decline in BCR-ABL levels, with a rapid first decline followed by a slower second decline. However, small populations of Ph+ cells persist over many years of treatment, and cessation of treatment generally leads to a rapid relapse.

3 Reducing the Agent-Based Model to a System of Difference Equations

Although the Roeder model has the advantage of being able to capture the dynamics of cell–cell interactions, simulations with a realistic number of agents is computationally very expensive. In the simulations in [24], the number of cells is down-scaled to 1∕10 of normal patient values, resulting in approximately 105 stem cells. Even with this reduction in the number of agents, a simulation of 20 years requires approximately 175,000 steps for each of the 105 agents. (Precursors and mature cells can be represented as populations, so the total number of agents is the total number of stem cells.) To address this limitation, the Roeder model is reduced to a system of PDEs in [11, 25] and a system of difference equations in [12]. In this section we follow [12] and provide a brief summary of the system of difference equations. A modified version of this system is what we later use for the numerical simulations of our modified version of the Roeder model.

In order to decrease the number of variables, Kim et al. [12] discretize the affinity state space. In [24], d = 1. 05 and r = 1. 1, so \(\log (d) =\rho = 0.0488 \approx \log (r)/2\). By setting d = e ρ and r = e 2ρ, any cell whose initial affinity is of the form \(a(t) = e^{-k\rho }\) for an integer k will continue to have this form. Since 0. 002 ≤ a(t) ≤ 1, k is restricted to 0 ≤ k ≤ 127. Because of the negative in the exponent, the maximum affinity corresponds to the minimum k value, and the minimum affinity corresponds to the maximum k value. More importantly, though, with these new values of r and d, it is no longer necessary to track individual agents. Rather, for each of the various k values, we can group stem cells into populations whose affinity \(a(t) = e^{-k\rho }\), for each of the finitely many k values.

Define A k (t) and Ω k, c (t) as follows:

$$\displaystyle\begin{array}{rcl} A_{k}(t)& =& \mbox{ Number of cells in $A$ at time $t$ with log $a(t) = -k\rho $},{}\end{array}$$
(6)
$$\displaystyle\begin{array}{rcl} G_{k,c}(t)& =& \mbox{ Number of cells in $\varOmega $ at time $t$ with log $a(t) = -k\rho $ and $c(t) = c$}.\quad \quad {}\end{array}$$
(7)

As mentioned earlier, k ∈ { 0, …, 127}, and c ∈ { 0, …, 48}. Given this discretization, the Roeder model is represented by the following system of difference equations:

$$\displaystyle\begin{array}{rcl} A_{k}(t + 1)& =& \left\{\begin{array}{ll} (A_{0}(t) - B_{0}(t)) + (A_{1}(t) - B_{1}(t)) + (A_{2}(t) - B_{2}(t)),&k = 0, \\ (A_{k+2}(t) - B_{k+2}(t)) +\sum\nolimits_{ c=0}^{31}\varPsi _{k,c}(t), &k = 1\ldots 125, \\ \sum _{c=0}^{31}\varPsi _{k,c}(t), &k = 126,127, \end{array} \right.{}\end{array}$$
(8)
$$\displaystyle\begin{array}{rcl} \varOmega _{k,c}(t + 1)& =& \left\{\begin{array}{ll} B_{0}(t), &k = 0,\,\,c = 32, \\ 2\varOmega _{k-1,48}(t), &k > 0,\,\,c = 0, \\ \varOmega _{k-1,c-1}(t) -\varPsi _{k-1,c-1}(t), &k > 0,\,\,c = 1,\ldots,31, \\ (\varOmega _{k-1,31}(t) -\varPsi _{k-1,31}(t)) + B_{k}(t),&k > 0,\,\,c = 32, \\ \varOmega _{k-1,c-1}(t), &k > 0,\,\,c = 33,\ldots,48, \\ 0, &\text{otherwise}. \end{array} \right.{}\end{array}$$
(9)

The terms B k represent the number of cells that leave A k and enter the cycling compartment Ω k, 32. Ψ k, c is the number of cells that leave Ω k, c and enter the quiescent compartment A k . These terms are defined by

$$\displaystyle\begin{array}{rcl} & & B_{k}(t) \sim \textrm{ Bin}\left(A_{k}(t),\omega (\varOmega (t),e^{-k\rho })\right),{}\end{array}$$
(10)
$$\displaystyle\begin{array}{rcl} & & \varPsi _{k,c}(t) \sim \textrm{ Bin}\left(\varOmega _{k,c}(t),\alpha (A(t),e^{-k\rho })\right),\ c = 0,\ldots,31,{}\end{array}$$
(11)

where Ω(t) = ∑ k, c Ω k, c (t) and A(t) = ∑ k A k (t) are the total number of cycling and quiescent stem cells, and the functions ω and α are defined in Eqs. (1) and (2). In our simulations, we replace these stochastic variables with their expected value and allow populations to be continuous variables.

At each time step, a quiescent cell may remain quiescent or enter the cell cycle. Cells that remain quiescent increase their affinity by a factor of r, which translates to a decrease in k by two. Equation (8) describes the number of quiescent cells in each compartment, at time t + 1. The first line (k = 0) represents the number of cells entering A 0, namely those cells previously in A 0, A 1, or A 2 that remain quiescent. In the second line (k = 1, …, 125), cells previously in A k+2 that remain quiescent enter A k . The summation term is the number of cycling cells in Ω k, c that become quiescent. The sum is over c ∈ { 0, …, 31} because only cells in G1 can become quiescent. Lastly, when k = 126 or k = 127, there are no quiescent cells with k > 127 to feed these compartments. Therefore, the only cells entering these compartment are cycling cells that become quiescent.

On the other hand, cycling cells that continue to cycle decrease their affinity by a factor of d, which translates to an increase in k by one. At each step, the cell cycle counter also increases by one. The cycling cells are described by Eq. (9). The first line (\(k = 0,c = 32\)) represents cells that have maximum affinity who are entering the S phase of the cell cycle. Since there are no cycling cells with greater affinity, the only cells entering this compartment are quiescent cells that have just entered the cell cycle. The second line (k > 0, c = 0) represents cells that have just completed the cell cycle. The constant 2 represents division into two daughter cells, whose cell cycle counters are reset to c(t) = 0. The third line (k > 0, c = 1, …, 31) represents cycling cells in the G1 phase. The right-hand side is the number of cycling cells in the (k − 1)st compartment that continue to cycle. The beginning of the S phase, marked by c(t) = 32, is where transitioning quiescent cells enter the cell cycle. The fourth line (k > 0, c = 32) is similar to the third, with an additional term for the quiescent cells that begin cycling. The fifth line (k > 0, c = 33, …, 48) represents cells in S, G2, and M. Because these cells have committed to division, they all progress to the next step in the cell cycle and increase their k value by one, until division. All other cycling cell compartments are zero at all times.

When a cycling cell’s affinity reaches its minimum, corresponding to k taking its maximum value of 127, the cell differentiates into a precursor cell. The precursor cell divides once per day for 20 days (480 h). Upon the last division, both daughter cells differentiate into mature cells, which live for another 8 days without dividing, and then die. The equations for these compartments are

$$\displaystyle\begin{array}{rcl} P_{j}(t + 1)& =& \left\{\begin{array}{ll} \sum _{c=0}^{48}\varOmega _{127,c}(t) -\sum _{c=0}^{31}\varPsi _{127,c}(t),&j = 0, \\ 2P_{j-1}(t), &j = 24,48,72,\ldots,456, \\ P_{j-1}(t), &\text{otherwise}, \end{array} \right.{}\end{array}$$
(12)
$$\displaystyle\begin{array}{rcl} M_{j}(t + 1)& =& \left\{\begin{array}{ll} 2P_{479}(t),&j = 0, \\ M_{j-1}(t),&\text{otherwise}. \end{array} \right.{}\end{array}$$
(13)

Here, P j (t) is the number of cells that have been precursors for j hours, where j ∈ { 0, …, 479}. M j (t) is the number of cells that have been mature for j hours, where j ∈ { 0, …, 191}. In Eq. (12), the first line on the right-hand side represents cycling stem cells that reach minimum affinity (k = 127), continue to cycle, and become precursors. The second line accounts for the division of precursor cells, which occurs every 24 h. For all other values of j, cells increase their age j by one per time step. In Eq. (13), precursor cells completing their final division become mature, which is the first line. The second line represents the fact that mature cells continue to age without dividing.

As in the Roeder model, cancer genesis is simulated by initializing a single Ph+ stem cell into the Ph− cell steady state. Both populations are described by the system of difference equations (Eqs. 8, 9, 12, 13). The two populations compete at the stem cell level and differ in their transition functions f ω and f α .

In simulating treatment, we divide the Ph+ population into two categories: those that are not affected by IM, which we denote Ph+/R, and those that are, which we denote Ph+/I. These two Ph+ populations differ in their transition function f ω , with the Ph+/I stem cells being much less likely to transition from quiescence to cycling. At the beginning of treatment, all Ph+ cells are not IM-affected. The effects of treatment are assumed to occur at the beginning of every time step. For each k and c, let \(\varOmega _{k,c}^{+/R}(t)\) be the number of cycling Ph+/R cells, and let \(\varOmega _{k,c}^{+/I}(t)\) be the number of Ph+/I cells. Each cell in \(\varOmega _{k,c}^{+/R}\) will become IM-affected with probability r inh . The number of cells in \(\varOmega _{k,c}^{+/R}\) that becomes IM-affected at that time step is given by \(\varOmega _{k,c}^{+/I,new}(t) \sim \textrm{ Bin}(\varOmega _{k,c}^{+/R}(t),r_{inh})\). We set

$$\displaystyle\begin{array}{rcl} \varOmega _{k,c}^{+/R}(t)&:=& \varOmega _{ k,c}^{+/R}(t) -\varOmega _{ k,c}^{+/I,new}(t),{}\end{array}$$
(14)
$$\displaystyle\begin{array}{rcl} \varOmega _{k,c}^{+/I}(t)&:=& \varOmega _{ k,c}^{+/I}(t) +\varOmega _{ k,c}^{+/I,new}(t).{}\end{array}$$
(15)

We additionally assume that all cycling Ph+ cells will apoptose with probability r deg . We therefore remove these cells from the Ph+ populations at the beginning of each time step, by subtracting them from Eqs. (14) and (15). In our simulations, we choose to make the effects of IM deterministic by setting the number of cells that become IM-affected and apoptose to the expected values rather than taking them from their binomial distributions. Once the values of Ω k, c (t) are updated, all three populations (Ph−, Ph+/R, Ph−/I) evolve following Eqs. (8), (9), (12), and (13).

4 Modifications to the Roeder Model

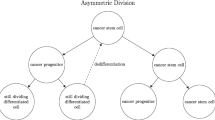
In this section we propose several modifications to the Roeder model [24]. Our model is summarized in Fig. 2. First, we consider three types of stem cell division:

  1. 1.

    Asymmetric division, in which one daughter cell remains a stem cell and the other differentiates into a precursor cell

  2. 2.

    Symmetric differentiation, in which both daughter cells differentiate into precursors

  3. 3.

    Symmetric renewal, in which both daughter cells remain stem cells.

Fig. 2
figure 2

A diagram of the modified Roeder model. (1) Stem cell transitions between quiescence and the cell cycle are unchanged. The affinity variable is updated in the same way as in the original model. (2) Cycling stem cells progress through G1, S, G2, and M. Stem cells enter the cell cycle at hour c(t) = 32. (3) At hour c(t) = 48, the cell divides, and each daughter cell will remain a stem cell with probability a STC (t) and will differentiate into a precursor with probability 1 − a STC (t). Precursor cells symmetrically renew ten times. For all subsequent divisions, up to a total of thirty divisions, the daughter cells will remain precursors with probability a P (t) and will differentiate into mature cells with probability 1 − a P (t). (4) On the last division, both precursor cells differentiate into mature cells. Mature cells provide feedback, marked by dashed lines, that affects the renewal fractions a STC (t) and a P (t) of the stem and precursor cells. After 8 days, mature cells die

Full size image

In the Roeder model, all dividing stem cells symmetrically renew. Differentiation into precursor cells is not tied to a division event, and stem cells whose affinity reaches a min instantaneously transform into precursor cells. Thus, the affinity variable controls both cell cycle transitions and differentiation.

By incorporating these three types of cell division, each with probability a ′, b ′, and c ′, where \(a^{{\prime}} + b^{{\prime}} + c^{{\prime}} = 1\), we provide a mechanism for differentiation that is independent of affinity, while still allowing a cell’s affinity to control transitions between quiescence and cycling. Several other modeling groups have represented differentiation in this way, including [19, 28]. Moreover, in [28], it is suggested that cancer stem cells tend to symmetrically renew, while healthy stem cells tend to divide asymmetrically. By associating differentiation with a cell division, it becomes possible to implement this hypothesis in the model.

Secondly, we allow precursor cells to divide a variable number of times before they differentiate into mature cells. To implement this, we allow precursors to go through the same three types of divisions as stem cells. Precursors can divide between 10 and 30 times before differentiating into mature cells. This range is centered around 20 divisions, which is assumed for all precursor cells in [24]. The lower bound to the number of divisions enforces a minimum number of divisions before maturation, and the upper bound prevents any precursor cells from living forever.

Lastly, it is known that hematopoiesis is a very closely regulated process that is affected by many different signals and cytokines [20]. For instance, granulocyte colony-stimulating factor (G-CSF) is known to play a significant role in granulopoiesis [20, 23]. Motivated by [19], we implement feedback inhibition from mature cells that affects less mature cells (precursors and stem cells). Consider a cytokine S(t) that is produced at a constant rate α, degraded at a constant rate d, and is consumed by mature cells at a rate β. Then

$$\displaystyle{ \frac{dS} {dt} =\alpha -dS -\beta SM, }$$
(16)

where M(t) is the number of mature cells. Since the cytokine dynamics occur on a faster time scale than cell division, we may assume that the cytokine exists at its quasi-steady state, which when scaled to s(t) ∈ [0, 1], is

$$\displaystyle{ s(t) = \frac{1} {1 + kM(t)}, }$$
(17)

where \(s = dS/\alpha\) and \(k =\beta /d\). We define the renewal fraction a of the stem cell population as

$$\displaystyle{ a = \frac{a^{{\prime}}} {2} + c^{{\prime}}. }$$
(18)

This quantity represents the probability that a daughter cell of a stem cell will also be a stem cell. In [19], feedback inhibition affects proliferation rates, renewal fractions, or both, in the less mature compartments. It is found that regulation of self-renewal fractions is essential for the system to be able to recover from events such as chemotherapy that deplete the mature blood cell population. Therefore, we choose to focus on feedback inhibition that affects renewal fractions a STC and a P of stem cells and precursors by defining

$$\displaystyle\begin{array}{rcl} a_{STC}(t)& =& \frac{a_{STC,max}} {1 + kM(t)},{}\end{array}$$
(19)
$$\displaystyle\begin{array}{rcl} a_{P}(t)& =& \frac{a_{P,max}} {1 + kM(t)}.{}\end{array}$$
(20)

Here, a STC, max and a P, max define the maximum renewal fractions of the stem cell and precursors, respectively. As M(t) becomes smaller, the renewal fractions of both stem cells and precursors increases, in order to expand both pools, which ultimately leads to an increase in mature cells.

We incorporate these changes into the system of difference equations defined by Eqs. (8), (9), (12), and (13). These changes do not change the form of Eq. (8). Line 2 in Eq. (9) is replaced by

$$\displaystyle{ \varOmega _{k,c}(t + 1) = 2a_{STC}(t)\varOmega _{k-1,48}(t),\qquad 0 < k < 127,\ c = 0, }$$
(21)

to incorporate asymmetric division of stem cells. Each of the two daughter cells of the dividing stem cell will remain a stem cell with probability a STC (t). Note that instead of choosing the number of daughter stem cells from a binomial distribution, we use the expected value. All other lines in Eq. (9) are unchanged, for 0 ≤ k < 127. However, when k = 127, we must account for the fact that cycling cells with minimum affinity are no longer differentiating into precursors but instead remain stem cells. Thus, when k = 127, we replace Eq. (9) with

$$\displaystyle\begin{array}{rcl} \varOmega _{127,c}(t + 1)& =& \left\{\begin{array}{ll} 2a_{STC}(t)(\varOmega _{126,48}(t) +\varOmega _{127,48}(t)), &c = 0, \\ \sum\nolimits_{k=126}^{127}\varOmega _{k,c-1}(t) -\varPsi _{k,c-1}(t), &c = 1\ldots 31, \\ \sum\nolimits_{k=126}^{127}(\varOmega _{k,31}(t) -\varPsi _{k,31}(t)) + B_{k}(t),&c = 32, \\ \varOmega _{126,c-1}(t) +\varOmega _{127,c-1}(t), &c = 33,\ldots,48. \end{array} \right.{}\end{array}$$
(22)

The precursor cells are described by

$$\displaystyle\begin{array}{rcl} P_{j}(t + 1)& =& \left\{\begin{array}{ll} 2(1 - a_{STC}(t))\sum\nolimits_{k}\varOmega _{k,48}(t),&j = 0, \\ 2P_{j-1}(t), &j = 24,48,72,\ldots,240, \\ 2a_{P}(t)P_{j-1}(t), &j = 264,288,312,\ldots,696, \\ P_{j-1}(t), &\text{otherwise}. \end{array} \right.{}\end{array}$$
(23)

Since the precursors can now live for up to 30 days, j = 0, …, 719. Line 1 in Eq. (23) represents new precursor cells. Stem cells differentiate into precursors during cell divisions, each of which produces two daughter cells. Each daughter cell will become a precursor with probability 1 − a STC (t). All progenitor cells divide every 24 h. The first 10 divisions are symmetric renewals, which is represented by line 2 in Eq. (23). For each subsequent division, up to a total of 30 divisions, daughter cells will remain precursors with probability a P (t). For all other times, precursor cells age by 1 h.

The mature cells are described by

$$\displaystyle\begin{array}{rcl} M_{j}(t + 1)& =& \left\{\begin{array}{ll} 2P_{719}(t) + 2(1 - a_{P}(t))\sum\nolimits_{d=11}^{29}P_{24d-1}(t),&j = 0, \\ M_{j-1}(t), &\text{otherwise}. \end{array} \right.{}\end{array}$$
(24)

The only difference from Eq. (13) is when j = 0. This line represents the source of mature cells. The first term of line 1 of Eq. (24) represents precursors who are completing their 30th division and must undergo symmetric differentiation. The second term represents the contributions of all precursors who are completing their d th division, where d = 11, …, 29. For these divisions, each of the two daughter cells differentiates with probability 1 − a P (t). We use this modified system of difference equations to produce the simulations that are discussed in Sect. 5.

5 Numerical Results

For our simulations, we use the system of difference equations in [12], modified to incorporate the changes discussed in Sect. 4. For all parameters that are present in the original Roeder model, we choose the same values given in [24]. In order to allow the stem cell compartment to grow or shrink, we must set a STC, max  > 0. 5. We choose a STC, max  = 0. 52 and a P, max  = 0. 51. In determining the value of k, we observe that at steady state, the total number of stem cells should be constant. In this model, this occurs when the renewal fraction of the stem cells a STC (t) = 0. 5. Thus, if we want a steady-state solution with M(t) = M ′, then we should choose

$$\displaystyle{ k = \frac{2a_{STC,max} - 1} {M^{{\prime}}}. }$$
(25)

We set M ′ = 6. 8246(10)10 cells, which is the mature healthy cell steady-state value in [12] and apply Eq. (25) to determine k.

Using these parameters, numerical simulations of healthy cells produce a shift in the stem cell population toward their cycling state, when compared to the simulations in [12, 24]. This shift had to be addressed since it is known that the stem cells tend to be quiescent [2]. In order to restore the quiescent stem cell population, we reduce the function f ω by a factor of 10, in comparison to the function used in the original Roeder model. In other words, we reduce the probability that a quiescent stem cell will enter the cell cycle. This modification restores the balance of stem cells, with 91 % in quiescence at steady state. The parameters, including this modification of f ω , are given in Table 1.

Table 1 Parameters for the simulations in Sect. 5
Full size table

In implementing carcinogenesis, as in [24], we introduce a single Ph+ stem cell into the healthy cell population at its steady state. As mentioned previously, in [24], Ph− and Ph+ cells compete at the stem cell level. They differ in their transition functions f ω and f α . We decrease f ω for both populations by a factor of 10, in order to maintain the same relative difference between these functions for the Ph− and Ph+ cells. We additionally assume that Ph− and Ph+ stem cells compete for cytokine, which is consumed by the mature cells of both populations. We choose a smaller value of k for the Ph+ population, which represents cancer’s decreased sensitivity to environmental signals. Specifically, we set k cancer = k healthy ∕2.

Figure 3 shows a simulation of cancer genesis for the parameter values described above. The simulation shows a long latency time during which Ph− (solid) and Ph+ (dashed) cells coexist. The Ph+ population becomes greater than the Ph− population between years 5 and 6. These simulations show similar behavior to the simulations of cancer genesis in [12, 24].

Fig. 3
figure 3

A simulation of cancer genesis. The solid line represents mature Ph− cells, and the dashed line represents mature Ph+ cells

Full size image

A simulation of a treatment is shown in Fig. 4. The initial conditions are taken from the end of the cancer simulation in Fig. 3. The number of quiescent stem cells, number of mature cells, and BCR-ABL ratio are displayed as functions of time. In comparison with results from [12, 24], we observe a much slower decline in the BCR-ABL ratio and the number of cancer cells during treatment. This difference can be understood by considering the Ph+ stem cells. First, recall that quiescent Ph+ stem cells are assumed to be unaffected by IM. These cells are only affected by IM if they enter the cell cycle. Thus, a decrease in the transition rate of stem cells from quiescence to cycling results in quiescent Ph+ stem cells that will remain quiescent for longer periods of time, during which they will remain protected from IM. Figure 4a illustrates this phenomenon, as the number of quiescent Ph+ stem cells decreases by less than one order and remains above 104, after 20 years of treatment. As a result, the number of mature Ph+ cells, shown in Fig. 4b, remains above 107. The BCR-ABL ratio, shown in Fig. 4c, decreases by about 3.5 orders. The simulated patient achieves a MMR, or a 3-log decrease in BCR-ABL ratio, at year 4. However, MMR4 (a 4-log decrease in BCR-ABL ratio) and MMR5 (a 5-log decrease) are not achieved.

Fig. 4
figure 4

A simulation of treatment. (a) Quiescent stem cells. (b) Mature cells. (c) BCR-ABL ratio. In (a, b), Ph− cells are represented by a solid line, Ph+ cells that are not affected by IM are represented by a dashed line, and Ph+ cells that are affected by IM are represented by a dotted line

Full size image

We consider varying the two treatment parameters, r deg and r inh , in order to simulate patients that achieve MMR4 and MMR5. We find that increasing r deg , the rate at which IM kills cycling Ph+ stem cells, results in an increase in the rate at which cancer is cleared, as illustrated in Fig. 5. By increasing r deg , our simulated patient achieves MMR4 (r deg  = 0. 066 h−1) and MMR5 (r deg  = 0. 132 h−1).

Fig. 5
figure 5

BCR-ABL ratio is plotted during treatment, for three different values of r deg : 0.033 h−1 (solid), 0.066 h−1(dashed), and 0.132 h−1 (dotted). As r deg increases, the BCR-ABL ratio declines more rapidly. For all three simulations, r inh  = 0. 05 h−1

Full size image

On the other hand, r inh has a non-monotonic relationship with the rate of cancer clearance. The parameter r inh describes the rate at which cycling Ph+ stem cells become IM-affected, meaning they become less likely to enter the cell cycle. Decreasing the transitions of quiescent Ph+ stem cells to cycling has two contrasting effects. On one hand, Ph+ stem cells are prevented from cycling, limiting the number of mature Ph+ cells. On the other hand, these quiescent Ph+ stem cells cannot be eliminated from the stem cell population, as IM does not kill non-cycling Ph+ stem cells.

For large r inh , the Ph+ population rapidly shifts toward these decreased transition rates. As a result, initially the simulations show a sharper decline in mature Ph+ cells, compared to simulations with smaller r inh values. However, Ph+ stem cells with IM-affected transition rates remain quiescent for longer periods of time and are protected from the degradation effect of IM. Eventually, the number of mature Ph+ cells for r inh large becomes greater than the number of mature Ph+ cells for r inh smaller. Figure 6b shows the effects of treatment on mature Ph+ cells over time, for different values of r inh .

Fig. 6
figure 6

Number of quiescent Ph+ stem cells and BCR-ABL ratio during treatment, for three different values of r inh : 0 h−1 (solid), 0.05 h−1 (dashed), 0.1 h−1 (dotted). (a) Quiescent Ph+ stem cells. (b) BCR-ABL ratio. Initially, a higher value of r inh leads to faster cancer clearance, but later the lower values of r inh become more favorable. For all three simulations, r deg  = 0. 033 h−1

Full size image

Figure 6a shows the number of quiescent Ph+ stem cells over time for different values of r inh . Here, the relationship is more straightforward. As r inh increases, Ph+ stem cells become IM-affected more rapidly, and as a result, the number of quiescent Ph+ stem cells increases.

Conclusion

In this chapter we modify the Roeder model [24] by adding more biological detail. Specifically, we incorporate asymmetric division of stem cells and precursors, allow precursors to live for a variable amount of time before maturing, and add feedback inhibition from mature cells that affects stem cells and precursors. A more accurate representation of hematopoiesis can lead to more realistic simulations of CML genesis and treatment.

Parametrization of our model suggests that healthy stem cells transition between the quiescent and proliferating compartments at rates that are lower than the rates obtained in the original Roeder model. In the Roeder model, at healthy steady state, approximately 1 quiescent stem cell enters the cell cycle per 1,000 quiescent stem cells per time step. Thus, quiescent cells enter the cell cycle, on average, once per 1.4 months. In contrast, in our simulations, 1 quiescent stem cell enters the cell cycle per 10,000 cells, which translates to quiescent cells entering the cell cycle, on average, once every 14 months. This lower rate of entry into the cell cycle by stem cells is supported by [17, 26].

Lower stem cell transition rates have a significant effect on the results of IM therapy. In our model, we assume that IM only affects cycling Ph+ cells. By decreasing the transition rates of Ph+ stem cells, quiescent Ph+ stem cells can never mind evade the effects of IM during treatment. During 20 years of simulated treatment, we see an initial phase of a few months when IM kills most cycling Ph+ stem cells. Once the cycling Ph+ population is depleted, the majority of the remaining Ph+ stem cell population is quiescent and is therefore protected from IM. What follows is a very slow decline in the number of quiescent Ph+ cells over time, since only a few of these cells enter the cell cycle every hour. Our treatment simulations indicate a much larger residual cancer population than those in [24]. These results suggest that IM alone, acting through the implemented mechanisms, can never fully eradicate the cancer population.

The Stop Imatinib trial [18] sought to determine whether patients who responded well to IM therapy could be safely taken off treatment without relapsing. They found that while 61 % of patients relapsed, 39 % remained in remission for the duration of the 2-year study. It is possible that some of the patients in sustained remission had no Ph+ cells remaining when they stopped IM. If this is the case, it may imply that there is an additional action of IM that is not included in the model. Alternatively, patients that remain in sustained remission after stopping IM may still harbor small populations of Ph+ cells. Remaining in remission after stopping IM would then require some other mechanism (e.g., the immune response) to control the Ph+ population and prevent it from expanding.

Still, the fact that many patients do relapse after being taken off IM motivates studying methods by which IM therapy can be improved. Our results suggest that IM therapy may greatly benefit from quiescent Ph+ stem cell activation. IFN-α has been shown to activate quiescent stem cells [6] and is therefore a strong candidate for combination therapy. A detailed analysis of immunotherapy in this context is left for a future study.