Keywords

5.1 Introduction

Panel data are useful because of the opportunity they afford the researcher to control for unobserved heterogeneity or effects that do not vary over time. Typically, exploiting this opportunity means employing the fixed-effects (FE) estimator, because it produces consistent estimates of the coefficients of time-varying variables under weak assumptions about their relationship with the effects. As is well-understood, the FE estimator achieves this through a data transformation that eliminates the effects. The downside to FE estimation, however, is that this data transformation also eliminates any time-invariant variables. Consequently, the FE estimator is sometimes abandoned entirely for a random-effects (RE) approach, whose requirements for consistency frequently are not satisfied, since unobserved heterogeneity is often correlated with the regressors.

While the partial effects of time-invariant variables can be recovered in a second-step regression, this fact is generally omitted in most textbook treatments of panel-data methods (Wooldridge 2010 is an exception). The practical necessity of recovering the partial effects of time-invariant variables shows up in many different empirical contexts. In the familiar exercise of estimating wage regressions, human-capital variables such as experience and tenure are taken to be correlated with the unobserved effect, which is commonly interpreted as “ability”. While FE estimation eliminates such time-invariant unobservables, it also eliminates race, gender and education (when schooling is completed before the sample period), the effects of which are of great interest. Similarly, when estimating production relationships, inputs may be correlated with fixed “environmental” factors, which again would swept away by the FE estimator. However, policy-relevant firm characteristics, such as public or private ownership in the case of electric utilities, would be swept away as well.

Interest in recovering the partial effects of time-invariant variables may be even more common in panels of state and country-level aggregates, as with empirical growth and comparative political-economy studies, where policy-relevant fixed institutional variables are differenced out of a FE regression. The recovery of these partial effects motivated the work of Plümper and Troeger (2007), who proposed a three-step method for estimating the effects of time-invariant variables in linear panel-data models. Plümper’s and Troeger’s so-called “fixed-effects vector decomposition” (FEVD) became widely utilized through their Stata program (xtfevd) that computes the estimator and corresponding standard errors. However, as shown in the critiques of Breusch et al. (2011) and Greene (2011), the main substantive claims about the FEVD estimator are false. Importantly, from our perspective, the standard errors produced by the FEVD estimator are incorrect, because their method does not estimate the correct asymptotic covariance matrix, which should incorporate the first-step estimated covariance matrix.

In this paper, we focus on the two-step estimation procedure and compare conventional inference based on the asymptotic formula to bootstrap alternatives. Bootstrapping has a natural appeal, because of the complications associated with estimating the asymptotic covariance matrix and the inherent finite-sample bias of the resulting standard errors. Our paper contributes to the panel data and bootstrapping literature in four ways. First, we derive the correct asymptotic covariance matrix for the second-step coefficient estimators, allowing for heteroskedasticity and autocorrelation of unknown form. Second, we develop the steps required to perform bootstrap estimation of the covariance matrix of the second-step estimated coefficients. Third, we prove that the pairs and wild bootstrap coefficient estimators are unbiased. This stands in contrast to Flachaire (2005) who asserts that the pairs is a biased estimator. Unbiasedness implies that the error in rejection probability (ERP) of corresponding t-tests, measured as the difference between their actual and nominal size, should be small.

Finally, using Monte Carlo methods, we compare the size and power of the naive asymptotic estimator, which ignores the first-step estimation error, the correct asymptotic covariance matrix estimator, which does not, and the bootstrap alternatives. We consider a variety of panel sizes (N) and lengths (T) relevant to the common large-N, small-T setting. We find that the bootstrap methods consistently provide more accurate inference than the asymptotic formulae. The performance gain is largest for N less than 250 and shrinks as N grows. Although a small ERP remains for the correct asymptotic covariance matrix estimator when N = 1, 000, as N grows to 250 and beyond, both bootstrap estimators generally produce the correct size. Comparing the two bootstrap methods, the pairs tends to moderately over-reject and the wild to moderately under-reject for smaller values of N, with the pairs having a slightly smaller ERP. While we find a slight advantage of the pairs method over the others in terms of power with N = 250 and T = 5, few differences are observed with larger values of N.

The remainder of this paper is organized as follows. Section 5.2 introduces the model and two-step estimator. Section 5.3 presents the correct asymptotic covariance matrix for the second-step estimator and outlines the bootstrap alternatives for second-step standard-error estimation. In Sect. 5.4, we review previous studies of the wild and pairs procedures and prove that they are both unbiased for the problems we address. Section 5.5 explains our Monte Carlo experiments and reports our findings on the size and power of t-tests produced by conventional and bootstrap procedures. Conclusions follow in Sect. 5.6.

5.2 The Two-Step Model and Parameter Estimation

We consider estimation of linear panel-data models of the form

$$\displaystyle{ y_{it} = \mathbf{x}_{it}\beta + \mathbf{z}_{i}\gamma +\xi _{it}\quad i = 1,\ldots,N;t = 1,\ldots,T, }$$
(5.1)

where \(\xi _{it} = c_{i} + e_{it}\), y it is the dependent variable, x it is a (1 × K) vector of time-varying regressors, z i is a (1 × G) vector of time-invariant regressors, c i is an unobserved effect that is fixed for the cross-section unit, and e it is an error term.Footnote 1 The e it may be heteroscedastic and serially correlated. The coefficient vectors, β and γ, are (K × 1) and (G × 1), respectively. For most of the discussion that follows we work with the form of the model that combines all T observations for each cross-section unit:

$$\displaystyle{ \mathbf{y}_{i} = \mathbf{X}_{i}\beta + (\mathbf{j}_{T} \otimes \mathbf{z}_{i})\gamma + +\mathbf{j}_{T}c_{i} + \mathbf{e}_{i}, }$$
(5.2)

where X i is (T × K), j T is a T-vector of ones, and y i and e i are (T × 1) vectors.

Our interest is in estimating γ, allowing for the possibility that some or all of the variables in X i are correlated with the unobserved effect. Formally, we adopt the standard FE assumption that

$$\displaystyle{ E(e_{it}\,\vert \,\mathbf{X}_{i},\mathbf{z}_{i},c_{i}) = 0,\quad t = 1,\ldots,T. }$$
(5.3)

Additionally, we assume

$$\displaystyle{ E(c_{i}\,\vert \,\mathbf{z}_{i}) = 0, }$$
(5.4)

which treats the time-invariant variables as uncorrelated with the unobserved effects. We invoke (5.4) to focus attention on the transmission of the first-step estimation error to the second step, without the confounding influence of endogeneity in z i . While this is a strong assumption, it is reasonable in some of the empirical contexts referenced above. For example, in the production relationships category, Agee et al. (2009, 2012) use directional distance functions to estimate the efficiency of a household’s production of health and human capital in children. In both cases, all time-invariant child and household characteristics are treated as exogenous on the grounds that the characteristics are either fixed by nature (e.g., race and gender) or by circumstances of the household or the parents. County, state, and country-level panels provide other examples, many of which come from social science papers outside of economics (as described in Plümper and Troeger (2007)). A common practice has been either to include time-invariant variables in a pooled ordinary least-squares (POLS) or RE regression, or use FE estimation and ignore them. Knack (1993), which is concerned with the relationship between the prospect of jury service and voter registration, does both. Over Knack’s two-year panel, certain state characteristics, like whether there is a senate contest, are time-invariant. Because the timing of senate contests are fixed by law, this indicator is exogenous. Knack estimates OLS regressions on each year separately, including the fixed characteristics, and FE regressions using both years of the panel, dropping these characteristics.Footnote 2

In the two-step approach to estimating γ, we begin by applying FE to (5.1), which produces

$$\displaystyle{ \hat{\beta }_{FE} ={\biggl (\sum _{i}\mathbf{X}_{i}^{\prime}\mathbf{Q}_{T}\mathbf{X}{_{i}\biggr )}}^{-1}\sum _{ i}\mathbf{X}_{i}^{\prime}\mathbf{Q}_{T}\mathbf{y}_{i}, }$$
(5.5)

where \(\mathbf{Q}_{T} = \mathbf{I}_{T} -\mathbf{j}_{T}{(\mathbf{j}_{T}^{\prime}\mathbf{j}_{T})}^{-1}\mathbf{j}_{T}^{\prime}\) is the idempotent projection that time de-means the data. The FE estimator is unbiased and consistent under (5.3).

Next, we take \(\hat{\beta }_{FE}\) and compute individual or group-level residuals,

$$\displaystyle{ \hat{\delta _{i}} =\bar{ y}_{i} -\bar{\mathbf{x}}_{i}\hat{\beta }_{FE}, }$$
(5.6)

and formulate the second-step regression model

$$\displaystyle{ \hat{\delta _{i}} = \mathbf{z}_{i}\gamma + u_{i}, }$$
(5.7)

where

$$\displaystyle{ u_{i} =\bar{\xi } _{i} -\bar{\mathbf{x}}_{i}(\hat{\beta }_{FE}-\beta ), }$$
(5.8)

\(\bar{\xi }_{i} = c_{i} +\bar{ e}_{i}\), the over-bar indicates the sample-period mean for unit i (e.g., \(\bar{\mathbf{x}}_{i} = \frac{1} {T}\sum _{t}\mathbf{x}_{it}\)), and the first element of z i is 1. Equation (5.8) is obtained by combining (5.7), (5.6), and the sample-period mean for unit i of (5.2). We then estimate γ by applying OLS to (5.7).Footnote 3 The resulting estimator, which we label \(\hat{\gamma }_{FE}\) because it is derived from \(\hat{\beta }_{FE}\), can be written as

$$\displaystyle{ \hat{\gamma }_{FE} ={\biggl (\sum _{i}\mathbf{z}_{i}^{\prime}\mathbf{z}{_{i}\biggr )}}^{-1}{\biggl (\sum _{ i}\mathbf{z}_{i}^{\prime}\hat{\delta _{i}}\biggr )}. }$$
(5.9)

5.3 Second-Step Standard-Error Estimation

In this section, we first derive the asymptotic covariance matrix of \(\hat{\gamma }_{FE}\) and explain how to estimate it consistently. Then we outline the procedures for computing the wild and pairs bootstrap alternatives.

5.3.1 Asymptotic Covariance Matrix

As Wooldridge (2010) points out, the asymptotic covariance matrix for \(\hat{\gamma }_{FE}\) can be obtained by applying standard arguments for two-step estimators (see, for example, Murphy and Topel 1985). We begin by writing the sampling error of \(\hat{\gamma }_{FE}\) as

$$\displaystyle{ \hat{\gamma }_{FE} -\gamma ={\biggl (\sum _{i}\mathbf{z}_{i}^{\prime}\mathbf{z}{_{i}\biggr )}}^{-1}{\biggl (\sum _{ i}\mathbf{z}_{i}^{\prime}u_{i}\biggr )}. }$$
(5.10)

Then we can show that \(\sqrt{N}(\hat{\gamma }_{FE} -\gamma )\) is asymptotically normal with a limiting covariance matrix that can be expressed as

$$\displaystyle{ {(\mathbf{B}_{zz})}^{-1}\,\mathbf{A}\,{(\mathbf{B}_{ zz})}^{-1}, }$$
(5.11)

where, \(\mathbf{B}_{zz} =\mathrm{ plim} \frac{1} {N}\sum _{i}\mathbf{z}_{i}^{\prime}\mathbf{z}_{i}\). As implied by (5.8)

$$\displaystyle{ \mathbf{A} =\mathrm{ plim} \frac{1} {N}\sum _{i}\bar{\xi }_{i}^{2}\mathbf{z}_{ i}^{\prime}\mathbf{z}_{i} +\mathrm{ plim} \frac{1} {N}\sum _{i}\mathbf{z}_{i}^{\prime}\bar{\mathbf{x}}_{i}\,\mathbf{V}_{\hat{\beta }_{FE}}\,\bar{\mathbf{x}}_{i}^{\prime}\mathbf{z}_{i}, }$$
(5.12)

where \(\mathbf{V}_{\hat{\beta }_{FE}}\) is the limiting covariance matrix of \(\sqrt{N}(\hat{\beta }_{FE}-\beta )\).

A consistent estimator of the asymptotic covariance matrix of \(\hat{\gamma }_{FE}\) hinges on the consistent estimation of A. The latter is accomplished by utilizing the robust covariance matrix estimator of \(\mathbf{V}_{\hat{\beta }_{ FE}}\),

$$\displaystyle{ \hat{\mathbf{V}}_{\hat{\beta }_{FE}} ={\biggl (\sum _{i}\mathbf{X}_{i}^{\prime}\mathbf{Q}_{T}\mathbf{X}{_{i}\biggr )}}^{-1}\sum _{ i}\mathbf{X}_{i}^{\prime}\mathbf{Q}_{T}\hat{\mathbf{e}}_{i}\hat{\mathbf{e}}_{i}^{\prime}\mathbf{Q}_{T}\mathbf{X}_{i}{\biggl (\sum _{i}\mathbf{X}_{i}^{\prime}\mathbf{Q}_{T}\mathbf{X}{_{i}\biggr )}}^{-1} }$$
(5.13)

(see Arellano 1987), and extracting an estimator of ξ i from the group-level version of (5.1) evaluated at \((\hat{\beta }_{FE},\hat{\gamma }_{FE})\).

5.3.2 Bootstrap Methods

There are two important reasons to prefer bootstrap estimators of standard errors to estimators based on asymptotic formulae. First, bootstrapping standard errors is often easier than estimating the asymptotic covariance matrix. Second, bootstrapping often produces better small-sample performance in terms of ERP.

We consider the wild and pairs bootstrap procedures because they produce estimated standard errors that are robust to heteroskedasticity. Davidson and Flachaire (2008) have shown that the wild bootstrap yields a heteroskedasticity-consistent covariance matrix estimator when the residuals are divided by h i , the diagonal element of the projection matrix corresponding to the right-hand-side variables of the original equation estimated. T. Lancaster (2003, A note on bootstraps and robustness, unpublished manuscript. Department of Economics, Brown University) has proven that the pairs bootstrap yields a similar covariance estimator. Below we outline how each can be adapted to our two-step estimation problem.

Following Cameron and Trivedi (2005), for fixed-T panels, consistent (as N → ∞) standard errors can be obtained by using cross-sectional resampling. Hence, we employ this method for both the pairs and wild bootstrap, assuming no cross-sectional or temporal dependence.Footnote 4

5.3.2.1 Wild Bootstrap Estimator

The wild bootstrap procedure can the applied to the estimation of the standard errors of \(\hat{\gamma }_{FE}\) by executing the following steps.

  1. 1.

    Compute \(\hat{\beta }_{FE}\) in (5.5).

  2. 2.

    Using \(\hat{\beta }_{FE}\), compute \(\hat{\delta }_{i}\) in (5.6).

  3. 3.

    Compute \(\hat{\gamma }_{FE}\) in (5.9).

  4. 4.

    Since \(\xi _{it} = c_{i} + e_{it}\) in (5.1), compute

    $$\displaystyle{ \hat{\xi }_{it} = y_{it} -\mathbf{x}_{it}\hat{\beta }_{FE} -\mathbf{z}_{i}\hat{\gamma }_{FE}, }$$
    (5.14)

    Then define \(f(\hat{\xi }_{it})\) as:

    $$\displaystyle{f(\hat{\xi }_{it}) = \frac{\hat{\xi }_{it}} {{(1 - h_{it})}^{1/2}},}$$

    where h it is the diagonal element of the projection matrix corresponding to the right-hand-side variables of (5.2). Thus, the transformed residual is homoskedastic by definition so long as the error term, ξ it , is homoskedastic.Footnote 5

  5. 5.

    We follow Davidson and Flachaire (2008) and MacKinnon (2002) and define ε i as the two-point Rademacher distribution:

    $$\displaystyle{ \epsilon _{i} = \left \{\begin{array}{rl} - 1&\mathrm{with\ probability}\ \frac{1} {2} \\ 1&\mathrm{with\ probability}\ \frac{1} {2}\end{array} \right.. }$$
    (5.15)

    This assigns the same value to all T observations for each i. Then, we generate

    $$\displaystyle{ y_{it}^{w} = \mathbf{x}_{ it}\hat{\beta }_{FE} + \mathbf{z}_{i}\hat{\gamma }_{FE} +\xi _{ it}^{w}, }$$
    (5.16)

    where

    $$\displaystyle{ \xi _{it}^{w} = f(\hat{\xi }_{ it})\epsilon _{i}. }$$
    (5.17)

    Davidson and Flachaire (2008) provide evidence that this version of the wild bootstrap is superior to other wild methods. This is due to the fact that \(E(\epsilon _{i}) = 0,E(\epsilon _{i}^{2}) = 1,E(\epsilon _{i}^{3}) = 0,\) and \(E(\epsilon _{i}^{4}) = 1\). Since \(\hat{\xi }_{it}\) and ε i are independent, \(E(\xi _{it}^{w}) = E(\hat{\xi }_{it})\epsilon _{i}\vartheta = 0\), its variance is that of \(\hat{\xi }_{it}\vartheta\), its third moment is zero (which implies zero skewness in \(\hat{\xi }_{it}\)), but its fourth moment is again that of \(\hat{\xi }_{it}\vartheta\). Thus, the first, second, and fourth moments of \(\hat{\xi }_{it}\vartheta\) are reproduced exactly in the wild bootstrap data using (5.15).

  6. 6.

    Compute the FE estimator of \(\hat{\beta }\) using the wild bootstrap data:

    $$\displaystyle{ \hat{\beta }_{FE}^{w} ={\biggl (\sum _{ i}\mathbf{X}_{i}^{\prime}\mathbf{Q}_{T}\mathbf{X}{_{i}\biggr )}}^{-1}\sum _{ i}\mathbf{X}_{i}^{\prime}\mathbf{Q}_{T}\mathbf{y}_{i}^{w}. }$$
    (5.18)
  7. 7.

    Compute the group-mean residuals as

    $$\displaystyle{ \delta _{i}^{w} =\bar{ y}_{ i}^{w} -\bar{\mathbf{x}}_{ i}\hat{\beta }_{FE}^{w}. }$$
    (5.19)

    Note that in step (5) it was necessary to generate \(y_{it}^{w}\) rather than time-demeaned y it , because in the current step one must compute group means to generate the residuals. Group means cannot be recovered from the time-demeaned data.

  8. 8.

    Formulate the true bootstrap model

    $$\displaystyle{ \delta _{i}^{w} = \mathbf{z}_{ i}\hat{\gamma }_{FE} + u_{i}^{w}, }$$
    (5.20)

    where \(u_{i}^{w}\) is a bootstrap error, and compute the second-step estimator of \(\hat{\gamma }_{FE}\) using the bootstrap data:

    $$\displaystyle{ \hat{\gamma }_{FE}^{w} ={\biggl (\sum _{ i}\mathbf{z}_{i}^{\prime}\mathbf{z}{_{i}\biggr )}}^{-1}\sum _{ i}\mathbf{z}_{i}^{\prime}\delta _{i}^{w}. }$$
    (5.21)
  9. 9.

    Iterate steps 5–8 and compute the sample standard deviation of \(\hat{\gamma }_{FE}^{w}\), \(s_{\hat{\gamma },w}\), as an estimator of the standard error of \(\hat{\gamma }_{FE}\), where w denotes the wild procedure.

5.3.2.2 Pairs Bootstrap Estimator

The pairs bootstrap procedure discussed in T. Lancaster (2003, A note on bootstraps and robustness, unpublished manuscript. Department of Economics, Brown University) can be extended to our problem as follows:

  1. 1.

    Compute \(\hat{\beta }_{FE}\) in (5.5).

  2. 2.

    Using \(\hat{\beta }_{FE}\), compute \(\hat{\delta }_{i}\) in (5.6).

  3. 3.

    Compute \(\hat{\gamma }_{FE}\) in (5.9).

  4. 4.

    Draw randomly with replacement among i = 1, …, N blocks, using all T observations in the chosen block, with probability 1∕T from \(\{y_{it},\mathbf{x}_{it},\mathbf{z}_{it}\}\) to obtain \(\{y_{it}^{p},\mathbf{x}_{it}^{p},\mathbf{z}_{it}^{p}\}\), where the superscript denotes the pairs estimator. Resampling all variables in this manner preserves the correlation of the corresponding time-invariant and group-mean variables in the second-step regression with the first-step variables.

  5. 5.

    For the pairs bootstrap, define \(\boldsymbol{\xi }_{i}^{p}\) as a (T × 1) vector made up of \(\{\xi _{i1}^{p},\ldots,\xi _{iT}^{p}\}\) for observation i. Write the first-step regression model with unknown error term, \(\boldsymbol{\xi }_{i}^{p}\), as

    $$\displaystyle{ \mathbf{y}_{i}^{p} = \mathbf{X}_{ i}^{p}\hat{\beta }_{ FE} + (\mathbf{j}_{T} \otimes \mathbf{z}_{i}^{p})\hat{\gamma }_{ FE} +\boldsymbol{\xi }_{ i}^{p}. }$$
    (5.22)

    Compute the FE estimator of \(\hat{\beta }\) using the pairs bootstrap data \((\mathbf{y}_{i}^{p},\mathbf{X}_{i}^{p})\)

    $$\displaystyle{ \hat{\beta }_{FE}^{p} ={\biggl (\sum _{ i}\mathbf{X}_{i}^{p^{\prime}}\mathbf{Q}_{ T}\mathbf{X}_{i}^{{p}\biggr )}}^{-1}\sum _{ i}\mathbf{X}_{i}^{p^{\prime}}\mathbf{Q}_{ T}\mathbf{y}_{i}^{p}. }$$
    (5.23)
  6. 6.

    Using \(\hat{\beta }_{FE}^{p}\) compute the residuals

    $$\displaystyle{ \delta _{i}^{p} =\bar{ y}_{ i}^{p} -\bar{\mathbf{x}}_{ i}^{p}\hat{\beta }_{ FE}^{p}. }$$
    (5.24)
  7. 7.

    Formulate the second-step pairs bootstrap model as

    $$\displaystyle{ \delta _{i}^{p} = \mathbf{z}_{ i}^{p}\hat{\gamma }_{ FE} + u_{i}^{p}, }$$
    (5.25)

    where \(u_{i}^{p}\) is the pairs second-step error, then compute the second-step estimator of \(\hat{\gamma }_{FE}\) using the bootstrap data:

    $$\displaystyle{ \hat{\gamma }_{FE}^{p} ={\biggl (\sum _{ i}\mathbf{z}_{i}^{p^{\prime}}\mathbf{z}_{ i}^{{p}\biggr )}}^{-1}\sum _{ i}\mathbf{z}_{i}^{p^{\prime}}\delta _{ i}^{p}. }$$
    (5.26)
  8. 8.

    Iterate steps 4–7 and compute the sample standard deviation of \(\hat{\gamma }_{FE}^{p},s_{\hat{\gamma },p}\), as an estimator of the standard error of \(\hat{\gamma }_{FE}\).

5.4 The Size and Power of Bootstrap Estimators

5.4.1 Previous Studies of the Size and Power of Bootstrap Estimators

We are unaware of any Monte Carlo study that examines the ERP and size of estimator t-values for two-step panel-data models of the type we consider. However, there is a substantial literature on bootstrap performance in cross-section regressions. Horowitz (2001) compares the actual size of the pairs and wild bootstrap to the size associated with the asymptotic formula for White’s information matrix test, the t-test in a heteroskedastic regression model, and the t-test in a Box-Cox regression model. For relatively small sample sizes, he finds that the wild and pairs dramatically reduce the ERP of the asymptotic formulas, and in many cases the wild essentially eliminates this error. The wild method outperforms the pairs and both outperform the jackknife method. Davidson and Flachaire (2008) obtain similar results when they compare the wild and pairs estimators to those obtained using the asymptotic formula. Using an Edgeworth expansion, they trace the wild’s advantage to the fact that the ERPs of the pairs depend on more higher-order raw moments of the original errors and the bootstrap residuals, which are greater under heteroskedasticity. With homoskedastic errors, there is little difference between the wild and pairs estimators and their ERP is very small. The results we present below are consistent with this finding. Inference based on the asymptotic formula also improves, but exhibits a substantially larger ERP.

In summary, for single-equation models with heteroskedastic errors, Monte Carlo results generally show that the wild bootstrap outperforms the pairs and that both improve on inference based on the estimator of the asymptotic formula. However, we are not aware of bootstrap performance comparisons that address the empirical context of a two-step panel data model, where estimation error from the first step is the primary complicating factor. Next, we analytically examine the wild and pairs procedures for the two-step estimation problem, identifying the conditions required for both to be unbiased.

5.4.2 The Unbiasedness of Our Two-Step Bootstrap Estimators

The unbiasedness of the first and second-step wild estimators follows directly from the fact that the ε i are zero-mean random variables generated independently of ξ it . See Theorems 1 and 2 in the Appendix. Flachaire (2005) compares the conditional expectation of the bootstrap error given the explanatory variables for the wild versus pairs methods in a simple linear model. In terms of our setup, he asserts that the wild bootstrap satisfies \(E(u_{i}^{w}\vert \mathbf{z}_{i}) = 0\), and hence is unbiased.

He also asserts that the pairs does not satisfy \(E(u_{i}^{p}\vert \mathbf{z}_{i}^{p})\neq 0\), and therefore is biased (because \(u_{i}^{p}\) depends on \(\mathbf{z}_{i}^{p}\)). Thus, he argues that the wild should produce a smaller ERP than the pairs estimator. In the Appendix, however, we prove that both estimators are unbiased given the exogeneity conditions (5.3) and (5.4).

To show that the pairs estimator is unbiased, we need to reformulate it in terms of the residual of the original model. Since by definition \(\mathbf{y}_{i}\) equals the fitted model plus the residual for observation i,

$$\displaystyle{ \sqrt{v_{i}}\mathbf{y}_{i} = \sqrt{v_{i}}\mathbf{X}_{i}\hat{\beta }_{FE} + \sqrt{v_{i}}(\mathbf{j}_{T} \otimes \mathbf{z}_{i})\hat{\gamma }_{FE} + \sqrt{v_{i}}\boldsymbol{\hat{\xi }}_{i}, }$$
(5.27)

where v i specifies number of times (from 0 to N) that each (\(\mathbf{y}_{i},\mathbf{X}_{i})\) pair for observation i is reused in the pairs bootstrap sample. Using \((\sqrt{v_{i}}\mathbf{y}_{i},\sqrt{v_{i}}\mathbf{X}_{i})\) we obtain an alternative formulation of the pairs first-step estimator as

$$\displaystyle{ \hat{\beta }_{FE}^{p} ={\biggl (\sum _{ i}v_{i}\mathbf{X}_{i}^{\prime}\mathbf{Q}_{T}\mathbf{X}{_{i}\biggr )}}^{-1}\sum _{ i}v_{i}\mathbf{X}_{i}^{\prime}\mathbf{Q}_{T}\mathbf{y}_{i}. }$$
(5.28)

Hence, (5.28) becomes a weighted regression version of (5.23), where \(\mathbf{y}_{i}^{p}\) is replaced by \(\sqrt{v_{i}}\mathbf{y}_{i}\), \(\mathbf{X}_{i}^{p}\) is replaced by \(\sqrt{v_{i}}\mathbf{X}_{i}\), and \((\mathbf{j}_{T} \otimes \mathbf{z}_{i}^{p})\) is replaced by \(\sqrt{v_{ i}}(\mathbf{j}_{T} \otimes \mathbf{z}_{i})\). Again by definition, reformulate (5.25) as

$$\displaystyle{ \sqrt{v_{i}}\delta _{i} = \sqrt{v_{i}}\mathbf{z}_{i}\hat{\gamma }_{FE} + \sqrt{v_{i}}\hat{u}_{i}. }$$
(5.29)

where \(\hat{u}_{i}\) is the residual computed from (5.7) and obtain a more useful formulation of the second-step pairs estimator as

$$\displaystyle{ \hat{\gamma }_{FE}^{p} ={\biggl (\sum _{ i}v_{i}\mathbf{z}_{i}^{\prime}\mathbf{z}{_{i}\biggr )}}^{-1}\sum _{ i}v_{i}\mathbf{z}_{i}^{\prime}\delta _{i}. }$$
(5.30)

Theorem 3 says that the pairs estimator is unbiased in the first step if \(E(\mathbf{Q}_{T}\boldsymbol{\hat{\xi }}_{i}\vert v_{i},\mathbf{X}_{i}) = 0\). This result also applies to any linear, single-equation model estimated by the pairs estimator. Finally, using (5.30), and assuming that (5.3), (5.4), and Theorem 3 hold, Theorem 4 shows that in the second step, the pairs estimator is unbiased for \(\hat{\gamma }_{FE}\).

Davidson and MacKinnon (1999) demonstrate that the ERP depends on estimator bias. Thus, a biased bootstrap estimator should have a larger ERP than an unbiased estimator assuming that the errors, ξ i , are i.i.d.Footnote 6 The size of t-values for both the second-step wild and pairs estimators should be highly accurate since their biases are zero, given that the assumptions in (5.3) and (5.4) hold.

5.5 Monte Carlo Estimation

5.5.1 Data Generation

We create the data for the Monte Carlo experiments in the following steps.

  1. 1.

    Generate the x itk and z itg (\(k = 1,\ldots,10;\;g = 1,\ldots,3\)) as multivariate normal with zero means and unit variances. We set \(cov(z_{g},z_{g^{\prime}}) = 0.2,\,\,g\neq g^{\prime}\) (implying simple correlations of 0.2), \(cov(x_{k},x_{k^{\prime}}) = 0.3,\,\,k\neq k^{\prime}\). We also set \(cov(x_{k},z_{g}) = 0.3\) and draw x itk and z itg . For each g, we then create the group mean of z itg and use this for z ig (which is time invariant) so that the group means of x k and z g have correlation of 0.3.

  2. 2.

    Generate c i and e it as i.i.d. normal random variables with mean zero and variance of 10 and 100, respectively. The large variance for e it guarantees a relatively low R 2 for the first-step regression. This in turn implies a greater difference between the estimated “naive” and correct asymptotic covariance matrices for the second-step coefficients.

  3. 3.

    Using the data from steps 1–2, generate y it in Eq. (5.1).

The bootstrap estimators do not require the i.i.d. assumption. As described in Sect. 5.3.2, they have heteroskedastic-consistent covariance matrices. Using cross-sectional resampling as defined above, these bootstrap methods will deal with dependent data by generating correlated errors that exhibit approximately the same pattern of autocorrelation as ξ it . However, in this paper we focus on the i.i.d. case (as defined in step two), because our primary interest here is how the bootstrap estimators handle the transmission of the first-step estimation error to the second step relative to the analytical alternative in the simplest of contexts. In Atkinson and Cornwell (2013), we explore the effects, in some cases substantial, of heteroskedasticity and serial correlation in the ξ it on the second-step inference problem.

5.5.2 Monte Carlo Results

We perform a number of Monte Carlo experiments to compare the actual size and power of the t-statistics derived from four estimators of the covariance matrix of \(\hat{\gamma }\)– a “naive” method which is the asymptotic formula without adjusting for the first-step parameter estimators, the correct asymptotic formula which makes this adjustment, the pairs bootstrap, and the wild bootstrap. For our size calculations, we assume that \(\beta =\gamma = 1\) during data generation and test the null that γ = 1 using a two-sided equal-tailed 95 % confidence interval, so that the total type-I error is α = 0. 05.

We set the number of bootstrap draws, B, to 399 following MacKinnon (2002) who states that while this number may be smaller than should be used in practice, any randomness due to B of this size averages out across the replications. We find this to be true for our experiments where larger values of B did not change our results on ERP up to three significant digits beyond the decimal point. Within each of M(m = 1, …, M) Monte Carlo trials, for each bootstrap method, we estimate the unrestricted model and obtain \(\hat{\gamma }_{m,b,g}^{{\ast}}\), the bootstrap estimator of \(\hat{\gamma }_{m,g}\), b = 1, …, B. For each m, we calculate the actual size of the test-statistic,

$$\displaystyle{ t_{m,g}^{{\ast}} = (\hat{\gamma }_{ m,g} -\gamma _{g})/s_{m,g}^{{\ast}},\quad g = 1,\ldots,G, }$$
(5.31)

where \(s_{m,g}^{{\ast}}\) is the bootstrap estimator of the standard error of \(\hat{\gamma }_{m,g}\), computed as the standard deviation of \(\hat{\gamma }_{m,b,g}^{{\ast}}\) over all bootstrap replications. Note that the \(t_{m,g}^{{\ast}}\) statistic is not asymptotically pivotal and no asymptotic refinements obtain; however, we employ it since applied researchers may have difficulty computing the asymptotic formula. See MacKinnon (2002) for details.

For each Monte Carlo trial, m, we calculate the size for each bootstrap estimator as the percentage of \(t_{m,g}^{{\ast}}\) values greater than the nominal level of \(t_{\alpha /2}^{{\ast}} = 1.96\) or less than the nominal level of \(t_{1-\alpha /2}^{{\ast}} = -1.96\), with α = 0. 05. We choose M = 1, 999, so that \(\frac{1} {2}\alpha (M + 1)\) is an integer.

For each Monte Carlo trial, we compute the size for the naive and asymptotic formula methods using

$$\displaystyle{ t_{m,g} = (\hat{\gamma }_{m,g} -\gamma _{g})/s_{\hat{\gamma }_{m,g}}, }$$
(5.32)

where \(s_{\hat{\gamma }_{m,g}}\) for the naive method is the standard error estimator ignoring the existence of first-step random variables and for the asymptotic method is the square root of the gth diagonal element of (5.13). Then, we estimate size over all M observations as the percentage of times that t m, g exceeds the nominal level of \(t_{\alpha /2}^{{\ast}} = 1.96\) or is less than the nominal level of \(t_{1-\alpha /2}^{{\ast}} = -1.96\) for α = 0. 05.

Because we are interested in performance under large-N asymptotics, we consider the following cases: N = 50, 100, 250, 500 and 1, 000 crossed with T = 5, 10 and 20. We compute the actual size, also termed type-I error or rejection probability (RP), and the absolute value of the ERP. Table 5.1 reports actual RPs, while Table 5.2 reports the sum over all parameters of the absolute ERPs.

Table 5.1 Monte Carlo actual size calculations
Full size table
Table 5.2 Total Monte Carlo ERP
Full size table

Table 5.1 shows that the naive and asymptotic methods seriously over-reject for small values of N, the pairs bootstrap slightly over-rejects, and the wild bootstrap under-rejects. Both bootstrap methods are considerably more accurate than the non-bootstrap methods, with the advantage going to the pairs. For N = 50, actual sizes are 0. 051 for the pairs and between 0. 046 and 0. 047 for the wild, but range from 0. 069 to 0. 088 for the non-bootstrap methods. Thus, the upward bias of the pairs is extremely small (2 %); the downward bias of the wild is larger (6–8 %), but still far smaller than the bias of the conventional methods (at least 40 %).

Increasing N generally improves the accuracy of all methods, but the performance rankings do not change. By N of 250, the bootstrap methods produces the correct, or very close to the correct, size in every case, while the conventional methods still overstate the significance of t-values by at least 10 % in more than half of the cases. Increasing N to 500 and then 1,000 brings actual and nominal size into alignment in every bootstrap case. However, even when N = 1, 000, the conventional approaches get the size right in only two cases and are off by as much as 12 % in the others.

The sums of absolute ERPs in Table 5.2 concisely summarize the advantage of the bootstrap methods. For N > 50, the pairs bootstrap absolute ERP sum never exceeds 0. 001. The wild bootstrap is not as impressive for smaller values of N, but competes with the pairs when N is at least 250. In contrast, the absolute ERP sums of conventional methods are often an order of magnitude larger, even for N as large as 500.

To quantify the roles of N and T in reducing size distortions we regress the ln(actual size) for each estimated coefficient on the logs of N and T by method, where the observations are the 15 combinations of N and T considered in Table 5.3. Asymptotic t-values are reported in parentheses. The results show that increasing N by a given percentage affects size to a considerably greater degree than increasing T by the same percentage. The cross-section dimension effect is also always highly significant, whereas the panel length is never significant at even the 10- % level. This makes sense, because T affects second-step estimation only through its effect on \(\hat{\beta }_{FE}\) and its estimated covariance matrix.

Table 5.3 Regressions explaining ln (actual size) (number of observations = 15)
Full size table

Finally we examine the power of the conventional and bootstrap tests, computed using level-adjusted sizes. Since both bootstrap methods always reject less frequently than the conventional methods, the former will appear to have less power. Therefore, we compute power based on level-adjusted t m, g ∗ values, so that critical values are used for which the actual RP is exactly equal to the nominal RP.Footnote 7 These levels, \(t_{\alpha /2,g}^{{\ast}}\) and \(t_{1-\alpha /2,g}^{{\ast}}\), are the α∕2 and \(1 -\alpha /2\) quantiles of the sorted \(t_{m,g}^{{\ast}}\). For each Monte Carlo replication, they are found by first sorting the \(t_{m,g}^{{\ast}}\) values from large to small and then taking the \((\alpha /2)(B + 1)\) and \((1 -\alpha /2)(B + 1)\) values for each g. We compute the power curves for γ 3 for each method as the alternative value of γ 3 (denoted as ALT in the figures) is increased from − 1 to 1 in increments of.1 by calculating the percentage of the B bootstrap estimates that fall outside the critical region. For the conventional methods, we use the same range of alternative parameter values to compute power as the percentage of M Monte Carlo estimates that falls outside the interval defined by their level-adjusted t-values, computed using the same sorting method just described.

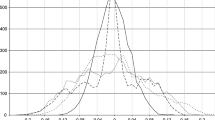
Figures 5.1–5.3 present the power curves for N = 250, 500, and 1000, where T = 5 throughout. With N = 250, the pairs method holds a slight advantage in terms of power. However, with larger values of N, all methods are highly similar. With N = 250 the power of all methods is quite low relative to N = 1000, where power has risen to approximately. 7 for alternatives of − 1 and 1.

Fig. 5.1
figure 1

Power vs. H A for N = 250, t = 5 for γ 3

Full size image
Fig. 5.2
figure 2

Power vs. H A for N = 500, t = 5 for γ 3

Full size image
Fig. 5.3
figure 3

Power vs. H A for N = 1000, t = 5 for γ 3

Full size image

5.6 Conclusions

The primary advantage of panel data is the ability they provide to control for unobserved heterogeneity or effects that are time-invariant. The fixed-effects (FE) estimator is by far the most popular technique for exploiting this advantage, because it makes no assumption about the relationship between the explanatory variables in the model and the effects. However, a well-known problem with the FE estimator is that any time-invariant regressor in the model is swept away by the data transformation that eliminates the effects. The partial effects of time-invariant variables can be estimated in a second-step regression, but this fact is generally overlooked in textbook discussions of panel-data methods.

In this paper, we have shown how to conduct inference on the coefficients of time-invariant variables in linear panel-data models, estimated in a two-step framework. Our estimation framework is rooted in Hausman and Taylor’s (1981) “consistent, but inefficient” estimator, albeit under weaker FE assumptions. We derive the asymptotic covariance matrix of the two-step estimator and compare inference based on the asymptotic standard errors with bootstrap alternatives. Bootstrapping has a natural appeal, because of the complications associated with estimating the asymptotic covariance matrix and the inherent finite-sample bias of the resulting standard errors. We adapt the pairs and wild bootstrap to this two-step problem. Then we prove that both bootstrap coefficient estimators are unbiased, a result that is important since bootstrap ERPs are a function of bias. Using Monte Carlo methods, we compare the size and power of the naive asymptotic estimator, which ignores the first-step estimation error, the correct asymptotic covariance matrix estimator, which does not, and the bootstrap alternatives.

In terms of size, bootstrap methods are the clear winners. For values of N less than 250, the pairs somewhat over-rejects and the wild somewhat under-rejects, with the pairs having a small advantage. The positive ERP of the pairs is 2 %, while the negative ERP of the wild is 6–8 %. In contrast, both are considerably more accurate than the methods based on asymptotic formulae, which are typically biased by more than 40 %. For values of N equal to 250 and larger, the bootstrap methods converge to the correct size and the advantage of the pairs becomes negligible. The correct asymptotic covariance matrix estimator remains somewhat biased even for N = 1, 000. The pairs bootstrap method slightly out-performs the other methods in terms of power with N = 250, although power curves are highly similar with larger values of N.

The Monte Carlo findings are consistent with the results of our analytical examination of the pairs and wild bootstrap procedures. The implication of these results is that both bootstrap ERPs should be very close to zero. The bottom line of both our Monte Carlo exercise and analytical results is that researchers interested in estimating the effects of time-invariant variables in a two-step framework should rely on bootstrapped standard errors. This conclusion holds particularly strongly in small-N panels like those encountered in cross-state and cross-country studies.

What remains is to consider the advantages to bootstrapping when some of the second-step regression variables may be correlated with the unobserved effects and when the true model errors are heteroskedastic and autocorrelated. Atkinson and Cornwell (2013) extend the work of this paper to that case.