Keywords

10.1 Introduction

In this chapter we present a dynamic-network model of the bank technology which can be used to measure bank performance. The model accounts for exogenous inputs, excess reserves which can be carried over from period to period and final outputs that include desirable outputs and jointly produced undesirable by-products in the form of nonperforming loans . The framework is based on the performance measures of Fukuyama and Weber (2013, 2015a, b, 2016). These models measure bank performance accounting for the following characteristics of the bank technology: (i) banks face a two-stage network technology where deposits and other funds are produced in a first stage and then in a second stage those deposits are used to generate a portfolio of interest-bearing assets (loans) and non-interest bearing assets (securities investments), (ii) banks face credit risk in that the loan production process generates a jointly produced by-product of nonperforming loans, (iii) in the second stage of production bank managers can choose to make loans and securities investments or carry-over some excess reserves for use in a future period, (iv) nonperforming loans produced in one period become an undesirable input to the first stage of production in a future period.

The dynamic aspect of the technology incorporates two outcomes of current period production on future production. First, a bank can choose to either produce final outputs of securities investments and loans, including jointly produced nonperforming loans or they can choose to carry-over some of their raised funds to the second stage of production in a future period. Thus, current production decisions affect future production possibilities. Second, nonperforming loans generated in the current period have a negative effect on the first stage of production in a subsequent period. This is because when nonperforming loans are generated, a bank must raise more financial equity capital or curtail their deposit taking and other fund-raising activities. Thus, static performance indicators that account for only current period outputs and inputs are biased to the extent that bank managers optimize over many periods. Although the lending process links desirable and jointly produced undesirable outputs, securities investments made by the bank are not linked to nonperforming loans .Footnote 1 As a consequence we separate the jointly produced linked outputs of performing and nonperforming loans and the unlinked outputs of securities investments following Epure and Lafuente (2015) and Fukuyama and Weber (2016). Since nonperforming loans are an unavoidable by-product of loan production and negatively affect the ability of banks to raise deposits, they are treated as an undesirable input to stage 1 in a subsequent period. On the other hand, carryover assets from a previous period augment future lending and investment opportunities and are treated as a desirable input to stage 2.

10.2 Selective Literature Review

10.2.1 Network DEA and Dynamic DEA

In the static black-box form of data envelopment analysis (DEA ) due to Farrell (1957) and Charnes et al. (1978), inputs and outputs are assumed to be independent across production periods. That is, the inputs and outputs observed in one period have no effect on the production technology in future periods. Färe and Grosskopf (1996) extended the static black box technology and laid the theoretical foundation for network DEA. A two-stage network model where intermediate products are produced in stage 1 and then become the only inputs to stage 2 is commonly used (see Fig. 10.1). The popularity of this model is mainly due to its simple mathematical structure although this network model can be easily extended to more than two stages and to parallel production technologies as well. Sexton and Lewis (2003), Liang et al. (2008), Chen et al. (2009b) and Chen et al. (2010) investigated the static two-stage network method without undesirable outputs. Fukuyama and Weber (2010) presented a static two-stage network model of bank production accounting for the undesirable output of nonperforming loans. Their model used the directional technology distance function to measure performance and accounted for slacks in the constraints that define the DEA technology.

Fig. 10.1
figure 1

Static two-stage network production with bad outputs. Legend: T1 tSN : static network stage 1 technology; T2 tSN : static network stage 2 technology; SN: static network

Full size image

Lewis and Sexton (2004) developed a multi-stage network DEA model which extended the Sexton and Lewis (2003) two-stage network model. Kao and Hwang (2008) provided a two-stage method that simultaneously determined the efficiency of each division and the entire system. Tone and Tsutsui (2009) introduced a network DEA method that compared actual division outputs with potential outputs accounting for slacks in the output and inputs constraints that defined the network technology. Kao (2009) used a multiplier form and introduced a network DEA method by considering the relations among sub-process efficiencies in terms of series, parallel, and mixed methods.

Fukuyama and Mirdehghan (2012) and Mirdehghan and Fukuyama (2016) suggested a two-phase algorithm for identifying the Pareto-Koopmans efficiency status of the decision making unit (DMU ). Lozano (2015) presented a network DEA model that compared outputs of all divisions with the outputs of all divisions that could be produced if a central decision-maker allocated inputs to each division or sub-process instead of taking divisional inputs as given. Extending Fukuyama and Weber’s (2010) two-stage network SBI (slack-based inefficiency) model, Lozano (2016) generalized Fukuyama and Weber’s (2010) two-stage network model by accounting for undesirable outputs. A comprehensive survey of the literature on network DEA is provided by Kao (2014) who categorized network DEA models into nine classes: (i) independent models, (ii) system distance measure models, (iii) process distance models, (iv) factor distance models, (v) slacks-based measure models, (vi) ratio-form system (overall) efficiency models, (vii) ratio-form sub-process efficiency models, (viii) game theoretic models, and (ix) value-based models.

While dynamic DEA studies are sparse compared to those of network DEA, the number of dynamic network DEA studies has been growing. Färe, Grosskopf and Margaritis (2011) extended Shephard and Färe’s (1980) basic dynamic production framework by connecting a sequence of single-period technologies and allowing producers to produce either final outputs or carryover some output to augment production in a subsequent period. Färe and Grosskopf (1996) used investment spending as an example of a carryover with producers deciding the mix of GDP to be allocated to the final output of consumer spending and private investment spending that enhances future production possibilities. Sengupta (1994) and Nemoto and Goto (2003) used adjustment cost theory and provided optimal control-theoretic models for assessing the dynamic efficiency of DMUs. To examine the impact of public capital investment on private productivity, Bogetoft et al. (2009) derived a DEA model and calculated the optimal paths and levels of public and private investment spending. Tone and Tsutsui (2014) proposed a slacks-based dynamic-network model that allowed carryover assets to have positive or negative effects on future production. In an examination of Bangladeshi banks Akther et al. (2013) constrained the current-period bank technology on the amount of nonperforming loans generated in a previous period. Fukuyama and Weber (2013, 2015a, b, 2016) extended Akther et al. (2013) to multiple periods and allowed a bank to reduce the current production of loans and securities investments and to save carryovers for use in a future period if future production could be enhanced by more than the loss of current production.

Färe et al. (1992) and Färe et al. (1994) proposed static Malmquist productivity indices which can be decomposed into indexes of efficiency change and technological change. Färe et al. (2011) presented a multiplicative dynamic Malmquist index that allowed DMUs to make inter-temporal decisions on the allocation of scarce resources so as to maximize production over all periods. Similarly, Fukuyama and Weber (2015b, 2016) proposed a dynamic-network Luenberger bank productivity indicator and its additive components of efficiency change and technological change.

De Mateo et al. (2006) and Fallah-Fini et al. (2014) addressed various inter-temporal aspects of production technologies and performance measures. De Mateo et al. (2006) studied various concepts associated with inter-temporal production including the cost, path, and period of adjustment, the appraisal period, profits, and dynamic DEA. Fallah-Fini et al. (2014) determined five main factors that influence the inter-temporal dependence between inputs and outputs: production delays, inventories, quasi-fixed factors, adjustments costs, and disembodied technical change.

10.2.2 Bank Production and Risk

Berger and Humphrey (1997) provide a comprehensive survey of financial institution performance measures. Here we selectively examine studies that estimated bank performance controlling for the effects of bank risk. McAllister and McManus (1993) showed that large US banks had even greater measured scale economies controlling for bank risk. Altunbas et al. (2000) estimated a parametric cost frontier for a sample of Japanese commercial banks to examine the impact of risk and quality factors on bank costs. Altunbas et al. (2000) defined the loan quality as the ratio of nonperforming loans to total loans. For a sample of Japanese banks operating in 1996, Drake and Hall (2003) reported evidence that financial capital had the greatest impact on scale efficiency.

Liu and Tone (2008) used the ratio of credit costs to potential loan losses as an input and found that Japanese banks appeared to be “learning by doing” as efficiency improved during the sample period of 1997–2001. Park and Weber (2006) and Fukuyama and Weber (2003, 2004, 2005) controlled for bank risk by using financial equity capital as an input in their static measures of bank performance. Fukuyama and Weber (2008a, b) estimated the shadow price of nonperforming loans. Drake et al. (2009) documented the importance of accounting for loans and risk in the analysis of Japanese bank efficiency.

Fukuyama and Weber (2010) proposed a two-stage network model for Japanese cooperative Shinkin banks. In stage 1 banks use labor, physical capital and financial equity capital to produce deposits. Then, in stage 2 those deposits serve as an input as banks produce a portfolio of securities investments and loans with some of the loans becoming nonperforming. In a study of Bangladeshi banks Akther, Fukuyama and Weber (2013) advanced this specification by allowing nonperforming loans generated in a preceding period to decrease the production possibility set in a subsequent period. All above-mentioned bank efficiency studies have the view that risk associated to nonperforming loans need to be considered in bank efficiency measurement.

Compared with network DEA, fewer studies have been devoted to the dynamic DEA studies of bank efficiency. Fukuyama and Weber (2013) extended the Färe and Grosskopf (1996) dynamic model to a network setting by specifying a bank technology where a bank can forego current loans and the jointly produced nonperforming loans by expanding carryover assets (excess reserves) for use in a subsequent period when better lending conditions might exist. Although their dynamic model considered only three periods for bank managers to optimize over Fukuyama and Weber (2015b, 2016) extended the model to more than three periods. Fukuyama and Weber (2015a) added a financial regulatory restraint that constrained the feasible technology by requiring banks to hold a minimum ratio of financial equity capital to assets. Furthermore, Fukuyama and Weber (2015a, b) showed how the primal envelopment form that incorporated the regulatory constraint could be estimated by its dual multiplier form with financial regulatory restraint and how the Luenberger dynamic productivity indicator could be decomposed into productivity gains due to technological progress and productivity gains due to greater efficiency. Epure and Lafuente (2015) accounted for bank risk and distinguished between desirable outputs linked to nonperforming loans and desirable outputs such as securities investments and service fees not linked to jointly produced undesirable outputs.

Table 10.1 presents a summary of the assumptions behind the models of Fukuyama and Weber (2013, 2015a, b, 2016) and the data sets on Japanese banks used in their empirical work. The primary purpose of the current study is to unify these models and provide an extension by incorporating the condition of weak disposability between desirable outputs and jointly produced undesirable outputs when banks operate under variable returns to scale.

Table 10.1 Previous dynamic-network bank efficiency studies with NPLs
Full size table

10.3 Preliminaries

10.3.1 Black-Box Technology

Let the exogenous inputs that can be employed by a bank in period t be represented by \( {\mathbf{x}}^t=\left({x}_1^t,\dots, {x}_N^t\right)\in {\Re}_{+}^N \) and let total desirable outputs be represented by \( {\mathbf{y}}^t=\left({y}_1^t,\dots, {y}_M^t\right)\in {\Re}_{+}^M \). The static black-box (SBB) technology for period t is defined as

$$ {T}_{\mathrm{SBB}}^t=\left\{\left({\mathbf{x}}^t,\kern0.5em {\mathbf{y}}^t\right)\in {\Re}_{+}^N\times {\Re}_{+}^M\left|\kern0.5em {\mathbf{x}}^t\kern0.5em \mathrm{can}\ \mathrm{produce}\kern0.5em {\mathbf{y}}^t\right.\right\}. $$
(10.1)

The SBB technology considers only one period and neglects the possible effects of past production outcomes such as nonperforming loans and carryover assets that might make a bank appear less efficient than it would otherwise be if those carryover assets were incorporated into the technology. We assume that T tSBB satisfies strong disposability of exogenous inputs x t and desirable outputs y t along with other standard properties (Shephard 1970; Färe and Primont 1995). Strong disposability of inputs and outputs means that if \( \left({\mathbf{x}}_0^t,\kern0.5em {\mathbf{y}}_0^t\right)\in {T}_{\mathrm{SBB}}^t \) then \( \left({\mathbf{x}}_0^t,-{\mathbf{y}}_0^t\right)\le \left({\mathbf{x}}_1^t,-{\mathbf{y}}_1^t\right) \) implies \( \left({\mathbf{x}}_1^t,\kern0.5em {\mathbf{y}}_1^t\right)\in {T}_{\mathrm{SBB}}^t \). That is, it is feasible for banks to use more input to produce less output.

10.3.2 Network Technology with Bad Outputs

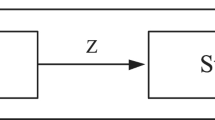
To specify a bank technology and measure DMU performance researchers must determine what inputs are used to produce what outputs. In their examination of Japanese banks Fukuyama and Weber (2003, 2004, 2005) adopted the intermediation approach of Sealey and Lindley (1977) and assumed that Japanese banks employed variable inputs of labor, physical capital, and deposits and a quasi-fixed input in the form of financial equity capital to produce loans and securities investments. Although the SBB technology represented by (10.1) has frequently been used in bank efficiency measurement studies, disagreement exists regarding whether deposits should be treated as an output or as an input. Berger and Humphrey (1997) and Fethi and Pasiouras (2010) provide background on this on-going discussion. To cope with this problem, various authors have used static two-stage network models where deposits are an intermediate output of stage 1 production and an intermediate input of stage 2 production. Let \( {\mathbf{z}}^t=\left({z}_1^t,\dots, {z}_Q^t\right)\in {\Re}_{+}^Q \) represent the vector of intermediate products that are produced in stage 1 and then subsequently used as an input in stage 2. The static stage 1 network (SN) technology is denoted

$$ T{1}_{\mathrm{SN}}^t=\left\{\left(\kern0.1em {\mathbf{x}}^t,{\mathbf{z}}^t\right)\in {\Re}_{+}^N\times {\Re}_{+}^Q\left|\kern0.5em {\mathbf{x}}^t\in {\Re}_{+}^N\kern0.6em \mathrm{can}\kern0.5em \mathrm{produce}\kern1em {\mathbf{z}}^t\in {\Re}_{+}^Q\right.\right\}. $$
(10.2)

In the second stage of production it is commonly assumed that the main activity of a bank is lending to the customers and hence it faces the credit risk associated with lending, i.e., nonperforming loans arise in the stage 2 production process. Let \( {\mathbf{b}}^t=\left({b}_1^t,\dots, {b}_L^t\right)\in {\Re}_{+}^L \) represent the undesirable outputs that are jointly produced as part of the lending process. Accounting for these undesirable outputs the static stage 2 network technology is denoted

$$ T{2}_{\mathrm{SN}}^t=\left\{\left(\kern0.1em {\mathbf{z}}^t,{\mathbf{y}}^t,{\mathbf{b}}^t\right)\in {\Re}_{+}^N\times {\Re}_{+}^M\times {\Re}_{+}^L\left|\kern0.5em {\mathbf{x}}^t\kern0.6em \mathrm{can}\kern0.5em \mathrm{produce}\kern1em \left({\mathbf{y}}^t,{\mathbf{b}}^t\right)\right.\right\}\kern0.1em . $$
(10.3)

Nonperforming loans are generally classified by the various stages of delinquency–loans delinquent for less than 3 months, loans delinquent less than 6 months but more than 3 months, etc. Following Wang et al. (1997) and Chen et al. (2009a, b, 2010) the SBB technology can be extended to a static two-stage network technology that accounts for undesirable outputs. This static network technology is denoted

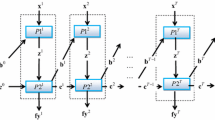
$$ {T}_{\mathrm{SN}}^t=\left\{\left(\kern0.1em {\mathbf{x}}^t,{\mathbf{z}}^t,{\mathbf{y}}^t\right)\in {\Re}_{+}^N\times {\Re}_{+}^M\left|\kern0.5em \left(\kern0.1em {\mathbf{x}}^t,{\mathbf{z}}^t\right)\in T{1}_{\mathrm{SN}}^t,\kern1em \left(\kern0.1em {\mathbf{z}}^t,{\mathbf{y}}^t,{\mathbf{b}}^t\right)\in T{2}_{\mathrm{SN}}^t\right.\right\}. $$
(10.4)

Figure 10.1 depicts the two-stage network system with undesirable outputs.

10.3.3 Dynamic Technology with Carryovers

To move from a static to a dynamic technology we follow Färe and Grosskopf (1996) and assume that bank managers have discretion in how to allocate total output produced, \( {\mathbf{y}}^t=\left({\mathbf{y}}_1^t,\dots, {\mathbf{y}}_M^t\right)\in {R}_{+}^M \), between final outputs, \( \mathbf{f}{\mathbf{y}}^t=\left(\mathbf{f}{\mathbf{y}}_1^t,\dots, \mathbf{f}{\mathbf{y}}_M^t\right)\in {R}_{+}^M \), and carryover assets, \( {\mathbf{c}}^t=\left({c}_1^t,\dots, {c}_M^t\right)\in {\Re}_{+}^M \) where

$$ {\mathbf{y}}^t=\mathbf{f}{\mathbf{y}}^t+{\mathbf{c}}^t\in {\Re}_{+}^M. $$
(10.5)

See also Fukuyama and Weber (2013, 2015a, b). For instance, total outputs can be thought of as the total amount of assets–less required reserves and physical capital assets–that can be allocated to the various divisions that make loans and securities investments. After the managers of those divisions receive their allocation (y t) they can choose to use their funds to make loans or securities investments (fy t) or they can save their allocation for use in a future period (c t) when better lending and investment opportunities might be available because of technological progress or because of a more robust economy (Fig. 10.2).

Fig. 10.2
figure 2

Bank intermediation process with NPLs and carryovers. Notes: T1t: dynamic network Stage 1 technology; T2t: dynamic network Stage 2 technology; NPLs: nonperforming loans

Full size image

Therefore, we define the dynamic black-box (DBB) technology as

$$ {T}_{\mathrm{DBB}}=\left\{\left(\mathbf{x},\kern0.15em \mathbf{f}\mathbf{y},\mathbf{c},\kern0.15em \mathbf{b}\right)\left|\begin{array}{c}\hfill \kern0.5em \left({\mathbf{c}}^{t-1},{\mathbf{b}}^{t-1},\kern0.5em {\mathbf{x}}^t,\mathbf{f}{\mathbf{y}}^t+{\mathbf{c}}^t,{\mathbf{b}}^t\right)\ \mathrm{is}\ \mathrm{a}\ \mathrm{f}\mathrm{easible}\hfill \\ {}\hfill \mathrm{production}\ \mathrm{plan}\ \mathrm{f}\mathrm{o}\mathrm{r}\ t=1,\dots, T\hfill \end{array}\right.\ \right\} $$
(10.6)

where \( \mathbf{x}=\left({\mathbf{x}}^1,{\mathbf{x}}^2,\dots, {\mathbf{x}}^T\right) \), \( \mathbf{f}\mathbf{y}=\left(\mathbf{f}{\mathbf{y}}^1,\kern0.5em \mathbf{f}{\mathbf{y}}^2,\dots, \kern0.5em \mathbf{f}{\mathbf{y}}^T\right) \), \( \mathbf{c}=\left({\mathbf{c}}^0,{\mathbf{c}}^1,\kern0.5em \dots, \kern0.5em {\mathbf{c}}^T\right) \) and \( \mathbf{b}=\left({\mathbf{b}}^0,{\mathbf{b}}^1,\dots, {\mathbf{b}}^T\right) \). Akther et al. (2013) considered lagged nonperforming loans as an undesirable input when studying the efficiency of commercial banks in Bangladesh.

10.3.4 Dynamic-Network Technology

Our final goal is to link the static network technology with the dynamic black box technology. Nonperforming loans generated in a previous period, \( {\mathbf{b}}^{t-1} \), are an undesirable input to stage 1 in period t. Undesirable inputs have the property that if the current level of production is to be maintained, greater use of the undesirable input must be offset by the use of larger amounts of the desirable inputs. For instance, financial equity capital is necessary for banks to engage in fund raising activities. When some of a bank’s loans become nonperforming, the ratio of equity capital to total assets falls and bank regulations require banks to either seek additional sources of financial equity capital (the desirable stage 1 input) or reduce fund raising activities. Therefore, we define the dynamic-network stage 1 technology as

$$ T{1}^t=\left\{\left({\mathbf{b}}^{t-1},{\mathbf{x}}^t,{\mathbf{z}}^t\right)\in {\Re}_{+}^M\times {\Re}_{+}^N\times {\Re}_{+}^Q\left|\kern0.5em \left({\mathbf{b}}^{t-1},{\mathbf{x}}^t\right)\in {\Re}_{+}^N\kern0.6em \mathrm{can}\kern0.5em \mathrm{produce}\kern1em {\mathbf{z}}^t\in {\Re}_{+}^Q\right.\right\}. $$
(10.7)

Stage 2 of production also has a dynamic element. Along with the intermediate outputs of raised funds and deposits, carryover assets from a previous period are a desirable input in the production of the portfolio of loans and securities investments in the current period. When lending and other investment opportunities are plentiful in the current period, bank managers might seek to keep carryover assets (excess reserves) to a minimum which reduces production possibilities in a subsequent period. In contrast, bank managers might choose to keep final outputs relatively small and hold a large amount of carryover assets for use in a future, more positive lending environment. Thus, carryover assets, \( {\mathbf{c}}^t=\left({c}_1^t,\dots, {c}_M^t\right)\in {\Re}_{+}^M \) represent the unused assets in period t that are held until period t + 1, similar to an inventory. When current economic conditions are weakening or when technological progress is expected a bank can delay some portion of the assets for use to a future period at the expense of the current production of outputs. Therefore, we denote the stage 2 technology as

$$ T{2}^t=\left\{\left({\mathbf{c}}^{t-1},\kern0.1em {\mathbf{z}}^t,\mathbf{f}{\mathbf{y}}^t,{\mathbf{b}}^t\right)\in {\Re}_{+}^N\times {\Re}_{+}^M\times {\Re}_{+}^L\left|\kern0.5em \left({\mathbf{c}}^{t-1},{\mathbf{z}}^t,\mathbf{f}{\mathbf{y}}^t+{\mathbf{c}}^t,{\mathbf{b}}^t\right)\kern0.5em \mathrm{is}\ \mathrm{feasible}\right.\right\}\kern0.5em . $$
(10.8)

We combine (10.7) and (10.8) to obtain the period t network technology

$$ N{T}^t=\left\{\left({\mathbf{b}}^{t-1},{\mathbf{c}}^{t-1},\kern0.5em {\mathbf{x}}^t,\kern0.5em {\mathbf{z}}^t,\kern0.5em \mathbf{f}{\mathbf{y}}^t,\kern0.5em {\mathbf{b}}^t,{\mathbf{c}}^t\right)\kern0.62em \left|\begin{array}{l}\kern0.5em \left({\mathbf{b}}^{t-1},\kern0.5em {\mathbf{x}}^t,\kern0.5em {\mathbf{z}}^t\right)\in T{1}^t,\\ {}\kern0.5em \left({\mathbf{c}}^{t-1},\kern0.1em {\mathbf{z}}^t,\mathbf{f}{\mathbf{y}}^t,{\mathbf{b}}^t\right)\in T{2}^t\end{array}\right.\right\}. $$
(10.9)

The dynamic-network technology (DNT) is formed by extending (10.9) over \( t=1,\dots, T \) periods:

$$ DNT=\left\{\left(\mathbf{x},\kern0.5em \mathbf{y},\mathbf{c},\kern0.5em \mathbf{b}\right)\left|\begin{array}{l}\kern0.5em \left({\mathbf{b}}^0,{\mathbf{c}}^0,\kern0.5em {\mathbf{x}}^1,\kern0.5em {\mathbf{z}}^1,\kern0.5em \mathbf{f}{\mathbf{y}}^1,\kern0.5em {\mathbf{b}}^1,{\mathbf{c}}^1\right)\in N{T}^1,\\ {}\kern2.5em \vdots \\ {}\kern0.5em \left({\mathbf{b}}^{T-1},{\mathbf{c}}^{T-1},\kern0.5em {\mathbf{x}}^T,\kern0.5em {\mathbf{z}}^T,\kern0.5em \mathbf{f}{\mathbf{y}}^T,\kern0.5em {\mathbf{b}}^T,{\mathbf{c}}^T\right)\in N{T}^T\end{array}\right.\right\}. $$
(10.10)

To measure bank performance we use a variant of the directional distance function . Directional distance functions were developed by Chambers et al. (1998) as a functional representation of the production technology, similar to Luenberger’s (1992, 1995) benefit function that was used to represent the consumer’s choice problem. A single period directional distance function measures the simultaneous expansion in desirable outputs and contraction in undesirable outputs and inputs for the directional scaling vector \( \mathbf{g}=\left({\mathbf{g}}_{fy},{\mathbf{g}}_b,{\mathbf{g}}_x\right) \). We extend the directional distance function to the dynamic network technology given by (10.10). Let \( {\Omega}_k=\left({\mathbf{b}}_k^{t-1},\kern0.5em {\overset{.}{\mathbf{c}}}_k^{t-1},\kern0.5em {\ddot{\mathbf{c}}}_k^{t-1},\kern0.5em {\mathbf{b}}_k^t,\kern0.5em {\mathbf{x}}_k^t,\kern0.5em \mathbf{f}{\overset{.}{\mathbf{y}}}_k^t,\kern0.5em {\overset{.}{\mathbf{c}}}_k^t,\kern0.5em \mathbf{f}{\ddot{\mathbf{y}}}_k^t,\kern0.5em {\ddot{\mathbf{c}}}_k^t,\kern0.5em \forall t=1,\dots, T\right) \) represent the observed inputs, outputs, and carryovers for bank k in each production period. We define a weighted DN-directional distance function as

$$ \begin{array}{ll}DN\overrightarrow{D}\left({\Omega}_k;\mathbf{g}\right)=& \underset{\beta^t,\kern0.5em {\mathbf{z}}^t,\kern0.5em {\mathbf{c}}^t}{\operatorname{maximize}}\kern0.5em \left\{{\displaystyle \sum_{t=1}^T{w}^t{\beta}^t}\right.\hfill \\ {}& \kern2em \left.\kern1em \left|\begin{array}{l}\kern0.5em \left({\mathbf{b}}^0,{\mathbf{c}}^0,\kern0.5em {\mathbf{x}}^1-{\beta}^1{\mathbf{g}}_x,\kern0.5em {\mathbf{z}}^1,\kern0.5em \mathbf{f}{\mathbf{y}}^1+{\beta}^1{\mathbf{g}}_y,\kern0.5em {\mathbf{b}}^1-{\beta}^1{\mathbf{g}}_b,{\mathbf{c}}^1\right)\in N{T}^1,\\ {}\kern0.5em \left({\mathbf{b}}^1-{\beta}^1{\mathbf{g}}_b,{\mathbf{c}}^1,\kern0.5em {\mathbf{x}}^2-{\beta}^2{\mathbf{g}}_x,\kern0.5em {\mathbf{z}}^2,\kern0.5em \mathbf{f}{\mathbf{y}}^2+{\beta}^2{\mathbf{g}}_y,\kern0.5em {\mathbf{b}}^2-{\beta}^2{\mathbf{g}}_b,{\mathbf{c}}^2\right)\in N{T}^1,\\ {}\kern2.5em \vdots \\ {}\kern0.5em \left({\mathbf{b}}^{T-1}-{\beta}^{T-1}{\mathbf{g}}_b,{\mathbf{c}}^{T-1},\kern0.5em {\mathbf{x}}^T-{\beta}^T{\mathbf{g}}_x,\kern0.5em {\mathbf{z}}^T,\kern0.5em \mathbf{f}{\mathbf{y}}^T+{\beta}^T{\mathbf{g}}_y,\kern0.5em {\mathbf{b}}^T-{\beta}^T{\mathbf{g}}_b,{\mathbf{c}}^T\right)\in N{T}^T.\end{array}\right.\right\}\hfill \end{array} $$
(10.11)

The weights (w t) for each period are exogenously chosen. Following Nemoto and Goto (2003), De Mateo et al. (2006) and Fukuyama and Weber (2015a, b, 2016) one might choose the present value factors for the predetermined weights. That is, \( {w}^t={\left(1+R\right)}^{t-1} \), where R is the producer’s rate of time preference. Inefficient producers have \( DN\overrightarrow{D}\left({\Omega}_k;\mathbf{g}\right)>0 \) and in stage 1 of period t they can contract inputs by β t g x while in stage 2 of the same period they can simultaneously expand desirable outputs by β t g y and contract undesirable outputs by β t g b . The contraction in stage 2’s undesirable outputs means that in the next period the amount of undesirable inputs that enter stage 1 will also decline. A producer who is efficient in a single period has \( {\beta}^t=0 \) and a producer who is efficient in every period has \( DN\overrightarrow{D}\left({\Omega}_k;\mathbf{g}\right)=0 \). We note that in the initial period the lagged value of undesirable outputs (b 0) are fixed. Furthermore, while the producer chooses the amount of carryover assets (c t) in each of the \( t=1,\dots, T \) periods, the lagged value of carryover assets (c 0) in period \( t=1 \) are taken as exogenous. Figure 10.3 depicts the multi-period dynamic-network structure for a bank.

Fig. 10.3
figure 3

Dynamic network structure of bank production. Note: We adapted the multi-period dynamic-network representations given in Fukuyama and Weber (2015b, 2016)

Full size image

10.4 DEA Implementation

We specify the dynamic network technology and estimate the performance of each DMU using DEA. To incorporate the idea that nonperforming loans from a previous period are an undesirable input to stage 1 of the current period we assume that nonperforming loans \( \left({\mathbf{b}}^{t-1}\right) \) and other inputs (x t) satisfy joint weak input disposability (JWID). The condition of JWID is written as

$$ \mathrm{JWID}:\kern1em \left({\mathbf{b}}^{t-1},\kern0.5em {\mathbf{x}}^t,\kern0.5em {\mathbf{z}}^t\right)\in T{1}^t\subseteq {\Re}_{+}^{L+N+Q}\kern1em \mathrm{and}\kern1em \varphi \ge 1\kern1em \Rightarrow \kern1em \left(\varphi {\mathbf{b}}^{t-1},\kern0.5em \varphi {\mathbf{x}}^t,\kern0.5em {\mathbf{z}}^t\right)\in T{1}^t $$
(10.12)

which indicates that any proportional expansion of undesirable inputs \( {\mathbf{b}}^{t-1} \) and current desirable inputs x t can still feasibly produce a fixed level of intermediate products z t.

Our DEA technology also distinguishes between desirable outputs that are linked to undesirable byproducts and desirable outputs that are not linked to undesirable outputs. To make the distinction we assume that \( \overset{.}{M} \) of the desirable outputs are linked to undesirable outputs and that \( \ddot{M} \) of the desirable outputs are not linked to undesirable outputs where \( M=\overset{.}{M}+\ddot{M} \). That is,

$$ {\mathbf{y}}^t=\mathbf{f}{\mathbf{y}}^t+{\mathbf{c}}^t=\left(\mathbf{f}{\overset{.}{\mathbf{y}}}^t+{\overset{.}{\mathbf{c}}}^t,\mathbf{f}{\ddot{\mathbf{y}}}^t+{\ddot{\mathbf{c}}}^t\right). $$
(10.13)

In addition to JWID we assume that stage 2 desirable outputs linked to undesirable outputs satisfy joint weak output disposability (JWOD). This condition is written as follows:

$$ \begin{array}{l}\mathrm{JWOD}:\kern1em \left({\mathbf{z}}^t,\kern1em \mathbf{f}{\overset{.}{\mathbf{y}}}^t+\kern0.5em {\overset{.}{\mathbf{c}}}^t,\kern0.5em \mathbf{f}{\ddot{\mathbf{y}}}^t+\kern0.5em {\ddot{\mathbf{c}}}^t,\kern0.5em {\mathbf{b}}^t\right)\in T{2}^t\subseteq {\Re}_{+}^{Q+\overset{.}{M}+\ddot{M}+L}\hfill \\ {}\kern1em \mathrm{and}\kern1em 0\le {\theta}^t\le 1\kern10em \Rightarrow \kern1em \left({\mathbf{z}}^t,\kern0.5em {\theta}^t\left(\mathbf{f}{\overset{.}{\mathbf{y}}}^t+{\overset{.}{\mathbf{c}}}^t\right),\kern0.5em \mathbf{f}{\ddot{\mathbf{y}}}^t+\kern0.5em {\ddot{\mathbf{c}}}^t,\kern0.5em \theta {\mathbf{b}}^t\right)\in T{2}^t\hfill \end{array} $$
(10.14)

which means that it is feasible to produce proportionally less of the desirable and undesirable outputs with the same amount of input. Weak disposability of outputs is in contrast to the more typical assumption of strong disposability where it is possible to produce less of a single output. Weak disposability means there is an opportunity cost of producing fewer undesirable outputs–fewer desirable outputs must also be produced.

To fully specify the DEA technology we assume that there are j = 1,…, J banks observed in \( t=1,\dots, T \) periods. Let \( {\boldsymbol{\uplambda}}^{1t}=\left({\lambda}_1^{1t},\dots, {\lambda}_J^{1t}\right)\in {\Re}_{+}^J \) and \( {\boldsymbol{\uplambda}}^{2t}=\left({\lambda}_1^{2t},\dots, {\lambda}_J^{2t}\right)\in {\Re}_{+}^J \) represent the intensity variable vectors that form convex combinations of observed inputs for the stage 1 and stage 2 technologies. Accounting for JWID, the stage 1 DEA technology in period t is

$$ \begin{array}{ll}T{1}^t& =\left\{\left({\mathbf{b}}^{t-1},{\mathbf{x}}^t,\kern0.5em {\mathbf{z}}^t\right)\kern0.5em \left|\left({\mathbf{b}}^{t-1},\kern0.5em {\mathbf{x}}^t\right)\ \mathrm{can}\ \mathrm{produce}\ {\mathbf{z}}^t\right.\right\}\hfill \\ {}& \kern1.74em =\left\{\left({\mathbf{b}}^{t-1},\kern0.5em {\mathbf{x}}^t,\kern0.5em {\mathbf{z}}^t\right)\in {\Re}_{+}^{L+N+Q}\kern0.62em \left|\begin{array}{l}\kern0.5em {\mathbf{b}}^{t-1}\ge {\displaystyle {\sum}_{j=1}^J{\varphi}^t{\mathbf{b}}_j^{t-1}{\lambda}_j^{1t}},\kern1em {\mathbf{x}}^t\ge {\displaystyle {\sum}_{j=1}^J{\varphi}^t{\mathbf{x}}_j^t{\lambda}_j^{1t}},\\ {}\kern0.5em {\mathbf{z}}^t\le {\displaystyle {\sum}_{j=1}^J{\mathbf{z}}_j^t{\lambda}_j^{1t}},\kern0.5em {\boldsymbol{\uplambda}}^{1t}\ge \mathbf{0},\kern1em {\varphi}^t\ge 1\end{array}\right.\right\}\hfill \end{array} $$
(10.15)

where “0” indicates an appropriate dimensional zero vector. The existence of nonperforming loans from a preceding period requires the bank to raise a greater amount of equity capital and utilize more of the other inputs.

The stage 2 DEA technology for period t is denoted by

$$ \begin{array}{ll}T{2}^t& =\left\{\left({\mathbf{z}}^t,\kern0.5em \mathbf{f}{\mathbf{y}}^t+\kern0.5em {\mathbf{c}}^t,\kern0.5em {\mathbf{b}}^t\right)\in {\Re}_{+}^{Q+L+M}\left|\kern1em \left({\mathbf{c}}^{t-1},\kern0.5em {\mathbf{z}}^t\right)\ \mathrm{can}\ \mathrm{produce}\ \left({\mathbf{y}}^t+\kern0.5em {\mathbf{c}}^t,\kern0.5em {\mathbf{b}}^t\right)\right.\right\}\hfill \\ {}& \kern1.74em =\left\{\left(\begin{array}{l}{\mathbf{z}}^t,\kern0.5em \mathbf{f}{\overset{.}{\mathbf{y}}}^t+\kern0.5em {\overset{.}{\mathbf{c}}}^t,\kern0.5em {\mathbf{b}}^t,\\ {}\mathbf{f}{\ddot{\mathbf{y}}}^t+{\ddot{\mathbf{c}}}^t\end{array}\right)\in {\Re}_{+}^{Q+L+M}\kern0.62em \left|\begin{array}{l}\kern0.5em {\displaystyle {\sum}_{j=1}^J{\mathbf{z}}_j^t{\lambda}_j^t}\le {\mathbf{z}}^{2t},\kern1em {\mathbf{b}}^t\ge {\displaystyle {\sum}_{j=1}^J{\theta}^t{\mathbf{b}}_j^t{\lambda}_j^{2t}},\kern0.5em \\ {}\kern0.5em \mathbf{f}{\overset{.}{\mathbf{y}}}^t+{\overset{.}{\mathbf{c}}}^t\le {\displaystyle {\sum}_{j=1}^J{\theta}^t{\overset{.}{\mathbf{y}}}_j^t{\lambda}_j^{2t}},\kern0.5em \\ {}\kern0.5em \mathbf{f}{\ddot{\mathbf{y}}}^t+{\ddot{\mathbf{c}}}^t\le {\displaystyle {\sum}_{j=1}^J{\ddot{\mathbf{y}}}_j^t{\lambda}_j^{2t}},\\ {}\kern0.5em {\overset{.}{\mathbf{c}}}^{t-1}\ge {\displaystyle {\sum}_{j=1}^J{\overset{.}{\mathbf{c}}}_j^{t-1}{\lambda}_j^{2t}},\kern1em {\ddot{\mathbf{c}}}^{t-1}\ge {\displaystyle {\sum}_{j=1}^J{\ddot{\mathbf{c}}}_j^{t-1}{\lambda}_j^{2t}},\kern0.5em \\ {}\kern0.5em {\boldsymbol{\uplambda}}_j^{2t}\ge \mathbf{0},\kern1em 0\le {\theta}^t\le 1,\kern1em \forall t=1,\dots, T\end{array}\right.\right\}.\hfill \end{array} $$
(10.16)

Combining (10.15) and (10.16), we obtain the DEA-based technology for t denoted as

$$ \begin{array}{ll}\hfill & N{T}^t\\ {}& =\left\{\left(\begin{array}{l}{\mathbf{b}}^{t-1},\kern0.5em {\mathbf{x}}^t,\kern0.5em {\mathbf{c}}^{t-1},\\ {}\mathbf{f}{\overset{.}{\mathbf{y}}}^t+\kern0.5em {\overset{.}{\mathbf{c}}}^t,\kern0.5em \\ {}\mathbf{f}{\ddot{\mathbf{y}}}^t+{\ddot{\mathbf{c}}}^t,\kern0.5em {\mathbf{b}}^t\end{array}\right)\kern0.5em \in {\Re}_{+}^{L+N+M+\overset{.}{M}+\ddot{M}+L}\kern0.62em \left|\begin{array}{l}\kern0.5em {\mathbf{b}}^{t-1}\ge {\displaystyle \sum_{j=1}^J{\varphi}^t{\mathbf{b}}_j^{t-1}{\lambda}_j^{1t}},\kern1em {\mathbf{x}}^t\ge {\displaystyle {\sum}_{j=1}^J{\varphi}^t{\mathbf{x}}_j^t{\lambda}_j^{1t}},\\ {}\kern0.5em {\displaystyle {\sum}_{j=1}^J{\mathbf{z}}_j^t\left({\lambda}_j^{1t}-{\lambda}_j^{2t}\right)}\ge \mathbf{0},\kern1em {\mathbf{b}}^t\ge {\displaystyle {\sum}_{j=1}^J{\theta}^t{\mathbf{b}}_j^t{\lambda}_j^{2t}},\kern0.5em \\ {}\kern0.5em \mathbf{f}{\overset{.}{\mathbf{y}}}^t+{\overset{.}{\mathbf{c}}}^t\le {\displaystyle \sum_{j=1}^J{\theta}^t{\overset{.}{\mathbf{y}}}_j^t{\lambda}_j^{2t}},\kern1em \\ {}\kern0.5em \mathbf{f}{\ddot{\mathbf{y}}}^t+{\ddot{\mathbf{c}}}^t\le {\displaystyle {\sum}_{j=1}^J{\ddot{\mathbf{y}}}_j^t{\lambda}_j^{2t}},\\ {}\kern0.5em {\overset{.}{\mathbf{c}}}^{t-1}\ge {\displaystyle {\sum}_{j=1}^J{\overset{.}{\mathbf{c}}}_j^{t-1}{\lambda}_j^{2t}},\kern1em {\ddot{\mathbf{c}}}^{t-1}\ge {\displaystyle {\sum}_{j=1}^J{\ddot{\mathbf{c}}}_j^{t-1}{\lambda}_j^{2t}},\kern1em {\mathbf{z}}^t\ge \mathbf{0},\\ {}\kern0.5em {\boldsymbol{\uplambda}}^{1t}\ge \mathbf{0},\kern1em {\boldsymbol{\uplambda}}^{2t}\ge \mathbf{0},\kern1em {\varphi}^t\ge 1,\kern1em 0\le {\theta}^t\le 1,\kern1em \forall t=1,\dots, T\end{array}\right.\right\}.\hfill \end{array} $$
(10.17)

We use \( {\mathbf{b}}^t\ge {\displaystyle {\sum}_{j=1}^J{\theta}^t{\mathbf{b}}_j^t{\lambda}_j^{2t}} \) rather than \( {\mathbf{b}}^t={\displaystyle {\sum}_{j=1}^J{\theta}^t{\mathbf{b}}_j^t{\lambda}_j^{2t}} \) in (10.16) and (10.17), but this treatment does not indicate that undesirable outputs are inputs due to the condition that \( 0\le {\theta}^t\le 1 \). In fact, Färe et al. (2016) also replaced the equality “=” by the inequality “\( \ge \)” in a static black-box setting where no distinction was made between desirable outputs linked with jointly produced undesirable outputs and desirable outputs not linked to undesirable outputs. They stated that such a treatment was consistent with treating b t as undesirable outputs, rather than inputs.

In (10.17) two sets of constraints link the two stages of production. These constraints are for the intermediate outputs produced in stage 1 which are then used as an input to stage 2. The constraints are

$$ {\displaystyle \sum_{j=1}^J{\mathbf{z}}_j^t{\lambda}_j^{1t}}\ge \mathbf{z}\kern1em \mathrm{and}\kern0.5em {\displaystyle \sum_{j=1}^J{\mathbf{z}}_j^t{\lambda}_j^{2t}}\le \mathbf{z}\kern1.5em \iff \kern1em {\displaystyle \sum_{j=1}^J{\mathbf{z}}_j^t\left({\lambda}_j^{1t}-{\lambda}_j^{2t}\right)}\ge \mathbf{0}. $$
(10.18)

See Fukuyama and Weber (2010, 2014) and see also Chen et al. (2009b) and Chen et al. (2010). Equation (10.18) allows some of the intermediate outputs produced in stage 1 to be wasted in that not all of the intermediate outputs are needed to produce the final outputs in stage 2. Fukuyama and Weber (2015a) found that Japanese commercial banks produced more deposits in stage 1 than were needed to produce the portfolio of loans and securities investments in stage 2. An et al. (2015) also studied the relation between the degree of centralization and the internal resource waste for a two-stage network DEA problem. Fukuyama and Mirdehghan (2012) and Mirdehghan and Fukuyama (2016) examined (10.18) in a more general network DEA framework from a Pareto-Koopmans efficiency perspective.

The dynamic network directional distance function can be estimated using DEA by substituting the dynamic network DEA technology (10.17) into (10.11). Let \( \mathbf{g}=\left({\mathbf{g}}_x,\kern0.15em {\mathbf{g}}_{\overset{.}{y}}\kern-0.15em ,\kern0.15em {\mathbf{g}}_{\ddot{y}},\kern0.15em {\mathbf{g}}_b\right) \) be a predetermined directional vector for exogenous inputs, linked outputs, unlinked outputs and undesirable outputs and let w t represent the pre-determined weights for each period. The T-period DN-directional technology distance function is estimated using DEA as

$$ \begin{array}{l}DN\overrightarrow{D}\left({\Omega}_k;\mathbf{g}\right)\kern1em =\underset{\beta^t,\kern0.5em {\overset{.}{\mathbf{c}}}^t,\kern0.5em {\ddot{\mathbf{c}}}^t,\kern0.5em {\boldsymbol{\uplambda}}^{1t},\kern0.5em {\boldsymbol{\uplambda}}^{2t},\kern0.5em {\varphi}^t,\kern0.5em {\theta}^t}{\mathrm{maximize}}\kern0.5em {w}^1{\beta}^1+{w}^2{\beta}^2+\dots +{w}^T{\beta}^T\\ {}\kern0.75em \mathrm{subject}\ \mathrm{t}\mathrm{o}:\\ {}\boxed{\mathrm{bank}\ k\ \mathrm{in}\ t=1\ \mathrm{and}\ \mathrm{t}\mathrm{echnology}\ \mathrm{at}\ t=1}\\ {}\kern2em {\mathbf{b}}_k^0\ge {\displaystyle {\sum}_{j=1}^J{\varphi}^1{\mathbf{b}}_j^0{\lambda}_j^{1,1}},\kern1em {\mathbf{x}}_k^1-{\beta}^1{\mathbf{g}}_x\ge {\displaystyle {\sum}_{j=1}^J{\varphi}^1{\mathbf{x}}_j^1{\lambda}_j^{1,1}},\kern1em {\displaystyle {\sum}_{j=1}^J{\mathbf{z}}_j^1\left({\lambda}_j^{1,1}-{\lambda}_j^{2,1}\right)}\ge \mathbf{0},\\ {}\kern2em {\overset{.}{\mathbf{c}}}_k^0\ge {\displaystyle {\sum}_{j=1}^J{\overset{.}{\mathbf{c}}}_j^0{\lambda}_j^{2,1}},\kern1em {\ddot{\mathbf{c}}}_k^0\ge {\displaystyle {\sum}_{j=1}^J{\ddot{\mathbf{c}}}_j^0{\lambda}_j^{2,1}},\kern1em {\mathbf{b}}_k^1-{\beta}^1{\mathbf{g}}_b\ge {\displaystyle \sum_{j=1}^J{\theta}^1{\mathbf{b}}_j^1{\lambda}_j^{2,1}},\\ {}\kern2em \mathbf{f}{\overset{.}{\mathbf{y}}}_k^1+{\overset{.}{\mathbf{c}}}^1+{\beta}^1{\mathbf{g}}_{\overset{.}{y}}\le {\displaystyle {\sum}_{j=1}^J{\theta}^1{\overset{.}{\mathbf{y}}}_j^1{\lambda}_j^{2,1}},\kern1em \mathbf{f}{\ddot{\mathbf{y}}}_k^1+{\ddot{\mathbf{c}}}^1+{\beta}^1{\mathbf{g}}_{\ddot{y}}\le {\displaystyle {\sum}_{j=1}^J{\ddot{\mathbf{y}}}_j^1{\lambda}_j^{2,1}},\\ {}\kern2em {\beta}^1\ge 0,\kern1em {\boldsymbol{\uplambda}}^{1,1}\ge \mathbf{0},\kern1em {\boldsymbol{\uplambda}}^{2,1}\ge \mathbf{0},\kern1em {\overset{.}{\mathbf{c}}}^1\ge \mathbf{0},\kern1em {\ddot{\mathbf{c}}}^1\ge \mathbf{0}\kern0.5em ,\kern1em {\varphi}^1\ge 1,\kern1em 0\le {\theta}^1\le 1\end{array} $$
(10.19)
$$ \begin{array}{l}\boxed{\mathrm{bank}\ k\ \mathrm{in}\ t=2,\dots T\ \mathrm{and}\ \mathrm{technology}\ \mathrm{at}\ t=2,\dots, T}\\ {}\kern3em {\mathbf{b}}_k^{t-1}-{\beta}^{t-1}{\mathbf{g}}_{\mathbf{b}}\ge {\displaystyle {\sum}_{j=1}^J{\varphi}^t{\mathbf{b}}_j^{t-1}{\lambda}_j^{1t}},\kern1em {\mathbf{x}}_k^t-{\beta}^t{\mathbf{g}}_x\ge {\displaystyle {\sum}_{j=1}^J{\varphi}^t{\mathbf{x}}_j^t{\lambda}_j^{1t}},\kern1em {\displaystyle {\sum}_{j=1}^J{\mathbf{z}}_j^t\left({\lambda}_j^{1t}-{\lambda}_j^{2t}\right)}\ge \mathbf{0},\\ {}\kern3em {\overset{.}{\mathbf{c}}}^{t-1}\ge {\displaystyle {\sum}_{j=1}^J{\overset{.}{\mathbf{c}}}_j^{t-1}{\lambda}_j^{2,t}},\kern1em {\ddot{\mathbf{c}}}^{t-1}\ge {\displaystyle {\sum}_{j=1}^J{\ddot{\mathbf{c}}}_j^{t-1}{\lambda}_j^{2,t}},\kern1em {\mathbf{b}}_k^t-{\beta}^t{\mathbf{g}}_b\ge {\displaystyle {\sum}_{j=1}^J{\theta}^t{\mathbf{b}}_j^t{\lambda}_j^{2t}},\\ {}\kern3em \mathbf{f}{\overset{.}{\mathbf{y}}}_k^t+{\beta}^t{\mathbf{g}}_{\overset{.}{y}}+{\overset{.}{\mathbf{c}}}^t\le {\displaystyle {\sum}_{j=1}^J{\theta}^t{\overset{.}{\mathbf{y}}}_j^t{\lambda}_j^{2t}},\kern1em \mathbf{f}{\ddot{\mathbf{y}}}_k^t+{\beta}^t{\mathbf{g}}_{\ddot{y}}+{\ddot{\mathbf{c}}}^t\le {\displaystyle {\sum}_{j=1}^J{\ddot{\mathbf{y}}}_j^t{\lambda}_j^{2t}},\\ {}\kern3em {\beta}^t\ge 0,\kern1em {\boldsymbol{\uplambda}}^{1t}\ge \mathbf{0},\kern1em {\boldsymbol{\uplambda}}^{2t}\ge \mathbf{0},\kern1em {\overset{.}{\mathbf{c}}}^t\ge \mathbf{0},\kern1em {\ddot{\mathbf{c}}}^t\ge \mathbf{0},\kern1em {\varphi}^t\ge 1,\kern1em 0\le {\theta}^t\le 1.\end{array} $$

The T-period DN-directional technology distance function is a dynamic network version of the directional technology distance function due to Chambers et al. (1996).

Although (10.19) is a nonlinear program it can be transformed into a linear program by transforming the intensity variables using the Kuosmanen’s (2005) procedure. Let \( {\gamma}_j^{1t}={\varphi}^t{\lambda}_j^{1t} \) and let \( {\mu}_j^{1t}=\left(1-{\varphi}^t\right){\lambda}_j^{1t} \) where \( {\mu}_j^{1t}\kern1em \left(j=1,\dots, J\right) \) are non-positive. Consequently, the stage 1 intensity variables can be written as \( {\lambda}_j^{1t}={\gamma}_j^{1t}+{\mu}_j^{1t} \). Similarly, let \( {\gamma}_j^{2t}={\theta}^t{\lambda}_j^{2t} \) and let \( {\mu}_j^{2t}=\left(1-{\theta}^t\right){\lambda}_j^{2t} \) where \( {\mu}_j^{2t}\kern1em \left(j=1,\dots, J\right) \) are non-negative. Thus, the stage 2 intensity variables can be written as \( {\lambda}_j^{2t}={\gamma}_j^{2t}+{\mu}_j^{2t} \). Note that γ 1t j  and γ 2t j are non-negative. Substituting these transformed variables into (10.19) yields

$$ \begin{array}{l}{\displaystyle {\sum}_{t=1}^T{w}^t{\beta}^t\left[t\right]}\kern1em =\underset{\beta^t,\kern0.5em {\overset{.}{\mathbf{c}}}^t,\kern0.5em {\ddot{\mathbf{c}}}^t,\kern0.5em {\gamma}_j^{1t},\kern0.5em {\mu}_j^{1t},\kern0.5em {\gamma}_j^{2t},\kern0.5em {\mu}_j^{2t}}{\mathrm{maximize}}{w}^1{\beta}^1+{w}^2{\beta}^2+\dots +{w}^T{\beta}^T\\ {}\mathrm{subject}\ \mathrm{t}\mathrm{o}:\\ {}\boxed{\mathrm{bank}\ k\ \mathrm{in}\ t=1\ \mathrm{and}\ \mathrm{t}\mathrm{echnology}\ \mathrm{in}\ t=1}\\ {}\kern2em {\mathbf{b}}_k^0\ge {\displaystyle {\sum}_{j=1}^J{\mathbf{b}}_j^0{\gamma}_j^{1,1}},\kern1em {\mathbf{x}}_k^1-{\beta}^1{\mathbf{g}}_x\ge {\displaystyle {\sum}_{j=1}^J{\mathbf{x}}_j^1{\gamma}_j^{1,1}},\kern1.5em \\ {}\kern2em {\displaystyle {\sum}_{j=1}^J{\mathbf{z}}_j^1\left(\left({\gamma}_j^{1,1}+{\mu}_j^{1,1}\right)-\left({\gamma}_j^{2,1}+{\mu}_j^{2,1}\right)\right)}\ge \mathbf{0},\kern1em \\ {}\kern2em {\overset{.}{\mathbf{c}}}_k^0\ge {\displaystyle {\sum}_{j=1}^J{\overset{.}{\mathbf{c}}}_j^0\left({\gamma}_j^{2,1}+{\mu}_j^{2,1}\right)},\kern1em {\ddot{\mathbf{c}}}_k^0\ge {\displaystyle {\sum}_{j=1}^J{\ddot{\mathbf{c}}}_j^0\left({\gamma}_j^{2,1}+{\mu}_j^{2,1}\right)},\\ {}\kern2em {\mathbf{b}}^1-{\beta}^1{\mathbf{g}}_b\ge {\displaystyle {\sum}_{j=1}^J{\mathbf{b}}_j^1{\gamma}_j^{2,1}},\kern1em \\ {}\kern2em \mathbf{f}{\overset{.}{\mathbf{y}}}_k^1+{\beta}^1{\mathbf{g}}_{\overset{.}{y}}+{\overset{.}{\mathbf{c}}}^1\le {\displaystyle {\sum}_{j=1}^J{\overset{.}{\mathbf{y}}}_j^1{\gamma}_j^{2,1}},\kern1em \\ {}\kern2em \mathbf{f}{\ddot{\mathbf{y}}}_k^1+{\beta}^1{\mathbf{g}}_{\ddot{y}}+{\ddot{\mathbf{c}}}^1\le {\displaystyle {\sum}_{j=1}^J{\ddot{\mathbf{y}}}_j^1\left({\gamma}_j^{2,1}+{\mu}_j^{2,1}\right)},\kern1.5em \\ {}\kern2em {\beta}^1\ge 0,\kern1em {\boldsymbol{\uplambda}}^{1,1}\ge \mathbf{0},\kern1em {\boldsymbol{\uplambda}}^{2,1}\ge \mathbf{0},\kern1em {\overset{.}{\mathbf{c}}}^1\ge \mathbf{0},\kern1em {\ddot{\mathbf{c}}}^1\ge \mathbf{0}\kern0.5em ,\kern1em \\ {}\kern2em {\gamma}_j^{1,1}\ge 0,\kern1em {\mu}_j^{1,1}\le 0,\kern1em {\gamma}_j^{2,1}\ge 0,\kern1em {\mu}_j^{2,1}\ge 0\kern1em \left(j=1,\dots, J\right)\\ {}\kern2em {\gamma}_j^{1,1}+{\mu}_j^{1,1}\ge 0\kern1em \left(j=1,\dots, J\right),\kern0.5em {\gamma}_j^{2,1}+{\mu}_j^{2,t}\ge 0\kern1em \left(j=1,\dots, J\right),\end{array} $$
(10.20)
$$ \begin{array}{l}\boxed{\mathrm{bank}\ k\ \mathrm{in}\ t=2,\dots T\ \mathrm{and}\ \mathrm{technology}\ \mathrm{at}\ t=2,\dots, T}\\ {}\kern2em {\mathbf{b}}_k^{t-1}-{\beta}^{t-1}{\mathbf{g}}_b\ge {\displaystyle {\sum}_{j=1}^J{\mathbf{b}}_j^{t-1}{\gamma}_j^{1t}},\kern1em {\mathbf{x}}_k^t-{\beta}^t{\mathbf{g}}_b\ge {\displaystyle {\sum}_{j=1}^J{\mathbf{x}}_j^t{\gamma}_j^{1t}},\kern1.5em ,\\ {}\kern2em {\displaystyle {\sum}_{j=1}^J{\mathbf{z}}_j^t\left(\left({\gamma}_j^{1t}+{\mu}_j^{1t}\right)-\left({\gamma}_j^{2t}+{\mu}_j^{2t}\right)\right)}\ge \mathbf{0},\\ {}\kern2em {\overset{.}{\mathbf{c}}}^{t-1}\ge {\displaystyle {\sum}_{j=1}^J{\overset{.}{\mathbf{c}}}_j^{t-1}\left({\gamma}_j^{2t}+{\mu}_j^{2t}\right)},\kern1em {\ddot{\mathbf{c}}}^{t-1}\ge {\displaystyle {\sum}_{j=1}^J{\ddot{\mathbf{c}}}_j^{t-1}\left({\gamma}_j^{2t}+{\mu}_j^{2t}\right)},\\ {}\kern2em {\mathbf{b}}^t-{\beta}^t{\mathbf{g}}_b\ge {\displaystyle {\sum}_{j=1}^J{\mathbf{b}}_j^t{\gamma}_j^{2t}},\kern1em \\ {}\kern2em \mathbf{f}{\overset{.}{\mathbf{y}}}_k^t+{\beta}^t{\mathbf{g}}_{\overset{.}{y}}+{\overset{.}{\mathbf{c}}}^t\le {\displaystyle {\sum}_{j=1}^J{\overset{.}{\mathbf{y}}}_j^t{\gamma}_j^{2t}},\kern1em \\ {}\kern2em \mathbf{f}{\ddot{\mathbf{y}}}_k^t+{\beta}^t{\mathbf{g}}_{\ddot{y}}+{\ddot{\mathbf{c}}}^t\le {\displaystyle {\sum}_{j=1}^J{\ddot{\mathbf{y}}}_j^t\Big({\gamma}_j^{2t}}+{\mu}_j^{2t}\Big),\kern1.5em \\ {}\kern2em {\beta}^t\ge 0,\kern1em {\boldsymbol{\uplambda}}^{1t}\ge \mathbf{0},\kern1em {\boldsymbol{\uplambda}}^{2t}\ge \mathbf{0},\kern1em {\overset{.}{\mathbf{c}}}^t\ge \mathbf{0},\kern1em {\ddot{\mathbf{c}}}^t\ge \mathbf{0}\kern0.5em ,\kern1em \\ {}\kern2em {\gamma}_j^{1t}\ge 0,\kern1em {\mu}_j^{1t}\le 0,\kern1em {\gamma}_j^{2t}\ge 0,\kern1em {\mu}_j^{2t}\ge 0\kern2em \left(j=1,\dots, J\right)\\ {}\kern2em {\gamma}_j^{1t}+{\mu}_j^{1t}\ge 0\kern1em \left(j=1,\dots, J\right),\kern1.5em {\gamma}_j^{2t}+{\mu}_j^{2t}\ge 0\kern1em \left(j=1,\dots, J\right),\kern1em t=2,\dots, T.\end{array} $$

where carryover assets, \( {\overset{.}{\mathbf{c}}}^t \), \( {\ddot{\mathbf{c}}}^t\kern1em \left(\forall t=1,\dots, T\right) \) are choice variables and the optimized values β t[t] represent bank inefficiency in period t with \( DN\overrightarrow{D}\left({\Omega}_k;\mathbf{g}\right)={\displaystyle {\sum}_{t=1}^T{w}^t{\beta}^t\left[t\right]} \).

The dynamic-network performance problem (10.20) selects the maximal value of the weighted sum of scaling factors related to exogenous inputs, the undesirable output of nonperforming loans and the desirable outputs of loans and securities investments. The model (10.20) differs from those of Fukuyama and Weber (2013, 2015a, b) by incorporating joint weak input-disposability (JWID) given by (10.12) and joint weak output-disposability (JWOD) given by (10.14). The multi-period dynamic-network directional distance function \( DN\overrightarrow{D}\left({\Omega}_k;\mathbf{g}\right) \) extends the static black-box directional technology distance function due to Chambers et al. (1998). The optimal values of the intermediate outputs, z t, can be calculated using the optimal intensity variables with \( {\displaystyle {\sum}_{j=1}^J{\mathbf{z}}_j^t\left({\gamma}_j^{1t}+{\mu}_j^{1t}\right)} \) providing an upper bound estimate for z t and \( {\displaystyle {\sum}_{j=1}^J{\mathbf{z}}_j^t\left({\gamma}_j^{2t}+{\mu}_j^{2t}\right)} \) providing a lower bound estimate of z t. Values of \( DN{\overrightarrow{D}}_k=DN\overrightarrow{D}\left({\Omega}_k;\mathbf{g}\right)=0 \) indicate that DMU k is efficient in every period with no ability to simultaneously expand final outputs and contract undesirable outputs given the DEA technology. When \( DN{\overrightarrow{D}}_k>0 \), DMU k is inefficient with larger values indicating greater inefficiency.

The objective function of (10.20) is a weighted bank performance score equal to the sum of the product of the weights (w t) and the period t directional technology distance functions β t[t] over the \( t=1,\dots, T \) periods. For the estimation of various productivity indicators we need to calculate cross-period directional technology distance functions \( {\beta}^{t+1}\left[t\right] \) and \( {\beta}^t\left[t+1\right] \), \( t=1,\dots, T-1 \), where \( {\beta}^{t+1}\left[t\right] \) measures the distance of the observed banks inputs and outputs in period t relative to the technology in period t + 1 and \( {\beta}^t\left[t+1\right] \) measures the observed bank’s inputs and outputs in period t + 1 relative to the technology in period t. We estimate the cross-period DN-directional technology distance functions by building on Pastor, Asmild, and Lovell’s (2011) biennial Malmquist index and Färe et al. (2011) dynamic Malmquist index.

Using the cross-period estimates, the DN-Luenberger productivity indicator \( \left(DN{L}^{t,t+1}\right) \) is obtained as

$$ \begin{array}{l}DN{L}^{t,t+1}=\frac{1}{2}\left[\left({w}^t{\beta}^t\left[t\right]-{w}^t{\beta}^t\left[t+1\right]\right)+\left({w}^{t+1}{\beta}^{t+1}\left[t\right]-{w}^{t+1}{\beta}^{t+1}\left[t+1\right]\right)\right],\\ {}\kern3.28em t=1,\dots, T-1.\end{array} $$
(10.21)

A DMU experiences productivity growth (decline) between periods t and t + 1 if \( DN{L}^{t,t+1} \) is positive (negative). The DN-Luenberger productivity indicator extends Chambers' (2002) static Luenberger productivity indicator for a dynamic network technology. The DN-Luenberger productivity indicator can also be thought of as an additive version of the static Malmquist productivity index of Färe et al. (1994).

To estimate \( {\beta}^t\left[t+1\right] \) we solve the following optimization problem:

$$ \begin{array}{l}{\displaystyle {\sum}_{t=1}^{T-1}{w}^t{\beta}^t\left[t+1\right]}\kern1em =\kern1em \underset{\beta^t,\kern0.5em {\overset{.}{\mathbf{c}}}^t,\kern0.5em {\ddot{\mathbf{c}}}^t,\kern0.5em {\gamma}_j^{1t},\kern0.5em {\mu}_j^{1t},\kern0.5em {\gamma}_j^{2t},\kern0.5em {\mu}_j^{2t}}{\operatorname{maximize}}\kern1em {\displaystyle {\sum}_{t=1}^{T-1}{w}^t{\beta}^t}\\ {}\mathrm{subject}\ \mathrm{t}\mathrm{o}:\\ {}\boxed{\mathrm{bank}\ k\ \mathrm{in}\ t=2\ \mathrm{and}\ \mathrm{t}\mathrm{echnology}\ \mathrm{in}\ t=1}\\ {}\kern2em {\mathbf{b}}_k^1\ge {\displaystyle {\sum}_{j=1}^J{\mathbf{b}}_j^0{\gamma}_j^{1,1}},\kern1em {\mathbf{x}}_k^2-{\beta}^1{\mathbf{g}}_x\ge {\displaystyle {\sum}_{j=1}^J{\mathbf{x}}_j^1{\gamma}_j^{1,1}},\kern1.5em \\ {}\kern2em {\displaystyle {\sum}_{j=1}^J{\mathbf{z}}_j^1\left(\left({\gamma}_j^{1,1}+{\mu}_j^{1,1}\right)-\left({\gamma}_j^{2,1}+{\mu}_j^{2,1}\right)\right)}\ge \mathbf{0},\kern0.5em {\overset{.}{\mathbf{c}}}_k^1\ge {\displaystyle {\sum}_{j=1}^J{\overset{.}{\mathbf{c}}}_j^0\left({\gamma}_j^{2,1}+{\mu}_j^{2,1}\right)},\\ {}\kern2em {\ddot{\mathbf{c}}}_k^1\ge {\displaystyle {\sum}_{j=1}^J{\ddot{\mathbf{c}}}_j^0\left({\gamma}_j^{2,1}+{\mu}_j^{2,1}\right)},\kern1em {\mathbf{b}}^2-{\beta}^1{\mathbf{g}}_b\ge {\displaystyle {\sum}_{j=1}^J{\mathbf{b}}_j^1{\gamma}_j^{2,1}},\kern0.5em \\ {}\kern2em \mathbf{f}{\overset{.}{\mathbf{y}}}_k^2+{\beta}^1{\mathbf{g}}_{\overset{.}{y}}+{\overset{.}{\mathbf{c}}}^2+\kern0.5em {\overset{.}{\mathbf{s}}}^2={\displaystyle {\sum}_{j=1}^J{\overset{.}{\mathbf{y}}}_j^1{\gamma}_j^{2,1}},\\ {}\kern2em \mathbf{f}{\ddot{\mathbf{y}}}_k^2+{\beta}^1{\mathbf{g}}_{\ddot{y}}+{\ddot{\mathbf{c}}}^2+\kern0.5em {\ddot{\mathbf{s}}}^2={\displaystyle {\sum}_{j=1}^J{\ddot{\mathbf{y}}}_j^1\Big({\gamma}_j^{2,1}+}{\mu}_j^{2,1}\Big),\kern1.5em \\ {}\kern2em {\beta}^1:\kern0.5em \mathrm{free},\kern1em {\boldsymbol{\uplambda}}^{1,1}\ge \mathbf{0},\kern1em {\boldsymbol{\uplambda}}^{2,1}\ge \mathbf{0},\kern1em {\overset{.}{\mathbf{c}}}^2\ge \mathbf{0},\kern1em {\ddot{\mathbf{c}}}^2\ge \mathbf{0}\kern0.5em ,\kern1em {\overset{.}{\mathbf{s}}}^2:\kern0.5em \mathrm{free},\kern1em {\ddot{\mathbf{s}}}^2:\kern0.5em \mathrm{free},\\ {}\kern2em {\gamma}_j^{1,1}\ge 0,\kern1em {\mu}_j^{1,1}\le 0,\kern1em {\gamma}_j^{2,1}\ge 0,\kern1em {\mu}_j^{2,1}\ge 0\kern1em \left(j=1,\dots, J\right)\\ {}\kern2em {\gamma}_j^{1,1}+{\mu}_j^{1,1}\ge 0\kern1em \left(j=1,\dots, J\right),\kern1em {\gamma}_j^{2,1}+{\mu}_j^{2,1}\ge 0\kern1em \left(j=1,\dots, J\right)\end{array} $$
(10.22)
$$ \begin{array}{l}\boxed{\mathrm{bank}\ k\ \mathrm{in}\ t=3,\dots T\ \mathrm{and}\ \mathrm{technology}\ \mathrm{at}\ t=2,\dots, T-1}\\ {}\kern2em {\mathbf{b}}_k^t-{\beta}^{t-1}{\mathbf{g}}_{\mathbf{b}}\ge {\displaystyle {\sum}_{j=1}^J{\mathbf{b}}_j^{t-1}{\gamma}_j^{1t}},\kern1em {\mathbf{x}}_k^{t+1}-{\beta}^t{\mathbf{g}}_x\ge {\displaystyle {\sum}_{j=1}^J{\mathbf{x}}_j^t{\gamma}_j^{1t}},\kern1em \\ {}\kern2em {\displaystyle {\sum}_{j=1}^J{\mathbf{z}}_j^t\left(\left({\gamma}_j^{1t}+{\mu}_j^{1t}\right)-\left({\gamma}_j^{2t}+{\mu}_j^{2t}\right)\right)}\ge \mathbf{0},\\ {}\kern2em {\overset{.}{\mathbf{c}}}^t\ge {\displaystyle {\sum}_{j=1}^J{\overset{.}{\mathbf{c}}}_j^{t-1}\left({\gamma}_j^{2t}+{\mu}_j^{2t}\right)},\kern1em {\ddot{\mathbf{c}}}^t\ge {\displaystyle {\sum}_{j=1}^J{\ddot{\mathbf{c}}}_j^{t-1}\left({\gamma}_j^{2t}+{\mu}_j^{2t}\right)},\\ {}\kern2em {\mathbf{b}}_k^{t+1}-{\beta}^t{\mathbf{g}}_b\ge {\displaystyle {\sum}_{j=1}^J{\mathbf{b}}_j^t{\gamma}_j^{2t}},\kern0.5em \\ {}\kern2em \mathbf{f}{\overset{.}{\mathbf{y}}}_k^{t+1}+{\beta}^t{\mathbf{g}}_{\overset{.}{y}}+{\overset{.}{\mathbf{c}}}^{t+1}+\kern0.5em {\overset{.}{\mathbf{s}}}^{t+1}={\displaystyle {\sum}_{j=1}^J{\overset{.}{\mathbf{y}}}_j^t{\gamma}_j^{2t}},\\ {}\kern2em \mathbf{f}{\ddot{\mathbf{y}}}_k^{t+1}+{\beta}^t{\mathbf{g}}_{\ddot{y}}+{\ddot{\mathbf{c}}}^{t+1}+\kern0.5em {\ddot{\mathbf{s}}}^{t+1}={\displaystyle {\sum}_{j=1}^J{\ddot{\mathbf{y}}}_j^t\Big({\gamma}_j^{2t}}+{\mu}_j^{2t}\Big),\kern1.5em \\ {}\kern2em {\beta}^t:\kern0.5em \mathrm{free}\ \mathrm{in}\ \mathrm{sign},\kern1em {\overset{.}{\mathbf{c}}}^t\ge \mathbf{0},\kern1em {\ddot{\mathbf{c}}}^t\ge \mathbf{0}\kern0.5em ,\\ {}\kern2em {\overset{.}{\mathbf{s}}}^{t+1}:\kern0.5em \mathrm{free}\ \mathrm{in}\ \mathrm{sign},\kern1em {\ddot{\mathbf{s}}}^{t+1}:\kern0.5em \mathrm{free}\ \mathrm{in}\ \mathrm{sign},\kern0.5em \\ {}\kern2em {\gamma}_j^{1t}\ge 0,\kern1em {\mu}_j^{1t}\le 0,\kern1em {\gamma}_j^{2t}\ge 0,\kern1em {\mu}_j^{2t}\ge 0\kern1em \left(j=1,\dots, J\right),\kern1em t=2,\dots, T-1\\ {}\kern2em {\gamma}_j^{1t}+{\mu}_j^{1t}\ge 0\kern1em \left(j=1,\dots, J\right),\kern1em {\gamma}_j^{2t}+{\mu}_j^{2t}\ge 0\kern1em \left(j=1,\dots, J\right),\kern1em t=2,\dots, T-1.\end{array} $$

The cross-period distance functions , \( {\beta}^{t+1}\left[t\right],\kern0.5em t=1,2,\dots, T-1 \), measure how far a bank’s observed inputs and outputs in period t are from the period t + 1 production frontier. These cross-period distance functions are found by solving the linear programming problem

$$ \begin{array}{l}{\displaystyle {\sum}_{t=1}^{T-1}{w}^{t+1}{\beta}^{t+1}\left[t\right]}=\underset{\beta^t,\kern0.5em {\overset{.}{\mathbf{c}}}^t,\kern0.5em {\ddot{\mathbf{c}}}^t,\kern0.5em {\gamma}_j^{1t},\kern0.5em {\mu}_j^{1t},\kern0.5em {\gamma}_j^{2t},\kern0.5em {\mu}_j^{2t}}{ \max}\kern1em {\displaystyle {\sum}_{t=1}^{T-1}{w}^{t+1}{\beta}^{t+1}}\\ {}\mathrm{subject}\ \mathrm{t}\mathrm{o}:\\ {}\boxed{\mathrm{bank}\ k\ \mathrm{in}\ t=1\ \mathrm{and}\ \mathrm{t}\mathrm{echnology}\ \mathrm{in}\ t=2}\\ {}\kern2em {\mathbf{b}}_k^0\ge {\displaystyle {\sum}_{j=1}^J{\mathbf{b}}_j^1{\gamma}_j^{1,2}},\kern1em {\mathbf{x}}_k^1-{\beta}^2{\mathbf{g}}_x\ge {\displaystyle {\sum}_{j=1}^J{\mathbf{x}}_j^2{\gamma}_j^{1,2}},\\ {}\kern2em {\displaystyle {\sum}_{j=1}^J{\mathbf{z}}_j^2\left(\left({\gamma}_j^{1,2}+{\mu}_j^{1,2}\right)-\left({\gamma}_j^{2,2}+{\mu}_j^{2,2}\right)\right)}\ge \mathbf{0},\\ {}\kern2em {\overset{.}{\mathbf{c}}}_k^0\ge {\displaystyle {\sum}_{j=1}^J{\overset{.}{\mathbf{c}}}_j^1\left({\gamma}_j^{2,2}+{\mu}_j^{2,2}\right)},\kern1em {\ddot{\mathbf{c}}}_k^0\ge {\displaystyle {\sum}_{j=1}^J{\ddot{\mathbf{c}}}_j^1\left({\gamma}_j^{2,2}+{\mu}_j^{2,2}\right)},\\ {}\kern2em {\mathbf{b}}_k^1-{\beta}^2{\mathbf{g}}_b\ge {\displaystyle {\sum}_{j=1}^J{\mathbf{b}}_j^1{\gamma}_j^{2,2}},\kern0.5em \\ {}\kern2em \mathbf{f}{\overset{.}{\mathbf{y}}}_k^1+{\beta}^2{\mathbf{g}}_{\overset{.}{y}}+{\overset{.}{\mathbf{c}}}^1+{\overset{.}{\mathbf{s}}}^1={\displaystyle {\sum}_{j=1}^J{\overset{.}{\mathbf{y}}}_j^2{\gamma}_j^{2,2}},\\ {}\kern2em \mathbf{f}{\ddot{\mathbf{y}}}_k^1+{\beta}^2{\mathbf{g}}_{\ddot{f}}+{\ddot{\mathbf{c}}}^1+{\ddot{\mathbf{s}}}^1={\displaystyle {\sum}_{j=1}^J{\ddot{\mathbf{y}}}_j^2\Big({\gamma}_j^{2,2}}+{\mu}_j^{2,2}\Big),\\ {}\kern2em {\beta}^2:\ \mathrm{free}\ \mathrm{in}\ \mathrm{sign},\kern1em {\overset{.}{\mathbf{c}}}^1\ge \mathbf{0},\kern1em {\ddot{\mathbf{c}}}^1\ge \mathbf{0},\\ {}\kern2em {\overset{.}{\mathbf{s}}}^1:\kern0.5em \mathrm{free}\ \mathrm{in}\ \mathrm{sign},\kern1em {\ddot{\mathbf{s}}}^1:\kern0.5em \mathrm{free}\ \mathrm{in}\ \mathrm{sign},\\ {}\kern2em {\gamma}_j^{1,2}\ge 0,\kern1em {\mu}_j^{1,2}\le 0,\kern1em {\gamma}_j^{2,2}\ge 0,\kern1em {\mu}_j^{2,2}\ge 0\kern1em \left(j=1,\dots, J\right)\\ {}\kern2em {\gamma}_j^{1,2}+{\mu}_j^{1,2}\ge 0\kern1em \left(j=1,\dots, J\right),\kern1em {\gamma}_j^{2,2}+{\mu}_j^{2,2}\ge 0\kern1em \left(j=1,\dots, J\right)\kern0.5em \end{array} $$
(10.23)
$$ \begin{array}{l}\boxed{\mathrm{bank}\ k\ \mathrm{in}\ t=2,\dots T-1\ \mathrm{and}\ \mathrm{technology}\ \mathrm{at}\ t=3,\dots, T}\\ {}\kern2em {\mathbf{b}}_k^{t-1}-{\beta}^t{\mathbf{g}}_b\ge {\displaystyle {\sum}_{j=1}^J{\mathbf{b}}_j^t{\gamma}_j^{1,t+1}},\kern1em {\mathbf{x}}_k^t-{\beta}^{t+1}{\mathbf{g}}_x\ge {\displaystyle {\sum}_{j=1}^J{\mathbf{x}}_j^{t+1}{\gamma}_j^{1,t+1}},\kern1em \\ {}\kern2em {\displaystyle {\sum}_{j=1}^J{\mathbf{z}}_j^{t+1}\left(\left({\gamma}_j^{1,t+1}+{\mu}_j^{1,t+1}\right)-\left({\gamma}_j^{2,t+1}+{\mu}_j^{2,t+1}\right)\right)}\ge \mathbf{0},\\ {}\kern2em {\overset{.}{\mathbf{c}}}^{t-1}\ge {\displaystyle {\sum}_{j=1}^J{\overset{.}{\mathbf{c}}}_j^t\left({\gamma}_j^{2,t+1}+{\mu}_j^{2,t+1}\right)},\kern0.5em {\ddot{\mathbf{c}}}^{t-1}\ge {\displaystyle {\sum}_{j=1}^J{\ddot{\mathbf{c}}}_j^t\left({\gamma}_j^{2,t+1}+{\mu}_j^{2,t+1}\right)},\\ {}\kern2em {\mathbf{b}}_k^t-{\beta}^{t+1}{\mathbf{g}}_b\ge {\displaystyle {\sum}_{j=1}^J{\mathbf{b}}_j^t{\gamma}_j^{2t}},\kern0.5em \\ {}\kern2em \mathbf{f}{\overset{.}{\mathbf{y}}}_k^t+{\beta}^{t+1}{\mathbf{g}}_{\overset{.}{y}}+{\overset{.}{\mathbf{c}}}^t+\kern0.5em {\overset{.}{\mathbf{s}}}^t={\displaystyle {\sum}_{j=1}^J{\overset{.}{\mathbf{y}}}_j^{t+1}{\gamma}_j^{2,t+1}},\\ {}\kern2em \mathbf{f}{\ddot{\mathbf{y}}}_k^t+{\beta}^{t+1}{\mathbf{g}}_{\ddot{y}}+{\ddot{\mathbf{c}}}^t+\kern0.5em {\ddot{\mathbf{s}}}^t={\displaystyle {\sum}_{j=1}^J{\ddot{\mathbf{y}}}_j^{t+1}\left({\gamma}_j^{2,t+1}+{\mu}_j^{2,t+1}\right)},\kern1em \\ {}\kern2em {\beta}^{t+1}:\ \mathrm{free}\ \mathrm{in}\ \mathrm{sign},\kern1.5em {\overset{.}{\mathbf{c}}}^t\ge \mathbf{0},\kern1em {\ddot{\mathbf{c}}}^t\ge \mathbf{0}\kern0.5em ,\kern0.5em \\ {}\kern2em {\overset{.}{\mathbf{s}}}^t:\kern0.5em \mathrm{free}\ \mathrm{in}\ \mathrm{sign},\kern1em {\ddot{\mathbf{s}}}^t:\kern0.5em \mathrm{free}\ \mathrm{in}\ \mathrm{sign},\kern0.5em \\ {}\kern2em {\gamma}_j^{1t}\ge 0,\kern1em {\mu}_j^{1t}\le 0,\kern1em {\gamma}_j^{2t}\ge 0,\kern1em {\mu}_j^{2t}\ge 0\kern2em \left(j=1,\dots, J\right),\kern1em t=2,\dots, T-1\\ {}\kern2em {\gamma}_j^{1,t+1}+{\mu}_j^{1,t+1}\ge 0\kern1em \left(j=1,\dots, J\right),\kern1em {\gamma}_j^{2,t+1}+{\mu}_j^{2,t+1}\ge 0\kern1em \left(j=1,\dots, J\right),\kern1em t=2,\dots, T-1.\end{array} $$

After solving the linear programming problems (10.20), (10.22), and (10.23), we can obtain the DN-Luenberger productivity indicator, \( DN{L}^{t,t+1} \), given in (10.21). This productivity indicator can be decomposed into a dynamic-network efficiency change indicator, \( DNE{C}^{t,t+1} \), and a dynamic-network technical change indicator, \( DNT{C}^{t,t+1} \):

$$ \begin{array}{l}DN{L}^{t,t+1}=\underset{DNE{C}^{t,t+1}}{\underbrace{w^t{\beta}^t\left[t\right]-{w}^{t+1}{\beta}^{t+1}\left[t+1\right]}}\\ {}\kern4.5em +\kern.1em \underset{DNT{C}^{t,t+1}}{\underbrace{\frac{1}{2}\left[\left\{{w}^{t+1}{\beta}^{t+1}\left[t\right]-{w}^t{\beta}^t\left[t\right]\right\}+\left\{{w}^{t+1}{\beta}^{t+1}\left[t+1\right]-{w}^t{\beta}^t\left[t+1\right]\right\}\right]}},\hfill \end{array} $$
(10.24)

A bank exhibits an efficiency gain (loss) if \( DNE{C}^{t,t+1} \) is positive (negative). Similarly, a bank exhibits technological progress (regress) if \( DNT{C}^{t,t+1} \) is positive (negative).

10.5 A Choice of Variables and Regulatory Constraints

10.5.1 Variable Selection: An Example

In this sub-section, we describe the bank inputs and outputs that were used by Fukuyama and Weber (2015a) in their dynamic network model. In their basic model, banks transform labor (x 1), physical capital (x 2) and financial equity capital (x 3) to produce deposits (z 1) and other raised funds (z 2) in stage 1. Then, in stage 2, banks use the intermediate products of stage 1 as inputs in producing loans \( \left(f{\overset{.}{y}}_{\kern-0.15em 1}\right) \) and securities investments (fÿ 2) as well as carryover assets \( \left(\mathbf{c}=\left({\overset{.}{c}}_1,\kern0.5em {\ddot{c}}_2\right)\right) \) and an undesirable by-product of nonperforming loans (b 1). Carryover assets are divided into carryover assets that come from loans \( \left({\overset{.}{c}}_1\right) \) and carryover assets that come from securities \( \left({\ddot{c}}_2\right) \). The total carryover assets \( \left({\overset{.}{c}}_{\kern-0.2em 1}+\kern0.5em {\ddot{c}}_2\right) \) are derived as:

$$ \begin{array}{ll}{\overset{.}{c}}_1+{\ddot{c}}_2=& \mathrm{Assets}-\mathrm{Required}\kern0.35em \mathrm{Reserves}-\mathrm{Physical}\kern0.35em \mathrm{capital}\left({x}_2\right)\kern1em \\ {}& -\mathrm{Performing}\kern0.35em \mathrm{loans}\left(f{\overset{.}{y}}_1\right)\kern1.85em -\mathrm{Securities}\kern0.35em \mathrm{investments}\kern0.5em \left(f{\ddot{y}}_2\right)\kern1em \\ {}& -\mathrm{Nonperforming}\kern0.35em \mathrm{loans}\kern0.5em \left({b}_1\right).\kern1em \end{array} $$
(10.25)

In their study, all carryover assets correspond with securities, i.e., c 1 = 0 and \( {c}_2>0 \). Since all carryovers are from securities investments, the network technology (10.17) exhibits null-jointness, because a proportional reduction in linked desirable and undesirable outputs is technologically feasible given the condition of JWOD. For the calculation of required reserves, see Fukuyama and Weber (2013, 2015a, b).

10.5.2 Imposing Bank Regulatory Constraint

Banks face a variety of financial regulations which constrain their ability to reduce certain kinds of inputs such as financial equity capital or to expand deposits and other raised funds without the use of extra financial equity capital, even if the technology would allow them to do so. In addition, financial regulations also constrain the ability of banks to make certain kinds of risky loans without additional financial equity capital. Fukuyama and Weber (2015a) incorporated these financial regulatory constraints into the DEA technology. Since Japanese domestic banks are required to have qualifying equity capital as a percent of risk-weighted assets (wA t k ) greater than 4 %, bank k’s capital adequacy ratio is expressed as

$$ CA{R}_k^t=\frac{Tier\kern0.5em {1}_k^t+ Tier\kern0.5em {2}_k^t- deduc{t}_k^t}{w{A}_k^t}\ge 0.04 $$
(10.26)

where Tier 1 t k is core tier 1 bank capital (primarily shareholders’ equity), Tier 2 t k is supplementary bank capital and deduct t k is a deduction that includes goodwill. Domestically operating banks are required to have a capital adequacy ratio of at least 4 %, whereas the international banks need to have a capital adequacy ratio of at least 8 % (see for example Montgomery and Shimizutani 2009).

Weber and Devaney (1999) and Färe et al. (2004) were the early DEA studies which incorporated risk-based capital constraints in bank efficiency measurement. Let W t ka be the risk-weight of asset a and let A t ka be the value of asset a. For assets \( a=1,\dots, Z \) the weighted sum \( w{A}_k^t={\displaystyle \sum_{a=1}^Z{W}_{ka}^t}{A}_{ka}^t \) represents risk-weighted assets.

The dynamic-network model of Fukuyama and Weber (2015a) assumed that equity capital equals the sum of Tier 1 and Tier 2 capital, less deductions. Their data source did not report the risk-weights for loans and securities although it did report total risk-weighted assets (wA t k ). Therefore, they imputed the risk-weights for the two outputs of loans and securities investments from total risk-weighted assets and by using the regulatory risk-weights for various classes of assets. Their imputation procedure is as follows. A bank’s total securities consist of central government bonds (Gov t k ), local and municipal bonds (Local t k ), corporate bonds (Corp t k ), and other securities (otherSec t k ), and securities have risk weights between zero and one with various government bonds having lower risk weights than corporate bonds and other securities. Following Fukuyama and Weber (2015a) the risk-weight for total securities can be computed as \( {W}_{2k}^t=\frac{0\times Go{v}_k^t+0.2\times Loca{l}_k^t+0.75\times Cor{p}_k^t+1\times otherSe{c}_k^t}{f{y}_{2k}^t} \). Fukuyama and Weber (2015a) also assumed that cash representing carryover assets has a risk weight of 0 and physical capital has a risk weight of 1; and other assets (otherA t k ) have a risk-weight of 1. Since \( w{A}_k^t=0\times Cas{h}_k^t+{W}_{1k}^tf{y}_{1k}^t+{W}_{2k}^tf{y}_{2k}^t+1\times {x}_{2k}^t+1\times other{A}_k^t \), the risk-weight for loans is computed as \( {W}_{1k}^t=\frac{w{A}_k^t-{W}_{2k}^t\times f{y}_{2k}^t-1\times {x}_{2k}^t-1\times other{A}_k^t}{f{y}_{1k}^t} \). Therefore, the capital adequacy restriction given by (10.26) can be written as \( \frac{x_{3k}^t}{W_{1k}^t\times f{y}_{1k}^t+{W}_{2k}^t\times f{y}_{2k}^t+1\times {x}_{2k}^t+1\times other{A}_k^t}\ge 0.04 \) which can be rearranged to yield \( \frac{x_{3k}^t}{0.04}\ge \left({W}_{1k}^t\times f{y}_{1k}^t+{W}_{2k}^t\times f{y}_{2k}^t+1\times {x}_{2k}^t+1\times other{A}_k^t\right) \). Thus, taking inefficiency into consideration yields the following regulatory inequality constraint:

$$ \frac{x_{3k}^t}{0.04}\ge {W}_{1k}^t\times f{y}_{1k}^t+{W}_{2k}^t\times f{y}_{2k}^t+{x}_{2k}^t+ other{A}_k^t+{\beta}^t\left({W}_{1k}^t\times {g}_{y1}+{W}_{2k}^t\times {g}_{y2}-{g}_{x2}+\frac{g_{x3}}{.04}\right). $$
(10.27)

Therefore, the financial regulatory constraints can be expressed as

$$ {F}_k^t\ge {\beta}^t{G}_k^t\kern1em \left(t=1,\dots, T\right). $$
(10.28)

where \( {F}_k^t=\frac{x_{3k}^t}{0.04}-{W}_{1k}^t\times f{y}_{1k}^t-{W}_{2k}^t\times f{y}_{2k}^t-{x}_{2k}^t- other{A}_k^t \) and \( {G}_k^t={W}_{1k}^t\times {g}_{y1}+{W}_{2k}^t\times {g}_{y2}-{g}_{x2}+\frac{g_{x3}}{0.04} \). Therefore, the financial regulatory constraint can be imposed by adding (10.28) to (10.19). A consequence of financial regulatory constraints is that measures of inefficiency–the ability to expand desirable outputs and contract inputs–is less than what might be achieved given the technology without the financial regulatory constraint.

Note that the dual multiplier representation of (10.19) with the financial regulatory constraint (10.28) can be developed similar to the method of Fukuyama and Weber (2015a).

10.6 A Summary

Specifying an appropriate technology and measuring financial institution performance has been a fertile area among operations researchers in the past 30 years. Much of the early work relied on a black box technology where inputs entered and outputs emerged from the black box and the performance of a particular financial institution was measured relative to the best-practice producer in a single period. This research was extended to network models that allowed various production divisions within a financial institution to contribute to the production of final outputs. One of the common network models assumed that banks used various exogenous inputs in stage 1 to produce intermediate outputs of deposits and then used those deposits as an input in stage 2 to generate a portfolio of interest bearing assets such as loans and securities investments. These network models were extended to account for the fact that the lending process generates a jointly produced undesirable output in the form of delinquent or nonperforming loans. Furthermore, nonperforming loans generated in one period constrain bank production possibilities in future periods. In addition, instead of immediately making loans as deposits are generated banks can instead choose to carryover some of their deposits if they expect enhanced future production possibilities. Dynamic models extended the black box technology by allowing inter temporal dependence between the input and output decisions of one period on the production possibilities of subsequent periods.

In this chapter, the dynamic network bank technology and performance measures developed by Fukuyama and Weber (2013, 2015a, b) were studied and extended accounting for weak disposability between desirable and undesirable inputs and accounting for weak disposability between desirable and undesirable outputs. Static black box efficiency measures tend to be biased because they ignore inter-temporal dependencies among inputs and outputs. The performance measures that were developed in this chapter help reduce the bias in static black box efficiency measures by comparing observed bank input and output decisions relative to a dynamic best-practice technology that accounts for the effects of input and output decisions of one period on the ability of banks to produce in future periods.