Measuring Environmental Efficiency: An Application to U.S. Electric Utilities

Abstract

This chapter highlights limitations of some DEA (data envelopment analysis) environmental efficiency models, including directional distance function and radial efficiency models, under weak disposability assumption and various return-to-scale technology. It is found that (1) these models are not monotonic in undesirable outputs (i.e., a firm’s efficiency score may increase when polluting more, and vice versa), (2) strongly dominated firms may appear efficient, and (3) some firms’ projection points derived from the optimal environmental efficiency scores are strongly dominated, thus they cannot be the right direction for the improvement. To address these problems, we propose a weighted additive model, i.e., the Median Adjusted Measure (MAM) model. An application to measuring the environmental efficiency of 94 U.S. electric utilities is presented to illustrate the problems and to compare the existing models with our MAM model. The empirical results show that the directional distance function and radial efficiency models may generate spurious efficiency estimates, and thus it must be with caution.

This chapter is prepared based on Chen (2013, 2014). The authors thank Springer and Elsevier for granting the rights for reusing the contents of these two papers. The authors also thank Maria Montes-Sancho for preparing the data used in this article.

11.1 Introduction

When measuring environmental efficiency, we seek to answer the following question: Can a firm produce more desirable outputs while generating lower quantities of undesirable outputs than its competitors? The answer to this question can help managers and policymakers act pro-actively in strategy-making and resource allocation to ensure both corporate and environmental sustainability. However, measuring environmental efficiency can be challenging for several reasons. First, calculating environmental efficiency scores requires an articulation of weights or preferences for productive inputs and outputs, but both eliciting and combining preferences are difficult in a multi-stakeholder environment (Baucells and Sarin 2003). Second, most undesirable outputs, such as greenhouse gas emissions and toxic releases, do not have a well-established market from which we can obtain reliable price signals. This makes prioritizing different environmental factors difficult. For example, it can be difficult to assign specific weights to different dimensions of corporate social performance, such as environmental consciousness and community relationship (Chen and Delmas 2011).

The absence of reliable price information for environmental impacts makes data envelopment analysis (DEA) a useful tool for assessing environmental efficiency. DEA does not require explicit assumptions about weights, production functions, and probability distributions for environmental inefficiency. Weights are optimized based on which input(s) a specific firm excels at utilizing, or which output(s) a firm excels at generating in comparison to the other firms in the sample. In this way, each firm can endogenously determine the weights used to evaluate its eco-efficiency . Applications of DEA to environmental efficiency have also been in a variety of problem contexts where undesirable outputs are consequential, including banking and finance, electricity generation, manufacturing, and transportation. The goal of this chapter is to review the commonly used DEA models for measuring environmental efficiency and talk about their potential limitations.

In the DEA literature, the directional distance function (DDF) (Chung et al. 1997) and radial efficiency models (e.g., Zhou et al. 2007; Färe et al. 1989) are among the two most widely used. Compared with other DEA models (e.g., Seiford and Zhu 2002), the DDF and radial efficiency models usually adopt an additional assumption on undesirable outputs, i.e., weak disposability assumption (WDA) on undesirable outputs (Shephard 1970), which specifies the trade-off (and boundary) relationship between a firm’s capability to produce good and bad outputs in the production possibility set. This chapter reveals three problems associated with these two models under the weak disposability assumption: (1) Non-monotonicity in undesirable outputs: a firm’s efficiency obtained from the two models may increase when polluting more, and vice versa, (2) misclassification of efficiency status: strongly dominated firms may be identified efficient, and (3) strongly dominated projection targets: environmental efficiency scores may be computed against strongly dominated points. Our findings suggest that the DDF and radial efficiency models should be used with caution. We also examine modelling issues under variable returns-to-scale (VRS) production technology . As a solution, we propose an alternative model based on the weighted additive model (Cooper et al. 1999), and compare our model with the existing models by an illustrative application of evaluating the environmental efficiency of 94 U.S. electric utilities in year 2007.

In the next section, we introduce the production technology assumptions, the DDF and radial efficiency models for environmental efficiency evaluation, and identified issues and problems. In Sect. 11.3, we develop a model to avoid the problems of the existing models. In Sect. 11.4 we include a case study for measuring the environmental efficiency of 94 U.S. electric utilities. Section 11.5 gives conclusions.

11.2 Production Models with Undesirable Outputs for Environmental Efficiency

11.2.1 Production Technology Assumptions

We consider n decision-making units (DMU). Each DMU uses m inputs to produce s desirable outputs and p undesirable outputs. The input vector of DMU q is denoted by ${X}_q=\left({x}_{q1},\dots, {x}_{qm}\right)$, desirable output vector by ${Y}_q=\left({y}_{q1},\dots, {y}_{qs}\right)$, and undesirable output vector by ${B}_q=\left({b}_{q1},\dots, {b}_{qp}\right)$. The correspondence between the three vectors can be described as:

$$ f\left({X}_q\right)\triangleq \left\{\left({Y}_q,{B}_q\right):\ \left({Y}_q,{B}_q\right)\ \mathrm{can}\ \mathrm{b}\mathrm{e}\ \mathrm{produced}\ \mathrm{b}\mathrm{y}\ \mathrm{using}\ {X}_q\right\}. $$

(11.1)

The function f captures the relationship between inputs and outputs and hence represents the production technology. A common behavioural assumption is that producer q should maximize Y _q and minimize B _q for a given X _q . We define output efficiency as:

Definition 1 (output efficiency)

DMU q is output efficient if there does not exist a non-zero vector $\left({S}^Y,{S}^B\right)\in {\mathrm{\Re}}_{+}^s\times {\mathrm{\Re}}_{+}^p$ , such that $\left({Y}_q+{S}^Y,{B}_q-{S}^B\right)\in f\left({X}_q\right)$ .

Definition 1 means that a DMU is output efficient if it is impossible to improve any of its outputs given the current input level. Note that output efficiency defined here is similar to but different from the Pareto-Koopmans efficiency (Cooper et al. 2007, pp. 45–46), in that output efficiency does not consider input-side inefficiency and slacks (i.e., reductions in some of the inputs).

The definition of output efficiency implies that firms can improve output efficiency by either increasing Y _q , decreasing B _q , or both. This entails the question of how to model the trade-off relationship between the desirable and undesirable outputs. One possibility is to assume there is no such trade-off, ceteris paribus. In this situation (i.e., free disposability ), the technology set (X, f(X)) allows lowering undesirable outputs without losing desirable outputs; i.e., $\left({Y}_q,{B}_q\right)\in f\left({X}_q\right)\Rightarrow \left({Y}_q,{B}_q^{*}\right)\in f\left({X}_q\right)$ for ${B}_q^{*}\geqq {B}_q$, and $\left({Y}_q,{B}_q\right)\in f\left({X}_q\right)\Rightarrow \left({Y}_q^{*},{B}_q\right)\in f\left({X}_q\right)$, for all ${Y}_q^{*}\leqq {Y}_q$ and ${Y}_q^{*}\in {\mathrm{\Re}}_{+}^s$, “$\leqq$” being the component-wise inequality. Alternatively, one may assume reducing undesirable outputs should not be “free” and impose a weak disposability assumption on undesirable outputs. Denoting the technology set under the weak disposability assumption as f _w (X _q ), the weak disposability assumption satisfies the following three conditions (Shephard 1970): (i) $\left({Y}_q,{B}_q\right)\in {f}_w\left({X}_q\right)$ implies that $\left({Y}_q^{*},{B}_q\right)\in f\left({X}_q\right)$ for all ${Y}_q^{*}\leqq {Y}_q$, (ii) $\left({Y}_q,{B}_q\right)\in {f}_w\left({X}_q\right)$ and $0\le \theta \le 1$ implies that $\left(\theta {Y}_q,\theta {B}_q\right)\in {f}_w\left({X}_q\right)$, and (iii) $\left({Y}_q,{B}_q\right)\in {f}_w\left({X}_q\right)$ implies that $\left({Y}_q,{B}_q\right)\in f\left({X}_q^{*}\right)$ for all ${X}_q^{*}\geqq {X}_q$.

The first condition means that if (X _q , Y _q , B _q ) is observed, the existence of this observation implies that it is feasible to produce a lower amount of desirable outputs with given X _q and B _q . The second condition stipulates that proportional reduction of the joint output vector (Y _q , B _q ) is feasible. The first two conditions imply that a reduction in B _q must be accompanied by a reduction in desirable outputs Y _q , while the converse is not true. The weak disposability assumption condition is meant to reflect that generation and disposal of undesirable outputs should not be free, in a sense that reducing undesirable outputs will come at the expense of lowering desirable outputs. Clearly, the technology set f _w (X _q ) is a subset of f(X _q ), because of these additional constraints associated with the weak disposability assumption.

The technology f _w can be formulated as a linear system under the following axioms: f _w (X _q ) is convex, and f _w (X _q ) is the intersection of all sets satisfying the convexity axiom and disposability assumptions; i.e., the production set ${f}_w={\displaystyle \underset{j=1}{\overset{n}{\cap }}{f}_w^{\prime}\left({X}_q\right)}$, where f _w ^′(X _q ) is any convex set satisfying the disposability assumption for DMU j (Banker et al. 1984). The model can be expressed as:

$$ {f}_w\left({X}_q\right)=\left\{\left(Y,B\right):{\displaystyle \sum_{j=1}^n}{\lambda}_j{x}_{ji}\le {x}_{qi},i=1,\dots, m,{\displaystyle \sum_{j=1}^n}{\lambda}_j{y}_{jr}\ge {y}_{qr},r=1,\dots, s,\right.\left.{\displaystyle \sum_{j=1}^n}{\lambda}_j{b}_{jk}={b}_{qk},k=1,\dots, p,{\lambda}_j\ge 0,j=1,\dots, n\right\} $$

(11.2)

The boundary of (11.2) consists of non-negative linear combinations of all DMUs’ input and output vectors. The λ _j represents the production intensity of the jth DMU, which can take different values to populate different areas of (X _q , f _w (X _q )). The weak disposability assumption is enforced by the equality constraints associated with undesirable outputs. See p. 50 in Färe and Grosskopf (2006) for the proof that shows (11.2) satisfies the weak disposability assumption. If on contrary we assume that undesirable outputs are freely disposable, the new technology set f _f (X _q ) can be recast by replacing the equality constraints with “$\le$” inequality constraints, meaning that the efficient level of undesirable outputs are bounded below by the left-hand-side value and undesirable outputs can be improved independently from desirable outputs.

Note that the convex set (X _q , f _w (X _q )) satisfies the constant returns-to-scale (CRS) assumption ; i.e., $\left(Y,B\right)\in {f}_w(X)$ implies that $\left(\delta Y,\delta B\right)\in {f}_w\left(\delta X\right),\delta \ge 0$. A number of studies on environmental efficiencies assume a VRS technology (Chen 2013). These studies follow Banker et al. (1984) and add a convexity constraint on the intensity variables to represent the VRS assumption imposed (e.g., Mandal and Madheswaran 2010; Oggioni et al. 2011; Riccardi et al. 2012). However, it is a general misconception that simply adding a convexity constraint to the CRS model with weak disposability means that the new model is one with a VRS technology with weak disposability, as shown in Färe and Grosskopf (2003). As such, many studies used an incorrect VRS formulation in the literature (Chen 2013).

The correct VRS formulation with weak disposability assumption first appeared in Shephard (1970). However, the Shephard’s VRS formulation with weak disposability is highly nonlinear and thus the model has difficulties in computation. Also the production set under the Shephard’s VRS formulation is not convex, which means that some of the feasible points in the production set under the convexity axiom in nonparametric production models (see, e.g., Banker et al. 1984) may be deemed infeasible in Shephard’s formulation . Kuosmanen (2005) and Kuosmanen and Podinovski (2009) extend Shephard’s VRS formulation by developing a convex and fully linearizable model (i.e., linearizable for all common types of efficiency indexes):

$$ {f}_{VRS}\left({X}_q\right)\kern-.25em =\kern-.15em \left\{\left(Y,B\right)\kern-.18em :\kern-.15em {\displaystyle \sum_{j=1}^n}\left({\lambda}_j+{\mu}_j\right){x}_{ji}\le {x}_{qi},i=1,\dots, m;{\displaystyle \sum_{j=1}^n}{\lambda}_j{y}_{jr}\ge {y}_{qr},r=1,\dots, s;\right.\left.{\displaystyle \sum_{j=1}^n}{\lambda}_j{b}_{jk}={b}_{qk},k=1,\dots, p;{\displaystyle \sum_{j=1}^n}\left({\lambda}_j+{\mu}_j\right)=1;{\lambda}_j,{\mu}_j\ge 0,j=1,\dots, n\right\} $$

(11.3)

It is shown that the Shephard’s VRS formulation is a special case of the Kuomanen’s VRS formulation (Kuosmanen 2005). More importantly, the efficiency models constructed based on (11.3) become linear programming problems and can be solved easily. However, to date few papers in the literature have employed this general and correct VRS formulation in environmental efficiency analysis (Chen 2013). Next, we introduce the DDF and radial efficiency models based on Kuosmanen’s formulation .

11.2.2 Directional Distance Function

The formulation of the directional distance function (DDF) is shown in (11.4). Specifically, the DDF model calculates the environmental efficiency score of a firm according to the maximum improvement in outputs that this firm can make in the direction (g ^Y, g ^B), such that the firm remains in f _VRS (X _q ) after this improvement. Therefore environmentally efficient firms in the DDF model are those obtaining a zero optimal value (i.e., ${\theta}^{*}=0$), in a sense that these firms cannot improve their outputs following the pre-determined direction .

$$ \mathrm{Max}\theta $$

$$ \mathrm{s}.\mathrm{t}.{\displaystyle \sum_{j=1}^n}\left({\lambda}_j+{\mu}_j\right){x}_{ji}\le {x}_{qi},i=1,\dots, m $$

$$ {\displaystyle \sum_{j=1}^n}{\lambda}_j{y}_{jr}\ge {y}_{qr}+\theta {g}_r^Y,r=1,\dots, s $$

$$ {\displaystyle \sum_{j=1}^n}{\lambda}_j{b}_{jk}={b}_{qk}-\theta {g}_k^B,k=1,\dots, p $$

$$ {\displaystyle \sum_{j=1}^n}\left({\lambda}_j+{\mu}_j\right)=1 $$

$$ {\lambda}_j,{\mu}_j\ge 0,j=1,\dots, n $$

(11.4)

We can calculate the projection point for each DMU according to the efficiency score obtained from (11.4). For example, $\left({X}_q,{Y}_q+{\theta}^{*}{g}^Y,{B}_q-{\theta}^{*}{g}^B\right)$ is the projection point of DMU q under DDF, where θ* is the optimal solutions to the corresponding efficiency model (11.4). Clearly, the projection point is at the boundary of the production set. As noted, the projection point is the linear combination of different observed DMUs. We define the reference set for an evaluated DMU as the collection of DMUs that forms the projection point. The λ’s associated with these active DMUs are positive in the optimal solution (Cooper et al. 2007). Thus this also means that an efficient DMU is its own reference set and projection point.

11.2.3 Radial Efficiency Models

Studies with a radial efficiency index (Charnes et al. 1978; Farrell 1957) under the weak disposability assumption are found in the literature. The number of papers using radial efficiency models increases rapidly over past years (Chen 2013). These models with a radial efficiency index can be classified into the follow three types¹: the index associated with desirable outputs and undesirable outputs, desirable outputs only, and undesirable outputs only, which can be modelled by (11.5).

$$ \mathrm{Max}\kern0.15em \theta \kern0.75em \left( or\ \mathrm{M}\mathrm{i}\mathrm{n}\kern0.2em {\delta}^b\right) $$

$$ \mathrm{s}.\mathrm{t}.{\displaystyle \sum_{j=1}^n}\left({\lambda}_j+{\mu}_j\right){x}_{ji}\le {x}_{qi},i=1,\dots, m $$

$$ {\displaystyle \sum_{j=1}^n}{\lambda}_j{y}_{jr}\ge \theta {y}_{qr},r=1,\dots, s $$

$$ {\displaystyle \sum_{j=1}^n}{\lambda}_j{b}_{jk}={\delta}^b{b}_{qk},k=1,\dots, p $$

$$ {\displaystyle \sum_{j=1}^n}\left({\lambda}_j+{\mu}_j\right)=1 $$

$$ {\lambda}_j,{\mu}_j\ge 0,j=1,\dots, n $$

(11.5)

Before illustrate the limitations associated with the DDF and radial efficiency models in the next section, we list the four types of environmental efficiency models introduced thus for (M1 to M4 in Table 11.1). It should be noted that DMUs’ efficiency scores obtained from models M1 to M4 have different ranges and different values for efficient observations. To be specific, a DMU having lower score in M1, M2 and M4 is considered more efficient, but M1 is equal or greater than zero while M2 and M4 have a lower bound of one. DMUs obtaining higher scores in M3 are considered more efficient and the range of M3 is from zero to one. The projection point for DMU q according to the efficiency score and optimal solutions obtained from radial efficiency models is (X _q , θ*Y _q , δ ^b * B _q ), which is at the boundary of the production set.

Table 11.1 Efficiency models classification for measuring environmental efficiency (Chen 2013)

11.2.4 Problems Illustration by a Numerical Example

We present a simple numerical example to show problems of the DDF and radial efficiency models with the WDA and Kuosmanen’s VRS assumptions .

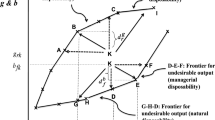
In this numerical sample, there are four observed DMUs (DMU A to D) with one input, one desirable, and one undesirable output, shown in Table 11.2. For the ease graphical presentation, all four DMUs are assumed to consume the same amount of inputs. The output set f _VRS (X) for this sample based on the production technology model (11.3) is represented by the region ‘0ABCE0’ in Fig. 11.1. When WDA is not imposed, the output set expands and becomes the area under the line segment ‘0A’ and the horizontal line extended from A to its right. More specifically, for the desirable output y, which is freely disposable, the area below the line segments ‘0A’ are considered feasible (c.f. the inequality constraint for y in (11.3)). Observe that the frontier under the WDA (i.e., the boundary of f _VRS (X)) may include points dominated in both y and b, which correspond to the problem of misclassification of efficiency status. For example, DMUs B and C produce a lower amount of y but more b than DMU A. However, DMUs B and C are in the boundary set of f _VRS (X). DMU D may be projected to the dominated portion of the boundary set (i.e., the line segment between A and B) w ith certain choices of directional vectors. The same thing may occur in the radial efficiency models (e.g., M2 projects D to B, and M4 may project D to the line segment between A and B by a hyperbolical locus). This potential problem for DMU D is called the problem of strongly dominated projection targets. If we increase the undesirable output of D from 25 to 35, the inefficient DMU D would become efficient DMU C. That is to say, an increase in a DMU’s undesirable outputs may improve the DMU’s efficiency score, which correspond to the problem of non-monotonicity in undesirable outputs.

Table 11.2 A numerical example for problems illustration

Fig. 11.1

Output set f _VRS under the WDA and Kuosmanen’s VRS technology

Chen (2014) proves the above three problems associated with the DDF and HEM (M4) models under CRS technology. In the next section, we introduce a weighted additive model for environmental efficiency evaluation as a solution.

11.3 A Median Adjusted Measure (MAM) Model for Environmental Efficiency

As noted earlier, weighted additive models have been shown to be able to project all DMUs onto the efficient facet (Charnes et al. 1985), which resolves the dilemma of choosing between free and weak disposability for undesirable outputs. Weighted additive models are a general class of models that include many variants (Charnes et al. 1985; Seiford and Zhu 2005; Färe and Grosskopf 2010). One important issue for implementing the weighted additive model is that we must specify weights. This is particular a problem as DEA models are known as a weight-free approach and do not require subjective weight assignments. Chen and Delmas (2012) use the DMU’s own outputs to normalize the output improvements and then calculate environmental efficiency as the average normalized score. This approach has a potential limitation in that different DMUs would be based its own production but miss information about distributions of different outputs across the entire sample, which may carry significant practical implications. Some studies assign weights based on the sample statistics, such as the range adjusted measure (RAM) model proposed by Cooper et al. (1999):

$$ \mathrm{Max}\varGamma =\frac{1}{s+p}\left({\displaystyle \sum_{r=1}^s}\frac{s_r^{+}}{R_r^{+}}+{\displaystyle \sum_{k=1}^p}\frac{s_k^{-}}{R_k^{-}}\right) $$

$$ \mathrm{s}.\mathrm{t}.{\displaystyle \sum_{j=1}^n}\left({\lambda}_j+{\mu}_j\right){x}_{ji}\le {x}_{qi},i=1,\dots, m $$

$$ {\displaystyle \sum_{j=1}^n}{\lambda}_j{y}_{jr}={y}_{qr}+{s}_r^{+},r=1,\dots, s $$

$$ {\displaystyle \sum_{j=1}^n}{\lambda}_j{b}_{jk}={b}_{qk}-{s}_k^{-},k=1,\dots, p $$

$$ {\displaystyle \sum_{j=1}^n}\left({\lambda}_j+{\mu}_j\right)=1;{\lambda}_j,{\mu}_j\ge 0,j=1,\dots, n $$

$$ {\lambda}_j,{\mu}_j\ge 0, j=1,\dots, n $$

$$ {s}_r^{+},{s}_k^{-}\ge 0,r=1,\dots, s;k=1,\dots, p $$

(11.6)

where ${R}_r^{+}$ is the range of the rth desirable output and ${R}_k^{-}$ is the range of the pth undesirable output. Note that the RAM model can also incorporate slacks variables for inputs. When the inputs slacks are taken into consideration, we need to replace the objective function in (11.6) by $\mathrm{Max}\frac{1}{m+s+p}\left({\displaystyle \sum_{i=1}^m\frac{s_i^{-}}{R_i^{-}}+{\displaystyle \sum_{r=1}^s\frac{s_r^{+}}{R_r^{+}}+{\displaystyle \sum_{k=1}^p\frac{s_k^{-}}{R_k^{-}}}}}\right)$ where ${R}_i^{-}$ is the range of the ith input, and change the input inequality constraints in (11.6) to ${\displaystyle \sum_{j=1}^n\left({\lambda}_j+{\mu}_j\right)}\ {x}_{ji}={x}_{qi}-{s}_i^{-},i=1,\dots, m$. For the purpose of the current paper, we focus on the output-oriented RAM model. For the economic intuition behind the RAM model, see Cooper et al. (1999) for an excellent exposition of the rationale behind the additive efficiency model and its use to measure allocative, technical, and overall inefficiencies.

We propose a model based on the concept from the RAM model, as Cooper et al. (1999) point out that the RAM-type of efficiency models come with a number of desirable properties, including (i) the efficiency score is bounded in [0,1], (ii) the model is unit invariant, (iii) the model is strongly monotonic in slacks, and (iv) the model is translation invariant under the variable returns-to-scale technological assumption (Banker et al. 1984). However, we find using ranges as the normalizing factors problematic, and choose to use other normalizing variables instead of ranges in the original model. For example, it is stated in Cooper et al. (1999) that $0\le \varGamma \le 1$, where a zero value indicates efficiency and a value of one indicates full efficiency. As the slacks are usually much lower in magnitude than their corresponding ranges, the efficiency scores obtained from the original RAM model tends to be low in both magnitude and variation (Cooper et al. 1999; Steinmann and Zweifel 2001). Therefore the RAM scores cannot effectively differentiate the performance of different DMUs. Furthermore, if we observe extremely inefficient firms that makes certain ${R}_r^{+}$ and/or ${R}_k^{-}$ larger. These extremely inefficient firms may be those that produce lower than minimal observed desirable outputs but higher than maximum observed undesirable outputs at a fixed input level. The efficiency scores of all the other firms may decrease markedly, and most firms would appear more efficient although the efficient frontier remains unaltered. As it is not uncommon to observe “heavy polluters” in applications, using ranges or other dispersion measures of outputs do not seem appropriate. Also note that if a weighted additive model is used, the disposability assumption on undesirable outputs will not have any impact on the resultant efficiency scores.

Another problem of using ranges is that ranges cannot reveal the relative magnitude of the output. For example, suppose we obtain for a particular DMU that its slack for an output is 5 and the corresponding range for that output is 50. The managerial implication of this output slack for this DMU may be quite different if the maximum and minimum of the output are respectively 10 and 60 rather than 500 and 550, for example. As the main purpose of the normalizing factors are to obtain unit invariance, we opt for using the median of outputs to replace the range used in the objective function of model (11.6), which is more robust than ranges or averages as the basic statistical properties of these measures. We call our efficiency measure based on median the “Median Adjusted Measure” (MAM). The MAM score then has an intuitive interpretation as the average of slacks compared to the sample median of the corresponding output variables. Note that one may designate the normalizing parameters in the original range adjusted model in other ways; see, e.g., Cooper et al. (2011) for a comprehensive discussion.

11.4 An Application to Measuring Environmental Efficiency of U.S. Electric Utilities

The electricity sector has been under stringent scrutiny for its environmental performance (Majumdar and Marcus 2001; Fabrizio et al. 2007; Delmas et al. 2007). Following previous studies (e.g., Majumdar and Marcus 2001; Delmas et al. 2007), we consider plant value, total operation & maintenance expenditure, labor cost, and electricity purchased from other firms as four input variables. The desirable output considered is total sales in MWH, and three undesirable outputs are sulfur dioxide (SO₂), nitrogen oxide (NO_x), and carbon dioxide (CO₂), of which SO₂ and NO_x are regulated by the U.S. Environmental Protection Agency (EPA) under the Acid Rain Program .

The data are collected from the U.S. Federal Energy Regulatory Commission (FERC ) Form Number 1 (U.S. DOE, FERC Form 1), from the U.S. Energy Information Administration (Forms EIA-860, EIA-861, and EIA-906), and from the U.S. Environmental Protection Agency Clean Air Market Program’s website. Our sample consists of 94 major investor-owned electric utilities in 2007. Table 11.3 reports t he statistics summary of the electric utilities’ input, desirable and undesirable outputs, which show that the 94 utilities vary significantly in their production scales, thus a VRS technology assumption is employed to reflect the industry production technology. In the application of the 94 U.S. electric utilities, we apply the DDF and radial efficiency models to show the limitations under the WDA and VRS technologies, and also apply our proposed median adjusted measures model as an illustration.

Table 11.3 Variables and data set descriptive statistics (n=94)

We applied the models M1–M4. For DDF (M1), an all-one vector is employed as the directional vector which is fixed. Another commonly used directional vectors includes ${g}_q=\left({Y}_q,{B}_q\right)$, (0, B _q ), or (Y _q , 0), or sample average values of outputs. Although not shown here, the three problems mentioned in the previous sections will still persist under these alternative directional vectors.

Table 11.4 shows the environmental efficiency results and optimal slacks values from the MAM models. There are 17 firms identified as strongly efficient by the MAM model, because they have zero optimal slacks in both desirable and undesirable outputs and are efficient across all of M1 to M4 models at the same time. However, some of the firms appear efficient in models M1 to M4 are strongly dominated in their outputs such as firms #2, #5, and #17. The rate of misclassification is rather high for the DDF and radial efficiency models (average higher than 30 %).

Table 11.4 Environmental efficiency scores and optimal slack values

We have obtained the optimal efficiency scores of all the firms by models M1 to M4 and the efficiency classification. These optimal efficiency scores can also be used to compute the projection points for those inefficient firms. To examine the problem of strongly dominated projection targets, we add the obtained projection points into the original data set, and use the MAM model to evaluate the efficiency of the projection points. Table 11.5 shows the efficiency results of those firms’ projection points under models M1 to M4. Besides those output efficient firms under MAM, the efficiency scores of the other firms’ projection targets under M1, M2, M3 and M4 are larger than zero (except DMU #57 under M1, DMU #27 and #87 under M3, and DMU #14 under M3). Thus, those projection targets are not strongly efficient and some are not even efficient in a weak sense.

Table 11.5 Efficiency results of projection points

11.5 Conclusions

In this chapter, we examine three critical implementation issues of the DDF and radial efficiency models which are widely used for the environmental efficiency evaluation in the literature: non-monotonicity, misclassification of efficiency status, and strongly dominated projection targets. Our analysis shows that the classical weak disposability assumption on undesirable outputs can create a portion of the output-dominated frontier, which can be considered the root cause for the three issues. Our findings provide important implications for both empirical and theoretic researchers of environmental efficiency. We suggest that researchers should be cautious when imposing the classical weakly disposability assumption on undesirable outputs under both CRS and VRS production technologies, which has been the standard assumption in a large stream of studies.

As the importance of environmental efficiency is growing, findings from this study have an important theoretical implication. Further, the application areas of the environmental efficiency model can be applied to many other dimensions of corporate operations when both positive and negative consequences of an activity or policy (e.g., debts in banking, labor accidents and litigations in transportation and manufacturing). Researchers are encouraged to explore more application areas in other emerging contexts.