Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

8.1 Introduction

Smart materials-based actuators are popularly employed for actuation in various precision engineering applications such as micropositioning, micromanipulation, and microassembly. As a typical smart actuator, piezoelectric actuators are particularly attractive owing to the merits of subnanometer positioning resolution and rapid response speed [14]. Even though intensive works have concentrated on the research and applications of piezoelectric actuators, the nonlinear piezoelectric effects, especially the hysteresis, still pose big challenges to precise positioning nowadays.

To fulfill the requirements of ultrahigh-precision positioning, the piezoelectric hysteresis behavior has to be suppressed by developing a suitable control strategy [20]. It has been shown that the hysteresis can be greatly alleviated by using a charge-driven approach or a capacitor insertion method [12]; it is however at the cost of stroke reduction. Thus, voltage actuation is still widely adopted in practice. Generally, the existing control schemes fall into two categories of hysteresis model-based and hysteresis model-free methods. In the first approach, a hysteresis model (e.g., Preisach model) is generated and used to construct an inverse-based feedforward compensator [1, 2]. It is known that the inverse model-based compensation is capable of achieving an accurate positioning, whereas the result is very sensitive to the model accuracy [5, 6]. In order to suppress the residual hysteresis as well as creep effects, a combination of feedforward with feedback control can be adopted [3, 15]. The major advantage of the second approach is that no hysteresis model is required. Instead, the unmodeled hysteresis is considered as an uncertainty or a disturbance [19] to the nominal system, which is tolerated by a robust or adaptive control technique. For instance, the sliding mode control [19], H ∞ robust control [18], fuzzy logic control [4], and neural network control [10] have been applied in recent works.

Even though it is possible to compensate the hysteresis nonlinearity by designing an advanced feedback controller without modeling the hysteresis effect, it is true that a feedforward controller by resorting to a simple hysteresis model in combination with a simple feedback (e.g., PID) controller makes it more feasible to suppress the hysteresis effect. The reason lies in that the latter approach allows the relief of burden to develop complicated modern controllers. For example, it has been shown that by modeling the hysteresis with Prandtl–Ishlinskii model [9], a feedforward compensator combined with a PID feedback controller is capable of effectively compensating the nonlinear hysteresis. Nevertheless, the majority of existing works on model-based hysteresis compensation employ an inverse hysteresis model. Hence, both a forward model and an inverse hysteresis model are required for the purposes of hysteresis characterization and compensation. Recently, it has been shown that it is possible to compensate the hysteresis by using a simple Bouc–Wen hysteresis model without adopting the hysteresis inverse [7, 13].

The purpose of the current research is to characterize and compensate the piezoelectric hysteresis by only using an intelligent hysteresis model without solving the hysteresis inverse. It has been shown that support vector machine (SVM) is superior to artificial neural networks (ANN) in terms of global optimization and higher generalization capability, hence SVM is widely employed to estimate nonlinear system models accurately [16]. Specifically, in the current research, a least squares support vector machine (LSSVM)-based hysteresis model is established and a feedforward compensator is developed without modeling the hysteresis inverse. It is shown that the LSSVM model is more effective than Bouc–Wen model in terms of both hysteresis modeling and hysteresis compensation.

8.2 Modeling of Dynamics with Hysteresis Behavior

The Bouc–Wen model has been extensively applied in piezoelectric hysteresis modeling. It has been shown that the entire dynamic model of the piezoactuated system can be established as follows [7, 11]:

$$\displaystyle\begin{array}{rcl} & & M\ddot{y}(t) + B\dot{y}(t) + Ky(t) = K[Du(t) - H(t)]{}\end{array}$$
(8.1)
$$\displaystyle\begin{array}{rcl} & & \dot{H}(t) =\alpha D\dot{u}(t) -\beta \vert \dot{u}(t)\vert H(t) -\gamma \dot{ u}(t)\vert H(t)\vert {}\end{array}$$
(8.2)

where t is the time variable, parameters M, B, K, and y represent the mass, damping coefficient, stiffness, and displacement response of the piezoactuated system, respectively; D is the piezoelectric coefficient, u denotes the input voltage, and H indicates the hysteretic loop in terms of displacement whose magnitude and shape are determined by parameters α, β, and γ.

The hysteresis model describes the relationship between the input voltage and output displacement of the piezostage system. On the other hand, the input voltage used to produce a desired displacement value is obtained by solving (8.1).

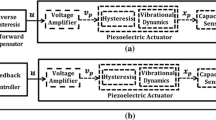
$$\displaystyle{ u(t) = \frac{1} {KD}[M\ddot{y}(t) + B\dot{y}(t) + Ky(t) + KH(t)]. }$$
(8.3)

It is observed that the feedforward control signal (8.3) is generated by using the hysteresis term H(t) without solving the inverse hysteresis model. A block diagram constructed with Matlab and Simulink software is given in [7].

Motivated by the hysteresis compensation using Bouc–Wen model which does not solve the hysteresis inverse, an intelligent model based on LSSVM is proposed below.

The dynamic model (8.1) of the system is written into the form

$$\displaystyle{ \ddot{y}(t) + 2\xi \omega _{n}\dot{y}(t) +\omega _{ n}^{2}y(t) = du(t) + h(t) }$$
(8.4)

where ξ and ω n denote the damping ratio and natural frequency of the piezoactuated system, respectively, d is a positive parameter, and h represents the hysteresis effect in terms of acceleration.

If the hysteresis model h is established, a feedforward hysteresis compensator can be constructed.

$$\displaystyle{ u(t) = \frac{1} {d}[\ddot{y}(t) + 2\xi \omega _{n}\dot{y}(t) +\omega _{ n}^{2}y(t) - h(t)] }$$
(8.5)

which uses the hysteresis model directly without solving the inverse hysteresis model. The hysteresis model based on LSSVM is established in the following discussions.

8.3 Hysteresis Modeling Using LSSVM

It is well known that the hysteresis effect is rate-dependent. Specifically, the hysteresis behavior is dependent not only on the amplitude but also on the frequency of input voltage signals. Moreover, due to the hysteresis nonlinearity, an input voltage corresponds to multiple position outputs. Typically, LSSVM only treats the problem of single-valued mapping between the input and output. Hence, one of the challenges in modeling the hysteresis behavior with LSSVM lies in how to convert the multivalued mapping problem into a single-valued one.

In previous work [21] of the authors, a one-to-one mapping is constructed by introducing the current input value and input variation rate as one data set. Nevertheless, in the case that the input data are accompanied with noises, the variation rate is not smooth and will induce modeling error. Moreover, it is unknown how many orders of the variation rate are sufficient to establish the mapping. Later, a regression model of hysteresis is developed in [17] by employing the current and previous inputs and previous outputs as exogenous inputs to transform the multivalued mapping is into a single-valued one. Yet, the above work takes the voltage and position as the input and output variables, respectively, which is different from the situation in the current research as shown below.

8.3.1 Regression Model Development

In the current research, the hysteresis term is expressed by taking into account (8.4):

$$\displaystyle{ h(t) =\ddot{ y}(t) + 2\xi \omega _{n}\dot{y}(t) +\omega _{ n}^{2}y(t) - du(t). }$$
(8.6)

It is observed from (8.6) that the output variable is the hysteresis term h, whereas both input voltage u and output position y appear as input variables. It is different from the scenario in [17].

Using LSSVM, a nonlinear regression model is formulated to capture the hysteresis behavior

$$\displaystyle{ \hat{h}(t) = f(\mathbf{x}_{k}) }$$
(8.7)

with

$$\displaystyle{ \mathbf{x}_{k} = [u_{k},\ldots,u_{k-m},y_{k},\ldots,y_{k-n},h_{k-1},\ldots,h_{k-l}] }$$
(8.8)

where \(\hat{h}_{k}\) denotes the predicted hysteresis term by LSSVM at the current time instant k. u k − 1, y k − 1, and h k − 1 represent the input voltage, output position, and hysteresis term at previous time instant k − 1, respectively. In addition, m ≥ 0, n ≥ 0, and l ≥ 1 define the order of the model.

8.3.2 Modeling with LSSVM

It is known that the LSSVM maps the input data into a high-dimensional feature space and constructs a linear regression function therein [17, 21]. The unknown hysteresis function is approximated by the equation

$$\displaystyle{ h(\mathbf{x}) ={ \mathbf{w}}^{T}\varphi (\mathbf{x}) + b }$$
(8.9)

with the given training data set \(\{\mathbf{x}_{k},h_{k}\}_{k=1}^{N}\) where N represents the number of training data set, \(\mathbf{x}_{k} \in {\mathbf{R}}^{m+n+l+2}\) is an input vector as shown in (8.8), and h k  ∈ R are the output data. Additionally, w is a weight vector, \(\varphi (\cdot )\) denotes a nonlinear mapping from the input space to a higher-dimensional feature space, and b is the bias.

The LSSVM approach formulates the regression as an optimization problem in the primal weight space. Then, the conditions for optimality are obtained by solving a series of partial derivatives, which are used to construct the dual formulation, i.e.,

$$\displaystyle{ \left [\begin{array}{cc} 0\ \ & \mathbf{1}_{N}^{T} \\ \mathbf{1}_{N}\ \ &\boldsymbol{\Omega } {+\gamma }^{-1}\mathbf{I}_{N} \end{array} \right ]\left [\begin{array}{c} b\\ \boldsymbol{\alpha } \end{array} \right ] = \left [\begin{array}{c} 0\\ \mathbf{h} \end{array} \right ] }$$
(8.10)

where \(\boldsymbol{\alpha }= {[\alpha _{1},\alpha _{2},\ldots,\alpha _{N}]}^{T}\) is called the support vector. The support values are \(\alpha _{k} =\gamma e_{k}\) with \(\gamma \in \mathbb{R}\) denoting the regularization factor. In addition, \(\mathbf{1}_{N} = {[1,1,\ldots,1]}^{T}\), \(\mathbf{h} = {[h_{1},h_{2},\ldots,h_{N}]}^{T}\), and I N is an identity matrix. Besides, the kernel trick is employed to derive that

$$\displaystyle{ \Omega _{kj} =\varphi {(\mathbf{x}_{k})}^{T}\varphi (\mathbf{x}_{ j}) = K(\mathbf{x}_{k},\mathbf{x}_{j}),\quad k,j = 1,2,\ldots,N }$$
(8.11)

where K is a predefined kernel function. The purpose of introducing the kernel function is to avoid the explicit computation of the map \(\varphi (\cdot )\) in dealing with the high-dimensional feature space.

After calculating b and \({\alpha }\) from (8.10), one can obtain the solution for the regression problem

$$\displaystyle{ h(\mathbf{x}) =\sum _{ k=1}^{N}\alpha _{ k}K(\mathbf{x},\mathbf{x}_{k}) + b }$$
(8.12)

where K is the kernel function satisfying Mercer’s condition, x k is the training data, and x denotes the new input data.

By adopting the radial basis function (RBF) as kernel function,

$$\displaystyle{ K(\mathbf{x},\mathbf{x}_{k}) =\exp \left (-{\frac{\|\mathbf{x} -\mathbf{x}{_{k}\|}^{2}} {\sigma }^{2}} \right ) }$$
(8.13)

with σ > 0 denoting the width parameter (which specifies the kernel sample variance σ 2) and \(\|\cdot \|\) representing the Euclidean distance, the LSSVM model for the hysteresis model estimation becomes

$$\displaystyle{ h(\mathbf{x}) =\sum _{ k=1}^{N}\alpha _{ k}\exp \left (-{\frac{\|\mathbf{x} -\mathbf{x}{_{k}\|}^{2}} {\sigma }^{2}} \right ) + b. }$$
(8.14)

With the assigned regularization parameter γ and kernel parameter σ, the purpose of the training process is to determine the support values α k and the bias b. A good generalization ability of the LSSVM model relies on an appropriate tuning of the two hyperparameters (γ and σ). In the current research, the leave-one-out cross-validation approach is adopted to infer the values of the hyperparameters.

8.4 Experimental Investigations on Hysteresis Modeling

In this section, the hysteresis modeling based on Bouc–Wen model and LSSVM approach is carried out by experimental studies.

8.4.1 Experimental Setup

Figure 8.1 depicts the experimental setup, where a four-layer piezoelectric bimorph actuator with the dimension of 28 × 5 × 0. 86 mm3 is driven by a high-voltage amplifier. A USB-6259 board (from National Instruments Corp.) with 16-bit DAC and ADC channels is adopted to produce an analog voltage, which is then amplified by a high-voltage amplifier (model: EPA-104 from Piezo Systems, Inc.) with an adjustable gain of 10 to provide a high voltage for driving the piezo-actuator. The output displacement at the end point of piezo-bimorph is measured by a laser displacement sensor (model: LK-H055, from Keyence Corp.). The analog voltage output of the sensor signal conditioner is acquired by a PC through one ADC channel of the USB-6259 board. Moreover, LabVIEW software is employed to implement a real-time control of the piezoactuated system.

Fig. 8.1
figure 1

Experimental setup of a piezoactuated system

Full size image

8.4.2 Bouc–Wen Model Results

8.4.2.1 Bouc–Wen Model Identification

To identify the hysteresis model, the input voltage signal is chosen as shown in Fig. 8.2a, and the corresponding output data are depicted in Fig. 8.2b.

Fig. 8.2
figure 2

Results of the identified Bouc–Wen model. (a) Input voltage; (b) experimental result and Bouc–Wen model output; (c) displacement–voltage hysteresis loops; (d) Bouc–Wen model output errors

Full size image

It has been shown that the seven parameters (M, B, K, D, α, β, and γ) of the Bouc–Wen model can be identified by minimizing the following fitness function [7]:

$$\displaystyle{ f(M,B,K,D,\alpha,\beta,\gamma ) = \frac{1} {N}\sum _{i=1}^{N}{\left (y_{ i} - y_{i}^{\mathrm{BW}}\right )}^{2} }$$
(8.15)

where N denotes the total number of samples and \(y_{i} - y_{i}^{\mathrm{BW}}\) represents the error of the ith sample which is calculated as the deviation of Bouc–Wen model output (\(y_{i}^{\mathrm{BW}}\)) from experimental result (y i ).

By setting a time interval of 0.02 s, 500 training data sets are obtained as shown in Fig. 8.2a, b. Note that the voltage signal is applied to the high-voltage amplifier. Then, the Bouc–Wen model is identified by optimizing the seven parameters to minimize the fitness function (8.15). Specifically, the particle swarm optimization (PSO) is adopted, and the identified model parameters are shown in Table 8.1. It is noticeable that the mass M is normalized as 1 in order to reduce the number of the model parameters.

Table 8.1 Parameters of the Bouc–Wen hysteresis model
Full size table

8.4.2.2 Modeling Results

The experimental output and the Bouc–Wen model output are plotted in Fig. 8.2b–d. It is found that the Bouc–Wen model cannot exactly represent the complicated hysteresis of the piezostage system. A relatively large error exists between the identified model output and the experimental result as shown in Fig. 8.2d. Specifically, the maximum model error is \(13.63\,\mu \mathrm{m}\), which accounts for 5.8% of the travel range of the piezo-actuator. The root-mean-square error (RMSE) is \(3.71\,\mu \mathrm{m}\), which accounts for 1.6% of the travel range. It is observed that smaller model error is obtained when the input has lower magnitude and frequency. Hence, the model errors vary greatly at different amplitudes and frequencies of the input signal, which indicates that the Bouc–Wen model cannot capture the rate dependency of the hysteresis precisely.

8.4.2.3 Generalization Study

To test the generalization of the Bouc–Wen model, a new input signal is selected as shown in Fig. 8.3a. The model output is depicted in Fig. 8.3b, c. The model error with respect to the actual output (y d ) obtained by experiments is illustrated in Fig. 8.3d. It is observed that the Bouc–Wen model produces an RMSE of \(2.86\,\mu \mathrm{m}\), which accounts for 2.1% of the motion range.

Fig. 8.3
figure 3

Generalization test results of the Bouc–Wen model. (a) Input voltage; (b) experimental result and Bouc–Wen model output; (c) displacement-voltage hysteresis loops; (d) Bouc–Wen model output error

Full size image

8.4.3 LSSVM Model Results

8.4.3.1 Dynamic Model Identification

Before developing the LSSVM model, a linear dynamic model of the system plant is identified by the swept-sine approach. The magnitudes of frequency responses obtained from the experimental data and the identified model are compared in Fig. 8.4. It is found that the first resonant mode occurs around 404 Hz, and the identified second-order model matches the system dynamics well in the frequencies below 600 Hz. The identified transfer function is

$$\displaystyle{ G_{c}(s) = \frac{1.247 \times 1{0}^{8}} {{s}^{2} + 1.847s + 6.477 \times 1{0}^{6}} }$$
(8.16)

which is employed to demonstrate the effectiveness of the proposed hysteresis modeling and compensation scheme.

Fig. 8.4
figure 4

Magnitude of frequency response of the system plant

Full size image

By comparing the parameters of (8.4) and (8.16), one can deduce that \(\omega = 2.5450 \times 1{0}^{3}\,\mathrm{rad/\!\!s}\), \(\xi = 3.6287 \times 1{0}^{-4}\), and \(d = 1.247 \times 1{0}^{8}\,\mu \mathrm{{m/s}}^{2}\mbox{ -}\mathrm{V}\).

8.4.3.2 LSSVM Modeling and Testing

To train the LSSVM model, the same exciting voltage signal as shown in Fig. 8.5a is employed. In order to accurately capture the hysteresis behavior based on LSSVM model, a suitable input vector (8.8) is required to be determined. Without loss of generality, the position and hysteresis terms are considered as input variables in the current research.

Fig. 8.5
figure 5

The hysteresis term h. (a) Time history of input voltage; (b) time history of h; (c) h versus input voltage; (d) h versus output position

Full size image

By setting n = 2 and l = 2, the LSSVM model is trained by using the corresponding input variables and the output variables, i.e., the hysteresis term h as shown in Fig. 8.5b–d which is generated by resorting to (8.6). The training results of the LSSVM model are shown in Fig. 8.6. By employing the input signal (see Fig. 8.3a), the testing results are illustrated in Fig. 8.7.

Fig. 8.6
figure 6

Results of the trained LSSVM model. (a) Hysteresis term versus voltage; (b) displacement–voltage hysteresis loops

Full size image
Fig. 8.7
figure 7

Generalization test results of the LSSVM model. (a) Hysteresis term versus voltage; (b) displacement–voltage hysteresis loops

Full size image

It is observed that the LSSVM model is trained to produce an RMSE of 0.01% for the hysteresis term h, which leads to a percent RMSE of 1.05% for the output position x. With the new testing signal, the LSSVM model generates an RMSE of 0.77% for h, which results in 1.42% RMSE for the output position x.

It is evident that the LSSVM model has reduced the testing error of output position by 32% in comparison with the Bouc–Wen model. Therefore, the effectiveness of LSSVM model is confirmed by the hysteresis modeling results.

8.5 Feedforward Hysteresis Compensation and Results

In this section, the feedforward control schemes based on the developed Bouc–Wen and LSSVM models are realized to compensate for the hysteresis effect.

To suppress the hysteresis nonlinearity, a feedforward (FF) control (8.3) based on the Bouc–Wen model is first implemented. Moreover, the block diagram of LSSVM model-based FF control is depicted in Fig. 8.8. It is obvious that only the hysteresis model is needed whereas no inverse hysteresis model is required in the implementation of the feedforward compensation.

Fig. 8.8
figure 8

Block diagram of LSSVM model-based feedforward control scheme

Full size image

In order to demonstrate the superiority of LSSVM over Bouc–Wen model for hysteresis compensation, several experimental studies have been carried out. For instance, concerning a desired position trajectory as shown in Fig. 8.9a, the FF control results of Bouc–Wen model and LSSVM model are illustrated in Fig. 8.9a, c, and the tracking errors are compared in Fig. 8.9b. It is observed that the Bouc–Wen model gives an RMSE of \(7.92\,\mu \mathrm{m}\) (i.e., 5.8% of motion range), and the LSSVM model produces a \(1.02\mbox{ -}\mu \mathrm{m}\) RMSE (i.e., 0.7% of motion range). As compared with Bouc–Wen model, the LSSVM is capable of suppressing the tracking error more by 88%, which leads to a negligible hysteresis as depicted in Fig. 8.9c. Thus, the effectiveness of LSSVM in the hysteresis compensation is demonstrated by the experimental results.

Fig. 8.9
figure 9

Feedforward compensation results. (a) Reference and actual positions; (b) displacement errors of Bouc–Wen and LSSVM models-based FF compensation; (c) actual versus reference positions

Full size image

Although some degree of compensation error exists as evident from Fig. 8.9b, it can be easily reduced by combining a feedback controller as shown in [8].

8.6 Conclusion

This chapter is dedicated to hysteresis modeling and compensation of piezoelectric actuators. It is shown that the nonlinear hysteresis can be well compensated by resorting to a trained intelligent hysteresis model without modeling the hysteresis inverse. That means that the established hysteresis model can be used for both hysteresis characterization and compensation, which is more computationally effective than most of existing approaches where both a hysteresis model and an inverse hysteresis model are employed. Experimental results confirm that the LSSVM model is superior to the Bouc–Wen model in terms of hysteresis modeling accuracy and hysteresis compensation effectiveness. Furthermore, the proposed approach applies to hysteresis modeling and compensation of other smart materials-based actuators as well.