Interval Modeling and Robust Feedback Control of Piezoelectric-Based Microactuators

Abstract

This chapter presents the modeling and the control of piezoelectric-based microactuators. Typified by uncertainties of models, we propose to use intervals to bound the uncertain parameters. These uncertainties are particularly due to the difficulties to perform precise identification and to the high sensivity of the systems at the micro/nanoscale. In order to account the models uncertainties, we propose therefore to combine interval tools and classical control theory to derive robust controllers. Experimental results confirm the predicted theory and demonstrate the efficiency of the proposed method.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

6.1 Introduction

This chapter presents the control of piezoelectric actuators used in microgrippers generally dedicated to micromanipulation or to microassembly. Piezoelectric actuators are well recognized for their high resolution (submicrometric), their high bandwidth (up to several tens of kiloHertz), their high force density, and for their ease of control (control signal is electrical). However, like other microactuators (thermal, electrostatic, etc.), piezoelectric microactuators suffer from the high sensivity face to the environment due to their small sizes. For instance, small mechanical vibrations or small thermal noises surrounding the microactuators would generate nonnegligible unwanted movement of them. All these make the used models have uncertain or varying parameters and consequently may lead to the loss of performances or even the loss of stability during the utilization of the actuators.

In order to achieve the required performances in micromanipulation and microassembly tasks, linear modeling with Δ-matrix uncertainties has been used and classical robust control laws ($H_{2},\ H_{\infty }$, and $\mu$-synthesis) were applied for each piezocantilever [4, 14–16]. The efficiency of these advanced methods was proved in several applications (SISO and MIMO microsystems). However their major disadvantage is the derivation of high-order controllers which are time consuming and which limit their embedding possibilities, as required for real packaged microsystems.

An alternative possibility to classical robust control laws is the use of interval analysis which is a way to model the parametric uncertainties. The principle of the controller design is therefore based on the combination of the interval arithmetic with a linear control theory. In addition to its principle simplicity to model the uncertain parameters, the main advantage is the derivation of low-order controllers.

In this chapter, interval tools are used to design robust controllers for piezoelectric microactuators and to check a posteriori their performances. Two methods are proposed for the control design, a method based on the Performances Inclusion Theorem [13] and a method based on the combination of the H _∞ and interval tools. Experimental results demonstrate the efficiency of the proposed approaches and show their real interest for uncertain systems such as piezoelectric microactuators.

The chapter is organized as follows. We give first some preliminaries on interval tools in Sect. 6.2. Section 6.3 is devoted to the design of robust controller using the Performances Inclusion Theorem while the method based on the combination of H _∞ tool and interval tools is presented in Sect. 6.4. In Sect. 6.5, we present the a posteriori performances analysis still by using H _∞ tool and interval tools. Finally, the experimental results are presented in Sect. 6.6.

6.2 Preliminaries on Intervals

6.2.1 Definitions

We remind here some basics on intervals that will be used in the rest of the chapter. The readers who are interested to see more in details the techniques of intervals are suggested to read the references [6, 12].

A real interval [x] is a closed interval such that

$$\displaystyle{ [x] = [{x}^{-},{x}^{+}] }$$

(6.1)

where x ⁻ and x ⁺ are called lower bound and upper bound, respectively. We have, ${x}^{-}\leq {x}^{+}$. Having ${x}^{-} = {x}^{+}$ means that the interval [x] is degenerate. By convention, a degenerate interval [a] = [a, a] is identified by the real number a. The designation point number is similar to the designation degenerate interval number. While the set of real point numbers is $\mathbb{R}$, the set of real intervals (or real interval numbers) is $\mathbb{I}\mathbb{R}$.

Instead of using the notation in (6.1), one can also identify a real interval number by its midpoint $\mathrm{mid}\left ([x]\right )$ and its radius $\mathrm{rad}\left ([x]\right )$ such that

$$\displaystyle{ \left \{\begin{array}{l} \mathrm{mid}\left ([x]\right ) = \frac{\left ({x}^{+}+{x}^{-}\right )} {2} \\ \mathrm{rad}\left ([x]\right ) = \frac{\left ({x}^{+}-{x}^{-}\right )} {2} = \frac{w\left ([x]\right )} {2}\\ \end{array} \right. }$$

(6.2)

where $w\left ([x]\right )$ is the width of the interval.

6.2.2 Operations on Intervals

In the arithmetics of intervals, the basic operations are extended to interval numbers. Consider two intervals $[x] = [{x}^{-},{x}^{+}]$ and $[y = {y}^{-},{y}^{+}]$. So we have

$$\displaystyle{ [x] + [y] = [{x}^{-} + {y}^{-},{x}^{+} + {y}^{+}] }$$

(6.3)

and

$$\displaystyle{ [x] - [y] = [{x}^{-}- {y}^{+},{x}^{+} - {y}^{-}] }$$

(6.4)

Consequently, we have, [x] − [x]≠0, except for ${x}^{-} = {x}^{+}$.

The multiplication and division are defined as follows

$$\displaystyle{ \begin{array}{l} \left [x\right ].\left [y\right ] = \left [\min \left ({x}^{-}{y}^{-},{x}^{-}{y}^{+},{x}^{+}{y}^{-},{x}^{+}{y}^{+}\right ),\right. \\ \left.\max \left ({x}^{-}{y}^{-},{x}^{-}{y}^{+},{x}^{+}{y}^{-},{x}^{+}{y}^{+}\right )\right ]\\ \end{array} }$$

(6.5)

and

$$\displaystyle{ \begin{array}{*{20}c} \left [x\right ]/\left [y\right ] = \left [x\right ].\left [1/{y}^{+},1/{y}^{-}\right ],&0\notin \\ \end{array} \left [y\right ] }$$

(6.6)

We say that an interval $\left [x\right ]$ is included in an interval $\left [y\right ]$, i.e. $\left [x\right ] \subset \left [y\right ]$, if and if only $\left [x\right ] \cap \left [y\right ] = \left [x\right ]$. We have $\left [x\right ]> \left [y\right ]$ if ${x}^{-}> {y}^{+}$. The real interval $\left [x\right ]$ is said to be positive if x ⁻ > 0. The distributive law does not hold in general for interval. However, the following relation, called subdistributivity, holds, $\left [x\right ]\left (\left [y\right ] + \left [z\right ]\right ) \subseteq \left [x\right ]\left [y\right ] + \left [x\right ]\left [z\right ]$. In addition, if $\left [x\right ] + \left [y\right ] = \left [x\right ] + \left [z\right ]$, the cancellation law for addition holds, and $\left [y\right ] = \left [z\right ]$. The same property holds for multiplication, if $\left [x\right ]\left [y\right ] = \left [x\right ]\left [z\right ]$ and $0\notin \left [x\right ]$, thus $\left [y\right ] = \left [z\right ]$.

If f is a function $f : \mathbb{R} \rightarrow \mathbb{R}$, then its interval counterpart $\left [f\right ]$ satisfies

$$\displaystyle{ \left [f\right ]\left (\left [x\right ]\right ) = \left [\left \{f\left (x\right ) : x \in \left [x\right ]\right \}\right ] }$$

(6.7)

The interval function $\left [f\right ]$ is called inclusion function because $f\left (\left [x\right ]\right ) \subseteq \left [f\right ]\left (\left [x\right ]\right )$, for all $\left [x\right ] \in \mathbb{I}\mathbb{R}$. An inclusion function $\left [f\right ]$ is thin if for any degenerate interval $\left [x\right ] = x$, $\left [f\right ](x) = f(x)$. It is minimal if for any $\left [x\right ]$, $\left [f\right ]\left (\left [x\right ]\right )$ is the smallest interval that contains $f\left (\left [x\right ]\right )$. The minimal inclusion function for f is unique and is denoted by ${\left [f\right ]}^{{\ast}}\left (\left [x\right ]\right )$.

An easy way to compute an inclusion function for f is to replace each variable x in the expression of f by $\left [x\right ]$ and all operations on points by their interval counterpart. Thus, one obtains the natural inclusion function.

6.2.3 Interval Systems

An interval system is a transfer function representation, a state space representation or a differential representation where the parameters are intervals. For an interval transfer function, which is the interest of this chapter, the representation is as follows

$$\displaystyle{ \left [G\right ]\left (s\right ) = \frac{\left [b_{m}\right ]{s}^{m} + \cdots + \left [b_{1}\right ]{s}^{1} + \left [b_{0}\right ]} {\left [a_{n}\right ]{s}^{n} + \cdots + \left [a_{1}\right ]{s}^{1} + \left [a_{0}\right ]} = \frac{\sum \limits _{l=0}^{m}\left [b_{l}\right ]{s}^{l}} {\sum \limits _{k=0}^{n}\left [a_{k}\right ]{s}^{k}} }$$

(6.8)

where s is the Laplace variable and where m ≤ n, n being the order of the interval system [G](s). The parameters $\left [a_{k}\right ]$ and $\left [b_{l}\right ]$ are considered to be constant real intervals in order to assume linear time invariant (LTI) systems. The notation $\left [G\right ]\left (s\right )$ shall be used if the intervals $\left [a_{k}\right ]$ and $\left [b_{l}\right ]$ are known. Instead, the notation $\left [G\right ]\left (\left [a_{k}\right ],\left [b_{l}\right ],s\right )$ is used when they are unknown and to be sought for.

The notion of inclusion of systems should also be defined. Consider two interval systems having the same polynomials degrees m and n, i.e. having the same structure

$$\displaystyle{ \begin{array}{*{20}c} \left [G_{1}\right ](s) = \frac{\sum \limits _{l=0}^{m}\left [b_{ 1l}\right ]\cdot {s}^{l}} {\sum \limits _{k=0}^{n}\left [a_{1k}\right ]\cdot {s}^{k}} &,&\left [G_{2}\right ](s) = \frac{\sum \limits _{l=0}^{m}\left [b_{ 2l}\right ]\cdot {s}^{l}} {\sum \limits _{k=0}^{n}\left [a_{2k}\right ]\cdot {s}^{k}}\\ \end{array} }$$

(6.9)

$\left [G_{1}\right ]\left (s\right ) \subseteq \left [G_{2}\right ]\left (s\right )$ is equivalent to saying that for any s ∈ [0, ∞), we have $\left [G_{1}\right ] \subseteq \left [G_{2}\right ]$.

Lemma 2.1.

If $\left [b_{1l}\right ] \subseteq \left [b_{2l}\right ]$ and $\left [a_{1k}\right ] \subseteq \left [a_{2k}\right ]$ , ∀k,l, then $\left [G_{1}\right ]\left (s\right ) \subseteq \left [G_{2}\right ]\left (s\right )$ .

Proof.

See [13].

6.2.4 The Performances Inclusion Theorem [13]

Consider two interval systems having the same polynomials degrees m and n

$$\displaystyle{ \begin{array}{*{20}c} \left [G_{1}\right ](s) = \frac{\sum \limits _{l=0}^{m}\left [b_{ 1l}\right ]\cdot {s}^{l}} {\sum \limits _{k=0}^{n}\left [a_{1k}\right ]\cdot {s}^{k}} &,&\left [G_{2}\right ](s) = \frac{\sum \limits _{l=0}^{m}\left [b_{ 2l}\right ]\cdot {s}^{l}} {\sum \limits _{k=0}^{n}\left [a_{2k}\right ]\cdot {s}^{k}}\\ \end{array} }$$

(6.10)

The performances inclusion theorem (PIT) which will be used to further design a controller is composed of two results.

Theorem 2.1.

The performances inclusion in the frequency domain

$$\displaystyle{\begin{array}{l} \mathrm{if}\left \{\begin{array}{*{20}l} \begin{array}{*{20}c} \left [a_{1k}\right ] \subseteq \left [a_{2k}\right ],&\forall k = 1,\ldots,n\\ \end{array} \\ \mathrm{and} \\ \begin{array}{*{20}l} \left [b_{1l}\right ] \subseteq \left [b_{2l}\right ],&\forall l = 1,\ldots,m\\ \end{array}\\ \end{array} \right. \\ \\ \Rightarrow \left \{\begin{array}{*{20}l} \left [\rho \right ]\left (\left [G_{1}\right ](j\omega )\right ) \subseteq \rho \left (\left [G_{2}\right ](j\omega )\right ) \\ \mathrm{and} \\ \left [\varphi \right ]\left (\left [G_{1}\right ](j\omega )\right ) \subseteq \varphi \left (\left [G_{2}\right ](j\omega )\right )\\ \end{array} \right. \\ \end{array} }$$

Theorem 2.2.

The performances inclusion in the time domain

$$\displaystyle{\begin{array}{l} \mathrm{if}\left \{\begin{array}{*{20}l} \begin{array}{*{20}l} \left [a_{1k}\right ] \subseteq \left [a_{2k}\right ],&\forall k = 1,\ldots,n\\ \end{array} \\ \mathrm{and} \\ \begin{array}{*{20}l} \left [b_{1l}\right ] \subseteq \left [b_{2l}\right ],&\forall l = 1,\ldots,m\\ \end{array}\\ \end{array} \right. \\ \\ \begin{array}{*{20}c} \Rightarrow &\left [g_{1}\right ](t) \subseteq \left [g_{2}\right ](t)\\ \end{array}\\ \end{array} }$$

where

• $[\rho ]\left ([G_{i}](j\omega )\right )$ is the modulus of the system [G _i ].

• $[\varphi ]\left ([G_{i}](j\omega )\right )$ is the argument.

• [g _i ](t) is the impulse response.

Proof.

See [13].

6.3 PIT-Based Robust Control Design

Consider the feedback system shown in Fig. 6.1, where an uncertain system modeled by an interval transfer function $[G](s,[\mathbf{a}],[\mathbf{b}])$ is controlled by a controller [C](s). y _c (t) is the reference input, y(t) is the output signal, and u(t) is the input control signal.

Fig. 6.1

A unity feedback interval control system

Let us define the SISO interval system $[G](s,[\mathbf{a}],[\mathbf{b}])$ as follows

$$\displaystyle{ [G](s,[\mathbf{a}],[\mathbf{b}]) = \frac{[N](s,[\mathbf{b}])} {[D](s,[\mathbf{a}])}\;, }$$

(6.11)

where $[N](s,[\mathbf{b}])$ and $[D](s,[\mathbf{a}])$ are known polynomial with interval coefficients

$$\displaystyle{ \begin{array}{l} [D](s,[\mathbf{a}]) = [a_{0}] + [a_{1}]s + [a_{2}]{s}^{2} + \cdots + [a_{n}]{s}^{n}\\ \\{} [N](s,[\mathbf{b}]) = 1 + [b_{1}]s + [b_{2}]{s}^{2} + \cdots + [b_{m}]{s}^{m}\\ \end{array} }$$

(6.12)

with m ≤ n and the interval vectors $[\mathbf{a}]$ and $[\mathbf{b}]$ are defined by

$$\displaystyle{[\mathbf{a}] = \left (\begin{array}{l} [a_{0}] \\ {}[a_{1}] \\ {}[a_{2}]\\ \ \ \vdots \\{} [a_{n}]\\ \end{array} \right )\ \ \ [\mathbf{b}] = \left (\begin{array}{l} \ \ 1 \\{} [b_{1}] \\{} [b_{2}]\\ \ \ \vdots \\{} [b_{m}]\\ \end{array} \right )}$$

The natural question in control design approaches for interval systems is: How can one derive a candidate controller for which the closed-loop system of Fig. 6.1 meets some performance requirements whatever the coefficients a _i and b _j ranging in their intervals [a _i ] and [b _j ] (for i = 0, …, n and j = 1, …, m), respectively. This point will be presented next.

Let us define a controller [C](s, [θ]) with a prior knowledge on its order l ≤ k as follows

$$\displaystyle{ [C](s,[\theta ]) = \frac{[N_{c}](s)} {[D_{c}](s)} }$$

(6.13)

where the interval polynomials [D _c ](s) and [N _c ](s) are given as follows

$$\displaystyle{ \begin{array}{l} [D_{c}](s) = [c_{0}] + [c_{1}]s + [c_{2}]{s}^{2} + \cdots + [c_{k}]{s}^{k}\\ \\ {}[N_{c}](s) = [d_{0}] + [d_{1}]s + [d_{2}]{s}^{2} + \cdots + [d_{l}]{s}^{l}\\ \end{array} }$$

(6.14)

with the interval parameters vector of the controller $[\theta ]={\left ([c_{0}],\ldots,[c_{k}],[d_{0}],\ldots,[d_{l}]\right )}^{T}$ is assumed to be unknown.

Let us denote the closed-loop model of Fig. 6.1 by $[H_{\mathrm{cl}}](s,[\mathbf{p}],[\mathbf{q}])$. This latter can be computed using the interval model (6.11) and the imposed controller (6.13) as follows

$$\displaystyle{ [H_{\mathrm{cl}}](s,[\mathbf{p}],[\mathbf{q}]) = \frac{1} { \frac{1} {[C](s,[\theta ])[G](s,[\mathbf{a}],[\mathbf{b}])} + 1} }$$

(6.15)

where the interval vectors $[\mathbf{q}]$ and $[\mathbf{p}]$ are function of the intervals $[\mathbf{a}]$, $[\mathbf{b}]$, and [θ].

The closed-loop form given in (6.15) allows to avoid a multi-occurrence of the interval terms $[G](s,[\mathbf{a}],[\mathbf{b}])$ and [C](s, [θ]) which can produce an overestimation during the closed-loop computation.

After replacing $[G](s,[\mathbf{a}],[\mathbf{b}])$ and [C](s, [θ]) in (6.15), we get

$$\displaystyle{ [H_{\mathrm{cl}}](s,[\mathbf{p}],[\mathbf{q}]) = \frac{[N](s,[\mathbf{b}])[N_{c}](s)} {[N](s,[\mathbf{b}])[N_{c}](s) + [D](s,[\mathbf{a}])[D_{c}](s)} }$$

(6.16)

which can be written after developing as follows

$$\displaystyle{ [H_{\mathrm{cl}}](s,[\mathbf{p}],[\mathbf{q}]) = \frac{[N_{\mathrm{cl}}](s,[\mathbf{q}])} {[D_{\mathrm{cl}}](s,[\mathbf{p}])} }$$

(6.17)

with

$$\displaystyle{ \begin{array}{l} [D_{\mathrm{cl}}](s,[\mathbf{p}]) = [p_{0}] + [p_{1}]s + [p_{2}]{s}^{2} + \cdots + [p_{r}]{s}^{r}\\ \\ {}[N_{\mathrm{cl}}](s,[\mathbf{q}]) = 1 + [q_{1}]s + [q_{2}]{s}^{2} + \cdots + [q_{e}]{s}^{e}\\ \end{array} }$$

(6.18)

where $e = m + l$, $r = n + k$, and

$$\displaystyle{[\mathbf{p}] = \left (\begin{array}{l} [p_{0}] \\ {}[p_{1}] \\ {}[p_{2}]\\ \ \ \vdots \\ {}[p_{r}]\\ \end{array} \right )\ \ \ [\mathbf{q}] = \left (\begin{array}{l} \ \ 1 \\{} [q_{1}] \\ {}[q_{2}]\\ \ \ \vdots \\ {}[q_{e}]\\ \end{array} \right )}$$

Consider a family of wanted closed-loop behaviors described by a known interval transfer function, called interval reference model. If the controller defined in (6.13) for a given θ ensures that the set of all possible closed-loop plants (6.17) is included in the set of all feasible reference models, then robust performances are achieved.

Let’s denote by $[H](s,[\overline{\mathbf{p}}],[\overline{\mathbf{q}}])$ the interval reference model that describes the required performance measures. Also, let Θ be the set of admissible values of the controller parameters allowing to ensure required performances. Thus, the design problem to be addressed can be viewed as finding the set Θ for which the following inclusion holds [7, 8, 11], i.e., robust performances achieve.

$$\displaystyle{ \Theta = \left \{\theta \in \mathcal{D}\vert [H_{\mathrm{cl}}](s,[\mathbf{p}],[\mathbf{q}]) \subseteq [H](s,[\overline{\mathbf{p}}],[\overline{\mathbf{q}}])\right \} }$$

(6.19)

where $\mathcal{D}$ is the definition domain of θ.

Assume that an interval reference model is available and can be defined as follows

$$\displaystyle{ [H](s,[\overline{\mathbf{p}}],[\overline{\mathbf{q}}]) = \frac{[\overline{N}](s,[\overline{\mathbf{q}}])} {[\overline{D}](s,[\overline{\mathbf{p}}])} }$$

(6.20)

where

$$\displaystyle{ \begin{array}{l} [\overline{D}](s,[\overline{\mathbf{p}}]) = [\overline{p}_{0}] + [\overline{p}_{1}]s + [\overline{p}_{2}]{s}^{2} + \cdots + [\overline{p}_{\overline{r}}]{s}^{\overline{r}}\\ \\ {}[\overline{N}](s,[\overline{\mathbf{q}}]) = 1 + [\overline{q}_{1}]s + [\overline{q}_{2}]{s}^{2} + \cdots + [\overline{q}_{\overline{e}}]{s}^{\overline{e}}\\ \end{array} }$$

(6.21)

such as $\overline{e} \leq \overline{r}$ and

$$\displaystyle{[\overline{\mathbf{p}}] = \left (\begin{array}{l} [\overline{p}_{0}] \\ {}[\overline{p}_{1}] \\ {}[\overline{p}_{2}]\\ \ \ \vdots \\ {}[\overline{p}_{\overline{r}}]\\ \end{array} \right )\ \ \ [\overline{\mathbf{q}}] = \left (\begin{array}{l} \ \ 1 \\{} [\overline{q}_{1}] \\ {}[\overline{q}_{2}]\\ \ \ \vdots \\ {}[\overline{q}_{\overline{e}}]\\ \end{array} \right )}$$

In order to check the inclusion $[H_{\mathrm{cl}}](s,[\mathbf{p}],[\mathbf{q}]) \subseteq [H](s,[\overline{\mathbf{p}}],[\overline{\mathbf{q}}])$ by applying the parameter by parameter inclusion as given in the PIT theorem in Sect. 6.2.4, the interval reference model $[H](s,[\overline{\mathbf{p}}],[\overline{\mathbf{q}}])$ must have the same structure than the closed-loop transfer $[H_{\mathrm{cl}}](s,[\mathbf{p}],[\mathbf{q}])$ defined in (6.17). For that, let’s assume that the interval polynomials $[\overline{D}](s,[\overline{\mathbf{p}}])$ and $[\overline{N}](s,[\overline{\mathbf{q}}])$ of the interval reference model have the same order as in the polynomials $[D_{\mathrm{cl}}](s,[\mathbf{p}])$ and $[N_{\mathrm{cl}}](s,[\mathbf{q}])$, respectively, as follows

$$\displaystyle{ \begin{array}{l} [\overline{D}](s,[\overline{\mathbf{p}}]) = [\overline{p}_{0}] + [\overline{p}_{1}]s + [\overline{p}_{2}]{s}^{2} + \cdots + [\overline{p}_{r}]{s}^{r}\\ \\ {}[\overline{N}](s,[\overline{\mathbf{q}}]) = 1 + [\overline{q}_{1}]s + [\overline{q}_{2}]{s}^{2} + \cdots + [\overline{q}_{e}]{s}^{e}\\ \end{array} }$$

(6.22)

According to the PIT theorem in Sect. 6.2.4, if the following set of inclusions

$$\displaystyle{ \left \{\begin{array}{l} [q_{j}] \subseteq [\overline{q}_{j}],\begin{array}{*{20}c} \\ \end{array} \mathrm{for}\begin{array}{*{20}c} \\ \end{array} j = 1,\ldots,e \\{} [p_{i}] \subseteq [\overline{p}_{i}],\begin{array}{*{20}c} \\ \end{array} \mathrm{for}\begin{array}{*{20}c} \\ \end{array} i = 0,\ldots,r\\ \end{array} \right. }$$

(6.23)

hold, then the set of all possible closed-loop plants $[H_{\mathrm{cl}}](s,[\mathbf{p}],[\mathbf{q}])$ belong to the set of all admissible plants $[H](s,[\overline{\mathbf{p}}],[\overline{\mathbf{q}}])$, and therefore the performances defined by $[H_{\mathrm{cl}}](s,[\mathbf{p}],[\mathbf{q}])$ are included in those of the wanted closed-loop $[H](s,[\overline{\mathbf{p}}],[\overline{\mathbf{q}}])$. As a result, the controller [C](s, [θ]) that guarantees the above inclusions will effectively ensures the required performances for any system G(s) in the interval model $[G](s,[\mathbf{a}],[\mathbf{b}])$.

Remark 1.

The interval vectors $[\overline{\mathbf{p}}]$ and $[\overline{\mathbf{q}}]$ are known and they can be easily computed from the required specifications, while the interval parameters [p _i ] and [q _j ] (for i = 0, …, r and j = 1, …, e) depend on the controller parameters which are unknown.

Finally, the design problem given in (6.19) can be reduced as finding the set-solution Θ of the admissible values of the controller parameters that ensure the following set of inclusions

$$\displaystyle{ \Theta = \left \{\theta \in \mathcal{D}\left \vert \left \{\begin{array}{l} [q_{j}]([\theta ]) \subseteq [\overline{q}_{j}],\forall j = 1,\ldots,m + l \\ {}[p_{i}]([\theta ]) \subseteq [\overline{p}_{i}],\forall i = 0,\ldots,n + k\\ \end{array} \right.\right.\right \} }$$

(6.24)

where $\mathcal{D}$ is the definition domain of θ.

The above problem described in (6.24) is known as a set-inversion problem which can be solved using interval techniques. The set inversion operation consists to compute the reciprocal image of a compact set called subpaving. The set-inversion algorithm SIVIA (more details are given in [5, 6]) allows to solve the design problem given in (6.24) and provides an approximation with subpavings of the set solution Θ. This approximation is realized with an inner and outer subpavings, respectively, $\underline{\Theta }$ and $\overline{\Theta }$, such that $\underline{\Theta } \subseteq \Theta \subseteq \overline{\Theta }$. The subpaving Θ corresponds to the controller parameter vector for which the problem (6.24) holds. If $\Theta = \emptyset$, then it is guaranteed that no solution exists for (6.24).

We give in Table 6.1 the recursive SIVIA algorithm allowing to solve the control problem (6.24) with guaranteed solution. SIVIA algorithm requires a search box [θ ₀] (possibly very large) also called initial box within which $\overline{\Theta }$ is guaranteed to belong. The inner and outer subpavings ($\underline{\Theta }$ and $\overline{\Theta }$ ) are initially empty. ε represents the wanted accuracy of computation.

Table 6.1 SIVIA algorithm for solving a set-inversion problem [5, 6]

Quite often we are interested to compute an inner approximation $\underline{\Theta }$ for which we are sure that $\underline{\Theta }$ is included in the set solution Θ, i.e., $\underline{\Theta } \subseteq \Theta$, but when no inner approximation exists i.e., $\underline{\Theta } = \emptyset$, it is possible to choose parameters inside the outer subpaving, i.e., choose $\theta \in \overline{\Theta }$.

Remark 2.

The number of unknown parameters in (6.24) is $l + k + 2$, while the number of inclusions is $r + e + 1$. Since $e = m + l$ and $r = n + k$, we can write $r + e + 1 \geq l + k + 2$. Therefore, there are more inclusions than unknown variables. So, the set solution Θ can be obtained by the intersection of the set solution of each inclusion in (6.24) as follows

$$\displaystyle{\Theta =\bigcap \limits _{ i=1}^{r+e+1}(set{\_}sol)_{ i}}$$

such as, $(set{\_}sol)_{i}$ is the set solution of the ith inclusion.

Remark 3.

If the set-inversion problem is not feasible, i.e., $\Theta = \emptyset$, the initial box of the parameters must be changed and/or one must modify the controller structure and/or the required performance specifications.

6.4 Design of a Robust Controller by Combining Standard H _∞ and Interval Tools

In this part, another approach to design robust controllers for interval systems is proposed. The method is based on the standard H _∞ technique and interval tools. While the specifications and wanted performances are transcribed in terms of weighting transfers and the standard H _∞ is used to formulate the objective or problem, interval tools are used to compute the controllers.

Consider the closed-loop pictured in Fig. 6.1, where the controlled system $[G](s,[\mathbf{a}],[\mathbf{b}])$ is a general nth-order interval system defined by the following transfer function

$$\displaystyle{ [G](s,[\mathbf{a}],[\mathbf{b}]) = \frac{[b_{0}] + [b_{1}]s + [b_{2}]{s}^{2} + \cdots + [b_{m}]{s}^{m}} {[a_{0}] + [a_{1}]s + [a_{2}]{s}^{2} + \cdots + [a_{n}]{s}^{n}} }$$

(6.25)

where m ≤ n and

$$\displaystyle{[\mathbf{a}] = \left (\begin{array}{l} [a_{0}] \\ {}[a_{1}] \\ {}[a_{2}]\\ \ \ \vdots \\ {}[a_{n}]\\ \end{array} \right )\ \ \ [\mathbf{b}] = \left (\begin{array}{l} [b_{0}] \\{} [b_{1}] \\ {}[b_{2}]\\ \ \ \vdots \\ {}[b_{m}]\\ \end{array} \right )}$$

Similar to the design problem presented in the previous section, the main objective is to design robust controller for which robust performances hold for any system G(s) part of the family of systems defined by $[G](s,[\mathbf{a}],[\mathbf{b}])$. Also, in addition to the desired performance specifications of the closed-loop system, it is often desired to design low-order controllers for simplicity of implementation, especially for embedded systems. For that, a fixed structure of the controller can be a priori imposed as follows

$$\displaystyle{ [C](s,[\theta ]) = \frac{[d_{0}] + [d_{1}]s + [d_{2}]{s}^{2} +\ldots +[d_{l}]{s}^{l}} {[c_{0}] + [c_{1}]s + [c_{2}]{s}^{2} + \cdots + [c_{k}]{s}^{k}} }$$

(6.26)

where $[\theta ] ={ \left ([c_{0}],\cdots \,,[c_{k}],[d_{0}],\ldots,[d_{l}]\right )}^{T}$ is an unknown vector of interval parameters and l ≤ k to have the causality of the controller.

The issue is to find the set (or subset) of the suitable values of the controller parameters so that the closed-loop system respects some given performances despite the parametric uncertainties considered in the transfer function of the controlled system. For that, the controller parameters can be adjusted using H _∞ -criterion. Such criterion is defined as the H _∞ -norm of some weighted transfer functions of the closed-loop to be less than or equal to one.

Let’s remind the H _∞ -standard principle that considers the tracking performances and the input control limitation [3, 18]. It is based on the standard block pictured in Fig. 6.2b where P(s) is called the augmented system. This standard scheme is derived from the weighted closed-loop in Fig. 6.2a. While the weighting W ₁(s) is used to transcribe the tracking performances, the weighting W ₂(s) is used to transcribe the input control limitation.

Fig. 6.2

Standard H _∞ control scheme (a): the weighted closed-loop block-diagram. (b): the corresponding standard form

The H _∞ problem is to find a controller stabilizing the closed-loop system and achieving the following H _∞ -criterion

$$\displaystyle{ \left \|F_{l}(P(s),C(s))\right \|_{\infty } \leq \gamma }$$

(6.27)

where γ is a positive scalar. If γ ≤ 1, the nominal (specified) performances are achieved.

The linear fractional transformation F _l (P(s), C(s)) is the transfer between the weighted outputs and the exogenous inputs of Fig. 6.2b. It is defined as follows

$$\displaystyle{ F_{l}(P(s),C(s)) = z(s)\ y_{c}^{-1}(s) }$$

(6.28)

with $z = \left (\begin{array}{l} z_{1} \\ z_{2}\\ \end{array} \right )$

From Fig. 6.2a F _l (P(s), C(s)) is given by

$$\displaystyle{ F_{l}(P(s),C(s)) = \left (\begin{array}{*{20}c} W_{1}(s)S(s) \\ W_{2}(s)C(s)S(s)\\ \end{array} \right ) }$$

(6.29)

where $S(s) ={ \left (1 + C(s)G(s)\right )}^{-1}$ is the sensivity function.

Applying the H _∞ standard problem in (6.27) to (6.28) and (6.29), we obtain the following conditions to be satisfied

$$\displaystyle{ \left \{\begin{array}{l} \left \|W_{1}(s)S(s)\right \|_{\infty }\leq \gamma \\ \left \|W_{2}(s)C(s)S(s)\right \|_{\infty }\leq \gamma \\ \end{array} \right. }$$

(6.30)

Now we reapply the same H _∞ principle presented above to design robust controller for systems modeled by an interval transfer function $[G](s,[\mathbf{a}],[\mathbf{b}])$. Since the system is interval, the augmented plant will also be interval, $[P](s,[\mathbf{a}],[\mathbf{b}])$. Moreover, the H _∞ -criterion $\left \|F_{l}([P](s,[\mathbf{a}],[\mathbf{b}]),[C](s,[\theta ]))\right \|_{\infty } \leq \gamma$ is given by

$$\displaystyle{ \left \{\begin{array}{l} \left \|W_{1}(s)[S](s)\right \|_{\infty }\leq \gamma \\ \left \|W_{2}(s)[C](s,[\theta ])[S](s)\right \|_{\infty }\leq \gamma \\ \end{array} \right. }$$

(6.31)

In this case, if γ ≤ 1, the robust performances are achieved.

Let’s denote by Θ the set of the suitable values corresponding to the controller parameters that ensures the requirements. Based on the H _∞ principle above, the design problem can be formulated as follows [7, 9, 10].

Find the set Θ so that H _∞ performance holds for any positive number γ ≤ 1, i.e.,

$$\displaystyle{ \Theta = \left \{\theta \in \mathcal{D}\left \vert \left \{\begin{array}{l} \left \|W_{1}(s)[S](s)\right \|_{\infty }\leq \gamma \\ \left \|W_{2}(s)[C](s,[\theta ])[S](s)\right \|_{\infty }\leq \gamma \\ \end{array} \right.\right.\right \} }$$

(6.32)

where $\mathcal{D}$ is the definition domain of θ. The interval sensivity function [S](s) is defined as follows

$$\displaystyle{ [S](s) = \frac{1} {1 + [C](s,[\theta ])[G](s,[\mathbf{a}],[\mathbf{b}])} }$$

(6.33)

However, the resolution of the problem (6.32) requires the computation of the H _∞ -norm of certain interval transfers. This computation can be done by applying the following theorems which are due to the results in [1, 2, 17].

Theorem 4.1.

Consider an interval system $[G](s,[\mathbf{a}],[\mathbf{b}])$ defined as in (6.25) . The H _∞ -norm of [G] is the maximal among the H _∞ -norm of the sixteen transfers,

$$\displaystyle{ \left \|\left [G\right ]\right \|_{\infty } =\mathop{ \max }\limits _{i=1\rightarrow 16}\left \|{G}^{(i)}\right \|_{ \infty } }$$

(6.34)

where G ⁽ⁱ⁾ , for $i = 1,2,\ldots,16$ are sixteen (point) systems based on the eight Kharitonov vertex polynomials corresponding to the numerator and denominator of the interval system, i.e., sixteen transfer functions formed by combining the four Kharitonov vertex polynomials of the numerator of $[G](s,[\mathbf{a}],[\mathbf{b}])$ and the four Kharitonov vertex polynomials of its denominator.

Proof.

see [1, 2].

When the interval system [G] is weighted by a weighting function (not interval transfer) W(s), it is not advised to compute the multiplication W[G] first and then compute the H _∞ -norm of the resulting interval plant afterwards. Indeed, developing the multiplication of the intervals polynomials produces a multi-occurrence of the parameters and therefore a overestimation of the resulting intervals. Thus, the H _∞ -norm of W[G] is defined as follows [1, 2]

$$\displaystyle{ \left \|W\left [G\right ]\right \|_{\infty } =\mathop{ \max }\limits _{i=1\rightarrow 16}\left \|W{G}^{(i)}\right \|_{ \infty } }$$

(6.35)

Also, in this control approach, we need to compute the H _∞ -norm of the sensivity function of an interval system $[G](s,[\mathbf{a}],[\mathbf{b}])$. This has been addressed in the following theorem proposed by Long-Wang [17].

Theorem 4.2.

Consider an interval system $[G](s,[\mathbf{a}],[\mathbf{b}])$ and its sensivity function $[S] = \frac{1} {1+[G]} = \frac{[D]} {[N]+[D]}$ , where [N] and [D] are the numerator and denominator polynomials of [G]. The H _∞ -norm of the sensivity [S] is defined by the maximal among the H _∞ -norm of twelve vertex systems out of sixteen vertex systems,

$$\displaystyle{ \left \|[S]\right \|_{\infty } = \left \| \frac{[D]} {[N] + [D]}\right \|_{\infty } =\mathop{ \max }\limits _{i=1\rightarrow 12}\left \|{S}^{\left (i\right )}\right \|_{ \infty } }$$

(6.36)

Proof.

see [17].

The computation of $\left \|W_{1}(s)[S](s)\right \|_{\infty }$ and $\left \|W_{1}(s)[C](s,[\theta ])[S](s)\right \|_{\infty }$ given in (6.32) can be easily carried out by applying the above theorems.

$$\displaystyle{ \begin{array}{l} \left \|W_{2}[C][S]\right \|_{\infty } =\mathop{ \max }\limits _{i=1\rightarrow 16}\left \|W_{2}{M}^{\left (i\right )}\right \|_{\infty }\\ \\ \left \|W_{1}[S]\right \|_{\infty } =\mathop{ \max }\limits _{i=1\rightarrow 12}\left \|W_{1}{S}^{\left (i\right )}\right \|_{\infty }\\ \end{array} }$$

(6.37)

where [M] = [C][S] and ${M}^{\left (i\right )}$ (i = 1, 2, …, 16) are the sixteen vertex of [M].

The problem given in (6.32) is known as a set-inversion problem which can be solved using set inversion algorithms. By using SIVIA algorithm [5, 6], it is possible to approximate the set solution Θ corresponding to the controller parameters for which the problem (6.32) is fulfilled. In fact, testing the existing or not of a solution (existing of a candidate controller) for the problem (6.32) requires to have a knowledge on the minimum and the maximum values of the H _∞ -norm of the involved interval transfers. However, Theorems 4.1 and 4.2 allow only to evaluate the maximum value of the H _∞ -norm of interval transfers. For that, we present in Fig. 6.3, a flow chart describing the recursive SIVIA algorithm allowing to solve the above design problem (6.32). The controller computation requires a search box [θ ₀] also called initial box. The subpaving Θ is initially empty. ε represents the wanted accuracy of computation. Note that, contrary to the standard H _∞ problem (for point systems) where the optimal value of γ is found by dichotomy, its value here is directly set to one, γ = 1. The objective is to find directly the controller parameters for which the specified performances are met.

Fig. 6.3

Flow chart corresponding to the SIVIA algorithm used for solving the problem (6.32)

Remark 4.

The controller computation based on the algorithm shown in Fig. 6.3 takes more time due to the high number of bisections carried out on the domain of the parameters θ.

6.5 A Posteriori Performances Analysis Using Standard H _∞ and Interval Tools Combined

Contrary to the problem presented in the two last sections where the objective was to design robust controller for interval systems, in this part, we deal with the inverse problem. This latter is as follows.

Consider an uncertain system modeled by an interval transfer $[G](s,[\mathbf{a}],[\mathbf{b}])$ and controlled by a controller C(s) (see Fig. 6.4) to ensure for the closed-loop system a more desirable behavior.

Fig. 6.4

Closed-loop control system

Assume that a candidate controller C ^∗(s) is available (for example, computed using the method presented in Sect. 6.3), then the natural question: How can one check if a such controller C ^∗(s) achieves the required performance specifications for the closed-loop system? This point can be carried out by means of H _∞ approach combined with interval analysis.

The principle of H _∞ synthesis combined with interval analysis discussed in Sect. 6.4 consists first in transcribing during the synthesis, the requirements into weighting functions (see Fig. 6.5), then computing a controller for which a H _∞ criterion holds,

$$\displaystyle{ \left \|F_{l}([P](s,[\mathbf{a}],[\mathbf{b}]),C(s)\right \|_{\infty }\leq 1 }$$

(6.38)

where F _l (P(s), C(s)) is the transfer of the interconnection between C(s) and the augmented plant $[P](s,[\mathbf{a}],[\mathbf{b}])$.

Fig. 6.5

H _∞ -standard problem

In our case the controller C ^∗(s) is known, so we need to check the fulfillment of the condition (6.38) for the controller C(s) = C ^∗(s). From Fig. 6.5, the H _∞ criterion becomes,

$$\displaystyle{ \left \{\begin{array}{l} \left \|W_{1}(s)[S](s)\right \|_{\infty }\leq \gamma \\ \left \|W_{2}(s)C(s)[S](s)\right \|_{\infty }\leq \gamma \\ \end{array} \right. }$$

(6.39)

then satisfying the conditions defined in (6.39) for C(s) = C ^∗(s), means that the controller C ^∗(s) guarantees robust performances for any G(s) within the interval system [G](s). The computation of the maximal H _∞ norm of the interval transfers given in (6.39) can be carried out by applying the Theorems 4.1 and 4.2.

Remark 5.

The H _∞ conditions given in (6.39) are only sufficient, so if these constraints are not satisfied, then no conclusion on the achievement of the desired performances can be done.

6.6 Application to Piezocantilevers and Experimental Results

The aim of this section is to apply the interval control methods previously presented to control piezoelectric microactuators used in microgrippers. In fact, a piezoelectric microgripper is composed of two piezoelectric cantilevers (microactuators) generally with rectangular section. Figure 6.6 pictures a microgripper made at the AS2M department of FEMTO-ST Institute manipulating a small gear.

Fig. 6.6

A piezoelectric microgripper manipulating a small gear

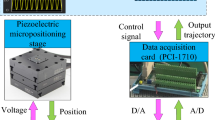
In general, one of the two actuators that compose the microgripper is used for the precise positioning while the second actuator is used to measure or control the manipulation force. In this application, we are interested by the modeling and control of the positioning. The actuator used is a unimorph cantilever made up of one piezoelectric layer (PZT material) and one passive layer (Copper material). Figure 6.7 presents the setup used for the rest of the chapter which includes,

• The piezoelectric actuator itself.

• A computer and a dSPACE board for the data acquisition, for generating the control signal or the reference signal and for the controller implementation. The Matlab-Simulink is used for the implementation and the sampling time is set equal to T _s  = 0. 2 ms.

• An optical sensor (Keyence LC-2420) which is set to have a resolution of 50 nm.

• A high-voltage (HV) amplifier ( ± 200 V).

Fig. 6.7

Setup used for the experiments

Modeling and identification of microsystems are very delicate because of their small sizes, their fragility, and the lack of convenient (accurate and high bandwidth) sensors to report precise measurements. These systems are also very sensitive to environmental disturbances (temperature, vibrations, manipulated objects, etc.). As a result, their behavior parameters may change during their functioning or during the tasks and therefore the wanted performances or even the stability may be lost. In this application, we bound the uncertain parameters of piezocantilever models by intervals that are able to account the above complex characteristics. Afterwards, control design approaches presented previously can be easily applied to improve the performances of piezocantilevers.

6.6.1 Interval Model Derivation

The models of piezocantilevers are often subjected to variation due to the environment (small thermal variation, manipulated object, etc.). In fact, these characteristics stem from the relatively small sizes of the piezoelectric actuators used in micromanipulation and micropositioning applications which finally make them very sensitive to any minor variation. The model parameters can be considered as uncertain and thus bounded by intervals within its range of variation in order to further design a robust controller. However, for an ease of identification in this application, we will not characterize the parameter variations of the piezoelectric actuator during a micropositioning or a micromanipulation task. We will use two unimorph piezocantilevers denoted by P ₁ and P ₂. The first piezocantilever P ₁ has the dimensions $length \times width \times thickness = 16\,\mathrm{mm} \times 1\,\mathrm{mm} \times 0.45\,\mathrm{mm}$, while the second one P ₂ has dimensions of $14\,\mathrm{mm} \times 1\,\mathrm{mm} \times 0.45\,\mathrm{mm}$. The difference in their length generate nonnegligible difference on their model parameters. The interval model $[G](s,[\mathbf{a}],[\mathbf{b}])$ which represents a family of piezocantilever models is derived using the two point models G ₁(s) and G ₂(s) corresponding to the used piezocantilevers P ₁ and P ₂, respectively, where the models G ₁(s) and G ₂(s) are identified without performing the above tasks. After a frequency identification for each piezocantilever and performing some computation, we obtain the following interval model $[G](s,[\mathbf{a}],[\mathbf{b}])$,

$$\displaystyle{ [G](s,[\mathbf{a}],[\mathbf{b}]) = \dfrac{[b_{2}]{s}^{2} + [b_{1}]s + [b_{0}]} {[a_{2}]{s}^{2} + [a_{1}]s + [a_{0}]} }$$

(6.40)

where

$$\displaystyle{ \begin{array}{l} [b_{2}] = [7.042,8.0313] \times 1{0}^{-8} \\ {}[b_{1}] = [1.808,1.809] \times 1{0}^{-4} \\ {}[b_{0}] = 1 \\{} [a_{2}] = [8.802,9.794] \times 1{0}^{-8} \\ {}[a_{1}] = [5.24,5.364] \times 1{0}^{-6} \\ {}[a_{0}] = [1.291,1.44]\\ \end{array} }$$

In order to increase the stability margin and to ensure that the interval model really contains the models of the two piezocantilevers, we propose to expand by 10 % the interval width of each parameter of the model $[G](s,[\mathbf{a}],[\mathbf{b}])$. This choice is a compromise. If the widths are too large, it is difficult to find a controller that respects both the stability and performances for the closed-loop. Finally, the extended interval model that will be used for the computation of a controller is as follows

$$\displaystyle\begin{array}{rcl} [G](s,[\mathbf{a}],[\mathbf{b}]) = \frac{[6.992,8.08] \times 1{0}^{-8}{s}^{2} + [1.807,1.809] \times 1{0}^{-4}s + 1} {[8.753,9.844] \times 1{0}^{-8}{s}^{2} + [5.234,5.37] \times 1{0}^{-6}s + [1.283,1.448]}& &{}\end{array}$$

(6.41)

6.6.2 Specifications and Controller Structure

Piezocantilevers are very resonant (more than 60 % of overshoot). Such overshoot is not desirable in micromanipulation and microassembly tasks. The following specifications are therefore considered for the closed-loop,

• Zero or very small overshoot.

• Settling time tr _5 %  ≤ 8 ms.

• Static error $\left \vert \varepsilon \right \vert \leq 1\,\%$.

These specifications often correspond to the requirement in micropositioning tasks for microassembly and micromanipulation that use piezoelectric microgrippers.

To ensure the above requirements, the control design approach does not require any specified structure for the controller. So, any structure can be chosen for the controller [C](s) as long as Remark 2 is satisfied. In this example, we consider a PI (Proportional–Integral) structure because of its low-order (two parameters) and its wide use in the industry

$$\displaystyle{ [C](s,[K_{p}],[K_{i}]) = \dfrac{[K_{p}]s + [K_{i}]} {s} }$$

(6.42)

where [K _p ] and [K _i ] are the proportional and integral gains, respectively.

Next, the both proposed control approaches will be applied to achieve these requirements.

6.6.3 PI Controller Computation Using PIT Approach

Based on the interval model in (6.41) and the interval controller in (6.42), the general model of the closed-loop can be expressed as follows

$$\displaystyle{ [H_{\mathrm{cl}}](s,[\mathbf{p}],[\mathbf{q}]) = \dfrac{[q_{3}]{s}^{3} + [q_{2}]{s}^{2} + [q_{1}]s + 1} {[p_{3}]{s}^{3} + [p_{2}]{s}^{2} + [p_{1}]s + [p_{0}]} }$$

(6.43)

where $[q_{3}] = \dfrac{[K_{p}][b_{2}]} {[K_{i}]}$, $[q_{2}] = \dfrac{[K_{p}][b_{1}]} {[K_{i}]} + [b_{2}]$, $[q_{1}] = \dfrac{[K_{p}]} {[K_{i}]} + [b_{1}]$,$[p_{3}] = \dfrac{[a_{2}] + [K_{p}][b_{2}]} {[K_{i}]}$, $[p_{2}] = \dfrac{[a_{1}] + [K_{p}][b_{1}]} {[K_{i}]} + [b_{2}]$, $[p_{1}] = \dfrac{[a_{0}] + [K_{p}]} {[K_{i}]} + [b_{1}]$ and [p ₀] = 1.

Concerning the reference model, its computation is carried out according to the closed-loop (6.43) and to the required specifications. According to the specifications (see Sect. 6.6.2), a first order model can be used for the reference model.

$$\displaystyle{ [H](s,[K],[\tau ]) = \dfrac{[K]} {[\tau ]s + 1} }$$

(6.44)

where the parameters [K] and $[\tau ]$ define the static error and settling time, respectively:

• $[K] = 1+\varepsilon = [0.99,1.01]$.

• $[\tau ] = \dfrac{[tr_{5\,\%}]} {3} = [0,2.66\,\mathrm{ms}]$.

However, it is necessary that the interval reference model has the same structure than that of the closed-loop in order to apply the parameter by parameter inclusion as required in (6.24). Thus we add some poles and zeros far from the imaginary axis to (6.44)

$$\displaystyle{ [H](s,[K],[\tau ]) = \dfrac{[K]{\left ( \dfrac{[\tau ]} {10}s + 1\right )}^{3}} {([\tau ]s + 1).{\left ( \dfrac{[\tau ]} {10}s + 1\right )}^{2}} }$$

(6.45)

which can also be rewritten as follows:

$$\displaystyle{ [H](s,[\overline{\mathbf{p}}],[\overline{\mathbf{q}}]) = \dfrac{[\overline{q}_{3}]{s}^{3} + [\overline{q}_{2}]{s}^{2} + [\overline{q}_{1}]s + 1} {[\overline{p}_{3}]{s}^{3} + [\overline{p}_{2}]{s}^{2} + [\overline{p}_{1}]s + [\overline{p}_{0}]} }$$

(6.46)

where $[\overline{q}_{3}] = 0.001{[\tau ]}^{3}$, $[\overline{q}_{2}] = 0.03{[\tau ]}^{2}$, $[\overline{q}_{1}] = 0.3[\tau ]$, $[\overline{p}_{3}] = 0.01 \dfrac{{[\tau ]}^{3}} {[K]}$,$[\overline{p}_{2}] = 0.21 \dfrac{{[\tau ]}^{2}} {[K]}$, $[\overline{p}_{1}] = 1.2 \dfrac{[\tau ]} {[K]}$ and $[\overline{p}_{0}] = \dfrac{1} {[K]}$.

According to the control method discussed in Sect. 6.3, the admissible values of the PI controller parameters that guarantee the required specifications for the interval model (6.41) can be obtained by solving the following system of inclusions.

$$\displaystyle{ \begin{array}{l} \dfrac{[K_{p}][b_{2}]} {[K_{i}]} \subseteq 0.001{[\tau ]}^{3}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \dfrac{[a_{1}] + [K_{p}][b_{1}]} {[K_{i}]} + [b_{2}] \subseteq \dfrac{0.21{[\tau ]}^{2}} {[K]} \\ \dfrac{[K_{p}][b_{1}]} {[K_{i}]} + [b_{2}] \subseteq 0.03{[\tau ]}^{2}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \dfrac{[a_{0}] + [K_{p}]} {[K_{i}]} + [b_{1}] \subseteq \dfrac{1.2[\tau ]} {[K]} \\ \dfrac{[K_{p}]} {[K_{i}]} + [b_{1}] \subseteq 0.3[\tau ]\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 1 \subseteq \dfrac{1} {[K]} \\ \dfrac{[a_{2}] + [K_{p}][b_{2}]} {[K_{i}]} \subseteq \dfrac{0.01{[\tau ]}^{3}} {[K]}\end{array} }$$

(6.47)

The application of the SIVIA algorithm implemented in the Matlab-Software, with an initial box $[K_{p0}] \times [K_{i0}] = [0,1] \times [0.1,1000]$, provides the subpaving shown in Fig. 6.8. The dark colored subpaving ($\underline{\Theta }$ ) corresponds to the inner approximation, i.e., the set parameters [K _p ] and [K _i ] of the controller (6.42) that ensures the above inclusions and consequently that meets the performances for the interval model.

Fig. 6.8

Set solution of the parameters [K _p ] and [K _i ] ensuring the wanted performances

The controller $[C](s,[K_{p}],[K_{i}])$ is an interval and is not directly implementable. Point parameters K _p and K _i within the set solution $\underline{\Theta }$ must be chosen and the corresponding point controller $C(s,K_{p},K_{i}) = C(s)$ has to be implemented. In this example, we test the following PI controller

$$\displaystyle{ C(s) = \dfrac{0.1s + 900} {s} }$$

(6.48)

This controller has been independently tested on the both piezocantilevers P ₁ and P ₂. A step response analysis is performed on each closed-loop by applying a step reference of amplitude $40\,\mu$ m. The application of the implemented controller C(s) to the both piezocantilevers leads to the experimental results shown in Fig. 6.9.

Fig. 6.9

Experimental step responses when testing the implemented controller C(s)

As shown in Fig. 6.9, the implemented controller has played its role and achieved the wanted performances for the closed-loops. Indeed, the experimental settling times are about tr ₁ = 4 ms and tr ₂ = 4. 7 ms with the piezocantilever P ₁ and P ₂, respectively. Moreover, the obtained behaviors are with very small overshoot and the experimental static errors are neglected and belong to the required interval $\left \vert \varepsilon \right \vert \leq 1\,\%$.

6.6.4 PI Controller Computation by Combining the H _∞ Technique with Interval Analysis

In this section, we apply the robust control approach proposed in Sect. 6.4 to control the deflection (position) of piezocantilevers having model inside the interval model $[G](s,[\mathbf{a}],[\mathbf{b}])$ defined in (6.41). The same requirements presented in Sect. 6.6.2 are considered here. Moreover, it is necessary to limit the applied voltage in order to avoid any damage of the actuators. For that, we add a condition on the amplitude of the input voltage U applied to the piezocantilever. We particularly choose a maximal voltage ${U}^{\max } = 2.5$  V for each $1\,\mu$ m of reference. Also, without loss of generality, we consider the design of the previous PI (Proportional–Integral) controller structure (6.42).

Figure 6.10a presents the closed-loop scheme for the controller design, where the weighting function W ₁(s) is added to transcribe the tracking performances and W ₂(s) for the input control limitation.

Fig. 6.10

(a) The closed-loop scheme with the weighting functions. (b) The H _∞ -standard scheme

The weighting functions W ₁(s) and W ₂(s) were chosen according to the required performances. We choose

$$\displaystyle{ \left \{\begin{array}{l} W_{1}(s) = \dfrac{0.002667s + 1} {0.002667s + 0.01}\\ \\ W_{2}(s) = \dfrac{1} {2.5}\\ \end{array} \right. }$$

(6.49)

We aim to find the set-solution Θ of the PI controller parameters that ensures H _∞ performance for γ = 1, i.e.,

$$\displaystyle{ \Theta = \left \{\theta \in [\theta ]\left \vert \left \{\begin{array}{l} \left \|W_{1}(s)[S](s)\right \|_{\infty }\leq \gamma \\ \left \|W_{2}(s)[C](s,[\theta ])[S](s)\right \|_{\infty }\leq \gamma \\ \end{array} \right.\right.\right \} }$$

(6.50)

where $[S](s) = {(1 + [C](s,[\theta ])[G](s,[\mathbf{a}],[\mathbf{b}]))}^{-1}$ is the sensivity function defined as follows:

$$\displaystyle\begin{array}{rcl} [S](s) = \dfrac{\dfrac{[a_{2}]} {[K]}{s}^{3}+\dfrac{[a_{1}]} {[K]}{s}^{2}+ \dfrac{1} {[K]}s} {\dfrac{[a_{2}]} {[K]}{s}^{3}+\dfrac{[a_{1}]} {[K]}{s}^{2}+ \dfrac{1} {[K]}s+[K_{p}][b_{2}]{s}^{3}+\left ([K_{i}][b_{2}]+[K_{p}][b_{1}]\right ){s}^{2}+\left ([K_{p}]+[K_{i}][b_{1}]\right )s+[K_{i}]}& &{}\end{array}$$

(6.51)

Now, we solve the set-inversion problem in (6.50) using the recursive algorithm presented in Fig. 6.3. We choose an initial box for the controller parameters $[K_{p0}] \times [K_{i0}] = [0,1.2] \times [0.1,1200]$. The resulting subpaving is presented in Fig. 6.11. The dark colored subpaving $\underline{\Theta }$ corresponds to the set parameters [K _p ] and [K _i ] of the PI controller (6.42) that ensures the performances defined by the H _∞ -criterion (6.50).

Fig. 6.11

Set-solution of the parameters [K _p ] and [K _i ] ensuring the wanted performances

Note that any choice of the parameters [K _p ] and [K _i ] within the dark colored subpaving $\underline{\Theta }$ (see Fig. 6.11) satisfies the conditions (6.50) and consequently ensures the required performances. In the case where the problem (6.50) is not feasible (with the imposed controller), i.e., $\Theta = \emptyset$, the initial box of the parameters $[K_{p0}] \times [K_{i0}]$ must be changed and/or the structure of the controller must be modified (increase the order, for example) and/or the specifications must be modified (degrade the specifications).

Similar to the previous case, the controller C(s) to be implemented is chosen by taking any point parameters K _p and K _i within the set-solution $\underline{\Theta }$ in Fig. 6.11. In this example, we test the following controller:

$$\displaystyle{ C(s) = \dfrac{s + 1,000} {s} }$$

(6.52)

In order to prove that the inequalities (6.50) are satisfied, the magnitudes of the bounds $\left \vert \frac{1} {W_{1}(s)}\right \vert$ and $\left \vert \dfrac{1} {W_{2}(s)}\right \vert$ are compared to the magnitudes of the sensivity function $\left \vert [S](s)\right \vert$ and of the transfer $\left \vert C(s)[S](s)\right \vert$, respectively, when using the implemented controller (6.52). This comparison is given by Fig. 6.12.

Fig. 6.12

Magnitudes of the bounds compared to the sensivity [S](s) and to the input transfer C(s)[S](s)

The obtained results in Fig. 6.12 prove that the magnitudes of [S](s) and C(s)[S](s) are effectively bounded by that of $\frac{1} {W_{1}(s)}$ and $\frac{1} {W_{2}(s)}$, respectively, when using the computed controller C(s). This fact confirms that the specified performances are effectively ensured.

Now, we implement the computed controller C(s) using the first piezocantilever with length l = 16 mm then the second one with length l = 14 mm. Figure 6.13 shows the experimental results when a step reference of $40\,\mu$ m is applied. As shown on the Fig. 6.13, the implemented controller (6.52) has played its role since the closed-loop piezocantilevers satisfy the wanted specifications. Indeed, experimental settling times obtained with the piezocantilevers P ₁ and P ₂ are about tr ₁ = 5. 2 ms and tr ₂ = 7 ms, respectively. The overshoots and static errors are neglected (D _1, 2 ≈ 0, $\varepsilon _{1,2} \approx 0 <1\,\%$ ). Furthermore, the maximal voltages U applied to the both piezocantilevers are less than 40 ×2. 5 = 100 V, which should be the limit for a displacement of $40\,\mu$ m. Indeed, the experiments show that the maximal input voltage is ${U}^{\max } = 97$  V.

Fig. 6.13

Experimental step responses of the piezocantilevers when using C(s)

6.7 Conclusion

This chapter presents the modeling and robust control of piezoelectric microactuators. These latters are characterized by models with uncertain parameters and need convenient modeling and robust control laws. The challenge in micromanipulation, microassembly, and micropositioning application is to ensure robust performances despite the variation in model parameters. For that, interval analysis has been introduced to describe uncertain parameters in the models of microactuators. The main advantage of a such description by interval is the ease and natural way to bound these uncertainties. Moreover, interval techniques can be used to solve many engineering problems, such as control system problems. In the second part of this chapter, two control design approaches for interval systems have been proposed. The first control design method is based on the inclusion of interval transfers and their time and frequency responses, while the second one combines the H _∞ -standard method with interval techniques. The main advantage of the proposed approaches is that they can provide low-order controllers that are able to ensure robust performances for uncertain systems and that are convenient for real-time embedded systems. It has been noted that these proposed control methods are based on some sufficient conditions. This is one limitation of these proposed methods, since sometimes the fulfillment of the constrained conditions does not hold for a given controller, however the required performances measures can be met with this latter. Also, based on the principle of the second control approach, it has been shown that it is possible to perform a posteriori analysis of the performances of interval closed-loop system when the controller is assumed to be known. At the end of this chapter, the proposed control design methods have been applied to control the deflection of piezocantilevers which are typically uncertain systems. The derived controllers were with very low-order (first order) that are suitable for embedded systems. The obtained experimental results confirmed the robustness of the implemented controllers and also the efficiency of the proposed control approaches. As a conclusion interval analysis can be viewed as a guaranteed and powerful tool to represent uncertainties in real systems. Moreover, it can be introduced also to formulate and solve many engineering problems.