Identification of Restoring Force Surfaces in Nonlinear MDOF Systems from FRF Data Using Nonlinearity Matrix

Abstract

The sensitivity of the response characteristics of a nonlinear structure to load level may prevent us to predict the linear behavior of a nonlinear system. The nonlinear identification method recently proposed by the authors is based on the measured linear and nonlinear Frequency Response Functions (FRFs). The method is easy to implement and requires standard testing methods. The data required is limited with measured linear and nonlinear FRFs. In order to obtain the linear FRFs in a nonlinear system, it is the general practice to use low level forcing, unless the nonlinearity is due to dry friction. However, depending on the level of nonlinearity it may not be possible to lower the harmonic forcing amplitude beyond a practical limit, and this may not be sufficient to obtain linear FRFs. The approach presented in this study aims to perform the nonlinear identification directly from a series of measured nonlinear FRFs. It is shown that Restoring Force Surfaces (RFS) can be identified more accurately by employing this approach. The verification of the method is demonstrated with simulated and experimental case studies.

5.1 Introduction

Traditionally, for system identification in structural dynamics, we tend to apply linear identification theories, which are well established [1, 2]. However, with the increasing need to understand nonlinear characteristics of complicated structures, there were several studies published on nonlinear system identification. For instance, see [3–15]. Nonlinearities can be localized at joints or boundaries or else the structure itself can be nonlinear. There are various types of nonlinearities, such as hardening stiffness, clearance, coulomb friction etc. [4].

Nonlinear system identification methods can be divided into two groups as time and frequency domain methods [11], and time domain methods can be further divided as discrete and continuous time methods [5]. Most of the methods available require some foreknown data for the system. Some methods require all or part of mass, stiffness and damping values [7–9] whereas some methods [10–14] require linear frequency response function (FRF) of the analyzed structure. In these methods nonlinearity type is usually foreknown or determined by inspecting the describing function footprints (DFF) visually. However, although the user interpretation may be possible for a single type of nonlinearity, it may not be so easy when there is more than one type of nonlinearity present in the system [4].

The Restoring Force Surface (RFS) method, proposed by Masri et al. [9], constitutes one of the first attempts to identify nonlinear structures. A variant of this method was later independently developed by Crawley et al. [16, 17] and was named as force-state mapping method. Masri et al. [18] extended the RFS method to MDOF systems in 1982.

The RFS method requires the time histories of the displacement and its derivatives, and the applied force to be measured or calculated. Furthermore, the mass and damping matrices can be needed. In theory, the RFS method is applicable to MDOF systems. However, a number of practical considerations diminish this capability, and its scope is practically bound to systems with a few degrees of freedom only [19].

The RFS method has been studied experimentally for several systems with few degrees of freedom. Kerschen et al. [20] demonstrated experimental identification of impacting cantilever beams with symmetrical or asymmetrical piecewise linear stiffness using the RFS method. Another experimental application of the RFS method studied by Kerschen et al. [21] was the VTT benchmark, which consists of wire rope isolators mounted between a load mass and a base mass. The RFS method was also used in vehicle suspension system characterization [22]. Recently, Noel et al. [19] demonstrated the application of the RFS method for an elastomeric connection on a real life spacecraft structure.

There are studies in the literature obtaining the nonlinear RFS [23, 24] using variants of RFS method or other similar approaches like neural networks and optimization [5, 25]. Application of optimization methods in nonlinear system identification is rather a new and promising approach. The major disadvantage of these methods is generally the computational time required.

Nonlinearity identification method presented in this study is an improved version of the method developed earlier by Özer et al. [11]. The improvement includes performing the nonlinear identification directly from a series of measured nonlinear FRFs without the need to measure the linear FRFs. Furthermore, it is shown that Restoring Force Surfaces (RFS) can be identified more accurately by employing this approach.

5.2 Theory

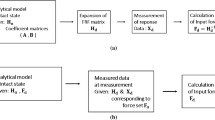
Representation of nonlinear forces in matrix multiplication form using describing functions has been first given by Tanr$\imath$kulu et al. [26], and employed in identification of structural nonlinearities by Özer et al. [11]. The method presented here is based on the basic theory of the identification method which is given in detail in reference [11]. Here, only the related equations are given with a brief summary.

The nonlinear internal forces in the system can be expressed in matrix form using describing functions. This approach makes it possible to represent the nonlinear stiffness and damping properties of the system in compact form as a response dependent matrix which can easily be included into the dynamic stiffness matrix of the linear system in the frequency domain. From the mathematical expressions of the FRF matrix of the nonlinear system [H ^NL] and FRF matrix of the linear part of the system [H] (see reference [11] for details) the response dependent “nonlinearity matrix” [$\Delta (x,\dot{\chi })$] can be obtained as

$$\displaystyle{ \left [\Delta \right ] ={ \left [{H}^{NL}\right ]}^{-1} -{\left [H\right ]}^{-1} }$$

(5.1)

where the elements of the nonlinearity matrix are expressed in terms of describing functions v [26].

In general applications, the linear model of the system can be obtained by using FEM, and experiments are made only on the nonlinear system. Alternatively, the FRFs of the underlying linear system can be obtained from FRF measurements in the system at very low forcing levels, where the nonlinear internal forces will be negligible. However, when there is only friction type of nonlinearity, FRFs measured at low amplitude of vibration will not represent FRFs of the underlying linear system; on the contrary, the FRFs measured at high response levels will represent FRFs of the linear counterpart. Comparison of FRFs measured at different response levels will reveal whether or not there is only friction type of nonlinearity so that the FRF measured at high response level can be taken as the FRF for the underlying linear system. Yet, if the system has multiple nonlinearities including friction type of nonlinearity, it may be difficult to measure the FRF of the underlying linear system experimentally, and using finite element model of the system seems to be the only alternative to obtain linear FRF of the linear counterpart.

In an attempt to obtain the nonlinearity matrix directly from nonlinear FRFs, the following methodology is proposed;

The nonlinearity matrix at forcing level F₁can be defined as

$$\displaystyle{ \left [\Delta _{1}\right ] ={ \left [H_{1}^{NL}\right ]}^{-1} -{\left [H\right ]}^{-1} }$$

(5.2)

Changing the forcing to another level F₂, Eq. (5.2) becomes

$$\displaystyle{ \left [\Delta _{2}\right ] ={ \left [H_{2}^{NL}\right ]}^{-1} -{\left [H\right ]}^{-1} }$$

(5.3)

Subtracting Eq. (5.2) from Eq. (5.3) yields

$$\displaystyle{ \left [\Delta _{2}\right ] -\left [\Delta _{1}\right ] ={ \left [H_{2}^{NL}\right ]}^{-1} -{\left [H_{ 1}^{NL}\right ]}^{-1} }$$

(5.4)

For a SDOF system, Eq. (5.4) reduces to

$$\displaystyle{ \Delta _{2} - \Delta _{1} = \frac{1} {H_{2}^{NL}} - \frac{1} {H_{1}^{NL}} }$$

(5.5)

where the nonlinearity matrix reduces to the describing function ν.

The describing function will be a function of the displacement amplitude only, when there is displacement dependent nonlinearity in the system. As the values Δ ₁ and Δ ₂ are obtained from the same describing function, evaluated at two different displacement amplitude levels; if a polynomial form (as shown below) is assumed for the describing function and nonlinear FRFs at two load levels (H ₁ ^NL and H ₂ ^NL) are measured experimentally, the coefficients of the function that describes the nonlinearity can be calculated:

$$\displaystyle{ \Delta (X) =\sum \limits _{ i=1}^{\infty }c_{ i}{X}^{i} }$$

(5.6)

where X represents the amplitude of the harmonic response.

For a MDOF system the difference matrix ([Δ ₂] – [Δ ₁]) is obtained from Eq. (5.4). Then, a polynomial is fitted to each element of the difference matrix separately and the coefficients of the functions that describe the nonlinearities at different coordinates can be calculated. The only difference between one nonlinear location and multiple nonlinear locations will be the number of curve fitting operations required.

5.2.1 Application of the Method

The first step is to test the nonlinear structure at two excitation levels. Equation (5.4) requires having the inverses of the measured nonlinear FRFs, and therefore is sensitive to noise. In order to minimize this effect, the excitation levels can be chosen high enough or averaging can be performed. However, if the forcing levels are high then friction type nonlinearities will not depict themselves in the measured values. In order to identify friction type nonlinear elements a low forcing test can also be performed. Equation (5.4) will give a complex result, whose real part represents the stiffness nonlinearity and the imaginary part represents the damping nonlinearity.

In order to solve Eq. (5.4) we need as many equations as the order of the polynomial that has been assumed. These equations can be generated from the nonlinear FRF values, which have distinct displacement values for each frequency. In other words, if we assume a polynomial, for instance up to the third order for the nonlinearity, we will need three equations. The following equations show the calculation procedure:

$$\displaystyle\begin{array}{rcl} & & (c_{1}X_{2} + c_{2}X_{2}^{2} + c_{ 3}X_{2}^{3}) - (c_{ 1}X_{1} + c_{2}X_{1}^{2} + c_{ 3}X_{1}^{3}) = \frac{1} {H_{2}^{NL}} - \frac{1} {H_{1}^{NL}}{}\end{array}$$

(5.7)

$$\displaystyle\begin{array}{rcl} & & \left [\begin{array}{lll} X_{2} - X_{1} & X_{2}^{2} - X_{1}^{2} & X_{2}^{3} - X_{1}^{3}\\ \end{array} \right ]\left [\begin{array}{l} c_{1} \\ c_{2} \\ c_{3}\\ \end{array} \right ] = \frac{1} {H_{2}^{NL}} - \frac{1} {H_{1}^{NL}}{}\end{array}$$

(5.8)

$$\displaystyle\begin{array}{rcl} & & \left [\begin{array}{lll} \begin{array}{lll} x_{2}(\omega _{1}) - x_{1}(\omega _{1})&X_{2}^{2}(\omega _{1}) - X_{1}^{2}(\omega _{1})&X_{2}^{3}(\omega _{1}) - X_{1}^{3}(\omega _{1})\\ \end{array} \\ \begin{array}{lll} x_{2}(\omega _{2}) - x_{1}(\omega _{2})&X_{2}^{2}(\omega _{2}) - X_{1}^{2}(\omega _{2})&X_{2}^{3}(\omega _{2}) - X_{1}^{3}(\omega _{2})\\ \end{array} \\ \begin{array}{lll} x_{2}(\omega _{3}) - x_{1}(\omega _{3})&X_{2}^{2}(\omega _{3}) - X_{1}^{2}(\omega _{3})&X_{2}^{3}(\omega _{3}) - X_{1}^{3}(\omega _{3})\\ \end{array}\\ \end{array} \right ]\left [\begin{array}{lll} c_{1} \\ c_{2} \\ c_{3}\\ \end{array} \right ] = \left [\begin{array}{lll} \frac{1} {H_{2}^{NL}(\omega _{1})} - \frac{1} {H_{1}^{NL}(\omega _{1})} \\ \frac{1} {H_{2}^{NL}(\omega _{2})} - \frac{1} {H_{1}^{NL}(\omega _{2})} \\ \frac{1} {H_{2}^{NL}(\omega _{3})} - \frac{1} {H_{1}^{NL}(\omega _{3})}\\ \end{array} \right ]{}\end{array}$$

(5.9)

where ω represents the response frequency.

The FRF values at each frequency give us one equation. In general we will have more frequency values than the number of equations that is required to solve the equation for unknown coefficients. Thus, if we use “n” frequencies, Eq. (5.9) can be expanded as

$$\displaystyle{ \left [\begin{array}{lll} x_{2}(\omega _{1}) - x_{1}(\omega _{1}) &X_{2}^{2}(\omega _{1}) - X_{1}^{2}(\omega _{1}) &X_{2}^{3}(\omega _{1}) - X_{1}^{3}(\omega _{1}) \\ x_{2}(\omega _{2}) - x_{1}(\omega _{2}) &X_{2}^{2}(\omega _{2}) - X_{1}^{2}(\omega _{2}) &X_{2}^{3}(\omega _{2}) - X_{1}^{3}(\omega _{2}) \\ x_{2}(\omega _{3}) - x_{1}(\omega _{3}) &X_{2}^{2}(\omega _{3}) - X_{1}^{2}(\omega _{3}) &X_{2}^{3}(\omega _{3}) - X_{1}^{3}(\omega _{3})\\ \vdots &\vdots &\vdots \\ x_{2}(\omega _{n}) - x_{1}(\omega _{n})&X_{2}^{2}(\omega _{n}) - X_{1}^{2}(\omega _{n})&X_{2}^{3}(\omega _{n}) - X_{1}^{3}(\omega _{n})\\ \end{array} \right ]\left [\begin{array}{l} c_{1} \\ c_{2} \\ c_{3}\\ \end{array} \right ] = \left [\begin{array}{lll} \frac{1} {H_{2}^{NL}(\omega _{1})} - \frac{1} {H_{1}^{NL}(\omega _{1})} \\ \frac{1} {H_{2}^{NL}(\omega _{2})} - \frac{1} {H_{1}^{NL}(\omega _{2})} \\ \frac{1} {H_{2}^{NL}(\omega _{3})} - \frac{1} {H_{1}^{NL}(\omega _{3})}\\ \vdots \\ \frac{1} {H_{2}^{NL}(\omega _{n})} - \frac{1} {H_{1}^{NL}(\omega _{n})}\\ \end{array} \right ] }$$

(5.10)

Equation (5.10) can be solved by pseudo inversion which will give us a least square fit solution for the polynomial coefficients. After successful identification of high forcing effective nonlinearities, the linear FRFs can be evaluated from Eq. (5.2). Thus, using Eq. (5.2) again with nonlinear FRFs obtained from low forcing level, and calculated linear FRFs, we can obtain the describing function values for low forcing nonlinearities such as friction.

The describing function inversion approach introduced recently [27] can now easily be integrated to the method proposed here. The verification and effective application of the method are shown with the case studies and experimental studies given next.

5.3 Case Studies

5.3.1 Case Study 1

The nonlinear identification approach proposed in this study is applied to a SDOF discrete system with a nonlinear elastic element represented by k₁ ^∗ (a linear stiffness of 1,000 N/m with a backlash of 0.005 m) and a coulomb friction element $\mathrm{c}_{1}^{{\ast}}(= 0.001sgn(\dot{x})\,N)$, as shown in Fig. 5.1.

Fig. 5.1

SDOF discrete system with two nonlinear elements

The numerical values of the linear system elements are given as follows:

$$\displaystyle\begin{array}{rcl} k_{1}& =& 500\,\mathrm{N/m} \\ c_{1}& =& 5\,\mathrm{Ns/m} \\ m_{1}& =& 1\,\mathrm{kg} {}\end{array}$$

(5.11)

The time response of the system is first calculated with MATLAB by using the ordinary differential equation solver ODE45. The simulation was run for 32 s at each frequency to ensure that transients die out. The frequency range used during the simulations is between 0.0625 and 16 Hz with frequency increments of 0.0625 Hz. Three forcing levels (0.01, 3, 20 N) are used, in turn, in the simulations. The FRF functions obtained are presented in Fig. 5.1. Before using the calculated FRFs as simulated experimental data, they are polluted by using the “rand” function of MATLAB with zero mean, normal distribution and standard deviation of 5 % of the maximum amplitude of the FRF value. A sample comparison for the nonlinear FRFs (H ₁₁) is given in Fig. 5.2 for three different forcing levels.

Fig. 5.2

Nonlinear FRF plots for different forcing levels

Using the method proposed, the describing functions representing these nonlinear elements are calculated from simulated experimental results and are plotted in Fig. 5.3.

Fig. 5.3

Identified and exact DFs, (a) stiffness type (backlash) nonlinear element, (b) damping type (friction) nonlinear element

Alternatively, the types of nonlinear elements can be identified more easily if DF inversion method proposed in the previous study [27] is used. The calculated RF plots are presented in Fig. 5.4. By first fitting curves to the calculated RF plots, parametric identification can easily be made.

Fig. 5.4

Identified and exact RF plots, (a) stiffness type (backlash) nonlinear element, (b) damping type (friction) nonlinear element

Although the DF inversion formulations are based on polynomial type describing functions, it is shown in this case study that they work, with an acceptable accuracy, for even discontinuous nonlinearities such as backlash, as well as for multiple nonlinearities.

5.3.2 Case Study 2

The proposed method is again applied to the same SDOF discrete system with a nonlinear elastic element represented by k₁ ^∗ (a nonlinear hardening cubic $\mathrm{spring} = 1{0}^{6}{x}^{2}\,\mathrm{N/m}$) and a coulomb friction element $\mathrm{c}_{1}^{{\ast}}(= 0.001 =\, \mathrm{sgn}(\dot{x})\,\mathrm{N})$, as shown in Fig. 5.1. The nonlinear FRFs (H ₁₁) are given in Fig. 5.5 for three different forcing levels.

Fig. 5.5

Nonlinear FRF plots for different forcing levels

Following the same procedure we obtain the describing functions representing these nonlinear elements as given in Fig. 5.6.

Fig. 5.6

Identified and exact DFs, (a) stiffness type (cubic stiffness) nonlinear element, (b) damping type (friction) nonlinear element

Similarly, the types of nonlinear elements can be identified more easily if DF inversion method is used. These plots are given in Fig. 5.7.

Fig. 5.7

Identified and exact RF plots, (a) stiffness type (cubic stiffness) nonlinear element, (b) damping type (friction) nonlinear element

5.3.3 Case Study-3

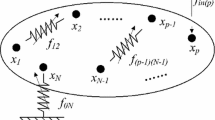
The nonlinear identification approach proposed in this study is applied to a 4 DOF discrete system with a nonlinear elastic element represented by k₄ ^∗ (a linear stiffness of 100 N/m with a backlash of 0.005 m) and a nonlinear hardening cubic spring $\mathrm{k}_{4}^{{\ast}{\ast}}(= 1{0}^{6}{x}^{2}\,\mathrm{N/m})$ between coordinates 3 and 4, as shown in Fig. 5.8.

Fig. 5.8

Four DOFs discrete system with two nonlinear elements

The numerical values of the linear system elements are given as follows:

$$\displaystyle\begin{array}{rcl} k_{1}& =& k_{2} = k_{3} = k_{4} = k_{5} = 500\,\mathrm{N/m} \\ c_{1}& =& c_{2} = c_{3} = c_{4} = c_{5} = 5\,\mathrm{Ns/m} \\ m_{1}& =& 0.5\,\mathrm{kg},\quad m_{2} = 1\,\mathrm{kg},\quad m_{3} = 1.5\,\mathrm{kg},\quad m_{4} = 3\,\mathrm{kg}{}\end{array}$$

(5.12)

A sample comparison for the nonlinear and linear FRFs (H ₁₁) is given in Fig. 5.9.

Fig. 5.9

Nonlinear FRF plots for different forcing levels

In this case study, the forcing is first applied from third coordinate with two forcing levels, and then from fourth coordinate. Employing the method suggested and by using FRFs of the third and fourth coordinates only, the describing functions representing these nonlinear elements are obtained as given in Fig. 5.10. As it is the case in the previous example, the total restoring force of nonlinear elements can be identified more easily when DF inversion method is used.

Fig. 5.10

Identified and exact, (a) DFs, (b) RFs

5.4 Experimental Study

The proposed approach is also tested on the experimental setup used in a recent study [28]. The tests carried out in previous study [28] were repeated with better frequency resolution (0.1 Hz) and force control. The experimental setup and FRF plots obtained with constant amplitude harmonic forces are given in Figs. 5.11 and 5.12, respectively.

Fig. 5.11

Setup used in the experimental study

Fig. 5.12

Constant force driving point FRF curves for different forcing levels

The test rig consists of a linear cantilever beam with its free end held between two thin identical beams which generate cubic spring effect. The cantilever beam and the thin nonlinear beams were manufactured from St37 steel. The beam can be taken as a single DOF system with a nonlinear cubic stiffness located between the ground and the equivalent mass representing the cantilever beam. This test rig is preferred for its simplicity in modeling the dynamic system since the thin beams yield only hardening stiffness nonlinearity and the structure itself can be modeled as a single degree of freedom system.

For a single degree of freedom system, the nonlinearity matrix reduces to the describing function defining the nonlinearity [11]:

$$\displaystyle{ v = \frac{H - {H}^{NL}} {{H}^{NL}H} }$$

(5.13)

As discussed in Sect. 5.2, the method requires the linear FRFs. Thus, we may assume that the lowest force level that we can achieve gives the linear FRF. However, the method proposed in this study shows that the linear FRF may not always be obtained accurately by low forcing even though there is no friction type of nonlinearity (Fig. 5.13).

Fig. 5.13

Linear FRF curves

If we cannot apply sufficiently low forcing level or if there is friction type of nonlinearity in the system then the approach proposed becomes more valuable. The describing function representation of the nonlinearity (ν) can be graphically shown as a function of response amplitude, which makes it possible to identify the type of nonlinearity and to make parametric identification by using curve fitting (Fig. 5.14a). The restoring force plot is also given in Fig. 5.14b. From Fig. 5.14b the nonlinearity coefficient is found by curve fitting as 6.18 10⁸ N∕m².

Fig. 5.14

(a) DF curve and fitted curve, (b) RF curve and fitted curve

The nonlinear FRFs are calculated [11] using the identified nonlinearity coefficient at forcing levels of 0.5 and 1 N and are compared with experimentally measured values in Fig. 5.15. As can be seen from the figure, better agreements are obtained between experimental and predicted responses with the new method.

Fig. 5.15

Identified and measured nonlinear FRF curves at forcing level of (a) 0.5 N, (b) 1 N

5.5 Conclusions

It was recently shown [27] with an experimental case study that the method developed by Özer et al. [11] for detecting, localizing and parametrically identifying nonlinearity in MDOF systems is a promising method that can be used in industrial applications. In the study presented here some improvements are suggested to eliminate some of the practical limitations of the previously developed method. The verification of the approach proposed is demonstrated with three case studies. The main improvement is obtaining the nonlinearity matrix directly from nonlinear FRFs eliminating the need for obtaining linear FRFs.

The original method requires dynamic stiffness matrix of the linear part of the system which can be obtained by constructing a numerical model for the system and updating it using experimental measurements. Alternatively, low forcing measurements can be used to obtain the linear FRFs. However, low forcing testing may not always give the linear FRFs accurately when nonlinearity is high, and furthermore, if nonlinearity is due to dry friction, low forcing level testing will not give linear FRFs at all, since its effect will be dominant at low level vibrations. For this type of nonlinearity, on the contrary, high forcing testing will yield the linear FRFs. To overcome such problems, in the approach developed in this study it is proposed to test the structure at two forcing levels and calculate the nonlinearity matrix directly from these measurements.

The approach suggested is first applied to lumped parameter systems and it is shown that identification of nonlinear elements can successfully be achieved even when there is more than one nonlinear element with different characters at the same coordinate.

The application of the approach proposed is also demonstrated on a real structural test system, and it is concluded that the accuracy in parametric determination of nonlinearity by the proposed method gives better results than the method of Özer et al. [11] where low forcing tests were used to obtain linear FRFs. It is concluded in this study that the approach proposed is very promising to be used in practical systems, especially when there are multiple nonlinear elements at the same location.