A Multi-item Risk-Averse Newsvendor with Law Invariant Coherent Measures of Risk

Abstract

I consider a multi-product risk-averse newsvendor under the law-invariant coherent measures of risk. I first establish a few fundamental properties of the model regarding the convexity of the problem and the symmetry of the solution, and study the impacts of risk aversion and shift in mean demand to the optimal solution with independent demands. Specifically, I show that for identical products with independent demands, increased risk aversion leads to decreased orders. For a large but finite number of heterogenous products with independent demands, I derive closed-form approximations for the optimal order quantities. The approximations are as simple to compute as the classical risk-neutral solutions. I also show that the risk-neutral solution is asymptotically optimal as the number of products tends to be infinity, and thus risk aversion has no impact in the limit. For a risk-averse newsvendor with dependent demands, I show that positively (negatively) dependent demands lead to a lower (higher) optimal order quantities than independent demands. Using a numerical study, I examine the convergence rates of the approximations and develop additional insights on the interplay between dependent demands and risk aversion.

1 Introduction

1.1 Motivation

The multi-product newsvendor model is a classical model in the inventory control literature. In this model, there are multiple products to be sold in a single selling season. On the one hand, when demand exceeds supply for any product, the excessive demand is lost. On the other hand, when supply exceeds demand, the excessive inventory is sold at a loss. The firm’s objective is to determine the optimal order quantity for each product so as to maximize a certain performance measure. This model finds its applications in many manufacturing, distribution, and retailing firms that handle short life cycle products.

The literature of the multi-product newsvendor model has mainly used risk-neutral performance measures as an objective function. For example, the company optimizes the expected average profit or average cost per product. Under these objective functions, the model is decomposable and one can consider each product separately as multiple single-product newsvendor models, unless resource constraints are imposed nor demand substitution is allowed. Under risk-averse objective functions, however, the model is generally not decomposable. One needs to consider all products simultaneously, as a portfolio.

Below, I first review the literature of risk-neutral multi-product inventory models by ways products interact. Then, I review the literature of risk models and its recent applications in supply chain inventory management.

Hadley and Whitin (1963) consider a multi-product newsvendor model with storage capacity or budget constraints, and provide the solution methods based on Lagrangian multiplier. Porteus (1990) presents a thorough review of various newsvendor models. Veinott (1965) considers the dynamic version of the multi-product inventory models in a multi-period setting, with general assumptions in demand process, cost parameters, and lead times. Conditions under which myopic policy is optimal are identified. Ignall and Veinott (1969) and Heyman and Sobel (1984) extend the work by identifying new conditions for the myopic policy in models with risk-neutral assumption, see Aviv and Federgruen (2001), Decroix and Arreola-Risa (1998); Evans (1967), and Federgruen (1984) for exact analysis and approximations. Other than resource constraints, multi-product newsvendor models are also studied under demand substitution, where unsatisfied demand of one product can be satisfied by on-hand inventory of another product. I refer to van Ryzin and Mahajan (1999) for a review on multi-item inventory systems with substitution.

My aim is to replace the risk-neutral performance measure by measures taking risk aversion into account. Such a model is generally not decomposable, and one needs to consider all products simultaneously, as a portfolio. In this paper, I lay the foundations of the multi-product newsvendor model under coherent measures of risk and derive its basic properties. They provide insight into the impact of risk aversion on the multi-product newsvendor with either independent or dependent demands. Moreover, I study asymptotic properties of the solution as the number of products tends to infinity and develop simple yet accurate approximations of risk-averse solutions, which allow fast computation of large-scale problems.

Below, I first review the literature of risk measures and their recent applications in supply chain inventory management. Then, I summarize my model and main results.

1.2 Risk Measures

The risk-neutral inventory models provide the best decision on average. This may be justified by the Law of Large Numbers. However, one cannot always rely on repeated similar chances. The first few outcomes may turn out to be very bad and entail unacceptable losses. Schweitzer and Cachon (2000) provide experimental evidence suggesting that inventory managers may be risk-averse for high-value products. Because of these reasons, attempts to overcome the drawbacks of the expected value optimization have a long history and there exist four typical approaches to model decision making under risk. They are expected utility theory, stochastic dominance, chance constraints, and mean-risk analysis. These approaches are related and consistent to some extent.

The expected utility theory of von Neumann and Morgenstern (1944) derives, from simple axioms, the existence of a nondecreasing utility function, which transforms in a nonlinear way the observed outcomes. The decision maker optimizes, instead of the expected outcome, the expected value of the utility function. In the maximization context, when the outcome represents profit, risk-averse decision makers have concave and nondecreasing utility functions.

The second approach is based on the theory of stochastic dominance, developed in statistics and economics (see Lehmann 1955; Hadar and Russell 1969 and references therein). Stochastic dominance relations are partial orders on the space of distributions, and thus allow for pairwise comparison of different solutions. An important feature of the stochastic dominance theory is its universal character with respect to utility functions. More specifically, the distribution of a random outcome V is preferred to random outcome Y in terms of a stochastic dominance relation if and only if expected utility of V is preferred to expected utility of Y for all utility functions in a certain class, called the generator of the relation. In particular, the second-order stochastic dominance corresponds to all concave nondecreasing utility functions, and is thus well suited to model risk-averse preferences. For an overview of these issues, see Müller and Stoyan (2002) and Levy (2006). Unfortunately, the stochastic dominance approach does not provide a simple computational recipe. In fact, it is a multiple criteria model with a continuum of criteria. Therefore, it has been used as a constraint (see Dentcheva and Ruszczyński 2003), and also utilized as a reference standard whether a particular solution approach is appropriate (see Ogryczak and Ruszczyński 1999; Ruszczyński and Vanderbei 2003).

The third approach specifies constraints on probabilities of unfavorable events. Prékopa (2003) provides a thorough overview of the state of the art of the optimization theory with chance constraints. Theoretically, a chance constraint is a relaxed version of the stochastic dominance relation of the first-order, and thus it is related to the expected utility theory, but there is no equivalence. In finance, chance constraints are known under the name of Value-at-Risk (VaR) constraints. Chance constraints sometimes lead to nonconvex formulations of the resulting optimization problems.

The fourth approach, originating from finance, is the mean-risk analysis. It quantifies the problem in a lucid form of two criteria: the mean (the expected value of the outcome), and the risk (a scalar measure of the variability of the outcome). In the maximization context, one selects from the universe of all possible solutions those that are efficient: for a given value of the mean they minimize the risk, or equivalently, for a given value of risk they maximize the mean. Such an approach has many advantages: it allows one to formulate the problem as a parametric optimization problem, and it facilitates the trade-off analysis between mean and risk.

In the context of portfolio optimization, Markowitz (1959) used the variance of the return as the risk. It is easy to compute, and it reduces the financial portfolio selection problem to a parametric quadratic programming problem. One can, however, construct simple counterexamples that show the imperfection of the variance as the risk measure: it treats over-performance equally as under-performance, and more importantly it may suggest a portfolio which is stochastically dominated by another portfolio. Table 2.1 below summarizes a defect of mean-variance models. In Table 2.1, let me consider two policies, policy 1 and 2, defined at the two equally likely events, “Bad” and “Good.” Then, policy 2 is stochastically bigger than policy 1. Here, both $-\mu + {\sigma }_{1}$ and $-\mu + {\sigma }_{2}$ are coherent risk measures. Then, with these two risk measures, policy 2 is preferred to policy 1, which shows consistency with stochastic dominance relations. However, with a mean-variance model, policy 1 may be preferred to policy 2 implying contradiction to stochastic dominance.

Table 2.1 A counterexample to show problems of mean-variance models

To overcome the drawbacks of the mean-variance analysis, the general theory of coherent measures of risk was suggested by Artzner et al. (1999) and extended to general probability spaces by Delbaen (2002). For further generalizations, see Föllmer and Schied (2002, 2004); Kusuoka (2003); Ruszczyński and Shapiro (2005) and Ruszczyński and Shapiro (2006a). Dynamic version for a multi-period case were analyzed, among others, by Kusuoka and Morimoto (2004); Riedel (2004), Cheridito et al. (2006) and Ruszczyński and Shapiro (2006b). In this theory, an integrated performance measure is proposed, comprising both the mean and variability measures, and four axioms (Convexity, Monotonicity, Translation Equivariance, and Positive Homogeneity; see Sect. 2.3 for a precise definition) are imposed. Coherent measures of risk are extensions of the mean-risk analysis. It is known that coherent measures of risk are consistent with the 1st and 2nd order stochastic dominance relations (see Shapiro et al. 2009).

More specifically, in a multi-product newsvendor problem, these four axioms have following implications to guarantee consistency with intuition about rational risk-averse decision making. Thus, by satisfying the axioms, a coherent risk measure has certain attractive features, as compared to these measures, making it worth considering. First, Convexity axiom means that the global risk of a portfolio should be equal or less than the sum of its partial risks. Thus, this axiom is consistent with diversification effects. Second, Monotonicity axiom is consistent with the first-order stochastic dominance relation. Third, Translation Equivariance axiom means that adding a constant cost is equivalent to increasing the vendors performance measure by the same amount. On the contrary, adding a constant gain is equivalent to decreasing the vendors performance measure by the same amount. Therefore, by excluding the impact of constant gains or losses, fixed parts can be separated equivalently from the vendors random performance measure at every possible state of nature. Lastly, Positive Homogeneity axiom guarantees that the optimal solution does not change to rescaling of units.

Among the four axioms aforementioned, expected utility models and coherent risk measures share the properties of convexity and consistency with stochastic dominance. In addition, the coherent risk measures satisfy the axioms of Translation Equivariance and Positive Homogeneity. However, under expected utility theory, these two axioms typically do not hold; see, e.g., the exponential utility function in Howard (1988).

For inventory systems where the initial endowment effect is significant, i.e., when the initial wealth could affect the decision of a risk-averse manager, or when constant demand for some products could affect order quantities of other products, an expected utility model may be preferred to a model with a coherent risk measure, because the latter ignores the endowment effect. In newsvendor models, where inventory managers are mainly concerned about the overage and underage costs associated with random demand, and in other problems, where risk is primarily associated with uncertainty, coherent risk measures may capture risk preferences better. The following arguments speak in favor of coherent measures of risk: (1) Translation Equivariance allows them to properly rank risky alternatives by excluding the impact of constant gains or losses (see Artzner et al. 1999). (2) The Positive Homogeneity axiom ensures that their attitude to risk will not change when the unit system is changed (e.g., from dollars to cents). More importantly, this axiom indicates no diversification effect when demands are completely correlated. To see this, it is well known that the subadditivity property, $\rho (X + Y ) \leq \rho (X) + \rho (Y )$, implies ρ(nX) ≤ nρ(X). However ρ(nX) < nρ(X) would imply diversification effect even when the random demands are completely correlated. To avoid this counter-intuitive effect, it is left with ρ(nX) = nρ(X) which is the Positive Homogeneity axiom.

Several modifications and extensions of coherent measures of risk have been suggested in the literature, including convex measures of risk, insurance risk measures, natural risk statistic, and tradeable measures of risk. I point out that all these risk measures ignore the initial endowment effect, implying consistency with Translation Equivariance.

Föllmer and Schied (2002) consider convex measures of risk, in which the Positive Homogeneity axiom is relaxed. Again, in my context, this may lead to a diversification effect when demands are completely correlated; it may also lead to counterintuitive effects of changing risk attitudes when the outcomes are rescaled, by changing the currency in which profits are calculated, or by considering the average profit per product.

The other three risk measures do not satisfy the convexity axiom in general. They are based on the reality of financial markets where noncoherent risk measures, such as VaR (Value-at-Risk), are widely used. Wang et al. (1997) suggest insurance risk measures which are law invariant, and satisfy the axioms of conditional state independence, monotonicity, comonotone additivity and continuity. Heyde (2006) propose the natural risk statistics, which is also law invariant, and in which the convexity axiom is required only for comonotone random variables. Ahmed et al. (2008) show that such a risk measure can be represented as a composition of a coherent measure of risk and a certain law preserving transformation, and thus the insights into models with coherent measures of risk are relevant for natural risk statistics. Pospišil et al. (2008) propose tradeable measures of risk. They argue that the proper risk measures should be constructed by historically realized returns. When compared to the coherent measures of risk, these risk measures appear to be much more difficult to handle, due to nonconvexity and/or nondifferentiability of the resulting model. I shall see that even in the case of coherent measures of risk the technical difficulties are substantial.

1.3 Risk-Averse Inventory Models

In recent years, risk-averse inventory models have received increasing attention in the supply chain management literature. Table 2.2 classifies the literature by inventory models and risk measures. Because there is no research so far directly applying stochastic dominance to this field, I drop it from the table.

Table 2.2 Summary of the literature on risk-averse inventory models

Most work to date dealt with single-product inventory models. For newsvendor models, research focused on finding the optimal solution under a risk-averse measure, and studying the impact of the degree of risk aversion (among other model parameters) on the optimal solution. A typical finding is that as the degree of risk aversion increases, the optimal order quantity tends to decrease.

For single-product but multi-period dynamic inventory models under risk aversion, the literature focuses on characterizing the structure of the optimal ordering or pricing policies and quantifying the impact of the degree of risk aversion on the optimal polices. Chen et al. (2006) review results in this direction.

For multi-product risk-averse newsvendor models, Tomlin and Wang (2005) study how characteristics of products (e.g., profit margin, demand correlation), resource reliability and firm’s risk attitude affect the preference of resource flexibility and supply diversification. Under a downside risk measure and Conditional Value at Risk (CVaR), they show that for a risk-averse firm with unreliable resources, a supply chain can prefer dedicated resources than a flexible resource even if the cost of the latter is smaller than the former.

Newsvendor networks are studied by van Mieghem (2007), with many products and many resources under mean-variance and utility function approaches. The networks feature resource diversification, flexibility (e.g., ex post inventory capacity allocation) and/or demand pooling. The paper addresses the question of how the aforementioned operational strategies reduce total risk and create value. It shows that a risk-averse newsvendor may invest more resources in certain networks than a risk-neutral newsvendor (i.e., operational hedging) because such resources may reduce the profit variance and mitigate risk in the network. Among the three networks, the dedicated one is mostly related to my model. In this network, there are two products with correlated demand. The author characterizes the impact of demand correlation on the optimal order quantities in two extreme cases of complete positive or negative correlation. A numerical study is conducted to cover cases other than the extreme ones.

Finally, Ağrali and Soylu (2006) conduct a numerical investigation on a two-product newsvendor model under the risk measure of CVaR. Assuming a discretized multi-variate normal demand distribution, the authors studied the sensitivity of the optimal solution with respect to the mean and variance of demand, demand correlation, and various cost parameters. Interestingly, the report shows that as the demand correlation increases, the optimal order quantities tend to decrease.

For multi-echelon or multi-agent models, so far all papers consider single-product and single-period models. Lau and Lau (1999) study a manufacturer’s pricing strategy and return policy under the mean-variance risk measure. Agrawal and Seshadri (2000b) introduce a risk-neutral intermediaries to offer mutually beneficial contracts to risk-averse retailers. Tsay (2002) studies how a manufacturer can use return policies to share risk under the mean-standard deviation measure. Gan et al. (2004) study Pareto-optimality for suppliers and retailers under various risk-averse measures. Gan et al. (2005) design coordination schemes of buyback and risk-sharing contracts in a supply chain under a Value-at-Risk constraint. For a review of the literature on risk aversion in capacity investment models and on operational hedging, see van Mieghem (2003).

1.4 My Model and Main Results

This paper considers a multi-product risk-averse newsvendor using a law-invariant coherent risk measure (see Sects. 2.2 and 2.3). As I argued in Sect. 2.1.2, coherent risk measures can be more attractive than the expected utility theory in the multi-product newsvendor problem due to their properties of Translation Equivariance and Positive Homogeneity.

The model presents a considerable challenge, both analytically and computationally, because the objective function cannot be decomposed by each product and one has to look at the totality of all products as a portfolio. In particular, one has to characterize the impact of risk aversion and demand dependence on the optimal solution, identify efficient ways to find the optimal solution, and connect this model to the financial portfolio theory. While Tomlin and Wang (2005) study a two-product system under CVaR, their focus is on the design of material flow topology and thus is different from mine.

I should also point out that in most practical cases where this model is relevant (either manufacturing or retailing), firms may have a large number of heterogenous products. Due to the complex nature of risk optimization models, they become practically intractable for problems of these dimensions. Thus, it is theoretically interesting and practically useful to study the asymptotic behavior of the system as the number of products tends to infinity and obtain fast approximation for large-size problems.

This work contributes to literature in the following ways: I first establish a few fundamental properties regarding the convexity of the model and the symmetry of the solution for the model in Sect. 2.4, and study the impacts of risk aversion and shift in mean demand to the optimal solution with independent demands in Sect. 2.5. I then consider large but finite number of independent heterogenous products, for which I develop closed-form approximations in Sect. 2.6 which are exact in the single-product case. The approximations are as simple to compute as the risk-neutral solutions. I also show that under certain regularity conditions, the risk-neutral solutions are asymptotically optimal under risk aversion, as the number of products tends to be infinity. This asymptotic result has an important economic implication: companies with many products or product families with low demand dependence need to look only at risk-neutral solutions, even if they are risk-averse.

The impact of dependent demands under risk aversion poses a substantial analytical challenge. By utilizing the concept of associated random variables, I prove in Sect. 2.7 that in a risk-averse two-product model with positively dependent demands the optimal order quantities are lower than for independent demands, while for negatively dependent demands the optimal order quantities are higher. Using a sample-based optimization, I conduct in Sect. 2.8 a numerical study, which demonstrates that the approximations converge quickly to the optimal solutions as the number of products increases. It also provides additional insights into the impact of dependent demands. Specifically, I identify counterexamples to show that increased risk aversion can lead to greater optimal order quantities for strongly negatively dependent demands. In Sect. 2.9, I summarize the paper and compare the multi-product risk-averse newsvendor model to the financial portfolio problem.

2 Problem Formulation

Given products j = 1, …, n, let x = (x ₁, x ₂, …, x _n ) be the vector of ordering quantities and let $D = ({D}_{1},\ldots ,{D}_{n})$ be the demand vector. I also define $r = ({r}_{1},\ldots ,{r}_{n})$ to be the price vector, $c = ({c}_{1},\ldots ,{c}_{n})$ to be cost vector, and $s = ({s}_{1},\ldots ,{s}_{n})$ to be the vector of salvage values. Finally, let f _j ( ⋅) and F _j ( ⋅) be the marginal probability density function (pdf), if it exists, and the marginal cumulative distribution function (cdf) of D _j , respectively. Denote $\bar{{F}}_{j}(\xi ) = 1 - {F}_{j}(\xi )$.

Setting $\bar{{c}}_{j} = {c}_{j} - {s}_{j}$ and $\bar{{r}}_{j} = {r}_{j} - {s}_{j}$, I can write the profit function as follows:

$$\Pi (x,D) ={ \sum \limits _{j=1}^{n}}{\Pi }_{ j}({x}_{j},{D}_{j}),$$

(2.1)

where

$$\begin{array}{rcl}{ \Pi }_{j}({x}_{j},{D}_{j})& = -\bar{{c}}_{j}{x}_{j} +\bar{ {r}}_{j}\min \{{x}_{j},{D}_{j}\} & \\ & = ({r}_{j} - {c}_{j}){x}_{j} - ({r}_{j} - {s}_{j}){({x}_{j} - {D}_{j})}^{+},\quad j = 1,\ldots ,n,&\end{array}$$

(2.2)

with ${(x)}^{+} =\max \{ x,0\}$. I assume that the demand vector D is random and nonnegative. Thus, for every x ≥ 0 the profit Π(x, D) is a real bounded random variable.

The risk-neutral multi-product newsvendor optimization problem is to maximize the expected profit:

$${ \max _{x\geq 0}}\mathbb{E}[\Pi (x,D)].$$

(2.3)

This problem can be decomposed into independent problems, one for each product. Thus, under risk neutrality, a multi-product newsvendor problem is equivalent to multiple single-product newsvendor problems. However, as I have mentioned it in the introduction, this formulation is inappropriate, if one is concerned with few (or just one) realizations and the Law of Large Numbers cannot be invoked.

Under a coherent risk measure, the optimization problem of the risk-averse newsvendor is defined as follows:

$${ \min _{x\geq 0}}\rho [\Pi (x,D)],$$

(2.4)

where ρ[ ⋅] is a law-invariant coherent measure of risk, and Π(x, D) represents the profit of the newsvendor, as defined in (2.1). It is worth stressing that problem (2.4) cannot be decomposed into independent subproblems, one for each product. Thus, it is necessary to consider the portfolio of products as a whole.

3 Coherent Measures of Risk

I present a formal definition of the coherent measures of risk following the abstract approach of Ruszczyński and Shapiro (2005, 2006a). Let (Ω, ℱ) be a certain measurable space. In my case, Ω is the probability space on which D is defined. An uncertain outcome (in my case, Π(x, D)) is represented by a measurable function V : Ω → ℝ. I specify the vector space $\mathcal{Z}$ of possible functions; in my case it is sufficient to consider $\mathcal{Z} = {\mathcal{L}}_{\infty }(\Omega ,\mathcal{F},P)$, which is the space of all bounded measurable functions on [0, 1]. Indeed, for a fixed order quantity x, the function ω → Π(x, D(ω)) is bounded. For any V and Y $\in \mathcal{Z}$, I write V ≽ Y if V ≥ Y almost surely (or with probability 1).

In the minimization context, a coherent measure of risk is a function $\rho : \mathcal{Z}\rightarrow \mathbb{R}$ satisfying the following axioms:

$\rho (\alpha V + (1 - \alpha )Y ) \leq \alpha \rho (V ) + (1 - \alpha )\rho (Y )$, for all $V,Y \in \mathcal{Z}$ and all α ∈ [0, 1].

If $V,Y \in \mathcal{Z}$ and V ≽ Y , then ρ(V ) ≤ ρ(Y ).

If a ∈ ℝ and $V \in \mathcal{Z}$, then $\rho (V + a) = \rho (V ) - a$.

If t ≥ 0 and $V \in \mathcal{Z}$, then ρ(tV ) = tρ(V ).

A coherent measure of risk ρ( ⋅) is called law invariant, if the value of ρ(V ) depends only on the distribution of V , that is, ρ(V ₁) = ρ(V ₂) if V ₁ and V ₂ have identical distributions. It implies that only the distribution matters, but not particular realizations. This axiom may look so natural. However, each random variable is actually defined by probability distribution as well as the field of events with a sigma-algebra structure. Although all practical risk measures are all law invariant, it is theoretically possible to construct a non law-invariant risk measure. From now on, without loss of generality, “coherent risk measures” actually mean “law-invariant coherent risk measures” unless mentioned explicitly. For more details of mathematical properties of law invariance, see Acerbi and Tasche (2002); Delbaen (2002) and Kusuoka (2003).

Important examples of law-invariant coherent measures of risk are obtained from mean–risk models of form:

$$\rho (V ) = -\mathbb{E}[V ] + \lambda r[V ],$$

(2.5)

where λ > 0 and r[ ⋅] is a variability measure of the random outcome V. Popular examples of r[ ⋅] are the semideviation of order p ≥ 1:

$${\sigma }_{p}[V ] = \mathbb{E}{\left [\{{(\mathbb{E}[V ] - V ){}^{+}\}}^{p}\right ]}^{\frac{1} {p} },$$

(2.6)

and weighted mean-deviation from quantile:

$${r}_{\beta }[V ] {=\min _{\eta \in \mathbb{R}}}\mathbb{E}\left [\max \left ((1 - \beta )(\eta - V ),\beta (V - \eta )\right )\right ],\quad \beta \in (0,1).$$

(2.7)

The optimal η in the problem above is the β-quantile of V. Optimization models with (2.6) and (2.7) were considered in Ogryczak and Ruszczyński (1999, 2001, 2002). In the maximization context, from the practical point of view, it is most reasonable to consider β ∈ (0, 1 ∕ 2], because then r _β[V ] penalizes the left tail of the distribution of V much higher than the right tail.

The equation ρ[ ⋅] defined at (2.5), with r[ ⋅] = σ _p [ ⋅] and p ≥ 1, is a coherent measure of risk, provided that λ ∈ [0, 1]. When r[ ⋅] = r _β[ ⋅], (2.5) is a coherent measure of risk, if λ ∈ [0, 1 ∕ β]. All these results can be found in Ruszczyński and Shapiro (2006a).

The mean-deviation from quantile r _β[ ⋅] is connected to the Average Value-at-Risk (AVaR), also known as expected shortfall or CVaR in Rockafellar and Uryasev (2000), as follows:

$${ \text{ AVaR}}_{\beta }(V ) = {-\max _{\eta \in \mathbb{R}}}\left \{\eta - \frac{1} {\beta }\mathbb{E}\left [{(\eta - V )}^{+}\right ]\right \} = -\mathbb{E}[V ] + \frac{1} {\beta }{r}_{\beta }[V ].$$

(2.8)

All these relations can be found in Föllmer and Schied (2004), Ogryczak and Ruszczyński (2002) and Ruszczyński and Vanderbei (2003) (with obvious adjustments for the sign of V ). The relation (2.8) allows me to interpret { AVaR}_β(V ) as a special case of the mean–risk model where r[V ] is a deviation from quantile in (2.7) with $\lambda = 1/\beta$.

One of the fundamental results in the theory of law-invariant measures is the theorem of Kusuoka (2003): For every lower semicontinuous law-invariant coherent measure of risk ρ[⋅] on ℒ _∞ (Ω,ℱ,P), with an atomless probability space (Ω,ℱ,P), there exists a convex set ℳ of probability measures on (0,1] such that

$$\rho [V ] {=\sup _{\mu \in \mathcal{M}}}{\int \nolimits }_{0}^{1}{\mathrm{AVaR}}_{ \beta }[V ]\,\mu (\mathrm{d}\beta ).$$

(2.9)

Using identity (2.8), I can rewrite ρ[V ] as follows:

$$\rho [V ] = -\mathbb{E}[V ] {+\sup _{\mu \in \mathcal{M}}}{\int \nolimits }_{0}^{1} \frac{1} {\beta }{r}_{\beta }[V ]\,\mu (\mathrm{d}\beta ).$$

(2.10)

This means that every problem (2.4) with a coherent law-invariant measure of risk is a mean–risk model, with the variability measure

$${\varkappa }_{\mathcal{M}}[V ] {=\sup _{\mu \in \mathcal{M}}}{\int \nolimits }_{0}^{1} \frac{1} {\beta }{r}_{\beta }[V ]\,\mu (\mathrm{d}\beta ).$$

(2.11)

To illustrate the impact of scaling (the unit system) on risk measurement, I compare solutions of a single-product risk-averse newsvendor model under the coherent risk measure with (2.5) and (2.7), the entropic exponential utility function $\frac{1} {\lambda }\ln \mathbb{E}\left [{\mathrm{e}}^{-\lambda \Pi (x;D)}\right ]$ and the mean-variance model. The entropic exponential utility function is an example of a convex measure of risk which is not coherent and is equivalent to an exponential utility function by a certainty equivalent operator.

I select parameters for each risk measure so that they have the same optimal solution when the unit of profit measurement is one dollar. Specifically, I set r = 15, c = 10, and s = 7 (in dollars) for all three risk measures. Demand follows a lognormal distribution with μ = 3 and σ = 0. 4724. This demand distribution is used in all instances. For the coherent measure of risk, I set β = 0. 5 and $\lambda = {\lambda }_{1} = 0.2$. By the sample-based LP method, the optimal solution is $\hat{{x}}^{\mathrm{R{A}_{1}}} = 20.7824$. For the entropic exponential utility function model, defined as

$${ \min _{x\geq 0}} \frac{1} {{\lambda }_{2}}\ln \mathbb{E}\left [{\mathrm{e}}^{-{\lambda }_{2}\Pi (x;D)}\right ].$$

(2.12)

I set λ₂ = 0. 0072, which results in a sample-based solution $\hat{{x}}^{\mathrm{R{A}_{2}}} = 20.7786$. For the mean-variance model, defined as

$${ \min _{x\geq 0}} - \mathbb{E}\left [\Pi (x;D)\right ] + {\lambda }_{3}\mathbb{V}\mathrm{ar}\left [\Pi (x;D)\right ].$$

(2.13)

I set λ₃ = 0. 0037, which results in a sample-based solution $\hat{{x}}^{\mathrm{R{A}_{3}}} = 20.7918$. Then I change the unit of r (price), c (cost) and s (salvage value) from dollar to 30 cents, 10 cents, 3 cents and 1 cent while keeping all other parameters unchanged. My results are summarized in Table 2.3.

Table 2.3 The impact of rescaling on solutions—a coherent measure of risk, entropic exponential utility function, and a mean–variance model

As one can see from this table, while the numerical solution under a coherent measure of risk is invariant with respect to the unit system, it varies significantly under other risk measures.

4 Basic Analytical Results

In this section, I prove two fundamental results for a multi-product risk-averse newsvendor model. As I do not assume independent demands for the two results in this section, Propositions 1 and 2 hold true both in independent and dependent demands. These two Propositions also take a role of key intermediate steps for further analysis in Sects. 2.5–2.7.

Proposition 1 (Convexity of the Model). 

If ρ[⋅] is a coherent measure of risk, then ρ[Π(x,D)] is a convex function of x.

Proof.

I first note that $\Pi (x,D) ={ \sum \nolimits }_{j=1}^{n}{\Pi }_{j}({x}_{j},{D}_{j})$ is concave in x. That is, for any 0 ≤ α ≤ 1 and all x and y,

$$\Pi (\alpha x + (1 - \alpha )y,D) \geq \alpha \Pi (x,D) + (1 - \alpha )\Pi (y,D)\quad \mbox{ for all $D$.}$$

Using the monotonicity axiom, I obtain

$$\begin{array}{rcl} & \rho [\Pi (\alpha x + (1 - \alpha )y,D)] \leq \rho [\alpha \Pi (x,D) + (1 - \alpha )\Pi (y,D)]& \\ & \leq \alpha \rho [\Pi (x,D)] + (1 - \alpha )\rho [\Pi (y,D)]. & \\ \end{array}$$

The second inequality follows by the axiom of convexity.

Proposition 1 shows the convexity of my model. It means the convexity preserves in a risk-averse model as well as in a risk-neutral model. Observe that I did not use the axiom of positive homogeneity, and thus Proposition 1 extends to more general models (e.g., convex measures of risk). I next prove the intuitively clear statement that identical products should be ordered in equal quantities under coherent measures of risk.

Proposition 2 (Symmetry of the Solution). 

Assume that all products are identical, i.e., prices, ordering costs, and salvage values are the same across all products. Furthermore, let the joint probability distribution of the demand be symmetric, that is, invariant with respect to permutations of the demand vector. Then, for every law-invariant coherent measure of risk ρ[⋅], one of the optimal solutions of problem (2.4) is a vector with equal coordinates, $\hat{{x}}_{1}^{\mathrm{RA}} =\hat{ {x}}_{2}^{\mathrm{RA}} = \cdots =\hat{ {x}}_{n}^{\mathrm{RA}}$ .

Proof.

An optimal solution exists, because with no loss of generality I can assume that x is bounded by some large constant, and ρ[Π(x, D)] is continuous with respect to x (see Ruszczyński and Shapiro 2006a).

Let me consider an arbitrary order vector $x = ({x}_{1},\ldots ,{x}_{n})$ and let P be an n ×n permutation matrix. Then, the distribution of profit associated with Px is the same as that associated with x. There are n! different permutations of x and let me denote them ${x}^{1},\ldots ,{x}^{n!}$. Consider the point

$$y = \frac{1} {n!}{\sum \nolimits }_{i=1}^{n!}{x}^{i}.$$

It has all coordinates equal to the average of the coordinates x _j . As the joint probability distribution of ${D}_{1},{D}_{2},\ldots ,{D}_{n}$ is symmetric, the distribution of Π(x ⁱ, D) is the same for each i. By Proposition 1 and law invariance of ρ[ ⋅] I obtain

$$\rho [\Pi (y,D)] \leq \frac{1} {n!}{\sum \nolimits }_{i=1}^{n!}\rho [\Pi ({x}^{i},D)] = \rho [\Pi (x,D)].$$

This means that for every plan x, the corresponding plan y with equal orders is at least as good. As an optimal plan exists, there is an optimal plan with equal orders.

Note that Proposition 2 only requires symmetric joint demand distribution, but not independent demands.

5 Analytical Results for Independent Demands

In this section, I assume demand independence and provide two analytical results (impact of degree of risk aversion and impact of shift in mean demand) for the multi-product newsvendor model under coherent risk measures. First, to study the impact of the degree of risk aversion, let me first focus on a specific variability measure—the weighted mean-deviation from quantile, given by (2.7). The corresponding measure of risk has the form,

$$\rho [V ] = -\mathbb{E}[V ] + \lambda {r}_{\beta }[V ].$$

(2.14)

By (2.8), I can write

$$\rho [V ] = -(1 - \lambda \beta )\mathbb{E}[V ] + \lambda \beta {\mathrm{AVaR}}_{\beta }[V ].$$

(2.15)

I consider the problem

$${ \min _{x\geq 0}}\left \{-\mathbb{E}[\Pi (x,D)] + \lambda {r}_{\beta }[\Pi (x,D)]\right \}.$$

(2.16)

Proposition 3 (Monotonicity of the Solution with a mean-deviation from quantile). 

Assume that all products are identical and demands for all products are iid (independently and identically distributed) and have a continuous distribution. Let $\hat{{x}}^{{\mathrm{RA}}_{1}}$ be the solution of problem (2.16) for λ = λ ₁ > 0, having equal coordinates. If λ ₂ ≥ λ ₁ then there exists a solution $\hat{{x}}^{{\mathrm{RA}}_{2}}$ of problem (2.16) for λ = λ ₂ , having equal coordinates and such that $\hat{{x}}_{j}^{{\mathrm{RA}}_{2}} \leq \hat{ {x}}_{j}^{{\mathrm{RA}}_{1}}$ , j = 1,…,n.

For the proof of Proposition 3, refer to Choi et al. (2011). Then, my goal is to extend the monotonicity property to all law-invariant coherent measures of risk. Observe that my assumption about continuous distribution of the demand implies that the probability space is nonatomic. Consider the problem

$${ \min _{x\geq 0}}\left \{-\mathbb{E}[\Pi (x,D)] + \lambda {\varkappa }_{\mathcal{M}}[\Pi (x,D)]\right \}\!,$$

(2.17)

where ${\varkappa }_{\mathcal{M}}[V ]$ is given by (2.11).

Proposition 4 (Monotonicity of the Solution with every coherent measure of risk). 

Assume that all products are identical and demands for all products are iid and have a continuous distribution. Let $\hat{{x}}^{{\mathrm{RA}}_{1}}$ be the solution of problem (2.17) for λ = λ ₁ > 0, having equal coordinates. If λ ₂ ≥ λ ₁ then there exists a solution $\hat{{x}}^{{\mathrm{RA}}_{2}}$ of problem (2.17) for λ = λ ₂ , having equal coordinates and such that $\hat{{x}}_{j}^{{\mathrm{RA}}_{2}} \leq \hat{ {x}}_{j}^{{\mathrm{RA}}_{1}}$ , j = 1,…,n.

Proof.

As in the proof of Proposition 3, each function x↦r _β[Π(x, D)] is nondecreasing, for every β ∈ (0, 1). Then the integral over β with respect to any nonnegative measure μ is nondecreasing as well. Taking the supremum in (2.11) does not change this property. Therefore, Proposition 4 holds true also for the mean–risk model with the risk $r[\cdot ] = {\varkappa }_{\mathcal{M}}[\cdot ]$.

Finally, I discuss the impact of the shift in mean demand on the optimal order quantities under general coherent measures of risk.

Proposition 5 (Impact of the Shift in Mean Demand). 

Assume that all products are identical and demands for all products are iid except that ${\mu }_{j} = \mathbb{E}[{D}_{j}]$ , $j = 1,\ldots ,n$ . If ${\mu }_{1} \geq {\mu }_{2} \geq \cdots \geq {\mu }_{n}$ , then $\hat{{x}}_{1}^{\mathrm{RA}} \geq \hat{ {x}}_{2}^{\mathrm{RA}} \geq \cdots \geq \hat{ {x}}_{n}^{\mathrm{RA}}$ .

Proof.

Consider the demand vector $\tilde{{D}}_{j} = {D}_{j} - {\mu }_{j} + {\mu }_{1}$. As it has identical and iid components, by Proposition 2 there exists an optimal order vector $\tilde{x}$ with equal coordinates: $\tilde{{x}}_{1} =\tilde{ {x}}_{2} = \cdots =\tilde{ {x}}_{n}$, for the risk-averse multi-product newsvendor with $\tilde{D}$ as the demand vector. I can interpret the demand D as a sum of the random demand $\tilde{D}$ and a deterministic demand vector h with coordinates ${h}_{j} = {\mu }_{j} - {\mu }_{1}$. If $\tilde{{x}}_{j} > 0$, then by the Translation Equivariance axiom, it is easy to see that $\hat{x} =\tilde{ x} + h$ is the solution of the problem

$${\min _{x\geq 0}}\rho [\Pi (x,D)],$$

for every coherent measure of risk ρ[ ⋅].

6 Asymptotic Analysis and Closed-Form Approximations

6.1 Asymptotic Optimality of Risk-Neutral Solutions

In this section, I study the asymptotic behavior of the risk-averse newsvendor model when the number of products tends to infinity. I assume heterogenous products with independent demands.

I start from the derivation of error bounds for the risk-neutral solution. Consider a sequence of products $j = 1,2,\ldots$, with corresponding prices r _j , costs c _j , and salvage values s _j . I assume that s _j  < c _j  < r _j , and that all these quantities are uniformly bounded for $j = 1,2\ldots$.

Consider the risk-neutral optimal order quantities

$$\hat{{x}}_{j}^{\mathrm{RN}} =\bar{ {F}}_{ j}^{-1}\left (\frac{\bar{{c}}_{j}} {\bar{{r}}_{j}}\right ),\quad j = 1,2,\ldots.$$

(2.18)

I assume that the following conditions are satisfied:

• (i) There exist x ^min > 0 and x ^max such that

  $${x}^{\min } \leq \hat{ {x}}_{j}^{\mathrm{RN}} \leq {x}^{\max },\quad j = 1,2,\ldots.$$

• (ii) There exists σ_min > 0 such that

  $$\mathbb{V}\mathrm{ar}\left [\min \left (\hat{{x}}_{j}^{\mathrm{RN}},{D}_{ j}\right )\right ] \geq {\sigma }_{\min }^{2},\quad j = 1,2,\ldots.$$

My intention is to evaluate the quality of the risk-neutral solution $\hat{{x}}^{\mathrm{RN}}$ in the risk-averse problem

$${ \min }_{{x}_{1},\ldots ,{x}_{n}}\rho \left [ \frac{1} {n}{\sum \nolimits }_{j=1}^{n}{\Pi }_{ j}({x}_{j},{D}_{j})\right ]\!.$$

(2.19)

Observe that in problem (2.19) I consider the average profit per product, rather than the total profit, as in problem (2.4). The reason is that I intend to analyze properties of the optimal value of this problem as n → ∞ and I want the limit of the objective value of problem (2.19) to exist. Owing to the Positive Homogeneity axiom, problems (2.19) and (2.4) are equivalent.

I denote by $\hat{{\rho }}_{n}$ the optimal value of problem (2.19). I also introduce the following notation,

$$\begin{array}{rcl} {\mu }_{j}^{\mathrm{RN}}& = \mathbb{E}\left [\min (\hat{{x}}_{ j}^{\mathrm{RN}},{D}_{ j})\right ],\qquad \bar{{\mu }}_{n} = \frac{1} {n}{ \sum \limits _{j=1}^{n}}\bar{{r}}_{j}{\mu }_{j}^{\mathrm{RN}}, & \\ {\left ({\sigma }_{j}^{\mathrm{RN}}\right )}^{2}& = \mathbb{V}\mathrm{ar}\left [\min \left (\hat{{x}}_{ j}^{\mathrm{RN}},{D}_{ j}\right )\right ],\qquad \bar{{s}}_{n}^{2} = \frac{1} {{n}^{2}} { \sum \limits _{j=1}^{n}}\bar{{r}}_{j}^{2}{\left ({\sigma }_{j}^{\mathrm{RN}}\right )}^{2}.& \\ \end{array}$$

Finally, I denote by $\mathcal{N}$ the standard normal variable. Then, I will show asymptotic convergence of risk-neutral solution to the true risk-averse solution.

Proposition 6 (Asymptotic Convergence of Risk-Neutral Solution with Error Bound). 

Assume that ρ[⋅] is a law-invariant coherent measure of risk and the space (Ω,ℱ,P) is nonatomic. Then

$$\rho \left [ \frac{1} {n}{\sum \limits _{j=1}^{n}}{\Pi }_{ j}(\hat{{x}}_{j}^{\mathrm{RN}},{D}_{ j})\right ] {\leq \min }_{{x}_{1},\ldots ,{x}_{n}}\rho \left [ \frac{1} {n}{\sum \limits _{j=1}^{n}}{\Pi }_{ j}({x}_{j},{D}_{j})\right ] + O\left ( \frac{1} {\sqrt{n}}\right )\!.$$

(2.20)

For the proof, refer to Choi et al. (2011). Asymptotically, the difference between the optimal objective value (the first term of the right-hand side of (2.20)) and the value obtained by using the risk-neutral solution (the term in the left-hand side of (2.20)) disappears at the rate of $1/\sqrt{n}$. Such difference can be considered as the error bound of a risk-neutral solution given as an “o” function of $1/\sqrt{n}$. Thus, for a firm dealing with very many products having independent demands, the risk-neutral solution is a reasonable sub-optimal alternative to the risk-averse solution.

6.2 Adjustments in the Mean-Deviation from Quantile Model

In this section, I develop close-form approximations to the optimal risk-averse solution when the number of products is moderately large. My idea is to use the risk-neutral solution as the starting point, and to calculate an appropriate correction to account for risk aversion.

I first consider the mean-deviation from quantile model in which the measure of variability is defined at (2.7). Recall that the corresponding mean–risk model in (2.14) is equivalent to the minimization of a combination of the mean and the Conditional Value-at-Risk, as in (2.15). I then consider the general coherent risk measure in Sect. 2.6.3. I finally discuss several iterative methods that are based on the approximations in Sect. 2.6.4.

I use the notation ${Z}_{x}^{n} = \frac{1} {n}{ \sum \nolimits }_{j=1}^{n}\bar{{r}}_{j}\min ({x}_{j},{D}_{j})$ (with x as a subscript to stress the dependence of Z _x ⁿ on x). Using (2.1) and (2.2), I can calculate the average profit per product as follows:

$$\bar{\Pi }(x,D) = \frac{1} {n}{\sum \limits _{j=1}^{n}}{\Pi }_{ j}({x}_{j},{D}_{j}) = -\frac{1} {n}{\sum \limits _{j=1}^{n}}\bar{{c}}_{ j}{x}_{j} + {Z}_{x}^{n}.$$

Thus,

$$\begin{array}{ccc} \rho [\bar{\Pi }(x,D)]& = \frac{1} {n}{ \sum \limits _{j=1}^{n}}\bar{{c}}_{j}{x}_{j} + \left (-\mathbb{E}[{Z}_{x}^{n}] + \lambda {r}_{\beta }({Z}_{x}^{n})\right ) \\ & = \frac{1} {n}{ \sum \limits _{j=1}^{n}}\bar{{c}}_{j}{x}_{j} + \left (\mathbb{E}[{Z}_{x}^{n}](\lambda \beta - 1) - \lambda {\beta \max }_{\eta \in \mathbb{R}}\left \{\eta - \frac{1} {\beta }\mathbb{E}\left [{(\eta - {Z}_{x}^{n})}^{+}\right ]\right \}\right ).\end{array}$$

(2.21)

Let me denote $\hat{\eta }$ to be the maximizer in (2.21), among η ∈ ℝ, at a fixed x. $\hat{\eta }$ is the β-quantile of Z _x ⁿ. To take the partial derivative of $\rho [\bar{\Pi }(x,D)]$ with respect to x _j , I consider two cases.

Case (i): $\hat{\eta } < \frac{1} {n}{ \sum \nolimits }_{j=1}^{n}\bar{{r}}_{j}{x}_{j}$.

Assuming that the quantile $\hat{\eta }$ is unique and differentiating (2.21), I observe again that

$$\frac{\partial \rho [\bar{\Pi }(x,D)]} {\partial {x}_{j}} = \frac{\bar{{c}}_{j}} {n} + \frac{\bar{{r}}_{j}(\lambda \beta - 1)} {n} \mathbb{P}[{D}_{j} > {x}_{j}] -\frac{\bar{{r}}_{j}\lambda } {n} \mathbb{P}\left [\{{Z}_{x}^{n} <\hat{ \eta }\} \cap \{ {D}_{ j} > {x}_{j}\}\right ].$$

(2.22)

Here I used (Bonnans and Shapiro 2000, Theorem 4.13) to avoid differentiating with respect to $\hat{\eta }$.

Let me analyze the last term on the right-hand side in (2.22) for j = 1, 2, …, n:

$$\begin{array}{rcl} & \mathbb{P}\left [\{{Z}_{x}^{n} <\hat{ \eta }\} \cap \{ {D}_{j} > {x}_{j}\}\right ] = \mathbb{P}\left [{Z}_{x}^{n} <\hat{ \eta }\vert {D}_{j} > {x}_{j}\right ]\mathbb{P}[{D}_{j} > {x}_{j}]& \\ & = \mathbb{P}\left [ \frac{1} {n}{ \sum \limits _{k\not =j}^{n}}\bar{{r}}_{k}\min ({x}_{k},{D}_{k}) <\hat{ \eta } -\frac{\bar{{r}}_{j}{x}_{j}} {n} \right ] \cdot \mathbb{P}[{D}_{j} > {x}_{j}].&\end{array}$$

(2.23)

Suppose x _j  ≥ x _min, $j = 1,2,\ldots ,$. Owing to conditions (i) and (ii), exactly as in Sect. 2.6.1, for large n the random variable Z _x ⁿ is approximately normally distributed with the mean $\bar{{\mu }}_{n} = \frac{1} {n}{ \sum \nolimits }_{j=1}^{n}\bar{{r}}_{j}{\mu }_{j}$ and the variance $\bar{{s}}_{n}^{2} = \frac{1} {{n}^{2}} { \sum \nolimits }_{j=1}^{n}\bar{{r}}_{j}^{2}{\sigma }_{j}^{2}$, where ${\mu }_{j} = \mathbb{E}[\min \{{x}_{j},{D}_{j}\}]$ and ${\sigma }_{j}^{2} = \mathbb{V}\mathrm{ar}(\min \{{x}_{j},{D}_{j}\})$. Under normal approximation, the β-quantile of Z _x ⁿ can be approximated by $\hat{\eta } \simeq \bar{ {\mu }}_{n} + {z}_{\beta }\bar{{s}}_{n},$ where z _β is the β-quantile of the standard normal variable. Similarly, $\frac{1} {n-1}{ \sum \nolimits }_{k\not =j}^{n}\bar{{r}}_{k}\min ({x}_{k},{D}_{k})$ is approximately normal with mean $\frac{1} {n-1}{ \sum \nolimits }_{k\not =j}^{n}\bar{{r}}_{k}{\mu }_{k}$ and variance $\frac{1} {{(n-1)}^{2}} { \sum \nolimits }_{k\not =j}^{n}\bar{{r}}_{k}^{2}{\sigma }_{k}^{2}$. Using these approximations and denoting by $\mathcal{N}$ the standard normal random variable, I obtain:

$$\begin{array}{ccc} &\mathbb{P}\left [ \frac{1} {n}{ \sum \nolimits }_{k\not =j}^{n}\bar{{r}}_{k}\min ({x}_{k},{D}_{k}) <\hat{ \eta } -\frac{\bar{{r}}_{j}{x}_{j}} {n} \right ] \simeq \mathbb{P}\left [\mathcal{N} < \frac{-\bar{{r}}_{j}({x}_{j}-{\mu }_{j})+{z}_{\beta }\sqrt{{\sum \nolimits }_{k=1}^{n}\bar{{r}}_{k}^{2}{\sigma }_{k}^{2}}} {\sqrt{{\sum \nolimits }_{k\not =j}\bar{{r}}_{k}^{2}{\sigma }_{k}^{2}}} \right ] \\ & \quad = \mathbb{P}\left [\mathcal{N} < \frac{-\bar{{r}}_{j}({x}_{j}-{\mu }_{j})} {\sqrt{n-1}{\gamma }_{nj}} + {z}_{\beta }\sqrt{1 + \frac{\bar{{r}}_{j }^{2 }{\sigma }_{j }^{2 }} {(n-1){\gamma }_{nj}^{2}}} \right ]\!,\end{array}$$

(2.24)

where ${\gamma }_{nj} = \sqrt{ \frac{1} {n-1}{ \sum \nolimits }_{k\not =j}\bar{{r}}_{k}^{2}{\sigma }_{k}^{2}}$. As $\bar{{r}}_{k}^{2}{\sigma }_{k}^{2}$ is uniformly bounded from above and below across all products, I conclude that γ _nj is bounded from above and below for all j and n.

This estimate can be put into (2.23), and thus (2.22) can be approximated as follows:

$$\begin{array}{rcl} & & \frac{\partial \rho [\bar{\Pi }(x,D)]} {\partial {x}_{j}} \simeq \frac{\bar{{c}}_{j}} {n} + \frac{\bar{{r}}_{j}\mathbb{P}[{D}_{j} > {x}_{j}]} {n} \\ & & \quad \; \times \left (\lambda \beta - 1 - \lambda \mathbb{P}\left [\mathcal{N} < \frac{-\bar{{r}}_{j}({x}_{j} - {\mu }_{j})} {\sqrt{n - 1}{\gamma }_{nj}} + {z}_{\beta }\sqrt{1 + \frac{\bar{{r}}_{j }^{2 }{\sigma }_{j }^{2 }} {(n - 1){\gamma }_{nj}^{2}}}\right ]\right ).\qquad \end{array}$$

(2.25)

My next step is to approximate the probability on the right-hand side of (2.25). To this end, I derive its limit and calculate a correction to this limit for a finite n. When n → ∞, I have

$$\mathbb{P}\left [\mathcal{N} < \frac{-\bar{{r}}_{j}({x}_{j} - {\mu }_{j})} {\sqrt{n - 1}{\gamma }_{nj}} + {z}_{\beta }\sqrt{1 + \frac{\bar{{r}}_{j }^{2 }{\sigma }_{j }^{2 }} {(n - 1){\gamma }_{nj}^{2}}}\right ] \rightarrow \beta $$

(2.26)

and thus

$$\frac{\partial \rho [\bar{\Pi }(x,D)]} {\partial {x}_{j}} \rightarrow \frac{1} {n}(\bar{{c}}_{j} -\bar{ {r}}_{j}\mathbb{P}[{D}_{j} > {x}_{j}]).$$

This means that the conditions of the risk-averse solution

$$\frac{\partial \rho [\bar{\Pi }(x,D)]} {\partial {x}_{j}} = 0,\quad j = 1,2,\ldots ,n,$$

(2.27)

approaches that of the risk-neutral solution in (2.18). Thus the risk-neutral solution will be used as the base value, to which corrections will be calculated.

I can estimate the difference between the probability in (2.26) and β for a large but finite n, by assuming that x is close to $\hat{{x}}^{\mathrm{RN}}$. Thus, μ _j is close to ${\mu }_{j}^{\mathrm{RN}} = \mathbb{E}[\min \{\hat{{x}}_{j}^{\mathrm{RN}},{D}_{j}\}]$ and σ _j is close to ${\sigma }_{j}^{\mathrm{RN}} = \sqrt{\mathbb{V}\mathrm{ar } (\min \{\hat{{x}}_{j }^{\mathrm{RN } }, {D}_{j } \})}$. Considering only the leading term with respect to $1/\sqrt{n - 1}$, I obtain

$$\begin{array}{rcl} \mathbb{P}\left [\mathcal{N} < \frac{-\bar{{r}}_{j}({x}_{j} - {\mu }_{j})} {\sqrt{n - 1}{\gamma }_{nj}} + {z}_{\beta }\sqrt{1 + \frac{\bar{{r}}_{j }^{2 }{\sigma }_{j }^{2 }} {(n - 1){\gamma }_{nj}^{2}}}\right ]\simeq \,\mathbb{P}\left [\mathcal{N} < \frac{-\bar{{r}}_{j}(\hat{{x}}_{j}^{\mathrm{RN}} - {\mu }_{j}^{\mathrm{RN}})} {\sqrt{n - 1}{\gamma }_{nj}^{\mathrm{RN}}} + {z}_{\beta }\right ]\!,& & \\ \end{array}$$

where ${\gamma }_{nj}^{\mathrm{RN}} = \sqrt{ \frac{1} {n-1}{ \sum \nolimits }_{k\not =j}\bar{{r}}_{k}^{2}{({\sigma }_{k}^{\mathrm{RN}})}^{2}}$. The last probability can be estimated by the linear approximation derived at z _β. Observing that $P[\mathcal{N} < {z}_{\beta }] = \beta$ and that its derivative at z = z _β is the standard normal density at z _β, I get

$$\mathbb{P}\left [\mathcal{N} < \frac{-\bar{{r}}_{j}(\hat{{x}}_{j}^{\mathrm{RN}} - {\mu }_{j}^{\mathrm{RN}})} {\sqrt{n - 1}{\gamma }_{nj}^{\mathrm{RN}}} + {z}_{\beta }\right ] \simeq \beta - {\delta }_{nj}^{\mathrm{RN}},$$

with

$${\delta }_{nj}^{\mathrm{RN}} = \frac{{\mathrm{e}}^{-{z}_{\beta }^{2}/2 }} {\sqrt{2\pi }} \frac{\bar{{r}}_{j}(\hat{{x}}_{j}^{\mathrm{RN}} - {\mu }_{j}^{\mathrm{RN}})} {\sqrt{n - 1}{\gamma }_{nj}^{\mathrm{RN}}} ,\quad j = 1,\ldots ,n.$$

(2.28)

These estimates can be substituted to (2.25) for the derivative and yield

$$\frac{\partial \rho [\bar{\Pi }(x,D)]} {\partial {x}_{j}} \simeq \frac{\bar{{c}}_{j}} {n} + \frac{\bar{{r}}_{j}} {n} \left (-1 + \lambda {\delta }_{nj}^{\mathrm{RN}}\right )\mathbb{P}[{D}_{ j} > {x}_{j}].$$

(2.29)

Using the above approximations of the derivatives in (2.27), I obtain the first-order approximation of the risk-averse solution:

$$\hat{{x}}_{j}^{\mathrm{APR}} =\bar{ {F}}_{ j}^{-1}\left [ \frac{\bar{{c}}_{j}} {\bar{{r}}_{j}(1 - {\delta }_{nj}^{\mathrm{RN}}\lambda )}\right ],\quad j = 1,2,\ldots ,n.$$

(2.30)

Clearly, this approximation of $\hat{{x}}_{j}^{\mathrm{APR}}$ is increasing in n, decreasing in λ, and tends to the risk-neutral solution as n → ∞. Similar to the analysis in Sect. 2.6.1, the error bound of this approximation in (2.30) is given as follows:

$$0 \leq -\frac{\partial \rho \left (\bar{\Pi }\left (\hat{{x}}_{j}^{\mathrm{APR}},D\right )\right )} {\partial {x}_{j}} \leq O(1/{n}^{3/2}).$$

(2.31)

It implies that as the number of products increases, the convergence rate of my approximate solution to the risk-averse solution in (2.31), $O(1/{n}^{3/2})$, is much faster than the rate of the risk-neutral solution in (2.20), $O(1/{n}^{1/2})$.

Case (ii): $\hat{\eta } = \frac{1} {n}{ \sum \limits _{j=1}^{n}}\bar{{r}}_{j}{x}_{j}$.

I have

$$\begin{array}{rcl} \rho [\bar{\Pi }(x,D)]& =& \frac{1} {n}{\sum \nolimits }_{j=1}^{n}\bar{{c}}_{ j}{x}_{j} + \left (\mathbb{E}[{Z}_{x}^{n}](\lambda \beta - 1)\right. \\ & & \left.-\lambda \beta \left \{\frac{1} {n}{\sum \limits _{j=1}^{n}}\bar{{r}}_{ j}{x}_{j} - \frac{1} {\beta }\mathbb{E}\left [ \frac{1} {n}{\sum \limits _{j=1}^{n}}\bar{{r}}_{ j}{x}_{j} - {Z}_{x}^{n}\right ]\right \}\right )\!.\end{array}$$

Taking derivative with respect to x _j yields,

$$\frac{\partial \rho [\bar{\Pi }(x,D)]} {\partial {x}_{j}} = \frac{1} {n}\left [\bar{{c}}_{j} +\bar{ {r}}_{j}\lambda (1 - \beta ) +\bar{ {r}}_{j}\mathbb{P}[{D}_{j} > {x}_{j}]\left (\lambda (\beta - 1) - 1\right )\right ].$$

Equating the right-hand side to 0, I get

$$\hat{{x}}_{j}^{\mathrm{RA}} =\bar{ {F}}_{ j}^{-1}\left ( \frac{\bar{{c}}_{j} +\bar{ {r}}_{j}\lambda (1 - \beta )} {\bar{{r}}_{j}(1 + \lambda (1 - \beta ))}\right ).$$

(2.32)

Note that the solution in Case (ii) is an exact solution and free of the number of products, n. Clearly, if λ = 0, $\hat{{x}}_{j}^{\mathrm{RA}} =\hat{ {x}}_{j}^{\mathrm{RN}}$. As λ increases, $\hat{{x}}_{j}^{\mathrm{RA}}$ is decreasing. For any 0 ≤ λ ≤ 1 ∕ β, $\hat{{x}}_{j}^{\mathrm{RA}}$ is well defined.

It should be emphasized that Case (i) is more important, because for large n the distribution of Z _x ⁿ is close to normal and for a small β, the β-quantile of Z _x ⁿ tends to be smaller than $\frac{1} {n}{ \sum \nolimits }_{j=1}^{n}\bar{{r}}_{j}{x}_{j}$, for the values of x of interest.

Consider the special case of identical products. With a slight abuse of notation, let c _j  = c, r _j  = r and s _j  = s for all j = 1, 2, …, n. In Case (i), the first-order approximation of the risk-averse solution yields:

$$\frac{\mathrm{d}\rho [\bar{\Pi }(x,D)]} {\mathrm{d}x} \simeq \bar{ c} +\bar{ r}\mathbb{P}[{D}_{1} > x]({\delta }_{n}^{\mathrm{RN}}\lambda - 1),$$

with

$${\delta }_{n}^{\mathrm{RN}} = \frac{{\mathrm{e}}^{-{z}_{\beta }^{2}/2 }} {\sqrt{2\pi }} \frac{\hat{{x}}^{\mathrm{RN}} - {\mu }_{ x}^{\mathrm{RN}}} {\sqrt{n - 1}{\sigma }_{x}^{\mathrm{RN}}},$$

(2.33)

where $\hat{{x}}^{\mathrm{RN}}$, μ _x ^RN, and σ _x ^RN are the counterparts of $\hat{{x}}_{j}^{\mathrm{RN}}$, μ _j ^RN, and σ _j ^RN, respectively. Equating the right hand side to 0, I obtain

$$\hat{{x}}_{1}^{\mathrm{APR}} =\bar{ {F}}_{ 1}^{-1}\left ( \frac{\bar{c}} {\bar{r}(1 - {\delta }_{n}^{\mathrm{RN}}\lambda )}\right ),\quad j = 1,\ldots ,n.$$

(2.34)

Here, (2.34) is similar to (2.30) except that the terms $\bar{{c}}_{j}$, $\bar{{r}}_{j}$ and δ _nj ^RN are now identical for all j. In Case (ii), (2.32) reduces to

$$\hat{{x}}_{1}^{\mathrm{RA}} =\bar{ {F}}_{ 1}^{-1}\left ( \frac{\bar{c} +\bar{ r}\lambda (1 - \beta )} {\bar{r}(1 + \lambda (1 - \beta ))}\right ).$$

In the special case of a single-product problem, by (2.22) in Case (i) I obtain

$$\frac{\mathrm{d}\rho [\bar{\Pi }(x,D)]} {\mathrm{d}x} =\bar{ c} +\bar{ r}(\lambda \beta - 1)\mathbb{P}[D > x] -\bar{ r}\lambda \mathbb{P}\left [\{{Z}_{x} <\hat{ \eta }\} \cap \{ D > x\}\right ],$$

where Z _x  = min(x, D). Observe that in Case (i),$\mathbb{P}\left [\{{Z}_{x} <\hat{ \eta }\} \cap \{ D > x\}\right ] = \mathbb{P}\left [{Z}_{x} <\hat{ \eta }\vert D > x\right ]\mathbb{P}[D > x] = 0.$ Therefore, $\frac{\mathrm{d}\rho [\bar{\Pi }(x,D)]} {\mathrm{d}x} =\bar{ c} +\bar{ r}(\lambda \beta - 1)\mathbb{P}[D > x].$ This yields the exact solution of the single product problem

$$\hat{{x}}^{\mathrm{RA}} =\bar{ {F}}^{-1}\left ( \frac{\bar{c}} {\bar{r}(1 - \lambda \beta )}\right ) \leq \bar{ {F}}^{-1}\left (\frac{\bar{c}} {\bar{r}}\right ) =\hat{ {x}}^{\mathrm{RN}}.$$

This special case solution is the same as the solution obtained by Gotoh and Takano (2007). To determine whether Case (i) or Case (ii) applies, one can compute $\hat{{x}}^{\mathrm{RA}}$ for both cases, and then compute $\hat{\eta }$ to check the case conditions.

6.3 General Law-Invariant Coherent Measures of Risk

So far my analysis focused on a special risk measure, weighted mean-deviation from quantile, given in (2.7). I now generalize the results to any law-invariant coherent risk measure ρ[ ⋅].

Consider problem (2.17) where ${\varkappa }_{\mathcal{M}}[V ]$ is given by (2.11). By Kusuoka theorem, for nonatomic spaces, every law-invariant coherent measure of risk has such representation. Thus, I focus on Case (i) solution only. Then (2.21) can be replaced by

$$\begin{array}{rcl} \rho [\bar{\Pi }(x,D)]& =& \frac{1} {n}{\sum \limits _{j=1}^{n}}\bar{{c}}_{ j}{x}_{j} {+\sup }_{\mu \in \mathcal{M}}{\int \limits _{0}^{1}}\left (\mathbb{E}[{Z}_{ x}^{n}](\lambda \beta - 1)\right. \\ & & \left.-\lambda {\beta \max }_{\eta \in \mathbb{R}}\left \{\eta - \frac{1} {\beta }\mathbb{E}\,\left [{(\eta - {Z}_{x}^{n})}^{+}\right ]\right \}\right )\,\mu (\mathrm{d}\beta ).\end{array}$$

Suppose the maximum over ℳ is attained at a unique measure $\hat{\mu }$ (this is certainly true for spectral measures of risk, where the set ℳ has just one element). Similarly to (2.29),

$$\frac{\partial \rho [\bar{\Pi }(x,D)]} {\partial {x}_{j}} \simeq \frac{\bar{{c}}_{j}} {n} + \frac{\bar{{r}}_{j}} {n} \left (-1 + \lambda {\int \nolimits }_{0}^{1}{\delta }_{ nj}^{\mathrm{RN}}(\beta )\,\hat{\mu }(\mathrm{d}\beta )\right )\mathbb{P}[{D}_{ j} > {x}_{j}].$$

(2.35)

I denote here the quantity given in (2.28) by δ _nj ^RN(β), to stress its dependence on β​. Let me approximate $\hat{\mu }$ by the measure $\hat{{\mu }}^{\mathrm{RN}}$, obtained for the risk-neutral solution $\hat{{x}}^{\mathrm{RN}}$. Equating the approximate derivatives in (2.35) to zero, I obtain an approximate solution:

$$\hat{{x}}_{j}^{\mathrm{APR}} =\bar{ {F}}_{ j}^{-1}\left ( \frac{\bar{{c}}_{j}} {\bar{{r}}_{j}\left (1 - \lambda {\int \nolimits \nolimits }_{0}^{1}{\delta }_{ nj}^{\mathrm{RN}}(\beta )\,\hat{{\mu }}^{\mathrm{RN}}(\mathrm{d}\beta )\right )}\right )\!,\quad j = 1,2,\ldots ,n.$$

(2.36)

Again, δ _nj ^RN(β) ↓ 0 as n → ∞, and thus $\hat{{x}}_{j}^{\mathrm{APR}}$ increases in n and approaches the risk-neutral solution $\hat{{x}}_{j}^{\mathrm{RN}}$. This is consistent with Proposition 6 and the analysis in Sect. 2.6.2.

In the special case of identical products, the approximate solution is

$$\hat{{x}}_{1}^{\mathrm{APR}} =\bar{ {F}}_{ 1}^{-1}\left ( \frac{\bar{{c}}_{j}} {\bar{{r}}_{j}\left (1 - \lambda {\int \nolimits \nolimits }_{0}^{1}{\delta }_{ n}^{\mathrm{RN}}(\beta )\,\hat{{\mu }}^{\mathrm{RN}}(\mathrm{d}\beta )\right )}\right )\!,\quad j = 1,2,\ldots ,n,$$

(2.37)

where δ _n ^RN is defined at (2.33).

In the single-product problem, I obtain

$$\begin{array}{rcl} \rho [\bar{\Pi }(x,D)]& =\bar{ c}x {+\sup }_{\mu \in \mathcal{M}}{\int \nolimits }_{0}^{1}\left (\mathbb{E}[{Z}_{x}](\lambda \beta - 1)\right. & \\ & \quad \left.-\lambda {\beta \max }_{\eta \in \mathbb{R}}\left \{\eta - \frac{1} {\beta }\mathbb{E}\left [{(\eta - {Z}_{x})}^{+}\right ]\right \}\right )\,\mu (\mathrm{d}\beta ).&\end{array}$$

(2.38)

Assuming that $\hat{\mu }$ is the unique maximizer in (2.38), I obtain

$$\frac{\mathrm{d}\rho [\bar{\Pi }(x,D)]} {\mathrm{d}x} =\bar{ c} +{ \int \nolimits }_{0}^{1}\left (\bar{r}(\lambda \beta - 1)\mathbb{P}[D > x] -\bar{ r}\lambda \mathbb{P}\left [\{{Z}_{ x} <\hat{ \eta }\} \cap \{ D > x\}\right ]\right )\,\hat{\mu }(\mathrm{d}\beta ).$$

Similarly to the model with mean-deviation from quantile case, $\mathbb{P}\left [\{{Z}_{x} <\hat{ \eta }\}\cap \right.$ $\left.\{D > x\}\right ] = \mathbb{P}\left [{Z}_{x} <\hat{ \eta }\vert D > x\right ]\mathbb{P}[D > x] = 0.$ Thus,

$$\begin{array}{rcl} \frac{\mathrm{d}\rho [\bar{\Pi }(x,D)]} {\mathrm{d}x} & =\bar{ c} +{ \int \nolimits }_{0}^{1}\left (\bar{r}(\lambda \beta - 1)\mathbb{P}[D > x]\right )\,\hat{\mu }(\mathrm{d}\beta ) & \\ & =\bar{ c} +\bar{ r}\left (-1 + {\lambda \sup }_{\mu \in \mathcal{M}}{\int \nolimits }_{0}^{1}\beta \hat{\mu }(\mathrm{d}\beta )\right )\mathbb{P}[D > x].& \\ \end{array}$$

Therefore, the closed-form exact solution for general coherent measures of risk is given by:

$$\hat{{x}}^{\mathrm{RA}} =\bar{ {F}}^{-1}\left ( \frac{\bar{c}} {\bar{r}(1 - \lambda \bar{\beta })}\right ) \leq \bar{ {F}}^{-1}\left (\frac{\bar{c}} {\bar{r}}\right ) =\hat{ {x}}^{\mathrm{RN}},\quad \text{ where }\bar{\beta } ={ \int \nolimits }_{0}^{1}\beta \hat{{\mu }}^{\mathrm{RN}}(\mathrm{d}\beta ).$$

6.4 Iterative Methods

So far, I discussed approximations based on expansions about the risk-neutral solution $\hat{{x}}^{\mathrm{RN}}$. But exactly the same argument can be used to develop an iterative method, in which the best approximation known so far is substituted for the risk-neutral solution. I explain the simplest idea for the approximation developed in Sect. 2.6.2; the same idea applies to general coherent measures of risk discussed in Sect. 2.6.3.

The idea of the iterative method is to generate a sequence of approximations $\hat{{x}}^{(\nu )}$, $\nu = 0,1,2,\ldots$. I set $\hat{{x}}^{(0)} =\hat{ {x}}^{\mathrm{RN}}$. Then I calculate $\hat{{x}}^{(1)}$ by applying (2.30). In the iteration $\nu = 1,2,\ldots$, I use $\hat{{x}}^{(\nu )}$ instead of $\hat{{x}}^{\mathrm{RN}}$ in my approximation, calculating:

$$\begin{array}{rcl} {\mu }_{j}^{(\nu )}& = \mathbb{E}\left [\min \left \{\hat{{x}}_{ j}^{(\nu )},{D}_{ j}\right \}\right ],\quad {\sigma }_{j}^{(\nu )} = \sqrt{\mathbb{V}\mathrm{ar } \left (\min \left \{\hat{{x}}_{ j}^{(\nu )},{D}_{j}\right \}\right )}, & \\ {\gamma }_{nj}^{(\nu )}& = \sqrt{ \frac{1} {n-1}{ \sum \nolimits }_{k\not =j}\bar{{r}}_{k}^{2}{\left \{\left ({\sigma }_{k}^{(\nu )}\right )\right \}}^{2}},\quad {\delta }_{nj}^{(\nu )} = \frac{{\mathrm{e}}^{-{z}_{\beta }^{2}/2}} {\sqrt{2\pi }} \frac{\bar{{r}}_{j}\left (\hat{{x}}_{j}^{(\nu )}-{\mu }_{ j}^{(\nu )}\right )} {\sqrt{n-1}{\gamma }_{nj}^{(\nu )}} ,\quad j = 1,\ldots ,n.& \\ \end{array}$$

Finally, (2.30) is applied to generate the next approximate solution $\hat{{x}}^{(\nu +1)}$, and the iteration continues.

The iterative method is efficient if the initial approximation $\hat{{x}}^{(0)}$ is sufficiently close to the risk-averse solution. This is true when the risk aversion coefficient κ = λβ is close to zero or the number of products is very large. I must point out that the iterative method does not guarantee convergence to the optimal risk-averse solution. One reason is that my approximation in (2.30) may result in infeasible solutions as the term $\frac{\bar{{c}}_{j}} {\bar{{r}}_{j}\left (1-{\delta }_{nj}^{(\nu )}\lambda \right )}$ can be negative or greater than 1 (due to approximation). When this occurs less likely, one can say that the approximation is more stable. Generally, the approximation is more stable for larger number of products and smaller κ. To improve stability, I propose a more accurate method called the continuation method. In this approach, I apply the iterative method for a small value of κ, starting from the risk-neutral solution. Then I increase κ a little, and I apply the iterative method again, but starting from the best solution found for the previous value of κ. In this way, I gradually increase κ, until I reach the risk aversion coefficients which are of interest (usually, between 0 and 1). The stability of the iterative and continuation methods is summarized in Sect. 2.8.2.

7 Impact of Dependent Demands

In this section, I provide some insights on the impact of dependent demands. Due to significant analytical challenges, I focus on a two-product system and the mean-deviation from quantile model.

Under the risk-neutral measure, dependence of product demands has no impact on the optimal order quantities. However, under risk-averse measures, it can greatly affect the optimal order decisions for the newsvendor. Intuitively, positively (negatively) dependent demands entail larger (smaller) variability and thus increase (decrease) risk, as compared to independent demands. Thus, one tends to decrease (increase) the order quantity in case of positively (negatively) dependent demands relative to the case of independent demand.

To characterize the impact of demand dependence on the optimal order quantity under the coherent risk measure, I utilize the concept of “associated” random variables. Consider random variables D ₁, D ₂, …, D _n , denote vector D = (D ₁, D ₂, …, D _n ). The following definition is due to Esary et al. (1976); see Tong (1980) for a review.

Definition 1.

The random variables D ₁ ,D ₂ , …,D _n are associated, if ℂov [f(D),g(D)]  ≥  0, or, equivalently, $\mathbb{E}[f(D)g(D)]\: \geq \: \mathbb{E}[f(D)]\mathbb{E}[g(D)]$ , for all nondecreasing real functions f,g for which $\mathbb{E}[f(D)], \mathbb{E}[g(D)]$ and $\mathbb{E}[f(D)g(D)]$ exist.

Lemma 1.

• (i) Any subset of a set of associated random variables is associated.

• (ii) If two sets of associated random variables are independent of each other, their union is a set of associated random variables.

• (iii) Nondecreasing (or nonincreasing) functions of associated random variables are associated.

• (iv) If D ₁ ,D ₂ ,…,D _n are associated, then for all (y ₁ ,y ₂ ,…,y _n ) ∈ R ⁿ

  $$\begin{array}{rcl} \mathbb{P}\{{D}_{1} \leq {y}_{1},{D}_{2} \leq {y}_{2},\ldots ,{D}_{n} \leq {y}_{n}\}& \:\geq \: {\Pi }_{k=1}^{n}\mathbb{P}\{{D}_{k} \leq {y}_{k}\},& \\ \mathbb{P}\{{D}_{1} \geq {y}_{1},{D}_{2} \geq {y}_{2},\ldots ,{D}_{n} \geq {y}_{n}\}& \:\geq \: {\Pi }_{k=1}^{n}\mathbb{P}\{{D}_{k} \geq {y}_{k}\}.& \\ \end{array}$$

I refer to Tong (1980) for proofs.

Association is closely related to correlation. By (Tong, 1980, p. 99), a set of multi-variate normal random variables is associated if their correlation matrix has the structure l (Tong, 1980, p. 13) in which the correlation coefficient ρ _ij  = γ _i γ _j for all i ≠ j and 0 ≤ γ _i  < 1 for all i. This means that I can represent the demands as having one common factor:

$${D}_{i} = {\gamma }_{i}{D}_{0} + {\Delta }_{i},\quad i = 1,\ldots ,n,$$

where D ₀ and Δ _i , $i = 1,\ldots ,n$, are independent. A special case is the bi-variate normal random variable with a positive correlation coefficient.

Consider a system with two identical products and a solution with equal coordinates. Let ${Z}_{x} =\min \{ x,{D}_{1}\} +\min \{ x,{D}_{2}\}$. Clearly, $\Pi (x,D) = -2\overline{c}x + \overline{r}{Z}_{x}$ and

$$\begin{array}{rcl} & \rho (\Pi (x,D)) = 2\overline{c}x + \overline{r}\rho ({Z}_{x}), &<EquationNumber>2.39</EquationNumber> \\ & \rho ({Z}_{x}) = \mathbb{E}({Z}_{x})(\lambda \beta - 1) - \lambda {\beta \max }_{\eta \in \mathbb{R}}\left \{\eta - \frac{1} {\beta }\mathbb{E}[{(\eta - {Z}_{x})}^{+}]\right \}.&\end{array}$$

(2.40)

Let $\hat{\eta }$ be the maximizer. If $\hat{\eta }$ is not an atom of the distribution of Z _x , similar to Case (i) analysis in Sect. 2.6.2, I obtain

$$\frac{\mathrm{d}\rho ({Z}_{x})} {\mathrm{d}x} =\frac{\mathrm{d}\mathbb{E}[{Z}_{x}]} {\mathrm{d}x} (\lambda \beta - 1) + \lambda \frac{\mathrm{d}\mathbb{E}[{(\hat{\eta } - {Z}_{x})}^{+}]} {\mathrm{d}x} ,$$

where $\hat{\eta }$ is the β-quantile of Z _x and $\hat{\eta } < 2x$. Because the first term depends only on the marginal distributions of the demands, I focus on the second term, which is affected by the dependence of D ₁ and D ₂. I have

$$\frac{\mathrm{d}\mathbb{E}[{(\hat{\eta } - {Z}_{x})}^{+}]} {\mathrm{d}x} =-{\sum \limits _{j=1}^{2}}\mathbb{P}\left [\{{Z}_{ x} <\hat{ \eta }\} \cap \{ {D}_{j} > x\}\right ]=-2\mathbb{P}[\min \{x,{D}_{2}\} <\hat{ \eta }-x,{D}_{1} > x].$$

(2.41)

Consider three cases of (D ₁, D ₂), with the same the marginal distributions of D ₁ and D ₂. In case 1, (D ₁, D ₂) are associated random variables, and I use $\hat{{\eta }}_{P}$ to denote the β-quantile of the corresponding Z _x ; In case 2, (D ₁, D ₂) are independent with $\hat{{\eta }}_{I}$ as the β-quantile of Z _x ; In case 3, (D ₁, − D ₂) are associated random variables with $\hat{{\eta }}_{N}$ as the β-quantile of Z _x . I also let x _P ^∗, x _I ^∗, and x _N ^∗ be the optimal order quantities in cases 1, 2, and 3, respectively.

Proposition 7 (Impact of Demand Correlation). 

If $\hat{{\eta }}_{P} \leq \hat{ {\eta }}_{I} \leq \hat{ {\eta }}_{N} < 2x$ , then

$${x}_{P}^{{_\ast}}\leq {x}_{ I}^{{_\ast}}\leq {x}_{ N}^{{_\ast}}.$$

(2.42)

That is, positively (negatively) dependent (D ₁ ,D ₂ ) results in smaller (larger) optimal order quantities than independent (D ₁ ,D ₂ ).

Proof.

I first consider associated (D ₁, D ₂). I have

$$\begin{array}{rcl} & \mathbb{P}[\min \{x,{D}_{2}\} <\hat{ {\eta }}_{P} - x,{D}_{1} > x] & \\ & \quad = \mathbb{P}[{D}_{2} <\hat{ {\eta }}_{P} - x,{D}_{1} > x] & \\ & \quad = \mathbb{P}[{D}_{1} > x] - \mathbb{P}[{D}_{2} \geq \hat{ {\eta }}_{P} - x,{D}_{1} > x] \leq \mathbb{P}[{D}_{1} > x] - \mathbb{P}[{D}_{2} \geq \hat{ {\eta }}_{P} - x]\mathbb{P}[{D}_{1} > x]& \\ & \quad = \mathbb{P}[{D}_{2} <\hat{ {\eta }}_{P} - x]\mathbb{P}[{D}_{1} > x] \leq \mathbb{P}[{D}_{2} <\hat{ {\eta }}_{I} - x]\mathbb{P}[{D}_{1} > x]. & \\ \end{array}$$

The first inequality follows by Lemma 1 part (iv). The second inequality follows by $\hat{{\eta }}_{P} \leq \hat{ {\eta }}_{I}$. Note that the last term corresponds to independent (D ₁, D ₂). Thus, by (2.41), associated (D ₁, D ₂) have the derivatives dρ(Z _x ) ∕ dx at least as large as independent (D ₁, D ₂), which implies that x _P ^∗ ≤ x _I ^∗.

I then consider associated (D ₁, − D ₂). I obtain

$$\begin{array}{rcl} \mathbb{P}[{D}_{2} <\hat{ {\eta }}_{N} - x,{D}_{1} > x]& = \mathbb{P}[-{D}_{2} > -\hat{{\eta }}_{N} + x,{D}_{1} > x] & \\ & \quad \geq \mathbb{P}[-{D}_{2} > -\hat{{\eta }}_{N} + x]\mathbb{P}[{D}_{1} > x] & \\ & = \mathbb{P}[{D}_{2} <\hat{ {\eta }}_{N} - x]\mathbb{P}[{D}_{1} > x] \geq \mathbb{P}[{D}_{2} <\hat{ {\eta }}_{I} - x]\mathbb{P}[{D}_{1} > x].& \\ \end{array}$$

The first inequality follows by Lemma 1 part (iv). The second inequality follows by $\hat{{\eta }}_{I} \leq \hat{ {\eta }}_{N}$. Note that the last term corresponds to independent (D ₁, D ₂). Thus, by (2.41), associated (D ₁, − D ₂) have the derivatives dρ(Z _x ) ∕ dx no larger than independent (D ₁, D ₂), which implies that x _I ^∗ ≤ x _N ^∗.

The condition $\hat{{\eta }}_{P} \leq \hat{ {\eta }}_{I} \leq \hat{ {\eta }}_{N}$ holds when Y ₁ = min{x, D ₁} and Y ₂ = min{x, D ₂} follow bivariate normal distribution and β ≤ 0. 5. One can approximate the joint distribution of Y ₁ and Y ₂ very closely by bivariate normal when (D ₁, D ₂) follow bivariate normal and x is set to cover most of the demand, which is very likely in practice when the underage cost r − c is much greater than the overage cost c − s.

8 Numerical Examples

The objective of this section is twofold. First, I study the accuracy and the convergence rates of the approximations. Second, I provide insights (in addition to the analysis in Sects. 2.5–2.7) on the impact of demand dependence and risk aversion. I first introduce the sample-based optimization method.

8.1 Sample-Based Optimization

In all examples considered, I apply sample-based optimization to solve the resulting stochastic programming problems. I generate a sample ${D}^{1},{D}^{2},\ldots ,{D}^{T}$ of the demand vector, where

$${D}^{t} = ({d}_{ 1t},{d}_{2t},\ldots ,{d}_{nt}),\quad t = 1,\ldots ,T.$$

Then I replace the original demand distribution by the empirical distribution based on the sample, that is, I assign to each of the sample points the probability ${p}_{t} = 1/T$. It is known that when T → ∞, the optimal value of the sample problem approaches the optimal value of the original problem (see Shapiro 2007). In all my examples, I used T = 10, 000.

For the empirical distribution, the corresponding optimization problem (2.16) has an equivalent linear programming formulation. For each $j = 1,\ldots ,n$ and $t = 1,\ldots ,T$, I introduce the variable w _jt to represent the salvaged number of product j in scenario t. The variable u _t represents the shortfall of the profit in scenario t to the quantile η. It is also convenient to introduce the parameter κ = λβ to represent the relative risk aversion (0 ≤ κ ≤ 1). I obtain the formulation

$$\begin{array}{rcl} \max \quad & (1 - \kappa ){\sum \limits _{j=1}^{n}}\left [({r}_{j} - {c}_{j}){x}_{j} - ({r}_{j} - {s}_{j}){\sum \nolimits }_{t=1}^{T}{p}_{t}{w}_{jt}\right ] + \kappa \left (\eta - \frac{1} {\beta }{ \sum \limits _{t=1}^{T}}{p}_{t}{u}_{t}\right )& \\ \mbox{subject to}\quad & {\sum \limits _{j=1}^{n}}\left [({r}_{j} - {c}_{j}){x}_{j} - ({r}_{j} - {s}_{j}){w}_{jt}\right ] + {u}_{t} \geq \eta ,\quad t = 1,\ldots ,T, & \\ & \quad {x}_{j} - {d}_{jt} \leq {w}_{jt},\quad j = 1,\ldots ,n;\quad t = 1,\ldots ,T, & \\ & \quad {w}_{jt} \geq 0,\quad j = 1,\ldots ,n;\quad t = 1,\ldots ,T, & \\ & \quad {u}_{t} \geq 0,\quad t = 1,\ldots ,T, & \\ & \quad {x}_{j} \geq 0,\quad j = 1,\ldots ,n.\quad & \\ \end{array}$$

(2.43)

To explain this formulation, suppose the order quantities x _j are fixed. Then ${w}_{jt} = {({x}_{j} - {d}_{jt})}^{+}$ and ${u}_{t} = {(\eta - \Pi (x,{D}^{t}))}^{+}$ are optimal, and I maximize with respect to η the last term in problem (2.43), that is,

$${\max }_{\eta }\left \{\eta - \frac{1} {\beta }\mathbb{E}\left [{(\eta - \Pi (x,D))}^{+}\right ]\right \} = -{\text{ AVaR}}_{ \beta }\left [\Pi (x,D)\right ].$$

In the last expression, I used (2.8). Therefore, (2.43) is equal to $(1 - \kappa )\mathbb{E}\left [\Pi (x,D)\right ] - \kappa {\text{ AVaR}}_{\beta }\left [\Pi (x,D)\right ]$.

8.2 Accuracy of Approximations

In this section, I assess the accuracy of the closed-form approximations of Sect. 2.6. I first consider identical products, then nonidentical products.

For identical products, I assume that all products have identical cost structure, and iid demands. I set r = 15, c = 10, and s = 7. I set the demand distribution of each product to be lognormal with μ = 3 and σ = 0. 4724 (to achieve the desirable coefficient of variance (cv) of 0.5). Thus, the mean and standard deviation of each demand are ${\mathrm{e}}^{\mu +{\sigma }^{2}/2 } = 22.46$ and ${\mathrm{e}}^{\mu +{\sigma }^{2}/2 } \cdot \sqrt{({\mathrm{e} }^{{\sigma }^{2 } } - 1)} = 11.23$. Because the joint demand distribution is invariant with respect to the permutations of the demand vector, there exists an order vector with equal coordinates, which is optimal for the model.

I choose the number of products, n, to be 1, 3, 10, and 30, and I study the impact of the number of products on the gap between the sample-based LP solutions and the approximate solutions (generated by the iterative method with ν = 3, see Sect. 2.6.4). The sample-based LP solutions can take hours to solve, especially for large n and T. For instance, with n = 30 and a sample size of 10,000, the running time by CPLEX 9.0 at an Intel Pentium 4 PC is 32,607 s for identical products and 50,889 s for heterogenous products. In contrast, the approximate solution can be obtained within one or two seconds. I use β = 0. 5, that is, I am concerned with the shortfall below the median.

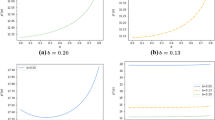
In my numerical study of identical products, I set the optimal order quantities for different products to be identical by Proposition 2. In model (2.43), all variables x _j are replaced by a single variable x. The corresponding results are illustrated in Fig. 2.1, where on the horizontal axis I display the relative risk aversion parameter κ = λβ. The term “exact,” “numerical,” and “approximation” represent the solution obtained by the exact calculation, the sample-based LP, and the closed-form approximation, respectively.

Fig. 2.1

Identical products with independent demands—Approximate or exact solutions vs. sample-based solutions. The terms “exact,” “numerical,” and “approximation” refer to exact solutions, solutions of the sample-based model, and closed-form approximations, respectively

Figure 2.1 shows that my analytical solution is very close to the numerical solution when n = 1. This is obvious as my solution is exact for the single-product case (here, the case $\hat{\eta } = x$ is valid). In the case of a three-product model, the approximation does not work well, which is quite understandable as the approximation is based on the Central Limit Theorem. As the number of products increases, my approximations become more accurate and the gap becomes negligible when n ≥ 10. I also observe that the order quantities decrease as the degree of risk-aversion increases, which confirms Proposition 3; and as the number of products increases, the error of the risk neutral solution decreases (consistent with Proposition 6).

For independent but heterogenous products, I tested the accuracy of the approximations on 30 randomly generated problems, 10 for each number of products n = 3, 10, 30. At each value of κ = 0. 2, 0. 4, 0. 6, 0. 8, 1, I calculated the sample-based LP solution and an approximate solution by the continuation method with ν = 1. My numerical study shows that the continuation method is much more stable and accurate than the iterative method with ν = 1, especially for smaller numbers of products, when the difference between risk-neutral solution and risk-averse solution is larger (e.g., κ is larger). For n = 30, both methods work very well.

For each instance in which the continuation method can generate a feasible solution, I compute the absolute percentage error of the approximate solution relative to the sample-based LP solution, which is defined by the absolute difference between the approximate solution and the sample-based LP solution over the sample-based LP solution. For comparison, I also compute the absolute percentage error of the risk-neutral solution relative to the sample-based LP solution. Then for each value of n and κ, I compute the average and maximum percentage error over all the solutions generated. The average (and maximum) percentage errors of the risk-neutral solutions and of the solutions obtained by the continuation method are displayed in Figs. 2.2 and 2.3, respectively).

Fig. 2.2

Heterogeneous products with independent demands—The average percentage error of the approximate solutions and risk-neutral solutions

Fig. 2.3

Heterogeneous products with independent demands—The maximum percentage error of the approximate solutions and risk-neutral solutions

In all cases, in terms of the average and maximum errors, my approximation outperforms the risk-neutral solution. Furthermore, in most cases, the improvement brought by the approximation is significant. Often, the approximation cuts the error of the risk-neutral solution by 3–6 times, although only one step of the continuation method was made at each κ. Second, I observe that the approximation is quite accurate for all cases of n = 10 and n = 30. However, the approximation does not work well for n = 3, which is similar to what I observed in the identical products case. Finally, I observe that the average and maximum errors of the risk-neutral solutions are decreasing in n, as established in Proposition 6.

8.3 Impact of Dependent Demands Under Risk Aversion

I first consider a simple system with two identical products, then a system with two heterogenous products. The numerical results here are obtained by the sample-based LP.

I choose the following cost parameters for the system with two identical products: ${r}_{1} = {r}_{2} = 15$, ${c}_{1} = {c}_{2} = 10$ and ${s}_{1} = {s}_{2} = 7$. I assume that demand follows bivariate lognormal distribution, which is generated by exponentiating a bivariate normal with the parameters ${\mu }_{1} = {\mu }_{2} = 3$, ${\sigma }_{1} = {\sigma }_{2} = 0.4724$ and a correlation coefficient of $-1,-0.8,-0.6,\ldots ,1$. Thus, the mean and standard deviation of each marginal distribution are 22. 46 and 11. 23 respectively with cv = 0. 5. The numerical results are summarized in Fig. 2.4.

Fig. 2.4

Identical products with dependent demands—The impact of demand correlation and risk aversion κ

Consistent with my analysis in Sect. 2.5, risk aversion reduces optimal order quantities for independent or positively correlated demands, relative to the risk-neutral solution. But interestingly, this observation may not hold for strongly negatively correlated demands, where increased risk aversion can result in a greater optimal order quantity. To explain the intuition behind these counterexamples, let me consider two identical products with perfectly negatively correlated demands, D ₁ and D ₂. A larger order quantity, Q, increases negative correlation between the sales min(D ₁, Q) and min(D ₂, Q), and thus leads to smaller variability of the total sales min(D ₁, Q) + min(D ₂, Q). Choi (2009) also studied a special case of a two-identical product system with bivariate uniform distribution and perfectly negative demand correlation. As a result, a closed-form optimal solution is obtained which is an increasing function of degree of risk aversion.

Figure 2.4 also shows that consistent with my analysis in Sect. 2.7, negatively correlated demands result in higher optimal order quantities than independent demands under risk aversion, while positively correlated demand leads to lower optimal order quantity under risk aversion. Indeed, the impact of demand correlation is almost monotonic with small deviations due to random sample errors.

These observations imply that if the firm is risk-averse, then demand dependence can have a significant impact on its optimal order quantities. They agree with the intuition that stronger positively (negatively) correlated demands indicate higher (lower) risk, and therefore lead to lower (higher) order quantities. More interestingly, while in most cases, the order quantity decreases in the degree of risk aversion, it can increase when the demands are strongly negatively correlated.

For heterogenous products, I consider a simple system with two products and the following parameters: ${r}_{1} = 15,{c}_{1} = 10,{s}_{1} = 7$ and ${r}_{2} = 30,{c}_{2} = 10,{s}_{2} = 4$. The demand is bivariate lognormal generated by exponentiating a bivariate normal with ${\mu }_{1} = {\mu }_{2} = 3$, σ₁ = 0. 4724, σ₂ = 1. 26864 and a correlation coefficient of $-1,-0.8,-0.6,\ldots ,1$. The marginal demand distributions of products 1 and 2 have means 22. 46 and 44. 913, standard deviations 11. 23 and 89. 826, and cv’s 0. 5 and 2, respectively. Intuitively, product 1 is less risky and less profitable than product 2.

My numerical study shows that for product 1, the impact of demand correlation is similar to that for identical products; see Fig. 2.5. For product 2, however, the optimal ordering quantity always decreases in κ but not in correlation, see Fig. 2.6.

Fig. 2.5

Heterogenous products with dependent demands—The impact of demand correlation and risk aversion κ for the product with low risk and low profit

Fig. 2.6

Heterogenous products with dependent demands—The impact of demand correlation and risk aversion κ for the product with high risk and high profit

The implication is that for heterogenous products, the impact of demand correlation under risk aversion can be very different in each product. Specifically, as the firm becomes more risk-averse, it should always order less of the more risky and more profitable products. However, for the less risky and less profitable products, while it should order less when demands are positively correlated, it may order more when demands are strongly negatively correlated.

For more details on the numerical study, see Choi (2009).

9 Conclusions

The multi-product newsvendor problem with coherent measures of risk does not decompose into independent problems, one for each product. The portfolio of products has to be considered as a whole. My analytical results focus on the impact of risk aversion and demand dependence on the optimal order quantities. I analyze the asymptotic behavior of the optimal risk-averse solution. Then I derive (2.30) and (2.36) for general law-invariant coherent measures of risk, which are simple and accurate approximations of the optimal order quantities for a large number of products with independent demands. My numerical study confirms the accuracy of these approximations for the numbers of products as small as 10, and enriches my understanding of the interplay of demand dependence and risk aversion.

It is perhaps appropriate to conclude this paper by comparing the multi-product risk-averse newsvendor problem (2.4) to the risk-averse portfolio optimization problem. In a portfolio problem, one has n assets with random returns ${R}_{1},\ldots ,{R}_{n}$ and the objective is to determine investment quantities ${x}_{1},\ldots ,{x}_{n}$ to obtain desirable characteristics of the total portfolio return $P(x,R) = {R}_{1}{x}_{1} + \cdots + {R}_{n}{x}_{n}$. In the classical mean-variance approach of Markowitz (1959), the mean of the return and its variance are used to find efficient portfolio allocations. See also Elton et al. (2006). In more modern approaches (e.g., Konno and Yamazaki 1991; Miller and Ruszczyński 2008; Ruszczyński and Vanderbei 2003) more general mean–risk models and coherent measures of risk are used, similarly to problem (2.4). There are, however, fundamental structural differences which make the multi-product newsvendor problem significantly different from the financial portfolio problem.

The most important difference is that the portfolio return P(x, R) is linear with respect to the decision vector x, while the newsvendor profit Π(x, D) is concave and nonlinear with respect to the order quantities x. This leads to the following different properties of the problems.

• The risk-neutral portfolio problem has no solution, unless the total amount invested (e.g., to 1) is restricted, in which case the optimal solution is to invest everything in the asset(s) having highest expected returns. On the contrary, the risk-neutral newsvendor problem always has a solution, because of natural limitations of the demand.

• The effect of using risk measures in the portfolio problem is a diversification of the solution, which otherwise would remain completely nondiversified. In the newsvendor problem the use of risk measures results in changes of the already diversified risk-neutral solution, by ordering more of products having less variable or negatively correlated demands and less of products having more variable or positively correlated demands. Products are unlikely to be eliminated because of risk aversion, because very small amounts will almost always be sold and thus they introduce very little risk.

• In the portfolio problem, independently of the number of assets considered, the risk-neutral solution remains structurally different from the risk-averse solution. On the contrary, in the newsvendor problem the risk-neutral solution is asymptotically optimal under risk aversion, when the number of independent products approaches infinity.

Finally, it is worth stressing that the nonlinearity of the newsvendor profit Π(x, D) is the source of formidable technical difficulties in the analysis of the composite function (2.4), which involves two nondifferentiable functions.