Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Maritime industry plays a major role in our life and in the economy of the world. Most of the merchandize and goods like electronics, cars, food, clothes, are transported from producers to end consumers by ship containers from one end of the world to the other end. Over the last decades, shipping industry has experienced a continuous growing both in their fleets and in the total trade volume. As a consequence of this growing, it has been necessary the design of new ships and vessels capable of transporting as much as possible of products. This is the reason why nowadays ships are designed using cutting edge technology in order to find an optimal design looking mainly at economic aspects. For instance, modern container ships hulls feature a bow flare and stern overhang in combination with a flow-optimized geometry below the water line. This design is twofold: at one hand it provides maximum space for container storage and at the other hand it provides a minimal water resistance. However, modern designs of vessels and ships seem to be prone to a phenomenon called parametric roll.

Parametric roll is an undesired phenomenon because it may produce cargo damage, delay or even suspension of the activities performed by the crew, seasickness in passengers and crew and in the limit case it can lead to the capsizing of the ship [13]. It has been suggested (c.f. [5]) that the onset of parametric roll is due to the occurrence of the following conditions: the ship is sailing in head seas, the natural period of roll is approximately twice the wave encounter period, the roll damping is low, the wave height exceeds a critical level and the wavelength is close to the ship length.

Probably, the earliest studies about this phenomenon are due to William Froude (1810–1879), who in 1857 started a serious research in order to find the causes and conditions that lead to parametric roll resonance. It was the time when the Great Eastern, a ship that was so big in comparison with the size of any other ship, was under construction. The designer, I. K. Brunel was concerned because he thought that the ship could behave in an unexpected manner. Brunel then asked Froude to start a theoretical study on parametric roll. One of Froude’s early discoveries was that the roll angle can increase rapidly when the period of the ship is in resonance with the period of wave encounter. He also came to the conclusion that the roll motion is not produced by the waves hitting the side of the hull, but rather because of the pressure of the waves acting on the hull. Although Froude made several simplifications in his analysis because of the intractable mathematics, his research ended with a theory of rolling in waves and its stabilization by the introduction of bilge keels (c.f. [3, 13], and the references therein).

Because modern ships still experience dangerous roll motions, it continues being a hot topic not only in the research field but also in the maritime industry. We mention two incidents, where millions of dollars were lost. In 1998, a post-Panamax C11 class container was caught by a violent storm and experienced parametric roll with roll angles close to 40 ∘ . As a consequence one-third of the on-deck containers were lost overboard and a similar amount were severely damaged [5]. More recently, in January 2003, another Panamax container vessel encountered a storm in the North Atlantic. It was reported that the ship experienced violent rolling with angles close to 47 ∘ . As a result, 133 containers were lost overboard and other 50 presented severe damage [4].

So far, several models of different sophistication have been proposed by the researchers in order to analyze the dynamical behavior of a ship in a seaway. In particular, there are models that have been developed for the study of parametric roll, for instance, we mention the simplified nonlinear models presented in [12, 8], where three DOF are considered (heave, pitch, and roll). Furthermore, some authors have derived their models by using an analogy of the ship motions to a mechanical system [16, 10]. Besides the development of models there is the issue of finding stabilization techniques in order to cope with parametric roll phenomenon. Hence, in the literature we can find different stabilization techniques as for example, the use of bilge keels [10], passive and active U-tanks [1, 7], rudders [2] and fins stabilizers [6].

In this work, we present an experimental study of parametric roll occurring in a container ship. As a “towing tank” we use an electro-mechanical platform consisting of two (controllable) mass-spring-damper oscillators mounted on an elastically supported (controllable) beam. The stiffness and damping in the system have been identified experimentally and the state vector is reconstructed by using the position measurements. Then, via computer controlled feedback, the dynamical properties of the system are modified by canceling the inherent dynamics of the setup and enforcing the dynamics of a 3-DOF (heave, pitch, and roll) container ship. The heave and pitch motions are represented by the displacement of the oscillators and the supporting beam is used to mimic the roll motion. Additionally, the experimental setup is masked with the dynamics of a mechanical system consisting of two masses restrained by elastic springs and supporting two identical pendula. Such model was developed to simulate heave-pitch-roll motion of a ship in longitudinal waves.

At the end of the day, we want to show that our experimental setup is suitable for the experimental analysis of parametric roll and that can facilitate the understanding of ship dynamics. Actually, we want to show that the setup can be seen as a testbed for controllers ad hoc designed to stabilize the roll motion.

The rest of the manuscript is organized as follows. In Sect. 14.2 we describe in detail the experimental setup. Then, in Sect. 14.3 we present experimental results related to the onset and stabilization of parametric roll in a container ship. Next, in Sect. 14.4 we conduct an experimental analysis of the dynamics corresponding to a mechanical system developed to simulate the most general case of heave-pitch-roll motion in a vessel. Finally, in Sect. 14.5 we draw some conclusions.

2 The Experimental Setup

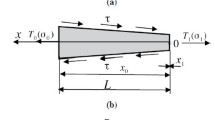
In this section, we describe the electro-mechanical device depicted in Fig. 14.1 which has been used for the experiments. It consists of two oscillators mounted on an elastically supported beam. The system has three DOF corresponding to the axial displacement of the oscillators and the beam. Moreover, each DOF is equipped with a voice coil actuator and with a linear variable differential transformer position sensor. The maximum stroke of the oscillators and the beam is approximately 6 mm. and the position sensors are calibrated such that 1 [V] = 5 [mm]. In the other hand, the actuators have a limited input of ± 0.42 [V].

Fig. 14.1
figure 1

Photo of the experimental setup at Eindhoven University of Technology

Full size image

The experimental setup is schematically depicted in Fig. 14.2. The masses corresponding to the oscillators are given by m i ∈ ℝ  +  (i = 1, 2) and the mass of the supporting beam is denoted by m 3 ∈ ℝ  + . This mass may be varied by a factor 10. The stiffness and damping characteristics present in the system are assumed to be linear with constants coefficients κi,βi ∈ ℝ  +  respectively. However, the experimental setup allows modeling of different types of springs (for instance, linear or cubic) and any other desired effect within the physical limitations of the setup. The electric actuator force for subsystem i (i = 1…3) is denoted as u i. Finally, x i ∈ ℝ (i = 1, 2, 3) are the displacements of the oscillators and the supporting beam respectively. Using Newton’s 2nd law, it follows that the idealized – i.e. assuming that no friction is present – equations of motion of the system of Fig. 14.2 are

$$ \begin{array}{rcl}{ m}_{1}\ddot{{x}}_{1}& =& -{\kappa }_{1}({x}_{1} - {x}_{3}) - {\beta }_{1}(\dot{{x}}_{1} -\dot{ {x}}_{3}) + {u}_{1}, \\ {m}_{2}\ddot{{x}}_{2}& =& -{\kappa }_{2}({x}_{2} - {x}_{3}) - {\beta }_{2}(\dot{{x}}_{2} -\dot{ {x}}_{3}) + {u}_{2}, \\ {m}_{3}\ddot{{x}}_{3}& =& {\sum \nolimits }_{i=1}^{2}\left [{\kappa }_{ i}({x}_{i} - {x}_{3}) + {\beta }_{i}(\dot{{x}}_{i} -\dot{ {x}}_{3}) - {u}_{i}\right ] - {\kappa }_{3}{x}_{3} - {\beta }_{3}\dot{{x}}_{3} + {u}_{3}. \\ \end{array} $$
(14.1)

For convenience, system (14.1) is written in the following manner

$$ \begin{array}{rcl} \ddot{{x}}_{1}& =& -{\omega }_{1}^{2}({x}_{ 1} - {x}_{3}) - 2{\zeta }_{1}{\omega }_{1}(\dot{{x}}_{1} -\dot{ {x}}_{3}) + \frac{1} {{m}_{1}}{u}_{1}, \\ \ddot{{x}}_{2}& =& -{\omega }_{2}^{2}({x}_{ 2} - {x}_{3}) - 2{\zeta }_{2}{\omega }_{2}(\dot{{x}}_{2} -\dot{ {x}}_{3}) + \frac{1} {{m}_{2}}{u}_{2}, \\ \ddot{{x}}_{3}& =& {\sum \nolimits }_{i=1}^{2}{\mu }_{ i}\left [{\omega }_{i}^{2}({x}_{ i} - {x}_{3}) + 2{\zeta }_{i}{\omega }_{i}(\dot{{x}}_{i} -\dot{ {x}}_{3}) - \frac{1} {{m}_{i}}{u}_{i}\right ] - {\omega }_{3}^{2}{x}_{ 3} - 2{\zeta }_{3}{\omega }_{3}\dot{{x}}_{3} + \frac{1} {{m}_{3}}{u}_{3}, \\ & &\\ \end{array} $$
(14.2)

where \({\omega }_{i} = \sqrt{ \frac{{\kappa }_{i } } {{m}_{i}}}\) [rad s − 1], \({\zeta }_{i} = \frac{{\beta }_{i}} {2{\omega }_{i}{m}_{i}}\) [ − ] are the angular eigenfrequency and dimensionless damping coefficient present in subsystem i (i = 1, 2, 3), the coupling strength is denoted by \({\mu }_{i} = \frac{{m}_{i}} {{m}_{3}}\) (i = 1, 2). After a suitable parametric identification of model (14.2) the parameters presented in Table 14.1 were obtained (see [14]).

Fig. 14.2
figure 2

Schematic model of the setup

Full size image
Table 14.1 Parameters values for the experimental setup according to model (14.2)
Full size table

The potential of this experimental setup to perform experiments on several dynamical systems relies on the fact that the properties of the system can be adjusted or modified by a suitable design of the control inputs u i. These inputs are generated as follows: a data acquisition system reads data from the sensors and forwards the converted data to a computer. In the computer the state vector is reconstructed by an observer [15] and the reconstructed state vector is used to construct the new desired dynamics. With this data, the output u i is generated, it consists of a feed forward part (to cancel the original dynamics) plus compensation terms plus the desired dynamics. Then, it is clear that by means of state feedback, the original dynamics are masked with the dynamics that we want. For example, in [14] the setup is used for experimentally testing synchronization of coupled oscillators.

By means of two experiments we show the capabilities of the experimental setup to conduct experiments on parametric roll. As a first example we implement the dynamics of a 3-DOF nonlinear container ship model navigating in head seas and as a second example the dynamics of a mechanical model for simulating heave-pitch-roll motion of a ship in longitudinal waves.

In both cases, a controller is implemented in order to stabilize the parametric roll resonance condition. Since the experimental setup is fully actuated, the choice of the controller is arbitrary and therefore many controllers can be implemented and tested in the setup.

3 Case 1: A High-Fidelity 3-DOF Nonlinear Container Ship Model

A ship can be seen as a rigid body that can be modeled as a 6-DOF system. Three of these DOF, named surge, sway, and yaw, correspond to unrestored motions in the horizontal plane while the other three DOF named heave, pitch, and roll, correspond to oscillating motions in the vertical plane. However, some simplifications can be done in the model, depending on the desired analysis. For instance, for the study of parametric roll, some authors [8, 17, 12, 9] agree in the fact that a 3rd order model (considering heave, pitch, and roll) is enough to study the phenomenon, since the restoring forces that may produce resonance on the ship roll motion only act when the ship is subjected to motions in the vertical plane.

In this section, the dynamical behavior of the experimental setup presented in the previous section is modified in order to mimic the dynamics of a nonlinear container ship model developed in [8]. Additionally, we implement a control strategy for the stabilization of the roll motion. Such control law is presented in [6] and is based in a combined speed and fin stabilizer control.

3.1 The Model and Its Implementation in the Setup

Consider the following nonlinear container ship model

$$\begin{array}{rcl} \ddot{s} = {(M + A)}^{-1}\left ({c}_{\mathrm{ ext}}(\zeta, \dot{\zeta },\ddot{\zeta }) - B(\dot{\phi })\dot{s} - {c}_{\mathrm{res}}(s,\zeta )\right ),& &\end{array}$$
(14.3)

where

$$\begin{array}{rcl} s(t) ={ \left [z(t)\ \ \phi (t)\ \ \theta (t)\right ]}^{\mathrm{T}}& &\end{array}$$
(14.4)

is the generalized vector which contains the three restoring degrees of freedom, heave, roll, and pitch, respectively. M ∈ ℝ 3 ×3 is the generalized mass matrix, A ∈ ℝ 3 ×3 describes the hydrodynamic added mass matrix and B ∈ ℝ 3 ×3 represents the hydrodynamic damping matrix. c res ∈ ℝ 3 ×1 contains the nonlinear restoring forces and moments dependent on the relative motions between ship hull and wave elevation ζ(t). Finally, the generalized vector c ext ∈ ℝ 3 ×1 contains the external forces exerted by the waves. These forces are depending on weave heading, encounter frequency, wave amplitude, and time. For the derivation of the model, as well as for definitions and expressions for M, A, B, c res, and c ext, the reader is referred to [8, 12].

Indeed, system (14.3) has the following structure

$$\begin{array}{rcl} \left [\begin{array}{c} \ddot{z}\\ \ddot{\phi } \\ \ddot{\theta } \end{array} \right ] ={ \left [\begin{array}{ccc} {a}_{11} & {a}_{12} & {a}_{13} \\ {a}_{21} & {a}_{22} & {a}_{23} \\ {a}_{31} & {a}_{32} & {a}_{33} \end{array} \right ]}_{{(M+A)}^{-1}}\left ({\left [\begin{array}{c} {c}_{\mathrm{ext}z} \\ {c}_{\mathrm{ext}\phi } \\ {c}_{\mathrm{ext}\theta } \end{array} \right ]}_{{c}_{\mathrm{ext}}(\zeta, \dot{\zeta },\ddot{\zeta })} -{\left [\begin{array}{c} {c}_{\mathrm{res}z} \\ {c}_{\mathrm{res}\phi } \\ {c}_{\mathrm{res}\theta } \end{array} \right ]}_{{c}_{\mathrm{res}}(z,\phi, \theta, \zeta )}\right ) -{\left [\begin{array}{ccc} {c}_{11} & {c}_{12} & {c}_{13} \\ {c}_{21} & {c}_{22} & {c}_{23} \\ {c}_{31} & {c}_{32} & {c}_{33} \end{array} \right ]}_{{(M+A)}^{-1}B}\left [\begin{array}{c} \dot{z}\\ \dot{\phi } \\ \dot{\theta } \end{array} \right ].\qquad & &\end{array}$$
(14.5)

For convenience, we rewrite (14.5) as

$$\begin{array}{rcl} \ddot{z}& =& {F}_{z}(z,\phi, \theta, \zeta, \dot{\zeta },\ddot{\zeta }) - {c}_{11}\dot{z} - {c}_{12}\dot{\phi } - {c}_{13}\dot{\theta },\end{array}$$
(14.6)
$$\begin{array}{rcl} \ddot{\phi }& =& {F}_{\phi }(z,\phi, \theta, \zeta, \dot{\zeta },\ddot{\zeta }) - {c}_{21}\dot{z} - {c}_{22}\dot{\phi } - {c}_{23}\dot{\theta },\end{array}$$
(14.7)
$$\begin{array}{rcl} \ddot{\theta }& =& {F}_{\theta }(z,\phi, \theta, \zeta, \dot{\zeta },\ddot{\zeta }) - {c}_{31}\dot{z} - {c}_{32}\dot{\phi } - {c}_{33}\dot{\theta },\end{array}$$
(14.8)

where \({F}_{z}(\cdot ) = {a}_{11}{c}_{\mathrm{ext}z} + {a}_{12}{c}_{\mathrm{ext}\phi } + {a}_{13}{c}_{\mathrm{ext}\theta } - {a}_{11}{c}_{\mathrm{res}z} - {a}_{12}{c}_{\mathrm{res}\phi } - {a}_{13}{c}_{\mathrm{res}\theta }\). Expressions for F ϕ and F θ can be derived from (14.5).

As we mention before, the experimental setup not only allows for the implementation of other dynamics (like the dynamics of a ship) but also a wide variety of controllers can be implemented and validated within the physical limits of the setup. Hence, a controller is incorporated in order to stabilize the parametric roll resonance condition occurring in system (14.6)–(14.8).

For the time being, we use the controller presented in [6]. This controller has two objectives: to avoid that the encounter frequency approaches twice the roll natural frequency ωϕ, and to increase the damping in roll.

Since in deep water, the encounter frequency (c.f. [11]) is given by

$$\begin{array}{rcl}{ \omega }_{e} = \omega -\frac{{\omega }^{2}} {g} U\cos (\mu ),& &\end{array}$$
(14.9)

where ω is the wave frequency, U is the forward velocity of the ship and μ is the heading angle. Then, it is clear that the first objective is achieved by varying the forward velocity of the vessel. Different to [6], we do not generate the velocity in a dynamical way; rather we consider that the velocity is given by a setpoint that can be increased/decreased with a prescribed acceleration/deceleration rate. The setpoint is changed whenever the roll angle achieves a certain threshold. In this way, we do not need to increase the model to a 4th order model.

The second objective is achieved by including fin stabilizers. The hydraulic machinery, that generates the fin-induced roll moment τϕ is modeled as follows (see [6])

$$\begin{array}{rcl} \dot{{\tau }}_{\phi } = \frac{1} {{t}_{\mathrm{r}}}{\tau }_{\max }\mbox{ sat}\left (\frac{{\tau }_{\mathrm{c}}} {{\tau }_{\max }} \right ) - \frac{1} {{t}_{\mathrm{r}}}{\tau }_{\phi },& &\end{array}$$
(14.10)

where τmax is the maximum moment that can be provided by the fins, τc is the moment generated by the controller and is given in [6]. The time constant t r corresponds to the time constant of the hydraulic machinery.

Consequently, it follows from (14.6)–(14.8) and (14.10) that the simplified nonlinear ship container model with fin stabilizer control is given by

$$\begin{array}{rcl} \ddot{z}& =& {F}_{z}(z,\phi, \theta, \zeta, \dot{\zeta },\ddot{\zeta }) - {c}_{11}\dot{z} - {c}_{12}\dot{\phi } - {c}_{13}\dot{\theta },\end{array}$$
(14.11)
$$\begin{array}{rcl} \ddot{\phi }& =& {F}_{\phi }(z,\phi, \theta, \zeta, \dot{\zeta },\ddot{\zeta }) + {\tau }_{\phi } - {c}_{21}\dot{z} - {c}_{22}\dot{\phi } - {c}_{23}\dot{\theta },\end{array}$$
(14.12)
$$\begin{array}{rcl} \ddot{\theta }& =& {F}_{\theta }(z,\phi, \theta, \zeta, \dot{\zeta },\ddot{\zeta }) - {c}_{31}\dot{z} - {c}_{32}\dot{\phi } - {c}_{33}\dot{\theta }. \end{array}$$
(14.13)

The experimental setup depicted in Fig. 14.1 can be adjusted to mimic the container ship dynamics (14.11)–(14.13). First, we make an analogy between the electro-mechanical experimental setup and the heave, roll, and pitch motion of the ship. In other experiments (related with synchronization), we have found that under some circumstances, the oscillators can be in an oscillating state while the beam is at rest. Therefore, the following choice seems to be logic: displacement of oscillator 1 will correspond to heave displacement, displacement of oscillator 2 will represent the rotation angle in pitch and the supporting beam will denote the rotation angle in roll.

Next, the virtual coordinate system s = z ϕ θT is obtained by choosing the appropriate coordinate transformation. Since in the experimental setup all the displacements are translational, the coordinate transformation should be chosen such that translational displacements are mapped to rotation angles. Then, we write:

$$\begin{array}{rcl} \left [\begin{array}{c} z\\ \phi \\ \theta \end{array} \right ] = \left [\begin{array}{ccc} \frac{1} {{x}_{1}^{{_\ast}}} & 0 & 0 \\ 0 & 0 & \frac{{\gamma }_{1}} {{x}_{3}^{{_\ast}}} \\ 0 & \frac{{\gamma }_{2}} {{x}_{2}^{{_\ast}}} & 0 \end{array} \right ]\left [\begin{array}{c} {x}_{1} \\ {x}_{2} \\ {x}_{3}\end{array} \right ],& &\end{array}$$
(14.14)

where x i  ∗ , i = 1, 2, are the maximal displacements of the oscillators and x 3  ∗  is the maximal displacement of the supporting beam. In the sequel, these values are taken to be \({x}_{1}^{{_\ast}} = {x}_{2}^{{_\ast}} = {x}_{3}^{{_\ast}} = 5\) [mm]. This mapping assures rotation angles of ± γi [rad].

In order to complete the adjustment of the experimental setup we choose the actuator forces as follows

$$\begin{array}{rcl}{ u}_{1}& =& {m}_{1}\left ({\omega }_{1}^{2}\Delta {x}_{ 1} + 2{\zeta }_{1}{\omega }_{1}\dot{\Delta }{x}_{1} + {F}_{z}(\cdot ) - {c}_{11}\dot{z} - {c}_{12}\dot{\phi } - {c}_{13}\dot{\theta }\right ),\end{array}$$
(14.15)
$$\begin{array}{rcl}{u}_{2}& =& {m}_{2}\left ({\omega }_{2}^{2}\Delta {x}_{ 2} + 2{\zeta }_{2}{\omega }_{2}\dot{\Delta }{x}_{2} + {F}_{\theta }(\cdot ) - {c}_{31}\dot{z} - {c}_{32}\dot{\phi } - {c}_{33}\dot{\theta }\right ),\end{array}$$
(14.16)
$$\begin{array}{rcl}{u}_{3}& =& {m}_{3}\left ({\omega }_{3}^{2}{x}_{ 3} - 2{\zeta }_{3}{\omega }_{3}\dot{{x}}_{3} + {\mu }_{1}\left ({F}_{z}(\cdot ) - {c}_{11}\dot{z} - {c}_{12}\dot{\phi } - {c}_{13}\dot{\theta }\right )\right. \\ & & +{\mu }_{2}\left ({F}_{\theta }(\cdot ) - {c}_{31}\dot{z} - {c}_{32}\dot{\phi } - {c}_{33}\dot{\theta }\right ) + {F}_{\phi }(\cdot ) \\ & & \left.+{\tau }_{\phi } - {c}_{21}\dot{z} - {c}_{22}\dot{\phi } - {c}_{23}\dot{\theta }\right ), \end{array}$$
(14.17)

where \(\Delta {x}_{i} = ({x}_{i} - {x}_{3})\), \(\dot{\Delta }{x}_{i} = (\dot{{x}}_{i} -\dot{ {x}}_{3})\).

In closed loop, the dynamics of system (14.2) with controllers (14.15)–(14.17) coincides with dynamics (14.11)–(14.13). Therefore, the electro-mechanical experimental setup has been “converted” into a container ship.

3.2 Experimental and Numerical Analysis

In order to demonstrate that the experimental setup can actually mimic the dynamical behavior of a ship, in particular the onset and stabilization of parametric roll, we present two experiments: one corresponding to the uncontrolled case, where oscillations in roll appear and the other one corresponding to the controlled case, where parametric roll is stabilized. Indeed, the second experiment shows the capability of the setup to test and validate controllers that have been designed to cope with the problem of parametric roll.

For the first experiment, we consider system (14.11)–(14.13) with parameters listed in [8]. Such parameters correspond with a 1 : 45 scale model ship. Furthermore, the following experimental conditions are assumed: wave amplitude A ω = 2. 5 [m], wave frequency ω = 0. 4640 [rad/s], encounter angle μ = 180 ∘ , and encounter frequency, w e = 0. 5842 [rad/s]. For this experiment the forward velocity of the ship is taken to be 5. 4806 [m/s]. Note that the forward velocity of the ship is directly related with the surge motion of the ship and therefore it cannot be related to the velocity of the experimental setup, where heave, pitch, and roll motions are being reproduced by the oscillators and the beam respectively. In this analysis, the forward velocity is considered as a control parameter given by a setpoint implemented in software and its changes are reflected in adjustments in the value of the encounter frequency (see (14.9)). Ultimately, this is reflected in changes in the dynamical behavior of system (14.11)–(14.13).

The initial conditions for the oscillators and the beam are as follows: x 1(0) = 125 [μm], x 2(0) = 0, x 3(0) = 58. 178 [μm], \(\dot{{x}}_{1} =\dot{ {x}}_{2} =\dot{ {x}}_{3} = 0\). These initial conditions are related to the initial conditions of system (14.11)–(14.13) by means of (14.14). In this experiment, we want to investigate the onset of parametric roll, therefore the control input τϕ in (14.12) is taken to be zero.

Figure 14.3 shows the experimental (solid line) and numerical (dotted line) results corresponding to heave, roll, and pitch. The onset of parametric roll becomes immediately clear from the graph in the middle of Fig. 14.3 and after 400 s it stabilizes with an amplitude of ± 15 ∘ . The figure also reveals that the experimental results are in fair agreement with the simulation results. Indeed, in steady-state it is hard to distinguish the difference.

Fig. 14.3
figure 3

Onset of parametric roll. Solid line: experiment, dotted line: simulation

Full size image

In a second experiment, we implement controller (14.10) in order to stabilize parametric roll. All the initial conditions and parameters are as in experiment one. The controller is activated when the rotational angle in roll achieves a threshold angle of 10 ∘ . Furthermore, when controller (14.10) is activated, the forward velocity of the vessel is increased 35% with an acceleration rate of 0. 04 [m/s2]. This increment in the forward velocity is also reflected in the value of the encounter frequency, which is also increased from 0. 5842 [rad/s] to 0. 6263 [rad/s]. In the same way, the value of the external wave forces and the values of the entries of the added mass matrix and hydrodynamic damping matrix are updated. In our experiment, the hydraulic machinery has been implemented in software and we have considered a time constant t r = 1 [msec] since the data acquisition system of the setup has a maximum sampling period of 1 [msec].

Initially, the controller is switched-off, but when the rotation angle in roll reaches the threshold value ϕ = 10 ∘ , the controller is switched-on and after the transient, the oscillations in roll are “quenched” as depicted in Fig. 14.4.

Fig. 14.4
figure 4

Experimental result. Parametric roll is stabilized

Full size image

For the mapping (14.14) we have used γ1 = 0. 035 [rad], which assures a maximal rotation in pitch of θ =  ± 2 ∘  and γ2 = 0. 3 [rad], which yields a maximal rotation in roll of ϕ =  ± 17 ∘ . This mapping not only allows to convert translational displacements to rotational angles but also yields the signals in a range that is suitable for the experimental setup as can be seen in Fig. 14.5, where the inputs u i (see equations (14.15)–(14.17)) are depicted. From this figure it is evident that the inputs of the actuators are far from saturation, since the maximum voltage input allowed by the actuators is ± 0. 42 [V].

Fig. 14.5
figure 5

Control inputs u i sent to the experimental setup

Full size image

4 Case 2: Mechanical Model for Simulating Heave-Pitch-Roll Motions

In this section, we investigate the onset of parametric roll by using the mechanical model depicted in Fig. 14.6, which has been developed to simulate heave-pitch-roll motions of a ship in longitudinal waves and it has been presented in [17]. As in the previous case, we present experiments related to the uncontrolled and controlled situations.

Fig. 14.6
figure 6

Mechanical model for simulating heave-pitch-roll motion

Full size image

4.1 The Model and Its Implementation in the Setup

Consider the mechanical system depicted in Fig. 14.6. It consists of two masses restrained by elastic springs and supporting two equal pendulums rigidly connected by means of a weightless rod. Each mass is externally excited by a harmonic force. These external forces have the same amplitude and frequency but there is a phase lag between them. This phase shift is to include the delayed effects of the wave propagating along the ship. This model was developed to simulate the heave-pitch-roll motion of a ship in longitudinal waves. For more details about the model, the reader is referred to [17].

The equations of motion for the system of Fig. 14.6 are:

$$\begin{array}{rcl} & & \left ({m}_{1} + m\right )\left (\ddot{{z}_{1}} - \alpha {\omega }^{2}\cos \omega \mbox{ t}\right ) + {d}_{ 1}\dot{{z}}_{1} + {k}_{1}{z}_{1} + ml\left (\ddot{\varphi }\sin \varphi +\dot{ {\varphi }}^{2}\cos \varphi \right ) = 0,\end{array}$$
(14.18)
$$\begin{array}{rcl} \left ({m}_{2} + m\right )\left (\ddot{{z}}_{2} - \alpha {\omega }^{2}\cos (\omega \mbox{ t} - \psi )\right ) + {d}_{ 2}\dot{{z}}_{2} + {k}_{2}{z}_{2} + ml\left (\ddot{\varphi }\sin \varphi +\dot{ {\varphi }}^{2}\cos \varphi \right ) = 0,\end{array}$$
(14.19)
$$\begin{array}{rcl}\frac{1} {2}ml\left (\ddot{{z}}_{1} - \alpha {\omega }^{2}\cos \omega \mbox{ t} +\ddot{ {z}}_{ 2} - \alpha {\omega }^{2}\cos (\omega \mbox{ t} - \psi )\right )\sin \varphi \\ & & \qquad \quad + m{l}^{2}\ddot{\varphi } + c\dot{\varphi } + mgl\sin \varphi = {\tau }_{\mathrm{ p}}, \end{array}$$
(14.20)

where τp is an external torque for the pendula. By defining the new time variable \(\tau = \sqrt{\frac{g} {l}} \mbox{ t}\), system (14.18)–(14.20) is rewritten in the following dimensionless form (see [17])

$$\begin{array}{rcl}{ \omega }_{1}^{\prime\prime} + {\kappa }_{ 1}{\omega }_{1}^{\prime} + {q}_{ 1}^{2}{\omega }_{ 1} + {\mu }_{m1}\left ({\varphi }^{\prime\prime}\sin \varphi + {\varphi }^{\prime 2}\cos \varphi \right ) = a{\eta }^{2}\cos \eta \tau, & &\end{array}$$
(14.21)
$$\begin{array}{rcl}{ \omega }_{2}^{\prime\prime} + {\kappa }_{ 2}{\omega }_{2}^{\prime} + {q}_{ 2}^{2}{\omega }_{ 2} + {\mu }_{m2}\left ({\varphi }^{\prime\prime}\sin \varphi + {\varphi }^{\prime 2}\cos \varphi \right ) = a{\eta }^{2}\cos (\eta \tau - \psi ),\ \ \ \;& &\end{array}$$
(14.22)
$$\begin{array}{rcl} \frac{1} {2}\left [{\omega }_{1}^{\prime\prime} - a{\eta }^{2}\cos \eta \tau + {\omega }_{ 2}^{\prime\prime} - a{\eta }^{2}\cos (\eta \tau - \psi )\right ]\sin \varphi + {\varphi }^{\prime\prime} + {\kappa }_{ 0}{\varphi }^{\prime} +\sin \varphi = {\tau }_{ \varphi },& & \\ & &\end{array}$$
(14.23)

where \({\omega }_{i} = \frac{{z}_{i}} {l}\), \({\kappa }_{i} = \frac{{d}_{i}} {{\omega }_{0}\left ({m}_{i}+m\right )}\), \({q}_{i}^{2} = \frac{{k}_{i}} {{\omega }_{0}^{2}\left ({m}_{i}+m\right )}\), \({\mu }_{mi} = \frac{m} {\left ({m}_{i}+m\right )}\) for i = 1, 2 and \({\omega }_{0} = \sqrt{\frac{g} {l}}\), \({\kappa }_{0} = \frac{c} {{\omega }_{0}m{l}^{2}}\), \(\eta = \frac{\omega } {{\omega }_{0}}\), \(a = \frac{\alpha } {l}\) and \({\tau }_{\varphi } = \frac{{\tau }_{\mathrm{p}}} {m{l}^{2}{\omega }_{0}^{2}}\).

It can be shown that this system (with τφ = 0) has a steady-state solution which has the property \({\sum \nolimits }_{i=1}^{2}[{\omega }_{i}^{2} +\dot{ {\omega }}_{i}^{2}]\neq 0\), \(\varphi =\dot{ \varphi } = 0\). This solution can become unstable in certain intervals of the frequency of excitation, denoted as ω in (14.18)–(14.20). When the solution becomes unstable, parametric roll resonance will appear (φ≠0).

For the case where parametric roll resonance appears, it is necessary to stabilize it. Then, we derive a controller by following the derivations presented in [6]. This controller is designed by using backstepping. Note however that, at this stage, we can adopt any controller for the experimental setup to be tested.

For the design of the control, we use the uncoupled equation for roll ((14.23) with \({\omega }_{1}^{\prime\prime} = {\omega }_{2}^{\prime\prime} = 0\)) and it follows that the control model verifies:

$$\begin{array}{rcl} & {\varphi }^{\prime\prime} + {\kappa }_{0}{\varphi }^{\prime\prime} +\sin \varphi + \frac{1} {2}\left [-a{\eta }^{2}\cos \eta \tau - a{\eta }^{2}\cos (\eta \tau - \psi )\right ]\sin \varphi = {\tau }_{ \varphi },\end{array}$$
(14.24)
$$\begin{array}{rcl}\dot{{\tau }}_{\varphi } + \frac{1} {{t}_{\mathrm{r}}}{\tau }_{\varphi } = \frac{1} {{t}_{\mathrm{r}}}{\tau }_{\max }\mbox{ sat}\left (\frac{{\tau }_{\mathrm{c}}} {{\tau }_{\max }} \right ), &\end{array}$$
(14.25)

where t r is a time constant that coincides with the sampling period of the data acquisition system of the experimental setup (1 msec), τmax is the maximum input that can be delivered to the system and τc verifies

$$\begin{array}{rcl}{ \tau }_{\mathrm{c}} = -{Q}_{3}{z}_{2} - {Q}_{2}{z}_{1} - {\kappa }_{0}{Q}_{1}\varphi +\sin \varphi + {Q}_{1}^{2}\varphi - {Q}_{ 2}\dot{{z}}_{1}{t}_{\mathrm{r}},& &\end{array}$$
(14.26)

where \({z}_{1} =\dot{ \varphi } + {Q}_{1}\varphi \), \({z}_{2} = {\tau }_{\varphi } + {Q}_{2}{z}_{1} + {\kappa }_{0}{Q}_{1}\varphi -\sin \varphi - {Q}_{1}^{2}\varphi \), Q 1 > 0, \({Q}_{2} > ({Q}_{1} + 2\gamma - {\kappa }_{0}\)), \(\gamma = \frac{a{\eta }^{2}} {2}\), Q 3 > 0.

After the derivation of the controller, the system (14.21)–(14.23) with controller (14.25) is implemented in the experimental setup of Fig. 14.1. The analogy between system of Fig. 14.6 and the setup of Fig. 14.1 is as follows: the vertical displacement corresponding to mass 1 is represented by oscillator 1, the vertical displacement of mass 2 is represented by oscillator 2 and the rotation angle of pendula is represented by the supporting beam.

The next step is to obtain the virtual coordinate system \(s :={ \left [\begin{array}{ccc} {\omega }_{1} & {\omega }_{2} & \varphi \end{array} \right ]}^{\mathrm{T}}\). Then, we use the transformation

$$\begin{array}{rcl} \left [\begin{array}{c} {\omega }_{1} \\ {\omega }_{2} \\ \varphi \end{array} \right ] = \left [\begin{array}{ccc} \frac{{\epsilon }_{1}} {{x}_{1}^{{_\ast}}} & 0 & 0 \\ 0 & \frac{{\epsilon }_{2}} {{x}_{2}^{{_\ast}}} & 0 \\ 0 & 0 & \frac{\alpha } {{x}_{3}^{{_\ast}}} \end{array} \right ]\left [\begin{array}{c} {x}_{1} \\ {x}_{2} \\ {x}_{3}\end{array} \right ],& &\end{array}$$
(14.27)

where x i  ∗  has the same meaning as in (14.14). With this transformation, the translational displacement of the supporting beam is mapped to rotation angle and assures angles in roll of ± α [rad]. The constants εi > 0 are scaling factors used in order to leave the signal corresponding to the vertical displacement of mass i between suitable ranges for the setup.

The adjustment continues by defining the actuator forces of the setup as follows:

$$\begin{array}{rcl}{ u}_{1}& =& {m}_{1}\left ({\omega }_{1}^{2}\Delta {x}_{ 1} + 2{\zeta }_{1}{\omega }_{1}\dot{\Delta }{x}_{1} + {\omega }_{1}^{\prime\prime}\right ),\end{array}$$
(14.28)
$$\begin{array}{rcl}{u}_{2}& =& {m}_{2}\left ({\omega }_{2}^{2}\Delta {x}_{ 2} + 2{\zeta }_{2}{\omega }_{2}\dot{\Delta }{x}_{2} + {\omega }_{2}^{\prime\prime}\right ),\end{array}$$
(14.29)
$$\begin{array}{rcl}{u}_{3}& =& {m}_{3}\left ({\omega }_{3}^{2}{x}_{ 3} + 2{\zeta }_{3}{\omega }_{3}\dot{{x}}_{3} + {\mu }_{1}{\omega }_{1}^{\prime\prime} + {\mu }_{ 2}{\omega }_{2}^{\prime\prime} + {\varphi }^{\prime\prime}\right )\end{array}$$
(14.30)

with ωi ′, i = 1, 2 and φ′ as given in (14.21)–(14.23). It is clear that the closed-loop dynamics of the experimental setup coincides with the dimensionless dynamics of the mechanical system depicted in Fig. 14.6.

4.2 Experimental and Simulation Results

Some experimental results are provided in order to show the capability of the experimental setup to mimic the dynamics of the mechanical model of Fig. 14.6 used to simulate the heave-pitch-roll motion of a ship. The onset of parametric roll is analyzed for the controlled and uncontrolled situations. We also analyze the effect in the roll motion when the mass of the pendula (corresponding to the mass of the supporting beam) is varied.

For the experiments, we consider model (14.21)–(14.23) with the following parameters: m = 8. 1 [kg], \({m}_{1} = {m}_{2} = 0.210\) [kg], l = 9. 81 [m], α = 0. 5689 [-], \(\psi = \frac{\pi } {8}\) [rad], g = 9. 81 [m/s2], \({k}_{1} = {k}_{2} = 8.0698\) [N/s] \({d}_{1} = {d}_{2} = 67.06\) [Ns/m], c = 60 [Nms/rad], ω = 2 [rad/s].

In the first experiment, we investigate the occurrence of parametric roll resonance. The initial conditions for the oscillators and the beam are as follows: x 1(0) = 0. 0011 [m], x 2(0) = 0. 001 [m], x 3(0) = 0. 00001 [m], \(\dot{{x}}_{1}(0) =\dot{ {x}}_{2}(0) =\dot{ {x}}_{3}(0) = 0\). These initial conditions are related with the initial conditions of system (14.21)–(14.23) by means of (14.27). In this experiment, parametric roll is not stabilized, hence we consider τφ = 0 in (14.23).

Figure 14.7 shows the time series for heave, pitch, and roll. The oscillations in roll are slowly increasing until certain steady-state value (approximately 30 ∘ ) as becomes evident from the graph at the bottom of the figure. The behavior in heave and pitch motions is as expected, since the masses are excited with the same amplitude and frequency but with a phase lag of \(\frac{\pi } {8}\) [rad]. However, the phase difference is a bit lower, in part, due to the “disturbance” produced by the oscillations in roll, since we have verified in other experiments that when parametric roll does not appear, the phase difference in heave and pitch is precisely \(\frac{\pi } {8}\) [rad]. The experimental and numerical results are fairly comparable and in steady-state (around 350 s) the differences are negligible. The small differences between experimental and numerical results observed in the transient are rather quantitative than qualitative and the most probable cause is the slightly different initial conditions and the natural damping present in the setup which is not perfectly canceled. In a second experiment, controller (14.25) is included in order to stabilize the parametric roll resonance condition. The parameters of the controller are τmax = 0. 01 [Nm], t r = 1 [msec], with gains Q 1 = 5, Q 2 = 10. 155, and Q 3 = 7. The parameters for the model and the initial conditions are as in experiment one except for x 3(0) = 0. 0002 and m = 6 [kg]. The controller is activated when the roll angle achieves the threshold angle φ = 10 ∘ . The experimental results are presented in Fig. 14.8. From this figure it is possible to realize that parametric roll has been stabilized. The control law τφ has been implemented in software and is sent to the setup by means of the data acquisition system. Finally, we present an experiment in which one of the parameters of the system is varied during the experiment. In [17] it has been shown that the stability threshold of the semi-trivial solution \({\sum \nolimits }_{i=1}^{2}[{\omega }_{i}^{2} +\dot{ {\omega }}_{i}^{2}]\neq 0\), \(\varphi, \dot{\varphi } = 0\) is dependent on the parameters of the system. Indeed, in experiments one and two, we have chosen the parameters such that the semi-trivial solution is unstable (parametric roll occurs). However, we also find that by considering m = 4. 1 [kg] and with the same parameters as in experiment one, the stability threshold is not violated and therefore no parametric roll appears. This is illustrated experimentally. First, experiment one is repeated but with m = 4. 1 [kg], therefore no parametric roll occurs. At t = 100 s, we add extra mass in the supporting beam. As a consequence, we can observe resonance in the roll motion. At t ≈ 120 s, we remove the extra mass and the resonance in roll disappears, as depicted in Fig. 14.9. Clearly, we can see that by varying the mass of the supporting beam we can trigger the onset of parametric roll.

Fig. 14.7
figure 7

Heave, pitch, and roll motions. Solid line: experimental results. Dotted line: simulation results

Full size image
Fig. 14.8
figure 8

Parametric roll is stabilized

Full size image
Fig. 14.9
figure 9

In this experiment parametric roll is triggered by varying the mass of the beam

Full size image

5 Conclusions

We have presented an electro-mechanical setup which is capable of conducting parametric roll experiments. The dynamical behavior of the system has been modified such that we were able to mimic the dynamics of a simplified 3-DOF nonlinear container ship model and the dynamics of a mechanical model which simulates the heave-pitch-roll motion of a ship in a longitudinal sea. In both cases, the oscillators are used to represent the heave and pitch motions and the supporting beam is used to reproduce the roll motion. The experiments have been supported by numerical results and are quite comparable with results that already have been presented in the literature.

One of the advantages of this approach is the low implementation cost since for the experiments we do not require additional equipment. The only requirement is a computer and a data acquisition system. The rest is implemented in software. This brings another advantage: in this setup it is possible to implement any external excitation and hence, it is possible to create, for example, an excitation corresponding to the waves of a rough sea or the situation in which the ship is navigating in random seas. In the same way, it is possible to study the influence of specific parameters in the onset of parametric roll, since we are able to change/update any parameter at any time. Ultimately, this experimental testbed can be seen as an alternative for the validation of models and mainly, for testing controllers ad hoc designed for the stabilization of parametric roll, with the final aim of improving its performance in real applications.