Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In the last decade, there has been a considerable interest to the applications of fractional calculus such that many processes in the nature have been successfully modeled by a set of axioms, definitions, and methods of fractional calculus (see  [1,  2,  3,  4]). One of these processes is anomalous diffusion which is a phenomenon occurs in complex and nonhomogeneous mediums. The phenomenon of anomalous diffusion may be based on generalized diffusion equation which contains fractional order space and/or time derivatives [5]. Turski et al.  [6] presented the occurrence of the anomalous diffusion from the physical point of view and also explained the effects of fractional derivatives in space and/or time to diffusion propagation. Agrawal  [7] represented an analytical technique using eigenfunctions for a fractional diffusion-wave system and therefore provided that this formulation could be applied to all those systems for which the existence of eigenmodes is guaranteed. Agrawal  [8] also formulated a general solution using finite sine transform technique for a fractional diffusion-wave equation in a bounded domain whose fractional term was described in sense of Caputo. Herzallah et al.  [9] researched the solution of a fractional diffusion wave model which is more accurate and provides the existence, uniqueness, and continuation of the solution. Huang and Liu  [10] considered a sort of generalized diffusion equation which is defined as a space-time fractional diffusion equation in sense of Caputo and Riemann-Liouville operators. In addition, Huang and Liu [11] found the fundamental solution of the space-time fractional advection-dispersion equation with Riesz–Feller derivative. Langlands [12] proposed a modified fractional diffusion equation on an infinite domain and therefore found the solution as an infinite series of Fox functions. Sokolov et al. [13] analyzed different types of distributed-order fractional diffusion equations and investigated the effects of different classes of such equations. Saichev and Zaslavsky [14] presented the solutions of a symmetrized fractional diffusion equation with a source term applying a method similar to separation of variables. Mainardi et al. [15] researched the fundamental solution of a Cauchy problem for the space-time fractional diffusion equation obtained from the standard diffusion equation by replacing the second-order space derivative by a fractional Riesz or Riesz–Feller derivative, and the first-order time derivative by a fractional Caputo derivative. Gorenflo and Mainardi [16,  17] analyzed a space-fractional (or Levy–Feller) diffusion process governed by a generalized diffusion equation which generates all Levy stable probability distributions and also approximated these processes by random walk models, discreted space and time based on Gr ünwald-Letnikov (GL) approximation. Özdemir et al. [18] presented the numerical solution of a diffusion-wave problem in polar coordinates using GL approximation. Özdemir and Karadeniz [19] also applied GL formula to find the numerical results for a diffusion problem in cylindrical coordinates. Povstenko [20,  21,  22,  23] researched the solutions of axial-symmetric fractional diffusion-wave equations in cylindrical and spherical coordinates.

In addition, numerical schemes are fine research topics in fractional calculus. Because the analytical solutions of the fractional differential equations are usually obtained in terms of Green and Fox functions which are difficult to calculate explicitly. For this reason, there are many research related to numerical approximation of space or space-time fractional diffusion equations. Shen and Liu [24] investigated the error analysis of the numerical solution of a space fractional diffusion equation obtained using an explicit finite difference method. Liu et al. [25] formulated the numerical solution of a space-time fractional advection-dispersion equation in terms of Caputo and RL derivatives using an implicit and an explicit difference methods. Lin et al. [26] considered a nonlinear fractional diffusion equation in terms of generalized Riesz fractional derivative and applied an explicit finite-difference method to find numerical solutions. Özdemir et al. [27] researched the numerical solutions of a two-dimensional space-time fractional diffusion equation in terms of Caputo and Riesz derivatives. Ciesielski and Leszczynski [28] proposed a new numerical method for the spatial derivative called Riesz–Feller operator, and hence found the numerical solutions to a fractional partial differential equation which describe an initial-boundary value problem in one-dimensional space. Ciesielski and Leszczynski [29] also presented the numerical solutions of a boundary value problem for an equation with the Riesz–Feller derivative. Liu et al. [30] presented a random walk model for approximating a Levy–Feller advection-dispersion process and proposed an explicit finite difference approximation for Levy–Feller advection-dispersion process, resulting from the GL discretization of fractional derivatives. Zhang et al. [31] considered the Levy–Feller diffusion equation and investigated their probabilistic interpretation and numerical analysis in a bounded spatial domain. Moreover, Machado [32] presented a probabilistic interpretation to the fractional-order derivatives.

The plan of this work as follows. In this work, we consider a two-dimensional anomalous diffusion problem in terms of Caputo and Riesz–Feller derivatives. For this purpose, we give some basic definitions necessary for our formulations in Sect. 2. In Sect. 3, we formulate our considerations and find the analytical solution of the problem. We apply GL definition to find the numerical solution in Sect. 4. In Sect. 5, we choose an example and therefore show the effectiveness of the numerical approximation for our problem. Finally, we conclude our work in Sect. 6.

2 Mathematical Background

In this work, we consider an anomalous diffusion equation in two-dimensional space. We define our problem in terms of Caputo time and Riesz–Feller fractional derivatives. Therefore, let we remind the well-known definitions and origins of these operators.

Originally, Riesz introduced the pseudo-differential operator x I 0 α whose symbol is \({\left \vert \kappa \right \vert }^{-\alpha }\), well defined for any positive α with the exclusion of odd integer numbers, then was called Riesz Potential. The Riesz fractional derivative \({}_{x}{D}_{0}^{\alpha } = -\) x I 0 α defined by analytical continuation can be represented as follows:

$$ \begin{array}{rcl}{ }_{x}{D}_{0}^{\alpha }& =& -{\left \vert \kappa \right \vert }^{\alpha } \\ & =& -{\left ({\kappa }^{2}\right )}^{\frac{\alpha } {2} } \\ & =& -{\left (- \frac{{{\mathrm d}}^{2}} {{\mathrm d}{x}^{2}}\right )}^{\frac{\alpha } {2} }.\end{array}$$
(21.1)

In addition, Feller [33] generalized the Riesz fractional derivative to include the skewness parameter θ of the strictly stable densities. Feller showed that the pseudo-differential operator D θ α is as the inverse to the Feller potential, which is a linear combination of two Riemann–Liouville { or Weyl} integrals:

$$ \begin{array}{rcl}{ }_{x}{I}_{+}^{\alpha }f\left (x\right )& =& \frac{1} {\Gamma \left (\alpha \right )} \int _{-\infty }\limits^{x}{\left (x - \xi \right )}^{\alpha -1}f\left (\xi \right ){\mathrm d}\xi,\end{array}$$
(21.2)
$$ \begin{array}{rcl}{ }_{x}{I}_{-}^{\alpha }f\left (x\right )& =& \frac{1} {\Gamma \left (\alpha \right )} \int _{x}\limits^{ + \infty }{\left (\xi - x\right )}^{\alpha -1}f\left (\xi \right ){\mathrm d}\xi,\end{array}$$
(21.3)

where α > 0. By these definitions, the Feller potential can be defined as follows:

$${ }_{x}{I}_{\theta }^{\alpha }f\left (x\right ) = {c}_{ +}{\left (\alpha,\theta \right )}_{x}{I}_{+}^{\alpha }f\left (x\right ) + {c}_{ -}{\left (\alpha,\theta \right )}_{x}{I}_{-}^{\alpha }f\left (x\right ),$$
(21.4)

where the real parameters α and θ are always restricted as follows:

$$\begin{array}{rcl} 0& <& \alpha \leq 2,\text{ }\alpha \neq 1, \\ \left \vert \theta \right \vert & \leq & \min \left \{\alpha,2 - \alpha \right \}, \\ \end{array}$$

and also the coefficients are

$$\begin{array}{rcl} {c}_{+}\left (\alpha,\theta \right )& =& \frac{\sin \left (\frac{\left (\alpha -\theta \right )\pi } {2} \right )} {\sin \left (\alpha \pi \right )}, \\ {c}_{-}\left (\alpha,\theta \right )& =& \frac{\sin \left (\frac{\left (\alpha +\theta \right )\pi } {2} \right )} {\sin \left (\alpha \pi \right )}.\end{array}$$
(21.5)

Using the Feller potential, Mainardi and Gorenflo [16] defined the Riesz–Feller derivative

$$\frac{{\partial }^{\alpha }f\left (x\right )} {\partial {\left \vert x\right \vert }_{\theta }^{\alpha }} = {-}_{x}{I}_{\theta }^{-\alpha }f\left (x\right ) = -\left [{c}_{ +}{\left (\alpha,\theta \right )}_{x}{D}_{+}^{\alpha }f\left (x\right ) + {c}_{ -}{\left (\alpha,\theta \right )}_{x}{D}_{-}^{\alpha }f\left (x\right )\right ],$$

where x D  ±  α fx are Weyl fractional derivatives defined as follows:

$${ }_{x}{D}_{\pm }^{\alpha }f\left (x\right ) = \left \{\begin{array}{cc} \pm \frac{{\mathrm d}} {{\mathrm d}x}\left [{}_{x}{I}_{\pm }^{1-\alpha }f\left (x\right )\right ]\!,&\text{ }0 < \alpha < 1, \\ \frac{{{\mathrm d}}^{2}} {{\mathrm d}{x}^{2}} \left [{}_{x}{I}_{\pm }^{2-\alpha }f\left (x\right )\right ]\!, &\text{ }1 < \alpha \leq 2. \end{array} \right.$$
(21.7)

The Caputo fractional derivative is defined as follows:

$$\frac{{\partial }^{\beta }u(t)} {\partial {t}^{\beta }} = \frac{1} {\Gamma \left (n - \beta \right )} \int ^{t}\limits_{0}{\left (t - \tau \right )}^{n-\beta -1}{\left ( \frac{{\mathrm d}} {{\mathrm d}\tau }\right )}^{n}u\left (\tau \right ){\mathrm d}\tau,$$
(21.8)

where \(0 < \beta \leq n,n \in \mathbb{Z}.\) Now, we can formulate our problem after these preliminaries.

3 Formulation of the Main Problem

Let us consider the following space-time fractional anomalous diffusion problem:

$$\begin{array}{rcl} & \frac{{\partial }^{\beta }u(x,y,t)} {\partial {t}^{\beta }} = \text{ }\frac{{\partial }^{\alpha }u(x,y,t)} {\partial {\left \vert x\right \vert }_{{\theta }_{1}}^{\alpha }} + \text{ }\frac{{\partial }^{\mu }u(x,y,t)} {\partial {\left \vert y\right \vert }_{{\theta }_{2}}^{\mu }},&\end{array}$$
(21.9)
$$\begin{array}{rcl} & u(x,y,0) = {u}_{0}\left (x,y\right ),&\end{array}$$
(21.10)
$$\begin{array}{rcl} & \mathop{\lim }\limits_{x,y \rightarrow \pm \infty }u(x,y,t) = 0,&\end{array}$$
(21.11)

where x, y ∈ ℝ; β, α, μ are real parameters restricted as 0 < β ≤ 1, 0 < α < 1, 1 < μ ≤ 2; the skewness parameters θ1 θ1 ≤ minα, 1 − α and θ2 θ2 ≤ minμ, 2 − μ are measures of the asymmetry of the probability distribution of a real-valued random variable among the x and y coordinate axes. Note that many simplistic mathematical models are defined under the Gaussian (normal) distribution; i.e., the skewness parameter is zero. However, in reality, random variables may not distribute symmetrically. Therefore, the behavior of such anomalous diffusion problem differs with the changing of θ1 and θ2 parameters. We first assume that the solution and the initial condition functions can be expanded into the complex Fourier series, respectively:

$$\begin{array}{rcl} u(x,y,t)& =& {\sum \nolimits }_{n=1}^{\infty }{\sum \nolimits }_{m=1}^{\infty }{u}_{ nm}\left (t\right ){{\mathrm e}}^{{\mathrm inx}}{{\mathrm e}}^{{\mathrm imy}},\end{array}$$
(21.12)
$$\begin{array}{rcl}{ u}_{0}\left (x,y\right )& =& {\sum \nolimits }_{n=1}^{\infty }{\sum \nolimits }_{m=1}^{\infty }{u}_{{\mathrm 0nm}}{{\mathrm e}}^{{\mathrm inx}}{{\mathrm e}}^{{\mathrm imy}},\end{array}$$
(21.13)

where \({i}^{2} = -1.\) Under these assumptions, we calculate the fractional derivative terms in the right-hand side of (21.9), respectively, as follows: We start with the calculation of \(\frac{{\partial }^{\alpha }u(x,y,t)} {\partial {\left \vert x\right \vert }_{{\theta }_{1}}^{\alpha }}\) term which dependent on x variable and 0 < α < 1. Let us remind the definition:

$$\frac{{\partial }^{\alpha }u(x,y,t)} {\partial {\left \vert x\right \vert }_{{\theta }_{1}}^{\alpha }} = -\left [{c}_{+}{\left (\alpha,{\theta }_{1}\right )}_{-\infty }{D}_{x}^{\alpha }u(x,y,t) + {c}_{ -}{\left (\alpha,{\theta }_{1}\right )}_{x}{D}_{+\infty }^{\alpha }u(x,y,t)\right ],$$
(21.14)

where

$${ }_{-\infty }{D}_{x}^{\alpha }u(x,y,t) = \frac{\partial } {\partial x}\left ( \frac{1} {\Gamma \left (1 - \alpha \right )} \int ^{x}\limits_{ -\infty }\frac{u(\xi,y,t)} {{\left (x - \xi \right )}^{\alpha }}{\mathrm d}\xi \right )$$
(21.15)

and

$${ }_{x}{D}_{+\infty }^{\alpha }u(x,y,t) = - \frac{\partial } {\partial x}\left ( \frac{1} {\Gamma \left (1 - \alpha \right )} \int _{x}\limits^{\infty }\frac{u\left (\xi,y,t\right )} {{\left (\xi - x\right )}^{\alpha }}{\mathrm d}\xi \right )$$
(21.16)

are the left- and the right-side Weyl fractional derivatives. Now, substituting (21.12) into (21.15), we have

$$ \begin{array}{rcl} {}_{-\infty }{D}_{x}^{\alpha }u(x,y,t)& =& \frac{\partial } {\partial x}\left ( \frac{1} {\Gamma \left (1 - \alpha \right)}{\sum \nolimits }_{n=1}^{\infty }{\sum \nolimits }_{m=1}^{\infty }{u}_{ nm}\left (t\right){{\mathrm e}}^{{\mathrm imy}}{ \int \nolimits \nolimits }_{-\infty }^{x} \frac{{{\mathrm e}}^{{\mathrm in}\xi }} {{\left (x - \xi \right )}^{\alpha }}{\mathrm d}\xi \right ) \\ & =& \frac{1} {\Gamma \left (1 - \alpha \right )} \sum _{n = 1}\limits^{\infty } \sum _{m = 1}\limits^{\infty }{u}_{{\mathrm nm}}\left (t\right){{\mathrm e}}^{{\mathrm imy}} \frac{{\mathrm d}} {{\mathrm dx}}\left ({{\mathrm e}}^{{\mathrm inx}}\mathop{ \int \nolimits \nolimits }\limits^{\infty }\limits_{0}\frac{{{\mathrm e}}^{-{\mathrm inr}}} {{r}^{\alpha }} {\mathrm d}r\right ) \\ & =& \frac{1} {\Gamma \left (1 - \alpha \right )} \sum _{n = 1}\limits^{\infty } \sum _{m = 1}\limits^{\infty }{u}_{{\mathrm nm}}\left (t\right){{\mathrm e}}^{{\mathrm imy}} \frac{{\mathrm d}} {{\mathrm dx}}\left ({{\mathrm e}}^{{\mathrm inx}}{\left (in\right )}^{\alpha -1}\Gamma \left (1 - \alpha \right )\right ) \\ & =& \sum _{n = 1}\limits^{\infty } \sum _{m = 1}\limits^{\infty }{\left ({\mathrm in}\right )}^{\alpha }{u}_{{\mathrm nm}}\left (t\right){{\mathrm e}}^{{\mathrm imy}}{{\mathrm e}}^{{\mathrm inx}} \\ \end{array}$$

and with the similar manipulations,

$${ }_{x}{D}_{+\infty }^{\alpha }u(x,y,t) =\mathop{ \sum \nolimits }\limits_{n = 1}\limits^{\infty } \sum _{m = 1}\limits^{\infty }{\left (-{\mathrm in}\right )}^{\alpha }{u}_{{\mathrm nm}}\left (t\right){{\mathrm e}}^{{\mathrm imy}}{{\mathrm e}}^{{\mathrm inx}}.$$

Hence, for 0 < α < 1, 

$$\frac{{\partial }^{\alpha }u(x,y,t)} {\partial {\left \vert x\right \vert }_{{\theta }_{1}}^{\alpha }} = - \sum _{n = 1}\limits^{\infty } \sum _{m = 1}\limits^{\infty }{n}^{\alpha }\left \{{c}_{ +}\left (\alpha,{\theta }_{1}\right ){\left (i\right )}^{\alpha } + {c}_{ -}\left (\alpha,{\theta }_{1}\right ){\left (-i\right )}^{\alpha }\right \}{u}_{{\mathrm nm}}\left (t\right ){{\mathrm e}}^{{\mathrm imy}}{{\mathrm e}}^{{\mathrm inx}}.$$
(21.17)

Now, we obtain a similar computation of \(\frac{{\partial }^{\mu }u(x,y,t)} {\partial {\left \vert y\right \vert }_{{\theta }_{2}}^{\mu }}\) for the case of 1 < μ ≤ 2. Therefore, we get

$$ \begin{array}{rcl} {}_{-\infty }{D}_{y}^{\mu }u(x,y,t)& =& \frac{{\partial }^{2}} {\partial {y}^{2}}\left ( \frac{1} {\Gamma \left (2 - \mu \right)} \int ^{y}\limits_{ -\infty } \frac{u(x,\eta,t)} {{\left (y - \eta \right )}^{\mu -1}}{\mathrm d}\eta \right ) \\ & =& \frac{{\partial }^{2}} {\partial {y}^{2}}\left ( \frac{1} {\Gamma \left (2 - \mu \right )} \sum _{n = 1}\limits^{\infty } \sum _{m = 1}\limits^{\infty }{u}_{{\mathrm nm}}\left (t\right ){{\mathrm e}}^{{\mathrm inx}}\mathop{ \int \nolimits \nolimits }\limits^{y}\limits_{ -\infty } \frac{{{\mathrm e}}^{{\mathrm im}\eta }} {{\left (y - \eta \right )}^{\mu -1}}{\mathrm d}\eta \right ) \\ & =& \frac{1} {\Gamma \left (2 - \mu \right )} \sum _{n = 1}\limits^{\infty } \sum _{m = 1}\limits^{\infty }{u}_{{\mathrm nm}}\left (t\right ){{\mathrm e}}^{{\mathrm inx}} \frac{{{\mathrm d}}^{2}} {{\mathrm d}{y}^{2}}\left ({{\mathrm e}}^{{\mathrm imy}}\mathop{ \int \nolimits \nolimits }\limits^{\infty }\limits_{0}\frac{{{\mathrm e}}^{-{\mathrm imk}}} {{k}^{\mu -1}} {\mathrm d}k\right ) \\ & =& \frac{1} {\Gamma \left (2 - \mu \right )} \sum _{n = 1}\limits^{\infty } \sum _{m = 1}\limits^{\infty }{u}_{{\mathrm nm}}\left (t\right ){{\mathrm e}}^{{\mathrm inx}} \frac{{{\mathrm d}}^{2}} {{{\mathrm dy}}^{2}}\left ({{\mathrm e}}^{{\mathrm imy}}{\left ({\mathrm im}\right )}^{\mu -2}\Gamma \left (2 - \mu \right )\right ) \\ & =& \sum _{n = 1}\limits^{\infty } \sum _{m = 1}\limits^{\infty }{\left ({\mathrm im}\right )}^{\mu }{u}_{{\mathrm nm}}\left (t\right ){{\mathrm e}}^{{\mathrm inx}}{{\mathrm e}}^{{\mathrm imy}} \\ \end{array}$$

Hence, we obtain

$$\frac{{\partial }^{\mu }u(x,y,t)} {\partial {\left \vert y\right \vert }_{{\theta }_{2}}^{\mu }} =\mathop{ -\sum \nolimits }\limits_{n = 1}\limits^{\infty } \sum _{m = 1}\limits^{\infty }\left \{{c}_{+}\left (\mu,{\theta }_{2}\right ){\left ({\mathrm im}\right )}^{\mu } + {c}_{ -}\left (\mu,{\theta }_{2}\right ){\left (-{\mathrm im}\right )}^{\mu }\right \}{u}_{{\mathrm nm}}\left (t\right ){{\mathrm e}}^{{\mathrm imy}}{{\mathrm e}}^{{\mathrm inx}}.$$
(21.18)

Consequently, substituting (21.17) and (21.18) into (21.9) we take the following time fractional differential equation

$$\begin{array}{rcl} \frac{{\partial }^{\beta }{u}_{{\mathrm nm}}\left (t\right )} {\partial {t}^{\beta }} & =& -\left \{{n}^{\alpha }\left [{c}_{ +}\left (\alpha,{\theta }_{1}\right ){\left ({\mathrm i}\right )}^{\alpha } + {c}_{ -}\left (\alpha,{\theta }_{1}\right ){\left (-{\mathrm i}\right )}^{\alpha }\right ]\right. \\ & & \left.\quad \; +\; {m}^{\mu }\left [{c}_{ +}\left (\mu,{\theta }_{2}\right ){\left ({\mathrm i}\right )}^{\mu } + {c}_{ -}\left (\mu,{\theta }_{2}\right ){\left (-{\mathrm i}\right )}^{\mu }\right ]\right \}{u}_{ nm}\left (t\right ).\qquad \;\qquad \qquad \end{array}$$
(21.19)

Therefore, we reduce the (21.9) to a fractional differential equation with one fractional term. To find the u nm t, we apply Laplace transform to (21.19) and obtain

$${s}^{\beta }{u}_{{\mathrm nm}}\left (s\right ) - {s}^{\beta -1}{u}_{{\mathrm nm}}\left (0\right ) + A{u}_{{\mathrm nm}}\left (s\right ) = 0$$
(21.20)

where

$$\begin{array}{rcl} & & A\,=\,{n}^{\alpha }\left [{c}_{ +}\left (\alpha,{\theta }_{1}\right ){\left ({\mathrm i}\right )}^{\alpha }+{c}_{ -}\left (\alpha,{\theta }_{1}\right ){\left (-{\mathrm i}\right )}^{\alpha }\right ]+{m}^{\mu }\left [{c}_{ +}\left (\mu,{\theta }_{2}\right ){\left ({\mathrm i}\right )}^{\mu } + {c}_{ -}\left (\mu,{\theta }_{2}\right ){\left (-{\mathrm i}\right )}^{\mu }\right ]\!.\end{array}$$
(21.21)

Using inverse Laplace transform, (21.20) reduces to

$${u}_{{\mathrm nm}}\left (t\right ) = {u}_{{\mathrm nm}}\left (0\right ){E}_{\beta,1}\left (-A{t}^{\beta }\right ),$$
(21.22)

where E β, 1(. ) is a well-known Mittag–Leffler function. The Fourier coefficients of the (21.13) can be found by

$${u}_{0nm} = \frac{1} {{(2\pi )}^{2}}\mathop{ \int \nolimits \nolimits }\limits_{-\pi }\limits^{\pi } \int _{-\pi }\limits^{\pi }{u}_{0}\left (x,y\right ){{\mathrm e}}^{-{\mathrm inx}}{{\mathrm e}}^{-{\mathrm imy}}{\mathrm d}x{\mathrm d}y.$$
(21.23)

After some manipulations, we take u nm0 = u 0nm and also u nm t = u 0nm E β, 1 − At β. Now, we can rewrite the solution series after these computations:

$$u\left (x,y,t\right ) =\mathop{ \sum \nolimits }\limits_{n = 1}\limits^{\infty } \sum _{m = 1}\limits^{\infty }{u}_{{\mathrm 0nm}}\left (0\right ){E}_{\beta,1}\left (-A{t}^{\beta }\right ){{\mathrm e}}^{{\mathrm inx}}{{\mathrm e}}^{{\mathrm imy}}.$$
(21.24)

4 Grünwald–Letnikov Approximation for Numerical Solution

In this section, we show the numerical solution of the problem by applying GL approximation for Caputo derivative. Let us first give the relation between the left RL and Caputo definitions:

$${ }_{a}{D}_{t}^{\beta }u\left (t\right ) ={ \text{ }}_{ a}^{C}{D}_{ t}^{\beta }u\left (t\right ) +\mathop{ \sum \nolimits }\limits_{r = 0}\limits^{m - 1} \frac{{{\mathrm d}}^{r}} {{\mathrm d}{t}^{r}}u\left (t\right )\mathop{\mid }\limits_{t = a} \frac{{\left (t - a\right )}^{r-\beta }} {\Gamma \left (r - \beta + 1\right )},$$

where m ∈ ℕ, m − 1 < β ≤ m, a ∈ ℝ. Note that under the assumption \(\left \vert \mathop{\lim }\limits_{a \rightarrow -\infty }\frac{{{\mathrm d}}^{r}} {{\mathrm d}{t}^{r}}u\left (t\right )\mathop{\mid }\limits_{x = a}\right \vert < \infty \) for \(r = 0,1,...,m - 1,\) we have

$${ }_{-\infty }{D}_{x}^{\beta }u\left (t\right ) ={ \text{ }}_{ -\infty }^{C}{D}_{ x}^{\beta }u\left (t\right ).$$

It is also valid for the upper limit case and similar assumption as follows:

$${ }_{x}{D}_{+\infty }^{\beta }u\left (t\right ) ={ \text{ }}_{ x}^{C}{D}_{ +\infty }^{\beta }u\left (t\right ).$$

We remind that the order of Caputo derivative is 0 < β ≤ 1, the lower limit of derivative a = 0, and so we obtain

$${ }_{0}^{C}{D}_{ x}^{\beta }u\left (t\right ) ={ \text{ }}_{ 0}{D}_{x}^{\beta }u\left (t\right )\text{ } - u\left (0\right ) \frac{{t}^{-\beta }} {\Gamma \left (1 - \beta \right )}.$$

It is well known that if a function has suitable properties, i.e., it has first-order continuous derivatives and its second-order derivative is integrable, the β-order derivatives of function in both RL and GL senses are the same. By this property, we discretize the RL operator applying GL definition to (21.19), and therefore we take the approximation of Caputo derivative as

$${ }_{0}^{C}{D}_{ t}^{\beta }{u}_{{\mathrm nm}}\left (t\right ) \approx \frac{1} {{h}^{\beta }}\mathop{ \sum \nolimits }\limits_{r = 0}\limits^{M}{w}_{r}^{\left (\beta \right )}{u}_{{\mathrm nm}}\left ({\mathrm hM} -{\mathrm rh}\right ) - {u}_{{\mathrm nm}}\left (0\right ) \frac{{\left (hM\right )}^{-\beta }} {\Gamma \left (1 - \beta \right )},$$
(21.25)

where \(M = \frac{t} {h}\) represents the number of sub-time intervals, h is step size, and w r β are the coefficients of GL formula:

$$\begin{array}{cc} {w}_{0}^{\beta } = 1,&{w}_{r}^{\beta } = \left (1 -\frac{\beta +1} {r} \right ){w}_{(r-1)}^{\beta }.\end{array}$$
(21.26)

Substituting (21.25) into (21.19) and after some arranging, we get

$${ u}_{{\mathrm nm}}\left ({\mathrm hM}\right ) = \frac{1} {\left ( \frac{1} {{h}^{\beta }}{w}_{0}^{\left (\beta \right )} + A\right )}\left \{{u}_{{\mathrm nm}}\left (0\right ) \frac{{\left ({\mathrm hM}\right )}^{-\beta }} {\Gamma \left (1 - \beta \right )} - \frac{1} {{h}^{\beta }}\mathop{ \sum \nolimits }\limits_{r = 1}\limits^{M}{w}_{r}^{\left (\beta \right )}{u}_{{\mathrm nm}}\left ({\mathrm hM} -{\mathrm rh}\right )\right \},$$
(21.27)

where A is given by (21.21).

5 Numerical Example

In this section, we consider the following initial condition:

$$u\left (x,y,0\right ) =\sinh (x + y).$$

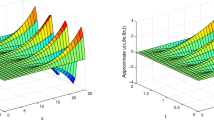
In Fig. 21.1, we first validate the efficiency of numerical method by comparison of analytical and numerical solutions for \(x = \frac{\pi } {5},\) \(y = \frac{\pi } {4},\) t = 5, h = 0. 01 and \(n = m = 10\). It is clear from the figure that the analytical solution is in a good agreement with the numerical solution. Figure 21.2 shows the behavior of problem under the variations of μ values for \(x = \frac{\pi } {5},\) \(y = \frac{\pi } {4},\) t = 5, h = 0. 01, β = 1, α = 0. 3 and θ1 = 0. 3. Similarly, Fig. 21.3 shows the response of the problem for variable order of α for t = 5, β = 0. 5, μ = 1. 5 and θ2 = 0. 5. Figure 21.4 indicates changing behaviors of problem with respect to the variations of α, β, and μ parameters for \(x = \frac{\pi } {5},\) \(y = \frac{\pi } {4},\) t = 5. In Fig. 21.5, we get the three-dimensional surface of the problem (21.9) with respect to x and t for \(y = \frac{\pi } {4},\) β = 0. 7, \(\alpha = 0.5,{\theta }_{1} = 0.5\) and \(\mu = 1.8,{\theta }_{2} = 0.1.\) Finally, we obtain the surface of the problem (21.9) with respect to x and y for β = 0. 7, α = 0. 5, θ1 = 0. 5, and μ = 1. 8, θ2 = 0. 1 and h = 0. 01 in Fig. 21.6.

Fig. 21.1
figure 1_21

Comparison of analytical and numerical solutions for β = 1

Full size image
Fig. 21.2
figure 2_21

Variations of μ parameter

Full size image
Fig. 21.3
figure 3_21

Variations of α parameter

Full size image
Fig. 21.4
figure 4_21

Variations of β, α, and μ parameters

Full size image
Fig. 21.5
figure 5_21

Surface of the whole solution with respect to x and t

Full size image
Fig. 21.6
figure 6_21

Surface of the whole solution with respect to x and y

Full size image

6 Conclusions

In this chapter, we have defined a two-dimensional anomalous diffusion problem with time and space fractional derivative terms. These have been described in the sense of Caputo and Riesz–Feller operators, respectively. We have purposed to find the exact and the numerical solutions of the problem under some assumptions. Therefore, we use Laplace and Fourier transforms for analytical solution and also prefer to apply GL definition. However, we first reduce the main problem to a fractional differential equation with time fractional term. By this way, we have obtained numerical results more easily. Finally, we apply the formulations to an example. After that we present some figures under different considerations about variations of parameters. In addition, we deduce from the comparison of the analytical and the numerical solutions that the GL approximation can be applied successfully to such type of anomalous diffusion problems.