Progressive Censoring Methodology

Abstract

Progressive censoring has received great attention in the last decades especially in life testing and reliability. This review highlights fundamental applications, related models, and probabilistic and inferential results for progressively censored data. Based on the fundamental models of progressive type I and type II censoring, we present related models like adaptive and hybrid censoring as well as, e.g., stress-strength and competing risk models for progressively censored data. Focusing on exponentially and Weibull distributed lifetimes, an extensive bibliography emphasizing recent developments is provided.

1 Introduction and Fundamental Models

Monograph-length accounts on progressive censoring methodology have been provided by Balakrishnan and Cramer [1] and Balakrishnan and Aggarwala [2], while detailed reviews are due to [3] and [4]. In particular, [1] provides an up-to-date account to progressive censoring including many references and detailed explanations. Therefore, we provide essentially the basic models and results in the following, accompanied by recent developments and references which are not covered in the mentioned monograph.

1.1 Basic Ideas of Progressive Censoring

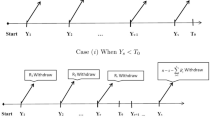
According to [5], a progressively censored life testing experiment is conducted as follows. n items are put simultaneously on a test. At times τ₁ < ⋯ < τ_m, some items are randomly chosen among the surviving ones and removed from the experiment (see Fig. 9.1). In particular, at time τ_j, R_j items are withdrawn from the experiment. Originally, [5] had introduced two versions of progressive censoring, called type I and type II progressive censoring. In progressive type I censoring, the censoring times τ₁ < ⋯ < τ_m are assumed to be fixed in advance (e.g., as prefixed inspection or maintenance times). For a better distinction, fixed censoring times are subsequently denoted by T₁ < ⋯ < T_m. Moreover, the censoring plan $\mathscr {R}=(R_1,\dots , R_m)$ is prespecified at the start of the life test. But, as failures occur randomly, it may happen that at some censoring time T_j, less than R_j items have survived. In that case, all the remaining items are withdrawn, and the life test is terminated at T_j. Notice that, due to this construction, observations beyond the largest censoring time T_m are possible. At this point, it is worth mentioning that the understanding of progressive type I censoring has changed over time. As has been noted in [6], the understanding of the term progressive type I censoring has been used differently after the publication of monograph [2] [see also 7]. Since then, right censoring has been considered as a feature of progressive type I censoring, that is, T_m is considered as a termination time of the experiment (see Fig. 9.2). Therefore, in progressive type I censoring, we distinguish the initially planned censoring plan $\mathscr {R}^0=(R^0_1,\dots , R^0_{m-1})$ from the effectively applied one denoted by $\mathscr {R}=(R_1,\dots , R_{m-1})$. Notice that we drop the mth censoring number R_m in the plan since it is always random due to the right censoring. In order to distinguish these scenarios, [6] called the original scenario Cohen’s progressive censoring scheme with fixed censoring times.

Fig. 9.1

Progressive censoring scheme with censoring times τ₁ < ⋯ < τ_m and censoring plan $\mathscr {R}=(R_1,\dots , R_m)$

Fig. 9.2

Progressive type I censoring with censoring times T₁ < ⋯ < T_m−1, time censoring at T_m, and initial censoring plan $\mathscr {R}^0=(R^0_1,\dots , R^0_{m-1})$

Notation	Explanation
cdf	Cumulative distribution function
pdf	(Probability) density function
iid	Independent and identically distributed
BLUE	Best linear unbiased estimator
MLE	Maximum likelihood estimator
UMVUE	Uniformly minimum variance unbiased estimator
PHR model	Proportional hazard rates model
$\mathbb {R}$	Set of real numbers
$\mathbb {N}, \mathbb {N}_0$	Set of positive and nonnegative integers, respectively
F ←	Quantile function of a cdf F
$\mathbb {I}_{A}(t)$	Indicator function for a set A; $\mathbb {I}_{A}(t)=1$ for t ∈ A, $\mathbb {I}_{A}(t)=0$, otherwise
$\overset {d}=$	Identical in distribution
x m	xm = (x1, …, xm)
xn ∧yn	$\boldsymbol {x}_n \wedge \boldsymbol {y}_n= (\min (x_1, y_1),\dots , \min (x_n, y_n))$
xn ∨yn	$\boldsymbol {x}_n \vee \boldsymbol {y}_n= (\max (x_1, y_1),\dots , \max (x_n, y_n))$
[x]+	$\max (x, 0)$
d •m	$d_{\bullet m}=\sum _{i=1}^{m} d_i$ for $d_1,\dots , d_m\in \mathbb {R}$
$\mathscr {R}$	Censoring plan $\mathscr {R}=(R_1,\dots , R_m)$ with censoring numbers R1, …, Rm
$\mathscr {C}^m_{m,n}$	Set of admissible (progressive type II) censoring plans defined in (9.1)
(γ1, …, γm)	$\gamma _i=\sum _{j=i}^{m}(R_j+1)$, 1 ≤ i ≤ m, for a censoring plan $\mathscr {R}=(R_1,\dots , R_m)$
X1:m:n, …, Xm:m:n, $X_{1:m:n}^{\mathscr {R}},\dots , X_{m:m:n}^{\mathscr {R}}$	Progressively type II censored order statistics based on a sample X1, …, Xn and censoring plan $\mathscr {R}$
$\boldsymbol {X}^{\mathscr {R}}$	$\boldsymbol {X}^{\mathscr {R}}=(X_{1:m:n}^{\mathscr {R}},\dots , X_{m:m:n}^{\mathscr {R}})$
U1:m:n, …, Um:m:n	Uniform progressively type II censored order statistics
$X_{1:K:n}^{I}, \ldots , X_{K:K:n}^{I}$	Progressively type I censored order statistics or progressively censored order statistics with fixed censoring times based on a sample X1, …, Xn
$\boldsymbol {X}^{I,\mathscr {R}}$	$\boldsymbol {X}^{I,\mathscr {R}}=(X_{1:K:n}^{I}, \ldots , X_{K:K:n}^{I})$
X1:n, …, Xn:n	Order statistics based on a sample X1, …, Xn
Exp(μ, 𝜗)	Two-parameter exponential distribution with pdf $f(t)=\frac {1}{\vartheta } \mbox{\textsf {e}}^{-(t-\mu )/\vartheta }$, t > μ
Exp(𝜗) = Exp(0, 𝜗)	Exponential distribution with mean 𝜗 and pdf $f(t)=\frac {1}{\vartheta } \mbox{\textsf {e}}^{-t/\vartheta }$, t > 0
$F_{\exp }$	cdf of standard exponential distribution Exp(1); $F_{\exp }(t)=1- \mbox{\textsf {e}}^{-t}$, t ≥ 0
Wei(𝜗, β)	Weibull distribution with parameters 𝜗, β > 0 and pdf $f(t)=\frac {\beta }{\vartheta }t^{\beta -1} \mbox{\textsf {e}}^{-t^\beta /\vartheta }$, t > 0
U(0, 1)	Uniform distribution on the interval (0, 1)
χ2(r)	χ2-distribution with r degrees of freedom
X ∼ F	X is distributed according to a cdf F
$X_1,\dots , X_n\overset {\text{iid}}\sim F$	X1, …, Xn are independent and identically distributed according to a cdf F

The second version of progressive censoring proposed by Cohen [5] is called progressive type II censoring which may be considered as the most popular version of progressive censoring. Here, the censoring times are induced by the lifetimes of the surviving units in the sense that the next withdrawal is carried out the first failure after the removal of items. Suppose the items are numbered by 1, …, n with lifetimes X₁, …X_n and denote by the set $\mathcal {R}_j$ the numbers of the items available before the jth removal. Then, the next removal time is defined by $X_{j:m:n} = \min _{i\in \mathcal {R}_j} X_i$ (see Fig. 9.3), j = 1, …, m. Clearly, $\mathcal {R}_1=\{1,\dots , n\}$ and X_1:m:n = X_1:n is given by the minimum of the lifetimes. Furthermore, $|\mathcal {R}_j|=n-j+1 -\sum _{i=1}^{j-1}R_i=\gamma _j$, j = 1, …, m. The censoring times are iteratively constructed and random so that they are not known in advance (in contrast to the type I censoring scheme). However, the censoring plan and the sample size are fixed here. In fact, given n and m, the set of admissible progressive type II censoring plans is given by

$$\displaystyle \begin{aligned} \mathscr{C}^m_{m,n} =\Big\{ (r_1,\ldots,r_m)\in \mathbb{N}_0^m :~ \sum_{i=1}^m r_i= n-m\Big\}. \end{aligned} $$

(9.1)

Fig. 9.3

Progressive type II censoring with censoring times X_1:m:n < ⋯ < X_m:m:n and censoring plan $\mathscr {R}=(R_1,\dots , R_m)$

Based on the above fundamental models, further versions of progressive censoring have been proposed. Progressive type I interval censoring uses only partial information from a progressively type I censored life test. In particular, it is assumed that only the number D_j of items failing in an interval (T_j−1, T_j] is known (see Fig. 9.4 for Cohen’s progressive censoring with fixed censoring times). The corresponding situation under type I right censoring is depicted in Fig. 9.5.

Fig. 9.4

Progressive interval censoring with censoring times T₁ < ⋯ < T_m, initial censoring plan $\mathscr {R}^0=(R_1^0,\dots , R_m^0)$, and random counters D₁, …, D_m+1

Fig. 9.5

Progressive type I interval censoring with censoring times T₁ < ⋯ < T_m−1, time censoring at T_m, initial censoring plan $\mathscr {R}^0=(R^0_1,\dots , R^0_{m-1})$, and random counters D₁, …, D_m

The above censoring schemes have been extended in various directions. For instance, a wide class of models called progressive hybrid censoring has been generated by combining type I and type II censoring procedures. In type I progressive hybrid censoring, a type I censoring mechanism has been applied to progressively type II censored data X_1:m:n, …, X_m:m:n by Childs et al. [8] [see also 9, 10], extending a model of [11] by introducing a threshold T. The resulting time censored data $X^{h,I}_{j:m:n}=\min \{X_{j:m:n}, T\}$, j = 1, …, m, will be discussed further in Sect. 9.4.2. Considering the so-called extended progressively type II censored sample by dropping the right censoring (see (9.15)), that is, $X_{1:m+R_m:n},\dots , X_{m+R_m:m+R_m:n}$, a type II progressively hybrid censored sample can be defined by the condition $X_{K:m+R_m:n}\le T< X_{K+1:m+R_m:n}$, m ≤ K ≤ m + R_m. Further versions have been summarized in [12]. An extensive survey on (progressive) hybrid censoring schemes is provided in the recent monograph by [380].

Motivated by the Ng-Kundu-Chan modelintroduced in [13], adaptive progressive censoring schemes have been proposed by Cramer and Iliopoulos [14] and Cramer and Iliopoulos [15]. In these models, censoring plans and censoring times may be chosen adaptively according to the observed data. Such models are presented briefly in Sect. 9.4.3.

In most cases, progressive censoring is studied under the assumption that the underlying lifetimes X₁, …, X_n are independent and identically distributed (iid) random variables. If not noted explicitly, all results presented in the following are based on this assumption. However, relaxations of this assumption have been made. For instance, [16] discussed the case of heterogeneous distributions, that is, X_i ∼ F_i, 1 ≤ i ≤ n, are independent random variables but may have a different cumulative distribution function (see also [17, 18]). Rezapour et al. [19, 20] assumed dependent underlying lifetimes. For a review, we refer to [1, Chapter 10].

1.2 Notation

Throughout, we use the following notation and abbreviations.

1.3 Organization of the Paper

In the following sections, we discuss the most popular versions of progressive censoring in detail, that is, progressive type II censoring (Sect. 9.2) and progressive type I censoring (Sect. 9.3). Further, progressive censoring with fixed censoring times is also addressed in Sect. 9.3. In Sect. 9.4, related data like progressive interval censoring, progressive hybrid censoring, and adaptive progressive censoring as well as applications in reliability and lifetime analysis are discussed. Due to their importance, we focus on exponentially and Weibull distributed lifetimes. Except when otherwise stated, the underlying lifetimes X₁, …, X_n are supposed to be independent and identically distributed according to a cdf F, that is, $X_1,\dots , X_n\overset {\text{iid}}\sim F$.

2 Progressive Type II Censoring

2.1 Probabilistic Results

Fundamental tools in studying properties of progressively type II censored order statistics are the joint pdf of X_1:m:n, …, X_m:m:n and the quantile representation. The joint pdf of progressively type II censored order statistics X_1:m:n, …, X_m:m:n based on an (absolutely continuous) cdf F with pdf f is given by

$$\displaystyle \begin{aligned} f^{\boldsymbol{X}^{\mathscr{R}}} (\boldsymbol{x}_m) = \begin{cases} \prod_{j=1}^m\left[ \gamma_j f(x_j) (1-F(x_j))^{R_j}\right], & x_1 \le \dots \le x_m\\ 0, & \text{otherwise} \end{cases} \end{aligned} $$

(9.2)

where $\gamma _j=\sum _{i=j}^{m}(R_i+1)$ denotes the number of items remaining in the experiment before the jth failure, 1 ≤ j ≤ m. Notice that n = γ₁ > ⋯ > γ_m ≥ 1. It is immediate from (9.2) that progressively type II censored order statistics are connected to the distributional model of generalized order statistics (see [21,22,23]) which covers progressively type II censored order statistics as a particular case (for details, see [1], Section 2.2).

2.1.1 Exponential Distributions

From (9.2), the pdf for an exponential population Exp(μ, 𝜗) can be directly obtained, that is, the pdf of exponential progressively type II censored order statistics $\boldsymbol {X}^{\mathscr {R}} =(X_{1:m:n},\dots , X_{m:m:n})$ is given by

$$\displaystyle \begin{aligned} f^{\boldsymbol{X}^{\mathscr{R}}} (\boldsymbol{x}_m) = & \frac{1}{\vartheta^m} \Big(\prod_{j=1}^m\gamma_j\Big) \exp\Big(-\frac{1}{\vartheta} \sum_{j=1}^{m}(R_j+1)(x_j-\mu)\Big), \quad \\ &\mu\le x_1 \le \dots \le x_m. \end{aligned} $$

This expression is important in deriving, e.g., properties of exponential progressively type II censored order statistics as well as in developing statistical inference. As pointed out by Thomas and Wilson [24] (see also [25]), the normalized spacings $S_j^{\mathscr {R}} =\gamma _j (X_{j:m:n}-X_{j-1:m:n})$, 1 ≤ j ≤ m, with X_0:m:n = μ defined as left endpoint of support are iid random variables, that is (see [1], Theorem 2.3.2),

$$\displaystyle \begin{aligned} S_1^{\mathscr{R}},\dots, S_m^{\mathscr{R}} \overset{\text{iid}}\sim \mbox{\textsf{Exp}}(\vartheta). \end{aligned} $$

(9.3)

On the other hand, exponential progressively type II censored order statistics can be written in terms of their spacings yielding the identity

$$\displaystyle \begin{aligned} X_{r:m:n} = \mu+ \sum_{i=1}^{r} \frac{1}{\gamma_i}S_i^{\mathscr{R}} =X_{r-1:m:n} +\frac{1}{\gamma_r}S_r^{\mathscr{R}},\quad 1\le r\le m, \end{aligned} $$

(9.4)

where X_0:m:n = μ. This representation allows us to derive many properties of exponential progressively type II censored order statistics. For instance, using (9.3) and (9.4), the one-dimensional marginal pdfs and cdfs are given by (see also [26])

$$\displaystyle \begin{aligned} \begin{array}{rcl} f^{X_{r:m:n}}(t) & = &\displaystyle \Big(\prod^r_{j=1} \gamma_j\Big) \sum_{j=1}^r a_{j,r} \mbox{\textsf{e}}^{-\gamma_j t},\quad \\ F^{X_{r:m:n}}(t) & = &\displaystyle 1- \Big(\prod^r_{i=1} \gamma_i\Big) \sum_{j=1}^r \frac{1}{\gamma_j} a_{j,r} \mbox{\textsf{e}}^{-\gamma_j t}, \quad t>0 , \end{array} \end{aligned} $$

where $a_{j,r} = \prod ^r_{\substack {i=1\\ i\neq j}} \frac {1}{\gamma _i-\gamma _j}$, 1 ≤ j ≤ r ≤ n. Representations of bivariate and arbitrary marginals can be found in [1, Section 2.4], (see also [27, 28]). Moreover, it follows from (9.4) that X_1:m:n, …, X_m:m:n form a Markov chain, that is, for 2 ≤ r ≤ m,

$$\displaystyle \begin{aligned} &X_{r:m:n}\mid (X_{r-1:m:n}=x_{r-1},\dots, X_{1:m:n}=x_{1}) \\ &\quad \overset{d}= X_{r:m:n}\mid (X_{r-1:m:n}=x_{r-1}) \\ &\quad \overset{d}= \frac{1}{\gamma_r}S_r^{\mathscr{R}} + x_{r-1} \sim \mbox{\textsf{Exp}}(x_r, \vartheta/\gamma_r). \end{aligned}$$

Furthermore, $X_{1:m:n} \overset {d}= \mbox{\textsf {Exp}}(\mu , \vartheta /\gamma _1)$. These representations allow direct calculation of moments. For instance, one gets

$$\displaystyle \begin{aligned} E X_{r:m:n} &=\mu+\vartheta \sum_{ j=1}^{r} \frac{1}{\gamma_j}, \quad \operatorname{\mathrm{\text{Var}}} X_{r:m:n} =\vartheta^2 \sum_{ j=1}^{r} \frac{1}{\gamma_j^2},\\ \operatorname{\mathrm{\text{Cov}}} (X_{r:m:n}, X_{s:m:n}) &=\operatorname{\mathrm{\text{Var}}} X_{r:m:n}=\vartheta^2 \sum_{ j=1}^{r} \frac{1}{\gamma_j^2},\quad 1\le r\le s \le m. \end{aligned} $$

(9.5)

Further results on moments, e.g., higher order moments, existence of moments, bounds, and recurrence relations, can be found in [1] and the references cited therein.

2.1.2 Other Distributions

Probabilistic results for other distributions can be obtained from the pdf in (9.2) or, alternatively, from the results obtained for the exponential distribution and the following result due to [29, 30] (for a proof, see [1]). It shows that most of the distributional results can be obtained for a uniform distribution and then transformed to an arbitrary cdf F.

Theorem 9.2.1

Suppose X_1:m:n, …, X_m:m:n and U_1:m:n, …, U_m:m:n are progressively type II censored order statistics based on a cdf F and a uniform distribution, respectively. Then,

$$\displaystyle \begin{aligned} (X_{j:m:n})_{1\le j\le m} \overset{d}= \left(F^{\leftarrow}(U_{j:m:n})\right)_{1\le j\le m}.\end{aligned} $$

Theorem 9.2.1, together with the representation of the joint pdf for uniform distributions, yields an expression for progressively type II censored order statistics based on an arbitrary cdf F, that is,

$$\displaystyle \begin{aligned} F^{X_{r:m:n}}(t) = 1- \Big(\prod^r_{i=1} \gamma_i\Big) \sum_{j=1}^r \frac{1}{\gamma_j} a_{j,r} (1-F(t))^{\gamma_j}, \quad t\in\mathbb{R}. \end{aligned}$$

If F is absolutely continuous with pdf f, then the pdf is given by

$$\displaystyle \begin{aligned} f^{X_{r:m:n}}(t) = \Big(\prod^r_{j=1} \gamma_j\Big) f(t) \sum_{j=1}^r a_{j,r} (1-F(t))^{\gamma_j-1},\quad t\in\mathbb{R}.\end{aligned} $$

Similar representations can be obtained for multiple progressively type II censored samples (see [1], p.41, [28, 31]). Log-concavity and unimodality properties of the distributions are studied in [32,33,34,35,36].

From (9.4), it follows that $F_{\exp }(X_{r:m:n}) = 1-\prod _{j=1}^r \left (\mbox{\textsf {e}}^{-S_j^{\mathscr {R}}/\vartheta }\right )^{1/\gamma _j}$ with $S_1^{\mathscr {R}},\dots , S_m^{\mathscr {R}}$ as in (9.3). Thus, $U_j= \mbox{\textsf {e}}^{-S_j^{\mathscr {R}}/\vartheta }$, 1 ≤ j ≤ m, are independent uniformly distributed random variables. This yields the identity

$$\displaystyle \begin{aligned} U_{r:m:n}\overset{d}= 1- \prod_{j=1}^r U_j^{1/\gamma_j}, \quad 1\le r\le m, \end{aligned} $$

of U_r:m:n as a product of independent random variables. Combining this expression with the quantile representation from Theorem 9.2.1, we arrive at the following representation [see also 37].

Theorem 9.2.2

Let X_1:m:n, …, X_m:m:n be progressively type II censored order statistics from an arbitrary cdf F and $U_1,\dots U_m \overset {\mathit{\text{iid}}}\sim \mathit{\mbox{\textsf {U}}}(0, 1)$. Then,

$$\displaystyle \begin{aligned} X_{1:m:n},\dots, X_{m:m:n} \overset{d}= F^{\leftarrow}\bigg( 1-\prod_{j=1}^r U_j^{1/\gamma_j}\bigg), \quad 1\le r\le m. \end{aligned}$$

As has been noticed in [38], this representation provides an alternative method to simulate progressively type II censored order statistics from a cdf F (for a survey on simulation methods, see [1, Chapter 8]). Alternatively, one can also write

$$\displaystyle \begin{aligned} X_{r:m:n} \overset{d}= F^{\leftarrow}\bigg( F_{\exp} \Big (\sum_{j=1}^r\frac{1}{\gamma_j}Z_j\Big) \bigg), \quad 1\le r\le m, \end{aligned}$$

with $Z_1,\dots , Z_m \overset {\text{iid}}\sim \mbox{\textsf {Exp}}(1)$. This result illustrates that X_1:m:n, …, X_m:m:n form a Markov chain with transition probabilities

$$\displaystyle \begin{aligned} P(X_{r:m:n}\le t\mid X_{r-1:m:n}=s)=1- \left(\frac{1-F(t)}{1-F(s)}\right)^{\gamma_r},\!\!\quad s{\,\le\,} t \text{ with } F(s){\,<\,}1. \end{aligned}$$

Further results on the dependence structure of progressively type II censored order statistics are available. For instance, [28] has shown that progressively type II censored order statistics exhibit the MTP₂-property which implies that progressively type II censored order statistics are always positively correlated. The block independence property has been established by Iliopoulos and Balakrishnan [39]. In order to formulate the result, we introduce the number of progressively type II censored order statistics that do not exceed a threshold T, i.e., $D=\sum _{j=1}^m \mathbb {I}_{(-\infty , T]}(X_{j:m:n})$. Then, the probability mass functionof D is given by the probabilities

$$\displaystyle \begin{aligned} P(D=0) &= (1-F(T))^n, \\ P(D=d)&= \Big(\prod^{d}_{i=1} \gamma_i\Big) \sum_{j=1}^{d+1} a_{j,d+1} (1-F(T))^{\gamma_j}, \quad d=1,\dots,m-1, \\ P(D=m)&= F^{X_{m:m:n}}(T). \end{aligned}$$

Given d ∈{1, …, m − 1}, a cdf F, and a censoring plan $\mathscr {R}=(R_1,\dots , R_m)$, the block independence property is as follows: Conditionally on D = d, the random vectors (X_1:m:n, …, X_d:m:n) and (X_d+1:m:n, …, X_m:m:n) are independent with

$$\displaystyle \begin{aligned} (X_{1:m:n},\dots, X_{d:m:n}) & \overset{d}= \left( V_{1:d:\kappa_d}^{\boldsymbol{K}_d},\dots, V_{d:d:\kappa_d}^{\boldsymbol{K}_d}\right),\\ (X_{d+1:m:n},\dots, X_{m:m:n}) & \overset{d}=\left( W_{1:m-d:\gamma_d},\dots, W_{m-d:m-d:\gamma_d}\right) \end{aligned} $$

(9.6)

where K_d = (K₁, …, K_d) is a random censoring plan on the Cartesian product with probability mass function

$$\displaystyle \begin{aligned} p^{\boldsymbol{K}_d}(\boldsymbol{k}_d)= \frac{1}{P(D=d)} F^{\eta_1(d)}(T) (1-F(T))^{n-\eta_1(d)}\prod_{i=1}^d \frac{\gamma_i}{\eta_i(d)} \binom{R_i}{k_i} , \end{aligned}$$

$\kappa _d=\sum _{j=1}^d (1+K_j)$, and $\eta _i(d)=\sum _{j=i}^d(k_j+1)$, 1 ≤ i ≤ d. Further:

• 1. V₁, …, V_n are iid random variables with right truncated cdf F_T given by $F_T(t)= \frac {F(t)}{F(T)}$, t ≤ T.

• 2. $W_1,\dots , W_{\gamma _d}$ are iid random variables with left truncated cdf G_T given by $G_T(t)=1-\frac {1-F(t)}{1-F(T)}$, t ≥ T.

The sample size κ_d of the progressively type II censored order statistics $V_{1:d:\kappa _d}^{{\mathbf {K}}_{d}},\dots$, $V_{d:d:\kappa _d}^{{\mathbf {K}}_{d}}$ is a random variable. The above representation means that the distribution of (X_1:m:n, …, X_d:m:n), given D = d, is a mixture of distributions of progressively type II censored order statistics with mixing distribution $p^{{\mathbf {K}}_{d}}$. It is well known that right truncation of progressively type II censored order statistics does not result in progressively type II censored order statistics from the corresponding right truncated distribution [see, e.g., 2]. This is due to the fact that those observations (progressively) censored before T could have values larger than T.

2.1.3 Connection to Order Statistics and Other Models of Ordered Data

Order statistics [see, e.g., 40, 41] can be interpreted as special progressively type II censored order statistics by choosing the censoring plan $\mathscr {O}=(0,\dots , 0)$. Then, we have m = n and $X_{j:n:n}^{\mathscr {O}}=X_{j:n}$, 1 ≤ j ≤ n. Furthermore, the censoring plan $\mathscr {O}^*=(0,\dots , 0,R_m)$ with n = m + R_m yields $X_{j:m:n}^{\mathscr {O}}=X_{j:m+R_m}$, 1 ≤ j ≤ m, leading to a type II right censored sample. Thus, all the results developed for progressively type II censored order statistics can be specialized to order statistics. Detailed accounts to order statistics are provided by Arnold et al. [40] and David and Nagaraja [41].

As mentioned above, progressively type II censored order statistics can be seen as particular generalized order statistics and sequential order statistics, respectively (see [21, 23, 37]). In this regard, results obtained in these models hold also for progressively type II censored order statistics by specifying model parameters and distributions suitably. For pertinent details, we refer to the references given above.

2.1.4 Moments

Many results on moments have been obtained for progressively type II censored order statistics (see, e.g., [1], Chapter 7). This discussion includes explicit results for selected distributions, e.g., exponential distributions (see (9.5)), Weibull, Pareto, Lomax, reflected power, and extreme value distributions. Further topics are existence of moments (see [42, 43]), bounds (see, e.g., [32, 44, 45]), recurrence relations (see, e.g., [27, 46]), and approximations (see, e.g., [47]). Furthermore, the accurate computation of moments has been discussed in [48] (see also [49]). It should be noted that an enormous number of papers have discussed moments as well as related recurrence relations for particular distributions.

2.1.5 Stochastic Orders and Stochastic Comparisons

Results on various stochastic orders of progressively type II censored order statistics have been mostly established in terms of generalized and sequential order statistics (see [1], Section 3.2). Therefore, the results can be applied to progressively type II censored order statistics by choosing particular parameter values. For information, we present definitions of the most important stochastic orders discussed for progressively type II censored order statistics. For a general discussion, we refer to [50, 51], and [52]. A review of results on multivariate stochastic orderings for generalized order statistics is provided in [53] (see also [1]).

Let X ∼ F, Y ∼ G be random variables and let f and g denote the respective pdfs. For simplicity, it is assumed that the supports are subsets of the set of positive values. In the following, we present some selected results on stochastic orderings under progressive type II censoring and provide references for further reading.

Stochastic Order/Multivariate Stochastic Order

• (i) X is said to be stochastically smaller than Y , that is, X ≤_stY  or F ≤_stG, iff $\overline {F}(x) \le \overline {G}(x)$ for all x ≥ 0.

• (ii) Let X = (X₁, …, X_n)′, Y  = (Y₁, …, Y_n)′ be random vectors. Then, X is said to be stochastically smaller than Y , that is, X ≤_stY or F^X ≤_stF^Y, iff Eϕ(X) ≤ Eϕ(Y ) for all nondecreasing functions $\phi :\mathbb {R}^n\longrightarrow \mathbb {R}$ provided the expectations exist.

Notice that, for n = 1, the definition of the multivariate stochastic order is equivalent to the (common) definition in the univariate case.

Belzunce et al. [54] has established the preservation of the stochastic order when the baseline distributions are stochastically ordered.

Theorem 9.2.3

Let $\boldsymbol {X}^{\mathscr {R}}$ and $\boldsymbol {Y}^{\mathscr {R}}$ be vectors of progressively type II censored order statistics from continuous cdfs F and G with censoring plan $\mathscr {R}$, respectively. Then, for F ≤_stG, $\boldsymbol {X}^{\mathscr {R}} \le _{\textsf {st}} \boldsymbol {Y}^{\mathscr {R}}$.

A comparison in terms of the univariate stochastic order has been established by Khaledi [55] using the following partial ordering of γ-vectors (see [56, 57]). Let $\mathscr {R}$ and $\mathscr {S}$ be censoring plans with corresponding γ-values $\gamma _i(\mathscr {R})=\sum _{k=i}^{m_1} (R_k+1)$ and $\gamma _i(\mathscr {S})=\sum _{k=i}^{m_2} (S_k+1)$. For 1 ≤ j ≤ i,

$$\displaystyle \begin{aligned} (\gamma_1(\mathscr{S}),\ldots,\gamma_j(\mathscr{S}))\le_{\textsf{p}}(\gamma_{i-j+1}(\mathscr{R}),\ldots,\gamma_i(\mathscr{R})) \end{aligned} $$

(9.7)

iff

$$\displaystyle \begin{aligned} \prod_{k=1}^\ell \gamma_{i-k+1}(\mathscr{R}) \le \prod_{k=1}^\ell \gamma_k(\mathscr{S}) \text{ for }\ell=1,\ldots, j.\end{aligned}$$

Theorem 9.2.4

Let F, G be continuous cdfs with F ≤_stG and X ∼ F, Y ∼ G. Moreover, let $\mathscr {R}\in \mathscr {C}_{m_1,n_1}^{m_1}, \mathscr {S}\in \mathscr {C}_{m_2,n_2}^{m_2}$ with $m_1, m_2\in \mathbb {N}$ be censoring plans. Then:

• (i) $X_{i:m_1:m_1}^{\mathscr {R}}\le _{\textsf {st}} Y_{i:m_1:m_1}^{\mathscr {R}}$, 1 ≤ i ≤ m₁.

• (ii) If 1 ≤ j ≤ i and condition (9.7) holds, then $X_{j:m_2:m_2}^{\mathscr {S}} \le _{\textsf {st}} Y_{i:m_1:m_1}^{\mathscr {R}}$.

Applications to stochastic ordering of spacings of progressively type II censored order statistics can be found in [58].

Failure Rate/Hazard Rate Order, Reversed Hazard Rate Order

• (i) X is said to be smaller than Y  in the hazard rate order, that is, X ≤_hrY  or F ≤_hrG, iff $\overline {F}(x)\overline {G}(y) \le \overline {F}(y)\overline {G}(x)$ for all 0 ≤ y ≤ x.

• (ii) X is said to be smaller than Y  in the reversed hazard rate order, that is, X ≤_rhY  or F ≤_rhG, iff F(x)G(y) ≤ F(y)G(x) for all 0 ≤ y ≤ x.

For the hazard rate order, the ratio $\frac {\overline {F}(x)}{\overline {G}(x)}$ is nonincreasing in x ≥ 0 where $\frac {a}{0}$ is defined to be ∞. If F and G are absolutely continuous cdfs with pdfs f and g, respectively, then hazard rate ordering is equivalent to increasing hazard rates, that is,

$$\displaystyle \begin{aligned} \lambda_F(x) =\frac{f(x)}{1- F(x)} \le \frac{g(x)}{1- G(x)} =\lambda_G(x) \text{ for all }x\ge 0.\end{aligned}$$

For the reversed hazard rate order, the ratio $\frac {F(x)}{G(x)}$ is nonincreasing in x ≥ 0, where $\frac {a}{0}$ is defined to be ∞.

Results for (multivariate) hazard rate orders of progressively type II censored order statistics have been obtained by Belzunce et al. [54], Khaledi [55], and Hu and Zhuang [59]. For instance, replacing the stochastic order by the hazard rate order in Theorem 9.2.4, an analogous result is true (see [1, Theorem 3.2.3]).

Likelihood Ratio Order/Multivariate Likelihood Ratio Order

• (i) X is said to be smaller than Y  in the likelihood ratio order, that is, X ≤_lrY  or F ≤_lrG, iff f(x)g(y) ≤ f(y)g(x) for all 0 ≤ y ≤ x.

• (ii) Let X = (X₁, …, X_n)′, Y  = (Y₁, …, Y_n)′ be random vectors with pdfs f^X and f^Y. Then, X is said to be smaller than Y in the multivariate likelihood ratio order, that is, X ≤_lrY or F^X ≤_lrF^Y, iff

  $$\displaystyle \begin{aligned} f^{\boldsymbol{X}}(\boldsymbol{x}_n) f^{\boldsymbol{Y}}( \boldsymbol{y}_n) \le f^{\boldsymbol{X}}(\boldsymbol{x}_n \wedge \boldsymbol{y}_n) f^{\boldsymbol{Y}}(\boldsymbol{x}_n \vee \boldsymbol{y}_n) \end{aligned}$$

  for all $\boldsymbol {x}=(x_1,\dots , x_n)', \boldsymbol {y}=(y_1,\dots , y_n)'\in \mathbb {R}^n$.

The (multivariate) likelihood ratio order has been discussed, e.g., by Korwar [60], Hu and Zhuang [59], Cramer et al. [61], Belzunce et al. [54], Zhuang and Hu [62], Balakrishnan et al. [63], Sharafi et al. [64], and Arriaza et al. [65]. The following result is due to [60] (see [59] for generalized order statistics).

Theorem 9.2.5

Let $\mathscr {R}\in \mathscr {C}_{m_1,n_1}^{m_1}, \mathscr {S}\in \mathscr {C}_{m_2,n_2}^{m_2}$ with $m_1, m_2\in \mathbb {N}$ be censoring plans and $X_{j:m_2:m_2}^{\mathscr {S}} , X_{i:m_1:m_1}^{\mathscr {R}}$ be progressively type II censored order statistics from the same absolutely continuous cdf F. If 1 ≤ j ≤ i and $\gamma _k(\mathscr {R})\le \gamma _k(\mathscr {S})$, k = 1, …, j, then $X_{j:m_2:m_2}^{\mathscr {S}} \le _{\textsf {lr}} X_{i:m_1:m_1}^{\mathscr {R}}$.

Comparisons of vectors of progressively type II censored order statistics (generalized order statistics) with different cdfs and different censoring plans have been considered in [54]. In particular, they found the following property.

Theorem 9.2.6

Let $X_{i:m:n}^{\mathscr {R}}, Y_{i:m:n}^{\mathscr {R}}$, 1 ≤ i ≤ m ≤ n, be progressively type II censored order statistics from absolutely continuous cdfs F and G, respectively, with F ≤_lrG and censoring plan $\mathscr {R}$. Then, $X_{i:m:n}^{\mathscr {R}}\le _{\textsf {lr}} Y_{i:m:n}^{\mathscr {R}}$, 1 ≤ i ≤ m.

Ordering of p-spacings is discussed in [54, 66,67,68].

Dispersive Order

X is said to be smaller than Y  in the dispersive order, i.e., X ≤_dispY  or F ≤_dispG, iff F^←(x) − F^←(y) ≤ G^←(x) − G^←(y) for all 0 < y < x < 1.

Results for the (multivariate) dispersive order are established in [55, 69,70,71]. For instance, [55] has shown a result as in Theorem 9.2.4 for the dispersive order provided that the cdf F has the DFR-property. Belzunce et al. [54] have shown that $\boldsymbol {X}^{\mathscr {R}} \le _{\textsf {disp}} \boldsymbol {Y}^{\mathscr {R}}$ and that $X_{i:m:n}^{\mathscr {R}}\le _{\textsf {disp}} Y_{i:m:n}^{\mathscr {R}}$, 1 ≤ i ≤ m, when F ≤_dispG.

Further orderings like mean residual life, total time on test, and excess wealth orders have also been discussed (see [72,73,74,75]). Results for the increasing convex order of generalized order statistics have been established in [76]. Orderings of residual life are discussed in [77, 78]. Stochastic orderings of INID progressively type II censored order statistics have been studied in [79].

2.1.6 Ageing Notions

Ageing properties have also been studied for progressively type II censored order statistics. For general references on ageing notions and their properties, we refer to, e.g., [80,81,82]. Results have been obtained for various ageing notions, e.g., increasing/decreasing failure rate (IFR/DFR), increasing/ decreasing failure rate on average (IFRA/DFRA), and new better/worse than used (NBU/NWU). Fundamental results on progressively type II censored order statistics for the most common ageing notions are mentioned subsequently.

IFR/DFR

A cdf F is said to be IFR (DFR) iff the ratio $\frac {F(t+x)-F(t)}{1-F(t)}$ is increasing (decreasing) in x ≥ 0 for all t with F(t) < 1.

If F exhibits a pdf then the IFR-/DFR-property means that the hazard rate function λ_F = f∕(1 − F) is increasing (decreasing).

IFRA/DFRA

A cdf F is said to be IFRA (DFRA) iff, for the hazard function $R=-\log \overline {F}$, the ratio R(x)∕x is increasing (decreasing) in x > 0.

NBU/NWU

A cdf F is said to be NBU (NWU) iff $\overline {F}(t+x)\le (\ge ) \overline {F}(t)\overline {F}(x)$ for all x, t ≥ 0.

The IFR- and IFRA-property of progressively type II censored order statistics have been investigated in [33]. It has been shown that all progressively type II censored order statistics are IFR/IFRA provided that the baseline cdf F is IFR/IFRA. The respective result for the NBU-property as well as further results can be found in [83] in terms of sequential order statistics (see also [84]). Preservation properties are presented in [23], e.g., it has been proved that the DFR-property is preserved by spacings (see also [21]). The reversed hazard rate has been studied in [85]. Belzunce et al. [86] considered multivariate ageing properties in terms of nonhomogeneous birth processes and applied their results to generalized order statistics. A restriction to progressive censoring shows that progressively type II censored order statistics $\boldsymbol {X}^{\mathscr {R}}$ are M-IFR if F is an IFR-cdf. Moreover, $\boldsymbol {X}^{\mathscr {R}}$ is multivariate Polya frequency of order 2 (MPF₂) if the pdf of F is log-concave. Further notions of multivariate IFR/DFR and its applications to generalized order statistics have been discussed in [87]. The connection of ageing properties and residual life has been considered in [88] in terms of generalized order statistics.

2.1.7 Further Topics

The following probabilistic topics have also been discussed in progressive type II censoring, but, for brevity, we only mention them here briefly. Many publications deal with various kinds of characterizations of probability distributions [see, e.g., 1, Chapter 3.1]. Limit theorems have also been established imposing different assumptions on the censoring plans and distributions. For instance, [89] considered normal approximations using an approach inspired by Hoadley [90]. Cramer [91] discussed extreme value analysis which includes extreme, central, and intermediate progressively type II censored order statistics [see also 92, 93]. Counting process approaches in combination with limiting distributions have been extensively discussed in [94] [see also 95, 96]. Hofmann et al. [97] has discussed a block censoring approach.

Information measures have also found some interest [see, e.g., 1, Chapter 9]. Results on the Fisher information have been established in, e.g., [98,99,100,101,102]. A detailed approach in terms of the more general model of generalized order statistics is discussed in [103, 104]. Asymptotic results are provided in [105]. Entropy-type measures are investigated in [106,107,108,109,110]. Kullback-Leibler-related measures are addressed in [106, 107, 111,112,113,114,115]. Pitman closeness for progressively type II censored data has been considered in, e.g., [116,117,118,119].

Concomitants for progressively type II censored order statistics have been addressed [120,121,122] (see also [1]).

As already mentioned above, progressive type II censoring has also been discussed under nonstandard conditions. Specifically, the underlying random variables X₁, …, X_n are supposed to be distributed according to some (multivariate) distribution function $F^{X_1,\dots , X_n}$. A general mixture representation of the distribution in terms of distributions of order statistics has been established by Fischer et al. [17]. Assuming independence but possibly different marginals, [16] found representations of the joint density functions. Inference in such a model has been discussed in [123]. Given a copula of the lifetimes X₁, …, X_n, [19, 20] addressed dependent random variables. Progressive censoring of random vectors has been discussed in [124] [see also 125, 126].

2.2 Inference

Inference for progressively type II censored data has been widely discussed in the literature. Most of the material is devoted to parametric inference. In the following, we present a selection of results for exponential and Weibull distribution. In addition, references to other distributions are provided. A standard reference for all these results is [1]. If nothing else is mentioned, we discuss inference on a single progressively type II censored sample X_1:m:n, …, X_m:m:n.

2.2.1 Point Estimation

The most popular parametric estimation concepts applied to progressively type II censored data are linear, likelihood, and Bayesian estimation. Assuming a location-scale family of distributions

$$\displaystyle \begin{aligned} \mathscr{F}= \Big\{ F_{\mu,\vartheta}=F\Big(\frac{\cdot - \mu}\vartheta\Big)\,\Big|\, \mu\in\mathbb{R},\vartheta>0 \Big\}, \end{aligned}$$

with a known cdf F, a progressively type II censored sample $\boldsymbol {X}^{\mathscr {R}}$ from F_μ,𝜗 can be written as a linear model:

$$\displaystyle \begin{aligned} \boldsymbol{X}^{\mathscr{R}} = \mu\cdot \boldsymbol{1} + \vartheta \boldsymbol{Y}^{\mathscr{R}} =\mu\cdot \boldsymbol{1} +\vartheta E\boldsymbol{Y}^{\mathscr{R}} +\boldsymbol{W}^{\mathscr{R}} = B\boldsymbol{\theta} +\boldsymbol{W}^{\mathscr{R}}, \end{aligned}$$

where $E\boldsymbol {W}^{\mathscr {R}}=0$, $\operatorname {\mathrm {\text{Cov}}}(\boldsymbol {W}^{\mathscr {R}})= \vartheta ^2\Sigma$ denotes the variance-covariance matrix of $\boldsymbol {W}^{\mathscr {R}}$, $\Sigma = \operatorname {\mathrm {\text{Cov}}}(\boldsymbol {Y}^{\mathscr {R}})$, B = [1, b] is the known design matrix, and θ = (μ, 𝜗)′ is the (unknown) parameter vector. Notice that the distribution of $\boldsymbol {Y}^{\mathscr {R}}$ is parameter free, and it depends only on the standard member F.

Thus, as pointed out in [1, Chapter 11], least squares estimation can be applied in order to obtain the best linear unbiased estimator (BLUE) of θ (see, e.g., [127]) as

$$\displaystyle \begin{aligned} \widehat{\boldsymbol{\theta}}= (B'\Sigma^{-1}B)^{-1} B'\Sigma^{-1} \boldsymbol{X}^{\mathscr{R}}. \end{aligned}$$

Obviously, the estimator can be applied when the first and second moments of $\boldsymbol {X}^{\mathscr {R}}$ can be computed (at least numerically). This has been done for many distributions. For instance, given exponential distributions, explicit expressions result since the respective moments have a closed form expression (see, e.g., [128,129,130]). For m ≥ 2, the BLUEs $\widehat \mu _{\textsf {LU}}$ and $\widehat \vartheta _{\textsf {LU}}$ are given by

$$\displaystyle \begin{aligned} \widehat{\mu}_{\textsf{LU}}& =X_{1:m:n}-\frac{\widehat{\vartheta}_{\textsf{LU}}}n,\\ \widehat{\vartheta}_{\textsf{LU}} &=\frac{1}{m-1}\sum_{j=2}^m (R_j+1)(X_{j:m:n}-X_{1:m:n}). \end{aligned} $$

Further results for particular distributions are summarized in [1, Chapter 11]. In case of Weibull distributions, the model can be transformed to a linear model from extreme value distributions by a log-transformation of the data. Thus, estimators of the Weibull parameters can be obtained by using the BLUEs of the transformed parameters when the data results from an extreme value distribution. Results in this direction can be found in [24, 131, 132]. The mixture representation in terms of order statistics can also be utilized to compute the moments (see [17, 133, 134]).

Similar to least squares estimation, one can consider the best linear equivariant estimators (BLEEs). This problem has been discussed, e.g., by Balakrishnan et al. [135], Burkschat [136] (see also [137] for the best linear (risk) invariant estimators).

The most popular approach to the estimation problem is likelihood inference since the joint pdf given in (9.2) leads to tractable expressions in many situations (see [1, Chapter 12]). For generalized Pareto distributions, explicit expressions result. For exponentially distributed lifetimes with mean 𝜗, the MLE is given by

$$\displaystyle \begin{aligned} \widehat\vartheta_{\textsf{MLE}}= \frac{1}{m}\sum_{j=1}^m(R_j+1)X_{j:m:n} =\frac{1}{m}\sum_{j=1}^m S_j^{\mathscr{R}}, \end{aligned} $$

(9.8)

which is also the BLUE in this model. The representation in terms of the spacings $S_1^{\mathscr {R}},\dots , S_m^{\mathscr {R}}$ is important in the analysis of the MLE since it enables easy derivation of the exact distribution of the MLE. For two-parameter exponential distribution, explicit expressions for the MLEs are also available. For Weibull distribution Wei(𝜗, β), the MLE $(\widehat \vartheta ,\widehat \beta )$ of (𝜗, β) uniquely exists (see [138]). They are given by $\widehat \vartheta =\frac {1}{m}\sum _{j=1}^m(R_j+1)X_{j:m:n}^{\widehat \beta }$ where, for the observed data X_j:m:n = x_j, 1 ≤ j ≤ m, the estimate $\widehat \beta$ is the unique solution of the equation:

$$\displaystyle \begin{aligned} \frac{m}\beta+\sum_{j=1}^m \log x_j-\frac{\sum_{j=1}^m(R_j+1)\log(x_j) x_j^\beta}{\sum_{j=1}^m(R_j+1) x_j^\beta}=0. \end{aligned}$$

The above equation has to be solved numerically, e.g., by the Newton-Raphson procedure. Ng et al. [98] proposed an EM-algorithm approach to compute the MLE (see also [139]) which, suitably adapted, has successfully been applied for other distributions, too. Results on likelihood inference for other distributions can be found in [1, Chapter 12]. Recent references for other distributions are, e.g., [140] (Rayleigh), [141] (modified Weibull), [142, 143] (Lindley), and [144] (Gompertz).

For some distributions, related concepts like modified and approximate maximum likelihood estimation have been discussed. The latter concept due to [145] has been successfully applied in many cases, e.g., for extreme value distribution [146] and Weibull distributions [147] (see also [1, Chapter 12.9.2]).

Bayesian inference has also been discussed considerably for progressively type II censored data under various loss functions (see [1, Chapter 15]). Under squared error loss function, the Bayes estimate of the scale parameter α = 1∕𝜗 of an exponential lifetime is given by the posterior mean

$$\displaystyle \begin{aligned} \widehat\alpha_{\textsf{B}} = \frac{a+m}{ b+\sum_{j=1}^m (R_j+1) X_{j:m:n}^\beta} \end{aligned}$$

given a gamma prior

$$\displaystyle \begin{aligned} \pi_{a, b}( \alpha) = \frac{b^a}{\Gamma(a)}\alpha^{a-1} \mbox{\textsf{e}}^{-b\alpha}, \quad \alpha>0, \end{aligned}$$

with hyperparameters a, b > 0. Using a similar inverse gamma prior, [148] obtained the corresponding Bayes estimator of 𝜗 as

$$\displaystyle \begin{aligned} \widehat\vartheta_{\textsf{B}}= \frac{1}{a+m-1}\Big(\sum_{j=1}^m \gamma_j(X_{j:m:n}-X_{j-1:m:n})+b\Big), \end{aligned}$$

where X_0:m:n = 0. Two-parameter Weibull distribution with appropriate priors has been discussed in [149] and [150]. For further results, we refer to [1, Chapter 15].

Using a counting process approach, [94] and [151] have addressed nonparametric inference with progressively type II censored lifetime data for the population cdf F and the survival function. For instance, they presented a Nelson-Aalen-type estimator and a smoothed hazard rate estimator as well as asymptotic results for these estimators. A survey is provided in [1, Chapter 20].

2.2.2 Statistical Intervals

Various kinds of statistical intervals have been discussed for progressively type II censored data. In particular, confidence intervals have been studied under different assumptions. In some situations, exact confidence intervals with level 1 − α can be constructed using properties of the estimators. For exponential distribution, it follows from the independence of the spacings (9.3) that the distribution of the MLE $\widehat \vartheta _{\textsf {MLE}}$ in (9.8) can be obtained as $2m\widehat \vartheta _{\textsf {MLE}}/\vartheta \sim \chi ^2 (2m)$. Hence, $\left [\frac {2m\widehat {\vartheta }_{\textsf {MLE}}}{\chi ^2_{1-\alpha /2}(2m)}, \frac {2m\widehat {\vartheta }_{\textsf {MLE}}}{\chi ^2_{\alpha /2}(2m)}\right ]$ is a two-sided (1 − α)-confidence interval for 𝜗. Similarly, one may obtain confidence intervals and confidence regions for the two-parameter exponential distribution (see [1, Chapter 17], [152]). For Wei(𝜗, β)-distribution, [153] has obtained confidence intervals for the scale and shape parameters of a Wei(𝜗, β)-distribution using a transformation to exponential data and the independence of the spacings. An exact (1 − α)-confidence interval for β is given by

$$\displaystyle \begin{aligned} \mathscr{K}=\Big[ \psi^*(\boldsymbol{X}^{\mathscr{R}},\textsf{F}_{\alpha/2}(2(m-1),2)), \psi^*(\boldsymbol{X}^{\mathscr{R}},\textsf{F}_{1-\alpha/2}(2(m-1),2)) \Big],\end{aligned}$$

where $\psi ^*(\boldsymbol {X}^{\mathscr {R}}, \omega )$ is the unique solution for β of the equation

$$\displaystyle \begin{aligned} \sum_{j=2}^m (R_j+1)\Big(\frac{X_{j:m:n}}{X_{1:m:n}}\Big)^\beta =\gamma_2+n(m-1) \omega. \end{aligned}$$

Wang et al. [154] established a confidence interval for β using the pivotal quantity

$$\displaystyle \begin{aligned} \tau(\boldsymbol{X}^{\mathscr{R}},\beta) = 2\sum_{j=1}^{m-1} \log \left(\frac{\sum_{i=1}^{m} (R_i+1)X_{i:m:n}^\beta}{\sum_{i=1}^{j-1} (R_i+1)X_{i:m:n}^\beta+\gamma_jX_{j:m:n}^\beta}\right).\end{aligned}$$

They showed that an exact (1 − α)-confidence interval for β is given by

where $\tau ^{-1}(\boldsymbol {X}^{\mathscr {R}}, \omega )$ is the unique solution for β of the equation $\tau (\boldsymbol {X}^{\mathscr {R}}, \beta )=\omega$ with ω > 0. A simultaneous confidence region has been obtained by Wu [153]. The same ideas may be applied to Pareto distributions (see [155,156,157,158]). In [158, 159], and [160], optimal confidence regions are discussed (for a location-scale family, see [161]). Nonparametric confidence intervals for quantiles have been discussed in [133] (for multiple samples, see [162, 163]). Exact confidence intervals based on conditional inference have been proposed for progressively type II censored data by Viveros and Balakrishnan [25] (see also [2, Chapter 9]). In particular, exponential, extreme value, log-gamma distributions, Pareto, and Laplace have been discussed. Asymptotic confidence intervals have been applied in various situations by assuming asymptotic normality of some pivotal quantities. The asymptotic variance is estimated by the observed likelihood. Generalized confidence intervals for distribution parameters using Weerahandi’s approach (see [164]) can be found in [154].

Furthermore, prediction intervals and tolerance intervals have been discussed. References for the latter concept are [134, 162, 165, 166]. The highest posterior density credible intervals have been established in [148, 149], and [167].

2.2.3 Prediction

Prediction problems have been discussed for both point and interval prediction, respectively (see [1, Chapter 16 & 17.4]). In particular, they have been considered for:

• (I) Progressively censored failure times at censoring steps 1, …, m; in particular, the progressively censored ordered failure times $W_{j,1:R_j},\dots , W_{j,R_j:R_j}$, 1 ≤ j ≤ m, are predicted.

• (II) For future observations in the same sample (this is a particular case of (I) in the sense that the lifetimes of the items removed in the final progressive censoring step are predicted).

• (III) Observations of an independent future sample from the same population.

Problem (I) has been considered by Basak et al. [168] (the special case $W_{m,1:R_m},\dots , W_{m,R_m:R_m}$ is addressed by Balakrishnan and Rao [169]). Given exponential lifetimes with unknown mean 𝜗, they found that the best unbiased predictor of the rth ordered progressively censored lifetime $W_{j,r:R_j}$ in step j is given by

$$\displaystyle \begin{aligned} \widehat{W}_{j,r:R_j}(\boldsymbol{X}^{\mathscr{R}}) =X_{j:m:n} +\widehat\vartheta_{\textsf{MLE}} \sum_{k=1}^r \frac{1}{R_j-k+1}, \end{aligned}$$

where $\widehat \vartheta _{\textsf {MLE}}$ is the MLE of 𝜗. Further results have been obtained for extreme value distribution [168], normal distribution [170], and Pareto distribution [171]. Prediction intervals based on various prediction concepts (e.g., best linear unbiased prediction, maximum likelihood prediction, and median unbiased prediction) have been obtained for exponential and extreme value distributions in [168]. Normal and Pareto distributions are considered in [170] and [171], respectively. Generalized exponential and Rayleigh distributions are discussed in [172] and [173], respectively.

The best linear unbiased/equivariant prediction of future observations X_r+1:m:n, …, X_m:m:n, based on the first r progressively type II censored order statistics X_1:m:n, …, X_r:m:n, has been discussed in [136]. The same problem has been investigated in a Bayesian framework, too, and the corresponding results can be found in [148] and [152]. Prediction intervals for a general class of distributions, including exponential, Weibull, and Pareto distributions, can be seen in [174]. Results for Weibull distribution have also been presented in [175].

Problem (III) has mainly been discussed in a Bayesian framework. Relevant references are [141, 143, 175,176,177,178,179,180,181,182,183]. Results on nonparametric prediction of future observations can be found in [134, 162, 184].

2.2.4 Testing

Statistical tests under progressive censoring have mainly been discussed in the context of precedence-type testing, homogeneity, and goodness-of-fit tests. A good source for precedence-type tests is [185] (see also [1, Chapter 21]). Particular results can be found in [186] and [187]. Homogeneity tests based on several progressively type II censored samples have been addressed in [188]. For related results in terms of sequential order statistics, we refer to [23]. A review on goodness-of-fit-tests for exponential distributions, including a power study, has recently been presented in [114] (see also [1, Chapter 19]). Goodness-of-fit tests for location-scale families are discussed in, e.g., [189]. Tests have been constructed by means of spacings and deviations from the uniform distribution as well as from the empirical distribution function (e.g., Kolmogorov-Smirnov-type statistics; see [190, 191]). Furthermore, information measures like (cumulative) Kullback-Leibler information and entropy have been used (see [106, 111, 113]).

2.3 Experimental Design

Initiated by Balakrishnan and Aggarwala [2, Chapter 10], problems of experimental design have been discussed extensively for progressively type II censored lifetime experiments. A review on various results and optimality criteria has been provided by Balakrishnan and Cramer [1, Chapter 26]. Assuming that progressive type II censoring is carried out by design, the experimenter has to choose an appropriate censoring plan prior to the start of the experiment. Thus, assuming the sample size n and the number m of observed items as fixed, the censoring plan $\mathscr {R}=(R_1,\dots , R_m)$ has to be chosen in an optimal way. Burkschat [58] has formulated the problem as a mathematical optimization problem in a very general way (see also [192, 193]), that is, given a criterion $\psi : \mathscr {C}^m_{m,n}\longrightarrow \mathbb {R}$, a censoring plan $\mathscr {S}$ is said to be ψ-optimal if

$$\displaystyle \begin{aligned}\psi (\mathscr{S}) =\min_{\mathscr{R} \in \mathscr{C}^m_{m,n}} \psi (\mathscr{R}), \end{aligned}$$

where $\mathscr {C}^m_{m,n}$ is given in (9.1). Various optimality criteria have been used, e.g., probabilistic criteria [58], variance criteria [2, 139, 192,193,194], information measures like Fisher information [100, 104, 105, 139] and entropy [107, 195, 196], optimal estimation of quantiles [139, 149, 197, 198], Pitman closeness [117], and optimal block censoring [97]. A detailed review is provided in [1, Chapter 26].

It turns out that the optimal designs depend heavily on both the optimality criterion to be used and the distributional assumption made. Due to the large number of admissible censoring plans, i.e., $\binom {n-1}{m-1}$ (see [1, p. 531]), [199] proposed a variable neighborhood search algorithm to identify optimal plans in a reasonable time. It should be mentioned that the so-called one-step censoring plans turn out to be optimal in many cases. This means that progressive censoring is carried out only at one failure time, whereas at the other failure times no censoring occurs. Such plans are discussed in [100, 102], and [200]. Recently, restrictions on censoring plans have been addressed in [49].

2.4 Connection of Progressive Type II Censoring to Coherent Systems

Cramer and Navarro [201] established a connection of failure data from coherent systems to progressively type II censored order statistics. They showed that the joint distribution of the component failures (Y₍₁₎, …, Y_(m)) (given the number M = m of component failures leading to the system failure) in a coherent system can be seen as a mixture of progressively type II censored order statistics:

$$\displaystyle \begin{aligned} P^{Y_{(1)},\dots, Y_{(m)}|M=m} = \sum_{\boldsymbol{r}\in \mathcal{S}_m} P(\mathscr{R}=\boldsymbol{r}|M=m)P^{X_{1:m:n}^{\boldsymbol{r}},\dots, X_{m:m:n}^{\boldsymbol{r}}}, \end{aligned} $$

(9.9)

where $\mathcal {S}_m$ denotes the set of all admissible censoring plans r = (r₁, …, r_m) of length m. The probabilities $P(\mathscr {R}=\boldsymbol {r}|M=m)$ depend only on the structure of the coherent system and therefore can be calculated directly [see also 202]. Utilizing this connection, inference for coherent system data can be carried out using inferential methods for progressively type II censored data. For exponentially distributed lifetimes as well as PHR models, we refer to [201], while Weibull distribution is discussed in [203].

Cramer and Navarro [202] applied this connection to define a progressive censoring signature (PC-signature)which can be used to compare the lifetimes of different coherent systems with respect to stochastic orderings.

2.5 Connection of Progressive Type II Censoring to Ordered Pooled Samples

In (9.9), a mixture of some random variables in terms of progressively type II censored order statistics has been established. A similar mixture representation has been found in the context of pooling two independent type II censored samples. Let X_1:n, …, X_r:n and Y_1:m, …, Y_s:m be independent right censored samples from a uniform distribution with sample sizes n and m, respectively. Without loss of any generality, let r ≥ s and denote the ordered pooled sample by W₍₁₎ ≤⋯ ≤ W_(r+s). Then, [162] showed that the joint distribution of the ordered pooled sample W₍₁₎, …, W_(r+s) is a mixture of uniform progressively type II censored order statistics, that is,

$$\displaystyle \begin{aligned} P^{W_{(1)}, \dots, W_{(r+s)}} &= \sum_{j=0}^{r-1} \pi_j P^{(T_{1:r+s:n+m}^{\mathscr{R}_j},\dots, T_{r+s:r+s:n+m}^{\mathscr{R}_j})} \\ &\quad + \sum_{j=0}^{s-1} \pi_j^* P^{(T_{1:r+s:n+m}^{\mathscr{R}_j^*},\dots, T_{r+s:r+s:n+m}^{\mathscr{R}_j^*})}, \end{aligned} $$

with appropriately chosen discrete probability distributions π₀, …, π_r−1 and $\pi _0^*,\dots , \pi _{s-1}^*$ and two-step censoring plans $\mathscr {R}_j$, 0 ≤ j ≤ r − 1 and $\mathscr {R}_j^*$, 0 ≤ j ≤ s − 1, respectively [162], [1, Section 17.1.6]. An extension to multiple pooled samples is presented in [204].

3 Progressive Type I Censoring

As mentioned in Sect. 9.1, progressive type I censoring as introduced in [5] does not have a prefixed termination time, that is, the last censoring time T_m (see Fig. 9.1) has not been considered as termination time. As pointed out in [6], inference for this model has been considered up to the early 1990s (see, e.g., [5, 205,206,207,208,209], and the monographs by Nelson [210] and Cohen and Whitten [211]). In the following, we call this censoring scheme Cohen’s progressive censoring with fixed censoring times. The understanding of T_m as a time censoring point seems to have changed after the publication of the monograph [2] [see also 7]. Since then, almost all publications dealing with progressive type I censoring interpret T_m as the termination time of the experiment.

3.1 Distributional Results for Cohen’s Progressive Censoring with Fixed Censoring Times

We start with a short review of progressive censoring with fixed censoring times as presented in [6]. In principle, the procedure is quite similar to progressive type II censoring, but the censoring times are fixed in advance. Due to this property, we have to distinguish the initially planned censoring plan $\mathscr {R}^0 = (R_1^0, \ldots , R_{m}^0)$ and the effectively applied censoring plan $\mathscr {R} = (R_1, \ldots , R_{m})$ (see [1, 2]) where

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathscr{R}^0 & =&\displaystyle \left(R_1^0, \ldots, R_{m}^0\right)\in \mathscr{C}^{m}_{l,n} \\ & =&\displaystyle \Big\{\big(r_1, \ldots, r_{m}\big) \in \mathbb{N}_0^{m} \, \big| \, r_{\bullet m} \leq n - l\Big\}, \quad l \in \{0, \ldots, n\}, \end{array} \end{aligned} $$

with $m, n\in \mathbb {N}$ and $0\le R_j\le R_j^0$, 1 ≤ j ≤ m, and $\mathscr {C}^{m}_{l,n}$ denotes the set of admissible censoring plans. As mentioned in the introduction, the censoring times of a progressively type I censored life test are prefixed, and the number of observations is random. Thus, we get a sample $X_{1:K:n}^{I} \leq \cdots \leq X_{K:K:n}^{I}$ with random censoring plan $\mathscr {R}$ and random sample size K. Notice that the important difference between progressive censoring with fixed censoring times and progressive type I censoring is the fact that we can ensure a minimum number of observations, that is, $K\ge n - R_{\bullet m}^0 \geq n - (n - l) = l$. Moreover, it is possible to observe values exceeding the threshold T_m. Progressive type I censoring can be interpreted as a type I hybrid version of progressive censoring with fixed censoring times (see Sect. 9.4.2). Denoting the number of observations in the intervals

$$\displaystyle \begin{aligned} (-\infty, T_1], \ (T_1, T_2], \ \ldots, \ (T_{m-1}, T_{m}], \ (T_{m}, \infty)\end{aligned}$$

by the random variables D₁, D₂, …, D_m, D_m+1 and by d₁, …, d_m+1 their realizations, the effectively applied censoring numbers are given by

$$\displaystyle \begin{aligned} R_j =R_j(\boldsymbol{d}_{j})= \min\big\{R_j^0, [n - d_{\bullet j} - R_{\bullet j-1}]_+\big\}, \quad 1 \leq j \leq m, \end{aligned}$$

where n − d_•i − R_•i−1 equals the number of units still remaining in the experiment before the ith withdrawal at time T_i. Notice that D_m+1 is a (deterministic) function of D₁, …, D_m, i.e., D_m+1 = n − D_•m − R_•m. Then, the set

$$\displaystyle \begin{aligned} \mathfrak{D}_{(m+1)} = \big\{\boldsymbol{a}_{m+1} \in \mathbb{N}_0^{m+1} \, \big| \, a_i &\leq [n - a_{\bullet i-1} - R_{\bullet i-1}(\boldsymbol{a}_{i-1})]_+, \\ &\quad i = 1, \ldots, m, \\ &\quad a_{m+1} =[n - a_{\bullet m} - R_{\bullet m}(\boldsymbol{a}_{m})]_+ \big\} \end{aligned}$$

denotes the support of (D₁, …, D_m+1) for a progressively censored life test with fixed censoring times.

Similarly to Theorem 9.2.1, we get the following quantile representation.

Theorem 9.3.1

Suppose $X_{1:K:n}^{I} \leq \cdots \leq X_{K:K:n}^{I}$ and $U_{1:K:n}^{I} \leq \cdots \leq U_{K:K:n}^{I}$ are progressively censored order statistics with fixed censoring times based on a continuous cdf F and a standard uniform distribution, respectively. The censoring times are given by T₁, …, T_m and F(T₁), …, F(T_m), respectively. Then,

$$\displaystyle \begin{aligned}\Big(X_{1:K:n}^{I}, \ldots, X_{K:K:n}^{I}\Big) \mathop{=}\limits^{\textsf{d}} {} \Big(F^{\leftarrow}\big(U_{1:K:n}^{I}\big), \ldots, F^{\leftarrow}\big(U_{K:K:n}^{I}\big)\Big).\end{aligned}$$

Assuming $X_1, \ldots , X_n \overset {\text{iid}}\sim F$ with an absolutely continuous cdf F and a pdf f, T_m+1 = ∞, and R_m+1 = 0, the joint pdf $f^{\boldsymbol {X}^{I},\boldsymbol {D}_{m+1}}$ of $\boldsymbol {X}^{I,\mathscr {R}}=(X_{1:K:n}^{I}, \ldots , X_{K:K:n}^{I})$ and D_m+1 = (D₁, …, D_m+1) is given by

$$\displaystyle \begin{aligned} &f^{\boldsymbol{X}^{I,\mathscr{R}},\boldsymbol{D}_{m+1}}(\boldsymbol{x}_k,\boldsymbol{d}_{m+1}) \\ &\ \ = \!\biggl\{ \prod_{j=1}^{{m+1}} \binom{n - d_{\bullet j-1} - R_{\bullet j-1}}{d_j} d_j! \, \big[1 {-} F(T_j)\big]^{R_j}\biggr\} \biggl\{ \prod_{i=1}^{k} f(x_{i})\biggr\} \end{aligned} $$

(9.10)

for $\boldsymbol {d}_{m+1} \in \mathfrak {D}_{(m+1)}$ with k = d_•m+1 and x₁ ≤⋯ ≤ x_k. Clearly, (9.10) can be rewritten as

$$\displaystyle \begin{aligned} f^{\boldsymbol{X}^{I,\mathscr{R}},\boldsymbol{D}_{m+1}}(\boldsymbol{x}_k,\boldsymbol{d}_{m+1}) = C(\boldsymbol{d}_{m+1}) \prod_{j=1}^{{m+1}} \big[1 - F(T_j)\big]^{R_j} \prod_{i=1}^{k} f(x_{i})\end{aligned}$$

which illustrates the structural similarities to the pdf under progressive type II censoring given in (9.2). Notice that the value of D_(m+1) is defined uniquely by $\boldsymbol {X}^{I,\mathscr {R}}=(X_{1:K:n}^{I}, \ldots , X_{K:K:n}^{I})$.

The joint probability mass function $p^{\boldsymbol {D}_{m+1}}$ of D_m+1 is given by

$$\displaystyle \begin{aligned} p^{\boldsymbol{D}_{m+1}}(\boldsymbol{d}_{m+1}) &= \prod_{j=1}^{m+1} \binom{n - d_{\bullet j-1} - R_{\bullet j-1}}{d_j} \, \big[F(T_j)-F(T_{j-1})\big]^{d_j} \\ &\quad \times \big[1 - F(T_j)\big]^{R_j}, \boldsymbol{d}_{m+1} \in \mathfrak{D}_{(m+1)}. \end{aligned} $$

Further, the conditional density function of $\boldsymbol {X}^{I,\mathscr {R}}$, given D_m+1, is given by

$$\displaystyle \begin{aligned} f^{\boldsymbol{X}^{I,\mathscr{R}}|\boldsymbol{D}_{m+1}} (\boldsymbol{x}_k \mid \boldsymbol{d}_{m+1}) = \prod_{j=1,d_j>0}^{{m+1}} f^{(j)}_{1 \ldots d_j:d_j}(\boldsymbol{x}_{d_j}) \, {\mathbb{I}}_{(T_{j-1},T_j]}(\boldsymbol{x}_{d_j}) \end{aligned} $$

(9.11)

for $\boldsymbol {d}_{m+1} \in \mathfrak {D}_{(m+1)}$ with m = d_•m+1 and x₁ ≤⋯ ≤ x_k. $f^{(j)}_{1 \ldots d_j:d_j}$ denotes the density function of order statistics $X^{(j)}_{1:d_j}, \ldots , X^{(j)}_{d_j:d_j}$ from the (doubly) truncated cdf F in the interval (T_j−1, T_j].

As for progressive type II censoring, the conditional block independence of progressively censored order statistics with fixed censoring times holds which for progressive type I censoring and progressive type II censoring has first been established by Iliopoulos and Balakrishnan [39]. It follows directly from the joint pdf. Conditionally on (D₁, …, D_m+1) = (d₁, …, d_m+1), the progressively censored order statistics with fixed censoring times are block independent, that is, the random vectors

$$\displaystyle \begin{aligned} \Big(X_{d_{\bullet j-1}+1:d_{\bullet {m^*+1}}:n}^{I}, \ldots, X_{d_{\bullet j}:d_{\bullet {m^*+1}}:n}^{I}\Big), \quad j\in\{1 \leq i \leq m+1 \mid d_i>0\}, \end{aligned} $$

are independent with

$$\displaystyle \begin{aligned} &\Big(X_{d_{\bullet j-1}+1:d_{\bullet {m^*+1}}:n}^{I}, \ldots, X_{d_{\bullet j}:d_{\bullet {m^*+1}}:n}^{I}\Big) \\ &\quad \overset{d}= \Big(X^{(j)}_{1:d_j}, \ldots, X^{(j)}_{d_j:d_j}\Big), \quad j\in\{1 \leq i \leq m+1 \mid d_i>0\}, \end{aligned} $$

where $X^{(j)}_{1:d_j}, \ldots , X^{(j)}_{d_j:d_j}$ are order statistics from the (doubly) truncated cdf F in the interval (T_j−1, T_j], j ∈{1 ≤ i ≤ k∣d_i > 0}.

3.2 Distributional Results for ProgressiveType I Censoring

Since progressive type I censoring results from Cohen’s progressive censoring model with fixed censoring times by interpreting the final censoring time T_m as a threshold or termination point, the respective sample results from $X_{1:K:n}^{I} \leq \cdots \leq X_{K:K:n}^{I}$ is given by $\boldsymbol {X}^{I,\mathscr {R},T_m}=(X_{1:K:n}^{I} ,\dots , X_{D_{\bullet m}:K:n}^{I})$. Notice that this sample may result in an empty sample when all items are either progressively censored at T₁, …, T_m−1 or right censored at T_m. Thus, no failures have been observed due to the time censoring at T_m. As a consequence, inferential results are often obtained and discussed subject to the assumption that at least one failure has been observed, that is, D_•m ≥ 1 which happens with probability

$$\displaystyle \begin{aligned}P(D_{\bullet m}\ge1) =1-\prod_{i=1}^m\big(1-F(T_i)\big)^{R_i^0}. \end{aligned}$$

Then, the distributional results presented before can be applied to progressive type I censoring. For instance, the quantile representation in Theorem 9.3.1 holds, too. The pdf of $\boldsymbol {X}^{I,\mathscr {R},T_m}$ and D_m can be seen as a marginal pdf of (9.10) with an appropriate restriction on the domain. This leads to the pdf

$$\displaystyle \begin{aligned} & f^{\boldsymbol{X}^{I,\mathscr{R},T_m}, \boldsymbol{D}_{m}}(\boldsymbol{x}_k, \boldsymbol{d}_m) \\ &\quad =\left\{\prod_{i=1}^m \binom{n-d_{\bullet i-1}-R_{\bullet i-1}}{d_i} d_i![ 1-F(T_i)]^{R_i}\right\}\\ &\qquad \qquad \qquad \qquad \qquad \qquad \qquad \Big\{\prod_{j=1}^{k} f(x_{j}) \Big\}\end{aligned} $$

(9.12)

for $\boldsymbol {d}_m\in \mathfrak {D}_{(m)}$ with k = d_•m ≥ 1 and x₁ ≤⋯ ≤ x_k ≤ T_m (see [1, p. 121]). Notice that R_m is defined differently in comparison with (9.10).

Apart from the above presented results, almost no probabilistic results seem to be available for (Cohen’s) progressively type I censored order statistics. Obviously, this is caused by the problems due to the random sample size K and the random censoring plan $\mathscr {R}$. Nevertheless, numerous inferential results have been obtained.

3.3 Inference

Most of the results established in progressive type I censoring are connected to likelihood inference. Since the likelihood functions are given by the joint pdfs (9.10) and (9.12), respectively, the MLEs can be obtained by direct optimization. In the following, we present only the progressive type I censoring model (with time censoring). Similar results can be obtained for Cohen’s progressive censoring with fixed censoring times model (see, e.g., [6]). A summary with more details is provided in [1, Chapter 12]. Notice that, due to the similarity of the likelihood function to the progressive type II censoring case, the computation of MLEs proceeds quite similarly to this case. In particular, explicit expressions result in the same cases, and the likelihood equations are similar (replace the censoring time T_i in progressive type I censoring by the observed failure time X_i:m:n in progressive type II censoring; cf. (9.8) and (9.13)). For exponentially distributed lifetimes with mean 𝜗, one gets the MLE as

$$\displaystyle \begin{aligned} \widehat\vartheta_{\textsf{MLE}}^{I} = \frac{1}{K}\left[\sum_{i=1}^K X_{i:K:n}^{I} + \sum_{j=1}^{m} R_j T_j\right]. \end{aligned} $$

(9.13)

Although the structure is similar to the MLE under progressive type II censoring, the distribution of the estimator is quite complicated. Using a moment generating function approach, [212] established the conditional pdf of $\widehat \vartheta ^{I}_{\textsf {MLE}}$, given D_•m ≥ 1, as a generalized mixture of (shifted) gamma distributions (for a direct approach under progressive censoring with fixed censoring times, see [6]). Establishing the stochastic monotonicity of the (conditional) survival function by the three monotonicity lemmas (see also [212,213,214]), constructed exact (conditional) confidence intervals for 𝜗 using the method of pivoting the cdf (see [215,216,217]). A multi-sample model has been studied in [218] who presented an alternate representation of the pdf in terms of B-spline functions. Two-parameter exponential distribution Exp(μ, 𝜗) has been considered, e.g., in [211, 219], and [220]. Cohen [219] proposed also modified MLEs. Weibull distribution has been discussed in [205, 219, 221, 222], and [2]. Explicit expressions for the MLEs are not available, and the estimates have to be computed by numerical procedures. Balakrishnan and Kateri [138] have established the existence and uniqueness of the MLEs. Three-parameter Weibull distributions are considered in [206, 208], and [223]. Further distributions considered are, e.g., extreme value distribution [219], normal distribution [5], Burr-XII distribution [209], and logistic distribution [224].

4 Sampling Models Based on Progressively Censored Data

Progressively type I and type II censored data have been considered as a basis for inferential purposes in various models. In the following, we sketch some of these applications and provide some recent references.

4.1 Progressive (Type I) Interval Censoring

In progressive type I censoring, the number of observations observed between censoring times is random. It is assumed that only these numbers are observed (see Fig. 9.5), whereas the exact values of the failure times are not observed. This kind of data has been introduced in [7] (see also [1, Chapter 12]) assuming an absolutely continuous cdf F_θ. This yields the likelihood function (cf. (9.11))

$$\displaystyle \begin{aligned} L (\boldsymbol{\theta}) \propto \prod_{j=1}^m \big(F_{\boldsymbol{\theta}}(T_j)-F_{\boldsymbol{\theta}}(T_{j-1})\big)^{d_j}\overline{F}^{R_j}_{\boldsymbol{\theta}}(T_j), \end{aligned}$$

where $\boldsymbol {\theta }=(\theta _1,\dots , \theta _p)'\in \Theta \subseteq \mathbb {R}^p$ denotes the parameter vector and d₁, …, d_m are realizations of the number of observed failures D₁, …, D_m. T₀ = −∞ < T₁ < ⋯ < T_m are the censoring times, and $\mathscr {R}=(R_1,\dots , R_m)$ is the effectively applied censoring plan.

Inferential results have been established for various distributions. Asymptotic results for MLEs with general distribution have been established in [225]. Exponential distribution has been discussed in [7] and [226]. For (inverse) Weibull distribution, we refer to [226, 227], and [228]. Further distributions considered are generalized exponential distributions [228,229,230], generalized Rayleigh distribution [231], gamma distribution [232], and Burr-XII [233]. Further examples are given in [1, Chapter 18].

Under progressive type I censoring, the optimal choice of both inspection times and censoring proportions has been addressed by many authors [1, Chapter 18.2 & 18.3]. Other relevant references in this direction are [225, 233,234,235,236,237,238,239,240,241].

4.2 Progressive Hybrid Censoring

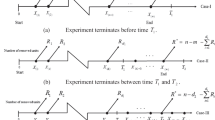
In progressive hybrid censoring, progressive type II censored data is subject to, e.g., additional time censoring at some threshold T. There are many variations available in the literature so far. For reviews, see [242], [1, Chapter 5 & 14], [12, 243, 244] and the recent monograph [380]. For illustration, we sketch the idea of the two basic hybrid censoring models under progressive censoring. Let $D= \sum _{i=1}^m \mathbb {I}_{(-\infty , T]}(X_{i:m:n})$ denote the total number of observed failures. As in [10], we perceive the data with possibly less than m observed failure times as a sample of size m by adding the censoring time in the required number. For a progressively type II censored sample X_1:m:n, …, X_m:m:n with censoring plan $\mathscr {R}$, type I progressively hybrid censored order statistics $X^{h,I}_{1:m:n},\dots , X^{h,I}_{m:m:n}$ are defined via

$$\displaystyle \begin{aligned} X^{h,I}_{j:m:n} = \min (X_{j:m:n}, T), \quad 1\le j\le m. \end{aligned} $$

(9.14)

Notice that the names type I/type II progressive hybrid censoring are differently used in the literature which may result in some confusion. From (9.14), it is evident that the sample may include both observed failure times and censoring times. Conditionally on D = d, d ∈{0, …, m}, we have

For d = 0, the experiment has been terminated before observing the first failure, and, thus, the sample is given by the constant data $(T,\dots , T)\in \mathbb {R}^m$. Some probabilistic results have been obtained (see [1, Chapter 5], [10]). For instance, as under progressive type II censoring, a quantile representation similar to that given in Theorem 9.2.1 holds. The (conditional) joint pdf is given by Childs et al. [see also 8, 9]:

$$\displaystyle \begin{aligned} & f^{X^{h,I}_{j:m:n}, 1\le j\le m|D=d}(\boldsymbol{t}_d,T^{*(m-d})\\ &\quad = \frac{C_d}{P(D=d)} (1-F(T))^{\gamma_{d+1}} f_{1,\dots, d:d:n-\gamma_{d+1}}^{\mathscr{R}_d}(\boldsymbol{t}_d), \quad t_1\le \dots \le t_d\le T, \end{aligned} $$

where $f_{1,\dots , d:d:n-\gamma _{d+1}}^{\mathscr {R}_d}$ denotes the pdf of the progressively type II censored sample with a censoring plan $\mathscr {R}_d$. In case of the exponential distribution, [10] established the (conditional) joint density function of the spacings $W^{h,I}_{j:m:n}= \gamma _j (X^{h,I}_{j:m:n}-X^{h,I}_{j-1:m:n})$, 1 ≤ j ≤ d, as

$$\displaystyle \begin{aligned} & f^{W^{h,I}_{j:m:n}, 1\le j\le d|D=d}(\boldsymbol{w}_{d}) = \frac{\gamma_{d+1}\mbox{\textsf{e}}^{-\gamma_{d+1}(T-\mu)/\vartheta}}{\vartheta f_{d+1:m:n}(T)} \\ &\qquad \qquad \qquad \qquad \times \left[\prod_{j=1}^d \frac{1}{\vartheta}\exp\left\{-\Big(1-\frac{\gamma_{d+1}}{\gamma_j} \Big)\frac{w_j}\vartheta\right\}\right], \\ &\qquad \qquad \qquad \qquad \boldsymbol{w}_d\in \mathcal{W}_d(T), \end{aligned} $$

with support

$$\displaystyle \begin{aligned} \mathcal{W}_d(T) = \Big\{ \boldsymbol{w}_d \mid w_j\ge 0, 1\le j\le d, \sum_{j=1}^d \frac{w_j}{\gamma_j} \le T-\mu \Big\}.\end{aligned}$$

As a difference to the case of progressive type II censoring, the spacings are no longer independent although the pdf exhibits a product structure. These results can be utilized to obtain the exact distribution of the MLE for exponential lifetimes. A moment generating function approach is advocated in, e.g., [8]. The MLE of 𝜗 exists provided D > 0 and is given by

$$\displaystyle \begin{aligned} \widehat\vartheta= \frac{1}{D} \left[\sum_{j=1}^D \gamma_j(X^{h,I}_{j:m:n}-X^{h,I}_{j-1:m:n}) +{\gamma}D_{d+1}T\right] . \end{aligned}$$

Its distribution can be written in terms of B-spline functions (see [10]) or in terms of shifted gamma functions (see [8]). The connection of the particular representations has been studied in [243]. The result can be applied to construct exact (conditional) confidence intervals by pivoting the cdf since the corresponding survival function is stochastically monotone (see [213, 214, 245]). For the multi-sample case, we refer to [246]. Results for two-parameter exponential distribution are given in [10] and [247]. Inference for Weibull distribution has been discussed in [248]. Results for other distributions can be found in, e.g., [249,250,251,252,253,254,255]. Optimal censoring plans are discussed in [256, 257].

Childs et al. [8] and Kundu and Joarder [9] proposed an alternative hybrid censoring procedure called type II progressive hybrid censoring. Given a (fixed) threshold time T, the life test terminates at $T_2^*=\max \{X_{m:m:n},T\}$. This approach guarantees that the life test yields at least the observation of m failure times. Given the progressively type II censored sample X_1:m:n, …, X_m:m:n with an initially planned censoring plan $\mathscr {R}=(R_1,\dots , R_m)$, the right censoring at time X_m:m:n is not carried out. The monitoring of the failure times after X_m:m:n is continued until time T is reached or the maximum in the extended progressively type II censored sample

$$\displaystyle \begin{aligned} X_{1:m+R_m:n},\dots, X_{m:m+R_m:n}, X_{m+1:m+R_m:n},\dots, X_{m+R_m:m+R_m:n} \end{aligned} $$

(9.15)

is observed. Notice that this sample can be viewed as progressively type II censored data with extended censoring plan $\mathscr {R}^*=(R_1,\dots , R_{m-1}, 0,\dots , 0)$ of length m + R_m. Furthermore, $\gamma _j=\sum _{i=j}^m(R_i+1)$, j = 1, …, m − 1, γ_j = m + R_m − j + 1, j = m, …, m + R_m. As in the case of type I progressive hybrid censoring, the random counter $D= \sum _{i=1}^{m+R_m} \mathbb {I}_{(-\infty , T]}(X_{i:m+R_m:n})$ represents the sample size having support {0, …, m + R_m}. Again, the exact distribution of the MLE given by

$$\displaystyle \begin{aligned} \widehat\vartheta = \begin{cases}\displaystyle \frac{1}{m}\sum_{j=1}^m (R_j+1) X_{j:m:n}, & D<m\\ \displaystyle \frac{1}{D} \bigg(\sum_{j=1}^m (R_j+1) X_{j:m:n} +\sum_{j=m+1}^D X_{j:m+R_m:n} + \gamma_{D+1}T\bigg), & D\ge m \end{cases} \end{aligned}$$

can be obtained. Furthermore, exact confidence intervals can be established (see [8, 258]) since the cdf is stochastically monotone (see [214]). For the multi-sample case, we refer to [259]. Inferential results for this kind of data have been obtained in, e.g., [8, 9, 258, 260]. Mokhtari et al. [261], Alma and Arabi Belaghi [262], and Noori Asl et al. [263].

There are many extensions on this basic progressive hybrid censoring. Generalized progressive hybrid censoring is discussed in, e.g., [243, 264,265,266,267,268,269,270]. Further extensions can be found in [12] and [271]. The Fisher information in hybrid censoring schemesis discussed in [272] and [273]. Furthermore, interval censored data have been studied in [274].

4.3 Adaptive Progressive Censoring

A common feature of the abovementioned progressive censoring schemes is that the design of the experiment (i.e., initially planned censoring plan, censoring times) is prefixed, that is, these quantities are known in advance. Since such a design may not be possible or be useful in practical situations, [13] came up with the idea that the censoring plan may be adapted during the experiment. Given some prefixed censoring plan $\mathscr {S}=(S_1,\ldots , S_m)$ and a threshold T, the plan is adapted after step $j^*=\max \{j:X_{j:m:n}<T\}$ such that no further censoring is carried out until the mth failure time has been observed. Hence, the censoring plan is changed at the progressive censoring step j^∗ + 1, i.e., at the first observed failure time exceeding the threshold T. The effectively applied censoring plan in the Ng-Kundu-Chan model is given by $\mathscr {S}^*=(S_1,\ldots , S_{j^*},0,\dots , 0,n-m-\sum _{i=1}^{j^*} S_i)$. This model has been extensively investigated, and many results have been obtained (see [248, 260, 275, 276]).

A general approach to adaptive progressive censoring has been proposed by Cramer and Iliopoulos [15] allowing for a flexible choice of the censoring plan and the censoring times. This approach covers both adaptive progressive type I and adaptive progressive type II censoring. Adaptive progressive type II censoring has been discussed in detail in [14] who particularly showed that the model covers the Ng-Kundu-Chan model as well as the model of progressive type II censoring with random removals (see also [1, Chapter 6]). The latter model has been proposed by Yuen and Tse [277] assuming that the censoring numbers are chosen according to some probability distribution on the set of possible censoring numbers. Further references discussing this model are, e.g., [278,279,280]. For interval censored data, we refer to [281] and [282]. Flexible progressive censoring introduced in [283] can also be seen as a special adaptive progressive censoring model (see also [284, 285]).

4.4 Reliability and Stress-Strength Reliability

Applications in reliability based on progressively type II censored data have been addressed by many authors. The analysis is mostly based on a single progressively type II censored sample X_1:m:n, …, X_m:m:n, but the situation of multiple samples has also been taken into account. In the following, we summarize some scenarios where this kind of data has been considered.

Given a lifetime X with cdf F, the reliability function $R=\overline {F}=1-F$ can be estimated parametrically and nonparametrically. Nonparametric estimators under progressive censoring are mentioned in Sect. 9.2.2. Parametric estimators of R_θ can be constructed as plug-in estimators by replacing θ by an appropriate estimator $\widehat {\theta }$, e.g., the MLE (see, e.g., [142, 286,287,288,289,290,291]). Furthermore, Bayesian approaches have also been extensively discussed. However, for exponential distributions and $t\in \mathbb {R}$, the UMVUE of R_𝜗(t) = P_𝜗(X > t) is given by (see (9.8))

$$\displaystyle \begin{aligned} \widehat{R}(t)=\left(1- \frac{t}{m \widehat\vartheta_{\textsf{MLE}}}\right)^{m-1} \mathbb{I}_{[t, \infty)}(m\widehat\vartheta_{\textsf{MLE}})\end{aligned}$$

(see [292]). The result can be slightly extended to an exponential family with cdf F_𝜗 defined by $F_\vartheta (t) =1-\exp (-g(t)/\vartheta )$ and a suitable function g (see, e.g., [23, 293]).

Inference for the stress-strength reliability R = P(X < Y ) has also been addressed under progressive censoring for various distributions (for a general account, see [294]). For exponential distribution, the problem has been considered in terms of Weinman exponential distributions in [295] and [296]. For two independent progressively type II censored samples $X_{1:m:n}^{\mathscr {R}},\dots , X_{m:m:n}^{\mathscr {R}}$ and $Y_{1:r:s}^{\mathscr {S}},\dots , Y_{r:r:s}^{\mathscr {S}}$, based on exponential distributions Exp(𝜗₁) and Exp(𝜗₂), the MLEs of the parameters are given by $\widehat \vartheta _{j,\textsf {MLE}}$, j = 1, 2, as in (9.8). Then, the MLE of $R=\frac {\vartheta _2}{\vartheta _1+\vartheta _2}$ is given by $R_{\textsf {MLE}}=\frac {\widehat \vartheta _2}{\widehat \vartheta _1+\widehat \vartheta _2}$. Furthermore, the UMVUE is given by

$$\displaystyle \begin{aligned} \widehat R_{\textsf{UMVUE}}=\begin{cases} \sum\limits_{j=0}^{r-1} (-1)^j \frac{\binom{r-1}j}{\binom{m+j-1}j} \bigg(\frac{m\widehat\vartheta_{1,\textsf{MLE}}}{r\widehat\vartheta_{2,\textsf{MLE}}}\bigg)^j, & m\widehat\vartheta_{1,\textsf{MLE}} \le r\widehat\vartheta_{2,\textsf{MLE}} \\ 1- \sum\limits_{j=0}^{m-1} (-1)^j \frac{\binom{m-1}j}{\binom{r+j-1}j} \bigg(\frac{r\widehat\vartheta_{2,\textsf{MLE}}}{m\widehat\vartheta_{1,\textsf{MLE}}}\bigg)^j, & m\widehat\vartheta_{1,\textsf{MLE}}> r\widehat\vartheta_{2,\textsf{MLE}} \end{cases} \end{aligned}$$

Saraçoğlu et al. [see also 297, who addressed Bayesian inference, too]. Confidence intervals are discussed in [295, 296], and [297]. Two-parameter exponential distributions with common location parameter are investigated in [295, 296] [see also 1, Chapter 24]. Other distributions considered in the literature are generalized (inverted) exponential distribution [289, 298], Weibull distribution [299, 300], generalized Pareto distributions [301], the PHR model [302, 303], Birnbaum-Saunders distribution [304], generalized logistic distribution [305], and finite mixtures [306].

Stress-strength models under joint progressive censoring have been considered in [307]. Progressively type I interval censored data has been discussed by Bai et al. [306].

4.5 Competing Risks

In competing risk modeling, it is assumed that a unit may fail due to several causes of failure. For two competing risks, the lifetime of the ith unit is given by

$$\displaystyle \begin{aligned} X_i = \min\left\{X_{1i}, X_{2i}\right\}, \quad i=1,\ldots,n,\end{aligned}$$

where X_ji denotes the latent failure time of the ith unit under the jth cause of failure, j = 1, 2. In most models considering competing risks under a progressive censoring scheme, the latent failure times are assumed to be independent with X_ji ∼ F_j, j = 1, 2, i = 1, …, m. Additionally, the sample X₁, …, X_n is progressively type II censored, and it is assumed that the cause of each failure is known. Therefore, the available data are given by

$$\displaystyle \begin{aligned} \left(X_{1:m:n}, C_1\right), \left(X_{2:m:n}, C_2\right), \ldots, \left(X_{m:m:n}, C_m\right),\end{aligned}$$

where C_i = 1 if the ith failure is due to first cause and C_i = 2 otherwise. The observed data is denoted by (x₁, c₁), (x₂, c₂), …, (x_m, c_m). Further, we define the indicators

$$\displaystyle \begin{aligned} \mathbb{I}_{\{j\}}(C_i) = \begin{cases} 1,& C_i=j \\ 0,& \text{otherwise} \end{cases}. \end{aligned}$$

Thus, the random variables $m_1 = \sum _{i=1}^m \mathbb {I}_{\{1\}}(C_i)$ and $m_2 = \sum _{i=1}^m \mathbb {I}_{\{2\}}(C_i)$ describe the number of failures due to the first and the second cause of failure, respectively. Given the assumptions, m₁ and m₂ are binomials with sample size m and probability of success R = P(X₁₁ ≤ X₂₁) and 1 − R, respectively. For a given censoring plan $\mathscr {R}=(R_1,\ldots , R_m)$, the joint pdf is given by Kundu et al. [see 308]

$$\displaystyle \begin{aligned} &f^{\boldsymbol{X}^{\mathscr{R}},\boldsymbol{C}} (\boldsymbol{x}_m,\boldsymbol{c}_m)\\ &\quad =\Big( \prod_{j=1}^m \gamma_j\Big) \prod_{i=1}^m\Big[\left[f_1(x_i)\overline{F}_2(x_i)\right]^{\mathbb{I}_{\{1\}}(c_i)}\, \left[f_2(x_i)\overline{F}_1(x_i)\right]^{ \mathbb{I}_{\{2\}}(c_i)} \left[\overline{F}_1(x_i)\overline{F}_2(x_i)\right]^{R_i} \Big]. \end{aligned} $$

[308] discussed competing risks for Exp(𝜗_j)-distributions, j = 1, 2, under progressive type II censoring. The MLEs of the parameters are given by

$$\displaystyle \begin{aligned} \widehat\vartheta_j= \frac{1}{m_j}\sum_{i=1}^m (R_i+1)X_{i:m:n}, \quad j=1,2, \end{aligned}$$

provided that m_j > 0. In this framework, inferential topics like point and interval estimation as well as prediction problems have been discussed. To keep things short, we provide references for further reading. Competing risks under progressive type II censoring have been considered for, e.g., Weibull distribution [309,310,311], Lomax distribution [312], half-logistic distribution [313], and Kumaraswamy distribution [314].

Progressive type I interval censoring in the presence of competing risks has been investigated by Wu et al. [234], Azizi et al. [315], and Ahmadi et al. [316]. Competing risks under hybrid censoring are investigated in, e.g., [317,318,319,320,321,322,323,324,325].

4.6 Applications to System Data

In the standard models of progressive censoring, it is assumed that the underlying random variables are iid random variables distributed according to a cdf F. Progressive censoring has also been studied in terms of iid system data $Y,\dots , Y_n\overset {\text{iid}}\sim G$, where G = h ∘ F with some known function h and a cdf F. F is supposed to model the component lifetime, whereas h describes the technical structure of the system. In a series system with s components, we have G = F^s with h(t) = t^s. For a parallel system with s components, the function h is given by h(t) = 1 − (1 − t)^s.

As pointed out in [1, Chapter 25], the case of progressively type II censored series system data is included in the standard model by adapting the censoring plan appropriately. Given a censoring plan $\mathscr {R}=(R_1,\dots , R_m)$ and series systems with s components, the corresponding progressively type II censored system data can be interpreted as standard progressively type II censored data with censoring plan

$$\displaystyle \begin{aligned} \mathscr{S}=s\mathscr{R} +(s-1)(1^{*m}), \text{ i.e., } S_j = sR_j +s-1, j=1,\dots, m.\end{aligned}$$

This kind of data has also been entitled first-failure censored data (see, e.g., [326, 327]), and many results have been published for this model. However, as mentioned before, the respective results are covered in the standard model by adapting the censoring plan.

The situation is more involved for parallel or, more general, for coherent systems. Parallel systems are studied in [166, 328, 329], and [330]. k out-of-n system data is addressed in [331], and coherent systems are addressed in [332].

4.7 Applications in Quality Control

Applications of progressively censored data in quality control have been discussed in terms of reliability sampling plans (acceptance sampling plans) and the lifetime performance index, respectively.

Reliability sampling plans based on progressively type II censored exponential lifetimes have been considered by Balasooriya and Saw [333], Balakrishnan and Aggarwala [2], and [334] [see also 1, Chapter 22]. For a progressively censored sample $\boldsymbol {X}^{\mathscr {R}}$ from an Exp(μ, 𝜗)-distribution, the MLEs of the parameters are used to estimate the parameters and, thus, to construct the decision rule. Since the distributions of the MLEs do not depend on the censoring plan $\mathscr {R}$, the resulting sampling plans coincide with those for type II right censoring. Pérez-González and Fernández [335] established approximate acceptance sampling plans in the two-parameter exponential case. Balasooriya et al. [147] addressed reliability sampling plans for a Weibull distribution employing the Lieberman-Resnikoff procedure for a lower limit using the approximate MLEs of the parameters. Ng et al. [139] tackled the same problem using the MLEs. Fernández et al. [336] considered progressively censored group sampling plans for Weibull distributions. For a log-normal distribution, [337] applied the Lieberman-Resnikoff approach using approximate BLUEs for the location and scale parameters. Further reference in this direction is [338].

Inference for the lifetime performance index (or capability index) has been discussed for various distributions in [339] including exponential and gamma distributions (see also [340,341,342,343]). Weibull distribution has been considered in [344, 345], and Rayleigh distribution in [341]. Lomax and Pareto distributions are discussed by Mahmoud et al. [346] and Ahmadi and Doostparast [347], respectively. Progressively type I interval censored data has been considered in [348,349,350].

4.8 Accelerated Life Testing

In accelerated life testing, progressive censoring has been mostly discussed in terms of step-stress testing. Recent reviews on the topic are provided by Kundu and Ganguly [351] and Balakrishnan and Cramer [1, Chapter 23] (see also [352]). Assuming a cumulative exposure model for the lifetime distribution, the basic model in simple step-stress model with a single stress change point is applied to progressively type II censored data, that is, at a prefixed time τ, the stress level is to be increased to a level s₁ > s₀ (see Fig. 9.6). Then, the data

$$\displaystyle \begin{aligned} X_{1:r:n} < \cdots < X_{D:r:n} \leq \tau < X_{D+1:r:n} < \cdots < X_{r:r:n} \end{aligned}$$

results where D denotes the number of failures observed before τ. Obviously, the sample X_1:r:n, …, X_D:r:n is a type I progressive hybrid censored sample so that the inferential results can be taken from this area. Assuming exponential lifetimes with means 𝜗₁ and 𝜗₂ (before and after τ) as well as a cumulative exposure model, the MLEs of the parameters are given by

$$\displaystyle \begin{aligned} \begin{array}{rcl} \widehat\vartheta_1 & =&\displaystyle \frac{1}{D}\left(\sum^{D}_{k=1} (R_k + 1)X_{k:r:n} + \tau\gamma_{D+1}\right),\quad \\ \widehat\vartheta_2 & =&\displaystyle \frac{1}{r-D}\sum^r_{k=D+1} (R_k + 1)(X_{k:r:n} - \tau), \end{array} \end{aligned} $$

provided that 1 ≤ D ≤ r − 1. As mentioned above, distributional results for $\widehat \vartheta _1$ are directly obtained from type I progressive hybrid censoring leading to, e.g., exact (conditional) confidence intervals (see [353, 354]). Using the result in (9.6), we get $2(r-D)\widehat \vartheta _2/\vartheta _2|D=d \sim \chi ^2(2r-2d)$, d < r. In particular, $E(\widehat \vartheta _2|D=d) =\vartheta _2$ and $\operatorname {\mathrm {\text{Var}}}(\widehat \vartheta _2|D=d)=\vartheta ^2_2/(r-d)$. Weibull lifetimes are investigated in [355]. Extensions to multiple stress changing times are discussed in [356, 357]. The model has also been discussed for progressive type I interval censored data (see [358,359,360]).

Fig. 9.6

Step-stress testing with single stress change time τ

Wang and Yu [361] discussed a simple step-stress model where the stress changing time τ is replaced by a failure time $X_{r_1:r:n}$. It is shown in [1, p. 492] that this model is connected to sequential order statistics which can be utilized to establish easily properties of the resulting MLEs. Following the ideas of [362], a multiple step-stress model with additional progressive censoring has been proposed in [1, p. 503]. The resulting model corresponds to that proposed in [361] and is further discussed in [363].

Another kind of accelerated life testing model in the presence of progressive censoring, called progressive stress model, has been proposed by Abdel-Hamid and AL-Hussaini [364].

4.9 Stage Life Testing

A common argument used to justify progressive censoring is that the intentionally removed objects are utilized for other tests (cf., e.g., [2, p. 3], [365, p. 336]). In order to include such an information in the statistical analysis, [366] connected the notion of progressive censoring with ideas from accelerated life testing and proposed a stage life testing model with a single stage change time. In fact, they adapted the idea of step-stress testing and assumed that the removed objects are tested on a different level, whereas the remaining items are still tested under standard conditions. The basic situation with a single censoring time τ and two stages s₀, s₁ is depicted in Fig. 9.7.

Fig. 9.7

Stage life testing with single stage change time τ

Inspired by simple step-stress testing (see Fig. 9.6), the stage life testing model is introduced as follows. Assume that n identical objects are placed on a life test. The initial conditions are called stage s₀. At the prefixed stage-change time τ, $0\le R_1^\star \le n$ of the surviving items are randomly withdrawn (if possible) and further tested on stage s₁. Notice that this may be regarded as a different life test with used components. The testing of the remaining items is continued on stage s₀. The life test terminates when all n objects have failed.

Let D₁ and D₂ denote the random number of failures occurring on stage s₀ before and after τ₁, respectively. Furthermore, M = D₁ + D₂ and

• $\boldsymbol {Y}_{1,D_1} = \big (Y_{1:M:n}, \ldots , Y_{D_1:M:n}\big )$ denote the (ordered) observations on stage s₀ before τ.

• $\boldsymbol {Y}_{2,D_2} = \big (Y_{D_1+1:M:n}, \ldots , Y_{D_1+D_2:M:n}\big )$ denote the (ordered) observations on stage s₀ after τ.

• $\boldsymbol {Z}_{R^{\star }_1} = \big (Z_{1:R^{\star }_1}, \ldots , Z_{R^{\star }_1:R^{\star }_1}\big )$ denote the (ordered) observations on stage s₁ after τ with $Y_{D_1:M:n} \leq \tau < Z_{1:R^{\star }_1}$.

The order statistics on stage s₀ and the order statistics on stage s₁ are represented by the random vectors $\boldsymbol {Y} = \big (\boldsymbol {Y}_{1,D_1} , \boldsymbol {Y}_{2,D_2}\big )$ and Z, respectively. Figure 9.7 illustrates this representation of the stage life testing order statistics.

Assuming a cumulative exposure model with cdfs F₀ and F₁ and utilizing progressive censoring with fixed censoring times (see [6]), inferential results have been obtained for exponential, Weibull, and other lifetime distributions. The results are based on the joint pdf $f^{\boldsymbol {Y},\boldsymbol {Z},D_1}_{1 \ldots n}$ of (Y , Z) and D₁ given by

$$\displaystyle \begin{aligned} & f^{\boldsymbol{Y},\boldsymbol{Z},D_1}_{1 \ldots n}(\boldsymbol{y}_{1,d_1},\boldsymbol{y}_{2,d_2},\boldsymbol{z},d_1) \\ & \quad = \binom{n}{d_1} d_1! \, d_2! \, r^{\star}_1! \, \prod_{h = 1}^{d_1+d_2} f_0(y_{h:m:n}) \,\prod_{j = 1}^{r^{\star}_1} f_1(z_{j:r^{\star}_1} + v_1 - \tau), \end{aligned} $$

for $\boldsymbol {y}_{1,d_1} {=} (y_{1:m:n}, \ldots , y_{d_1:m:n})$, $\boldsymbol {y}_{2,d_2} {=} (y_{d_1+1:m:n}, \ldots , y_{d_1+d_2:m:n})$, and $\boldsymbol {z} = (z_{1:r^{\star }_1}, \ldots , z_{r^{\star }_1:r^{\star }_1})$, where $d_2 = n - d_1 -r^{\star }_1$, and $r^{\star }_1 = \varrho (d_1)$ denotes the number of objects selected for testing on stage s₁. f_i denotes the pdf of F_i, i ∈{0, 1}.

In fact, the function ϱ may be chosen according to the needs of the experimenter. Inspired by procedures to generate the censoring number in progressive censoring (see [7]), [366] proposed two options to define $R^{\star }_1$, that is,

$$\displaystyle \begin{aligned} R^{\star}_1 &= \varrho(D_1) \quad \text{with} \quad \\ \varrho(x) &= \begin{cases} \lfloor \pi_1 \cdot (n-x) \rfloor, & \text{Type-P} \\[1ex] \min\big\{n - x,R^0_1\big\}, & \text{Type-M} \end{cases}, \quad x\in \{0,\dots, n\}, \end{aligned} $$

where the proportion π₁ ∈ [0, 1] and the number $R^0_1 \in \mathbb {N}$ are prespecified, respectively. Under the type P scheme, at τ, a (fixed) proportion π₁ of the surviving objects is selected for testing on stage s₁. In case of the type M scheme, given a prefixed number $R_1^0$, it is intended to select at τ as many items as possible (at most $R_1^0$) for testing on stage s₁.

Assuming exponential lifetimes with means 𝜗₀ and 𝜗₁, the corresponding MLEs are obtained as

$$\displaystyle \begin{aligned} \widehat{\vartheta}_0 &= \frac{1}{D_1 + D_2} \left( \sum_{i = 1}^{D_1+D_2} Y_{i:M:n} + R^{\star}_1 \tau \right), \\ \widehat{\vartheta}_1 & =\frac{1}{R^{\star}_1} \left(\sum_{j = 1}^{R^{\star}_1} Z_{j:R^{\star}_1} - R^{\star}_1 \tau \right) \ (\text{provided that }R^{\star}_1 > 0). \end{aligned} $$

As for other progressive censoring models, exact inferential results, e.g., exact confidence intervals, can be established. An extension to multiple stage change times τ₁ < ⋯ < τ_m has been introduced in [367]. Stage changes at failure times are discussed in [368]. For a survey on these models as well as more details, we refer to [369].

4.10 Joint Progressive Censoring Schemes

In joint progressive type II censoring, the sample is based on two baseline samples $X_1,\dots , X_{n_1}\overset {\text{iid}}\sim F_1$ (product/type A) and $Y_1,\dots , Y_{n_2}\overset {\text{iid}}\sim F_2$ (product/type B) of independent random variables. The progressive censoring is applied to the pooled sample $X_1,\dots , X_{n_1}, Y_1,\dots , Y_{n_2}$ given a prefixed censoring $\mathscr {R}\in \mathscr {C}^m_{m,n_1+n_2}$. Moreover, it is assumed that the type of the failed unit as well as the types of withdrawn units are known. Therefore, the sample is given by $(\boldsymbol {C}, \boldsymbol {W}^{\mathscr {R}}, \mathscr {S})$, where

$$\displaystyle \begin{aligned} \boldsymbol{C} &= (C_1,\dots, C_m)\in \{0, 1\}^m, \\ \boldsymbol{W}^{\mathscr{R}} &= (W_{1:m:n_1+n_2},\dots, W_{m:m:n_1+n_2}), \mathscr{S} = (S_1,\dots, S_m). \end{aligned} $$

The indicators C_j have the value 1 if the failed unit is of type A, and otherwise C_j = 0. W_j:m:n denotes the jth failure time in the progressively censored experiment. Finally, $\mathscr {S}$ denotes a random censoring plan. S_j is the number of removed units of type A in the jth withdrawal. Thus, R_j − S_j denotes the numbers of withdrawn units of type B at the jth censoring step. This model has been discussed in [370,371,372,373,374,375,376]. Joint progressive type I censoring has been proposed in [377]. A hybrid version is discussed in [378]. Another version of joint progressive censoring leading to more tractable results has been investigated in [376] and [379].