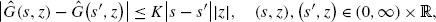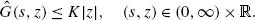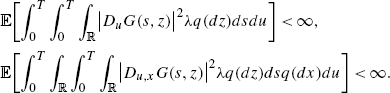Abstract
We solve linear BSDEs which may arise in actuarial applications. Since solving a linear BSDE requires to find the predictable representation of a random variable, we show how to derive the predictable representation of an insurance payment process. We consider the case of a life insurance and a non-life insurance payment process under systematic and unsystematic claims risk. We apply both the Itô’s formula and the Malliavin calculus to derive the control processes of linear BSDEs. The representations of the control processes involve conditional expectations which can be explicitly calculated or estimated by Monte Carlo methods.
Access provided by Autonomous University of Puebla. Download chapter PDF
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
In this chapter we solve linear BSDEs which may arise in actuarial applications. We illustrate two methods based on the Itô’s formula and the Malliavin calculus which can be used to derive the control processes of linear BSDEs. Linear BSDEs are important for applications. In Chap. 9 a linear BSDE is used to characterize the replicating strategy for a liability, and in Chap. 10 linear BSDEs are used to characterize the optimal (in the mean-square sense) hedging strategy for a liability. We also remark that nonlinear BSDEs which we face when investigating pricing and hedging of liabilities under model ambiguity and the entropic risk measure may be reduced to linear BSDEs, see Propositions 3.3.3 and 3.4.3 and Example 3.4. Since solving a linear BSDE requires to find the predictable representation of a random variable, in this chapter we show how to derive the predictable representation of an insurance payment process. We consider the case of a life insurance and a non-life insurance payment process under systematic and unsystematic claims risk.
1 The Application of the Itô’s Formula
Let us investigate the financial model

and the equity-linked (life insurance) liabilities

where J denotes the deaths counting process for a life insurance portfolio consisting of n policies. We assume that the mortality intensity is given by the dynamics

For an actuarial and financial motivation we refer to Examples 7.2 and 7.7. We model the longevity risk by a stochastic process which solves a forward SDE describing the time evolution of the mortality intensity. Such stochastic models are advocated in the actuarial literature, see Russo et al. (2011) and Schrager (2006). We can also assume that r depends on S and allow for time-dependent dynamics. Then, we can follow the same arguments to derive the control processes of a BSDE. Let us recall that the jump measure N of the point process J has the compensator ϑ(dt,{1})=(n−J(t−))λ(t)dt.
The value of the insurance liabilities is given by

If we consider the market-consistent value, then the expectation should be taken under an equivalent martingale measure, see Sect. 9.1. From Propositions 3.3.1 and 3.4.1 we conclude that the value process (8.1) satisfies the linear BSDE

The dynamics (8.2) is formulated under the real-world probability measure \({\mathbb{P}}\). If we took the expectation (8.1) under an equivalent probability measure \({\mathbb{Q}}\), then the BSDE (8.2) would be formulated under \({\mathbb{Q}}\). Introducing the process \(V(t)=U(t)-\hat{G}(S(t))\) and recalling the forward dynamics of S and λ, we can investigate the FBSDE

The goal is to characterize the control processes (Z 1,Z 2,V) of the linear BSDE (8.3). We use the Itô’s formula.
Proposition 8.1.1
Consider the linear BSDE (8.3). Assume that
-
(i)
the jump measure N of the point process J has the compensator ϑ(dt,{1})=(n−J(t−))λ(t)dt,
-
(ii)
the processes S and λ are positive,
-
(iii)
the functions μ:(0,∞)→[0,∞),σ:(0,∞)→[0,∞) and μ λ:(0,∞)→[0,∞),σ λ:(0,∞)→[0,∞) are Lipschitz continuous,
-
(iv)
the functions \(\hat{F}:(0,\infty)\rightarrow[0,\infty),\hat {H}:(0,\infty)\rightarrow[0,\infty)\) and \(\hat{G}:(0,\infty)\rightarrow [0,\infty)\) are Lipschitz continuous.
We define measurable functions \(\hat{h}:[0,T]\times[0,T]\times(0,\infty )\rightarrow[0,\infty),\hat{f}:[0,T]\times[0,T]\times(0,\infty )\rightarrow[0,\infty), \hat{g}:[0,T]\times[0,T]\times(0,\infty )\rightarrow[0,\infty), p:[0,T]\times[0,T]\times(0,\infty)\rightarrow (0,\infty)\) and \(\hat{p}:[0,T]\times[0,T]\times(0,\infty)\rightarrow [0,\infty)\) such that for 0≤t≤u≤T we set

and for 0≤u<t≤T we set \(\hat{h}=\hat{f}=\hat{g}=p=\hat{p}=0\). We further assume that
-
(v)
for each 0≤u≤T the functions \(\hat{h}(.,u,.),\hat {f}(.,u,.), \hat{g}(.,u,.)\), p(.,u,.) and \(\hat{p}(.,u,.)\) are of the class
 .
.
The control processes \((Z_{1},Z_{2},V)\in\mathbb{H}^{2}({\mathbb{R}})\times\mathbb {H}^{2}({\mathbb{R}})\times\mathbb{H}^{2}_{N}({\mathbb{R}})\) of the BSDE (8.3) take the form

where \(\hat{f}_{s}(t,u,s)=\frac{\partial}{\partial s}\hat{f}(t,u,s)\), \(\hat {h}_{s}(t,u,s)=\frac{\partial}{\partial s}\hat{h}(t,u,s)\), \(\hat {g}_{s}(t,u,s)=\frac{\partial}{\partial s}\hat{g}(t,u,s)\), \(p_{\lambda}(t,u,\lambda)=\frac{\partial}{\partial\lambda}p(t,u,\lambda)\), \(\hat {p}_{\lambda}(t,u,\lambda)=\frac{\partial}{\partial\lambda}\hat {p}(t,u,\lambda)\).
Proof
By Theorems 3.1.1 and 4.1.1 there exists a unique solution (Y,Z 1,Z 2,V,S,λ) to (8.3) and the processes S and λ have finite moments. From Propositions 3.3.1 and 3.4.1 we can deduce that the control processes (Z 1,Z 2,V) are obtained from the predictable representation of the martingale

Let us consider the first martingale

We can derive

where we use representation (7.4), the property of conditional expectations, the exponential conditional distribution of τ i and the independence of W and B. We get

The Lipschitz property of \(\hat{F}\), the moment estimate (4.2) for S and square integrability of S imply that  is square integrable. Hence, there exists a unique predictable representation of the martingale
is square integrable. Hence, there exists a unique predictable representation of the martingale  in \(\mathbb {H}^{2}({\mathbb{R}})\times\mathbb{H}^{2}({\mathbb{R}})\times\mathbb{H}^{2}_{N}({\mathbb{R}})\) and the martingale
in \(\mathbb {H}^{2}({\mathbb{R}})\times\mathbb{H}^{2}({\mathbb{R}})\times\mathbb{H}^{2}_{N}({\mathbb{R}})\) and the martingale  can be represented as a sum of three square integrable stochastic integrals driven by W,B and \(\tilde{N}\). Since \(\hat{f}\),
can be represented as a sum of three square integrable stochastic integrals driven by W,B and \(\tilde{N}\). Since \(\hat{f}\),  , we can apply the Itô’s formula and we immediately get the dynamics
, we can apply the Itô’s formula and we immediately get the dynamics

We remark that the Lebesque integral in the Itô’s formula must vanish by the martingale property. Since  and ΔJ(T)=0 a.s. by quasi-left continuity, then
and ΔJ(T)=0 a.s. by quasi-left continuity, then  , and in \(\mathbb{L}^{2}({\mathbb{R}})\) by the dominated convergence theorem. By the growth properties of \(\hat{f}_{s}\), p, \(\hat {f}, p_{\lambda}\), which can be deduced from (4.2) and (8.4), the three stochastic integrals in (8.7) are well-defined square integrable martingales on [0,T]. Hence, we take the limit in \(\mathbb{L}^{2}({\mathbb{R}})\) and we derive
, and in \(\mathbb{L}^{2}({\mathbb{R}})\) by the dominated convergence theorem. By the growth properties of \(\hat{f}_{s}\), p, \(\hat {f}, p_{\lambda}\), which can be deduced from (4.2) and (8.4), the three stochastic integrals in (8.7) are well-defined square integrable martingales on [0,T]. Hence, we take the limit in \(\mathbb{L}^{2}({\mathbb{R}})\) and we derive

We deal with the second martingale

Fix u∈[0,T]. We introduce the process

Following the arguments which led to (8.8), we can obtain

together with the representation

where we introduce the processes  ,
,  and
and  . If we apply the a priori estimate (3.4) to the BSDE (8.9) and we use the Lipschitz property of \(\hat{H}\) and the moment estimate (4.2) for S, then we can derive
. If we apply the a priori estimate (3.4) to the BSDE (8.9) and we use the Lipschitz property of \(\hat{H}\) and the moment estimate (4.2) for S, then we can derive

with K independent of u. Estimate (8.10) also yields

We now obtain the representation of the second martingale  . Using (8.9), we get
. Using (8.9), we get

By the measurability assumptions and property (8.11) we can apply the Fubini’s theorem for stochastic integrals, see Theorem IV.65 in Protter (2004). We change the order of integration in (8.12) and we derive the representation

The representation of the third martingale

is obtained analogously to (8.13). From the representation of the martingale  and Propositions 3.3.1 and 3.4.1 we deduce the formulas for the control processes (Z
1,Z
2,V). □
and Propositions 3.3.1 and 3.4.1 we deduce the formulas for the control processes (Z
1,Z
2,V). □
The assumptions of Proposition 8.1.1 should hold in many cases. We remark that the Lipschitz continuity assumptions of Proposition 8.1.1 can be relaxed, but additional existence and moment assumptions for S and λ would have to be introduced instead. The assumption that the functions \(\hat{f}\), \(\hat{h}\), \(\hat{g}\), \(\hat{p}\) and p are of the class  is mathematically convenient. In fact, this is the key assumption which allows us to apply the Itô’s formula and, consequently, to find the predictable representation and the control processes of the linear BSDE. We recall that prices of call options, put options and survival probabilities in classical financial and actuarial models are sufficiently smooth under appropriate conditions, see Sect. 12.1 in Cont and Tankov (2004) and Chap. 5 in Filipovic (2009). However, the smoothness of prices is not guaranteed and it may require very strong assumptions.
is mathematically convenient. In fact, this is the key assumption which allows us to apply the Itô’s formula and, consequently, to find the predictable representation and the control processes of the linear BSDE. We recall that prices of call options, put options and survival probabilities in classical financial and actuarial models are sufficiently smooth under appropriate conditions, see Sect. 12.1 in Cont and Tankov (2004) and Chap. 5 in Filipovic (2009). However, the smoothness of prices is not guaranteed and it may require very strong assumptions.
The representation of the control processes from Proposition 8.1.1 involve derivatives. If we deal with the classical Black-Scholes model and we assume that the mortality intensity follows the Cox-Ingersoll-Ross process, then \(\hat{f}_{s}\), \(\hat {h}_{s}\), \(\hat{g}_{s}\), \(\hat{p}_{\lambda}\) and p λ have closed form solutions, see Chap. 5 in Shreve (2004) and Chap. 5 in Filipovic (2009). If we consider a more general model, then we can use Proposition 4.1.2 to calculate (or estimate) the derivatives.
2 The Application of the Malliavin Calculus
We investigate the financial model

and the equity-linked (non-life insurance) liabilities

where the random measure N is generated by a compound Poisson process with intensity λ and jump size distribution q. For an actuarial and financial motivation we refer to Examples 7.9 and 7.10.
The value of the insurance liabilities is given by

Following the reasoning that led to (8.3), we consider the FBSDE

Using the Malliavin calculus and the results for FBSDEs from Chap. 4, we show how to derive the control processes (Z,V) without applying the Itô’s formula. The Malliavin calculus allows us to relax smoothness assumptions in our models.
Proposition 8.2.1
Consider the linear BSDE (8.14). Assume that
-
(i)
the random measure N is generated by a compound Poisson process with intensity λ and jump size distribution q,
-
(ii)
the process S is positive,
-
(iii)
the functions μ:(0,∞)→[0,∞) and σ:(0,∞)→(0,∞) are twice continuously differentiable with bounded derivatives,
-
(iv)
the function \(\hat{G}:(0,\infty)\times {\mathbb{R}}\rightarrow [0,\infty)\) is measurable, Lipschitz continuous in the sense that
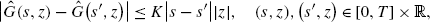
and satisfies the growth condition
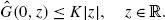
The control processes \((Z,V)\in\mathbb{H}^{2}({\mathbb{R}})\times\mathbb{H}^{2}_{N}({\mathbb{R}})\) of the BSDE (8.14) take the form

where

and \(\hat{G}_{s}(s,z)=\frac{\partial}{\partial s}\hat{G}(s,z)\).
Proof
By Theorems 3.1.1 and 4.1.1 there exists a unique solution (Y,Z,V,S) to (8.14). Since we deal with the Markovian dynamics, we have Y(t)=u(t,S(t)) where

By Theorem 4.1.2 the law of S is absolutely continuous. From Theorem 4.1.2 we conclude that S is Malliavin differentiable and, next, from Propositions 2.6.4–2.6.5 we deduce that \(\int_{{\mathbb{R}}}\hat{G}(S(s),z)\lambda q(dz)\) is Malliavin differentiable for 0≤s≤T. Hence, Theorem 4.1.4 yields the control processes

By the Lipschitz property of \(\hat{G}\) and the moment estimates (4.2) we obtain the inequalities

and

for all \((t,u,s,s',z)\in[0,T]\times[0,t]\times(0,\infty)\times(0,\infty )\times {\mathbb{R}}\). From (8.16) we deduce that the family

is uniformly integrable for fixed \((t,u,s,z)\in[0,T]\times[0,T]\times (0,\infty)\times {\mathbb{R}}\), see the proof of Proposition 4.1.2. By (8.15), the dominated convergence theorem, the uniform integrability of A s′ and Fubini’s theorem we finally derive

where

and we use the fact that \(s\mapsto\hat{G}(S^{t,s}(u),z)\) is a.s. differentiable for \(z\in {\mathbb{R}}\), u∈(t,T]. □
The proof of Proposition 8.2.1 relies on Theorem 4.1.4 which we established for a FBSDE driven by a Brownian motion and a compensated Poisson random measure. It is interesting to note that Theorem 4.1.4 can be applied to BSDEs driven by more general random measures provided that appropriate modifications are introduced.
Let us investigate the financial model

and the equity-linked (non-life insurance) liabilities

where the random measure N is generated by a compound Cox process with compensator ϑ(dt,dz)=λ(S(t))q(dz)dt. Since the intensity λ is contingent on the stock, the systematic claims risk is now considered. For an actuarial and financial motivation we again refer to Examples 7.9 and 7.10. We show that we can replace the random measure N generated by a compound Cox process with a Poisson random measure.
Let us assume that the intensity λ is bounded and set E={y:0≤y≤sup
s>0
λ(s)}. Let N
p denote a Poisson random measure on  . We assume that the compensator of the Poisson random measure N
p is ϑ(dt,dz,dy)=q(dz)dydt. We introduce the random measure
. We assume that the compensator of the Poisson random measure N
p is ϑ(dt,dz,dy)=q(dz)dydt. We introduce the random measure

We can notice that

is a martingale for  by Theorem 2.3.3. Hence, by Definition 2.1.4 the random measure
by Theorem 2.3.3. Hence, by Definition 2.1.4 the random measure  has the compensator λ(S(t))q(dz)dt. From Theorem 11.5 in He et al. (1992) we conclude that the measures N and
has the compensator λ(S(t))q(dz)dt. From Theorem 11.5 in He et al. (1992) we conclude that the measures N and  are indistinguishable. Consequently, we can use the results derived for BSDEs driven by Poisson random measures also in the case when we deal with random measures generated by Cox processes.
are indistinguishable. Consequently, we can use the results derived for BSDEs driven by Poisson random measures also in the case when we deal with random measures generated by Cox processes.
The value of the insurance liability is given by

and we investigate the FBSDE

Proposition 8.2.2
Consider the linear BSDE (8.18). Assume that
-
(i)
the process S is positive,
-
(ii)
the function λ:(0,∞)→E is positive and Lipschitz continuous, and the set E is bounded,
-
(iii)
the random measure N p is defined on
 and it is a Poisson random measure with the compensator
ϑ(dt,dz,dy)=q(dz)dydt
such that
\(q({\mathbb{R}})=1\)
and
\(\int_{{\mathbb{R}}}|z|^{2}q(dz)<\infty\),
and it is a Poisson random measure with the compensator
ϑ(dt,dz,dy)=q(dz)dydt
such that
\(q({\mathbb{R}})=1\)
and
\(\int_{{\mathbb{R}}}|z|^{2}q(dz)<\infty\), -
(iv)
the functions μ:(0,∞)→[0,∞) and σ:(0,∞)→(0,∞) are twice continuously differentiable with bounded derivatives,
-
(v)
the function \(\hat{G}:(0,\infty)\times {\mathbb{R}}\rightarrow[0,\infty )\) is measurable, Lipschitz continuous in the sense that
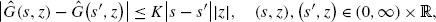
and satisfies the growth condition
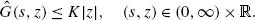
The control processes \((Z,V)\in\mathbb{H}^{2}({\mathbb{R}})\times\mathbb {H}^{2}_{N^{p}}({\mathbb{R}})\) of the BSDE (8.18) take the form

where

and \(\hat{G}_{s}(s,z)=\frac{\partial}{\partial s}\hat{G}(s,z)\).
Proof
We cannot apply Proposition 8.2.1 since the indicator function in the generator of (8.18) is not smooth enough. Let E={y:0≤y≤c} where c=sup
s>0
λ(s). Choose a smooth function  such that φ(x)=1, x≤0, and φ(x)=0, x≥1. It is easy to show
such that φ(x)=1, x≤0, and φ(x)=0, x≥1. It is easy to show

By Theorems 3.1.1 and 4.1.1 there exists a unique solution (Y,Z,V,S) to (8.18), and by Theorem 4.1.2 the law of S is absolutely continuous with respect to the Lebesgue measure. Consider the FBSDE

By Theorems 3.1.1 and 4.1.1 there also exists a unique solution (Y n,Z n,V n,S) to (8.20). The a priori estimates (3.4) and (3.6) together with the Cauchy-Schwarz inequality yield

and by the dominated convergence theorem and (8.19) we get

In order to find the solution (Z,V), we find the solution (Z n,V n) to the BSDE (8.20) and we take the limit. We can now apply Proposition 8.2.1 to (8.20). We obtain the control processes

Notice that for a.a. s>0, for which the derivative λ′(s) exists, we have

and

where we use properties of φ. Combining (8.21) with (8.22), we get

and the limit of Z n can be established by the dominated convergence theorem and properties (8.19), (8.23). □
The results derived so far are only applicable to Markovian dynamics. The power of the Malliavin calculus lies in the fact that it can be applied in a general non-Markovian setting. Let us investigate the financial model

and the liabilities

where the random measure N is generated by a compound Poisson process with intensity λ and jump size distribution q. The drift and volatility of the stock S and the claim G are non-Markov processes. We consider the BSDE

The next proposition shows the benefit of the Malliavin calculus in the theory and applications of BSDEs. Recalling the key results established for the Malliavin derivative and FBSDEs, we can immediately derive the control processes (Z,V) of the BSDE (8.24).
Proposition 8.2.3
Let us consider the natural filtration
 generated by a Brownian motion and a compound Poisson process with intensity
λ
and jump size distribution q. We investigate the linear BSDE (8.24). Assume that
generated by a Brownian motion and a compound Poisson process with intensity
λ
and jump size distribution q. We investigate the linear BSDE (8.24). Assume that
-
(i)
(C1)–(C4) from Chap. 7 hold,
-
(ii)
υ-a.e. \((s,z)\in[0,T]\times {\mathbb{R}}\) the random variable G(s,z) is Malliavin differentiable, and the Malliavin derivative satisfies
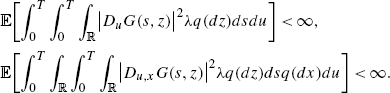
The control processes \((Z,V)\in\mathbb{H}^{2}({\mathbb{R}})\times\mathbb{H}^{2}_{N}({\mathbb{R}})\) of the BSDE (8.24) take form

where
 denotes the predictable projection of the process.
denotes the predictable projection of the process.
Proof
The result follows from Theorem 3.5.1, Propositions 3.5.2, 2.6.3 and 2.6.5. □
Proposition 8.2.1 arises now as a special case of Proposition 8.2.3.
Let us remark that in applications we may face a linear BSDE with a generator which also have a linear term in the control processes (Z,U). By Propositions 3.3.1 and 3.4.1 such a linear term may be absorbed by the random noises and the change of measure. We end up with a linear BSDE with a generator independent of (Z,U) with the dynamics under a different probability measure. After the change of measure, we can use the techniques presented in this chapter to derive the control processes.
We have discussed two methods which can be applied to derive the predicable representations of random variables and representations of the control processes of linear BSDEs. The representations involve expectations of state processes. Such representations are useful since we can use Monte Carlo simulations in numerical applications. As the control processes of BSDEs determine hedging strategies, the results of this chapter point out methods which can be used to establish implementable formulas for hedging strategies.
Bibliographical Notes
In the proof of Proposition 8.1.1 we closely follow the proof from Delong (2010), see also Møller (2001). The idea of replacing a random measure generated by a Cox process by a Poisson random measure is taken from Ankirchner and Imkeller (2008). In the proof of Proposition 8.2.2 we closely follow the arguments from Ankirchner and Imkeller (2008). For applications of the Malliavin calculus to linear BSDEs driven by Brownian motions we refer to El Karoui et al. (1997b).
References
Ankirchner, S., Imkeller, P.: Quadratic hedging of weather and catastrophe risk by using short term climate prediction. Preprint (2008)
Cont, R., Tankov, P.: Financial Modelling with Jump Processes. Chapman and Hall/CRC Press, London (2004)
Delong, Ł.: An optimal investment strategy for a stream of liabilities generated by a step process in a financial market driven by a Lévy process. Insur. Math. Econ. 47, 278–293 (2010)
El Karoui, N., Peng, S., Quenez, M.C.: Backward stochastic differential equations in finance. Math. Finance 7, 1–71 (1997b)
Filipovic, D.: Term-Structure Models. Springer, Berlin (2009)
He, S., Wang, J., Yan, J.: Semimartingale Theory and Stochastic Calculus. CRC Press, Boca Raton (1992)
Møller, T.: Risk minimizing hedging strategies for insurance payment processes. Finance Stoch. 5, 419–446 (2001)
Protter, P.: Stochastic Integration and Differential Equations. Springer, Berlin (2004)
Russo, V., Giacometti, R., Ortobelli, S., Rachev, S., Fabozzi, F.: Calibrating affine stochastic mortality models using term assurance premiums. Insur. Math. Econ. 49, 53–60 (2011)
Schrager, D.: Affine stochastic mortality. Insur. Math. Econ. 38, 81–97 (2006)
Shreve, S.E.: Stochastic Calculus for Finance II: Continuous-Time Models. Springer, Berlin (2004)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer-Verlag London
About this chapter
Cite this chapter
Delong, Ł. (2013). Linear BSDEs and Predictable Representations of Insurance Payment Processes. In: Backward Stochastic Differential Equations with Jumps and Their Actuarial and Financial Applications. EAA Series. Springer, London. https://doi.org/10.1007/978-1-4471-5331-3_8
Download citation
DOI: https://doi.org/10.1007/978-1-4471-5331-3_8
Publisher Name: Springer, London
Print ISBN: 978-1-4471-5330-6
Online ISBN: 978-1-4471-5331-3
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


 .
.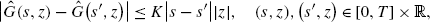
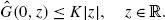
 and it is a Poisson random measure with the compensator
ϑ(dt,dz,dy)=q(dz)dydt
such that
and it is a Poisson random measure with the compensator
ϑ(dt,dz,dy)=q(dz)dydt
such that