Abstract
We investigate pricing and hedging of the insurance payment process under quadratic objectives. Four types of quadratic loss functions are considered. First, we deal with a minimal hedging error in a mean-square sense. The hedging error is evaluated both under an equivalent martingale measure and the real-world measure. Next, we investigate locally risk minimizing strategies which lead to non-self-financing investment portfolio processes. Finally, we minimize an instantaneous mean-variance risk measure of the insurer’s surplus to derive a hedging strategy. The pricing and hedging strategies are characterized by linear and nonlinear BSDEs.
Access provided by Autonomous University of Puebla. Download chapter PDF
Keywords
- Price Process
- Hedging Strategy
- Portfolio Selection Problem
- Equivalent Martingale Measure
- Hedging Portfolio
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
Since a self-financing investment portfolio cannot perfectly replicate the insurance payment process, we aim to find an investment strategy which hedges the payment process with a minimal replication error. It is natural to measure the replication error with a quadratic function. In this chapter we investigate four types of quadratic objectives for pricing and hedging in incomplete markets. Quadratic objectives have gained their importance in portfolio optimization since Markowitz (1952) solved a one-period portfolio selection problem. We point out that the Markowitz mean-variance portfolio selection is used in practice for investment decision making and asset-liability management, see Zenios and Ziemba (2006) and Adam (2007). Let us also remark that replicating portfolios for insurance liabilities are constructed in practice by means of a mean-square criterion, see Boekel et al. (2009).
1 Quadratic Pricing and Hedging Under an Equivalent Martingale Measure
Let an equivalent martingale measure  be given. We formulate our pricing and hedging objective under the measure \({\mathbb{Q}}\). First, we define a class of admissible strategies under \({\mathbb{Q}}\).
be given. We formulate our pricing and hedging objective under the measure \({\mathbb{Q}}\). First, we define a class of admissible strategies under \({\mathbb{Q}}\).
Definition 10.1.1
A strategy π:=(π(t),0≤t≤T) is called admissible under the measure \({\mathbb{Q}}\), written  , if it satisfies the conditions:
, if it satisfies the conditions:
-
(i)
\(\pi:[0,T]\times\varOmega\rightarrow\mathbb{R}\) is a predictable process,
-
(ii)
\(\mathbb{E}^{{\mathbb{Q}}}[\int_{0}^{T} |\pi(t)\sigma(t) |^{2}dt]<\infty\),
-
(iii)
there exists a unique càdlàg, adapted solution X π to (7.11) on [0,T].
If assumptions (C2)–(C4) hold under \({\mathbb{Q}}\), then the wealth process X
π is square integrable under \({\mathbb{Q}}\) for any admissible strategy  , see (7.12).
, see (7.12).
The insurer faces the payment process (7.3). We control the wealth of the insurer at time T which may denote the planning horizon in an ALM study or the point of time when the insurance portfolio terminates. The goal is to find an initial capital x and an admissible investment strategy  which minimize the mean-square hedging error
which minimize the mean-square hedging error

where the investment portfolio process X π,x is given by (7.11). Hence, we aim to find an investment portfolio which hedges the insurance payment process with a minimal replication error at time T. The use of the mean-square objective for measuring the replication error is very natural. The formulation of the objective under an equivalent martingale measure is mathematically and practically convenient, as we discuss later. The optimal capital, or the initial value of the optimal hedging portfolio, yields the price of the payment process.
Theorem 10.1.1
Let an equivalent martingale measure
 be given and assume that (C1)–(C4) from Chap. 7
hold under
\({\mathbb{Q}}\). We consider the quadratic pricing and hedging problem (10.1).
be given and assume that (C1)–(C4) from Chap. 7
hold under
\({\mathbb{Q}}\). We consider the quadratic pricing and hedging problem (10.1).
-
(a)
There exists a unique solution \((Y,Z_{1},Z_{2},U)\in\mathbb {S}^{2}({\mathbb{R}})\times\mathbb{H}^{2}({\mathbb{R}})\times\mathbb{H}^{2}({\mathbb{R}})\times\mathbb {H}^{2}_{N}({\mathbb{R}})\) to the BSDE
 (10.2)
(10.2)where the square integrability conditions for (Y,Z 1,Z 2,U) hold under \({\mathbb{Q}}\).
-
(b)
The optimal initial value of the hedging portfolio x ∗ and the optimal admissible hedging strategy
 for the payment process
P
take the form
for the payment process
P
take the form

Proof
(a) The assertion follows from Theorem 3.1.1.
(b) We recall that the dynamics of X π,x is described by (7.11). By the change of measure, the Girsanov’s theorem and discounting we obtain

From (10.3) we conclude that the mean-square error (10.1) is given by

and by (10.2) we get

Taking the squares and using moment properties of stochastic integrals, see Theorem 2.3.3, we derive

Finally, property (5.5) yields the hedging error

and the optimality of (x ∗,π ∗) follows. The admissability of π ∗ is clear. □
The price and the hedging strategy for the payment process P are characterized by the predictable representation of the discounted payments (or by the linear BSDE (10.2)). The price x ∗ is arbitrage-free. Recalling the interpretation given in Sect. 9.2 and Theorem 4.2.1, we can conclude that the hedging strategy π ∗ is a delta-hedging strategy. The hedging strategy π ∗ is updated with the current information on the financial and the insurance risk.
Example 10.1
We consider the classical Black-Scholes model with constant coefficients r, μ, σ and an insurer who issues a portfolio of n unit-linked endowment policies with a capital guarantee. We are interested in pricing and hedging the claim F=(n−J(T))(K−S(T))+ where J is the deaths counting process for the insurance portfolio. We consider a constant mortality intensity λ and we choose the equivalent martingale measure \({\mathbb{Q}}^{*}\) defined in Theorem 9.2.1. In order to find the price and the optimal hedging strategy for the claim F, we have to solve the BSDE

From Proposition 8.1.1 and formula (9.34) we conclude that the solution to the BSDE (10.4) is given by the triple

By Theorem 10.1.1 the optimal hedging strategy is given by the formula

and the price of the claim, and the initial value of the optimal hedging portfolio, is equal to

The value of the optimal hedging portfolio is determined by the process

The solution to the optimization problem (10.1) is easy to derive but the objective (10.1) has two drawback from the financial point of view. Firstly, we have to choose the equivalent martingale measure \({\mathbb{Q}}\). This choice determines the price. When we investigate pricing in incomplete markets we expect to find the equivalent martingale measure. Consequently, the equivalent martingale measure used for pricing should be the output of an optimization problem, rather than the input. Secondly, the use of an equivalent martingale measure for evaluating the hedging error is questionable. Profits and losses or the performance of the hedging portfolio should be evaluated under the real-world measure.
2 Quadratic Pricing and Hedging Under the Real-World Measure
We aim to find an investment portfolio which hedges the insurance payment process (7.3) with a minimal replication error at time T and we evaluate the performance of the hedging portfolio under the real-world measure. The goal is to find an initial capital x and an admissible investment strategy  which minimize the mean-square hedging error
which minimize the mean-square hedging error

where X
π,x is given by (7.11), and we use the class of admissible strategies  from Definition 7.3.1. If one prefers to minimize the hedging error (10.5) for the discounted quantities as in (10.1), then obvious modifications should be introduced.
from Definition 7.3.1. If one prefers to minimize the hedging error (10.5) for the discounted quantities as in (10.1), then obvious modifications should be introduced.
We deal with two backward stochastic differential equations

and

Equation (10.6) is called a stochastic Riccati equation. First, we establish existence and uniqueness results for these two BSDEs.
Proposition 10.2.1
Assume that (C1)–(C2) from Chap. 7 hold. There exists a unique solution \((Y,Z)\in\mathbb{S}^{\infty}({\mathbb{R}})\times \mathbb{H}^{2}({\mathbb{R}})\) to the BSDE (10.6) such that Y(t)≥k>0, 0≤t≤T. Moreover, the process \((\int_{0}^{t}Z(s)dW(s), 0\leq t\leq T)\) is a BMO-martingale.
Proof
Since we look for a process Y which is uniformly bounded away from zero, we can introduce new variables

The Itô’s formula yields

We end up with a linear BSDE. By Proposition 3.3.1 there exists a unique solution \((\hat{Y},\hat{Z})\in\mathbb{S}^{2}({\mathbb{R}})\times \mathbb{H}^{2}({\mathbb{R}})\) to the linear BSDE (10.8). From the representation of the solution \(\hat{Y}\) and boundedness of θ and r we deduce that \(0< k\leq\hat{Y}(t)\leq K\), 0≤t≤T. Hence, we conclude that there exists a unique solution (Y,Z) to the nonlinear BSDE (10.6) and 0<k≤Y(t)≤K, 0≤t≤T. We now prove the BMO property. By the Itô’s formula we obtain

and

where we use boundedness of r, θ and Y, strict positivity of Y and inequality (3.10). Choosing α sufficiently large and taking the expectation, we derive

and the BMO property is proved. □
We will need higher moment estimates for the control process Z. From estimate (10.9) we deduce that for any p≥2 we have

We choose α sufficiently large, take the expected value, apply the Burkholder-Davis-Gundy inequality and we obtain the inequality

Starting with (10.10), by iteration we can derive the moment estimate

We use estimate (10.12) in the sequel.
We now investigate the second BSDE.
Proposition 10.2.2
Assume that (C1)–(C4) from Chap. 7 hold.
-
(a)
There exists a unique solution
 to the BSDE (10.7). The process
to the BSDE (10.7). The process
 has the representation
has the representation
 (10.13)
(10.13)where the equivalent martingale measure \({\mathbb{Q}}^{*}\) is given by

-
(b)
If

for some p>2, then
 (10.14)
(10.14)
Proof
(a) The existence and the uniqueness follow from Theorem 3.1.1. Representation (10.13) can be derived by following the arguments from Proposition 3.3.1 and the fact that the compensator of N remains unchanged under \({\mathbb{Q}}^{*}\), see also the proof of Theorem 9.4.1.
(b) By the Burkholder-Davis-Gundy inequality, the dynamics of the BSDE (10.7), the Cauchy-Schwarz inequality and boundedness of r, θ we obtain

Assume now that the time horizon T is sufficiently small. We get the inequality

From representation (10.7), the Cauchy-Schwarz inequality and boundedness of r and θ we deduce

which leads to the estimate

where we use the Doob’s martingale inequality, the Jensen’s inequality and inequality (10.15). If T is sufficiently small, then we conclude that  . To prove estimate (10.14) for an arbitrary T, we divide the interval [0,T] into sufficiently small subintervals [T
i
,T
i+1] and we consider the BSDEs
. To prove estimate (10.14) for an arbitrary T, we divide the interval [0,T] into sufficiently small subintervals [T
i
,T
i+1] and we consider the BSDEs

We can establish the assertion  on each subinterval. The global estimate for
on each subinterval. The global estimate for  on [0,T] follows by combining a finite number of local estimates. □
on [0,T] follows by combining a finite number of local estimates. □
We now derive the solution the quadratic optimization problem (10.5).
Theorem 10.2.1
Assume that (C1)–(C4) from Chap. 7 hold, and let

for some p>2. We consider the quadratic hedging problem (10.5). The strategy of the form

where (Y,Z) and
 solve the BSDEs (10.6) and (10.7), and the process
X
∗
is given by
solve the BSDEs (10.6) and (10.7), and the process
X
∗
is given by

are the optimal admissible hedging strategy
 and the optimal hedging portfolio for the payment process
P.
and the optimal hedging portfolio for the payment process
P.
Proof
1. The optimality. The proof is based on the method of completing the squares. Consider the BSDEs (10.6) and (10.7) written in the shorthand notation

where the generators f and f′ are appropriately defined. Key properties of the solutions to the BSDEs (10.6) and (10.7) are established in Propositions 10.2.1 and 10.2.2. We use these properties in the proof. We introduce the process

The Itô’s formula yields the dynamics

where

and

We choose an admissible strategy  and we consider the investment portfolio process X
π given by (7.11). By the Itô’s formula we derive the dynamics
and we consider the investment portfolio process X
π given by (7.11). By the Itô’s formula we derive the dynamics

and

We can notice that the stochastic integrals with respect to W, B and \(\tilde{N}\) are locally square integrable local martingales since X
π and  are càdlàg, Y is bounded, π,
are càdlàg, Y is bounded, π,  ,
,  and
and  are square integrable, see Theorem 2.3.1. Furthermore, the stochastic integrals with respect to N have locally integrable compensators since X
π and
are square integrable, see Theorem 2.3.1. Furthermore, the stochastic integrals with respect to N have locally integrable compensators since X
π and  are càdlàg, Y is bounded, G and
are càdlàg, Y is bounded, G and  are square integrable. Consequently, the compensated integrals are local martingales, see Theorem 2.3.2. Let (τ
n
)
n≥1 denote a localizing sequence for the local martingales such that τ
n
→T, n→∞. We obtain the expectations
are square integrable. Consequently, the compensated integrals are local martingales, see Theorem 2.3.2. Let (τ
n
)
n≥1 denote a localizing sequence for the local martingales such that τ
n
→T, n→∞. We obtain the expectations

and

From (10.19)–(10.20), after some tedious calculations, we deduce the formula

and by the definition of the generators f and \(\hat{f}\) from (10.6) and (10.18) we obtain

where the process φ collects all terms independent of π. We let n→∞. We have to justify the interchange of the limit n→∞ and the expectation. First, we recall that Y is uniformly bounded,  since
since  solves (10.7) and \(\mathbb{E}[\sup_{t\in[0,T]}|X^{\pi}(t)|^{2}]<\infty\) by (7.12). From these properties we can conclude that Y(τ
n
)|X
π(τ
n
)|2,
solves (10.7) and \(\mathbb{E}[\sup_{t\in[0,T]}|X^{\pi}(t)|^{2}]<\infty\) by (7.12). From these properties we can conclude that Y(τ
n
)|X
π(τ
n
)|2,  and
and  are bounded uniformly in n by an integrable random variable. Next, we deduce from the moment estimates (10.12) and (10.14) that the process
are bounded uniformly in n by an integrable random variable. Next, we deduce from the moment estimates (10.12) and (10.14) that the process  is square integrable. Finally, under our assumptions the process φ is integrable i.e. \({\mathbb{E}}[\int_{0}^{T}|\varphi (t)|dt]<\infty\). Hence, we apply the monotone convergence theorem to the first expectation on the right hand side of (10.21), the dominated convergence theorem to the second expectation on the right hand side of (10.21) and the dominated convergence theorem on the left hand side of (10.21). We end up with
is square integrable. Finally, under our assumptions the process φ is integrable i.e. \({\mathbb{E}}[\int_{0}^{T}|\varphi (t)|dt]<\infty\). Hence, we apply the monotone convergence theorem to the first expectation on the right hand side of (10.21), the dominated convergence theorem to the second expectation on the right hand side of (10.21) and the dominated convergence theorem on the left hand side of (10.21). We end up with

Since the last term in (10.22) does not depend on π, the optimal strategy can be immediately derived from (10.22) and (10.17).
2. The admissability. Let \(\pi^{*}(t)=A(t)X^{\pi ^{*}}(t-)+B(t)\). The dynamics of the investment portfolio (7.11) under the candidate strategy (10.16) is given by

Since (10.23) is a linear forward SDE, there exists a unique càdlàg, adapted solution \(X^{\pi^{*}}\) to (10.23), see Theorem V.7 in Protter (2004). We can now conclude that π ∗ is a predictable process.
We are left with proving the square integrability of the strategy π
∗. From (10.21) and integrability of the processes  and φ we can deduce the uniform estimate
and φ we can deduce the uniform estimate

and by Fatou’s lemma we get

Consequently, we can prove square integrability of the investment portfolio by noticing that

where we use the lower bound k≤Y(t). Consider now the BSDE

Since \({\mathbb{E}}[|X^{\pi^{*}}(T)|^{2}]<\infty\), there exists a unique solution \((\bar{Y},\bar{Z},\bar{U})\in\mathbb{S}^{2}({\mathbb{R}})\times\mathbb{H}^{2}({\mathbb{R}})\times\mathbb{H}^{2}_{N}({\mathbb{R}})\) to the BSDE (10.24). By (10.23) we get \(\bar{Y}(t)=X^{\pi^{*}}(t), \bar {Z}(t)=\pi^{*}(t)\sigma(t), \bar{U}(t,z)=0\). The admissibility of π ∗ has been proved. □
We remark that the arguments from the proof of Theorem 10.2.1 can be applied to solve a general linear quadratic control problem, see Lim (2004), Lim (2005) and Øksendal and Hu (2008).
Equation (10.22) gives the minimal hedging error under the optimal strategy π ∗. We can easily find the optimal initial capital.
Proposition 10.2.3
Under the assumptions of Propositions 10.2.1, 10.2.2 and Theorem 10.2.1 the initial value of the investment portfolio which minimizes the quadratic hedging error (10.5) takes the form

where the equivalent martingale measure \({\mathbb{Q}}^{*}\) is given by

The price and the hedging strategy for the payment process P can be obtained by solving the nonlinear BSDE (10.6) and the linear BSDE (10.7). The price (10.25), the initial value of the hedging portfolio, is arbitrage-free. We notice that the risk premiums for the systematic insurance risk and the unsystematic insurance risk are equal to zero and the insurance risk is not priced under the measure \({\mathbb{Q}}^{*}\). In contrast to Sect. 10.1 where the pricing measure were assumed to be given, here the pricing measure \({\mathbb{Q}}^{*}\) is derived by solving the optimization problem (10.5). We remark that the pricing measure which arises from solving the quadratic pricing and hedging problem (10.5) is called a minimal variance measure, see Lim (2004) and Schweizer (2010). The optimal hedging strategy (10.16) consists of two terms: the first term is a delta hedging strategy and the second term is a correction factor taking into account discrepancies between the optimal hedging portfolio X
∗ and the market-consistent value  of the insurance payment process (the reserve required for P). The second term adjusts the delta hedging strategy according to the shortfall or the surplus of the assets over the liabilities.
of the insurance payment process (the reserve required for P). The second term adjusts the delta hedging strategy according to the shortfall or the surplus of the assets over the liabilities.
Example 10.2
We consider the classical Black-Scholes model with constant coefficients r, μ, σ and an insurer who issues a portfolio of n unit-linked endowment policies with a capital guarantee. We are again interested in pricing and hedging the claim F=(n−J(T))(K−S(T))+ where J is the deaths counting process for the insurance portfolio. We consider a constant mortality intensity λ. In order to find the price and the optimal hedging strategy for the claim F, we have to solve the BSDEs


It is straightforward to notice that the solution to the BSDE (10.26) is of the form

Recalling the results from Example 9.5, we conclude that the solution to the BSDE (10.27) is given by the triple

By Theorem 10.2.1 and Proposition 10.2.3 the optimal hedging strategy is given by the feedback formula

where the optimal hedging portfolio is determined by the process

and the price of the claim, and the initial value of the optimal hedging portfolio, is equal to

The quadratic objective (10.5) can be generalized by keeping its mathematical tractability. We can solve the quadratic optimization problem

where a running cost is added. Under the objective (10.28) an investment strategy is chosen in such a way that the investment portfolio is as close as possible, in the mean-square sense, to the targets β and ξ. The targets β and ξ may represent solvency constraints or profit expectations, see Detemple and Rindisbacher (2008) and Delong (2010). We can also solve the Markowitz portfolio selection problem

where the variance of the terminal wealth is minimized given the constraint on the expected return. We remark that the Markowitz portfolio selection is commonly used for investment decision making and asset-liability management, see Chap. 4 in Zenios and Ziemba (2006) and Sect. 23.2 in Adam (2007).
Notice that in order to apply the investment strategy (10.16) we have to estimate the drift μ. The advantage of the quadratic optimization under an equivalent martingale measure (10.1) over the quadratic optimization under the real-world measure (10.5) is that the drift of the stock does not enter the optimal strategy in the former case. It is known that the estimation of the drift is challenging. Consequently, the quadratic pricing and hedging under the real-world measure may be difficult to implement in practice, see Sect. 10.4.3 in Cont and Tankov (2004) for a discussion.
3 Quadratic Pricing and Hedging Under Local Risk-Minimization
We now investigate the objective of local risk-minimization which was developed in Schweizer (1991) and Schweizer (2008). Local risk-minimization is an important alternative to global quadratic hedging. We will see that the locally risk-minimizing strategy is derived by optimizing an objective formulated under the real-world measure but at the same time the optimal strategy does not depend on the drift of the stock.
Let \(\hat{S}(t)=e^{-\int_{0}^{t}r(s)ds}S(t)\). The discounted stock price satisfies the dynamics

We introduce a class of admissible investment strategies.
Definition 10.3.1
A strategy Π:=(Π(t),0≤t≤T) is called admissible, written  , if it satisfies the conditions:
, if it satisfies the conditions:
-
(i)
\(\varPi:\varOmega\times[0,T]\rightarrow\mathbb{R}\) is a predictable process,
-
(ii)
\(\mathbb{E} [\int_{0}^{T} |\hat{S}(t)\varPi(t)\sigma(t) |^{2}dt ]<\infty\).
A strategy Γ:=(Γ(t),0≤t≤T) is called admissible, written  , if it satisfies the conditions:
, if it satisfies the conditions:
-
(i)
\(\varGamma:\varOmega\times[0,T]\rightarrow\mathbb{R}\) is an adapted process,
-
(ii)
the process
 is right-continuous and square integrable.
is right-continuous and square integrable.
A strategy (Π,λ) is called admissible for the local risk-minimization problem, written  , if
, if  and
and 
We remark that the strategy Π denotes the number of stock which are held in the investment portfolio, Γ denotes the position in the bank account and  is the discounted value of the investment portfolio. We point out that the investment portfolio
is the discounted value of the investment portfolio. We point out that the investment portfolio  is not self-financing under
is not self-financing under  .
.
We define the cost process and the risk process of a hedging strategy.
Definition 10.3.2
Assume that (C1)–(C4) from Chap. 7 hold. The cost process of an admissible strategy  related to hedging the payment process P is given by
related to hedging the payment process P is given by

The risk process of an admissible strategy  related to hedging the payment process P is given by
related to hedging the payment process P is given by

Since  , the integral \(\int_{0}^{t}\varPi (s)d\hat{S}(s)\) is well-defined and C
Π,Γ is square integrable.
, the integral \(\int_{0}^{t}\varPi (s)d\hat{S}(s)\) is well-defined and C
Π,Γ is square integrable.
The cost process C
Π,Γ describes accumulated discounted costs or profits (cash inflows or outflows) for the insurer who applies an investment strategy (Π,Γ), pays the benefits P and holds the investment portfolio  . If the payment process can be perfectly replicated by (Π,Γ), then
. If the payment process can be perfectly replicated by (Π,Γ), then

and the cost process related to hedging P is equal to the initial premium  - the cost of setting the replicating portfolio which matches the liability. If the payment process cannot be perfectly replicated, then the insurer has to inject capital or withdraw capital during the lifetime of the policy in order to match the assets with the liabilities. These inflows and outflows of capital from the investment portfolio are modelled by the cost process.
- the cost of setting the replicating portfolio which matches the liability. If the payment process cannot be perfectly replicated, then the insurer has to inject capital or withdraw capital during the lifetime of the policy in order to match the assets with the liabilities. These inflows and outflows of capital from the investment portfolio are modelled by the cost process.
The idea of local risk-minimization is to find an admissible hedging strategy  which minimizes the risk process R
Π,Γ for all t∈[0,T]. The precise definition of the hedging objective is very technical and it involves limit considerations and local perturbations of investment strategies, see Schweizer (1991) and Schweizer (2008). We can say that under the local risk-minimization we aim to find an asset portfolio which perfectly matches the liability with a minimal mean-square cost of matching. We point out that the hedging objective, the risk process, is evaluated under the real-world measure, as it should be.
which minimizes the risk process R
Π,Γ for all t∈[0,T]. The precise definition of the hedging objective is very technical and it involves limit considerations and local perturbations of investment strategies, see Schweizer (1991) and Schweizer (2008). We can say that under the local risk-minimization we aim to find an asset portfolio which perfectly matches the liability with a minimal mean-square cost of matching. We point out that the hedging objective, the risk process, is evaluated under the real-world measure, as it should be.
We give the key result which characterizes a locally risk-minimizing strategy.
Theorem 10.3.1
Assume that (C1)–(C4) from Chap. 7
hold. The payment process
P
admits an admissible locally risk-minimizing strategy
 if and only if the discounted payment process has the representation
if and only if the discounted payment process has the representation

where
 , and
, and
 is a right-continuous, square integrable martingale which is strongly orthogonal to the martingale component of
\(\hat{S}\)
and verifies
is a right-continuous, square integrable martingale which is strongly orthogonal to the martingale component of
\(\hat{S}\)
and verifies
 . In this case, we define
. In this case, we define

Proof
The result follows from Proposition 5.2 from Schweizer (2008). □
We remark that two square integrable martingales are strongly orthogonal if \({\mathbb{E}}[M^{1}(t)M^{2}(t)]=0\).
Decomposition (10.30) is called the Föllmer-Schweizer decomposition. The locally risk-minimizing strategy (Π
∗,Γ
∗) is called mean-self-financing as the optimal cost process  is a martingale, i.e. the average future cost is equal to zero. The strategy (Π
∗,Γ
∗) is also called 0-achieving as
is a martingale, i.e. the average future cost is equal to zero. The strategy (Π
∗,Γ
∗) is also called 0-achieving as  and all claims are covered.
and all claims are covered.
The next result shows that the Föllmer-Schweizer decomposition can be derived from a BSDE.
Proposition 10.3.1
Assume that (C1)–(C4) from Chap. 7 hold.
-
(a)
The Föllmer-Schweizer decomposition of the discounted payment process is given by

where \((Y,Z_{1},Z_{2},U)\in\mathbb{S}^{2}({\mathbb{R}})\times\mathbb{H}^{2}({\mathbb{R}})\times \mathbb{H}^{2}({\mathbb{R}})\times\mathbb{H}^{2}_{N}({\mathbb{R}})\) is the unique solution to the BSDE
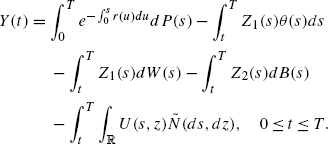 (10.31)
(10.31) -
(b)
The admissible locally risk-minimizing strategy
 and the optimal discounted hedging portfolio for the payment process
P
are given by
and the optimal discounted hedging portfolio for the payment process
P
are given by

Proof
(a) Consider the BSDE

where the generator f will be specified in the sequel. Assume there exists a solution \((Y,Z_{1},Z_{2},U)\in\mathbb{S}^{2}({\mathbb{R}})\times\mathbb {H}^{2}({\mathbb{R}})\times\mathbb{H}^{2}({\mathbb{R}})\times\mathbb{H}^{2}_{N}({\mathbb{R}})\) to (10.32). From the BSDE (10.32) we get the representation of the discounted payments

From property (5.5) we deduce that the stochastic integrals driven by B and \(\tilde{N}\) are strongly orthogonal to the martingale component of \(\hat{S}\), i.e. the stochastic integral driven by W. The discounted payment process (10.33) would now satisfy the Föllmer-Schweizer decomposition (10.30) if for some  we had
we had

Since

we should choose

With this choice, there exists a unique solution \((Y,Z_{1},Z_{2},U)\in \mathbb{S}^{2}({\mathbb{R}})\times\mathbb{H}^{2}({\mathbb{R}})\times\mathbb{H}^{2}({\mathbb{R}})\times \mathbb{H}^{2}_{N}({\mathbb{R}})\) to (10.32) and  . From (10.33) and (10.34) we deduce the Föllmer-Schweizer decomposition.
. From (10.33) and (10.34) we deduce the Föllmer-Schweizer decomposition.
(b) The formulas for Π
∗ and  follow from item (a), (10.32)–(10.34) and Theorem 10.3.1. □
follow from item (a), (10.32)–(10.34) and Theorem 10.3.1. □
We state an important corollary.
Corollary 10.3.1
Under the assumptions of Theorem 10.3.1 and Proposition 10.3.1 the optimal hedging portfolio process has the representation

where

and the optimal amount invested in the stock is given by

Proof
Since  , the representation of X
∗ follows from Proposition 10.3.1 and the representation of the solution Y to the linear BSDE (10.31). Since π
∗(t)=Π
∗(t)S(t), the formula for π
∗ follows immediately from Proposition 10.3.1. □
, the representation of X
∗ follows from Proposition 10.3.1 and the representation of the solution Y to the linear BSDE (10.31). Since π
∗(t)=Π
∗(t)S(t), the formula for π
∗ follows immediately from Proposition 10.3.1. □
The hedging portfolio (10.35) and the optimal amount invested in the stock (10.36) can be obtained by solving the linear BSDE (10.31). The price of the insurance payment process, which is the initial value of the hedging portfolio, is arbitrage-free. The insurance risk is not priced under the measure \({\mathbb{Q}}^{*}\). The hedging strategy π
∗ is a delta-hedging strategy which is updated with the current information on the financial and the insurance risk. We notice that the optimal hedging portfolio and the optimal hedging strategy are characterized under the equivalent martingale measure \({\mathbb{Q}}^{*}\), hence the drift of the stock does not enter the solution. We point out that under the locally risk-minimizing strategy (Π
∗,Γ
∗) there is no mismatch between the assets and the liabilities. The hedging portfolio is forced to match the market-consistent value of the liabilities, see Corollary 10.3.1. This equivalence holds since the investment portfolio process  is not self-financing. By Proposition 10.3.1 we obtain
is not self-financing. By Proposition 10.3.1 we obtain

Using π ∗, we derive the dynamics of the hedging portfolio

The stochastic integrals driven by B and \(\tilde{N}\) are interpreted as cash inflows/outflows which guarantee that  for all 0≤t≤T. As already noticed, the expected value of the cash inflows/outflows is zero
for all 0≤t≤T. As already noticed, the expected value of the cash inflows/outflows is zero

and the hedging portfolio (10.37) is mean-self-financing. We remark that the locally risk-minimizing strategy (10.36) for the stock would coincide with the minimum mean-square error strategy for the stock derived in Theorem 10.1.1 if the measure \({\mathbb{Q}}^{*}\) from Corollary 10.3.1 were chosen in the global quadratic hedging problem. However, the investment strategy from Theorem 10.1.1 is obtained in the framework of self-financing portfolios and  except at the inception of the contract.
except at the inception of the contract.
4 Quadratic Pricing and Hedging Under an Instantaneous Mean-Variance Risk Measure
As discussed at the end of Sect. 10.2, the Markowitz mean-variance objective is often used by financial institutions. In this chapter we investigate a local version of the mean-variance objective.
In Sects. 10.1–10.2 where we were only interested in finding the price of the payment process P at the initial time t=0. We are now interested in dynamic pricing of the payment process P over the period [0,T]. We assume that the price Y of the payment process P solves the BSDE

with a generator f. By Propositions 3.3.1 and 3.4.1 an arbitrage-free price of P, i.e.  ,
,  , has to solve a BSDE of the form (10.38). Hence, it is reasonable to assume a priori that the price process satisfies (10.38). In the sequel we use a local mean-variance objective to derive the generator f of the BSDE (10.38), the price process and the hedging strategy.
, has to solve a BSDE of the form (10.38). Hence, it is reasonable to assume a priori that the price process satisfies (10.38). In the sequel we use a local mean-variance objective to derive the generator f of the BSDE (10.38), the price process and the hedging strategy.
We recall that the investment portfolio X
π under an admissible investment strategy  is given by (7.11). We assume that there exists a solution \((Y,Z_{1},Z_{2},U)\in\mathbb{S}^{2}({\mathbb{R}})\times\mathbb{H}^{2}({\mathbb{R}})\times\mathbb {H}^{2}({\mathbb{R}})\times\mathbb{H}^{2}_{N}({\mathbb{R}})\) to the BSDE (10.38). We introduce a surplus process
is given by (7.11). We assume that there exists a solution \((Y,Z_{1},Z_{2},U)\in\mathbb{S}^{2}({\mathbb{R}})\times\mathbb{H}^{2}({\mathbb{R}})\times\mathbb {H}^{2}({\mathbb{R}})\times\mathbb{H}^{2}_{N}({\mathbb{R}})\) to the BSDE (10.38). We introduce a surplus process  which models the excess of the wealth of the insurer over the price of the payment process. We set
which models the excess of the wealth of the insurer over the price of the payment process. We set

We can derive the dynamics of the surplus process. We get the equation

with the initial condition  , since we should have X(0)=Y(0). We remark that
, since we should have X(0)=Y(0). We remark that  is square integrable for any
is square integrable for any  . Since Y can be interpreted as the market-consistent reserve for the liabilities, the surplus process
. Since Y can be interpreted as the market-consistent reserve for the liabilities, the surplus process  models the excess of the assets over the liabilities—the net asset wealth. The surplus process
models the excess of the assets over the liabilities—the net asset wealth. The surplus process  models the profit earned by the insurer. We recall that the net asset wealth is the key object investigated in Solvency II Directive, see European Commission QIS5 (2010). In Leitner (2007) the process
models the profit earned by the insurer. We recall that the net asset wealth is the key object investigated in Solvency II Directive, see European Commission QIS5 (2010). In Leitner (2007) the process  is called a tracking error.
is called a tracking error.
We define the mean-variance Markowitz risk measure

where the parameter L is a risk aversion coefficient which sets the trade-off between variance minimization and expected return maximization. Following Leitner (2007), we apply the risk measure (10.40), with a time-varying risk aversion coefficient L, to the infinitesimal change in the surplus process  . We investigate the instantaneous mean-variance risk measures
. We investigate the instantaneous mean-variance risk measures

The quadratic variation is now used for modelling the instantaneous variance. The moments in (10.41) are derived by Theorems 2.3.2–2.3.3. The goal is to find an admissible hedging strategy  which minimizes the instantaneous risk measures
which minimizes the instantaneous risk measures  for all t∈[0,T] and choose a generator f of the price dynamics Y which makes the instantaneous risk measures vanish
for all t∈[0,T] and choose a generator f of the price dynamics Y which makes the instantaneous risk measures vanish  for all t∈[0,T]. This is a reasonable pricing and hedging objective. The insurer should be interesting in applying an investment strategy under which the expected excess return on the surplus over the risk-free return on the surplus is maximized. At the same time, the insurer should choose an investment strategy under which the return on the surplus (the tracking error) is not volatile. Hence, the mean-variance objective is used for choosing the hedging strategy. The insurance payment process is next priced by requiring that the instantaneous Sharpe ratio of the surplus process equals a pre-specified target L, i.e. the insurance payment process is priced by requiring that
for all t∈[0,T]. This is a reasonable pricing and hedging objective. The insurer should be interesting in applying an investment strategy under which the expected excess return on the surplus over the risk-free return on the surplus is maximized. At the same time, the insurer should choose an investment strategy under which the return on the surplus (the tracking error) is not volatile. Hence, the mean-variance objective is used for choosing the hedging strategy. The insurance payment process is next priced by requiring that the instantaneous Sharpe ratio of the surplus process equals a pre-specified target L, i.e. the insurance payment process is priced by requiring that

We can now interpret L as a process which controls the ratio of the expected earned surplus (the net asset wealth) to its deviation over time or as a profit, specified by a Sharpe ratio, which is demanded by the insurer who sells the insurance contract. We assume that L(t)≥θ(t)+ε, ε>0. The former inequality is obvious since the investment in the payment process P carries an additional risk compared to the investment in the risky stock S and the insurer is interested in earning a risk premium strictly above θ, which is the risk premium earned by investing in the stock. For the instantaneous Sharpe ratio pricing we refer to Bayraktar and Young (2007), Young (2008), Bayraktar and Young (2008) and Bayraktar et al. (2009), for the connection with the cost of capital pricing we refer to Pelsser (2011).
Theorem 10.4.1
Assume that (C1)–(C4) from Chap. 7
hold and let
L
be a predictable process such that
L(t)≥θ(t)+ε,ε>0, and
L(t)≤K, 0≤t≤T. The admissible investment strategy
 which minimizes the risk measures (10.41) for all
t∈[0,T] and the generator
f
∗
which makes the risk measures (10.41) vanish for all
t∈[0,T] take the form
which minimizes the risk measures (10.41) for all
t∈[0,T] and the generator
f
∗
which makes the risk measures (10.41) vanish for all
t∈[0,T] take the form

where \((Y,Z_{1},Z_{2},U)\in\mathbb{S}^{2}({\mathbb{R}})\times\mathbb{H}^{2}({\mathbb{R}})\times \mathbb{H}^{2}({\mathbb{R}})\times\mathbb{H}^{2}_{N}({\mathbb{R}})\) is the unique solution to the BSDE

Proof
The form of the generator and the strategy are deduced from properties of the function

It is straightforward to find a unique minimizer π ∗ of the function w and f ∗ such that w(π ∗)=0. We now study the BSDE (10.44). By the Schwarz inequality

we can prove the following inequality

Hence, the generator (10.44) is Lipschitz continuous in the sense of Theorem 3.1.1. From (3.22) and Theorem 3.1.1 we conclude that there exists a unique solution to the BSDE (10.44). It is clear that the investment strategy (10.43) is admissible. □
The price process of the payment process P solves the nonlinear BSDE (10.44). It is important to point out that the price process (10.44) may not be represented as the expected value of the future discounted claims under an equivalent martingale measure. We also remark that the price process (10.44) may not satisfy the property of monotonicity with respect to the claim in the sense that a more severe claim may have a lower price. Hence, the price derived in Theorem 10.4.1 may give rise to arbitrage opportunities. In the language of BSDEs the solution to the BSDE (10.44) does satisfy the comparison principle with respect to the terminal condition and the BSDE (10.44) does not have a measure solution. This problem, which arises for BSDEs with jumps, was pointed out in Sect. 3.2.
Example 10.3
We consider the classical Black-Scholes model with constant coefficients r, μ, σ and an insurer who issues an endowment policy. We are interested in pricing and hedging the claim F=1−J(T) where J is the death counting process for the policy. We consider a constant mortality intensity λ and a constant Sharpe ratio L. In order to find the optimal price process and the optimal investment strategy for the claim F, we have to solve the BSDE

Clearly, we can set Z(t)=0, 0≤t≤T. Let us guess that U(t)=−Y(t−), Y(t)≥0, 0≤t≤T. We end up with the equation

First, it is straightforward to derive the dynamics

Integrating and taking the expected value, we can obtain the candidate solution

where we use the fact that J(T)=0 implies J(t)=0, 0≤t≤T. Next, from (10.49) we derive the dynamics

and

which agrees with (10.48). Our candidate solution (Y,Z,U), where Y is given by (10.49), Z(t)=0, U(t)=−Y(t−), 0≤t≤T, is square integrable. Hence, the unique solution to the BSDE (10.47) is found. By Theorem 10.4.1 the optimal price process is defined by

the optimal investment strategy is given by

We have obtained the unique solution to the pricing and hedging problem under the instantaneous mean-variance risk measure. If \(\lambda -\sqrt{L^{2}-\theta^{2}}\sqrt{\lambda}\leq0\), then the price of the endowment policy is larger than e −r(T−t) which is the price of the bond paying 1 at the maturity. The property of monotonicity of the pricing operator with respect to the claim is not satisfied. The insurer can buy the bond which hedges the payment from the endowment policy and earns a risk-free profit. We can conclude that the price (10.50) may give rise to arbitrage opportunities. To get the arbitrage-free price, we have to introduce the constraint \(\lambda-\sqrt{L^{2}-\theta^{2}}\sqrt{\lambda}>0\), or equivalently L 2<λ+θ 2.
We are now interested in pricing and hedging the claim F=(1−J(T))(K−S(T))+. In order to find the optimal price process and the optimal hedging strategy for the claim F, we have to solve the BSDE

We can conclude that the unique solution to the BSDE (10.51) is given by the triple

where we use (9.6) and (9.7). The optimal price process is defined by

and the optimal hedging strategy is given by

The price (10.52) is arbitrage-free if L 2<λ+θ 2.
We also give an example which shows that the price from Theorem 10.4.1 may be arbitrage-free without any additional assumptions on the parameters. It turns out that arbitrage-free prices arise for specific types of claims.
Example 10.4
Let the assumptions from Example 10.3 hold. We consider an insurer who issues a life insurance policy paying 1 at maturity of the contract provided that the policyholder dies within the duration of the contract. We are interested in pricing and hedging the claim F=J(T) where J is the death counting process for the policy. In order to find the optimal price process and the optimal investment strategy for the claim F, we have to solve the BSDE

Clearly, we can set Z(t)=0, 0≤t≤T. Let us guess that U(t)≥0, 0≤t≤T. We end up with the BSDE

By Proposition 3.4.1 and a similar reasoning as in Example 10.3, the solution to the BSDE (10.54) is of the form

and we see that U(t)≥0, 0≤t≤T. Our candidate solution (Y,Z,U), where (Y,Z) is given by (10.55), Z(t)=0, 0≤t≤T, is square integrable. Hence, the unique solution to the BSDE (10.53) is found. By Theorem 10.4.1 the arbitrage-free optimal price process is defined by

and the optimal investment strategy is given by the formula

By Theorem 10.4.1 the hedging strategy for the payment process P is characterized by the control processes of the nonlinear BSDE (10.44). The investment strategy (10.43) is studied in Chap. 12 where the results of this chapter are derived again under different pricing and hedging objectives. In Chap. 12 we also give conditions which guarantee that the price process (10.44) derived under the instantaneous mean-variance risk measure is arbitrage-free.
Instead of the mean-variance minimization, we can use the approach proposed by Bayraktar and Young (2007), Young (2008), Bayraktar and Young (2008), Bayraktar et al. (2009), and we can find a hedging strategy π
∗ which minimizes the instantaneous variation  for all t∈[0,T] together with a generator f
∗ which makes the instantaneous mean-variance risk measures vanish
for all t∈[0,T] together with a generator f
∗ which makes the instantaneous mean-variance risk measures vanish  for all t∈[0,T]. We obtain
for all t∈[0,T]. We obtain

where \((Y,Z_{1},Z_{2},U)\in\mathbb{S}^{2}({\mathbb{R}})\times\mathbb{H}^{2}({\mathbb{R}})\times \mathbb{H}^{2}({\mathbb{R}})\times\mathbb{H}^{2}_{N}({\mathbb{R}})\) is the unique solution to the BSDE

Again, the price process (10.57) may lead to arbitrage opportunities.
Bibliographical Notes
For a review on quadratic pricing and hedging we refer to Schweizer (2010). The proof of Theorem 10.1.1 is classical, see Sect. 10.4 in Cont and Tankov (2004) and Ankirchner and Imkeller (2008). Riccati backward stochastic differential equation is studied in Lim (2004), Kohlmann and Tang (2002), Kohlmann and Tang (2003). Higher moment estimates for a solution to a BSDE driven by a Brownian motion are investigated in El Karoui et al. (1997b). The proof of the optimality in Theorem 10.2.1 is taken from Delong (2010), see also Lim (2004) and Øksendal and Hu (2008) for the method of completing the squares. In the proof of the admissability in Theorem 10.2.1 we closely follow the arguments from Lim (2004). For Markowitz mean-variance optimization problems in finance and insurance we refer to Lim (2004), Øksendal and Hu (2008), Xie (2009), Xie et al. (2008), Kharroubi et al. (2012). It is worth mentioning that quadratic hedging problems in a financial model with assets driven by quasi-left continuous semimartingales with bounded jumps and in a financial model with assets driven by general semimartingales were solved in Kohlmann et al. (2010) and Jeanblanc et al. (2012) where the authors applied semimartingale BSDEs. The proof of Proposition 10.3.1 is inspired by Ankirchner and Heine (2012). For locally risk-minimizing strategies we refer to Ankirchner and Heine (2012), Dahl and Møller (2006), Dahl et al. (2008), Møller (2001) and Vandaele and Vanmaele (2008). Section 10.4 is taken from Delong (2012a).
References
Adam, A.: Handbook of Asset and Liability Management. Wiley, New York (2007)
Ankirchner, S., Heine, G.: Cross hedging with stochastic correlation. Finance Stoch. 16, 17–43 (2012)
Ankirchner, S., Imkeller, P.: Quadratic hedging of weather and catastrophe risk by using short term climate prediction. Preprint (2008)
Bayraktar, E., Young, V.: Hedging life insurance with pure endowments. Insur. Math. Econ. 40, 435–444 (2007)
Bayraktar, E., Young, V.: Pricing options in incomplete equity markets via the instantaneous Sharpe ratio. Ann. Finance 4, 399–429 (2008)
Bayraktar, E., Milevsky, M., Promislow, S., Young, V.: Valuation of mortality risk via the instantaneous Sharpe ratio: applications to life annuities. J. Econ. Dyn. Control 33, 676–691 (2009)
Boekel, P., Delft, L., Hoshino, T., Ino, R., Reynolds, C., Verheugen, H.: Replicating portfolios. Milliman Research. http://publications.milliman.com/research/life-rr/pdfs/replicating-portfolios-rr.pdf (2009)
Cont, R., Tankov, P.: Financial Modelling with Jump Processes. Chapman and Hall/CRC Press, London (2004)
Dahl, M., Møller, T.: Valuation and hedging of life insurance liabilities with systematic mortality risk. Insur. Math. Econ. 39, 193–217 (2006)
Dahl, M., Melchior, M., Møller, T.: On systematic mortality risk and risk-minimization with survival swaps. Scand. Actuar. J. 2, 114–146 (2008)
Delong, Ł.: An optimal investment strategy for a stream of liabilities generated by a step process in a financial market driven by a Lévy process. Insur. Math. Econ. 47, 278–293 (2010)
Delong, Ł.: No-good-deal, local mean-variance and ambiguity risk pricing and hedging for an insurance payment process. ASTIN Bull. 42, 203–232 (2012a)
Detemple, J., Rindisbacher, M.: Dynamic asset liability management with tolerance for limited shortfalls. Insur. Math. Econ. 43, 281–294 (2008)
El Karoui, N., Peng, S., Quenez, M.C.: Backward stochastic differential equations in finance. Math. Finance 7, 1–71 (1997b)
European Commission: Fifth quantitative impact study: call for advice and technical specifications. http://ec.europa.eu/internal_market/insurance/solvency/index_en.htm (2010)
Jeanblanc, M., Mania, M., Santacroce, M., Schweizer, M.: Mean-variance hedging via stochastic control and BSDEs for general semimartingales. Ann. Appl. Probab. 22, 2388–2428 (2012)
Kharroubi, I., Lim, T., Ngoupeyou, A.: Mean-variance hedging on uncertain time horizon in a market with a jump. Preprint (2012)
Kohlmann, M., Tang, S.: Global adapted solutions of one-dimensional backward stochastic Riccati equations, with applications to the mean-variance hedging. Stoch. Process. Appl. 97, 255–288 (2002)
Kohlmann, M., Tang, S.: Multidimensional backward stochastic Riccati equations and applications. SIAM J. Control Optim. 41, 1696–1721 (2003)
Kohlmann, M., Xiong, D., Ye, Z.: Mean-variance hedging in a general jump model. Appl. Math. Finance 27, 29–57 (2010)
Leitner, J.: Pricing and hedging with globally and instantaneously vanishing risk. Stat. Decis. 25, 311–332 (2007)
Lim, A.: Quadratic hedging and mean-variance portfolio selection with random parameters in an incomplete market. Math. Oper. Res. 29, 132–161 (2004)
Lim, A.: Mean-variance hedging when there are jumps. SIAM J. Control Optim. 44, 1893–1922 (2005)
Markowitz, H.: Portfolio selection. J. Finance 7, 77–91 (1952)
Møller, T.: Risk minimizing hedging strategies for insurance payment processes. Finance Stoch. 5, 419–446 (2001)
Øksendal, B., Hu, Y.: Partial information linear quadratic control for jump diffusions. SIAM J. Control Optim. 47, 1744–1761 (2008)
Pelsser, A.: Pricing in incomplete markets. Preprint (2011)
Schweizer, M.: Option hedging for semimartingales. Stoch. Process. Appl. 37, 339–363 (1991)
Schweizer, M.: Local risk minimization for multidimensional assets and payment streams. Banach Cent. Publ. 83, 213–229 (2008)
Schweizer, M.: Mean-variance hedging. In: Cont, R. (ed.) Encyclopedia of Quantitative Finance, pp. 1177–1181. Wiley, New York (2010)
Vandaele, N., Vanmaele, M.: A locally risk-minimizing hedging strategies for unit-linked life insurance contracts in a Lévy process financial market. Insur. Math. Econ. 42, 1128–1137 (2008)
Xie, S.: Continuous-time mean-variance portfolio selection with liability and regime switching. Insur. Math. Econ. 45, 148–155 (2009)
Xie, S., Li, Z., Wang, S.: Continuous-time portfolio selection with liability: mean-variance model and stochastic LQ approach. Insur. Math. Econ. 42, 943–953 (2008)
Young, V.: Pricing life insurance under stochastic mortality via the instantaneous Sharpe ratio. Insur. Math. Econ. 42, 691–703 (2008)
Zenios, S.A., Ziemba, W.T.: Handbook of Asset and Liability Management. North-Holland, Amsterdam (2006)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer-Verlag London
About this chapter
Cite this chapter
Delong, Ł. (2013). Quadratic Pricing and Hedging. In: Backward Stochastic Differential Equations with Jumps and Their Actuarial and Financial Applications. EAA Series. Springer, London. https://doi.org/10.1007/978-1-4471-5331-3_10
Download citation
DOI: https://doi.org/10.1007/978-1-4471-5331-3_10
Publisher Name: Springer, London
Print ISBN: 978-1-4471-5330-6
Online ISBN: 978-1-4471-5331-3
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)



 for the payment process
P
take the form
for the payment process
P
take the form

 to the BSDE (
to the BSDE ( has the representation
has the representation




 is right-continuous and square integrable.
is right-continuous and square integrable.
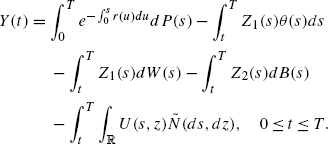
 and the optimal discounted hedging portfolio for the payment process
P
are given by
and the optimal discounted hedging portfolio for the payment process
P
are given by
