Abstract
Structure theory of the group G=SL2(ℝ) is introduced, an explicit Haar measure is computed. The notion of a continuous representation is given and an more abstract way of viewing modular forms is given by showing that they are representation vectors. The exponential map of the group G is described and it is shown how it gives rise to invariant differential operators.
Access provided by Autonomous University of Puebla. Download chapter PDF
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
In this chapter we will show that cusp forms can be viewed as representation vectors for Lie groups. This opens the way for the application of representation theory to automorphic forms.
3.1 Haar Measures and Decompositions
The group G=SL2(ℝ) acts on the upper half plane by linear fractionals  . Let
. Let  be in the stabilizer of i∈ℍ, i.e. gi=i. Then one gets \(\frac{ai+b}{ci+d}=i\) or ai+b=−c+di, which gives a=d and b=−c by comparison of real and imaginary parts. It follows that the stabilizer of i∈ℍ is the group
be in the stabilizer of i∈ℍ, i.e. gi=i. Then one gets \(\frac{ai+b}{ci+d}=i\) or ai+b=−c+di, which gives a=d and b=−c by comparison of real and imaginary parts. It follows that the stabilizer of i∈ℍ is the group
This is the group of all matrices of the form
The action of G on ℍ is transitive (i.e. there is only one orbit), because for z=x+iy∈ℍ one has
So the map

is a bijection which identifies the upper half plane with the quotient G/K.
The group G is a subset of M2(ℝ)≅ℝ4, and thus inherits a natural topology. A sequence  converges in G to an element
converges in G to an element  if and only if a
n
→a, b
n
→b, c
n
→c and d
n
→d. The action on ℍ is continuous in that the map
if and only if a
n
→a, b
n
→b, c
n
→c and d
n
→d. The action on ℍ is continuous in that the map

is a continuous map. (See Exercise 3.2.)
Theorem 3.1.1
(Iwasawa decomposition)
Let
A
be the group of all diagonal matrices in
G
with positive entries. Let
N
be the group of all matrices of the form
 with
s∈ℝ. Then
G=ANK. More precisely, the map
with
s∈ℝ. Then
G=ANK. More precisely, the map

is a homeomorphism.
Proof
Let g∈G and let gi=x+yi. With
one has gi=ani and so g −1 an lies in K, i.e. there is k∈K with g=ank. By means of the formula \(gi=\frac{ai+b}{ci+d}\) we can determine the inverse map as follows. Let
be given by \(\phi(g)=(\underline{a} (g),\underline{n} (g),\underline{k}(g))\), where

It is an easy computation to show that ϕψ=Id and ψϕ=Id. □
The notation \(\underline{a}(g)\), \(\underline{n}(g)\) and \(\underline{k}(g)\) will be used in the sequel. For x,t,θ∈ℝ we write

Definition 3.1.2
Let k∈ℕ0. A function f:G→ℂ is said to be k-times continuously differentiable if the map ℝ3→ℂ, given by
is k-times continuously differentiable. The map is called smooth if it is infinitely often continuously differentiable. The set of smooth functions on G is written as C ∞(G). The set of smooth functions of compact support is written as \(C_{c}^{\infty}(G)\).
The group G is a locally compact Hausdorff space, since G is a closed subset of ℝ4. Further, G is a topological group, i.e. the group operations,
are continuous maps. A topological group, which is locally compact and Hausdorff, is called a locally compact group.
Examples 3.1.3
-
An arbitrary group G becomes a locally compact group, if we equip it with the discrete topology (i.e. every set is open). In that case, one speaks of a discrete group.
-
The groups \(\operatorname{GL}_{2}(\mathbb{R})\) and SL2(ℝ) are locally compact groups when equipped with the subspace topology of ℝ4.
-
We will construct further examples using p-adic numbers and adeles later.
Lemma 3.1.4
Let G be a locally compact group. Every function f∈C c (G) is uniformly continuous, which means that for every ε>0 there exists a neighborhood U of the unit element of G, such that for x,y∈G with x −1 y∈U or yx −1∈U one has |f(x)−f(y)|<ε.
Proof
We show only the case x −1 y∈U, as the other case is analogous. Let S be the support of f. Choose ε>0 and a compact neighborhood V of the unit in G. Since f is continuous, for given x∈G there exists an open unit neighborhood V x ⊂V such that y∈xV x ⇒|f(x)−f(y)|<ε/2. As the group multiplication is continuous, there is an open unit neighborhood U x such that \(U_{x}^{2}\subset V_{x}\). The sets xU x , with x∈SV, form an open covering of the compact set SV. So there exist x 1,…,x n ∈KV such that SV⊂x 1 U 1∪…∪x n U n , where we have written U j for \(U_{x_{j}}\). Let U=U 1∩…∩U n . Then U is an open unit neighborhood. Let x,y∈G with x −1 y∈U. If x∉SV, then y∉S, since x∈yU −1=yU⊂yV. In that case we conclude f(x)=f(y)=0. So let x∈SV. Then there is j with x∈x j U j , so y∈x j U j U⊂x j V j . We get
as claimed. □
Definition 3.1.5
A measure μ, defined on the Borel σ-algebra of a locally compact Hausdorff space X, is called a Radon measure if the following conditions are met:
-
(a)
μ(K)<∞ for every compact subset K;
-
(b)
μ(A)=inf U⊃A μ(U), where the infimum runs over all open subsets with U⊃A and A⊂X is measurable; this property is called outer regularity;
-
(c)
μ(A)=sup K⊂A μ(K), where the supremum runs over all compact subsets K⊂X, which lie in A, and A is open or of finite measure; this property is called inner regularity.
Examples 3.1.6
-
If X is discrete, i.e. every set is open, then the counting measure
$$\mu(A) = \begin{cases} n&\text{if }A\text{ is finite with }n\text{ elements,} \\ \infty&\text{otherwise,} \end{cases} $$is a Radon measure.
-
If X=ℝ, then the Lebesgue measure is a Radon measure.
Proposition 3.1.7
Let μ be a Radon measure on the locally compact Hausdorff space X. For every 1≤p≤∞ the space C c (X) is dense in L p(X).
Proof
Let f∈L p(X). We want to write f as a limit of a sequence in C c (X). We can decompose f into real and imaginary parts and these again into positive and negative parts. If we can write all these as limits of C c (X) functions, then we can do so for f. So it suffices to assume f≥0. One can write f as the point-wise limit of a monotonically increasing sequence of Lebesgue step functions. It therefore suffices to assume that f is a Lebesgue step-function. By linearity it suffices to consider the case f=1 A for a set A of finite measure. By outer regularity there exists a sequence U n of open sets, U n ⊃U n+1⊃A, such that μ(U n )→μ(A), i.e. \(\|\mathbf{1}_{A}-\mathbf {1}_{U_{n}}\|_{p}\to0\). So we can assume that A is open. By inner regularity there exists a sequence of compact sets K n ⊂K n+1⊂A such that \(\|\mathbf{1}_{A}-\mathbf {1}_{K_{n}}\|_{p}\to0\). By the lemma of Urysohn, A.3.2, there is, for each n, a function φ n ∈C c (X) with \(\mathbf{1}_{K_{n}}\le\varphi_{n}\le \mathbf{1}_{A}\). Then the sequence φ n converges to 1 A in the L p-norm. □
If μ is a Radon measure on X, then the integral I=I μ :φ↦∫ X φ(x) dμ(x) is a linear map C c (X)→ℂ, which is positive in the sense that φ≥0 ⇒ I(φ)≥0. The Representation Theorem of Riesz says that the map μ↦I μ is a bijection between the set of all Radon measures and the set of all positive linear functionals on C c (X).
Theorem 3.1.8
Let G be a locally compact group. Then there exists a Radon measure μ≠0 on the Borel σ-algebra, which is left-invariant, i.e. one has μ(xA)=μ(A) for every x∈G and every measurable set A⊂G. This measure μ is uniquely determined up to scaling by positive numbers. It is called a Haar measure of G.
Every open set has positive Haar measure, and every compact set has finite Haar measure. The Haar measure is finite if and only if the group is compact.
Proof
One finds a proof for instance in each of the books [DE09, Str06]. □
Note that a Radon measure μ on a locally compact group G is a Haar measure if and only if
holds for every f∈L 1(G)and every x∈G.
Examples 3.1.9
-
If G is a discrete group, then the counting measure is a Haar measure.
-
For the group G=(ℝ,+), the Lebesgue measure dx is a Radon measure.
-
A Haar measure on the group G=(ℝ×,×) is given by \(\frac{dx}{x}\).
-
A Haar measure for the group \(G=\operatorname{GL}_{2}(\mathbb{R})\) is given by
$$\frac{dx\,dy\,dz\,dw}{|xw-yz|^2}, $$where the coordinates are the entries of the matrix
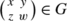 . This is easily shown by change of variables.
. This is easily shown by change of variables.
Convention
For simplicity we will write dx instead of dμ(x), when integrating over a Haar measure μ, where we always assume a fixed choice of Haar measure. So we write
instead of ∫ G f(x) dμ(x). The volume μ(A) of a measurable set A⊂G will be denoted as
Definition 3.1.10
Let G be a locally compact group with Haar measure dx. For f,g∈L 1(G) the convolution is defined by
Proposition 3.1.11
Let G be a locally compact group with Haar measure dx. For f,g∈L 1(G) the convolution integral f∗g(x) exists for x outside a set of measure zero and the so-defined function f∗g lies in L 1(G). More precisely, one has ∥f∗g∥1≤∥f∥1∥g∥1. Equipped with the convolution product, the space L 1(G) is an algebra over ℂ, i.e. for all f,g,h∈L 1(G) one has
and for every λ∈ℂ the equalities
hold.
Proof
The proposition follows from simple applications of the invariance of Haar measure. As an example, we will prove the first assertion. Let f,g∈L 1(G). Then we compute, formally at first,

The existence of the integrals on the right-hand side implies their existence on the left. The existence of f∗g(x) outside a set of measure zero follows from Fubini’s theorem, A.2.3. □
3.1.1 The Modular Function
A Haar measure μ needn’t be right-invariant as well, i.e. in general one has μ(Ax)≠μ(A). For given x∈G let
Then μ x is a left-invariant measure, as
The uniqueness of Haar measures implies that there is a unique number Δ(x)>0 with μ x =Δ(x)μ. The resulting function Δ=Δ G :G→(0,∞) is called the modular function of G. The modular function is a group homomorphism of G to the multiplicative group \(\mathbb{R}^{\times}_{>0}\), since
Further one shows that Δ is a continuous function (see [DE09], Chap. 1).
Example 3.1.12
Let B denote the group of all real matrices of the form  with y≠0. Then the modular function of B is
with y≠0. Then the modular function of B is  (see Exercise 3.4).
(see Exercise 3.4).
Definition 3.1.13
Let the set X be equipped with a σ-algebra. Assume the group G acts on X by measurable maps. A measure μ on X is called an invariant measure if for every measurable set A⊂X and every g∈G one has μ(gA)=μ(A). We will examine the case when X is the coset space G/H of a subgroup H of G.
Lemma 3.1.14
Let G be a locally compact group and let H be a closed subgroup. Then H is again a locally compact group and the quotient space G/H, equipped with the quotient topology, is a locally compact Hausdorff space.
Proof
[DE09]. □
Theorem 3.1.15
-
(a)
Let H⊂G be a closed subgroup of the locally compact group G. On the locally compact space G/H there exists a non-trivial, G-invariant Radon measure if and only if
$$\varDelta _G(h) = \varDelta _H(h) $$holds for every h∈H. If it exists, the invariant measure is unique up to scaling. Given Haar measures on G and H it can be normalized such that for every f∈L 1(G) the integral formula
$$\int_Gf(x)\,dx = \int_{G/H}\int _Hf(yh)\,dh\,dy $$holds.
-
(b)
For y∈G and f∈L 1(G) one has
$$\int_G f(xy)\,dx = \varDelta \bigl(y^{-1}\bigr) \int_G f(x)\,dx. $$ -
(c)
The equation
$$\int_G f\bigl(x^{-1}\bigr)\,\varDelta \bigl(x^{-1}\bigr)\,dx = \int_G f(x)\,dx $$holds for every f∈L 1(G).
-
(d)
If H⊂G is a closed subgroup and K⊂G a compact subgroup such that G=HK, then one can normalize the Haar measures of G,H,K in such a way that for every integrable function f the identity
$$\int_G f(x)\,dx = \int_H\int _Kf(hk)\,dk\,dh $$holds.
Proof
Example 3.1.16
The upper half plane ℍ can be identified with the quotient G/K=SL2(ℝ)/SO(2). The invariant measure \(d\mu=\frac{dx\,dy}{y^{2}}\) is a measure as in the theorem. Therefore the G-invariance determines the measure μ uniquely up to scaling.
A locally compact group G is called unimodular if Δ≡1.
Examples 3.1.17
-
If G is abelian, then G is unimodular.
-
If G is compact, then G is unimodular, since the image Δ(G) is a compact subgroup of \(\mathbb{R}_{>0}^{\times}\), so Δ(G)={1}.
-
If G is a discrete group, then G is unimodular, since the cardinality of a set A⊂G equals the cardinality of Ax for every x∈G.
Proposition 3.1.18
The group G=SL2(ℝ) is unimodular.
Proof
Let \(\phi: G\to\mathbb{R}^{\times}_{+}\) be a continuous group homomorphism. We show that ϕ is trivial. Firstly, we have that ϕ(K) is a compact subgroup of (0,∞), but the latter group has only one compact subgroup, the trivial one. Hence it follows that ϕ(K)=1. The restriction of ϕ to A is a continuous group homomorphism, so there exists a real number x∈ℝ such that ϕ(a
t
)=e
tx for every t∈ℝ. Let  . Then wa
t
w
−1=a
−t
, and therefore e
tx=ϕ(a
t
)=ϕ(wa
t
w
−1)=e
−tx for every t∈ℝ. This means x=0 and so ϕ(A)=1. Analogously we have ϕ(n
x
)=e
rx for some r∈ℝ. By \(a_{t} n_{x}a_{t}^{-1}=n_{e^{2t}x}\) it follows that \(e^{rs}=e^{re^{2t}s}\) for every t∈ℝ, so r=0 and ϕ(N)=1. By the Iwasawa decomposition we infer that ϕ(G)=ϕ(ANK)=ϕ(A)ϕ(N)ϕ(K)=1. □
. Then wa
t
w
−1=a
−t
, and therefore e
tx=ϕ(a
t
)=ϕ(wa
t
w
−1)=e
−tx for every t∈ℝ. This means x=0 and so ϕ(A)=1. Analogously we have ϕ(n
x
)=e
rx for some r∈ℝ. By \(a_{t} n_{x}a_{t}^{-1}=n_{e^{2t}x}\) it follows that \(e^{rs}=e^{re^{2t}s}\) for every t∈ℝ, so r=0 and ϕ(N)=1. By the Iwasawa decomposition we infer that ϕ(G)=ϕ(ANK)=ϕ(A)ϕ(N)ϕ(K)=1. □
Let g∈G=SL2(ℝ). We write \(\underline{t}(g)\) for the unique t∈ℝ with \(\underline{a}(g)=a_{t}\), i.e. we have
Theorem 3.1.19
(Iwasawa integral formula)
Let G=SL2(ℝ) and A,N,K⊂G as in Theorem 3.1.1. For any given Haar measures on three of the groups G,A,N,K there is a unique Haar measure on the fourth, such that for every f∈L 1(G) the equality
holds.
In the sequel, we will choose fixed Haar measures as follows. On the compact group K we choose the unique Haar measure of volume 1. On A we choose the measure 2dt, where \(t=\underline{t}(a)\), and on N we choose ∫ℝ f(n s ) ds. The factor of 2 in the measure on A was put in to grant compatibility with the measure \(\frac{dx\,dy}{y^{2}}\) on the upper half plane.
Proof of the Theorem
Let B=AN be the subgroup of all upper triangular matrices with positive diagonal entries. It is easy to show that db=da dn is a Haar measure on B and that B is not unimodular. Indeed, one has Δ B (a t )=e −2t, as the equation \(a_{t}n_{x}a_{s}n_{y}=a_{t+s}n_{y+e^{-2s}x}\) yields. Let \(\underline{b}:G\to B\) be the projection \(\underline{b}(g)=\underline{a}(g)\underline{n}(g)\). The map B→G/K≅ℍ, sending b to bK, is a B-equivariant homeomorphism. Every G-invariant measure on G/K≅ℍ gives a Haar measure on B and the uniqueness of these measures implies that every B-invariant measure on G/K already is G-invariant. The formula ∫ G f(x) dx=∫ G/K ∫ K f(xk) dk dx gives ∫ G f(x) dx=∫ B ∫ K f(bk) dk db. Since db=da dn, the integral formula follows. □
3.2 Representations
We define the notion of a continuous representation of a topological group on a Banach space V.
Definition 3.2.1
Let G be a topological group. A representation of G is a pair (π,V) consisting of a Banach space V and a group homomorphism \(\pi: G \to \operatorname{GL}(V)\), such that the map
is continuous.
Examples 3.2.2
-
Let χ:G→ℂ× be a continuous group homomorphism, i.e. a so-called quasi-character. One can consider χ as a representation, since naturally, \(\mathbb{C}^{\times}\cong\operatorname{GL}(\mathbb{C})\).
-
Let G=SL2(ℝ). This group has a canonical representation on the Banach space ℂ2, given by matrix multiplication.
Now assume that V is even a Hilbert space. A representation π of the group G on V is called a unitary representation if π(g) is unitary for every g∈G. This means that π is unitary if and only if for every g∈G and all v,w∈V one has 〈π(g)v,π(g)w〉=〈v,w〉.
Lemma 3.2.3
A representation π of a topological group G on a Hilbert space V is unitary if and only if π(g −1)=π(g)∗ holds for every g∈G.
Proof
An operator T is unitary if and only if it is invertible and satisfies T −1=T ∗. A representation π is a group homomorphism, so it satisfies π(g −1)=π(g)−1 for every g∈G. These two assertions give the claim. □
Example 3.2.4
Let χ:G→ℂ× be a quasi-character. As a representation, χ is unitary if and only if its image lies in the compact torus \(\mathbb{T}=\{ z\in\mathbb{C}: |z|=1\}\). In this case we say that χ is a character.
We will next consider an important example. Let G be a locally compact group and let x∈G. On the Hilbert space L 2(G), we define an operator L x by
Lemma 3.2.5
The map x↦L x is a unitary representation of the locally compact group G. It is called the left regular representation.
Proof
We first show that L x is a unitary operator. This is a consequence of the left-invariance of the Haar measure:

Next we show that x↦L x is a group homomorphism. This is immediate by
It remains to show continuity of the map Φ:G×L 2(G)→L 2(G); (x,φ)↦L x φ. For this let φ 0∈L 2(G) be given. An open neighborhood of φ 0 in L 2(G) is given by the set B r (φ 0) of all φ∈L 2(G) with ∥φ−φ 0∥<r, where r>0 and ∥⋅∥ is the L 2-norm. We have to show that S=Φ −1(B r (φ 0)) is an open subset of the product G×L 2(G). Let (x,φ)∈S, so ∥L x φ−φ 0∥<r. The claim asserts that there are open neighborhoods U of x and V of φ with U×V⊂S. To prove this, we estimate for y∈G and ψ∈L 2(G),

The last summand is strictly smaller that r. Set
The claim follows, if we can show that there are neighborhoods U of x and V of φ, such that for (y,ψ)∈U×V the estimate
holds. So let V be the set of all ψ∈L 2(G) with ∥φ−ψ∥<ε/2. We show that there exists an open neighborhood U of x, such that for every y∈U one has ∥(L x −L y )φ∥<ε/2. By Proposition 3.1.7 there exists a g∈C c (G) with ∥φ−g∥<ε/8. It follows that

Let C⊂G be a compact set such that g≡0 outside C. We can assume that C has positive Haar measure vol(C)>0. By uniform continuity of g, i.e. Lemma 3.1.4, there exists an open neighborhood U of x, such that for all y∈U and all t∈G the inequality
holds. So
We integrate this over t∈G to get for y∈U,

Taking square roots, we get ∥(L x −L y )g∥<ε/4 and the lemma is proven. □
We define the right regular representation x↦R x on the Hilbert space L 2(G) by
where Δ is the modular function of G. Analogous to the right regular case, one shows that R is a unitary representation as well.
Definition 3.2.6
Two representations (π,V π ) and (η,V η ) of a topological group G are called equivalent representations if there exists a linear operator T:V π →V η , such that
-
T is continuous, invertible, and the inverse T −1 is continuous as well, and further
-
Tπ(g)=η(g)T holds for every g∈G.
The second property can also be written as π(g)=T −1 η(g)T. Every such operator T is called an intertwining operator between the two representations π and η. If V π and V η are Hilbert spaces, and there is a unitary intertwining operator, then the representations are said to be unitarily equivalent.
Let (π 1,V 1) and (π 2,V 2) be two unitary representations. On the direct sum V=V 1⊕V 2 there is a direct sum representation π=π 1⊕π 2. More generally, one can define direct sum representations of infinitely many summands as follows.
Definition 3.2.7
Let I be an index set and for every i∈I let a Hilbert space V i be given. The Hilbert direct sum
is the set of all v∈∏ i∈I V i such that
The algebraic direct sum ⨁ i∈I V i of all v∈∏ i∈I V i such that v i =0 for almost all i∈I is a subset of the Hilbert direct sum.
Since the set I may be uncountable, it is not immediately clear how the sum ∑ i∈I ∥v i ∥2 is defined. It is defined to be the integral with respect to the counting measure on I of the function i↦∥v i ∥2. By definition of the integral one gets

where the supremum is extended over all finite subsets E of I. The reader not familiar with integration theory may take the right-hand side of this equality as the definition of the left-hand side. The condition ∑ i∈I ∥v i ∥2<∞ then implies that there exists a countable subset J⊂I such that ∥v i ∥=0 for all i∈I∖J and the sum ∑ i∈J ∥v i ∥2 converges in any order (see Exercise 3.8).
Note that by the definition it is not clear that V is a vector space, i.e. it is not clear why with v,w∈V their sum v+w lies in V.
Lemma 3.2.8
The direct Hilbert sum \(V=\widehat{\bigoplus}_{i\in I}V_{i}\) is a sub vector space of ∏ i V i . It is a Hilbert space with inner product
The algebraic direct sum is a dense subspace.
If for every i∈I there is given a unitary representation π i of the topological group G on the space V i , then
defines a unitary representation of G on V, called the direct sum representation.
Notation
In the sequel, we will often leave out the hat in the direct sum. So we write ⨁ i∈I V i when it is clear from the context that we really mean \(\widehat{\bigoplus}_{i\in I}V_{i}\).
Proof
Let v,w∈V. We shall show that the sum v+w lies in V, if v does. Also, we shall show that the sum ∑ i∈I 〈v i ,w i 〉 i converges absolutely (see Exercise 3.8).
If we equip the set I with the counting measure defined on the σ-algebra of all subsets of I, the corresponding L 2-space is the space ℓ 2(I) of all functions φ:I→ℂ with ∥φ∥2=∑ i∈I |φ(i)|2<∞. This is a Hilbert space with the inner product \(\langle \varphi ,\psi \rangle =\sum_{i\in I}\varphi (i)\overline{\psi(i)}\). For v∈V, the map φ v (i)=∥v i ∥ is in ℓ 2(I) and one has ∥φ v ∥=∥v∥. We now apply the Cauchy–Schwarz inequality first for the Hilbert spaces V i and then for ℓ 2(I) to get
This implies the claimed absolute convergence of the sum 〈v,w〉 and by
we infer the Cauchy–Schwarz inequality for this inner product, so that for v,w∈V we have

so that finally we get that V indeed is a sub vector space of ∏ i V i . The last claim is trivial. □
Example 3.2.9
Let G=ℝ/ℤ. The left regular representation L of G lives on the Hilbert space V=L 2(ℝ/ℤ). By the theory of Fourier series, L is isomorphic to the direct sum representation on \(\widehat{V}=\widehat{\bigoplus}_{k\in\mathbb{Z}}\mathbb{C}v_{k}\), where G acts on ℂv k by the character χ −k (x)=e −2πix, i.e. we have π(t)v=χ −k (t)v if v lies in the one-dimensional space ℂv k .
Definition 3.2.10
A representation (π,V π ) is called a subrepresentation of a representation (η,V η ), if V π is a closed, G-stable linear subspace of V η and π(g) is the restriction of η(g) to V π . So every G-stable, closed linear subspace gives a subrepresentation of η.
A representation (π,V π ) is called irreducible if V π ≠0 and it has no proper subrepresentations, i.e. if for every closed linear subspace U⊂V π , which is G-stable, one has U=0 or U=V π .
Example 3.2.11
Let G=SL2(ℂ) and V=ℂ2. Let π be the standard representation of G on V given by matrix multiplication. Then π is irreducible. For a proof let e 1=(1,0)t be the first standard basis vector. For g∈G the vector π(g)e 1 equals the first column of g. Therefore, for every v∈V∖{0} there exists a g∈G with v=π(g)e 1. This implies irreducibility as follows. Let 0≠U⊂V be a G-stable linear subspace. We have to show that U=V. Let 0≠v∈V be arbitrary. Choose a 0≠u∈U. Then there are g,h∈G such that π(g)e 1=u and π(h)e 1=v. Then π(g −1)u=e 1 and so π(hg −1)u=π(h)e 1=v. As U is stable under the G-action, we conclude v∈U. Since v is arbitrary, U=V.
3.3 Modular Forms as Representation Vectors
Lemma 3.3.1
Let G be a locally compact group and let Γ⊂G be a discrete subgroup. Then Γ is closed in G.
Proof
Let g be in the closure \(\overline{\varGamma }\) of Γ. We want to show that g∈Γ, so we assume the contrary. Since \(g\in\overline{\varGamma}\), every neighborhood of g contains an element of Γ. If U is a neighborhood of the unit, then gU is a neighborhood of g, and hence contains an element γ U of Γ. Since g≠γ U , we get g −1 γ U ≠1, so, by the Hausdorff property, there is a neighborhood V⊂U of the unit such that γ U ∉gV. As gV again contains an element γ V of Γ, we infer that γ V ≠γ U , so we get that for every unit neighborhood U there exist two different elements γ U ≠τ U of Γ with γ U ,τ U ∈gU.
As Γ is discrete, there exists a unit neighborhood V⊂G such that V∩Γ={1}. Since the multiplication of G is a continuous map, there exists a unit neighborhood U with U 2⊂V, where
Since U −1={u −1:u∈U} again is a unit neighborhood, we can, by replacing U with U∩U −1, assume that U=U −1. This means in particular that for any two u 1,u 2∈U we have \(u_{1}^{-1}u_{2}\in V\). Consider γ U ,τ U ∈gU. Then g −1 γ U ,g −1 τ U ∈U; hence
Since \(\gamma_{U}^{-1}\tau_{U}\in\varGamma \) this implies \(\gamma_{U}^{-1}\tau_{U}=1\), in contradiction with γ U ≠τ U . Hence the assumption is false, so Γ is indeed closed. □
The group K=SO(2) is isomorphic with \(\mathbb {T}\)={z∈ℂ:|z|=1} via  . Any character of K is of the form
. Any character of K is of the form
Let Γ⊂G=SL2(ℝ) be a congruence subgroup. The topology of G makes Γ a discrete subgroup. By Lemma 3.3.1 it is a closed subgroup. As Γ is discrete, the counting measure is a Haar measure, so Γ is unimodular. Since G is unimodular, too, Theorem 3.1.15 implies that there exists a non-trivial G-invariant Radon measure on G/Γ. It is now convenient to switch between left and right cosets, since we will use left cosets with respect to the subgroup K. The map

is a homeomorphism sending the left translation action of G to the right translation action. It transports the invariant Radon measure on G/Γ to a right G-invariant Radon measure on Γ∖G. Let L 2(Γ∖G) be the corresponding L 2-space. This is a Hilbert space with an action of G by right translations:
Lemma 3.3.2
The representation R of G on the Hilbert space L 2(Γ∖G) is unitary.
Proof
We have to show that for g∈G the operator R g :L 2(Γ∖G)→L 2(Γ∖G) is unitary, i.e. that
for all φ,ψ∈L 2(Γ∖G). We compute
where we have used the G-invariance of the measure. Further we have to show that the representation is continuous. This is proven analogously to the proof of Lemma 3.2.5. □
For ν∈ℤ recall the character \(\varepsilon_{\nu}:K\to \mathbb{T}\) given by
Let L 2(Γ∖G)1 be the space of all φ∈L 2(Γ∖G) which are continuously differentiable; the latter means that φ as a function on G is continuously differentiable in the sense of Definition 3.1.2.
Lemma 3.3.3
-
(a)
The space L 2(Γ∖G)1 is dense in the Hilbert space L 2(Γ∖G).
-
(b)
The space L 2(Γ∖G) is a direct Hilbert sum
$$L^2(\varGamma \backslash G) = \bigoplus _{\nu\in\mathbb {Z}}L^2(\varGamma \backslash G) ( \varepsilon_\nu), $$where
$$L^2(\varGamma \backslash G) (\varepsilon_\nu) = \bigl\{ \varphi \in L^2(\varGamma \backslash G): \varphi (xu)= \varepsilon_\nu(u)\varphi (x)\ \forall u\in K\bigr\}. $$
Proof
(a) It suffices to show that the orthogonal space W=L 2(Γ∖G)1,⊥ is zero. Let ψ∈L 2(Γ∖G), let \(f\in C_{c}^{\infty}(G)\) and define
Then R(f)ψ is continuously differentiable, as the second representation shows. The first representation shows that R(f)ψ is still Γ-invariant on the left. To show that R(f)ψ lies in L 2(Γ∖G)1 it suffices to show that its L 2-norm is finite. Let C⊂G be the support of f and let M=∫ C |f(y)|2 dy. We use the Hölder inequality and the Fubini theorem to get

So we see that R(f) is an operator on L 2(Γ∖G) with image inside L 2(Γ∖G)1. Now let ψ∈W, i.e. we have 〈ψ,φ〉=0 for every φ∈L 2(Γ∖G)1. We want to show that ψ=0. We first show that R(f)ψ∈W again. To see this, let φ∈L 2(Γ∖G)1 and compute

where \(f^{*}(y)=\overline{f(y^{-1})}\). Now R(f ∗)φ lies in L 2(Γ∖G)1 as we have seen, so the latter product is zero. It follows that R(f)ψ lies in L 2(Γ∖G)1 and its orthogonal space; hence it is zero. Being a continuous function, it must vanish everywhere, so R(f)ψ=0 holds for every \(f\in C_{c}^{\infty}(G)\). We finally deduce ψ=0 from this. As ψ is continuous at x, for given ε>0 there exists a unit neighborhood U such that for every y∈U one has |ψ(xy)−ψ(x)|<ε. Let f be a function in \(C_{c}^{\infty}(G)\) with support in U, such that f≥0 and ∫ G f(x) dx=1. Such a function exists for every U by Exercise 3.6. Then

Since R(f)ψ=0 for all f, we infer that ψ=0 as claimed.
For part (b) we first show that L 2(Γ∖G)(ε ν )⊥L 2(Γ∖G)(ε μ ) for ν≠μ. For this let φ∈L 2(Γ∖G)(ε ν ) and ψ∈L 2(Γ∖G)(ε μ ). Then

So the sum is indeed orthogonal.
Let φ∈L 2(Γ∖G) be continuously differentiable, which means that φ as a function on G is continuously differentiable in the sense of Definition 3.1.2. For given x∈G the group \(K\cong\mathbb{T}\) acts on xK⊂G. By the theory of Fourier series we have
where the series converges absolutely. The function φ ν (x) is given by
This implies that φ ν ∈L 2(Γ∖G)(ε ν ) and that we have the desired decomposition for the subspace L 2(Γ∖G)1 of all continuously differentiable functions. As this space is dense in L 2 by part (a), the claim follows. □
Let f∈S
k
(Γ) for a congruence subgroup Γ⊂Γ(1). Then f(γz)=(cz+d)k×f(z) holds for every  . For g∈G set
. For g∈G set
if  . For
. For  and z∈ℍ set μ(g,z)=(cz+d)k. A computation shows
and z∈ℍ set μ(g,z)=(cz+d)k. A computation shows
for all g,h∈G and all z∈ℍ. For u∈SO(2) one also has
Proposition 3.3.4
The map f↦ϕ f is an isometric injection of the Hilbert space S k (Γ) into the space L 2(Γ∖G)(ε −k ).
Proof
We show that ϕ f is invariant under Γ. For this let γ∈Γ and g∈G. Then
We see that this map is an isometry by noting that

The image lies in L 2(Γ∖G)(ε −k ), as for u∈K,
□
Let G=SL2(ℝ). By Lemma 3.3.2, the representation of G on L 2(Γ∖G) is unitary.
Definition 3.3.5
An automorphic form is a function φ in L 2(Γ∖G). Later we will extend this notion to include functions of the adele valued group which are invariant under \(\operatorname{GL}_{2}(\mathbb{Q})\).
The word automorphic indicates the invariance φ(γx)=φ(x) under the Γ-left-translation. It derives from the Greek word for of the same form, meaning unchanged under the transform. Felix Klein formed this notion in his paper Zur Theorie der Laméschen Functionen which appeared in the year 1890.
The Automorphic Spectral Problem
Can the unitary representation (R,L 2(Γ∖G)) be decomposed into a direct sum of irreducible subrepresentations? We will show that a positive solution of this problem solves the spectral problem for each of the operators Δ k . This problem admits a positive solution if and only if Γ is cocompact. If Γ is not cocompact, there will also be the so-called continuous spectrum.
3.4 The Exponential Map
Let n∈ℕ. The following assertions will be used subsequently only in the case n=2. But as the proofs are the same for any dimension n, we prove them in general.
On the real vector space M n (ℝ) of all real n×n matrices we consider the Euclidean norm
where we have written the entries of a matrix A as A i,j . For matrix multiplication we have ∥AB∥≤∥A∥∥B∥, since by means of the Cauchy–Schwarz inequality we get
A series \(\sum_{j=0}^{\infty}A_{j}\) of matrices in M n (ℝ) is said to be absolutely convergent if ∑ j ∥A j ∥<∞. In this case, the series converges in M n (ℝ) and the limit doesn’t change under reordering of the series.
For a given real n×n matrix X∈M n (ℝ), the exponential series
converges absolutely in M n (ℝ), as follows from the estimate ∥X ν∥≤∥X∥ν and the absolute convergence of the ℝ-valued exponential series.
Proposition 3.4.1
-
(a)
If the matrices A,B∈M n (ℝ) commute, i.e. AB=BA, then
$$\exp(A+B) = \exp(A)\exp(B). $$ -
(b)
For every A∈M n (ℝ) the matrix exp(A) is invertible and we have exp(A)−1=exp(−A).
-
(c)
The exponential map is a smooth map \(\mathrm{M}_{n}(\mathbb{R})\cong\mathbb{R}^{n^{2}}\to\mathrm {M}_{n}(\mathbb{R})\), the image of which lies in \(\operatorname{GL}_{n}(\mathbb{R})\), and whose differential at zero \(D\exp(0):\mathbb{R}^{n^{2}}\to\mathbb{R}^{n^{2}} \) is an invertible linear map.
-
(d)
In the group \(\operatorname{GL}_{n}(\mathbb{R})\) there is a unit neighborhood U, which does not contain any subgroup of \(\operatorname{GL}_{n}(\mathbb{R})\) other than the trivial one.
Proof
The equality AB=BA implies \((A+B)^{\nu}=\sum_{k=0}^{\nu}\binom{\nu}{k}A^{k}B^{\nu-k}\) for every ν∈ℕ. Therefore,

This proves (a). Part (b) follows from part (a), as exp(A)exp(−A)=I. For part (c) note that the entries of the matrix exp(A) are convergent power series in the entries of A. So the exponential map is infinitely differentiable. We compute the directional derivative in the direction X∈M2(ℝ) as follows
This means Dexp(0)=Id, so the claim follows.
(d) Since the Jacobi matrix of exp is invertible, there exists an open neighborhood \(\tilde{V}\subset\mathrm{M}_{n}(\mathbb{R})\) of zero in M n (ℝ), such that \(\tilde{V}\) is mapped diffeomorphically to an open neighborhood V of the unit matrix in \(\operatorname{GL}_{n}(\mathbb{R})\) by the exponential map. We may choose \(\tilde{V}\) to be bounded. Let \(\tilde{U}=\frac{1}{2}\tilde{V}\) and \(U=\exp(\tilde{U})\). Then U contains no non-trivial subgroup. To see this let a=exp(X)∈U with \(X\in\smash{\tilde{U}}\) and assume X≠0. Then there exists ν∈ℕ with \(\nu X\in\tilde{V}\smallsetminus \tilde{U}\). Assuming that a ν=exp(νX) lies in U, there exists \(Y\in \tilde{U}\) with exp(Y)=a ν=exp(νX), so the two elements Y and νX of \(\tilde{V}\) have the same image under the exponential map, and hence they are equal, contradicting \(\nu X\notin\tilde{U}\). □
Every X∈M n (ℝ) defines, by taking right derivatives, a differential operator of first order \(\tilde{R}_{X}\) on \(G=\operatorname {GL}_{n}(\mathbb{R})\) by
Analogously, there is a differential operator \(\tilde{L}_{X}\) given by left derivatives,
Let (π,V π ) be a representation of the group \(G=\operatorname{GL}_{n}(\mathbb{R})\). A vector v∈V π is called a smooth vector if the map
as a map from the open set \(\operatorname{GL}_{n}(\mathbb{R})\subset\mathrm{M}_{n}(\mathbb {R})\cong\mathbb{R}^{n^{2}}\) into the Banach space V π is infinitely differentiable. The set \(V_{\pi}^{\infty}\) of all smooth vectors in V π is a linear subspace of the vector space V π .
Let v∈V π be a smooth vector and let X∈M n (ℝ). Then the map t↦π(exp(tX))v is differentiable, so the limit
exists.
Lemma 3.4.2
-
(a)
The operator \(\tilde{R}_{X}\), X∈M n (ℝ) is left-invariant, i.e. \(L_{x}\tilde{R}_{X}L_{x^{-1}}=\tilde{R}_{X}\), where \(x \in G=\operatorname{GL}_{n}(\mathbb{R})\) and L x f(y)=f(x −1 y) for every smooth function f on G. Analogously, the operator \(\tilde{L}_{X}\) is right-invariant, i.e. \(R_{x}\tilde{L}_{X}R_{x^{-1}}=\tilde{L}_{X}\) with R x f(y)=f(yx).
-
(b)
A continuous intertwining operator T:V π →V η between two representations of \(G=\operatorname {GL}_{n}(\mathbb{R})\) maps smooth vectors to smooth vectors, i.e. \(T(V_{\pi}^{\infty})\subset V_{\eta}^{\infty}\).
-
(c)
For v∈V π and \(f\in C_{c}^{\infty}(G)\), the vector π(f)v is smooth. The space of smooth vectors is dense in V π . For X∈M n (ℝ) we have
$$\tilde{\pi}(X)\pi(f)v = \pi(\tilde{L}_Xf)v. $$ -
(d)
Let \(f\in C_{c}^{\infty}(G)\) and let φ be a locally square-integrable function on G, that is, for every x∈G there exists a neighborhood U of x, such that φ| U ∈L 2(U). Then the integral
$$R(f)\varphi (x) = \int_Gf(y)\varphi (xy)\,dy $$exists for every given x∈G and defines a smooth function R(f)φ. For every X∈M n (ℝ) one has
$$\tilde{R}_X\bigl(R(f)\varphi \bigr) = R(\tilde{L}_Xf) \varphi . $$
Proof
(a) Let f be a differentiable function on \(\operatorname{GL}_{n}(\mathbb{R})\). We have to show that \(\tilde{R}_{X}L_{x}f=L_{x}\tilde{R}_{X}f\), where L x f(y)=f(x −1 y). For \(y\in\operatorname{GL}_{n}(\mathbb{R})\) we compute

(b) If f:ℝN→V is a smooth map into a Banach space and if T:V→W is a continuous linear map between Banach spaces, then T∘f:ℝN→W is smooth.
Now for (c). Since the differential of the exponential function is surjective, a vector v is smooth if and only if for every x∈G the map X↦π(exp(X)x)v as a map M n (ℝ)→V π is smooth. So the smoothness, as well as the claimed formula, follow from
Finally we have to show that smooth vectors are dense. This follows if we show that vectors of the form π(f)v for \(f\in C_{c}^{\infty}(G)\) are dense. Let ε>0 and v∈V π . By continuity of π there exists a neighborhood U of the unit in G such that ∥π(x)v−v∥<ε for every x∈U. Let \(f\in C_{c}^{\infty}(G)\) be supported inside U, satisfy f≥0 and ∫ G f(x) dx=1; see Exercise 3.6 for the existence of such a function. For v∈V π we get
So the set of all vectors of the form π(f)v for v∈V π and \(f\in C_{c}^{\infty}(G)\) is indeed dense in V π .
(d) follows similar to (c). □
3.5 Exercises and Remarks
Exercise 3.1
Prove Proposition 3.1.11.
Exercise 3.2
Show that the map SL2(ℝ)×ℍ→ℍ, given by (g,z)↦gz is continuous.
Exercise 3.3
Let K=SO(2) and let D be the set of all diagonal matrices in G=SL2(ℝ) or in \(G=\operatorname{GL}_{2}(\mathbb{R})\). Show in both cases that G=KDK.
Exercise 3.4
Let B be the group of all real matrices of the form  with y≠0. Show that the modular function is
with y≠0. Show that the modular function is  .
.
Exercise 3.5
Let μ be a Haar measure of the locally compact group G. Let ∅≠U⊂G be an open subset. Show that μ(U)>0.
Exercise 3.6
-
(a)
Show that the function
$$f(t)= \begin{cases}0&\text{if }t\le0,\\ e^{-t}&\text{if } t>0, \end{cases} $$is infinitely differentiable on ℝ.
-
(b)
Show that for every neighborhood U of zero in ℝ there exists a function f≥0 on ℝ which is infinitely differentiable, has support in U and satisfies ∫ℝ f(x) dx=1.
-
(c)
Let G=SL2(ℝ). Show that for every unit neighborhood U there exists a function \(f\in C_{c}^{\infty}(G)\) such that f≥0, the integral ∫ G f(x) dx is equal to 1 and f has support inside U. Show the same for \(G=\operatorname{GL}_{n}(\mathbb{R})\).
Exercise 3.7
-
(a)
Show that the map f↦ϕ f with
$$\phi_f(g) = (ci+d)^{-k} f(gi) $$defines a bijection between the set C ∞(ℍ) of all smooth maps on ℍ and the set V k of all smooth functions ϕ on SL2(ℝ) with ϕ(xu)=ε −k (u) for every u∈SO(2).
(Hint: the inverse map is given by ϕ↦f ϕ with
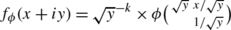 .)
.) -
(b)
Let
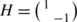 ,
, 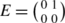 and
and 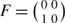 . For ϕ∈V
k
define the differential operator
$$D\phi(g) = \frac{d}{dt}\bigg\vert_{t=0}\phi\bigl(g\exp(tH) \bigr)-i\phi \bigl(g\exp(tE)\bigr)-i\phi\bigl(g\exp(tF)\bigr). $$
. For ϕ∈V
k
define the differential operator
$$D\phi(g) = \frac{d}{dt}\bigg\vert_{t=0}\phi\bigl(g\exp(tH) \bigr)-i\phi \bigl(g\exp(tE)\bigr)-i\phi\bigl(g\exp(tF)\bigr). $$Show that \(f_{D\phi}=-2iy\bar{\partial}f_{\phi}\), where \(\bar{\partial}=\frac{\partial}{\partial x}+i\frac{\partial}{\partial y}\). Conclude that f is holomorphic if and only if f is continuously differentiable and Dϕ f =0.
Exercise 3.8
Let I be an index set and for each i∈I let a i ∈ℂ be given. We define
Suppose that ∑ i∈I |a i |<∞. Show that there is a countable subset C⊂E such that a i =0 if i∉C and that the sum
converges in any order, always yielding the same complex number. We call this number the sum ∑ i∈I a i and say that this sum converges absolutely.
Exercise 3.9
Assume that the series \(L(s)=\sum_{n=1}^{\infty}a_{n}n^{-s}\) converges in s=s 0∈ℂ. Show that the series converges locally uniformly absolutely in \(\operatorname{Re}(s)>\operatorname{Re}(s_{0})+1\).
Exercise 3.10
Let \(L(a,s)=\sum_{n=1}^{\infty}a_{n}n^{-s}\) and \(L(b,s)=\sum_{n=1}^{\infty}b_{n}n^{-s}\) both convergent for some s∈ℂ. Assume L(a,s ν )=L(b,s ν ) for a sequence s ν ∈ℂ with \(\operatorname{Re}(s_{\nu})\to\infty\). Show that a n =b n for every n∈ℕ.
Exercise 3.11
A sequence (a n ) of complex numbers is called weakly multiplicative if a mn =a n a m for every coprime pair of natural numbers (m,n). The sequence is called strongly multiplicative or just multiplicative if this holds for every pair of natural numbers. Let \(L(s)=\sum_{n=1}^{\infty}a_{n}n^{-s}\) be absolutely convergent for \(\operatorname{Re}(s)>\sigma_{0}\). Show:
-
The sequence (a n ) is weakly multiplicative if and only if for every s∈ℂ with \(\operatorname{Re}(s)>\sigma_{0}\) one has
$$L(s) = \prod_p\sum _{k=0}^\infty a_{p^k}p^{_ks}. $$ -
The sequence (a n ) is strongly multiplicative if and only if for every s∈ℂ with \(\operatorname{Re}(s)>\sigma_{0}\) one has
$$L(s) = \prod_p\frac{1}{1-a_pp^{-s}}. $$
Remarks
We have encountered classical modular forms \(\mathcal{M}_{k}(\varGamma )\) and cusp forms S k (Γ), and we have seen how to attach L-functions L(f,s) to these.
The L-functions have Euler products if the forms are Hecke eigenforms. Finally we saw how to embed S k (Γ) into the space L 2(Γ∖G), where the latter space carries a unitary representation of G=SL2(ℝ). The spectral problem of decomposition of this representation into irreducibles is a central problem in the theory of automorphic forms.
We shall show that sometimes, f∈S k (Γ)⊂L 2(Γ∖G) generates an irreducible subrepresentation π. We want to define L(f,s) using π, but there are data missing to do that. These data are encoded in the Hecke action.
Let Γ⊂SL2(ℤ) be a congruence subgroup. Recall that the Hecke action comes about by the operation of the group \(G_{\mathbb{Q}}=\operatorname{GL}_{2}(\mathbb{Q})\). For α∈G ℚ the group Γ∩αΓα −1 is again a congruence subgroup. the Hecke operator T α can be defined by the action of α: f↦f|α, which maps S k (Γ) to S k (Γ∩αΓα −1), followed by a sum over Γ/(Γ∩αΓα −1), the latter mapping to S k (Γ) again. This summation is just the orthogonal projection onto the subspace S k (Γ) in the Hilbert space S k (Γ∩αΓα −1). By projecting, one loses information. If we leave out the projection, the Hecke operator does not map the space S k (Γ) to itself. We solve this problem by enlarging the space to
where Γ runs through all congruence subgroups of Γ. This is a vector space with a linear action of the group G ℚ. The space
inherits an inner product, if one normalizes the inner products on the space L 2(Γ∖G) as follows:
Let H be the completion of the resulting pre-Hilbert space. One can define Hecke operators on this space. However, in the current description, this space is not easy to understand.
Here comes the punch line: There exists a natural ring \(\mathbb{A}\), the ring of adeles, such that as SL2(ℝ)-module,
Given the definition of H, this assertion seems ridiculous. More precisely, one has \(\mathbb{A}=\mathbb{A}_{\mathrm{fin}}\times\mathbb{R}\), where \(\mathbb{A}_{\mathrm{fin}}\) is called the ring of finite adeles. The group \(\mathrm{SL}_{2}(\mathbb{A})=\mathrm{SL}_{2}(\mathbb{A}_{\mathrm{fin}})\times\mathrm{SL}_{2}(\mathbb{R})\) acts by right translations on H. The action of SL2(ℝ) is the same as before. It turns out that the action of \(\mathrm{SL}_{2}(\mathbb{A}_{\mathrm{fin}})\) is, in a sense to be made precise, equivalent to the action of the Hecke algebra! Consequently, a decomposition of H into \(\mathrm{SL}_{2}(\mathbb {A})\)-irreducibles gives Hecke eigenforms with Euler products. So the L-function should be expressible in representation-theoretic terms of the group \(\mathrm{SL}_{2}(\mathbb{A})\).
References
Deitmar, A., Echterhoff, S.: Principles of Harmonic Analysis. Universitext. Springer, New York (2009)
Stroppel, M.: Locally Compact Groups. EMS Textbooks in Mathematics. European Mathematical Society (EMS), Zürich (2006)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer-Verlag London
About this chapter
Cite this chapter
Deitmar, A. (2013). Representations of SL2(ℝ). In: Automorphic Forms. Universitext. Springer, London. https://doi.org/10.1007/978-1-4471-4435-9_3
Download citation
DOI: https://doi.org/10.1007/978-1-4471-4435-9_3
Publisher Name: Springer, London
Print ISBN: 978-1-4471-4434-2
Online ISBN: 978-1-4471-4435-9
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


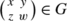 . This is easily shown by change of variables.
. This is easily shown by change of variables.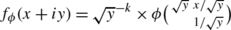 .)
.)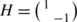 ,
, 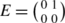 and
and 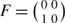 . For ϕ∈V
k
define the differential operator
. For ϕ∈V
k
define the differential operator