Basic MPC Formulation

Abstract

Model predictive control (MPC) is a modern optimization based control strategy, which has been predominantly used for applications with slow dynamics so far. The implementation of MPC for fast systems such as active vibration attenuation (AVC) requires a firm theoretical knowledge of the method, its issues and limitations. This chapter is aimed at the reader with little or no prior contact with model predictive control. Discussing basic concepts like prediction, penalty, cost and optimization helps the reader to get up to speed using the most straightforward approach possible. Taking the basic building blocks of MPC and assembling them, one should ultimately understand how the optimal, constrained, quadratic programming-based MPC algorithm works. The chapter starts with an introduction of the fundamental idea behind model predictive control, followed by a review of the historic development of this field of control engineering. Next, generating a sequence of future states based on the current measurement and a state-space model is presented. Assembling a numerical indicator of the quality of control from the grounds up is just as important as predicting the sequence of future states, thus essentials of creating a quadratic cost are also presented. With the cost function available, one is able to create a simple MPC control law in the absence of constraints. Finally, the formulation of process constraints is described, and the resulting quadratic programming (QP) optimization problem is reviewed. The mathematical problem of quadratic programming is presented through an example, along with two basic solution algorithms for QP. The chapter is finished by the discussion of the important infinite horizon cost dual-mode MPC algorithm.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Model predictive control (MPC) is an advanced optimization- based control method that has been in use for applications with slow dynamics, such as petrochemical plants since the 1980s (Fig. 6.1). Unlike linear quadratic (LQ) control, in addition to providing an optimal control process, MPC offers the explicit handling of process constraints that arise from natural requirements, for example cost effectiveness, safety, actuator limits and others. In fact due to the active interest of industry, the early theoretical development of MPC has been influenced greatly by the requirements of corporate users. A review of the industrial applications for those interested is given in [35, 43–45]. The design of MPC controllers is nowadays supported by numerous off-the-shelf commercial packages [45]. These tools typically contain means for model identification , controller design, controller tuning and controller performance analysis and are intended for the industrial user without a deep knowledge of the theoretical aspects of MPC.

Control decisions in MPC are computed online using an internal model of the plant dynamics. The big advantage of MPC over other control strategies is that it can handle process constraints on an algorithmic level. Unfortunately, the inclusion of constraints renders the MPC law nonlinear, which has dramatic effects on its stability properties. Just as in the case of any other well-designed system employing an arbitrary control law, the closed-loop stability of constrained MPC needs to be investigated and if possible guaranteed as well.

Given an otherwise stable plant model, it is always possible to conceive a system state, which can render the MPC controller unstable . A constrained MPC control law (in its primal, online optimization- based form) does not have an explicit closed-loop form, therefore stability guarantees can be given only by applying additional constraints which have a task to ensure future feasibility and stability . The stability aspects of model predictive control will be discussed in the following chapter, that is in Chap. 7.

The aim of this chapter is to introduce model predictive control to the reader who has no or minimal prior knowledge of this advanced control strategy. For this reason, we are beginning our discussion from the essentials and build a controller from the grounds up. Fundamental concepts such as prediction, cost and penalization are explained first in order to introduce the simplest possible MPC control law, which in the absence of constraints can be expressed in a closed form. By the end of this chapter, the reader shall be familiar with the theoretical fundamentals of the popular dual-mode formulation of the quadratic programming-based MPC strategy.

Fig. 6.1

The petrochemical industry was the first to recognize the merits of MPC and adopt it in everyday operations [22]

After an introduction of the underlying idea of model predictive control, a historic overview of the development of MPC is presented in the first section. Here the development from fixed feedback laws based on finite impulse responses up to the constrained and stable online optimization strategies used today are briefly reviewed. This is followed by a section discussing how we can predict the evolution of states based on a state-space model, and how all of this can be given in a compact matrix notation. Section 6.3 introduces the idea of the cost function, which can give a clear numerical measure of the performance of a control law formulating the basis of the optimization task in MPC. Following this, further building blocks of the predictive strategy are discussed, namely the penalization matrices that help to fine tune the behavior of the controlled system. The first working MPC control law is derived in Sect. 6.6, which thanks to the absence of constraints is just a fixed feedback matrix. As one of the main advantages of using MPC over classical methods is its ability to handle process constraints, the formulation of constraints is reviewed in the following section. Following this Sect. 6.8 finally arrives at the central element of the predictive strategy: the most common dual-mode constrained MPC law. This MPC formulation is evaluated online using the mathematical optimization tool called quadratic programming. The chapter ends with a short section discussing the idea of different predictive and control horizons while briefly examining the problem of tracking in state-space systems as well.

The style of presentation and the content of this chapter is aimed at the reader unfamiliar with model predictive control. The ultimate objective is to present constrained MPC based on quadratic programming in a straightforward manner, without distractions leading the reader off-course. This however requires omitting some aspects of predictive control from the explanation. The theoretical view on stability , feasibility and efficiency of MPC is discussed in the subsequent chapters. In case one is interested in MPC formulations based on transfer function models, impulse or step responses, we suggest to read one of the excellent books discussing the basics and more advanced concepts of model predictive control, such as the popular books by Maciejowski [34], Rossiter [48] or several other publications [ 6, 7, 26, 36].

1 The MPC Idea

In essence, an MPC controller is based on an iterative, finite horizon (constrained) optimization of a plant model. At each discrete sampling time $(k)$ the plant is sampled and the actual state ¹ ${\mathbf{x}}_k$ is measured or estimated using observers. The performance of the controller is expressed by a so-called cost function . Based on a dynamic model of the plant, this cost function is formulated in such a way that it expresses the performance of the MPC controller in the future, given a current plant state ${\mathbf{x}}_k$ and a sequence of future inputs ${\mathbf{u}}_k$. In other words, this predicted cost function gives a numerical indicator of the quality of control, assuming that the current plant state is influenced by a certain sequence of past inputs. The question is not what the performance of the controller will be, but rather what the sequence of inputs ${\mathbf{u}}_k$ is which will produce the best performance. To calculate the optimal sequence of inputs, one must minimize the cost function at each sampling interval using a numerical optimization algorithm. As in the case of most real plants inputs, outputs and states can be bounded by physical constraints, which can be easily incorporated into the numerical minimization task. Of the sequence of future inputs ${\mathbf{u}}_k$ only the first is applied, then the process is repeated based on brand new measured state information. This type of repeated measure-predict-optimize-apply cycle is called receding horizon control.

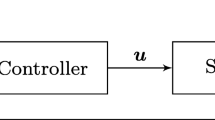
The model predictive control algorithm is schematically illustrated in Fig. 6.2. The structure of this scheme illustrates that essentially MPC is a form of a feedback control algorithm, where instead of a fixed feedback law a dynamic online optimization process determines inputs based on the actual measurements.

A model predictive controller is based on the following concepts:

• using a mathematical model of the plant dynamics

• predicting future plant dynamics

• expressing process optimality by a cost function

• predicting cost of future plant dynamics

• cost function minimization (optimal control)

• receding horizon control

Fig. 6.2

Schematic representation of the model predictive control algorithm

Figure 6.3 illustrates the concept of the receding horizon model predictive controller. At the time step $(k)$ the controller measures or observes the current plant state from the outputs, denoted by the black dot. An optimal course of inputs is calculated, which is associated with a predicted output course. At time $(k)$ however, only the first element of the sequence is applied to the plant. At the next step $(k\,{+}\,1)$ the whole process is repeated, shifting the horizon one step further.

An interesting view of predictive control is presented by Camacho and Bordons in [6, 7], where the control process is represented by the analogy of driving a motor vehicle. While model predictive control represents driving based on the information gathered by looking out the front windshield, classical feedback control is closer to looking out the back window or the rear-view mirror. A real driver uses an MPC-like approach in steering the car, since it looks forward and chooses an ideal action based on possible future outcomes, taking the real characteristics of the car into consideration. A hypothetical driver using a classical control engineering approach (e.g. PID) would only look out the back window, trying to steer the vehicle based on information about its past behavior. Moreover, our hypothetical driver would not take into consideration the real limits and boundaries of its vehicle: it would try to drive through a curve with a semi-truck, assuming it handles just like a sports car.

Fig. 6.3

Model predictive control demonstrating the receding horizon control idea—new state measurements (observations) are used to compute a new optimal sequence of inputs shifting the horizon forward at all times

While this is an oversimplified approach, the analogy has more to offer. The driver of a car bases his or her judgments at the current time on predictions of the future. The driver is familiar with a mental image of the car, knows how it can accelerate, how fast it can stop and how it handles in general. This mental image of the car is substituted by a simplified internal mathematical model in MPC. In good visibility, a driver may see far ahead in the horizon, and thus go fast. If the visibility conditions are bad, the horizon in front of the driver is also short and one may easily misjudge the situation. The portion of the road one can see while driving is represented by the prediction horizon in MPC. Instability may occur in MPC if the prediction horizon is too short, this would be the equivalent of crashing the car because of entering an unknown curve too fast in low visibility conditions. A real driver continuously updates its decisions, it does not make a plan before starting the engine and stick to it by all means. Similarly, MPC continuously updates the decisions in real-time and it uses only the most recent one, then repeats this procedure. Since just like the real driver the MPC law updates its decisions at all times, the MPC horizon is receding forward in time. Of course, one of the most important aspects of driving is given by the essential requirement of not leaving the road and crashing the car. We can think of this as a type of constraint, along with other constraints such as the physical properties of the vehicle. With a limited portion of the road ahead, one may misjudge its current actions leaving the road: the trajectory and handling of the car becomes unstable, leading to dramatic consequences. Similarly, in MPC the mere presence of constraints can complicate the situation and affect the stability of the control course.

1.1 Historical Overview

Historically, we can differentiate between three independent lines of development of model predictive control [6, 25, 26, 51]:

• model predictive control

• generalized predictive control

• receding horizon control

The first general category is model predictive control (MPC) which encompasses for example model algorithmic control (MAC) based on finite impulse response (FIR) models and dynamic matrix control (DMC) which is based on finite step response (FSR) models. Successful application of MAC has been introduced in [47], while DMC has been first characterized and applied to a chemical process in [14]. The acceptance of these methods in the industry is backed by the use of impulse- and step response-based models that are very easy and convenient to identify. The drawback of FIR- and FSR-based models is, however that it is very difficult to generalize and apply them to more complex systems, moreover they cannot be formulated for unstable systems.

A second line of development is represented by generalized predictive control (GPC). GPC methods are based on single-input single-output (SISO) models such as the ones often utilized in adaptive control. Some of the control approaches falling under this category are the minimum variance (MV) [2] and the generalized minimum variance (GMV) [10] methods. Unfortunately, these methods have been sensitive to modeling errors and could not guarantee stability of non-minimum phase systems. These problems lead to further development of control theory and the introduction of GPC [12, 13], long-range predictive control [11], extended horizon adaptive control [53] and extended prediction self-adaptive control [15]. Later GPC has been formulated for a continuous time system [16] and MIMO models [27, 50] as well. A GPC predictive controller with guaranteed stability has been presented in [23].

The third and final line of development is called receding horizon control (RHC) where the research direction has been given on modifications and development of linear quadratic controllers. Initially the method did not assume the presence of system constraints. An RHC method minimizing a quadratic criterion with a terminal equality constraint ensuring stability has been introduced in [30, 31]. Reference tracking has been added to this formulation later in [29] while [33] has been dealing with state-space interpretation based closed-loop RHC control.

The different directions of research introduced previously have been evolving independently at first. Later the more general state-space representation of RHC allowed the investigation of the connections between the different predictive control approaches [38, 54]. We may state that receding horizon control is in fact the most general interpretation containing GPC or MPC as its special cases. In fact, the one-shot solution of GPC and recursive form of RHC is identical in the absence of constraints. Moreover, there is an analogy between the state observers used in RHC and the optimal predictors of GPC. The state-space representation of the predictive control problem allows the use of MIMO models and more intricate tools in ensuring stability . This book will assume the use of state-space models for representing vibration dynamics as well. Although the state-space representation allows more complex formulations and is now generally accepted in both theoretical and practical works, the simpler FIR- and FSR-based methods remain popular in the industry.

The difference among MPC, GPC and RHC research directions have been decreasing with time and predictive control has arrived at a merging point. Currently, the term predictive control or model predictive control is used in a general sense, and denotes the same concept. An overview of the connections between the different model predictive control interpretations and a unifying view is discussed for example in [4, 32, 51]. A review and discussion of the current predictive control methods and issues is presented for example in [34, 48].

1.2 Nonlinear Model Predictive Control

The plant models assumed in this work are linear or are linearized. Although in many cases this is only an approximation of real dynamics, control engineering practice has demonstrated that plants with complex dynamics can be often controlled using simplified linearized models. A version of MPC using nonlinear plant models is referred to as nonlinear MPC or NMPC. In linear MPC, the optimization task is convex and can be carried out relatively easily. NMPC however creates a non-convex optimization problem, which not only makes the online optimization task considerably difficult but also raises many questions associated with stability .

In practice the inherent mathematical properties of NMPC are exploited to speed up the online solution process, such as the fact that if NMPC problems are solved in sequence, they tend to be fairly similar to each other. This book does not deal with nonlinear models or the application of NMPC to vibration attenuation.

2 Prediction

Let us consider a linear system described by state-space equation:

$$ \begin{aligned} {\mathbf{x}}_{k\,{+}\,1} \,{=}\,{\mathbf{A}}{\mathbf{x}}_k\,{+}\,{\mathbf{B}}{\mathbf{u}}_k\\ {\mathbf{y}}_k \,{=}\, {\mathbf{C}}{\mathbf{x}}_k\,{+}\,{\mathbf{D}}{\mathbf{u}}_k \end{aligned} $$

(6.1)

where ${\mathbf{A}}$ is the state matrix, ${\mathbf{B}}$ is the input matrix and ${\mathbf{C}}$ is the output matrix of dimensions ${\mathbf{A}} \in {\mathbb{R}}^{{n_x}\times{n_x}}$, ${\mathbf{B}} \in {\mathbb{R}}^{{n_y}\times{n_x}}$ and ${\mathbf{C}} \in {\mathbb{R}}^{{n_y}\times{n_x}}$. Since ${\mathbf{D}}$ represents the direct input–output feedthrough, it is omitted in most models based on real-life systems.

Vectors and matrices are marked with a bold upright font in this book, for example the state vector is denoted as ${\mathbf{x}}_k$, in the case of a general multi-input system inputs are ${\mathbf{u}}_k$ and the outputs with ${\mathbf{y}}_k$. To simplify our notation in the upcoming sections and chapters we will now replace these with italic fonts as in $x_k$, $u_k$ and $y_k$. We will reserve the bold upright notation as in ${\mathbf{x}}_k,{\mathbf{u}}_k$ and $\mathbf{y}_k$   rather for future predicted or computed sequences of the quantities expressed by ${{x}}_k,{{u}}_k$ and ${y}_k$ .

In predictive control the state and successively the output of the system is predicted several time steps ahead of the current time. The idea is simply iterating the state-space model several times in succession, while always utilizing the new state update to get the next step. A discrete state-space system is in fact a state predictor, one step into the future. If our discrete time is marked by $(k)$ and our state at that time is given by $x_k$ we may iterate a one-step ahead prediction of the state using a discrete state-space model:

$$ x_{k\,{+}\,1}\,{=}\,{\mathbf{A}}x_{k}\,{+}\,{\mathbf{B}}u_{k} $$

(6.2)

While the system output at the current step is defined by the second equation in (6.1), we can predict the output at the next step as well simply by substituting the actual predicted state $x_{k\,{+}\,1}$:

$$ y_{k\,{+}\,1}\,{=}\,{\mathbf{C}}x_{k\,{+}\,1} $$

(6.3)

Let u suppose the current time is marked by the discrete time step $(k)$. At time $(k)$ we have the state $x_{k}$ based on real readings from the available sensors. ² We may calculate the predicted state at step $(k\,{+}\,1)$, that is $x_{k\,{+}\,1}$. If we take our predicted state $x_{k\,{+}\,1}$ and perform the previous step once more, we get a prediction at time $(k\,{+}\,2)$, that is $x_{k\,{+}\,2}$. Therefore, the state is substituted into the basic state-space equation recursively. The process may be repeated arbitrary times: if we repeat it $n_p$ times we have a $n_p$ steps long prediction horizon:

$$ \begin{array}{lll} k &x_k \,{=}\,x_k\\ k\,{+}\,1\quad &x_{k\,{+}\,1} \,{=}\,{\mathbf{A}}x_{k}\,{+}\,{\mathbf{B}}u_{k}\\ k\,{+}\,2\quad & x_{k\,{+}\,2} \,{=}\,{\mathbf{A}}x_{k\,{+}\,1}\,{+}\,{\mathbf{B}}u_{k\,{+}\,1}\,{=}\, {\mathbf{A}}^2x_{k}\,{+}\,{\mathbf{A}}{\mathbf{B}}u_{k}\,{+}\,{\mathbf{B}}u_{k\,{+}\,1}\\ k\,{+}\,3\quad & x_{k\,{+}\,3}\,{=}\,{\mathbf{A}}x_{k\,{+}\,2}\,{+}\,{\mathbf{B}}u_{k\,{+}\,2}\,{=}\, {\mathbf{A}}^3x_{k}\,{+}\,{\mathbf{A}}^2{\mathbf{B}}u_{k} \,{+}\,{\mathbf{A}}{\mathbf{B}}u_{k\,{+}\,1}\,{+}\,{\mathbf{B}}u_{k\,{+}\,2}\\ \vdots &\vdots \\ k\,{+}\,n_p\quad &x_{k\,{+}\,n_p} \,{=}\,{\mathbf{A}}x_{k\,{+}\,n_p-1}\,{+}\,{\mathbf{B}}u_{k\,{+}\,n_p-1}\\ &\hspace*{2.20pc}\,{=}\,{\mathbf{A}}^{n_p}x_{k}\,{+}\,{\mathbf{A}}^{n_p-1}{\mathbf{B}}u_{k} \,{+}\,\cdots\,{+}\,{\mathbf{A}}{\mathbf{B}}u_{k\,{+}\,n_p}\,{+}\,{\mathbf{B}}u_{k\,{+}\,n_p-1} \end{array} $$

(6.4)

An autonomous system does not assume an input to the system. It is possible to predict the dynamic behavior of a freely vibrating system subject to an initial disturbance by simply ignoring the terms featuring input $u_i$:

$$ \begin{array}{ll} k\,{+}\,i\quad\longrightarrow & x_{k\,{+}\,i}\,{=}\,{\mathbf{A}}^{i}x_{k} \end{array} $$

(6.5)

with $i\,{=}\,0,1,2,\ldots,n_p$. Figure 6.4 demonstrates that given a good model it is possible to predict the behavior of a vibrating system quite precisely. In this example, the state at time step $23$ has been observed from the experimentally measured output—the deflection data of a vibrating cantilever beam. The state and successively the output have been iterated six steps forward, through using a state-space model as a basis for the predictions. Continuing this process tens or hundreds of steps onwards, the error would be likely to build up because of modeling errors and the recursive nature of the process.

Fig. 6.4

Six (several) steps ahead model prediction of the state and original measured output

A predictive controller iterates the state-space model several steps ahead in time to see how the system will behave in the future and adjusts the inputs $u_k$ at the current time accordingly. Naturally, this must be done at each sampling instant, since the output measurements and the estimated states are always updated in real-time.

To automate the process of recursive iteration into the future the prediction matrices must be defined and constructed. Let us now denote the sequence of future predicted states at time $(k)$ as an $n_{\!p}$ elements long a row vector ${\mathbf{x}}_k$, the sequence of planned inputs as ${\mathbf{u}}_k$ and the sequence of predicted outputs as ${{\mathbf{y}}}_k$. The subscript $k$ denotes that the vector has been last actualized at time $(k)$ and contains the predictions starting from this discrete time point. According to this, these vectors can be described as follows:

$$ {\mathbf{x}}_k\,{=}\,\left[\begin{array}{l}x_{k}\\ x_{k\,{+}\,1}\\ x_{k\,{+}\,2}\\ \vdots\\ x_{k\,{+}\,n_{\!p}-2}\\ x_{k\,{+}\,n_{\!p}-1}\\ x_{k\,{+}\,n_{\!p}}\\ \end{array}\right] \quad {\mathbf{y}}_k\,{=}\,\left[\begin{array}{l} y_{k}\\ y_{k\,{+}\,1}\\ y_{k\,{+}\,2}\\ \vdots\\ y_{k\,{+}\,n_{\!p}-2}\\ y_{k\,{+}\,n_{\!p}-1}\\ y_{k\,{+}\,n_{\!p}}\\ \end{array}\right]\quad {\mathbf{u}}_k\,{=}\,\left[\begin{array}{l}u_{k}\\ u_{k\,{+}\,1}\\ u_{k\,{+}\,2}\\ \vdots\\ u_{k\,{+}\,n_{\!p}-3}\\ u_{k\,{+}\,n_{\!p}-2}\\ u_{k\,{+}\,n_{\!p}-1}\\ \end{array}\right] \\ $$

(6.6)

Note the terms in Eq. (6.4) which are multiplied by $x_i$. As we proceed from time $(k)$ to the end of the prediction horizon, that is as $k\,{=}\,k,k\,{+}\,1,\ldots,k\,{+}\,n_{\!p}-1,k\,{+}\,n_{\!p}$ the term in front of $x_k$ is simply $A^i$. Therefore, for an autonomous system the vector of predicted states can be calculated by:

$$ {\mathbf{x}}_{k}\,{=}\,{\mathbf{M}}x_k\,{=}\,\left[\begin{array}{l}{\mathbf{A}}^0\\ {\mathbf{A}}^1\\ {\mathbf{A}}^2\\ \vdots\\ {\mathbf{A}}^{n_{\!p}-2}\\ {\mathbf{A}}^{n_{\!p}-1}\\ {\mathbf{A}}^{n_{\!p}}\\ \end{array}\right]x_k \\ $$

(6.7)

The prediction matrix ³ ${\mathbf{M}}$ for this autonomous system is also valid for systems with input (the general case), although here we must take care of the terms which are multiplied by the input $u_{i}$. Again, if we look at Eq. (6.4) carefully, we may rearrange its terms so we can get the prediction matrices for a general case:

$$ {\mathbf{x}}_{k}\,{=}\,{\mathbf{M}}x_k\,{+}\,{\mathbf{N}}{\mathbf{u}}_k $$

(6.8)

where ${\mathbf{N}}$, the second prediction matrix may be intuitively interpreted as the impulse response matrix which is an example of a convolution matrix. Note that instead of a direct input ${\mathbf{u}}$ most industrial controllers use a difference in input $\triangle {\mathbf{u}}$ as a degree of freedom. In that case, the prediction matrix can be interpreted as the step response matrix. The impulse response matrix ${\mathbf{N}}$ is calculated according to:

$$ {\mathbf{N}}\,{=}\,\left[\begin{array}{ccccccc}{\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \ldots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}}\\ {\mathbf{B}} & {\mathbf{0}} & {\mathbf{0}} & \ldots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}}\cr {\mathbf{AB}} & {\mathbf{B}} & {\mathbf{0}} & \ldots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}}\\ {\mathbf{A}}^2{\mathbf{B}} & {\mathbf{AB}} & {\mathbf{B}} & \ldots & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}}\\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ {\mathbf{A}}^{n_{\!p}-3}{\mathbf{B}} & {\mathbf{A}}^{n_{\!p}-4}{\mathbf{B}} & {\mathbf{A}}^{n_{\!p}-5}{\mathbf{B}} & \ldots & {\mathbf{B}} & {\mathbf{0}} & {\mathbf{0}}\\ {\mathbf{A}}^{n_{\!p}-2}{\mathbf{B}} & {\mathbf{A}}^{n_{\!p}-3}{\mathbf{B}} & {\mathbf{A}}^{n_{\!p}-4}{\mathbf{B}} & \ldots & {\mathbf{AB}} & {\mathbf{B}} & {\mathbf{0}}\cr {\mathbf{A}}^{n_{\!p}-1}{\mathbf{B}} & {\mathbf{A}}^{n_{\!p}-2}{\mathbf{B}} & {\mathbf{A}}^{n_{\!p}-3}{\mathbf{B}} & \ldots & {\mathbf{A}}^2{\mathbf{B}} & {\mathbf{AB}} & {\mathbf{B}}\end{array}\right] $$

(6.9)

Note that the first block row of matrix ${\mathbf{N}}$ is zero in order to get $x_k$ as the first element of ${\mathbf{x}}_k$. For a time-invariant state-space model, we only have to construct the prediction matrices ${\mathbf{M}}$ and ${\mathbf{N}}$ once. For an adaptive system, these matrices have to be constructed online. To get the vector of predicted states, we simply substitute for the prediction matrices and obtain ${\mathbf{x}}_{k}$.

Let us denote the $i$-th block row ⁴ of matrix ${\mathbf{M}}$ with ${\mathbf{M}}_i$ according to:

$$ {\mathbf{M}}_i\,{=}\,{\mathbf{A}}^i $$

(6.10)

with ${\mathbf{M}}_0\,{=}\,{\mathbf{I}}$. Similarly, one may consider the $i$-th block row section of matrix ${\mathbf{N}}$ as defined by (6.9) and denote it with ${\mathbf{N}}_i$

$$ {{\mathbf{N}}_i}\,{=}\,\left[\begin{array}{lllllll}{\mathbf{A}}^{i}{\mathbf{B}} & {\mathbf{A}}^{i-1}{\mathbf{B}} & {\mathbf{A}}^{i-2}{\mathbf{B}} & \ldots & {\mathbf{A}}^2{\mathbf{B}} & {\mathbf{AB}} & {\mathbf{B}}\end{array}\right] $$

(6.11)

$$ {\mathbf{N}}_0\,{=}\,\left[\begin{array}{ccccc}{\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & \ldots & {\mathbf{0}}\end{array} \right] $$

(6.12)

and use it to get the predicted state at any time $(k\,{+}\,i)$, where $i\,{=}\,0,1,2,\ldots,n_{\!p}$ by using the following expression:

$$ x_{k\,{+}\,i}\,{=}\,{\mathbf{M}}_{i}x_k\,{+}\,{\mathbf{N}}_i {\mathbf{u}}_k\,{=}\,{\mathbf{A}}^{i}x_k\,{+}\,{\mathbf{N}}_i {\mathbf{u}}_k $$

(6.13)

By computing the sequence of predicted states, we may also estimate the future system output by multiplying with ${\mathbf{C}}^{i\,{+}\,1}$ according to:

$$ y_{k\,{+}\,i}\,{=}\,{\mathbf{C}}^{i\,{+}\,1}x_{k\,{+}\,i}\,{=}\,{\mathbf{C}}^{i\,{+}\,1} {\mathbf{A}}^{i}x_k\,{+}\,{\mathbf{C}}^{i\,{+}\,1}{\mathbf{N}}_i {\mathbf{u}}_k $$

(6.14)

Of course, it is not possible to calculate the vector of future states or outputs, unless the sequence of inputs ${{\mathbf{u}}_{\mathbf{k}}}$ is known beforehand. Fortunately, this problem can be reversed, and instead of asking what the sequence of outputs or states will be, we can ask what sequence of inputs is necessary to achieve the desired sequence of outputs or states.

3 Cost Functions

A cost function is an important part of a predictive controller because it is an indicator of the degree of optimality of a dynamic response, resulting a sequence of control inputs ${\mathbf{u}}_k$ applied to the system. This degree of optimality may express how close we are to the desired output or state levels including how much effort is needed to get there, and in MPC this is referred to as the cost. In the controller itself the role of the cost function is reversed, and we are aiming to calculate the best series of control inputs ${\mathbf{u}}_k$ which results in a minimal cost.

In control engineering we want to keep output as close to the reference as possible. Reference is often located at zero; this is a common case in vibration attenuation, as we would like to keep the vibrating structure at equilibrium . We may designate the difference between the desired level with an error, which can be expressed at any moment by a numerical indicator. This numerical indicator called the cost does not necessarily have a physical meaning, and the mathematical way to calculate the cost is to set up a cost function .

Let us calculate a simple scalar indicator $J$, a cost describing how good our control will be in the future: from the next step up to the horizon defined by the prediction horizon $n_{\!p}$. This indicator only depends on the current measured or observed state $x_k$ and the input sequence ${\mathbf{u}}_k$ we will implement at the next step and the time up to the end of the horizon:

$$ J\,{=}\,f(x_k,{\mathbf{u}}_k) $$

(6.15)

Theoretically, this function can be arbitrary: for example it may contain numerical indicators expressing how close is the desired value at any given moment to the reference or how much input $u_k$ is needed to keep it there, etc. Although a cost function can be arbitrary, it is better to prefer certain constructions for the cost function , as proper formulations may aid the evaluation and optimization procedures later. The most common form for the cost function in MPC is a quadratic cost function .

Having a cost, we can use it to calculate the sequence of future control inputs ${\mathbf{u}}_k$ by formulating the following problem:

${\boldsymbol{\it{Given\, a\, current\, state}}}$ $\,\,x_k \,\,{\boldsymbol{what\,is\,the\,sequence\, of\, future\, control\, inputs, \mathbf{u}}_k \,\,{\boldsymbol{which}}}$ ${\boldsymbol{will\, keep\, the\, cost}}$ ${J} {\boldsymbol{at\, its\, minimum?}}$

In other words, we have to minimize the cost function with the argument ${\mathbf{u}}_k$ to get an optimal sequence of inputs denoted with ${\mathbf{u}}^{\ast}_k$:

$$ {\mathbf{u}}^{\ast}_k\,{=}\,arg\min_{{\mathbf{u}}} J(x_k,{{\mathbf{u}}_k}) $$

(6.16)

The above statement defines an optimal control problem.

3.1 Building a Quadratic Cost Function

As it has been previously stated, the aim of a control system is to keep the outputs $y_k$ as close to the reference as possible. The difference between the reference value $r_k$ and output $y_k$ is called the control error and it is simply defined by:

$$ e_k\,{=}\,r-y_k $$

(6.17)

where $e_k$ is the error vector. ⁵ Let us consider a zero reference since defining a nonzero $r$ is just a matter of shifting it to the desired tracking level or using a controller that produces input increments $\triangle u_k$. A zero reference is $r\,{=}\,0$, in other words means that any type of output is an error:

$$ e_k\,{=}\,r-y_k\,{=}\,0-y_k\,{=}\,-y_k $$

(6.18)

Instead of the relative value of the output it is better to consider the square of the error, this way negative values are eliminated and deviation from the equilibrium is penalized with an equal value. The square of the output is in this case a unit-less indicator of control quality $j_k$ at the given sampling time $(k)$. The less its value is, the better is our control:

$$ j_k\,{=}\,y_k^Ty_k $$

(6.19)

Note that due to a simplification in notation $y_k$ is still a vector, therefore we are using $y_k^Ty_k$ instead of $y_k^2$. Since the output in real systems is given by ${y}_k\,{=}\,{\mathbf{C}}x_k$ we may substitute that into (6.19) and get:

$$ j_k\,{=}\,x_k^T{\mathbf{C}}^T{\mathbf{C}}x_k $$

(6.20)

For a state-space model this is a very good quality indicator, and expresses the cost of control at a given instant. In addition to removing negative outputs $-y$ from the cost the square representation has one more advantage. As the state is a column vector, taking a matrix square results in a scalar valued cost.

When formulating a cost function it is good to take into account the work performed by the actuators, or in other words the effect of control input $u_k$. In certain situations, it is not necessary to limit actuation, nevertheless it may be necessary to preserve functionality and lengthen the lifetime of actuators. For example, if an actuator is adjusting the position of a mechanical structure continuously and aggressively, even if there is only a minimal disturbance—this may limit the lifetime of the actuators itself, the structure or possibly other system components. Aggressive controller action is another reason to include the effect of actuators into the cost function . For example, a vibration control system for aircraft or spacecraft shall not generate actuator inputs, which seriously affect the overall attitude and maneuverability of the system. Finally, the cost function may also express cost in the economic terms: as energy is needed to drive the actuators, there are financial aspects of every adjustment. A civil engineering structure requires actuators that may be expensive to drive: in a normal situation, their action should be minimal, however if the structure is subjected to an earthquake, the actuators should perform their task as well as possible. To summarize this paragraph, some of the reasons to include control input in the cost function are:

• lifetime prolongation

• design

• safety

• economic

• others$\ldots$

In addition to the quadratic effect of the output defined by (6.20) we may therefore simply add the square of the control input. This will create a numerical indicator, a cost function for the time step $(k)$:

$$ j_k\,{=}\,x_k^T{\mathbf{C}}^T{\mathbf{C}}x_k\,{+}\,u_k^Tu_k $$

(6.21)

4 State and Input Penalization

In a predictive controller, in addition to the prediction or control horizon there are two more important settings that can affect the overall type and performance of the controller and its resulting actions. These settings are the so-called penalization matrices. Let us introduce a matrix ${\mathbf{R}}$ that will affect the contribution of the second term into the overall cost:

$$ j_k\,{=}\,x_k^T{\mathbf{C}}^T{\mathbf{C}}x_k\,{+}\,u_k^T{\mathbf{R}}u_k $$

(6.22)

where ${\mathbf{R}}$ is the so-called input penalization matrix. The value of ${\mathbf{R}}$ always depends on the application, and it is set by the control engineer. If it is not important to consider the effect of the work performed by the actuators, it is possible to use ${\mathbf{R}}\,{=}\,0$ or a very low level and the second term will be practically eliminated from the cost function . On the other hand, the contribution of the second term can be fine tuned by raising the level of ${\mathbf{R}}$ to higher numbers.

With a multiple input system—that is having more actuators—by setting some elements of the matrix ${\mathbf{R}}$ to a higher value, we indicate the need to lower the input to certain actuators. Their effect will be penalized, as every action will be represented by a higher cost contribution. On the other hand, if one uses a very low number, the actuator will not be represented significantly in the overall cost and its actions are not penalized. ${\mathbf{R}}$ is therefore the input penalization matrix, a tuning parameter adjustable by the user.

The first part of the expression in (6.21) contains the state vector and its transpose, which encloses ${\mathbf{C}}^T{\mathbf{C}}$. In predictive control, we may replace this by the so-called state penalization matrix denoted by ${\mathbf{Q}}$.

$$ j_k\,{=}\,x_k^T{\mathbf{Q}}x_k\,{+}\,u_k^T{\mathbf{R}}u_k $$

(6.23)

The structure of this matrix depends on the given system and on the particular choice of the control engineer. If one chooses ${\mathbf{Q}}\,{=}\,{\mathbf{C}}^T{\mathbf{C}}$ then essentially the states are recalculated into outputs $y_k$. An arbitrary ${\mathbf{Q}}$ matrix may be chosen as well. This allows the control engineer to include or exclude effects of given states. For example consider the vibration of a system which is modeled by a second order state-space model, in which the first state describes the position of the structure while the second its velocity. If the state penalty matrix is constructed in the following way

$$ {\mathbf{Q}}\,{=}\,\left[\begin{array}{ll}1 & 0\\ 0 & 0\\ \end{array}\right] $$

(6.24)

then one is penalizing the position, and the velocity does not play a role in the final cost. On the other hand, if one utilizes the penalization matrix

$$ {\mathbf{Q}}\,{=}\,\left[\begin{array}{ll}1 & 0\\ 0 & 10\\ \end{array}\right] $$

(6.25)

the velocity is an order of magnitude more important in the final cost than position. The possible number of combinations to tune penalization matrices is endless and it is always up to the given application and the control engineer to choose a suitable Q and R matrix.

Based on the formerly introduced definition of the cost function it makes natural sense to use the output in the cost function , that is to choose ${\mathbf{Q}}\,{=}\,{\mathbf{C}}^T{\mathbf{C}}$. If there is no preference as to which state has to be penalized more (e.g. which is more important) then it is also common to choose ${\mathbf{Q}}$ to be equal with the identity matrix

$$ {\mathbf{Q}}\,{=}\,{\mathbf{I}}\,{=}\,\left[\begin{array}{ll}1 & 0\\ 0 & 1\\ \end{array} \right] $$

(6.26)

for a second order system. The identity matrix ${\mathbf{I}}$ is a matrix of ones on the diagonal and zeros elsewhere. It is also a square matrix , and its size equals to the model order $n_x$.

In case of a single input system, if the input contribution of the actuators is not important in the cost, the input penalization ${\mathbf{R}}\,{=}\,r$ is chosen as a small number $r\,{=}\,$1E-3. If the input contribution shall be included in the cost more dominantly, one may increase this value. Analogically, for a multiple input system we may use the identity matrix or its scalar multiples:

$$ {\mathbf{R}}\,{=}\,{\mathbf{I}} r $$

(6.27)

where ${\mathbf{I}}$ is again the identity matrix, and $r$ is a tunable scalar multiplier.

5 Cost of the Future States and Inputs

Instead of just considering the cost of the current step as in (6.23), a predictive controller needs to calculate the cost of future inputs, or in other words the predicted cost. A predicted cost at any time $(k)$ is a sum of individual cost contributions according to (6.23) from the time $(k)$ up to the end of the prediction horizon, that is $(k\,{+}\,n_{\!p})$ [1, 20, 23, 36]:

$$ J_k\,{=}\,\sum_{i\,{=}\,0}^{n_{\!p}-1} j_{k\,{+}\,i}\,{=}\,\sum_{i\,{=}\,0}^{n_{\!p}-1} \left(x_{k\,{+}\,i}^T{\mathbf{Q}}x_{k\,{+}\,i}\,{+}\,u_{k\,{+}\,i}^T{\mathbf{R}}u_{k\,{+}\,i}\right) $$

(6.28)

Note that while $j_k$ is a cost just at the current time, $J_k$ now denotes cost from $(k)$ up to the end of the prediction (or control) horizon. This is called a finite horizon predicted cost calculated at the time $(k)$. The cost in (6.28) expresses the cost of control inputs and its effects up to the prediction horizon.

Figure 6.5 illustrates a finite horizon MPC control law, where the effect of control inputs is only included in the predicted cost and thus the optimization problem for the length of the horizon. The effect of inputs is assumed zero beyond this horizon. The actual zero input level may or may not be ever reached, since the horizon is receding forward. However, input effects beyond the horizon are excluded from the optimization altogether.

Fig. 6.5

Finite horizon model predictive control. The control law assumes free variables within the horizon, but predicts zero input afterward. The effect of inputs beyond the horizon is not included in the predicted cost

Fig. 6.6

Model predictive control demonstrating the receding horizon control idea. New state measurements (observations) are used to compute a new optimal sequence of inputs shifting the horizon forward at all times

For a finite horizon cost, there is no guarantee that the control law will achieve the optimal predicted performance. This situation may be solved by predicting the cost for an infinite horizon, that is [1, 42]:

$$ J_k\,{=}\,\sum_{i\,{=}\,0}^{\infty} \left(x_{k\,{+}\,i}^T{\mathbf{Q}}x_{k\,{+}\,i}\,{+}\,u_{k\,{+}\,i}^T{\mathbf{R}}u_{k\,{+}\,i}\right) $$

(6.29)

Unfortunately, this would create an optimization problem with an infinite number of variables within ${\mathbf{u}}_k$. Luckily, it is possible to express the cost of the control inputs and their effects beyond the prediction horizon in such a way that the number of optimization parameters still remains finite.

For this, it is necessary to employ a method which approximates the cost for an infinite horizon but with a finite number of inputs: the so-called dual-mode control paradigm. In the dual-mode paradigm, the predictive controller calculates the control explicitly up to a fixed horizon. The cost is calculated up to the very last step of the horizon, which is up to $(k\,{+}\,n_{\!p}-1)$. Instead of just considering the cost of the last state $x_{k\,{+}\,n_{\!p}}$ as usual, this state is used to compute a so-called terminal cost . This terminal cost can be made equivalent to the cost $J_\infty$ ranging from $(k\,{+}\,n_{\!p}-1)$ up to infinite time $k\,{=}\,\infty$. To express this cost, one has to use a special penalty matrix called the terminal weighting matrix denoted as ${\mathbf{P}}_{\!\!f}$ and express the new cost according to [34, 46, 48, 49]:

$$ J_k\,{=}\,\sum_{i\,{=}\,0}^{n_{\!p}-1} \left(x_{k\,{+}\,i}^T{\mathbf{Q}}x_{k\,{+}\,i}\,{+}\,u_{k\,{+}\,i}^T{\mathbf{R}}u_{k\,{+}\,i}\right) \,{+}\,x_{k\,{+}\,n_{\!p}}^T{\mathbf{P}}_{\!\!f}x_{k\,{+}\,n_{\!p}} $$

(6.30)

In dual-mode control, not only will the cost be divided into two modes, but the control inputs as well. The first mode will contain free optimization variables, while the second mode (associated with the last state) will be steered into equilibrium by a stabilizing fixed feedback law, usually a linear quadratic control law. The two modes from the view of the inputs $u_{i}$ are:

$$ u_{i}\,{=}\,\left\{\begin{array}{lll}\hbox{free variables} &\quad i\,{=}\,k,k\,{+}\,1,\ldots, n_{\!p}-1 &\quad \hbox{Mode 1} \\ {\mathbf{K}}x_{k\,{+}\,i} &\quad i\,{=}\,n_{\!p},n_{\!p}\,{+}\,1,\ldots,\infty &\quad \hbox {Mode 2} \end{array} \right. $$

(6.31)

Since the cost in (6.30) needs to be evaluated explicitly only up to the end of the horizon, a proper choice for the terminal weighting matrix ${\mathbf{P}}_{\!\!f}$ is necessary. If we assume that the control moves in mode 2 will be computed by a fixed feedback law $u_{k\,{+}\,n_{\!p}\,{+}\,i}\,{=}\,{\mathbf{K}}x_{k\,{+}\,n_{\!p}}$, then the terminal weighting matrix ${\mathbf{P}}_{\!\!f}$ is the solution of the following Lyapunov equation [25, 39, 41, 48]:

$$ {\mathbf{P}}_{\!\!f}-({\mathbf{A}}\,{+}\,{\mathbf{B}}{\mathbf{K}})^T {\mathbf{P}}_{\!\!f}({\mathbf{A}}\,{+}\,{\mathbf{B}} {\mathbf{K}})\,{=}\,{\mathbf{Q}}\,{+}\,{\mathbf{K}}^T{\mathbf{R}}{\mathbf{K}} $$

(6.32)

where given the LTI system and the calculated fixed stabilizing feedback law ${\mathbf{K}}$, the terminal weighting matrix can be easily calculated.

The cost at a given time $(k)$ and onwards up to the infinity is given by (6.30). Using the notation established earlier in (6.6), we can use a vector of a series of predicted inputs ${\mathbf{u}}_k$ and reformulate the infinite horizon cost to be more suitable for the optimization task. The cost function in the current sum based form is not appropriate for an MPC controller, where a compact matrix notation is preferred. If one substitutes for ${x_k}$ at the current time and ${{\mathbf{u}}_k}$ for all future inputs up to the end of the horizon, obtains a transformed cost function after rearranging the terms. This transformed cost function does not use the sum operator anymore, matrix algebra is necessary to evaluate the cost of control actions ${{\mathbf{u}}_k}$ up to infinity. The transformed cost will be given by [8, 25, 39]:

$$ J_k\,{=}\,{\mathbf{u}}_k^T{\mathbf{H}}{\mathbf{u}}_k\,{+}\,2x_k^T{\mathbf{G}}^T {\mathbf{u}}_k\,{+}\,x_k^T{\mathbf{F}}x_k $$

(6.33)

where

$$ {\mathbf{H}}\,{=}\,\sum_{i\,{=}\,0}^{n_{\!p}-1} {\mathbf{N}}^T_i{\mathbf{Q}}{\mathbf{N}}_i\,{+}\, {\mathbf{N}}_{n_{\!p}}^T{\mathbf{P}}_{\!\!f}{\mathbf{N}}_{n_{\!p}}\,{+}\,{\fancyscript{R}} $$

(6.34)

$$ {\mathbf{G}}\,{=}\,\sum_{i\,{=}\,0}^{n_{\!p}-1} {\mathbf{N}}^T_i{\mathbf{Q}}{\mathbf{M}}_i\,{+}\,{\mathbf{N}}_{n_{\!p}}^T {\mathbf{P}}_{\!\!f}{\mathbf{M}}_{n_{\!p}} $$

(6.35)

$$ {\mathbf{F}}\,{=}\,\sum_{i\,{=}\,0}^{n_{\!p}-1}{\mathbf{M}}^T_i{\mathbf{{\mathbf{Q}}}} {\mathbf{M}}_i\,{+}\,{\mathbf{M}}_{n_{\!p}}^T{\mathbf{P}}_{\!\!f}{\mathbf{M}}_{n_{\!p}} $$

(6.36)

where $i$ denotes the $i$-th block row, respectively $n_{\!p}$ denotes the last block row of ${\mathbf{N}}$ and ${\mathbf{M}}$. Matrix ${\fancyscript{R}}$ is a block matrix having the input penalty ${\mathbf{R}}$ on its main diagonal, that is:

$$ {\fancyscript{R}}\,{=}\,\left[\begin{array}{cccc}{\mathbf{R}} & 0 & \ldots & 0\\ 0 &{\mathbf{R}} & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & {\mathbf{R}} \\ \end{array}\right] $$

(6.37)

Given a linear time-invariant model matrices ${\mathbf{H}}$, ${\mathbf{G}}$ and ${\mathbf{F}}$ can be computed offline.

If one inspects the cost function in (6.33) closely, finds a vector of future predicted control inputs ${\mathbf{u}}_k$ in the first two terms. In the MPC controller this is the unknown or free variable, in other words the aim of the controller is to find the optimal ${\mathbf{u}}_k$ which minimizes the cost function (6.33). There is one more variable in the cost function $x_k$ but that is dependent on the actual measured or observed state, and is updated accordingly at every $(k)$. If everything is constant in (6.33) except the input vector, then the cost function is in fact a matrix analogy of the scalar quadratic function:

$$ j\,{=}\,au^2\,{+}\,bu\,{+}\,c $$

(6.38)

The cost function is therefore quadratic. From the pure mathematical optimization point of view, such a quadratic function has beneficial properties making its evaluation easier. There is one more fact to note about the formulation in (6.33). The last part of the expression containing $x_k^T{\mathbf{F}}x_k$ does not depend on the inputs ${\mathbf{u}}_k$. The last part contributes to the final cost a steady amount regardless of the sequence of planned inputs. Since in MPC we are interested in minimizing the cost, we may just simply leave out this static part since it does not carry any useful information:

$$ J_k\,{=}\,{\mathbf{u}}_k^T{\mathbf{H}}{\mathbf{u}}_k\,{+}\,2x_k^T {\mathbf{G}}^T{\mathbf{u}}_k $$

(6.39)

6 Unconstrained Model Predictive Control

The simplest possible formulation of a model predictive controller is a controller without constraints: in other words without limits on the input, output or the states. This is actually an exception in the field of MPC, as it can be expressed in a closed form. If one minimizes the cost function in (6.33) without a regard to constraints, a closed form expressed by a fixed matrix feedback law is obtained. This feedback law is explicit and it does not have to be recalculated at each iteration in the case of an LTI system. Unlike in the absence of constraints, it is not possible to obtain constrained MPC in a closed form. If constraints are assumed the optimization has to be performed by a numerical optimization algorithm, online and at every sampling instant $(k)$.

The aim of an MPC controller can be defined stating that we want to find the sequence of input values ${\mathbf{u}}_k$ which produces a minimal cost function $J_k$ given a measured or observed state $x_k$ at time $(k)$. In this way we get a sequence of optimal inputs ${\mathbf{u}}^{\ast}_k$ or mathematically [34, 48]:

$$ {\mathbf{u}}^{\ast}_k\,{=}\,arg\min_{{\mathbf{u}}_k} J_k(x_k,{{\mathbf{u}}_k}) $$

(6.40)

$$ {\mathbf{u}}_k \,{=}\,arg\min_{{\mathbf{u}}_k} \left\{ \sum_{i\,{=}\,0}^{n_{\!p}-1} \left(x_{k\,{+}\,i}^T{\mathbf{Q}}x_{k\,{+}\,i}\,{+}\,u_{k\,{+}\,i}^T{\mathbf{R}} u_{k\,{+}\,i}\right)\,{+}\,x_{k\,{+}\,n_{\!p}}^T{\mathbf{P}}_{\!\!f}x_{k\,{+}\,n_{\!p}} \right\} $$

(6.41)

The quadratic infinite time cost in a simplified collected way has been defined previously by (6.39). The matrices ${\mathbf{H}}$, ${\mathbf{G}}$ can be calculated in advance and are not variable given an LTI system while the optimization task can be computed beforehand as well, resulting a closed form control law. The optimization task is to minimize:

$$ {\mathbf{u}}^{\ast}_k\,{=}\,arg\min_{{\mathbf{u}}_k} \left({\mathbf{u}}_k^T{\mathbf{H}}{\mathbf{u}}_k\,{+}\,2x_k^T{\mathbf{G}}^T {\mathbf{u}}_k\right) $$

(6.42)

The gradient of the cost function with respect to ${\mathbf{u}}$ will be [6, 8]:

$$ \nabla {J_k}\,{=}\,2{\mathbf{H}}{\mathbf{u}}_k\,{+}\,2{\mathbf{G}}x_k $$

(6.43)

The minimum of $J_k$ is satisfied at $\nabla {J_k}$. If ${\mathbf{H}}$ is nonsingular, then the optimization result is unique and is given by [6, 25]

$$ {\mathbf{u}}^{\ast}_k\,{=}\,-\!{\mathbf{H}}^{-1}{\mathbf{G}}x_k $$

(6.44)

where ${\mathbf{H}}$ and ${\mathbf{G}}$ are according to (6.34) and the actual measured or observed state is $x_k$. The result is a sequence of optimal inputs ${\mathbf{u}}_k$ of which only the first element or in the case of a multiple input system the first block element is required. An actual controller uses the first element of ${\mathbf{u}}_k$, then the inputs are re-evaluated based on new observed states. For an LTI system this reduces to a static control law, which is the first $n_u$ wide block row of $-{\mathbf{H}}^{-1}{\mathbf{G}}$ used in the following fashion:

$$ u_{k}\,{=}\,-{\fancyscript{K}}x_k\,{=}\,-[\begin{array}{ccccc}{\mathbf{I}}_{n_u} {\mathbf{0}} & {\mathbf{0}} & \ldots & {\mathbf{0}}]\end{array}{\mathbf{H}}^{-1}{\mathbf{G}} x_k $$

(6.45)

where ${\fancyscript{K}}$ is the resulting fixed unconstrained MPC law and ${\mathbf{I}}_{n_u}$ is a square matrix of the size equivalent to the number of inputs $n_u$.

The usual and obvious choice for the mode 2 fixed stabilizing feedback ${\mathbf{K}}$ is the LQ optimal gain. Because the predictions in the unconstrained MPC law will be optimal in both modes and the previously formulated cost is equivalent to the cost used in LQ controllers, the unconstrained MPC gain ${\fancyscript{K}}$ will be identical to the LQ gain ${\mathbf{K}}$. The future optimal sequence of the outputs ${\mathbf{u}}^{\ast}_k$ will be related to the LQ gain as well.

7 Constraint Formulation

The real power of MPC lies in computing optimal control actions for systems, which incorporate constraints. In this case, however, the feedback law cannot be computed beforehand, given a knowledge of the plant model. Instead, the optimization procedure must be performed online, in between samples $(k)$ and $(k\,{+}\,1)$.

The quadratic cost determined by (6.30) and then subsequently simplified by (6.33) still holds. What we have in addition is a set of constraints, or limits on the input variables, output or possibly states. These inputs are defined as follows [1, 8, 39]:

$$ \underline {u} \,{\leq}\,u_k \leq \overline{u} $$

(6.46)

$$ \underline {x} \,{\leq}\,x_k \leq \overline{x} $$

(6.47)

These constraints have to be rewritten in a form suitable for a predictive controller. This form is more compact than the above notation and collects the constraints in such a way that they are expressed in terms of the argument, that is $u_k$. The constrained MPC control law has to be evaluated online using a quadratic programming (QP) algorithm and most QP solvers process optimization constraints in the following generic form [5]:

$$ {\mathbf{A_c}} u_{k} \,{\leq}\,{\mathbf{b_0}} $$

(6.48)

where ${\mathbf{A_c}}$ and ${\mathbf{b_0}}$ define the constraints. The input constraints 6.47 can be divided into the following two equivalent constraints:

$$ \begin{aligned} \underline {u} \,&{\leq}\,u_k\\ -\overline{u} \,&{\leq}\,{-}u_k \end{aligned} $$

(6.49)

If this holds for each input $u_k$ then it is necessary to redefine it until the end of the mode 1 predictions, ⁶ that is for all free variables. The constraints shall cover $u_k, u_{k\,{+}\,1},\ldots,u_{k\,{+}\,n_p-1}$. This can be written in the following equivalent matrix form:

$$ \left[ \begin{array}{r} {\mathbf{I}} \\ -{\mathbf{I}} \end{array}\right] {\mathbf{u}}_k \,{\leq}\, \left[\begin{array}{r} {\mathbf{1}}\overline{u}\\ -{\mathbf{1}}\underline{u} \end{array}\right] $$

(6.50)

where ${\mathbf{I}}$ is an identity matrix, while ${\mathbf{1}}$ is a vector of ones for a single input system and $\left[{\mathbf{1}}\,{=}\,\begin{array}{cccc}{\mathbf{I}} & {\mathbf{I}} & \ldots & {\mathbf{I}}\end{array}\right]$ with $n_u$ sized identity matrices if the system has $n_u$ inputs.

State constraints can be similarly rewritten. State constraints from (6.47) have to be applied not for the current step $x_k$ but similarly to the input for the future free variables $x_{k\,{+}\,1}, x_{k\,{+}\,2},\ldots,x_{k\,{+}\,n_p}$ as well. We can divide the state constraints (6.47) in two parts and we get

$$ \begin{aligned} \underline {x} \,&{\leq}\,x_k\\ -\overline{x} \,&{\leq}\,{-}x_k \end{aligned} $$

(6.51)

One must change this direct state formulation, so that the states are expressed in the terms of the inputs. From the prediction equations it is possible to calculate the next state $x_{k\,{+}\,1}\,{=}\,{\mathbf{M}}_i x_k \,{+}\, {\mathbf{N}}_i {\mathbf{u}}_k$ at each $i\,{=}\,1,2,3,\ldots,n_p$, we can rewrite the state constraints to obtain the following simplified form [8]:

$$ \left[\begin{array}{c}{\mathbf{N}}_i\\ -{\mathbf{N}}_i\end{array}\right] {\mathbf{u}}_k \,{\leq}\,\left[\begin{array}{c} \overline{x}\\ -\underline{x}\end{array}\right] \,{+}\, \left[\begin{array}{c}-{\mathbf{M}}_i\\ {\mathbf{M}}_i \end{array}\right]x_k $$

(6.52)

substituting for each block row of ${\mathbf{M}}_i$ and ${\mathbf{N}}_i$ $i\,{=}\,1,2,\ldots,n_p$. Note that $i\,{=}\,0$, or first block row of ${\mathbf{M}}$ and ${\mathbf{N}}$ is missing, since we cannot take into account the currently measured or observed state $x_k$ at the time $(k\,{+}\,i),i\,{=}\,0$.

The input and state constraints from (6.50) and (6.52) may be combined, since the usual QP algorithm accepts constraints on the optimized variables in the following form:

$$ {\mathbf{A_c}} u_{k} \,{\leq}\,{\mathbf{b}}_0 \,{+}\, {\mathbf{B}}_0 x_k $$

(6.53)

where the matrices ${\mathbf{A_c}}$, ${\mathbf{b}}_0$ and ${\mathbf{B}}_0$ are constant and can be determined offline.

7.1 Hard Saturation Versus Constraint Handling

One might wonder why we need constrained MPC if natural actuator boundaries can be effectively incorporated into a control law by using simple saturation limits. Saturation is a commonly used technique, where the real inputs computed by an arbitrary control strategy are clipped to the allowable level according to:

$$ \begin{array}{l@{\quad}l@{\quad}l@{\quad}l} u_k\,{=}\,u_k &\quad\textrm{if} &\quad\underline {u} < &u_k <\overline{u}\\ u_k\,{=}\,\overline{u} &\quad\textrm{if} & &u_k \geq \overline{u}\\ u_k\,{=}\,\underline {u} &\quad\textrm{if} & & u_k \,{\leq}\,\underline {u} \end{array} $$

(6.54)

In case the controller computes an input in between the lower and upper bounds, the input is directly used in the closed-loop system as intended. As soon as the input exceeds the lower or upper limits, it is clipped to the allowable level by hard saturation limits. This is the essential technique used by most traditional controllers to incorporate constraints imposed by physical or technological limits of the actuators.

The use of saturation limits creates a discrepancy between the inputs computed by the controller (assumed to be ideal or even optimal), and the real ones which are simply clipped to the allowable maximal or minimal level. The closed-loop system acquires a completely different set of inputs than it was originally intended by the controller. By clipping the inputs using saturation, we also introduce a level of nonlinearity into the control law. All of this essentially creates two very serious problems with:

• optimality

• stability.

Let us use the linear quadratic controller introduced earlier in Sect. 4.3 to illustrate the problems with saturation limits. LQ is an ideal controller to compare with MPC, since a properly formulated infinite horizon unconstrained MPC law is essentially equivalent to its LQ analogy. If one designs an LQ controller without the constraints in mind, but then imposes saturation limits on the inputs, eventually ends up with an completely different control law than originally intended. This different and nonlinear control law may not work as planned and may perform much less efficiently. Moreover, traditional closed-loop stability guarantees will not be valid anymore, as a fundamentally different nonlinear strategy is taking over the plant instead of the initial design. It is also possible to take into account the saturation limits right at the stage of control system design. If the LQ controller is penalized enough in order not to invoke constraints too often, there is a greater chance that the closed-loop system will remain stable, although stability still cannot be guaranteed beforehand. Nevertheless, this conservativeness implies a great loss of efficiency and performance.

A constrained MPC control law with stability guarantees works in a completely different manner. Inputs are not simply clipped to the level of constraints, but actively considered at the online optimization task. Thanks to the unique formulation of the MPC law, at each sampling interval inputs are computed in a manner that they are as optimal as possible while still guaranteeing closed-loop stability. As one may clearly see, not even an input saturated LQ (or other) control law shall be directly compared to constrained MPC, since the essential methodology of manipulating with input limits is entirely different. Saturated LQ is simply not equivalent to constrained MPC, imposing hard saturation limits is a separate concept to constraint handling through online optimization.

Note that the performance difference between saturated LQ (or any other saturated control law) and constrained MPC with stability guarantees is likely to manifest with increasing problem dimensionality and plant complexity. Although the performance loss of a saturated LQ law in comparison with MPC is only barely detectable in the simple SISO case introduced in the upcoming chapters, a MIMO system with several inputs and outputs is much more likely to demonstrate the advantages of constrained MPC. We are not interested in making a point that constrained MPC is better than a simple saturated law, as this point has been made by numerous authors before us [34, 48]. What is more important, industrial users have clearly taken a stance with implementing numerous MPC controllers in MIMO plants with slow dynamics [43–45], ultimately gaining a performance advantage over saturated control strategies. After all, what is advantageous for a slow plant shall also be favorable for active vibration control.

8 Constrained Quadratic Programming-Based MPC

The unconstrained model predictive control law can be expressed in a closed form as demonstrated previously in Sect. 6.6. For this, it is enough to perform differentiation on the matrix cost function and we obtain a fixed feedback matrix as a result, which in the case of a linear time-invariant system can be used at each sampling interval. With the addition of constraints, the problem cannot be expressed explicitly in closed form as before, and the optimization procedure has to be performed at every sampling interval repeatedly.

Once again, our aim is to minimize the quadratic cost function , only this time with constraints. The minimization of a quadratic function with constraints is known in mathematics as a quadratic programming problem. The general logic of the MPC algorithm will stay the same, only the means and the method of the optimization task will be changed.

Let us now assume that we would like to steer the system state of (6.1) into the origin so that we drive our vibrating system into equilibrium . Furthermore, let us assume that the problem requires the implementation of constraints as well. We may define the following MPC algorithm [8, 26]:

Algorithm 6.1

To find the solution of the constrained model predictive control problem, perform the following set of operations at each sampling instant:

• Observe or measure actual system state at sample $x_k$.

• Minimize the following cost function with respect to constraints:

  $$ \min_{{\mathbf{u}}_k} J({\mathbf{u}}_k,x_k)\,{=}\, \sum^{n_c-1}_{i\,{=}\,0}\left(x^T_{k\,{+}\,i} {\mathbf{Q}}x_{k\,{+}\,i}\,{+}\,{\mathbf{u}}^T_{k\,{+}\,i}{\mathbf{R}}{\mathbf{u}}_{k\,{+}\,i}\right) \,{+}\,x^T_{k\,{+}\,n_c}{\mathbf{P}}_{\!\!f}x_{k\,{+}\,n_c} $$

  where ${{\mathbf{u}}_k\,{=}\,\left[u_k,u_{k\,{+}\,1},u_{k\,{+}\,2},\ldots,u_{k\,{+}\,n_c-1}\right]}$, ${{\mathbf{Q}}\,{=}\,{\mathbf{Q}}^T\geq0}$ is a state penalization matrix, ${{\mathbf{R}}\,{=}\,{\mathbf{R}}^T\geq0}$ is an input penalization matrix, $n_c$ is both the prediction and control horizon ⁷ and ${\mathbf{P}}_{\!\!f}$ is the solution of the unconstrained, infinite horizon quadratic regulation problem. The typical MPC cost function must be subject to the following constraints:

  $$ \underline{\it u}\,{\leq}\,u_{k\,{+}\,i} \,{\leq}\,\overline {u}, i\,{=}\,0,1,2,\ldots,n_{c}-1 $$

  (6.55)
  $$ \begin{aligned} \underline{\it x}\,{\leq}\,x_{k\,{+}\,i} \,{\leq}\,\overline {x}, i\,{=}\,1,2,\ldots,n_{c} \end{aligned} $$

  (6.56)
  $$ x_{k\,{+}\,0}\,{=}\,x_{k} $$

  (6.57)
  $$ x_{k\,{+}\,i\,{+}\,1}\,{=}\,{\mathbf{A}}x_{k\,{+}\,i}\,{+}\,{\mathbf{B}}u_{k\,{+}\,i}, i\geq0 $$

  (6.58)
  $$ y_{k\,{+}\,i}\,{=}\,{\mathbf{C}}x_{k\,{+}\,i}, i\geq0 $$

  (6.59)
  $$ u_{k\,{+}\,i}\,{=}\,{\mathbf{K}}x_{k\,{+}\,i}, i\geq n_c $$

  (6.60)

  where ${\mathbf{K}}$ is a stabilizing feedback gain.

• Apply the first element of the vector of optimal control moves ${\mathbf{u}}_k$ to the controlled system, and re-start the procedure.

8.1 Quadratic Programming

The core of algorithm 6.1 defined above is the minimization of the cost function with subject to constraints. The quadratic cost function can be rewritten in a compact matrix form as introduced by (6.33), while the constraints can be collected by (6.53). This minimization task is referred to as a quadratic programming (QP) optimization in mathematics.

In general, a quadratic programming optimization problem minimizes a multi-variable quadratic function, which is subject to linear constraints on the variables. Let us assume ${\mathbf{u}}$ is in general a vector containing the optimization variables, while ${\mathbf{H}}$ is a symmetric matrix and ${\mathbf{G}}$ is a vector. A quadratic programming problem is then defined by [5, 28]:

$$ \begin{array}{ccc} \hbox{minimize} & \quad & f({\mathbf{u}})\,{=}\, {\frac{1}{2}}{\mathbf{u}}^T{\mathbf{H}}{\mathbf{u}}\,{+}\,{\mathbf{G}}^T{\mathbf{u}}\\ \hbox{subject to} & \quad & {\mathbf{A_c}}{\mathbf{u}} \,{\leq}\, {\mathbf{b}}_0\\ & \quad & {\mathbf{A_e}}{\mathbf{u}} \,{=}\, {\mathbf{b}}_e \end{array} $$

(6.61)

where the first constraint is a so-called inequality constraint and the second is an equality constraint. If ${\mathbf{H}}$ is a positive semidefinite matrix, then the function $f({\mathbf{u}})$ is convex and it has a global minimizer, if there exists a feasible vector ${\mathbf{u}}$. Feasibility means that the variable ${\mathbf{u}}$ satisfies all constraints. Given a positive definite ${\mathbf{H}}$ and a feasible ${\mathbf{u}}$ the global minimizer of the QP is unique.

Fig. 6.7

Surface and contour plot of the cost function in quadratic programming

8.1.1 Geometric Representation of QP

One may interpret the definition of the quadratic programming problem in an intuitive geometrical representation as well. Instead of presenting a generic treatment of the geometrical representation of the QP problem, we will use an example to illustrate the idea of quadratic programming. In order to preserve the clarity of the presentation, let us imagine an optimization variable ${\mathbf{u}}$ which is defined in a two-dimensional space, having only two elements. To illustrate the various aspects of quadratic programming, let us choose a simple quadratic cost function: $f({\mathbf{u}})\,{=}\,f(u_1,u_2)$. This function depends on variables $u_1$ and $u_2$ for which we will try to find the minimum:

$$ f({\mathbf{u}})\,{=}\,f(u_1,u_2)\,{=}\,u_1^2\,{+}\,9u_2^2-10u_1-54u_2 $$

(6.62)

This cost function has different values for different combinations of $u_1$ and $u_2$ and it can be plotted in a three-dimensional space. The surface created by this example is illustrated in Fig. 6.7 where the different contours of the function are shown as well. Without constraints, the minimum of our function is the “bottom” of the three-dimensional surface. In mathematical terms, the minimum of the unconstrained cost function is found if we find where the partial derivative equals zero with respect to all of the variables:

$$ \nabla_{{\mathbf{u}}} f({\mathbf{u}})\,{=}\,0 $$

(6.63)

$$ {\frac{\partial f(u_1,u_2)}{\partial u_1}}\,{=}\,0 $$

(6.64)

$$ {\frac{\partial f(u_1,u_2)}{\partial u_2}}\,{=}\,0 $$

(6.65)

Evaluating the partial differentiation with respect to $u_1$ yields $5$, while with respect to $u_2$ yields 3, meaning that the unconstrained minimum of this cost function is to be found at the coordinates ${\mathbf{u}}^{\blacktriangle}\,{=}\,[5 \quad 3]^T$. In absence of constraints it is trivial to find the minimum of a quadratic function, but the addition of constraints creates a quadratic programming problem.

Let us confine the pool of valid solutions for our minimization problem in (6.62) in the ${\mathbf{u}}$-space by a set of linear constraints:

$$ \begin{aligned} u_1 &\geq 0\\ u_2 &\geq 0\\ u_2 &\,{\leq}\,4 - u_1 \\ \end{aligned} $$

(6.66)

and let us not consider equality constraints for our example. In the two-dimensional space these constraints form lines, while in a general multidimensional space constraints form hyperplanes. The first constraint here is coincident with the horizontal axis, the second with the vertical axis and the third is simply a diagonal line. The constraints and the feasible space from which it is possible to select the optimization variables $u_1$ and $u_2$ are shown in Fig. 6.8. The shaded area represents the feasible subspace of ${\mathbf{u}}$, while the thick black lines illustrate the linear constraints given by (6.66).

Fig. 6.8

The shaded triangular area illustrates the restricted space in which the choice of variables ${\mathbf{u}}$ are limited by the linear constraints represented by the black lines. The constraints are presented in (a) in the ${\mathbf{u}}$ space, a view of the quadratic cost surface in the space of $u_2$ is depicted in (b), while the constraints are shown with the cost function $f({\mathbf{u}})$ in (c) in three dimensions

Fig. 6.9

Quadratic programming example showing the contour lines of the cost function $f({\mathbf{u}})$ (dash-dot), the constraints (continuous), the unconstrained solution ${\mathbf{u}}^{\blacktriangle}$ (triangle) and the constrained QP solution ${\mathbf{u}}^{\ast}$ (asterisk) and the contour line containing the solution (dashed)

To evaluate this constrained minimization problem, we will utilize the quadprog quadratic programming solver, which is a part of the Matlab Optimization Toolbox [52]. First, it is necessary to convert the problem formulation so that it resembles the general formulation of (6.61). We may write the cost function (6.62) in a matrix form by expressing it as:

$$ \begin{aligned}[b] f({\mathbf{u}})\,{=}\,f(u_1,u_2)&\,{=}\,{\frac{1}{2}}\left[\begin{array}{ll} u_1&u_2\end{array}\right] \left[\begin{array}{cc}2 & 0\\ 0 & 18\end{array}\right] \left[\begin{array}{c}u_1\\ u_2\end{array}\right]\,{+}\,\left[ \begin{array}{ll}-10 & -54\end{array}\right]\left[\begin{array}{c} u_1\\ u_2\end{array}\right]\\ &\,{=}\,{\frac{1}{2}}{\mathbf{u}}^T{\mathbf{H}} {\mathbf{u}}\,{+}\,{\mathbf{G}}^T{\mathbf{u}} \end{aligned} $$

(6.67)

The constraints may also be rearranged to the form given by (6.61) by changing them to:

$$ \begin{aligned} -u_1 &\,{\leq}\,0 \\ -u_2 &\,{\leq}\,0\\ u_1 \,{+}\, u_2 &\,{\leq}\,4 \end{aligned} $$

(6.68)

which in a matrix form will be rendered to

$$ \begin{aligned} \left[\begin{array}{cc}-1 & 0 \\ 0 & -1 \\ 1 & 1\end{array}\right] \left[\begin{array}{l}u_1\\ u_2\end{array}\right] &\,{\leq}\, \left[\begin{array}{c} 0\\ 0\\ 4\end{array}\right]\\ {\mathbf{A_c}}{\mathbf{u}} &\;{\leq}\;{\mathbf{b}}_0 \end{aligned} $$

(6.69)

Passing the matrices and vectors defined by ${\mathbf{H}},{\mathbf{G}},{\mathbf{A_c}}$ and ${\mathbf{b}}_0$ to the quadprog solver in Matlab using the syntax

$$ {\mathsf{[u\_{ast}},f]\,{=}\,\texttt{quadprog}(\hbox{H},\hbox{G},\hbox{Ac},\hbox{b0})} $$

will yield in the optimal solution ${\mathbf{u}}^{\ast}\,{=}\,\left[\begin{array}{ll}1.4& 2.6\end{array}\right]^T$ in merely two iterations. Figure 6.9illustrates this process in the space of the variables ${\mathbf{u}}$. The optimal solution for the unconstrained case ${\mathbf{u}}^{\blacktriangle}$ is visible as the center point of the contour lines of the cost function $f({\mathbf{u}})$. Because the problem is constrained, this solution is not feasible anymore and the algorithm has to choose from the inside of (including the boundaries) the triangular space enclosed by the constraints. The optimal solution ${\mathbf{u}}^{\ast}$ lies on the third constraint and the contour-line encompassing it is also illustrated. Different methods and algorithms may be used to solve a quadratic programming problem, including [5, 8, 34]:

• active set

• interior point

• conjugate gradient

• gradient projection

• variations of the simplex algorithm

• others.

8.1.2 Active Set Quadratic Programming Method

One of the best-known quadratic programming algorithms is referred to as the active set (AS) algorithm [20]. In essence, the active set algorithm finds the optimal solution of the constrained QP optimization by evaluating problems involving only equality constraints. The active set QP algorithm is used with medium-scale optimization problems, which are typical for model predictive control. The big advantage of the active set algorithm is that it can be warm started. Warm starting means that, due to the nature of the MPC problem, it is possible to find the solution much faster at time step $(k\,{+}\,1)$ if the algorithm can use knowledge gained from the solution evaluated at previous time $(k)$.

Let us have a look at the general inequality constraint formulation in (6.61) again. Each row of the matrix inequality formulation is an individual linear constraint, which we can denote with a simple sequential number $i$. Therefore, we may separate the individual constraints if we denote the rows of ${\mathbf{A}}_c$ with $A_c^i$ and the rows of ${\mathbf{b}}_0$ with $b_0^i$ to get $A_c^i {\mathbf{u}} \,{\leq}\,b_0^i$ for each constraint. A certain constraint is said to be inactive if the term $A_c^i {\mathbf{u}}^\ast < b_0^i$ holds. However, in case the term $A_c^i {\mathbf{u}}^\ast \,{=}\, b_0^i$ holds, then the $i$-th constraint is said to be active. It is also possible for the active set to be empty if none of the inequality constraints are in effect at the solution [34].

If we number the constraints (6.69) in our previous example with the sequential number $i$, we will get three constraints, which can be either active or inactive. Figure 6.10 illustrates the solution for our example, from which it is clear that two constraints are inactive (1, 2) while number 3 is active for ${\mathbf{u}}^{\ast}$. It is possible to remove the inactive constraints without affecting the solution [8]. The optimal solution of the problem is the solution of an equality constrained problem where only the active equality constraints are considered while the rest is discarded. We can denote this by:

$$ \begin{array}{rl}\hskip5pt{\hbox{minimize}} &\quad f({\mathbf{u}})\,{=}\, {\frac{1}{2}}{\mathbf{u}}^T{\mathbf{H}}{\mathbf{u}}\,{+}\,{\mathbf{G}}^T{\mathbf{u}} \\ {\hbox{subject to}} &\quad A_c^i {\mathbf{u}} \,{=}\, b_0^i, \quad i \in {\mathbf{a}}^\ast \end{array} $$

(6.70)

where ${\mathbf{a}}^{\ast}\,{=}\,\{ i : A_c^i {\mathbf{u}}^{\ast} \,{=}\, b_0^i \}$ is the configuration of the active constraints at the solution of the quadratic programming problem [8].

Fig. 6.10

Illustration of the active set in the active set quadratic programming method. Two constraints are inactive, while one is active. The inactive constraints can be removed from the problem, leaving only a constrained quadratic minimization problem to be solved

Naturally, one does not know in advance the ideal combination of the active and inactive constraints ${\mathbf{a}}^{\ast}$ which eventually leads to an optimal solution ${\mathbf{u}}^{\ast}$. However, it is possible to devise a strategy in which the equality problem associated with the current active set yields an improved solution at each iteration, while determining optimality and managing the active set at the same time. In a well-designed active set QP algorithm the active sets are not selected randomly, various strategies exist which help to avoid the necessity to test a large number of active/inactive constraint permutations. For example, it is possible to select successive sets in a way that the value of the cost function $f({\mathbf{u}})$ will be decreased at each successive iteration.

The rough outline of an active set quadratic programming algorithm may be given by [5, 8, 19, 34]:

Algorithm 6.2

To solve a quadratic programming problem (given a feasible initial solution ${\mathbf{u}}_0$ and an active set ${\mathbf{a}}_0$), at each iteration $p$ perform the following procedure:

• solve the equality problem corresponding to the active set ${\mathbf{a}}_p$ given by (6.70)

• test the optimality of the solution

  • if the solution is optimal (${\mathbf{u}}_p\,{=}\,{\mathbf{u}}^\ast$), terminate

  • if the solution is not optimal, continue

• find which constraint $i$ violated feasibility and add it to the active set to create a new active set ${\mathbf{a}}_{p\,{+}\,1}$. Repeat the procedure to find an improved solution ${\mathbf{u}}_{p\,{+}\,1}$.

Let us now focus on the subproblem described by the second item in Algorithm 6.2, namely determining whether the solution of the equality problem is really the global solution of the QP. The optimality of the partial solution with a certain active set can be determined from the Lagrange multipliers of the associated equality problem. To verify the optimality in an unconstrained optimization problem defined by:

$$ \hbox{minimize} \quad f({\mathbf{u}}) $$

(6.71)

we have to test whether its gradient equals zero, that is whether

$$ \nabla_{{\mathbf{u}}} f({\mathbf{u}}^\ast) \,{=}\, 0 $$

(6.72)

holds. In general, a constrained optimization problem with $m$ constraints can be expressed by the following formulation:

$$ \begin{array}{ccc} \hbox{minimize} & \quad & f({\mathbf{u}})\\ \hbox{subject to} & \qquad & g_i({\mathbf{u}})\,{=}\,0, \quad i\,{=}\,1,\ldots,m \end{array} $$

(6.73)

which is also true for a given active set ${\mathbf{a}}$ and the corresponding equality problem of (6.70), where $m$ constraints are given by $g_i({\mathbf{u}})\,{=}\,A_c^i {\mathbf{u}} - b_0^i$. To test the optimality of the solution after evaluating the equality problem it is not sufficient to fulfill the gradient condition (6.72) anymore. Instead, this gradient condition is augmented by the effect of the constraints. For a single constraint (m = 1) the optimality condition would be transformed to:

$$ \nabla_{{\mathbf{u}}} f({\mathbf{u}}^\ast) \,{=}\, - \lambda \nabla_{{\mathbf{u}}} g({\mathbf{u}}^\ast) $$

(6.74)

meaning that the direction of the gradient of the minimized function at ${\mathbf{u}}^\ast$ must be exactly opposite to the direction of the gradient of the constraint. The scalar $\lambda$ is a Lagrange multiplier and it is necessary in the formulation because, although the directions of the gradients are opposite, their magnitude is not necessarily the same.

This concept is illustrated in Fig. 6.11 on the example discussed before. Here constraints number 1 and 2 can be removed from the active set without affecting the solution, only constraint 3 is considered. After the equality problem (6.70) is solved, we have to make sure whether the trial solution is truly the optimal solution. As we are following the contour line of the constraint $g({\mathbf{u}})$ the value of the cost function may vary, the contour lines of $g({\mathbf{u}})$ cross the constraint at several points. The value of the cost function is neither increased, nor decreased only when the contour lines touch but do not cross. In other words, when the constraint touches the contour lines of the cost function tangentially we have found our solution ${\mathbf{u}}^\ast$. Mathematically expressed, the two function contours touch when the tangent vectors of the contours are parallel. The gradients of a function are perpendicular to the contour line, thus we may equivalently say that the gradients of functions $f({\mathbf{u}})$ and $g({\mathbf{u}})$ are parallel but with magnitudes different by a scalar value $\lambda$.

Fig. 6.11

Illustration of the gradients of the minimized function $f({\mathbf{u}})$ and the active equality constraint $g({\mathbf{u}})\,\,{=}\,\,0$. At the optimal solution, the direction of the gradients is opposite, their magnitude is scaled by the Lagrange multiplier $\lambda$

This constrained optimality condition can be easily converted into a multi constraint formulation as well. If for the actual active set ${\mathbf{a}}_p$ at iteration $p$ the variable ${\mathbf{u}}_p\,{=}\,{\mathbf{u}}^\ast$ is really the solution of the constrained equality problem given by (6.70), then we can find Lagrange multipliers $\lambda_i^{\ast},i\,{=}\,1,2,\ldots,m$ which will satisfy [9]:

$$ \begin{aligned} \nabla_{{\mathbf{u}}} f({\mathbf{u}}^\ast) \,{+}\, \sum_{i\,{=}\,1}^m \lambda_i^{\ast} \nabla_{{\mathbf{u}}} g_i({\mathbf{u}}^\ast) &\,{=}\, 0, \quad i\,{=}\,1,2,\ldots,m\\ g_i({\mathbf{u}}^\ast) &\,{=}\, 0, \quad i\,{=}\,1,2,\ldots,m \end{aligned} $$

(6.75)

In other words, if we can find a set of $\lambda_i^{\ast}$ for the trial solution which fulfills the condition above, the trial solution is in fact the solution of the QP problem.

The optimality condition of (6.75) can be extended to a case of $n$ additional equality constraints given by $h({\mathbf{u}})\,{=}\,{\mathbf{A}}_e{\mathbf{u}}-{\mathbf{b}}_e$ as well. The necessary and sufficient conditions for ${\mathbf{u}}^\ast$ to be the global optimum are given by the so-called Karush–Kuhn–Tucker (KKT) conditions [5, 19]:

$$ \begin{array}{l@{\quad}l} \nabla_{{\mathbf{u}}} f({\mathbf{u}}^\ast) \,{+}\, \sum_{i\,{=}\,1}^m \lambda_i^{\ast} \nabla_{{\mathbf{u}}}g_i({\mathbf{u}}^\ast)\,{+}\, \sum_{i\,{=}\,1}^n {\it v}_i^{\ast} \nabla_{{\mathbf{u}}}h_i({\mathbf{u}}^\ast) \,{=}\, 0, &i\,{=}\,1,2,\ldots,m \\ & i\,{=}\,1,2,\ldots,n\\ g_i({\mathbf{u}}^\ast) \,{=}\, 0,&i\,{=}\,1,2,\ldots,m\\ h_i({\mathbf{u}}^\ast) \,{=}\, 0,&i\,{=}\,1,2,\ldots,n\\ \end{array} $$

(6.76)

According to the KKT conditions if vectors of Lagrange multipliers $\lambda \geq 0$ and ${\it v}$ exist, then ${\mathbf{u}}^\ast$ is the global optimizer. After substitution and differentiation, the KKT conditions for the quadratic cost function $f({\mathbf{u}})$, inequality and equality constraints defined by (6.61) will be reduced to [34]:

$$ {\mathbf{H}}{\mathbf{u}}\,{+}\,{\mathbf{A}}_c^T\lambda \,{+}\,{\mathbf{A}}_e^T{\it v}\,{=}-{\mathbf{G}} $$

(6.77)

$$ {\mathbf{A}}_c{\mathbf{u}}\,{=}\,{\mathbf{b}}_0 $$

(6.78)

$$ {\mathbf{A}}_e{\mathbf{u}}\,{=}\,{\mathbf{b}}_e $$

(6.79)

where the elements of $\lambda$ corresponding to the inactive inequality constraints must remain zero (this can be ensured by an additional complementary condition). To put it differently, only elements corresponding to the active set need to be evaluated and, if all of them are nonnegative, then the solution ${\mathbf{u}}$ is the global optimum of the QP problem.

A valid strategy to implement the rough algorithm outlined in Algorithm 6.2 [34] can be created by modifying our original cost function in (6.70) by replacing absolute values of the solution ${\mathbf{u}}_p$ at iteration $p$ with increments ${\mathbf{u}}_p\,{+}\,\triangle{\mathbf{u}}$. Substituting this into Algorithm 6.2 in $f({\mathbf{u}})$ yields a new incremented cost:

$$ f({\mathbf{u}}_p\,{+}\,\triangle{\mathbf{u}})\,{=}\, {\frac{1}{2}}({\mathbf{u}}_p\,{+}\,\triangle{\mathbf{u}})^T{\mathbf{H}} ({\mathbf{u}}_p\,{+}\,\triangle{\mathbf{u}})\,{+}\,{\mathbf{G}}^T ({\mathbf{u}}_p\,{+}\,\triangle{\mathbf{u}}) $$

(6.80)

which after factoring out and simplification can be reduced to

$$ f({\mathbf{u}}_p\,{+}\,\triangle{\mathbf{u}})\,{=} f({\mathbf{u}}_p)\,{+}\, {\frac{1}{2}}\triangle{\mathbf{u}}^T{\mathbf{H}}\triangle{\mathbf{u}} \,{+}\,({\mathbf{G}}^T\,{+}\,{\mathbf{u}}_p^T{\mathbf{H}})\triangle{\mathbf{u}} $$

(6.81)

and the equality constrained minimization problem (6.70) can be equivalently stated by the new cost function $f(\triangle{\mathbf{u}})$:

$$ \begin{array}{rl} \hskip7pt\hbox{minimize} & \quad f(\triangle{\mathbf{u}})\,{=}\, {\frac{1}{2}}\triangle{\mathbf{u}}^T{\mathbf{H}} \triangle{\mathbf{u}}\,{+}\,{\mathbf{G}}^T_p\triangle{\mathbf{u}}\\ \hbox{subject to} &\quad A_c^i \triangle{\mathbf{u}} \,{=}\, 0, \quad i \in {\mathbf{a}}^\ast \end{array} $$

(6.82)

where ${\mathbf{G}}_p^T\,{=}\,({\mathbf{G}}^T\,{+}\,{\mathbf{u}}_p^T{\mathbf{H}})$. Note that the inequality constraints in this new formulation have also changed, $b_0^i$ has been removed. This can be explained by substituting the new incremental optimization variable ${\mathbf{u}}_p\,{+}\,\triangle{\mathbf{u}}$ into the equality constraint in (6.70) to get:

$$ A_c^i{\mathbf{u}}_p\,{+}\, A_c^i\triangle{\mathbf{u}} \,{=}\, b_0^i $$

(6.83)

from which we only have to ensure that $g_i(\triangle{\mathbf{u}})\,{=}\,A_c^i\triangle{\mathbf{u}}\,{=}\,0$ in order to maintain the validity of the original equality constraint.

Let us now use this new equality constraint $g(\triangle{\mathbf{u}})$ with the cost function $f(\triangle{\mathbf{u}})$ and substitute it back to the conditions of optimality in (6.75), with using a new vector of Lagrange multipliers $\triangle\lambda$:

$$ \begin{aligned} \nabla f(\triangle{\mathbf{u}}) \,{+}\, \triangle\lambda \nabla g_{{\mathbf{a}}}(\triangle{\mathbf{u}}) &\,{=}\, 0\\ g_{{\mathbf{a}}}(\triangle{\mathbf{u}}) &\,{=}\, 0 \end{aligned} $$

(6.84)

where subscript ${\mathbf{a}}$ marks that only equality constraints from the active set ${\mathbf{a}}_p$ at iteration $p$ is utilized. After substitution and differentiation with respect to $\triangle{\mathbf{u}}$ this will be reduced to [5, 34]:

$$ {\mathbf{H}}\triangle{\mathbf{u}}\,{+}\,{{\mathbf{A}}^{{\mathbf{a}}}_c}^T \triangle\lambda\,{=}-{\mathbf{G}}_p $$

(6.85)

$$ {\mathbf{A}}^{{\mathbf{a}}}_c\triangle{\mathbf{u}}\,{=}\,0 $$

(6.86)

which can be easily expressed in a matrix form:

$$ \left[\begin{array}{ll} {\mathbf{H}} & {{\mathbf{A}}^{{\mathbf{a}}}_c}^T\\ {\mathbf{A}}^{{\mathbf{a}}}_c & 0\end{array}\right] \left[\begin{array}{c}\triangle{\mathbf{u}}\\ \triangle \lambda\end{array}\right]\,{=}\, \left[\begin{array}{c}-{\mathbf{G}}_p\\ 0\end{array}\right] $$

(6.87)

The equality optimization problem expressed by (6.82) thus can be conveniently expressed with the above matrix equation. The problem may be expanded for a general quadratic programming case with both equality and inequality constraints by using the Karush-Kuhn-Tucker conditions in (6.76) to get [5, 20, 34]:

$$ {\mathbf{H}}\triangle{\mathbf{u}}\,{+}\,{{\mathbf{A}}^{{\mathbf{a}}}_c}^T \triangle\lambda\,{+}\,{{\mathbf{A}}^{{\mathbf{a}}}_e}^T \triangle{\it v}\,{=}-{\mathbf{G}}_p $$

(6.88)

$$ {\mathbf{A}}^{{\mathbf{a}}}_c\triangle{\mathbf{u}}\,{=}\,0 $$

(6.89)

$$ {\mathbf{A}}^{{\mathbf{a}}}_e\triangle{\mathbf{u}}\,{=}\,0 $$

(6.90)

which can be expressed in a matrix form as well:

$$ \left[\begin{array}{ccc} {\mathbf{H}}& {{\mathbf{A}}^{{\mathbf{a}}}_c}^T & {{\mathbf{A}}^{{\mathbf{a}}}_e}^T \\ {\mathbf{A}}^{{\mathbf{a}}}_c& 0& 0\\ {\mathbf{A}}^{{\mathbf{a}}}_e & 0 & 0 \end{array}\right] \left[\begin{array}{c} \triangle{\mathbf{u}}\\ \triangle \lambda\\ \triangle \nu \end{array}\right] \,{=}\,\left[\begin{array}{c} -{\mathbf{G}}_p\\ 0\\ 0\end{array}\right] $$

(6.91)

A new active set strategy using these ideas can be outlined [34]:

Algorithm 6.3

To solve a quadratic programming problem (given a feasible initial solution ${\mathbf{u}}_0$ and an initial active set ${\mathbf{a}}_0$), at each iteration $p$ perform the following procedure [34]:

• given ${\mathbf{u}}_p$ solve the modified equality problem (6.70) corresponding to the active set ${\mathbf{a}}_p$ by evaluating (6.87) to get a solution improvement ${\mathbf{u}}_p\,{+}\,\triangle{\mathbf{u}}$

• test the feasibility of this improved solution ${\mathbf{u}}_p\,{+}\,\triangle{\mathbf{u}}$ by evaluating ${\mathbf{A}}_c{\mathbf{u}}_p\,{\leq}\,{\mathbf{b}}_0$ and

  • if the solution is feasible, accept as an improved optimization variable at the next iteration ${\mathbf{u_{p\,{+}\,1}}}\,{=}\;{\mathbf{u}}_p\,{+}\;\triangle{\mathbf{u}}$ and maintain the current active set ${\mathbf{a}}_{p}\,{=}\;{\mathbf{a}}_{p\,{+}\,1}$

  • if the solution is infeasible perform a line search pointing in the direction of $\triangle{\mathbf{u}}$ and locate the point ${\mathbf{u_{p\,{+}\,1}}}\,{=}\;{\mathbf{u}}_p\,{+}\,\alpha_l\triangle{\mathbf{u}}$ at which the feasibility is lost (where $0<\alpha_l<1$). Add this new active constraint to the active set, creating ${\mathbf{a}}_{p\,{+}\,1}$

• determine the optimality of the improved solution ${\mathbf{u}}_{p\,{+}\,1}$ by checking the Lagrange multipliers according to (6.75) and then

  • if it is not the constrained optimum of the QP, restart the procedure

  • if it is the constrained optimum of the QP, terminate the procedure

Let us review the procedure of Algorithm 6.3 once more on the simple example familiar from our previous discussion and illustrate the steps in Fig. 6.12. Without going into details, suppose that we have a feasible initial solution ${\mathbf{u}}_0$ at our disposition and an empty active set ${\mathbf{a}}_0\,{=}\,\left[\begin{array}{ccc}0 & 0 & 0\end{array}\right]^T$. In the first step $p\,{=}\,1$(a) the matrix expression (6.87) is evaluated, obtaining an improvement $\triangle {\mathbf{u}}_1$ in the solution. As the active set is empty, the new solution is equivalent to the unconstrained optimum of the cost function. The feasibility of this new solution ${\mathbf{u}}_1\,\,{=}\,\,{\mathbf{u}}^{\blacktriangle}\,\,{=}\,\,{\mathbf{u}}_0\,{+}\;\triangle {\mathbf{u}}_0$ must be then determined. By evaluating ${\mathbf{A}}_c{\mathbf{u}}_1\,{\leq}\;{\mathbf{b}}_0$ the solution is clearly infeasible, thus ${{\mathbf{u}}_1\!\neq {\mathbf{u}}_0\,\,{+}\,\,\triangle {\mathbf{u}}_0}$. A line search is made in the direction of ${\mathbf{u}}_0$ to determine where feasibility has been lost. The line search coefficient $\alpha_l$ determines the new partial solution at iteration $p\,\,{=}\,\,1$(b) which is given by ${\mathbf{u}}_1\,{=}\;{\mathbf{u}}_0\,{+}\,\alpha_l\triangle{\mathbf{u}}_0$. A new active set is created by adding constraint number 3, resulting in ${\mathbf{a}}_1\,{=}\,\left[\begin{array}{ccc}0 & 0 & 1\end{array}\right]^T$. We have to see whether this solution is the global optimum of the quadratic programming problem, by computing the Lagrange coefficients of the problem at ${\mathbf{u}}_1$ according to (6.75). As it turns out this is not the global optimum of the QP, so one more iteration $p\,{=}\,2$ is initiated.

Fig. 6.12

Illustration of the iterations in an active set quadratic programming method. The solution for this simple problem is found in merely two iterations of the algorithm

By evaluating (6.87) utilizing the new solution improvement ${\mathbf{u}}_1$ and the next active set ${\mathbf{a}}_1$ we arrive at the solution ${\mathbf{u}}_2\,{=}\;{\mathbf{u}}_1\,{+}\,\triangle{\mathbf{u}}_1$. This solution is feasible, as ${\mathbf{A}}_c{\mathbf{u}}_2 \,{\leq}\,{\mathbf{b}}_0$ holds. Testing the optimality of the solution by computing the Lagrange multipliers according to (6.75) shows that this new solution is the global optimum. As no further improvement is possible ${\mathbf{u}}^\ast\,{=}\;{\mathbf{u}}_2$ and the sequence is terminated. ⁸

8.1.3 Interior Point Quadratic Programming Method

The interior point (IP) quadratic programming algorithm [37, 40] is mostly used for large-scale problems in the range of hundreds of optimization variables. Although it is a more recent algorithm, it is not necessarily better than active set methods [34]. Unlike the active set algorithm the interior point algorithm cannot be warm started, in other words, we cannot reduce computational load by applying prior knowledge on the previous solution. The advantage of interior point methods is that their computational complexity is generally a polynomial function of parameters (for example $3n_x \,{+}\, n_u$) whereas active set and most other algorithms require a computational time which grows exponentially depending on the problem parameters (for example ${n_x\,{+}\,n_u}^3$) [34]. The use of interior point algorithms in model predictive control is less typical for this reason.

The idea behind the interior point algorithm is to convert the QP problem into an unconstrained optimization problem by augmenting the cost function by a so-called barrier function. The role of the barrier function is to supply a finite value to the minimized function, when the solution satisfies the constraints. The value of the boundary function tends to infinity, whenever solution approaches the constraint boundary. This can be expressed mathematically as [9, 34]:

$$ \hbox{minimize} \quad \mu [f({\mathbf{u}})\;{=}\;{\frac{1}{2}}{\mathbf{u}}^T{\mathbf{H}} {\mathbf{u}}\,{+}\,{\mathbf{G}}^T{\mathbf{u}})] \,{+}\, \psi({\mathbf{u}}) $$

(6.92)

where $f({\mathbf{u}})$ is the quadratic cost, $\psi({\mathbf{u}})$ is the boundary function based on the constraints and $\mu$ is a scalar value. In case we have constraints formed as $A_c^i {\mathbf{u}} \,{=}\, b_0^i$ a typical choice for a barrier function could be:

$$ \psi({\mathbf{u}})\,{=}\,\sum_{i\,{=}\,1}^m - \log (b_0^i-A_c^{iT} {\mathbf{u}}) $$

(6.93)

although other formulations are also possible. As it has been previously noted, the value of $\psi({\mathbf{u}})$ approaches infinity as the solution ${\mathbf{u}}$ approaches the constraint boundaries. The solution of the unconstrained interior point minimization problem (6.93) will satisfy constraints for any given scalar $\mu$. In other words, by minimizing $f({\mathbf{u}})$ the solution will always remain within the feasible region, because the barrier function prevents the search from leaving it [34].

As we increase $\mu$ the solution will tend to get closer and closer to the optimal solution ${\mathbf{u}}^{\ast}$:

$$ {\mathbf{u}} \longrightarrow {\mathbf{u}}^{\ast} \quad \hbox{as} \quad \mu \longrightarrow \infty $$

(6.94)

If an initial feasible solution can be found in the vicinity of ${\mathbf{u}}_0$, then this solution can be continually improved by increasing $\mu$ until the difference between the partial solution ${\mathbf{u}}$ and the real optimal solution ${\mathbf{u}}^\ast$. An interior point algorithm therefore successively increases the value of $\mu$ until the constraints are met within a given tolerance [8]:

Algorithm 6.4

• increase the value of $\mu$

• minimize the unconstrained problem (6.93)

• if solution meets constraints within tolerance terminate, otherwise restart the procedure

The initial point of the algorithm ${\mathbf{u}}_0$ is known as the analytic center of the constraints, while the path traced out by the successively improving partial solutions ${\mathbf{u}}$ is known as the central path [34].

While iterations of the active set algorithm search along the points on the boundary of the feasible region, as the name implies interior point algorithms search in the interior of this region. This approach requires an initial feasible solution but will remain feasible through all iterates. This strategy is not the most efficient and the iterates of modern IP algorithms are not always feasible, that is until the end of the search [34].

A central problem to active set algorithms is the possible numerical ill-conditioning caused by the logarithmic nature of the barrier function. As we are successively increasing the value of $\mu$ to get better and better solutions, the value of the barrier function starts to rise very rapidly, thus rendering the optimization problem (6.92) numerically ill-conditioned. This may cause that the algorithm results infeasible or sub-optimal solutions. A well-designed interior point algorithm is relatively complicated and amongst others contains algorithmic tools to prevent the problem described above. Currently the most effective interior point algorithms referred to as primal-dual are based on solving the convex optimization problems and their dual problems simultaneously [5].

Figure 6.13 illustrates a very simple interior point algorithm solving the demonstration example familiar from our previous discussion on quadratic programming. The algorithm starts from the analytic center of the feasible region, located at ${\mathbf{u}}_0\,{=}\,[4/3 \quad 4/3]$. The original cost function is augmented by the barrier function, and the new unconstrained cost function (6.93) is minimized. To solve our simple example in Matlab the new cost function (6.93) has been programmed as a function objfun, which is then minimized by a derivative-free method through the built-in fminsearch algorithm. The syntax to minimize the objective function is:

$$ \mathtt{[u,fval]\,=\,} \user2{\mathtt{fminsearch}}\;\mathtt{(f,u0)} $$

where u is the solution of the interior point algorithm and ${\mathbf{u}}_0$ is the analytical center of the feasible region. The central path is generated by supplying this problem with different values of $\mu$, spanning a logarithmic space from $0.001$ to $100$ in $40$ steps. The algorithm starts from the analytic center and the solutions marked with a cross are improving with increasing $\mu$ along the central path. The solutions get very close to the optimal solution marked with a triangle, as computed previously by the active set algorithm implemented in quadprog. The two solutions match very closely, the contour lines of $f({\mathbf{u}})$ corresponding to the different algorithms are practically indistinguishable.

Fig. 6.13

The iterations of an interior point quadratic programming algorithm are shown in (a) while sub optimal and infeasible solutions due to numerical ill-conditioning are demonstrated in (b). The figures show the analytical center (square), the solution of an active set algorithm (triangle) the iterations of the interior point QP algorithm (cross), constraints (thick black line), contours of the original cost (dashed gray line), contour of the active set solution (thin black line), contour of the interior point solution (thin dashed black line)

The possible numerical issues with simple interior point algorithms are demonstrated in Fig. 6.13b where the detail in the neighborhood of the solution is shown. As it is clear from the figure, even this very basic interior point algorithm yields good approximations of the optimal ${\mathbf{u}}^\ast$. Note, however, that certain solutions for increasing $\mu$ tend to be very suboptimal, while some are even infeasible. This is caused by the previously mentioned numerical ill-conditioning of the unconstrained optimization problem. There is for example a point ${\mathbf{u}}_0\,{=}\,[1.59 \quad 2.41]$ which is not only suboptimal but also outside the feasible region.

8.2 MPC and Quadratic Programming

Now, it is clear that the cost function in (6.33) and the constraints (6.53) in fact formulate a quadratic programming problem, which is given by [48]:

$$ \begin{array}{cc} \hbox{minimize} & J_k({\mathbf{u}}_k)\;{=}\;{\mathbf{u}}_k^T{\mathbf{H}}{\mathbf{u}}_k\,{+}\,2x_k^T {\mathbf{G}}^T{\mathbf{u}}_k\\ \hbox{subject to} & {\mathbf{A_c}} {\mathbf{u}}_{k}\;{\leq}\;{\mathbf{b}}_0 \,{+}\, {\mathbf{B}}_0 x_k \end{array} $$

(6.95)

where ${\mathbf{H}}$ and ${\mathbf{G}}$ are the predetermined prediction matrices, ${\mathbf{A_c}}$, ${\mathbf{b}}_0$, and ${\mathbf{B}}_0$ define the constraints, $x_k$ is the actually measured or observed state and ${\mathbf{u}}_k$ is the optimization variable—that is the unknown sequence of future optimal control inputs.

To solve the quadratic programming problem given by the MPC formulation (6.95) in Matlab, we can use the built-in quadprog function, which at each time step will solve the QP given by the following syntax ⁹:

$$ \mathtt{u\,{=}\,}\user2{\mathtt{quadprog}}\;\mathtt{(H,G*x,Ac,b0\,{+}\,B0*x)} $$

where $x$ is the actual measured or observed state, ${\mathbf{H}}$ and ${\mathbf{G}}$ are prediction matrices, ${\mathbf{A}}_c$, ${\mathbf{b}}_0$ and ${\mathbf{B}}_0$ are given by the constraints and ${\mathbf{u}}$ is the optimal input trajectory of which only the first element is utilized. The function quadprog is only usable in the Matlab environment, and cannot be employed in a real-time environment. For the online optimization task in traditional QP based MPC (QPMPC) a dedicated solver is required, preferably a C language version of either generic quadratic programming software or one which is optimized for MPC usage. Such a solver is for example qpOASES developed by Ferreau et al. [17–19] which is utilized as a benchmark for traditional optimal MPC in the upcoming chapters.

Quadratic programming solvers specifically designed to solve MPC problems utilize some of the unique properties of the QP problem arising due to the predictive control formulation. These properties are [34]:

• the QP problem is sparse

• it is possible to warm start

After reordering the variables in the QP problem arising from the MPC formulation the problem becomes sparse, meaning that the matrices are mainly populated with zeros. The second condition comes from the fact that unless there are excessive disturbances acting on the controlled plant, the successive solutions at times $(k)$ and $(k\,{+}\,1)$ are very much alike. For this reason, it is possible to warm start the algorithm based on the previous solution to save on computational time. The MPC tuned implementations of active set algorithms are more common; however, examples of interior point algorithms utilizing the structure and properties of MPC exist as well.

9 Prediction and Control Horizon

In the previous sections, the prediction horizon—that is the point in the future up to which predictions are made—was identical to the control horizon. The control horizon can be understood as a point in the future up to which control moves are calculated.

Let us denote the control horizon by $n_c$ and the prediction horizon as $n_{\!p}$ as illustrated in Fig. 6.14. The control and prediction horizon can be equivalent, though they are often different: the cost is predicted further into the future, but in order to reduce the number of free variables the control horizon $n_c$ is considered to be shorter than the prediction horizon $n_{\!p}$. A common approach is when the controller computes the control moves in such a manner that it assumes that the control inputs will remain on the same level after the control horizon ends. The control input may vary up to the end of $n_c$. The control input vector will have two different domains:

$$ {\mathbf{u}}_k\,{=}\,[\begin{array}{lllllll}u_{k} & u_{k\,{+}\,1} & \ldots & u_{k\,{+}\,n_c} & u_{ss} & u_{ss} & u_{ss}\end{array}]^T $$

(6.96)

where $u_{ss}$ is the steady-state control input. If we take a simple regulation example where the output needs to be driven to zero, we can divide the prediction matrix ${\mathbf{N}}$ to two parts: one for the control moves which may vary, and one which is assumed to be steady-state:

$$ \begin{aligned}[b] {\mathbf{x}}_k \,&{=}\,{\mathbf{M}}x_k\,{+}\,{\mathbf{N}}{\mathbf{u}}_k\,\\&{=}\, {\mathbf{M}}x_k\,{+}\,{\mathbf{N}}_1[u_0 \ldots u_{n_c}]^T+\,{\mathbf{N}}_2[1 \ldots 1]^Tu_{ss}\\&{=}\,{\mathbf{M}}x_k\,{+}\,\tilde{{\mathbf{N}}}[u_0 \ldots u_{n_c}u_{ss}]^T \end{aligned} $$

(6.97)

Fig. 6.14

The control horizon $n_c$ may be shorter than the prediction horizon $n_{\!p}$, however it is very common to choose these two horizons to have equal lengths

In most predictive control applications the control horizon $n_c$ actually equals the prediction horizon $n_{\!p}$. Similarly, the ongoing discussion will not differentiate these two concepts. From now on it will be assumed that $n_c\,{=}\,n_{\!p}$ and the control horizon will be simply marked by $n_c$, expecting predictions to be computed up to this point in time as well and vice versa.

10 Fixed Target Tracking

The problem statement has to be slightly changed if the goal of the control application is to keep the output at a predetermined level, instead of keeping it at zero. The formulation is similar, but the zero is shifted toward the new required value. The desired output will be designated as $y_d$ and the corresponding control input as $u_d$. When the system reaches $y_d$ it will be true:

$$ \begin{aligned} x_d &\,{=}\, {\mathbf{A}}x_d \,{+}\, {\mathbf{B}}u_d \\ y_d&\,{=}\,r\,{=}\,{\mathbf{C}}x_d \end{aligned} $$

(6.98)

From this, the reference state and the required steady-state input can be calculated:

$$ \begin{aligned} x_d&\,{=}\,({\mathbf{I}}-{\mathbf{A}})^{-1}{\mathbf{B}}u_d\\ r&\,{=}\,{\mathbf{C}}({\mathbf{I}}-{\mathbf{A}})^{-1}{\mathbf{B}}u_d \\ \end{aligned} $$

(6.99)

The term ${\mathbf{C}}({\mathbf{I}}-{\mathbf{A}})^{-1}{\mathbf{B}}$ is often referred to as the DC gain. If we denote the difference between the actual and the desired state as $x_e\,{=}\,x-x_d$, and also $u_e \,{=}\, u-u_d$ the model may be modified to:

$$ x_{e(k\,{+}\,1)}\,{=}\,{\mathbf{A}}x_{e(k)}\,{+}\,{\mathbf{B}}(u-u_d) $$

(6.100)

Using this notation to create and evaluate a cost function results a calculated set of future control differences $u_e$. One must use $u_e$ instead of $u$, and similarly $x_e$ instead of $x$. The control move must be recalculated properly as well, before it can be applied to the system. For example a controller may take a form of $u\,{=}\,{\mathbf{K}}x_e$ and the required output shall be $u\,{=}\,{\mathbf{I}}u_d\,{+}\,{\mathbf{K}}x_e$.

Problems arise with calculating the required steady-state values. Since no model can be perfectly correct, there will always be some challenges. If the desired steady-state values are incorrect, offset-free tracking is not possible. There are several techniques to overcome this problem and ensure offset-free regulation.

The most common control aim in active vibration control is to steer the structure into equilibrium and to keep it there. This equilibrium point is the origin of the state-space system. Alternatively, the system model can be transformed and shifted to have the origin as an equilibrium point. Further discussion in this book will not assume the use of tracking (fixed target or any other sort), the systems will rather be steered into the origin of the state-space formulation, which is coincident with the physical equilibrium of the mechanical system.

11 Integral Action

In this work, we will assume that the control input $u_k$ will be computed by the predictive controller in its absolute form. However, this is not the only way to produce inputs to the plant. Just as PID controllers often use an incremental or velocity ¹⁰ input [3], we may also define an MPC controller in a similar way. Instead of computing the absolute level of the input $u_k$, only its changes will be computed which are given by $\triangle u_k$. This formulation is also referred to as discrete-time integration formulation [34]. The reason to use a controller formulation with integral action is to get offset-free tracking. To achieve offset-free tracking, the minimum of the cost function $J$ must be consistent with zero tracking errors in steady-state and the predicted control move must also be zero to maintain zero tracking [48].

There are several valid ways to express the controller input in its incremental, integrating form. All of the methods involve augmenting the state vector with an additional block of elements. Let us therefore consider a new augmented state, which is denoted by:

$$ \tilde{x}_{k} \,{=}\, \left[\begin{array}{l}x_k\\ u_{k-1}\end{array}\right] $$

(6.101)

where our new augmented vector ¹¹ will be denoted by $x_{k}$ and it will contain the original state vector $x_k$ and the previous value of the input $u_{k-1}$ at time $(k-1)$. The next iteration of this vector at time $k\,{+}\,1$ would be [34]:

$$ \left[\begin{array}{l} x_{k\,{+}\,1}\\ u_{k}\end{array}\right] \,{=}\,\left[\begin{array}{cc}{\mathbf{A}} & {\mathbf{B}}\\ {\mathbf{0}} & {\mathbf{I}}\end{array}\right] \left[\begin{array}{l}x_k\\ u_{k-1}\end{array}\right] \,{+}\,\left[\begin{array}{c}{\mathbf{B}}\\ {\mathbf{I}}\end{array}\right] \triangle u_k $$

(6.102)

where the dimensionality of the zero matrix ${\mathbf{0}}$ and ${\mathbf{I}}$ depend on the number of inputs. Similarly, the outputs can be defined by:

$$ y_k \,{=}\,\left[\begin{array}{ll}{\mathbf{C}} & {\mathbf{0}}\end{array}\right] \left[\begin{array}{l}x_k\\ u_{k-1}\end{array}\right] $$

(6.103)

Figure 6.15 illustrates the boundary between the actual MPC controller and the controlled plant. It is often convenient to consider the discrete-time integration operation to be a part of the plant dynamics. This integration operator computes the absolute value of the inputs $u_k$ from the increments $\triangle u_k$, thus creating an augmented MPC plant. In this way we may utilize an MPC controller producing an incremental input $\triangle u_k$, which may be used to control the plant augmented by the discrete-time integration operation.

Fig. 6.15

The boundary between the actual controller and plant depends on our view. A real plant augmented by an integration operation may be controlled by an algorithm computing input increments $\triangle u_k$

A slightly less intuitive way to create a discrete-time integration formulation of the predictive controller is to augment the state-space equation in the following way [34]:

$$ \tilde{x}_{k} \,{=}\,\left[\begin{array}{r} \triangle x_k \\y_k\end{array}\right] $$

(6.104)

where $\triangle x_k$ is simply the first difference of the state $\triangle x_k \,{=}\, x_k - x_{k-1}$ and $\tilde{x}_{k}$ is the augmented state. Considering a simple state-space system given by 1 for time $(k)$ and $(k-1)$ we will get

$$ x_{k\,{+}\,1} \,{=}\,{\mathbf{A}} x_k \,{+}\, {\mathbf{B}} u_k $$

(6.105)

$$ x_{k} \,{=}\,{\mathbf{A}} x_{k-1}\,{+}\,{\mathbf{B}} u_{k-1} $$

(6.106)

and subtracting these will yield the state difference $\triangle x_k$ according to

$$ \triangle x_{k\,{+}\,1} \,{=}\, {\mathbf{A}} \triangle x_k\,{+}\,{\mathbf{B}} \triangle u_k $$

(6.107)

From the second output equation in (6.1) we can also deduct:

$$ y_{k\,{+}\,1} \,{=}\, {\mathbf{C}} x_{k\,{+}\,1} $$

(6.108)

$$ \,{=}\, {\mathbf{C}}[\triangle x_{k\,{+}\,1} \,{+}\, x_k] $$

(6.109)

$$ \,{=}\, {\mathbf{C}}[{\mathbf{A}} \triangle x_k\,{+}\,{\mathbf{B}} \triangle u_k] \,{+}\, y_k $$

(6.110)

so the new state-space representation will be changed to

$$ \left[\begin{array}{r}\triangle x_{k\,{+}\,1} \\y_{k\,{+}\,1}\end{array}\right] \,{=}\,\left[\begin{array}{cc}{\mathbf{A}} & {\mathbf{0}}\\ {\mathbf{CA}} & {\mathbf{I}}\end{array}\right] \left[\begin{array}{r}\triangle x_k\\ y_{k}\end{array}\right] \,{+}\,\left[\begin{array}{c}{\mathbf{B}}\\ {\mathbf{CB}}\end{array}\right] \triangle u_k $$

(6.111)

$$ y_{k} \,{=}\, \left[\begin{array}{cc} {\mathbf{0}} & {\mathbf{I}}\end{array}\right] \left[\begin{array}{cc} \Delta x_k &\, y_{k}\end{array}\right] $$

(6.112)