Incremental Statistical Measures

Abstract

Statistical measures provide essential and valuable information about data and are needed for any kind of data analysis. Statistical measures can be used in a purely exploratory context to describe properties of the data, but also as estimators for model parameters or in the context of hypothesis testing. For example, the mean value is a measure for location, but also an estimator for the expected value of a probability distribution from which the data are sampled. Statistical moments of higher order than the mean provide information about the variance, the skewness, and the kurtosis of a probability distribution. The Pearson correlation coefficient is a measure for linear dependency between two variables. In robust statistics, quantiles play an important role, since they are less sensitive to outliers. The median is an alternative measure of location, the interquartile range an alternative measure of dispersion. The application of statistical measures to data streams requires online calculation. Since data come in step by step, incremental calculations are needed to avoid to start the computation process each time new data arrive and to save memory so that not the whole data set needs to be kept in the memory. Statistical measures like the mean, the variance, moments in general, and the Pearson correlation coefficient render themselves easily to incremental computations, whereas recursive or incremental algorithms for quantiles are not as simple or obvious. Nonstationarity is another important aspect of data streams that needs to be taken into account. This means that the parameters of the underlying sampling distribution might change over time. Change detection and online adaptation of statistical estimators is required for nonstationary data streams. Hypothesis tests like the χ²- or the t-test can be a basis for change detection, since they can also be calculated in an incremental fashion. Based on change detection strategies, one can derive information on the sampling strategy, for instance the optimal size of a time window for parameter estimations of nonstationary data streams.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Statistics and statistical methods are used in almost every aspect of modern life, like medicine, social surveys, economy, and marketing, only to name few of application areas. A vast number of sophisticated statistical software tools can be used to search and test for structures and patterns in data. Important information about the data generating process is provided by the simple summary statistics. Characteristics of the data distribution can be described by summary statistics like the following one.

• Measures of location: The mean and quantiles provide information about location of the distribution. Mean and median are representatives for the center of the distribution.

• Measures of spread: Common measures for the variation in the data are standard deviation, variance, and interquartile range.

• Shape: The third and fourth moments provide information about the skewness and the kurtosis of a probability distribution.

• Dependence: For instance, the Pearson correlation coefficient is a measure for the linear dependency between two variables. Other common measures for statistical dependency between two variables rank correlation coefficients like Spearman’s rho or Kendall’s tau.

Apart from providing information about location and spread of the data distribution, quantiles also play an important role in robust data analysis, since they are less sensitive to outliers.

Summary statistics can be used in a purely exploratory context to describe properties of the data, but also as estimators for model parameters of an assumed underlying data distribution.

More complex and powerful methods for statistical data analysis are for instance hypothesis tests. Statistical hypothesis testing allows us to discover the current state of affairs and therefore help us to make decisions based on the gained knowledge. Hypothesis test can be applied to a great variety of problems. We may need to test just a simple parameter or the whole distribution of the data.

However, classical statistics operates with a finite, fixed data set. On the other hand, nowadays it is very important to continuously collect and analyze data sets increasing with time, since the (new) data may contain useful information. Sensor data as well as the seasonal behavior of markets, weather, or animals are in the focus of diverse research studies. The amount of recorded data increases each day. Apart from the huge amount of data to be dealt with, another problem is that the data arrive continuously in time. Such kind of data is called data stream. A data stream can be characterized as an unlimited sequence of values arriving step by step over time. One of the main problems for the analysis of data streams is limited computing and memory capabilities. It is impossible to hold the whole data set in the main memory of a computer or computing device like an ECU (electronic control unit) that might also be responsible for other tasks than just analyzing the data. Moreover, the results of the analysis should be presented in acceptable time, sometimes even under very strict time constraints, so that the user or system can react in real time. Therefore, the analysis of data streams requires efficient online computations. Algorithms based on incremental or recursive computation schemes satisfy the above requirements. Such methods do not store all historical data and do not need to browse through old data to update an estimator or an analysis, in the ideal case, each data value is touched only once.

Consequently the application of statistical methods to data streams requires modifications to the standard calculation schemes in order to be able carry out the computations online. Since data come in step by step, incremental calculations are needed to avoid to start the computation process from scratch each time new data arrive and to save memory, so that not the whole data set must be kept in the memory. Statistical measures like the sample mean, variance and moments in general and the Pearson correlation coefficient render themselves easily incremental computation schemes, whereas, for instance, for standard quantiles computations the whole data is needed. In such cases, new incremental methods must be developed that avoid sorting the whole data set, since sorting requires in principal to check the whole data set. Several approaches for the online estimation of quantiles are presented for instance in [1, 9, 19, 25].

Another important aspect in data stream analysis is that the data generating process does not remain static, i.e., the underlying probabilistic model cannot be assumed to be stationary. The changes in the data structure may occur over time. Dealing with nonstationary data requires change detection and on-line adaptation. Different kinds of nonstationarity have been classified in [2]:

• Changes in the data distribution: the change occurs in the data distribution. For instance, mean or variance of the data distribution may change over time.

• Changes in concept: here concept drift refers to changes of a target variable. A target variable is a variable, whose values we try to predict based on the model estimated from the data, for instance for linear regression it is the change of the parameters of the linear relationship between the data.

  • Concept drift: concept drift describes gradual changes of the concept. In statistics, this usually called structural drift.

  • Concept shift: concept shift refers to an abrupt change which is also referred to as structural break.

Hence change detection and online adaptation of statistical estimators are required for nonstationary data streams. Various strategies to handle nonstationarity are proposed, see for instance [11] for a detailed survey of change detection methods. Statistical hypothesis tests may also be used for change detection. Since we are working with data streams, it is required that the calculations for the hypothesis tests can be carried out in an incremental way. For instance, the χ²-test and the t-test¹ render themselves easily to incremental computations. Based on change detection strategies, one can derive information on the sampling strategy, for instance the optimal size of a time window for parameter estimations of nonstationary data streams [3, 26].

This chapter is organized as follows. Incremental computations of the mean, variance, third and fourth moments and the Pearson correlation coefficient are explained in Sect. 2.2. Furthermore two algorithms for the on-line estimation of quantiles are described in Sect. 2.3. In Sect. 2.4 we provide on-line adaptations of statistical hypothesis test and discuss different change detection strategies.

2 Incremental Calculation of Moments and the Pearson Correlation Coefficient

Statistical measures like sample central moments provide valuable information about the data distribution. So the sample mean or empirical mean (first sample central moment) is the measure of the center of location of the data distribution, the measure of variability is sample variance (second sample central moment). The third and fourth central moments are used to compute skewness and kurtosis of the data sample. Skewness provides us the information about the asymmetry of the data distribution and kurtosis give us an idea about the degree of peakedness of the distribution.

Another important statistic is the correlation coefficient. The correlation coefficient is a measure for linear dependency between two variables.

In this section, we introduce incremental calculations for these statistical measures.

In the following, we consider a real-valued sample x ₁, …, x _t , … (${x}_{i} \in \mathbb{R}$ for all i ∈ 1, …, t, …).

Definition 2.1.

Let x ₁, …, x _t be a random sample from the distribution of the random variable X.

The sample or empirical mean of the sample of size t, denoted by $\bar{{x}}_{t}$, is given by the formula

$$\bar{{x}}_{t} = \frac{1} {t}{\sum _{i=1}^{t}{x}_{ i}}.$$

(2.1)

Equation (2.1) cannot be applied directly in the context of data streams, since it would require to consider all sample values at each time step. Fortunately, (2.1) can be easily transformed into an incremental scheme.

$$\begin{array}{rcl} \bar{{x}}_{t}& =& \frac{1} {t}{\sum \limits _{i=1}^{t}}{x}_{ i} \\ & =& \frac{1} {t}\left ({x}_{t} +{ \sum \limits _{i=1}^{t-1}}{x}_{ i}\right ) \\ & =& \frac{1} {t}\left ({x}_{t} + \left (t - 1\right )\bar{{x}}_{t-1}\right ) \\ & =& \bar{{x}}_{t-1} + \frac{1} {t}\left ({x}_{t} -\bar{ {x}}_{t-1}\right ).\end{array}$$

(2.2)

The incremental update (2.2) requires only three values to calculate the sample mean at time point t:

• The mean at time point t − 1.

• The sample value at time point t.

• The number of sample values so far.

The empirical or sample variance can be calculated in an incremental fashion in a similar way.

Definition 2.2.

Let x ₁, …, x _t be a random sample from the distribution of the random variable X. The empirical or sample variance of a sample of size t is given by

$${s}_{t}^{2} = \frac{1} {t - 1}{\sum \limits _{i=1}^{t}}{({x}_{ i} -\bar{ {x}}_{t})}^{2}$$

(2.3)

Furthermore, ${s}_{t} = \sqrt{{s}_{t }^{2}}$ is called the sample standard deviation.

In order to simplify the calculation, we use following notation:

$$\tilde{{m}}_{2,t} ={ \sum \limits _{i=1}^{t}}{({x}_{ i} -\bar{ {x}}_{t})}^{2}$$

(2.4)

In the following, the formula for incremental calculation is derived from (2.4) using (2.2).

$$\begin{array}{rcl} \tilde{{m}}_{2,\,t} -\tilde{ {m}}_{2,\,t-1}& =& {\sum \limits _{i=1}^{t}}{x}_{ i}^{2} - t\bar{{x}}_{ t}^{2} -{\sum \limits _{i=1}^{t-1}{x}_{ i}^{2}} + \left (t - 1\right )\bar{{x}}_{ t-1}^{2} \\ & =& {x}_{t}^{2} - t\bar{{x}}_{ t}^{2} + \left (t - 1\right )\bar{{x}}_{ t-1}^{2} \\ & =& {x}_{t}^{2} -\bar{ {x}}_{ t-1}^{2} + t\left (\bar{{x}}_{ t-1}^{2} -\bar{ {x}}_{ t}^{2}\right ) \\ & =& {x}_{t}^{2} -\bar{ {x}}_{ t-1}^{2} + t\left (\bar{{x}}_{ t-1} -\bar{ {x}}_{t}\right )\left (\bar{{x}}_{t-1} +\bar{ {x}}_{t}\right ) \\ & =& {x}_{t}^{2} -\bar{ {x}}_{ t-1}^{2} + t\left (\bar{{x}}_{ t-1} -\bar{ {x}}_{t-1} -\frac{1} {t}\left ({x}_{t} -\bar{ {x}}_{t-1}\right )\right )\left (\bar{{x}}_{t-1} +\bar{ {x}}_{t}\right ) \\ & =& {x}_{t}^{2} -\bar{ {x}}_{ t-1}^{2} + \left (\bar{{x}}_{ t-1} - {x}_{t}\right )\left (\bar{{x}}_{t-1} +\bar{ {x}}_{t}\right ) \\ & =& \left ({x}_{t} -\bar{ {x}}_{t-1}\right )\left ({x}_{t} +\bar{ {x}}_{t-1} -\bar{ {x}}_{t-1} -\bar{ {x}}_{t}\right ) \\ & =& \left ({x}_{t} -\bar{ {x}}_{t-1}\right )\left ({x}_{t} -\bar{ {x}}_{t}\right ).\end{array}$$

Consequently, we obtain the following recurrence formula for the second central moment:

$$\tilde{{m}}_{2,\,t} =\tilde{ {m}}_{2,\,t-1} + \left ({x}_{t} -\bar{ {x}}_{t-1}\right )\left ({x}_{t} -\bar{ {x}}_{t}\right )$$

(2.5)

The unbiased estimator for the variance of the sample according to (2.5) is given by

$${s}_{t}^{2} = \frac{1} {t - 1}{M}_{2,\,t} = \frac{\left (t - 2\right ){s}_{t-1}^{2} + \left ({x}_{t} -\bar{ {x}}_{t-1}\right )\left ({x}_{t} -\bar{ {x}}_{t}\right )} {t - 1}.$$

(2.6)

Definition 2.3.

Let x ₁, …, x _t be a random sample from the distribution of the random variable X. Then the k-th central moment of a sample of size t is defined by

$${m}_{k,\,t} = \frac{1} {t}{\sum \limits _{i=1}^{t}}{({x}_{ i} -\bar{ {x}}_{t})}^{k}.$$

(2.7)

In order to simplify the computations and to facilitate the readability of the text, we use the following expression for the derivation.

$$\tilde{{m}}_{k,\,t} ={ \sum \limits _{i=1}^{t}}{({x}_{ i} -\bar{ {x}}_{t})}^{k},$$

(2.8)

therefore $\tilde{{m}}_{k,t} = t \cdot {m}_{k,t}$.

For the third- and fourth-order moments, which are needed to calculate skewness and kurtosis of the data distribution, incremental formulae can be derived in a similar way, in the form of pairwise update equations for $\tilde{{m}}_{3,t}$ and $\tilde{{m}}_{4,t}$.

$$\begin{array}{rcl} \tilde{{m}}_{3,\,t}& =& {\sum \limits _{i=1}^{t-1}}{\left ({x}_{ i} -\bar{ {x}}_{t}\right )}^{3} +{ \left ({x}_{ t} -\bar{ {x}}_{t}\right )}^{3} \\ & =& {\sum \limits _{i=1}^{t-1}}{\left ({x}_{ i} -\bar{ {x}}_{t-1} -\frac{1} {t}\left ({x}_{t} -\bar{ {x}}_{t-1}\right )\right )}^{3} +{ \left ({x}_{ t} -\bar{ {x}}_{t-1} -\frac{1} {t}\left ({x}_{t} -\bar{ {x}}_{t-1}\right )\right )}^{3} \\ & =& {\sum \limits _{i=1}^{t-1}}{\left (\left ({x}_{ i} -\bar{ {x}}_{t-1}\right ) - b\right )}^{3} +{ \left (tb - b\right )}^{3} \\ & =& {\sum \limits _{i=1}^{t-1}}\left ({\left ({x}_{ i} -\bar{ {x}}_{t-1}\right )}^{3} - 3b{\left ({x}_{ i} -\bar{ {x}}_{t-1}\right )}^{2} + 3{b}^{2}\left ({x}_{ i} -\bar{ {x}}_{t-1}\right ) - {b}^{3}\right ) +{ \left (t - 1\right )}^{3}{b}^{3} \\ & =& \tilde{{m}}_{3,\,t-1} - 3b\tilde{{m}}_{2,\,t-1} - (\left (t - 1\right ){b}^{3} +{ \left (t - 1\right )}^{3}{b}^{3} \\ & =& \tilde{{m}}_{3,\,t-1} - 3b\tilde{{m}}_{2,\,t-1} + t\left (t - 1\right )\left (t - 2\right ){b}^{3} \end{array}$$

(2.9)

where $b = \frac{{x}_{t}-\bar{{x}}_{t-1}} {t}$.

From (2.9), we obtain a one-pass formula for the third-order centered statistical moment of a sample of size t:

$$\tilde{{m}}_{3,\,t} =\tilde{ {m}}_{3,\,t-1} - 3\frac{\left ({x}_{t} -\bar{ {x}}_{t-1}\right )} {t} \tilde{{m}}_{2,\,t-1} + \frac{\left (t - 1\right )\left (t - 2\right )} {{t}^{2}}{ \left ({x}_{t} -\bar{ {x}}_{t-1}\right )}^{3}.$$

(2.10)

The derivation for the fourth-order moment is very similar to (2.9) and thus is not detailed here.

$$\begin{array}{rcl} \tilde{{m}}_{4,\,t}& =& \tilde{{m}}_{4,\,t-1} - 4\frac{\left ({x}_{t} -\bar{ {x}}_{t-1}\right )} {t} \tilde{{m}}_{3,\,t-1} + 6{\left (\frac{{x}_{t} -\bar{ {x}}_{t-1}} {t} \right )}^{2}\tilde{{m}}_{ 2,\,t-1} \\ & & +\frac{\left (t - 1\right )\left ({t}^{2} - 3t + 3\right )} {{t}^{3}}{ \left ({x}_{t} -\bar{ {x}}_{t-1}\right )}^{4}. \end{array}$$

(2.11)

The results presented above offer the essential formulae for efficient, one-pass calculations of statistical moments up to the fourth order. Those are important when the data stream mean, variance, skewness, and kurtosis should be calculated. Although these measures cover the needs of the vast majority of applications for data analysis, sometimes higher-order statistics should be used. For the computation of higher-order statistical moments, see for instance [6].

Now we derive a formula for the incremental calculation of the sample correlation coefficient.

Definition 2.4.

Let x ₁, …, x _t be a random sample from the distribution of the random variable X and y ₁, …, y _t be a random sample from the distribution of the random variable Y. Then the sample Pearson correlation coefficient of the sample of size t, denoted by r _xy, t , is given by the formula

$${r}_{xy,\,t} = \frac{{\sum \limits _{i=1}^{t}}\left ({x}_{i} -\bar{ {x}}_{t}\right )\left ({y}_{i} -\bar{ {y}}_{t}\right )} {\left (t - 1\right ){s}_{x,\,t}{s}_{y,\,t}}$$

(2.12)

where $\bar{{x}}_{t}$ and $\bar{{y}}_{t}$ are the sample means of X and Y and s _x, t and s _y, t are the sample standard deviations of X and Y, respectively.

The incremental formula for the sample standard deviation can be easily derived from the incremental formula for sample variance (2.6). Hence, only the numerator of (2.12) needs to be considered further. Furthermore, the numerator of (2.12) represents the sample covariance s _xy, t .

Definition 2.5.

Let x ₁, …, x _t be a random sample from the distribution of the random variable X and y ₁, …, y _t be a random sample from the distribution of the random variable Y. Then the sample covariance s _xy, t of the sample of size t is given by t

$${s}_{xy,\,t} = \frac{{\sum \nolimits _{i=1}^{t}}\left ({x}_{i} -\bar{ {x}}_{t}\right )\left ({y}_{i} -\bar{ {y}}_{t}\right )} {t - 1}$$

(2.13)

where $\bar{{x}}_{t}$ and $\bar{{y}}_{t}$ are the sample means of X and Y and s _x, t and s _y, t are the sample standard deviations of X and Y , respectively.

The formula for the incremental calculation of the covariance is given by

$$\begin{array}{rcl} \left (t - 1\right ){s}_{xy,\,t}& =& {\sum \limits _{i=1}^{t-1}}\left ({x}_{ i} -\bar{ {x}}_{t}\right )\left ({y}_{i} -\bar{ {y}}_{t}\right ) + \left ({x}_{t} -\bar{ {x}}_{t}\right )\left ({y}_{t} -\bar{ {y}}_{t}\right ) \\ & =& {\sum \limits _{i=1}^{t-1}}\left (\left ({x}_{ i} -\bar{ {x}}_{t-1}\right ) - {b}_{x}\right )\left (\left ({y}_{i} -\bar{ {y}}_{t-1}\right ) - {b}_{y}\right ) +{ \left (t - 1\right )}^{2}{b}_{ x}{b}_{y} \\ & =& \left (t - 2\right ){s}_{xy,\,t-1} + t\left (t - 1\right ){b}_{x}{b}_{y} \end{array}$$

(2.14)

where ${b}_{x} = \frac{\left ({x}_{t}-\bar{{x}}_{t-1}\right )} {t}$ and ${b}_{y} = \frac{\left ({y}_{t}-\bar{{y}}_{t-1}\right )} {t}$. Hence, the incremental formula for the sample covariance is

$${s}_{xy,\,t} = \frac{\left (t - 2\right )} {\left (t - 1\right )}{s}_{xy,\,t-1} + \frac{1} {t}\left ({x}_{t} -\bar{ {x}}_{t-1}\right )\left ({y}_{t} -\bar{ {y}}_{t-1}\right )$$

(2.15)

Therefore, to update the Pearson correlation coefficient, we have to compute the sample standard deviation and covariance first and subsequently use (2.12).

Above in this section, we presented incremental calculations for the empirical mean, empirical variance, third and fourth sample central moments and sample correlation coefficient. These statistical measures can also be considered as estimators of the corresponding parameters of the data distribution. Therefore, we are interested in the question how many values x _i do we need to get a “good” estimation of the parameters. Of course, as we deal with a data stream, in general we will have a large amount of data. However, some application are based on time window techniques. For instance, for change detection methods presented in the section (Sect. 2.4). Here we need to compare at least two samples of data; on that account, the data have to be split into smaller parts. To answer the question about the optimal amount of data for statistical estimators, we have to analyze the variances of the parameter estimators. The variance of an estimator shows how efficient this estimator is.

Here we restrict our considerations to a random sample from a normal distribution with expected value 0. Let X ₁, …, X _t be independent and identically distributed (i.i.d.) random variables following a normal distribution, X _i  ∼ N0,  σ² and x ₁, …, x _t are observed values of these random variables.

The variance of the estimator of the expected value² $\bar{{X}}_{t} = \frac{1} {t} { \sum \limits_{i=1}^{t}{X}_{i}}$ is given by

$$V ar\left (\bar{{X}}_{t}\right ) = \frac{{\sigma }^{2}} {t}.$$

(2.16)

The variance of the unbiased estimator of the variance ${S}^{2} = \frac{1} {t-1}{ \sum \limits_{i=1}^{t}}{\left ({X}_{i} -\bar{ {X}}_{t}\right )}^{2}$ is given by

$$V ar\left ({S}_{t}^{2}\right ) = \frac{2} {\left (t - 1\right )}{\sigma }^{4}.$$

(2.17)

The variance of the distribution of the third moment is shown in (2.18) (see [6] for more detailed information)

$$V ar\left ({M}_{3,\,t}\right ) = \frac{6\left (t - 1\right )\left (t - 2\right )} {{t}^{3}} {\sigma }^{6}.$$

(2.18)

Figure 2.1 shows (2.16), (2.17), and (2.18) as functions in t for σ² = 1 (standard normal population). It is obvious that for small amounts of data, the variance of the estimators is quite large, consequently more values are needed to obtain a reliable estimation of distribution parameters. Furthermore, the optimal sample size depends on the statistic to be computed. For instance, for the sample mean and a sample of size 50, the variance is already small enough, whereas for the third moment estimator to have the same variance, many more observations are needed.

Fig. 2.1

Variances from bottom to top of parameter estimators for the expected value, the variance and the third moment of a standard normal distribution

We apply the same considerations to the sample correlation coefficient. Let X and Y be two random variables following normal distributions and let X ₁, …, X _t and Y ₁, …, Y _t be i.i.d. samples of X and Y , respectively: X _i  ∼ N0,  σ _x ² and Y _i  ∼ N0,  σ _y ². Assume the correlation between X and Y is equal to ρ _XY . Then the asymptotic variance of the sample correlation coefficient is given by (see [7])

$$V ar\left ({R}_{XY,\,t}\right ) \approx \frac{{\left (1 - {\rho }_{XY }^{2}\right )}^{2}} {t}.$$

(2.19)

Attention should be paid to the asymptotic nature of (2.19). This formula can be used only for sufficiently large t (see [7]). Equation (2.19) is illustrated in Fig. 2.2 as a function in t for ρ _XY  = 0. 9. Since for different values of ρ _XY , the plots are very similar, they are not shown here.

Fig. 2.2

Asymptotic variance of the sample correlation coefficient

In this section, we have provided equations for incremental calculation of the sample mean, sample variance, third and fourth moments and the Pearson correlation coefficient. These statistics allow us to summarize a set of observations analytically. Since we assume that the observations reflect the population as a whole, these statistics give us an idea about the underlying data distribution. Other important summary statistics are sample quantiles. Incremental approaches for quantiles estimation are described in the next section.

3 Incremental Quantile Estimation

Quantiles play an important role in statistics, especially in robust statistics, since they are not or less sensitive to outliers. For q ∈ (0, 1), the q-quantile has the property that q ⋅100% of the data are smaller and (1 − q) ⋅100% of the data are larger than this value. Themedian, i.e., the 50% quantile, is a robust measure of location and the interquartile range³ is a robust measure of spread. Incremental or recursive techniques for quantile estimation are not as obvious as for statistical moments, since for the sample quantile computation the entire sorted data are needed. Nevertheless, there are techniques for incremental quantile estimation. In this section, we describe two different approaches. First approach is restricted to continuous symmetric unimodal distributions. Therefore, this method is not very useful for all real world data. The second approach is not restricted to any kind of distribution and is not limited to continuous random variables. We also provide experimental results for both algorithms for different kinds of distributions.

3.1 Incremental Quantile Estimation for Continuous Random Variables

Definition 2.6.

For a random variable X with cumulative distribution function F _X , the q-quantile (q ∈ (0, 1)) is defined as $\inf \{x \in \mathbb{R}\mid {F}_{X}(x) \geq q\}$. If x _q is the q-quantile of a continuous random variable, this implies P(X ≤ x _q ) = q and P(X ≥ x _q ) = 1 − q.

For continuous random variables, an incremental scheme for quantile estimation is proposed in [10]. This approach is based on the following theorem.

Theorem 2.1.

Let ξ _{t t=0,1,…} be a sequence of identically distributed independent (i.i.d.) random variables with cumulative distribution function F _ξ . Assume that the density function f _ξ (x) exists and is continuous in the α-quantile x _α for an arbitrarily chosen α (0 < α < 1). Further let the inequality

$${f}_{\xi }({x}_{\alpha }) > 0$$

(2.20)

be fulfilled. Let c _{t t=0,1,…} be a (control) sequence of real numbers satisfying the conditions

$${\sum \limits _{t=0}^{\infty }}{c}_{ t} = \infty , {\sum \limits _{t=0}^{\infty }{c}_{ t}^{2} < \infty}.$$

(2.21)

Then the stochastic process X _t defined by

$$\begin{array}{rcl}{ X}_{0}& =& {\xi }_{0},\end{array}$$

(2.22)

$$\begin{array}{rcl}{ X}_{t+1}& =& {X}_{t} + {c}_{t}{Y }_{t+1}\left ({X}_{t},\;{\xi }_{t+1}\right ),\end{array}$$

(2.23)

with

$$\begin{array}{rcl}{ Y }_{t+1}& =& \left \{\begin{array}{ll} \alpha - 1&\mbox{ if }{\xi }_{t+1} < {X}_{t}, \\ \alpha &\mbox{ if }{\xi }_{t+1} \geq {X}_{t}, \end{array} \right.\end{array}$$

(2.24)

almost surely converges to the quantile x _α .

The proof of the theorem is based on stochastic approximation and can be found in [18]. A standard choice of the sequence c _{t t = 0, 1, …} is c _t  = 1 ∕ t. However, convergence might be extremely slow for certain distributions. Therefore, techniques to choose a suitable sequence c _{t t = 0, 1, …} , for instance, based on an estimation of the probability density function of the sampled random variable, are proposed in [10, 17].

Although this technique of incremental quantile estimation has only minimum memory requirement, it has certain disadvantages.

• It is only suitable for continuous random variables.

• Unless the sequence c _{t t = 0, 1, …} is well chosen, convergence can be extremely slow.

• When the sampled random variable changes over time, especially when the c _t are already close to zero, the incremental estimation of the quantile will remain almost constant and the change will be unnoticed.

In the following, we present an algorithm to overcome these problems.

3.2 Incremental Quantile Estimation

Here we provide a more general approach which is not limited to continuous random variables. First we describe an algorithm for incremental median estimation, which can be generalized to arbitrary quantiles. Since this algorithm is not very suitable for noncentral quantiles, we modify this approach in such a way that it yields good results for all quantiles.

3.2.1 Incremental Median Estimation

Before we discuss the general problem of incremental quantile estimation, we first focus on the special case of the median, since we will need the results for the median to develop suitable methods for arbitrary quantiles.

For the incremental computation of the median we store a fixed number, a buffer of m sorted data values a ₁, …, a _m in the ideal case the $\frac{m} {2}$ closest values left and the $\frac{m} {2}$ closest values right of the median, so that the interval [a ₁, a _m ] contains the median. We also need two counters L and R to store the number of values outside the interval [a ₁, a _m ], counting the values left and right of the interval separately. Initially, L and R are set to zero.

The algorithm works as follows. The first m data points x ₁, …, x _m are used to fill the buffer. They are entered into the buffer in increasing order, i.e., a _i  = x _[i] where x _[1] ≤ … ≤ x _[m] are the sorted values x ₁, …, x _m . After the buffer is filled, the algorithm handles the incoming values x _t in the following way:

• 1. If x _t  < a ₁, i.e., the new value lies left of the interval supposed to contain the median, then L ^new : = L ^old + 1.

• 2. If x _t  > a _m , i.e., the new value lies right of the interval supposed to contain the median, then R ^new : = R ^old + 1.

• 3. If a _i  ≤ x _t  ≤ a _i + 1 (1 ≤ i < m), x _t is entered into the buffer at position a _i or a _i + 1. Of course, the other values have to be shifted accordingly and the old left bound a ₁ or the old right bound a _m will be dropped. Since in the ideal case, the median is the value in the middle of the buffer, the algorithm tries to achieve this by balancing the number of values left and right of the interval [a ₁, a _m ]. Therefore, the following rule is applied:

  • a. If L < R, then remove a ₁, increase L, i.e. L ^new : = L ^old + 1, shift the values a ₂, …, a _i one position to the left and enter x _t in a _i .

  • b. Otherwise remove a _m , increase R, i.e. R ^new : = R ^old + 1, shift the values a _i + 1, …, a _m − 1 one position to the right and enter x _t in a _i + 1.

In each step, the median $\hat{{q}}_{0.5}$ can be easily calculated from the given values in the buffer and the counters L and R by

$$\hat{{q}}_{0.5}\; =\; \left \{\begin{array}{cl} {a}_{\frac{L+m+R} {2} -L} &\mbox{ if $t$ is odd,} \\ \frac{{a}_{\frac{L+m+R-1} {2} -L}+{a}_{\frac{L+m+R+1} {2} -L}} {2} & \mbox{ if $t$ is even.} \end{array} \right.$$

(2.25)

It should be noted that it can happen that at least one of the indices $\frac{L+m+R} {2} - L$, $\frac{L+m+R-1} {2} - L$ and $\frac{L+m+R+1} {2} - L$ are not within the bounds 1, …, m of the buffer indices and the computation of the median fails. The interval length a _m  − a ₁ can only decrease and at least for continuous distributions X with probability density function f _X (q _0. 5) > 0, where q _0. 5 is the true median of X, it will tend to zero with increasing sample size. In an ideal situation, the buffer of m stored values contains exactly the values in the middle of the sample. Here, we assume that at this point in time the sample consists of m + t values (Table 2.1).

Table 2.1 A small example data set

Table 2.2 illustrates how this algorithm works with an extremely small buffer of size m = 4 based on the data set given in Table 2.1.

Table 2.2 The development of the buffer and the two counters for the small example data set in Table 2.1

In the following, we generalize and modify the incremental median algorithm proposed in the previous section and analyze the algorithm in more detail.

3.2.2 An Ad hoc Algorithm

This algorithm for incremental median estimation can be generalized to arbitrary quantiles in a straightforward manner. For the incremental q-quantile estimation (0 < q < 1), only case 3 requires a modification. Instead of trying to get the same values for the counters L and R, we now try to balance the counters in such a way that qR ≈ (1 − q)L holds. This means, step 3a is applied if L < (1 − q)t holds, otherwise step 3b is carried out. t is the number of data sampled after the buffer of length m has been filled.

Therefore, in the ideal case, when we achieve this balance, a proportion of q of the data points lies left and a proportion of (1 − q) lies right of the interval defined by the buffer of length m.

Now we are interested in the properties of the incremental quantile estimator presented above. Since we are simply selecting the k-th order statistic of the sample, at least for continuous random variables and larger pre-sampling sizes, we can provide an asymptotic distribution of the order statistic and therefore for the estimator.

Assume, the sample comes from a continuous random variable X and we are interested in an estimation of the q-quantile x _q . Assume furthermore that the probability density function f _X is continuous and positive at x _q . Let ξ _k ^t (k = tq + 1) denote the k-th order statistic from an i.i.d. sample. Then ξ _k ^t has an asymptotic normal distribution [7]

$$N\left ({x}_{q};\ \frac{q\left (1 - q\right )} {t{f}^{2}\left ({x}_{q}\right )} \right )$$

(2.26)

From (2.26), we can obtain valuable information about the quantile estimator.

In order to have a more efficient and reliable estimator, we want the variance of (2.26) to be as small as possible. Under the assumption that we know the data distribution, we can compute the variance of ξ _k ^t.

Let X be a random variable following a standard normal distribution and assume we have a sample x ₁, …, x _t of X, i.e., these values are realizations of the i.i.d. random variables X _i  ∼ N0,  1. We are interested in the median of X. According to (2.26), the sample median ξ_{0. 5t + 1} ^t follows asymptotically a normal distribution:

$${\xi }_{\left \lfloor 0.5t\right \rfloor +1}^{t} \sim N\left (0;\ \frac{\pi } {2t}\right ).$$

(2.27)

Figure 2.3 shows the variance of the order statistic ξ_{0. 5t + 1} ^t as a function in t when the chosen quantile is q = 0. 5, i.e., the median, and the original distribution from which the sample comes is a standard normal distribution N(0; 1). The second curve in the figure corresponds to the variance of the sample mean.

Fig. 2.3

Variance from bottom to top of $\bar{X}$ and ξ _k ^t under the assumption of a standard normal distribution of X

The variance of the sample mean $\bar{X}$ is only slightly better than that of the order statistic ξ_{0. 5t + 1} ^t, nevertheless we should keep in mind the asymptotic character of the distribution (2.26).

Furthermore, from (2.26) we obtain the other nice property of the incremental quantile estimator: It is an asymptotically unbiased estimator of sample quantiles. It is even a consistent estimator.

Unfortunately, as it was shown in [25], the probability for the algorithm to fail is much smaller for the estimation of the median than for arbitrary quantiles. Therefore, despite the nice properties of this estimator this simple generalization of the incremental median estimation algorithm to arbitrary quantiles is not very useful in practice. In order to amend this problem, we provide a modified algorithm based on pre-sampling.

3.2.3 Incremental Quantile Estimation With Presampling iQPres

Here we introduce the algorithm iQPres (incremental quantile estimation with pre-sampling) [25]. As already mentioned above, the failure probability for the incremental quantile estimation algorithm in Sect. 2.3.2.2 is lower for the median than for extreme quantiles. Therefore, to minimise the failure probability we introduce an incremental quantile estimation algorithm with pre-sampling.

Assume we want to estimate the q-quantile. We pre-sample n values and we simply take the l-th smallest value x _(l) from the pre-sample for some fixed l ∈ { 1, …, n}. At the moment, l does not even have to be related to the q-quantile. The probability that x _(l) is smaller than the q-quantile of interest is

$${ p}_{l} ={ \sum \limits _{i=0}^{l}}\left (\begin{array}{l} n\\ i \end{array} \right )\cdot {q}^{i}\cdot {\left (1 - q\right )}^{n-i}.$$

(2.28)

So when we apply pre-sampling in this way, we obtain the new (presampled) distribution (order statistic) ξ _l ⁿ. From (2.28), we can immediately see that the (1 − p _l )-quantile of ξ _l ⁿ is the same as the q-quantile of X. Therefore, instead of estimating the q-quantile of X, we estimate the (1 − p _l )-quantile of ξ _l ⁿ. Of course, this is only helpful, when l is chosen in such a way that the failure probabilities for the (1 − p _l )-quantile are significantly lower than the failure probabilities for the q-quantile. In order to achieve this, l should be chosen in such a way that (1 − p _l ) is as close to 0. 5 as possible.

We want to estimate the q-quantile (0 < q < 1). Fix the parameters m, l, n. (For an optimal choice see [25].)

• 1. Presampling: n succeeding values are stored in increasing order in a buffer b _n of length n. Then we select the l-th element in the buffer. The buffer is emptied afterwards for the next presample of n values.

• 2. Estimation of the (1 − p _l )-quantile based on the l-th element in the buffer for pre-sampling: this is carried out according to the algorithm described in Sect. 2.3.2.2.

The quantile is then estimated in the usual way, i.e., 

$$\begin{array}{rcl} k& =& \left \lceil (m + L + R) {_\ast} (1 - {p}_{l}) - l + 0.5\right \rceil , \\ r& =& (m + L + R) {_\ast} (1 - {p}_{l}) - l + 0.5 - k, \\ \hat{q}& =& (1 - r) \cdot {a}_{k-R} + r \cdot {a}_{k-R+1} \mbox{ (quantile estimator).} \\ \end{array}$$

Of course, this does only work when the algorithm has not failed, i.e., the corresponding index k is within the buffer of m values.

3.3 Experimental Results

In this section, we present an experimental evaluation of the presented algorithms iQPres and the algorithm described in Sect. 2.3.1. The evaluation is based on artificial data sets.

First, we consider estimations of the lower and upper quartile as well as the median for different distributions:

• Exponential distribution with parameter λ = 4 (Exp(4))

• Standard normal distribution (N(0;1))

• Uniform distribution on the unit interval (U(0,1))

• An asymmetric bimodal distribution given by a Gaussian mixture model (GM) of two normal distributions. The cumulative distribution function of this distribution is given by

  $$F(x)\; =\; 0.3 \cdot {F}_{\mbox{ N(-3;1)}} + 0.7 \cdot {F}_{\mbox{ N(1;1)}}$$

  where F _N(μ;σ ²) denotes the cumulative distribution function of the normal distribution with expected value μ and variance σ². Its probability density function is shown in Fig. 2.4.

Fig. 2.4

An example for an asymmetric, bimodal probability density function

The quantile estimations were carried out for samples of size of 10,000 that were generated from these distributions. We have repeated each estimation 1,000 times. Tables 2.3–2.5 show the average over all estimations for our algorithm (iQPres with a memory size of M = 150) and for the technique based on Theorem 2.1 where we used the control sequence ${c}_{t} = \frac{1} {t}$. The mean squared error over the 1,000 repeated runs is also shown in the tables.

Table 2.5 Estimation of the upper quartile q = 0. 75

Table 2.3 Estimation of the lower quartile q = 0. 25

Table 2.4 Estimation of the median q = 0. 5

For the uniform distribution, incremental quantile estimation based on (2.23) and iQPres leads to very similar and good results. For the normal distribution, both algorithms yield quite good results, but iQPres seems to be slightly more efficient with a smaller mean square error. For the bimodal distribution based on the Gaussian mixture model and a skewed distribution such as the exponential distribution, the estimations for the algorithm based on (2.23) are more or less useless, at least when no specific effort is invested to find an optimal control sequence c _{t t = 0, 1, …} . iQPres does not have any problems with these distributions. As already mentioned before, it is also not required for iQPres that the sampling distribution is continuous whereas it is a necessary assumption for the technique based on (2.23).

4 Hypothesis Tests and Change Detection

In this section we demonstrate how hypothesis testing can be adapted to an incremental computation scheme for the cases of the χ²-test and thet-test. Moreover, we discuss the problem of nonstationary data and explain various change detection strategies with the main focus on the use of statistical tests.

4.1 Incremental Hypothesis Tests

Statistical test are methods to check the validity of hypotheses about distributions or properties of distributions of random variables. Since statistical tests rely on samples, they cannot definitely verify or falsify a hypothesis. They can only provide probabilistic information supporting or rejecting the hypothesis under consideration.

Statistical tests usually consider a null hypothesis H ₀ and an alternative hypothesis H ₁. The hypotheses may concern parameters of a given class of distributions, for instance unknown expected value and variance of a normal distribution. Such tests are called parameter tests. In such cases, the a priori assumption is that the data definitely originate from a normal distribution. Only the parameters are unknown. In contrast to parameter tests, nonparametric tests concern more general hypothesis, for example, whether it is reasonable at all to assume that the data come from a normal distribution.

The error probability that the test will erroneously reject the null hypothesis, given the null hypothesis is true, is used as an indicator of the reliability of the test. Sometimes a so-called p-value is used. The p-value is smallest error probability that can be admitted, so that the test will still reject the null hypothesis for a given sample. Therefore, a low p-value is a good indicator for rejecting the null hypothesis. Usually, the acceptable error probability α (α-error) should be specified in advance, before the test is carried out. The smaller α is chosen, the more reliable is the test when the outcome is to reject the null hypothesis. However, when α is chosen too small, then the test will not tend to reject the null hypothesis, although the sample might not speak in favor of it.

Some of the hypothesis tests can be applied to data streams, since they can be calculated in an incremental fashion. We discuss in this section the incremental adaptation of two statistical tests, the χ²-test and the t-test. Note, that the application of hypothesis tests to data streams, using incremental computation or window techniques, requires the repeated execution of the test. This can cause the problem of multiple testing. The multiple testing problem is described later in this section.

4.1.1 χ²-test

The χ²-test has various applications. The principal idea of the χ²-test is the comparison of two distributions. One can check whether two samples come from the same distribution, a single sample follows a given distribution or also whether two samples are independent.

Example 2.1.

A die is thrown 120 times and the observed frequencies are as follows: 1 is obtained 30 times, 2–25, 3–18, 4–10, 5–22, and 6–15. We are interested in the question whether the die is fair or not.

The null hypothesis H ₀ for the χ²-test claims that the data follow a certain (cumulative) probability distribution F(x). The distribution of the null hypothesis is than compared to the distribution of the data. The null hypothesis can for instance be a given distribution, e.g., a uniform or a normal distribution, and the χ²-test can give an indication, whether the data strongly deviate from this expected distribution. For an independence test for two variables, the joint distribution of the sample is compared to the product of the marginal distributions. If these distributions differ significantly, this is an indication that the variables might not be independent.

The main idea of the χ²-test is to determine how well the observed frequencies fit the theoretical/expected frequencies specified by the null hypothesis. Therefore, the χ²-test is appropriate for data from categorical or nominally scaled random variables. In order to apply the test to continuous numeric data, the data domain should be partitioned into r categories first.

First we discus the χ²goodness of fit test. Here we assume to know from which distribution the data come. Then the H ₀ and H ₁ hypotheses can be stated as follows:

H ₀::

The sample comes from the distribution F _X

H ₁::

The sample does not come from the distribution F _X

Therefore the problem from Example 2.1 can be solved with the help of the χ² goodness of fit test. Consequently, the H ₀ and H ₁ hypotheses are chosen as follows:

H ₀::

$P(X = 1) = {p}_{1} = \frac{1} {6}$, … , $P(X = 6) = {p}_{6} = \frac{1} {6}$

H ₁::

$P(X = i)\neq \frac{1} {6}$ for at least one value i ∈ { 1, …, 6}

Let X ₁, …, X _n be i.i.d. continuous random variables and x ₁, …, x _n the observations from these random variables. Then the test statistic is computed as follows

$${\chi }^{2} ={ \sum \limits_{i=1}^{r}}\frac{{\left ({O}_{i} - {E}_{i}\right )}^{2}} {{E}_{i}}$$

(2.29)

where O _i are the observed frequencies and E _i are the expected frequencies.

Since we are dealing with continuous random variables, to compute the observed and expected frequencies we should carry out a discretisation of the data domain.

Let F _X (x) be the assumed cumulative distribution function. The x-axis have to be split into r pairwise disjoint sets or bin S _i . Then the expected frequency in bin S _i is given by

$${E}_{i} = n\left ({F}_{X}\left ({a}_{i+1}\right ) - {F}_{X}\left ({a}_{i}\right )\right ),$$

(2.30)

where a _i , a _i + 1 is interval corresponding to bin S _i .

Furthermore, for the observed frequencies we obtain

$${O}_{i} ={ \sum \limits _{{x}_{{k}_{ i}}\in {S}_{i}}1}.$$

(2.31)

O _i is therefore the amount of observations in the i-th interval.

The statistic (2.29) has an approximate χ²-distribution with r − 1 degrees of freedom under the following assumptions: First, the observations are independent from each other. Second, the categories—the bins S _i —are mutually exclusive and exhaustive. This means that no categories may have an expected frequency of zero, i.e. ∀i ∈ 1, …, r : E _i  > 0. Furthermore, no more than 20% of the categories should have an expected frequency less than five. If this is not the case, categories should be merged or redefined. Note that this might also lead to a different number of degrees of freedom.

Therefore, the hypothesis H ₀ that the sample comes from the particular distribution F _X is rejected if

$${\sum \limits_{i=1}^{r}}\frac{{\left ({O}_{i} - {E}_{i}\right )}^{2}} {{E}_{i}} > {\chi }_{1-\alpha }^{2},$$

(2.32)

where χ_1 − α ² is the 1 − α-quantile of the χ²-distribution with r − 1 degrees of freedom.

Table 2.6 summarizes the observed and expected frequencies and computations for Example 2.1. All E _i are greater than zero, even greater than 4. Therefore, there is no need to combine categories. The test statistic is computed as follows:

$$ {\sum \limits_{i=1}^{r}}\frac{{\left ({O}_{i} - {E}_{i}\right )}^{2}} {{E}_{i}} = 5 + 1.25 + 0.2 + 5 + 0.2 + 1.25 = 12.9 $$

(2.33)

The obtained result χ² = 12. 9 should be evaluated with 1 − α-quantile of the χ²-distribution. For that purposes table of the χ²-distribution ([7]). The corresponding degrees of freedom are computed as explained above r − 1 = (6 − 1) = 5. For α = 0. 05 the tabled critical value for 5 degrees of freedom is χ_0. 95 ² = 11. 07, which is smaller than computed test statistic. Therefore, the null hypothesis is rejected at the 0. 05 significance level. For significance level 0. 02, the critical value is χ_0. 98 ² = 13. 388 and therefore the null hypothesis cannot be rejected at this level. This result can be summarized as follows: χ² = 12. 9 with 5 degrees of freedom can be rejected for all significance levels bigger than 0. 024. This indicates that the die is unfair.

Table 2.6 Example 2.1

In order to adapt the χ² goodness of fit test to incremental calculation, the observed frequencies should be computed in an incremental fashion.

$${ O}_{i}^{\left (t\right )} = \left \{\begin{array}{ll} {O}_{i}^{\left (t-1\right )} + 1&\mbox{ if }{x}_{ t} \in {S}_{i}, \\ {O}_{i}^{\left (t-1\right )} & \mbox{ otherwise. } \end{array} \right.$$

(2.34)

The expected frequency should also be recalculated corresponding to the increasing amount of observations.

$${E}_{i}^{\left (t\right )} = \frac{{E}_{i}^{\left (t-1\right )}} {\left (t - 1\right )} t.$$

(2.35)

Another very common test is the χ² independence test. This test evaluates the general hypothesis that two variables are statistically independent from each other.

Let X and Y be two random variables and x ₁, y ₁, …, x _n , y _n are the observed values of these variables. For continuous random variables, the data domains should be partitioned into r and q categories, respectively. Therefore, the observed values of X can be assigned to one of the categories S ₁ ^X, …, S _r ^X and the observed values of Y to one of the categories S ₁ ^Y, …, S _q ^Y. Then O _ij is the frequency of occurrence of the observation $({x}_{{k}_{i}},{y}_{{k}_{j}})$, where ${x}_{{k}_{i}} \in {S}_{i}^{X}$ and ${y}_{{k}_{j}} \in {S}_{j}^{Y }$. Furthermore,

$${O}_{i\bullet } ={ \sum \limits_{j=1}^{q}{O}_{ ij}}$$

(2.36)

and

$${O}_{\bullet j} ={ \sum \limits_{i=1}^{r}{O}_{ ij}}$$

(2.37)

denote the marginal observed frequencies.

Table 2.7 illustrates the observed absolute frequencies. The total number of observations in the table is n. The notation O _ij represents the number of observations in the cell with index ij (i-th row and j-th column), O _i ∙ the number of observations in the i-th row and O _∙ j the number of observations in the j-th column. This table is called contingency table.

Table 2.7 Contingency table

It is assumed that the random variables X and Y are statistically independent. Let p _ij be the probability of being in the i-th category of the domain of X and the j-th category of the domain of Y. p _i ∙ and p _∙ j are the corresponding marginal probabilities. Then, corresponding to the assumption of independence for each pair

$${p}_{ij} = {p}_{i\bullet }\cdot {p}_{\bullet j}$$

(2.38)

holds. Equation (2.38) defines statistical independence. Therefore, the null and the alternative hypotheses are as follows:

H ₀::

p _ij  = p _i ∙ ⋅p _∙ j

H ₁::

p _ij ≠p _i ∙ ⋅p _∙ j

Thus, if X and Y are independent, then the expected absolute frequencies are given by

$${E}_{ij} = \frac{{O}_{i\bullet }\cdot {O}_{\bullet j}} {n}.$$

(2.39)

The test statistic, again checking the observed frequencies against the expected frequencies under the null hypothesis, is as follows.

$${\chi }^{2} ={ \sum \limits _{i=1}^{r}}{ \sum \limits_{j=1}^{q}}\frac{{\left ({O}_{ij} - {E}_{ij}\right )}^{2}} {{E}_{ij}}$$

(2.40)

The test statistic has an approximate χ²-distribution with r − 1s − 1 degrees of freedom. Consequently, the hypothesis H ₀ that X and Y are independent can be rejected if

$${\sum \limits _{i=1}^{r}}{ \sum \limits_{j=1}^{q}}\frac{{\left ({O}_{ij} - {E}_{ij}\right )}^{2}} {{E}_{ij}} \geq {\chi }_{1-\alpha }^{2}$$

(2.41)

where χ_1 − α ² is the 1 − α-quantile of the χ²-distribution with r − 1s − 1 degrees of freedom.

For the incremental computation of O _i ∙, O _∙ j , and O _ij corresponding formulae must be developed. For the time point t and the new observed values x _t , y _t , the incremental formulae are given by

$$\begin{array}{rcl}{ O}_{i\bullet }^{\left (t\right )}& =& \left \{\begin{array}{ll} {O}_{i\bullet }^{\left (t-1\right )} + 1&\mbox{ if }{x}_{ t} \in {S}_{i}^{X}, \\ {O}_{i\bullet }^{\left (t-1\right )} & \mbox{ otherwise. } \end{array} \right.\end{array}$$

(2.42)

$$\begin{array}{rcl}{ O}_{\bullet j}^{\left (t\right )}& =& \left \{\begin{array}{ll} {O}_{\bullet j}^{\left (t-1\right )} + 1&\mbox{ if }{y}_{ t} \in {S}_{j}^{Y }, \\ {O}_{\bullet j}^{\left (t-1\right )} & \mbox{ otherwise. } \end{array} \right.\end{array}$$

(2.43)

$$\begin{array}{rcl}{ O}_{ij}^{\left (t\right )}& =& \left \{\begin{array}{ll} {O}_{ij}^{\left (t-1\right )} + 1&\mbox{ if }{x}_{ t} \in {S}_{i}^{X} \wedge {y}_{ t} \in {S}_{j}^{Y }, \\ {O}_{ij}^{\left (t-1\right )} & \mbox{ otherwise. } \end{array} \right.\end{array}$$

(2.44)

The χ² goodness of fit test can be extended to a χ² homogeneity test ([22]). Whereas the χ² goodness of fit test can be used only for a single sample, the χ² homogeneity test is used to compare whether two or more samples come from the same population.

Let X ₁, …, X _m (m ≥ 2) be discrete random variables, or continuous random variables discretised into r categories S ₁, …, S _r . The data for each of the m samples from random variables X ₁, …, X _m (overall n values) are entered in a contingency table. This table is similar to the one for the χ² independence test.

The samples are represented by the columns and the categories by the rows of Table 2.8. We assume that each of the samples is randomly drawn from the same distribution. The χ² homogeneity test checks whether m samples are homogeneous with respect to the observed frequencies. If the hypothesis H ₀ is true, the expected frequency in the i-th category will be the same for all of the m random variables. Therefore, the null and the alternative hypotheses can be stated as follows:

H ₀::

p _ij  = p _i ∙ ⋅p _∙ j

H ₁::

p _ij ≠p _i ∙ ⋅p _∙ j .

Table 2.8 Contingency table

From H ₀ follows that the rows are independent of the column.

Therefore, the computation of an expected frequency can be summarized by

$${E}_{ij} = \frac{{O}_{i\bullet }\cdot {O}_{\bullet j}} {n}.$$

(2.45)

Although the χ² independence test and χ² homogeneity test evaluate different hypothesis, they are computed identically. Therefore, the incremental adaptation of the χ² independence test can also be applied to the χ² homogeneity test.

Commonly in case of two samples the Kolmogorov–Smirnov test is used, since it is an exact test and in contrast to the χ²-test can be applied directly without previous discretisation of continuous distributions. However, the Kolmogorov–Smirnov test does not have any obvious incremental calculation scheme. The Kolmogorov–Smirnov test is described in Sect. 2.4.2.2.

4.1.2 The t-Test

The next hypothesis test for which we want to provide incremental computation is the t-test. Different kinds of the t-test are used. We restrict our considerations to the one sample t-test and the t-test for two independent samples with equal variance.

The one sample t-test evaluates whether a sample with particular mean could be drawn from the population with known expected value μ₀. Let X ₁, …X _n be i.i.d. and X _i  ∼ Nμ; σ² with unknown variance σ². The null and the alternative hypotheses for two-sided test are:

H ₀::

μ = μ₀, the sample comes from the normal distribution with expected value μ₀.

H ₁::

μ≠μ₀, the sample comes from a normal distribution with an expected value differing from μ₀.

The test statistic is given by

$$T = \sqrt{n}\frac{\bar{X} - \mu } {S} ,$$

(2.46)

where $\bar{X}$ is the sample mean and S the sample standard deviation. The statistic (2.46) is t-distributed with (n − 1) degrees of freedom. H ₀ is rejected if

$$t < -{t}_{1-\alpha /2}\mbox{ or }t > {t}_{1-\alpha /2}$$

(2.47)

where t _{1 − α ∕ 2} is the 1 − α ∕ 2-quantile of the t-distribution with (n − 1) degrees of freedom and t is the computed value of the test statistic (2.46), i.e. $t = \sqrt{n}\frac{\bar{x}-{\mu }_{0}} {s}$.

One-sided tests are given by the following null and alternative hypotheses:

H ₀::

μ ≤ μ₀ and H ₁ :   μ > μ₀. H ₀ is rejected if t > t _1 − α.

H ₀::

μ ≥ μ₀ and H ₁ :   μ < μ₀. H ₀ is rejected if t <  − t _1 − α.

This test can be very easily adapted to incremental computation. For this purpose, the sample mean and the sample variance have to be updated as in (2.2) and (2.6), respectively, as described in Sect. 2.2. Note that the degrees of freedom of the t-distribution should be updated in each step as well.

$${t}_{n+1} = \sqrt{n + 1}\frac{\bar{{x}}_{n+1} - {\mu }_{0}} {{s}_{n+1}}$$

(2.48)

Unlike previous notations we use here n + 1 for the time point, since the letter t is already used for the computed test statistic. Furthermore, as mentioned above the 1 − α ∕ 2-quantile of the t-distribution with n degrees of freedom should be used to evaluate the null hypothesis. However for n ≥ 30, the quantiles of the standard normal distribution could be used as approximation of the quantiles of the t-distribution.

The t-test for two independent samples is used to evaluate whether two independent sample come from two normal distributions with the same expected value. The two sample means $\bar{x}$ and $\bar{y}$ are used to estimate the expected values μ _X and μ _Y of the underlying distributions. If the result of the test is significant, we assume that the samples come from two normal distributions with different expected values. Furthermore, we assume that the variances of the underlying distributions are unknown.

The t-test is based on the following assumptions:

• The samples are drawn randomly.

• The underlying distribution is a normal distribution.

• The variances of the underlying distributions are equal, i.e. σ _X ² = σ _Y ².

Let ${X}_{1},\ldots {X}_{{n}_{1}}$ i.i.d. and X _i  ∼ Nμ _X ; σ _X ² and ${Y }_{1},\ldots {Y }_{{n}_{2}}$ i.i.d. and Y _i  ∼ Nμ _Y ; σ _Y ² with unknown expected values and unknown variances and σ _X ² = σ _Y ².

The null and the alternative hypothesis can be defined as follows:

H ₀::

μ _X  = μ _Y , the samples come from the same normal distribution.

H ₁::

μ _X ≠μ _Y , the samples come from normal distributions with different expected values.

In this case, a two-sided test is carried out; however, similar to the one sample t-test also a one-sided test can be defined.

The test statistic is computed as follows.

$$T = \frac{\bar{X} -\bar{ Y }} {\sqrt{\frac{\left ({n}_{1 } -1 \right ) {S}_{X }^{2 }+\left ({n}_{2 } -1 \right ) {S}_{Y }^{2 }} {{n}_{1}+{n}_{2}-2}} }\sqrt{ \frac{{n}_{1 } {n}_{2 } } {{n}_{1} + {n}_{2}}}$$

(2.49)

where S _X ² and S _Y ² are the unbiased estimators for the variances of X and Y , respectively.

Equation (2.49) is a general equation for the t-test for two independent samples and can be used in both cases of equal and unequal sample sizes.

The statistic (2.49) has a t-distribution with n ₁ + n ₂ − 2 degrees of freedom.

Let

$$t = \frac{\bar{x} -\bar{ y}} {\sqrt{\frac{\left ({n}_{1 } -1 \right ) {s}_{X }^{2 }+\left ({n}_{2 } -1 \right ) {s}_{Y }^{2 }} {{n}_{1}+{n}_{2}-2}} }\sqrt{ \frac{{n}_{1 } {n}_{2 } } {{n}_{1} + {n}_{2}}}$$

(2.50)

be the computed value of the statistic (2.49). Then the hypothesis H ₀ that the samples come from the same normal distribution is rejected if

$$t < -{t}_{1-\alpha /2}\mbox{ or }t > {t}_{1-\alpha /2},$$

(2.51)

where t _{1 − α ∕ 2} is the 1 − α ∕ 2-quantile of the t-distribution with n ₁ + n ₂ − 2 degrees of freedom.

Similar to the one sample t-test, the t-test for two independent samples can be easily computed in an incremental fashion, since the sample means and the variance can be calculated in an incremental way. Here the degrees of freedom should also be updated with the new observed values.

4.1.3 Multiple Testing

Multiple testing refers to the application of number of tests simultaneously. Instead of a single null hypothesis, a tests for a set of null hypotheses H ₀, H ₁, …, H _n are considered. These null hypotheses do not have to exclude each other.

An example for multiple testing is a test whether m random variables X ₁, …X _m are pairwise independent. This means, the null hypotheses are H _1, 2, …, H _1, m , …, H _{m − 1, m} where H _i, j states that X _i and X _j are independent.

Multiple testing leads to the undesired effect of cumulating the α-error. The α-error α is the probability to reject the null hypothesis erroneously, given it is true. Choosing α = 0. 05 means that in 5% of the cases the null hypothesis would be rejected, although it is true. When k tests are applied to the same sample, then the error probability for each test is α. Under the assumption that the null hypotheses are all true and the tests are independent, the probability that at least one test will reject its null hypothesis erroneously is

$$\begin{array}{rcl} P\left (\mathcal{l} \geq 1\right )& =& 1 - P(\mathcal{l} = 0)\end{array}$$

(2.52)

$$\begin{array}{rcl} & =& 1 - (1 - \alpha ) \cdot (1 - \alpha )\ldots \cdot (1 - \alpha )\end{array}$$

(2.53)

$$\begin{array}{rcl} & =& 1 - {(1 - \alpha )}^{k}.\end{array}$$

(2.54)

ℓ is the number of tests rejection the null hypothesis.

A variety of approaches have been proposed to handle the problem of cumulating the α-error. In the following, two common methods will be introduced shortly.

The simplest and most conservative method is Bonferroni correction [21]. When k null hypotheses are tested simultaneously and α is the desired overall α-error for all tests together, then the corrected α-error for each single test should be chosen as $\tilde{\alpha } = \frac{\alpha } {k}$. The justification for this correction is the inequality

$$P\left ({\bigcup \limits _{i}{A}_{i}}\right ) \leq {\sum \limits _{i}P}\left ({A}_{i}\right ).$$

(2.55)

For Bonferroni correction, A _i is the event that the null hypothesis H _i is rejected, although it is true. In this way, the probability that one or more of the tests rejects its corresponding null hypothesis is at most α. In order to guarantee the significance level α, each single test must be carried out with the corrected level $\tilde{\alpha }$.

Bonferroni correction is a very rough and conservative approximation for the true α-error. One of its disadvantages is that the corrected significance level $\tilde{\alpha }$ becomes very low, so that it becomes almost impossible to reject any of the null hypotheses.

The simple single step Bonferroni correction has been improved by Holm [12]. The Bonferroni–Holm method is a multistep procedure in which the necessary corrections are carried out stepwise. This method usually yields larger corrected α-values than the simple Bonferroni correction.

When k hypotheses are tested simultaneously and the overall α-error for all tests is α, for each of the tests the corresponding p-value is computed based on the sample x and the p-values are sorted in ascending order.

$${p}_{[1]}(x) \leq {p}_{[2]}(x) \leq \ldots \leq {p}_{[k]}(x)$$

(2.56)

The null hypotheses H _i are ordered in the same way.

$${H}_{[1]},{H}_{[2]},\ldots ,{H}_{[k]}$$

(2.57)

In the first step, H _[1] is tested by comparing p _[1] with $\frac{\alpha } {k}$. If ${p}_{[1]} > \frac{\alpha } {k}$ holds, then H _[1] and the other null hypotheses H _[2], …, H _[k] are not rejected. The method terminates in this case. However, if ${p}_{[1]} \leq \frac{\alpha } {k}$ holds, H _[1] is rejected and the next null hypothesis H _[2] is tested by comparing the p-value p _[2] and the corrected α-value $\frac{\alpha } {k-1}$. If ${p}_{[2]} > \frac{\alpha } {k-1}$ holds, H _[2] and the remaining null hypotheses H _[3], …, H _[k] are not rejected. If ${p}_{[2]} \leq \frac{\alpha } {k-1}$ holds, H _[2] is rejected and the procedure continues with H _[3] in the same way.

The Bonferroni–Holm method tests the hypotheses in the order of their p-values, starting with H _[1]. The corrected α _i -values $\frac{\alpha } {k}, \frac{\alpha } {k-1},\ldots \alpha$ are increasing. Therefore, the Bonferroni–Holm method rejects at least those hypotheses that are also rejected by simple Bonferroni correction, but in general more hypotheses can be rejected.

4.2 Change Detection Strategies

Detecting changes in data streams has become a very important area of research in many application fields, such as stock market, web activities, or sensors measurements, just to name a few. The main problem for change detection in data streams is limited memory capacity. It is unrealistic to store the full history of the data stream. Therefore, efficient change detection strategies tailored to the data stream should be used. The main requirements for such approaches are: low computational costs, fast change detection, and high accuracy. Moreover it is important to distinguish between true changes and false alarms. Abrupt changes as well as slow drift in the data generating process can occur. Therefore, a “good” algorithm should be able to detect both kinds of changes.

Various strategies are proposed to handle this problem, see for instance [11] for a detailed survey of change detection methods. Most of these approaches are based on time window techniques [2, 15]. Furthermore, several approaches are presented for evolving data streams as they are discussed in [8, 13, 14].

In this section, we introduce two types of change detection strategies: incremental computation and window technique-based change detection. Furthermore, we put the main focus on statistical tests. We assume to deal with numeric data streams. As already mentioned in the introduction, two types of change are identified: concept change and change of data distribution. We do not differentiate in this work between both of them, since the distribution of the target variable will be changed in both cases.

4.2.1 iQPres for Change Detection

The incremental quantile estimator iQPres from Sect. 2.3.2.3 can be used for change detection [25]. In case, the sampling distribution changes, having a drift of the quantile to be estimated as a consequence, such changes will be noticed, since the simple version of iQPres without shifted parallel estimations will fail in the sense that it is not able to balance the counters L and R any more.

In order to illustrate how iQPres can be applied to change detection, we consider daily measurements for gas production in a waste water treatment plant over a period of more than eight years. The measurements are shown in Fig. 2.5.

Fig. 2.5

An example of change detection for time series data from a waste water treatment plant

iQPress has been applied to this data set to estimate the median with a memory size of M = 30. The optimal choice for the sizes of the buffers for pre-sampling and median estimation is then n = 3 and m = 27, respectively. At the three time points 508, 2,604, and 2,964, the buffer cannot be balanced anymore, indicating that the median has changed. These three time points are indicated by vertical lines in Fig. 2.5. The arrows indicate whether the median is increased or decreased. An increase corresponds to an unbalanced buffer with the right counter R becoming too large, whereas a decrease leads to an unbalanced buffer with the left counter L becoming too large. The median increases at the first point at 508 from 998 before and 1,361 after this point. At time point 2,604, the median increases to 1,406 and drops again to 1,193 at time point 2,964.

Note that algorithms based on Theorem 2.1 mentioned in Sect. 2.3.1 are not suitable for change detection.

By using iQPres for change detection in the data distribution, we assume that the median of the distribution changes with the time, however, if this is not the case and only another parameter like the variance of the underlying distribution changes, other strategies for change detection should be used.

4.2.2 Statistical Tests for Change Detection

The theory of hypothesis testing is the main background for change detection. Several algorithms for change detection are based on hypothesis tests.

Hypothesis tests could be applied to change detection in two different ways:

• Change detection through incremental computation of the tests: by this approach the test is computed in an incremental fashion, for instance, as it is explained in Sect. 2.4.1. Consequently the change can be detected if the test starts to yield different results as before.

• Window techniques: by this approach the data stream divided into time windows. A sliding window could be used as well as nonoverlapping windows. In order to detect potential changes, we need either to compare data from an earlier window with data from newer one or to test only the new data (for instance, whether the data follow a known or assumed distribution). When the window size is not too large, it is not necessary to be able to compute the tests in an incremental fashion. Therefore, we are not restricted to tests that render themselves to incremental computations, but many other tests could be used. Hybrid approaches combining both techniques are also possible. Of course, window techniques with incremental computations within the window will lead to less memory consumptions and faster computations.

We will not give a detailed description for change detection based on incremental computation here, since the principles of these methods are explained in Sect. 2.4.1. However, the problem of multiple testing as discussed in Sect. 2.4.1 should be taken into account when a test is applied again and again over time. Even if the underlying distribution does not change over time, any test will erroneously reject the null hypothesis of no change in the long run if we only carry out the test often enough. Different approaches to solve this problem are presented in Sect. 2.4.1.3. Another problem of this approach is the “burden of old data”. If a large amount of data has been analyzed already and the change is not very drastic, it may happen that the change will be detected with large delay or not detected at all when a very large window is used. On that account it may be useful to re-initialize the test from time to time.

To detect changes with by window technique, we need to compare two samples of data and have to decide whether the hypothesis H ₀ that they come from the same distribution is true.

First we will present a general meta-algorithm for change detection based on a window technique, without any specific fixed test. This algorithm is presented in Fig. 2.6. The constant step specifies, after how many new values the change detection should checked again.

Fig. 2.6

General scheme of a change detection algorithm based on time windows and statistical tests

This approach follows an simple idea: when the data from two subwindows of W are judged as “distinct enough”, the change is detected. Here “distinct enough” is specified by the selected statistical test for distribution change. In general, we assume the splitting of W into two subwindows of equal size. Nevertheless, any “valid” splitting can be used. Valid is meant in terms of the amount of data that is needed for the test to be reliable.

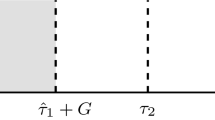
However, by a badly selected cut point the change can be detected with large delay as Fig. 2.7 shows. The rightmost part indicates a change in the data stream. As the change occurs almost at the end of the subwindow W ₁, it is most likely that the change remains at first undetected. Of course, since the window will be moved forward with new data points arriving, at some point the change will be detected, but it may be from essential interest, to detect the change as early as possible. To solve this problem, we modify the algorithm in Fig. 2.6 in the following way: instead of splitting window W only once, the splitting is carried out several times. Figure 2.8 shows the modified part of the algorithm in Fig. 2.6 starting at step 9. How many times the window should be split, should be decided based on the required performance and precision of the algorithm. We can run the test for each sufficiently large subwindow of W, although the performance of the algorithm will decrease, or we can carry out fixed number of splits. Note that also for the windows technique-based approach, attention should be paid to the problem of multiple testing (see Sect. 2.4.1.3). Furthermore, we do not specify here the effect of the detected change. The question whether the window should be re-initialized depends on the application. A change in the variance of the data stream might have a strong effect on the task to be fulfilled with the online analysis of the data stream or it might have no effect as long as the mean value remains more or less stable.

Fig. 2.7

Subwindows problem

Fig. 2.8

Modification of the algorithm for change detection to avoid the sub-windows problem

For the hypothesis test in step 10, of the algorithm, any appropriate test for the distribution change can be chosen. Since we do not necessarily have to apply an incremental scheme for the hypothesis test, the Kolmogorov–Smirnov test can also be considered for change detection. The Kolmogorov–Smirnov test is designed to compare two distribution, whether they are equal or not. Therefore, two kinds of questions could be answered with the help of the Kolmogorov–Smirnov test:

• Does the sample arise from a particular known distribution?

• Do two samples coming from different time windows have the same distribution?

We are particularly interested in the second question. For this purpose, the two sample Kolmogorov–Smirnov goodness-of-fit test should be used.

Let X ₁, …, X _n and Y ₁, …, Y _m be two independent random samples from distributions with cumulative distribution functions F _X and F _Y , respectively. We want to test the hypothesis H ₀ :  F _X  = F _Y against the hypothesis H ₁ :  F _X ≠F _Y . The Kolmogorov–Smirnov statistic is given by

$${D}_{n,m} {=\sup }_{t}\left \vert {S}_{X,n}\left (x\right ) - {S}_{Y,m}\left (x\right )\right \vert ,$$

(2.58)

where S _X, n x and S _Y, m x are corresponding empirical cumulative distribution function⁴ of the first and second sample. H ₀ is rejected at level α if

$$\sqrt{ \frac{nm} {m + n}}{D}_{n,m} > {K}_{\alpha }$$

(2.60)

where K _α is the α-quantile of the Kolmogorov distribution.

To adapt the Kolmogorov–Smirnov test as a change detection algorithm, first the significance level α should be chosen (we can also use for instance the Bonferroni correction to avoid the multiple testing problem). The value of K _α needs either numerical computation or should be stored in a table.⁵ Furthermore, values from the subwindows W ₀ and W ₁ represent two samples x ₁, …, x _n and y ₁, …, y _m . Then the empirical cumulative distribution functions S _X, n x and S _Y, m x and the Kolmogorov–Smirnov statistic should be computed. Note that for the computation of S _X, n x and S _Y, m x in case of unique splitting the samples have to be sorted only initially, afterward the new values have to be inserted and the old values must be deleted from the sorted lists. In case of multiple splitting we have to decide either to sort each time from scratch or to save sorted lists for each kind of splitting.

An implementation of the Kolmogorov–Smirnov test is for instance available in the R statistics library (see [4] for more information).

Algorithm 2.8 based on the Kolmogorov–Smirnov test as the hypothesis test in step 10 has been implemented in Java using R-libraries and has been tested with artificial data. For the data generation process, the following model was used:

$${Y }_{t} ={ \sum \limits_{i=1}^{t}{X}_{ i}}.$$

(2.61)

We assume the random variables X _i to be normally distributed with expected value μ = 0 and variance σ², i.e. X _i  ∼ N0,  σ². Here Y _t is a one dimensional random walk [24]. To make the situation more realistic, we consider the following model:

$${Z}_{t} \sim N\left ({y}_{t},1\right ).$$

(2.62)

The process (2.62) can be understood as a constant model with drift and noise, the noise follows a normal distribution whose expected value equals the actual value of the random walk and whose variance is 1.

The data were generated with the following parameters: σ₁ = 0. 02, σ₂ = 0. 1. Therefore, the data have a slow drift and are furthermore corrupted with noise.

Algorithm 2.8 has been applied to this data set. The size of the window W was chosen to be 500. The window is always split into two subwindows of equal size, i.e., 250. The data are identified by the algorithm as nonstationary. Only very short sequences are considered to be stationary by the Kolmogorov–Smirnov test. These sequences are marked by the darker areas in Fig. 2.9. In the interval, 11, 14, 414, 445 stationary parts are mixed with occasionally occurring small nonstationary parts. For easier interpretation, we joined these parts to one larger area. Of course, since we are dealing with the window, the real stationary areas are not exactly the same as shown in the figure. The quality of change detection depends on the window. For slow gradual changes in the form of concept drift a larger window is a better choice, whereas for abrupt changes in terms of a concept shift a smaller window is of advantage.

Fig. 2.9

An example of change detection for the data generated by the process (2.62)

5 Conclusions

We have introduced incremental computation schemes for statistical measures or indices like the mean, the median, the variance, the interquartile range, or the Pearson correlation coefficient. Such indices provide information about the characteristics of the probability distribution that generates the data stream. Although incremental computations are designed to handle large amounts of data, it is not extremely useful to calculate the above mentioned statistical measures for extremely large data sets, since they quickly converge to the parameter of the probability distribution they are designed to estimate as can be seen in Figs. 2.1–2.3. Of course, convergence will only occur when the underlying data stream is stationary.

It is therefore very important to use such statistical measure or hypothesis tests for change detection. Change detection is a crucial aspect for nonstationary data streams or “evolving systems.” It has been demonstrated in [26] that naïve adaption without taking any effort to distinguish between noise and true changes of the underlying sample distribution can lead to very undesired results. Statistical measures and tests can help to discover true changes in the distribution and to distinguish them from random noise.

Applications of such change detection methods can be found in areas like quality control and manufacturing [16, 20], intrusion detection [27] or medical diagnosis [5].

The main focus of this chapter are univariate methods. There also extensions to multidimensional data [23] which are out of the scope of this contribution.